Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-20T08:29:21.662Z Has data issue: false hasContentIssue false
  • English
  • Français

FORBIDDEN INDUCED SUBGRAPHS AND THE ŁOŚ–TARSKI THEOREM

Part of: General logic Model theory

Published online by Cambridge University Press:  04 January 2024

YIJIA CHEN  and
JÖRG FLUM
YIJIA CHEN*
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE SHANGHAI JIAO TONG UNIVERSITY SHANGHAI, CHINA
JÖRG FLUM
Affiliation:
MATHEMATISCHES INSTITUT UNIVERSITÄT FREIBURG FREIBURG, GERMANY E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 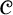$\mathscr {C}$ be a class of finite and infinite graphs that is closed under induced subgraphs. The well-known Łoś–Tarski Theorem from classical model theory implies that 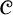$\mathscr {C}$ is definable in first-order logic by a sentence 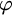$\varphi $ if and only if 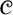$\mathscr {C}$ has a finite set of forbidden induced finite subgraphs. This result provides a powerful tool to show nontrivial characterizations of graphs of small vertex cover, of bounded tree-depth, of bounded shrub-depth, etc. in terms of forbidden induced finite subgraphs. Furthermore, by the Completeness Theorem, we can compute from 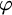$\varphi $ the corresponding forbidden induced subgraphs. This machinery fails on finite graphs as shown by our results:

  • – There is a class 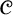$\mathscr {C}$ of finite graphs that is definable in first-order logic and closed under induced subgraphs but has no finite set of forbidden induced subgraphs.

  • – Even if we only consider classes 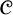$\mathscr {C}$ of finite graphs that can be characterized by a finite set of forbidden induced subgraphs, such a characterization cannot be computed from a first-order sentence 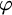$\varphi $ that defines 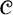$\mathscr {C}$ and the size of the characterization cannot be bounded by 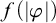$f(|\varphi |)$ for any computable function f.

Besides their importance in graph theory, the above results also significantly strengthen similar known theorems for arbitrary structures.

Keywords

preservation theorem for graphsfinite model theory

MSC classification

Primary: 03B70: Logic in computer science 03C13: Finite structures
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 2 , June 2024 , pp. 516 - 548
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alechina, N. and Gurevich, Y., Syntax vs. semantics on finite structures , Structures in Logic and Computer Science, A Selection of Essays in Honor of Andrzej Ehrenfeucht (J. Mycielski, G. Rozenberg, and A. Salomaa, editors), Lecture Notes in Computer Science, 1261, Springer, Berlin, 1997, pp. 14–33.Google Scholar
Atserias, A., Dawar, A., and Grohe, M., Preservation under extensions on well-behaved finite structures . SIAM Journal on Computing , vol. 38 (2008), pp. 1364–1381.CrossRefGoogle Scholar
Chen, Y. and Flum, J., FO-definability of shrub-depth . 28th EACSL Annual Conference on Computer Science Logic, CSL 2020 , 13–16 January 2020, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Barcelona, Spain, 2020, pp. 1–15.Google Scholar
Chen, Y. and Flum, J., Forbidden induced subgraphs and the Łoś–Tarski theorem . 36th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2021 . IEEE, 2021, pp. 1–13.Google Scholar
Dawar, A., Grohe, M., Kreutzer, S., and Schweikardt, N., Model theory makes formulas large . Automata, Languages and Programming, 34th International Colloquium, ICALP 2007 , Springer, Wroclaw, Poland, 9–13 July 2007, 2007, pp. 913–924.Google Scholar
Dawar, A. and Sankaran, A., Extension preservation in the finite and prefix classes of first order logic . 29th EACSL Annual Conference on Computer Science Logic, CSL 2021 , LIPIcs, 183, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2021, pp. 1–18.Google Scholar
Ding, G., Subgraphs and well-quasi-ordering . Journal of Graph Theory , vol. 16 (1992), no. 5, pp. 489–502.CrossRefGoogle Scholar
Downey, R. G. and Fellows, M. R., Parameterized Complexity , Springer, New York, 1999.CrossRefGoogle Scholar
Duris, D., Extension preservation theorems on classes of acyclic finite structures . SIAM Journal on Computing , vol. 39 (2010), no. 8, pp. 3670–3681.CrossRefGoogle Scholar
Dvorák, Z., Giannopoulou, A. C., and Thilikos, D. M., Forbidden graphs for tree-depth . European Journal of Combinatorics , vol. 33 (2012), no. 5, pp. 969–979.CrossRefGoogle Scholar
Ebbinghaus, H.-D. and Flum, J., Finite Model Theory , Perspectives in Mathematical Logic, Springer, Berlin, 1999.Google Scholar
Fellows, M. R., Private communication, 2019.Google Scholar
Fellows, M. R. and Langston, M. A., On search, decision, and the efficiency of polynomial-time algorithms . Journal of Computer and System Sciences , vol. 49 (1994), no. 3, pp. 769–779.CrossRefGoogle Scholar
Gajarský, J. and Kreutzer, S., Computing shrub-depth decompositions . 37th International Symposium on Theoretical Aspects of Computer Science, STACS 2020 , Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2020, pp. 1–56.Google Scholar
Ganian, R., Hlinený, P., Nesetril, J., Obdrzálek, J., and Ossona de Mendez, P., Shrub-depth: Capturing height of dense graphs . Logical Methods in Computer Science , vol. 15 (2019), no. 1, pp. 7:1–7:25.Google Scholar
Ganian, R., Hlinený, P., Nesetril, J., Obdrzálek, J., de Mendez, P. Ossona, and Ramadurai, R., When trees grow low: Shrubs and fast ${}_1$ . Mathematical Foundations of Computer Science 2012 – 37th International Symposium, MFCS 2012 , Springer, Bratislava, Slovakia, 27–31 August 2012, 2012, pp. 419–430.Google Scholar
Gurevich, Y., Toward logic tailored for computational complexity . Lecture Notes in Mathematics , vol. 1104 (1984), pp. 175–216.CrossRefGoogle Scholar
Lopez, A., When locality meets preservation . LICS’22: 37th Annual ACM/IEEE Symposium on Logic in Computer Science, 2022 , ACM, 2022, pp. 1–46.Google Scholar
Łoś, J., On the extending of models I . Fundamenta Mathematicae , vol. 42 (1955), pp. 38–54.CrossRefGoogle Scholar
McKee, T. A., Forbidden subgraphs in terms of forbidden quantifiers . Notre Dame Journal of Formal Logic , vol. 19 (1978), pp. 186–188.CrossRefGoogle Scholar
Rossman, B., Homomorphism preservation theorems . Journal of the ACM , vol. 55 (2008), no. 3, pp. 1–15.CrossRefGoogle Scholar
Rossman, B., Łoś–Tarski Theorem has non-recursive blow-up , Unpublished manuscript, 2012, pp. 1–2.Google Scholar
Sankaran, A., Revisiting the generalized Łoś–Tarski Theorem . Logic and Its Applications - 8th Indian Conference, ICLA 2019 , Delhi, 1–5 March 2019, Lecture Notes in Computer Science, 11600, Springer, 2019, pp. 76–88.Google Scholar
Sankaran, A., Adsul, B., and Chakraborty, S., A generalization of the Łoś–Tarski preservation theorem . Annals of Pure and Applied Logic , vol. 167 (2016), no. 3, pp. 189–210.CrossRefGoogle Scholar
Tait, W. W., A counterexample to a conjecture of Scott and Suppes, this Journal, vol. 24 (1959), no. 1, pp. 15–16.Google Scholar
Tarski, A., Contributions to the theory of models I–II . Indagationes Mathematicae , vol. 16 (1954), pp. 572–588.CrossRefGoogle Scholar
Vaught, R., Remarks on universal classes of relational systems . Indagationes Mathematicae , vol. 16 (1954), pp. 589–591.CrossRefGoogle Scholar
Zaslavsky, T., Forbidden induced subgraphs . Electronic Notes in Discrete Mathematics , vol. 63 (2017), pp. 3–10.CrossRefGoogle Scholar