1. INTRODUCTION
Reliable projections of ice-sheet mass loss and subsequent changes in sea level require understanding the relative contributions of the processes that couple ice sheets, oceans and climate (Favier and others, Reference Favier2014; Alley and others, Reference Alley2015; DeConto and Pollard, Reference DeConto and Pollard2016). In Antarctica, the dynamic response of glaciers to changes in ice-shelf thickness plays an important role in controlling net mass loss from the ice sheet (Pritchard and others, Reference Pritchard, Arthern, Vaughan and Edwards2009, Reference Pritchard2012; Rignot and others, Reference Rignot, Jacobs, Mouginot and Scheuchl2013; Joughin and others, Reference Joughin, Smith and Medley2014). Ice shelves, when confined along their margins or grounded at discrete points along their bases (pinning points), resist the seaward flow of ice and thereby influence the rate of ice discharge to the ocean (Thomas, Reference Thomas1979; Gudmundsson, Reference Gudmundsson2013; Kowal and others, Reference Kowal, Pegler and Worster2016). This buttressing effect is sensitive to changes in local ocean temperature because warmer seawater tends to melt, and therefore thin ice shelves, which can reduce buttressing and increase glacier velocities (Jenkins and Jacobs, Reference Jenkins and Jacobs2008; Holland and others, Reference Holland, Jenkins and Holland2010; Mouginot and others, Reference Mouginot, Rignot and Scheuchl2014; Seroussi and others, Reference Seroussi2014).
The importance of ice-shelf buttressing to glacier dynamics is well-established through models and observations (e.g., Rignot and others, Reference Rignot2004; Scambos and others, Reference Scambos, Bohlander, Shuman and Skvarca2004; Dupont and Alley, Reference Dupont and Alley2005; Rott and others, Reference Rott, Müller, Nagler and Floricioiu2011; De Rydt and others, Reference De Rydt, Gudmundsson, Rott and Bamber2015; Fürst and others, Reference Fürst2016). Here, we build upon this foundation by quantifying the response of outlet glaciers to observed ice-shelf thinning using dynamic modeling and recent observations. We focus on the Bellingshausen Sea sector (BSS), a region in West Antarctica that contains numerous outlet glaciers (Fig. 1a) that flow into buttressing ice shelves that are both confined along their margins and contain numerous pinning points (Fürst and others, Reference Fürst2016). Warm modified circumpolar deep water circulates beneath many of these ice shelves (Jenkins and Jacobs, Reference Jenkins and Jacobs2008; Zhang and others, Reference Zhang, Thompson, Flexas, Roquet and Bornemann2016), leading to variability in local ocean temperatures that likely accounts for the observed sustained thinning over portions of all BSS ice shelves (Fig. 1b) (Holland and others, Reference Holland, Jenkins and Holland2010; Paolo and others, Reference Paolo, Fricker and Padman2015). Observations of gravity anomalies, surface elevation and ice velocity indicate higher rates of mass loss over at least the past decade in BSS relative to most other regions of Antarctica (Wouters and others, Reference Wouters2015; Martín-Espanol and others, Reference Martín-Español, Zammit-Mangion, Clarke, Flament, Helm, King, Luthcke, Petrie, Rémy, Schön, Wouters and Bamber2016; Hogg and others, Reference Hogg2017). The onset of net mass loss appears to be contemporaneous across multiple glaciers (Wouters and others, Reference Wouters2015; Hogg and others, Reference Hogg2017) and exceeds the magnitude of interannual variability predicted by models of surface mass balance (van Wessem and others, Reference van Wessem2014, Reference van Wessem2016). Observed glacier-thinning rates are highest near the grounding lines (where ice goes afloat) of fast-flowing glaciers, show broad spatial correlation with observed ice-shelf thinning, and accompany grounding line retreat in some areas (Paolo and others, Reference Paolo, Fricker and Padman2015; Wouters and others, Reference Wouters2015; Christie and others, Reference Christie, Bingham, Gourmelen, Tett and Muto2016). Based on these observations, it has been hypothesized that ice-shelf thinning has driven increases in mass flux across the grounding lines (Wouters and others, Reference Wouters2015; Martín-Espanol and others, Reference Martín-Español, Zammit-Mangion, Clarke, Flament, Helm, King, Luthcke, Petrie, Rémy, Schön, Wouters and Bamber2016; Hogg and others, Reference Hogg2017). Here, we use recent observations of ice surface velocity and ice-shelf thinning rates along with an ice flow model to quantify the dynamic response of BSS outlet glaciers to ice-shelf thinning.

Fig. 1. Ice flow and thinning in BSS. (a) Modeled horizontal ice surface speed for 2014/15 (colormap). Blue labels are ice-shelf names and white labels are the major named glaciers. Red box in the inset shows the location of the model domain and sinuous red lines in the main panel outline the region of interest (drainage basins 23, which contains George VI Ice Shelf, and 24 as defined by Zwally and others (Reference Zwally, Giovinetto, Beckley and Saba2012)). (b) Instantaneous change in modeled dynamic thinning rates (red/blue colormap) in response to thinning of ice shelves (green/purple colormap; positive values indicate thinning). Glacier thinning rates are filtered over a 10 km window to match the spatial resolution of the surface elevation data in panel c. (c) Observed rate of change in surface elevation from Wouters and others (Reference Wouters2015) (red/blue colormap) and modeled sub-ice-shelf melt rates (green/purple colormap). Note that the green/purple colormaps in (b) and (c) differ. In all panels, heavy black lines indicate the modeled grounding line for 2014–2015 while gray contour lines show ice surface topography in 250-m increments. Gray-shaded areas in (b) and (c) are excluded from the analysis because they are outside the drainage basins or lack ice shelves.
2. DATA AND METHODS
2.1. Surface velocity observations
For ice surface velocity observations, we rely primarily on satellite imagery acquired by the Landsat 7 and Landsat 8 satellites in 2014 and 2015 (Fig. 2) (Gardner and others, Reference Gardner2018). These data feature fine (240-m) spatial resolution, have estimated errors <30 m a−1 (Gardner and others, Reference Gardner2018), resolve all of the main outlet glaciers within our area of interest, and are coincident with surface elevation data (collected from 2010 to 2014) previously used to show thinning of BSS glaciers (Helm and others, Reference Helm, Humbert and Miller2014; McMillan and others, Reference McMillan2014; Wouters and others, Reference Wouters2015). The Landsat-derived velocity data complement surface velocity fields derived from synthetic aperture radar data collected in 2007 and 2008 (Fig. 2) (Rignot and others, Reference Rignot, Mouginot and Scheuchl2011). These two datasets provide snapshots of ice velocities that bookend a 7-year period, during which dynamic mass losses in BSS reportedly increased (Wouters and others, Reference Wouters2015; Martín-Espanol and others, Reference Martín-Español, Zammit-Mangion, Clarke, Flament, Helm, King, Luthcke, Petrie, Rémy, Schön, Wouters and Bamber2016).

Fig. 2. Observed and modeled velocity fields, velocity changes and changes in thinning rates. (a,b) Observed surface velocity fields from (a) SAR data collected 2007/08 with the ALOS PALSAR instrument (Rignot and others, Reference Rignot, Mouginot and Scheuchl2011) and (b) Landsat 8 optical data collected 2014/15 (Gardner and others, Reference Gardner2018). (c) Changes in surface velocity (Δu = u 2014/15 − u 2007/08) and (d) changes in dynamic thinning rates calculated as the change in flux divergence (see Eqn 3) using data in (a and b). (e–h) Same as for (a–d) but for model results. Surface speeds shown in (f) are the initialized model state and speeds shown in (e) are calculated using the perturbed ice shelf thicknesses. The surface velocity field in (f) is the same as in Figure 1a, and the change in dynamic thinning rates (Δdh/dt) and observed ice-shelf thinning rates in (h) are the same as in Figure 1b. In (c) and (d), we set values with observed speed < 250 m a−1 to zero because of noise present in slower moving ice and potential differences in geolocation between the SAR and Landsat data. We applied a median filter with a 7 km square window to data in (c) before plotting. The ice shelves in (c) and (d) are masked because the SAR data, which are sensitive to both vertical and horizontal displacements, were not corrected for ocean tidal uplift and therefore contain tidal residuals over the ice shelf that corrupt the difference map. Tidal uplift is restricted to the ice shelves, so these residuals do not cause errors over grounded ice. Surface velocity data are unavailable where grounded areas are colored gray in (a–d).
2.2. Surface elevation, basal topography and ice thickness observations
We define the elevations of the ice surface, ice base and the bed by blending estimates of grounded-ice geometry from Bedmap2 (Fretwell and others, Reference Fretwell2013) with updated estimates of ice-shelf geometry based on data from CryoSat-2 (Chuter and Bamber, Reference Chuter and Bamber2015) (Fig. 3). Blending is done with a cosine taper that extends 8 km seaward from the grounding line. As a result, the surface and bed topography at (and inland of) the grounding line are given by Bedmap2; the surface and thickness data more than 8 km seaward of the grounding line are given by Chuter and Bamber (Reference Chuter and Bamber2015); and the surface and thickness data within 8 km of the grounding line are the weighted average of the two datasets with weights calculated from the cosine taper. We define the seaward extent of the ice shelves and ice sheet as the zero-ice-thickness contour.

Fig. 3. Ice geometry in the BSS: (a) surface elevation, (b) bathymetry and (c) ice thickness (Fretwell and others, Reference Fretwell2013; Chuter and Bamber, Reference Chuter and Bamber2015). Red lines in all panels outline the region of interest. Gray lines in (c) indicate flight tracks for ice penetrating radar used to define bathymetry.
2.3. Numerical model
For the modeling aspect of the study, we use the numerical ice-flow model Úa, a finite-element model that solves the continuity and momentum equations in two horizontal dimensions using the vertically integrated, shallow-shelf approximation (MacAyeal, Reference MacAyeal1989) and a non-Newtonian ice rheology (Gudmundsson and others, Reference Gudmundsson, Krug, Durand, Favier and Gagliardini2012; De Rydt and others, Reference De Rydt, Gudmundsson, Rott and Bamber2015). We define a static, anisotropic finite-element mesh containing ~250,000 elements that has a resolution of 1 km over the ice shelves and faster-flowing areas, coarsening to 10 km in grounded, slow-moving ice. To initialize the flow model, we apply adjoint, or control, methods (MacAyeal, Reference MacAyeal1992, Reference MacAyeal1993; Morlighem and others, Reference Morlighem, Seroussi, Larour and Rignot2013) to infer both the ice rheology and basal slipperiness fields (Fig. 4) that minimize the misfit between modeled and observed surface velocity fields (Fig. 5). The constitutive relation for ice is defined by the Nye-Glen flow law such that:
where n = 3 is a prescribed parameter, A is the inferred ice softness factor (Fig. 4a), ![]() $\dot {\varepsilon }_e$ is the effective strain rate, and τ e is effective stress. Both the effective stress and strain rate are calculated from the second invariant of their respective tensor such that
$\dot {\varepsilon }_e$ is the effective strain rate, and τ e is effective stress. Both the effective stress and strain rate are calculated from the second invariant of their respective tensor such that ![]() $\dot {\varepsilon }_e = \sqrt {\dot {\varepsilon }_{ij}\dot {\varepsilon }_{ij}/2}$, where
$\dot {\varepsilon }_e = \sqrt {\dot {\varepsilon }_{ij}\dot {\varepsilon }_{ij}/2}$, where ![]() $\dot {\varepsilon }_{ij}$ is the strain rate tensor, and
$\dot {\varepsilon }_{ij}$ is the strain rate tensor, and ![]() $\tau _e = \sqrt {\tau _{ij}\tau _{ij}/2}$, where τ ij is the deviatoric stress tensor. At the bed, we prescribe a Weertman-type sliding law given as:
$\tau _e = \sqrt {\tau _{ij}\tau _{ij}/2}$, where τ ij is the deviatoric stress tensor. At the bed, we prescribe a Weertman-type sliding law given as:
where τb is the basal shear traction, ub is the basal velocity vector, m = 3 is a prescribed parameter and C is the inferred basal slipperiness (Fig. 4b). The resulting modeled velocity fields are in generally good agreement within the areas of interest (Fig. 5). Given the errors in ice geometry (Fretwell and others, Reference Fretwell2013; Chuter and Bamber, Reference Chuter and Bamber2015), we were unable to achieve further reductions to the misfit between observed and modeled ice velocities. In this study, we consider only the instantaneous response of glacier flow to changes in ice-shelf thickness, and thus hold the inferred ice rheology and basal slipperiness fields constant.

Fig. 4. Inferred ice rheology and basal slipperiness fields. (a) Rate factor A from the flow law (Eqn 1). (b) Basal slipperiness defined from the basal boundary condition (Eqn 2). Values of C over the ice shelves are irrelevant, and therefore shown in gray, because we impose |τb| = 0 where ice is afloat. Gray shaded regions are the same as in Figure 1b.

Fig. 5. Comparison of observed and modeled surface velocity fields. (a) Observed surface speed (Gardner and others, Reference Gardner2018) used to initialize the model (same as Fig. 2b). (b) Modeled surface speed following model initialization (same as Fig. 2f). Black lines indicate the modeled grounding lines and magenta lines indicate the Bedmap2 grounding lines (Fretwell and others, Reference Fretwell2013). (c) Misfit of modeled surface speed; gray shaded regions are the same as in Figure 1b.
2.4. Ice-shelf thickness perturbations
We perturb ice-shelf thickness using the Gaussian-filtered mean 1994–2012 observed ice-shelf thinning rates given by Paolo and others (Reference Paolo, Fricker and Padman2015). We take these mean rates to be constant for the purposes of our study. From the mean rates, we calculate the total change in ice shelf thickness for two different time periods. In the first case, we consider the 7-year period preceding the collection of our reference (Landsat) velocity fields—which are derived from data collected in 2014 and 2015—in order to represent changes in ice-shelf thickness that occurred between those velocity fields and surface velocity fields given by Rignot and others (Reference Rignot, Mouginot and Scheuchl2011), which are derived from data collected in 2007 and 2008. Therefore, we multiply the mean ice-shelf-thinning rates (given in m a−1) by −7 years to get the total change in ice-shelf thickness. In the second case, our interest is in making plausible projections of the dynamically driven mass loss over the next decade. Thus, we calculate the total amount of ice-shelf thinning that we would expect over the next 10 years if the mean rates given by Paolo and others (Reference Paolo, Fricker and Padman2015) remain constant (i.e. we multiplied the mean rates, given in ma−1 BSS, by 10 yrs). In each case, we adjusted the values of observed ice-shelf thicknesses according to the total amount of ice-shelf thinning calculated for the given period, held all other model parameters fixed, and then reran the ice flow model to calculate the instantaneous change in flow velocities caused by the perturbations in ice-shelf thicknesses. From the instantaneous change in flow velocities, we calculated the inland dynamic thinning rates as:
where ![]() $\dot {a}$ is the surface mass balance and u is the horizontal velocity vector. Because we only consider instantaneous changes in velocity,
$\dot {a}$ is the surface mass balance and u is the horizontal velocity vector. Because we only consider instantaneous changes in velocity, ![]() $\dot {a}$ is unchanged. As a result, the change in dynamic thinning rate, Δdh/dt, is equal to the change in the flux divergence. To assess model errors, we undertook a Monte-Carlo simulation of changes in flux across the grounding line within drainage basins 23 and 24 (Fig. 1a) (Zwally and others, Reference Zwally, Giovinetto, Beckley and Saba2012) using a total of 2000 model runs. In each model run, we applied a Gaussian-distributed random error whose standard deviation is defined by the formal measurement error estimates for ice-shelf thinning (Paolo and others, Reference Paolo, Fricker and Padman2015), which we take to be spatially uncorrelated.
$\dot {a}$ is unchanged. As a result, the change in dynamic thinning rate, Δdh/dt, is equal to the change in the flux divergence. To assess model errors, we undertook a Monte-Carlo simulation of changes in flux across the grounding line within drainage basins 23 and 24 (Fig. 1a) (Zwally and others, Reference Zwally, Giovinetto, Beckley and Saba2012) using a total of 2000 model runs. In each model run, we applied a Gaussian-distributed random error whose standard deviation is defined by the formal measurement error estimates for ice-shelf thinning (Paolo and others, Reference Paolo, Fricker and Padman2015), which we take to be spatially uncorrelated.
Our focus here is on the dynamic response of glaciers to ice-shelf-thinning alone. Therefore, we consider only instantaneous changes in ice flow, thereby ignoring transient processes, and we make the conservative assumption that ice-shelf thinning occurs only in fully floating areas. These practical but justifiable considerations are driven primarily by the poor resolution of bedrock topography within our study area (Fig. 3). Both transient ice-flow models and the characteristics of grounding-line retreat are sensitive to bedrock topography, thus we would add complexity but not improve our model results by including finite timescales (transients) and grounding-line retreat. For the purposes of our study, ignoring transient changes in ice dynamics are justifiable given that increases in BSS mass loss occurred over decadal timescales (Wouters and others, Reference Wouters2015; Martín-Espanol and others, Reference Martín-Español, Zammit-Mangion, Clarke, Flament, Helm, King, Luthcke, Petrie, Rémy, Schön, Wouters and Bamber2016), which means that instantaneous stress transmission should be the dominant factor in variations in ice dynamics (Gudmundsson, Reference Gudmundsson2003; Williams and others, Reference Williams, Hindmarsh and Arthern2012). Our fixed-grounding-line assumption is reasonable because significant, observed grounding line retreat in BSS occurs either where there is no ice shelf to thin (note Fox Ice Stream in Fig. 1, which is excluded from our study) or in areas that show relatively small changes in surface elevation (Holt and others, Reference Holt, Glasser, Quincey and Siegfried2013; Christie and others, Reference Christie, Bingham, Gourmelen, Tett and Muto2016). The key advantage of the fixed-grounding-line assumption and our overall process-based approach is that they allow us to isolate and study the dynamic response of glaciers to ice-shelf thinning (De Rydt and others, Reference De Rydt, Gudmundsson, Rott and Bamber2015).
To isolate the impact of only ice-shelf thinning on glacier motion and to avoid nonphysical steep surface slopes at the grounding line, we tapered the prescribed ice-shelf thinning rates to zero at the grounding line. The profile used to taper the thinning rates varies from zero at the grounding line to unity over the freely floating ice shelf along a profile defined as a hyperbolic tangent whose argument scales with ice thickness above floatation. In BSS, this typically produces an increase in thinning rates from zero at the grounding line to the full thinning value over ~1 km, though in areas with numerous pinning points, this distance can be of order a few km. Because shear stress at the bed is relatively high (Fig. 6), small changes in grounding line position, which cannot be constrained by existing observations nor modeled because of the poorly constrained basal topography in many parts of BSS (Fretwell and others, Reference Fretwell2013) (Fig. 3), have a marked impact on ice flow. Therefore, we consider the assumption of thinning only over freely floating ice to be necessary to avoid skewing the model results with unrealistic grounding line migration driven by incorrect thinning rates, erroneous basal topography and nonphysically steep ice surface slopes (and therefore nonphysically high gravitational driving stresses) at the grounding line. While our tapering method could produce unrealistic ice surface slopes over freely floating ice, these slopes do not impact our results because longitudinal stresses (and therefore spreading rates) in fully floating ice are insensitive to surface slopes (e.g., Schoof, Reference Schoof2007).

Fig. 6. Basal shear stress and gravitational driving stress. (a) Inferred basal shear stress τ b corresponding to inferred values shown in Fig. 4 (b) Gravitational driving stress τ d = ρghα, where ρ is the density of ice, g is gravitational acceleration, h is ice thickness and α is the ice surface slope. τ d is averaged over 15 km, which is ~5 ice thicknesses in each direction. (c) Ratio of basal shear and gravitational driving stresses. Ice shelves are shown in gray because we impose |τb| = 0 where ice is afloat, rendering the ratio uninformative. In all panels, the black contour lines show ice surface topography in 250 m increments.
By integrating the ice-shelf thinning rates backward in time, we generally thicken the ice shelves (Fig. 1). In some areas, the applied thickening either exceeds the null-value prescribed where the sub-ice-shelf bathymetry is poorly constrained or is less than the errors in bathymetry (Fretwell and others, Reference Fretwell2013). Thus, to avoid erroneous grounding, we lowered the sub-ice-shelf bathymetry in all areas where the thickened ice shelves come into contact with the seafloor (Fretwell and others, Reference Fretwell2013). As a result, the total grounded area (i.e. the position of the grounding lines) remains constant across all model runs, a reasonable condition given our poor knowledge of sub-ice-shelf bathymetry in BSS (Fretwell and others, Reference Fretwell2013). Note that we do not attempt to account for potential regrounding on previously active pinning points due to uncertainties in ice-shelf thickness and the geometry of previously active pinning points.
3. RESULTS AND DISCUSSION
3.1. Glacier acceleration and mass loss
In this section, we describe the results for the first case of ice-shelf thickness perturbations, in which we calculated the total change in ice-shelf thickness over a 7-year period, adjusted the values of ice-shelf thickness used to initialize the flow model, and reran the ice flow model, holding all other model parameters constant. Our results show that perturbations in ice-shelf thickness induce instantaneous increases in ice velocities and dynamic thinning rates, both of which broadly agree with observed magnitudes and spatial patterns near (<10 km upstream of) the grounding line (Figs. 1, 2, and 7), the area most relevant for understanding dynamic mass loss over annual-to-decadal timescales. Modeled speedups are systematically lower than observed speedups, which we attribute to errors in bedrock topography, the instantaneous nature of the model, and the fact that we taper ice-shelf thinning rates to zero at the grounding line. However, the overall trends are consistent between the modeled and observed speedups (Fig. 7), suggesting that our model captures the salient dynamics and the impact of ice-shelf thinning on glacier flow. We do not expect agreement between our model and observations further upstream because these observed changes are either unrelated to recent ice-shelf thinning or are due to time-dependent processes intentionally excluded from our model (Williams and others, Reference Williams, Hindmarsh and Arthern2012). Since we only perturb ice-shelf thickness, we naturally expect poor agreement between modeled and observed speedups in glaciers and ice streams that lack ice shelves (e.g. Fox Ice Stream; Fig. 1a) or flow into ice shelves that are too small to be accurately represented using our approach, most notably Ferrigno Ice Stream (Fig. 1a). Ferrigno Ice Stream contains the majority of points in the bin centered on 700 m a−1 in Fig. 7, which explains the large disparity between modeled and observed speedup, Δu, in that bin.
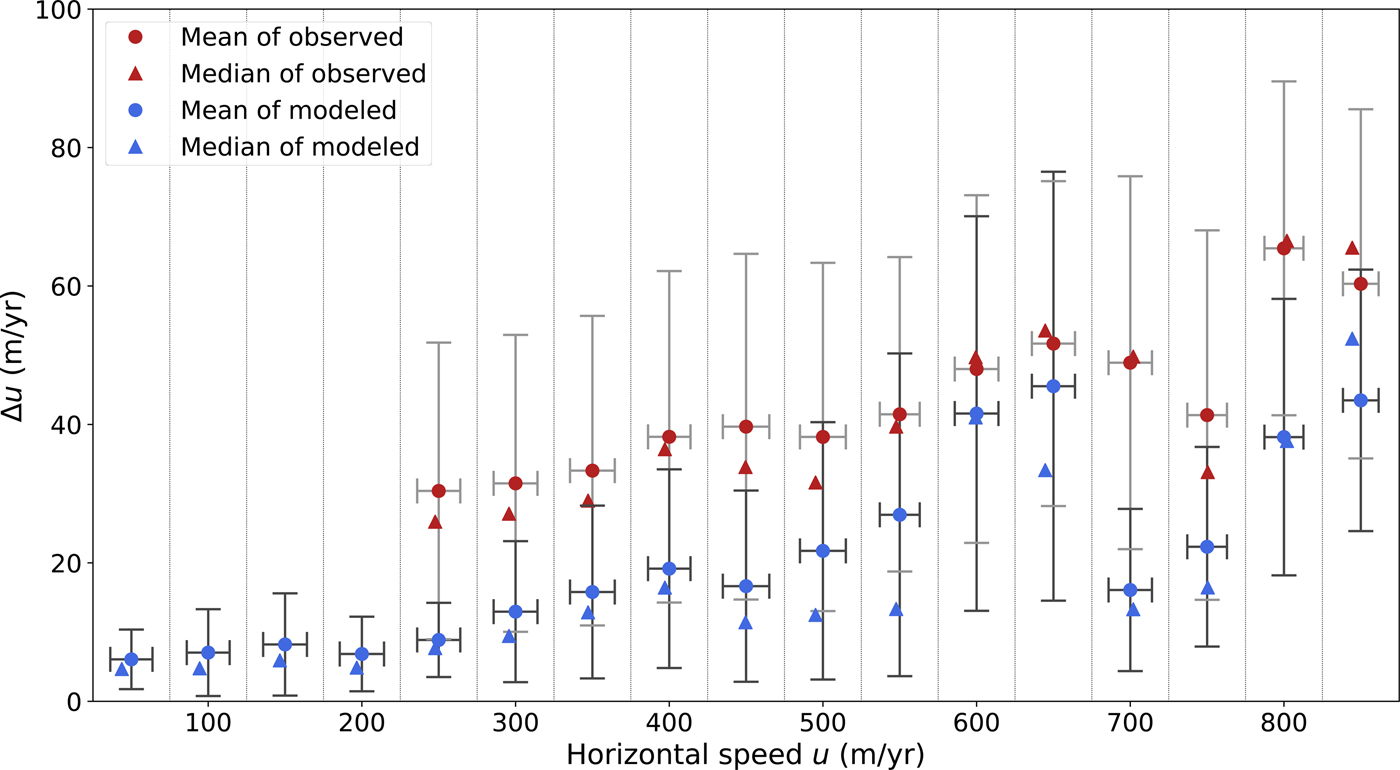
Fig. 7. Observed and modeled changes in horizontal flow speed in response to changes in ice-shelf thickness versus modeled horizontal flow speed u. Observed values with u < 250 m a−1 have been masked out because of high noise levels. Values are taken at the nodes of the finite element mesh and are binned by horizontal speed every 50 m a−1. Bin boundaries are shown by vertical dotted lines. Circles represent mean values, triangles show median values and error bars indicate one standard deviation about the mean.
The modeled instantaneous increase in flux across the grounding line (Fig. 1) in response to perturbations in ice shelf thickness is 3 ± 1 Gt a−1, which is ~2% of the total discharge (≈ 180 Gta−1). This change is consistent with changes in grounding line flux of 2 ± 3 Gt a−1 as calculated from observed surface velocities (Gardner and others, Reference Gardner2018). This agreement between modeled and observed changes in grounding line flux supports the hypothesis that ice-shelf thinning is a primary driver of increased grounding line discharge from BSS (Wouters and others, Reference Wouters2015; Hogg and others, Reference Hogg2017; Gardner and others, Reference Gardner2018). However, both modeled and observed changes in grounding line flux account for only ~5% of the previously published values of increases in mass loss over the same area and approximately the same time period (Wouters and others, Reference Wouters2015). Direct comparison of our values and previous results from Wouters and others (Reference Wouters2015) comes with two caveats: increases in ice discharge may have occurred prior to 2007/08 (Hogg and others, Reference Hogg2017; Gardner and others, Reference Gardner2018) (the years when previous velocity data were collected (Rignot and others, Reference Rignot, Mouginot and Scheuchl2011)) and our model may not reliably capture speedups in some of the ice streams that might be prominent contributors to BSS mass loss. These ice streams are Ferrigno Ice Stream, whose ice shelf is too small to be accurately represented using our modeling approach; Fox Ice Stream, which does not have an ice shelf (Fig. 1a); and Wiesnet and Williams Ice Streams, whose bathymetry is poorly constrained (Fig. 3) (Christie and others, Reference Christie, Bingham, Gourmelen, Tett and Muto2016). Nevertheless, observed and modeled changes in ice dynamics suggest that some portion of mass losses previously attributed to ice dynamics (Wouters and others, Reference Wouters2015) may be due to variations in snow accumulation that are not captured by the regional climate models used to make the previous estimates (van Wessem and others, Reference van Wessem2014, Reference van Wessem2016).
Modeled and observed glacier speedup and thinning rates are most pronounced in the southern extent of the English Coast (Fig. 1). Here, high ice-shelf thinning rates occur in areas with a high density of pinning points, which exert drag on the ice-shelf base and increase buttressing (Holt and others, Reference Holt, Glasser, Quincey and Siegfried2013; Joughin and others, Reference Joughin, Alley and Holland2012). Thinning the ice shelf in these regions leads to a considerable reduction in buttressing as the area of contact with the pinning points is diminished. Reduced buttressing is likely the primary driver of pronounced glacier speedups along the English Coast and helps explain why this area experiences higher inland dynamic thinning rates than other parts of George VI that have comparable ice-shelf thinning rates. Notably, the fast-flowing outlet glacier in the northern extent of the English Coast shows little speedup, despite similar observed ice-shelf thinning rates, relative to the comparably fast-flowing glaciers in the southern English Coast that are proximal to numerous pinning points. While localized grounding line retreat in the southern extent of the English Coast, which occurred between 1973 and 2010 (Holt and others, Reference Holt, Glasser, Quincey and Siegfried2013), potentially contributed to the observed changes in glacier velocity, the reported retreat is too localized to fully explain the observed or modeled pattern of glacier speedup (see Holt and others, Reference Holt, Glasser, Quincey and Siegfried2013, Fig. 8).
Dynamic changes in the rest of BSS are less pronounced than in the English Coast. Abbot Ice Shelf thinned little over the observation period. As a result, little dynamic thinning is modeled or observed in the outlet glaciers that feed the ice shelf. Venable Ice Shelf experienced the greatest thinning of any BSS ice shelf over the observational period. These high rates of ice-shelf thinning caused the model to predict the significant dynamic response of the two ice streams that flow into Venable Ice Shelf—Wiesnet and Williams Ice Streams—in contrast with observations; this disparity between our model and observations is likely due to poor constraints on subglacial topography and sub-ice-shelf bathymetry (cf. Fretwell and others, Reference Fretwell2013; Christie and others, Reference Christie, Bingham, Gourmelen, Tett and Muto2016).
The overall pattern of dynamical change shows that increases in modeled dynamic thinning rates are most substantial in fast-flowing outlet glaciers (Figs. 7 and 8) where ice-shelf thinning rates near the grounding line exceed 1 m a−1 (Fig. 1b) and where the glacier beds are relatively slippery (Figs. 4b and 8b). Slippery beds result in greater sensitivity to changes in ice-shelf buttressing than less slippery beds, causing perturbations in buttressing stresses to readily propagate upstream over distances of order tens of kilometers (Gudmundsson, Reference Gudmundsson2003; Schoof, Reference Schoof2007). Glacier width modulates the sensitivity of ice velocity to changes in ice-shelf buttressing because drag in the glacier margins provides an additional resistance to ice flow (Gudmundsson, Reference Gudmundsson2013). This dependence on width is especially important in BSS because many outlet glaciers flow through relatively narrow (usually <15 km) bedrock channels. Drag in the margins of BSS outlet glaciers and the existence of laterally confined and buttressing ice shelves may stabilize this region (i.e. suppress the marine ice sheet instability (e.g., Schoof, Reference Schoof2007)), even in areas where the bed deepens inland (Gudmundsson, Reference Gudmundsson2013; Pegler, Reference Pegler2016, Reference Peglerin press).
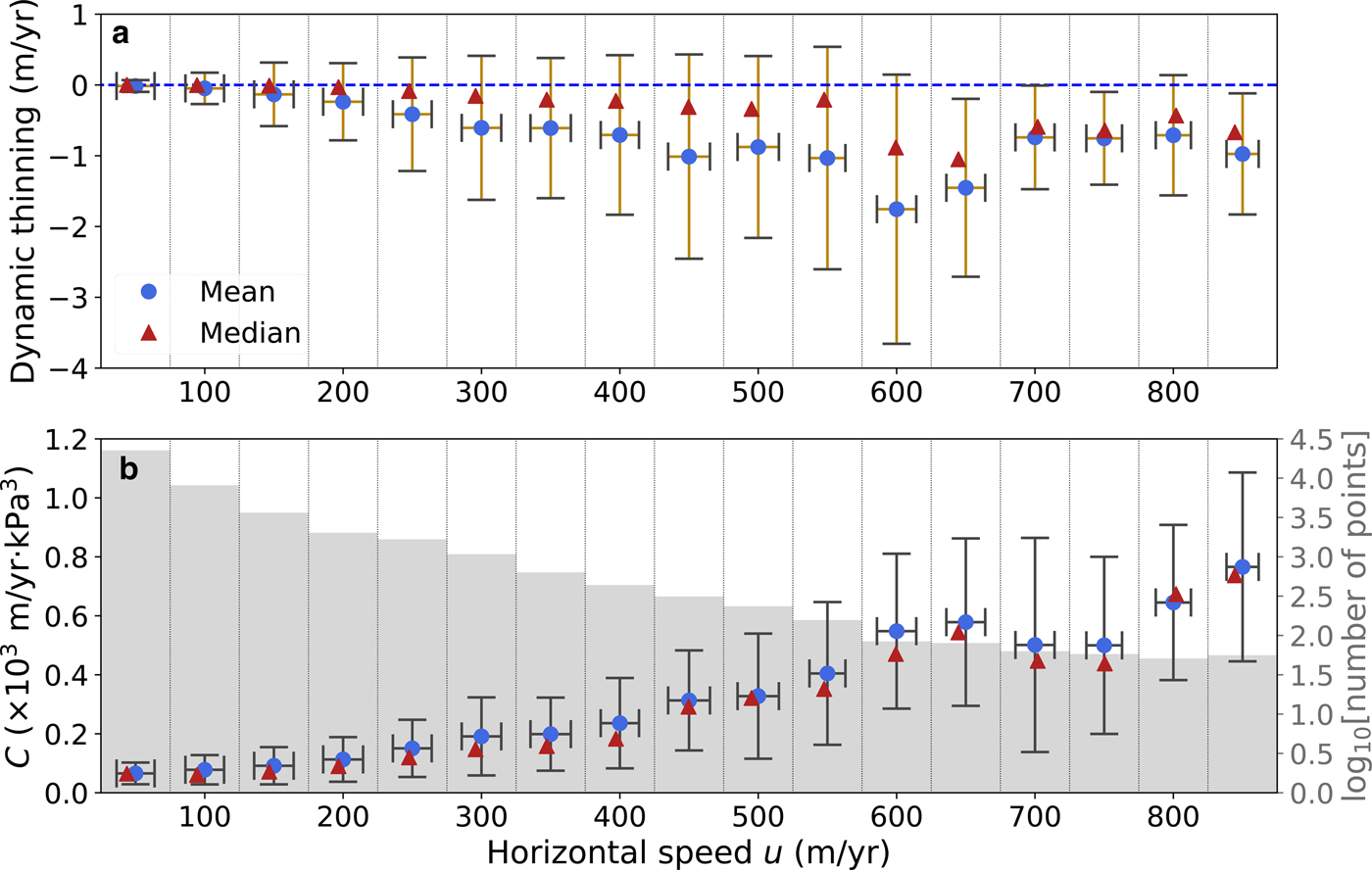
Fig. 8. Dynamic thinning rates and glacier characteristics. (a) Modeled changes in inland dynamic thinning rates (shown in map view in Fig. 1b) and (b) inferred basal slipperiness parameter C versus modeled horizontal flow speed u. In both panels, values are taken at the nodes of the finite element mesh and are binned by horizontal speed every 50 m a−1. Bin boundaries are shown by vertical dotted lines, and gray bars in (b) indicate the number of points per bin on a log scale. Blue circles represent mean values, red triangles show median values, and error bars indicate one standard deviation about the mean.
3.2. Projections of dynamically driven mass loss
To examine how dynamically driven mass loss from BSS might change over approximately the next decade, we followed the same procedure as in the previous section, but we calculated the total expected ice-shelf thinning over the next 10 years, assuming that the mean ice-shelf thinning rates remain constant. After adjusting the ice-shelf thickness from the initialized state, ice-shelf thicknesses within our model domain remain above zero everywhere. The resulting changes in flow velocity are qualitatively similar to those shown in Figures. 1b, 7, and 8; thus we do not repeat the figures. Instead, we quantify the model results by simply noting that if ice-shelf thinning rates remain unchanged and the grounding line of George VI Ice Shelf remains fixed—as it approximately did from 1973 to 2010 (Holt and others, Reference Holt, Glasser, Quincey and Siegfried2013)—grounding line flux in BSS could increase by up to 13 Gt a−1 before 2025. To estimate a plausible upper limit on mass loss, we increased ice-shelf thinning rates to three times the current values, reran the model, and found that grounding line flux could increase by as much as 30 Gt a−1. These estimates of mass losses exclude contributions of grounding line retreat because we only apply thickness perturbations to freely-floating ice. More reliable projections of dynamically driven mass loss would require better constraints on bed topography than are currently available, allowing for realistic representations of the effects of grounding line retreat on dynamically driven mass loss in BSS.
4. CONCLUSION
We used recent observations of ice surface velocity and ice-shelf thinning rates along with an ice flow model to isolate the impact of ice-shelf thinning on glacier mass loss in BSS. Our results indicate that increases in ice discharge contributed to observed changes in surface elevation and gravitational potential in BSS, in agreement with previous studies. We find instantaneous increases in glacier speeds and dynamically induced thinning rates in response to changes in ice-shelf thickness (alone) that broadly agree with observations. Glacier speedup and increases in dynamic thinning rates are most pronounced in the southern English Coast, where George VI Ice Shelf is rapidly thinning in areas with numerous pinning points. Modeled instantaneous increases in grounding line flux agree with changes in grounding line flux calculated from observed changes in surface velocity (Gardner and others, Reference Gardner2018), but are markedly lower than (~ 5% of) rates of dynamic mass loss estimated from observations of gravity anomalies and inland surface elevation along with outputs from a regional climate model (Wouters and others, Reference Wouters2015). We postulate that disparities in the estimates of grounding line flux and dynamic mass losses in BSS may be due primarily to variations in surface mass balance not accounted for in the regional climate model. Projections of dynamic mass loss over the next decade indicate that, in the absence of grounding line retreat in the English Coast, ice-shelf thinning alone could drive further BSS mass loss; these losses are unlikely to exceed 15% of the total discharge from this area. We are unable to model the dynamic response of BSS outlet glacier to local grounding line retreat, a potentially important process for understanding the future evolution of the ice sheet, because the bed in BSS is poorly resolved. Thus, our projections of BSS mass loss may be an underestimate, and it is important to continue to monitor mass changes in BSS using multiple observational platforms and to collect finer resolution, spatially comprehensive data on ice thickness and bed topography to enable more detailed model studies.
ACKNOWLEDGMENTS
We benefitted from discussions with J. Bamber and B. Wouters. Surface elevation changes were provided by B. Wouters, RACMO2.3 results were provided by J. M. Van Wessem, and ice shelf thickness measurements by S. Chuter. B.M. is funded by NSF Earth Sciences Postdoctoral Fellowship award EAR-1452587 and his work was completed while at the British Antarctic Survey.










