1. Introduction
The Global Navigation Satellite System (GNSS) community has experienced dramatic changes over the past decade after the completion of the Russian Global Navigation Satellite System (GLONASS) constellation and the advent of new global and regional navigation systems, for example the European Global Navigation Satellite System (Galileo), Chinese BeiDou Navigation Satellite System (BDS), Japanese Quasi-Zenith Satellite System (QZSS) and Indian Regional Navigation Satellite System (IRNSS). New navigation systems have also brought along considerable opportunities to enhance positioning, timing and navigation applications. In recent years, numerous studies indicated that it is possible to augment the performance of various GNSS applications with multi-GNSS integrations, for example precise point positioning (PPP) (Cai et al., Reference Cai, Gao, Pan and Zhu2015; Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015; Pan et al., Reference Pan, Chai and Kong2017a), real-time kinematic (RTK) positioning (Paziewski and Wielgosz, Reference Paziewski and Wielgosz2017; Paziewski et al., Reference Paziewski, Sieradzki and Baryla2018; Odolinski and Teunissen, Reference Odolinski and Teunissen2019), baseline positioning solutions (Paziewski and Sieradzki, Reference Paziewski and Sieradzki2017; Yalvac and Berber, Reference Yalvac and Berber2018; Li et al., Reference Li, Nie, Xu, Rovira-Garcia, Fang and Xu2020), real-time ambiguity resolved PPP–RTK (Li et al., Reference Li, Li, Yuan, Zhang, Zhang and Wickert2018; Psychas et al., Reference Psychas, Verhagen and Teunissen2020), PPP/INS (Inertial Navigation System) integration (Gao et al., Reference Gao, Zhang, Ge, Niu, Shen, Wickert and Schuh2017, Reference Gao, Li, Zhang, Ge and Schuh2018), single-frequency positioning (Pan et al., Reference Pan, Zhang, Liu, Li and Li2017b; Hong et al., Reference Hong, Tu, Zhang, Fan, Zhang and Han2020), precise time transfer (Zhang et al., Reference Zhang, Tu, Zhang, Gao and Cai2018; Ge et al., Reference Ge, Zhou, Dai, Qin, Wang and Yang2019) and GNSS reflectometry (Farzaneh et al., Reference Farzaneh, Parvazi and Shali2021; Kim and Park, Reference Kim and Park2021). On the other hand, the individual performance of new global navigation systems, such as Galileo and BDS, has recently taken more and more attention from the GNSS users, since it is projected that they reach full orbital capability in the short run. Therefore, some studies have recently been carried out to evaluate their individual performance in various GNSS applications (Hadaś et al., Reference Hadaś, Kazmierski and Sośnica2019; Bahadur and Nohutcu, Reference Bahadur and Nohutcu2020; Ge et al., Reference Ge, Ding, Qin, Zhou and Yang2020, Reference Ge, Chen, Wu, Fan, Qin, Zhou and Yang2021; Zhang et al., Reference Zhang, Li, He, Zhang and Miao2020; Su and Jin, Reference Su and Jin2021; Zhu et al., Reference Zhu, Zheng, Cui, Zhang, Jia, Zhang and Fan2021).
Being the only civilian system, Galileo is differentiated from the other navigation systems. The European Space Agency (ESA) initiated the Galileo operation in 2005 by launching the first in-orbit validation satellite. After a long while, the initial validation phase was started with the two pairs of operational Galileo satellites launched in 2011 and 2012, respectively. Nowadays, its full operational capability phase continues, and it is projected that the Galileo constellation will be completed soon with the launch of the remaining few satellites. As of May 2021, the Galileo constellation includes 22 usable satellites, which means its constellation reaches an important number of satellites that enables individual positioning and navigation operations (GSA, 2021). Hence, a considerable number of recent studies have concentrated on the performance of Galileo-only positioning solutions. For instance, Zhang et al. (Reference Zhang, Tu, Liu, Hong, Fan, Zhang and Lu2019) analysed Galileo's system performance in terms of satellite coverage and indicated that, by the end of June 2018, Galileo can provide at least four visible satellites on a global scale with a 90% probability. Also, Xia et al. (Reference Xia, Ye, Xia, Zhao, Jiang, Chen and Hu2019) evaluated Galileo-only PPP as regards positioning performance in kinematic and static modes and concluded that decimetre- and centimetre-level positioning accuracies can be acquired from post-processed Galileo-only PPP, respectively. Hadaś et al. (Reference Hadaś, Kazmierski and Sośnica2019) carried out a performance assessment for dual-frequency absolute positioning with Galileo satellites and exhibited that Galileo-only PPP solution that employs broadcast ephemeris provides higher positioning accuracy in kinematic and static modes as compared with the corresponding GPS solution. Bahadur and Nohutcu (Reference Bahadur and Nohutcu2020) concisely assessed the performance of single-frequency Galileo-based PPP with the final precise ephemeris of different International GNSS Service (IGS) Multi-GNSS Experiment (MGEX) agencies and demonstrated that the Galileo solution could provide a positioning performance comparable with a GPS solution. In addition, Su and Jin (Reference Su and Jin2021) recently developed new PPP models including five frequencies of Galileo and showed that the Galileo PPP with five-frequency improves the positioning performance in comparison with its dual- and triple-frequency PPP solutions. More recently, Yalvac (Reference Yalvac2021) investigated the historical development of Galileo-based relative positioning and concluded that nowadays the performance of Galileo relative positioning is highly comparable to the GPS solution.
On the other hand, positioning solutions with single-frequency standalone receivers have recently attracted enormous interest from the GNSS community. The growing attention can be explained by the fact that relatively low-cost receivers still dominate the GNSS market due to mobile devices and these kind of receivers are mostly compatible with single-frequency positioning solutions (GSA, 2019). Nonetheless, to achieve optimum performance with single-frequency positioning solutions, their typical problems, such as mitigation of ionospheric effect and the higher noise level of measurements, must be handled appropriately. For this reason, several attempts have been made to overcome these drawbacks and therefore acquire better positioning performance from single-frequency positioning solutions (Ning et al., Reference Ning, Han and Zhang2018; Fan et al., Reference Fan, Guan, Zhu, Peng and Xiang2019; Li et al., Reference Li, Wang, Wang, Liu, Yuan and Zhang2019; Zheng et al., Reference Zheng, Gu, Gong, Lou, Fan and Shi2020). Furthermore, the fundamental requirement of single-frequency GNSS applications is to achieve real-time positioning results. Standard point positioning (SPP), which is the essential positioning approach with broadcast ephemeris, can conventionally be employed for instantaneous positioning. Nevertheless, the orbits and clock corrections provided within broadcast ephemeris cannot provide sufficient accuracy for precise positioning. Also, the utmost 75% of total ionospheric delay can be mitigated with global ionosphere models disseminated with the broadcast ephemeris (Orus Perez, Reference Orus Perez2017), for example Klobuchar (Reference Klobuchar1987), BDGIM (Yuan et al., Reference Yuan, Wang, Li and Huo2019) and NeQuick-G (EC, 2016). Another alternative is to employ the corrections that are broadcast by IGS through its real-time service (RTS) for instantaneous positioning applications (Hadaś and Bosy, Reference Hadaś and Bosy2015). IGS–RTS products involve satellite orbits and clock corrections along with the real-time ionospheric corrections, by this means they offer better positioning performance compared with conventional SPP solution. Although IGS–RTS products include only GPS satellites at the beginning, there are currently several analysis centres generating and disseminating real-time corrections for multi-GNSS satellites, including Galileo. To employ IGS–RTS products, an external connection is required, as they are disseminated with an online stream using the NTRIP protocol. Over the past few years, numerous studies have indicated that IGS–RTS products can be utilised effectively for many GNSS applications with both dual- and single-frequency receivers (De Bakker and Tiberius, Reference de Bakker and Tiberius2017; Shi et al., Reference Shi, Yuan, Cai and Wang2017; Zhao et al., Reference Zhao, Yao and Yao2018; Jin and Su, Reference Jin and Su2019; Nie et al., Reference Nie, Liu and Gao2020). Still, the real-time positioning performance of newly emerged navigation systems is an interesting topic for GNSS users.
Until now, existing studies have mostly been limited to the evaluation of Galileo dual-frequency positioning performance or the performance assessment of Galileo single-frequency positioning employing the final precise products. In the literature, there has been no considerable study that specifically concentrates on the real-time Galileo single-frequency precise positioning. Considering also that the Galileo constellation is progressed, and the precision of its orbits and clock corrections are improving each day, this study aims to evaluate the most recent performance of the Galileo constellation in real-time single-frequency precise positioning applications. In this study, two positioning models, single-frequency code-based positioning and code-phase combination, are adopted for real-time Galileo-based positioning. Section 2 explains the single-frequency positioning models comprehensively. Then, Section 3 presents experimental tests performed for the performance evaluation of real-time single-frequency precise positioning with Galileo satellites, including data description, satellite visibility analysis, detailed processing strategies, comprehensive results, and performance analyses. Finally, Section 4 provides the conclusions drawn from this study.
2. Single-frequency positioning models
Single-frequency receivers are mostly able to record code pseudo-range measurements only. However, some types of receivers can provide carrier phase measurements in addition to code measurements, and their presence in the market are increasing daily (GSA, 2019). Therefore, in this study, two positioning models, namely single-frequency code-based positioning and code-phase combination, are utilised for the performance assessment of real-time Galileo precise positioning. This section introduces two single-frequency positioning models in detail after describing the fundamental observation equations of code and phase measurements.
Fundamentally, code ($P$![]() ) and phase observations ($L$
) and phase observations ($L$![]() ) on the $i$
) on the $i$![]() th frequency can be expressed in meters by the following equations (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2021a):
th frequency can be expressed in meters by the following equations (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2021a):
where superscripts s and k denote the GNSS index (E: Galileo, G: GPS), and satellite number, while subscript r indicates the receiver. $\rho _r^{s,k}$![]() demonstrates the geometric distance from the satellite to the receiver in meters, c denotes the speed of light in vacuum ($m/s$
demonstrates the geometric distance from the satellite to the receiver in meters, c denotes the speed of light in vacuum ($m/s$![]() ), $dt_r^s$
), $dt_r^s$![]() and $d{T^{s,k}}$
and $d{T^{s,k}}$![]() denote the receiver and satellite clock offsets in seconds, $T_r^{s,k}$
denote the receiver and satellite clock offsets in seconds, $T_r^{s,k}$![]() is the tropospheric delay in meters, $I_i^{s,k}$
is the tropospheric delay in meters, $I_i^{s,k}$![]() indicates the first-order ionospheric delay on the $i$
indicates the first-order ionospheric delay on the $i$![]() th frequency in meters, $b_{i,r}^s$
th frequency in meters, $b_{i,r}^s$![]() and $b_i^{s,k}$
and $b_i^{s,k}$![]() denote the receiver and satellite code hardware biases on the $i$
denote the receiver and satellite code hardware biases on the $i$![]() th frequency in seconds, $B_{i,r}^s$
th frequency in seconds, $B_{i,r}^s$![]() and $B_i^{s,k}$
and $B_i^{s,k}$![]() are the receiver and satellite phase hardware biases on the $i$
are the receiver and satellite phase hardware biases on the $i$![]() th frequency in seconds, $\lambda _i^s$
th frequency in seconds, $\lambda _i^s$![]() demonstrates the wavelength of the corresponding GNSS signal in meters, $N_i^{s,k}$
demonstrates the wavelength of the corresponding GNSS signal in meters, $N_i^{s,k}$![]() denotes the integer ambiguity parameter in cycles and $\varepsilon$
denotes the integer ambiguity parameter in cycles and $\varepsilon$![]() indicates the observation noise and multipath.
indicates the observation noise and multipath.
2.1 Single-frequency code-based positioning
For a Galileo satellite ($k$![]() ), the equation of code pseudo-range observation on the first frequency (E1) can be rewritten using Equation (2.1) as
), the equation of code pseudo-range observation on the first frequency (E1) can be rewritten using Equation (2.1) as
where $\widetilde {dt}_r^E$![]() and ${\widetilde {dT}^{E,k}}$
and ${\widetilde {dT}^{E,k}}$![]() demonstrate the reformed receiver and satellite clock offsets which are
demonstrate the reformed receiver and satellite clock offsets which are
Equation (2.4) reveals that the reformed receiver clock offset contains both the actual receiver clock offset and receiver code hardware bias. Typically, they are estimated together as the reformed receiver clock offset in the estimation process due to their high correlation. In addition, an external clock source, such as precise ephemeris or broadcast ephemeris, is employed to correct the reformed satellite clock offset that contains satellite code hardware bias as well as the actual satellite clock offset. However, a particular signal or signal combination is utilised in the generation of satellite clock corrections provided in broadcast ephemeris and IGS precise ephemeris. For Galileo satellites, the reference signal combination is the dual-frequency ionosphere-free (IF) combination of code observations on E1 and E5a frequencies, while the similar IF combination on L1 and L2 frequencies is utilised to generate the satellite corrections for GPS satellites (Steigenberger et al., Reference Steigenberger, Hugentobler, Loyer, Perosanz, Prange, Dach, Uhlemann, Gendt and Montenbruck2015). Therefore, it is not possible to employ satellite clock corrections that embrace additional code hardware biases directly for single-frequency positioning. Accordingly, the satellite clock correction that is produced based on the dual-frequency IF combination on two distinct frequencies ($i = 1,\; 2$![]() ) is given as
) is given as
Using Equation (2.4) and Equation (2.5), satellite clock correction can be rearranged for single-frequency positioning as
where ${T_{GD}}$![]() indicates the timing (or total) group delay and it is also represented as proportional to $({b_1^{E,j} - b_2^{E,j}} )$
indicates the timing (or total) group delay and it is also represented as proportional to $({b_1^{E,j} - b_2^{E,j}} )$![]() , which indicates the differential code biases (DCBs) between the related frequencies (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2021b). In the single-frequency positioning, the timing group delay is must be corrected for aligning the satellite clock correction. For this purpose, the broadcast ephemeris includes the timing-group delay corrections for single-frequency users. Furthermore, some IGS analysis centres generate and disseminate the DCB parameters routinely and they can be employed to align the satellite clock corrections with corresponding clock reference. After correcting the reformed satellite clock offset considering the timing-group delay, for single-frequency code-based positioning, Equation (2.3) can be rewritten as
, which indicates the differential code biases (DCBs) between the related frequencies (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2021b). In the single-frequency positioning, the timing group delay is must be corrected for aligning the satellite clock correction. For this purpose, the broadcast ephemeris includes the timing-group delay corrections for single-frequency users. Furthermore, some IGS analysis centres generate and disseminate the DCB parameters routinely and they can be employed to align the satellite clock corrections with corresponding clock reference. After correcting the reformed satellite clock offset considering the timing-group delay, for single-frequency code-based positioning, Equation (2.3) can be rewritten as
For the single-frequency code-based positioning, Equation (2.7) represents the functional model containing four parameters to be estimated, for example three position components and one receiver clock offset. On the other hand, the tropospheric delay is generally split into two parts, namely the hydrostatic (dry) and nonhydrostatic (wet) components. While the dry component can be corrected using the empirical models depending on the station position and atmospheric parameters, modelling the wet component is quite troublesome because of the rapid variations in water vapor content (Davis et al., Reference Davis, Herring, Shapiro, Rogers and Elgered1985). Therefore, the typical procedure is to estimate the wet tropospheric component as an additional unknown parameter. Also, it is necessary to correct the ionospheric delay in the single-frequency code-based positioning model since the IF combinations are not applicable. Finally, Equation (2.7) is given for the single-system single-frequency positioning. If the multiple constellations are integrated, it is required to introduce the inter-system bias (ISB) parameters for each additional system with respect to a selected reference constellation (Cai and Gao, Reference Cai and Gao2013; Li et al., Reference Li, Ge, Dai, Ren, Fritsche, Wickert and Schuh2015).
2.2 Single-frequency code-phase combination
Once phase observations are available together with code pseudo-ranges, a single-frequency code-phase combination, namely the single-frequency IF combination ($\mathrm{\Phi }$![]() ), can be constructed for the first frequency of Galileo as (Yunck, Reference Yunck1993)
), can be constructed for the first frequency of Galileo as (Yunck, Reference Yunck1993)
From Equation (2.1) and Equation (2.2), the observation equation of single-frequency code-phase combination is written using the reformed receiver and satellite clock offset as
where $\tilde{N}_1^{E,j}$![]() denotes the reformed ambiguity parameter which contains the integer ambiguity parameter together with code and phase hardware biases, and it is expressed by
denotes the reformed ambiguity parameter which contains the integer ambiguity parameter together with code and phase hardware biases, and it is expressed by
Here, it should be mentioned that the satellite-dependent part of code and phase hardware biases, such as temporally stable part, is absorbed by the reformed ambiguity parameter, while the satellite-independent part, which is temporally variable, is absorbed by the receiver clock offset in this combination (Sterle et al., Reference Sterle, Stopar and Pavlovčič Prešeren2015; Pan et al., Reference Pan, Zhang, Liu, Li and Li2017b; Ge et al., Reference Ge, Zhou, Dai, Qin, Wang and Yang2019). After the correction of the reformed satellite clock offset with the timing group delay, the single-frequency code-phase combination is given by
For the single-frequency code-phase combination, Equation (2.11) constitutes the functional model, which includes a float ambiguity parameter for each observed satellite as the additional estimated parameter to the single-frequency code-based positioning model. The single-frequency code-phase combination is presumed to be ionosphere-free because the ionosphere delays in phase and code observations have equal magnitudes in reverse directions. Furthermore, the noise level of code pseudo-range observations is considerably reduced with the single-frequency code-phase combination thanks to phase observations which have a lower noise level. Still, in the combination, phase ambiguities are no longer integer numbers because of the accumulation of hardware biases in the phase ambiguity parameters. Hence, the combination requires a relatively long initial period for converging the float phase ambiguity parameters, and therefore achieving the desired positioning accuracy.
3. Experimental test and results
This study includes two fundamental experiments that have been performed for assessing the latest performance of Galileo satellites in real-time single-frequency precise positioning. Firstly, the detailed description of navigation data utilised in the experimental tests and the satellite visibility analysis are presented in this section. Afterwards, the experimental tests with their results and performance assessments are presented in this section comprehensively.
3.1 Data description and satellite visibility
The daily observation dataset of 15 IGS stations over the two-week period of 3–16 January 2021 were employed in the experimental tests. The stations were randomly selected to represent the globe evenly, as much as possible. Figure 1 illustrates the geographical locations of the selected stations. All the stations are among the IGS MGEX network and are equipped with GNSS receivers that can record multi-GNSS observations, including Galileo and GPS satellites. In addition, the observation sampling interval of the observation dataset is 30 s. On the other hand, the real-time corrections disseminated by the Centre National d'Etudes Spatiales (CNES) through the IGS–RTS stream, namely the ‘SSRA00CNE0’ message, was used for the single-frequency positioning. CNES product contains real-time corrections for GPS and Galileo satellites as well as GLONASS and BDS.

Figure 1. Geographical locations of the selected IGS stations
Satellite visibility is one of the critical factors influencing the real-time single-frequency positioning performance. The visibility of Galileo satellites at the selected stations is investigated in comparison with the GPS constellation. Figure 2 depicts the station-based maximum, average and minimum visible satellite numbers per epoch for the GPS and Galileo constellation over the observation period. Considering each epoch over the two-week observation period, that is 40,320 individual epochs; minimum and maximum numbers indicate the fewest and greatest satellite numbers that appear per epoch during this period, while the average number is calculated as the mean of satellite numbers in all epochs. As can be observed from the figure, the station-based minimum satellite numbers range from 3 to 7 for the GPS constellation, whereas the minimum numbers of Galileo satellites are between 2 and 6. The maximum satellite numbers at the selected stations range from 11 to 14 for the GPS constellation, while the corresponding numbers alter between 8 and 11 for Galileo satellites. Also, the average numbers of visible GPS satellites are computed between 7⋅60 and 9⋅87. The station-based average numbers change between 4⋅47 and 7⋅47 for the Galileo constellation. Considering all stations, the average numbers of visible GPS and Galileo satellites are calculated as 8⋅93 and 6⋅61. Additionally, when the results of all stations are analysed, it can be said that the GPS constellation provides at least four visible satellites at nearly all epochs, excluding a few specific epochs. As regards Galileo, there similarly exist at least four visible satellites at almost all epochs for the selected stations, except for the ISTA and LHAZ stations. In these two stations, the percentages of epochs having at least four visible satellites within the whole epochs are considerably lower than those of the other stations. Especially, at the LHAZ station, the 16% of total epochs over the two-week observation period have three or fewer visible Galileo satellites. In addition, for the Galileo constellation, the average satellite numbers are calculated as 5⋅36 and 4⋅47 at the ISTA and LHAZ stations, which are the lowest averages. The result is not surprising because these two stations are located between the northern latitudes of 25 and 45 degrees, which is one of the weakest regions in terms of Galileo satellite visibility, depending on the longitude (Zhang et al., Reference Zhang, Tu, Liu, Hong, Fan, Zhang and Lu2019). In addition, the stations near the equatorial and polar regions, the NKLG, OHI3 and REYK stations, have average satellite numbers higher than 7 for the Galileo constellation. Consequently, although its satellite visibility changes depending on the station's location, the Galileo constellation has a considerable number of usable satellites at most stations utilised in the experiment.
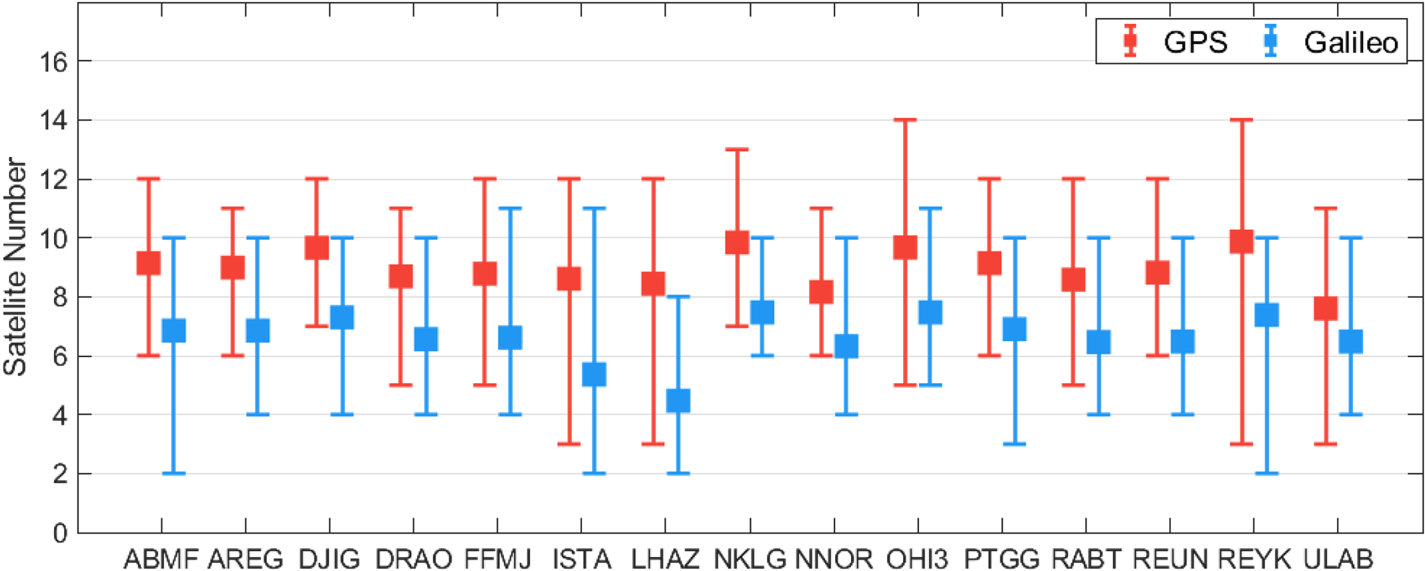
Figure 2. Station-based maximum, average and minimum visible satellite numbers for the GPS and Galileo constellation during the observation period
3.2 Processing method
As a part of this study, an enhanced version of PPPH (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2018), which enables real-time positioning processes, was employed to perform the Galileo real-time single-frequency positioning solutions. To compare the Galileo positioning results and to understand the contribution of the Galileo constellation, the observation dataset was also processed under two additional processing scenarios, which are GPS-only and GPS/Galileo combination. Since single-frequency receivers mostly require kinematic or dynamic positioning conditions, the kinematic mode, with a spectral density of ${10^2}\; {m^2}{s^{ - 1}},\;$![]() was adopted in the processing of all positioning solutions. To access the real-time satellite products and observations, a Bundesamt für Kartographie und Geodasie (BKG) NTRIP client program (BNC) was utilised in this study (BKG, 2021). Table 1 presents the detailed processing strategies applied for the real-time single-frequency positioning processes.
was adopted in the processing of all positioning solutions. To access the real-time satellite products and observations, a Bundesamt für Kartographie und Geodasie (BKG) NTRIP client program (BNC) was utilised in this study (BKG, 2021). Table 1 presents the detailed processing strategies applied for the real-time single-frequency positioning processes.
Table 1. Processing details adopted in PPPH for real-time single-frequency positioning

3.3 Performance analysis of single-frequency code-based positioning
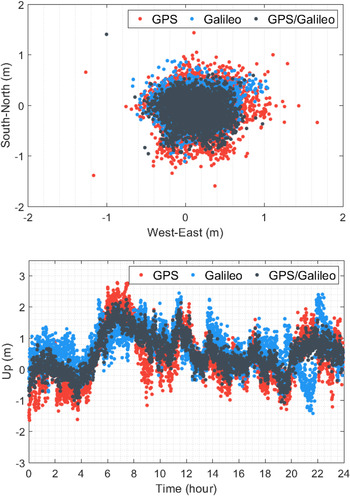
The results were analysed as regards positioning accuracy for the real-time single-frequency code-based positioning with Galileo satellites. For this purpose, the positioning error specified as the coordinate difference between the related positioning solution and ground truth was utilised to evaluate the positioning performance. Typically, IGS provides precise coordinates of its stations routinely and IGS weekly solutions were employed as the reference source for the precise station coordinates in this study. Accordingly, the positioning errors were computed in the local coordinate system for each separate epoch in which the positioning process was performed. As previously mentioned, to compare the Galileo positioning results, a similar procedure was employed for the GPS and GPS/Galileo positioning solutions. Figure 3 presents the horizontal (north and east directions) and vertical (up direction) positioning errors at the FFMJ station on 3 January 2021 for the GPS, Galileo, and GPS/Galileo single-frequency code-based positioning solutions. As shown in the figure, the GPS solution mostly has higher horizontal and vertical positioning errors in comparison with the Galileo solution. The positioning performance of single-system solutions is augmented with the GPS/Galileo integration, as expected. For the daily GPS, Galileo and GPS/Galileo solutions, root mean square (RMS) errors are calculated as 0⋅548, 0⋅399 and 0⋅375 m for the horizontal component. Similarly, for the vertical component, the RMS errors computed for the GPS, Galileo and GPS/Galileo solutions are 0⋅914, 0⋅881 and 0⋅783 m, respectively. The results denote that, compared with the GPS solution, the Galileo solution acquires better positioning accuracy.
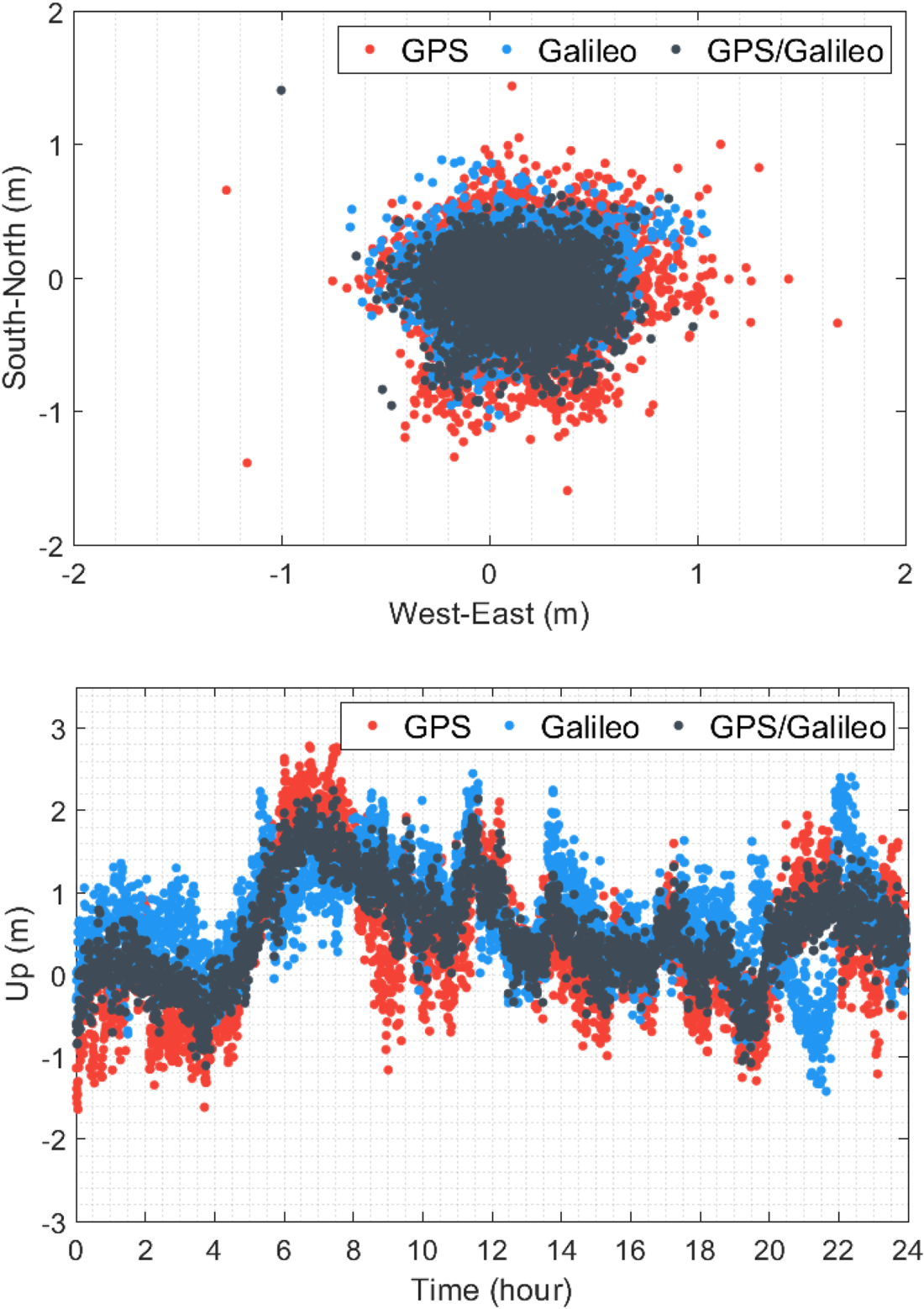
Figure 3. Horizontal and vertical positioning errors for the GPS, Galileo and GPS/Galileo single-frequency code-based solutions at FFMJ station on 3 January 2021
The observation residuals computed after the estimation processes can also be used for the evaluation of positioning performance as they represent the harmony between the defined system model and measurements. Moreover, the observation residuals reveal the noise characteristics of observations, including orbit errors, multipath effect and unmodelled errors. Figure 4 illustrates the observation residuals computed for the GPS and Galileo single-frequency code-based positioning solutions at the FFMJ station on 3 January 2021. The figure also provides the RMS values calculated when taking all daily observation residuals into consideration. The RMS values of residuals are computed as 0⋅319 and 0⋅198 m for the GPS and Galileo observations. The observation residuals of Galileo are approximately 38% fewer than those of GPS, on average, which indicates that Galileo code observations have a considerably lower noise level in comparison to GPS observations.
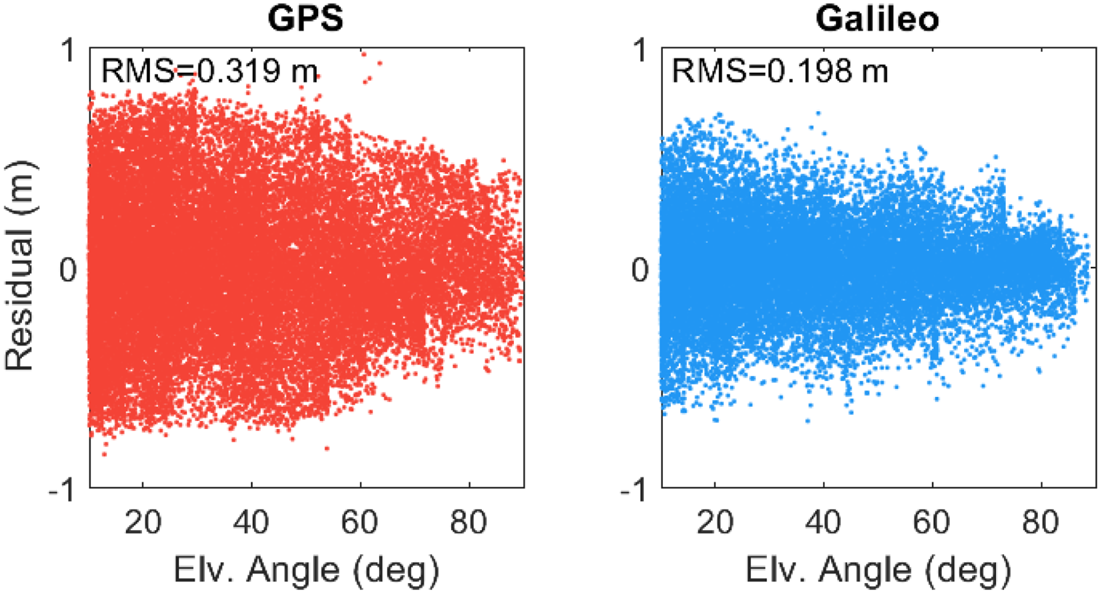
Figure 4. Observation residuals computed for the GPS and Galileo single-frequency code-based solutions at FFMJ station on 3 January 2021
On the other hand, Figure 5 provides the distributions of positioning errors computed in the north, east and up directions for the GPS, Galileo and GPS/Galileo solutions. In the generation of distributions, epoch-wise positioning solutions of 15 stations during the two-week observation period were considered. In the figure, the error distributions are presented as the probability percentages which are based on the ratio of error frequencies to the total number of epochs, instead of actual error frequencies. Therefore, the positioning solutions at the whole epochs, 604,800 epochs in total (2880 epochs in a day over two weeks for 15 different stations) were used when generating the error distributions. Furthermore, the figure demonstrates the mean and RMS errors computed in each direction, respectively. As shown in the figure, the RMS errors are 0⋅707, 0⋅622 and 1⋅876 m in the north, east and up directions for the GPS solution, while the corresponding errors are computed as 0⋅515, 0⋅429 and 1⋅401 m for the Galileo solution. The results denote that the Galileo solution provides a better positioning performance by 27⋅1%, 31⋅0% and 25⋅3% in the north, east and up directions, respectively, in comparison with the GPS solution. The GPS/Galileo solution has the related RMS values of 0⋅477, 0⋅377 and 1⋅289 m, respectively, which demonstrates that it considerably augments the positioning accuracy of the single-system solutions in all directions.
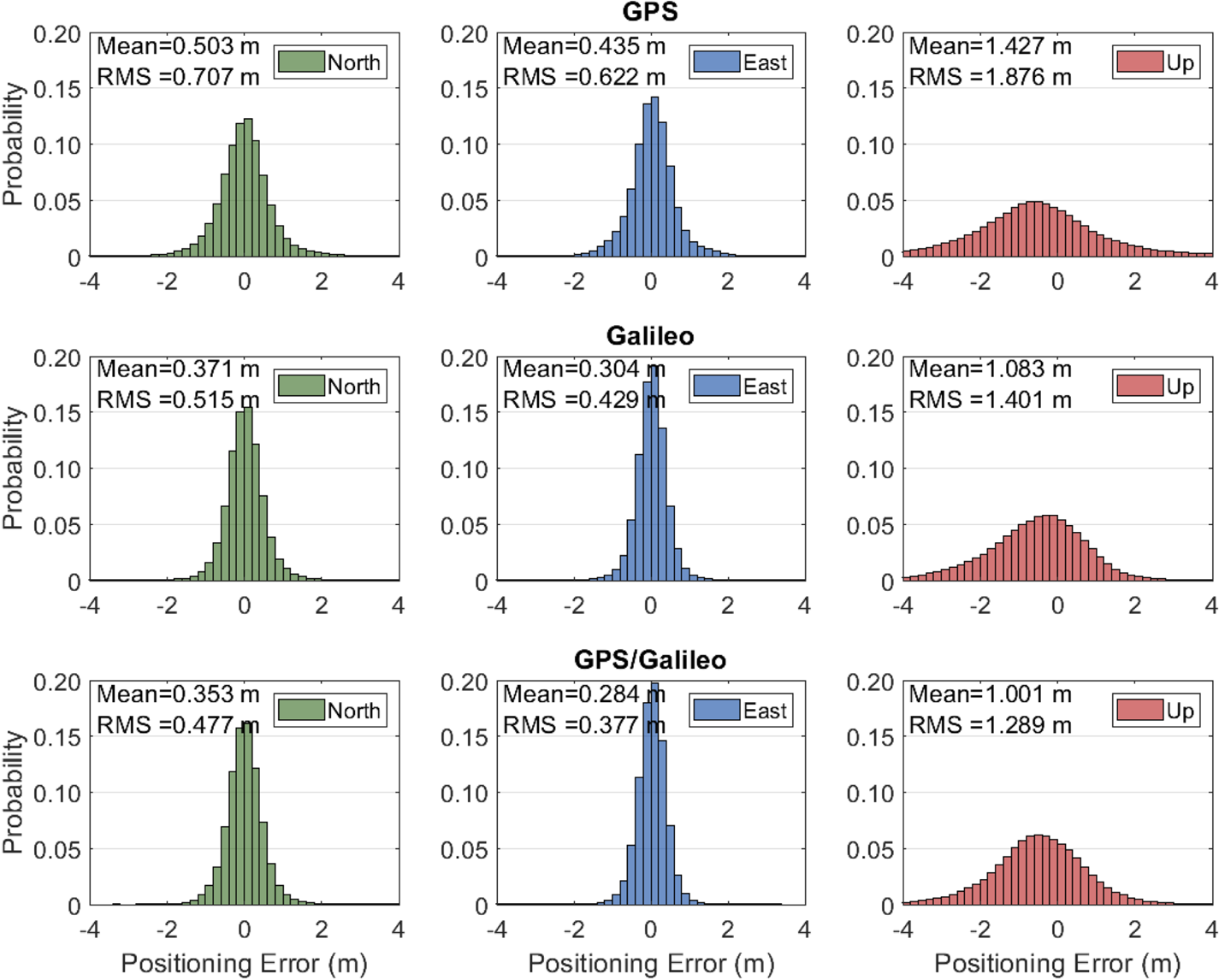
Figure 5. Error distributions for the GPS, Galileo and GPS/Galileo single-frequency code-based solutions
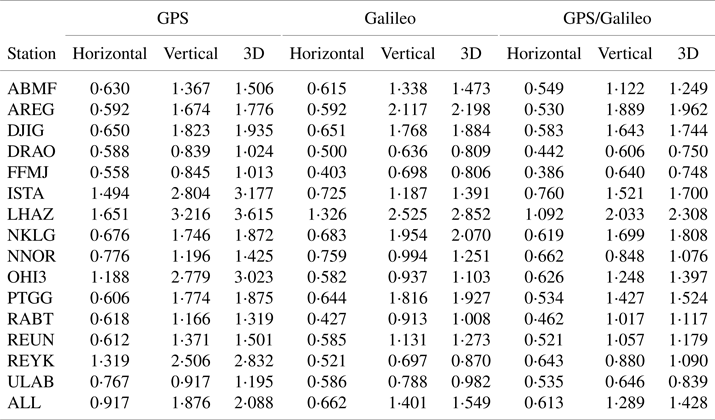
As regards the GPS, Galileo and GPS/Galileo solutions, Table 2 demonstrates the station-based RMS values computed for horizontal, vertical and three-dimensional (3D) positioning errors considering the whole positioning processes over the two-week period. The table also demonstrate the average RMS values of horizontal, vertical and 3D positioning errors computed, taking all stations into consideration. Except for the AREG, NKLG and PTGG stations, the Galileo solution presents considerably better positioning accuracy in all positioning components than that of the GPS solution for all stations. The Galileo solution augments the positioning accuracy of the GPS solution by 25⋅8% on average when the 3D RMS errors are considered. Also, its improvement percentages for the horizontal and vertical components are 27⋅9% and 25⋅3%, respectively. The 3D improvements of the Galileo solution reach 63⋅5% and 69⋅6% for the OHI3 and REYK stations located near the polar regions where the visibility of Galileo is quite strong. When it comes to the GPS/Galileo solution, it has the best positioning performance in all the stations excluding the AREG station. The GPS/Galileo integration presents a better 3D positioning accuracy than the GPS and Galileo solutions by the ratios of 31⋅6% and 7⋅9%.
Table 2. Station-based RMS values of horizontal, vertical and 3D positioning errors for the GPS, Galileo and GPS/Galileo single-frequency code-based solutions (in:m)
3.4 Performance analysis of single-frequency code-phase combination
The observation dataset was also processed for the single-frequency code-phase combination with the GPS, Galileo and GPS/Galileo solutions. To converge the non-integer phase ambiguity parameters, an initial period is necessary in this combination, called the ‘convergence time.’ Therefore, the convergence time was also utilised in the assessment of positioning performance of the single-frequency code-phase combination together with the positioning accuracy. Figure 6 depicts the horizontal and vertical positioning errors at the FFMJ station on 3 January 2021 for the GPS, Galileo and GPS/Galileo single-frequency code-phase combination solutions. When the figure is analysed, it is apparent that the horizontal positioning accuracy of the GPS solution is mostly lower than that of the Galileo solution. The daily horizontal RMS errors are computed as 0⋅266, 0⋅184 and 0⋅173 m for the GPS, Galileo and GPS/Galileo solutions, respectively. In addition, the daily vertical RMS errors of the GPS, Galileo and GPS/Galileo solutions are 0⋅322, 0⋅285 and 0⋅206 m, respectively. The results indicate that the Galileo solution presents slightly better positioning accuracy than does the GPS solution horizontally and vertically, while the best positioning performance comes from the GPS/Galileo solution.
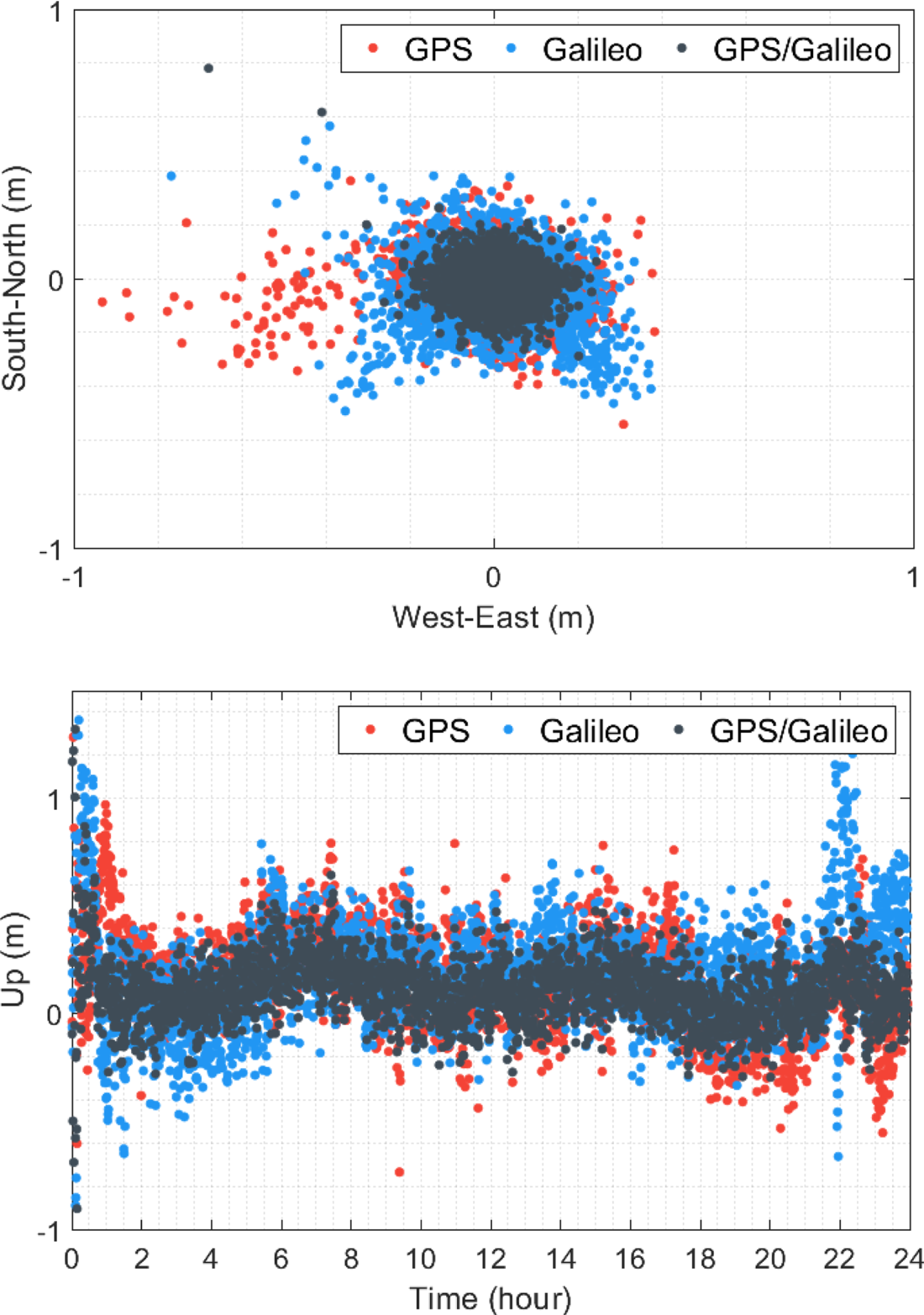
Figure 6. Horizontal and vertical positioning errors for the GPS, Galileo and GPS/Galileo single-frequency code-phase combination solutions at FFMJ station on 3 January 2021
Similarly, for the GPS and Galileo single-frequency code-phase combination solutions, Figure 7 illustrates the observation residuals computed at the FFMJ station on 3 January 2021. When compared with the single-frequency code-based positioning, the observation residuals are substantially smaller for the single-frequency code-phase combination, owing to the presence of phase observations. The RMS values computed from all daily observation residuals are 0⋅082 and 0⋅064 m for the GPS and Galileo solutions, which means that the observation residuals of Galileo are averagely 21⋅9% lower than those of GPS. The results confirm that the noise level of GPS single-frequency observations is substantially higher than Galileo observations.
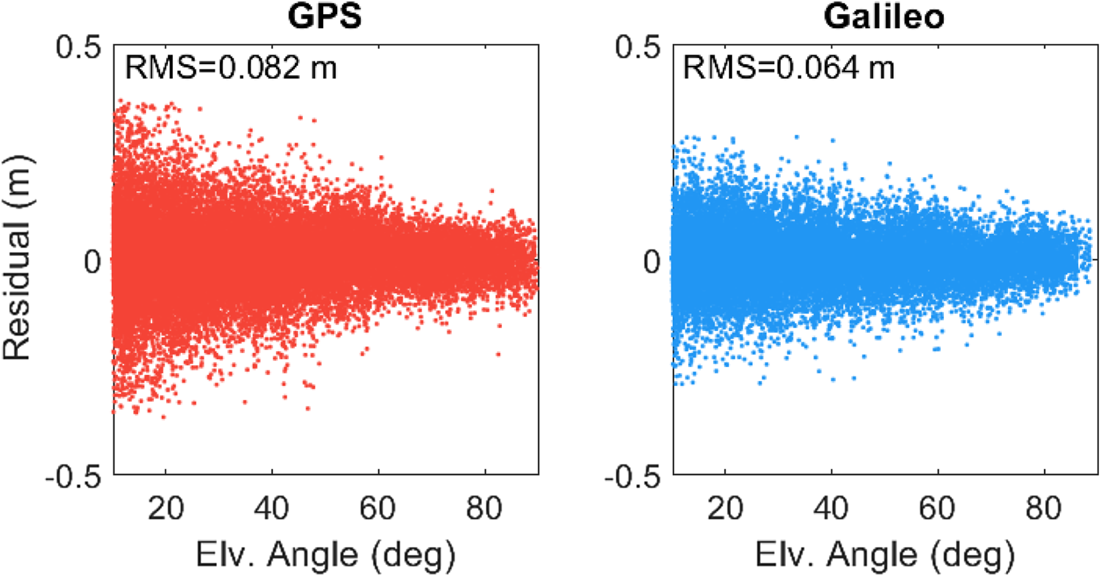
Figure 7. Observation residuals computed for the GPS and Galileo single-frequency code-phase combination solutions at FFMJ station on 3 January 2021
On the other hand, Figure 8 provides the error distributions in local directions for the GPS, Galileo and GPS/Galileo single-frequency code-phase combination solutions. Here, it should be clarified that the positioning errors at the first-hour period of each positioning solution were excluded from the probability distributions to avoid the influence of unconverged phase ambiguity parameters. The RMS errors are 0⋅192, 0⋅262 and 0⋅403 m in the north, east and up directions for the GPS solution, respectively, while these errors are computed as 0⋅179, 0⋅260 and 0⋅347 m for the Galileo solution. The results reveal that the performance of Galileo solution is better than that of the GPS solution by 6⋅7%, 1⋅0% and 13⋅9% in the north, east and up directions, respectively. Likewise, the GPS/Galileo combination provides the best positioning performance with the RMS errors of 0⋅111, 0⋅141 and 0⋅246 m. Furthermore, the convergence time was assessed as an additional indicator of the performance of single-frequency code-phase combination. The time or epoch where the 3D positioning error falls under 1 m and does not pass over the 1 m threshold for the following 10 min was utilised as the convergence time criteria in this study (Bahadur and Nohutcu, Reference Bahadur and Nohutcu2021a). According to this definition, the average convergence times computed from all positioning results over the observation period are 66⋅68, 50⋅43 and 33⋅24 min for the GPS, Galileo and GPS/Galileo solutions, respectively. The results demonstrate that the Galileo solution has a 24⋅4% shorter convergence time on average in comparison with the GPS solution, while the GPS/Galileo solution presents the best convergence performance, thanks to the increasing number of visible satellites.

Figure 8. Error distributions for the GPS, Galileo and GPS/Galileo single-frequency code-phase combination solutions
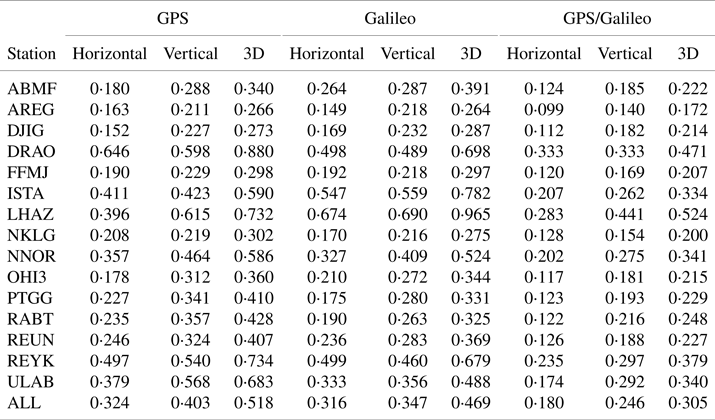
Finally, Table 3 shows the station-based RMS values of horizontal, vertical and 3D positioning errors, considering all positioning processes during the two-week period for the GPS, Galileo and GPS/Galileo solutions. The Galileo solution, compared with the GPS solution, has a better positioning performance in all stations, except for the ABMF, DJIG, ISTA and LHAZ stations. Especially, the performance of the Galileo solution is considerably worse at the ISTA and LHAZ stations, which have the lowest average numbers for visible Galileo satellites over the two-week observation period. As the single-frequency code-phase combination is a rank-deficient model, which contains more unknown parameters than the number of measurements, the satellite number has a considerable influence on the positioning performance of this model. Therefore, it can be said that the poor positioning performance at these two stations mainly stems from the low visibility of Galileo satellites. Considering the 3D RMS errors of all stations for the single-frequency code-phase combination, the performance of the Galileo solution is better than that of the GPS solution by 9⋅4%. The positioning accuracy is enhanced with the integration of GPS and Galileo constellation significantly. The GPS/Galileo solution improves the 3D positioning accuracies obtained from the GPS and Galileo solutions by 41⋅2% and 35⋅1%, respectively.
Table 3. Station-based RMS values of horizontal, vertical and 3D positioning errors for the GPS, Galileo and GPS/Galileo single-frequency code-phase combination solutions (in:m)
4. Conclusions
This study investigates the most recent performance of the Galileo constellation in real-time single-frequency precise positioning. Two single-frequency positioning models, namely single-frequency code-based positioning and code-phase combination, were adopted for the performance assessment in this study. In this context, several experimental tests were performed to evaluate the performance of real-time Galileo single-frequency positioning and its contribution to the GPS-only solution. Additionally, as one of the important factors that have a substantial influence on the positioning performance, the satellite visibility of the Galileo constellation was analysed as a part of this study.
The results demonstrated that the Galileo constellation mostly provides a considerable satellite resource for single-frequency positioning, while its satellite visibility can alter depending on the station's location. Especially, it was observed from the results that the visibility of Galileo satellites is quite strong near the polar regions. In addition, the results demonstrated that the observation residuals acquired from single-frequency measurements of Galileo satellites are considerably lower than those of GPS satellites. Based on these results, it was concluded that the single-frequency Galileo observations have relatively better quality and less influenced by multipath and other unmodelled errors compared with the GPS observations. For the real-time single-frequency code-based positioning, the GPS solution provided a 3D positioning accuracy of 2⋅088 m on average, while the 3D positioning accuracy was computed as 1⋅549 m for the Galileo solution. These results indicated that the Galileo solution presents better positioning performance than the GPS solution by 25⋅8%, on average. Moreover, its improvement percentages relative to the GPS solution reached 63⋅5% and 69⋅6% at the OHI3 and REYK stations located near the polar regions. Similarly, the results showed that a 9⋅4% better 3D positioning accuracy is acquired from the Galileo solutions for the single-frequency code-phase combination compared with the GPS solution. In addition, the convergence times were computed as 66⋅68 and 50⋅43 min for the GPS and Galileo solutions, which means the Galileo solution has a 24⋅4% shorter convergence time, on average. Still, the results depicted that the positioning performance of the Galileo single-frequency code-phase combination solution can be considerably worse at the stations where its satellite visibility is relatively poor. Moreover, the results indicated that the GPS/Galileo integration enhances the positioning performance of single-system solutions significantly for both positioning models. Consequently, this study concluded that Galileo could provide considerably better positioning performance in comparison with GPS and contribute to the GPS solution substantially for the real-time single-frequency precise positioning. Considering also that the Galileo constellation and its products are improving each day, Galileo is an important alternative to the GPS constellation for real-time single-frequency GNSS applications.