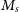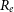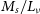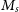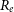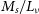1. Introduction
Over the past many decades, astronomers have identified commonalities in clusters of stars ranging from small groups to large galaxies. Hot stellar systems (HSS) are a class of celestial objects consisting of globular clusters, nuclear star clusters, compact ellpitical galaxies, giant elliptical galaxies, ultra compact dwarf elliptical galaxies, nuclear star clusters and so on. These HSS are very important to understand processes such as the formation of stars or black holes, evolution of galaxies and so on. Indeed, the physical properties of these objects have been directly linked to galaxy interactions and have been extensively studied. One of the most useful concepts (Burstein et al. Reference Burstein, Bender, Faber and Nolthenius1997; Bernardi et al. Reference Bernardi2003; Kormendy et al. Reference Kormendy, Fisher, Cornell and Bender2009; Misgeld & Hilker Reference Misgeld and Hilker2011) in studying these objects is the set of fundamental plane relations (Brosche Reference Brosche1973). These planes are typically constructed with parameters such as luminosity, surface brightness, stellar magnitude or central velocity dispersion and help understand important properties of these stellar systems. Different HSS sub-groups typically have different fundamental planes, photometric properties and other types of interpretations (Kormendy Reference Kormendy1985; Djorgovski Reference Djorgovski1995; McLaughlin & van der Marel Reference McLaughlin and van der Marel2005; Meylan et al Reference Meylan2001; Forbes et al. Reference Forbes, Lasky, Graham and Spitler2008; Harris, Pritchet, & McClure Reference Harris, Pritchet and McClure1995; Webbink Reference Webbink1985; Ichikawa, Wakamatsu, & Okamura Reference Ichikawa, Wakamatsu and Okamura1986; Kormendy et al. Reference Kormendy, Fisher, Cornell and Bender2009; Bender et al. Reference Bender, Burstein and Faber1992). But the origins of these relations, the underlying evolutionary processes involved and the statistical reliability of these results are not well understood and remain as significant challenges. A huge volume of data has been collected and catalogued in the last fifteen years to effectively address these challenges. For example Jordán et al. (Reference Jordán2008) catalogued and studied 12 763 candidate globular clusters (GCs) from the Virgo Cluster Survey during the eleventh Hubble Space Telescope observation cycle. A more comprehensive catalogue was compiled by Misgeld & Hilker (Reference Misgeld and Hilker2011) which included 693 additional HSS along with those of Jordán et al. (Reference Jordán2008). Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) pointed out that several studies have previously compared stellar systems such as globular clusters and dwarf spheroidals using two-point correlations between different projections of the fundamental plane of galaxies. Given our lack of understanding about HSS groups, their evolution and relationships, an important step forward is a firm understanding of which groups are demonstrably different in observational parameter spaces, and which may be more closely related. These important questions can be answered by modern multivariate statistical analysis methods, and one effort to do so was by Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) who used k-means clustering with the jump statistic (Sugar & James Reference Sugar and James2003) and found five and four homogeneous groups in the 693 non-candidate and the larger 13 456 HSS datasets.
Clustering (Kettenring Reference Kettenring2006; Xu & Wunsch Reference Xu and Wunsch2009; Everitt Reference Everitt2011) is an unsupervised learning technique that groups observations without a response variable. While there are many kinds of clustering algorithms, most of them can broadly be categorised into hierarchical and non-hierarchical approaches. Hierarchical clustering algorithms yield a tree-like grouping hierarchy while non-hierarchical algorithms, such as from k-means or model-based clustering (MBC) methods, typically optimise an objective function using iterative greedy algorithms—these algorithms typically require a specified number of groups. The objective function is often multimodal and requires careful initialisation (Maitra Reference Maitra2009). A detailed review on MBC is provided, for instance, in McLachlan & Peel (Reference McLachlan and Peel2000) or Melnykov & Maitra (Reference Melnykov and Maitra2010); additionally, Chattopadhyay & Maitra (Reference Chattopadhyay and Maitra2017) reviewed it in the context of astronomical applications. Even though model-based methods are an improvement over traditional hierarchical and non-hierarchical methods, they are still mostly limited to finding regular-structured groups. For example, the most common technique of Gaussian-mixtures MBC (GMMBC) assumes spherical or ellipsoidally structured spreads in their groups. Very often, however, the underlying groups in a dataset are irregular in shape and do not all neatly fit the assumptions underlying MBC. Thus advanced methods are necessary to identify and analyse complex-structured groups. Almodóvar-Rivera & Maitra (Reference Almodóvar-Rivera and Maitra2020) proposed a novel method of identifying such groups by using syncytial clustering which incorporates the results from standard clustering methods and then merges them to reveal the complex general structure in data. Specifically, their approach reveals a multi-layered group structure that provides insight into not just the groups but also their underlying sub-group structure, which may have regular structure at some level. We analyse the 13 456 HSS of Misgeld & Hilker (Reference Misgeld and Hilker2011) that is briefly summarised in Section 2 using syncytial clustering methods (introduced in Section 3) with initial clustering results obtained using t-mixtures MBC (tMMBC). We analyse the HSS using these methods in Section 4. Further, in all such investigations involving astronomical data, parameter estimation in statistical clustering algorithms is accompanied by uncertainty in those estimates and careful assessment of these estimates is often required to judge their results and their impact on the obtained groupings. We analyse this uncertainty by using a nonparametric bootstrap procedure (Efron Reference Efron1979) to calculate the confidence of classification of each data point into a group. The paper concludes with some discussion about the physical properties of the obtained groups and to pointers for future work.
2. The HSS dataset
The dataset used in our analysis was compiled from different sources by Misgeld & Hilker (Reference Misgeld and Hilker2011) and contains measurements on 13 456 HSS of different types: globular clusters (GC), giant ellipticals (gE), compact ellipticals (cE), ultra compact dwarf galaxies (UCD), dwarf globular transition objects (DGTO), nuclear of star clusters (NuSc), bulges of spiral galaxy (Sbul) and nuclei of nucleated dwarf galaxies (dE,N). There are 12 763 HSS in this dataset that are candidate GCs (GC_VCC) from the Virgo Globular Cluster survey meaning it is ambiguous if these systems are GC’s or not. Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) primarily excluded these candidate GCs from their analysis, focusing mainly on the 673 stellar systems consisting of confirmed GC’s and other different types of stellar systems. We call these 673 systems non-candidate HSS. The main parameters in Misgeld & Hilker (Reference Misgeld and Hilker2011) are stellar mass (
$M_s$
), effective radius (
$R_e$
), mass surface density averaged over projected effective radius (
$S_e$
) and absolute magnitude in the V band (
$M_\nu$
). Following Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) we use the logarithm (base 10) of
$M_s$
,
$R_e$
and mass-to-luminosity ratio (
$M_s / L_\nu$
) in solar luminosity (
$M_{s,\odot}$
) units in our analysis. The
$M_s/L_\nu$
ratio was obtained using the standard magnitude-luminosity relation.
\begin{equation} \frac{M_s}{M_{s,\odot}} = -2.5\left(\frac{L_\nu}{L_{\nu,\odot}}\right)\end{equation}
where
$L_{\nu,\odot}$
denotes the luminosity of the sun. The parameter
$\log_{10}S_e$
is taken into account while interpreting the results but, as in Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013), is not used in the clustering mechanism. Figure 1 provides pairwise scatterplots of the three parameters for both candidate and non-candidate objects along with density plots of the parameters used in clustering. From Figure 1 we see that the densities of the non-candidates display moderate univariate bimodality, and especially in the context of effective radius and mass-luminosity ratio. There is therefore evidence of grouping, certainly so at the univariate level. Also, the correlation values indicate that
$M_s$
and
$R_e$
are moderately positively correlated, as expected in stellar objects. But mass-luminosity ratio has a weak linear association with both
$M_s$
and
$R_e$
. It therefore points to complex structure in the dataset and so in the coming sections, we outline methodology to uncover and understand it from astronomical perspectives.
Figure 1. Pairwise scatterplots, estimated densities and correlation coefficients of the logarithm (base 10) of the parameters in the HSS dataset. Here Ms denotes mass, Re effective radius and R the mass-luminosity ratio. In the scatterplot, orange indicates the non-candidates and blue the candidates. For the density plots the blue curves represent the non-candidates. Note that the calculated correlations are for all 13 456 HSS in the dataset (including the non-candidates and candidates).
3. Statistical methodology
In this section we briefly describe our methodology for analysing the 13 456 HSS. Our methodology is a model-based analogue of the syncytial clustering algorithm of Almodóvar-Rivera & Maitra (Reference Almodóvar-Rivera and Maitra2020). Our procedure involves an initial clustering of the data using tMMBC followed by merging of the tMMBC mixture components using pairwise overlap measure and generalised overlap, calculated using Monte Carlo methods, as described next.
3.1. Initial MBC using a mixture of multivariate-t densities
MBC provides a principled way to find homogeneous regular-shaped groups in a given dataset. It scores over classical clustering algorithms like k-means due to its ability to better model heterogeneity in groups. As pointed out by Chattopadhyay & Maitra (Reference Chattopadhyay and Maitra2017) assuming spherically dispersed homogeneous groups when such assumption is not valid can lead to erroneous results. In MBC (Melnykov & Maitra Reference Melnykov and Maitra2010; McLachlan & Peel Reference McLachlan and Peel2000) the observations
$X_1,X_2,\ldots,X_N$
are assumed to be realisations from a G-component mixture model (McLachlan & Peel Reference McLachlan and Peel2000) with probability density function (PDF)
\begin{equation} f(x;\ \unicode{x03B8}) = \sum_{g=1}^{\textit{G}}\pi_g f_g(x;\ \unicode{x03B7}_g) \end{equation}
where
$f_g(\cdot;\ \unicode{x03B7}_g)$
is the density of the gth group,
$\unicode{x03B7}_g$
the vector of unknown parameters and
$\pi_g = Pr[x_i \in\mathcal{G}_g]$
is the mixing proportion of the gth group,
$g=1,2,\ldots,G$
, and
$\sum_{g=1}^{\textit{G}}\pi_g = 1$
. The component density
$f_g(\cdot;\ \unicode{x03B7}_g)$
can be chosen according to the specific needs of the application—the most popular choice is the multivariate Gaussian density (Chattopadhyay & Maitra Reference Chattopadhyay and Maitra2017; Fraley & Raftery Reference Fraley and Raftery1998, Reference Fraley and Raftery2002). Another useful family of mixture models proposed by McLachlan & Peel (Reference McLachlan and Peel1998) specifies
$f_g(\cdot;\unicode{x03B7}_g)$
to be the multivariate-t density. That is,
\begin{align} & f_g(z;\ \unicode{x03BC}_g , \Sigma_g, \nu_g) \nonumber \\[3pt] & = \frac{\Gamma (\nu_g/2 + p/2)}{\Gamma(\nu_g/2) {{\nu_g}^{\frac{p}{2}}}{{\pi_g}^{\frac{p}{2}}}{|\Sigma_g|}^\frac{1}{2}} \Big[1+ \frac{1}{\nu_g}(z-\unicode{x03BC}_g)^T\Sigma_g^{-1}(z-\unicode{x03BC}_g)\Big], \end{align}
for
$z\in\mathbb{R}^p$
, where
$\unicode{x03BC}_g$
denotes the mean vector,
$\Sigma_g$
the scale matrix and
$\nu_g$
the degrees of freedom, all for the gth mixture component,
$g=1,2,\ldots,G$
. Our analysis uses, instead of a Gaussian mixture model (GMM), the multivariate-t mixture model (tMM) (Goren & Maitra Reference Goren and Maitra2022) because the multivariate-tMM better allows for thicker tails in the component mixture densities. Subsequent steps in clustering involve obtaining maximum likelihood (ML) estimates of the parameters
$\unicode{x03B7}_g$
,
$g = 1, 2,\ldots,G$
using the Expectation-Maximisation (EM) algorithm (Dempster, Laird, & Rubin Reference Dempster, Laird and Rubin1977; McLachlan & Krishnan Reference McLachlan and Krishnan2008; Chattopadhyay & Maitra Reference Chattopadhyay and Maitra2017; Chattopadhyay & Maitra Reference Chattopadhyay and Maitra2018) and assigning each individual observation based on the maximum posterior probability that it belongs to a given group. We use the Bayesian Information Criterion (BIC) (Schwarz Reference Schwarz1978; Chattopadhyay & Maitra Reference Chattopadhyay and Maitra2017) to decide G.
3.2. Merging mixture components using overlap
After obtaining the parameter estimates of (2), mixture components can be merged using one of several criteria described in Melnykov (Reference Melnykov2016). Here we use the pairwise overlap measure (Maitra & Melnykov Reference Maitra and Melnykov2010; Melnykov & Maitra Reference Melnykov and Maitra2011; Melnykov, Chen, & Maitra Reference Melnykov, Chen and Maitra2012). The pairwise overlap takes value in [0, 1] and provides us with a sense of the distinctiveness between groups obtained using a particular clustering method, with values closer to 1 indicating that the two groups are poorly separated. We now provide details on how to obtain these overlap measures.
3.2.1. Pairwise overlap between simple groups
A simple group (Almodóvar-Rivera & Maitra Reference Almodóvar-Rivera and Maitra2020) is obtained from the initial classifications, in our case by tMMBC. For a G-component tMM (2), the probability that an observation X, originally from a mth component distribution (that is, belonging to the mth group) gets misclassified to the nth group is
\begin{equation} \omega_{n|m} = P(\pi_nf_n(x;\ \unicode{x03BC}_n, \Sigma_n, \nu_n) > \pi_mf_m(x;\ \unicode{x03BC}_m, \Sigma_m, \nu_m)) \end{equation}
where
$f_g(x;\ \unicode{x03BC}_g, \Sigma_g, \nu_g)$
has density as in (3). The pairwise overlap (Maitra & Melnykov Reference Maitra and Melnykov2010) between the mth and nth group is then defined as
\begin{equation} \omega_{mn} = \omega_{n|m} + \omega_{m|n} \end{equation}
For illustration, we display in the appendix (Figure A.1) sample two-component three-dimensional distributions with varying degrees of overlap.
Unlike in the case of GMM, the misclassification probability
$\omega_{n|m}$
cannot be readily calculated using analytical methods, so we use Monte Carlo methods as follows:
-
1. Generate M realisations
$x_i^*$
,
$i=1,2,\ldots M$
from the density
$f_m(x ;\ \unicode{x03BC}_m, \Sigma_m, \nu_m)$
. -
2.
$\omega_{n|m}$
can then be approximated as (6)where
\begin{align} &\hat{\omega}_{n|m} \nonumber \\[3pt] & = \frac{1}{M}\sum_{i=1}^{M}I\{\pi_nf_n(x_i^*;\ \unicode{x03BC}_n, \Sigma_n, \nu_n) > \pi_mf_m(x_i^*;\ \unicode{x03BC}_m, \Sigma_m, \nu_m)\} \end{align}
$I(\cdot)$
is the indicator function, that in this case is 1 for a given i if
$\pi_nf_n(x_i^*;\ \unicode{x03BC}_n, \Sigma_n, \nu_n) > \pi_mf_m(x_i^*;\ \unicode{x03BC}_m, \Sigma_m, \nu_m)$
and 0 otherwise.
The pairwise overlap provides us with a sense of the distinctiveness between groups obtained using a particular clustering method. As mentioned earlier, these values lie inside [0, 1] with values near zero indicating perfect separation between groups and those closer to unity indicating poor separation. Melnykov & Maitra (Reference Melnykov and Maitra2011) used methods developed in Maitra (Reference Maitra2010) to define the generalised overlap
$\ddot{\omega}$
to summarise the
$G\times G$
matrix
$\Omega$
of pairwise overlaps which is given by
$(\lambda_{\Omega}-1)/(G-1)$
where
$\lambda_{\Omega}$
is the largest eigenvalue of
$\Omega$
. Typically, smaller values of
$\ddot{\omega}$
indicate distinctive groupings while larger values indicate more overlap between groups.
Figure 2. From left to right: (a) Original Gaussian mixture model clustering solution according to BIC. (b) Five clusters obtained after first phase merging. (c) Final clustering solution obtained after second phase merging.
3.2.2. Pairwise overlap between composite groups
Let
$\mathcal{G}_p$
and
$\mathcal{G}_q$
be two composite groups having probability densities
$\sum_{h \epsilon \mathcal{G}_p }\pi_hf_h(x;\ \unicode{x03BC}_h, \Sigma_h, \nu_h)$
and
$\sum_{r \epsilon \mathcal{G}_q}\pi_rf_h(x;\ \unicode{x03BC}_r, \Sigma_r, \nu_r)$
respectively, possibly formed by merging one or more components of (2). The probability of an observation X actually from
$\mathcal{G}_p$
being misclassified to
$\mathcal{G}_q$
is
\begin{equation} \omega_{\mathcal{G}_q|\mathcal{G}_p} = P\Bigg(\frac{\sum_{r \epsilon \mathcal{G}_q }\pi_rf_r(x;\ \unicode{x03BC}_r, \Sigma_r, \nu_r)}{\sum_{h \epsilon \mathcal{G}_p }\pi_hf_h(x;\ \unicode{x03BC}_h, \Sigma_h, \nu_h)} > 1\Bigg) \end{equation}
where
$f_g(x;\ \unicode{x03BC}_g, \Sigma_g, \nu_g)$
has density given by (3). The pairwise overlap between
$\mathcal{G}_p$
and
$\mathcal{G}_q$
, denoted by
$\omega_{\mathcal{G}_p \mathcal{G}_q}$
, is then computed as
$\omega_{\mathcal{G}_q|\mathcal{G}_p} + \omega_{\mathcal{G}_p|\mathcal{G}_q}$
. The misclassification probability
$\omega_{\mathcal{G}_q|\mathcal{G}_p}$
can be estimated as follows:
-
1. Generate M samples
$x_i^*$
,
$i=1,2,\ldots M$
from the density
$\sum_{h \epsilon \mathcal{G}_p }\pi_h^*f_r(x;\ \unicode{x03BC}_h, \Sigma_h, \nu_h)$
, where
$\pi_h^*$
is a standardised probability obtained as
$\pi_h^* = \pi_h/\sum_{h \epsilon \mathcal{G}_p } \pi_h$
. -
2.
$\omega_{\mathcal{G}_q|\mathcal{G}_p}$
can then be approximated as (8)where
\begin{equation} \hat{\omega}_{\mathcal{G}_q|\mathcal{G}_p} = \frac1M\sum\nolimits_{i=1}^MI\left\{\frac{\sum_{r \epsilon \mathcal{G}_q }\pi_rf_r(x_i^*;\ \unicode{x03BC}_r, \Sigma_r, \nu_r)}{\sum_{h \epsilon \mathcal{G}_p}\pi_hf_h(x_i^*;\ \unicode{x03BC}_h, \Sigma_h, \nu_h)} > 1\right\}, \end{equation}
$I(\cdot)$
is the indicator function, as before.
3.3. The model-based syncytial clustering algorithm
Our syncytial clustering algorithm consists of three phases, the tMMBC phase, the initial overlap calculation phase and the merging phase:
-
1. The initial clustering phase: This phase fits a G-component tMM to the data using the EM algorithm (McLachlan & Peel Reference McLachlan and Peel2000), with G chosen using BIC (Schwarz Reference Schwarz1978).
-
2. Merging Phase: This phase gets triggered only if the generalised overlap
$\ddot{\omega}^{(1)}$
of the original clustering solution is not negligible, that is if
$\ddot{\omega}^{(1)} \not\approx 0$
and atleast one pairwise overlap of the original clustering solution is greater than
$\ddot{\omega}^{(1)}$
. Specifically this phase involves the following steps:-
(a) Find the pairwise overlaps between ith and jth group
$\omega_{ij}$
for the
$G(G-1)/2$
pairs of groups using the method described in Section 3.2.1. Also find the generalised overlap
$\ddot{\omega}$
. -
(b) Merge the ith and jth groups if
$\omega_{ij} > \unicode{x03BA}\ddot{\omega}$
, with
$\unicode{x03BA}$
as discussed shortly, and relabel the merged groups, as needed. -
(c) Calculate the updated pairwise overlaps of the newly formed composite groups using the method described in Section 3.2.2. Also calculate
$\ddot\omega$
of the new clustering solution. Repeat Step (b) with the updated pairwise overlaps and the generalised overlap.
-
-
3. Termination Phase: Terminate the merging in Step 2. if the generalised overlap of the current phase clustering solution, or its change, is negligible (in this paper defined to be
$\leq10^{-3}$
): that is, if
$\ddot{\omega}^{(l)} \approx \ddot{\omega}^{(l-1)}$
or
$\ddot{\omega}^{(l)}$
where
$\ddot{\omega}^{(l-1)}$
is the generalised overlap of the previous phase clustering solution.
Selection of
$\unicode{x03BA}$
: The parameter
$\unicode{x03BA}$
determines the propensity of merging, and hence the characteristics of the composite groups formed at each merging phase. With larger values of
$\unicode{x03BA}$
, few pairs merge at each phase while smaller values of
$\unicode{x03BA}$
mean that many components are merged simultaneously at each phase. A data-driven approach proposed by Almodóvar-Rivera & Maitra (Reference Almodóvar-Rivera and Maitra2020) for selecting
$\unicode{x03BA}$
, that we also adopt, runs the algorithm for several values of
$\unicode{x03BA}$
and uses the final clustering solution with the smallest terminating
$\ddot\omega$
.
Choice of mixture model: The description of our algorithm uses tMMBC in the initial clustering phase, however, our algorithm applies to other mixture models with appropriate modifications. Indeed, in our paper, we have used tMMBC (which by default, includes GMMBC, when the degrees of freedom for each mixture component are infinite), with degrees of freedom also estimated, and then decided on the initial clustering solution with the higher BIC.
3.4. An illustrative example
We illustrate our model-based syncytial clustering algorithm on the synthetic 2D Bananas-Arcs dataset in Almodóvar-Rivera & Maitra (Reference Almodóvar-Rivera and Maitra2020). From Figure 2 it is evident that this dataset has four complex-structured clusters. We fit both GMMBC and tMMBC to this dataset using the methods in Chattopadhyay & Maitra (Reference Chattopadhyay and Maitra2017) and (2018) and selected the best clustering solution as well as the number of groups using BIC. For this dataset, GMMBC with 15 groups provided the best solution (Figure 2a) with
$\ddot\omega=8.2\times 10^{-3}$
. The first of the merging phases (with the best
$\unicode{x03BA}=3$
) provided the five clusters of Figure 2b with
$\ddot\omega=1.4\times 10^{-4}$
. Therefore this merged solution provides a more distinctive grouping than the Gaussian mixture model solution. The second phase of merging resulted in the four groups of Figure 2c with
$\ddot\omega=1.368\times 10^{-4}$
. Since the generalised overlap of this phase is nearly indisinguishable from that obtained at the end of the first phase of merging, the merging terminates here. This example clearly illustrates the effectiveness of syncytial clustering over regular methods in capturing complex structure and irregular-shaped clusters. Additionally, the multi-staged solution provides us with the ability to understand each of these complex structures in terms of their component (simpler) homogeneous groups. Our data-driven approach results in a terminating
$\ddot\omega$
that is much smaller than the original tMMBC solution indicating a preference for the complex-structured solution in providing distinctive groups. We now analyse the 13 456 HSS using our syncytial clustering algorithm.
Figure 3. BIC for each G upon performing G-component tMMBC with 13 456 HSS from Misgeld & Hilker (Reference Misgeld and Hilker2011).
4. Characterisation of HSS
4.1. Cluster analysis
4.1.1. The initial clustering phase
We performed G-component tMMBC, for
$G \in \{1, 2,\ldots,9\}$
on
$M_s$
,
$R_e$
and
$M_s/L_\nu$
, all in the
$\log_{10}$
-scale, of the 13 456 HSS. Figure 3 indicates that a eight-component tMMBC provides an optimal fit, as per BIC. The eight-component tMMBC solution was better, as per BIC, than the optimal GMMBC solution. Our results here are different from that of Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) who, upon using k-means with the Jump statistic (Sugar & James Reference Sugar and James2003), found five groups when excluding the candidate GCs of Jordán et al. (Reference Jordán2008) and four groups on the full HSS dataset.
Figure 4 shows the pairwise overlaps of the eight groups obtained using tMMBC. A 3D scatterplot of the eight tMMBC groups is also provided in Figure 5. Table 1 provides the group means and standard deviations for the eight groups. The composition of the eight groups in terms of the different kinds of stellar objects are in Table 2. Since tMMBC assumes ellipsoidally dispersed groups (with fatter tails) some of the groups exhibit substantial overlap (Figure 4). These large overlap values point to the possibility of complex group structure in the data that is not accounted for by using tMMBC (or GMMBC). We therefore explore if we can use our algorithm to reveal this potentially complex structure.
Figure 4. Pairwise overlap measures between any two groups obtained by our eight-component tMMBC solutions.
4.1.2. The merging phases
The first phase: Based on the pairwise overlap map of Figure 4, and for
$\unicode{x03BA}=1$
(determined to be the solution with the lowest terminating
$\ddot\omega$
), Groups 1-4, 7 and 8 all merge into one group. Thus, at the end of this merging phase, we have three groups and a generalised overlap of
$\ddot\omega =0.13$
. To facilitate easy reference, we relabel the erstwhile Groups 5 and 6 as the merged (first phase) Groups (i)-5 and (ii)-6 respectively and the merged entity as Group (iii), with the component individual groups as Group (iii)-1 through Group (iii)-4 and Group (iii)-7 and Group (iii)-8. A 3D scatterplot of the three first-phase merged groups is provided in Figure 6, while Tables 3 and 4 summarise the mean parameter values and the types of objects in the three merged groups. The pairwise overlap between Groups (i) and (ii) is 0.01 and between Groups (ii) and (iii) is 0.1. the overlap between Groups (i) and (iii) is negligible. Figure 6 immediately points out how the first phase mergers based on the pairwise overlaps have been able to capture the non-ellipsoidal structure present in the data. But the pairwise overlaps and the generalised overlap (and the logic of our method) suggest that there might be additional structure which might have been missed in the first phase merge. So we proceed with another merging phase.
Table 1. Mean and standard deviation (in brackets) of parameter values for each of the eight groups obtained using tMMBC.
Figure 5. Three viewing angles of the scatterplot of the full dataset with different colours representing different groups, and intensity of the colour indicating the underlying confidence in that particular grouping. Darker shades indicate higher confidence of classification of that particular object.
Table 2. Types of objects in each of the eight groups obtained by tMMBC.
Table 3. Mean and standard deviation (in brackets) of parameter values for each of the three groups after phase one merging. The third group is the merged group.
Figure 6. Two viewing angles of the scatterplot of the full dataset after the first stage merging. Here, different colours representing different groups: intensity of the colour indicates the degree of underlying confidence in that particular grouping. Darker shades indicate higher confidence of classification of that particular object.
The second phase: In the second phase, Groups (ii)-6 and (iii) merge to yield two complex-structured groups. We label the newly-merged group as Group II—with component merged sub-groups as Groups II-(ii) and II-(iii), and correspondingly down the hierarchy—and the original group as Group I (with sub-groups classification of Group I-(i) and Group I-(i)-5, to indicate the three-stages of classifications). A 3D scatterplot of the two new groups is given in Figure 7, with numerical summaries provided in Tables 5 and 6. The scatterplot clearly depicts that the second merge has captured the complex general-shaped group structures in the dataset well and also obtained to a good extent the two well-separated groups. The pairwise overlap between these two groups is 0.0013. Since the pairwise overlap between Groups I and II is very close to
$10^{-3}$
the algorithm terminates at this stage.
Table 4. Types of objects in each of the three groups after phase one merge.
Table 5. Mean and standard deviation (in bracket) of parameter values for each of the two groups after phase two merging. The second group is the new merged group.
4.2. Measuring uncertainty in the obtained groupings through bootstrapping
We assess the uncertainty in the parameter estimates in each phase and the corresponding classification using a nonparametric bootstrap technique where we repeatedly resample from the dataset with replacement and analyse each resample to obtain estimated properties of the parameters of interest. Refer to Efron (Reference Efron1979) for a detailed study on the bootstrap.
Table 6. Types of objects in each of the two groups after the phase two mergers.
In our scenario, the parameters of interest are the group memberships. Here, a well-done cluster analysis is expected to produce the same group memberships for most of the observations at each bootstrap replicate. We now describe the steps to obtain the confidence of classification of each observation for the original clustering solution using tMMBC.
-
(i) First we perform tMMBC on the original 13 456 HSS as described in Section 2. This matches the analysis so far and yields eight tMMBC groups.
-
(ii) Sample, with replacement, 13 456 HSS from the dataset and again cluster the resampled data using the classifications obtained in Step (i) as the initial estimates for the groupings. Repeat this procedure B times to obtain B sets of classification estimates. Let us denote these B sets by
$C_1, C_2,\ldots,C_{B}$
. Also let
$C_{ij}$
be 1 if the classification of the jth data point in the ith bootstrap replicate is the same as the original classification of the jth datapoint and 0 otherwise, where
$i = 1, 2,\ldots B$
and
$j = 1, 2,\ldots,13\,456$
. -
(iii) The classification probability for the jth HSS is obtained as
(9)where
\begin{equation} p_j = \frac{1}{B}\sum_{i=1}^{B} C_{ij} \end{equation}
$j = 1, 2,\ldots,13\,456$
. In our analysis, we took
$B=1\,000$
, that is, we resampled 1 000 times from the dataset.
In each merging phase, the confidence of classification is obtained by relabeling each of the B bootstrap replicates to the solution obtained from the original clustering results and then repeating Steps (i)-(iii) of our algorithm with the relabelled bootstrap replicates. Table 7 gives the number of HSS in each class having confidences in seven intervals (0, 0.30], (0.30, 0.60], (0.60, 0.85], (0.85, 0.90], (0.90, 0.95] and (0.95. 1], at the two merging stages. The fact that the majority of HSS have a high confidence of classification in both the stages provides reassurance in our clustering results for the 13 456 HSS.
We end our discussion in this section by noting that we could have also obtained an estimate of the confidence of classification based on the posterior probability of classification. However, we use a nonparametric bootstrap technique for estimating the classification probabilities in order to account for the uncertainty in the modelling and to account for possible model misspecification. The choice of the nonparametric bootstrap technique provides us with more robust estimates of the confidence of classification compared to using the posterior probability of classification because it accounts for possible model misspecification in the calculation of the classification confidence.
4.3. Analysis of results
4.3.1. Properties of identified groups
Table 2 gives the numbers of different types of HSS in each of the tMMBC groups and Tables 4, 6 give the numbers of different types of HSS in each group at each phase of the algorithm. The means and standard deviations of the parameters for the tMMBC solution are provided in Table 1 while those for each group at each of the merging phases is in Tables 3 and 5. Additionally, different colours in Figures 5, 6 and 7 indicate the group to which each HSS belongs, with different shades indicating the confidence of that particular HSS. Darker shades indicate higher confidences for that particular HSS. From the figures and Table 7a and b it is clear that most of the HSS have high confidence coefficients, indicating that the classification method has worked well in identifying the non-ellipsoidal structure that was demonstrated after the initial clustering using tMMBC. After the first mergers, the most notable groups are Groups (i)-5 and (iii) which have most of the HSS. Most of the GC_VCCs are in Group (iii) after the first merge and only ten are in Group (ii)-6. The stellar systems in Group (ii)-6 have lower confidence compared to the other two groups due to which inferences about the HSS in this group will be more uncertain compared to the HSS in other groups. From Table 6 we see that after the second phase, all the candidates (GC_VCC) were classified to Group II. All the GCs were also classified to this group, as also a number of UCDs and dE,Ns. These group compositions and means can help us infer about the kinematic properties of these stellar systems. After the final merge, Group I has a larger
$M_s$
and a much larger
$R_e$
than Group II. The effective magnitude is also significantly larger for the second group. The
$M_s/L_\nu$
ratio is quite similar for both groups. We now interpret our results.
Table 7. Number of candidate HSS (C) and non-candidate HSS (NC) having confidences in each of the seven intervals for each of the (a) three groups after the first merge and (b) two groups after the second merge. Here
$(\alpha, \beta]$
denotes the interval with left endpoint
$\alpha$
(not included) and right endpoint
$\beta$
(included). Entries in the table are left blank when there are no members in that group.
Figure 7. Two viewing angles of the scatterplot of the entire dataset after the final merging stage with different colours representing different groups and intensity of the colour signifying the underlying confidence in that particular grouping. Darker shades indicate higher confidence of classification of that particular HSS.
4.3.2. Interpretations
In this section, we understand the physical and evolutionary properties of the objects in each of the two groups after the final merge using stellar mass surface density and absolute magnitude. To analyse the two complex-structured groups at the end of the final merge, we carefully look at the properties of the ellipsoidal groups obtained by tMMBC and group structures obtained with the original eight-group clustering solution and after the two mergers, and obtain deeper insight into the evolutionary and physical properties of these celestial objects.
From Table 2 it is evident that Group 7 is the largest group obtained by tMMBC and also contains the maximum number of GC_VCCs. Table 1 indicates that the HSS in this group have moderate mass and a low effective radius. The surface density is towards the higher side compared to other groups like Group 5 and this group also has a moderate mass-luminosity ratio. Thus intuition dictates that the HSS in this group are bright and newer compared to other groups like Groups 1, 4 and 8. Indeed, the last group, which is mostly composed of GC_VCCs has a higher mass-luminosity ratio and surface density compared to Group 7 indicating that that the HSS in these groups are older compared to that of Group 7 and also brighter. But the HSS in this group are typically smaller compared to those of Group 7 and also heavier which gives some indication as to why the HSS in this group are brighter even though they are older compared to those of Group 7. Group 4 which is composed of only globular clusters (both candidate and non-candidate HSS) have properties similar to those HSS in Group 7. The same can be said about Group 3. This similarity in terms of kinematic properties also indicates this group having a high overlap as seen in Figure 4. Group 1 also exhibits similarity with Group 8 with respect to kinematic properties. The HSS in Group 2 exhibit kinematic properties that are close to that of Group 4 but are somewhat smaller since they have a higher mass-luminosity ratio than that in Group 4. Thus it is very clear that many of the eight tMMBC groups exhibit a good degree of similarity in terms of kinematic properties which satisfies the intuition of many of the groups getting merged to reveal only two complex-structured groups with a low overlap. We now study the kinematic properties of the complex groups obtained at each merging phase.
At the end of the final merge, Group 1 is essentially Group 5 of the tMMBC solution. From Table 5, we see that the HSS in this group have higher mass and effective radius compared to the second group. The mass-luminosity ratio for this group is slightly higher compared to the second group which indicates that the stellar systems in this group have probably lost most of their massive stars and are mostly composed of low-mass stars, further indicating that these HSS are typically older than those in the second group. Since this group is similar to Group 5 from the tMMBC solution, and did not change during the merging phases, we conclude that there is no complex structure present in this group as compared to Group II. The conclusions for this group might be a little uncertain for one stellar object that has a low confidence of classification.
Group II is much larger in size than Group I and as mentioned earlier, contains all the GC_VCCs and GCs, dE,Ns and most of the UCDs, with many of the HSS assignments having low confidence of classification, mainly because this group is formed by merging Groups (ii)-6 and (iii). So, it would be more helpful to analyse this group by separately looking at the properties of Groups (ii)-6 and (iii) to get a better understanding of the properties of this group.
For Group (iii) at the end of the first merging phase, it can be inferred that the GC_VCCs in this group (and also Group (ii)-6) are typically smaller HSS compared to that of Group I (or Group (i)-5). Also the HSS in this group have a higher surface density compared to the other groups formed after the first phase, indicating that these objects are typically brighter compared to objects in the first group. These inferences are a little uncertain for the sixteen HSS with low confidence of classification.
The stellar systems in Group (ii)-6 have slightly higher mass compared to Group (iii). The effective radius is also higher for the HSS in this group which indicates that these stellar systems are larger compared to the objects in Group (iii). The mass-luminosity ratio is significantly low compared to the other two groups formed in the first merging phase,and indicates that these stellar systems are relatively young as compared to other HSS. A marginally low surface density compared to that of Group (iii) indicates that these HSS are not as bright as those in Group (iii) although they are substantially brighter than those in Group (i)-5. These inferences are highly uncertain since a good number of stellar systems in this group have low confidence of classification.
An important aspect of our analysis is how our algorithm is able to capture the actual number of well-separated groups present in this dataset. Previous analyses like those of Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) indicated that there are four spherically dispersed groups but Figures 5, 6, 7 clearly show that the actual number of well-separated groups is two. The additional groups found by Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) (and even tMMBC in our initial stage) is due to the inability of k-means and tMMBC to detect complex group structures. Our algorithm is able to capture this complex structure through an effective merging mechanism in multiple (here, two) phases. Another important aspect is the confidence of classification for each HSS that allows us to assess how well our clustering algorithm performed for this dataset. The fact that most of the HSS have high confidence of classification indicates that our clustering algorithm has been able to reliably capture the complex structure present in the data.
5. Conclusions
Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013) performed statistical cluster analysis on 673 HSS from Misgeld & Hilker (Reference Misgeld and Hilker2011) to determine the homogeneous groups present in the HSS data. Using the k-means clustering algorithm together with the jump statistic (Sugar & James Reference Sugar and James2003), they arrived at five optimal groups whose properties were explored using fundamental plane relations and other physical parameters. Their main analysis excluded the candidate GCs (GC_VCCs), because of concerns that including them would render the data unfit for clustering. Their analysis hinges on an assumption of homogeneous spherically dispersed groups, that underlies the k-means algorithm, and that may not be appropriate and can lead to erroneous results, especially when there is a complex structure present in the underlying statistical groups as found in our analysis. We initially grouped all 13 456 HSS of Misgeld & Hilker (Reference Misgeld and Hilker2011) using tMMBC and BIC to optimally find eight groups. Motivated from a syncytial clustering technique developed by Almodóvar-Rivera & Maitra (Reference Almodóvar-Rivera and Maitra2020), we objectively, in a data-driven manner, merged components of the tMMBC solution which revealed two complex-structured groups. Using a nonparametric bootstrap technique, we further determined the confidence of classification for each of the 13 456 HSS at each stage of merging to quantify how correctly the stellar systems have been assigned to their correct groups. We then studied the physical and evolutionary properties of the objects in each of the two groups by analysing their mean stellar mass, surface density and effective radius. We found that Group I (that is, Group 5 from the original tMMBC solution) typically consists of large and old stellar systems. Group II which is made up by merging Groups 1-4, 6-8 of the original tMMBC solution consists of younger stellar systems which are brighter than those of Group I and also smaller in size compared to those in Group I. All the GC_VCCs were classified to this group along with all the GCs and some other HSS. Our results point to the fact that the GCs are indeed different from elliptical galaxies which includes the dwarf ellipticals (dEs). These results support earlier conclusions (Kormendy Reference Kormendy1985). Our results also confirm that the GC_VCCs are most likely to be GCs and that there is very less chance that these are dwarfs.
A reviewer has asked whether our merging stages can, for instance, result in erasing of correlations between parameters that may have physical meaning, and whether this presents a limitation for our method. We note that correlation only measures linear association (or relationships) and is inadequate for describing other kinds of relationships. The possible reduction or erasure of the correlation between parameters in complex-structured groups formed by merging, is a consequence more of the complex structure of the well-separated groups: note also that relationships (including linear ones) continue to be described, as necessary, at the appropriate sub-group level. Therefore, we do not necessarily consider our methodology to have a limitation here: rather, we feel that it provides a more nuanced understanding of the group structure present in the HSS data. Finally, we note that the goal of clustering is to find different groups of homogeneous observations. How the clustering is done is dependent on the resolution (which is analogous to the merging level) and the properties that we would like our clusters to portray. For instance, if we want ellipsoidally shaped groups, then the eight-component tMMBC solution provides a good description of the HSS. At the same time, we can see which of these groups of HSS are closer (or more similar) to each other, at the different resolution levels, and how they form into more generally shaped groups. Our approach here formally helps determine the groups that combine (i.e., are similar) at each level and provides an objective approch to describe where the groups are distinct enough to require separate consideration and understanding of their properties. As we see in Section 4.3.2, this sort of understanding of the underlying complex group structure can better inform our understanding of the characteristics of the different kinds of HSS.
There are a number of issues that merit further investigation. For example it would be useful to explore if the logarithmic transformation used on the parameters is plausible or is detrimental to the objective of finding groups of HSS. It is possible that some other transformation may lead to better-separated groups. Our analysis may also be extended to larger and more comprehensive data sets than in this study, in order to analyse whether similar results hold for the HSS from other sources. Also with additional information like temperature and colour indices of the stars present in the system, it might be possible to obtain deeper understanding of the evolution of these systems possibly through HR diagrams. Apart from this it would also be interesting to analyse how fundamental plane relations hold in conjunction with these results. Thus we see that while our analysis has provided some interesting insights into the different types of HSS, additional issues remain that deserve further attention.
Acknowledgement
We sincerely thank T. Chattopadhyay for providing us with the dataset of Chattopadhyay & Karmakar (Reference Chattopadhyay and Karmakar2013). We are also very grateful to C. Struck for helpful comments on clarifying and interpreting our results. Our sincere appreciation also to an Associate Editor and an anonymous reviewer whose thorough and insightful comments greatly improved an earlier version of this article.
Appendix 1. Illustration of the pairwise overlap
In this section, we demonstrate the kinds of 3D distributions that may be obtained with specification of different pairwise overlap measures. Using the R (R Core Team 2017) package MixSim (Melnykov et al. Reference Melnykov, Chen and Maitra2012), we simulated 1 000 observations from two-component GMMs with pairwise overlap
$\omega = 10^{-5}, 0.001, 0.01, 0.05, 0.1$, and
$0.5$. The simulated data are displayed in Figure A.1. Each component distribution is also specified by means of its 95% ellipsoid of concentration. The figure shows very good separation with
$\omega=10^{-5}$, and even with
$\omega=0.001$, modest separation for
$\omega=0.01$, substantially poor separation for
$\omega=0.05$, and worsening separation with higher values of
$\omega$.
Figure A.1. Realisations from sample two-component Gaussian mixture distributions having pairwise overlap measures of (a)
$\omega = 0.00001$, (b)
$\omega = 0.001$, (c)
$\omega = 0.01$ (d)
$\omega = 0.05$, (e)
$\omega = 0.1$ and (f)
$\omega = 0.5$. For each component, we also provide the 95% ellipsoid of concentrations.
Open access
