1. Introduction
Fluid–structure interactions appear at many different scales on our planet, and perhaps the largest one is the continental plate tectonics (Plummer, McGeary & Carlson Reference Plummer, Carlson and Hammersley2001). It is believed that this tectonic motion results from the thermal convection in Earth's mantle (Kious & Tilling Reference Kious and Tilling1996), where the mantle materials behave like a fluid (Turcotte & Schubert Reference Turcotte and Schubert2002) that is heated from the core and cooled at the surface of Earth. Under gravity, this configuration of heating and cooling leads to thermal convection, whose circulation provides forcing to the continental plates through shearing. This is considered to be the simplest picture of plate tectonics; however, many details of the plate dynamics, like the periodic formation of supercontinents and the associated geological Wilson cycle (Burke Reference Burke2011), require further investigation.
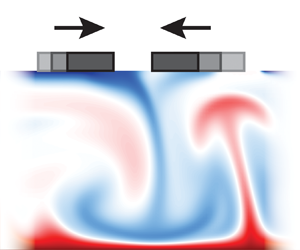
Laboratory experiments have proven to be an effective way of understanding the fluid–structure interaction behind the plate tectonics, with many successful studies that couple the thermally convective fluid to solid structures (Elder Reference Elder1967; Howard, Malkus & Whitehead Reference Howard, Malkus and Whitehead1970; Whitehead Reference Whitehead1972). Aimed at recovering the plate dynamics and understanding the associated fluid–structure interactions, a series of laboratory experiments was later conducted by Zhang & Libchaber (Reference Zhang and Libchaber2000) and Zhong & Zhang (Reference Zhong and Zhang2005, Reference Zhong and Zhang2007a,Reference Zhong and Zhangb). Shown in figure 1(a), this experiment employs water as the working fluid, and a heater beneath provides heating while the ventilation at the water–air interface provides cooling, resulting in Rayleigh–Bénard convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). A floating plate of size ![]() $d$ is carefully placed on top of this convective domain of total length
$d$ is carefully placed on top of this convective domain of total length ![]() $D$. This moving plate with centre location
$D$. This moving plate with centre location ![]() $x_p$ has only fluid force acting on it, unless it hits the wall on the left or the right. Large-scale circulations (Araujo, Grossmann & Lohse Reference Araujo, Grossmann and Lohse2005; Brown & Ahlers Reference Brown and Ahlers2007; Moore & Huang Reference Moore and Huang2023) are observed to form in the convective fluid, as shown in figures 1(a) and 1(c). Depending on the location
$x_p$ has only fluid force acting on it, unless it hits the wall on the left or the right. Large-scale circulations (Araujo, Grossmann & Lohse Reference Araujo, Grossmann and Lohse2005; Brown & Ahlers Reference Brown and Ahlers2007; Moore & Huang Reference Moore and Huang2023) are observed to form in the convective fluid, as shown in figures 1(a) and 1(c). Depending on the location ![]() $x_p$, the plate can be either transported by the circulating fluid, or situated on top of a converging or diverging centre of the surface flow (this is the case shown in figure 1a). Interestingly, different plate motions are observed depending on its size: when the ratio between plate size
$x_p$, the plate can be either transported by the circulating fluid, or situated on top of a converging or diverging centre of the surface flow (this is the case shown in figure 1a). Interestingly, different plate motions are observed depending on its size: when the ratio between plate size ![]() $d$ and tank width
$d$ and tank width ![]() $D$ is smaller than a critical number near
$D$ is smaller than a critical number near ![]() $0.58$, the plate oscillates between the two sidewalls as shown in figure 1(b); When this ratio is above the critical value, the plate is trapped at the centre of tank, as shown in figures 1(b) and 1(c).
$0.58$, the plate oscillates between the two sidewalls as shown in figure 1(b); When this ratio is above the critical value, the plate is trapped at the centre of tank, as shown in figures 1(b) and 1(c).

Figure 1. Rayleigh–Bénard convection coupled to a free-floating plate leads to different dynamics of plate motion. (a) Schematics of the interaction between Rayleigh–Bénard convection and the floating plate. The fluid is heated from below and has an open free surface; the floating plate on this free surface is transported by the fluid force exerted from below. (b) Different states of plate motion. A small plate with ![]() $d/D=0.2$ oscillates between two sidewalls of the convection cell, while a big plate with
$d/D=0.2$ oscillates between two sidewalls of the convection cell, while a big plate with ![]() $d/D = 0.7$ is trapped in the middle of the convection cell. Here,
$d/D = 0.7$ is trapped in the middle of the convection cell. Here, ![]() $L = (D-d)/2$ is the bound of plate centre
$L = (D-d)/2$ is the bound of plate centre ![]() $x_p$. (c) Flow visualization reveals two counter-rotating large-scale circulations when the plate is located at the centre of the convection cell. Image credit: Zhong & Zhang (Reference Zhong and Zhang2007b) and Huang et al. (Reference Huang, Zhong, Zhang and Mertz2018).
$x_p$. (c) Flow visualization reveals two counter-rotating large-scale circulations when the plate is located at the centre of the convection cell. Image credit: Zhong & Zhang (Reference Zhong and Zhang2007b) and Huang et al. (Reference Huang, Zhong, Zhang and Mertz2018).
Zhong, Zhang, and others investigated this transition of behaviours, and they discovered that the so-called thermal blanket effect is responsible here (Zhang & Libchaber Reference Zhang and Libchaber2000; Zhong & Zhang Reference Zhong and Zhang2005, Reference Zhong and Zhang2007a,Reference Zhong and Zhangb; Huang et al. Reference Huang, Zhong, Zhang and Mertz2018; Mao, Zhong & Zhang Reference Mao, Zhong and Zhang2019; Mao Reference Mao2021; Lowenstein Reference Lowenstein2024). In this theory, the floating plate serves as an insulator (like a blanket) on top of the convective fluid, hence the fluid beneath becomes warmer due to the lack of ventilation. The warm fluid then rises, creating a diverging surface flow as shown in figure 1(a) that can transport the plate. The coupling between the fluid and the floating plate therefore goes two ways: the plate modifies the flow temperature and leads to thermal convection; the formed convective flows transport the floating plate. Their interplay leads to non-trivial dynamics of the plate shown in figure 1(b), and the physically inspired Zhong–Zhang model (Zhong & Zhang Reference Zhong and Zhang2005, Reference Zhong and Zhang2007a,Reference Zhong and Zhangb) successfully captures the transition of dynamics. Recently, more careful investigations on the Zhong–Zhang model have lead to new advancements in the stochastic (Huang et al. Reference Huang, Zhong, Zhang and Mertz2018) and dynamical (Lowenstein Reference Lowenstein2024) modelling of fluid–structure interactions.
While the laboratory experiments are conducted in a domain of fluid with finite size, numerical simulations can be conducted in a domain that resembles the mantle of Earth. The numerical work of Gurnis (Reference Gurnis1988) provides one of the first time-dependent simulations of continental drift, where the fluid domain is two-dimensional and periodic. After this, many more numerical works have investigated the details of continental drift (Zhong & Gurnis Reference Zhong and Gurnis1993; Lowman & Jarvis Reference Lowman and Jarvis1993, Reference Lowman and Jarvis1995, Reference Lowman and Jarvis1999; Lowman & Gable Reference Lowman and Gable1999; Zhong et al. Reference Zhong, Zuber, Moresi and Gurnis2000; Lowman, King & Gable Reference Lowman, King and Gable2001), engaging higher resolutions, more detailed modelling of fluid–structure interactions, and three-dimensional simulations of the interior of Earth. In recent years, the mobility of the continental plate has become a focus of numerical study, where persistent motion is observed for larger plates, while small plates tend to move sporadically (Gurnis Reference Gurnis1988; Whitehead & Behn Reference Whitehead and Behn2015; Mao et al. Reference Mao, Zhong and Zhang2019; Mao Reference Mao2021). In these works, the thermal blanket effect is once again recognized as an important factor causing the diverse plate dynamics.
This work is a continuation of an earlier investigation, Huang (Reference Huang2024), where the thermal and mechanical coupling between one floating plate and convective fluid is modelled through a simple stochastic model. This model shows that the covering ratio ![]() $Cr$, defined as the ratio of the plate area to the total surface area, is a direct measure of the thermal blanket effect. A critical covering ratio
$Cr$, defined as the ratio of the plate area to the total surface area, is a direct measure of the thermal blanket effect. A critical covering ratio ![]() $Cr^*$ is identified to distinguish the dynamics of the plate: for a small plate with
$Cr^*$ is identified to distinguish the dynamics of the plate: for a small plate with ![]() $Cr\ll Cr^*$, the plate is passive to the flow field and exhibits little motion; for a plate with
$Cr\ll Cr^*$, the plate is passive to the flow field and exhibits little motion; for a plate with ![]() $Cr \gg Cr^*$, the strong thermal blanket effect leads to persistent plate translation. For plates with
$Cr \gg Cr^*$, the strong thermal blanket effect leads to persistent plate translation. For plates with ![]() $Cr\approx Cr^*$, more complicated transitioning dynamics is observed.
$Cr\approx Cr^*$, more complicated transitioning dynamics is observed.
In this work, we first introduce an efficient two-dimensional spectral solver that can accurately capture the motions and interactions of multiple floating plates on top of Rayleigh–Bénard convection. In a periodic domain shown in figure 2, this solver can handle the Navier–Stokes flows presented in laboratory experiments, with simple modifications available for the geophysical Stokes flows in the mantle. Moreover, multiple floating plates can be simulated as fast as a single-plate problem, as the floating plates are simply treated as an area with different boundary conditions. A specially tailored spectral solver handles the resulting inhomogeneous Robin conditions for both the temperature and the stream function, allowing for efficient time stepping and spectral accuracy. This enables us to systematically introduce one, two and many floating plates, and to show how the thermal blanket effect dictates their interactions with the convective flow beneath and each other. The covering ratio ![]() $Cr$ is once again identified as a key factor affecting the plate dynamics and the stable formation of supercontinents.
$Cr$ is once again identified as a key factor affecting the plate dynamics and the stable formation of supercontinents.

Figure 2. Schematics of the floating plate problem. The fluid domain ![]() $\varOmega$ is heated from the bottom surface
$\varOmega$ is heated from the bottom surface ![]() $\partial \varOmega _0$, and has an open surface on top (
$\partial \varOmega _0$, and has an open surface on top (![]() $\partial \varOmega _1$). Floating plates
$\partial \varOmega _1$). Floating plates ![]() $P_1, P_1, P_2,\dots$ cover part of this open surface, and shield the heat from leaving the fluid.
$P_1, P_1, P_2,\dots$ cover part of this open surface, and shield the heat from leaving the fluid.
This paper is arranged as follows. In § 2, we will mathematically formulate the Rayleigh–Bénard convection and its coupling to the plate motion. In § 3, a numerical scheme and its implementation for solving this free-boundary problem will be introduced. In § 4, numerical simulations of single, double and multiple plate dynamics will be included and discussed. Finally, we will discuss extensions and future works in § 5.
2. Mathematical formulation
2.1. Flow and temperature equations
We consider a dimensionless set of equations by rescaling the length scale by the cell height ![]() $H$, the time scale by the diffusion time
$H$, the time scale by the diffusion time ![]() $H^2/\kappa$ (where
$H^2/\kappa$ (where ![]() $\kappa$ is thermal diffusivity), and temperature by the temperature difference
$\kappa$ is thermal diffusivity), and temperature by the temperature difference ![]() $\Delta T$ between the heater and the free surface. The
$\Delta T$ between the heater and the free surface. The ![]() $x$ direction of the fluid domain is periodic with period
$x$ direction of the fluid domain is periodic with period ![]() $\varGamma = D/H$ (where
$\varGamma = D/H$ (where ![]() $D$ is the domain width), so the overall computational domain is
$D$ is the domain width), so the overall computational domain is ![]() $x\in (0,\varGamma )$,
$x\in (0,\varGamma )$, ![]() $y\in (0,1)$, as shown in figure 2. With the Boussinesq approximation, the resulting partial differential equations (PDEs) for flow speed
$y\in (0,1)$, as shown in figure 2. With the Boussinesq approximation, the resulting partial differential equations (PDEs) for flow speed ![]() ${\boldsymbol {u}} = (u,v)$, pressure
${\boldsymbol {u}} = (u,v)$, pressure ![]() $p$ and temperature
$p$ and temperature ![]() $\theta \in [0,1]$ are
$\theta \in [0,1]$ are
Two dimensionless numbers appear during this non-dimensionalization: the Rayleigh number ![]() $Ra = \alpha g\,\Delta T\,H^3 /\nu \kappa$, and the Prandtl number
$Ra = \alpha g\,\Delta T\,H^3 /\nu \kappa$, and the Prandtl number ![]() $Pr = \nu /\kappa$, with
$Pr = \nu /\kappa$, with ![]() $\nu$,
$\nu$, ![]() $\alpha$ and
$\alpha$ and ![]() $g$ denoting kinematic viscosity, thermal expansion coefficient of the fluid, and the acceleration due to gravity. We have further assumed that the physical properties of the fluid depend on temperature weakly, so
$g$ denoting kinematic viscosity, thermal expansion coefficient of the fluid, and the acceleration due to gravity. We have further assumed that the physical properties of the fluid depend on temperature weakly, so ![]() $Ra$ and
$Ra$ and ![]() $Pr$ do not depend on
$Pr$ do not depend on ![]() $\theta$.
$\theta$.
As our simulation is two-dimensional, it is convenient to write the Navier–Stokes equation in a vorticity and stream function format (Peyret Reference Peyret2002):
Instead of solving directly for ![]() ${\boldsymbol {u}}$ and
${\boldsymbol {u}}$ and ![]() $p$, the
$p$, the ![]() $z$-component of vorticity
$z$-component of vorticity ![]() $\omega = \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {\nabla }\times {\boldsymbol {u}}$ and the stream function defined by
$\omega = \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {\nabla }\times {\boldsymbol {u}}$ and the stream function defined by ![]() ${\boldsymbol {u}} = \boldsymbol {\nabla }_\perp \psi = (\psi _y, -\psi _x)$ are solved first.
${\boldsymbol {u}} = \boldsymbol {\nabla }_\perp \psi = (\psi _y, -\psi _x)$ are solved first.
2.2. Boundary conditions
While (2.4)–(2.6) are standard for modelling Rayleigh–Bénard convection, the boundary conditions become complicated when floating plates are present. Shown in figure 2, the fluid domain ![]() $\varOmega$ is bounded between the bottom heating wall
$\varOmega$ is bounded between the bottom heating wall ![]() $y=0$ (
$y=0$ (![]() $\partial \varOmega _0$) and the top free surface
$\partial \varOmega _0$) and the top free surface ![]() $y=1$ (
$y=1$ (![]() $\partial \varOmega _1$). The segments of top surface covered by the floating plates are labelled as
$\partial \varOmega _1$). The segments of top surface covered by the floating plates are labelled as ![]() $P_1, P_2, \ldots\,$, whose centres are
$P_1, P_2, \ldots\,$, whose centres are ![]() $x_p^{(1)}, x_p^{(2)}, \ldots\,$.
$x_p^{(1)}, x_p^{(2)}, \ldots\,$.
The boundary conditions for the bottom heating wall are set straightforwardly as constant temperature and no-slip:
For the vorticity–stream function format,
The top condition consists of two types of regions: for the free surface (not covered by ![]() $P_i$), the temperature is low and the flow is shear-free; for the region covered by the plate
$P_i$), the temperature is low and the flow is shear-free; for the region covered by the plate ![]() $P_i$, the heat flux is zero and the flow shares the same velocity as the plate. The zero-flux condition originates from the ‘thermal blanket’ effect caused by the low heat conduction of solids. The boundary conditions at
$P_i$, the heat flux is zero and the flow shares the same velocity as the plate. The zero-flux condition originates from the ‘thermal blanket’ effect caused by the low heat conduction of solids. The boundary conditions at ![]() $y = 1$ can be summarized as
$y = 1$ can be summarized as
Here, ![]() $u_p^{(i)} = \dot {x}_p^{(i)}$ is the velocity of
$u_p^{(i)} = \dot {x}_p^{(i)}$ is the velocity of ![]() $i$th plate
$i$th plate ![]() $P_i$. For convenience, we can also write the top boundary conditions in a more compact way:
$P_i$. For convenience, we can also write the top boundary conditions in a more compact way:
 \begin{equation} \begin{cases} (1-a)\theta + a\theta_y = 0,\\ au+(1-a)u_y = g\quad\mbox{at } y = 1,\\ v = 0. \end{cases} \end{equation}
\begin{equation} \begin{cases} (1-a)\theta + a\theta_y = 0,\\ au+(1-a)u_y = g\quad\mbox{at } y = 1,\\ v = 0. \end{cases} \end{equation}For the vorticity–stream function format,
 \begin{equation} \begin{cases} (1-a)\theta + a\theta_y = 0,\\ a\psi_y+(1-a)\psi_{yy} = g\quad \mbox{at } y = 1,\\ \psi = 0. \end{cases} \end{equation}
\begin{equation} \begin{cases} (1-a)\theta + a\theta_y = 0,\\ a\psi_y+(1-a)\psi_{yy} = g\quad \mbox{at } y = 1,\\ \psi = 0. \end{cases} \end{equation}
Here, ![]() $a(x) = \sum _{i}\mathbb{1}_{x\in P_i}$,
$a(x) = \sum _{i}\mathbb{1}_{x\in P_i}$, ![]() $g(x) = \sum _{i}u_p^{(i)}\mathbb{1}_{x\in P_i}$, and
$g(x) = \sum _{i}u_p^{(i)}\mathbb{1}_{x\in P_i}$, and ![]() $\mathbb{1}_{x\in P_i}$ is the characteristic function such that
$\mathbb{1}_{x\in P_i}$ is the characteristic function such that
 \begin{equation} {}\mathbb{1}_{x\in P_i} = \begin{cases} 1 & \mbox{if } x\in P_i,\\ 0 & \mbox{otherwise.} \end{cases} \end{equation}
\begin{equation} {}\mathbb{1}_{x\in P_i} = \begin{cases} 1 & \mbox{if } x\in P_i,\\ 0 & \mbox{otherwise.} \end{cases} \end{equation} On plate ![]() $P_i$, two types of forces drive its motion: the fluid force
$P_i$, two types of forces drive its motion: the fluid force ![]() $f^{(i)}$ due to the shear from convective flows, and the interacting force
$f^{(i)}$ due to the shear from convective flows, and the interacting force ![]() $f_l^{(i)}$ or
$f_l^{(i)}$ or ![]() $f_r^{(i)}$ when the left or right neighbouring plate (
$f_r^{(i)}$ when the left or right neighbouring plate (![]() $P_{i-1}$ or
$P_{i-1}$ or ![]() $P_{i+1}$) makes contact with plate
$P_{i+1}$) makes contact with plate ![]() $P_i$.
$P_i$.
For the fluid force, we simply integrate the fluid shear stress:
The interaction forces ![]() $f_l^{(i)}$ and
$f_l^{(i)}$ and ![]() $f_r^{(i)}$ are modelled as a short-range interaction force to ensure a fully elastic collision between plates. The numerical implementations will be included in § 3.3.
$f_r^{(i)}$ are modelled as a short-range interaction force to ensure a fully elastic collision between plates. The numerical implementations will be included in § 3.3.
Finally, we add all the forces together and evolve the plate location as
 $$\begin{gather}\dot{u}_p^{(i)} = a_p^{(i)} = m^{{-}1}\left[\,f_l^{(i)}+f_r^{(i)}-Pr \int_0^{\varGamma} u_y(x,1,t)\,\mathbb{1}_{x\in P_i}\, {{\rm d}\kern0.7pt x}\right]. \end{gather}$$
$$\begin{gather}\dot{u}_p^{(i)} = a_p^{(i)} = m^{{-}1}\left[\,f_l^{(i)}+f_r^{(i)}-Pr \int_0^{\varGamma} u_y(x,1,t)\,\mathbb{1}_{x\in P_i}\, {{\rm d}\kern0.7pt x}\right]. \end{gather}$$
Here, ![]() $a_p^{(i)}$ is the acceleration of
$a_p^{(i)}$ is the acceleration of ![]() $P_i$, and
$P_i$, and ![]() $m$ is the dimensionless mass of plate.
$m$ is the dimensionless mass of plate.
3. Numerical methods
3.1. Time stepping
We discretize time with the second order Adams–Bashforth backward differentiation method. At time step ![]() $t_n = n\,\Delta T$, (2.4)–(2.6) become
$t_n = n\,\Delta T$, (2.4)–(2.6) become
where
 \begin{gather}\begin{aligned} f_n &= Pr^{{-}1}\left[ 2 ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\boldsymbol{\nabla}}\omega)_{n-1} - ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\boldsymbol{\nabla}}\omega)_{n-2}\right] \nonumber\\ &\quad - (2\, Pr\, \Delta t)^{{-}1} \left(4\omega_{n-1}-\omega_{n-2}\right) -Ra \left( \frac{ \partial{\theta}}{ \partial x } \right)_{n},\end{aligned} \end{gather}
\begin{gather}\begin{aligned} f_n &= Pr^{{-}1}\left[ 2 ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\boldsymbol{\nabla}}\omega)_{n-1} - ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\boldsymbol{\nabla}}\omega)_{n-2}\right] \nonumber\\ &\quad - (2\, Pr\, \Delta t)^{{-}1} \left(4\omega_{n-1}-\omega_{n-2}\right) -Ra \left( \frac{ \partial{\theta}}{ \partial x } \right)_{n},\end{aligned} \end{gather}Equations (3.1)–(3.3) are Helmholtz equations that can be solved by standard numerical methods (Peyret Reference Peyret2002), and this implicit–explicit operator splitting scheme has been used in many numerical studies of thermal convection (Huang & Zhang Reference Huang and Zhang2022; Huang Reference Huang2024). However, modifications have to be made to accommodate the inhomogeneous Robin boundary conditions (2.12). We detail this modified Helmholtz solver in Appendices A–C, and a flow chart of the numerical procedure can be found in Appendix D.
In (3.5) and (3.6), nonlinear terms such as ![]() ${\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \theta$ and
${\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \theta$ and ![]() ${\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \omega$ are computed pseudo-spectrally, with a simple and efficient anti-aliasing filter (Hou & Li Reference Hou and Li2007). With given initial and boundary data, (3.2) can be solved first to obtain
${\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \omega$ are computed pseudo-spectrally, with a simple and efficient anti-aliasing filter (Hou & Li Reference Hou and Li2007). With given initial and boundary data, (3.2) can be solved first to obtain ![]() $\theta _{n}$, which is inserted in
$\theta _{n}$, which is inserted in ![]() $f_{n}$ so (3.1) can be solved next. Finally, (3.3) is solved with the known
$f_{n}$ so (3.1) can be solved next. Finally, (3.3) is solved with the known ![]() $\omega _{n}$. The spatial and temporal resolution of our study is also detailed in Appendix D.
$\omega _{n}$. The spatial and temporal resolution of our study is also detailed in Appendix D.
After solving for the flow and temperature fields, the acceleration ![]() $a_{p,n}^{(i)}$ of plate
$a_{p,n}^{(i)}$ of plate ![]() $P_i$ can be computed via (2.16), and (2.15) and (2.16) are integrated with a second-order Adams–Bashforth method:
$P_i$ can be computed via (2.16), and (2.15) and (2.16) are integrated with a second-order Adams–Bashforth method:
3.2. Smooth boundary conditions
In principle, the introduced fluid and heat solver is able to manage the inhomogeneous Robin boundary condition (2.11) at ![]() $y=1$. However, this boundary condition is not smooth, therefore limiting the accuracy of a numerical method with finite resolution. To overcome this, we aim to construct a smooth characteristic function
$y=1$. However, this boundary condition is not smooth, therefore limiting the accuracy of a numerical method with finite resolution. To overcome this, we aim to construct a smooth characteristic function ![]() $\hat {\mathbb{1}}_{x\in P_i}$ so it is compactly supported and sufficiently smooth.
$\hat {\mathbb{1}}_{x\in P_i}$ so it is compactly supported and sufficiently smooth.
We first construct a smooth step function in one dimension, whose derivative ![]() $\phi _{l,m}(r)$ is in the family of Wendland functions that are shaped like a Gaussian (Chernih, Sloan & Womersley Reference Chernih, Sloan and Womersley2014):
$\phi _{l,m}(r)$ is in the family of Wendland functions that are shaped like a Gaussian (Chernih, Sloan & Womersley Reference Chernih, Sloan and Womersley2014):
 \begin{equation} \phi_{l,m}(r) = \left\{
\begin{array}{ll} \dfrac{1}{\varGamma(m)\,2^{m-1}}
\displaystyle\int\nolimits_r^1
s(1-s)^l(s^2-r^2)^{m-1}\,{\rm d}s & \mbox{for } 0\leqslant
r\leqslant 1, \\ 0 & \mbox{for } r>1. \end{array} \right.
\end{equation}
\begin{equation} \phi_{l,m}(r) = \left\{
\begin{array}{ll} \dfrac{1}{\varGamma(m)\,2^{m-1}}
\displaystyle\int\nolimits_r^1
s(1-s)^l(s^2-r^2)^{m-1}\,{\rm d}s & \mbox{for } 0\leqslant
r\leqslant 1, \\ 0 & \mbox{for } r>1. \end{array} \right.
\end{equation}
The integer ![]() $m$ controls the smoothness of the Wendland function, and
$m$ controls the smoothness of the Wendland function, and ![]() $l = \lfloor {m+n/2}\rfloor + 1$ for spatial dimension
$l = \lfloor {m+n/2}\rfloor + 1$ for spatial dimension ![]() $n$. It can be shown that
$n$. It can be shown that ![]() $\phi _{l,m}\in C^{2m}(\mathbb {R}^+)$, and it is compactly supported. Next, we take
$\phi _{l,m}\in C^{2m}(\mathbb {R}^+)$, and it is compactly supported. Next, we take ![]() $m = 1$,
$m = 1$, ![]() $l = 2$ and construct a smooth step function
$l = 2$ and construct a smooth step function ![]() $W_\epsilon (x)$ that transitions from 0 to 1 on
$W_\epsilon (x)$ that transitions from 0 to 1 on ![]() $[-\epsilon,\epsilon ]$:
$[-\epsilon,\epsilon ]$:
 \begin{equation} W_\epsilon(x) = \frac{\displaystyle\int\nolimits_{-\infty}^x \phi_{2,1}(|s|/\epsilon)\,{\rm d}s}{\displaystyle\int\nolimits_{-\infty}^\infty \phi_{2,1}(|s|/\epsilon)\,{\rm d}s}. \end{equation}
\begin{equation} W_\epsilon(x) = \frac{\displaystyle\int\nolimits_{-\infty}^x \phi_{2,1}(|s|/\epsilon)\,{\rm d}s}{\displaystyle\int\nolimits_{-\infty}^\infty \phi_{2,1}(|s|/\epsilon)\,{\rm d}s}. \end{equation}
This function is plotted in figure 3(a) with various ![]() $\epsilon$, and it is easy to verify that
$\epsilon$, and it is easy to verify that ![]() $W_\epsilon (x) = 0$ when
$W_\epsilon (x) = 0$ when ![]() $x < -\epsilon$, and
$x < -\epsilon$, and ![]() $W_\epsilon (x) = 1$ when
$W_\epsilon (x) = 1$ when ![]() $x>\epsilon$. As the transition length
$x>\epsilon$. As the transition length ![]() $2\epsilon$ becomes smaller,
$2\epsilon$ becomes smaller, ![]() $W_\epsilon$ becomes sharper, approximating a step function. Moreover,
$W_\epsilon$ becomes sharper, approximating a step function. Moreover, ![]() $W_\epsilon \in C^3(\mathbb {R})$ when
$W_\epsilon \in C^3(\mathbb {R})$ when ![]() $\epsilon >0$ due to our choice of
$\epsilon >0$ due to our choice of ![]() $m = 1$, achieving our goal of constructing a smooth step function.
$m = 1$, achieving our goal of constructing a smooth step function.

Figure 3. Smooth step and indicator functions. (a) Smooth step function ![]() $W_\epsilon$ that has transition interval
$W_\epsilon$ that has transition interval ![]() $[-\epsilon,\epsilon ]$. Four values of
$[-\epsilon,\epsilon ]$. Four values of ![]() $\epsilon = 0.01,0.1,0.2,0.4$ are plotted. (b) Smooth indicator function
$\epsilon = 0.01,0.1,0.2,0.4$ are plotted. (b) Smooth indicator function ![]() $\hat {a}$ for locating the region of solid plates. The parameters plotted are
$\hat {a}$ for locating the region of solid plates. The parameters plotted are ![]() $x_p^{(1)} = 1$,
$x_p^{(1)} = 1$, ![]() $x_p^{(2)} = 3$,
$x_p^{(2)} = 3$, ![]() $d = 1$ and
$d = 1$ and ![]() $\epsilon = 0.05$.
$\epsilon = 0.05$.
We can further evaluate ![]() $W_\epsilon (x)$ as
$W_\epsilon (x)$ as
 \begin{equation} W_\epsilon(x)=\begin{cases} 0 & \mbox{if } x<{-}\epsilon,\\ \displaystyle-\frac{3}{4}\left(\frac{x}{\epsilon}\right)^5+\frac{5}{2}\left(\frac{x}{\epsilon}\right)^4 \mbox{sgn}(x)-\frac{5}{2}\left(\frac{x}{\epsilon}\right)^3+\frac{5}{4}\,\frac{x}{\epsilon}+\frac{1}{2} & \mbox{if } x\in[-\epsilon,\epsilon],\\ 1 & \mbox{if } x>\epsilon. \end{cases} \end{equation}
\begin{equation} W_\epsilon(x)=\begin{cases} 0 & \mbox{if } x<{-}\epsilon,\\ \displaystyle-\frac{3}{4}\left(\frac{x}{\epsilon}\right)^5+\frac{5}{2}\left(\frac{x}{\epsilon}\right)^4 \mbox{sgn}(x)-\frac{5}{2}\left(\frac{x}{\epsilon}\right)^3+\frac{5}{4}\,\frac{x}{\epsilon}+\frac{1}{2} & \mbox{if } x\in[-\epsilon,\epsilon],\\ 1 & \mbox{if } x>\epsilon. \end{cases} \end{equation} We next construct a smooth characteristic function ![]() $\hat {\mathbb{1}}_{x\in P}$ for a plate
$\hat {\mathbb{1}}_{x\in P}$ for a plate ![]() $P$ centred at
$P$ centred at ![]() $x_p$ with length
$x_p$ with length ![]() $d$:
$d$:
In our numerical examples, we take ![]() $\epsilon = 0.05d$ to ensure smoothness. Finally, we can write the Robin boundary conditions in the form
$\epsilon = 0.05d$ to ensure smoothness. Finally, we can write the Robin boundary conditions in the form
 \begin{equation} \begin{cases} (1-\hat{a})\theta + \hat{a}\theta_y = 0,\\ \hat{a}u+(1-\hat{a})u_y = \hat{g}\quad\mbox{at } y=1,\\ v = 0, \end{cases} \end{equation}
\begin{equation} \begin{cases} (1-\hat{a})\theta + \hat{a}\theta_y = 0,\\ \hat{a}u+(1-\hat{a})u_y = \hat{g}\quad\mbox{at } y=1,\\ v = 0, \end{cases} \end{equation}where
Noticing that ![]() $W_\epsilon (0) = 0.5$, it can be verified easily that
$W_\epsilon (0) = 0.5$, it can be verified easily that ![]() $\hat {a}(x)\in [0,1]$ as long as
$\hat {a}(x)\in [0,1]$ as long as ![]() $|x_p^{(i)}-x_p^{(j)}|\geqslant d$ for
$|x_p^{(i)}-x_p^{(j)}|\geqslant d$ for ![]() $i\neq j$. The function
$i\neq j$. The function ![]() $\hat {a}(x)$ for two plates centred at
$\hat {a}(x)$ for two plates centred at ![]() $x_p^{(1)} = 1$,
$x_p^{(1)} = 1$, ![]() $x_p^{(2)} = 3$ with plate length
$x_p^{(2)} = 3$ with plate length ![]() $d = 1$ is shown in figure 3(b).
$d = 1$ is shown in figure 3(b).
3.3. Dynamics of the moving plate
There are two types of forcing on each plate. One is the fluid force due to shear stress, and the other is the interaction force when two plates make contact.
For the fluid force, we simply integrate the shear stress by replacing the characteristic function with its smooth version:
As we are using an equally spaced periodic grid in ![]() $x$, the integration can be replaced with a numerical average of all grid values of the integrand, so
$x$, the integration can be replaced with a numerical average of all grid values of the integrand, so ![]() $\int _0^\varGamma f(x)\,{{\rm d}\kern0.7pt x} \approx \varGamma \langle \,f\rangle = (\varGamma /L)\sum _{k=1}^L f_k$, which is spectrally accurate (Trefethen Reference Trefethen2000).
$\int _0^\varGamma f(x)\,{{\rm d}\kern0.7pt x} \approx \varGamma \langle \,f\rangle = (\varGamma /L)\sum _{k=1}^L f_k$, which is spectrally accurate (Trefethen Reference Trefethen2000).
When solid plates make contact, a contact force between them keeps the plates separated. Inspired by the experiments of Zhong & Zhang (Reference Zhong and Zhang2005, Reference Zhong and Zhang2007a,Reference Zhong and Zhangb), we set the collision between neighbouring plates to be fully elastic, which means that their total momentum and kinetic energy are preserved after each collision. Numerically, we approximate the contact force by a function that is both short-ranged and smooth, so the force is zero when the plates are far away, but increases rapidly as they get close.
For plate number ![]() $i$, there are two forces for contact from the left neighbour and from the right neighbour:
$i$, there are two forces for contact from the left neighbour and from the right neighbour:
Here, the parameter ![]() $\delta$ models an ‘interaction length’, and
$\delta$ models an ‘interaction length’, and ![]() $f_{max}$ is the maximum interacting force between two plates. With the typical simulation parameters and no fluid forcing, we have verified that this choice of interacting force indeed conserves total momentum and results in a coefficient of restitution
$f_{max}$ is the maximum interacting force between two plates. With the typical simulation parameters and no fluid forcing, we have verified that this choice of interacting force indeed conserves total momentum and results in a coefficient of restitution ![]() $e > 0.99$. At each simulation,
$e > 0.99$. At each simulation, ![]() $\delta$ and
$\delta$ and ![]() $f_{max}$ are chosen according to the spatial and temporal resolution, so the ordinary differential equation (ODE) and PDE solvers can sufficiently resolve the plate motion and the associated boundary conditions.
$f_{max}$ are chosen according to the spatial and temporal resolution, so the ordinary differential equation (ODE) and PDE solvers can sufficiently resolve the plate motion and the associated boundary conditions.
4. Results
4.1. One-plate dynamics
In this subsection, we review the dynamics of a single plate motion. To simplify our study, the Rayleigh number is fixed at ![]() $Ra = 10^6$, the Prandtl number is
$Ra = 10^6$, the Prandtl number is ![]() $Pr = 7.9$, and the aspect ratio is
$Pr = 7.9$, and the aspect ratio is ![]() $\varGamma = 4$. These parameters are similar to those in a previous numerical study (Huang Reference Huang2024). For the plate, we set the mass as
$\varGamma = 4$. These parameters are similar to those in a previous numerical study (Huang Reference Huang2024). For the plate, we set the mass as ![]() $m = 4d$, so plates with various lengths
$m = 4d$, so plates with various lengths ![]() $d$ have the same density. For the numerical solver, there are
$d$ have the same density. For the numerical solver, there are ![]() $512$ Fourier modes in the
$512$ Fourier modes in the ![]() $x$ direction, and
$x$ direction, and ![]() $129$ Chebyshev nodes in the
$129$ Chebyshev nodes in the ![]() $y$ direction, and the time step size is
$y$ direction, and the time step size is ![]() $\Delta t = 10^{-6}$. These parameters yield accurate, stable and resolved numerical solutions.
$\Delta t = 10^{-6}$. These parameters yield accurate, stable and resolved numerical solutions.
To measure the size of the plate, we define the covering ratio ![]() $Cr = d/\varGamma$. Depending on the size of the plate, or
$Cr = d/\varGamma$. Depending on the size of the plate, or ![]() $Cr$, the dynamics of the plate motion can be very different. Figure 4 and supplementary movie 1 (available at https://doi.org/10.1017/jfm.2024.1231) show the dynamics of a small plate with
$Cr$, the dynamics of the plate motion can be very different. Figure 4 and supplementary movie 1 (available at https://doi.org/10.1017/jfm.2024.1231) show the dynamics of a small plate with ![]() $Cr = 0.1$, and its motion is a continuous random walk shown in figure 4(c). However in figure 5 and supplementary movie 2, a larger plate with
$Cr = 0.1$, and its motion is a continuous random walk shown in figure 4(c). However in figure 5 and supplementary movie 2, a larger plate with ![]() $Cr = 0.6$ shows completely different dynamics: it translates unidirectionally as shown in figure 5(c).
$Cr = 0.6$ shows completely different dynamics: it translates unidirectionally as shown in figure 5(c).

Figure 4. Motion of a small plate (![]() $Cr = 0.1$) is random and bidirectional. (a) A snapshot of flow and temperature fields beneath a plate. The small plate is trapped at a cool converging centre. (b) Vertically averaged temperature
$Cr = 0.1$) is random and bidirectional. (a) A snapshot of flow and temperature fields beneath a plate. The small plate is trapped at a cool converging centre. (b) Vertically averaged temperature ![]() $\bar {\theta }$ and vertical velocity
$\bar {\theta }$ and vertical velocity ![]() $\bar {v}$ at the same moment as in (a). The shaded region indicates the location of the plate. At the converging centre, the averaged temperature is low and the flow moves downwards. (c,d) The displacement
$\bar {v}$ at the same moment as in (a). The shaded region indicates the location of the plate. At the converging centre, the averaged temperature is low and the flow moves downwards. (c,d) The displacement ![]() $x_p$ and velocity
$x_p$ and velocity ![]() $u_p$ of the plate show behaviour of a random walk with jumps.
$u_p$ of the plate show behaviour of a random walk with jumps.

Figure 5. Motion of a large plate (![]() $Cr = 0.6$) is unidirectional. (a,b) Flow and temperature fields beneath the plate. (c,d) The displacement
$Cr = 0.6$) is unidirectional. (a,b) Flow and temperature fields beneath the plate. (c,d) The displacement ![]() $x_p$ and velocity
$x_p$ and velocity ![]() $u_p$ of the moving plate, which shows unidirectional motion with non-zero mean velocity.
$u_p$ of the moving plate, which shows unidirectional motion with non-zero mean velocity.
In Huang (Reference Huang2024), the two dynamics are analysed in detail, and we summarize the key interplay between the plate and the fluid below.
In figure 4, the small plate tends to be attracted by the converging centre of the fluid – the location where the fluid sinks. This converging centre can be seen clearly in figures 4(a) and 4(b), located at the minimum of both the vertically averaged temperature ![]() $\bar {\theta }(x,t) = \int _0^1 \theta (x,y,t)\,{{\rm d}y}$ and the averaged vertical flow speed
$\bar {\theta }(x,t) = \int _0^1 \theta (x,y,t)\,{{\rm d}y}$ and the averaged vertical flow speed ![]() $\bar {v}(x,t) = \int _0^1 v(x,y,t)\,{{\rm d}y}$. This means that the plate velocity
$\bar {v}(x,t) = \int _0^1 v(x,y,t)\,{{\rm d}y}$. This means that the plate velocity ![]() $u_p = \dot {x}_p$ in figure 4(d) matches the translational velocity of the flow converging centre, which has a zero mean but is subject to noise due to random fluid forcing. In this case, the plate motion is passive and completely driven by the flow structure, and the converging centre of the surface flow serves as a stable equilibrium location for the plate.
$u_p = \dot {x}_p$ in figure 4(d) matches the translational velocity of the flow converging centre, which has a zero mean but is subject to noise due to random fluid forcing. In this case, the plate motion is passive and completely driven by the flow structure, and the converging centre of the surface flow serves as a stable equilibrium location for the plate.
For a larger plate with ![]() $Cr = 0.6$, figure 5 and supplementary movie 2 show that the plate motion becomes unidirectional. Increasing plate size clearly changes the flow and temperature distribution in the fluid, as the bulk fluid temperature in figures 5(a,b) is visibly higher than that in figures 4(a,b). This is a clear sign of the thermal blanket effect, as the bigger plate shields the heat from escaping, and the effective cooling area at
$Cr = 0.6$, figure 5 and supplementary movie 2 show that the plate motion becomes unidirectional. Increasing plate size clearly changes the flow and temperature distribution in the fluid, as the bulk fluid temperature in figures 5(a,b) is visibly higher than that in figures 4(a,b). This is a clear sign of the thermal blanket effect, as the bigger plate shields the heat from escaping, and the effective cooling area at ![]() $y=1$ is smaller. In this case, the plate is no longer passive, but creates a thermal blanket that warms the fluid beneath it. Unlike the situation of small plates, a large plate sitting on top of a converging centre cannot be stable in the long term, as eventually the temperature beneath the plate will become high enough to turn this converging centre into a divergent one. Shown in figure 5(b), the average temperature
$y=1$ is smaller. In this case, the plate is no longer passive, but creates a thermal blanket that warms the fluid beneath it. Unlike the situation of small plates, a large plate sitting on top of a converging centre cannot be stable in the long term, as eventually the temperature beneath the plate will become high enough to turn this converging centre into a divergent one. Shown in figure 5(b), the average temperature ![]() $\bar {\theta }$ is indeed higher below the plate, and the plate sits between the converging and diverging centres. This causes the unidirectional motion of the plate, and as the plate keeps affecting the temperature distribution beneath it, the temperature and flow fields move with the plate as shown in supplementary movie 2. The plate displacement
$\bar {\theta }$ is indeed higher below the plate, and the plate sits between the converging and diverging centres. This causes the unidirectional motion of the plate, and as the plate keeps affecting the temperature distribution beneath it, the temperature and flow fields move with the plate as shown in supplementary movie 2. The plate displacement ![]() $x_p$ and velocity
$x_p$ and velocity ![]() $u_p$ are shown in figures 5(c) and 5(d), where
$u_p$ are shown in figures 5(c) and 5(d), where ![]() $u_p$ has a non-zero mean and is subject to random forcing from the fluid.
$u_p$ has a non-zero mean and is subject to random forcing from the fluid.
The motions of plates with various ![]() $Cr$ are shown in figure 6. The displacement in figure 6(a) clearly shows that the small plate has a random motion whose net displacement grows slowly in time. As
$Cr$ are shown in figure 6. The displacement in figure 6(a) clearly shows that the small plate has a random motion whose net displacement grows slowly in time. As ![]() $Cr$ increases, the plate starts to have more persistent unidirectional motions; however, the random fluid forcing can easily reverse the travel direction of the plate, leading to reversals of direction in figure 6(a). Further increasing
$Cr$ increases, the plate starts to have more persistent unidirectional motions; however, the random fluid forcing can easily reverse the travel direction of the plate, leading to reversals of direction in figure 6(a). Further increasing ![]() $Cr$, the unidirectional motion becomes more persistent; however, the velocity (slope of
$Cr$, the unidirectional motion becomes more persistent; however, the velocity (slope of ![]() $x_p$) decreases. Defining the total travel of a plate as
$x_p$) decreases. Defining the total travel of a plate as ![]() $d_p(t) = \int _0^t |u_p(t')|\,{\rm d}t'$, figure 6(b) shows a peak of the plate travelling speed at approximately
$d_p(t) = \int _0^t |u_p(t')|\,{\rm d}t'$, figure 6(b) shows a peak of the plate travelling speed at approximately ![]() $Cr = 0.6$. To further verify this, we define the average plate speed as
$Cr = 0.6$. To further verify this, we define the average plate speed as ![]() $v_p = \lim _{t\to \infty } d_p(t)/t$ in figure 6(c), and a maximum indeed appears at
$v_p = \lim _{t\to \infty } d_p(t)/t$ in figure 6(c), and a maximum indeed appears at ![]() $Cr = 0.6$.
$Cr = 0.6$.

Figure 6. Plate displacement and velocity for different covering ratios ![]() $Cr$. (a) Sample trajectories of the plate location, where small plates are more affected by noise, and large plates have more persistent unidirectional motion. (b) Total travel of the plate reveals its speed; a maximum speed of travel can be seen at approximately
$Cr$. (a) Sample trajectories of the plate location, where small plates are more affected by noise, and large plates have more persistent unidirectional motion. (b) Total travel of the plate reveals its speed; a maximum speed of travel can be seen at approximately ![]() $Cr = 0.6$. (c) Average travel speed has a maximum at
$Cr = 0.6$. (c) Average travel speed has a maximum at ![]() $Cr = 0.56$, and unidirectional motions start to appear for plates larger than
$Cr = 0.56$, and unidirectional motions start to appear for plates larger than ![]() $Cr = 0.33$.
$Cr = 0.33$.
As the thermal blanket effect strengthens, there is an apparent transition of the plate dynamics. Figure 7 shows the time series (lower images) and histogram (upper images) of ![]() $u_p$ at various
$u_p$ at various ![]() $Cr$. For small
$Cr$. For small ![]() $Cr$, the histogram of plate velocity resembles a Gaussian distribution, whose zero mean suggests that the net plate displacement would be small. Increasing
$Cr$, the histogram of plate velocity resembles a Gaussian distribution, whose zero mean suggests that the net plate displacement would be small. Increasing ![]() $Cr$ beyond
$Cr$ beyond ![]() $0.3$, the plate dynamics starts to transition as figure 7(c) shows that the variance of
$0.3$, the plate dynamics starts to transition as figure 7(c) shows that the variance of ![]() $u_p$ increases. At
$u_p$ increases. At ![]() $Cr = 0.4375$ (figure 7d), the two translational states with
$Cr = 0.4375$ (figure 7d), the two translational states with ![]() $u_p = \pm v_p$ emerge, where
$u_p = \pm v_p$ emerge, where ![]() $u_p$ switches between the two directions due to the noise of fluid forcing. At even higher
$u_p$ switches between the two directions due to the noise of fluid forcing. At even higher ![]() $Cr $ (figure 7e), the unidirectional motion is persistent and the reversal becomes rare. The observation here matches the stochastic theory developed in Huang (Reference Huang2024), which consists of a simple model that recovers the mechanical and thermal interplay between the plate and the fluid. This stochastic model predicts that there is only a passive state (no net plate motion) for
$Cr $ (figure 7e), the unidirectional motion is persistent and the reversal becomes rare. The observation here matches the stochastic theory developed in Huang (Reference Huang2024), which consists of a simple model that recovers the mechanical and thermal interplay between the plate and the fluid. This stochastic model predicts that there is only a passive state (no net plate motion) for ![]() $Cr < Cr ^*$, where the critical covering ratio is
$Cr < Cr ^*$, where the critical covering ratio is ![]() $Cr ^* = 1/3$ for
$Cr ^* = 1/3$ for ![]() $\varGamma = 4$, and the translational states can exist only for plates with
$\varGamma = 4$, and the translational states can exist only for plates with ![]() $Cr > Cr ^*$, indeed matching figure 7.
$Cr > Cr ^*$, indeed matching figure 7.

Figure 7. Time series (lower images) and histogram (upper images) of the plate velocity ![]() $u_p$ at various
$u_p$ at various ![]() $Cr $. The plate velocity is normalized by its average travel speed
$Cr $. The plate velocity is normalized by its average travel speed ![]() $v_p$, so
$v_p$, so ![]() $u_p\approx \pm v_p$ suggests a unidirectional translation. (a–e) Covering ratios
$u_p\approx \pm v_p$ suggests a unidirectional translation. (a–e) Covering ratios ![]() $0.0625$,
$0.0625$, ![]() $0.3125$,
$0.3125$, ![]() $0.375$,
$0.375$, ![]() $0.4375$,
$0.4375$, ![]() $0.875$, respectively. The plate motion has a transition from the passive state in (a,b) to the translating state in (d,e), and the translation is also more persistent for large
$0.875$, respectively. The plate motion has a transition from the passive state in (a,b) to the translating state in (d,e), and the translation is also more persistent for large ![]() $Cr $ in (e).
$Cr $ in (e).
Finally, we investigate how the bulk properties of the flow respond to the moving plate. In figure 8, we show the Nusselt number ![]() $Nu = - [\varGamma (t_2-t_1)]^{-1}\int _{t_1}^{t_2} \,{\rm d}t \int _0^\varGamma \theta _y(x,0,t)\,{{\rm d}\kern0.7pt x}$ and the Reynolds number
$Nu = - [\varGamma (t_2-t_1)]^{-1}\int _{t_1}^{t_2} \,{\rm d}t \int _0^\varGamma \theta _y(x,0,t)\,{{\rm d}\kern0.7pt x}$ and the Reynolds number ![]() $Re = (t_2-t_1)^{-1}\int _{t_1}^{t_2} (\max _{(x,y)} |{\boldsymbol {u}}(x,y,t)|)\, {\rm d}t$, where
$Re = (t_2-t_1)^{-1}\int _{t_1}^{t_2} (\max _{(x,y)} |{\boldsymbol {u}}(x,y,t)|)\, {\rm d}t$, where ![]() $t_2-t_1$ is the interval for long-time average. The two groups of measurements are for a plate that is free to move by the flow (free), and for a plate that is fixed at a certain location (immobile). By setting the plate free, the Nusselt number changes slightly in figure 8(a), while the Reynolds number decreases significantly in figure 8(b). We also note that at the critical
$t_2-t_1$ is the interval for long-time average. The two groups of measurements are for a plate that is free to move by the flow (free), and for a plate that is fixed at a certain location (immobile). By setting the plate free, the Nusselt number changes slightly in figure 8(a), while the Reynolds number decreases significantly in figure 8(b). We also note that at the critical ![]() $Cr ^*$, the flow speed reaches a maximum for the immobile plate shown in figure 8(b). Moreover, the Nusselt number approaches its maximum at approximately
$Cr ^*$, the flow speed reaches a maximum for the immobile plate shown in figure 8(b). Moreover, the Nusselt number approaches its maximum at approximately ![]() $Cr = 0.6$, where the plate translates the fastest, as shown in figure 6(c). While we do not have a clear theory to explain the observations in figure 8, we believe that the free plate motion certainly modifies the flow and thermal structure of Rayleigh–Bénard convection. For example, the fluid shearing drives the plate motion, thus part of the fluid kinetic energy must be converted to the plate kinetic energy. This may explain why a significant decrease of
$Cr = 0.6$, where the plate translates the fastest, as shown in figure 6(c). While we do not have a clear theory to explain the observations in figure 8, we believe that the free plate motion certainly modifies the flow and thermal structure of Rayleigh–Bénard convection. For example, the fluid shearing drives the plate motion, thus part of the fluid kinetic energy must be converted to the plate kinetic energy. This may explain why a significant decrease of ![]() $Re$ is shown in figure 8(b).
$Re$ is shown in figure 8(b).

Figure 8. Nusselt and Reynolds numbers for the convecting flow. (a) The Nusselt number is a measure of the vertical heat passing through the flow. (b) The Reynolds number as a measure of flow speed. The free data are for the plate moving freely with the flow, and the immobile data are for the plate that is fixed.
4.2. Two-plate interactions
Adding multiple plates to the convective surface brings interactions between plates and leads to more diverse dynamics. In our numerical simulation, adding a second plate can be achieved easily through the indicator function method outlined in §§ 2 and 3. In the following numerical experiments, we set ![]() $ Ra = 10^6$,
$ Ra = 10^6$, ![]() $Pr = 7.9$,
$Pr = 7.9$, ![]() $\varGamma = 4$,
$\varGamma = 4$, ![]() $m = 4d$, as we did for the single-plate case. We additionally set the maximum interaction force
$m = 4d$, as we did for the single-plate case. We additionally set the maximum interaction force ![]() $f_{max{}} = 10^6$ and an interaction range
$f_{max{}} = 10^6$ and an interaction range ![]() $\delta = \epsilon$ that matches the size of the smoothing region of the indicator function in § 3.2. These two parameters define the force of interaction between the two plates through (3.16) and (3.17), and such interaction conserves both the kinetic energy and momentum of the plates.
$\delta = \epsilon$ that matches the size of the smoothing region of the indicator function in § 3.2. These two parameters define the force of interaction between the two plates through (3.16) and (3.17), and such interaction conserves both the kinetic energy and momentum of the plates.
The dynamics of a pair of small plates (figure 9) and a pair of large plates (figure 10) are quite different. In figure 9 and supplementary movie 3, two small plates with individual covering ratios ![]() $Cr _p = 0.1$ are released on the convective surface. The two plates tend to stay together, generating a ‘supercontinent’ as shown in figure 9(a). Further analysing the flow temperature and surface flow rate in figure 9(b), we see they are in fact attracted by a converging centre of the surface flow, and the surface flow pushes them into each other. The trajectories
$Cr _p = 0.1$ are released on the convective surface. The two plates tend to stay together, generating a ‘supercontinent’ as shown in figure 9(a). Further analysing the flow temperature and surface flow rate in figure 9(b), we see they are in fact attracted by a converging centre of the surface flow, and the surface flow pushes them into each other. The trajectories ![]() $x_p^{(1)}$ and
$x_p^{(1)}$ and ![]() $x_p^{(2)}$ of the plates are shown in figure 9(c), and the normalized plate distance
$x_p^{(2)}$ of the plates are shown in figure 9(c), and the normalized plate distance ![]() $d_{12} = [x_p^{(2)}-x_p^{(1)}]/\varGamma$ is plotted in figure 9(d). We see clearly that the two plates prefer to stay in contact, as the normalized distance stays near
$d_{12} = [x_p^{(2)}-x_p^{(1)}]/\varGamma$ is plotted in figure 9(d). We see clearly that the two plates prefer to stay in contact, as the normalized distance stays near ![]() $Cr _p$ or
$Cr _p$ or ![]() $1-Cr _p$ in figure 9(d).
$1-Cr _p$ in figure 9(d).

Figure 9. Dynamics of two small plates (![]() $Cr {}_p = 0.1$ each) forming a supercontinent of
$Cr {}_p = 0.1$ each) forming a supercontinent of ![]() $Cr = 0.2$. (a) Flow and temperature distribution beneath the supercontinent. The surface flow is converging, and the formation of the supercontinent is stable. (b) Vertically averaged temperature
$Cr = 0.2$. (a) Flow and temperature distribution beneath the supercontinent. The surface flow is converging, and the formation of the supercontinent is stable. (b) Vertically averaged temperature ![]() $\bar {\theta }$ and vertical velocity
$\bar {\theta }$ and vertical velocity ![]() $\bar {v}$ at the same moment as in (a), with the region of the two plates shaded. (c) The displacement of plates
$\bar {v}$ at the same moment as in (a), with the region of the two plates shaded. (c) The displacement of plates ![]() $x_p^{(1)}$ and
$x_p^{(1)}$ and ![]() $x_p^{(2)}$. (d) The normalized plate distance
$x_p^{(2)}$. (d) The normalized plate distance ![]() $d_{12} = [x_p^{(2)}-x_p^{(1)}]/\varGamma$ indicates that the two plates tend to stay in contact. The white region (plates separated) and grey region (plates in contact) are separated by
$d_{12} = [x_p^{(2)}-x_p^{(1)}]/\varGamma$ indicates that the two plates tend to stay in contact. The white region (plates separated) and grey region (plates in contact) are separated by ![]() $Cr _p$ and
$Cr _p$ and ![]() $1-Cr _p$.
$1-Cr _p$.

Figure 10. Two large plates (![]() $Cr {}_p = 0.3$ each) cannot form a stable supercontinent of
$Cr {}_p = 0.3$ each) cannot form a stable supercontinent of ![]() $Cr =2\,Cr {}_p = 0.6$. (a) The warm upwelling fluid creates a diverging surface flow beneath the plates. This diverging surface flow pulls the two plates apart, rendering the supercontinent formation unstable. (b) Vertically averaged temperature and vertical velocity of the fluid beneath the plates shown in (a). (c) Plate displacements
$Cr =2\,Cr {}_p = 0.6$. (a) The warm upwelling fluid creates a diverging surface flow beneath the plates. This diverging surface flow pulls the two plates apart, rendering the supercontinent formation unstable. (b) Vertically averaged temperature and vertical velocity of the fluid beneath the plates shown in (a). (c) Plate displacements ![]() $x_p^{(1)}$ and
$x_p^{(1)}$ and ![]() $x_p^{(2)}$. (d) The normalized plate distance
$x_p^{(2)}$. (d) The normalized plate distance ![]() $d_{12}$ stays in the white region where the two plates are separated.
$d_{12}$ stays in the white region where the two plates are separated.
The combined covering ratio of these two plates is ![]() $Cr = 2\,Cr _p = 0.2$, which is less than the critical covering ratio
$Cr = 2\,Cr _p = 0.2$, which is less than the critical covering ratio ![]() $Cr ^* = 1/3$ that we identified earlier. Therefore, the thermal blanket effect generated by this supercontinent is not strong enough to heat up the fluid beneath, and the surface flow stays converging and pushing the two plates together. Thus a supercontinent with combined
$Cr ^* = 1/3$ that we identified earlier. Therefore, the thermal blanket effect generated by this supercontinent is not strong enough to heat up the fluid beneath, and the surface flow stays converging and pushing the two plates together. Thus a supercontinent with combined ![]() $Cr < Cr ^*$ is stable in its formation and exhibits a passive motion.
$Cr < Cr ^*$ is stable in its formation and exhibits a passive motion.
Figure 10 and supplementary movie 4 show the dynamics of two plates with ![]() $Cr = 2\,Cr _p = 0.6$. In this case, the fluid beneath the supercontinent is warmed up due to the thermal blanket effect, and generates an upwelling flow. The resulting diverging surface flow separates the two plates, leading to an unstable supercontinent formation. Figures 10(c) and 10(d) show the plate trajectories and the normalized plate distance, and the two plates are seen to stay separated in figure 10(d) as their normalized distance is between
$Cr = 2\,Cr _p = 0.6$. In this case, the fluid beneath the supercontinent is warmed up due to the thermal blanket effect, and generates an upwelling flow. The resulting diverging surface flow separates the two plates, leading to an unstable supercontinent formation. Figures 10(c) and 10(d) show the plate trajectories and the normalized plate distance, and the two plates are seen to stay separated in figure 10(d) as their normalized distance is between ![]() $Cr _p$ and
$Cr _p$ and ![]() $1-Cr _p$, and the contact state is only transient.
$1-Cr _p$, and the contact state is only transient.
In figure 10, although the covering ratio for each plate satisfies ![]() $Cr _p < Cr ^*$, their combined ratio is
$Cr _p < Cr ^*$, their combined ratio is ![]() $Cr = 2\,Cr _p>Cr ^*$. The supercontinent, once formed, will become unstable as the warm fluid beneath creates a diverging surface flow that pulls the two plates apart.
$Cr = 2\,Cr _p>Cr ^*$. The supercontinent, once formed, will become unstable as the warm fluid beneath creates a diverging surface flow that pulls the two plates apart.
Figure 11 shows how the plate dynamics depends on the combined ![]() $Cr $. In figure 11(a), we define a normalized contact time
$Cr $. In figure 11(a), we define a normalized contact time ![]() $\tau = t_{c}/T$, where
$\tau = t_{c}/T$, where ![]() $t_c$ is the amount of time that the two plates are in contact, and
$t_c$ is the amount of time that the two plates are in contact, and ![]() $T$ is the total simulation time. A sharp decrease of
$T$ is the total simulation time. A sharp decrease of ![]() $\tau$ is seen near
$\tau$ is seen near ![]() $Cr ^* = 1/3$, beyond which a persistent formation of supercontinent is unlikely. This is consistent with our analysis earlier, as a supercontinent with
$Cr ^* = 1/3$, beyond which a persistent formation of supercontinent is unlikely. This is consistent with our analysis earlier, as a supercontinent with ![]() $Cr > Cr ^*$ would induce warm upwelling flows that disintegrate the supercontinent. The centre of mass velocity of plates also picks up when
$Cr > Cr ^*$ would induce warm upwelling flows that disintegrate the supercontinent. The centre of mass velocity of plates also picks up when ![]() $Cr > Cr ^*$ (figure 11b), suggesting that the two large plates are no longer passive but instead translate as we have seen in figure 6(c).
$Cr > Cr ^*$ (figure 11b), suggesting that the two large plates are no longer passive but instead translate as we have seen in figure 6(c).

Figure 11. Contact and motion of the plates depend on the covering ratio. (a) The normalized contact time ![]() $\tau$ decreases sharply when
$\tau$ decreases sharply when ![]() $Cr $ increases above
$Cr $ increases above ![]() $Cr ^* = 1/3$. (b) The plate centre of mass velocity
$Cr ^* = 1/3$. (b) The plate centre of mass velocity ![]() $v_{com}$ increases when
$v_{com}$ increases when ![]() $Cr >Cr ^*$, indicating that the plates are no longer passive to the flow.
$Cr >Cr ^*$, indicating that the plates are no longer passive to the flow.
We now see the role of ![]() $Cr ^*$ in the formation of supercontinents: it is possible to have a stable supercontinent only if its
$Cr ^*$ in the formation of supercontinents: it is possible to have a stable supercontinent only if its ![]() $Cr $ is less than
$Cr $ is less than ![]() $Cr ^*$.
$Cr ^*$.
4.3. Multiple plates
Further increasing the number of plates, the formation of supercontinents exhibits complex and intriguing dynamics. In figure 12 and supplementary movie 5, eight plates with ![]() $Cr _p = 0.057$ (total
$Cr _p = 0.057$ (total ![]() $Cr = 0.457$) are released on top of the convective fluid, where
$Cr = 0.457$) are released on top of the convective fluid, where ![]() $ Ra = 10^6$,
$ Ra = 10^6$, ![]() $ Pr = 7.9$,
$ Pr = 7.9$, ![]() $\varGamma = 4$,
$\varGamma = 4$, ![]() $m = 4d$. The plate maximum interaction force
$m = 4d$. The plate maximum interaction force ![]() $f_{max{}} = 10^6$ and interaction range
$f_{max{}} = 10^6$ and interaction range ![]() $\delta = \epsilon$ are the same as before.
$\delta = \epsilon$ are the same as before.

Figure 12. Dynamics of eight plates (![]() $Cr {}_p = 0.057$,
$Cr {}_p = 0.057$, ![]() $Cr = 8\,Cr {}_p = 0.457$) floating on top of the convecting fluid. (a) A snapshot of eight plates and the convective fluid beneath, where the centre locations of the plates are
$Cr = 8\,Cr {}_p = 0.457$) floating on top of the convecting fluid. (a) A snapshot of eight plates and the convective fluid beneath, where the centre locations of the plates are ![]() $(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$. (b) Trajectories of
$(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$. (b) Trajectories of ![]() $(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$; plates can be seen forming supercontinents over time. (c) Zoomed-in view of the trajectories in (b) in the time window
$(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$; plates can be seen forming supercontinents over time. (c) Zoomed-in view of the trajectories in (b) in the time window ![]() $t\in (3.5, 3.6)$.
$t\in (3.5, 3.6)$.
Figure 12(a) shows a moment when the eight plates form two supercontinents, with each supercontinent covering ![]() $4\,Cr _p = 0.23$ of the free surface. Each supercontinent thus has a covering ratio less than
$4\,Cr _p = 0.23$ of the free surface. Each supercontinent thus has a covering ratio less than ![]() $Cr ^* = 1/3$, and is thereby stable by our earlier argument. Indeed, the stable formation of a supercontinent of four plates can be seen on the plate trajectory
$Cr ^* = 1/3$, and is thereby stable by our earlier argument. Indeed, the stable formation of a supercontinent of four plates can be seen on the plate trajectory ![]() $(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$ shown in figure 12(b), whose zoomed-in view for
$(x_p^{(1)},x_p^{(2)},\ldots, x_p^{(8)})$ shown in figure 12(b), whose zoomed-in view for ![]() $t\in (3.5, 3.6)$ is shown in figure 12(c). Of course, the formation of a supercontinent with a different number of plates is possible, and our theory predicts that they are stable if the number of plates is
$t\in (3.5, 3.6)$ is shown in figure 12(c). Of course, the formation of a supercontinent with a different number of plates is possible, and our theory predicts that they are stable if the number of plates is ![]() $I<Cr ^*/Cr _p \approx 6$.
$I<Cr ^*/Cr _p \approx 6$.
To further analyse the formation of supercontinents, we define the formation number ![]() $I(t)$ as the number of plates forming the largest supercontinent at any given time
$I(t)$ as the number of plates forming the largest supercontinent at any given time ![]() $t$. A schematic of such a formation number is shown in figure 13(a), where five continents are formed and the largest supercontinent has
$t$. A schematic of such a formation number is shown in figure 13(a), where five continents are formed and the largest supercontinent has ![]() $I = 4$. The formation number can be tracked over time, and figure 13(b) shows the formation number of the simulation presented in figure 12, with the zoomed-in view of
$I = 4$. The formation number can be tracked over time, and figure 13(b) shows the formation number of the simulation presented in figure 12, with the zoomed-in view of ![]() $I(t)$ in the window of figure 12(c) shown in figure 13(c). We note that the formation number can actually take on all integer values between 1 and 8, although many of the formation numbers are transient (such as
$I(t)$ in the window of figure 12(c) shown in figure 13(c). We note that the formation number can actually take on all integer values between 1 and 8, although many of the formation numbers are transient (such as ![]() $I = 1$ and
$I = 1$ and ![]() $I = 8$). The most common and persistent formation number that we can see visually in figure 13(c) is
$I = 8$). The most common and persistent formation number that we can see visually in figure 13(c) is ![]() $I = 4$, and this is confirmed in the histogram of
$I = 4$, and this is confirmed in the histogram of ![]() $I(t)$ shown in figure 13(d).
$I(t)$ shown in figure 13(d).

Figure 13. Statistics of the formation number ![]() $I(t)$ that is the maximum number of plates in a supercontinent at time
$I(t)$ that is the maximum number of plates in a supercontinent at time ![]() $t$. (a) Schematic of
$t$. (a) Schematic of ![]() $I=4$. (b) Time series of
$I=4$. (b) Time series of ![]() $I(t)$ shows the possibility of forming supercontinents with various sizes. (c) Zoomed-in view of
$I(t)$ shows the possibility of forming supercontinents with various sizes. (c) Zoomed-in view of ![]() $I(t)$ in (b) for
$I(t)$ in (b) for ![]() $t\in (3.5, 3.6)$. (d) Histogram of
$t\in (3.5, 3.6)$. (d) Histogram of ![]() $I(t)$ indicates that
$I(t)$ indicates that ![]() $I=4$ is the most common supercontinent formation, while small and large supercontinents are unlikely to form. The histogram is plotted against the size of supercontinent
$I=4$ is the most common supercontinent formation, while small and large supercontinents are unlikely to form. The histogram is plotted against the size of supercontinent ![]() $Cr = I\,Cr _p$, and the formation number
$Cr = I\,Cr _p$, and the formation number ![]() $I$ is labelled on top of each bin.
$I$ is labelled on top of each bin.
In figure 13(d), each bin corresponds to the total number of appearances of supercontinents with size ![]() $I$ (shown on top of each bin), and the horizontal axis shows the corresponding covering ratio. We indeed see that
$I$ (shown on top of each bin), and the horizontal axis shows the corresponding covering ratio. We indeed see that ![]() $I = 4$ plates is the most frequent size of a supercontinent. For small supercontinents, they tend to merge and form a larger but stable supercontinent. For a large supercontinent, the random fluid forcing can trigger a disintegration and break it into many smaller ones. Especially for
$I = 4$ plates is the most frequent size of a supercontinent. For small supercontinents, they tend to merge and form a larger but stable supercontinent. For a large supercontinent, the random fluid forcing can trigger a disintegration and break it into many smaller ones. Especially for ![]() $I\geqslant 6$, our theory predicts that such formations are not stable, hence supercontinents with
$I\geqslant 6$, our theory predicts that such formations are not stable, hence supercontinents with ![]() $I\geqslant 6$ are rarely formed and (once formed) are unstable.
$I\geqslant 6$ are rarely formed and (once formed) are unstable.
The results shown in figures 12 and 13 are common for simulations with different numbers (![]() $N_p$) and sizes (
$N_p$) and sizes (![]() $Cr _p$) of plates. And we identify
$Cr _p$) of plates. And we identify ![]() $I\,Cr _p < Cr ^*$ as a clue for predicting the supercontinental size
$I\,Cr _p < Cr ^*$ as a clue for predicting the supercontinental size ![]() $I$.
$I$.
4.4. Convection with increased Ra and  $\varGamma$
$\varGamma$
In this subsection, we show examples with Rayleigh number ![]() $ Ra {} = 10^7$, Prandtl number
$ Ra {} = 10^7$, Prandtl number ![]() $ Pr {} = 7.9$, and domain aspect ratio
$ Pr {} = 7.9$, and domain aspect ratio ![]() $\varGamma = 10$. Although these parameters deviate from previous laboratory and numerical investigations, they are actually closer to the conditions of mantle convection (Whitehead & Behn Reference Whitehead and Behn2015).
$\varGamma = 10$. Although these parameters deviate from previous laboratory and numerical investigations, they are actually closer to the conditions of mantle convection (Whitehead & Behn Reference Whitehead and Behn2015).
We first investigate the single-plate dynamics in figure 14, where the typical flow and temperature fields are shown in figure 14(a). Much like the observations made in figures 4–6, figures 14(b) and 14(c) show that small plates have little motion and are passive to the flow structure, while large plates translate unidirectionally. Typical simulations for a small plate with ![]() $Cr {} = 0.125$ and a large plate with
$Cr {} = 0.125$ and a large plate with ![]() $Cr {} = 0.417$ are included as supplementary movies 6 and 7.
$Cr {} = 0.417$ are included as supplementary movies 6 and 7.

Figure 14. Single-plate dynamics for large aspect ratio convection, where ![]() $\varGamma = 10$,
$\varGamma = 10$, ![]() $ Ra {} = 10^7$ and
$ Ra {} = 10^7$ and ![]() $ Pr {} = 7.9$. (a) Typical convective flow field for a plate with covering ratio 0.2. (b) Trajectories of the plate location
$ Pr {} = 7.9$. (a) Typical convective flow field for a plate with covering ratio 0.2. (b) Trajectories of the plate location ![]() $x_p$, where small plates move passively but large plates translate unidirectionally. (c) Total travel of the plate
$x_p$, where small plates move passively but large plates translate unidirectionally. (c) Total travel of the plate ![]() $d_p$ shows the same trend as in (b). (d) Average travel speed
$d_p$ shows the same trend as in (b). (d) Average travel speed ![]() $v_p$ has a sharp increase near
$v_p$ has a sharp increase near ![]() $Cr ^* = 0.18$, which is the critical covering ratio for
$Cr ^* = 0.18$, which is the critical covering ratio for ![]() $\varGamma = 10$. Additional simulations of small and large plates can be found in supplementary movies 6 and 7.
$\varGamma = 10$. Additional simulations of small and large plates can be found in supplementary movies 6 and 7.
In figure 14(d), the plate velocity ![]() $v_p$ is significantly higher than in figure 6(c), where
$v_p$ is significantly higher than in figure 6(c), where ![]() $ Ra {} = 10^6$. This is consistent with the model introduced in Huang (Reference Huang2024), which suggests that the equilibrium plate velocity is proportional to the surface flow rate. From the classic scaling
$ Ra {} = 10^6$. This is consistent with the model introduced in Huang (Reference Huang2024), which suggests that the equilibrium plate velocity is proportional to the surface flow rate. From the classic scaling ![]() $Re\sim Ra {}^{0.5}$ of Rayleigh–Bénard convection (Huang & Zhang Reference Huang and Zhang2022), we infer that the flow rate for
$Re\sim Ra {}^{0.5}$ of Rayleigh–Bénard convection (Huang & Zhang Reference Huang and Zhang2022), we infer that the flow rate for ![]() $ Ra {} = 10^7$ should be
$ Ra {} = 10^7$ should be ![]() $\sqrt {10}$ times bigger than that of
$\sqrt {10}$ times bigger than that of ![]() $ Ra {} = 10^6$. The plate velocity in figure 14(d) is indeed approximately 3–5 times higher than the velocity shown in figure 6(c), which is consistent with our estimation. Therefore, the
$ Ra {} = 10^6$. The plate velocity in figure 14(d) is indeed approximately 3–5 times higher than the velocity shown in figure 6(c), which is consistent with our estimation. Therefore, the ![]() $ Ra {}$ value of the convecting fluid directly affects the plate speed, and we note that higher
$ Ra {}$ value of the convecting fluid directly affects the plate speed, and we note that higher ![]() $ Ra {}$ also introduces finer flow structures shown in figure 14(a) that can potentially modify the strength and distribution of the stochastic fluid forcing.
$ Ra {}$ also introduces finer flow structures shown in figure 14(a) that can potentially modify the strength and distribution of the stochastic fluid forcing.
Another difference between figures 14(d) and 6(c) is the critical covering ratio ![]() $Cr {}^*$ differentiating the passive and translating states of the plate. In figure 14(d), a significant increase in
$Cr {}^*$ differentiating the passive and translating states of the plate. In figure 14(d), a significant increase in ![]() $v_p$ appears at approximately
$v_p$ appears at approximately ![]() $Cr {}^* = 0.18$, which is smaller than
$Cr {}^* = 0.18$, which is smaller than ![]() $Cr {}^* = 0.33$ in figure 6(c), where
$Cr {}^* = 0.33$ in figure 6(c), where ![]() $\varGamma = 4$. In Huang (Reference Huang2024), the critical covering ratio
$\varGamma = 4$. In Huang (Reference Huang2024), the critical covering ratio ![]() $Cr ^*$ is shown to depend on the aspect ratio as
$Cr ^*$ is shown to depend on the aspect ratio as ![]() $Cr ^*(\varGamma )\sim \varGamma ^{-2/3}$. So
$Cr ^*(\varGamma )\sim \varGamma ^{-2/3}$. So ![]() $Cr {}^*(10) = Cr {}^*(4)\,(10/4)^{-2/3} = 0.18$, consistent with the data shown in figure 14(d). Therefore the critical covering ratio
$Cr {}^*(10) = Cr {}^*(4)\,(10/4)^{-2/3} = 0.18$, consistent with the data shown in figure 14(d). Therefore the critical covering ratio ![]() $Cr ^*$ decreases with increasing
$Cr ^*$ decreases with increasing ![]() $\varGamma$, while the associated plate length
$\varGamma$, while the associated plate length ![]() $d^* = \varGamma \,Cr ^* \sim \varGamma ^{1/3}$ increases weakly with
$d^* = \varGamma \,Cr ^* \sim \varGamma ^{1/3}$ increases weakly with ![]() $\varGamma$.
$\varGamma$.
We finally look at the formation of supercontinents at high ![]() $ Ra {}$ and
$ Ra {}$ and ![]() $\varGamma$. Figure 15(a) shows a typical moment of supercontinent formation, where continents formed by 6, 3, 2 and 5 plates can been seen. In figure 15, each plate has a covering ratio
$\varGamma$. Figure 15(a) shows a typical moment of supercontinent formation, where continents formed by 6, 3, 2 and 5 plates can been seen. In figure 15, each plate has a covering ratio ![]() $Cr _p = 0.0234$, and supplementary movie 8 shows this simulation.
$Cr _p = 0.0234$, and supplementary movie 8 shows this simulation.

Figure 15. Multiple plate dynamics for large aspect ratio convection. There are 16 plates with individual covering ratio ![]() $Cr _p = 0.0234$. The convection parameters are
$Cr _p = 0.0234$. The convection parameters are ![]() $\varGamma = 10$,
$\varGamma = 10$, ![]() $ Ra {} = 10^7$ and
$ Ra {} = 10^7$ and ![]() $ Pr {} = 7.9$. (a) Typical convective flow field below the 16 moving plates; small groups of supercontinents can be seen. (b) Formation number
$ Pr {} = 7.9$. (a) Typical convective flow field below the 16 moving plates; small groups of supercontinents can be seen. (b) Formation number ![]() $I(t)$ indicating the size of the largest supercontinent at time
$I(t)$ indicating the size of the largest supercontinent at time ![]() $t$. (c) Histogram of the formation number
$t$. (c) Histogram of the formation number ![]() $I$, showing that
$I$, showing that ![]() $I = 6$ is the most probable formation of supercontinents, and that the formation of supercontinents with covering ratio above critical is rare. Supplementary movie 8 is associated with this simulation.
$I = 6$ is the most probable formation of supercontinents, and that the formation of supercontinents with covering ratio above critical is rare. Supplementary movie 8 is associated with this simulation.
In figure 15(a), we can see that the largest supercontinent formation still sits on a converging centre of surface flow, thus making such a formation stable. As we have done in the previous subsection, we define the formation number ![]() $I$ as the size of the largest supercontinent at a given time, so
$I$ as the size of the largest supercontinent at a given time, so ![]() $I = 6$ for the moment shown in figure 15(a). The time series of this formation number is shown in figure 15(b), where a formation size of approximately 5–6 plates is common, but both the large and small formations are rare. The histogram of
$I = 6$ for the moment shown in figure 15(a). The time series of this formation number is shown in figure 15(b), where a formation size of approximately 5–6 plates is common, but both the large and small formations are rare. The histogram of ![]() $I(t)$ in figure 15(c) also shows that the most probable supercontinent formation has
$I(t)$ in figure 15(c) also shows that the most probable supercontinent formation has ![]() $I = 6$, whose total covering ratio
$I = 6$, whose total covering ratio ![]() $Cr {} = I\,Cr {}_p = 0.14$ is smaller than the critical covering ratio
$Cr {} = I\,Cr {}_p = 0.14$ is smaller than the critical covering ratio ![]() $Cr {}^* = 0.18$ that we identified earlier. In fact, figure 15(c) shows that the formation of
$Cr {}^* = 0.18$ that we identified earlier. In fact, figure 15(c) shows that the formation of ![]() $I = 7$ is not rare either, and this is consistent with our estimation that the largest stable supercontinent can have a size up to
$I = 7$ is not rare either, and this is consistent with our estimation that the largest stable supercontinent can have a size up to ![]() $Cr {}^*/Cr {}_p = 7.7$.
$Cr {}^*/Cr {}_p = 7.7$.
In the discussions above, we see once again that the condition ![]() $I\,Cr {}_p < Cr {}^*$ can serve as an indicator of stable supercontinent formation.
$I\,Cr {}_p < Cr {}^*$ can serve as an indicator of stable supercontinent formation.
5. Discussion
Through our numerical investigations, we clearly see the covering ratio as the main factor affecting the thermal blanket effect, which determines the plate dynamics. This is especially apparent during the formation of supercontinents – the continent covering ratio cannot exceed ![]() $Cr ^*$, as the strong thermal blanket effect will induce a diverging surface flow that pulls the formed supercontinent apart.
$Cr ^*$, as the strong thermal blanket effect will induce a diverging surface flow that pulls the formed supercontinent apart.
As our current study is inspired by laboratory experiments, we certainly look forward to future experimental investigations of the interaction between multiple plates. Besides the geometry presented in figures 1 and 2, the broader investigation of fluid–structure interactions in thermal convection also includes adding fixed obstacles to the convective domain (Bao et al. Reference Bao, Chen, Liu, She, Zhang and Zhou2015; Li, Chen & Xi Reference Li, Chen and Xi2024), modifying the convective boundary conditions (Zhang et al. Reference Zhang, Xia, Zhou and Chen2020; Huang & Zhang Reference Huang and Zhang2022), and allowing for moving boundaries that are driven by the fluid forcing (Mercier et al. Reference Mercier, Ardekani, Allshouse, Doyle and Peacock2014; Wang & Zhang Reference Wang and Zhang2023) or phase change (Huang, Shelley & Stein Reference Huang, Shelley and Stein2021; Huang & Moore Reference Huang and Moore2022; Weady et al. Reference Weady, Tong, Zidovska and Ristroph2022). Many of these works are certainly geophysically inspired, addressing long-standing mysteries such as the super rotation of Earth's inner core (Wang & Zhang Reference Wang and Zhang2023; Yang & Song Reference Yang and Song2023).
In order to simulate the geophysical plate tectonics more closely, there are several future directions to improve our model. The first is to investigate the plate tectonics in a three-dimensional geometry, including the mantle-like spherical shell and the rectangular cuboidal fluid domain that is periodic in two horizontal directions. Although our current numerical scheme is two-dimensional, it can be extended easily to a higher dimension: for the spherical shell geometry, we can adopt a Fourier–Chebyshev–Chebyshev method that solves the heat and flow equations in spherical coordinates; for the periodic cuboidal domain, another periodic horizontal direction can be accommodated by the Fourier method. We are currently working on the three-dimensional study of plate tectonics, and we note that pioneer works including Lowman & Gable (Reference Lowman and Gable1999), Mao et al. (Reference Mao, Zhong and Zhang2019) and Mao (Reference Mao2021) have investigated the fluid–structure interactions and plate interactions in these settings. They also used the geophysical parameters of the mantle, most notably Prandtl number approximately ![]() $10^{23}$ (Meyers et al. Reference Meyers1987). One modification to accommodate this high Prandtl number is to take an asymptotic limit
$10^{23}$ (Meyers et al. Reference Meyers1987). One modification to accommodate this high Prandtl number is to take an asymptotic limit ![]() $ Pr \to \infty$, so the Navier–Stokes equation (2.1) becomes a time-independent Stokes equation (Mao Reference Mao2021). This Stokes equation can be handled easily by the numerical method in § 3; however, we choose to keep the fluid inertia so our results can be validated by future laboratory experiments, where the working fluid (water) has
$ Pr \to \infty$, so the Navier–Stokes equation (2.1) becomes a time-independent Stokes equation (Mao Reference Mao2021). This Stokes equation can be handled easily by the numerical method in § 3; however, we choose to keep the fluid inertia so our results can be validated by future laboratory experiments, where the working fluid (water) has ![]() $ Pr = 1\unicode{x2013}10$.
$ Pr = 1\unicode{x2013}10$.
In our study, we have also set the bottom boundary condition to be no-slip, which is consistent with the experiments. However, this is different from past geophysical models of the mantle, where the bottom boundary is typically assumed to be stress-free at the liquid–liquid interface between the mantle and the outer core of Earth. In the future, we plan to adopt the stress-free bottom condition as it is more consistent with the geophysical settings. Descending deeper into Earth, the outer core meets the solid inner core that is known to rotate. Together with the recent discovery that this rotation is not unidirectional (Yang & Song Reference Yang and Song2023), a fluid–structure interaction problem thus arises: Does the outer-core convection provide enough shear stress to rotate the inner core? This possibility has inspired some recent experimental developments (Wang & Zhang Reference Wang and Zhang2023), and we wish to further engage with this fluid–structure interaction problem in the future.
The interaction between continental plates is also more complicated in geophysical plate tectonics, as the converging continental plates deform the contact region and form the tallest mountains of Earth. It is still an ongoing quest to understand the consequences of converging and diverging continents, with many recent works focusing on the deforming contact region and addressing its influence on the mantle flow beneath (Rozel et al. Reference Rozel, Golabek, Jain, Tackley and Gerya2017; Whitehead Reference Whitehead2023). Inspired by the geophysics, one modification to our current model could be changing the way in which neighbouring plates interact. This can be achieved through changing the coefficient of restitution to 0 during each collision, which better captures the collision between continental plates during a long time scale. Adding an attractive force between plates can also reveal interesting dynamics, as the diverging surface flow has to be strong enough to pull the plates apart. Thus a larger formation of translating supercontinent may stay stable in this case, and the contact state of plates would also become more persistent. Looking forward, more sophisticated models are required to capture different plate interactions and resulting plate dynamics, and they may reveal new insights into the physics and dynamics of the formation of supercontinents.
To conclude, we consider a toy model to predict the size of the largest continental plate. The aspect ratio of Earth's mantle is approximately ![]() $\varGamma _E = 10$, so the critical covering ratio there is
$\varGamma _E = 10$, so the critical covering ratio there is ![]() $Cr ^*_E \approx 0.18$, as we have estimated in § 4.4. This gives an estimated dimension of the largest stable continental plate of Earth,
$Cr ^*_E \approx 0.18$, as we have estimated in § 4.4. This gives an estimated dimension of the largest stable continental plate of Earth, ![]() $L \approx 2{\rm \pi} R_E Cr ^*_E$, where
$L \approx 2{\rm \pi} R_E Cr ^*_E$, where ![]() $R_E = 6400$ km is the radius of Earth. So the plate area is
$R_E = 6400$ km is the radius of Earth. So the plate area is ![]() $L^2 \approx 6\times 10^7\ {\rm km}^2$, slightly underestimating the largest continental plate, the North American Plate, whose area is
$L^2 \approx 6\times 10^7\ {\rm km}^2$, slightly underestimating the largest continental plate, the North American Plate, whose area is ![]() $7.59\times 10^7\ {\rm km}^2$.
$7.59\times 10^7\ {\rm km}^2$.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.1231.
Acknowledgements
I thank J.-Q. Zhong, J. Chu and J. Zhang for useful discussions.
Funding
I acknowledge support from the National Natural Science Foundation of China (12272237, 92252204).
Declaration of interests
The author reports no conflict of interest.
Appendix A. Helmholtz solver for Dirichlet problems
We outline the numerical solver for the following Helmholtz problem:
As the domain is periodic in ![]() $x\in (0,\varGamma ]$, we can discretize
$x\in (0,\varGamma ]$, we can discretize ![]() $x$ as
$x$ as ![]() $L$ equally spaced nodes so
$L$ equally spaced nodes so ![]() $x_l = l\,\Delta x$, where
$x_l = l\,\Delta x$, where ![]() $\Delta x = \varGamma /L$, and
$\Delta x = \varGamma /L$, and ![]() $l = 1,2,\dots, L$. We further require
$l = 1,2,\dots, L$. We further require ![]() $L$ to be odd. We can now approximate the solution
$L$ to be odd. We can now approximate the solution ![]() $u(x,y)$ as a truncated Fourier series in
$u(x,y)$ as a truncated Fourier series in ![]() $x$:
$x$:
 \begin{equation} u(x_l,y) = \sum_{k={-}({L-1})/{2}}^{({L-1})/{2}} \hat{u}_k(y)\exp(2{\rm \pi} \mathrm{i} k l/L), \end{equation}
\begin{equation} u(x_l,y) = \sum_{k={-}({L-1})/{2}}^{({L-1})/{2}} \hat{u}_k(y)\exp(2{\rm \pi} \mathrm{i} k l/L), \end{equation}
where ![]() $\mathrm {i}$ is the imaginary unit. The Fourier coefficients
$\mathrm {i}$ is the imaginary unit. The Fourier coefficients ![]() $\hat {u}_k$ then satisfy the ODE
$\hat {u}_k$ then satisfy the ODE
where
 $$\begin{gather}\hat{h}_k(y) = \frac{1}{L}\sum_{l = 1}^{L} h(x_l,y) \exp({-}2{\rm \pi} \mathrm{i} k l/L), \end{gather}$$
$$\begin{gather}\hat{h}_k(y) = \frac{1}{L}\sum_{l = 1}^{L} h(x_l,y) \exp({-}2{\rm \pi} \mathrm{i} k l/L), \end{gather}$$ $$\begin{gather}\hat{g}_{0,k}= \frac{1}{L}\sum_{l = 1}^{L} g_0(x_l) \exp({-}2{\rm \pi} \mathrm{i} k l/L), \end{gather}$$
$$\begin{gather}\hat{g}_{0,k}= \frac{1}{L}\sum_{l = 1}^{L} g_0(x_l) \exp({-}2{\rm \pi} \mathrm{i} k l/L), \end{gather}$$ $$\begin{gather}\hat{g}_{1,k} =\frac{1}{L}\sum_{l = 1}^{L} g_1(x_l) \exp({-}2{\rm \pi} \mathrm{i} k l/L). \end{gather}$$
$$\begin{gather}\hat{g}_{1,k} =\frac{1}{L}\sum_{l = 1}^{L} g_1(x_l) \exp({-}2{\rm \pi} \mathrm{i} k l/L). \end{gather}$$The computation of (A9)–(A11) can be done efficiently with the help of the fast Fourier transformation algorithm.
Now all that is left is a set of ODEs (A5)–(A7), which can be solved with methods such as finite differences. We instead use the Chebyshev method, and discretize ![]() $y\in [0,1]$ to
$y\in [0,1]$ to ![]() $M+1$ Chebyshev nodes, so
$M+1$ Chebyshev nodes, so ![]() $y_m = [1+\cos (m{\rm \pi} /M)]/2$ with
$y_m = [1+\cos (m{\rm \pi} /M)]/2$ with ![]() $m = 0,1,2,\dots, M$. An advantage of using the Chebyshev method is that the unevenly distributed Chebyshev nodes have a higher resolution near the boundaries
$m = 0,1,2,\dots, M$. An advantage of using the Chebyshev method is that the unevenly distributed Chebyshev nodes have a higher resolution near the boundaries ![]() $y=0$ and
$y=0$ and ![]() $y=1$, therefore resolving the boundary layer structures. The differentiation operator
$y=1$, therefore resolving the boundary layer structures. The differentiation operator ![]() ${{\rm d}}/{{\rm d}y}$ can be approximated by a discrete operator
${{\rm d}}/{{\rm d}y}$ can be approximated by a discrete operator ![]() $\boldsymbol{\mathsf{D}}$ (Trefethen Reference Trefethen2000; Peyret Reference Peyret2002) whose elements are
$\boldsymbol{\mathsf{D}}$ (Trefethen Reference Trefethen2000; Peyret Reference Peyret2002) whose elements are
Here, ![]() $c_0=c_M = 2$, and
$c_0=c_M = 2$, and ![]() $c_j = 1$ for
$c_j = 1$ for ![]() $1\leqslant j\leqslant M-1$.
$1\leqslant j\leqslant M-1$.
The discrete operation on the left-hand side of (A5) can therefore be written as
where ![]() $\boldsymbol{\mathsf{I}}$ is an
$\boldsymbol{\mathsf{I}}$ is an ![]() $M+1$ by
$M+1$ by ![]() $M+1$ identity matrix.
$M+1$ identity matrix.
Noticing that the Chebyshev nodes are ![]() $\boldsymbol {y} = [1, y_1, y_2, \dots,y_{M-1},0]^{\rm T}$, we can write the discrete solution to (A5)–(A7) at these locations as a column vector
$\boldsymbol {y} = [1, y_1, y_2, \dots,y_{M-1},0]^{\rm T}$, we can write the discrete solution to (A5)–(A7) at these locations as a column vector
The interior solution ![]() $\tilde {\boldsymbol{\mathsf{U}}}$ therefore satisfies
$\tilde {\boldsymbol{\mathsf{U}}}$ therefore satisfies
where the ![]() $(M-1)\times (M-1)$ matrix
$(M-1)\times (M-1)$ matrix ![]() $\tilde {\boldsymbol{\mathsf{A}}}$ is the interior of
$\tilde {\boldsymbol{\mathsf{A}}}$ is the interior of ![]() $\boldsymbol{\mathsf{A}}$ (by removing its first and last rows and columns), and
$\boldsymbol{\mathsf{A}}$ (by removing its first and last rows and columns), and
 \begin{equation} \tilde{\boldsymbol{\mathsf{H}}} = \begin{bmatrix} \hat{h}_k(y_1)-\hat{g}_{1,k}A_{1,1} - \hat{g}_{0,k}A_{1,M} \\ \hat{h}_k(y_2)-\hat{g}_{1,k}A_{2,1} - \hat{g}_{0,k}A_{2,M} \\ \vdots \\ \hat{h}_k(y_{M-1})-\hat{g}_{1,k}A_{M-1,1} - \hat{g}_{0,k}A_{M-1,M} \end{bmatrix}. \end{equation}
\begin{equation} \tilde{\boldsymbol{\mathsf{H}}} = \begin{bmatrix} \hat{h}_k(y_1)-\hat{g}_{1,k}A_{1,1} - \hat{g}_{0,k}A_{1,M} \\ \hat{h}_k(y_2)-\hat{g}_{1,k}A_{2,1} - \hat{g}_{0,k}A_{2,M} \\ \vdots \\ \hat{h}_k(y_{M-1})-\hat{g}_{1,k}A_{M-1,1} - \hat{g}_{0,k}A_{M-1,M} \end{bmatrix}. \end{equation}Equation (A17) is invertible, and the operator ![]() $\tilde {\boldsymbol{\mathsf{A}}}$ does not change during time stepping, while the boundary information
$\tilde {\boldsymbol{\mathsf{A}}}$ does not change during time stepping, while the boundary information ![]() $g$ and forcing
$g$ and forcing ![]() $h$ are contained in
$h$ are contained in ![]() $\tilde {\boldsymbol{\mathsf{H}}}$. This allows us to compute the LU decomposition of
$\tilde {\boldsymbol{\mathsf{H}}}$. This allows us to compute the LU decomposition of ![]() $\tilde {\boldsymbol{\mathsf{A}}}$ at the beginning so
$\tilde {\boldsymbol{\mathsf{A}}}$ at the beginning so ![]() $\tilde {\boldsymbol{\mathsf{A}}}\tilde {\boldsymbol{\mathsf{U}}}= \tilde {\boldsymbol{\mathsf{H}}}$ can be inverted efficiently through backward and forward substitutions during time stepping. With
$\tilde {\boldsymbol{\mathsf{A}}}\tilde {\boldsymbol{\mathsf{U}}}= \tilde {\boldsymbol{\mathsf{H}}}$ can be inverted efficiently through backward and forward substitutions during time stepping. With ![]() $\tilde {\boldsymbol{\mathsf{U}}}$ and
$\tilde {\boldsymbol{\mathsf{U}}}$ and ![]() $\boldsymbol{\mathsf{U}}$ solved, the Fourier coefficients
$\boldsymbol{\mathsf{U}}$ solved, the Fourier coefficients ![]() $\hat {u}_k$ can then be inserted into (A4), and the solution
$\hat {u}_k$ can then be inserted into (A4), and the solution ![]() $u(x,y)$ is therefore obtained.
$u(x,y)$ is therefore obtained.
Appendix B. Helmholtz solver for Robin boundary conditions
Next, we consider the Helmholtz solver for equations such as (3.2), where inhomogeneous Robin boundary conditions such as (2.11) are applied. In a general form, consider
The idea for solving these equations is to use the influence matrix method (Peyret Reference Peyret2002): a PDE with inhomogeneous Robin boundary conditions can be converted into a series of PDEs with homogeneous Dirichlet boundary conditions, which can be solved by the method detailed in Appendix A.
We first separate the solution into several subproblems, so
 \begin{equation} u(x,y) = \tilde{u}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{u}_l(x,y), \end{equation}
\begin{equation} u(x,y) = \tilde{u}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{u}_l(x,y), \end{equation}
where ![]() $\xi _l$ are unknown coefficients to be determined later, and
$\xi _l$ are unknown coefficients to be determined later, and
Here, ![]() $\eta _m$ represents the
$\eta _m$ represents the ![]() $m$th node on the boundary, so there are
$m$th node on the boundary, so there are ![]() $2L$ of them, and
$2L$ of them, and ![]() $\delta _{lm}$ is the Kronecker delta function. Now, the boundary conditions (B2) and (B3) indicate
$\delta _{lm}$ is the Kronecker delta function. Now, the boundary conditions (B2) and (B3) indicate
 \begin{equation} \left.\left[a_i(x) \left(\sum_{l=1}^{2L} \xi_l\bar{u}_l\right) + b_i(x) \left( \frac{ \partial{\tilde{u}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{u}_l}}{ \partial y } \right)-g_i(x) \right]\right\vert_{\eta_m} = 0\quad \mbox{for } \eta_m\in \partial\varOmega_i. \end{equation}
\begin{equation} \left.\left[a_i(x) \left(\sum_{l=1}^{2L} \xi_l\bar{u}_l\right) + b_i(x) \left( \frac{ \partial{\tilde{u}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{u}_l}}{ \partial y } \right)-g_i(x) \right]\right\vert_{\eta_m} = 0\quad \mbox{for } \eta_m\in \partial\varOmega_i. \end{equation}
Here, ![]() $i\in \{0,1\}$ indicates the bottom or top boundary. As (B9) holds on all the boundary nodes
$i\in \{0,1\}$ indicates the bottom or top boundary. As (B9) holds on all the boundary nodes ![]() $\eta _m$, it provides
$\eta _m$, it provides ![]() $2L$ equations for
$2L$ equations for ![]() $2L$ unknowns
$2L$ unknowns ![]() $\xi _l$, and such a linear system is invertible. With all
$\xi _l$, and such a linear system is invertible. With all ![]() $\xi _l$ solved, the solution of (B1)–(B3) can be recovered as
$\xi _l$ solved, the solution of (B1)–(B3) can be recovered as ![]() $u = \tilde {u} + \sum _{l = 1}^{2L} \xi _l \bar {u}_l$.
$u = \tilde {u} + \sum _{l = 1}^{2L} \xi _l \bar {u}_l$.
In fact, ![]() $\xi _m$ is exactly the Dirichlet data for
$\xi _m$ is exactly the Dirichlet data for ![]() $u$ at boundary node
$u$ at boundary node ![]() $\eta _m$, therefore the solution of (B1)–(B3) is the same as the solution of
$\eta _m$, therefore the solution of (B1)–(B3) is the same as the solution of
This method can directly solve the heat equation (3.2) with boundary conditions in (2.8) and (2.12), by assigning ![]() $a_0 = 1$,
$a_0 = 1$, ![]() $b_0 = 0$,
$b_0 = 0$, ![]() $g_0 = 1$ at the bottom, and
$g_0 = 1$ at the bottom, and ![]() $a_1 = 1-a$,
$a_1 = 1-a$, ![]() $b_1 = a$,
$b_1 = a$, ![]() $g_1 = 0$ at the top. Usually, the solutions of (B7) and (B8) are obtained and saved at the beginning. At each time step, (B5) and (B6) are solved, and the location of moving plates will determine
$g_1 = 0$ at the top. Usually, the solutions of (B7) and (B8) are obtained and saved at the beginning. At each time step, (B5) and (B6) are solved, and the location of moving plates will determine ![]() $a_i(x)$,
$a_i(x)$, ![]() $b_i(x)$ and
$b_i(x)$ and ![]() $g_i(x)$, so (B9) can be inverted to provide
$g_i(x)$, so (B9) can be inverted to provide ![]() $\xi _m$, which can be used as boundary data in (B10) and (B11), and the solution
$\xi _m$, which can be used as boundary data in (B10) and (B11), and the solution ![]() $\theta _n$ can therefore be determined.
$\theta _n$ can therefore be determined.
Appendix C. Flow solver with Robin boundary conditions
At each time step, the following flow problem must be solved:
Here, we have dropped all the subscripts. We can also solve these equations with the influence matrix method. Now we want to convert the Neumann boundary condition in (C3) and Robin boundary condition in (C4) to a Dirichlet boundary condition for vorticity ![]() $\omega$. We decompose
$\omega$. We decompose ![]() $\omega$ and
$\omega$ and ![]() $\psi$ as
$\psi$ as
 $$\begin{gather} \omega(x,y) = \tilde{\omega}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{\omega}_l(x,y), \end{gather}$$
$$\begin{gather} \omega(x,y) = \tilde{\omega}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{\omega}_l(x,y), \end{gather}$$ $$\begin{gather}\psi(x,y) = \tilde{\psi}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{\psi}_l(x,y). \end{gather}$$
$$\begin{gather}\psi(x,y) = \tilde{\psi}(x,y) + \sum_{l = 1}^{2L} \xi_l\,\bar{\psi}_l(x,y). \end{gather}$$The associated subproblems are
The Neumann boundary condition in (C3) and the Robin boundary condition in (C4) can now be enforced as
 $$\begin{gather} \left. \left( \frac{ \partial{\tilde{\psi}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{\psi}_l}}{ \partial y } \right) \right\vert_{\eta_m} = 0 \quad\mbox{for } \eta_m\in \partial\varOmega_0, \end{gather}$$
$$\begin{gather} \left. \left( \frac{ \partial{\tilde{\psi}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{\psi}_l}}{ \partial y } \right) \right\vert_{\eta_m} = 0 \quad\mbox{for } \eta_m\in \partial\varOmega_0, \end{gather}$$ $$\begin{gather}\left.\left[a \left( \frac{ \partial{\tilde{\psi}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{\psi}_l}}{ \partial y } \right) + (1-a) \left( \frac{ \partial{^2\tilde{\psi}}}{ \partial y^2 } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{^2\bar{\psi}_l}}{ \partial y^2 } \right) -g \right]\right\vert_{\eta_m} = 0 \quad\mbox{for } \eta_m\in \partial\varOmega_1. \end{gather}$$
$$\begin{gather}\left.\left[a \left( \frac{ \partial{\tilde{\psi}}}{ \partial y } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{\bar{\psi}_l}}{ \partial y } \right) + (1-a) \left( \frac{ \partial{^2\tilde{\psi}}}{ \partial y^2 } +\sum_{l=1}^{2L} \xi_l\, \frac{ \partial{^2\bar{\psi}_l}}{ \partial y^2 } \right) -g \right]\right\vert_{\eta_m} = 0 \quad\mbox{for } \eta_m\in \partial\varOmega_1. \end{gather}$$
Equations (C11) and (C12) are again ![]() $2L$ equations for
$2L$ equations for ![]() $2L$ unknowns
$2L$ unknowns ![]() $\xi _l$, and the linear system is invertible. Equations (C5) and (C6) can then be summed, and the solutions are obtained. In fact,
$\xi _l$, and the linear system is invertible. Equations (C5) and (C6) can then be summed, and the solutions are obtained. In fact, ![]() $\xi _l$ is exactly the boundary data for
$\xi _l$ is exactly the boundary data for ![]() $\omega$ at boundary node
$\omega$ at boundary node ![]() $\eta _l$, so we can instead solve
$\eta _l$, so we can instead solve
Appendix D. Summary of numerical methods
There are two stages during our numerical simulation, and below we list some of the key steps during each stage.
Pre-processing stage steps.
(i) The inverse
 $\tilde {\boldsymbol{\mathsf{A}}}^{-1}$ (or the LU decomposition of
$\tilde {\boldsymbol{\mathsf{A}}}^{-1}$ (or the LU decomposition of  $\tilde {\boldsymbol{\mathsf{A}}}$) in (A17) is prepared for operators in (3.1)–(3.3), by taking
$\tilde {\boldsymbol{\mathsf{A}}}$) in (A17) is prepared for operators in (3.1)–(3.3), by taking  $\sigma = 0, \sigma _1, \sigma _2$ in (A15).
$\sigma = 0, \sigma _1, \sigma _2$ in (A15).(ii) Subproblems (B7)–(B8) and (C9)–(C10) are solved, and the solutions
 $\bar {\theta }_l$,
$\bar {\theta }_l$,  $\bar {\omega }_l$ and
$\bar {\omega }_l$ and  $\bar {\psi }_l$ for
$\bar {\psi }_l$ for  $l = 1,2,\dots,2L$ are saved.
$l = 1,2,\dots,2L$ are saved.
Steps at the ![]() $n$th step of the time stepping stage.
$n$th step of the time stepping stage.
(i) The fluid and interaction forces on each plate are computed according to (3.15)–(3.17).
(ii) The location and velocity of each plate are evolved by (3.7) and (3.8), and the indicator function
 $\hat {a}$ is prepared by (3.14a,b).
$\hat {a}$ is prepared by (3.14a,b).(iii) The forcing term
 $h_n$ in (3.2) is prepared according to (3.6), and
$h_n$ in (3.2) is prepared according to (3.6), and  $\tilde {\theta }_l$ is solved from (B5) and (B6).
$\tilde {\theta }_l$ is solved from (B5) and (B6).(iv) Equation (B9) is inverted so the Dirichlet boundary data for
 $\theta _n$ are known; (B10) and (B11) are then solved for
$\theta _n$ are known; (B10) and (B11) are then solved for  $\theta _n$.
$\theta _n$.(v) The temperature
 $\theta _n$ is used to prepare
$\theta _n$ is used to prepare  $f_n$ according to (3.5), so
$f_n$ according to (3.5), so  $\tilde {\omega }_l$,
$\tilde {\omega }_l$,  $\tilde {\psi }_l$ can be solved from (C7a,b) and (C8).
$\tilde {\psi }_l$ can be solved from (C7a,b) and (C8).(vi) Equations (C11) and (C12) are inverted so the Dirichlet data for
 $\omega _n$ are known; (C14) and (C15) are finally solved to provide
$\omega _n$ are known; (C14) and (C15) are finally solved to provide  $\omega _n$ and
$\omega _n$ and  $\psi _n$.
$\psi _n$.
For simulations with ![]() $\varGamma = 4$, we use
$\varGamma = 4$, we use ![]() $L = 256$ Fourier nodes and
$L = 256$ Fourier nodes and ![]() $M+1 = 65$ Chebyshev nodes. For simulations with higher aspect ratio
$M+1 = 65$ Chebyshev nodes. For simulations with higher aspect ratio ![]() $\varGamma = 10$,
$\varGamma = 10$, ![]() $L = 512$ Fourier nodes and
$L = 512$ Fourier nodes and ![]() $M+1 = 65$ Chebyshev nodes are used instead. During time stepping, we typically set
$M+1 = 65$ Chebyshev nodes are used instead. During time stepping, we typically set ![]() $\Delta t = \tau _0 = 5\times 10^{-4} \, Ra ^{-1/2}$ considering that the flow speed is
$\Delta t = \tau _0 = 5\times 10^{-4} \, Ra ^{-1/2}$ considering that the flow speed is ![]() $|{\boldsymbol {u}}|\sim \sqrt { Ra }$.
$|{\boldsymbol {u}}|\sim \sqrt { Ra }$.
These parameters are tested to yield spatially and temporally resolved results. In table 1, time-averaged values of ![]() $Nu$,
$Nu$, ![]() $Re$ and
$Re$ and ![]() $v_p$ (plate speed) are measured at the dynamical equilibrium state of convection with
$v_p$ (plate speed) are measured at the dynamical equilibrium state of convection with ![]() $ Ra {} = 10^7$,
$ Ra {} = 10^7$, ![]() $ Pr {} = 7.9$ and
$ Pr {} = 7.9$ and ![]() $\varGamma = 10$, where a floating plate with
$\varGamma = 10$, where a floating plate with ![]() $Cr {} = 1/2$ is free to move on top. The convergence of these values shows that our choice of spatial and temporal resolution is sufficient to resolve the dynamics of the flow and the plate.
$Cr {} = 1/2$ is free to move on top. The convergence of these values shows that our choice of spatial and temporal resolution is sufficient to resolve the dynamics of the flow and the plate.
Table 1. Time-averaged dynamical quantities at different spatial and temporal resolutions for plate tectonics with ![]() $ Ra {} = 10^7$,
$ Ra {} = 10^7$, ![]() $ Pr = 7.9$,
$ Pr = 7.9$, ![]() $\varGamma = 10$ and
$\varGamma = 10$ and ![]() $Cr {} = 1/2$. Here,
$Cr {} = 1/2$. Here, ![]() $L$ is the number of Fourier modes,
$L$ is the number of Fourier modes, ![]() $M+1$ is the number of Chebyshev nodes, and
$M+1$ is the number of Chebyshev nodes, and ![]() $\Delta t$ is the time step size. The asterisked parameters are used in the direct numerical simulations of figures 14 and 15, where
$\Delta t$ is the time step size. The asterisked parameters are used in the direct numerical simulations of figures 14 and 15, where ![]() $\Delta t = \tau _0 = 5\times 10^{-4} \, Ra ^{-1/2}$.
$\Delta t = \tau _0 = 5\times 10^{-4} \, Ra ^{-1/2}$.