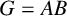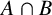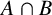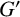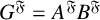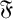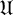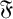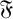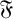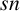1 Introduction
All groups considered in this article will be finite.
Let a group
![]() $G=AB$
be a product of two subgroups A and B. The structural influence of the structure of the subgroups A and B with certain permutability properties on the group
$G=AB$
be a product of two subgroups A and B. The structural influence of the structure of the subgroups A and B with certain permutability properties on the group
![]() $ G $
has been of interest to many authors for the past three decades (see [Reference Ballester-Bolinches, Esteban-Romero and Asaad1]). In this article we continue the investigation of generalised products of finite groups other than those considered in [Reference Ballester-Bolinches, Esteban-Romero and Asaad1].
$ G $
has been of interest to many authors for the past three decades (see [Reference Ballester-Bolinches, Esteban-Romero and Asaad1]). In this article we continue the investigation of generalised products of finite groups other than those considered in [Reference Ballester-Bolinches, Esteban-Romero and Asaad1].
We start by recalling some definitions and some notation. A group G is the mutually permutable product of the subgroups A and B if
![]() $G = AB$
and A permutes with every subgroup of B and B permutes with every subgroup of A. A group G is the weakly mutually permutable product of A and B if A permutes with every subgroup V of B such that
$G = AB$
and A permutes with every subgroup of B and B permutes with every subgroup of A. A group G is the weakly mutually permutable product of A and B if A permutes with every subgroup V of B such that
![]() $A\cap B\leqslant V $
, and B permutes with every subgroup U of A such that
$A\cap B\leqslant V $
, and B permutes with every subgroup U of A such that
![]() $A\cap B\leqslant U$
. A group G is the weakly mutually
$A\cap B\leqslant U$
. A group G is the weakly mutually
![]() $sn$
-permutable product of A and B if A permutes with every subnormal subgroup V of B such that
$sn$
-permutable product of A and B if A permutes with every subnormal subgroup V of B such that
![]() $A\cap B\leqslant V $
, and B permutes with every subnormal subgroup U of A such that
$A\cap B\leqslant V $
, and B permutes with every subnormal subgroup U of A such that
![]() $A\cap B\leqslant U$
. The classes of all finite nilpotent and supersoluble groups are denoted by
$A\cap B\leqslant U$
. The classes of all finite nilpotent and supersoluble groups are denoted by
![]() $ \mathfrak {N}$
and
$ \mathfrak {N}$
and
![]() $\mathfrak {U}$
, respectively.
$\mathfrak {U}$
, respectively.
In [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3] some results on mutually permutable products were extended to weakly mutually permutable products. In particular, the following theorem was shown, which is a generalisation of [Reference Ballester-Bolinches and Pedraza-Aguilera4, Theorem A].
Theorem 1.1 [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Theorem B].
Let
![]() $ \mathfrak {F} $
be a saturated formation containing
$ \mathfrak {F} $
be a saturated formation containing
![]() $ \mathfrak {U} $
. Let the group
$ \mathfrak {U} $
. Let the group
![]() $ G=AB $
be the weakly mutually permutable product of subgroups A and B. Suppose that A permutes with each Sylow subgroup of B and B permutes with each Sylow subgroup of A. If
$ G=AB $
be the weakly mutually permutable product of subgroups A and B. Suppose that A permutes with each Sylow subgroup of B and B permutes with each Sylow subgroup of A. If
![]() $ G' $
is nilpotent, then
$ G' $
is nilpotent, then
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $
.
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $
.
Our objective in this article is to generalise more results on mutually permutable products to weakly mutually permutable ones. We obtain new results on mutually permutable products as a consequence. In [Reference Ballester-Bolinches, Pérez-Ramos and Pedraza-Aguilera5], the following result was shown.
Theorem 1.2 [Reference Ballester-Bolinches, Pérez-Ramos and Pedraza-Aguilera5, Theorem 1].
Let
![]() $ G=AB $
be the mutually permutable product of subgroups A and B. If B is supersoluble and
$ G=AB $
be the mutually permutable product of subgroups A and B. If B is supersoluble and
![]() $G'$
is nilpotent, or B is nilpotent, then
$G'$
is nilpotent, or B is nilpotent, then
Part of this result was extended in [Reference Ballester-Bolinches and Pedraza-Aguilera4], were the authors proved that if
![]() $\mathfrak {F}$
is a saturated formation containing the class
$\mathfrak {F}$
is a saturated formation containing the class
![]() $\mathfrak {U}$
of supersoluble groups, then the
$\mathfrak {U}$
of supersoluble groups, then the
![]() $\mathfrak {F}$
-residual respects the operation of forming mutually permutable products with nilpotent commutator subgroup, that is,
$\mathfrak {F}$
-residual respects the operation of forming mutually permutable products with nilpotent commutator subgroup, that is,
![]() $G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}}$
. However, it turns out that the corresponding result is not true if B is nilpotent, even in the case where
$G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}}$
. However, it turns out that the corresponding result is not true if B is nilpotent, even in the case where
![]() $\mathfrak {F}$
is a Fitting class, as the following example shows.
$\mathfrak {F}$
is a Fitting class, as the following example shows.
Example 1.3. Let
![]() ${\mathfrak F}={{\mathfrak N}^2}$
be the class of metanilpotent groups. Then
${\mathfrak F}={{\mathfrak N}^2}$
be the class of metanilpotent groups. Then
![]() $\mathfrak F$
is a saturated Fitting formation containing
$\mathfrak F$
is a saturated Fitting formation containing
![]() $\mathfrak {U}$
, which is closed for subgroups. Consider
$\mathfrak {U}$
, which is closed for subgroups. Consider
![]() $G=AB$
the symmetric group of degree
$G=AB$
the symmetric group of degree
![]() $4$
, where B is a Sylow
$4$
, where B is a Sylow
![]() $2$
-subgroup of G and A is the alternating group of degree
$2$
-subgroup of G and A is the alternating group of degree
![]() $4$
. Then A and B are mutually permutable. Moreover, A is metanilpotent and B is nilpotent. But
$4$
. Then A and B are mutually permutable. Moreover, A is metanilpotent and B is nilpotent. But
![]() $1 = A^{\mathfrak N^2} \neq G^{\mathfrak N^2}=V $
, where
$1 = A^{\mathfrak N^2} \neq G^{\mathfrak N^2}=V $
, where
![]() $ V $
is the Klein
$ V $
is the Klein
![]() $4$
-group.
$4$
-group.
However, we have been able to prove the following extension of the result for weakly mutually permutable products.
Theorem A. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation containing
$ \mathfrak {F} $
be a subgroup-closed saturated formation containing
![]() $ \mathfrak {U} $
such that every group in
$ \mathfrak {U} $
such that every group in
![]() $ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
$ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
![]() $ G=AB $
be the weakly mutually permutable product of A and B. If B is nilpotent and permutes with each Sylow subgroup of A, then
$ G=AB $
be the weakly mutually permutable product of A and B. If B is nilpotent and permutes with each Sylow subgroup of A, then
As a corollary, we also obtain a result on weakly mutually
![]() $sn$
-permutable products.
$sn$
-permutable products.
A widely supersoluble group, or w-supersoluble group for short, is defined as a group
![]() $ G $
such that every Sylow subgroup of G is
$ G $
such that every Sylow subgroup of G is
![]() $\mathbb {P}$
-subnormal in G (a subgroup H of a group G is
$\mathbb {P}$
-subnormal in G (a subgroup H of a group G is
![]() $\mathbb {P}$
-subnormal in G whenever either
$\mathbb {P}$
-subnormal in G whenever either
![]() $H=G$
or there exists a chain of subgroups
$H=G$
or there exists a chain of subgroups
![]() $H=H_{0} \leqslant H_{1} \leqslant \cdots \leqslant H_{n-1} \leqslant H_{n}=G$
, such that
$H=H_{0} \leqslant H_{1} \leqslant \cdots \leqslant H_{n-1} \leqslant H_{n}=G$
, such that
![]() ${\vert }H_{i} {:} H_{i-1}{\vert }$
is a prime for every
${\vert }H_{i} {:} H_{i-1}{\vert }$
is a prime for every
![]() $i=1, \dots , n$
).
$i=1, \dots , n$
).
The class of w-supersoluble groups, denoted by
![]() $w\mathfrak {U} $
, is a subgroup-closed saturated formation containing
$w\mathfrak {U} $
, is a subgroup-closed saturated formation containing
![]() $\mathfrak {U} $
. Moreover, w-supersoluble groups have a Sylow tower of supersoluble type (see [Reference Valisev, Valiseva and Tyutyanov8, Corollary]).
$\mathfrak {U} $
. Moreover, w-supersoluble groups have a Sylow tower of supersoluble type (see [Reference Valisev, Valiseva and Tyutyanov8, Corollary]).
We recall some results we proved in [Reference Ballester-Bolinches, Madanha, Mudziiri Shumba and Pedraza-Aguilera2].
Theorem 1.4 [Reference Ballester-Bolinches, Madanha, Mudziiri Shumba and Pedraza-Aguilera2, Theorems A and C and Corollaries B and D].
Let
![]() $ \mathfrak {F}=\mathfrak {U} $
or
$ \mathfrak {F}=\mathfrak {U} $
or
![]() $ \mathfrak {F}=w\mathfrak {U} $
. Let
$ \mathfrak {F}=w\mathfrak {U} $
. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B, where
$sn$
-permutable product of the subgroups A and B, where
![]() $A, B\in \mathfrak {F}$
. Suppose that B permutes with each Sylow subgroup of A. Then
$A, B\in \mathfrak {F}$
. Suppose that B permutes with each Sylow subgroup of A. Then
![]() $ G\in \mathfrak {F} $
if one of the following assertions holds:
$ G\in \mathfrak {F} $
if one of the following assertions holds:
-
(a) B is nilpotent;
-
(b) A permutes with each Sylow subgroup of B and
 $ G' $
is nilpotent.
$ G' $
is nilpotent.
We unify these results by proving the following corollary.
Corollary B. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation such that
$ \mathfrak {F} $
be a subgroup-closed saturated formation such that
![]() $ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
$ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the
$sn$
-permutable product of the
![]() $ \mathfrak {F} $
-subgroups A and B. Suppose that either B or
$ \mathfrak {F} $
-subgroups A and B. Suppose that either B or
![]() $ G' $
is nilpotent. If B permutes with each Sylow subgroup of A, then the group
$ G' $
is nilpotent. If B permutes with each Sylow subgroup of A, then the group
![]() $ G $
belongs to
$ G $
belongs to
![]() $ \mathfrak {F} $
.
$ \mathfrak {F} $
.
The case where
![]() $ G' $
is nilpotent follows from the fact A and B are metanilpotent and so are supersoluble and hence
$ G' $
is nilpotent follows from the fact A and B are metanilpotent and so are supersoluble and hence
![]() $ G $
is supersoluble by Theorem 1.4.
$ G $
is supersoluble by Theorem 1.4.
In [Reference Ballester-Bolinches and Pedraza-Aguilera4], the authors showed that unfortunately the
![]() $\mathfrak {F}$
-projectors and thus the
$\mathfrak {F}$
-projectors and thus the
![]() $\mathfrak {F}$
-normalisers of a mutually permutable product with nilpotent commutator subgroup cannot be obtained from the corresponding projectors of the factor subgroups, as the following example shows. Let
$\mathfrak {F}$
-normalisers of a mutually permutable product with nilpotent commutator subgroup cannot be obtained from the corresponding projectors of the factor subgroups, as the following example shows. Let
![]() $ G=AB $
be the direct product of a cyclic group
$ G=AB $
be the direct product of a cyclic group
![]() $ \langle a \rangle $
of order
$ \langle a \rangle $
of order
![]() $ 3 $
with the alternating group
$ 3 $
with the alternating group
![]() $ \mathrm {A}_{4} $
of degree
$ \mathrm {A}_{4} $
of degree
![]() $ 4 $
. Let
$ 4 $
. Let
![]() $ V $
be the Klein group in
$ V $
be the Klein group in
![]() $ \mathrm {A}_{4} $
. Then G is the mutually permutable product of
$ \mathrm {A}_{4} $
. Then G is the mutually permutable product of
![]() $ A=\mathrm {A}_{4} $
and
$ A=\mathrm {A}_{4} $
and
![]() $ B=\langle a \rangle \times V $
. Moreover, B and
$ B=\langle a \rangle \times V $
. Moreover, B and
![]() $ G'=V $
are abelian. Note that B is the supersoluble projector of B and a Sylow
$ G'=V $
are abelian. Note that B is the supersoluble projector of B and a Sylow
![]() $ 3 $
-subgroup
$ 3 $
-subgroup
![]() $ A_{1} $
of
$ A_{1} $
of
![]() $ \mathrm {A}_{4} $
is a supersoluble projector of A. But
$ \mathrm {A}_{4} $
is a supersoluble projector of A. But
![]() $ A_{1}B $
is not supersoluble.
$ A_{1}B $
is not supersoluble.
Some conditions on
![]() $ \mathfrak {F} $
-projectors and
$ \mathfrak {F} $
-projectors and
![]() $ \mathfrak {F} $
-normalisers allow us to give the following result.
$ \mathfrak {F} $
-normalisers allow us to give the following result.
Theorem C. Let
![]() $ \mathfrak {F} $
be a formation. Assume that either
$ \mathfrak {F} $
be a formation. Assume that either
![]() $\mathfrak {F} = \mathfrak {U}$
or
$\mathfrak {F} = \mathfrak {U}$
or
![]() $\mathfrak {F}$
is a saturated Fitting formation containing
$\mathfrak {F}$
is a saturated Fitting formation containing
![]() $\mathfrak {U}$
. Let
$\mathfrak {U}$
. Let
![]() $G = AB$
be the weakly mutually permutable product of the subgroups A and B. Suppose that
$G = AB$
be the weakly mutually permutable product of the subgroups A and B. Suppose that
![]() $ G' $
is nilpotent,
$ G' $
is nilpotent,
![]() $ A_{1} $
is an
$ A_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of A such that
$ \mathfrak {F} $
-normaliser of A such that
![]() $ A\cap B \leqslant A_{1} $
and
$ A\cap B \leqslant A_{1} $
and
![]() $ B_{1} $
is an
$ B_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of B such that
$ \mathfrak {F} $
-normaliser of B such that
![]() $ A\cap B \leqslant B_{1} $
. Then
$ A\cap B \leqslant B_{1} $
. Then
![]() $ A_{1}B_{1}$
is an
$ A_{1}B_{1}$
is an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
.
$ G $
.
In this result, since
![]() $G'$
is nilpotent, we have
$G'$
is nilpotent, we have
![]() $G \in {\mathfrak N}{\mathfrak F}$
. Applying [Reference Doerk and Hawkes6, V, 4.2], the
$G \in {\mathfrak N}{\mathfrak F}$
. Applying [Reference Doerk and Hawkes6, V, 4.2], the
![]() $\mathfrak {F}$
-normalisers and the
$\mathfrak {F}$
-normalisers and the
![]() $\mathfrak {F}$
-projectors coincide, hence the result is also true for projectors.
$\mathfrak {F}$
-projectors coincide, hence the result is also true for projectors.
2 Preliminary results
In this section we first recall some properties of weakly mutually permutable products and then prove some results needed in the proof of our main results.
Lemma 2.1 [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Lemma 2.1].
Let
![]() $G = AB$
be the weakly mutually permutable product of subgroups A and B and let N be a normal subgroup of
$G = AB$
be the weakly mutually permutable product of subgroups A and B and let N be a normal subgroup of
![]() $ G $
. Then
$ G $
. Then
![]() ${G/N=(AN/N)(BN/N)} $
is the weakly mutually permutable product of
${G/N=(AN/N)(BN/N)} $
is the weakly mutually permutable product of
![]() $AN/N$
and
$AN/N$
and
![]() $BN/N$
.
$BN/N$
.
Lemma 2.2. Let
![]() $ G=AB $
be the weakly mutually permutable product of subgroups A and B.
$ G=AB $
be the weakly mutually permutable product of subgroups A and B.
-
(a) If
 $ H $
is a subgroup of A such that
$ H $
is a subgroup of A such that
 $ A\cap B \leqslant H $
and
$ A\cap B \leqslant H $
and
 $ K $
is a subgroup of B such that
$ K $
is a subgroup of B such that
 $ A\cap B\leqslant K $
, then
$ A\cap B\leqslant K $
, then
 $ HK $
is a weakly mutually permutable product of
$ HK $
is a weakly mutually permutable product of
 $ H $
and
$ H $
and
 $ K $
.
$ K $
. -
(b) If
 $ A\cap B=1 $
, then
$ A\cap B=1 $
, then
 $ G$
is the totally permutable product of the subgroups A and B, that is, every subgroup of A permutes with every subgroup of B.
$ G$
is the totally permutable product of the subgroups A and B, that is, every subgroup of A permutes with every subgroup of B. -
(c) If B permutes with a Sylow subgroup
 $ Q $
of A, then any subgroup of B containing
$ Q $
of A, then any subgroup of B containing
 $ A\cap B $
permutes with
$ A\cap B $
permutes with
 $ Q $
.
$ Q $
.
Proof. Assertions (a) and (b) are [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Lemma 2.2]. For (c), if
![]() $ K $
is such that
$ K $
is such that
![]() $ A\cap B\leqslant K \leqslant B $
, then for a Sylow subgroup
$ A\cap B\leqslant K \leqslant B $
, then for a Sylow subgroup
![]() $ Q $
of A, we have
$ Q $
of A, we have
![]() $ QK=Q((A\cap B)K)=(Q(A\cap B))K=K((A\cap B)Q)=KQ $
, as required.
$ QK=Q((A\cap B)K)=(Q(A\cap B))K=K((A\cap B)Q)=KQ $
, as required.
Lemma 2.3 [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Lemma 2.3].
Let
![]() $G = AB$
be the product of the subgroups A and B. If A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then
$G = AB$
be the product of the subgroups A and B. If A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then
![]() $ A\cap B $
also permutes with every Sylow subgroup of A and B. In particular,
$ A\cap B $
also permutes with every Sylow subgroup of A and B. In particular,
![]() $ A\cap B $
is a subnormal subgroup of
$ A\cap B $
is a subnormal subgroup of
![]() $ G $
.
$ G $
.
Our next lemma studies the behaviour of minimal normal subgroups of weakly mutually permutable products containing the intersection of the factors.
Lemma 2.4. Let
![]() $ G=AB $
be the weakly mutually permutable product of subgroups A and B. If N is a minimal normal subgroup of
$ G=AB $
be the weakly mutually permutable product of subgroups A and B. If N is a minimal normal subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ A\cap B\leqslant N $
, then either
$ A\cap B\leqslant N $
, then either
![]() $ A\cap N=B\cap N=1 $
or
$ A\cap N=B\cap N=1 $
or
![]() $ N=(N\cap A)(N\cap B) $
.
$ N=(N\cap A)(N\cap B) $
.
Proof. Note that
![]() $ A\cap N $
is a normal subgroup of A such that
$ A\cap N $
is a normal subgroup of A such that
![]() $ A\cap B\leqslant A\cap N$
and so
$ A\cap B\leqslant A\cap N$
and so
![]() $ H=(A\cap N)B $
is a subgroup of G. Observe that
$ H=(A\cap N)B $
is a subgroup of G. Observe that
![]() $ N\cap H = N\cap (A\cap N)B = (A\cap N)(B\cap N)$
. Since
$ N\cap H = N\cap (A\cap N)B = (A\cap N)(B\cap N)$
. Since
![]() $ N\cap H $
is a normal subgroup of
$ N\cap H $
is a normal subgroup of
![]() $ H $
, we see that B normalises
$ H $
, we see that B normalises
![]() $ N\cap H=(A\cap N)(B\cap N) $
.
$ N\cap H=(A\cap N)(B\cap N) $
.
Arguing as above,
![]() $ K=A(B\cap N) $
is a subgroup of
$ K=A(B\cap N) $
is a subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ K\cap N= A(B\cap N)\cap N=(A\cap N)(B\cap N) $
. Moreover, A normalises
$ K\cap N= A(B\cap N)\cap N=(A\cap N)(B\cap N) $
. Moreover, A normalises
![]() $ K\cap N=(A\cap N)(B\cap N) $
. Therefore,
$ K\cap N=(A\cap N)(B\cap N) $
. Therefore,
![]() $ (A\cap N)(B\cap N) $
is a normal subgroup of
$ (A\cap N)(B\cap N) $
is a normal subgroup of
![]() $ G $
. By the minimality of N, it follows that
$ G $
. By the minimality of N, it follows that
![]() $ A\cap N=B\cap N=1 $
or
$ A\cap N=B\cap N=1 $
or
![]() $ N=(N\cap A)(N\cap B) $
as required.
$ N=(N\cap A)(N\cap B) $
as required.
Lemma 2.5. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation containing
$ \mathfrak {F} $
be a subgroup-closed saturated formation containing
![]() $ \mathfrak {U} $
such that every group in
$ \mathfrak {U} $
such that every group in
![]() $ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
$ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
![]() $ G $
be a primitive group and let N be its unique minimal normal subgroup. Assume that
$ G $
be a primitive group and let N be its unique minimal normal subgroup. Assume that
![]() $ G/N $
belongs to
$ G/N $
belongs to
![]() $ \mathfrak {F} $
. If N is a
$ \mathfrak {F} $
. If N is a
![]() $ p $
-group, where
$ p $
-group, where
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ {\vert }G{\vert } $
, then
$ {\vert }G{\vert } $
, then
![]() $ N=F(G)=O_{p}(G) $
is a Sylow
$ N=F(G)=O_{p}(G) $
is a Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
.
$ G $
.
Proof. It is sufficient to show that N is a Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
. Note that
$ G $
. Note that
![]() $ {G=NM} $
for some maximal subgroup
$ {G=NM} $
for some maximal subgroup
![]() $ M $
of
$ M $
of
![]() $ G $
,
$ G $
,
![]() $ N\cap M=1 $
and
$ N\cap M=1 $
and
![]() $ C_{G}(N)=N $
since
$ C_{G}(N)=N $
since
![]() $ G $
is a primitive soluble group. By [Reference Doerk and Hawkes6, A, Theorem 15.6(b)],
$ G $
is a primitive soluble group. By [Reference Doerk and Hawkes6, A, Theorem 15.6(b)],
![]() $ O_{p}(M)=1 $
. But
$ O_{p}(M)=1 $
. But
![]() $ M\cong G/N \in \mathfrak {F}$
which means that
$ M\cong G/N \in \mathfrak {F}$
which means that
![]() $ M\in \mathfrak {F} $
and so has a Sylow tower of supersoluble type. Hence, a Sylow
$ M\in \mathfrak {F} $
and so has a Sylow tower of supersoluble type. Hence, a Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ M $
is normal in
$ M $
is normal in
![]() $ M $
and so
$ M $
and so
![]() $ p $
does not divide
$ p $
does not divide
![]() $ {\vert }M{\vert } $
, as required.
$ {\vert }M{\vert } $
, as required.
Lemma 2.6. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation containing
$ \mathfrak {F} $
be a subgroup-closed saturated formation containing
![]() $ \mathfrak {U} $
such that every group in
$ \mathfrak {U} $
such that every group in
![]() $ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
$ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
![]() $G = AB$
be the weakly mutually permutable product of the subgroups A and B, where B is nilpotent and A is an
$G = AB$
be the weakly mutually permutable product of the subgroups A and B, where B is nilpotent and A is an
![]() $ \mathfrak {F} $
-subgroup. If B permutes with each Sylow subgroup of A, then the group
$ \mathfrak {F} $
-subgroup. If B permutes with each Sylow subgroup of A, then the group
![]() $ G $
belongs to
$ G $
belongs to
![]() $ \mathfrak {F} $
.
$ \mathfrak {F} $
.
Proof. Suppose the result is not true and let
![]() $ G $
be a counterexample with
$ G $
be a counterexample with
![]() $ {\vert }G{\vert } $
minimal. We shall get to a contradiction by the following steps.
$ {\vert }G{\vert } $
minimal. We shall get to a contradiction by the following steps.
-
(a) G is a primitive soluble group with a unique minimal normal subgroup N and
 $N=C_{G}(N)=F(G)=O_{p}(G)$
for some prime p.
$N=C_{G}(N)=F(G)=O_{p}(G)$
for some prime p.
By [Reference Ballester-Bolinches, Madanha, Mudziiri Shumba and Pedraza-Aguilera2, Lemma 2.5], G is soluble since A soluble. Let N be a minimal normal subgroup of
![]() $ G $
. Note that
$ G $
. Note that
![]() $ G/N=(AN/N)(BN/N) $
satisfies the hypotheses of the theorem by Lemma 2.1 and this means that
$ G/N=(AN/N)(BN/N) $
satisfies the hypotheses of the theorem by Lemma 2.1 and this means that
![]() $ G/N $
belongs to
$ G/N $
belongs to
![]() $ \mathfrak {F} $
by the minimality of
$ \mathfrak {F} $
by the minimality of
![]() $ G $
. It follows that
$ G $
. It follows that
![]() $ G $
is a primitive soluble group since
$ G $
is a primitive soluble group since
![]() $ \mathfrak {F} $
is a saturated formation and so
$ \mathfrak {F} $
is a saturated formation and so
![]() $ G $
has a unique minimal normal subgroup N with
$ G $
has a unique minimal normal subgroup N with
![]() $ N=C_{G}(N)=F(G)=O_{p}(G) $
for some prime
$ N=C_{G}(N)=F(G)=O_{p}(G) $
for some prime
![]() $ p $
.
$ p $
.
-
(b)
 $N= (N\cap A)(N\cap B)$
,
$N= (N\cap A)(N\cap B)$
,
 $BN$
belongs to
$BN$
belongs to
 $\mathfrak {F}$
and
$\mathfrak {F}$
and
 $1\not = A\cap B\leqslant N $
.
$1\not = A\cap B\leqslant N $
.
If
![]() $ A\cap B=1 $
, then by Lemma 2.2(i),
$ A\cap B=1 $
, then by Lemma 2.2(i),
![]() $G=AB$
is the totally permutable product of subgroups A and B. By [Reference Ballester-Bolinches, Esteban-Romero and Asaad1, Theorem 5.2.1],
$G=AB$
is the totally permutable product of subgroups A and B. By [Reference Ballester-Bolinches, Esteban-Romero and Asaad1, Theorem 5.2.1],
![]() $ G $
belongs to
$ G $
belongs to
![]() $\mathfrak {F}$
, a contradiction. Hence,
$\mathfrak {F}$
, a contradiction. Hence,
![]() $A \cap B \neq 1$
. It follows that
$A \cap B \neq 1$
. It follows that
![]() $A\cap B$
is a nilpotent subnormal subgroup of
$A\cap B$
is a nilpotent subnormal subgroup of
![]() $ G $
using Lemma 2.3. Therefore,
$ G $
using Lemma 2.3. Therefore,
![]() $A\cap B \leqslant F(G)=N$
and so
$A\cap B \leqslant F(G)=N$
and so
![]() $N= (N\cap A)(N\cap B)$
by Lemma 2.4. Hence
$N= (N\cap A)(N\cap B)$
by Lemma 2.4. Hence
![]() $BN=B(N\cap B)(N\cap A)=B(N\cap A)$
is the weakly mutually permutable product of B and
$BN=B(N\cap B)(N\cap A)=B(N\cap A)$
is the weakly mutually permutable product of B and
![]() $ N\cap A $
. Since
$ N\cap A $
. Since
![]() $N\cap A$
has only one Sylow subgroup, namely itself, B trivially permutes with every Sylow subgroup of
$N\cap A$
has only one Sylow subgroup, namely itself, B trivially permutes with every Sylow subgroup of
![]() $N\cap A$
. Notice that
$N\cap A$
. Notice that
![]() $ BN $
satisfies the hypotheses of the theorem. If
$ BN $
satisfies the hypotheses of the theorem. If
![]() $ BN < G $
, then
$ BN < G $
, then
![]() $ BN $
belongs to
$ BN $
belongs to
![]() $\mathfrak {F}$
by the minimality of
$\mathfrak {F}$
by the minimality of
![]() $ G $
. Assume that
$ G $
. Assume that
![]() $G=BN$
. Let
$G=BN$
. Let
![]() $1 \neq M \leqslant A\cap B\leqslant N$
. Since N is abelian, M is a normal subgroup of N. Hence,
$1 \neq M \leqslant A\cap B\leqslant N$
. Since N is abelian, M is a normal subgroup of N. Hence,
![]() $ N=M^{G}=M^{NB}=M^{B}\leqslant B$
and
$ N=M^{G}=M^{NB}=M^{B}\leqslant B$
and
![]() $G=B$
, a contradiction. Thus
$G=B$
, a contradiction. Thus
![]() $BN$
belongs to
$BN$
belongs to
![]() $\mathfrak {F}$
, as required.
$\mathfrak {F}$
, as required.
-
(c) N is the unique Sylow p-subgroup of G and p is the largest prime dividing
 ${\vert }G{\vert }$
.
${\vert }G{\vert }$
.
Let
![]() $ q $
be the largest prime dividing
$ q $
be the largest prime dividing
![]() $ {\vert }G{\vert } $
and assume that
$ {\vert }G{\vert } $
and assume that
![]() $ q\not = p $
. Suppose first that
$ q\not = p $
. Suppose first that
![]() $ q $
divides
$ q $
divides
![]() $ {\vert }BN{\vert } $
. Note that
$ {\vert }BN{\vert } $
. Note that
![]() $ BN $
belongs to
$ BN $
belongs to
![]() $ \mathfrak {F} $
and so has a Sylow tower of supersoluble type. It follows that
$ \mathfrak {F} $
and so has a Sylow tower of supersoluble type. It follows that
![]() $ BN $
has a unique Sylow
$ BN $
has a unique Sylow
![]() $ q $
-subgroup,
$ q $
-subgroup,
![]() $ (BN)_{q} $
say. This means that
$ (BN)_{q} $
say. This means that
![]() $ (BN)_{q} $
centralises N. Since
$ (BN)_{q} $
centralises N. Since
![]() $ C_{G}(N)=N $
, we have
$ C_{G}(N)=N $
, we have
![]() $ (BN)_{q}=1 $
, a contradiction. Therefore, we may assume that
$ (BN)_{q}=1 $
, a contradiction. Therefore, we may assume that
![]() $ q $
divides
$ q $
divides
![]() $ {\vert }A{\vert } $
but does not divide
$ {\vert }A{\vert } $
but does not divide
![]() $ {\vert }BN{\vert } $
. Since A also has a Sylow tower of supersoluble type, it follows that A has a unique Sylow
$ {\vert }BN{\vert } $
. Since A also has a Sylow tower of supersoluble type, it follows that A has a unique Sylow
![]() $ q $
-subgroup,
$ q $
-subgroup,
![]() $ A_{q} $
say, and that
$ A_{q} $
say, and that
![]() $ A_{q} $
is a normal subgroup of
$ A_{q} $
is a normal subgroup of
![]() $ A_{q}(N\cap A) $
. Then
$ A_{q}(N\cap A) $
. Then
![]() $ A_{q}(N\cap B)=A_{q}(A\cap B)(N\cap B) $
is the weakly mutually permutable product of
$ A_{q}(N\cap B)=A_{q}(A\cap B)(N\cap B) $
is the weakly mutually permutable product of
![]() $ A_{q}(A\cap B) $
and
$ A_{q}(A\cap B) $
and
![]() $ N\cap B $
by Lemma 2.2. Also,
$ N\cap B $
by Lemma 2.2. Also,
![]() $ N\cap B $
permutes with each Sylow subgroup of
$ N\cap B $
permutes with each Sylow subgroup of
![]() $ A_{q}(A\cap B) $
. Suppose that
$ A_{q}(A\cap B) $
. Suppose that
![]() $ A_{q}(N\cap B) < G $
. Then
$ A_{q}(N\cap B) < G $
. Then
![]() $ A_{q}(N\cap B) $
belongs to
$ A_{q}(N\cap B) $
belongs to
![]() $ \mathfrak {F} $
by the minimality of
$ \mathfrak {F} $
by the minimality of
![]() $ G $
. In particular,
$ G $
. In particular,
![]() $ A_{q}(N\cap B) $
has a unique Sylow
$ A_{q}(N\cap B) $
has a unique Sylow
![]() $ q $
-subgroup since it has a Sylow tower of supersoluble type. Hence,
$ q $
-subgroup since it has a Sylow tower of supersoluble type. Hence,
![]() $ A_{q} $
is normalised by
$ A_{q} $
is normalised by
![]() $ N\cap B $
. Hence, in turn,
$ N\cap B $
. Hence, in turn,
![]() $ A_{q} $
is normalised by
$ A_{q} $
is normalised by
![]() $ (N\cap A)(N\cap B)=N $
. This means that
$ (N\cap A)(N\cap B)=N $
. This means that
![]() $ A_{q} $
centralises N, a contradiction. We may assume that
$ A_{q} $
centralises N, a contradiction. We may assume that
![]() $ A_{q}(N\cap B)=G $
. Then
$ A_{q}(N\cap B)=G $
. Then
![]() $ N \cap B=B $
and so B is an elementary abelian
$ N \cap B=B $
and so B is an elementary abelian
![]() $ p $
-group. Moreover,
$ p $
-group. Moreover,
![]() $ A=A_{q}(A\cap B) $
. Then
$ A=A_{q}(A\cap B) $
. Then
![]() $ A\cap B=N \cap A $
is a normal Sylow
$ A\cap B=N \cap A $
is a normal Sylow
![]() $ p $
-subgroup of A. Hence,
$ p $
-subgroup of A. Hence,
![]() $ A\cap B $
is normal in
$ A\cap B $
is normal in
![]() $ G $
because B is abelian. By the minimality of N, we have
$ G $
because B is abelian. By the minimality of N, we have
![]() $ N=A\cap B $
, that is,
$ N=A\cap B $
, that is,
![]() $ {G=A_{q}(N\cap B)=A_{q}(A \cap B)=A }$
, a contradiction. Therefore,
$ {G=A_{q}(N\cap B)=A_{q}(A \cap B)=A }$
, a contradiction. Therefore,
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ {\vert }G{\vert } $
. By Lemma 2.5, N is the unique Sylow
$ {\vert }G{\vert } $
. By Lemma 2.5, N is the unique Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
.
$ G $
.
-
(d) N is a subgroup of A and N is not contained in B.
Suppose that N is contained in B. Then a Hall
![]() $p'$
-subgroup
$p'$
-subgroup
![]() $B_{p'}$
of B must centralise
$B_{p'}$
of B must centralise
![]() $N = C_{G}(N)$
. Hence,
$N = C_{G}(N)$
. Hence,
![]() $B_{p'} = 1$
and B is a p-group. Then
$B_{p'} = 1$
and B is a p-group. Then
![]() $ G=AN $
. Let
$ G=AN $
. Let
![]() $ 1 \neq M\leqslant A\cap B $
. Then
$ 1 \neq M\leqslant A\cap B $
. Then
![]() $ N \leq M^{G}=M^{AN}=M^{A}\leqslant A $
and so
$ N \leq M^{G}=M^{AN}=M^{A}\leqslant A $
and so
![]() $ G = A $
, a contradiction. Therefore, N is not contained in B. Hence, B has a nontrivial Hall
$ G = A $
, a contradiction. Therefore, N is not contained in B. Hence, B has a nontrivial Hall
![]() $ p' $
-subgroup,
$ p' $
-subgroup,
![]() $ B_{p'} $
say, which is normal in B. Consequently,
$ B_{p'} $
say, which is normal in B. Consequently,
![]() $ AB_{p'}=A(A\cap B)B_{p'} $
is a subgroup of G. Then
$ AB_{p'}=A(A\cap B)B_{p'} $
is a subgroup of G. Then
![]() $ 1\not = B_{p'}^{G}\leqslant AB_{p'} $
and so
$ 1\not = B_{p'}^{G}\leqslant AB_{p'} $
and so
![]() $ N \leqslant AB_{p'}$
. Hence,
$ N \leqslant AB_{p'}$
. Hence,
![]() $ N\leqslant A $
, as required.
$ N\leqslant A $
, as required.
-
(e) Final contradiction.
Let
![]() $ A_{p'} $
be a Hall
$ A_{p'} $
be a Hall
![]() $ p' $
-subgroup of A. If
$ p' $
-subgroup of A. If
![]() $ A_{p'}=1 $
, then
$ A_{p'}=1 $
, then
![]() $ G=BN $
belongs to
$ G=BN $
belongs to
![]() $ \mathfrak {F} $
by step (b), a contradiction. Hence,
$ \mathfrak {F} $
by step (b), a contradiction. Hence,
![]() $ A_{p'}\not = 1 $
. Since B permutes with every Sylow subgroup of A, it follows that
$ A_{p'}\not = 1 $
. Since B permutes with every Sylow subgroup of A, it follows that
![]() $ A_{p'}B $
is a subgroup of
$ A_{p'}B $
is a subgroup of
![]() $ G $
. By step (d), N is not contained in B. Hence,
$ G $
. By step (d), N is not contained in B. Hence,
![]() $ A_{p'}B $
is a proper subgroup of
$ A_{p'}B $
is a proper subgroup of
![]() $ G $
. Since
$ G $
. Since
![]() $ NA_{p'}B=G $
, it follows that
$ NA_{p'}B=G $
, it follows that
![]() $ N\cap A_{p'}B=N\cap B $
is normal in
$ N\cap A_{p'}B=N\cap B $
is normal in
![]() $ G $
. The minimality of N implies that
$ G $
. The minimality of N implies that
![]() $ N=N\cap B $
or
$ N=N\cap B $
or
![]() $ N\cap B=1 $
. By step (d),
$ N\cap B=1 $
. By step (d),
![]() $ N \neq N\cap B $
. Therefore,
$ N \neq N\cap B $
. Therefore,
![]() $ N\cap B=1 $
, and then
$ N\cap B=1 $
, and then
![]() $ A\cap B\leqslant N\cap B=1 $
, contradicting step (b), our final contradiction.
$ A\cap B\leqslant N\cap B=1 $
, contradicting step (b), our final contradiction.
Theorem 2.7 [Reference Monakhov and Trofimuk7, Theorem 2.2].
Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation such that
$ \mathfrak {F} $
be a subgroup-closed saturated formation such that
![]() $ \mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}$
. Let
$ \mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}$
. Let
![]() $ G=AB $
be a product of
$ G=AB $
be a product of
![]() $ \mathbb {P} $
-subnormal subgroups A and B such that
$ \mathbb {P} $
-subnormal subgroups A and B such that
![]() $ A\in \mathfrak {F} $
and B is nilpotent. If B permutes with each Sylow subgroup of A, then
$ A\in \mathfrak {F} $
and B is nilpotent. If B permutes with each Sylow subgroup of A, then
![]() $ G $
belongs to
$ G $
belongs to
![]() $ \mathfrak {F} $
.
$ \mathfrak {F} $
.
Corollary 2.8. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation such that
$ \mathfrak {F} $
be a subgroup-closed saturated formation such that
![]() $ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
$ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
![]() $G = AB$
be the mutually
$G = AB$
be the mutually
![]() $sn$
-permutable product of the
$sn$
-permutable product of the
![]() $ \mathfrak {F} $
-subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then the group
$ \mathfrak {F} $
-subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then the group
![]() $ G $
belongs to
$ G $
belongs to
![]() $ \mathfrak {F} $
.
$ \mathfrak {F} $
.
Proof. By [Reference Valisev, Valiseva and Tyutyanov9, Lemma 4.5], A and B are
![]() $\mathbb {P}$
-subnormal subgroups of
$\mathbb {P}$
-subnormal subgroups of
![]() $ G $
. Using Theorem 2.7, we have
$ G $
. Using Theorem 2.7, we have
![]() $ G\in \mathfrak {F} $
, as required.
$ G\in \mathfrak {F} $
, as required.
We are in a position to prove Corollary B which we restate below.
Corollary 2.9. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation such that
$ \mathfrak {F} $
be a subgroup-closed saturated formation such that
![]() $ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
$ {\mathfrak {U}\subseteq \mathfrak {F} \subseteq w\mathfrak {U}}$
. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the
$sn$
-permutable product of the
![]() $ \mathfrak {F} $
-subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then the group
$ \mathfrak {F} $
-subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then the group
![]() $ G $
belongs to
$ G $
belongs to
![]() $ \mathfrak {F} $
.
$ \mathfrak {F} $
.
Proof. The argument is the same as in the proof of Lemma 2.6, taking into consideration Corollary 2.8 and some appropriate preliminary results in [Reference Ballester-Bolinches, Madanha, Mudziiri Shumba and Pedraza-Aguilera2].
3 Main results
In this section we prove our main results, which we shall restate.
Theorem 3.1. Let
![]() $ \mathfrak {F} $
be a subgroup-closed saturated formation containing
$ \mathfrak {F} $
be a subgroup-closed saturated formation containing
![]() $ \mathfrak {U} $
such that every group in
$ \mathfrak {U} $
such that every group in
![]() $ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
$ \mathfrak {F} $
has a Sylow tower of supersoluble type. Let
![]() $ G=AB $
be the weakly mutually permutable product of subgroups A and B. If B is nilpotent and permutes with each Sylow subgroup of A, then
$ G=AB $
be the weakly mutually permutable product of subgroups A and B. If B is nilpotent and permutes with each Sylow subgroup of A, then
Proof. Suppose the theorem is not true and let
![]() $ G $
be a counterexample with
$ G $
be a counterexample with
![]() $ {\vert }G{\vert } $
as small as possible. We shall get a contradiction by the following steps.
$ {\vert }G{\vert } $
as small as possible. We shall get a contradiction by the following steps.
-
(a)
 $ G^{\mathfrak {F}}=A^{\mathfrak {F}}N$
for each minimal normal subgroup N of G,
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}N$
for each minimal normal subgroup N of G,
 $F(G)=O_{p}(G)$
for some prime p and
$F(G)=O_{p}(G)$
for some prime p and
 $G^{\mathfrak {F}}$
is an abelian p-group. Moreover,
$G^{\mathfrak {F}}$
is an abelian p-group. Moreover,
 $A\cap B \neq 1$
is a p-group.
$A\cap B \neq 1$
is a p-group.
Since
![]() $ AG^{\mathfrak {F}}/G^{\mathfrak {F}}\cong A/(A\cap G^{\mathfrak {F}})\in \mathfrak {F} $
, we have
$ AG^{\mathfrak {F}}/G^{\mathfrak {F}}\cong A/(A\cap G^{\mathfrak {F}})\in \mathfrak {F} $
, we have
![]() $ A^{\mathfrak {F}}\leqslant G^{\mathfrak {F}} $
. Hence,
$ A^{\mathfrak {F}}\leqslant G^{\mathfrak {F}} $
. Hence,
![]() $ G^{\mathfrak {F}}\not = 1 $
. Moreover, by Lemma 2.6,
$ G^{\mathfrak {F}}\not = 1 $
. Moreover, by Lemma 2.6,
![]() $A^{\mathfrak {F}} \neq 1$
. Let N be a minimal normal subgroup of
$A^{\mathfrak {F}} \neq 1$
. Let N be a minimal normal subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ N\leqslant G^{\mathfrak {F}} $
. Then
$ N\leqslant G^{\mathfrak {F}} $
. Then
![]() $ G/N $
is the weakly mutually permutable product of
$ G/N $
is the weakly mutually permutable product of
![]() $ AN/N $
and
$ AN/N $
and
![]() $ BN/N $
. Moreover,
$ BN/N $
. Moreover,
![]() $ BN/N $
is nilpotent and permutes with each Sylow subgroup of
$ BN/N $
is nilpotent and permutes with each Sylow subgroup of
![]() $ AN/N $
. Hence,
$ AN/N $
. Hence,
![]() $ (G/N)^{\mathfrak {F}}=(AN/N)^{\mathfrak {F}} $
by the minimality of
$ (G/N)^{\mathfrak {F}}=(AN/N)^{\mathfrak {F}} $
by the minimality of
![]() $ G $
. This implies that
$ G $
. This implies that
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}N $
. Let
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}N $
. Let
![]() $ N_{1} $
be a minimal normal subgroup of
$ N_{1} $
be a minimal normal subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ N_{1}\nleqslant G^{\mathfrak {F}} $
. Then
$ N_{1}\nleqslant G^{\mathfrak {F}} $
. Then
![]() $ N_{1}\cap G^{\mathfrak {F}}=1 $
and
$ N_{1}\cap G^{\mathfrak {F}}=1 $
and
![]() $ G^{\mathfrak {F}}N_{1}=A^{\mathfrak {F}}N_{1} $
. Moreover,
$ G^{\mathfrak {F}}N_{1}=A^{\mathfrak {F}}N_{1} $
. Moreover,
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}(N_{1}\cap G^{\mathfrak {F}})=A^{\mathfrak {F}} $
, a contradiction. This means that every minimal normal subgroup of
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}(N_{1}\cap G^{\mathfrak {F}})=A^{\mathfrak {F}} $
, a contradiction. This means that every minimal normal subgroup of
![]() $ G $
is contained in
$ G $
is contained in
![]() $ G^{\mathfrak {F}} $
and so
$ G^{\mathfrak {F}} $
and so
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}N $
for each minimal normal subgroup N of G.
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}N $
for each minimal normal subgroup N of G.
We want to show that
![]() $ G^{\mathfrak {F}} $
is abelian. If
$ G^{\mathfrak {F}} $
is abelian. If
![]() $ A\cap B=1 $
, then
$ A\cap B=1 $
, then
![]() $ G=AB $
is the totally permutable product of A and B and so
$ G=AB $
is the totally permutable product of A and B and so
![]() $ A^{\mathfrak {F}}=G^{\mathfrak {F}} $
by [Reference Ballester-Bolinches, Pérez-Ramos and Pedraza-Aguilera5, Theorem 1], a contradiction. We may assume that
$ A^{\mathfrak {F}}=G^{\mathfrak {F}} $
by [Reference Ballester-Bolinches, Pérez-Ramos and Pedraza-Aguilera5, Theorem 1], a contradiction. We may assume that
![]() $ 1\not = A\cap B \leqslant F(G) $
by Lemma 2.3. Let N be a minimal normal subgroup of
$ 1\not = A\cap B \leqslant F(G) $
by Lemma 2.3. Let N be a minimal normal subgroup of
![]() $ G $
which is contained in
$ G $
which is contained in
![]() $ F(G) $
. Note that N is abelian. Suppose that N is contained in A. Since
$ F(G) $
. Note that N is abelian. Suppose that N is contained in A. Since
![]() $ A^{\mathfrak {F}} $
is a normal subgroup of A, N normalises
$ A^{\mathfrak {F}} $
is a normal subgroup of A, N normalises
![]() $ A^{\mathfrak {F}} $
and so
$ A^{\mathfrak {F}} $
and so
![]() $ A^{\mathfrak {F}} $
is a normal subgroup of
$ A^{\mathfrak {F}} $
is a normal subgroup of
![]() $ A^{\mathfrak {F}}N=G^{\mathfrak {F}} $
. Also
$ A^{\mathfrak {F}}N=G^{\mathfrak {F}} $
. Also
![]() $ G^{\mathfrak {F}}/A^{\mathfrak {F}} $
is abelian, which means that
$ G^{\mathfrak {F}}/A^{\mathfrak {F}} $
is abelian, which means that
![]() $ (G^{\mathfrak {F}})'\leqslant A^{\mathfrak {F}} $
. If
$ (G^{\mathfrak {F}})'\leqslant A^{\mathfrak {F}} $
. If
![]() $ (G^{\mathfrak {F}})'\not =1 $
, then
$ (G^{\mathfrak {F}})'\not =1 $
, then
![]() $ A^{\mathfrak {F}} $
contains a minimal normal subgroup N of
$ A^{\mathfrak {F}} $
contains a minimal normal subgroup N of
![]() $ G $
and therefore
$ G $
and therefore
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}N=A^{\mathfrak {F}} $
, a contradiction. We may assume that
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}N=A^{\mathfrak {F}} $
, a contradiction. We may assume that
![]() $ (G^{\mathfrak {F}})'=1 $
, that is,
$ (G^{\mathfrak {F}})'=1 $
, that is,
![]() $ G^{\mathfrak {F}} $
is abelian. Suppose that N is not contained in A. Consider
$ G^{\mathfrak {F}} $
is abelian. Suppose that N is not contained in A. Consider
![]() $ Y=AN $
. Then
$ Y=AN $
. Then
![]() $ Y=A(Y\cap B) $
is the weakly mutually permutable product of A and
$ Y=A(Y\cap B) $
is the weakly mutually permutable product of A and
![]() $ Y\cap B $
. Moreover,
$ Y\cap B $
. Moreover,
![]() $ Y\cap B $
is nilpotent and permutes with each Sylow subgroup of A. If
$ Y\cap B $
is nilpotent and permutes with each Sylow subgroup of A. If
![]() $ Y < G $
, then
$ Y < G $
, then
![]() $ Y^{\mathfrak {F}}=A^{\mathfrak {F}} $
and N normalises
$ Y^{\mathfrak {F}}=A^{\mathfrak {F}} $
and N normalises
![]() $ A^{\mathfrak {F}} $
, which implies that
$ A^{\mathfrak {F}} $
, which implies that
![]() $ G^{\mathfrak {F}} $
is abelian since
$ G^{\mathfrak {F}} $
is abelian since
![]() $ (G^{\mathfrak {F}})'\leqslant A^{\mathfrak {F}} $
. We assume that
$ (G^{\mathfrak {F}})'\leqslant A^{\mathfrak {F}} $
. We assume that
![]() $ G=Y=AN $
. Since B is nilpotent and
$ G=Y=AN $
. Since B is nilpotent and
![]() $ A\cap B $
is a subnormal subgroup of A,
$ A\cap B $
is a subnormal subgroup of A,
![]() $ (A \cap B)[A\cap B, A]=(A\cap B)^{A}\leqslant (A\cap B)^{G}\leqslant F(G) $
and
$ (A \cap B)[A\cap B, A]=(A\cap B)^{A}\leqslant (A\cap B)^{G}\leqslant F(G) $
and
![]() $ [A\cap B, A] $
is contained in A. It follows that
$ [A\cap B, A] $
is contained in A. It follows that
![]() $ [A\cap B, A] $
is a subnormal nilpotent subgroup of
$ [A\cap B, A] $
is a subnormal nilpotent subgroup of
![]() $ G $
. By [Reference Doerk and Hawkes6, A, 14.3],
$ G $
. By [Reference Doerk and Hawkes6, A, 14.3],
![]() $ [A\cap B, A] $
is normalised by N. Since
$ [A\cap B, A] $
is normalised by N. Since
![]() $ [A\cap B, A] $
is a normal subgroup of A,
$ [A\cap B, A] $
is a normal subgroup of A,
![]() $ [A\cap B, A] $
is a normal subgroup of
$ [A\cap B, A] $
is a normal subgroup of
![]() $ AN=G $
. If
$ AN=G $
. If
![]() $ [A\cap B, A]=1 $
, then
$ [A\cap B, A]=1 $
, then
![]() $ (A\cap B)^{A}=A\cap B $
is normalised by A and N, and thus
$ (A\cap B)^{A}=A\cap B $
is normalised by A and N, and thus
![]() $ A\cap B $
is a normal subgroup of
$ A\cap B $
is a normal subgroup of
![]() $ G $
. If
$ G $
. If
![]() $ [A\cap B, A] \neq 1 $
, then it is a normal subgroup of G contained in A and in
$ [A\cap B, A] \neq 1 $
, then it is a normal subgroup of G contained in A and in
![]() $F(G)$
. In both cases, there exists N, a minimal normal subgroup of G contained in
$F(G)$
. In both cases, there exists N, a minimal normal subgroup of G contained in
![]() $F(G)$
and in A. By the same argument as above,
$F(G)$
and in A. By the same argument as above,
![]() $ G^{\mathfrak {F}} $
is abelian.
$ G^{\mathfrak {F}} $
is abelian.
We now show that
![]() $ G^{\mathfrak {F}} $
is a
$ G^{\mathfrak {F}} $
is a
![]() $ p $
-group. Let
$ p $
-group. Let
![]() $ N_{2} $
be a minimal normal subgroup of
$ N_{2} $
be a minimal normal subgroup of
![]() $ G $
. Then
$ G $
. Then
![]() $ N_{2}\leqslant G^{\mathfrak {F}} $
is an elementary abelian
$ N_{2}\leqslant G^{\mathfrak {F}} $
is an elementary abelian
![]() $ p $
-group for some prime
$ p $
-group for some prime
![]() $ p $
. Since
$ p $
. Since
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}}N_{2} $
and
$ G^{\mathfrak {F}}=A^{\mathfrak {F}}N_{2} $
and
![]() $ G^{\mathfrak {F}}/A^{\mathfrak {F}} $
is a
$ G^{\mathfrak {F}}/A^{\mathfrak {F}} $
is a
![]() $ p $
-group,
$ p $
-group,
![]() $ O^{p}(G^{\mathfrak {F}})\leqslant A^{\mathfrak {F}} $
. If
$ O^{p}(G^{\mathfrak {F}})\leqslant A^{\mathfrak {F}} $
. If
![]() $ O^{p}(G^{\mathfrak {F}})\not =1 $
, then
$ O^{p}(G^{\mathfrak {F}})\not =1 $
, then
![]() $ O^{p}(G^{\mathfrak {F}}) $
is a normal subgroup of
$ O^{p}(G^{\mathfrak {F}}) $
is a normal subgroup of
![]() $ G $
and
$ G $
and
![]() $ A^{\mathfrak {F}} $
contains a minimal normal subgroup of
$ A^{\mathfrak {F}} $
contains a minimal normal subgroup of
![]() $ G $
. This means that
$ G $
. This means that
![]() $ G^{\mathfrak {F}}=A^{\mathfrak {F}} $
, a contradiction. Hence,
$ G^{\mathfrak {F}}=A^{\mathfrak {F}} $
, a contradiction. Hence,
![]() $ O^{p}(G^{\mathfrak {F}})=1 $
, that is,
$ O^{p}(G^{\mathfrak {F}})=1 $
, that is,
![]() $ G^{\mathfrak {F}} $
is a
$ G^{\mathfrak {F}} $
is a
![]() $ p $
-group for some prime
$ p $
-group for some prime
![]() $ p $
. Since
$ p $
. Since
![]() $ \textit {Soc}(G) $
is contained in
$ \textit {Soc}(G) $
is contained in
![]() $ G^{\mathfrak {F}} $
, we have
$ G^{\mathfrak {F}} $
, we have
![]() $ F(G)=O_{p}(G) $
.
$ F(G)=O_{p}(G) $
.
-
(b)
 $G^{\mathfrak {F}}$
is contained in B and
$G^{\mathfrak {F}}$
is contained in B and
 $A\cap B$
is the unique Sylow p-subgroup of A.
$A\cap B$
is the unique Sylow p-subgroup of A.
Consider
![]() $ (A\cap B)A_{p'} $
, where
$ (A\cap B)A_{p'} $
, where
![]() $ A_{p'} $
is a Hall
$ A_{p'} $
is a Hall
![]() $ p' $
-subgroup of A, and let
$ p' $
-subgroup of A, and let
![]() $ X $
be a maximal subgroup of A containing
$ X $
be a maximal subgroup of A containing
![]() $ (A\cap B)A_{p'} $
. Consider the subgroup
$ (A\cap B)A_{p'} $
. Consider the subgroup
![]() $ H=XB $
which is the weakly mutually permutable product of
$ H=XB $
which is the weakly mutually permutable product of
![]() $ X $
and B. Note that B permutes with all Sylow
$ X $
and B. Note that B permutes with all Sylow
![]() $ q $
-subgroups of
$ q $
-subgroups of
![]() $ X $
for
$ X $
for
![]() $ q\not =p $
, since they are all Sylow
$ q\not =p $
, since they are all Sylow
![]() $ q $
-subgroups of A, and B also permutes with all Sylow
$ q $
-subgroups of A, and B also permutes with all Sylow
![]() $ p $
-subgroups of
$ p $
-subgroups of
![]() $ X $
since they all contain
$ X $
since they all contain
![]() $ A\cap B $
(note that
$ A\cap B $
(note that
![]() $ A\cap B\leqslant O_{p}(X) $
which is contained in all Sylow
$ A\cap B\leqslant O_{p}(X) $
which is contained in all Sylow
![]() $ p $
-subgroups of
$ p $
-subgroups of
![]() $ X $
). If
$ X $
). If
![]() $G=H$
, then
$G=H$
, then
![]() $A=X(A \cap B)=X$
, a contradiction. Hence, H is a proper subgroup of G. It follows that
$A=X(A \cap B)=X$
, a contradiction. Hence, H is a proper subgroup of G. It follows that
![]() $ H^{\mathfrak {F}}=X^{\mathfrak {F}} $
and so
$ H^{\mathfrak {F}}=X^{\mathfrak {F}} $
and so
![]() $ H $
normalises
$ H $
normalises
![]() $ X^{\mathfrak {F}} $
. Note that
$ X^{\mathfrak {F}} $
. Note that
![]() $ X^{\mathfrak {F}}\leqslant A^{\mathfrak {F}} $
. If
$ X^{\mathfrak {F}}\leqslant A^{\mathfrak {F}} $
. If
![]() $ X^{\mathfrak {F}}\not = 1 $
, then
$ X^{\mathfrak {F}}\not = 1 $
, then
![]() $ (X^{\mathfrak {F}})^{G}\leqslant (X^{\mathfrak {F}})^{A} \leqslant A^{\mathfrak {F}} $
, a contradiction. Hence,
$ (X^{\mathfrak {F}})^{G}\leqslant (X^{\mathfrak {F}})^{A} \leqslant A^{\mathfrak {F}} $
, a contradiction. Hence,
![]() $ H^{\mathfrak {F}}=X^{\mathfrak {F}}=1 $
, that is,
$ H^{\mathfrak {F}}=X^{\mathfrak {F}}=1 $
, that is,
![]() $ H $
and
$ H $
and
![]() $ X $
belong to
$ X $
belong to
![]() $ \mathfrak {F} $
. Since
$ \mathfrak {F} $
. Since
![]() $ X $
is a maximal subgroup of A,
$ X $
is a maximal subgroup of A,
![]() $ X $
is an
$ X $
is an
![]() $ \mathfrak {F} $
-projector of A. Since
$ \mathfrak {F} $
-projector of A. Since
![]() $ A^{\mathfrak {F}} $
is abelian,
$ A^{\mathfrak {F}} $
is abelian,
![]() $ A^{\mathfrak {F}}X=A $
and
$ A^{\mathfrak {F}}X=A $
and
![]() $ X\cap A^{\mathfrak {F}}=1 $
by [Reference Doerk and Hawkes6, IV, 5.18]. This means that
$ X\cap A^{\mathfrak {F}}=1 $
by [Reference Doerk and Hawkes6, IV, 5.18]. This means that
![]() $ G=A^{\mathfrak {F}}XB=G^{\mathfrak {F}}H $
. By [Reference Doerk and Hawkes6, III, 3.2], there exists an
$ G=A^{\mathfrak {F}}XB=G^{\mathfrak {F}}H $
. By [Reference Doerk and Hawkes6, III, 3.2], there exists an
![]() $ \mathfrak {F} $
-projector
$ \mathfrak {F} $
-projector
![]() $ F $
of
$ F $
of
![]() $ G $
containing
$ G $
containing
![]() $ H $
and so
$ H $
and so
![]() $ G=G^{\mathfrak {F}}F $
and
$ G=G^{\mathfrak {F}}F $
and
![]() $ F\cap G^{\mathfrak {F}}=1 $
. Hence,
$ F\cap G^{\mathfrak {F}}=1 $
. Hence,
![]() $ {G^{\mathfrak {F}}=A^{\mathfrak {F}}(G^{\mathfrak {F}}\cap XB)=A^{\mathfrak {F}} }$
, a contradiction. Consequently,
$ {G^{\mathfrak {F}}=A^{\mathfrak {F}}(G^{\mathfrak {F}}\cap XB)=A^{\mathfrak {F}} }$
, a contradiction. Consequently,
![]() $ A=(A\cap B)A_{p'} $
. In particular,
$ A=(A\cap B)A_{p'} $
. In particular,
![]() ${ A^{\mathfrak {F}}\leqslant A\cap B \leqslant B }$
and
${ A^{\mathfrak {F}}\leqslant A\cap B \leqslant B }$
and
![]() $ A\cap B $
is the unique Sylow subgroup of A since
$ A\cap B $
is the unique Sylow subgroup of A since
![]() $ A\cap B $
is a subnormal subgroup of A. On the other hand,
$ A\cap B $
is a subnormal subgroup of A. On the other hand,
![]() $1 \neq (A \cap B)^{G}=(A \cap B)^{B} \leq B$
. Hence, there exists N, a minimal normal subgroup of G contained in B. Consequently,
$1 \neq (A \cap B)^{G}=(A \cap B)^{B} \leq B$
. Hence, there exists N, a minimal normal subgroup of G contained in B. Consequently,
![]() $G^{\mathfrak {F}}=A^{\mathfrak {F}}N \leq B$
.
$G^{\mathfrak {F}}=A^{\mathfrak {F}}N \leq B$
.
-
(c)
 $AF(G)$
is a proper subgroup of G.
$AF(G)$
is a proper subgroup of G.
Suppose that
![]() $ G=AF(G) $
. Let
$ G=AF(G) $
. Let
![]() $ Z $
be a maximal subgroup of
$ Z $
be a maximal subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ A\leqslant Z $
. Then
$ A\leqslant Z $
. Then
![]() $ Z=A(Z\cap B) $
is the weakly mutually permutable product of A and
$ Z=A(Z\cap B) $
is the weakly mutually permutable product of A and
![]() $ Z\cap B $
. Note that
$ Z\cap B $
. Note that
![]() $ Z\cap B $
permutes with each Sylow subgroup of A by Lemma 2.2. By the minimality of
$ Z\cap B $
permutes with each Sylow subgroup of A by Lemma 2.2. By the minimality of
![]() $ G $
, we have
$ G $
, we have
![]() $ Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
, that is,
$ Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
, that is,
![]() $ A^{\mathfrak {F}} $
is normal in
$ A^{\mathfrak {F}} $
is normal in
![]() $ Z $
. Also
$ Z $
. Also
![]() $ G=ZF(G) $
. Suppose that
$ G=ZF(G) $
. Suppose that
![]() $ G^{\mathfrak {F}} $
is not contained in
$ G^{\mathfrak {F}} $
is not contained in
![]() $ Z $
. Then
$ Z $
. Then
![]() $ G=G^{\mathfrak {F}}Z $
and so
$ G=G^{\mathfrak {F}}Z $
and so
![]() $ A^{\mathfrak {F}}=Z^{\mathfrak {F}} $
is normal in
$ A^{\mathfrak {F}}=Z^{\mathfrak {F}} $
is normal in
![]() $ G $
since
$ G $
since
![]() $ A^{\mathfrak {F}} $
is normal in
$ A^{\mathfrak {F}} $
is normal in
![]() $ G^{\mathfrak {F}} $
. Therefore,
$ G^{\mathfrak {F}} $
. Therefore,
![]() $ A^{\mathfrak {F}}=G^{\mathfrak {F}} $
, a contradiction. We may assume that
$ A^{\mathfrak {F}}=G^{\mathfrak {F}} $
, a contradiction. We may assume that
![]() $ G^{\mathfrak {F}}\leqslant Z $
. Let N be a minimal normal subgroup of
$ G^{\mathfrak {F}}\leqslant Z $
. Let N be a minimal normal subgroup of
![]() $ G $
. Since
$ G $
. Since
![]() $\mathit {Soc}(G) \leqslant G^{\mathfrak {F}} $
by step (a), we have
$\mathit {Soc}(G) \leqslant G^{\mathfrak {F}} $
by step (a), we have
![]() $ N\leqslant G^{\mathfrak {F}} $
. Note that
$ N\leqslant G^{\mathfrak {F}} $
. Note that
![]() $ F(G) $
centralises N. Hence, N is also a minimal normal subgroup of
$ F(G) $
centralises N. Hence, N is also a minimal normal subgroup of
![]() $ Z $
. This means that
$ Z $
. This means that
![]() $ N\cap Z^{\mathfrak {F}}\in \{ 1, N\} $
. If
$ N\cap Z^{\mathfrak {F}}\in \{ 1, N\} $
. If
![]() $ N\cap Z^{\mathfrak {F}}=N $
, then N is contained in
$ N\cap Z^{\mathfrak {F}}=N $
, then N is contained in
![]() $ A^{\mathfrak {F}} $
, a contradiction. Suppose that
$ A^{\mathfrak {F}} $
, a contradiction. Suppose that
![]() $ N\cap Z^{\mathfrak {F}}=1 $
. Then
$ N\cap Z^{\mathfrak {F}}=1 $
. Then
![]() $ NZ^{\mathfrak {F}}/Z^{\mathfrak {F}} $
is a minimal normal subgroup of
$ NZ^{\mathfrak {F}}/Z^{\mathfrak {F}} $
is a minimal normal subgroup of
![]() $ Z/Z^{\mathfrak {F}} $
. Since
$ Z/Z^{\mathfrak {F}} $
. Since
![]() $ Z/Z^{\mathfrak {F}}\in \mathfrak {F} $
, we have that N is
$ Z/Z^{\mathfrak {F}}\in \mathfrak {F} $
, we have that N is
![]() $ \mathfrak {F} $
-central in
$ \mathfrak {F} $
-central in
![]() $ Z $
and hence N is also
$ Z $
and hence N is also
![]() $ \mathfrak {F} $
-central in
$ \mathfrak {F} $
-central in
![]() $ G $
. This means that N is contained in every
$ G $
. This means that N is contained in every
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
using [Reference Doerk and Hawkes6, V, 3.2]. Let
$ G $
using [Reference Doerk and Hawkes6, V, 3.2]. Let
![]() $ F $
be such an
$ F $
be such an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
. Then
$ G $
. Then
![]() $ G=G^{\mathfrak {F}}F $
and
$ G=G^{\mathfrak {F}}F $
and
![]() $ G^{\mathfrak {F}}\cap F=1 $
, a contradiction.
$ G^{\mathfrak {F}}\cap F=1 $
, a contradiction.
-
(d) Final contradiction.
We want to show that
![]() $ G=AP $
, where
$ G=AP $
, where
![]() $ P $
is the Sylow
$ P $
is the Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
, to obtain our final contradiction. We also want to show that
$ G $
, to obtain our final contradiction. We also want to show that
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ {\vert }G{\vert } $
. Suppose that
$ {\vert }G{\vert } $
. Suppose that
![]() $ AQ $
is a proper subgroup of
$ AQ $
is a proper subgroup of
![]() $ G $
for every
$ G $
for every
![]() $ q $
dividing
$ q $
dividing
![]() $ {\vert }B{\vert } $
and every Sylow
$ {\vert }B{\vert } $
and every Sylow
![]() $ q $
-subgroup
$ q $
-subgroup
![]() $ Q $
of B. Then
$ Q $
of B. Then
![]() $ A(A\cap B)Q $
is the weakly mutually permutable product of A and
$ A(A\cap B)Q $
is the weakly mutually permutable product of A and
![]() $ (A\cap B)Q $
. By Lemma 2.2,
$ (A\cap B)Q $
. By Lemma 2.2,
![]() $ (A\cap B)Q $
permutes with each Sylow subgroup of A. Using the minimality of
$ (A\cap B)Q $
permutes with each Sylow subgroup of A. Using the minimality of
![]() $ G $
, we have
$ G $
, we have
![]() $ (AQ)^{\mathfrak {F}}=A^{\mathfrak {F}} $
. Therefore,
$ (AQ)^{\mathfrak {F}}=A^{\mathfrak {F}} $
. Therefore,
![]() $ A^{\mathfrak {F}} $
is normalised by every Sylow
$ A^{\mathfrak {F}} $
is normalised by every Sylow
![]() $ q $
-subgroup of B, that is,
$ q $
-subgroup of B, that is,
![]() $ A^{\mathfrak {F}} $
is normal in
$ A^{\mathfrak {F}} $
is normal in
![]() $ G $
, a contradiction. Hence,
$ G $
, a contradiction. Hence,
![]() $ G=AQ $
for some Sylow
$ G=AQ $
for some Sylow
![]() $ q $
-subgroup of B, Q say. Suppose that
$ q $
-subgroup of B, Q say. Suppose that
![]() $ q\not = p $
. Then
$ q\not = p $
. Then
![]() $ A^{\mathfrak {F}} $
is centralised by
$ A^{\mathfrak {F}} $
is centralised by
![]() $ Q $
and that means
$ Q $
and that means
![]() $ A^{\mathfrak {F}} $
is a normal subgroup of
$ A^{\mathfrak {F}} $
is a normal subgroup of
![]() $ G $
, a contradiction. Hence,
$ G $
, a contradiction. Hence,
![]() $ G=AP $
, where
$ G=AP $
, where
![]() $ P $
is a Sylow p-subgroup of B. In particular, B is a
$ P $
is a Sylow p-subgroup of B. In particular, B is a
![]() $ p $
-group and since
$ p $
-group and since
![]() $A=(A \cap B)A_{p'}$
, we have
$A=(A \cap B)A_{p'}$
, we have
![]() $G=A_{p'}P$
and P is a Sylow p-subgroup of G.
$G=A_{p'}P$
and P is a Sylow p-subgroup of G.
We now show that
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ {\vert }G{\vert } $
. Let
$ {\vert }G{\vert } $
. Let
![]() $ l $
be the largest prime dividing
$ l $
be the largest prime dividing
![]() $ {\vert }G{\vert } $
and
$ {\vert }G{\vert } $
and
![]() $ L $
be a Sylow
$ L $
be a Sylow
![]() $ l $
-subgroup of
$ l $
-subgroup of
![]() $ G $
. Suppose
$ G $
. Suppose
![]() $ l\not =p $
. We may assume that
$ l\not =p $
. We may assume that
![]() $ L\leqslant A $
. Note that
$ L\leqslant A $
. Note that
![]() $ LG^{\mathfrak {F}} $
is a normal subgroup of
$ LG^{\mathfrak {F}} $
is a normal subgroup of
![]() $ G $
since
$ G $
since
![]() $ G/G^{\mathfrak {F}}\in \mathfrak {F} $
and hence has a Sylow tower of supersoluble type. Let
$ G/G^{\mathfrak {F}}\in \mathfrak {F} $
and hence has a Sylow tower of supersoluble type. Let
![]() $ Z $
be a maximal subgroup of
$ Z $
be a maximal subgroup of
![]() $ G $
containing A. Then
$ G $
containing A. Then
![]() $ Z=(Z\cap B)A $
is the weakly mutually permutable product of A and
$ Z=(Z\cap B)A $
is the weakly mutually permutable product of A and
![]() $ Z\cap B $
, and
$ Z\cap B $
, and
![]() $ Z\cap B $
permutes with each Sylow subgroup of A. By the minimality of
$ Z\cap B $
permutes with each Sylow subgroup of A. By the minimality of
![]() $ G $
,
$ G $
,
![]() $ Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
. If
$ Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
. If
![]() $ G^{\mathfrak {F}} $
is not contained in
$ G^{\mathfrak {F}} $
is not contained in
![]() $ Z $
, then by the same argument as in step (c),
$ Z $
, then by the same argument as in step (c),
![]() $ A^{\mathfrak {F}} $
is a normal subgroup of
$ A^{\mathfrak {F}} $
is a normal subgroup of
![]() $ G $
, a contradiction. Hence,
$ G $
, a contradiction. Hence,
![]() $ G^{\mathfrak {F}} $
is contained in
$ G^{\mathfrak {F}} $
is contained in
![]() $ Z $
. Therefore,
$ Z $
. Therefore,
![]() $ LG^{\mathfrak {F}} $
is contained in
$ LG^{\mathfrak {F}} $
is contained in
![]() $ Z $
and so
$ Z $
and so
![]() $ (LG^{\mathfrak {F}})^{\mathfrak {F}}\leqslant Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
. If
$ (LG^{\mathfrak {F}})^{\mathfrak {F}}\leqslant Z^{\mathfrak {F}}=A^{\mathfrak {F}} $
. If
![]() $ (LG^{\mathfrak {F}})^{\mathfrak {F}}\not = 1 $
, then
$ (LG^{\mathfrak {F}})^{\mathfrak {F}}\not = 1 $
, then
![]() $ (LG^{\mathfrak {F}})^{\mathfrak {F}} $
is a normal subgroup of
$ (LG^{\mathfrak {F}})^{\mathfrak {F}} $
is a normal subgroup of
![]() $ G $
contained in
$ G $
contained in
![]() $ A^{\mathfrak {F}} $
, a contradiction. This means that
$ A^{\mathfrak {F}} $
, a contradiction. This means that
![]() $ LG^{\mathfrak {F}}\in \mathfrak {F} $
. In particular,
$ LG^{\mathfrak {F}}\in \mathfrak {F} $
. In particular,
![]() $ L $
is a normal subgroup of
$ L $
is a normal subgroup of
![]() $ G $
since it is a characteristic subgroup of the normal subgroup
$ G $
since it is a characteristic subgroup of the normal subgroup
![]() $ LG^{\mathfrak {F}} $
. It follows that
$ LG^{\mathfrak {F}} $
. It follows that
![]() $ L\leqslant F(G)= O_{p}(G) $
, a contradiction. Therefore,
$ L\leqslant F(G)= O_{p}(G) $
, a contradiction. Therefore,
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ {\vert }G{\vert } $
. Since
$ {\vert }G{\vert } $
. Since
![]() $ G^{\mathfrak {F}} \leqslant P $
and
$ G^{\mathfrak {F}} \leqslant P $
and
![]() $ P/G^{\mathfrak {F}} $
is a normal subgroup of
$ P/G^{\mathfrak {F}} $
is a normal subgroup of
![]() $ G $
,
$ G $
,
![]() $ P $
is a normal subgroup of
$ P $
is a normal subgroup of
![]() $ G $
. Hence,
$ G $
. Hence,
![]() $ P=F(G) $
and so
$ P=F(G) $
and so
![]() $ G=AF(G) $
, contradicting step (c). This contradiction concludes our proof.
$ G=AF(G) $
, contradicting step (c). This contradiction concludes our proof.
Theorem 3.2. Let
![]() $ \mathfrak {F} $
be a formation. Assume that either
$ \mathfrak {F} $
be a formation. Assume that either
![]() $\mathfrak {F} = \mathfrak {U}$
or
$\mathfrak {F} = \mathfrak {U}$
or
![]() $\mathfrak {F}$
is a saturated Fitting formation containing
$\mathfrak {F}$
is a saturated Fitting formation containing
![]() $\mathfrak {U}$
. Let
$\mathfrak {U}$
. Let
![]() $G = AB$
be the weakly mutually permutable product of the subgroups A and B. Suppose that
$G = AB$
be the weakly mutually permutable product of the subgroups A and B. Suppose that
![]() $ G' $
is nilpotent,
$ G' $
is nilpotent,
![]() $ A_{1} $
is an
$ A_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of A such that
$ \mathfrak {F} $
-normaliser of A such that
![]() $ A\cap B \leqslant A_{1} $
and
$ A\cap B \leqslant A_{1} $
and
![]() $ B_{1} $
is an
$ B_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of B such that
$ \mathfrak {F} $
-normaliser of B such that
![]() $ A\cap B \leqslant B_{1} $
. Then
$ A\cap B \leqslant B_{1} $
. Then
![]() $ A_{1}B_{1}$
is an
$ A_{1}B_{1}$
is an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
.
$ G $
.
Proof. Suppose that the result is not true and let
![]() $ G $
be a counterexample with
$ G $
be a counterexample with
![]() $ {\vert }G{\vert } + {\vert }A{\vert } + {\vert }B{\vert } $
minimal. If A and B are both
$ {\vert }G{\vert } + {\vert }A{\vert } + {\vert }B{\vert } $
minimal. If A and B are both
![]() $\mathfrak {F}$
-groups, then G is an
$\mathfrak {F}$
-groups, then G is an
![]() $\mathfrak {F}$
-group by [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Lemma 2.6]. Hence, we may assume without loss of generality that
$\mathfrak {F}$
-group by [Reference Ballester-Bolinches, Madanha and Pedraza-Aguilera3, Lemma 2.6]. Hence, we may assume without loss of generality that
![]() $ 1\not = A^{\mathfrak {F}} $
. Since
$ 1\not = A^{\mathfrak {F}} $
. Since
![]() $ \mathfrak {F} $
is a saturated formation,
$ \mathfrak {F} $
is a saturated formation,
![]() $ A^{\mathfrak {F}} $
is not contained in
$ A^{\mathfrak {F}} $
is not contained in
![]() $ \Phi (A) $
. There is a subgroup
$ \Phi (A) $
. There is a subgroup
![]() $ T $
of A such that
$ T $
of A such that
![]() $ F(A^{\mathfrak {F}}/(\Phi (A)\cap A^{\mathfrak {F}}))=T/(\Phi (A)\cap A^{\mathfrak {F}})\not = 1 $
. Note that
$ F(A^{\mathfrak {F}}/(\Phi (A)\cap A^{\mathfrak {F}}))=T/(\Phi (A)\cap A^{\mathfrak {F}})\not = 1 $
. Note that
![]() $ T\cap \Phi (A)=A^{\mathfrak {F}}\cap \Phi (A) $
. Using [Reference Doerk and Hawkes6, V, 3.7], it follows that
$ T\cap \Phi (A)=A^{\mathfrak {F}}\cap \Phi (A) $
. Using [Reference Doerk and Hawkes6, V, 3.7], it follows that
![]() $ T $
is a nilpotent subgroup of
$ T $
is a nilpotent subgroup of
![]() $ G $
. Moreover, since
$ G $
. Moreover, since
![]() $G^{\mathfrak {F}} \leq G'$
, it follows that
$G^{\mathfrak {F}} \leq G'$
, it follows that
![]() $G^{\mathfrak {F}}$
is nilpotent. Therefore, T is a subnormal subgroup of G. Let
$G^{\mathfrak {F}}$
is nilpotent. Therefore, T is a subnormal subgroup of G. Let
![]() $ M $
be a maximal subgroup of A such that
$ M $
be a maximal subgroup of A such that
![]() $ T $
is not contained in
$ T $
is not contained in
![]() $ M $
. Then
$ M $
. Then
![]() $ A=TM=A^{\mathfrak {F}}M=F(A)M $
. Thus
$ A=TM=A^{\mathfrak {F}}M=F(A)M $
. Thus
![]() $ M $
is an
$ M $
is an
![]() $ \mathfrak {F} $
-critical maximal subgroup of A. By [Reference Doerk and Hawkes6, V, 3.7], every
$ \mathfrak {F} $
-critical maximal subgroup of A. By [Reference Doerk and Hawkes6, V, 3.7], every
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ M $
is an
$ M $
is an
![]() $ \mathfrak {F} $
-normaliser of A. By [Reference Doerk and Hawkes6, V, 3.2],
$ \mathfrak {F} $
-normaliser of A. By [Reference Doerk and Hawkes6, V, 3.2],
![]() $ \mathfrak {F} $
-normalisers of A are conjugate and so we may assume that
$ \mathfrak {F} $
-normalisers of A are conjugate and so we may assume that
![]() $ A_{1} \leqslant M $
. Note that
$ A_{1} \leqslant M $
. Note that
![]() $ G=T(MB)=F(G)(MB)=G^{\mathfrak {F}}(MB) $
. If
$ G=T(MB)=F(G)(MB)=G^{\mathfrak {F}}(MB) $
. If
![]() $ G=MB $
, then
$ G=MB $
, then
![]() $ G $
is the weakly mutually permutable product of subgroups
$ G $
is the weakly mutually permutable product of subgroups
![]() $ M $
and B and also
$ M $
and B and also
![]() $ {\vert }G{\vert } + {\vert }M{\vert } + {\vert }B{\vert } < {\vert }G{\vert } + {\vert }A{\vert } + {\vert }B{\vert } $
. By the choice of
$ {\vert }G{\vert } + {\vert }M{\vert } + {\vert }B{\vert } < {\vert }G{\vert } + {\vert }A{\vert } + {\vert }B{\vert } $
. By the choice of
![]() $ G $
,
$ G $
,
![]() $ A_{1}B_{1} $
is an
$ A_{1}B_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
, a contradiction. We may assume that
$ G $
, a contradiction. We may assume that
![]() $ MB<G $
. Note that
$ MB<G $
. Note that
![]() $ MB $
is a maximal
$ MB $
is a maximal
![]() $ \mathfrak {F} $
-critical subgroup of
$ \mathfrak {F} $
-critical subgroup of
![]() $ G $
. Thus
$ G $
. Thus
![]() $ A_{1}B_{1} $
is an
$ A_{1}B_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ MB $
. Using [Reference Doerk and Hawkes6, V, 3.7], we find that
$ MB $
. Using [Reference Doerk and Hawkes6, V, 3.7], we find that
![]() $ A_{1}B_{1} $
is an
$ A_{1}B_{1} $
is an
![]() $ \mathfrak {F} $
-normaliser of
$ \mathfrak {F} $
-normaliser of
![]() $ G $
, a contradiction. This concludes our proof.
$ G $
, a contradiction. This concludes our proof.
As we said in the Introduction, the result is also true under these same hypotheses for projectors. However, the result is not true for saturated Fitting formations containing
![]() $\mathfrak {U}$
when B is nilpotent, as Example 1.3 shows.
$\mathfrak {U}$
when B is nilpotent, as Example 1.3 shows.