Introduction
Snow avalanche forecasting is defined here to include estimates of both current and futuresnow stability. The discussion is confined to the conventional, widely-practiced methods of avalanche forecasting based on a mix of meteorology, snow physics, and empirical experience. Purely statistical methods are omitted. Conventional forecasting has the following characteristics :
(1) A strong element of determinism based on the interaction of weather with physicalprocesses in the snow cover, coupled with largely non-deterministic decisions about actual forecasts.
(2) Reliance on diverse and often redundant sources of information about snow, weather, and avalanche occurrence.
(3) A high level of skill developed through empirical experience.
(4) A widespread inability on the part of practicing forecasters to explain the personal connection between experience and skill.
A concept which unifies these characteristics is found in the patterns of logic involved in avalanche forecasting. Deductive logic dominates the understanding of physical cause-and-effect involved in snow cover behavior, but, owing to intractable complexities on avalanche paths in the real world, actual forecasting decisions are reached through inductive logic, which carries with it uncertainty. Contrary to the idea conveyed by many texts and teachingmethods, avalanche forecasting as actually practiced does not work from the premises of deductive logic, arguing that each specific instance of snow stability can be deduced from general rules about snow mechanics. Rather, it follows the practical strategy most useful for dealing with the real world, the one which minimizes uncertainty. This paper is about minimizing uncertainty.
The Data Base
Inductive logic in avalanche forecasting has been identified by analyzing information from the following sources:
(1) A three-year project to design, set up, and operate a central avalanche forecasting facility for western Washington State was carried out during the period 1975-78.During this time the working forecasters maintained an on-going dialogue about their techniques, kept detailed notes on procedures, and compiled an algorithm outlining decision methods (Reference LaChapelle and LaChapelleLaChapelle and others, 1978).
(2) Extensive travel in the western United States during the winter of 1977-78 afforded a chance to interview some twenty-five experienced avalanche forecasters in the U.S. Forest Service, ski industry, and state highway departments. Although the levels of experience and skills among these individuals was uniformly high, the amount of useful information they communicated varied widely. In no case was a clear analytical forecasting method volunteered in detail; the underlying principles were brought out only by persistent questioning,
(3) The most valuable data came from ten case histories of specific forecasting episodes which had either been recorded in the past or written in response to this research. The contributors were few because the abilities of introspection, self-analysis, and exposition are only rarely combined in one individual, but these case histories provided the key insights into avalanche forecasting. Space limitations preclude reproducing them here and they will be published elsewhere.
The Fundamental Forecasting Process
The fundamental forecasting process
First, review of the data sources outlined above identifies several recurring patterns inforecasting.
(1) There are few surprises for the experienced forecaster. Though high forecasting precision is difficult to achieve, complete failures are rare. Enough inferences can usually be drawn to prepare a reasonable estimate of snow stability. Experience in interpreting the interaction between weather and snow is essential.
(2) There are no instant avalanche forecasts. No fixed formula is available to produce a snow stability rating from arbitrary snow and weather parameters. The forecast, instead, is integrated through time with evidence accumulating by increments. The timescale can range from hours to months, but integration in some form is pervasive throughout the sources.
(3) Information about snow conditions is highly diverse. Weather, snow structure, avalanche occurrence past and present, test ski-ing, artificial release, and local climate history all go into the forecast. Every available item, no matter how trivial, uncertain or seemingly irrelevant, enters the integration.
(4) The diversity of useful data is not random. These data readily fall into three categories that deal respectively with meteorology, snow-cover structure, and mechanical state of snow on a slope.
In the light of these observations, avalanche forecasting thus is seen to be the cumulativeintegration through time of a widely diverse body of information. This process is intuitively understood and practiced by every successful avalanche forecaster, but there is surprisingly little formal description of it in the literature. Of recent authors, Reference WilsonWilson (1977) has mostclearly expressed the principles involved: “No single clue will tell you all you need to know;you’ll have to be observant, and you’ll have to make a continuing evaluation ” (emphasis added).
Formally stated, the steps in avalanche forecasting are these:
(1) Available data are collected about the place and time in question. Some of these data may be vague, anecdotal, or general in nature (second-hand reports, climatology, past weather trends), while others may be quite precise (snow-fall records, avalanche records, weather maps)
(2) A hypothesis about snow stability is formed on the basis of the initially available data.(A first estimate may see an unstable snow pattern, or the amount of snow required to overload a slope may be anticipated.)
(3) The hypothesis is tested through observation and experiment. (Field checks are made for avalanche occurrence, mechanical tests are made for failure planes in new snow, or artificial release is attempted.)
(4) On the basis of the tests, the hypothesis is confirmed or revised. This test-revision process may be repeated a number of times over time spans ranging anywhere from hours to months, if a sufficiently reliable picture about snow stability has not yet emerged.
(5) Finally, the hypothesis is revised or confirmed to the point that it is seen to represent current reality of the snow cover. An evaluation or prediction is made. (Safe slopes are selected for ski-ing, a degree of hazard is estimated, or an avalanche warning is issued.)
(6) Actual avalanche occurrences (or non-occurrences) are monitored to check prediction accuracy.
Even though the whole process is often compressed at the expense of one or more steps, it is still clearly recognizable as inductive logic of the scientific method. Induction may proceed by a number of paths and heretofore it has been done largely at the intuitive level with little guidance from rational analysis. Avalanche forecasting as actually practiced uses inductive logic to combine varying sets of minute particulars, many of them obtained by deterministic methods, to identify again and again specific states of snow stability.
Iteration and Redundancy
The practical applications of inductive logic to avalanche forecasting follow well-known principles of information theory (Reference ShannonShannon, 1948). “Information” in this context does not in the usual semantic sense mean a quantity of knowledge conveyed, but rather the degree of uncertainty by a message receptor about what is going to be conveyed. A quantitative discussion of this concept is given below under Data categories. Here Shannon’s original term, entropy, is adopted and is equated, as many authors have done, with uncertainty. The avalanche forecasting practice of minimizing uncertainty, or entropy, often takes place by the use of iteration and redundancy.
Forecasting iteration consists of a winter-long evolution of snow stability estimates revised each day as current weather is seen to modify the previous day’s evaluation. This follows the principle of minimizing uncertainty by maximizing prior knowledge. The ideal goal, pursued but never achieved, is for the forecaster to gain a sufficiently perfect state of prior knowledge that the arrival of the next day’s snow and weather reports communicates zero additional knowledge about snow stability. In practice, each day’s imperfect state of prior knowledge is modified by new data, including avalanche occurrence reports, and becomes by iteration the next day’s prior knowledge. Conscious recognition of this practice has led to its explicit adoption at the avalanche-forecasting center for western Washington State in Seattle. The prevalent and strong reluctance of working forecasters to experience an interruption in their winter routine bears testimony to its widespread unconscious use. If an interruption does occur, for example, a week’s absence from the job, the train of iteration is broken and the returning forecaster must struggle to re-establish the base of prior knowledge. Iteration obviously is strongest for regional or local forecast centers where winter continuity can be established. It is weak and often highly telescoped in time for field situations which must be confronted without preparation, as on a ski tour in unknown terrain. Experienced forecasters exhibit remarkable ingenuity in developing prior knowledge even in these situations, leading to the general observation that they are seldom surprised. This importance of iteration suggests a fundamental axiom in avalanche forecasting: each avalanche forecast, for any path, at any time, begins with the first snow-fall of winter.
Redundancy is another route to reducing the uncertainty that goes with the imperfect flow of data from Nature to the forecaster. Errors in data transmission (noise) may be reduced by repetition, or weak insights into snow stability strengthened by multiple, reinforcing data sources describing snow structure, mechanics, or weather elements. A single data element may leave a high degree of uncertainty about snow stability, but as more elements accumulate, this uncertainly diminishes until a reasonably confident forecast can be made. Overlapping or complementary elements appear so frequently in avalanche forecasting, and are sought with such determination by practicing forecasters, that this phenomenon must perform a significant function in the inductive logic process. Striking evidence of redundancy turned up in one case history, where four forecasters worked for a winter in the San Juan Mountains of south-west Colorado as part of a research project in avalanche forecasting (Reference Armstrong, Armstrong, LaChapelle, Bovis and IvesArmstrong and others, 1974).These four took turns day by day in preparing avalanche forecasts for the vicinity of Red Mountain Pass. At the end of the winter they had very similar accuracy scores. Asked to list the data they considered important to their forecasting, they produced a list of 31 factors, of which, remarkably, only one, wind speed and direction, was common to all four. Only five factors were common to three of the four forecasters: study plot stratigraphy, precipitation intensity, old snow stability, new snow density and new snow crystal type. The individual factor lists ranged in length from 9 to 18, approximately in the order of experience. It seems that conventional forecasting methods embrace a sufficiently redundant data base that several inductive-logic paths exist and another axiom can be formulated: there is more than one way to forecast an avalanche.
Data Categories
The role of data categories in avalanche forecasting can be clarified by introducing the Shōda diagram (Fig. 1), derived from the work of the late avalanche scientist M. Shōda([Avalanches], 1973). This diagram outlines the chain of causation for snow avalanches, distinguishing the three data variables, meteorology, snow structure, and snow mechanics, as well as the fixed parameter (for a given site), terrain. For this discussion the elementary Shoda diagram (Fig. 2) is introduced with terrain omitted, giving fuller emphasis to the three variables which appeared independently in the analysis of forecasting techniques. Thenomenclature of set theory is followed here, with each data space made up of a series of eventclasses, each class consisting of a number of elementary events.
The forecasting data sequence, meteorology-snow structure-snow mechanics, follows the chain of causation from distant to proximate and also follows a sequence of decreasing number of event classes and especially a decreasing population of elementary events in each class. Snow-mechanics space needs extra comment, for in the present context it refers to those elements of mechanics which are directly observable and represent the integrated expression ofstresses and strains, namely, avalanche occurrence, fracture propagation, and failure-plane fig.1. fig.2.formation. Fundamental mechanical parameters like shear stress, viscosity, or tensile strength obviously are richly populated event classes which, though essential to theoretical under-standing, play little part in practical forecasting.
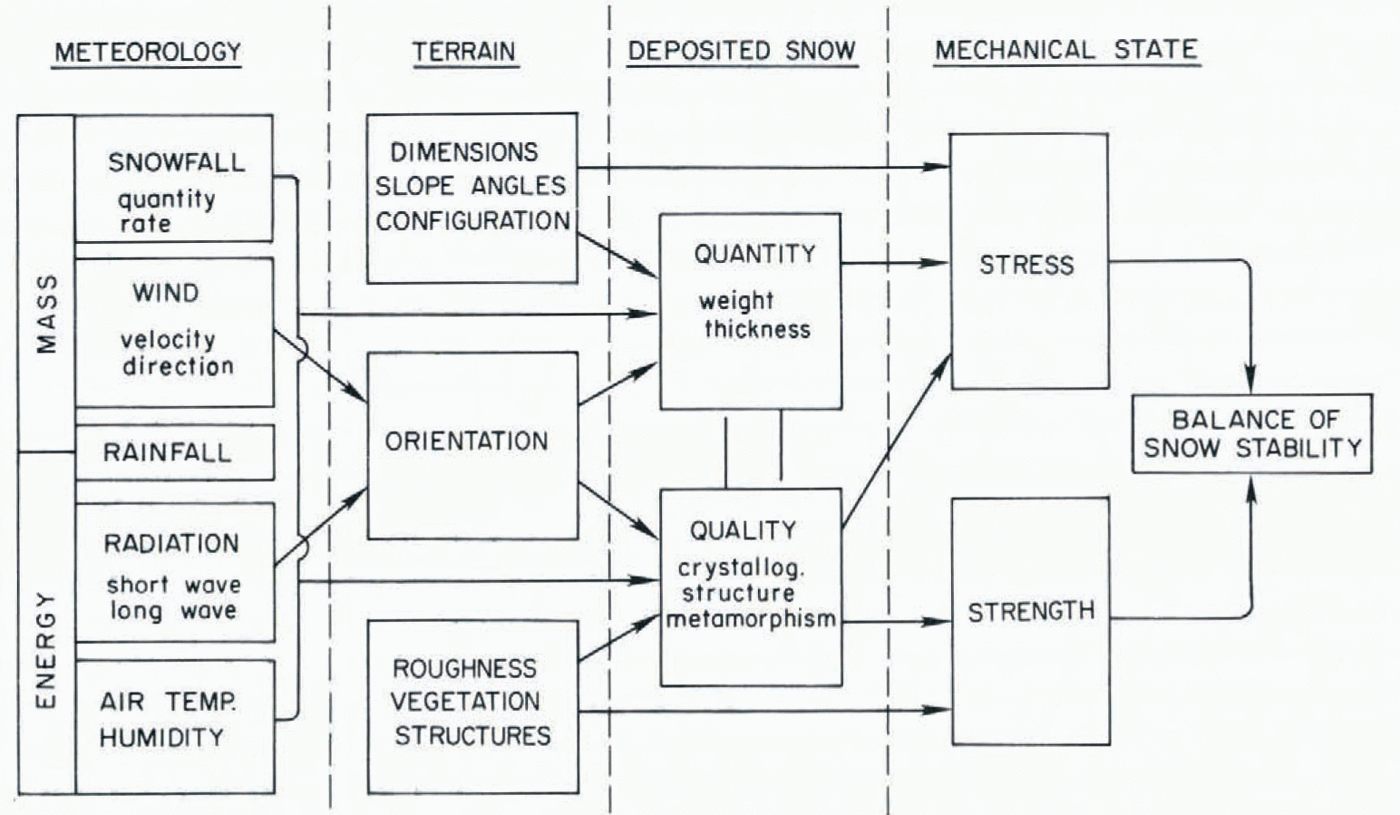
Fig. 1. The Shōda diagram illustrating the chain of causation in avalanche formation. Based on the work of the late M, Shōda([Avalanches], 1973).
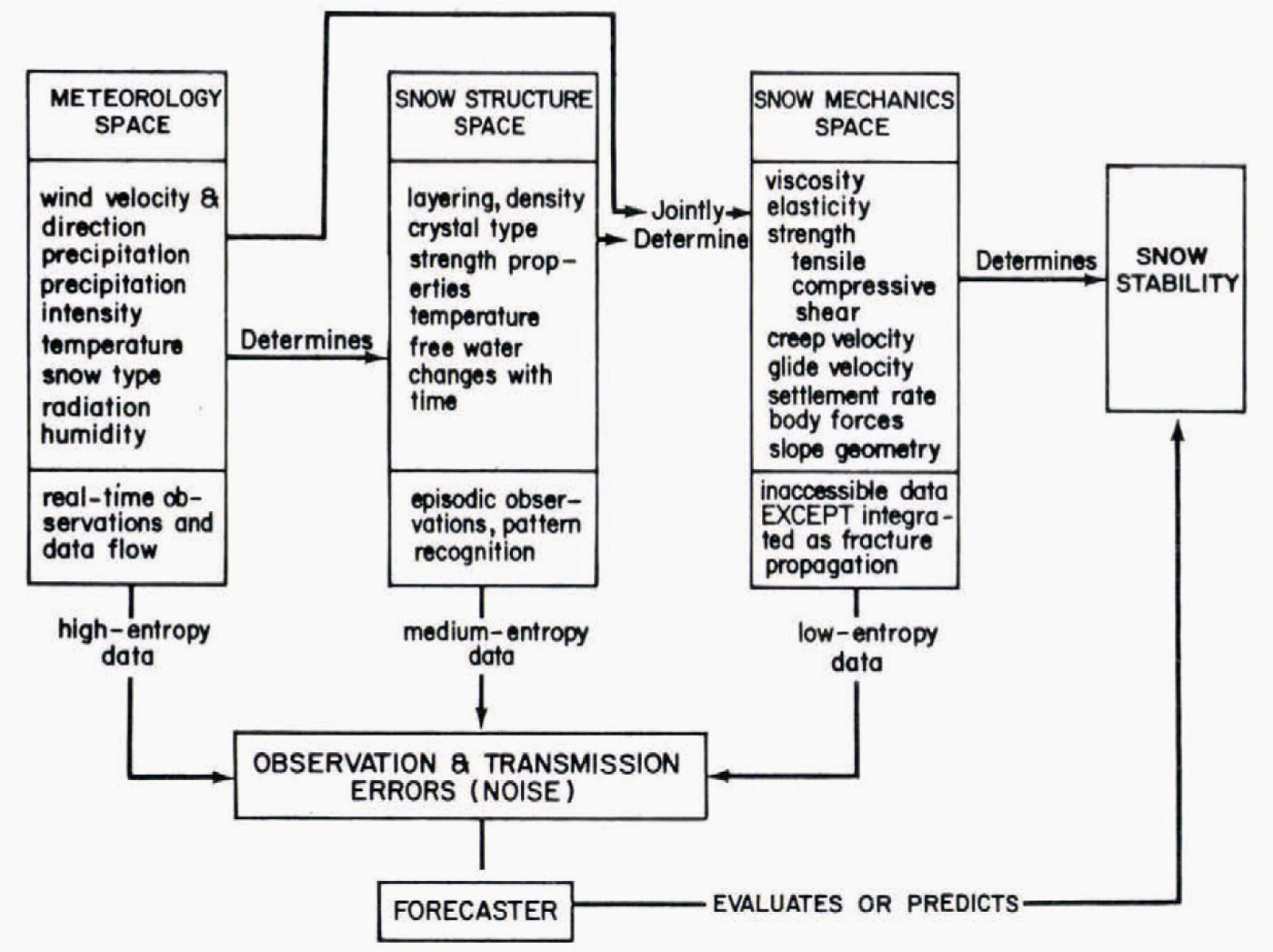
Fig. 2. The elementary Shōda diagram with the terrain parameter removed, showing the paths of data flow used in avalanche forecasting.
A rich population of elementary events means greater uncertainty and difficulty of interpretation. Air temperature in meteorological space is an example of such an event class. A given value like –5°C represents only one of many possible values within the climatological extremes, hence has associated with it a correspondingly large uncertainty of interpretation. At the other extreme, there are only two possible events in the class “avalanche occurrence”,either an avalanche falls or it does not, and interpretation is unequivocal.
Elementary information theory, introduced earlier, provides a quantitative measure of informational entropy directly related to the amount of prevailing uncertainty on the part of the receptor (forecaster). This quantity is defined as the average logarithm of the improbability of a message (Reference ShannonShannon, 1948)

where H is the measure of entropy in bits and p is the probability of each individual message element. When the probabilities of w elements are equal, then this reduces to ![]() In the latter case, the degree of uncertainty can be measured by the number of binary (yes–no answer) questions which have to be asked to elicit a single element of data. Reference GarnerGarner (1966) has summarized these concepts concisely: “the amount of information[al entropy] obtained form an event or act of communication is not a function of what does happen; rather, it is a function of what could have happened, but didn’t”. The latter is sometimes labeled potential information. fig.3. Meteorology space contains a very large body of potential information, snow-mechanicsspace (as defined above) contains very little, while snow-structure space lies somewhere between.
In the latter case, the degree of uncertainty can be measured by the number of binary (yes–no answer) questions which have to be asked to elicit a single element of data. Reference GarnerGarner (1966) has summarized these concepts concisely: “the amount of information[al entropy] obtained form an event or act of communication is not a function of what does happen; rather, it is a function of what could have happened, but didn’t”. The latter is sometimes labeled potential information. fig.3. Meteorology space contains a very large body of potential information, snow-mechanicsspace (as defined above) contains very little, while snow-structure space lies somewhere between.
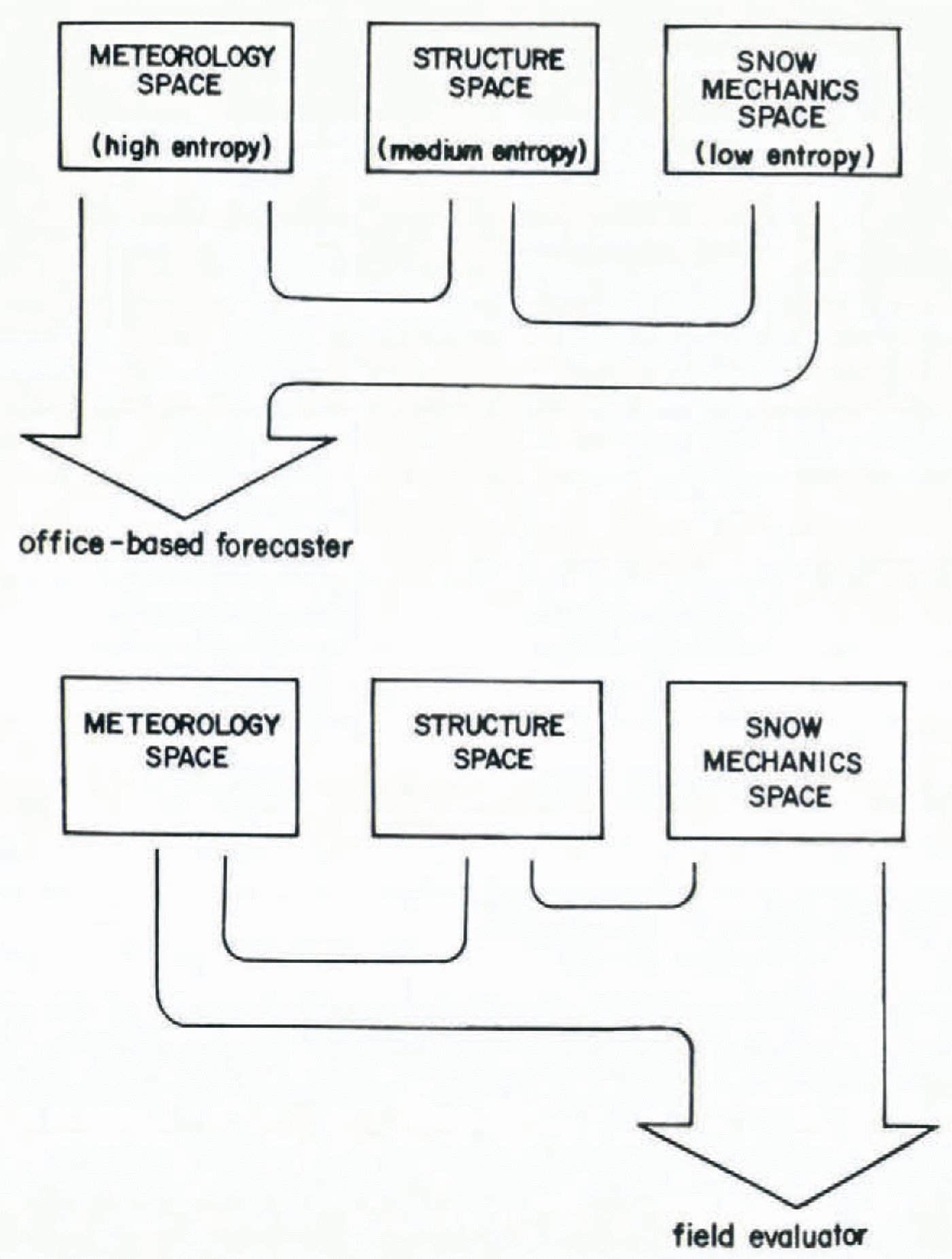
Fig. 3. The relative amounts of low, medium, and high-entropy data used for two basicalry different kinds of avalanche forecasting
The analysis of forecasting techniques upon which this paper is based showed a clear pattern in data use from the different categories. Office-based forecasters of necessity place greater emphasis on data with large potential information and cope with the greater un-certainty by such strateegems as iteration and redundancy. Field workers who need to make immediate, practical, safety decisions rely very strongly on low-entropy data from snow-mechanics space where they have to deal with a much smaller body of potential information. These concepts are summarized in Figure 3.
The Psychological Context
This paper identifies techniques of conventional avalanche forecasting which have evolved spontaneously in a practically successful fashion. This evolution follows basic human mental attributes for dealing with uncertainty, some of which have been identified by recent research in psychology and neurophysiology.
Reference GarnerGarner (1974) demonstrated the role of redundancy in surmounting basic limitations on perceiving and assimilating information. He distinguished between “state limitations” and“process limitations”. A state limitation interferes with a given stimulus getting through to the receptor and is shown to diminish with simple redundancy, or repetition of the stimulus. Collection of numerous snow-fall measurements to overcome natural variations or observation errors is an obvious example in avalanche forecasting; the “state limitation” for snow-fall data is clear and no one depends on a single measurement. A process limitation refers to the subject’s difficulties in recognizing or analyzing a stimulus clearly received. Redundancy again turns out to be the countermeasure in several different ways. Two redundant dimensions of stimuli may combine to form a new dimension easier to apprehend than either alone. Redundancy among stimuli can make it easier for the receptor to deal in memory with a large set of alternatives. Redundant dimensions are also shown to facilitate integration of numeric information, especially if two different dimensions appear in sequence. An obvious application can again be found in avalanche forecasting when several different lines of evidence about snow stability are considered, such as statistical records, contributor factors, and field reports on fracture propagation in snow. A reinforcing mechanism takes place to surmount the process limitations for interpreting each evidence individually.
Garner based his conclusions on extensive laboratory tests of pattern recognition, pre-dominantly for geometrical figures. A bold extension is made here to the more complex and varied stimuli flowing from the natural environment to the analyst. The analogy obviously is far from exact, but the underlying psychological principle shown to inhere in the way subjects deal with stimuli (data or information) by responding positively to several forms of redundancy, fits the intuitive nature of conventional avalanche forecasting like a glove.
If the basic psychological process of conventional avalanche forecasting consists of filling in the gaps in an often highly imperfect and highly redundant message (data set) about the current state of Nature, this leads to the fundamental conclusion that the whole inductive logic method described here originates in right-brain thinking. Because intuitive processes are difficult to describe in terms of left-brain, linear thinking, it should come as no surprise that experienced forecasters are often unable to communicate their methods. They may be able to identify kinds of data used and the relative weights given to various types of information, but the actual, intuitive leap of inductive logic which fills in the missing parts of Nature’s message has remained elusively buried in the right-brain function.
Applications
Identifying the actual practices of conventional avalanche forecasting suggests severalways existing skills can be improved, communicated, and tested.
(1) The role of statistical methods in the actual forecasting decision, as contrasted with deterministic analysis of snow—weather relations, becomes obvious in light of the fundamental observation that “probability is the calculus of inductive reasoning” (Laplace, quoted by Jowitt, unpublished). Likewise, informational entropy measures uncertainty only when a probability distribution is known. The step-wise revision of forecasts by iteration makes this an obvious candidate for probability analysis by Bayesian techniques, an approach hitherto largely neglected except for the solitary contribution of Reference GrakovichGrakovich (1976). Bayes’ equation shows how introducing new knowledge alters a probability assignment;

where the probability of A in the light of C is revised by the introduction of B. When p(A|C)is a current estimate of avalanche probability given the prior knowledge C, the next data increment, B, can generate a revised estimate p(A|BC).
(2) Uncertainty in forecasting can be minimized by emphasizing low-entropy data spaces whenever possible. This concept gives strong support to practical measures like test ski-ing, checking for fracture propagation in new snow, seeking failure planes by such direct shear tests as the tilt-table method (Reference Schleiss and SchleissSchleiss and Schleiss, 1970), or identifying failure planes with a wedge and classifying them by cluster analysis (La Reference LaChapelle and FergusonChapelle and Ferguson, 1980). When, as often is the case for regional forecasting centers, emphasis has to be placed on the flow of data from meteorological and snow-structure spaces, a large measure of redundancy needs to be provided. The network of instrumentation, observers, and connecting communication system needed to provide this redundancy should be defended as a necessity in the face of charges sometimes leveled by funding agencies that it is a luxury.
(3) Avalanche forecasting curiously relies on redundancy while at the same time suffering excesses of unnecessary information. The benefits of redundancy come from diversity, while the excesses stem from a surfeit of potential information in individual data sources. These excesses can be reduced by selecting observation, recording, and data-transmission techniques that minimize informational entropy. In meteorology space, for instance, the key event for avalanching if often a change in the weather which leads to a change in the mechanical- or thermal-energy state of the snow cover. Whether the weather changes or not is often more important than its current state reported in exhaustive detail.
This is also lower-entropy information, as seen in a simple example. Records from a certain mountain weather station show that in winter the probabilities of the wind blowing from the eight cardinal directions are as follows: S.; 0.37; S.W.: 0.17; W.: 0.23; N-W,: 0. 16;N.: 0.06; all others: nil. The informational entropy associated with a single direction report is H = 2.12 bits, but that associated with the report that the wind did, or did not, shift from direction X to direction Y highly significant for avalanche formation, is H = 1 bit.
Similar reasoning applies to wind velocity. The most important thing a forecaster wants to know is whether or not the velocity is above the critical value for transporting snow by drifting. (This value may vary with snow conditions.) A highly accurate anemometer which discriminates between velocities of, say, 26 and 27 km/h is simply introducing excess entropy, for such a distinction matters little for avalanche forecasting. A wind sensor which gave velocities in the Beaufort scale would be more useful for this purpose.
The role of air temperature in avalanche forecasting is ill served by a linear scale reading to the nearest degree Celsius over the entire climatic range. The really critical questions arewhether the temperature is above or below 0°C and which direction the most recent change has taken. Small changes close to the melting point are important, but at – 20°C they meanlittle in terms of avalanche formation. A non-linear temperature scale focused accurately around o°C and giving only broad ranges elsewhere could usefully reduce the entropy of this data element.
Such examples can be multiplied endlessly; the principle is clear—that informational entropy (uncertainty) can be minimized by proper selection of data-collection methods to eliminate unnecessary information. In his innovative effort to adapt inductive logic to pattern recognition, Reference BongardBongard (1970) summarized the principle: “…. every transformation of the input data that secures success should be degenerate, that is, should throw away information”.
(4) The varying entropy content of different data categories provides a rational basis for improving avalanche-danger rating schemes such as Contributory Factor Analysis (CFA)which are widely used implicitly and occasionally used explicitly. Reference Atwater and KoziolAtwater and Koziol (1952)proposed a CFA technique for predicting direct-action avalanches which introduced ten equally-weigh ted factors. Users of this scheme have long been aware that the weights in fact should not be equal, but lacked any basis beyond intuition to reassign them, A reasonable quantitative basis for doing this would be to assign a weight to each factor inversely proportional to its informational entropy. An immediate corollary follows that the weights will shift with climate and season, a shift long recognized empirically but lacking quantitative identification.
(5) Students of all kinds encounter much in education that is deterministic and many textbooks, especially in the physical sciences, that emphasize deductive logic. This approach is highly appropriate for students of avalanche science learning about physical processes in the snow cover and their response to weather, but it is inappropriate for teaching the actual decision-making process about snow stability, which works by inductive logic. Learning can be usefully speeded up if apprentice avalanche forecasters are introduced immediately to the iteration of hypothesis-forming, testing, and revision. The essence is always to have in hand an opinion, no matter how vague or ill-formed at first, about the current state of snow stability. The opinion can be revised and improved as more clues become available. The error is to have had no opinion at all, to have started building no prior knowledge, before a decision has to be made. The person who wonders about snow stability only when standing on the edge of an avalanche path about to be crossed has thought of the problem too late
(6) Once the underlying basis has been identified, skill in avalanche forecasting can readily be screened by testing. When needing to acquire knowledge about a new situation, an experienced forecaster immediately starts asking questions in low-entropy data spaces. The inexperienced person often attacks complex relations of snow and weather and ends up awash in a sea of potential information. The key first question does not deal with the lastweek’s range of snow-cover temperature gradients or yesterday’s sequence of freeze-thaw crustformations, but simply asks “has an avalanche fallen recently?”
Conclusions
Decisions about snow stability made in the face of uncertainty lead inevitably to the practice of inductive logic. This logic arises automatically at the intuitive level as a right-brain process. A fundamental attribute of the human bio-computer is that data affecting such decisions are selected and processed in order to minimize uncertainty and that this function is enhanced by the stress of survival. These principles can be identified, in some cases quantified, and used to enhance avalanche forecasting skills.





