2.1. Glaciar Perito Moreno

GPM (50.5° S, 73.2° W) covers an area of 259 km² (Fig. 1; Reference De AngelisDe Angelis, 2014). The glacier calves into two lakes, Brazo Rico and Canal de los Tempanos, which are part of Lago Argentino. The lake level is 185 m a.s.l. (Reference Rott, Stuefer, Nagler and RiedlRott and others, 2005). The mean AAR from 2002 to 2004 is reported as 0.70 (ELA = 1230 ± 40 m a.s.l.) based on analysis of Moderate Resolution Imaging Spectroradiometer (MODIS) images (Reference De AngelisDe Angelis, 2014). Based on field observations, Reference Stuefer, Rott and SkvarcaStuefer and others (2007) calculated surface mass balance in 1999/2000 and found the ELA to be 1170 m a.s.l.

GPM has shown only small terminus variations since 1920 compared to the other glaciers in Patagonia. Small variations that do occur are associated with the formation and collapse of an ice dam at the glacier front. Brazo Rico is often dammed by ice advancing onto Peninsula Magallanes (Fig. 1). Damming events have been observed repeatedly since the 1930s with intervals of a few years (Reference Skvarca and NaruseSkvarca and Naruse, 1997), but the occurrence is irregular. Since 1999 three events have been reported: September 2003–March 2004 (Reference Skvarca and NaruseSkvarca and Naruse, 2006), August 2005–March 2006 (Reference Stuefer, Rott and SkvarcaStuefer and others, 2007) and December 2007–July 2008; the outburst in July 2008 was the first observation of the icedam collapse in winter (Reference Pasquini and DepetrisPasquini and Depetris, 2011).

2.2. Glaciar Ameghino

GA (50.45° S, 73.3° W) covers an area of 76 km² (Fig. 1). The mean AAR between 2002 and 2004 was 0.55 and ELA = 940 ± 40 m a.s.l. (Reference De AngelisDe Angelis, 2014). GA now calves into Laguna Ameghino, which formed in 1967 as a result of glacier retreat. The lake, which is separated from Lago Argentino by 3 km, is 201 m a.s.l. (Reference Aniya and SatoAniya and Sato, 1995). After 1967, GA retreated rapidly for the next 9 years at a mean rate of 334 m a^–1 (Reference WarrenWarren, 1994). The rate decreased to 20 m a^–1 between 1976 and 1986, and the glacier continued to retreat, similar to many other glaciers in Patagonia. The surface velocity of GA is smaller than that of GPM, because the glacier is thinner and narrower. The surface velocity at the calving front was 0.79 m a^–1 in 1994, and a similar velocity was measured from satellite data in 2008 (Reference Floricioiu, Eineder, Rott and NaglerFloricioiu and others, 2008).

3.1. Surface elevation

Change in glacier surface elevation from February 2000 to 29 March 2008 was measured by differencing a DEM from the Shuttle Radar Topography Mission (SRTM) in February 2000 and a DEM produced from a stereo pair of satellite images obtained on 29 March 2008 by Panchromatic Remote-sensing Instruments for Stereo Mapping (PRISM) mounted on the Japanese Advanced Land Observation Satellite (ALOS). The horizontal resolution of the image was 2.5 m. The nadir- and forward-looking images with a processing level of 1B2 (geometrically corrected data) were distributed with rational polynomial coefficient (RPC) files by the Remote Sensing Technology Center (RESTEC) of Japan. Root-mean-square errors (RMSEs) of ALOS PRISM RPC were typically 1–5 m. We processed the stereo pair images for surface elevation with the aid of the Leica Photogrammetric Suite (LPS) in the ERDAS IMAGINE (Intergraph Co.) workstation. Surface elevation was measured by referring to stereoscopic three-dimensional images by LPS at gridpoints of the SRTM DEM as described below. The generated DEMs cover 35% and 75% of the total areas of GPM and GA, respectively. We were not able to generate DEMs in the accumulation areas because no visual contrast was available over snow-covered regions and dark shadow regions. The maximum error in DEMs produced by the same method is reported as ±4 m (Reference Lamsal, Sawagaki and WatanabeLamsal and others, 2011).

In addition to the ALOS DEM, we used a DEM generated by interferometric synthetic aperture radar (InSAR) measurement of the SRTM during 11 days in February 2000. We used SRTM v2.1 data with absolute accuracies in the horizontal and vertical directions of 20 and 16 m, respectively (Reference FarrFarr and others, 2007). The resolution of the SRTM DEM, after a projection on the area of study, was 73 m.

The DEMs were compared at gridpoints of the SRTM DEM to measure glacier surface elevation change from 2000 and 2008. Error in the measured elevation change was evaluated from changes obtained outside of the glaciers, where elevation change should be zero. This error evaluation was performed on different types of terrain near GPM and GA over an area of 3.1 km² and an elevation range of 187–1489 m a.s.l. indicated by light blue areas in Figure 2. The error is estimated to be ±2.4 m from the RMSE.

Fig. 2. Surface-elevation changes over GPM and GA from 2000 to 2008. Glacier margins and analyzed areas are indicated by the bold black and red curves. Contour intervals are 100 m. Dashdotted curves indicate the central flowlines used in Figure 3. The dashed lines indicate the ELA in 1999/2000 (after Reference Stuefer, Rott and SkvarcaStuefer and others, 2007). Accuracy of the DEM differentiation was evaluated in the light-blue areas.

3.2. Terminus position

We measured the terminus displacement of GPM and GA from January 1999 to October 2012, using orthorectified Landsat 7 Enhanced Thematic Mapper Plus (ETM+) band 8 and Landsat 5 Thematic Mapper (TM) band 3 (provided by the US Geological Survey at http://earthexplorer.usgs.gov/). Frontal margins of the glaciers were delineated by visual observations on a computer screen, using geographical information system software ArcGIS (ESRI, Inc.). The accuracy of this procedure was equal to the image resolutions, which were 15 and 30 m for Landsat 7 and 5 images, respectively. Changes in the terminus positions were calculated by dividing the changes in ice surface area by the width of the calving front (Reference Moon and JoughinMoon and Joughin, 2008).

4.1. Surface elevation

Surface-elevation changes were significantly different at GPM and GA. Results show ice thickening in GPM within 5 km of the terminus (Figs 2 and 3). The elevation change within this region was 10–30 m over the 8 years, which is equivalent to an ice volume increase of 0.25 ± 0.19 km³. Mean rate of elevation change over the studied 78 km² was 0.4 ± 0.3 m a^–1. During this period, the glacier advanced by 230 m.

Fig. 3. Surface elevation change in GPM and GA along the central flowlines indicated in Figure 2.

In contrast, GA showed surface lowering during the same period (Figs 2 and 3). The elevation change was more significant in the lower reaches, and the maximum change of –51 m (–6.4 m a^–1) was observed at 410 m from the terminus in 2000 (Fig. 3). The mean changing rate over the 40 km² covered by the ALOS DEM was –2.6 ± 0.3 m a^–1. This surface lowering is equivalent to an ice volume loss of 0.83 ± 0.09 km³.

4.2. Terminus position

Figure 4 shows variations in the terminus positions of GPM and GA from January 1999 to October 2012. GPM repeated relatively small advances and retreats, resulting in the total displacement of +30 m over the study period. The range of the variation was 270 m. The long-term variation was small, but the data show clear seasonal variations with a mean amplitude of 123 m. The glacier retreated primarily from January to June, and then advanced for the rest of the year. The mean rate of retreat from January to June was 293 m a^–1, whereas the rate of advance was 210 m a^–1.

Fig. 4. Changes in the terminus positions relative to 1999 in GPM and GA. A negative value indicates terminus retreat.

The total retreat of GA from 1999 to 2012 was 720 m, with a mean rate of 56 m a^–1 (Fig. 4). GA showed seasonal variations similar to GPM between 1999 and 2001, but it progressively retreated without a clear seasonal signal after 2001. According to previous studies, GA retreated at a rate of 334 m a^–1 between 1967 and 1976, and the rate then declined to 20 m a^–1 between 1976 and 1986 (Reference WarrenWarren, 1994). The rate of retreat between 1999 and 2012 is 36% greater than that between 1976 and 1986, which is similar to those reported for other calving glaciers in the SPI from 1944/45 to 2005 (Reference Masiokas, Rivera, Espizua, Villalba, Delgado and AravenaMasiokas and others, 2009; Reference Lopez, Chevallier, Favier, Pouyaud, Ordenes and OerlemansLopez and others, 2010).

4.3. Glacier-wide mass balance

Glacier-wide mass balance of a calving glacier is

(1)

where C _sfc and A _sfc are the surface mass balance over the accumulation area S _c and in the ablation area S _a, and D is the calving flux (Reference Cuffey and PatersonCuffey and Paterson, 2010; Reference CogleyCogley and others, 2011). Surface mass balance at elevation z is given by b(z) and integrated over the surface area S. Calving speed, glacier width and ice thickness at the calving front are denoted by u _D, W and H _i respectively. We evaluate the three components in the glacier-wide mass-balance Eqn (1) to investigate the driving mechanism of the mass changes in GPM and GA. Net surface mass balance above and below the ELA were computed using the elevation-dependent mass-balance profile reported for GPM by Reference Stuefer, Rott and SkvarcaStuefer and others (2007). To integrate the mass balance over the accumulation and ablation areas, we used hypsometry derived by the SRTM DEM in 2000 (Fig. 5a). The calving flux D in GPM was taken from the value estimated in Reference Stuefer, Rott and SkvarcaStuefer and others (2007), and that for GA was calculated from ice thickness (Reference Warren and AniyaWarren and Aniya, 1999), flow speed near the terminus (Reference Floricioiu, Eineder, Rott and NaglerFloricioiu and others, 2008) and terminus position changes obtained in this study.

Fig. 5. (a) Hypsometries for GPM and GA with elevation intervals of 100 m. (b) Mass-balance profile for 1999/2000 (after Reference Stuefer, Rott and SkvarcaStuefer and others, 2007) (bold). Gray thin lines are mass-balance profiles for changes in ELA by ±100 m, which are used for the sensitivity experiments.

Table 1 shows the glacier-wide mass balance and its components computed for GPM and GA for the 1999/2000 balance year. The glacier-wide mass balance is –0.1 ± 0.3 and –0.19 ± 0.05 km³ w.e. a^–1 for GPM and GA, respectively. These mass changes are equivalent to mean surface elevation changes of –0.4 ± 1.2 and –2.8 ± 1.2 m w.e. a^–1. Slightly negative mass change for GPM is consistent with the mean elevation change calculated by differencing DEMs over the period 2000–08 (0.4 ± 0.3 m w.e. a^–1) within the accuracy of the calculation, and the mass loss for GA agrees with the value from the DEMs (–2.6 ± 0.3 m w.e. a^–1) within the uncertainty. The computed mass balance for GA is more negative than the value estimated for 1995–2003 by Reference Stuefer, Rott and SkvarcaStuefer and others (2007) (–0.90 m w.e. a^–1). It is likely that the difference is a result of the different surface area and different AAR used in that study. Here we assume that our mass-balance calculation is sufficiently accurate to discuss processes controlling the mass change of the glaciers.

Table 1. Glacier-wide mass balance (Δ M), surface mass balance integrated over the accumulation area (C _sfc) and ablation area (A _sfc) and calving flux (D). C _sfc and A _sfc were calculated from the hypsometry (Fig. 5a) and the mass-balance profile reported by Reference Stuefer, Rott and SkvarcaStuefer and others (2007) for the 1999/2000 balance year (Fig. 5b). D for GPM is after Reference Stuefer, Rott and SkvarcaStuefer and others (2007) whereas D for GA was calculated in this study. Also indicated are glacier-wide specific mass balance (Δ M/S) and the rate of surface elevation change measured by the DEM differentiation (Δ h). The rate of elevation change represents the mean from 2000 to 2008 over the area analyzed in this study (Fig. 2)

5.1. Drivers of contrasting glacier variations

The changes in surface elevation (Figs 2 and 3) and terminus position (Fig. 4) indicate significantly different variations in GPM and GA. While GPM showed little change in terminus position and surface elevation, GA rapidly retreated and thinned during the study period. Below, we discuss the mechanism for the contrasting variations of these two glaciers by partitioning the mass balance into components (Table 1).

The three components of the mass-balance equation (C _sfc, A _sfc and D) in GA are smaller than those in GPM (Table 1) because GA is substantially smaller in dimension. Surface mass balance in the accumulation area (C _sfc) and calving flux (D) in GA are 11% and 13% respectively of those in GPM. Surface mass balance in the ablation area in GA is 36% of that in GPM, which is significantly greater than the other two components. Furthermore, the fraction of the negative mass balance in the ablation area to the total ablation A _sfc/(A _sfc – D) is 0.84 in GA, greater than the fraction in GPM (0.66). The fraction of surface mass balance in the accumulation and ablation areas (|A _sfc /C _sfc|) is greater in GA (2.27) than in GPM (0.72). These values indicate a relatively greater contribution of negative surface mass balance over the ablation area in the glacier-wide mass balance in GA. This analysis also suggests that A _sfc is the primary reason for the contrasting response of GA and GPM despite similar climate conditions.

The contrasting mass-balance regimes of the two glaciers are affected by the AAR. The accumulation area of GA is very steep and small compared to the flat ablation area extending in the lower elevation area (Figs 2 and 5a). In contrast, GPM has a relatively flat and large accumulation area (Figs 2 and 5a). If we apply the ELA reported for GPM in 1999/2000 (1170 m a.s.l.; Reference Stuefer, Rott and SkvarcaStuefer and others, 2007) to the SRTM DEM, accumulation and ablation areas are 36.5 and 29.4 km² (AAR = 0.45) for GA, and 190.6 and 72.1 km² (AAR = 0.73) for GPM (Fig. 5a).

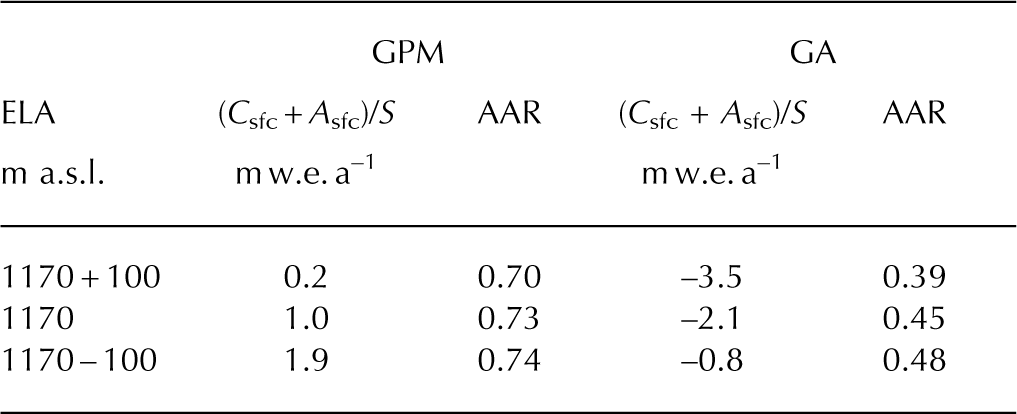
The mean AAR over the major calving glaciers in the SPI is 0.71 based on the AARs reported by Reference De AngelisDe Angelis (2014) and for the glaciers listed in Reference Aniya, Sato, Naruse, Skvarca and CasassaAniya and others (1997). The AAR of GA (0.45) is substantially smaller than the mean over the SPI, which resulted in the rapid retreat and thinning of this glacier. The AAR is small in GA because a large surface area is distributed slightly below the ELA (940 m a.s.l.) (Reference De AngelisDe Angelis, 2014). 28% of the surface area is at 800– 1000 m a.s.l. (Fig. 5a), which suggests that AAR is sensitive to recent increase in ELA. To investigate the sensitivity of mass balance to changes in ELA, we calculated surface accumulation and ablation based on the mass-balance profile reported by Reference Stuefer, Rott and SkvarcaStuefer and others (2007) (Fig. 5b). We kept calving flux constant in this experiment. When ELA is elevated by 100 m (Fig. 5b), the specific surface mass balance of GA decreases from –2.1 m w.e. a^–1 to –3.5 m w.e. a^–1 (Table 2). Mass balance of GPM also decreases (from 1.0 m w.e. a^–1 to 0.2 m w.e. a^–1), but the magnitude of the change is smaller. It is likely that the AAR plays a critical role in the greater sensitivity of GA because the decrease in AAR is greater (from 0.45 to 0.39) than for GPM (0.73 to 0.70). Mass balance and AAR of GA are also more sensitive to lowering ELA (–100 m). Results indicate that GA is more sensitive to climate forcing because of the characteristic surface area distribution (Fig. 5a).

Table 2. Glacier-wide specific surface mass balance (C _sfc + A _sfc)/S and AAR calculated for the ELA reported for 1999/2000 (1170 m a.s.l.) (Reference Stuefer, Rott and SkvarcaStuefer and others, 2007) and those after changes by ±100 m

Calving glaciers are expected to advance, irrespective of climatic forcing, when AAR exceeds 0.8 (Reference Post, O’Neel, Motyka and StrevelerPost and others, 2011). The AAR of GPM is similar to this number, thus explaining the stability of this glacier. The AAR of GPM (0.73) is slightly larger than the mean for SPI (0.71; Reference De AngelisDe Angelis, 2014), probably because of the geometry of the terminus region. Since GPM calves into two lakes, further advance was difficult in the past, and AAR has remained relatively constant and large. This is a plausible reason why GPM has shown no significant retreat compared to GA and other retreating glaciers in Patagonia.

5.2. Glacier fate

We believe that GA will continue to retreat in the future, because accumulation is not sufficient to counterbalance melting in the large ablation area. If we assume the surface mass balance and ELA in 1999/2000 (Reference Stuefer, Rott and SkvarcaStuefer and others, 2007), surface mass balance in the accumulation and ablation areas (C _sfc and A _sfc) balance when the terminus retreats to 700–800 m a.s.l. It takes ~100 years to reach this condition under the retreat rate observed for 1999–2012 (56 m a^–1). In fact, further retreat is necessary to reach the steady state because the accumulation area shrinks as the glacier thins and the surface lowers. We neglect calving flux (D) in the calculation because it currently accounts for only 20% of the total ablation and will likely decrease as the terminus retreats from the lake. Further, Reference Rasmussen, Conway and RaymondRasmussen and others (2007) discussed the importance of transition from solid to liquid precipitation under a warming climate. Because of the large area at low elevations, GA is more sensitive to such influence of temperature rise on snow accumulation.

Immediate change is not likely at GPM because AAR is large and the glacier has been stable for a long time in this geometry. Indeed, GPM thickened near the terminus in 2000–08 (Fig. 3). Presumably, ice is thickening in this region because the glacier is buttressed by Peninsula Magallanes. This hypothesis is supported by the fact that three damming events occurred between 2000 and 2008, whereas no event occurred in the 1990s (Reference Stuefer, Rott and SkvarcaStuefer and others, 2007). Our analysis demonstrates that contribution of the calving flux to the total ablation is relatively large (36%; Table 1), and thus glacier dynamics near the terminus may play a key role in future glacier change. Once the glacier accelerates, as has been observed in other calving glaciers in the SPI (Reference Rivera, Koppes, Bravo and AravenaRivera and others, 2012; Reference Sakakibara, Sugiyama, Sawagaki, Marinsek and SkvarcaSakakibara and others, 2013; Reference Sakakibara and SugiyamaSakakibara and Sugiyama, 2014), mass that is currently balanced would be altered in a way that causes the glacier to thin and retreat. Such a change can be triggered by meltwater increase and thinning of the glacier, because ice speed in the lower reaches of GPM is very sensitive to the effective pressure, i.e. ice overburden pressure minus subglacial water pressure (Reference SugiyamaSugiyama and others, 2011). Thus, glacier dynamics should be carefully monitored to predict a rapid change of GPM in the future.