Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-17T00:54:15.723Z Has data issue: false hasContentIssue false
  • English
  • Français

A variational principle for weighted topological pressure under 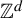$\mathbb {Z}^{d}$-actions

Part of: Dynamical systems with hyperbolic behavior Topological dynamics Smooth dynamical systems: general theory

Published online by Cambridge University Press:  04 October 2022

QIANG HUO  and
RONG YUAN
QIANG HUO*
Affiliation:
Laboratory of Mathematics, Complex Systems (Ministry of Education), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, PR China (e-mail: [email protected])
RONG YUAN
Affiliation:
Laboratory of Mathematics, Complex Systems (Ministry of Education), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, PR China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 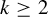$k\geq 2$ and 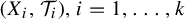$(X_{i}, \mathcal {T}_{i}), i=1,\ldots ,k$, be 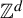$\mathbb {Z}^{d}$-actions topological dynamical systems with 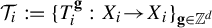$\mathcal {T}_i:=\{T_i^{\textbf {g}}:X_i{\rightarrow } X_i\}_{\textbf {g}\in \mathbb {Z}^{d}}$, where 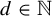$d\in \mathbb {N}$ and 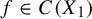$f\in C(X_{1})$. Assume that for each 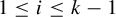$1\leq i\leq k-1$, 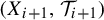$(X_{i+1}, \mathcal {T}_{i+1})$ is a factor of 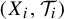$(X_{i}, \mathcal {T}_{i})$. In this paper, we introduce the weighted topological pressure 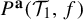$P^{\textbf {a}}(\mathcal {T}_{1},f)$ and weighted measure-theoretic entropy 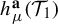$h_{\mu }^{\textbf {a}}(\mathcal {T}_{1})$ for 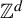$\mathbb {Z}^{d}$-actions, and establish a weighted variational principle as

$$ \begin{align*} P^{\textbf{a}}(\mathcal{T}_{1},f)=\sup\bigg\{h_{\mu}^{\textbf{a}}(\mathcal{T}_{1})+\int_{X_{1}}f\,d\mu:\mu\in\mathcal{M}(X_{1}, \mathcal{T}_{1})\bigg\}. \end{align*} $$

This result not only generalizes some well-known variational principles about topological pressure for compact or non-compact sets, but also improves the variational principle for weighted topological pressure in [16] from 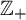$\mathbb {Z}_{+}$-action topological dynamical systems to 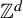$\mathbb {Z}^{d}$-actions topological dynamical systems.

Keywords

weighted topological pressureℤd-actionsvariational principlefactor mapsgeometric measure theory

MSC classification

Primary: 37C45: Dimension theory of dynamical systems
Secondary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37B40: Topological entropy
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 10 , October 2023 , pp. 3311 - 3340
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barral, J. and Feng, D.-J.. Weighted thermodynamic formalism on subshifts and applications. Asian J. Math. 16(2) (2012), 319–352.CrossRefGoogle Scholar
Biś, A.. An analogue of the variational principle for group and pseudogroup actions. Ann. Inst. Fourier (Grenoble) 63(3) (2013), 839–863.CrossRefGoogle Scholar
Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23(1) (2010), 217–245.CrossRefGoogle Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.CrossRefGoogle Scholar
Bowen, R.. Hausdorff dimension of quasicircles. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 11–25.CrossRefGoogle Scholar
Brin, M. and Katok, A.. On local entropy. Geometric Dynamic (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Ed. J. Palis Jr. Springer, Berlin, 1983, pp. 30–38.CrossRefGoogle Scholar
Cao, Y., Pesin, Y. and Zhao, Y.. Dimension estimates for non-conformal repellers and continuity of sub-additive topological pressure. Geom. Funct. Anal. 29(5) (2019), 1325–1368.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. and Varandas, P.. Quantitative recurrence for free semigroups. Nonlinearity 31(3) (2018), 864–886.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. B. and Varandas, P.. A variational principle for free semigroup actions. Adv. Math. 334 (2018), 450–487.CrossRefGoogle Scholar
Chung, N.-P.. Topological pressure and the variational principle for actions of sofic groups. Ergod. Th. & Dynam. Sys. 33(5) (2013), 1363–1390.CrossRefGoogle Scholar
Dinaburg, E. I.. A correlation between topological entropy and metric entropy. Dokl. Akad. Nauk SSSR 190 (1970), 19–22 (in Russian).Google Scholar
Dunford, N. and Schwartz, J. T.. Linear Operator Part I. General Theory. Interscience, New York, 1958.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259). Springer-Verlag London, 2011.CrossRefGoogle Scholar
Feng, D.-J.. Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.CrossRefGoogle Scholar
Feng, D.-J. and Huang, W.. Variational principles for topological entropies of subsets. J. Funct. Anal. 263(8) (2012), 2228–2254.CrossRefGoogle Scholar
Feng, D.-J. and Huang, W.. Variational principle for weighted topological pressure. J. Math. Pures Appl. (9) 106(3) (2016), 411–452.CrossRefGoogle Scholar
Fuda, T. and Tonozaki, M.. Brudno’s theorem for ${\mathbb{Z}}^d$ (or ${\mathbb{Z}}_{+}^d$ ) subshifts. Inform. and Comput. 253 (part 1) (2017), 155–162.CrossRefGoogle Scholar
Cánovas, J. S.. On entropy of non-autonomous discrete systems. Progress and Challenges in Dynamical Systems (Springer Proceedings in Mathematics and Statistics, 54). Eds. S. Ibáñez, J. S. Pérez del Río, A. Pumariño and J. Ángel Rodríguez. Springer, Heidelberg, 2013, pp. 143–159.CrossRefGoogle Scholar
Goodman, T. N. T.. Relating topological entropy and measure entropy. Bull. Lond. Math. Soc. 3 (1971), 176–180.CrossRefGoogle Scholar
Goodwyn, L. W.. Topological entropy bounds measure-theoretic entropy. Proc. Amer. Math. Soc. 23 (1969), 679–688.CrossRefGoogle Scholar
Kenyon, R. and Peres, Y.. Measures of full dimension on affine-invariant sets. Ergod. Th. & Dynam. Sys. 16(2) (1996), 307–323.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Entropy and the variational principle for actions of sofic groups. Invent. Math. 186(3) (2011), 501–558.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Soficity, amenability, and dynamical entropy. Amer. J. Math. 135(3) (2013), 721–761.CrossRefGoogle Scholar
Kolmogorov, A. N.. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Akad. Nauk SSSR 119 (1958), 861–864.Google Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–574.CrossRefGoogle Scholar
Liang, B. and Yan, K.. Topological pressure for sub-additive potentials of amenable group actions. J. Funct. Anal. 262(2) (2012), 584–601.CrossRefGoogle Scholar
Lin, X., Ma, D. and Wang, Y.. On the measure-theoretic entropy and topological pressure of free semi-groups. Ergod. Th. & Dynam. Sys. 38(2) (2018), 686–716.CrossRefGoogle Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146(2) (2001), 259–295.CrossRefGoogle Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics, Translated from the Portuguese by Silvio Levy (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 8). Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces, Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Misiurewicz, M.. A short proof the variational principle for a ${\mathbb{Z}}_{+}^N$ action on a compact space. International Conference on Dynamical Systems in Mathematical Physics (Rennes, 1975) (Astérisque, 40). Société Mathématique de France, Paris, 1976, pp. 147–157.Google Scholar
Ollagnier, J. M.. Ergodic Theory and Statistical Mechanics (Lecture Notes in Mathematics, 1115). Springer-Verlag, Berlin, 1985.CrossRefGoogle Scholar
Ollagnier, J. M. and Pinchon, D.. The variational principle. Studia Math. 72(2) (1982), 151–159.CrossRefGoogle Scholar
Ornstein, D. and Weiss, B.. The Shannon–McMillan–Breiman theorem for a class of amenable groups. Israel J. Math. 44(1) (1983), 53–60.CrossRefGoogle Scholar
Pesin, Y. B. and Pitskel’, B. S.. Topological pressure and the variational principle for non-compact sets. Funct. Anal. Appl. 18(4) (1984), 50–63.CrossRefGoogle Scholar
Ruelle, D.. Statistical mechanics on a compact set with ${\mathbb{Z}}^{\nu }$ action satisfying expansiveness and specification. Trans. Amer. Math. Soc. 187 (1973), 237–251.CrossRefGoogle Scholar
Ruelle, D.. Repellers for real analytic maps. Ergod. Th. & Dynam. Sys. 2(1) (1982), 99–107.CrossRefGoogle Scholar
Sinai, Y.. On the concept of entropy for a dynamical system. Dokl. Akad. Nauk SSSR 124 (1959), 768–771 (in Russian).Google Scholar
Stepin, A. M. and Tagi-Zade, A. T.. Variational characterization of topological pressure of the amenable groups of transformations Dokl. Akad. Nauk SSSR 254(3) (1980), 545–549 (in Russian).Google Scholar
Tang, X., Cheng, W.-C. and Zhao, Y.. Variational principle for topological pressures on subsets. J. Math. Anal. Appl. 424(2) (2015), 1272–1285.CrossRefGoogle Scholar
Tempel’man, A. A.. Specific characteristics and variational principle for homogeneous random fields. Z. Wahrsch. Verw. Gebiete. 65(3) (1984), 341–365.CrossRefGoogle Scholar
Walters, P.. A variational principle for the pressure of continuous transformations. Amer. J. Math. 97(4) (1975), 937–971.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer-Verlag, New York–Berlin, 1982.CrossRefGoogle Scholar
Yan, K.. Sub-additive and asymptotically sub-additive topological pressure for ${\mathbb{Z}}^d$ -actions. J. Dynam. Differential Equations 25(3) (2013), 653–678.CrossRefGoogle Scholar
Zhong, X. and Chen, Z.. Variational principle for topological pressure on subsets of free semigroup actions. Acta Math. Sin. (Engl. Ser.) 37(9) (2021), 1401–1414.CrossRefGoogle Scholar