The authors gave an example showing an error in [Reference Lee and Lee2, Lemma 3.3], and below offer at least a partial correction for that error under the unimodularity assumption. This makes all of the remaining results in [Reference Lee and Lee2] valid.
Consider the three-dimensional solvable non-unimodular Lie algebra ![]() $\mathfrak{S}$:
$\mathfrak{S}$:
This Lie algebra has a faithful matrix representation as follows:
 $$\begin{eqnarray}\left[\begin{array}{@{}cccc@{}}s & 0 & 0 & a\\ 0 & s & 0 & b\\ 0 & 0 & 0 & s\\ 0 & 0 & 0 & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cccc@{}}s & 0 & 0 & a\\ 0 & s & 0 & b\\ 0 & 0 & 0 & s\\ 0 & 0 & 0 & 0\end{array}\right].\end{eqnarray}$$ We can choose an ordered (linear) basis for ![]() $\mathfrak{S}$:
$\mathfrak{S}$:
 $$\begin{eqnarray}\mathbf{b}_{1}=\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right],\qquad \mathbf{b}_{2}=\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right],\qquad \mathbf{b}_{3}=\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{b}_{1}=\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right],\qquad \mathbf{b}_{2}=\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right],\qquad \mathbf{b}_{3}=\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\end{array}\right].\end{eqnarray}$$ They satisfy ![]() $[\mathbf{b}_{1},\mathbf{b}_{2}]=\mathbf{0}$,
$[\mathbf{b}_{1},\mathbf{b}_{2}]=\mathbf{0}$, ![]() $[\mathbf{b}_{3},\mathbf{b}_{1}]=\mathbf{b}_{1}$ and
$[\mathbf{b}_{3},\mathbf{b}_{1}]=\mathbf{b}_{1}$ and ![]() $[\mathbf{b}_{3},\mathbf{b}_{2}]=\mathbf{b}_{2}$. The connected and simply connected solvable Lie group
$[\mathbf{b}_{3},\mathbf{b}_{2}]=\mathbf{b}_{2}$. The connected and simply connected solvable Lie group ![]() $S$ associated with the Lie algebra
$S$ associated with the Lie algebra ![]() $\mathfrak{S}$ is
$\mathfrak{S}$ is
 $$\begin{eqnarray}S=\left\{\left.\left[\begin{array}{@{}cccc@{}}e^{t} & 0 & 0 & x\\ 0 & e^{t} & 0 & y\\ 0 & 0 & 1 & t\\ 0 & 0 & 0 & 1\end{array}\right]\right|x,y,t\in \mathbb{R}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}S=\left\{\left.\left[\begin{array}{@{}cccc@{}}e^{t} & 0 & 0 & x\\ 0 & e^{t} & 0 & y\\ 0 & 0 & 1 & t\\ 0 & 0 & 0 & 1\end{array}\right]\right|x,y,t\in \mathbb{R}\right\}.\end{eqnarray}$$ Let ![]() $g=((x,y),t)$ denote an element of
$g=((x,y),t)$ denote an element of ![]() $S$. Because
$S$. Because ![]() $\text{Ad}(g):\mathfrak{S}\rightarrow \mathfrak{S}$ is given by
$\text{Ad}(g):\mathfrak{S}\rightarrow \mathfrak{S}$ is given by ![]() $\text{Ad}(g)(A)=gAg^{-1}$ for
$\text{Ad}(g)(A)=gAg^{-1}$ for ![]() $A\in \mathfrak{S}$, a simple computation shows that the adjoint of
$A\in \mathfrak{S}$, a simple computation shows that the adjoint of ![]() $g$ is given by
$g$ is given by
 $$\begin{eqnarray}\text{Ad}(g)=\left[\begin{array}{@{}ccc@{}}e^{t} & 0 & -x\\ 0 & e^{t} & -y\\ 0 & 0 & 1\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\text{Ad}(g)=\left[\begin{array}{@{}ccc@{}}e^{t} & 0 & -x\\ 0 & e^{t} & -y\\ 0 & 0 & 1\end{array}\right].\end{eqnarray}$$ Let ![]() ${\it\varphi}$ be a Lie algebra homomorphism on
${\it\varphi}$ be a Lie algebra homomorphism on ![]() $\mathfrak{S}$. Since
$\mathfrak{S}$. Since ![]() $[\mathfrak{S},\mathfrak{S}]$ is generated by
$[\mathfrak{S},\mathfrak{S}]$ is generated by ![]() $\mathbf{e}_{1}$ and
$\mathbf{e}_{1}$ and ![]() $\mathbf{e}_{2}$, we have
$\mathbf{e}_{2}$, we have
 $$\begin{eqnarray}\displaystyle {\it\varphi}(\mathbf{b}_{1}) & = & \displaystyle m_{11}\mathbf{b}_{1}+m_{21}\mathbf{b}_{2},\nonumber\\ \displaystyle {\it\varphi}(\mathbf{b}_{2}) & = & \displaystyle m_{12}\mathbf{b}_{1}+m_{22}\mathbf{b}_{2},\nonumber\\ \displaystyle {\it\varphi}(\mathbf{b}_{3}) & = & \displaystyle p\mathbf{b}_{1}+q\mathbf{b}_{2}+m\mathbf{b}_{3}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\varphi}(\mathbf{b}_{1}) & = & \displaystyle m_{11}\mathbf{b}_{1}+m_{21}\mathbf{b}_{2},\nonumber\\ \displaystyle {\it\varphi}(\mathbf{b}_{2}) & = & \displaystyle m_{12}\mathbf{b}_{1}+m_{22}\mathbf{b}_{2},\nonumber\\ \displaystyle {\it\varphi}(\mathbf{b}_{3}) & = & \displaystyle p\mathbf{b}_{1}+q\mathbf{b}_{2}+m\mathbf{b}_{3}\nonumber\end{eqnarray}$$ for some ![]() $m_{ij},p,q,m\in \mathbb{R}$. Since
$m_{ij},p,q,m\in \mathbb{R}$. Since ![]() ${\it\varphi}$ preserves the bracket operations
${\it\varphi}$ preserves the bracket operations ![]() $[\mathbf{b}_{3},\mathbf{b}_{1}]=\mathbf{b}_{1}$ and
$[\mathbf{b}_{3},\mathbf{b}_{1}]=\mathbf{b}_{1}$ and ![]() $[\mathbf{b}_{3},\mathbf{b}_{2}]=\mathbf{b}_{2}$, it follows easily that
$[\mathbf{b}_{3},\mathbf{b}_{2}]=\mathbf{b}_{2}$, it follows easily that
Therefore, with respect to the basis ![]() $\{\mathbf{b}_{1},\mathbf{b}_{2},\mathbf{b}_{3}\}$ of
$\{\mathbf{b}_{1},\mathbf{b}_{2},\mathbf{b}_{3}\}$ of ![]() $\mathfrak{S}$,
$\mathfrak{S}$, ![]() ${\it\varphi}$ is one of the following:
${\it\varphi}$ is one of the following:
 $$\begin{eqnarray}\begin{array}{@{}rl@{}}\text{Type (I)} & \left[\begin{array}{@{}ccc@{}}m_{11} & m_{12} & p\\ m_{21} & m_{22} & q\\ 0 & 0 & 1\end{array}\right]\\ \text{Type (II)} & \left[\begin{array}{@{}ccc@{}}0 & 0 & p\\ 0 & 0 & q\\ 0 & 0 & m\end{array}\right]\quad \text{with}~m\neq 1.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rl@{}}\text{Type (I)} & \left[\begin{array}{@{}ccc@{}}m_{11} & m_{12} & p\\ m_{21} & m_{22} & q\\ 0 & 0 & 1\end{array}\right]\\ \text{Type (II)} & \left[\begin{array}{@{}ccc@{}}0 & 0 & p\\ 0 & 0 & q\\ 0 & 0 & m\end{array}\right]\quad \text{with}~m\neq 1.\end{array}\end{eqnarray}$$Now we can easily check that
 $$\begin{eqnarray}\displaystyle \det ({\it\varphi}-I) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}0\quad & \text{when}~{\it\varphi}~\text{is of type (I)},\\ m-1\quad & \text{when}~{\it\varphi}~\text{is of type (II);}\end{array}\right.\nonumber\\ \displaystyle \det ({\it\varphi}-\text{Ad}(g)) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}0\quad & \text{when}~{\it\varphi}~\text{is of type (I)},\\ e^{2t}(m-1)\quad & \text{when}~{\it\varphi}~\text{is of type (II).}\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det ({\it\varphi}-I) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}0\quad & \text{when}~{\it\varphi}~\text{is of type (I)},\\ m-1\quad & \text{when}~{\it\varphi}~\text{is of type (II);}\end{array}\right.\nonumber\\ \displaystyle \det ({\it\varphi}-\text{Ad}(g)) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}0\quad & \text{when}~{\it\varphi}~\text{is of type (I)},\\ e^{2t}(m-1)\quad & \text{when}~{\it\varphi}~\text{is of type (II).}\end{array}\right.\nonumber\end{eqnarray}$$ This example shows that [Reference Lee and Lee2, Lemma 3.3] is not true in general. We remark also that ![]() $S$ is not unimodular, and hence, as can be expected,
$S$ is not unimodular, and hence, as can be expected, ![]() $\det (\text{Ad}(g))=e^{2t}\neq 1$ for all
$\det (\text{Ad}(g))=e^{2t}\neq 1$ for all ![]() $t\neq 0$. We prove, however, that the lemma is true under the unimodularity assumption of the connected Lie group. That is, the following theorem.
$t\neq 0$. We prove, however, that the lemma is true under the unimodularity assumption of the connected Lie group. That is, the following theorem.
Theorem 1. Let ![]() $S$ be a connected and simply connected solvable Lie group, and let
$S$ be a connected and simply connected solvable Lie group, and let ![]() $D:S\rightarrow S$ be a Lie group homomorphism. If
$D:S\rightarrow S$ be a Lie group homomorphism. If ![]() $S$ is unimodular, then for any
$S$ is unimodular, then for any ![]() $x\in S$,
$x\in S$,
Remark 2. It is known that if a Lie group admits a lattice (discrete cocompact subgroup), then it is unimodular. Consequently, the remaining results of [Reference Lee and Lee2] are valid.
Lemma 3. Let ![]() $S$ be a connected and simply connected solvable Lie group, and let
$S$ be a connected and simply connected solvable Lie group, and let ![]() $D:S\rightarrow S$ be a Lie group homomorphism. Then, for any
$D:S\rightarrow S$ be a Lie group homomorphism. Then, for any ![]() $x\in S$,
$x\in S$, ![]() $I-D_{\ast }$ is an isomorphism if and only if
$I-D_{\ast }$ is an isomorphism if and only if ![]() $I-\text{Ad}(x)D_{\ast }$ is an isomorphism.
$I-\text{Ad}(x)D_{\ast }$ is an isomorphism.
Proof. Because ![]() $I-\text{Ad}(x^{-1})\text{Ad}(x)D_{\ast }=I-D_{\ast }$, it suffices to show the only if.
$I-\text{Ad}(x^{-1})\text{Ad}(x)D_{\ast }=I-D_{\ast }$, it suffices to show the only if.
Let ![]() $G=[S,S]$; then
$G=[S,S]$; then ![]() $G$ is nilpotent, and
$G$ is nilpotent, and ![]() $S/G\cong \mathbb{R}^{k}$ for some
$S/G\cong \mathbb{R}^{k}$ for some ![]() $k$. Then we have the following commutative diagram:
$k$. Then we have the following commutative diagram:
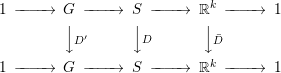
This induces the following commutative diagram:
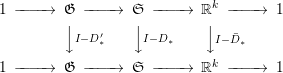
For ![]() $x\in S$, we denote by
$x\in S$, we denote by ![]() ${\it\tau}_{x}$ the inner automorphism on
${\it\tau}_{x}$ the inner automorphism on ![]() $S$ whose differential is
$S$ whose differential is ![]() $\text{Ad}(x)$. This induces an automorphism on
$\text{Ad}(x)$. This induces an automorphism on ![]() $G$, and we still denote it by
$G$, and we still denote it by ![]() ${\it\tau}_{x}$ and its differential is
${\it\tau}_{x}$ and its differential is ![]() $\text{Ad}^{\prime }(x)$. Then we can express
$\text{Ad}^{\prime }(x)$. Then we can express ![]() $I-D_{\ast }$ and
$I-D_{\ast }$ and ![]() $I-\text{Ad}(x)D_{\ast }$ as
$I-\text{Ad}(x)D_{\ast }$ as
 $$\begin{eqnarray}\displaystyle I-D_{\ast } & = & \displaystyle \left[\begin{array}{@{}cc@{}}I-\bar{D}_{\ast } & 0\\ \ast & I-D_{\ast }^{\prime }\end{array}\right],\nonumber\\ \displaystyle I-\text{Ad}(x)D_{\ast } & = & \displaystyle \left[\begin{array}{@{}cc@{}}I-\bar{D}_{\ast } & 0\\ \ast & I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }\end{array}\right]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I-D_{\ast } & = & \displaystyle \left[\begin{array}{@{}cc@{}}I-\bar{D}_{\ast } & 0\\ \ast & I-D_{\ast }^{\prime }\end{array}\right],\nonumber\\ \displaystyle I-\text{Ad}(x)D_{\ast } & = & \displaystyle \left[\begin{array}{@{}cc@{}}I-\bar{D}_{\ast } & 0\\ \ast & I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }\end{array}\right]\nonumber\end{eqnarray}$$ with respect to some linear basis for ![]() $\mathfrak{S}$.
$\mathfrak{S}$.
Assume that ![]() $I-\bar{D}_{\ast }$ is an isomorphism. We claim that
$I-\bar{D}_{\ast }$ is an isomorphism. We claim that ![]() $I-D_{\ast }^{\prime }$ is an isomorphism if and only if
$I-D_{\ast }^{\prime }$ is an isomorphism if and only if ![]() $I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }$ is an isomorphism.
$I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }$ is an isomorphism.
Since ![]() $I-\bar{D}$ is an isomorphism on
$I-\bar{D}$ is an isomorphism on ![]() $\mathbb{R}^{k}$,
$\mathbb{R}^{k}$, ![]() $\text{fix}(\bar{D})=\ker (I-\bar{D})$ is a trivial group. For any
$\text{fix}(\bar{D})=\ker (I-\bar{D})$ is a trivial group. For any ![]() $x\in S$, we consider the exact sequence of the Reidemeister sets
$x\in S$, we consider the exact sequence of the Reidemeister sets
![]() $\hat{p}^{x}$ is surjective, and
$\hat{p}^{x}$ is surjective, and ![]() $(\hat{p}^{x})^{-1}([\bar{1}])=\text{im}(\hat{i} ^{x})$. If
$(\hat{p}^{x})^{-1}([\bar{1}])=\text{im}(\hat{i} ^{x})$. If ![]() $\hat{i} ^{x}([g_{1}])=\hat{i} ^{x}([g_{2}])$ for some
$\hat{i} ^{x}([g_{1}])=\hat{i} ^{x}([g_{2}])$ for some ![]() $g_{1},g_{2}\in G$, then by definition there is
$g_{1},g_{2}\in G$, then by definition there is ![]() $y\in S$ such that
$y\in S$ such that ![]() $g_{2}=yg_{1}({\it\tau}_{x}D(y))^{-1}$. The image in
$g_{2}=yg_{1}({\it\tau}_{x}D(y))^{-1}$. The image in ![]() $S/G$ is then
$S/G$ is then ![]() $\bar{g}_{2}=\bar{y}\bar{g}_{1}\bar{D}(\bar{y})^{-1}$, which yields that
$\bar{g}_{2}=\bar{y}\bar{g}_{1}\bar{D}(\bar{y})^{-1}$, which yields that ![]() $\bar{y}\in \text{fix}(\bar{D})=\{\bar{1}\}$, and so
$\bar{y}\in \text{fix}(\bar{D})=\{\bar{1}\}$, and so ![]() $y\in G$. This shows that
$y\in G$. This shows that ![]() $\hat{i} ^{x}$ is injective for all
$\hat{i} ^{x}$ is injective for all ![]() $x\in S$. Because there is a bijection between the Reidemeister sets
$x\in S$. Because there is a bijection between the Reidemeister sets ![]() ${\mathcal{R}}[D]$ and
${\mathcal{R}}[D]$ and ![]() ${\mathcal{R}}[{\it\tau}_{x}D]$ given by
${\mathcal{R}}[{\it\tau}_{x}D]$ given by ![]() $[g]\mapsto [gx^{-1}]$, it follows that
$[g]\mapsto [gx^{-1}]$, it follows that ![]() $R(D^{\prime })=R({\it\tau}_{x}D^{\prime })$. On the other hand, by [Reference Dekimpe and Penninckx1, Lemma 3.4], since
$R(D^{\prime })=R({\it\tau}_{x}D^{\prime })$. On the other hand, by [Reference Dekimpe and Penninckx1, Lemma 3.4], since ![]() $I-\bar{D}_{\ast }$ is an isomorphism,
$I-\bar{D}_{\ast }$ is an isomorphism, ![]() $R(\bar{D})<\infty$, and
$R(\bar{D})<\infty$, and
This proves our claim.
Now assume that ![]() $I-D_{\ast }$ is an isomorphism. Then it follows that
$I-D_{\ast }$ is an isomorphism. Then it follows that ![]() $I-\bar{D}_{\ast }$ and
$I-\bar{D}_{\ast }$ and ![]() $I-D_{\ast }^{\prime }$ are isomorphisms. By the above claim,
$I-D_{\ast }^{\prime }$ are isomorphisms. By the above claim, ![]() $I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }$, and hence
$I-\text{Ad}^{\prime }(x)D_{\ast }^{\prime }$, and hence ![]() $I-\text{Ad}(x)D_{\ast }$ are isomorphisms.◻
$I-\text{Ad}(x)D_{\ast }$ are isomorphisms.◻
Proof of Theorem 1.
If ![]() $S$ is Abelian, then
$S$ is Abelian, then ![]() $\text{Ad}(x)$ is the identity and hence there is nothing to prove. We may assume that
$\text{Ad}(x)$ is the identity and hence there is nothing to prove. We may assume that ![]() $S$ is non-Abelian. Further, by Lemma 3, we may assume that
$S$ is non-Abelian. Further, by Lemma 3, we may assume that ![]() $I-D_{\ast }$ is an isomorphism. Hence,
$I-D_{\ast }$ is an isomorphism. Hence, ![]() $I-\bar{D}_{\ast }$ and
$I-\bar{D}_{\ast }$ and ![]() $I-\text{Ad}(x)D_{\ast }$ are isomorphisms for all
$I-\text{Ad}(x)D_{\ast }$ are isomorphisms for all ![]() $x\in S$.
$x\in S$.
Denote ![]() $G=[S,S]$ and
$G=[S,S]$ and ![]() ${\rm\Lambda}_{0}=S/G$. Then
${\rm\Lambda}_{0}=S/G$. Then ![]() $G$ is nilpotent, and
$G$ is nilpotent, and ![]() ${\rm\Lambda}_{0}\cong \mathbb{R}^{k_{0}}$ for some
${\rm\Lambda}_{0}\cong \mathbb{R}^{k_{0}}$ for some ![]() $k_{0}>0$. Consider the lower central series of
$k_{0}>0$. Consider the lower central series of ![]() $G$:
$G$:
where ![]() ${\it\delta}_{i+1}(G)=[G,{\it\delta}_{i}(G)]$. Let
${\it\delta}_{i+1}(G)=[G,{\it\delta}_{i}(G)]$. Let ![]() ${\rm\Lambda}_{i}={\it\delta}_{i}(G)/{\it\delta}_{i+1}(G)$. Then
${\rm\Lambda}_{i}={\it\delta}_{i}(G)/{\it\delta}_{i+1}(G)$. Then ![]() ${\rm\Lambda}_{i}\cong \mathbb{R}^{k_{i}}$ for some
${\rm\Lambda}_{i}\cong \mathbb{R}^{k_{i}}$ for some ![]() $k_{i}>0$. For each
$k_{i}>0$. For each ![]() $x\in S$, the conjugation
$x\in S$, the conjugation ![]() ${\it\tau}_{x}$ by
${\it\tau}_{x}$ by ![]() $x$ induces an automorphism on
$x$ induces an automorphism on ![]() $G$. Since each
$G$. Since each ![]() ${\it\delta}_{i}(G)$ is a characteristic subgroup of
${\it\delta}_{i}(G)$ is a characteristic subgroup of ![]() $G$,
$G$, ![]() ${\it\tau}_{x}\in \text{Aut}(G)$ restricts to an automorphism on
${\it\tau}_{x}\in \text{Aut}(G)$ restricts to an automorphism on ![]() ${\it\delta}_{i}(G)$, and hence on
${\it\delta}_{i}(G)$, and hence on ![]() ${\rm\Lambda}_{i}$. Now, if
${\rm\Lambda}_{i}$. Now, if ![]() $x\in G$, then we have observed that the induced action on
$x\in G$, then we have observed that the induced action on ![]() ${\rm\Lambda}_{i}$ is trivial. Consequently, there is a well-defined action of
${\rm\Lambda}_{i}$ is trivial. Consequently, there is a well-defined action of ![]() ${\rm\Lambda}_{0}=S/G$ on
${\rm\Lambda}_{0}=S/G$ on ![]() ${\rm\Lambda}_{i}$. Hence, there is a well-defined action of
${\rm\Lambda}_{i}$. Hence, there is a well-defined action of ![]() ${\rm\Lambda}_{0}$ on
${\rm\Lambda}_{0}$ on ![]() ${\rm\Lambda}_{i}$. This action can be viewed as a homomorphism
${\rm\Lambda}_{i}$. This action can be viewed as a homomorphism ![]() ${\it\mu}_{i}:{\rm\Lambda}_{0}\rightarrow \text{Aut}({\rm\Lambda}_{i})$. Note that
${\it\mu}_{i}:{\rm\Lambda}_{0}\rightarrow \text{Aut}({\rm\Lambda}_{i})$. Note that ![]() ${\it\mu}_{0}$ is trivial. Moreover, for any
${\it\mu}_{0}$ is trivial. Moreover, for any ![]() $x\in S$ denoting its image under
$x\in S$ denoting its image under ![]() $S\rightarrow {\rm\Lambda}_{0}$ by
$S\rightarrow {\rm\Lambda}_{0}$ by ![]() $\bar{x}$, the differential of conjugation
$\bar{x}$, the differential of conjugation ![]() ${\it\tau}_{x}$ by
${\it\tau}_{x}$ by ![]() $x$ can be expressed as a matrix of the form
$x$ can be expressed as a matrix of the form
 $$\begin{eqnarray}\text{Ad}(x)(={{\it\tau}_{x}}_{\ast })=\left[\begin{array}{@{}cccc@{}}I & 0 & \cdots \, & 0\\ \ast & {\it\mu}_{1}(\bar{x}) & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots \\ \ast & \ast & \cdots \, & {\it\mu}_{c}(\bar{x})\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}\text{Ad}(x)(={{\it\tau}_{x}}_{\ast })=\left[\begin{array}{@{}cccc@{}}I & 0 & \cdots \, & 0\\ \ast & {\it\mu}_{1}(\bar{x}) & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots \\ \ast & \ast & \cdots \, & {\it\mu}_{c}(\bar{x})\end{array}\right]\end{eqnarray}$$ by choosing a suitable basis of the Lie algebra ![]() $\mathfrak{S}$ of
$\mathfrak{S}$ of ![]() $S$.
$S$.
The homomorphism ![]() $D:S\rightarrow S$ induces homomorphisms
$D:S\rightarrow S$ induces homomorphisms ![]() $D_{i}:{\it\delta}_{i}(G)\rightarrow {\it\delta}_{i}(G)$ and hence homomorphisms
$D_{i}:{\it\delta}_{i}(G)\rightarrow {\it\delta}_{i}(G)$ and hence homomorphisms ![]() $\bar{D}_{i}:{\rm\Lambda}_{i}\rightarrow {\rm\Lambda}_{i}$, so that the following diagram is commutative:
$\bar{D}_{i}:{\rm\Lambda}_{i}\rightarrow {\rm\Lambda}_{i}$, so that the following diagram is commutative:
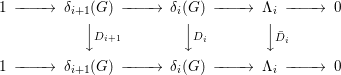
Hence, the differential of ![]() $D$ can be expressed as a matrix of the form
$D$ can be expressed as a matrix of the form
 $$\begin{eqnarray}D_{\ast }=\left[\begin{array}{@{}cccc@{}}\bar{D}_{0} & 0 & \cdots \, & 0\\ \ast & \bar{D}_{1} & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots \\ \ast & \ast & \cdots \, & \bar{D}_{c}\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}D_{\ast }=\left[\begin{array}{@{}cccc@{}}\bar{D}_{0} & 0 & \cdots \, & 0\\ \ast & \bar{D}_{1} & \cdots \, & 0\\ \vdots & \vdots & \ddots & \vdots \\ \ast & \ast & \cdots \, & \bar{D}_{c}\end{array}\right]\end{eqnarray}$$ with respect to the same basis for ![]() $\mathfrak{S}$ chosen as above.
$\mathfrak{S}$ chosen as above.
Furthermore, the above commutative diagram produces the following identities:
Let ![]() $x\in S$ with
$x\in S$ with ![]() $\bar{x}\in {\rm\Lambda}_{0}=\mathbb{R}^{k_{0}}$. Since
$\bar{x}\in {\rm\Lambda}_{0}=\mathbb{R}^{k_{0}}$. Since ![]() $I-\bar{D}_{0}:\mathbb{R}^{k_{0}}\rightarrow \mathbb{R}^{k_{0}}$ is invertible, we can choose
$I-\bar{D}_{0}:\mathbb{R}^{k_{0}}\rightarrow \mathbb{R}^{k_{0}}$ is invertible, we can choose ![]() $\bar{y}\in {\rm\Lambda}_{0}$ so that
$\bar{y}\in {\rm\Lambda}_{0}$ so that ![]() $(I-\bar{D}_{0})(\bar{y})=\bar{x}$. Now, using the above identities, we observe that
$(I-\bar{D}_{0})(\bar{y})=\bar{x}$. Now, using the above identities, we observe that
 $$\begin{eqnarray}\displaystyle \det (I-{\it\mu}_{i}(\bar{x})\bar{D}_{i}) & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{x}){\it\mu}_{i}(\bar{D}_{0}(\bar{y}))\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{x}+\bar{D}_{0}(\bar{y}))\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{y})\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}))\det (I-\bar{D}_{i})\det ({\it\mu}_{i}(\bar{y}))^{-1}\nonumber\\ \displaystyle & = & \displaystyle \det (I-\bar{D}_{i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det (I-{\it\mu}_{i}(\bar{x})\bar{D}_{i}) & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{x}){\it\mu}_{i}(\bar{D}_{0}(\bar{y}))\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{x}+\bar{D}_{0}(\bar{y}))\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}){\it\mu}_{i}(\bar{y})^{-1}-{\it\mu}_{i}(\bar{y})\bar{D}_{i}{\it\mu}_{i}(\bar{y})^{-1})\nonumber\\ \displaystyle & = & \displaystyle \det ({\it\mu}_{i}(\bar{y}))\det (I-\bar{D}_{i})\det ({\it\mu}_{i}(\bar{y}))^{-1}\nonumber\\ \displaystyle & = & \displaystyle \det (I-\bar{D}_{i}).\nonumber\end{eqnarray}$$Consequently, we have
 $$\begin{eqnarray}\displaystyle \det (I-\text{Ad}(x)D_{\ast }) & = & \displaystyle \det (I-\bar{D}_{0})\mathop{\prod }_{i=1}^{c}\det (I-{\it\mu}_{i}(\bar{x})\bar{D}_{i})\nonumber\\ \displaystyle & = & \displaystyle \det (I-\bar{D}_{0})\mathop{\prod }_{i=1}^{c}\det (I-\bar{D}_{i})=\det (I-D_{\ast }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det (I-\text{Ad}(x)D_{\ast }) & = & \displaystyle \det (I-\bar{D}_{0})\mathop{\prod }_{i=1}^{c}\det (I-{\it\mu}_{i}(\bar{x})\bar{D}_{i})\nonumber\\ \displaystyle & = & \displaystyle \det (I-\bar{D}_{0})\mathop{\prod }_{i=1}^{c}\det (I-\bar{D}_{i})=\det (I-D_{\ast }).\nonumber\end{eqnarray}$$This completes the proof of our theorem. ◻


