1 Introduction
Recently, modulation of the correlation functions of partially coherent beams has been studied widely[Reference Wolf1–Reference Chen, Gu, Wang and Cai9]. Correlation function provides a new freedom for manipulating optical field, e.g., creation of light beam with prescribed far-field intensity distribution. Various partially coherent beams with prescribed correlation functions have been investigated in both theory and experiment since Gori and collaborators derived the sufficient condition for constructing the genuine correlation functions[Reference Gori and Santarsiero2, Reference Gori, Sanchez, Santarsiero and Shirai3]. Recent studies have shown that specially correlated partially coherent beams display many unique but interesting properties, e.g., self-splitting effect appears in a Hermite–Gaussian correlated Schell-model beam on propagation[Reference Chen, Gu, Wang and Cai9–Reference Chen, Yu, Yuan, Wang and Cai11], partially coherent beams with multi-Gaussian, Bessel–Gaussian and cosine-Gaussian correlated Schell-model functions exhibit prescribed far-field intensity distributions[Reference Sahin and Korotkova12–Reference Liang, Wang, Liu, Cai and Korotkova15], Laguerre–Gaussian correlated Schell-model beam produces an optical cage near the focal plane[Reference Mei and Korotkova16, Reference Chen and Cai17]. Due to those extraordinary properties, specially correlated partially coherent beams are useful in some applications, such as optical imaging, particle trapping, atom guiding and free-space optical communications. We presented a review on specially correlated partially coherent beams in Ref. [Reference Cai, Chen and Wang4].
The nonuniform correlated partially coherent (NCPC) beam was first introduced in Ref. [Reference Lajunen and Saastamoinen18], and such beam exhibits self-focusing and self-shifting effect in free-space propagation. Propagation properties of an NCPC beam in the uniformly correlated media were studied in Ref. [Reference Tong and Korotkova19]. The evolution properties of the scintillation of an NCPC beam in atmospheric turbulence was illustrated in Ref. [Reference Gu and Gbur20], and it was found that an NCPC beam can not only have lower scintillation but also higher intensity than a conventional Gaussian–Schell-model (GSM) beam, and it will be useful for long-distance free-space optical communications. Recently, the scalar NCPC beam was extended to the electromagnetic case[Reference Tong and Korotkova21] and the statistical properties of such beam in turbulent atmosphere were also investigated[Reference Mei, Tong and Korotkova22]. Multi-Gaussian correlated Schell-model (MGCSM) beam introduced in Ref. [Reference Sahin and Korotkova12] displays far-field flat-topped beam profile although it has a Gaussian beam profile in the source plane[Reference Sahin and Korotkova12, Reference Korotkova, Sahin and Shchepakina23]. Both theoretical and experimental results have demonstrated that an MGCSM beam exhibits lower scintillation than a GSM beam in turbulence[Reference Yuan, Liu, Wang, Chen, Cai, Qu and Eyyuboglu24–Reference Avramov-Zamurovic, Nelson, Guth and Korotkova26].
All above-mentioned specially correlated partially coherent beams have the same correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions. However, in some specific applications, such as trapping and guiding anisotropic particles, beams with different intensity distributions in
$y$ directions. However, in some specific applications, such as trapping and guiding anisotropic particles, beams with different intensity distributions in ![]() $x$ and
$x$ and ![]() $y$ directions are required. In this paper, we introduce a new specially correlated partially coherent beam whose correlation functions in
$y$ directions are required. In this paper, we introduce a new specially correlated partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different, which is named nonuniform multi-Gaussian correlated (NMGC) partially coherent beam. The evolution properties of the intensity distribution of this new beam in free space are illustrated numerically, and we find that the NMGC partially coherent beam exhibits self-focusing and self-shifting in one direction and self-shaping in the other direction. The interesting properties of this new beam may find some applications, e.g., material thermal processing and laser carving, where a laser with high power and prescribed beam shape is required.
$y$ directions are different, which is named nonuniform multi-Gaussian correlated (NMGC) partially coherent beam. The evolution properties of the intensity distribution of this new beam in free space are illustrated numerically, and we find that the NMGC partially coherent beam exhibits self-focusing and self-shifting in one direction and self-shaping in the other direction. The interesting properties of this new beam may find some applications, e.g., material thermal processing and laser carving, where a laser with high power and prescribed beam shape is required.
2 Basic theory for constructing specially correlated partially coherent beam
In the space-time domain, partially coherent beam is characterized by the mutual intensity, which is restricted by the nonnegative definiteness requirement and can be expressed in the following form[Reference Wolf1–Reference Gori, Sanchez, Santarsiero and Shirai3],
where ![]() $I$ is a function that satisfies the nonnegative condition and
$I$ is a function that satisfies the nonnegative condition and ![]() $H$ is an arbitrary function. Various specially correlated partially coherent beams can be defined through choosing suitable functions of
$H$ is an arbitrary function. Various specially correlated partially coherent beams can be defined through choosing suitable functions of ![]() $H$ and
$H$ and ![]() $I$.
$I$.
In this paper, we consider a more general case. The correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different from each other, and the mutual intensity of this new beam is given as
$y$ directions are different from each other, and the mutual intensity of this new beam is given as ![]() $J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})=J_{0x}(x_{1},x_{2})J_{0y}(y_{1},y_{2})$. Then, to satisfy the nonnegative definiteness requirement,
$J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})=J_{0x}(x_{1},x_{2})J_{0y}(y_{1},y_{2})$. Then, to satisfy the nonnegative definiteness requirement, ![]() $J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})$ can be expressed in the following form,
$J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})$ can be expressed in the following form,
 $$\begin{eqnarray}\displaystyle J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}}) & = & \displaystyle \int I_{x}(u)H_{x}^{\ast }(x_{1},u)H_{x}^{\ast }(x_{2},u)\,du\nonumber\\ \displaystyle & & \displaystyle \times \,\int I_{y}(v)H_{y}^{\ast }(y_{1},v)H_{y}^{\ast }(y_{2},v)\,dv.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}}) & = & \displaystyle \int I_{x}(u)H_{x}^{\ast }(x_{1},u)H_{x}^{\ast }(x_{2},u)\,du\nonumber\\ \displaystyle & & \displaystyle \times \,\int I_{y}(v)H_{y}^{\ast }(y_{1},v)H_{y}^{\ast }(y_{2},v)\,dv.\end{eqnarray}$$ Under the condition of ![]() $I_{x}=I_{y}$ and
$I_{x}=I_{y}$ and ![]() $H_{x}=H_{y}$, Equation (2) reduces to Equation (1).
$H_{x}=H_{y}$, Equation (2) reduces to Equation (1).
After some operation, Equation (2) can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})=\int {\rm\Gamma}_{x}(u_{1},u_{2})H_{x}^{\ast }(x_{1},u_{1})H_{x}^{\ast }(x_{2},u_{2})\,du_{1}\,du_{2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int {\rm\Gamma}_{y}(v_{1},v_{2})H_{y}^{\ast }(y_{1},v_{1})H_{y}^{\ast }(y_{2},v_{2})\,dv_{1}\,dv_{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})=\int {\rm\Gamma}_{x}(u_{1},u_{2})H_{x}^{\ast }(x_{1},u_{1})H_{x}^{\ast }(x_{2},u_{2})\,du_{1}\,du_{2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int {\rm\Gamma}_{y}(v_{1},v_{2})H_{y}^{\ast }(y_{1},v_{1})H_{y}^{\ast }(y_{2},v_{2})\,dv_{1}\,dv_{2},\end{eqnarray}$$where
One sees from Equations (3) and (4) that ![]() $J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})$ and
$J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})$ and ![]() ${\rm\Gamma}_{x}(u_{1},u_{2}){\rm\Gamma}_{y}(v_{1},v_{2})$ represents the output and input mutual intensities, respectively.
${\rm\Gamma}_{x}(u_{1},u_{2}){\rm\Gamma}_{y}(v_{1},v_{2})$ represents the output and input mutual intensities, respectively. ![]() $H_{x}$ and
$H_{x}$ and ![]() $H_{y}$ denote the response functions of the optical paths in
$H_{y}$ denote the response functions of the optical paths in ![]() $x$ and
$x$ and ![]() $y$ directions between two planes, respectively.
$y$ directions between two planes, respectively. ![]() ${\rm\Gamma}_{x}(u_{1},u_{2})$ and
${\rm\Gamma}_{x}(u_{1},u_{2})$ and ![]() ${\rm\Gamma}_{y}(v_{1},v_{2})$ denote the mutual intensities of the incoherent source in
${\rm\Gamma}_{y}(v_{1},v_{2})$ denote the mutual intensities of the incoherent source in ![]() $x$ and
$x$ and ![]() $y$ directions, respectively. Thus, one can generate a specially correlated partially coherent beam whose correlation functions in
$y$ directions, respectively. Thus, one can generate a specially correlated partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different by varying
$y$ directions are different by varying ![]() $H_{x}$,
$H_{x}$, ![]() $H_{y}$,
$H_{y}$, ![]() $I_{x}$ and
$I_{x}$ and ![]() $I_{y}$ through propagation (see Figure 1).
$I_{y}$ through propagation (see Figure 1).

Figure 1. Schematic for forming a partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different through propagation.
$y$ directions are different through propagation.
3 Nonuniform multi-Gaussian correlated partially coherent beam
In this section, we introduce a typical kind of partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different named NMGC partially coherent beam, and explore its free-space propagation properties.
$y$ directions are different named NMGC partially coherent beam, and explore its free-space propagation properties.
The mutual intensity of a partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are different can be expressed as
$y$ directions are different can be expressed as
where ![]() $I$ denotes the intensity distribution,
$I$ denotes the intensity distribution, ![]() ${\it\mu}_{x}$ and
${\it\mu}_{x}$ and ![]() ${\it\mu}_{y}$ are the correlation functions in
${\it\mu}_{y}$ are the correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions, respectively. Now we introduce a new specially correlated partially coherent beam which has nonuniform correlation function in one direction and MGCSM function in the other direction, and we call this new beam as NMGC partially coherent beam. The intensity and correlation functions of an NMGC partially coherent beam at
$y$ directions, respectively. Now we introduce a new specially correlated partially coherent beam which has nonuniform correlation function in one direction and MGCSM function in the other direction, and we call this new beam as NMGC partially coherent beam. The intensity and correlation functions of an NMGC partially coherent beam at ![]() $z=0$ are written as
$z=0$ are written as
where ![]() ${\it\sigma}_{0}$ represents the beam width,
${\it\sigma}_{0}$ represents the beam width, ![]() $w_{x}$ and
$w_{x}$ and ![]() $w_{y}$ denote the coherence widths along
$w_{y}$ denote the coherence widths along ![]() $x$ and
$x$ and ![]() $y$ directions, respectively,
$y$ directions, respectively, ![]() $x_{0}$ is a real constant and
$x_{0}$ is a real constant and ![]() $\left(\!\begin{smallmatrix}M\\ m\end{smallmatrix}\!\right)$ stand for binomial coefficients.
$\left(\!\begin{smallmatrix}M\\ m\end{smallmatrix}\!\right)$ stand for binomial coefficients.
Figure 2 shows the density plot of the correlation functions of an NMGC partially coherent beam for various ![]() $x_{0}$ and
$x_{0}$ and ![]() $M$ in
$M$ in ![]() $x$ and
$x$ and ![]() $y$ directions. The green lines in Figure 2 denote the cross-lines with
$y$ directions. The green lines in Figure 2 denote the cross-lines with ![]() $x_{2}=0$ and
$x_{2}=0$ and ![]() $y_{2}=0$, respectively. During calculation, we set
$y_{2}=0$, respectively. During calculation, we set ![]() $w_{x}=w_{y}=0.2~\text{mm}$, and the values of other parameters are attached in Figure 2. We see from Figure 2 that the correlation function of the NMGC partially coherent beam in
$w_{x}=w_{y}=0.2~\text{mm}$, and the values of other parameters are attached in Figure 2. We see from Figure 2 that the correlation function of the NMGC partially coherent beam in ![]() $x$ direction is totally different from that in
$x$ direction is totally different from that in ![]() $y$ direction, i.e., the correlation function in
$y$ direction, i.e., the correlation function in ![]() $x$ direction is locally varying, but the correlation function in
$x$ direction is locally varying, but the correlation function in ![]() $y$ direction is independent of the lateral coordinate. Comparing Figures 2(a) and 2(c), we find that the highest value of the correlation function shifts to the position
$y$ direction is independent of the lateral coordinate. Comparing Figures 2(a) and 2(c), we find that the highest value of the correlation function shifts to the position ![]() $x_{0}$. Comparing Figures 2(b) and 2(d), we find that the number of the lobes of correlation function in
$x_{0}$. Comparing Figures 2(b) and 2(d), we find that the number of the lobes of correlation function in ![]() $y$ direction increases as the beam order
$y$ direction increases as the beam order ![]() $M$ increases. Due to the special distribution of the correlation functions, the NMGC partially coherent beam exhibits self-focusing and self-shaping effect during propagation as shown later.
$M$ increases. Due to the special distribution of the correlation functions, the NMGC partially coherent beam exhibits self-focusing and self-shaping effect during propagation as shown later.

Figure 2. Density plot of the correlation functions of an NMGC partially coherent beam for various ![]() $x_{0}$ and
$x_{0}$ and ![]() $M$ in
$M$ in ![]() $x$ and
$x$ and ![]() $y$ directions.
$y$ directions.
Paraxial propagation of the mutual intensity of an NMGC partially coherent beam through a stigmatic ABCD optical system can be studied by use of the generalized Collins formula[Reference Lin and Cai27],
 $$\begin{eqnarray}\displaystyle J({\bf\rho}_{1},{\bf\rho}_{2}) & = & \displaystyle \frac{1}{({\it\lambda}B)^{2}}\exp \left[-\frac{ikD}{2B}({\bf\rho}_{1}^{2}-{\bf\rho}_{2}^{2})\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left[-\frac{ikA}{2B}(\mathbf{r}_{1}^{2}-\mathbf{r}_{2}^{2})\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{ik}{B}\left(\mathbf{r}_{1}\boldsymbol{\cdot }{\bf\rho}_{1}-\mathbf{r}_{2}\boldsymbol{\cdot }{\bf\rho}_{2}\right)\right]d^{2}\mathbf{r}_{1}\,d^{2}\mathbf{r}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J({\bf\rho}_{1},{\bf\rho}_{2}) & = & \displaystyle \frac{1}{({\it\lambda}B)^{2}}\exp \left[-\frac{ikD}{2B}({\bf\rho}_{1}^{2}-{\bf\rho}_{2}^{2})\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }J_{0}(\mathbf{r}_{\mathbf{1}},\mathbf{r}_{\mathbf{2}})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left[-\frac{ikA}{2B}(\mathbf{r}_{1}^{2}-\mathbf{r}_{2}^{2})\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{ik}{B}\left(\mathbf{r}_{1}\boldsymbol{\cdot }{\bf\rho}_{1}-\mathbf{r}_{2}\boldsymbol{\cdot }{\bf\rho}_{2}\right)\right]d^{2}\mathbf{r}_{1}\,d^{2}\mathbf{r}_{2},\end{eqnarray}$$ where ![]() ${\bf\rho}_{1}$ and
${\bf\rho}_{1}$ and ![]() ${\bf\rho}_{2}$ are two arbitrary position vectors in the output plane,
${\bf\rho}_{2}$ are two arbitrary position vectors in the output plane, ![]() $k=2{\it\pi}/{\it\lambda}$ and
$k=2{\it\pi}/{\it\lambda}$ and ![]() ${\it\lambda}$ is the wavelength,
${\it\lambda}$ is the wavelength, ![]() $A$,
$A$, ![]() $B$,
$B$, ![]() $C$, and
$C$, and ![]() $D$ are the elements of the optical system transfer matrix.
$D$ are the elements of the optical system transfer matrix.

Figure 3. Normalized intensity distribution of an NMGC partially coherent beam on propagation in free space with ![]() $x_{0}=0$ and
$x_{0}=0$ and ![]() $M=5$.
$M=5$.
The intensity distribution in the output plane is obtained as
Let us consider the propagation of an NMGC partially coherent beam in free space. The elements of the transfer matrix between the source plane (at ![]() $z=0$) and output plane (at
$z=0$) and output plane (at ![]() $z$) in free space are given as
$z$) in free space are given as
By substituting Equations (5)–(9), (11) and (12) into Equation (10), we can easily study the evolution properties of the intensity distribution of an NMGC partially coherent beam on propagation in free space numerically. Figures 3 and 4 show the normalized intensity distribution of an NMGC partially coherent beam on propagation in free space for various ![]() $x_{0}$ and
$x_{0}$ and ![]() $M$. During calculation,
$M$. During calculation, ![]() ${\it\sigma}_{0}$ is set as 0.5 mm,
${\it\sigma}_{0}$ is set as 0.5 mm, ![]() $w_{x}$ and
$w_{x}$ and ![]() $w_{y}$ are equal to 0.2 mm. One finds from Figures 3 and 4 that the NMGC partially coherent beam has a Gaussian beam profile in the source plane, and the Gaussian beam profile generally evolves into needle-like beam profile on propagation, and the length of the needle increases as the beam order
$w_{y}$ are equal to 0.2 mm. One finds from Figures 3 and 4 that the NMGC partially coherent beam has a Gaussian beam profile in the source plane, and the Gaussian beam profile generally evolves into needle-like beam profile on propagation, and the length of the needle increases as the beam order ![]() $M$ increases. When
$M$ increases. When ![]() $x_{0}={\it\sigma}_{0}$, the position of maximum intensity shifts during propagation. Above propagation properties of an NMGC partially coherent beam in free space are also called self-shaping effect. Thus, modulating the correlation functions of
$x_{0}={\it\sigma}_{0}$, the position of maximum intensity shifts during propagation. Above propagation properties of an NMGC partially coherent beam in free space are also called self-shaping effect. Thus, modulating the correlation functions of ![]() $x$ and
$x$ and ![]() $y$ directions in different ways provides an effective method for manipulating the optical field, and it will be useful in various beam shaping applications.
$y$ directions in different ways provides an effective method for manipulating the optical field, and it will be useful in various beam shaping applications.
In order to observe the correlation-induced self-focusing effect, we calculate in Figures 5 and 6 the normalized intensity distribution of an NMGC partially coherent beam on propagation in free space in ![]() ${\it\rho}_{x}{-}z$ plane and
${\it\rho}_{x}{-}z$ plane and ![]() ${\it\rho}_{y}{-}z$ plane for various
${\it\rho}_{y}{-}z$ plane for various ![]() $x_{0}$ and
$x_{0}$ and ![]() $M$ and the corresponding cross-line. We find from Figure 5 that the NMGC partially coherent beam exhibits self-focusing effect in
$M$ and the corresponding cross-line. We find from Figure 5 that the NMGC partially coherent beam exhibits self-focusing effect in ![]() ${\it\rho}_{x}{-}z$ plane, i.e., the intensity at
${\it\rho}_{x}{-}z$ plane, i.e., the intensity at ![]() $z=80~\text{mm}$ is narrower and more powerful than that in the source plane, and exhibits self-shaping effect in
$z=80~\text{mm}$ is narrower and more powerful than that in the source plane, and exhibits self-shaping effect in ![]() ${\it\rho}_{y}{-}z$ plane, i.e., the intensity distribution evolves from a Gaussian beam profile to a flat-topped beam profile during propagation. From Figure 6, we see that the position of the maximum intensity shifts in
${\it\rho}_{y}{-}z$ plane, i.e., the intensity distribution evolves from a Gaussian beam profile to a flat-topped beam profile during propagation. From Figure 6, we see that the position of the maximum intensity shifts in ![]() ${\it\rho}_{x}{-}z$ plane under the condition of
${\it\rho}_{x}{-}z$ plane under the condition of ![]() $x_{0}={\it\sigma}_{0}$, and this phenomenon is called self-shifting[Reference Lajunen and Saastamoinen18].
$x_{0}={\it\sigma}_{0}$, and this phenomenon is called self-shifting[Reference Lajunen and Saastamoinen18].
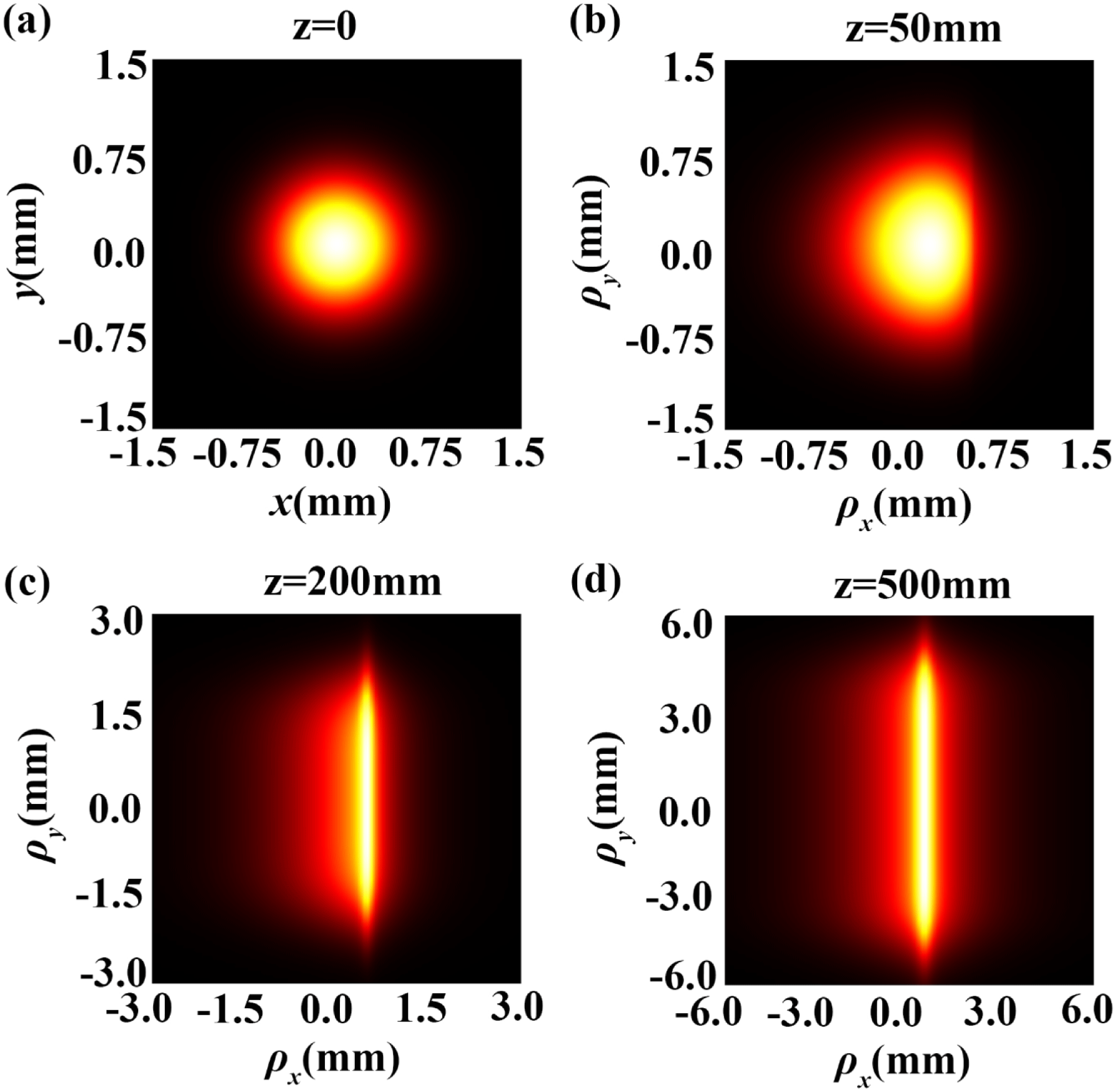
Figure 4. Normalized intensity distribution of an NMGC partially coherent beam on propagation in free space with ![]() $x_{0}={\it\sigma}_{0}$ and
$x_{0}={\it\sigma}_{0}$ and ![]() $M=20$.
$M=20$.

Figure 5. Normalized intensity distribution of an NMGC partially coherent beam on propagation in free space (a-1) in ![]() ${\it\rho}_{x}{-}z$ plane, and (b-1) in
${\it\rho}_{x}{-}z$ plane, and (b-1) in ![]() ${\it\rho}_{y}{-}z$ plane with
${\it\rho}_{y}{-}z$ plane with ![]() $x_{0}=0$ and
$x_{0}=0$ and ![]() $M=5$ and the corresponding cross-line.
$M=5$ and the corresponding cross-line.
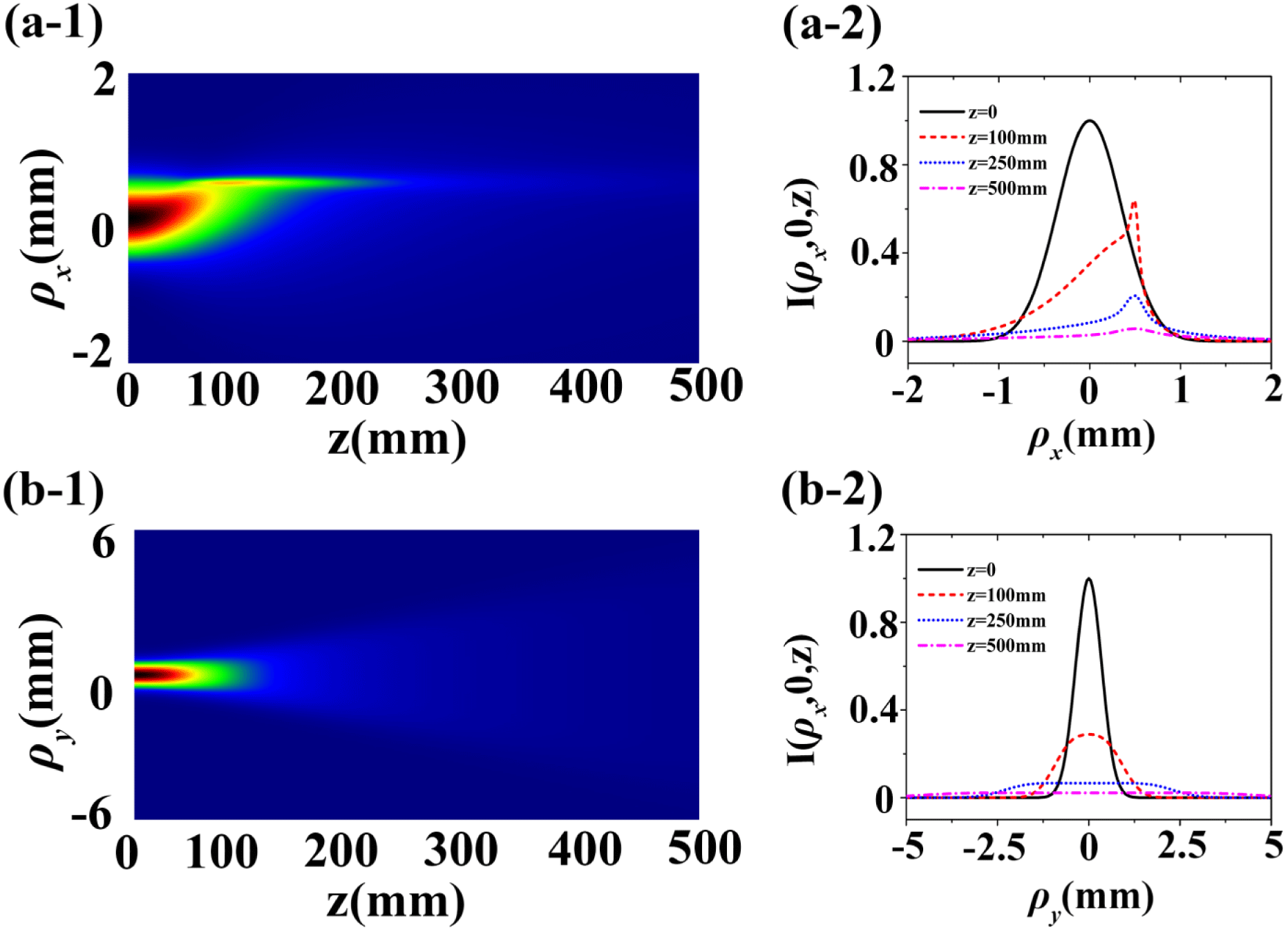
Figure 6. Normalized intensity distribution of an NMGC partially coherent beam on propagation in free space (a-1) in ![]() ${\it\rho}_{x}=z$ plane, and (b-1) in
${\it\rho}_{x}=z$ plane, and (b-1) in ![]() ${\it\rho}_{y}=z$ plane with
${\it\rho}_{y}=z$ plane with ![]() $x_{0}={\it\sigma}_{0}$ and
$x_{0}={\it\sigma}_{0}$ and ![]() $M=20$ and the corresponding cross-line.
$M=20$ and the corresponding cross-line.
4 Conclusions
As a summary, we have introduced a new specially correlated partially coherent beam named NMGC partially coherent beam whose correlation functions in ![]() $x$ and
$x$ and ![]() $y$ directions are totally different, and have outlined briefly the nonnegative definiteness for constructing the mutual intensity of this new beam. The propagation properties of this new beam in free space have been demonstrated numerically. Our results have shown that an NMGC partially coherent displays self-focusing and self-shifting effect in one direction and self-shaping effect in the other direction, and a needle-like beam profile can be formed on propagation. Our results suggest a new approach for optical field manipulation and will be useful in various beam shaping applications. The correlation-induced self-focusing and self-shaping effect will be useful in some applications where the high power and shaped laser is required.
$y$ directions are totally different, and have outlined briefly the nonnegative definiteness for constructing the mutual intensity of this new beam. The propagation properties of this new beam in free space have been demonstrated numerically. Our results have shown that an NMGC partially coherent displays self-focusing and self-shifting effect in one direction and self-shaping effect in the other direction, and a needle-like beam profile can be formed on propagation. Our results suggest a new approach for optical field manipulation and will be useful in various beam shaping applications. The correlation-induced self-focusing and self-shaping effect will be useful in some applications where the high power and shaped laser is required.
Acknowledgements
This research is supported by the National Natural Science Fund for Distinguished Young Scholar under grant no. 11525418, the National Natural Science Foundation of China under grant no. 11274005 and the project of the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions.










