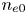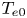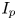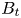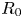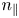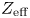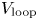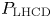1. Introduction
The ‘advanced tokamak’ (AT) concept (Kikuchi Reference Kikuchi1993; Goldston Reference Goldston1996) is a leading candidate for many steady-state fusion power plant designs (Galambos et al. Reference Galambos, Perkins, Haney and Mandrekas1995; Sips et al. Reference Sips2005; Najmabadi et al. Reference Najmabadi, Abdou, Bromberg, Brown, Chan, Chu, Dahlgren, El-Guebaly, Heitzenroeder and Henderson2006). An AT makes use of the pressure-gradient-driven bootstrap current to sustain a majority of the required plasma current, augmented by non-inductive current drive actuators (Houlberg & Attenberger Reference Houlberg and Attenberger1994). These auxiliary actuators may consist of neutral beams and/or radio frequency (RF) systems such as lower hybrid current drive (LHCD) and high harmonic fast wave (HHFW). RF actuators are well suited for use in fusion power plants. They do not require line-of-sight access through the breeding blanket and neutron shield surrounding the fusion plasma, and the technology readiness level (TRL) of the RF sources and power delivery systems is high. Control of AT operating scenarios requires detailed information on the RF heating and current drive profiles to maintain magnetohydrodynamic (MHD) stable overall current and pressure profiles (Moreau & Voitsekhovitch Reference Moreau and Voitsekhovitch1999; Luce Reference Luce2011). Moreover, additional current drive is often required at specific radial locations (on axis, off axis, rational $q$![]() surfaces) to augment the bootstrap current where it is insufficient, or to suppress instabilities such as tearing modes or kink modes.
surfaces) to augment the bootstrap current where it is insufficient, or to suppress instabilities such as tearing modes or kink modes.
Consequently, predicting RF wave heating and current drive is critical for present-day fusion experiments and to design and construct a fusion power plant. In fact, the commercialisation of fusion power requires an accurate accounting of plant energy in order to minimise the auxiliary system power usage and to optimise the plant operation cost, which requires advancement in high-fidelity modelling of RF actuators. In addition, accurate predictions of the current drive and heating profiles are needed in integrated modelling to assess the performance and stability of the plasma operating scenario.
An AT plasma is a complex integrated physics system with bi-directional coupling between heat/particle transport, temperature/density profiles, current profile, MHD stability, heat/particle exhaust and fusion reaction rate (Hayashi Reference Hayashi2010; Moreau et al. Reference Moreau, Walker, Ferron, Liu, Schuster, Barton, Boyer, Burrell, Flanagan and Gohil2013; Meneghini et al. Reference Meneghini, Smith, Lao, Izacard, Ren, Park, Candy, Wang, Luna and Izzo2015; Poli Reference Poli2018). Few of these quantities are directly controllable through external actuators. Control of the RF heating and current drive profiles, by varying the launched power and wavenumber of the system, is one of the few direct control knobs available on a tokamak. Having the capability to determine where the RF system is depositing power/current at the present moment (and how that may change with other plasma conditions) is crucial for the reliable operation of an AT. Although RF simulation tools are sophisticated and accurate, the computational resources required are considerable for high-fidelity simulations.
In this work, we propose using machine learning (ML) models to accurately predict RF power absorption and current density profiles and accelerate the time required for simulations, which will enable widespread use in parametric scenario scoping studies, time-dependent modelling and real-time control. We show that our models are able to quickly and accurately reproduce the results of GENRAY/CQL3D (Harvey & McCoy Reference Harvey and McCoy1992; Smirnov & Harvey Reference Smirnov and Harvey1995), with inference times on the order of milliseconds as compared with minutes for the ground-truth simulations.
The remainder of this paper is structured as follows. Section 2 reviews the state of surrogate models in fusion research and the physics we reproduce with our surrogate models. Section 3 covers the design and methods used in our research. Section 4 presents the results of our surrogate models and § 5 covers the paper conclusions and future work.
2. Background and previous work
In this section we review the relevant theoretical background on ray tracing Fokker–Plack (FP) modelling of heating and current drive, which is the basis for the input data of our designed ML models. We also review relevant works in the literature that use ML to accelerate computations and we provide a landscape of ML methods in the areas of plasma physics and fusion.
2.1. Ray tracing/FP modelling of heating and current drive
Several approaches are possible to simulate the RF current drive profile in tokamak plasmas. Analytical and reduced numerical (e.g. adjoint method) models provide a reasonable estimate of the total driven current but lack key physics necessary to determine the current profile shape that can only be realised by solving the FP equation. Moving upward in complexity to ray tracing/FP modelling includes the necessary wave propagation and quasi-linear Landau damping physics for accurate current profile prediction in several frequency ranges (lower hybrid, electron cyclotron). Ray tracing makes use of the simplifications of geometrical optics and reduces the problem from solving Maxwell's equations in toroidal geometry (the ‘fullwave’ method) to the following set of ray equations:
where $D_0$![]() is the wave dispersion relation, $\omega$
is the wave dispersion relation, $\omega$![]() is the wave frequency, $\boldsymbol {k}$
is the wave frequency, $\boldsymbol {k}$![]() is the wavenumber, $\tau$
is the wavenumber, $\tau$![]() is the ray step parameter, $t$
is the ray step parameter, $t$![]() is the time coordinate and $\boldsymbol {x}$
is the time coordinate and $\boldsymbol {x}$![]() is the spatial coordinate. Equation (2.1b) is trivial under the condition that the time variation of $D_0$
is the spatial coordinate. Equation (2.1b) is trivial under the condition that the time variation of $D_0$![]() is small on the timescale of the operating frequency $f_0$
is small on the timescale of the operating frequency $f_0$![]() , which is well satisfied for waves in the gigahertz range.
, which is well satisfied for waves in the gigahertz range.
Solving the FP equation is required for both fullwave and ray-tracing approaches to determine power absorption and current drive. The FP equation
describes the time evolution of the distribution function, $f$![]() , in the presence of RF damping, $RF$
, in the presence of RF damping, $RF$![]() , and collisions, $C$
, and collisions, $C$![]() . The RF term
. The RF term
depends on the distribution function and the quasi-linear diffusion operator, $D_{QL}$![]() . The wave solvers provide $D_{QL}$
. The wave solvers provide $D_{QL}$![]() as an input to the FP solver, as shown in figure 1. The FP solver then feeds information on power absorption back to the wave equation solver and the process iterates until convergence. In the ray-tracing approach, the ray trajectories need not be recalculated at each time step of the FP solver, only the power absorption along the ray. A schematic of the workflow between wave equation solvers and FP solvers is shown in figure 1. In this study we use the GENRAY (Smirnov & Harvey Reference Smirnov and Harvey1995) ray-tracing code coupled to CQL3D (Harvey & McCoy Reference Harvey and McCoy1992; Petrov & Harvey Reference Petrov and Harvey2016) for solving the FP equation, although the approach may be expanded to include other RF simulation tools such as TORIC (Brambilla Reference Brambilla1996) for fullwave simulations.
as an input to the FP solver, as shown in figure 1. The FP solver then feeds information on power absorption back to the wave equation solver and the process iterates until convergence. In the ray-tracing approach, the ray trajectories need not be recalculated at each time step of the FP solver, only the power absorption along the ray. A schematic of the workflow between wave equation solvers and FP solvers is shown in figure 1. In this study we use the GENRAY (Smirnov & Harvey Reference Smirnov and Harvey1995) ray-tracing code coupled to CQL3D (Harvey & McCoy Reference Harvey and McCoy1992; Petrov & Harvey Reference Petrov and Harvey2016) for solving the FP equation, although the approach may be expanded to include other RF simulation tools such as TORIC (Brambilla Reference Brambilla1996) for fullwave simulations.

Figure 1. Wave equation solvers (TORIC+Petra-M or GENRAY) couple to FP equation solvers (CQL3D) through the quasi-linear diffusion operator, $D_{QL}$![]() . The FP solver perturbs the distribution function and couples information on quasi-linear RF power absorption, $P_{abs}$
. The FP solver perturbs the distribution function and couples information on quasi-linear RF power absorption, $P_{abs}$![]() , back to the wave solver. This process iterates until the solutions converge. Rough per-iteration wall clock runtimes for each code are indicated in the figure. TORIC+Petra-M and GENRAY figures reproduced from Shiraiwa et al. (Reference Shiraiwa, Wright, Lee and Bonoli2017) and Wallace et al. (Reference Wallace, Parker, Bonoli, Hubbard, Hughes, LaBombard, Meneghini, Schmidt, Shiraiwa and Whyte2010), respectively.
, back to the wave solver. This process iterates until the solutions converge. Rough per-iteration wall clock runtimes for each code are indicated in the figure. TORIC+Petra-M and GENRAY figures reproduced from Shiraiwa et al. (Reference Shiraiwa, Wright, Lee and Bonoli2017) and Wallace et al. (Reference Wallace, Parker, Bonoli, Hubbard, Hughes, LaBombard, Meneghini, Schmidt, Shiraiwa and Whyte2010), respectively.
Both GENRAY and CQL3D require information about the plasma density, temperature and ion composition, as well as the magnetic equilibrium as inputs. In addition, CQL3D requires the toroidal DC electric field, whereas GENRAY requires the wave parameters (power, $n_{\|}$![]() spectrum, antenna position) as initial conditions. The outputs of GENRAY, namely the ray trajectories and quasi-linear diffusion operator, are of indirect rather than direct interest from the perspective of plasma control and integrated modelling. The outputs of CQL3D (wave power deposition and current profiles) are of direct interest and will be the prediction targets of our ML models.
spectrum, antenna position) as initial conditions. The outputs of GENRAY, namely the ray trajectories and quasi-linear diffusion operator, are of indirect rather than direct interest from the perspective of plasma control and integrated modelling. The outputs of CQL3D (wave power deposition and current profiles) are of direct interest and will be the prediction targets of our ML models.
2.2. Using ML to accelerate computations
Modern computational resources have advanced numerical simulation of physical systems to an increasing range of spatial and temporal scales. However, even with high-performance computing techniques, it is a challenge for real-time demand response in feedback control. Emerging data-driven methods have revolutionised how researchers model, predict and eventually control these complex systems in a diverse range of fields, including but not limited to automation, climate, combustion, fluids, high-energy physics, plasma science and plasmonics (Malkiel et al. Reference Malkiel, Mrejen, Nagler, Arieli, Wolf and Suchowski2018; Duraisamy, Iaccarino & Xiao Reference Duraisamy, Iaccarino and Xiao2019; Wilkes et al. Reference Wilkes, Emmett, Beltran, Woodward and Carling2020; Yellapantula et al. Reference Yellapantula, de Frahan, King, Day, Grout, H. and A.2020; Abbate, Conlin & Kolemen Reference Abbate, Conlin and Kolemen2021; Bai & Peng Reference Bai and Peng2021; Hatfield et al. Reference Hatfield, Gaffney, Anderson, Ali, Antonelli, Başeğmez du Pree, Citrin, Fajardo, Knapp and Kettle2021; Maschler & Weyrich Reference Maschler and Weyrich2021; Brunton & Kutz Reference Brunton and Kutz2022). A variety of ML techniques have been used such as deep neural networks (DNNs) to fit simulation data. The resulting surrogate models have been used in larger frameworks. For example, global climate models use ML models to represent kernels drawn from observations (Reichstein et al. Reference Reichstein, Camps-Valls, Stevens, Jung, Denzler, Carvalhais and Prabhat2019). A common thread is the use of numerical models and codes to generate training data to produce surrogate models with a low mean squared error (MSE). This is the approach of this paper.
2.3. The landscape of ML in plasma physics and fusion
The application of ML techniques to fusion energy and plasma physics dates to the late 20th century, with initial applications of neural networks to the topics of tokamak plasma control (Bishop et al. Reference Bishop, Cox, Haynes, Roach, Smith, Todd, Trotman and J.G.1992, Reference Bishop, Haynes, Smith, Todd and Trotman1995a; Wróblewski Reference Wróblewski1997), disruption prediction (Hernandez et al. Reference Hernandez, Vannucci, Tajima, Lin, Horton and McCool1996; Wroblewski, Jahns & Leuer Reference Wroblewski, Jahns and Leuer1997), energy confinement prediction (Allen & Bishop Reference Allen and Bishop1992) and data analysis (Lister & Schnurrenberger Reference Lister and Schnurrenberger1991; Bishop et al. Reference Bishop, Strachan, O'Rourke, Maddison and Thomas1993; Morabito & Versaci Reference Morabito and Versaci1997), among other topics. These early applications showed the promise of ML techniques in fusion research. Considerable advances in both computing hardware and ML techniques after the turn of the century resulted in renewed interest in ML applications for fusion in recent years.
ML continues to be an extremely effective tool in some of the early adopted topics, particularly disruption prediction (Rea & Granetz Reference Rea and Granetz2018; Rea et al. Reference Rea, Montes, Pau, Granetz and Sauter2020; Churchill, Tobias & Zhu Reference Churchill, Tobias and Zhu2020a; Churchill et al. Reference Churchill, Choi, Kube, Chang, Klasky, J., B., A., O., S. and T.2020b). A more recent application of ML to fusion research is in the area of accelerating computationally intensive simulation models. Researchers developed fast surrogate models for plasma transport (Meneghini et al. Reference Meneghini, Snoep, Lyons, McClenaghan, Imai, Grierson, Smith, Staebler, Snyder and Candy2020; van de Plassche et al. Reference van de Plassche, Citrin, Bourdelle, Camenen, Casson, Dagnelie, Felici, Ho and Van Mulders2020) and neutral beam heating/current drive (Boyer, Kaye & Erickson Reference Boyer, Kaye and Erickson2019; Morosohk, Boyer & Schuster Reference Morosohk, Boyer and Schuster2021), used surrogate model frameworks for validation of plasma transport codes (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, White, Creely, Greenwald, Howard, Sciortino and Wright2018) and also employed ML techniques to reduce computation time for codes such as XGC (Miller et al. Reference Miller, Churchill, Dener, Chang, Munson and Hager2021). The work of Boyer and Morosohk, in which they create a fast neural-network=based surrogate model for NUBEAM, is particularly relevant to the work presented in this paper. The work presented here represents the first efforts to create a ML-based surrogate model for RF heating and current drive.
3. Design and methods
To reduce the computational cost of ray tracing/FP modelling of heating and current drive, we implement and study three ML models to tackle the regression problem to predict both current profiles and wave power deposition. In the following, we first describe the details of the source data and input/output parameters used to design the ML models. Next, we describe the three ML models we implement in this study, multilayer perceptron (MLP), Gaussian processes and random forest, along with information about their design and hyperparameter optimisation.
3.1. Source data
Training ML models requires a database of simulations to draw training, validation and testing data. In the ML context, ‘validation’ refers to the process of using a holdout set of data to provide an unbiased evaluation of the model while tuning the hyperparameters. To this end, the ${\rm \pi}$![]() Scope (Shiraiwa et al. Reference Shiraiwa, Greenwald, Stillerman, Wallace, London and Thomas2018) workflow engine generates a set of $16\,384$
Scope (Shiraiwa et al. Reference Shiraiwa, Greenwald, Stillerman, Wallace, London and Thomas2018) workflow engine generates a set of $16\,384$![]() GENRAY (Smirnov & Harvey Reference Smirnov and Harvey1995)/CQL3D (Harvey & McCoy Reference Harvey and McCoy1992) input files and submits five of these simulations at a time to run in parallel on the MIT Engaging cluster at the Massachusetts Green High Performance Computing Center. The wall-clock time required to generate the entire database was approximately two weeks. As each GENRAY/CQL3D simulation completes, ${\rm \pi}$
GENRAY (Smirnov & Harvey Reference Smirnov and Harvey1995)/CQL3D (Harvey & McCoy Reference Harvey and McCoy1992) input files and submits five of these simulations at a time to run in parallel on the MIT Engaging cluster at the Massachusetts Green High Performance Computing Center. The wall-clock time required to generate the entire database was approximately two weeks. As each GENRAY/CQL3D simulation completes, ${\rm \pi}$![]() Scope incorporates the relevant input and output quantities into a NETCDF database. Because a single NETCDF file containing all simulation data would be too large for efficient data read/write, ${\rm \pi}$
Scope incorporates the relevant input and output quantities into a NETCDF database. Because a single NETCDF file containing all simulation data would be too large for efficient data read/write, ${\rm \pi}$![]() Scope chunks the NETCDF files with $100$
Scope chunks the NETCDF files with $100$![]() simulations per file.
simulations per file.
The GENRAY/CQL3D input files contain hundreds of parameters covering both the plasma and the numerical methods used in the simulation. The vast majority of these parameters do not vary in the simulation database, with nine zero-dimensional parameters describing the plasma and lower hybrid system varying across the ranges listed in table 1. The simulation database consists of LHCD simulations for the EAST tokamak (Wu et al. Reference Wu2007). The LHCD wave frequency is 4.6 GHz, and the antenna size/location match that of the LHCD antenna on EAST (Liu et al. Reference Liu, Ding, Li, Wan, Shan, Wang, Liu, Zhao, Li and Li2015). The kinetic profiles are analytic and defined by a central electron temperature/density ($n_{e0}$![]() , $T_{e0}$
, $T_{e0}$![]() ) and edge density/temperature ($n_{eb}$
) and edge density/temperature ($n_{eb}$![]() , $T_{eb}$
, $T_{eb}$![]() ) according to the equations
) according to the equations
and
where $\rho$![]() is the normalised minor radius. In the GENRAY/CQL3D database $n_{e0}$
is the normalised minor radius. In the GENRAY/CQL3D database $n_{e0}$![]() and $T_{e0}$
and $T_{e0}$![]() vary whereas $n_{eb}$
vary whereas $n_{eb}$![]() and $T_{eb}$
and $T_{eb}$![]() remain constant at $7.5 \times 10^{18}\,{\rm m}^{-3}$
remain constant at $7.5 \times 10^{18}\,{\rm m}^{-3}$![]() and 0.1 keV, respectively.
and 0.1 keV, respectively.
Table 1. Parameters varied in the GENRAY/CQL3D database.

The magnetic equilibrium is an analytic model based on the work described in (Guazzotto & Freidberg Reference Guazzotto and Freidberg2021). The major radius of the plasma, plasma current and toroidal magnetic field vary over typical ranges for the EAST tokamak in this database. However, other equilibrium parameters such as inverse aspect ratio (0.24), triangularity (0.5), elongation (1.8) and magnetic configuration (double null) remain constant for all simulations in the database.
For sampling the parameter space, we chose to use Latin hypercube sampling (LHS) (McKay, Conover & Whiteman Reference McKay, Conover and Whiteman1976). LHS covers a large dimension parameter space with far fewer sample points than a uniform grid and guarantees better uniformity across all columns/rows of the multi-dimensional parameter space than random sampling methods. Given the utility of this sampling method, ${\rm \pi}$![]() Scope now incorporates LHS functionality in parametric scans of input variables.
Scope now incorporates LHS functionality in parametric scans of input variables.
The parameter ranges in table 1 cover or exceed typical values for each parameter seen on the EAST tokamak, however not all combinations of parameters are relevant. In particular, a significant number of the simulations occur in the ‘slide-away’ regime where the collisional drag on fast electrons is insufficient to counteract the accelerating potential of the toroidal DC electric field:
where $m_e$![]() is the electron mass, $v$
is the electron mass, $v$![]() is the fast electron velocity, $\nu _{{\rm coll}}(v)$
is the fast electron velocity, $\nu _{{\rm coll}}(v)$![]() is the fast election collision frequency, $q$
is the fast election collision frequency, $q$![]() is the electron charge and $E_{{\rm crit}}$
is the electron charge and $E_{{\rm crit}}$![]() is the critical toroidal DC electric field. Using
is the critical toroidal DC electric field. Using
results in
which is the familiar expression for the Dreicer field (Dreicer Reference Dreicer1959). Taking $v = c/n_{\|}$![]() as the upper limit of the quasi-linear plateau for slide-away electrons (as opposed to $v=c$
as the upper limit of the quasi-linear plateau for slide-away electrons (as opposed to $v=c$![]() for true runaway electrons (Connor & Hastie Reference Connor and Hastie1975)) yields
for true runaway electrons (Connor & Hastie Reference Connor and Hastie1975)) yields
with $E_{{\rm crit}}$![]() measured in ${\rm V}\,{\rm m}^{-1}$
measured in ${\rm V}\,{\rm m}^{-1}$![]() . The slide-away regime can be modelled accurately with CQL3D by increasing the resolution and range of the electron energy grid, however this requires additional computational resources and the slide-away regime is generally avoided in LHCD experiments. A threshold of $E_{{\rm DC}}/E_{{\rm crit}} > 0.9$
. The slide-away regime can be modelled accurately with CQL3D by increasing the resolution and range of the electron energy grid, however this requires additional computational resources and the slide-away regime is generally avoided in LHCD experiments. A threshold of $E_{{\rm DC}}/E_{{\rm crit}} > 0.9$![]() delineates the slide-away regime to be filtered from the dataset, resulting in the final dataset used to design the ML models as described in the following.
delineates the slide-away regime to be filtered from the dataset, resulting in the final dataset used to design the ML models as described in the following.
3.2. ML models
This section describes the three different ML models designed to predict current profiles and power deposition. Each of these ML models carry different characteristics which may affect prediction performance in different ways. Our goal is to evaluate multiple ML models as surrogates for the traditional more expensive type of computation described in the previous section.
3.2.1. MLP
MLP (Bishop et al. Reference Bishop1995b) is a feed-forward artificial neural network composed of multiple layers of neurons (perceptrons) with activation functions. It typically consists of three types of layers of nodes, an input layer, one or more hidden layers and an output layer. Each node (with exception of the input layer) is a neuron that utilises a nonlinear activation function to learn the right representation of the data mathematically. MLP provides global approximations by mapping a set of input features to output features through a training process using the back-propagation algorithm (Rumelhart, Hinton & Williams Reference Rumelhart, Hinton and Williams1986). During this process, the parameters consisting of weights and biases are iteratively adjusted and optimised. MLP model has been broadly applied in classification and regression tasks in science (Gardill et al. Reference Gardill, Fuchs, Frank and Weigel2018; Yüksel, Soydaner & Bahtiyar Reference Yüksel, Soydaner and Bahtiyar2021). MLP is a supervised learning algorithm that relies on the existence of training data and is suitable for use in both classification and regression problems.
The hyperparameters of the neural network include the batch size, learning rate, the $L_2$![]() normalisation factor, the number of hidden layers and the number of neurons in each hidden layer. Considering the large search space of the hyperparameters in MLP, we employ the random search method by placing a reasonable set of range of the hyperparameters. We constrain the MLP to having four hidden layers, where the number of nodes in each layer is searched in the range $[20, 1000]$
normalisation factor, the number of hidden layers and the number of neurons in each hidden layer. Considering the large search space of the hyperparameters in MLP, we employ the random search method by placing a reasonable set of range of the hyperparameters. We constrain the MLP to having four hidden layers, where the number of nodes in each layer is searched in the range $[20, 1000]$![]() , the learning rate in $[10^{-5}, 10^{-2}$
, the learning rate in $[10^{-5}, 10^{-2}$![]() , the $L_2$
, the $L_2$![]() normalisation factor in $[1, 10]$
normalisation factor in $[1, 10]$![]() and the batch size in $[16, 128]$
and the batch size in $[16, 128]$![]() . We find the best hyperparameters separately for each prediction problem as reported in § 4.
. We find the best hyperparameters separately for each prediction problem as reported in § 4.
3.2.2. Random forest
Random forest (Breiman Reference Breiman2001) is a supervised learning algorithm that uses ensemble methods of bootstrap aggregation to solve classification or regression problems. It constructs multiple decision trees during training and then outputs the mean predictions of the individual tree models for testing. It leverages both the bagging method and feature randomness (Breiman Reference Breiman2001) to create an uncorrelated forest of decision trees. At each training step, the model creates a random subset of features and builds simplified trees using these subsets, and while splitting a node, the algorithm searches for the best features among the specific subset. A generalised result then combines the results of numerous uncorrelated models to output the prediction. Because the averaging of uncorrelated tress lowers the overall variance, the random forest model has a lower risk of overfitting and has been broadly applied to science and engineering domains (Jaiswal & Samikannu Reference Jaiswal and Samikannu2017; Resende & Drummond Reference Resende and Drummond2018).
The hyperparameters of the random forest model include the number of estimators, maximum of tree depth and minimum number of leaves required to split an internal node. To explore the best combinations of settings of the hyperparameters, we use GridSearchCV (Pedregosa et al. Reference Pedregosa, Varoquaux, Gramfort, Michel, Thirion, Grisel, Blondel, Prettenhofer, Weiss and Dubourg2011) with the ranges of $[100, 10\,000]$![]() , $[100, 2000]$
, $[100, 2000]$![]() and $[2, 4]$
and $[2, 4]$![]() for each of the above hyperparameters, respectively. In the following sections, we refer to the random forest regression model as RFR. We present detailed results for this process in § 4.
for each of the above hyperparameters, respectively. In the following sections, we refer to the random forest regression model as RFR. We present detailed results for this process in § 4.
3.2.3. Gaussian processes regression
The Gaussian processes regression (GPR) model is a probabilistic supervised ML framework that has been widely used for regression and classification tasks. This model can make predictions incorporating prior knowledge and provides uncertainty measures over predictions (Murphy Reference Murphy2013). Similar to other ML models, GPR is classified as a non-parametric model (Liu et al. Reference Liu, Ong, Shen and Cai2020), i.e. when conducting regressions using GPR, the complexity or flexibility of the model is not limited by the number of parameters. More specifically, the model does not assume a specific form for the function that maps the input to the output data, which would be the case for a linear regression model for example.
Formally, a Gaussian process mode is a probability distribution over possible functions that fit a set of points. The regression function modelled by a multivariate Gaussian is given as
where $\boldsymbol {X} = [\boldsymbol {x}_1,\ldots,\boldsymbol {x}_n]$![]() , $\boldsymbol {f} = [f(\boldsymbol {x}_1),\ldots,f(\boldsymbol {x}_n)]$
, $\boldsymbol {f} = [f(\boldsymbol {x}_1),\ldots,f(\boldsymbol {x}_n)]$![]() , $\boldsymbol {\mu } = [m(\boldsymbol {x}_1),\ldots,m(\boldsymbol {x}_n)]$
, $\boldsymbol {\mu } = [m(\boldsymbol {x}_1),\ldots,m(\boldsymbol {x}_n)]$![]() and $K_{ij} = k(\boldsymbol {x}_i,\boldsymbol {x}_j)$
and $K_{ij} = k(\boldsymbol {x}_i,\boldsymbol {x}_j)$![]() . Here $\boldsymbol {X}$
. Here $\boldsymbol {X}$![]() are the observed data points, $m$
are the observed data points, $m$![]() represents the mean function and $k$
represents the mean function and $k$![]() represents a positive-definite kernel function. With no observation, the mean function is default to be $m(\boldsymbol {X})=0$
represents a positive-definite kernel function. With no observation, the mean function is default to be $m(\boldsymbol {X})=0$![]() given that the data are often normalised to a zero mean. The Gaussian processes model is a distribution over functions whose shape is defined by $\boldsymbol {K}$
given that the data are often normalised to a zero mean. The Gaussian processes model is a distribution over functions whose shape is defined by $\boldsymbol {K}$![]() . If points $\boldsymbol {x}_i$
. If points $\boldsymbol {x}_i$![]() and $\boldsymbol {x}_j$
and $\boldsymbol {x}_j$![]() are considered to be similar by the kernel, function outputs of the two points, $f(\boldsymbol {x}_i)$
are considered to be similar by the kernel, function outputs of the two points, $f(\boldsymbol {x}_i)$![]() and $f(\boldsymbol {x}_j)$
and $f(\boldsymbol {x}_j)$![]() , are expected to be similar. In the regression process, given the observed data and a mean function $\boldsymbol {f}$
, are expected to be similar. In the regression process, given the observed data and a mean function $\boldsymbol {f}$![]() estimated by these observed points, predictions can be made at new points $\boldsymbol {X}_*$
estimated by these observed points, predictions can be made at new points $\boldsymbol {X}_*$![]() as $\boldsymbol {f}(\boldsymbol {X}_*)$
as $\boldsymbol {f}(\boldsymbol {X}_*)$![]() . Based on the definitions, one can directly derive the joint distribution of $\boldsymbol {f}$
. Based on the definitions, one can directly derive the joint distribution of $\boldsymbol {f}$![]() and $\boldsymbol {f}_*$
and $\boldsymbol {f}_*$![]() based on $\boldsymbol {K}$
based on $\boldsymbol {K}$![]() and, more importantly, the conditional distribution $P(\boldsymbol {f}_*|\boldsymbol {f},\boldsymbol {X},\boldsymbol {X}_*)$
and, more importantly, the conditional distribution $P(\boldsymbol {f}_*|\boldsymbol {f},\boldsymbol {X},\boldsymbol {X}_*)$![]() over $\boldsymbol {f}_*$
over $\boldsymbol {f}_*$![]() , which is needed for the regression process. These derivations are explained in detail in earlier work (Rasmussen & Williams Reference Rasmussen and Williams2005).
, which is needed for the regression process. These derivations are explained in detail in earlier work (Rasmussen & Williams Reference Rasmussen and Williams2005).
The hyperparameters of the GPR model consist of the kernel and its lengthscale and variance. In this work, we explore six different kernels: Exponential, Matern12, Matern32, Matern52, SquaredExponential and Rational Quadratic. Each of these kernels is added together with a Linear kernel. Generally speaking, the lengthscale controls the smoothness of the learnt functions and the variance controls the scale of values of the learnt functions. Given that the input dimension for our problem is nine, the dimension of the lengthscale is also nine. To optimise these hyperparameters, we perform a grid search using the interval $[0.25,2.1]$![]() for each lengthscale value for each input dimension, and the interval $[0.1,2.2]$
for each lengthscale value for each input dimension, and the interval $[0.1,2.2]$![]() for the variance of the kernels. This search is performed for all six different kernels. We present the final results for this optimisation process in § 4.
for the variance of the kernels. This search is performed for all six different kernels. We present the final results for this optimisation process in § 4.
3.3. Design and implementation
To implement the three proposed surrogate models we use Python and its supporting libraries. The MLP model is implemented using the Pytorch deep learning framework. We use the Adam solver (Kingma & Ba Reference Kingma and Ba2014), an extension of stochastic gradient descent in the implementation of optimising the weights of the MLP, which is computationally efficient and requires less tuning for hyperparameters.
As for the random forest model, we use scikit-learn (Pedregosa et al. Reference Pedregosa, Varoquaux, Gramfort, Michel, Thirion, Grisel, Blondel, Prettenhofer, Weiss and Dubourg2011), more specifically sklearn.ensemble.RandomForestRegressor, which provides the functions fit and predict for training and prediction, respectively.
Finally, to implement the GPR model, we use an existing Python library called GPflow (Matthews et al. Reference Matthews, van der Wilk, Nickson, Fujii, Boukouvalas, León-Villagrá, Ghahramani and Hensman2017), which is based on GPy (Sheffield Machine Learning Software 2012). Although these two libraries are very similar to each other, GPflow leverages TensorFlow for faster computation and gradient calculation, and focuses on variational inference and Markov Chain Monte Carlo methods. One special advantage about this library pertinent to our work is its recent extension to inter-domain approximations and multi-output priors (van der Wilk et al. Reference van der Wilk, Dutordoir, John, Artemev, Adam and Hensman2020), which is the case of our dataset. As mentioned previously, one essential component of a GPR model is the kernel function. GPflow provides implementations for the most well-known kernels used in the literature, including Exponential, Linear, Matern family, and others. The kernel selection is included in the hyperparameter optimisation process explained in § 3. For the optimisation process, we use the model gpflow.models.GPR also implemented in GPflow, along with gpflow.optimizers.Scipy for function minimisation.
4. Results and evaluation
Based on the designing process and hyperparameter optimisation explained in the previous section, we obtain the best three final ML models to be used as surrogates for the forward modelling problem, predicting current profiles and power deposition. This section presents the details of the final ML models along with their computational performance and prediction accuracy.
4.1. Computational environment and methodology
To create the database of simulations for training and testing the ML surrogate models, we used GENRAY version 10.10_170301 and CQL3D version cswim_170101.1 with the Intel FORTRAN compiler version 19.1.3.304 built and run on the MIT Engaging computing cluster at the Massachusetts Green High Performance Computing Center. The MIT PSFC partition of Engaging consists of 136 nodes, with $2\times 16$![]() Intel Xeon 2.1 GHz cores 128 GB RAM per node. The source code for GENRAY and CQL3D are available at https://github.com/compxco.
Intel Xeon 2.1 GHz cores 128 GB RAM per node. The source code for GENRAY and CQL3D are available at https://github.com/compxco.
Our ML experiments were performed on Cori, a multi-core platform maintained by the National Energy Research Scientific Computing Center (NERSC). All tests were run using Jupyter (https://docs.nersc.gov/services/jupyter/) on a shared CPU node, which consists of a large memory node running an AMD EPYC 7302 3.0 GHz with 32 physical cores, 2 threads per core, 2 sockets per node and has 2 TB of memory (https://docs.nersc.gov/systems/cori/). Appendix A presents more details specifically related to the Python environment used for reproducibility purposes.
The results reported in this section are based on the dataset filtered with the slide-away regime threshold as described in § 3.1. We randomly divide this database of simulations into two subsets: the training set and the test set. The training set is the largest and contains $80\,\%$![]() of the overall dataset ($10\,677$
of the overall dataset ($10\,677$![]() samples), whereas the test set contains $20\,\%$
samples), whereas the test set contains $20\,\%$![]() ($2670$
($2670$![]() samples). The training set is used for both hyperparameter optimisation and to build the final regression model used to predict samples in the test data as described in the next section. For all the models we report execution time for both training and testing, and prediction accuracy based on the MSE.
samples). The training set is used for both hyperparameter optimisation and to build the final regression model used to predict samples in the test data as described in the next section. For all the models we report execution time for both training and testing, and prediction accuracy based on the MSE.
4.2. Results of ML model performance and prediction accuracy
4.2.1. Hyperparameters
The first step in the design of the ML models is to optimise their hyperparameters, which is necessary for the selection of the best model for final predictions. In order to find the best hyperparameter set for each model, as described in § 3, the training set is used in a $5$![]() -fold cross-validation process using the MSE metric. For each fold, $8541$
-fold cross-validation process using the MSE metric. For each fold, $8541$![]() and $2136$
and $2136$![]() samples are used for train and validation, respectively, and the same $5$
samples are used for train and validation, respectively, and the same $5$![]() folds are used across all 3 models. A separate set of hyperparameters is obtained for each prediction problem (wave power deposition and current profiles).
folds are used across all 3 models. A separate set of hyperparameters is obtained for each prediction problem (wave power deposition and current profiles).
After the random search approach using the parameters’ ranges described in § 3, we find the best set of hyperparameters for the MLP model as presented in table 2. Owing to an existing bigger variation in the power profiles, we observe a denser network is selected with a smaller learning rate and larger batch size in the mini-batch gradient descent for convergence through training.
Table 2. Best hyperparameters obtained for the MLP model.

In figure 2, we report the hyperparameter selection of the random forest model for each prediction problem. The grid search results show that with an increase in the number of estimators, the cross-validated average MSE decreases. The cross-validated accuracy is not sensitive to the max depth of trees trained, for both the current and power profiles. Figure 2(d) presents a minuscule reduction of $5$![]() -fold validated accuracy when increasing the minimum sample split in a node. Therefore, we choose $2000$
-fold validated accuracy when increasing the minimum sample split in a node. Therefore, we choose $2000$![]() estimators, max depth of $100$
estimators, max depth of $100$![]() and minimum samples split of $2$
and minimum samples split of $2$![]() to balance the computational time and accuracy.
to balance the computational time and accuracy.

Figure 2. Hyperparameter tuning of the random forest regression model for the both current and power profiles: (a,c) cross-validated MSE versus the number of estimators using the maximum tree depth of 100, 1000 and 2000; (b,d) cross-validated MSE versus number of estimators using the minimum samples split of 2, 3 and 4.
Based on the grid search process using the different hyperparameters (with their respective ranges) related to the GPR model, we obtain a general overview of the cross-validated MSE values across all the $1200$![]() different sets of hyperparameters as shown in figure 3. Based on these results the GPR model presented a low cross-validated MSE variance throughout the hyperparameter optimisation process. For the problem of predicting current profiles, the best model used the Matern32 kernel with $0.75$
different sets of hyperparameters as shown in figure 3. Based on these results the GPR model presented a low cross-validated MSE variance throughout the hyperparameter optimisation process. For the problem of predicting current profiles, the best model used the Matern32 kernel with $0.75$![]() length scale value for all input dimensions, and variance $0.1$
length scale value for all input dimensions, and variance $0.1$![]() . The associated Linear kernel used variance value of $0.6$
. The associated Linear kernel used variance value of $0.6$![]() . In the case of predicting power deposition, the best model used the Exponential kernel with $1.25$
. In the case of predicting power deposition, the best model used the Exponential kernel with $1.25$![]() length scale value for all input dimensions and variance $2.1$
length scale value for all input dimensions and variance $2.1$![]() . The associated Linear kernel used variance value of $1.6$
. The associated Linear kernel used variance value of $1.6$![]() . In the following, we present the prediction results using the three ML models obtained based on the best set of hyperparameters.
. In the following, we present the prediction results using the three ML models obtained based on the best set of hyperparameters.

Figure 3. Results from the hyperparameter optimisation for the GPR models for both current profile and power deposition. For the current profile the Matern 32 kernel obtained superior results. In the case of power deposition the Exponential kernel performed the best, although the results are very similar among the different set of parameters and kernels.
4.2.2. Prediction results
Once the best hyperparameters are obtained, the models (based on these parameters) are retrained using the whole training data. Then, the final predictions are applied to the test set, which we will refer to as the ‘holdout’ set, as it includes samples from the simulation database never ‘seen’ by the models during either hyperparameter optimisation or training. The loss function used in all cases is the MSE, which is used to evaluate and compare our methods.
We start by presenting in figure 4 the results for predicting current profiles using the three ML models. Each column represents the ML model used and each row presents typical prediction cases for good fits, average fits, and poor fits. Our methodology for deciding which solution numbers to use for typical good, average, and poor fits is as follows. First, we ordered all prediction results for all methods by MSE. Then, from each set of results ordered by MSE, we considered a relatively small window size of solutions ($N=30$![]() ) with the lowest MSE and located the solution number common across this set. A similar methodology applies to those with the highest MSE. For the typical average MSE case, due to a high degree of variance in the middle of the MSE distribution, we used a larger window size ($N=160$
) with the lowest MSE and located the solution number common across this set. A similar methodology applies to those with the highest MSE. For the typical average MSE case, due to a high degree of variance in the middle of the MSE distribution, we used a larger window size ($N=160$![]() ) and display the solution number from the set of mid-range MSE values.
) and display the solution number from the set of mid-range MSE values.

Figure 4. Prediction results for current profiles: (a,d,g) MLP, (b,e,h) RFR and (c, f,i) GPR. (a–c) Good fits, (d–f) average fitsand (g–i) poor fits representations for the same test data using the three ML models.
This set of results shows that all three ML methods give an accurate quantitative prediction for the CQL3D current profile in cases with ‘good’ MSE ${<}0.005$![]() . In the case of ‘average’ MSE of ${\sim }0.1$
. In the case of ‘average’ MSE of ${\sim }0.1$![]() , the overall magnitude and peak structure of the ML inferences are in excellent agreement with the CQL3D ground truth. The differences between the ML model and the ground truth are within the level of experimental uncertainty in measuring the current profile, and also smaller than typical discrepancy between modelling and experiment. Only in the cases of worst disagreement between the ML model and the ground truth CQL3D model are qualitative differences observable between the two.
, the overall magnitude and peak structure of the ML inferences are in excellent agreement with the CQL3D ground truth. The differences between the ML model and the ground truth are within the level of experimental uncertainty in measuring the current profile, and also smaller than typical discrepancy between modelling and experiment. Only in the cases of worst disagreement between the ML model and the ground truth CQL3D model are qualitative differences observable between the two.
Similarly, Figure 5 presents the results for predicting wave power deposition. In the case of the power deposition profile, quantitative agreement is excellent for both the ‘good’ and ‘average’ cases, while the ‘poor’ case infers the correct location for the peak but with a magnitude that is too low by a factor of two. As with the current profiles, the level of agreement between the ML model and the ground truth is well within experimental uncertainty for the average case.

Figure 5. Prediction results for power deposition: (a,d,g) MLP, (b,e,h) RFR and (c, f,i) GPR. (a–c) Good fits, (d–f) average fits and (g–i) poor fits representations for the same test data using the three ML models.
Figures 4 and 5 only show representative prediction examples of ‘good’, ‘average’ and ‘poor’ cases for each ML model. However, in order to show the overall distribution of MSE values for the entire ‘holdout’ set containing $2670$![]() samples, we present in figure 6 the histograms of MSE values for the three ML models for each prediction problem. Based on these histograms, it is clear that the vast majority of predictions leads to small MSE values, around $10^{-1}$
samples, we present in figure 6 the histograms of MSE values for the three ML models for each prediction problem. Based on these histograms, it is clear that the vast majority of predictions leads to small MSE values, around $10^{-1}$![]() for the current profiles and $10^{-2}$
for the current profiles and $10^{-2}$![]() for the power deposition. Indeed, for the low error regime only MLP has MSE ${<}10^{-3}$
for the power deposition. Indeed, for the low error regime only MLP has MSE ${<}10^{-3}$![]() for the current profiles, and only MLP and RFR have MSE $< 5\times 10^{-4}$
for the current profiles, and only MLP and RFR have MSE $< 5\times 10^{-4}$![]() for the power deposition. MLP has a relative smaller distribution in the high-error regime and outperforms RFR and GPR in both cases. It is interesting to note that even though RFR has a larger distribution of MSE toward the very low-error regime compared with the other two models, it also shows a larger MSE at the high-error regimes for the power deposition prediction. For the current profile prediction, GPR in general has more predictions in the lower-error regime indicating a better performance in current profile prediction than RFR.
for the power deposition. MLP has a relative smaller distribution in the high-error regime and outperforms RFR and GPR in both cases. It is interesting to note that even though RFR has a larger distribution of MSE toward the very low-error regime compared with the other two models, it also shows a larger MSE at the high-error regimes for the power deposition prediction. For the current profile prediction, GPR in general has more predictions in the lower-error regime indicating a better performance in current profile prediction than RFR.

Figure 6. Histograms of the MSE in MLP, RFR and GPR ML models for (a) current and (b) power deposition.
Figures 7 and 8 compare the MSE of the current profile and power deposition using the three ML models for all the test examples. The highlighted spots correspond to the representative examples in figure 4 and 5. In general, the predictions of the three methods show a strong linear correlation. From a statistical perspective, MLP tends to have a smaller MSE than RFR and GPR in both the low- and high-error regimes for both the prediction cases. GPR shows a very comparable performance as MLP in the low-error regime of the current prediction. For the power prediction, RFR shows a cluster of relatively better performance in the low-error regime, which matches what we observed in the histogram plot of figure 6.

Figure 7. Pairwise comparisons of the entire MSE of current prediction among the MLP, RFR and GPR ML models for the inference records. The three representative good, average and poor test instances as in figure 4 are highlighted.

Figure 8. Pairwise comparisons of the entire MSE of power prediction among the MLP, RFR and GPR ML models for the inference records. The three representative good, average and poor test instances as in figure 5 are highlighted.
4.3. Discussion
Figures 4 and 5 show anecdotally that the accuracy of all three ML models is anti-correlated with the overall magnitude of the profile. This is potentially problematic as the model is of most interest in the regime where there is significant driven current and power absorption. The origin of this behaviour lies in the loss function used in the training of the ML models: MSE. The absolute MSE is naturally quite small for signals of small magnitude, whereas for larger-magnitude signals it is naturally larger. This is a double-edged sword. A loss function biased against large-magnitude signals actually improves the accuracy of the ML models in the large-magnitude regime as compared with a normalised loss function, which would weight the large- and small-magnitude signals equally in the training process. Training with a physics-based loss function, which is biased even more strongly against large-magnitude signals, may improve model performance further in the large-magnitude regime.
The previous section shows that the three ML-based surrogate models accurately reproduce the results of GENRAY/CQL3D across the range of inputs in the training database. The ultimate test of the ML-based surrogate models is whether they can produce inferences that are useful. To this end, we compare the MLP-based surrogate model with GENRAY/CQL3D simulations that use a full set of experimental inputs rather than the reduced set of nine zero-dimensional inputs. Figure 9 shows the inferred current density profile for a set of four well-diagnosed EAST discharges. The profiles in this figure use the MLP surrogate model, although the RFR and GPR inferences are substantially similar. The predicted current profiles from the surrogate model reproduce the same qualitative results shown in figure 11(b) of Garofalo et al. (Reference Garofalo, Gong, Qian, Chen, Li, Li, Li, Zhai, Bonoli and Brower2017), which used full profiles for the plasma density and temperature, a polarimeter-constrained equilibrium reconstruction, and LHCD power from antennas at 2.45 and 4.6 GHz. The ML surrogate model reproduces the current profile peak location accurately, although the magnitude of the current profile peak agrees less closely with the stand-alone GENRAY/CQL3D model in the previously published study. Note that these differences are a result of the reduced number of inputs (e.g. parabolic $n_e$![]() and $T_e$
and $T_e$![]() profiles as compared with the measured profiles, analytic plasma equilibrium as compared with EFIT reconstruction) to the GENRAY/CQL3D model used to generate the training database, and not inherent to the MLP-based surrogate model. Furthermore, the simulations in figure 9(b) include two frequencies of lower hybrid waves (2.45 and 4.6 GHz), whereas the surrogate model training data is for 4.6 GHz only. Neither figure 9(a) nor figure 9(b) include the effects of fast electron radial diffusion, which are known to be important in reproducing the experimental current profile on EAST (see the differences in figure 11(a–c) in Garofalo et al. Reference Garofalo, Gong, Qian, Chen, Li, Li, Li, Zhai, Bonoli and Brower2017).
profiles as compared with the measured profiles, analytic plasma equilibrium as compared with EFIT reconstruction) to the GENRAY/CQL3D model used to generate the training database, and not inherent to the MLP-based surrogate model. Furthermore, the simulations in figure 9(b) include two frequencies of lower hybrid waves (2.45 and 4.6 GHz), whereas the surrogate model training data is for 4.6 GHz only. Neither figure 9(a) nor figure 9(b) include the effects of fast electron radial diffusion, which are known to be important in reproducing the experimental current profile on EAST (see the differences in figure 11(a–c) in Garofalo et al. Reference Garofalo, Gong, Qian, Chen, Li, Li, Li, Zhai, Bonoli and Brower2017).

Figure 9. (a) Inferred current density profile using the MLP surrogate model for four well-diagnosed EAST discharges. (b) Current profiles for the same set of discharges published in a study by Garofalo. Data in subfigure (b) reproduced from figure 11(b) of Garofalo et al. (Reference Garofalo, Gong, Qian, Chen, Li, Li, Li, Zhai, Bonoli and Brower2017). The orange–red–blue–green legend applies to both figures.
The obtained prediction results clearly show that it is feasible to use ML methods as surrogates for the forward modelling problem achieving high prediction accuracy. Table 3 presents the overall accuracy results for the five-fold cross-validation and testing.
Table 3. Evaluation of our three ML models using MSE. For the five-fold cross-validation (CV) process we present the mean ($\mu$![]() ) and standard deviation ($\sigma$
) and standard deviation ($\sigma$![]() ) of the MSE across all folds. The second column presents the prediction results of each final model trained using the full training data.
) of the MSE across all folds. The second column presents the prediction results of each final model trained using the full training data.

Based on these results we can conclude that the three models are very stable throughout the cross-validation process, presenting very low standard deviation values for all cases. Moreover, all the three models are accurate in predicting current profiles and power deposition, with MLP and GPR presenting slightly better results compared with random forest.
An additional important point of consideration is the computational cost to achieve such results. Ideally, we would like to use these ML models to perform inference tasks in a fraction of the time required via traditional methods. We report the computational costs required for all the three ML models for both training and inference in table 4. The GPR model requires the highest amount of time to perform the five-fold cross-validation, taking $627.5$![]() and $771.1$
and $771.1$![]() min for current and power profiles, respectively. Random forest is the cheapest model, requiring only $3.2$
min for current and power profiles, respectively. Random forest is the cheapest model, requiring only $3.2$![]() and $1.6$
and $1.6$![]() min for each five-fold cross-validation task. Similar computational costs are obtained to train the final models based on the best set of hyperparameters. Most interestingly, all the three models present incredibly low inference times, just under 1 ms for MLP and random forest, and just above 2 ms for GPR, if compared with the 10 min required by the traditional method. This low computational costs easily allow for the applicability of these ML models in real experimental scenarios.
min for each five-fold cross-validation task. Similar computational costs are obtained to train the final models based on the best set of hyperparameters. Most interestingly, all the three models present incredibly low inference times, just under 1 ms for MLP and random forest, and just above 2 ms for GPR, if compared with the 10 min required by the traditional method. This low computational costs easily allow for the applicability of these ML models in real experimental scenarios.
Table 4. Timing requirements. The first column reports the total execution time needed to run the entire five-fold cross-validation (CV). The second column reports the time necessary to train each final model along with per sample inference time.

5. Conclusion and future work
The results of this paper demonstrate the feasibility of ML surrogate models for predicting the current profiles and power deposition of GENRAY/CQL3D, especially at the peak locations. The MLP and GPR generate more accurate estimates than RFR in terms of MSE for high-error regimes. On the other hand, RFR is a much more computationally efficient model that requires orders of magnitude less training time, even compared with the cost of one inference in the GENRAY/CQL3D simulation. Still, the computational resources needed to generate the training dataset far exceed the resources needed to train any of the ML surrogate models. Areas with large MSE are also near boundaries of model applicability and where experiments would not typically operate. Future work will include the study and development of customised loss functions based on the physics of the problem to replace MSE as a figure of merit. Similarly, we will work on improving the GPR model to use physics-based kernels aiming for higher prediction accuracy and more efficient training.
A surrogate model is only as accurate as the training data used to create it. The model presented here uses only a small subset of the many hundreds of possible input variables in GENRAY/CQL3D. Increasing the number of input variables will result in more accurate surrogate models at the cost of additional computational resources needed to create a larger training dataset. Even with a small set of zero-dimensional input parameters, the surrogate models reproduce the qualitative results obtained by GENRAY/CQL3D using full experimental profiles.
As noted in § 4, the effects of fast electron radial diffusion are important to reproducing the current profile in EAST with GENRAY/CQL3D. Including radial diffusion in CQL3D increases the computation time by a factor of 50–100. This represents both a challenge and a great opportunity for the ML surrogate models. On the one hand, generating the training database for the surrogate model is significantly more expensive when radial diffusion is included, whereas the time savings as compared with the original full-fidelity model are enhanced by an even greater factor. We hypothesise that it may be possible to reduce the size of the training database somewhat because radial diffusion smooths out the current profiles, which may allow for low MSE with a smaller database of simulations.
Ultimately, ML-based fast surrogate models will be incorporated into larger frameworks for plasma prediction and control. Control system development frameworks such as COTSIM (Pajares & Schuster Reference Pajares and Schuster2019, Reference Pajares and Schuster2020) and integrated models such as TRANSP (Jardin, Pomphrey & Delucia Reference Jardin, Pomphrey and Delucia1986; Wehner et al. Reference Wehner, Schuster, Boyer and Poli2019) or IPS-FASTRAN (Elwasif et al. Reference Elwasif, Bernholdt, Shet, Foley, Bramley, Batchelor and Berry2010; Park et al. Reference Park, Murakami, St. John, Lao, Chu and Prater2017) will benefit from more rapid estimates of power deposition and current drive profiles. To facilitate adoption of these surrogate models, we have made the trained models available online through Dataverse, as described in Appendix A. Rapid iteration times will allow increased exploration of parameter space to find optimal operating points using plasma ‘flight simulators’ prior to experiments, or in the design of new fusion reactors.
Acknowledgements
Editor Hartmut Zohm thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Director, Office of Science, Office of Fusion Energy Sciences, of the U.S. Department of Energy under Contract Nos. DE-SC0021202 and DE-AC02-05CH11231, through the grant ‘Accelerating Radio Frequency Modeling Using Machine Learning’. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231. The simulations presented in this paper were performed on the MIT-PSFC partition of the Engaging cluster at the MGHPCC facility (www.mghpcc.org) which was funded by DoE grant number DE-FG02-91-ER54109.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are openly available in Dataverse at https://doi.org/10.7910/DVN/5YY6PE and in GitHub at https://github.com/FusionRFModelingMachineLearning/genray-cql3d-ml. See additional details in Appendix A.
Appendix A. Reproducibility
This appendix provides information about accessing and using source code, trained models and sample data that will facilitate reproducing the work we have presented earlier in the paper. Our team is providing four sets of artifacts to facilitate reproducibility and potential application to additional fusion devices. These consist of the final trained models for each of the regression methods used (appendix A.1), the data for performing both training and inference using these methods (appendix A.2), source code to train the ML models using the same dataset used in this article (appendix A.3) and the source code for loading the trained models and sample data and then performing the inference computations (appendix A.4), as described in the following.
A.1 Trained models in ONNX and tensorflow formats
We leverage ONNX as much as possible for sharing our trained ML models. ONNX is a storage format and set of utilities for storing and loading ML models to/from disk files (Bai et al. Reference Bai, Lu and Zhang2019). The ONNX project is a collaboration of numerous partners from industry.
For each the MLP and RFR models we describe earlier (§ 3), we have saved each of these trained models in ONNX format. Owing to current limitations on the operations supported by ONNX, we are making the GPR trained model available using the Tensorflow format. Each trained model reflects the hyperparameter optimisation and training process we describe earlier (§ 3). The inference results we obtain (§ 4) come from these three trained models prior to export to ONNX and Tensorflow formats.Footnote 1
A.2 Data comprising database of simulations, training dataset and sample data for inference
We are providing several sets of data via Dataverse (https://doi.org/10.7910/DVN/5YY6PE). First is the set of NETCDF outputs generated for the full database of simulations, including additional code outputs (e.g. hard X-ray emission) not used in this work. Second is the dataset filtered with the slide-away regime threshold consisting of $13\,347$![]() samples, which can be used to train the three ML models described in this article using CSV format. The third is a sample dataset that can be leveraged to perform inference using the provided trained models in ONNX and Tensorflow using CSV format.
samples, which can be used to train the three ML models described in this article using CSV format. The third is a sample dataset that can be leveraged to perform inference using the provided trained models in ONNX and Tensorflow using CSV format.
A.3 Python scripts for training ML models
The source code used to train the three ML models presented here are available in our GitHub repository (https://github.com/FusionRFModelingMachineLearning/genray-cql3d-ml). These scripts allow for retraining the final models with the dataset containing $13\,347$![]() samples using the best parameters found via hyperparameter optimisation. Detailed information about the required computational environment and instructions to perform this tasks are available in the repository.
samples using the best parameters found via hyperparameter optimisation. Detailed information about the required computational environment and instructions to perform this tasks are available in the repository.
A.4 Python scripts for loading models, data and performing inference workload
In addition to the source code to train the ML models, we also provide Python scripts that directly load the trained models in ONNX and Tensorflow formats in order to perform inference with the provided sample data. We provide separate scripts for each one of the models as described in details in our GitHub repository.