1. Introduction
This paper describes results from two investigations designed to test the hypothesis that a temperate glacier may freeze to its bed in isolated patches. In the laboratory experiments an ice block, whose boundary was maintained at various temperatures close to the equilibrium melting temperature, was subjected to different hydrostatic loads for different periods, while careful measurements of the temperature (to ±0.005 K) were made at its centre with a thermocouple. In the field experiment, continuous records of strain down to 10−8 over a 10 m gauge length were made at three sites in two rock tunnels within 10 m of the ice/rock interface under the Glacier d’Argentière, Mont Blanc, France. The records show characteristic strain events lasting a few minutes that appear to be elastic changes in the rock resulting from changes in the surface tractions between the glacier and its bed.
Reference RobinRobin (1976) suggested two processes that would result in patches of the bed of a temperate glacier being colder than the pressure-melting point. The first process involves a heat-pump effect that is expected to occur during steady flow of a glacier over bedrock irregularities. The second process suggests that intermittent freezing of bedrock patches may result from time variations in the pressure of subglacial water and resultant changes of ice loading on bedrock protruberances.
The above processes depend on the assumption that if the hydrostatic pressure on a parcel of ice at the pressure-melting point is increased rapidly, the temperature through the parcel of ice will fall rapidly to the new pressure-melting point, the necessary heat balance being preserved by absorption of latent heat by melting within the ice mass. When the hydrostatic pressure is rapidly decreased it will quickly warm to the new warmer pressure-melting point as latent heat is absorbed by freezing of melt water only if there is sufficient melt water distributed throughout the parcel of ice. However if there is no melt water present, the ice will remain at the colder temperature of its former pressure-melting point until heat is supplied by conduction from the boundaries of the parcel or by the heat generated in deforming the ice mass.
The heat-pump hypothesis suggests that as basal glacier ice moves into a high-pressure zone up-stream of an obstacle and is cooled by increasing pressure, the resultant water is squeezed out through capillaries into the subglacial water film. Then when this ice moves on to regions of lower pressure, the ice remains cold because the capillaries have closed under pressure, and latent heat is no longer readily available. The effect may occur throughout the glacier sole of the order of decimetres or metres in thickness, and be sufficient to maintain cold patches of ice one or two metres across beneath a glacier moving at speeds of the order of 1 m d−1.
The second process envisages the major part of the weight of a glacier being supported by a water film at relatively low pressure and a smaller fraction by areas of high pressure over bedrock humps. Since the total weight must balance the total basal (water) pressure over a wide area, an increase of the low water pressure will produce a proportionally greater drop in pressure over the smaller high-pressure areas. If sufficient latent heat from water is not available within this ice mass, then it will not adjust to the warmer pressure-melting point, but will freeze to the bed.
If frozen patches are caused by either process, they are likely to produce a change of traction with time between the glacier and bedrock, since the ice will adhere to the rock in the absence of a water film. Since such patches could be some tenths of a degree Celsius below pressure-melting point, the shear tractions could be quite large (at least 0.1 MN m−2), and these would increase as the glacier moved forward. It would be expected, therefore, that from time to time a crack would run between the ice and the rock to relieve the stress. With a time constant, which depended on the diffusion of heat away from the crack faces, the crack would “heal” and the ice again become frozen to the rock. This effect would lead to a “jerky” sliding of the glacier over its bed.
Although Reference GoldthwaitGoldthwait (1973) observed jerky motion only at the upper surface of glaciers and not at bedrock, observations of the jerky nature of glacial sliding have been reported beneath Østerdalsisen in Norway by Reference TheakstoneTheakstone (1967) who recorded the motion of a peg driven into the ice roof of a cavity beneath the glacier. Reference Vivian and BocquetVivian and Bocquet (1973) also reported irregular sliding beneath Glacier d’Argentière. Care was taken to eliminate instrumental stick-slip in these observations, but the possibility of such effects remain. Our field observations give an independent indication of jerky sliding through our recording of strain events due to changing traction between the ice and rock.
2. Laboratory Studies
2.1. Introduction
The laboratory experiments had two objects. The first was to confirm that the adjustment of pressure-melting point under increasing pressure took place immediately following application of pressure. The second was to see if the heat-pump process could be shown to take place under laboratory conditions. It was expected that the results of these experiments would also confirm the accepted coefficient of change of melting point with pressure.
2.2. Apparatus
The apparatus is shown in Figure 1. Fine-grained snow formed by grinding ice (made from distilled water) in an electric coffee grinder, was packed in a cylinder around a small Chromel/Alumel thermocouple supported at the end of a stainless-steel tube. Distilled water was added to the snow and allowed to freeze to form a polycrystalline ice cylinder with randomly orientated grains and many air bubbles. The cylinder and a close-fitting piston were then lowered into an ice/salt/water bath and left for about one hour in the bath until a steady temperature was recorded. Loads were then applied to the piston via a simple hydraulic system and press; the pressure applied to the ram was monitored with a gauge, and the E.M.F. from the thermocouple junction compared to a second thermocouple junction in a triple-point cell, amplified and recorded on a chart recorder. A second thermocouple was used to measure the temperature on the outside of the cylinder. Temperature changes of 0.001 K could be resolved. The mixture in the ice/salt/water bath could be varied to change the temperature on the outside of the cylinder; the stress distribution in the ice block was assumed to be hydrostatic and equal to the load applied to the piston divided by its area. The temperature change in the middle of the ice block was measured for various boundary temperatures and changes in hydrostatic pressure.

Fig. 1. Apparatus used to load the ice at various hydrostatic pressures.
2.3. Results and discussion
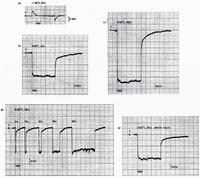
Compression of samples below the pressure-melting point shows adiabatic warming on compression that takes place at a similar rate to the increase of pressure. This indicates that our assumption that the hydrostatic pressure in the sample follows the changes of pressure of the hydraulic system is correct. When a constant pressure is left on the system (Fig. 2a), it then cools back to the ambient temperature with a time constant of the order of 30 s due to thermal conduction and the geometry of our experiment. When pressure is removed, adiabatic cooling of the order of 0. 1 K takes place and the process is reversed. The magnitude of this cooling is similar to that of the warming, which confirms the adiabatic effect.

Fig. 2. Temperature changes produced by loading and unloading the ice block: (a) ice at ‒ 1.09°C, load of 50 bars for 5 min; (b) ice at 0.00°C, load of 50 bars for 5 min; (c) ice at 0.00°C, load of 100 bars for 5 min; (d) ice at 0.00°C, load of 50 bars for times from 5 s to 300 s as shown; (e) ice at 0.00°C, load of 50 bars, with absorbent layer of talc compressed in chamber.
When the experiment is repeated on ice close to the pressure-melting point, we see in (Figure 2b) that instead of adiabatic warming due to compression, the sample cools rapidly as the pressure is applied so that there is no detectable time lag (less than 2 s) before the thermocouple records the new pressure-melting point within the sample. This shows that this temperature change is due to processes within the ice mass. Thermodynamic reasons in line with this argument given by A. B. Pippard (personal communication) are presented in the Appendix.
The above observation indicates that where temperate ice at the base of a glacier moves into a zone of increasing pressure, the temperature field will be determined directly by the pressure field throughout the ice mass.
The immediate lowering of temperature at 50 bars was 0.49±0.01 K (Fig. 2b), and at 100 bars 1.05±0.01 K (Fig. 2c). This is greater than the lowering expected for pure ice of 0.0074 K Per bar, and shows the additional lowering of 0.002 4 K per bar due to presence of air dissolved in water (Reference HarrisonHarrison, 1972). The main uncertainty in these observations is the measurement of pressure, which was read off an industrial pressure gauge.
When pressure is removed from the sample, which takes around two seconds, the temperature of the central thermocouple rises over the same time interval by a little over half of its previous fall in temperature, and it continues to rise slowly for one to five minutes to return to the temperature of the water bath (Fig. 2d). The time constant for this rise (I/e of temperature after release of pressure of 50 bars) varies from roughly 40 s after the pressure was applied for about 5 s, 60 s after applying the pressure for 90 s, and 90 s after applying the pressure for 300 s (Fig. 2b). We interpret these results as indicating that perhaps half the free water produced by compression remains distributed throughout the sample, while the remainder escapes possibly around the piston. For the run shown in Figure 2e a layer of around 0.5 cm of compressed talc was inserted above the ice, about 2 mm from the thermocouple, to see if this would absorb a large fraction of water produced during compression. No significant change is apparent.
The time constant for warming up following decompression of samples at 0.00°C is not less than that for decompression at ‒ 1.09°C, when no water is present. This indicates that the later part of the warming of samples initially at 0.00°C is due to thermal conduction processes, probably from the boundaries of the cylinder. It is clear that some redistribution of water within the cylinder has taken place, especially in the vicinity of the thermocouple. The major redistribution clearly takes place within 5 s at 50 bars pressure. To this extent we appear to have confirmed the presence of heat-pumping in the cylinder, and thus its probable importance beneath a glacier.
3. Continuous measurements of the strain changes in the rock Under Glacier d’ArgentiÈre
3.1. Instrumentation
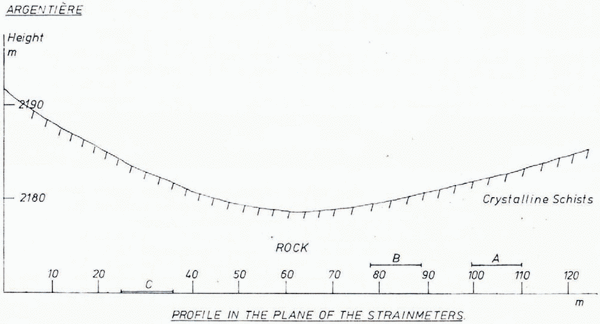
Under Glacier d’Argentière, Mont Blanc, France, a network of tunnels has been dug for a hydro-electric scheme. Some of these tunnels pass very close to the bed of the glacier. In two tunnels, which were within 10 m of the bed, three geophysical wire strainmeters (with a resolution of 1 in 108 strain, and 10 m gauge lengths) were installed and run for three-week periods between September 1975 and July 1976. Wire strainmeters have been used successfully for the measurement of earth tides (Reference King and BilhamKing and Bilham, 1973), and were not modified for this experiment. Data were recorded on three separate chart recorders, although the instruments did have a common a.c. power supply. A plan of the tunnel network at the site appears in Figure 3, and a profile showing the relation of the strainmeters to the glacier bed appears in Figure 4. The vertical plane containing the strainmeters was approximately perpendicular to the direction of flow of the glacier at the site. At this point, under about 80 m of ice, the glacier moves over a rock bar; about 20 m down-glacier of the instruments, a series of cavities have formed across the glacier, and on the surface there is an extensive crevasse field.

Fig. 3. A plan of the tunnel network under the Glacier d’Argentière. The contours are of the rock bed. The ice thickness above the cavity is about 80 m. ARGA, ARGB, and ARGC are the sites of the three wire strainmeters.

Fig. 4. The profile of the glacier bed in the plane of the three strainmeters.
The glacier has been well studied by R. A. Vivian and his co-workers. In particular they have installed in one of the cavities a device for measuring the sliding speed of the glacier (Reference Vivian and BocquetVivian and Bocquet, 1973), and have studied the fluctuations in volume of water discharged (Reference Vivian and ZumsteinVivian and Zumstein, 1973).
3.2. Observations
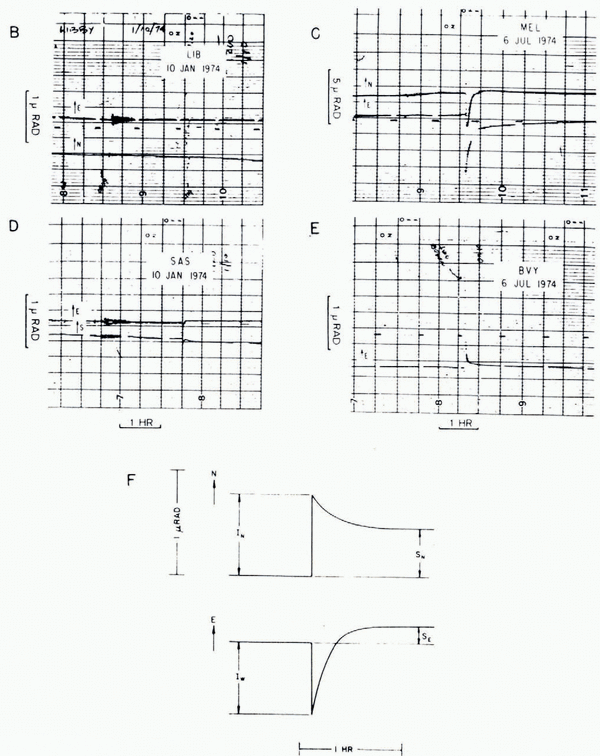
Good-quality strain data were collected on instruments A and C for three-week periods in September 1975, January 1976, and April 1976. The records all showed long-period strain changes, probably due to Earth tides, but also frequent but not regular strain excursions. Two types of events were observed; simple small offsets, and strain excursions which began with a very rapid (but not instantaneous) change followed by a slow decay back to the original value. Some examples are shown in Figure 5. The strain excursion events are strikingly similar to events observed on tilt-meters close to the San Andreas fault in California (Reference McHugh and JohnstonMcHugh and Johnston, 1977); on the fault the surfaces move relative to each other at only about 10 mm per year (see Fig. 6).

Fig. 5. Some examples of the events observed on the records of the strainmeters. The trace is a measure of the elastic strain changes in the rock tunnel as the glacier slides over its bed above the tunnel.

Fig. 6. Similar events observed in bore holes close to the San Andreas fault, California (from Reference McHugh and JohnstonMcHugh and Johnston, 1977).
The time between events for each instrument has been carefully analysed, and the resulting distributions compared with an exponential distribution, using a chi-squared test to examine whether the events are random. For each of the time series considered, the distribution was found to be exponential with an α value of better than 0.05; at this level of significance the events are random. Histograms showing the distributions are shown in Figure 7.

Fig. 7. Histograms showing number of events on individual strainmeters as a function of the time between events: (a) strainmeter A, 1 to 8 September 1975; (b) strainmeter A, 20 December 1975 to 13 January 1976; (C)strainmeter C, 20 December 1975 to 3 January 1976; (d) strainmeter C, 17 April to 16 May 1976.
Correlations between instruments A and C were also examined over a two-week period, and in 30% of the events the time at which they occurred was the same within the error of the time determination (c. 1O min). Because the instruments were some 70 m apart in different tunnels, and had different chart recorders and stabilized power supplies, the latter result is good evidence that the events are indeed real. In some cases, an offset event on one meter appeared to coincide with a strain excursion event on the other instrument.
For three days in April 1976 a vertical seismometer was operated alongside the strainmeter A. Many seismic events were observed when the magnetic tapes were replayed; a large proportion of the events had signatures which were similar to seismograms presented by Reference Neave and SavageNeave and Savage (1970), Reference VanWormer and BergVanWormer and Berg (1973), or Reference Weaver and MaloneWeaver and Malone (1976), who installed geophones or seismometers close to glaciers. Some of the seismic events could be correlated with events observed on the records from the strainmeters.
A comparison of events at different times of the year shows two features. Individual events in September show about three times the magnitude of the strain jump seen in April, when small offset events form a higher proportion of the total. To compare the time interval between events in summer and other seasons, we show on the diagrams the number of events per day on individual strainmeters at different times of the year. We see that in September events take place around twice as frequently as in December-January and nearly three times as frequently as in April.
Reference VivianVivian (1975) gives a table of glacier sliding speeds in the area of our observations for 1971 to 1973. The sliding speed in April of 17.4 mm h−1 was the slowest of the year, while it was 26.6 mm h−1 in September, a similar value to August, after more rapid sliding in June and July.
A search for a diurnal variation in the interval between events failed to show any such variation, although this variation might be expected in summer if the variations of pressure of the basal water film follow the pattern of water discharge in the main subglacial drainage system.
While seasonal variation indicates some possible link between events and summertime conditions of faster sliding and variable subglacial water supply, this is not apparent in the diurnal pattern.
3.3. Possible explanations of strain events
A Simple picture of such events is that a frozen patch which adheres to bedrock will experience an ever-increasing stress as the glacier moves forward so that eventually a crack runs part or all the way across the frozen patch and relieves the stress. Reference GoodmanGoodman (unpublished) has calculated the stress field due to a square patch with a side of 2 m and finds that if a shear traction of 0.1 MN m−2 were applied to the patch, the strain field would be large enough at 10 m to record strains of similar magnitude to those in Figure 2. Furthermore the strain field from a point force on the surface falls off as 1 /r4, where r is the distance from the force.
The apparent correlation of some seismic events with records from strainmeter A supports the idea of fast crack propagation due to stress. While this would be consistent with our simple offset events, the typical rise time of our strain excursion of the order of 10 s on the strainmeter does not fit this model. The coincidence in time between the two types of event in some observations suggests that they are associated in a common mechanism. Consider the effect if the frozen patch is not immediately adjacent to our strainmeter. If large events, such as crack propagation from large frozen patches, or the opening of surface cracks on the glacier, are too far from our strainmeter to be measured directly, that is at a distance much greater than 10 m, we may note the resultant effect of fracturing on the remainder of the glacier. Release of stress from large events will increase stresses on the surrounding bedrock with at least two consequences. The distribution of pressure and thickness in the basal water film will change, and in turn the flow of heat through rock and ice that is an essential part of the regelation process will be altered. The time constants of these two processes may differ widely. If one of the changes has a time constant of the order of ten seconds and the other one of some minutes, this could explain the form of the strain record, since both processes will affect traction at the ice/rock interface and hence elastic strains in the rock.
The increasing occurrence of strain events during summer and the larger amplitude of the events could fit the hypothesis of basal freezing due to changes of basal water pressure, although increasing surface fracturing due to faster flow offers another explanation. During winter months when the basal water flow is expected to be steady and of low discharge, and the glacier motion uniform, the heat-pump action may account for events.
Since one would expect some regularity of freezing action of any individual patch, either through time constants associated with flow and heat-pump action, or through increased changes of water pressure during daytime in summer months, the random time distribution of strain events does not appear to favour the freezing hypothesis. However if we are looking at events from a large number of freezing patches, each with a different time constant, the random timing of the sum of events is to be expected. To record a large number of events could involve a wide area of coverage. If this were the case, we should expect distant events to be recorded at all strainmeters. Since some 30% appear common to all strainmeters there is limited support for this hypothesis. As the surface is at least 80 m from our strain gauges, we should expect a high proportion of any events due to surface fracture to be common to all strain gauges. It appears however that we are dealing with more local phenomena for the majority of events, for which our hypothesis of fractured patches of ice frozen to bedrock can provide an explanation. While other explanations are also possible, the basic information on these events must be taken into account in any hypothesis of ice-bedrock sliding.
Acknowledgements
We are very grateful for the help of Professor R. A. Vivian in arranging access to the tunnels under the Glacier d’Argentière. G. Ballard, K. E. Evans, and J. Horsfall helped prepare and install the strainmeters. The equipment was purchased with grants from the Royal Society and the Science Research Council. During the field experiments D.J.G. was supported by the Science Research Council. Laboratory work was made possible by a grant from the Royal Society for the study of regelation effects (G. de Q.R.) and through provision of facilities in the Cavendish Laboratory by Professor D. Tabor, F.R.S., who is also thanked for helpful discussions.
Appendix
We consider an ice block, initially at its equilibrium melting temperature, when a pressure is suddenly applied. The immediate fall in temperature to the new equilibrium melting temperature is achieved by a small fraction of the ice block melting and extracting latent heat from the surrounding ice. A. B. Pippard (personal communication) has supplied a thermodynamic argument to show that the fraction of water in an ice/water block, α, will increase if the block is subjected, adiabatically to a pressure change. If S 1 is the entropy of the ice, and Sw the entropy of the water, the entropy of the block SB is
But S W –S1 = L/T, where L is the latent heat of ice, and T the temperature. Then for an adiabatic change dS = 0, and if S(p, T),

and the system moves along the solidus

d(L/T)/d p is very small compared to the other terms, (δS 1/δp)melting must be negative because

and consequently dα/dp is positive, and water is produced on compression.
Discussion
W. B. Kamb: In your experiments, if water were being expressed from the sample under the applied pressure, as needed in the heat-pump mechanism, one would expect the immediate temperature rise on release of pressure to be smaller the longer the time the pressure is applied, but your experiments do not appear to show that. Why?
G. de Q. Robin: One purpose of the experiments was to test this idea. We could not apply the pressure pulse for less than 5 s with our system, and it appears that the major redistribution of water took place in that time. Subsequently some blocking action may have prevented escape of water, as seems likely from the relatively large recovery of temperature shown on the last (300 s) pulse in our series experiments, in comparison with the two other 300 s pulses shown. It would be interesting to design an experiment in which much shorter time pulses were used, provided we could match them with the response time of our temperature measurement.