2.1. The inference problem

Our goal is to estimate the state of an unbounded two-dimensional vortical flow with vortex system (1.1), which we will call a vortex estimator, specified completely by the $n$-dimensional vector ($n=3N$)

(2.1)\begin{equation} \textit{x} = (\textit{x}_{1},\ldots,\textit{x}_{N})^{{\rm T}} \in \mathbb{R}^{3N}, \end{equation}

where

(2.2)\begin{equation} \textit{x}_{\textit{J}} \equiv (\boldsymbol{r}_{\textit{J}},\varGamma_{\textit{J}}) = (x_{\textit{J}},y_{\textit{J}},\varGamma_{\textit{J}}) ,\end{equation}

is the 3-component state of vortex ${\textit {J}}$. The associated state covariance matrix is written as

(2.3)\begin{equation} \varSigma_{\textit{x}} = \begin{pmatrix} \varSigma_{11} & \varSigma_{12} & \cdots & \varSigma_{1N} \\ \varSigma_{21} & \varSigma_{22} & \cdots & \varSigma_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ \varSigma_{N 1} & \varSigma_{N 2} & \cdots & \varSigma_{NN} \end{pmatrix} \in \mathbb{R}^{3N \times 3N}, \end{equation}

where each $3 \times 3$ block represents the covariance between vortex elements ${\textit {J}}$ and ${\textit {K}}$

(2.4)\begin{equation} \varSigma_{\textit{J}\textit{K}} \equiv \begin{pmatrix} \varSigma_{\boldsymbol{r}_{\textit{J}} \boldsymbol{r}_{\textit{K}}} & \varSigma_{\boldsymbol{r}_{\textit{J}} \varGamma_{\textit{K}}} \\ \varSigma_{\varGamma_{\textit{J}} \boldsymbol{r}_{\textit{K}}} & \varSigma_{\varGamma_{\textit{J}} \varGamma_{\textit{K}}} \end{pmatrix}. \end{equation}

Note that $\varSigma _{{\textit {K}}{\textit {J}}} = \varSigma ^{{\rm T}}_{{\textit {J}}{\textit {K}}}$.

Equation (1.2) expresses the pressure (relative to ambient), ${\rm \Delta} p(\boldsymbol {r}) \equiv p(\boldsymbol {r}) - p_{\infty }$, as a continuous function of space, $\boldsymbol {r}$. Here, we also explicitly acknowledge its dependence on the state, ${\rm \Delta} p(\boldsymbol {r},{\textit {x}})$. Furthermore, we will limit our observations to a finite number of sensor locations, $\boldsymbol {r} = \boldsymbol {s}_{\alpha }$, for $\alpha = 1,\ldots,d$, and define from this an observation operator, $h: \mathbb {R}^{n} \rightarrow \mathbb {R}^{d}$, mapping a given state vector ${\textit {x}}$ to the pressure at these sensor locations

(2.5)\begin{equation} h(\textit{x}) \equiv({\rm \Delta} p(\boldsymbol{s}_{1},\textit{x}), {\rm \Delta} p(\boldsymbol{s}_{2},\textit{x}),\ldots,{\rm \Delta} p(\boldsymbol{s}_{d},\textit{x}))^{{\rm T}} \in \mathbb{R}^{d}. \end{equation}

The objective of this paper is essentially to explore the extent to which we can invert function (2.5): from a given set of pressure observations ${\textit {y}}^{\ast } \in \mathbb {R}^{d}$ of the true system at $\boldsymbol {s}_{\alpha }$, $\alpha = 1,\ldots,d$, determine the state ${\textit {x}}$. In this work, the true sensor measurements ${\textit {y}}^{\ast }$ (the truth data) will be synthetically generated from the pressure field of a set of vortex elements in unbounded quiescent fluid, obtained from the same expression for pressure (1.2) that we use for $h({\textit {x}})$ in the estimator. Throughout, we will refer to the set of vortices that generated the measurements as the true vortices. However, there is inherent uncertainty in ${\textit {y}}^{\ast }$ due to random measurement noise $\varepsilon \in \mathbb {R}^{d}$, so we model the predicted observations ${\textit {y}}$ as

(2.6)\begin{equation} \textit{y} = h(\textit{x}) + \varepsilon, \end{equation}

where $\varepsilon$ is normally distributed about zero mean, $\mathcal{N}(\varepsilon | 0,\varSigma _{\mathcal{E}})$, and the sensor noise is assumed independent and identically distributed, so that its covariance is $\varSigma _{\mathcal{E}} = \sigma _{\mathcal {E}}^{2} I$ with $I \in \mathbb {R}^{d \times d}$ the identity. We seek a probabilistic form of the inversion of (2.6) when set equal to ${\textit {y}}^{\ast }$. That is, we seek the conditional probability distribution of states based on the observed data, ${\rm \pi} ({\textit {x}}\,|\,{\textit {y}}^{\ast })$: the peaks of this distribution would represent the most probable state(s) based on the measurements, and the breadth of the peaks would represent our uncertainty about the answer.

From Bayes’ theorem, the conditional probability of the state given an observation, ${\rm \pi} ({\textit {x}}\,|\,{\textit {y}})$, can be regarded as a posterior distribution over ${\textit {x}}$,

(2.7)\begin{equation} {\rm \pi}(\textit{x}\,|\,\textit{y}) = \frac{L(\textit{y}\,|\,\textit{x}) {\rm \pi}_{0}(\textit{x})}{{\rm \pi}(\textit{y})}, \end{equation}

where ${\rm \pi} _{0}({\textit {x}})$ is the prior distribution, describing our original beliefs about the state ${\textit {x}}$, and $L({\textit {y}}\,|\,{\textit {x}})$ is called the likelihood function, representing the probability of observing certain data ${\textit {y}}$ at a given state, ${\textit {x}}$. The likelihood function encapsulates our physics-based prediction of the sensor measurements, based on the observation operator $h({\textit {x}})$. Collectively, $L({\textit {y}}\,|\,{\textit {x}}) {\rm \pi}_{0}({\textit {x}})$ represents the joint distribution of states and their associated observations. The distribution of observations, ${\rm \pi} ({\textit {y}})$, is a uniform normalizing factor. Its value is unnecessary for characterizing the posterior distribution over ${\textit {x}}$, since only comparisons (ratios) of the posterior are needed during sampling, as we discuss below in § 2.4. Thus, we can omit the denominator in (2.7). We evaluate this unnormalized posterior at the true observations, ${\textit {y}}^{\ast }$, and denote it by $\tilde {{\rm \pi} }({\textit {x}}\,|\,{\textit {y}}^{\ast }) = L({\textit {y}}^{\ast }\,|\,{\textit {x}}) {\rm \pi}_{0}({\textit {x}})$.

Our goal is to explore and characterize this unnormalized posterior for the vortex system. Expressing our lack of prior knowledge, we write ${\rm \pi} _{0}({\textit {x}})$ as a uniform distribution within a certain acceptable bounding region $B$ on the state components (discussed in more specific detail below):

(2.8)\begin{equation} {\rm \pi}_{0}(\textit{x}) = \mathcal{U}_{n}(\textit{x}\,|\,B). \end{equation}

Following from our observation model (2.6) with Gaussian noise, the likelihood is a Gaussian distribution about the predicted observations, $h({\textit {x}})$,

(2.9)\begin{equation} L(\textit{y}\,|\,\textit{x}) = \mathcal{N}(\textit{y}\,|\,h(\textit{x}),\varSigma_{\mathcal{E}}) = \frac{1}{\sqrt{(2{\rm \pi})^{d}\det \varSigma_{\mathcal{E}}}} \exp\Big(-\frac{1}{2} \|\textit{y} - h(\textit{x})\|^{2}_{\varSigma_{\mathcal{E}}}\Big), \end{equation}

where we have defined the covariance-weighted norm

(2.10)\begin{equation} \|\textit{y}\|^{2}_{\varSigma} \equiv \textit{y}^{{\rm T}}\varSigma^{{-}1}\textit{y}. \end{equation}

Thus, our unnormalized posterior for the vortex estimator is given by

(2.11) \begin{equation} \tilde{\rm \pi}(\textit{x}\,|\,\textit{y}^{{\ast}}) = \frac{\mathcal{U}_{n}(\textit{x}\,|\,B)}{\sqrt{(2{\rm \pi})^{d}\det \varSigma_{\mathcal{E}}}} \exp\Big(-\frac{1}{2} \|\textit{y}^{{\ast}} - h(\textit{x})\|^{2}_{\varSigma_{\mathcal{E}}}\Big). \end{equation}

For practical purposes it is helpful to take the log of this probability, so that ratios of probabilities – some of them near machine zero – are assessed instead via differences in their logs. Because only differences are relevant, we can dispense with constants that arise from taking the log, such as the inverse square root factor. We note that the uniform probability distribution $\mathcal{U}_{n}({\textit {x}}\,|\,B)$ is uniform and positive inside $B$ and zero outside. Thus, to within an additive constant, this log posterior is

(2.12)\begin{equation} l(\textit{x}\,|\,\textit{y}^{{\ast}}) ={-} {\tfrac{1}{2}} \|\textit{y}^{{\ast}} - h(\textit{x})\|^{2}_{\varSigma_{\mathcal{E}}} + c_{B}(\textit{x}), \end{equation}

where $c_{B}({\textit {x}})$ is a barrier function arising from the log of the uniform distribution, equal to zero for any ${\textit {x}}$ inside of the restricted region $B$ of our uniform distribution, and $c_{B}({\textit {x}})= -\infty$ outside of $B$.

In the examples that we present in this paper, the pressure sensors will be uniformly distributed along a straight line on the $x$ axis, unless otherwise specified. and the set of vortices used for estimation purposes as the vortex estimator. To ensure finite pressures throughout the domain, both the true vortices and the vortex estimator are regularized as discussed in Appendix A.4, with a small blob radius $\epsilon = 0.01$ unless otherwise stated. To improve the scaling and conditioning of the problem, the pressure (relative to ambient) is implicitly normalized by $\rho \varGamma _{0}^{2}/L^{2}$, where $\varGamma _{0}$ is the strength of the largest-magnitude vortex in the true set and $L$ represents a characteristic distance of the vortex set from the sensors; all positions are implicitly normalized by $L$ and vortex strengths by $\varGamma _{0}$. Unless otherwise specified, the measurement noise is $\sigma _{\mathcal{E}} = 5 \times 10^{-4}$.

2.2. Symmetries and nonlinearity in the vortex-pressure system

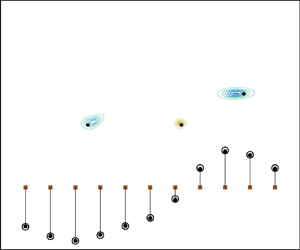
As mentioned in the introduction, there are many situations in which multiple solutions arise due to symmetries. This is easy to see from a simple thought experiment, depicted in figure 1(a). Suppose that we wish to estimate a single vortex from pressure sensors arranged in a straight line. A vortex on either side of this line of sensors will induce the same pressure on the sensors, and a vortex of either sign of strength will as well. Thus, in this simple problem, there are four possible states that are indistinguishable from each other, and we would need more information about the circumstances of the problem to rule out three of them. Such symmetries arise commonly in the problems we will study in this paper.

Figure 1. (a) Four configurations of vortices that would generate identical measurements for the set of pressure sensors (brown squares). (b) Two distinct vortex states that differ only in the vortex labelling but generate identical flow fields.

The symmetry with respect to the sign of vortex strength is due to the nonlinear relationship between pressure and vorticity. However, it is important to note that this symmetry issue is partly alleviated by the nonlinear relationship, as well, because of the coupling that it introduces between vortices. Figure 2 depicts the pressure fields for two examples of a pair of vortices: one in which the vortices in the pair have equal strengths and another in which the vortices have equal but opposite strengths. Although the pressure in the vortex cores of both pairs is similar and sharply negative, the pressures outside the cores are distinctly different because the interaction kernel enters the sum with different sign. At the positions of the sensors, the pressure has a small region of positive pressure in the case of vortices of opposite sign. These differences are essential for inferring the relative signs of vortex strengths in sets of vortices. However, it is important to stress that the pressure is invariant to a change of sign of all vortices in the set, so we would still need more prior information to discriminate one overall sign from the other.

Figure 2. Pressure fields and associated sensor measurements for two examples of a pair of vortex elements at $\boldsymbol {r}_{1} = (-1/2,1)$ and $\boldsymbol {r}_{2} = (1/2,1)$, respectively. Sensors are depicted in the pressure field plots as brown squares. Panels show (a,b) $\varGamma _{1} = 1$ and $\varGamma _{2} = 1$ and (c,d) $\varGamma _{1} = 1$ and $\varGamma _{2} = -1$. In both cases, pressure contours are between $-0.5$ (red) and $0.01$ (blue).

Another symmetry arises when there is more than one vortex to estimate, as in figure 1(b), because in such a case, there is no unique ordering of the vortices in the state vector. With each of the vortices assigned a fixed set of parameters, any of the $N!$ permutations of the ordering leads to the same pressure measurements. This vortex relabelling symmetry is a discrete analogue of the particle relabelling symmetry in continuum mechanics (Marsden & Ratiu Reference Marsden and Ratiu2013); it is also closely analogous to the non-identifiability issue of the mixture models that will be used for the probabilistic modelling in this paper. All of the $N!$ solutions are obviously equivalent from a flow field perspective, so this symmetry is not a problem if we assess estimator performance based on flow field metrics. However, the $N!$ solutions form distinct points in the state space and we must anticipate this multiplicity when we search for high-probability regions.

The barrier function $c_{B}({\textit {x}})$ in (2.12) allows us to anticipate and eliminate some modes that arise from problem symmetries, because we can use the bounding region $B$ to reject samples that fail to meet certain criteria. To eliminate some of the aforementioned symmetries, we will, without loss of generality, restrict our vortex estimator to search for vortices that lie above the line of sensors on the $x$ axis. For cases of multiple vortices in the estimator, we re-order the vortex entries in the state vector by their $x$ position at each Markov-chain Monte Carlo (MCMC) step to eliminate the relabelling symmetry. We also assume that the leftmost vortex has positive strength, which reduces the number of probable states by half; the signs of all estimated vortices can easily be switched a posteriori if new knowledge shows that this assumption is wrong.

2.3. The true covariance and rank deficiency

The main challenge of the vortex inference problem is that the observation operator is nonlinear, so the posterior (2.11) is not Gaussian. Thus, we will instead sample this posterior and develop an approximate model for the samples, composed of a mixture of Gaussians. However, we can obtain some important insight by supposing that we already know the true state and then linearizing the observation operator about it,

(2.13)\begin{equation} h(\textit{x}) \approx h(\textit{x}^{{\ast}}) + H \cdot (\textit{x}-\textit{x}^{{\ast}}), \end{equation}

where $H \equiv \boldsymbol {\nabla }h({\textit {x}}^{\ast }) \in \mathbb {R}^{d \times n}$, the Jacobian of the observation operator at the true state. Then we can derive an approximating $n$-dimensional Gaussian model about mean ${\textit {x}}^{\ast }$ (plus a bias due to noise in the realization of the true measurements) with covariance

(2.14)\begin{equation} \varSigma^{{\ast}}_{\textit{x}} = (H^{{\rm T}}\varSigma_{\mathcal{E}}^{{-}1}H)^{{-}1} \in \mathbb{R}^{n \times n}. \end{equation}

A brief derivation of this result is included in Appendix C.

We will refer to $\varSigma ^{\ast }_{{\textit {X}}}$ as the ‘true’ state covariance. It is useful to note that the matrix $H^{{\rm T}}\varSigma _{\mathcal{E}}^{-1}H$ is the so-called Fisher information matrix for our Gaussian likelihood (Cui & Zahm Reference Cui and Zahm2021), evaluated at the true state. In other words, it quantifies the information about the state of the system that is available in the measurements. Because all sensors have the same noise variance, $\sigma _{\mathcal{E}}^{2}$, then $\varSigma ^{\ast }_{{\textit {X}}} = \sigma _{\mathcal{E}}^{2}(H^{{\rm T}}H)^{-1}$. We can then use the singular value decomposition of the Jacobian, $H = U S V^{{\rm T}}$, to write a diagonalized form of the covariance,

(2.15)\begin{equation} \varSigma^{{\ast}}_{\textit{x}} = V \varLambda V^{{\rm T}}. \end{equation}

Here, the eigenvalue matrix is $\varLambda = \sigma _{\mathcal{E}}^{2} D^{-1}$, where $D = S^{{\rm T}}S \in \mathbb {R}^{n \times n}$ is a diagonal matrix containing squares $s^{2}_{j}$ of the singular values $S$ of $H$ in decreasing magnitude up to the rank $r \leq \min (d,n)$ of $H$ and padded with $n - r$ zeros. The uncertainty ellipsoid thus has semi-axis lengths

(2.16)\begin{equation} \lambda_{j}^{1/2} = \sigma_{\mathcal{E}}/s_{j}, \end{equation}

along the directions $v_{j}$ given by the corresponding columns of $V$. Thus, the greatest uncertainty $\lambda ^{1/2}_{n}$ is associated with the smallest singular value $s_{n}$ of $H$. The corresponding eigenvector, $v_{n}$, indicates the mixture of states for which we have the most confusion.

In fact, the smallest singular values of $H$ are necessarily zero if $n > d$, i.e. when there are fewer sensors than states and the problem is therefore underdetermined. In such a case, $H$ has a null space spanned by the last $n-r$ columns in $V$. However, ${\textit {x}}^{\ast }$ is not a unique solution in these problems; rather, it is simply one element of a manifold of vortex states that produce equivalent sensor readings (to within the noise). The covariance $\varSigma ^{\ast }_{{\textit {X}}}$ evaluated at any ${\textit {x}}^{\ast }$ on the manifold reveals the local tangent to this manifold – directions near ${\textit {x}}^{\ast }$ along which we get identical sensor values. The true covariance $\varSigma ^{\ast }_{{\textit {X}}}$ will also be very useful for illuminating cases in which the problem is ostensibly fully determined ($n \leq d$), but for which the arrangement of sensors and true vortices nonetheless creates significant uncertainty in the estimate. In some of these cases, the smallest singular values may still be zero or quite small, indicating that the effective rank of $H$ is smaller than $n$.

2.4. Sampling and modelling of the posterior

The true covariance matrix (2.14) and its eigendecomposition will be an important tool in the study that follows, but we generally will only use it when we presume to know the true state ${\textit {x}}^{\ast }$ and seek illumination on the estimation in the vicinity of the solution. To characterize the problem more fully and explore the potential multiplicity of solutions, we will generate samples of the posterior and then fit the samples with an approximate distribution $\hat {{\rm \pi} }_{{\textit {y}}^{\ast }}({\textit {x}}) \approx {\rm \pi}({\textit {x}}\,|\,{\textit {y}}^{\ast })$ over ${\textit {x}}$. The overall algorithm is shown in the flowchart in figure 3 in the context of an example of estimating one vortex with three sensors. For the sampling task, we use the Metropolis–Hastings method (see, e.g. Chib & Greenberg Reference Chib and Greenberg1995), a simple but powerful form of MCMC. This method relies only on differences of the log probabilities between a proposed chain entry and the current chain entry to determine whether the proposal is more probable than the previous entry and should be added to the chain of samples. To ensure that the MCMC sampling does not get stuck in one of possibly multiple high-probability regions, we use the method of parallel tempering (Sambridge Reference Sambridge2014).

Figure 3. One true vortex and one-vortex estimator using three sensors, with a flowchart showing the overall algorithm and references to figure panels. (a) True covariance ellipsoid. The ellipse on each coordinate plane represents the marginal covariance between the state components in that plane. The true vortex state is shown as a black dot. (b) True sensor data (filled circles) with noise levels (vertical lines), compared with sensor values from estimate (open circles), obtained from expected state of the sample set. (c) The MCMC samples (blue) and the resulting vortex position covariance ellipses (coloured unfilled ellipses) from the GMM. Thicker lines of the ellipses indicate higher weights in the mixture. The true vortex position is shown as a filled black circle, and the true covariance ellipse for vortex position (corresponding to the grey ellipse in (a)) is shown filled in grey. Sensor positions are shown as brown squares. (d) Contours of the expected vorticity field, based on the mixture model.

In practice, we generally have found good results in parallel tempering by using five parallel Markov chains exploring the target distribution raised to respective powers $3.5^{p}$, where $p$ takes integer values between $-4$ and $0$. We initially carry out $10^{4}$ steps of the algorithm with the MCMC proposal variance set to a diagonal matrix of $4\times 10^{-4}$ for every state component. Then, we perform $10^{6}$ steps with proposal variances set more tightly, uniformly equal to $2.5\times 10^{-5}$. The sample data set is then obtained from the $p = 0$ chain after discarding the first half of the chain (for burn in) and retaining only every $100$th chain entry of the remainder to minimize autocorrelations in the samples. On a MacBook Pro with a M1 processor, the overall process takes around 20 seconds in the most challenging cases (i.e. the highest-dimensional state spaces). There are other methods that move more efficiently in the direction of local maxima (e.g. such as hybrid MCMC, which uses the Jacobian of the log posterior to guide the ascent). However, the approach we have taken here is quite versatile for more general cases, particularly those in which the Jacobian is impractical to compute repetitively in a long sequential process.

To approximate the posterior distribution over ${\textit {x}}$ from the samples, we employ a Gaussian mixture model (GMM), which assumes the form of a weighted sum of $K$ normal distributions (the mixture components)

(2.17)\begin{equation} \hat{\rm \pi}_{\textit{y}^{{\ast}}}(\textit{x}) = \sum_{k=1}^{K}\alpha_{k} \mathcal{N}(\textit{x}\,|\,\bar{\textit{x}}^{(k)},\varSigma^{(k)}), \end{equation}

where $\bar {{\textit {x}}}^{(k)}$ and $\varSigma ^{(k)}$ are the mean and covariance of component $k$ of the mixture. Each weight $\alpha _{k}$ lies between 0 and 1 and represents the probability of a sample point ‘belonging to’ component $k$, so it quantifies the importance of that component in the overall mixture. For a given set of samples and a pre-selected number of components $K$, the parameters of the GMM ($\alpha _{k}$, $\bar {{\textit {x}}}^{(k)}$, and $\varSigma ^{(k)}$) are found via the expectation maximization algorithm (Bishop Reference Bishop2006). It is generally advantageous to choose $K$ to be large (${\sim }5$–$9$) because extraneous components are assigned little weight, resulting in a smaller number of effective components. It should also be noted that, for the special case of a single mode of small variance, a GMM with $K=1$ and a sufficient number of samples approaches the Gaussian approximation about the true state ${\textit {x}}^{\ast }$ described in § 2.3, with covariance $\varSigma ^{\ast }_{{\textit {X}}}$.

As we show in Appendix B, the GMM has a very attractive feature when used in the context of singular vortex elements because we can exactly evaluate the expectation of the vorticity field under the GMM probability,

(2.18)\begin{equation} E[\boldsymbol{\omega}](\boldsymbol{r}) = \sum_{k=1}^{K} \alpha_{k}\sum_{\textit{J}=1}^{N} [\bar{\varGamma}^{(k)}_{\textit{J}} + \varSigma^{(k)}_{\varGamma_{\textit{J}} \boldsymbol{r}_{\textit{J}}} {\varSigma^{(k)}_{\boldsymbol{r}_{\textit{J}} \boldsymbol{r}_{\textit{J}}}}^{{-}1} (\boldsymbol{r} - \bar{\boldsymbol{r}}^{(k)}_{\textit{J}} )] \mathcal{N}(\boldsymbol{r}\,|\,\bar{\boldsymbol{r}}_{\textit{J}}^{(k)}, \varSigma^{(k)}_{\boldsymbol{r}_{\textit{J}} \boldsymbol{r}_{\textit{J}}}), \end{equation}

where $\bar {\boldsymbol {r}}^{(k)}_{{\textit {J}}}$ and $\bar {\varGamma }^{(k)}_{{\textit {J}}}$ comprise the position and strength of the ${\textit {J}}$-vortex of mean state $\bar {{\textit {x}}}^{(k)}$ in (2.1), and $\varSigma ^{(k)}_{\boldsymbol {r}_{{\textit {J}}}\boldsymbol {r}_{{\textit {J}}}}$ and $\varSigma ^{(k)}_{\varGamma _{{\textit {J}}} \boldsymbol {r}_{{\textit {J}}}}$ are elements in the ${\textit {J}}{\textit {J}}$-block of covariance $\varSigma ^{(k)}$, defined in (2.4). Thus, under a GMM of the state, the expected vorticity field is itself composed of a sum of Gaussian-distributed vortices in Euclidean space (due to the first term in the square brackets), plus a sum of Gaussian-regularized dipole fields arising from covariance between the strengths and positions of the inferred vortex elements (the second term in square brackets).

3.1. Inference of a single vortex

In this section, we will explore cases in which both the true vortex system and our estimator consist of a single vortex. We will use this case to draw insight on many of the parameters of the inference problem. For most of the cases, a single line of sensors along the $x$ axis will be used. The true vortex will remain on the $y = 1$ line and have unit strength. Many of the examples that follow will focus on the true configuration $(x_{1},y_{1},\varGamma _{1}) = (0.5,1,1)$. (The subscript 1 is unnecessary with only one vortex, but allows us to align the notation with that of § 2.1). Note, however, that we will not presume knowledge of any of these states: the bounding region of our prior will be $x \in (-2,2)$, $y \in (0.01,4)$, $\varGamma \in (0,2)$.

All of the basic tools used in the present investigation are depicted in figure 3, in which the true configuration is estimated with three sensors arranged uniformly along the $x$ axis between $[-1,1]$ with $\sigma _{\mathcal{E}} = 5\times 10^{-4}$. Figure 3(a) shows the ellipsoid for covariance $\varSigma ^{\ast }_{{\textit {X}}}$, computed at the true vortex state. This figure particularly indicates that much of the uncertainty lies along a direction that mixes $y_{1}$ and $\varGamma _{1}$; indeed, the eigenvector corresponding to the direction of greatest uncertainty is $(0.08,0.79,0.61)$. This uncertainty is intuitive: as a vortex moves further away from the sensors, it generates very similar sensor measurements if its strength simultaneously increases in the proportion indicated by this direction. In figure 3(b), the samples obtained from the MCMC method are shown. Here, and in later figures in the paper, we show only the vortex positions of these samples in Euclidean space and colour their symbols to denote the sign of their strength (blue for positive, red for negative). The set of samples clearly encloses the true state, shown as a block dot; the expected value from the samples is $(0.51,1.07,1.05)$, which agrees well.

The samples also demonstrate the uncertainty of the estimated state. The filled ellipse in this figure corresponds to the exact covariance of figure 3(a) and is shown for reference. As expected, the samples are spread predominantly along the direction of the maximum uncertainty. This figure also depicts an elliptical region for each Gaussian component of the mixture computed from the samples. These ellipses correspond only to the marginal covariances of the vortex positions and do not depict the uncertainty of the vortex strength. The weight of the component in the mixture is denoted by the thickness of the line. One can see from this plot that the GMM covers the samples with components, concentrating most of the weight near the centre of the cluster with two dominant components. The composite of these components is best seen in figure 3(d), in which the expected vorticity field is shown. In the remainder of this paper, this expected vorticity field will be used extensively to illuminate the uncertainty of the vortex estimation. Finally, figure 3(c) compares the true sensor pressures with those corresponding to the expected state from the MCMC samples. These agree to within the measurement noise.

3.1.1. Effect of the number of sensors

In the last section, we found that three sensors were sufficient to estimate a single vortex's position and strength. In this section we investigate how this estimate of a single vortex depends on the number of sensors. In most cases, these sensors will again lie uniformly along the $x$ axis in the range $[-1,1]$. Intuitively, we expect that if we have fewer sensors than there are states to estimate, we will have insufficient information to uniquely identify the vortex. Figure 4 shows that this is indeed the case. In this example, only two sensors are used to estimate the same vortex as in the previous example. The MCMC samples are distributed along a circular arc, but are truncated outside of the aforementioned bounding region. In fact, this arc is a projection of a helical curve of equally probable states in the three-dimensional state space. The samples broaden from the arc the further they are from the sensors due to the increase in uncertainty with distance. The true covariance, $\varSigma ^{\ast }_{{\textit {X}}}$, cannot reveal the full shape of this helical manifold, which is inherently dependent on the nonlinear relationship between the sensors and the vortex. However, the rank of this covariance decreases to 2, so that the uncertainty along one of its principal axes must be infinite. This principal axis is tangent to the manifold of possible states, as shown by a line in the plot.

Figure 4. One true vortex and one-vortex estimator, using two sensors, showing MCMC samples (blue dots) and the resulting vortex position ellipses from the GMM. The estimator truncates the samples outside the bounding region. The true vortex position is shown as filled black circle. The circular curve represents the manifold of possible states that produce the same sensor pressures; the line tangent to the circle is the direction of maximum uncertainty at the true state.

What if there are more sensors than states? Figure 5(a–c) depicts expected vorticity fields for several cases in which there are increasing numbers of sensors arranged along a line, and figure 5(d) shows the expected vorticity when 5 sensors are instead arranged in a circle of radius 2.1 about the true vortex. (The choice of radius is to ensure that the smallest distance between the true vortex and a sensor is approximately 1 in all cases.) It is apparent that the uncertainty shrinks when the number of sensors increases from 3 to 4, but does so less notably when the number increases from 4 to 5. In figure 5(e), the maximum uncertainty is seen to drop by nearly half when one sensor is added to the basic set of 3 along a line, but decreases much more gradually when more than 4 sensors are used. The drop in uncertainty is more dramatic between 3 and 5 sensors arranged in a circle, but becomes more gradual beyond 5 sensors.

Figure 5. One true vortex and one-vortex estimator, using various numbers and configurations of sensors (shown as brown squares) arranged in a line between $-$1 and 1 (a–c) or in a circle of radius 2.1 (d). Each panel depicts contours of expected vorticity field. True vortex position shown as filled black circle in each. (e) Maximum length of the covariance ellipsoid with increasing number of sensors on line segment $x = [-1,1]$ (blue) or circle of radius $2.1$ (gold).

3.1.2. Effect of the true vortex position

It is particularly important to explore how the uncertainty is affected by the position of the true vortex relative to the sensors. We address this question here by varying this position relative to a fixed set of sensors with a fixed level of noise, $\sigma _{\mathcal{E}} = 5\times 10^{-4}$. Figure 6(a) depicts contours (on a log scale) of the resulting maximum length of the covariance ellipsoid, $\lambda _{n}^{1/2}$, based on four sensors placed on the $x$ axis between $-1$ and $1$. The contours reveal that there is little uncertainty when the true vortex is in the vicinity of the sensors, but the uncertainty increases sharply with distance when the vortex lies outside the extent of sensors. Indeed, one finds empirically that the rates of increase scale approximately as $\lambda _{n}^{1/2} \sim |y_{1}|^{5}$ and $\lambda _{n}^{1/2} \sim |x_{1}|^{6}$. This behaviour does not change markedly if we vary the number of sensors, as illustrated in figure 6(b). As the true vortex's $x$ position varies (and $y_{1}$ is held constant at 1), there is a similarly sharp rate of increase outside of the region near the sensors for 3, 4 or 5 sensors. However, although there is a small range of positions near $x_{1} = 0$ in which 3 sensors have less uncertainty than 4, there is generally less uncertainty at all vortex positions with increasing numbers of sensors. Furthermore, the uncertainty is less variable in this near region when 4 or 5 sensors are used.

Figure 6. One true vortex and one-vortex estimator, with noise $\sigma _{\mathcal{E}} = 5\times 10^{-4}$. (a) Contours (on a log scale) of maximum length of covariance ellipsoid, $\lambda _{n}^{1/2}$, as a function of true vortex position $(x_{1},y_{1})$ using four sensors, shown as brown squares. Contours are $10^{-2}$ through $10^{2}$, with $10^{-1}$ depicted with a thick black line. (b) Maximum length of covariance ellipsoid vs horizontal position of true vortex (with vertical position held fixed at $y_{1} = 1$), and varying number of sensors along line segment $x = [-1,1]$ ($d=3$, blue; $d = 4$, gold; $d = 5$, green).

3.1.3. Effect of sensor noise

From the derivation in § 2.3, we already know that the true covariance should depend linearly on the noise variance (2.16). In this section, we explore the effect of sensor noise on the estimation of a single vortex using MCMC and the subsequent fitting with a Gaussian mixture model. We keep the number of sensors fixed at 3 arranged along a line between $x = -1$ and $1$, and the true vortex in the original configuration, $(x_{1},y_{1},\varGamma _{1}) = (0.5,1,1)$. Figure 7 depicts the expected vorticity field as the noise standard deviation $\sigma _{\mathcal{E}}$ increases. Unsurprisingly, the expected vorticity distribution exhibits increasing breadth as the noise level increases. However, it is notable that this breadth becomes increasingly directed away from the sensors as the noise increases. Furthermore, the centre of the distribution lies somewhat further from the sensors than the true state, indicating a bias error. This trend toward increased bias error with increasing sensor noise is also apparent in other sensor numbers and arrangements.

Figure 7. One true vortex and one-vortex estimator, using three sensors (shown as brown squares), with noise levels (a) $\sigma _{\mathcal{E}} = 2.5 \times 10^{-4}$, (b) $5\times 10^{-4}$ and (c) $1\times 10^{-3}$. Each panel depicts contours of expected vorticity field. True vortex position shown as filled black circle in each.

3.1.4. Effect of true vortex radius

Throughout most of this paper, the radius of the true vortices is fixed at $\epsilon = 0.01$, and the estimator vortices share this same radius. However, for practical application purposes, it is important to explore the extent to which the estimation is affected by a mismatch between these. If the true vortex is more widely distributed, can an estimator consisting of a small-radius vortex reliably determine its position and strength? Furthermore, can the radius itself be inferred? These two questions are closely related, as we will show. First, it is useful to illustrate the effect of the vortex radius on the pressure field associated with a vortex, as in figure 8(a), which shows the vortex-pressure kernel $P_{\epsilon }$ for two different vortex radii, $\epsilon = 0.01$ and $\epsilon = 0.2$. As this plot shows, the effect of vortex radius is fairly negligible beyond a distance of 5 times the larger of these two vortex radii.

Figure 8. (a) Regularized vortex-pressure kernel $P_{\epsilon }$, with two different choices of blob radius. (b) The maximum length of uncertainty ellipsoid vs blob radius $\epsilon$, for one true vortex and four sensors, when blob radius is included as part of the state vector, for a true vortex at $(x_{1},y_{1},\varGamma _{1}) = (0.5,1,1)$. (c) Vorticity contours for a true vortex with radius $\epsilon =0.2$ (in grey) and expected vorticity from a vortex estimator with radius $\epsilon = 0.01$ (in blue), using four sensors (shown as brown squares).

As a result of this diminishing effect of vortex radius, one expects that it is very challenging to estimate this radius from pressure sensor measurements outside of the vortex core. Indeed, that is the case, as figure 8(b) shows. This figure depicts the maximum length of the covariance ellipsoid as a function of true vortex radius, when four sensors along the $x$ axis are used to estimate this radius (in addition to vortex position and strength), for a true vortex at $(0.5,1)$ with strength 1. The uncertainty is far too large for the radius to be observable until this radius approaches $\epsilon = 1$. Even when the sensors are within the core of the vortex, they are confused between the blob radius and other vortex states. In fact, one can show that the dependence of the maximum uncertainty on $\epsilon ^{-3}$ arises because of the nearly identical sensitivity that the pressure sensors have to changes of blob radius and changes in other states, e.g. vertical position in this case. The leading-order term of the difference is proportional to $\epsilon ^{3}$. Of course, if we presume precise knowledge of the other states, then vortex radius becomes more observable.

The insensitivity of pressure to vortex radius has a very important benefit, because it ensures that, even when the true vortex is relatively broad in size, a vortex estimator with small radius can still reliably infer the vortex's position and strength. This is illustrated in figure 8(c), which depicts the contours of a true vortex of radius $\epsilon = 0.2$ (with the same position and strength as in (b)), and the expected vorticity contours from an estimate carried out with a vortex element of radius $\epsilon = 0.01$. It is apparent from this figure that the centre of the vortex is estimated very well. In fact, the mean of the MCMC samples is $(\bar {x}_{1},\bar {y}_{1},\bar {\varGamma }_{1}) = (0.51, 1.08, 1.04)$, quite close to the true values.

3.2. Inference of multiple vortices

The previous sections have illustrated the crucial aspects of estimating a single vortex. In this section, we focus on inferring multiple vortices. As in the case with a single vortex, the eigenvalues and eigenvectors of the true covariance ellipsoid $\varSigma ^{\ast }_{{\textit {X}}}$ will serve an important role in revealing many of the challenges in this context. However, some of the multiple vortex cases will have multiple possible solutions, and we must rely on the MCMC samples to reveal these. In the examples carried out in this section, we use the same uniform prior as in the previous section, except that now the prior vortex strengths can be negative (lying in the range $(-2,2)$).

3.2.1. Two true vortices with a two-vortex estimator

In this section, we will study the inference of a pair of vortices using a two-vortex estimator. The basic configuration of true vortices consists of $(x_{1},y_{1},\varGamma _{1}) = (-0.75,0.75,1.2)$ and $(x_{2},y_{2},\varGamma _{2}) = (0.5,0.5,0.4)$, both of radius $\epsilon = 0.01$. As in the previous section, sensors have noise $\sigma _{\mathcal{E}} = 5\times 10^{-4}$. In figure 9 we demonstrate the estimation of this pair of vortices with eight sensors. The estimator is very effective at inferring the locations and strengths of the individual vortices: the mean state of the samples is $(\bar {x}_{1},\bar {y}_{1},\bar {\varGamma }_{1}) = (-0.75,0.77,1.23)$ and $(\bar {x}_{2},\bar {y}_{2},\bar {\varGamma }_{2}) = (0.50,0.50,0.39)$, and the pressure field predicted by the expected state matches well with the true pressure field.

Figure 9. True vortex configuration $(x_{1},y_{1},\varGamma _{1}) = (-0.75,0.75,1.2)$ and $(x_{2},y_{2},\varGamma _{2}) = (0.5,0.5,0.4)$, using two-vortex estimator with eight sensors. (a) The MCMC samples. True vortex positions shown as filled black circle in each. Ellipses correspond to the estimated covariance of the samples. (b) True pressure field, (c) the comparisons of sensor values between truth (filled circles) and estimate (open circles) and (d) estimated pressure field.

In this basic configuration, the vortices are widely separated so that the estimator's challenge is similar to that of two isolated single vortices, each estimated with four sensors. However, unique challenges arise as the true vortices become closer, as figure 10 shows. Here, we keep the strength and vertical position of each true vortex the same as in the basic case, but vary both vortices’ horizontal position – the left one is moved rightward and the right one is moved leftward – in such a manner that their average is invariant, $(x_{1}+x_{2})/2 = -0.125$. Three different numbers of sensors are used, $d = 6, 7, 8$, all uniformly distributed in the range $[-1,1]$. In figure 10(a), it is clear that using six sensors, although ostensibly sufficient to estimate the six states, is actually insufficient in a few isolated cases in which the maximum uncertainty becomes infinite. These cases are examples of rank deficiency in the vortex estimator. Importantly, this rank deficiency disappears when more than six sensors are used. An example of the estimator's behaviour in one of these rank-deficient configurations is depicted in figure 10(b,c). When six sensors are used (b), the MCMC samples are distributed more widely, along a manifold in the vicinity of the true state, with the eigenvector of the most-uncertain eigenvalue tangent to this manifold. However, when seven sensors are used (c), the MCMC samples are more tightly distributed around the true state.

Figure 10. Two true vortices with strengths $\varGamma _{1} = 1.2$ and $\varGamma _{2} = 0.4$ and two-vortex estimator. (a) Maximum length of uncertainty ellipsoid for varying horizontal distance between true vortices and varying number of sensors. (b,c) The MCMC samples from a two-vortex estimator, for the true vortex configuration with peak uncertainty at $x_{2} - x_{1} = 0.91$ (shown as a dashed vertical line in (a)), using (b) six sensors and (c) seven sensors. True vortex positions are shown as filled black circles in each. The thin lines in the six-sensor case indicate the direction of maximum uncertainty for each vortex position.

Thus, we can avoid rank deficiency by using more sensors than states. As a demonstration, we show in the left panels of figure 11 the expected vorticity field that results from estimating four different true vortex configurations with eight sensors. In each case, the locations of the vortices are accurately estimated with relatively little uncertainty, even as the vortices become closer to each other than they are to the array of sensors. However, with closer vortices there is considerable uncertainty in estimating the strengths of the individual vortices, as exhibited in the right panels of figure 11, each corresponding to the vortex configuration on the left.

Figure 11. Two true vortices with strengths $\varGamma _{1} = 1.2$ and $\varGamma _{2} = 0.4$, and two-vortex estimator with eight sensors (shown as brown squares in left panels). Varying separation between vortices: (a,b) $x_{2} - x_{1} = 1.75$, (c,d) $1.25$, (e,f) $0.75$, (g,h) $0.25$. Each left panel depicts contours of expected vorticity field, with true vortex positions shown as filled black circle in each. Each right panel depicts MCMC samples of vortex strengths, with true vortex strengths shown as black circle, and the longest axis of the true covariance ellipsoid depicted by the line.

As the true vortices become even closer than in the examples in figure 11, multiple solutions emerge. This is illustrated in figure 12, depicting the extreme case of one vortex just above the other. The MCMC identifies three modes of the posterior, each representing a different candidate solution for the estimator. One mode consists of vortices of opposite sign to either side of the true set, shown in the top row of figure 12. The second mode, in the middle row, comprises vortices very near the true set, although the strengths of the vortices are quite uncertain, as evidenced by the long ridge of samples in the strength plot in figure 12(d). Finally, the bottom row shows a mode that has positive vortices further apart than in the other two modes.

Figure 12. Two true vortices $(x_{1},y_{1},\varGamma _{1}) = (-0.125,0.75,1.2)$ and $(x_{2},y_{2},\varGamma _{2}) = (-0.125,0.5,0.4)$, and a two-vortex estimator with eight sensors (shown as brown squares). Each row depicts one mixture model component. In each left panel, true vortex positions are shown as filled black circles, and each vortex's corresponding position covariance is shown as filled grey ellipse. Red ellipses depict the position covariance of the mixture model component and the dots are the MCMC samples with greater than 50 % probability of belonging to that component (blue for positive strength; red for negative). Right panels depict the MCMC samples of vortex strengths, with true vortex strengths shown as black circle in each, and the longest axis of the true covariance ellipsoid depicted by the line.

It is natural to ask whether we can prefer one of these two candidate solutions over the other. One way to do so is to assess them based on their corresponding weights $\alpha _{k}$ in the mixture model, since each of these represents the probability of a given sample point belonging to that component. However, interpreting the mixture model's weights in this fashion requires that the MCMC has reached equilibrium, which can be challenging to determine with multimodal sampling. Instead, we follow the intuition that, if a mode is to be considered a more likely solution of the inference problem than another mode, then the samples belonging to that mode should be closer to the true observation. For this assessment we can compare the maxima of the log posterior (2.12) among the samples belonging to two modes. The mode with a significantly larger maximum (i.e. significantly closer to zero, since (2.12) is non-positive) is a superior candidate solution. For the two modes shown in figure 12, the maximum log posteriors are $-0.20$, $-0.11$ and $-14.83$, respectively, suggesting that the mode in the middle row is mildly superior to that of the top row and clearly superior to that of the bottom row. Indeed, the fact that this clearly inferior mode appears among the samples at all is likely due to incomplete MCMC sampling. Thus, in this example with two very closely spaced positive-strength vortices, the true solution is discernible from the two spurious solutions.

In figure 13 we carry out the same procedure of bringing two vortices closer together as in figure 11, but now we do so for one vortex of positive strength ($1.2$) and another of negative strength ($-1.0$). We get similar results as before, successfully estimating the vortex locations and strengths. The most challenging case among these is the first, in which the two vortices are furthest apart and near the extreme range of the sensors. Interestingly, no spurious solutions arise as the vortices become very close together, as they did in the previous example. In fact, when the two opposite-sign vortices are vertically aligned, as in figure 14, the estimator has no difficulty in identifying the individual vortices and their strengths. The figure ostensibly depicts two modes identified by the estimator, but in fact these modes are identical aside from the sign of their strengths. They remain distinct to the estimator only because they have eluded our simple mitigations for the relabelling and strength symmetries (of ordering the vortices by their $x$ position and assuming that the leftmost has positive strength). Clearly we could have chosen a different mitigation strategy to avoid this, but we include the separate modes here for illustration purposes.

Figure 13. Two true vortices with strengths $\varGamma _{1} = 1.2$ and $\varGamma _{2} = -1.0$, and two-vortex estimator with eight sensors (shown as brown squares in left panels). Varying separation between vortices: (a,b) $x_{2} - x_{1} = 1.75$, (c,d) $1.25$, (e,f) $0.75$, (g,h) $0.25$. Each left panel depicts contours of expected vorticity field, with true vortex positions shown as filled black circle in each. Each right panel depicts MCMC samples of vortex strengths, with true vortex strengths shown as black circle, and the longest axis of the true covariance ellipsoid depicted by the line.

Figure 14. Two true vortices $(x_{1},y_{1},\varGamma _{1}) = (-0.125,0.75,1.2)$ and $(x_{2},y_{2},\varGamma _{2}) = (-0.125,0.5,-1.0)$, and a two-vortex estimator with eight sensors (shown as brown squares). Each row depicts one mixture model component. In each left panel, true vortex positions are shown as filled black circles, and each vortex's corresponding position covariance is shown as filled grey ellipse. Red ellipses depict the position covariance of the mixture model component and the blue dots are the MCMC samples with greater than 50 % probability of belonging to that component (blue for positive strength; red for negative). Right panels depict the MCMC samples of vortex strengths, with true vortex strengths shown as black circle in each, and the longest axis of the true covariance ellipsoid depicted by the line.

3.2.2. Three true vortices

In this section we demonstrate the performance of the estimator on cases with three true vortices. In the first example, we will use three vortices in the estimator. Let the true state comprise ${\textit {x}}_{1} = (x_{1},y_{1},\varGamma _{1}) = (-0.5,0.5,1)$, ${\textit {x}}_{2} = (0.25,0.5,-1.2)$ and ${\textit {x}}_{3} = (0.75,0.75,1.4)$. Here, we apply the techniques shown to enhance performance in the previous sections: we use eleven sensors, two more than the marginal number, to avoid rank deficiency; and we choose a top candidate among the identified modes based on the maximum value of the log posterior. The resulting estimated solution has only a single candidate mode, whose mean is $\bar {{\textit {x}}}_{1} = (-0.47,0.53,1.10)$, $\bar {{\textit {x}}}_{2} = (0.25,0.51,-1.25)$, $\bar {{\textit {x}}}_{3} = (0.68,0.75,1.36)$. This is shown in figure 15. Both the expected vorticity field and the pressure field are captured very well by the estimator.

Figure 15. Three true vortices with states ${\textit {x}}_{1} = (x_{1},y_{1},\varGamma _{1}) = (-0.5,0.5,1)$, ${\textit {x}}_{2} = (0.25,0.5,-1.2)$ and ${\textit {x}}_{3} = (0.75,0.75,1.4)$, respectively, and a three-vortex estimator using eleven sensors, shown as brown squares. (a) Expected vorticity field, (b) true pressure field, (c) the comparisons of sensor values between truth (filled circles) and estimate (open circles) and (d) estimated pressure field.

It is important to note that, in the previous example, the estimator identifies another mode (not shown) in which the signs of the rightmost two vortices are switched. However, this candidate solution was discarded on the basis of the maximum log-posterior criterion: the selected mode's value is $-0.72$, while the discarded mode's is smaller, $-0.85$. This slight difference is entirely due to the nonlinear coupling between the vortices via the interaction kernel. By restricting the leftmost vortex to be positive, the signs of the middle and rightmost vortices are established through this coupling. Because the algebraic decay of both types of kernels in (1.2) is the same, the ability to discriminate the signs of the vortices requires a degree of balance between the vortex positions and the sensors. As a counterexample, when two of the three vortices form a compact pair that is well separated from the third, the estimator tends to be less able to prefer one choice of sign for the vortex pair over the other. An example is shown in figure 16, in which the rightmost pair of vortices has opposite sign in each mode. The corresponding pressure fields shown on the right are nearly identical because the coupling of the pair with the leftmost vortex is much weaker than in the pair itself. Thus, these modes are indistinguishable by our maximum log-posterior criterion: in the absence of additional prior knowledge, we cannot discern one from the other.

Figure 16. Three true vortices with states ${\textit {x}}_{1} = (x_{1},y_{1},\varGamma _{1}) = (-0.75,0.5,1)$, ${\textit {x}}_{2} = (0.45,0.5,-1.2)$ and ${\textit {x}}_{3} = (0.55,0.75,1.4)$, and a three-vortex estimator with 11 sensors (shown as brown squares). Each row depicts a mixture model component. In each left panel, true vortex positions are shown as filled black circles, and each vortex's corresponding position covariance is shown as filled grey ellipse. Red ellipses depict the position covariance of the mixture model component and the blue dots are the MCMC samples with greater than 50 % probability of belonging to that component (blue for positive strength; red for negative). Right panels depict contours of the estimated pressure field for that mode.

The three-vortex estimator must explore a nine-dimensional space for the solution, a challenging task even with the various MCMC and symmetry mitigation techniques we have used in this paper. Thus, it is useful to restrict the estimator to search a lower-dimensional space, and the easiest way to achieve this is by using fewer vortices in the estimator. In figure 17, we illustrate the behaviour of a two-vortex estimator on the three-vortex configuration in figure 15, in variations in which the signs of the right two true vortices are changed. The range of strengths in the prior is expanded in this problem to $(-4,4)$. In the first case, the true vortex strengths are all positive. The two-vortex estimator identifies a single mode, with mean vortex states $\bar {{\textit {x}}}_{1} = (-0.54, 0.37, 0.64)$ and $\bar {{\textit {x}}}_{2} = (0.48, 0.74, 3.25)$, and a maximum log posterior of $-30.7$. In other words, the estimator places one vortex near (and slightly weaker than) the leftmost true vortex, and another vortex near the centre of the rightmost pair, with a strength roughly equal to the sum of the pair. In the second case, the two rightmost vortices are both negative, and the estimator produces an analogous result, aggregating the two negative vortices into a single vortex. The estimated state is $\bar {{\textit {x}}}_{1} = (-0.34, 0.69, 1.27)$ and $\bar {{\textit {x}}}_{2} = (0.40, 0.62, -3.07)$, with maximum log posterior $-20.4$, so that the rightmost pair is once again approximated by a single vortex with roughly the sum of the pair's strength.

Figure 17. Estimated pressure fields for three true vortices with positions $(x_{1},y_{1}) = (-0.5,0.5)$, $(0.25,0.5)$ and $(0.75,0.75)$, using a two-vortex estimator with eight sensors (shown as brown squares). (a–c) True vortex strengths $\varGamma _{1} = 1$, $\varGamma _{2} = 1.2$ and $\varGamma _{3} = 1.4$; (d–f) $\varGamma _{1} = 1$, $\varGamma _{2} = -1.2$ and $\varGamma _{3} = -1.4$; (g–i) $\varGamma _{1} = 1$, $\varGamma _{2} = -1.2$ and $\varGamma _{3} = 1.4$. Rightmost panels depict contours of the estimated pressure field for each case.

The third case is the most interesting. Here, the true vortex configuration consists of positive, negative and positive vortices from left to right, so there is no pairing of like-sign vortices as in the previous two cases. The estimator identifies a solution consisting of $\bar {{\textit {x}}}_{1} = (0.40, 1.03, 3.50)$ and $\bar {{\textit {x}}}_{2} = (0.90, 0.97, -1.2)$. Neither of these vortices bears an obvious connection with one of the true vortices, so no aggregation is possible. The estimator has done the best in can in the lower-dimensional space available to it, aliasing the true flow onto a dissimilar flow state. The maximum log posterior is $-88.6$, significantly lower than in the other two cases.