I. INTRODUCTION
In a traditional electricity market, end users seldom participate in the market activities, where they simply accept a flat price of electricity. In recent years, there is an increasing attention to demand side management (DSM), which refers to programs implemented by utility companies to control energy consumption at the customer side [Reference Gellings and Chamberlin1–Reference Albadi and El-Saadany5]. Immediate benefits of DSM programs are mainly economic, including reduced electricity cost and price volatility in wholesale market [Reference Bompard, Ma, Napoli and Abrate6] by proper load reduction and load shifting. Many bulk services traditionally provided by power plants, such as frequency response, regulation, and contingency reserves, can partially be supplied from load resources at potentially lower cost [Reference Kueck, Snyder, Li and Snyder7]. In addition, DSM programs also improve the reliability of electricity network through load reduction, and therefore avoid or defer the need for distribution and transmission infrastructure reinforcements and upgrades. All the cost savings will be eventually translated into economic benefits to consumers through reduced electricity bills due to market competition or regulation. The DSM programs bring long-term environmental and sociological benefits as well, as improved energy efficiency through DSM will eventually reduce the energy usage and green house gas emission.
Traditionally, the DSM programs are mainly targeted at large commercial and industrial (C&I) users through direct load control (DLC) [Reference Ruiz, Cobelo and Oyarzabal8], where utility companies have the ability to remotely shut down participant equipments on a short notice based on an agreement between the utility companies and the customers [Reference Ruiz, Cobelo and Oyarzabal8]. Participation of residential users in DSM programs, if any, has been very limited. In recent years, with the increasing demand of balancing and reserve power due to penetration of renewable energy sources (RES), there is an increasing interest in extending DR program to residential users through price-based DSM programs [Reference Bloustein9,Reference Kirschen10]. DR programs encourage customers to voluntarily reduce or reschedule their consumption during peak periods through time-dependent electricity prices [Reference Gellings and Chamberlin1–Reference Albadi and El-Saadany5]. Several TDP schemes have been proposed for DR, including time-of-use (ToU) rate, critical peak price (CPP), extreme day pricing (EDP), and real-time pricing (RTP) [Reference Albadi and El-Saadany5].
Despite the promises, introducing TDP to residential users has lagged behind when compared to the wholesale market where sophisticated market mechanisms have been developed. Most retail markets have retained traditional flat price (FP) structure for end-users, which is adjusted to wholesale price movement at a much slower rate. Obstacles to TDP include concerns over cost and uncertainties of TDP, and privacy concern that the utility company is in the possession of too much energy consumption information from individual customers [Reference Mulligan, Wang and Burstein11]. It is thus important to establish appropriate mechanisms to overcome these concerns to pave the path for the future smart grid.
In this paper, we focus on these issues and design a TDP scheme to provide such a mechanism. The main contribution of this paper is a price-based incentive scheme for utility companies to launch DR programs in the electricity retail market where both FP and TDP schemes coexist. The TDP is calculated to minimize the total cost for the utility company. A benefit-sharing scheme is also proposed to distribute the economic benefits from DR between the utility company and end customers. Specifically, we consider a dual-price scheme that comprises both conventional regulated FP, and a voluntary TDP scheme. The FP scheme provides regulated flat electricity price to users, which is fixed and not subject to change by utility companies. On top of it, electricity users have the flexibility to opt for TDP to enjoy additional economic benefits. For TDP, the price signal is formulated as a cost minimization problem considering both the price response behaviors from electricity users and energy procurement costs. We focus on day-ahead TDP where the TDP prices are known to electricity users sufficiently ahead of time, so that they could plan their activities in advance based on the price information. It is shown that the proposed DR scheme is effective in terms of encouraging the desired consumption behaviors from electricity users towards more efficient grid operation. In addition, with proper price signaling, the proposed DR scheme can effectively reduce the total cost to the utility company, and at the same time provide incentive to TDP users to encourage the adoption of TDP. The privacy concern is also mitigated since the price signals in the proposed scheme are calculated base on aggregated loads rather than load scheduling of individual users.
Incorporating demand elasticity model in determining optimal TDP has been previously studied in [Reference David and Lee12–Reference Uturbey and Costa14] with focuses on economic dispatch and pricing problem for wholesale market. It has been shown in [Reference Roozbehani, Dahleh and Mitter15] that a naive approach which directly links the retail price to the wholesale price creates a close-loop feedback system in which price may oscillate or diverge to unacceptable limits. To address this issue, a stabilizing pricing algorithm has been proposed in [Reference Roozbehani, Dahleh and Mitter16]. Game-theoretic-based distributed algorithms were recently proposed in [Reference Samadi, Mohsenian-Rad, Schober, Wong and Jatskevich17,Reference Mohsenian-Rad, Wong, Jatskevich, Schober and Leon-Garcia18] where optimal energy consumption scheduling and electricity pricing that minimize energy costs are jointly determined from the Nash equilibrium of a cooperative game played among electricity users and utility company. Moreover, sharing of scheduling information between users and utility is necessary in order to derive the optimal results. In [Reference Caron and Kesidis19], a stochastic strategy was proposed to solve the electricity scheduling and pricing problem when there is only limited information, e.g., the instantaneous total load on the grid, shared among users, and utility company. Optimal day-ahead pricing was studied in [Reference Joe-Wong, Sen, Ha and Chiang20] based on cost minimization for utility, and in [Reference Li, Chen and Low21] based on social welfare maximization. Heterogeneous consumption behaviors of different loads were considered in these works at device level. In [Reference Yu, Yang and Rahardja22], the optimal TDP is calculated based on maximization of expected social welfare, where the price responsive behavior of aggregated demand from users are derived statistically from the time-utility models of different loads. In these works, it is commonly assumed that TDP is mandatory. The implications and consequences of having a dual-price scheme where both TFP and FP exist have not been studied.
The benefits, especially economic benefits, from DR programs with dynamic pricing schemes have been studied extensively [Reference Su and Kirschen23–Reference Borenstein25]. In [Reference Su and Kirschen23], a wholesale market with a day-ahead market clearing mechanism is considered to enable price-sensitive demand-side bids. The demand elasticity is modelled as a function of the load participation factor (LPF), which is the ratio of price-responsive demand to total demand. The benefits of increasing LPF to aggregate customers are analyzed, and results showed that DR benefits all bidders due to the decrease in the market-clearing price. The work in [Reference Yang, Yu and Nambiar24] considered a dual-price retail market with increasing shares of RTP subscribers, and focused on the benefits of RTP to various individual consumers with different levels of capacity and willingness for DR. The work in [Reference Borenstein25] analyzed the efficiency gains from RTP in a competitive, hybrid market where both RTP and time-invariant flat rate exist. While cross-elasticities are assumed to be zero throughout the analysis, results revealed that efficiency gains from RTP can be significant even with small self elasticities. The author also pointed out that incorporation of nonzero cross-elasticities would very likely increase the gains from RTP, which is supported in our work where non-zero self and cross-elasticities are both considered. A fundamental difference between [Reference Borenstein25] and our work is the mechanism used in determining the RTP of the electricity. In [Reference Borenstein25] the prices (both FP and RTP) of electricity are determined to allow the retailer to exactly break even on service to each group of customers, which are obtained based on the economic analysis of the equilibrium point in the deregulated competitive market [Reference Borenstein and Holland26]. In our work, we alleviate this constraint on the RTP, and provide a new RTP design that allows the utility to use RTP alone as a control signal to induce the desired electricity consumption behavior, and share the economic benefits among utility company and customers. Simulation results also show that our scheme provides more economic benefits to both utility company and customers compared to naive approach where the RTP is determined based on the clear price of the whole-sale market.
The rest of this paper is organized as follows. Section II introduces the system model as well as models for energy procurement cost and price-responsive energy consumption. In Section III, the problem of optimal day-ahead TDP under the dual-price scheme is formulated and the dynamic incentive scheme is introduced, followed by the analysis and derivation of the closed-form solution for the TDP. Numerical examples of the proposed pricing scheme are given in Section IV and finally, the paper concludes in Section V.
II. SYSTEM MODEL
The presumed electricity retail market is described as follows. Consider that a group of electricity customers are served by a utility company that works essentially as a regulated monopoly. The utility company procures electricity from the wholesale market, and makes profit by selling it to end-users.
We foresee that various pricing programs will arise for end customers to subscribe with different utility companies in a deregulated retail market. Therefore a hybrid market structure is assumed where multiple pricing schemes coexist. More specifically, consider a scenario where a dual-price scheme that comprises the traditional FP scheme and a voluntary TDP scheme is implemented by a utility company in the retail market (Fig. 1). In the FP scheme, the electricity price is fixed and regulated under the natural monopoly doctrine. FP customers, which are also called price-taking customers, can be guaranteed with prescribed electricity price without overspending. On the other hand, in the TDP scheme, electricity price will be pre-calculated by the utility company to minimize cost by considering both energy procurement cost and demand elasticity of end users, and will be broadcasted to users over communication networks. This pre-calculation feature is important to improve the predictability of TDP because it enables the utility company to announce the price signals sufficiently ahead of time (e.g., day-ahead) such that TDP customers, which are also called price-responsive customers, could have sufficient knowledge about future electricity prices in order to adjust their electricity consumption accordingly. Under the proposed scheme, customers have the flexibility to choose either FP scheme so that they can enjoy assured electricity price, or TDP scheme to enjoy its potential economic benefits.
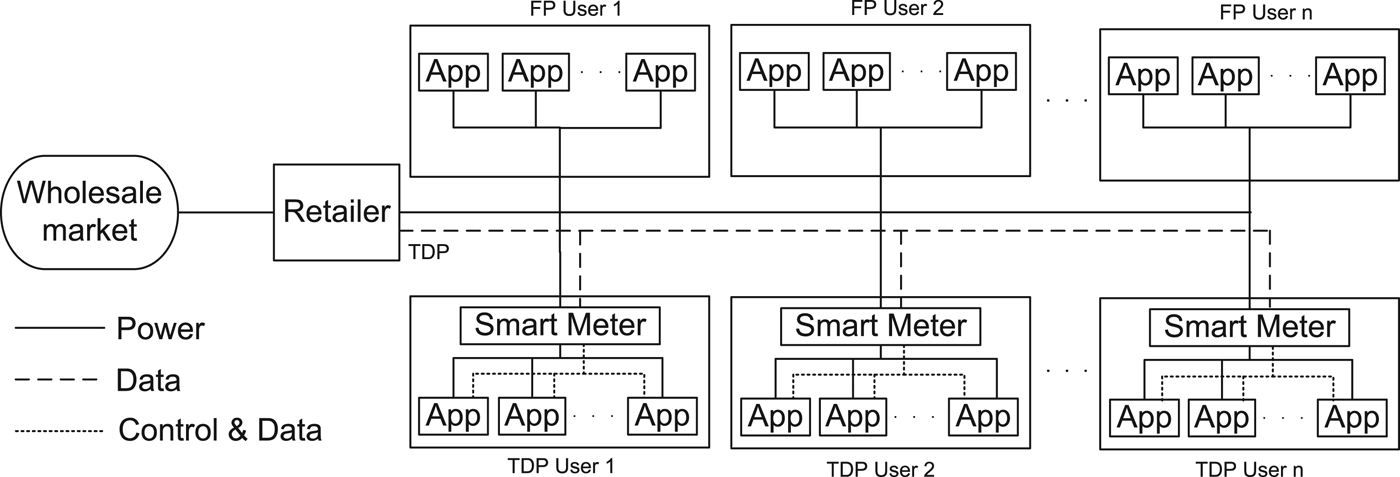
Fig. 1. Block diagram of a simplified smart grid system composed of a utility company implementing dual-price scheme. The time-dependent electricity price signals are announced to TDP users by utility company via digital communication network enabled by smart grid.
A) Utility company behavior
In a power supply system, electricity market may have a number of generating firms, which owns different number of units. Each unit submits an hourly bid according to its marginal cost curve to provide electricity to an independent system operator (ISO). Each bid is in the form of a linear nondecreasing marginal price function. The ISO then clears the market by ranking all of the bids in ascending order to form an aggregate supply curve and selecting the total quantity to clear supply and demand. According to the marginal cost of each unit and its corresponding operational constraints, the generation cost can be modeled as [Reference Su and Kirschen23]
 $$G_{t} = \sum_{l\, =\, 0}^{L-1} \left(u^{l\comma t}N^{l} +\sum_{b\, =\, 0}^{B-1}MP^{l\comma b}P_{S_g}^{l\comma b\comma t} + S^{l\comma t}\right)\comma \;$$
$$G_{t} = \sum_{l\, =\, 0}^{L-1} \left(u^{l\comma t}N^{l} +\sum_{b\, =\, 0}^{B-1}MP^{l\comma b}P_{S_g}^{l\comma b\comma t} + S^{l\comma t}\right)\comma \;$$
where, L is the number of generating units, B is the number of segments in the generator's offer curve, u l, t is the on/off status of the generating unit l at period t, N l is the no-load cost of generating unit l, MP l, b is the marginal production cost of generating unit l on segment b of its piecewise linear cost curve, P S g l,b,t is the output of generating unit l on segment b of its piecewise linear cost curve during period t, and S l, t is the start-up cost of generating unit l at period t.
The above model is complicated and very often leads to untrackable mathematical formulation. In practical applications, piecewise linear interpolation and quadratic function are two commonly used approaches to simplify this model.
The utility company procure electricity in the wholesale market and sell to end customers in the retail market. To simplify the problem, we assume a perfectly competitive market where the wholesale price is determined by the marginal cost of electricity as follows:
where d t is the total load at time t. Denote the load vector as d = [d 1,…,d t ], the total electricity procurement cost to the utility company is thus
B) Customer behaviors
Let the time period of the study be divided into T time slots, where T≜|Γ| and Γ is the set of all time slots. Without losing generality, hourly time slot is assumed in this paper. Let
![]() ${\tilde p}_t$
denote the TDP at time slot t ∈ Γ, and
${\tilde p}_t$
denote the TDP at time slot t ∈ Γ, and
![]() $\bar p$
the FP which is the same for all t. The original demands from all users without adoption of TDP is denoted by d
to
. With the adoption of TDP, the actual demand can be written as:
$\bar p$
the FP which is the same for all t. The original demands from all users without adoption of TDP is denoted by d
to
. With the adoption of TDP, the actual demand can be written as:
where
![]() $\bar{d}_{t}$
is the aggregated demand from the FP users, which may be written as
$\bar{d}_{t}$
is the aggregated demand from the FP users, which may be written as
![]() $\bar{d}_{t} = \lpar 1-\alpha\rpar d_{to}$
where α is a ratio defined as the percentage of electricity load under TDP, and
$\bar{d}_{t} = \lpar 1-\alpha\rpar d_{to}$
where α is a ratio defined as the percentage of electricity load under TDP, and
![]() ${\tilde d}_t$
is the aggregated demand from the TDP users.
${\tilde d}_t$
is the aggregated demand from the TDP users.
Price elasticity of demand is a basic concept in economics, which states that consumers tend to consume more of a good or service when its price decreases and vice versa. Unlike the demand of other types of commodities, the demand of electricity shows not only self-elasticity where the demand changes inversely proportional to the prevailing electricity prices, but also cross-time elasticity where demand at one time slot may also depend on the prices prevailing at other time slots [Reference David and Lee27,Reference Schweppe, Caramanis, Tabors and Bohn28]. The cross-time elasticity can be considered as an extension to the cross-elasticity in economics, which states that demand of one product or service will depend on price of its “alternative” product or service. To quantify the effect of price elasticity of demand, the price consumption relationship can be linearized around a given equilibrium point and the slopes of these linear functions are denoted, respectively, as self and cross-time elasticity factors defined as follows:
Here, ε tt is the self elasticity factor of time slot t, ε tτ is the cross-time elasticity factor that concerns the change in demand of time slot t with respect to price changes in time slot τ, and d to and p to are, respectively, demand and price values at the equilibrium point where elasticity is measured. Considering both self and cross-time elasticity, the change in electricity demand from the prices imposed to the consumers can be written in vector format as
where d≜(d 1,…,d T ) T , p≜(p 1,…,p T ) T , and E is the elasticity matrix in which the diagonal elements are self elasticities and the off-diagonal elements are cross-time elasticities. Here both prices and consumptions are assumed to be normalized to the equilibrium point (d to , p to ).
An elasticity matrix is called lossless [Reference Kirschen, Strbac, Cumperayot and de Paiva Mendes13] if the change in electricity price only induces load rescheduling without a reduction in energy consumption. In this case, the following relation holds between the elements of each column of the elasticity matrix:
where 1 is a row vector of all 1's. Otherwise, if load shedding exists due to high electricity price the relation becomes
In practice, the values of both self- and cross-time elasticity factors have to be determined through data analysis on customers' response to price signals. Privacy concerns can be avoided here if the data analysis is performed only on aggregated demands, or on a subset of voluntary customers who are willing to share their consumption information to help the efficient operation of power grid.
III. DYNAMIC INCENTIVE TDP UNDER DUAL-PRICE SCHEME
A) Optimization problem formulation
In this section, a dual-price scheme is proposed for the utility company with the objective to maximize profit, or equivalently, to minimize cost for the utility company. Based on the system model introduced in Section II, the problem of calculating the optimal TDP price signals under the dual-price DR program is formulated as an optimization problem. In addition, the benefits from DR program should be shared by the utility company as well as TDP customers so that both parties are rewarded by participating in TDP scheme. A practical method for benefit sharing is proposed to guarantee the benefits of both parties. The benefit-sharing method is implemented as a constraint of the optimization problem.
Considering the revenue that utility company receives from both FP and TDP users, the cost to utility company can be expressed as follows:
where C
p
is the energy costs as definedin (3),
![]() $\bar{{\bf d}} \triangleq \lpar \bar{d}_{1}\comma \; \ldots\comma \; \bar{d}_{T}\rpar ^{T}$
is the vector of aggregated demands from FP users,
$\bar{{\bf d}} \triangleq \lpar \bar{d}_{1}\comma \; \ldots\comma \; \bar{d}_{T}\rpar ^{T}$
is the vector of aggregated demands from FP users,
![]() $\tilde{{\bf d}} \triangleq \lpar \tilde{d}_{1}\comma \; \ldots\comma \; \tilde{d}_{T}\rpar ^{T}$
is the vector of aggregated demands from TDP users,
$\tilde{{\bf d}} \triangleq \lpar \tilde{d}_{1}\comma \; \ldots\comma \; \tilde{d}_{T}\rpar ^{T}$
is the vector of aggregated demands from TDP users,
![]() $\bar{{\bf p}}={\bf 1}^{T} \bar{p}_{t}$
is the FP vector, and
$\bar{{\bf p}}={\bf 1}^{T} \bar{p}_{t}$
is the FP vector, and
![]() $\tilde{{\bf p}} \triangleq \lpar \tilde{p}_{1}\comma \; \ldots\comma \; \tilde{p}_{T}\rpar ^{T}$
is the TDP price vector. Considering the demand elasticity,
$\tilde{{\bf p}} \triangleq \lpar \tilde{p}_{1}\comma \; \ldots\comma \; \tilde{p}_{T}\rpar ^{T}$
is the TDP price vector. Considering the demand elasticity,
![]() $\tilde{{\bf d}}$
is a function of TDP price vector and can be calculated by
$\tilde{{\bf d}}$
is a function of TDP price vector and can be calculated by
where d
o
≜(d
o1,…,d
oT
)
T
is the vector of original demand if all users are under FP scheme. Here it is assumed that demand elasticity factors are measured at the FP, and have been properly scaled according to equilibrium points
![]() $\lpar d_{ot}\comma \; \bar p\rpar \comma \; \forall t \in \Gamma$
. The aggregated demand from FP users is simply given by
$\lpar d_{ot}\comma \; \bar p\rpar \comma \; \forall t \in \Gamma$
. The aggregated demand from FP users is simply given by
Utility company offers monetary incentive to TDP customers in the electricity bill in order to encourage the adoption of TDP. One possible approach is to provide incentive in the form of discount. To provide such an incentive, the following constraint can be applied on the TDP:
such that the customers under TDP can enjoy a certain discount rate 0 < γ< 1 compared with FP. When high discount rate is given, users under TDP scheme may receive more monetary incentive from the utility company. Unfortunately, as will be demonstrated in the simulations, this incentive scheme considers only the benefit on the customer side and hence the profit of utility company cannot be guaranteed. To overcome this issue, we further propose a dynamic incentive scheme that consider the benefits of TDP to both utility company and electricity customers. Here the benefit to utility company is defined as
where
![]() ${\cal C}_{o}$
is the cost to utility company without TDP given by
${\cal C}_{o}$
is the cost to utility company without TDP given by
The benefit to the customers under TDP is the shrinkage in their electricity bill if they change from FP scheme to TDP scheme, and can be calculated as
The optimization problem can now be formulated as
subject to
where
![]() $\underline{p}_{t}$
and
$\underline{p}_{t}$
and
![]() $\overline{p}_{t}$
in (18) are the lower and upper price bounds to avoid extraneous results from the optimization process, (19) are the operating restrictions that specify the minimum demand (e.g., from critical loads) for each time slot, (20) guarantees benefits for TDP customers, and (21) is the constraint for dynamic incentive sharing such that the benefit partition between utility company and TDP customers is specified by the distribution factor β. Note that the utility company can adjust the distribution factor β to decide how the benefits from TDP are shared among the utility company and TDP customers. For example, a smaller β may be used during introduction of TDP scheme to give more monetary incentive to TDP customers to encourage adoption of TDP.
$\overline{p}_{t}$
in (18) are the lower and upper price bounds to avoid extraneous results from the optimization process, (19) are the operating restrictions that specify the minimum demand (e.g., from critical loads) for each time slot, (20) guarantees benefits for TDP customers, and (21) is the constraint for dynamic incentive sharing such that the benefit partition between utility company and TDP customers is specified by the distribution factor β. Note that the utility company can adjust the distribution factor β to decide how the benefits from TDP are shared among the utility company and TDP customers. For example, a smaller β may be used during introduction of TDP scheme to give more monetary incentive to TDP customers to encourage adoption of TDP.
B) Deriving optimal solution for TDP
This optimization problem is a standard non-linear programming (NLP) [Reference Bazaraa, Sherali and Shetty29] problem. For the special case where the demand elasticity factors are constants, and the energy cost is a quadratic function, the above optimization problem becomes a quadratically constrained quadratic programming (QCQP) problem [Reference Boyd and Vandenberghe30]. In the following, we present an analysis and derivation of the optimal solution for the TDP
![]() $\tilde{{\bf p}}$
.
$\tilde{{\bf p}}$
.
We consider the original optimization problem for the case of quadratic cost function
An example of the quadratic cost function is defined in (32). The Lagrange relaxation method is used to derive an easily computable lower bound on the optimal value. After going through a substantial amount of mathematical manipulation, we first write the original problem (17)–(21) in the form of QCQP problem as below:
 $$\eqalign{& \quad \quad \mathop{\min}_{\tilde{{\bf p}}} \, \, \tilde{{\bf p}}^T{\bf Q}_0^T \tilde{{\bf p}}+{\bf q}_0^T\tilde{{\bf p}} +r_0 \cr & {\rm subject}\, \, {\rm to} \cr & \quad \quad \tilde{{\bf p}}^T{\bf Q}_i^T \tilde{{\bf p}}+{\bf q}_i^T\tilde{{\bf p}} +r_i \le 0\comma \; \quad i=1\comma \; 2 \cr & \quad \quad - \tilde{{\bf p}}^T{\bf Q}_2^T \tilde{{\bf p}}-{\bf q}_2^T\tilde{{\bf p}} -r_2 \le 0\comma \; \cr & \quad \quad \tilde{{\bf p}}\le{\bf p}_{max}\comma \; \cr & \quad \quad \tilde{{\bf p}}\ge\hat{{\bf p}}_{min}\comma \; }$$
$$\eqalign{& \quad \quad \mathop{\min}_{\tilde{{\bf p}}} \, \, \tilde{{\bf p}}^T{\bf Q}_0^T \tilde{{\bf p}}+{\bf q}_0^T\tilde{{\bf p}} +r_0 \cr & {\rm subject}\, \, {\rm to} \cr & \quad \quad \tilde{{\bf p}}^T{\bf Q}_i^T \tilde{{\bf p}}+{\bf q}_i^T\tilde{{\bf p}} +r_i \le 0\comma \; \quad i=1\comma \; 2 \cr & \quad \quad - \tilde{{\bf p}}^T{\bf Q}_2^T \tilde{{\bf p}}-{\bf q}_2^T\tilde{{\bf p}} -r_2 \le 0\comma \; \cr & \quad \quad \tilde{{\bf p}}\le{\bf p}_{max}\comma \; \cr & \quad \quad \tilde{{\bf p}}\ge\hat{{\bf p}}_{min}\comma \; }$$
with the following denotations:
 $$\eqalign{&{\bf Q}_0 = \alpha^2 {\bf E}^T{\bf A}{\bf E} -\alpha{\bf E}\comma \; \cr & {\bf Q}_1 = \alpha{\bf E}\comma \; \cr & {\bf Q}_2 = \alpha^2 {\bf E}^T{\bf A}{\bf E} -\alpha \lpar 1+\beta\rpar {\bf E}\comma \; \cr & {\bf q}_0 = \alpha [ {\bf E}^T {\bf b}-{\bf d}_0 +{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf q}_1 = \alpha [ {\bf d}_0 -{\bf E} \bar{{\bf p}}-{\bf E}^T \bar{{\bf p}}] \comma \; \cr & {\bf q}_2 = \alpha [ { {\bf b}+ \lpar 1+\beta\rpar \lpar \bf E} \bar{{\bf p}}-{\bf E}^T {\bar{\bf p}\rpar -\lpar 1+\beta\rpar {\bf d}_0 }] \comma \; \cr & {\bf r}_0 = -\alpha^2 \bar{{\bf p}}^T {\bf E}^T{\bf A}{\bf E} \bar{{\bf p}}+\alpha {\bf b}^T [ {\bf d}_0 -{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf r}_1 = -\alpha \bar{{\bf p}}^T[ {\bf d}_0 +{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf r}_2 = -\alpha^2 \bar{{\bf p}}^T {\bf E}^T{\bf A}{\bf E} \bar{{\bf p}}+\alpha [ { {\bf b}^T- \lpar 1+\beta\rpar \bar{{\bf p}}}^T] [ {\bf d}_0 -{\bf E} {\bar{\bf p}\rpar }] \cr & \quad \quad +\lpar \bar{{\bf d}}^T_t {\bf A}+ {\bf b}^T\rpar \bar{{\bf d}}_t.}$$
$$\eqalign{&{\bf Q}_0 = \alpha^2 {\bf E}^T{\bf A}{\bf E} -\alpha{\bf E}\comma \; \cr & {\bf Q}_1 = \alpha{\bf E}\comma \; \cr & {\bf Q}_2 = \alpha^2 {\bf E}^T{\bf A}{\bf E} -\alpha \lpar 1+\beta\rpar {\bf E}\comma \; \cr & {\bf q}_0 = \alpha [ {\bf E}^T {\bf b}-{\bf d}_0 +{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf q}_1 = \alpha [ {\bf d}_0 -{\bf E} \bar{{\bf p}}-{\bf E}^T \bar{{\bf p}}] \comma \; \cr & {\bf q}_2 = \alpha [ { {\bf b}+ \lpar 1+\beta\rpar \lpar \bf E} \bar{{\bf p}}-{\bf E}^T {\bar{\bf p}\rpar -\lpar 1+\beta\rpar {\bf d}_0 }] \comma \; \cr & {\bf r}_0 = -\alpha^2 \bar{{\bf p}}^T {\bf E}^T{\bf A}{\bf E} \bar{{\bf p}}+\alpha {\bf b}^T [ {\bf d}_0 -{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf r}_1 = -\alpha \bar{{\bf p}}^T[ {\bf d}_0 +{\bf E} \bar{{\bf p}}] \comma \; \cr & {\bf r}_2 = -\alpha^2 \bar{{\bf p}}^T {\bf E}^T{\bf A}{\bf E} \bar{{\bf p}}+\alpha [ { {\bf b}^T- \lpar 1+\beta\rpar \bar{{\bf p}}}^T] [ {\bf d}_0 -{\bf E} {\bar{\bf p}\rpar }] \cr & \quad \quad +\lpar \bar{{\bf d}}^T_t {\bf A}+ {\bf b}^T\rpar \bar{{\bf d}}_t.}$$
where A = Diag[a
1, … a
T
] is a diagonal matrix with non-zero elements a
t
, and b = [b
1, …b
T
]
T
. Note that the second constraint in (23) is added to maintain the equality in the constraint (21) of the original problem. Moreover, in the last two constraints of (23),
![]() $\hat{{\bf p}}_{min}=\max \lpar {\bf 1}^{T} \underline{p}_{t}\comma \; {\bf E}^{-1}[ {\bf 1}^{T}\tilde{d}_{t\comma min}/\alpha-{\bf d}_{0}] \rpar $
, is the minimum constraint vector, and
$\hat{{\bf p}}_{min}=\max \lpar {\bf 1}^{T} \underline{p}_{t}\comma \; {\bf E}^{-1}[ {\bf 1}^{T}\tilde{d}_{t\comma min}/\alpha-{\bf d}_{0}] \rpar $
, is the minimum constraint vector, and
![]() ${\bf p}_{max}={\bf 1}^{T} \bar{p}_{t}$
is the maximum constraint vector for the TDP.
${\bf p}_{max}={\bf 1}^{T} \bar{p}_{t}$
is the maximum constraint vector for the TDP.
Next, we formulate the Lagrangian as follows:
 $$\eqalign{L\lpar \tilde{{\bf p}}\comma \; {\bf \underline{\lambda}}\comma \; {\bf \underline{\mu} }\comma \; {\bf \underline{\omega}}\rpar &= \tilde{{\bf p}}^T{\bf Q}_0^T \tilde{{\bf p}}+{\bf q}_0^T\tilde{{\bf p}} +r_0 \cr & \quad + \sum_{i=1}^{2} \lambda_i \lpar \tilde{{\bf p}}^T{\bf Q}_i^T \tilde{{\bf p}}+{\bf q}_i^T\tilde{{\bf p}} +r_i\rpar \cr & \quad - \lambda_3 \lpar \tilde{{\bf p}}^T{\bf Q}_2^T \tilde{{\bf p}}+{\bf q}_2^T\tilde{{\bf p}} +r_2\rpar \cr & \quad + {\bf \underline{\mu}}^T \lpar \tilde{{\bf p}}-{\bf p}_{max}\rpar -{\bf \underline{\omega}}^T\lpar \tilde{{\bf p}}-\hat{{\bf p}}_{min}\rpar .}$$
$$\eqalign{L\lpar \tilde{{\bf p}}\comma \; {\bf \underline{\lambda}}\comma \; {\bf \underline{\mu} }\comma \; {\bf \underline{\omega}}\rpar &= \tilde{{\bf p}}^T{\bf Q}_0^T \tilde{{\bf p}}+{\bf q}_0^T\tilde{{\bf p}} +r_0 \cr & \quad + \sum_{i=1}^{2} \lambda_i \lpar \tilde{{\bf p}}^T{\bf Q}_i^T \tilde{{\bf p}}+{\bf q}_i^T\tilde{{\bf p}} +r_i\rpar \cr & \quad - \lambda_3 \lpar \tilde{{\bf p}}^T{\bf Q}_2^T \tilde{{\bf p}}+{\bf q}_2^T\tilde{{\bf p}} +r_2\rpar \cr & \quad + {\bf \underline{\mu}}^T \lpar \tilde{{\bf p}}-{\bf p}_{max}\rpar -{\bf \underline{\omega}}^T\lpar \tilde{{\bf p}}-\hat{{\bf p}}_{min}\rpar .}$$
The vectors
![]() ${\underline{\lambda}}=[ {\matrix{\lambda_{1} & \lambda_{2} & \lambda_{3}\cr}}] ^{T} $
,
${\underline{\lambda}}=[ {\matrix{\lambda_{1} & \lambda_{2} & \lambda_{3}\cr}}] ^{T} $
,
![]() ${\bf \underline{\mu}}=[ \mu_{1} \ldots\mu_{T}] ^{T} $
,
${\bf \underline{\mu}}=[ \mu_{1} \ldots\mu_{T}] ^{T} $
,
![]() ${\bf \underline{\omega}}=[ \omega_{1} \ldots\omega_{T}] ^{T}$
are defined respectively for the Lagrange dual variables λ
i
, μ
i
, and ω
i
.
${\bf \underline{\omega}}=[ \omega_{1} \ldots\omega_{T}] ^{T}$
are defined respectively for the Lagrange dual variables λ
i
, μ
i
, and ω
i
.
To solve for the optimal TDP
![]() $\tilde{{\bf p}}$
, we then differentiate
$\tilde{{\bf p}}$
, we then differentiate
![]() $L\lpar \tilde{{\bf p}}\comma \; {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
with respect to
$L\lpar \tilde{{\bf p}}\comma \; {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
with respect to
![]() $\tilde{{\bf p}}$
, set
$\tilde{{\bf p}}$
, set
![]() $\nabla_{\tilde{{\bf p}}} L\lpar \tilde{{\bf p}}\comma \; {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar =0$
. By doing this, we arrive at the following closed form solution for the optimal TDP:
$\nabla_{\tilde{{\bf p}}} L\lpar \tilde{{\bf p}}\comma \; {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar =0$
. By doing this, we arrive at the following closed form solution for the optimal TDP:
where the
![]() ${\bf U}\lpar {\underline{\lambda}}\rpar $
and
${\bf U}\lpar {\underline{\lambda}}\rpar $
and
![]() ${\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
can be derived as
${\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
can be derived as
 $$\eqalign{{\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar &= \alpha {\bf E}^T{\bf b}+\lpar \lambda_2-\lambda_3\rpar {\bf b} \cr & \quad + [ \alpha\lpar \lambda_1-1\rpar -\lpar \lambda_2-\lambda_3\rpar \lpar 1+\beta\rpar ] {\bf d}_0 \cr & \quad +\alpha [ {\bf E} \bar{{\bf p}} + \lambda_1 \lpar {\bf E} \bar{{\bf p}} - {\bf E}^T \bar{{\bf p}}\rpar ] \cr & \quad +\alpha \lpar \lambda_2 - \lambda_3\rpar \lpar 1+\beta\rpar \lpar {\bf E} \bar{{\bf p}}-{\bf E}^T\bar{{\bf p}}\rpar \cr & \quad + {\underline{\mu}}+{\underline{\omega}}.} $$
$$\eqalign{{\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar &= \alpha {\bf E}^T{\bf b}+\lpar \lambda_2-\lambda_3\rpar {\bf b} \cr & \quad + [ \alpha\lpar \lambda_1-1\rpar -\lpar \lambda_2-\lambda_3\rpar \lpar 1+\beta\rpar ] {\bf d}_0 \cr & \quad +\alpha [ {\bf E} \bar{{\bf p}} + \lambda_1 \lpar {\bf E} \bar{{\bf p}} - {\bf E}^T \bar{{\bf p}}\rpar ] \cr & \quad +\alpha \lpar \lambda_2 - \lambda_3\rpar \lpar 1+\beta\rpar \lpar {\bf E} \bar{{\bf p}}-{\bf E}^T\bar{{\bf p}}\rpar \cr & \quad + {\underline{\mu}}+{\underline{\omega}}.} $$
Next, we proceed to solve for the Lagrange dual variables λ
i
. By substituting the optimal TDP
![]() $\tilde{{\bf p}}^{\ast}$
(26) into the objective function of (23), we obtain the dual function as
$\tilde{{\bf p}}^{\ast}$
(26) into the objective function of (23), we obtain the dual function as
where
 $$\eqalign {z\lpar {\underline{\lambda}}\rpar &= \alpha \lcub {\bf b}^T-\lambda_1 \bar{{\bf p}}^T+ \lpar \lambda_2-\lambda_3\rpar [ {\bf b}^T- \lpar 1+\beta\rpar \bar{{\bf p}}^T] \rcub \cr & \quad [ {\bf d}_0- {\bf E} \bar{{\bf p}}] -\alpha^2 \lpar 1+\lambda_2-\lambda_3\rpar \bar{{\bf p}}^T{\bf E}^T {\bf A} {\bf E} \bar{{\bf p}} \cr & \quad +\lpar \lambda_2-\lambda_3\rpar \lpar \bar{{\bf d}}^T_t {\bf A}+ {\bf b}^T\rpar \bar{{\bf d}}_t.} $$
$$\eqalign {z\lpar {\underline{\lambda}}\rpar &= \alpha \lcub {\bf b}^T-\lambda_1 \bar{{\bf p}}^T+ \lpar \lambda_2-\lambda_3\rpar [ {\bf b}^T- \lpar 1+\beta\rpar \bar{{\bf p}}^T] \rcub \cr & \quad [ {\bf d}_0- {\bf E} \bar{{\bf p}}] -\alpha^2 \lpar 1+\lambda_2-\lambda_3\rpar \bar{{\bf p}}^T{\bf E}^T {\bf A} {\bf E} \bar{{\bf p}} \cr & \quad +\lpar \lambda_2-\lambda_3\rpar \lpar \bar{{\bf d}}^T_t {\bf A}+ {\bf b}^T\rpar \bar{{\bf d}}_t.} $$
For given vectors
![]() ${\bf \underline{\mu}}$
and
${\bf \underline{\mu}}$
and
![]() ${\bf \underline{\omega}}$
, we can form the dual problem of (23) as follows:
${\bf \underline{\omega}}$
, we can form the dual problem of (23) as follows:
 $$\eqalign {& \quad \quad \quad {\max_{\underline{\lambda}}} \psi + z\lpar {\underline{\lambda}}\rpar \comma \; \cr & \hbox{subject to} \left[{\matrix{{\bf U}\lpar {\underline{\lambda}}\rpar & {\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar /2 \cr {\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar ^{T}/2 & -\psi \cr } } \right]\geq 0\comma \; \cr & \quad \quad \quad \quad \, \, {\lambda_i \ge 0\comma \; i=1\comma \; \ldots\comma \; 3.}} $$
$$\eqalign {& \quad \quad \quad {\max_{\underline{\lambda}}} \psi + z\lpar {\underline{\lambda}}\rpar \comma \; \cr & \hbox{subject to} \left[{\matrix{{\bf U}\lpar {\underline{\lambda}}\rpar & {\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar /2 \cr {\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar ^{T}/2 & -\psi \cr } } \right]\geq 0\comma \; \cr & \quad \quad \quad \quad \, \, {\lambda_i \ge 0\comma \; i=1\comma \; \ldots\comma \; 3.}} $$
where the
![]() ${\bf U}\lpar {\underline{\lambda}}\rpar $
and
${\bf U}\lpar {\underline{\lambda}}\rpar $
and
![]() ${\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
have been derived in (27) and (28), respectively.
${\bf v}\lpar {\underline{\lambda}}\comma \; {\underline{\mu} }\comma \; {\underline{\omega}}\rpar $
have been derived in (27) and (28), respectively.
The optimization in (31) is a semi-definite programming (SDP) problem, which is also convex and easy to solve or compute. It gives a lower bound on the optimal value of the original problem. The optimal values for
![]() ${\underline{\mu}}$
and
${\underline{\mu}}$
and
![]() ${\underline{\omega}}$
can be computed using the standard subgradient algorithms [Reference Boyd and Vandenberghe30] to meet the maximum and minimum constraints of the price variables.
${\underline{\omega}}$
can be computed using the standard subgradient algorithms [Reference Boyd and Vandenberghe30] to meet the maximum and minimum constraints of the price variables.
For more general cost function C p (d), the optimization involves minimising the objective function, which can be modeled as a polynomial over a set defined by the constraints which are polynomial inequalities. We can solve such polynomial optimization problem by rewriting it into the form of a QCQP programming problem using suitable change of variables [Reference Boyd and Vandenberghe30]. For example, for any objective function or constraint with a polynomial with the maximum degree term y 2n , we can introduce a new variable u, which is associated with the quadratic equality constraint u = y Reference Fahrioglu and Alvarado 2 . The resulting QCQP programming problem can then be solved using the above approach and solutions.
IV. CASE STUDY AND RESULTS ANALYSIS
The dynamic incentive TDP scheme described in Section III is implemented and simulation results are given in this section. Results demonstrate the load shifting and load shedding effects of the proposed dual-price system and its capabilities in distributing benefits from TDP to both utility company and end customers. The hourly initial demands assumed in our study are given in Fig. 2, which are assumed from electricity customers when they are under an FP of $ 649.55/MWh, which is calculated by (3) using the aggregated original load. We further allow TDP rates to fluctuate between a lower bound of $ 194.87/MWh and a higher bound of $ 1299.1/MWh over the time period as long as they, collectively, satisfy the constraint on dynamic incentive sharing.

Fig. 2. Original aggregated load from electricity users.
In our simulation, we further assume that the energy procurement cost of the utility company follows [Reference Su31] Appendix C.1, where a 10-Unit system is given. Based on this system, the corresponding cost function is generated and shown in Fig. 3. To simplify the problem, we use a quadratic cost function obtained through least-squares curve fitting to approximate the actual cost function, which is given as

Fig. 3. 10-Unit system cost function.
where d is power demand in MWh. The quadratic cost function is also shown in Fig. 3.
We use the coefficient of determination (R Reference Fahrioglu and Alvarado 2 ) to evaluate the accuracy of the quadratic function (32) in approximating the actual cost function. The coefficient of determination is calculated as
 $$R^2 = 1 - \displaystyle{{\sum\nolimits_d \lpar G_t - \hat{G}_t\rpar } \over {\sum\nolimits_d \lpar G_t - \bar{G}_t\rpar }}\comma \;$$
$$R^2 = 1 - \displaystyle{{\sum\nolimits_d \lpar G_t - \hat{G}_t\rpar } \over {\sum\nolimits_d \lpar G_t - \bar{G}_t\rpar }}\comma \;$$
where G
t
is the actual cost data,
![]() $\bar{G}_{t}$
is its expectation, and
$\bar{G}_{t}$
is its expectation, and
![]() $\hat{G}_{t}$
is its approximation. When the value of R
Reference Fahrioglu and Alvarado
2
is close to 1, high approximation accuracy is presented. We found that
$\hat{G}_{t}$
is its approximation. When the value of R
Reference Fahrioglu and Alvarado
2
is close to 1, high approximation accuracy is presented. We found that
![]() $\hat{G}_{t}$
achieves an R
Reference Fahrioglu and Alvarado
2
of 0.9998 for d ∈ [0, 5545], which shows that the quadric approximation given in (32) is highly accurate.
$\hat{G}_{t}$
achieves an R
Reference Fahrioglu and Alvarado
2
of 0.9998 for d ∈ [0, 5545], which shows that the quadric approximation given in (32) is highly accurate.
A) Case study
We start with the case where DR benefit is equally distributed between the utility company and the TDP customers, which is guaranteed by the constraint β = 1 in the optimization problem. In this case study, self- and cross-time elasticity factors of electricity users are specified as follows:
 $$\varepsilon_{t \tau} ={\left\{{ {\matrix{ -0.5\comma \; & {\rm mod}\lpar \tau-t\comma \; 24\rpar = 0 \cr \displaystyle{{1} \over {6}}\comma \; & {\rm mod}\lpar \tau-t\comma \; 24\rpar = 1 \cr \displaystyle{{1} \over {30}}\comma \; & \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 2\comma \; 3\comma \; 4\comma \; 22\comma \; 23 \cr \displaystyle{{1} \over {60}}\comma \; & \quad \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 5\comma \; 6\comma \; 7\comma \; 19\comma \; 20\comma \; 21 \cr \displaystyle{{1} \over {150}}\comma \; & \quad \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 8\comma \; 9\comma \; 10\comma \; 16\comma \; 17\comma \; 18 \cr \displaystyle{{1} \over {300}}\comma \; & \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 11\comma \; 12\comma \; 15 \cr 0\comma \; & \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 13\comma \; 14 \cr } } } \right.}.$$
$$\varepsilon_{t \tau} ={\left\{{ {\matrix{ -0.5\comma \; & {\rm mod}\lpar \tau-t\comma \; 24\rpar = 0 \cr \displaystyle{{1} \over {6}}\comma \; & {\rm mod}\lpar \tau-t\comma \; 24\rpar = 1 \cr \displaystyle{{1} \over {30}}\comma \; & \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 2\comma \; 3\comma \; 4\comma \; 22\comma \; 23 \cr \displaystyle{{1} \over {60}}\comma \; & \quad \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 5\comma \; 6\comma \; 7\comma \; 19\comma \; 20\comma \; 21 \cr \displaystyle{{1} \over {150}}\comma \; & \quad \quad \quad \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 8\comma \; 9\comma \; 10\comma \; 16\comma \; 17\comma \; 18 \cr \displaystyle{{1} \over {300}}\comma \; & \quad \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 11\comma \; 12\comma \; 15 \cr 0\comma \; & \quad \quad {\rm mod}\lpar \tau-t\comma \; 24\rpar = 13\comma \; 14 \cr } } } \right.}.$$
This elasticity matrix satisfies 1 · E ≺ 0, which indicates the existence of load shedding. The effect of TDP on the electricity market is measured by the total load, the peak load, the peak-to-average ratio (PAR) of the aggregated load curve, together with the benefit to utility company and aggregate/individual TDP users.
We compare the cases when α equals to 0.2 and 0.7. It can be seen that, when less users are involved in TDP program, these TDP users can get more benefit from TDP program. When more users participate into the TDP program, less benefit will be awarded to individual customer. Fig. 5 compared the aggregated load curves when α is 0.2 or 0.7 with the original demand. As can be seen from Fig. 5, when less users participate into TDP scheme (α = 0.2), the demand is in fact inelastic since the majority of electricity users are still under FP, resulting less load shifting from peak hours. The peak load is as high as 5842 MW at T = 18 and the PAR is 1.46. When more users are involved into TDP scheme (α = 0.7), more loads are shifted from peak hours to non-peak hours. The peak load becomes 4544 MW at T = 18 and the PAR is 1.14. Clearly, the reduced peak demand and improved load profile when more users participate into the TDP scheme will help to improve the reliability of the power grid.
The TDP price signals obtained from the optimization problem with dynamic incentive scheme β = 1 are illustrated in Fig. 4. It can be seen in both cases (α = 0.2 and 0.7), two price peaks are presented, which correspond to the peak load periods as shown in Fig. 2. In particular, when the level of TDP user participation is low (α = 0.2), more dramatic changing TDP is required in order to encourage load shifting from peak hours to non-peak hours. In this case, the TDP price signals closely resemble a simple ToU rate design that charges end users a higher rate during peak hours. The dynamic of TDP is reduced when more users participate into the TDP scheme, and the elasticity of electricity demand is improved (α = 0.7). This result implies a DR program with a simple ToU design may be as effective as TDP at a market with a low DR penetration, while more sophisticated TDP with hourly varying electricity price is relevant only when the grid is sufficiently elastic, i.e., there are sufficient number of DR customers existing in the power system.

Fig. 4. TDP prices (β = 1).
Table 1 further shows the comparison under different level of TDP participations when α varies from 0 to 1 with a step size of 0.1. Results clearly demonstrate that increased participation of TDP reduces the peak load and PAR of aggregated load curve, and increases utility and aggregate TDP consumers' benefits. However, the individual TDP user's benefit, which is the benefit measured as price per MW for an individual TDP user, decreases with increasing α. Note here the numbers for individual TDP user's benefit are calculated by assuming that the total number of consumers under the dual-price scheme is 1 million. The average TDP that the customer pays is calculated as a weighted average of the TDP vector by the actual load, i.e.,
![]() ${\rm TDP}_{avg}\lpar \tilde{{\bf d}}\rpar $
where
${\rm TDP}_{avg}\lpar \tilde{{\bf d}}\rpar $
where
Table 1. Market conditions with different participation (α) of TDP under dual-price scheme with dynamic incentive β = 1.
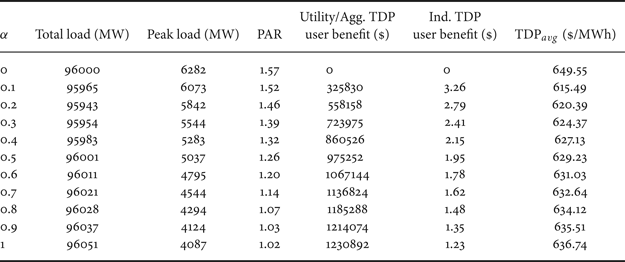
Note that when TDP is enabled, i.e., α > 0, TDP avg is always smaller than the flat rate which is $ 649.55/MWh.
B) Benefit sharing
It is interesting to compare the results, especially the benefits to utility company and customers, with those when a fixed discount rate as defined in (13) is given to the TDP customers. To this end, we repeated the simulation after replacing the constraint (20) with (13) and the results are compared with those for the dynamic incentive scheme in Fig. 6. It can be seen that in such a case, the profit of utility company cannot be guaranteed. When γ = 4%, i.e., 4% discount rate is given to the TDP customers, the profit of utility company may drop when more customers participate into the TDP program, and could even become negative, which is not desirable from the utility company's point of view. On the other hand, under the same simulation conditions, dynamic incentive scheme guarantees the profit of utility company, which could be a more favorable results for the utility company to promote the TDP program to its potential customers. This is evident from Fig. 6, which shows that the revenue to utility company in fact, increases when more users participate into the TDP scheme even when TDP users share the same benefit as the utility company.

Fig. 5. Aggregated electricity demand from all users under dual-price scheme with dynamic incentive β = 1.

Fig. 6. Comparison of aggregate benefits of TDP customers and utility company under different incentive schemes.
The total benefit gained from DR largely depends on the participation rate of TDP α, and the elasticity matrix E of that particular group of customers which reflects their capability for load rescheduling in response to price. In a fixed-discount benefit-sharing scheme, it is non-trivial to define the discount rate as a function of the α and E such that economic benefits to both utility company and customers are guaranteed. Instead, the proposed benefit-sharing scheme presents a practical and reasonable way to distribute the gains from DR between different parties and guarantees that both parties have positive profit, and is also controllable by changing the value of β.
Assuming quadratic generation cost and with fixed E, the benefit-sharing constraint (21) can actually be re-written in the form of
where M
1, M
2, and M
3 are quadratic functions of
![]() $\tilde{{\bf p}}$
. Therefore, α together with the upper and lower price bounds for TDP determines a feasible range of β. Figure 7 shows the benefits to utility and aggregate TDP customers under the proposed benefit-sharing scheme when α = 0.7 and β varies from 0.01 to 100.
$\tilde{{\bf p}}$
. Therefore, α together with the upper and lower price bounds for TDP determines a feasible range of β. Figure 7 shows the benefits to utility and aggregate TDP customers under the proposed benefit-sharing scheme when α = 0.7 and β varies from 0.01 to 100.

Fig. 7. Benefits to utility and aggregate TDP customers under the proposed benefit-sharing scheme with different β (α = 0.7).
C) Observations
Beyond the specific case study in the previous subsection, more observations are presented in details as below.
First of all, the scale of benefits brought by DR largely depend on the elasticity matrix of the TDP users. Highly price-responsive behavior leads to lower peak load, lower PAR and higher benefit. This can be demonstrated by Table 2 where other parameters fixed and the elasticity matrix is multiplied by a scale factor from 0.2 to 1.8 and compared with the original elasticity matrix as defined in (34).
Table 2. Results with different elasticity matrices (α = 0.7 and β = 1).
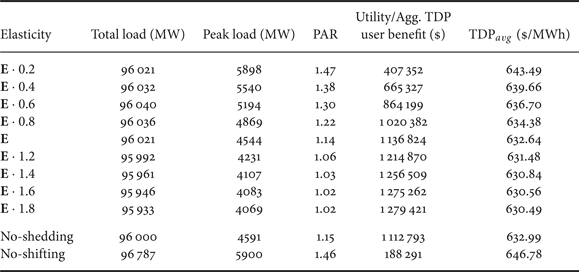
Secondly, the benefits come from both load shedding and load shifting. As in Table 2, for no-shedding case, the diagonal elements of E are set such that the row sums of E become zero, i.e., 1 · E = 0. The benefits from load shifting can be demonstrated by comparing the results of the no-shedding case with the original E case. For the no-shifting case, the non-diagonal elements of E are set to zero, i.e., ε tτ = 0, ∀t ≠ τ. An interesting observation is that when there is no load-shifting, enabling load shedding may lead to increase in the total consumption of load since customers may consume more electricity during non-peak hours due to lower electricity price.
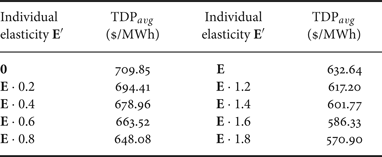
Thirdly, customers could lose when changing from FP to TDP if their loads are not price-responsive. Assume that the aggregate elasticity matrix for existing TDP users is E and one individual customer with a load vector d that has the same shape as the average load profile D averaged from all users, and a particular elasticity matrix E ′. Consider a market with α = 0.7 and β = 1, when the customer changed from FP to TDP, the average electricity prices TDP avg (d ′) are calculated as in (35) under different elasticity matrices, and the results are shown in Table 3. Given that the flat rate is $ 649.55/MWh, the results show that an individual TDP customer could lose if it has much lower elasticity values compared to other TDP customers. Note that here we assume the load profile of the individual customer has the same shape as the aggregated load profile and the results may differ if it is otherwise.
Table 3. Average electricity price ($ /MWh) for individual customer with average load profile under TDP with different elasticity matrices (FP $ 649.55/MWh).
Last but not least, we compare the proposed DR scheme with the case where wholesale market clearing price (MCP) is adopted directly as TDP to end customers, which is used in [Reference Borenstein25]. In such case the average electricity price that a TDP user pays is fixed at $ 639.74/MWh with the elasticity matrix as defined in (34). In Fig. 8, the benefits to utility company and aggregate TDP users w.r.t. different α are compared between the proposed TDP scheme (with β = 1) and using wholesale MCP directly as TDP. Results show that the proposed TDP brings more benefits to both utility company and aggregate TDP users.

Fig. 8. Comparison of benefits to utility company and aggregate TDP users between (1) the proposed TDP scheme and (2) using wholesale MCP directly as TDP.
D) Green energy study
In recent years, green energy, which includes but not limited to wind and solar power, becomes much popular in power supply. Green energy provides a low-cost power resource, which can be replenished constantly. However, the variability and intermittency of green energy present challenges to integrate green energy into the existing power grid. Traditional power generation has to replace green energy when the availability of green energy is low. This may increase the variation of load on traditional power generation, which is not desirable.
As discussed in this paper, the proposed TDP scheme can help to shift the demand in peak periods to non-peak periods, which reduces the overall load in peak periods. In this study, we will check the performance of proposed TDP scheme under power grid integration with green energy generation. Here, wind power is taken as an example. In the simulation, we assume the grid system under evaluation has an average wind energy penetration of 30%. The daily variation of wind energy generation as discussed in [Reference Fripp and Wiser32] is adopted in this study.
The simulation comparison results are given in Fig. 9. Three demand curves are presented: the original demand, the demand under the proposed TDP for a traditional power grid, and the demand under TDP for the integrated grid with 30% wind energy penetration as discussed above. In both cases, the same generator parameters as in previous study are assumed. From these results, it can be seen that the proposed TDP flattens the demand curve through incentive price. In addition, with the introduced of low-cost wind energy, less loads have been rescheduled to midnight (time slots 0 ~ 4). Instead, significant portions of those loads are now scheduled to time slots 19 ~ 21 and time slots 7 ~ 12 when wind energy is abundant, which is a favorable to customers as it helps to shorten the waiting time for re-scheduled loads.

Fig. 9. Comparison of loads under traditional power grid with proposed TDP (α = 0.5 and β = 1) and green-energy integrated power grid with proposed TDP.
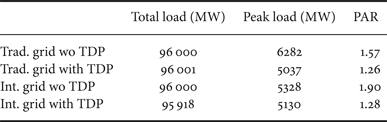
An important issue of green energy recourses such as wind or solar power is that they are not dispatchable, and their availability may not be necessarily coincident with the demand. Therefore, the introduction of this type of energy sources into a power grid may, in many cases, increases the variance of the loads on traditional power generation. This is undesired since the high variation of load presents substantial challenges to the traditional power generation. To study this issue, we compare the PAR of the loads on traditional power generation under different scenarios as illustrated in Table 4. From these results, it can be seen that the proposed TDP is effective in reducing the load variation on traditional power generation. We tested with α = 0.5 and β = 1. In the cases of no green energy integration, the introduction of TDP helps to reduce the PAR from 1.57 to 1.26. The reduction in PAR is more significant when wind energy is present, where the PAR is reduced from 1.90 without TDP to 1.28 with TDP. Note that the PAR in the latter case is already very close to that of the best case under TDP when wind energy is not present (PAR = 1.26). These results confirm the effectiveness of the proposed TDP scheme in terms of reduce the load variation in addition to its economic benefits to both utility company and electricity users.
Table 4. Comparison of loads in traditional power grid and green-energy integrated power grid with and without proposed TDP (α = 0.5, β = 1).
V. CONCLUSION
In this paper, dual-price based DR program that consists of both a conventional flat and regulated pricing scheme and a voluntary TDP scheme, is investigated. The TDP price signals provide a control signal to guide the power consumption toward more efficient operation of power grid, and simultaneously an economic tool for distributing cost saving to both utility company and TDP users as an incentive for them to adopt TDP scheme. An algorithm is proposed to calculate the optimal TDP based on a pre-defined distribution factor that determines the benefit distribution between utility company and TDP customers. We also present an analysis and derived a closed-form solution for the TDP. Simulation results show that the proposed method effectively distributes the benefit from TDP program to the utility company and TDP customers, so that they are both benefited from actively participating into TDP program. In addition, the results also show that the proposed TDP scheme can reduce the load variation on the traditional power generation, which helps to maintain the grid stability.















