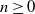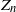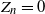1. Introduction
It is known that Galton–Watson processes are widely applied in nuclear physics, biology, ecology, epidemiology, and many other areas, and have been extensively studied; see [Reference Athreya and Ney2, Reference Haccou, Jagers and Vatutin10, Reference Kimmel and Axelrod18] and references therein. The study of Galton–Watson processes can be extended directly in two directions. One popular extension is the branching process in a random environment (BPRE), which has attracted much attention. Many interesting results arise from the existence of the random environment; we refer the reader to [Reference Kersting and Vatutin15] and references therein for details. Another interesting extension of the Galton–Watson process is the branching process in a varying environment (BPVE). Compared with BPREs, the the study of BPVEs has not been as successful. The main reason is that a BPVE is no longer a time-homogeneous Markov chain, but BPREs do have some homogeneous properties. Indeed, if the environments are assumed to be stationary and ergodic, then a BPRE is a time-homogeneous process under annealed probability. The emerging of the so-called varying environments also brings some strange phenomena to the branching processes. For example, the process may ‘fall asleep’ in some positive state [Reference Lindvall19], it may diverge at different exponential rates [Reference Macphee and Schuh21], and the tail probabilities of the surviving time may show some strange asymptotics [Reference Fujimagari9, Reference Wang and Yao29]. For other aspects of the study of BPVEs, we refer the reader to [Reference Bhattacharya and Perlman3–Reference Cohn and Wang5, Reference Dolgopyat, Hebbar, Koralov and Perlman7, Reference Jagers11, Reference Jones13, Reference Kersting14] and the references therein.
In this paper we study BPVEs with immigration. For simplicity, we assume that only one immigrant immigrates into the system in each generation. Roughly speaking, for
$n\ge0$
, let
$Z_n$
be the number of individuals in the nth generation, which does not count the immigrants entering the system at time n. If
$Z_n=0$
, we call n a regeneration time. Our aim is to provide the necessary and sufficient conditions to decide whether the process has finitely or infinitely many regeneration times. We should note that for Galton–Watson processes or BPREs with immigration, if the process has one regeneration time it must have infinitely many regeneration times. In other words, it will never happen that such a process owns finitely many regeneration times if there are any due to the time homogeneity.
Our motivation originates from two aspects, the regeneration structure of BPREs and the cutpoints of random walks in varying environments. On one hand, in [Reference Kesten, Kozlov and Spitzer16], in order to study the stable limit law of random walks in random environments, a regeneration structure of a single-type BPRE was constructed, and the tail probabilities of the regeneration time and the number of total progeny before the first regeneration time were estimated. Related problems in the multitype case of this regeneration structure can be found in [Reference Key17, Reference Roitershtein23, Reference Wang25]. Along these lines, it is natural for us to consider the number of regeneration times for BPVEs. On the other hand, in [Reference Csáki, Földes and Révész6, Reference James, Lyons and Peres12, Reference Lorentzen20, Reference Wang26], a class of questions related to the cutpoints of random walks in varying environments was considered. We find that the regeneration structures for BPVEs and the excursions between successive cutpoints share some similarities, so we aim to study the regeneration of BPVEs in this paper.
We currently treat only the regeneration times of one-type and two-type BPVEs with linear fractional offspring distributions. Basically, the one-type case is much easier, and the two-type case is very complicated. But the ideas in studying the two models are similar, so we omit the proofs of the one-type case. The difficulty in studying the two-type case arises from the fact that the probability that n is a regeneration time is written in terms of the product of
$2\times2$
nonnegative matrices, which are hard to estimate. To overcome this difficulty, we need some delicate analyses among the spectral radii, the tails of continued fractions, and the product of nonnegative matrices. These analyses lead to some interesting results in these fields, which may be of independent interest.
In Section 2, we precisely define the models and state the main results. In Section 3, we prove some properties of continued fractions that are useful for the proof of the main result. In Section 4, we focus on the proof of the main result. In Section 5, we construct some concrete examples that explicitly exhibit the new phenomena that arise from the existence of so-called varying environments.
2. Models and main results
Linear-fractional branching processes are of special interest as the iterations of their generating functions are again linear-fractional functions, allowing for explicit calculations of various entities of importance [Reference Athreya and Ney2, pp. 7--8]. Such explicit results illuminate the known asymptotic results concerning more general branching processes, and, on the other hand, may bring insight into less-investigated aspects of the theory of branching processes. So, in order to discuss the properties of the generation time of branching processes in varying environments (one-type and two-type), we study linear-fractional branching processes first.
2.1. One-type case
For
$k\ge1$
, suppose
$0<p_k\le \frac12$
,
$q_k>0$
are numbers such that
$p_k+q_k=1$
and
\begin{align*}f_k(s)=\frac{p_k}{1-q_ks}, \quad s\in [0,1].\end{align*}
Let
$\{Z_n\}_{n\ge0}$
be a Markov chain such that
$Z_0=0$
and
$E(s^{Z_n}\mid Z_0,\ldots,Z_{n-1}) = [f_{n}(s)]^{1+Z_{n-1}}$
,
$n\ge1$
. Clearly,
$\{Z_n\}_{n\ge0}$
forms a branching process in varying environments with exactly one immigrant in each generation. We now define the regeneration time with which we are concerned.
Definition 1. Let
$C=\{n\ge0\colon Z_n=0\}$
, and for
$k\ge1$
let
$C_k=\{n\colon n+i\in C, 0\le i\le k-1\}$
. If
$n\in C$
, n is called the regeneration time of the process
$\{Z_n\}$
. If
$n\in C_k$
, we call n a k-strong regeneration time of the process
$\{Z_n\}$
.
Remark 1. Here, we slightly abuse the term ‘regeneration time’. Notice that if
$R\in C$
then
$Z_R=0$
, i.e. the process temporarily dies out. But the process may get regenerated at time R, since there is an immigrant entering into the system at time R that may give birth to a number of individuals. In this point of view, we call R a regeneration time. We emphasize that the regeneration times here are different from the classical regeneration times of regenerative processes. In the literature (see, e.g., [Reference Sigman and Wolff24]), for a stochastic process
$X= \{X(t)\}_{t \ge 0}$
, if there is a random variable
$R > 0$
such that
$\{X(t + R)\}_{t \ge 0}$
is independent of
$\{\{X(t)\}_{t < R},R\}$
, and
$\{X(t + R) \}_{t \ge 0}$
equals
$\{X(t)\}_{t \ge 0}$
in distribution, then X is call a regenerative process and R is called a regeneration time. In our setting, for a regeneration time R, due to the existence of the so-called varying environments the distribution of
$\{Z_{R+n}\}_{n\ge 0}$
differs from that of
$\{Z_n\}_{n\ge 0}$
.
For
$k\ge1$
, let
$m_k=f^{\prime}_k(1)={q_k}/{p_k}$
. For
$n\ge k\ge 1$
, set
$D(k,n)\,:\!=\,1+\sum_{j=k}^n m_j\cdots m_n$
and write, for simplicity,
$D(n)\equiv D(1,n)$
.
The following theorem provides a criterion for the finiteness of the number of regeneration times.
Theorem 1. Suppose that, for some
$\varepsilon>0$
,
$\varepsilon <p_n\le \frac12$
,
$n\ge 1$
. Let D(n),
$n\ge1$
, be as defined above. If
\begin{align*}\sum_{n=2}^\infty\frac{1}{D(n)\log n}<\infty,\end{align*}
then
$\{Z_n\}$
has at most finitely many regeneration times, almost surely. If there exists some
$\delta>0$
such that
$D(n)\le \delta n\log n$
for n large enough and
\begin{align*}\sum_{n=2}^\infty\frac{1}{D(n)\log n}=\infty,\end{align*}
then
$\{Z_n\}$
has infinitely many k-strong regeneration times, almost surely.
2.2. Two-type case
Suppose
$a_k,b_k,d_k,\theta_k$
,
$k\ge 1$
, are positive real numbers and set
\begin{equation*} M_k \,:\!=\, \begin{bmatrix} a_k & \quad b_k \\ d_k & \quad \theta_k \end{bmatrix}, \quad k\ge 1.\end{equation*}
For
$n\ge1$
and
$ \mathbf{s}=(s_1,s_2)^\top\in [0,1]\times [0,1]$
, let
\begin{equation} \mathbf{f}_n(\mathbf{s}) = \big(f_n^{(1)}(\mathbf{s}),f_n^{(2)}(\mathbf{s})\big)^{\top} = \mathbf{1} - \frac{M_n(\mathbf{1} - \mathbf{s})}{1 + \mathbf{e}_1^{\top}M_n(\mathbf{1} - \mathbf{s})},\end{equation}
which is known as the probability-generating function of a linear-fractional distribution. Here and in what follows,
$a^{\top}$
denotes the transpose of the vector a,
$\mathbf{e}_1=(1,0)^{\top}$
,
$\mathbf{e}_2=(0,1)^{\top}$
, and
$\mathbf{1}={\mathbf{e}_1}+{\mathbf{e}_2}=(1,1)^{\top}$
.
Suppose
$\mathbf{Z}_n=(Z_{n,1},Z_{n,2})^{\top}$
,
$n\ge 0$
, is a two-type branching process with immigration satisfying
$E\big(s^{\mathbf{Z}_{n}}\mid\mathbf{Z}_0,\ldots,\mathbf{Z}_{n-1}\big)=\mathbf{f}_n(\mathbf{s})^{\mathbf{Z}_{n-1}+{\mathbf{e}_1}}$
for all
$n\ge1$
. Here,
$\mathbf{f}_n(\mathbf{s})^{\mathbf{Z}_{n-1}+{\mathbf{e}_1}}=\big[{f}^{(1)}_n(\mathbf{s})\big]^{Z_{n-1,1}+1}\big[{f}^{(2)}_n(\mathbf{s})\big]^{Z_{n-1,2}}$
.
We now define the regeneration times and the k-strong regeneration times of the two-type process
$\{\mathbf{Z}_n\}$
in a similar fashion to the one-type case.
Definition 2. Let
$C=\{n\ge0\colon\mathbf{Z}_n=(0,0)^\top\}$
and, for
$k\ge1$
, let
$C_k=\{n\colon n+i\in C, 0\le i\le k-1\}$
. If
$n\in C$
, we call n a regeneration time of the process
$\{\mathbf{Z}_n\}$
. If
$n\in C_k$
, we call n a k-strong regeneration time of the process
$\{\mathbf{Z}_n\}$
.
To study the regeneration times of the two-type branching process, we need the following condition on the sequences
$a_k,b_k,d_k,\theta_k$
,
$k\ge1$
.
Assumption 1. Suppose that
\begin{equation} \sum_{k=2}^\infty|a_k-a_{k-1}|+| b_k- b_{k-1}|+| d_k- d_{k-1}|+|\theta_{k}-\theta_{k-1}|<\infty, \end{equation}
and
$a_k\rightarrow a$
,
$b_k\rightarrow b$
,
$d_k\rightarrow d$
,
$\theta_k\rightarrow\theta$
as
$k\rightarrow\infty$
, where
$b,d>0$
and
$a,\theta\ge0$
are certain numbers such that
$a+\theta>0$
and
$bd-a\theta\neq0$
.
In what follows, for a matrix M we denote by
$\varrho(M)$
its spectral radius (the largest eigenvalue). For
$n\ge m\ge1$
, we set
\begin{equation} L(m,n)=1+\sum_{j=m}^{n}\prod_{i=j}^{n}\varrho(M_i), \end{equation}
and write L(1,n) as L(n) for simplicity. In the two-type case, we have the following criteria.
Theorem 2. Assume Assumption 1 holds, and that
$\varrho(M_k)\ge 1$
for all
$k\ge1$
.
(i) If
\begin{align*}\sum_{n=2}^\infty\frac{1}{L(n)\log n}<\infty\end{align*}
then
$\{\mathbf{Z}_n\}$
has at most finitely many regeneration times, almost surely.
(ii) If there exists some
$\delta>0$
such that
$L(n)\le \delta n\log n$
for n large enough and
\begin{align*}\sum_{n=2}^\infty\frac{1}{L(n)\log n}=\infty,\end{align*}
then
$\{\mathbf{Z}_n\}$
has infinitely many k-strong regeneration times, almost surely.
Remark 2. For branching processes with general offspring distributions, the probability-generating function of the population size cannot be computed explicitly in general, but, as seen in [Reference Agresti1, Reference Kersting and Vatutin15], it can be controlled from below and above by that of a branching process with linear-fractional offspring distributions. Based on this observation, our results may be generalized to branching processes with general offspring distributions.
Remark 3. We give some explanation on Assumption 1. The assumption in (2) allows us to show that
\begin{align*}\zeta \leq \frac{\varrho(M_{m} \cdots M_{n})}{\varrho(M_{m})\cdots\varrho(M_{n})} \leq \gamma\end{align*}
for some universal constant
$0<\zeta<\gamma<\infty$
, i.e. the spectral radius of the product of matrices can be uniformly bounded from below and above by the product of the spectral radii of these matrices; see Lemma 5. Such a result plays an important role in proving Theorem 2.
3. Products of
$2\times2$
matrices and continued fractions
The probability-generating function of
$\mathbf{Z}_n$
can be written in terms of the products of the mean offspring matrices, which are hard to compute directly since they are inhomogeneous. But it is known that the products of
$2\times2$
matrices can be written in terms of the products of the tails of certain continued fractions.
In this section, we focus on how to estimate the products of the mean offspring matrices by means of continued fractions. To begin with, we introduce some new matrices related to
$M_k$
,
$k\ge1$
. For
$k\ge1$
, set
\begin{equation*} A_k \,:\!=\, \begin{pmatrix} \tilde{a}_k & \quad \tilde{b}_k \\[3pt] \tilde{d}_k & \quad 0 \\ \end{pmatrix}, \quad \tilde{a}_k = a_k+\frac{b_k\theta_{k+1}}{b_{k+1}},\ \tilde{b}_k = b_k,\ \tilde{d}_k = d_k-\frac{a_k\theta_k}{b_k}, \end{equation*}
and write
\begin{align*}\Lambda_k \,:\!=\, \begin{pmatrix} 1 & \quad 0 \\[4pt] \theta_k/b_k & \quad 1 \\\end{pmatrix}. \end{align*}
Then, for
$n\ge k\ge1$
, we have
\begin{equation} A_k = \Lambda_k^{-1}M_k\Lambda_{k+1}, \qquad \mathbf{e}_1^{\top}\prod\limits_{i=k}^{n}M_i\mathbf{1} = \mathbf{e}_1^{\top}\prod\limits_{i=k}^{n}A_i(1,1-\theta_{n+1}/b_{n+1})^{\top},\end{equation}
and
$A_k\cdots A_n=\Lambda_k^{-1}M_k\cdots M_n\Lambda_{n+1}$
,
$n\ge k\ge 1$
. Since
$a_k$
,
$b_k$
,
$d_k$
, and
$\theta_k$
are all positive numbers, we have
\begin{alignat}{2} \mathbf{e}_1^{\top} A_k\cdots A_n \mathbf{e}_1 & = \mathbf{e}_1^{\top} M_k\cdots M_n(1,\theta_{n+1}/b_{n+1})^{\top}>0, & n & > k\ge1, \\ \mathbf{e}_1^{\top} A_k\cdots A_n \mathbf{e}_2 & = \mathbf{e}_1^{\top} M_k\cdots M_n\mathbf{e}_2>0, & n & > k\ge1, \nonumber \\ \mathbf{e}_2^{\top} A_k\cdots A_n \mathbf{e}_1 & = ({-}{\theta_k}/{b_k},1)M_k\cdots M_n(1,\theta_{n+1}/b_{n+1})^{\top}, \quad & n & \ge k\ge1. \nonumber \end{alignat}
Under Assumption 1, we have
\begin{equation*} \lim_{k\rightarrow\infty}M_k = M \,:\!=\, \begin{pmatrix} a & \quad b \\[3pt] d & \quad \theta \end{pmatrix},\qquad \lim_{k\rightarrow\infty}A_k = A \,:\!=\, \begin{pmatrix} a+\theta & \quad b \\[3pt] d-a\theta/b & \quad 0 \end{pmatrix},\end{equation*}
whose spectral radii are
\begin{align*} \varrho \,:\!=\, \varrho(M) = \varrho(A) & = \frac{a+\theta+\sqrt{(a+\theta)^2+4(bd- a\theta)}}{2}, \\ \varrho_1 \,:\!=\, \varrho_1(M) = \varrho_1(A) & = \frac{a+\theta-\sqrt{(a+\theta)^2+4(bd-a\theta)}}{2}. \end{align*}
Next, we introduce some basics on continued fractions. Let
$\beta_k,\alpha_k,k\ge 1$
be certain real numbers. For
$1\le k\le n$
, we denote by
\begin{equation} \xi_{k,n} \equiv \frac{\beta_k}{\alpha_k}\genfrac{}{}{0pt}{}{}{+} \frac{\beta_{k+1}}{\alpha_{k+1}}\genfrac{}{}{0pt}{}{}{+\cdots+} \frac{\beta_n}{\alpha_n} \,:\!=\, \dfrac{\beta_k}{\alpha_k+\dfrac{\beta_{k+1}}{\alpha_{k+1}+_{\ddots_{\textstyle+\frac{\textstyle\beta_{n}}{\textstyle\alpha_{n}}}}}}\end{equation}
the
$(n-k+1)$
th approximant of a continued fraction, and
\begin{equation} \xi_k \,:\!=\, \frac{\beta_{k}}{\alpha_{k}}\genfrac{}{}{0pt}{}{}{+} \frac{\beta_{k+1}}{\alpha_{k+1}}\genfrac{}{}{0pt}{}{}{+} \frac{\beta_{k+2}}{\alpha_{k+2}}\genfrac{}{}{0pt}{}{}{+\cdots}.\end{equation}
If
$\lim_{n\rightarrow\infty}\xi_{k,n}$
exists, we say that the continued fraction
$\xi_k$
is convergent and its value is defined as
$\lim_{n\rightarrow\infty}\xi_{k,n}$
. We call
$\xi_k$
,
$k\ge1$
, in (7) the tails, and
\begin{align*}h_k \,:\!=\, \frac{\beta_k}{\alpha_{k-1}}\genfrac{}{}{0pt}{}{}{+}\frac{\beta_{k-1}}{\alpha_{k-2}}\genfrac{}{}{0pt}{}{}{+\cdots+}\frac{\beta_2}{\alpha_1},\end{align*}
$k \ge2$
, the critical tails of the continued fraction
\begin{align*}{\frac{\beta_{1}}{\alpha_{1}}}\genfrac{}{}{0pt}{}{}{+}\frac{\beta_{2}}{\alpha_{2 }}\genfrac{}{}{0pt}{}{}{+\cdots},\end{align*}
respectively.
The following lemma gives the convergence of the tails and the critical tails of the continued fractions.
Lemma 1. If
$\lim_{n\rightarrow\infty}\alpha_n=\alpha\ne0$
,
$\lim_{n\rightarrow\infty}\beta_n=\beta$
, and
$\alpha^2+4\beta\ge0$
, then, for any
$k\ge1$
,
$\lim_{n\rightarrow\infty}\xi_{k,n}$
exists and, furthermore,
\begin{equation*} \lim_{k\rightarrow\infty}h_k = \lim_{k\rightarrow\infty}\xi_k = \frac{\alpha}{2}\Big(\sqrt{1+4\beta/\alpha^2}-1\Big). \end{equation*}
The proof of Lemma 1 can be found in many references. We refer the reader to [Reference Lorentzen20] (see the discussion between (4.1) and (4.2) on p. 81 therein).
For
$n\ge k\ge1$
, let
\begin{equation} y_{k,n} = \mathbf{e}_1^{\top}\prod\limits_{i=k}^{n}A_i\mathbf{e}_1, \qquad \xi_{k,n} = \frac{y_{k+1,n}}{y_{k,n}},\end{equation}
where we stipulate that
$y_{n+1,n}=1$
. Then we have
\begin{equation} \mathbf{e}_1^{\top}\prod\limits_{i=k}^{n}A_i\mathbf{e}_1 = \xi_{k,n}^{-1}\cdots\xi_{n,n}^{-1}, \quad n\ge k\ge1.\end{equation}
Lemma 2. For
$1\le k\le n$
,
$\xi_{k,n}$
defined in (8) coincides with the one in (6) with
$\beta_k=\tilde b_k^{-1}\tilde d_{k+1}^{-1}$
and
$\alpha_k=\tilde a_k\tilde b_k^{-1}\tilde d_{k+1}^{-1}$
.
Proof. Clearly,
\begin{align*} \xi_{n,n} = \frac{1}{y_{n,n}} = \frac{1}{\tilde a_n} = \frac{\tilde b_n^{-1}\tilde d_{n+1}^{-1}}{\tilde a_n\tilde b_n^{-1}\tilde d_{n+1}^{-1}} = \frac{\beta_n}{\alpha_n}. \end{align*}
For
$1\le k< n$
, note that
\begin{align*} \xi_{k,n} = \frac{y_{k+1,n}}{y_{k,n}} = \frac{\mathbf{e}_1^{\top} A_{k+1}\cdots A_{n}\mathbf{e}_1}{\mathbf{e}_1^{\top} A_k\cdots A_{n}\mathbf{e}_1} & = \frac{\mathbf{e}_1^{\top} A_{k+1}\cdots A_{n}\mathbf{e}_1} {\big(\tilde a_k\mathbf{e}_1^{\top}+\tilde b_k\mathbf{e}_2^{\top}\big) A_{k+1}\cdots A_{n}\mathbf{e}_1} \\ & = \frac{1}{\tilde a_k+\tilde b_k\dfrac{\mathbf{e}_2^{\top} A_{k+1}\cdots A_{n}\mathbf{e}_1} {\mathbf{e}_1^{\top} A_{k+1}\cdots A_{n}\mathbf{e}_1}} \\ & = \frac{1}{\tilde a_k+\tilde b_k\tilde d_{k+1}\dfrac{\mathbf{e}_1^{\top} A_{k+2}\cdots A_{n}\mathbf{e}_1} {\mathbf{e}_1^{\top} A_{k+1}\cdots A_{n}\mathbf{e}_1}} \\ & = \frac{\tilde b_k^{-1}\tilde d_{k+1}^{-1}}{\tilde a_k\tilde b_k^{-1}\tilde d_{k+1}^{-1}+\xi_{k+1,n}} = \frac{\beta_k}{\alpha_k+\xi_{k+1,n}}. \end{align*}
We come to the conclusion that the lemma is true by iterating this equation.
In the remainder of this section, we always assume that Assumption 1 holds, and
$\xi_k,\xi_{k,n}$
,
$n\ge k\ge1$
, are as defined in (6) and (7) with
$\beta_k=\tilde b_k^{-1}\tilde d_{k+1}^{-1}$
and
$\alpha_k=\tilde a_k\tilde b_k^{-1}\tilde d_{k+1}^{-1}$
. Since
\begin{align*} \lim_{k\rightarrow\infty}\beta_k \,=\!:\, \beta = (bd-a\theta)^{-1}\ne 0, \quad\!\!\! \lim_{k\rightarrow\infty}\alpha_k \,=\!:\, \alpha = \frac{a+\theta}{bd-a\theta}\ne 0, \quad\!\!\! \alpha^2+4\beta = \frac{(a-\theta)^2+4bd}{(bd-a\theta)^2}>0,\end{align*}
it follows from Lemma 1 that
\begin{equation} \lim_{n\rightarrow\infty}\xi_{k,n} = \xi_k, \qquad \lim_{k\rightarrow\infty}\xi_k \,=\!:\, \xi = \frac{\alpha}{2}\Big(\sqrt{1+4\beta/\alpha^2}-1\Big) = \varrho^{-1} > 0.\end{equation}
Moreover, consulting (5), (8), and the relationship
$\xi_k={\beta_k}/({\alpha_k+\xi_{k+1}})$
, we have
\begin{equation} \xi_k>0,\ \xi_{k,n}>0 \quad \text{for all } n\ge k\ge1.\end{equation}
The relationship between the entries
$\xi_{k+1}^{-1}\cdots\xi_{k+n}^{-1}$
and
$A_{k+1}\cdots A_{k+n}$
, which plays an important role in the proof of our main result, was established in [Reference Wang28, Theorem 2]. For convenience, we state it here.
Proposition 1. ([Reference Wang28, Theorem 2].) Let
$\xi_k$
be as in (7) for all
$k \ge 1$
. Suppose
$M_k\rightarrow M$
,
$a+\theta\neq 0$
,
$b\neq 0$
, and
$bd\neq a\theta$
. Then there exists a
$k_0>0$
such that, for
$k\ge k_0$
and
$i,j=1,2$
, we have
\begin{equation} \lim_{n\rightarrow\infty}\frac{e_i^{\top}A_{k+1}\cdots A_{k+n}e_j}{\xi_{k+1}^{-1}\cdots\xi_{k+n}^{-1}}=\varphi(i,j,k), \end{equation}
where the convergence is uniform in k, and
\begin{alignat*}{2} & \varphi(1) \,:\!=\, \varphi(1,1,k) = \frac{\varrho}{\varrho-\varrho_1}, \qquad & & \varphi(2) \,:\!=\, \varphi(1,2,k) = \frac{b}{\varrho-\varrho_1}, \\ & \varphi(2,1,k) = \frac{\rho}{\varrho-\varrho_1}\frac{\tilde{d}_{k+1}}{\xi^{-1}_{k+1}}, & & \varphi(2,2,k) = \frac{b}{\varrho-\varrho_1}\frac{\tilde{d}_{k+1}}{\xi^{-1}_{k+1}}. \end{alignat*}
Furthermore, if
$\rho\ge1$
then, for
$k\ge k_0$
, with the above
$i,j=1,2$
,
\begin{equation} \lim_{n\rightarrow\infty}\frac{\sum_{s=1}^{n+1}e_i^{\top}A_{k+s}\cdots A_{k+n}e_j} {\sum_{s=1}^{n+1}\xi_{k+s}^{-1}\cdots\xi_{k+n}^{-1}} = \varphi(i,j,k), \end{equation}
where the convergence is uniform in k.
4. Proof of the main result
Keep in mind that in what follows, unless otherwise specfied, c (with or without an index) is a positive constant whose value may be different from line to line.
For
$n\ge k\ge1$
, write
$\mathbf{f}_{k,n}(\mathbf{s})\,:\!=\,{\mathbf{f}_k(\mathbf{f}_{k+1}\cdots(\mathbf{f}_n(\mathbf{s}))\cdots\!)}$
. By iterating (1), we see that
\begin{equation*} \mathbf{f}_{k,n}(\mathbf{s}) = \mathbf{1} - \frac{M_k\cdots M_n(\mathbf{1}-\mathbf{s})} {1+\sum_{j=k}^n\mathbf{e}_1^{\top} M_j\cdots M_n (\mathbf{1}-\mathbf{s})}.\end{equation*}
As a consequence,
\begin{equation*} E\big(\mathbf{s}^{\mathbf{Z}_n}\mid\mathbf{Z}_0=0\big) = \prod_{k=1}^n\mathbf{e}_1^{\top}f_{k,n}(\mathbf{s}) = \frac1{1+\sum_{j=1}^n\mathbf{e}_1^{\top}M_j\cdots M_n(\mathbf{1}-\mathbf{s})},\end{equation*}
which implies that
\begin{equation} P(\mathbf{Z}_n=0\mid\mathbf{Z}_0=0) = \frac1{1+\sum_{j=1}^n\mathbf{e}_1^{\top}M_j\cdots M_n\mathbf{1}}.\end{equation}
Let
$G(k,n)\,:\!=\,1+\sum_{j=k}^n\mathbf{e}_1^{\top}M_j\cdots M_n\mathbf1$
,
$n\ge k\ge1.$
In order to study the regeneration times of the process
$\{\mathbf{Z}_n\}$
, we should estimate G(k,n). With Proposition 1 in hand, and using some other estimates, we can control G(k,n) by the entries
$\sum_{j=k}^{n}\varrho(M_j)\cdots\varrho(M_n)$
. We state the methods of the estimates in the following lemmas.
Lemma 3. Assume Assumption 1 holds, and
$\varrho(M_k)\ge 1$
. Then, for
$\varepsilon>0$
, there exist constants
$k_0$
and N such that, for all
$k> k_0$
and
$n-k> N$
,
\begin{equation} \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) - \varepsilon \le \frac{G(k,n)}{1+\sum_{j=k}^{n}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} \le \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) + \varepsilon, \end{equation}
where
$\varphi(1)$
and
$\varphi(2)$
are as defined in Proposition 1. Furthermore, for
$n>N$
,
\begin{equation} \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) - \varepsilon \le \frac{G(1,n)}{1+\sum_{j=1}^{n}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} \le \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) + \varepsilon. \end{equation}
Proof. In view of (4), we have
\begin{equation} G(k,n) = 1 + \sum_{j=k}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Bigg) + \bigg(1-\frac{\theta_{n+1}}{b_{n+1}}\bigg)\sum_{j=k}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_2\Bigg) \end{equation}
for all
$n\ge k\ge 1$
. Assumption 1 means that all the conditions of Proposition 1 are fulfilled. Then, in view of (13), we can see that for each
$\varepsilon>0$
there exists a constant
$N^{\prime}>0$
such that, for all
$n>N^{\prime}$
and
$k\ge k_0$
,
\begin{equation*} \varphi(l) - \varepsilon < \frac{\sum_{s=1}^{n+1}\mathbf{e}_1^{\top}A_{k+s}\cdots A_{k+n}\mathbf{e}_l} {\sum_{s=1}^{n+1}\xi_{k+s}^{-1}\cdots\xi_{k+n}^{-1}} < \varphi(l) + \varepsilon, \quad l=1,2. \end{equation*}
Thus, for
$k>k_0$
and
$n-k\ge N^{\prime}$
,
\begin{equation} \Bigg|\frac{\sum_{j=k}^{n+1}\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_l} {\sum_{j=k}^{n+1}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} - \varphi(l)\Bigg| = \Bigg|\frac{\sum_{s=1}^{n-k+2}\mathbf{e}_1^{\top}\prod_{i=(k-1)+s}^{(k-1)+n-(k-1)}A_i\mathbf{e}_l} {\sum_{s=1}^{n-k+2}\xi_{(k-1)+s}^{-1}\cdots\xi_{n}^{-1}} - \varphi(l)\Bigg| < \varepsilon \end{equation}
for
$l=1,2$
. Noticing that
$1-({\theta_{n+1}}/{b_{n+1}})\rightarrow1-({\theta}/{b})$
as
$n\rightarrow\infty$
, we conclude that (15) is true.
Now we turn to (16). For the above
$\varepsilon$
, it follows from (12) that there exist constants
$k_0$
and N” such that, for all
$k> k_0$
and
$n-k\ge N^{\prime\prime}$
,
\begin{equation} \bigg|\frac{e_1^{\top}A_k\cdots A_n e_l}{\xi_k^{-1}\cdots\xi_n^{-1}} - \varphi(l)\bigg| < \varepsilon, \quad l=1,2. \end{equation}
Taking (9) into account, we rewrite
\begin{align} \sum_{j=1}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Bigg) & = \sum_{j=1}^{k_0}\xi_{j,n}^{-1}\cdots\xi_{n,n}^{-1} + \sum_{j=k_0+1}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Bigg) \nonumber \\ & = \xi_{k_0+1,n}^{-1}\cdots\xi_{n,n}^{-1}\sum_{j=1}^{k_0}\xi_{j,n}^{-1}\cdots\xi_{k_0,n}^{-1} + \sum_{j=k_0+1}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Bigg) \nonumber \\ & = e_1^{\top}A_{k_0+1}\cdots A_n e_1\sum_{j=1}^{k_0}\xi_{j,n}^{-1}\cdots\xi_{k_0,n}^{-1} + \sum_{j=k_0}^n\Bigg(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Bigg). \end{align}
It follows from (10) that
\begin{equation} \lim_{n\rightarrow\infty}\frac{\sum_{j=1}^{k_0}\xi_{j,n}^{-1}\cdots\xi_{k_0,n}^{-1}} {\sum_{j=1}^{k_0+1}\xi_{j}^{-1}\cdots\xi_{k_0}^{-1}} = 1. \end{equation}
Then, using (18), (19), and (21) to estimate (20), we get, for
$n>\max\{N^{\prime}+k_0,N^{\prime\prime}+k_0\}$
,
\begin{equation} \Bigg|\frac{\sum_{j=1}^n\Big(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_1\Big)} {\sum_{j=1}^{n}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} - \varphi(1)\Bigg| < c\varepsilon. \end{equation}
We can rewrite the second summand in (17) as
\begin{align*} \frac{\sum_{j=1}^n\Big(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_2\Big)} {\sum_{j=1}^{n}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} = \frac{\sum_{j=1}^n\big(\mathbf{e}_1^{\top}A_j\cdots A_{n-1}\mathbf{e}_1\big)} {\sum_{j=1}^{n}\xi_{j}^{-1}\cdots\xi_{n-1}^{-1}}\frac{\tilde{b}_n}{\xi_n^{-1}}. \end{align*}
Then, taking the fact
$\varphi(1)\cdot\lim_{n\rightarrow\infty}{\tilde{b}_n}/{\xi_n^{-1}}=\varphi(2)$
and (22) into consideration, we get that there exists a constant K such that, for
$n>K$
,
\begin{equation} \Bigg|\frac{\sum_{j=1}^n\Big(\mathbf{e}_1^{\top}\prod_{i=j}^{n}A_i\mathbf{e}_2\Big)} {\sum_{j=1}^{n}\xi_{j}^{-1}\cdots\xi_{n}^{-1}} - \varphi(2)\Bigg| < c\varepsilon. \end{equation}
Therefore, taking (22), (23), and (17) together, we see that (16) is true.
Lemma 4. Suppose that Assumption 1 holds. Then there are constants
$0<c_1<c_2<\infty$
and numbers
$N_1,N_2$
, which may depend on
$c_1$
and
$c_2$
, such that, for all
$n-m>N_1$
,
$m>N_2$
,
\begin{align*}c_1<\frac{\mathbf{e}_1 A_m\cdots A_n\mathbf{e}_1^\top}{\varrho(M_m)\cdots\varrho(M_n)}<c_2.\end{align*}
The following is [Reference Wang27, Lemma 4]. For convenience, we state it here.
Lemma 5. ([Reference Wang27, Lemma 4].) Suppose that Assumption 1 holds. Then, for
$n\ge m\ge1$
,
\begin{equation*} \zeta \leq \frac {\varrho(M_{m} \cdots M_{n})}{\varrho(M_{m}) \cdots \varrho(M_{n})}\leq \gamma \end{equation*}
for some constants
$0<\zeta<\gamma<\infty$
independent of m and n.
Lemma 6. Suppose that Assumption 1 holds. Then there exist constants
$c_3>0$
,
$c_4>0$
and numbers
$N_1,N_3>0$
, which may depend on
$c_3$
and
$c_4$
, such that, for all
$n-m\ge N_1$
and
$m>N_3$
,
\begin{equation*} c_3<\frac{\varrho(A_{m} \cdots A_{n})}{\mathbf{e}_1 A_{m} \cdots A_{n} \mathbf{e}_1^\top}<c_4. \end{equation*}
The proof of this lemma is similar to that of [Reference Wang27, Lemma 5]; we just point out the differences.
Proof of Lemma 6. We write
\begin{align*} A_{m,n} \,:\!=\, A_{m} \cdots A_n = \left(\begin{array}{c@{\quad}c} A_{m,n}(11) & A_{m,n}(12) \\[5pt] A_{m,n}(21) & A_{m,n}(22) \end{array}\right), \quad n\ge m\ge 1. \end{align*}
From the proof of [Reference Wang27, Lemma 5], we get that
\begin{equation} \varrho(A_{m,n}) = \frac{A_{m,n}(11)+A_{m,n}(22)}2 + \frac{\sqrt{(A_{m,n}(11)+A_{m,n}(22))^2+4P_{m,n}}}2, \end{equation}
where
$P_{m,n}=A_{m,n}(12)A_{m,n}(21)-A_{m,n}(11)A_{m,n}(22)$
.
Applying Proposition 1, we have that for
$\varepsilon>0$
there exist
$k_0>0$
and
$N_1>0$
such that, for all
$m>k_0$
,
$n-m\ge N_1$
,
\begin{equation} \bigg|\frac{A_{m,n}(ij)}{A_{m,n}(11)} - \frac{\varphi(i,j,m-1)}{\varphi(1,1,m-1)}\bigg| < \varepsilon, \quad i,j=1,2. \end{equation}
It follows from Lemma 1 that
$\lim_{m\rightarrow\infty}\xi_m=-{\varrho_1}/({bd-a\theta})$
. As a result,
\begin{equation*} \lim_{m\rightarrow\infty}\bigg[1+\frac{\varphi(2,2,m-1)}{\varphi(1,1,m-1)}\bigg] = \lim_{m\rightarrow\infty}\bigg[1+\bigg(\frac{\theta_m}{b_m}-\xi_m\frac{a_m\theta_m-d_mb_m}{b_m}\bigg) \frac{b}{\varrho-\theta}\bigg] = \frac{\varrho-\varrho_1}{\varrho-\theta} > 0. \end{equation*}
On the other hand, note that
\begin{equation} R_m\,:\!=\,{\varphi(1,2,m-1)}{\varphi(2,1,m-1)} - \varphi(1,1,m-1){\varphi(2,2,m-1)} = 0. \end{equation}
We thus see that
\begin{align*} \lim_{m\rightarrow\infty}V_m & \,:\!=\, \lim_{m\rightarrow\infty}\bigg[\frac{\varphi(1,1,m-1)+\varphi(2,2,m-1)}{2\varphi(1,1,m-1)} + \frac{\sqrt{(\varphi(1,1,m-1)+\varphi(2,2,m-1))^2+4R_m}}{2\varphi(1,1,m-1)}\bigg] \\ & = \frac{\varrho-\varrho_1}{\varrho-\theta} > 0. \end{align*}
Consequently, there exist constants
$c^{\prime}_3>0$
,
$c^{\prime}_4>0$
, and
$k_1>0$
such that, for
$m>k_1$
,
\begin{equation} c^{\prime}_3<V_m<c^{\prime}_4. \end{equation}
Taking (25) and (24) into consideration, we have that, for all
$m>k_0$
and
$n-m\ge N_1$
, there exists a constant c’ such that
\begin{align*} -c^{\prime}\varepsilon < \frac{\varrho(A_{m} \cdots A_{n})}{\mathbf{e}_1 A_{m} \cdots A_{n}\mathbf{e}_1^\top} - V_m < c^{\prime}\varepsilon. \end{align*}
Therefore, in view of (27), we conclude that the lemma is true.
Lemma 7. Suppose Assumption 1 is fulfilled. Then there exist constants
$c_5<c_6<\infty$
and numbers
$N_1,N_4$
such that, for all
$n-m>N_1$
,
$m>N_4$
,
\begin{align*}c_5\varrho(M_m\cdots M_n)<{\varrho(A_m\cdots A_n)}<c_6{\varrho(M_m\cdots M_n)}.\end{align*}
Proof. Let
$A_{m,n}$
and
$P_{m,n}$
be as defined in Lemma 6. Define
\begin{align*}Q_{m,n}\,:\!=\,A_{m,n}(11)+A_{m,n}(22)+A_{m,n}(12)\bigg(\frac{\theta_m}{b_m}-\frac{\theta_{n+1}}{b_{n+1}}\bigg).\end{align*}
By some easy calculation, we have
$\varrho(M_m\cdots M_n)=\frac12(Q_{m,n}+\sqrt{Q_{m,n}^2+4P_{m,n}})$
.
Note that
\begin{align*} \lim_{n\rightarrow\infty}\lim_{m\rightarrow\infty}\bigg[1 + \frac{\varphi(2,2,k)}{\varphi(1,1,k)} + \frac{\varphi(1,2,k)}{\varphi(1,1,k)}\bigg(\frac{\theta_m}{b_m}-\frac{\theta_{n+1}}{b_{n+1}}\bigg)\bigg] = \frac{\varrho-\varrho_1}{\varrho-\theta}>0. \end{align*}
Thus, in view of (25) we get that there exist constants
$0<c^{\prime}_5<c^{\prime}_6<\infty$
and
$N_1>0,N^{\prime}_3>k_0$
such that. for all
$m>N^{\prime}_3, n-m>N_1$
,
\begin{equation} c^{\prime}_5<\frac{Q_{k,m}}{A_{m,n}(11)}<c^{\prime}_6. \end{equation}
Consulting (25) and (26), we have that there exists a constant
$c^{\prime}>0$
such that, for all
$n-m>N_1$
and
$m>k_0$
,
\begin{equation} -c^{\prime}\varepsilon<\frac{P_{m,n}}{A_{m,n}(11)}<c^{\prime}\varepsilon. \end{equation}
Taking (28) and (29) into account, we get that there exist constants
$0<c^{\prime\prime}_5<c^{\prime\prime}_6<\infty$
such that, for all
$m>N^{\prime}_3$
and
$ n-m>N_1$
,
\begin{align*}c^{\prime\prime}_5<\frac{\varrho(M_n\cdots M_n)}{A_{m,n}(11)}<c^{\prime\prime}_6.\end{align*}
For
$1\le m< n$
, let L(m,n) be as in (3) and write
\begin{equation} H(m,n) = 1 + \sum_{j=m}^{n}\xi_j^{-1}\cdots\xi_n^{-1}.\end{equation}
Also, we write H(1,n) as H(n) for simplicity.
We establish the relationship between L(n) and H(n) as follows.
Lemma 8. Suppose that Assumption 1 holds. Then there exist constants
$0<c_7<c_{8}<\infty$
,
$0<c_{9}<c_{10}<\infty$
and positive integers
$N_5,N_6,N_7$
such that, for
$n-m\ge N_5$
,
$m\ge N_6$
,
\begin{equation} c_7<\frac{\xi_m\cdots \xi_n}{\varrho^{-1}(M_m)\cdots\varrho^{-1}(M_n)}<c_{8}, \end{equation}
and for
$n>N_7$
,
\begin{equation} c_{9}L(n)\le H(n)\le c_{10} L(n). \end{equation}
Proof. Clearly, taking (12) and Lemma 4 together, we get (31).
For (32), first, by (31) we have that, for
$m>N_6$
and
$n>N_5+N_6$
,
\begin{equation} c_7\sum_{j=m}^{n-N_5}\varrho(M_j)\cdots\varrho(M_n) < \sum_{j=m}^{n-N_5}\xi_j^{-1}\cdots\xi_n^{-1} < c_{8}\sum_{j=m}^{n-N_5}\varrho(M_j)\cdots \varrho(M_n). \end{equation}
For
$n>N_5+N_6$
, we rewrite
\begin{equation} H(n) = 1 + \sum_{j=1}^{N_6}\xi_j^{-1}\cdots\xi_n^{-1} + \sum_{j=N_6+1}^{n-N_5}\xi_j^{-1}\cdots\xi_n^{-1} + \sum_{j=n-N_5+1}^{n}\xi_j^{-1}\cdots\xi_n^{-1}. \end{equation}
Since
\begin{align*} \sum_{j=n-N_5+1}^{n}\xi_j^{-1}\cdots\xi_n^{-1} \rightarrow \bigg(\frac{a\theta-bd}{\rho_1}\bigg)^{N_5}+\cdots+\frac{a\theta-bd}{\rho_1}>0, \end{align*}
$\sum_{j=n-N_5+1}^{n}\varrho(M_j)\cdots\varrho(M_n)\rightarrow\varrho^{N_5}+\cdots+\varrho>0$
as
$n\rightarrow\infty$
. Then there exist constants
$0<c_{11}<c_{12}<\infty$
and
$N^{\prime}_7>0$
such that, for all
$n>N^{\prime}_7$
,
\begin{equation} c_{11}\sum_{j=n-N_5+1}^{n}\varrho(M_j)\cdots\varrho(M_n) < \sum_{j=n-N_5+1}^{n}\xi_j^{-1}\cdots\xi_n^{-1} < c_{12}\sum_{j=n-N_5+1}^{n}\varrho(M_j)\cdots\varrho(M_n). \end{equation}
We rewrite
\begin{align*} \sum_{j=1}^{N_6}\xi_j^{-1}\cdots\xi_n^{-1} & = \xi_{N_6}^{-1}\cdots\xi_n^{-1}\frac{\sum_{j=1}^{N_6}\xi_j^{-1}\cdots\xi_{N_6-1}^{-1}} {\sum_{j=1}^{N_6}\varrho(M_j)\cdots\varrho(M_{N_6-1})}\sum_{j=1}^{N_6}\varrho(M_j)\cdots\varrho(M_{N_6-1}) \\ & \,=\!:\, \xi_{N_6}^{-1}\cdots\xi_n^{-1}\sum_{j=1}^{N_6}\varrho(M_j)\cdots\varrho(M_{N_6-1})\Delta. \end{align*}
Recalling that, by (11),
$\xi_j>0$
for all
$j>0$
, in view of the fact that
$\varrho(M_j)>0$
for all
$j>0$
we get that
$\Delta$
is a positive constant. Therefore, it follows from (31) that there exist constants
$0<c_{13}<c_{14}<\infty$
such that
\begin{align} c_{13}\sum_{j=1}^{N_6}\varrho(M_j)\cdots\varrho(M_n) \le \sum_{j=1}^{N_6}\xi_j^{-1}\cdots\xi_n^{-1} \le c_{14}\sum_{j=1}^{N_2}\varrho(M_j)\cdots\varrho(M_n). \end{align}
Taking (34), (33), (35), and (36) into consideration, we conclude that, for all
$n>N_7\,:\!=\,\max\{N_5+N_6, N^{\prime}_7\}$
, (32) is true.
Lemma 9. For every n and k,
\begin{equation*} P(n\in C_k)=\frac1{G(1,n)} \prod\limits_{i=n+1}^{n+k-1}\frac{1}{1+a_i+b_i}. \end{equation*}
Also, for every
$l>n+k$
,
\begin{equation*} P(n\in C_k,l\in C_k) = \frac1{G(1,n)}\frac1{G(n+k,l)}\prod_{i=n+1}^{n+k-1} \frac{1}{1+a_i+b_i}\prod_{i=l+1}^{l+k-1}\frac1{1+a_{i}+b_{i}}. \end{equation*}
Proof. Using the Markov property and (14), we have
\begin{align*} P(n\in C_k) & = P(\mathbf{Z}_n=0,\ldots,\mathbf{Z}_{n+k-1}=0) \\ & = P(\mathbf{Z}_n=0)\prod_{j=0}^{k-2}P(\mathbf{Z}_{n+j+1}=0\mid\mathbf{Z}_{n+j}=0) \\ & = \frac1{G(1,n)}\prod_{j=n+1}^{n+k-1}\frac{1}{1+a_{j}+b_{j}}, \\ P(n\in C_k,l\in C_k) & = P(n\in C_k)P(l\in C_k\mid n\in C_k) \\ & = P(n\in C_k)P(l\in C_k\mid\mathbf{Z}_{n+k-1}=0) \\ & = \frac1{G(1,n)}\prod_{i=n+1}^{n+k-1}\frac{1}{1+a_i+b_i}\times\frac1{G(n+k,l)} \prod_{i=l+1}^{l+k-1}\frac1{1+a_{i}+b_{i}}. \end{align*}
We thus complete the proof of the lemma.
Recalling the definitions in (30) and (3), by some easy computations we see that
\begin{equation} L(n+1) = 1 + \rho(M_{n+1})L(n) \end{equation}
and
\begin{equation} H(n+1) = 1 + \xi^{-1}_{n+1}H(n), \qquad \frac{H(k,n)}{H(n)} = 1 - \prod_{j=k-1}^n\bigg(1-\frac{1}{H(j)}\bigg). \end{equation}
Now we are ready to prove the main results.
Proof of Theorem
2. For
$j<i$
, set
$C_{j,i}=\{x\colon x\in(2^j, 2^i], x\in C\}$
and let
$A_{j,i}=|C_{j,i}|$
be the cardinality of the set
$C_{j,i}$
. On the event
$\{A_{m,m+1}>0\}$
, let
$l_m=\max\{k\colon k\in C_{m,m+1}\}$
be the largest regeneration time in
$C_{m,m+1}$
. Then, for
$m\ge1$
we have
\begin{align} & \sum_{j=2^{m-1}+1}^{2^{m+1}}P(j\in C) = E(A_{m-1,m+1}) \nonumber \\ & \qquad \ge \sum_{n=2^{m}+1}^{2^{m+1}}E(A_{m-1,m+1}, A_{m,m+1}>0,l_m=n) \nonumber \\ & \qquad = \sum_{n=2^{m}+1}^{2^{m+1}}P(A_{m,m+1}>0,l_m=n)E(A_{m-1,m+1}\mid A_{m,m+1}>0,l_m=n) \nonumber \\ & \qquad = \sum_{n=2^{m}+1}^{2^{m+1}}P(A_{m,m+1}>0,l_m=n)\sum_{i=2^{m-1}+1}^nP(i\in C\mid A_{m,m+1}>0,l_m=n) \nonumber \\ & \qquad \ge P(A_{m,m+1}>0)\min_{2^{m}<n\le 2^{m+1}}\sum_{i=2^{m-1}+1}^nP(i\in C\mid A_{m,m+1}>0,l_m=n) \,=\!:\,a_mb_m. \end{align}
Fix
$2^{m}+1\le n\le 2^{m+1}$
and
$2^{m-1}+1\le i\le n$
. Using Lemma 9 and the Markov property, we get that
\begin{align} & P(i\in C\mid A_{m,m+1}>0,l_m=n) \nonumber \\ & \qquad = \frac{P(Z_i=0,Z_n=0,Z_t\ne0,n+1\le t\le 2^{m+1})}{P(Z_n=0,Z_t\ne0,n+1\le t\le 2^{m+1})} \nonumber \\ & = \frac{P(Z_i=0,Z_n=0)}{P(Z_n=0)}\frac{P(Z_t\ne0,n+1\le t\le 2^{m+1}\mid Z_i=0,Z_n=0)} {P(Z_t\ne0,n+1\le t\le 2^{m+1}\mid Z_n=0)} \nonumber \\ & = \frac{P(Z_i=0,Z_n=0)}{P(Z_n=0)} = \frac{G(n)}{G(i)G(i+1,n)}. \end{align}
It follows from Lemma 3 that for fixed
$\varepsilon>0$
there exists a constant
$K_1>0$
such that, for all
$i>K_1$
and
$ n-i> K_1$
,
\begin{align} \frac{G(n)}{G(i)G(i+1,n)} > \frac{H(n)}{H(i)H(i+1,n)}\cdot \frac{\varphi(1)+(1-{\theta}/{b})\varphi(2)-\varepsilon} {[\varphi(1)+(1-{\theta}/{b})\varphi(2)+\varepsilon]^2}, \end{align}
\begin{align} G(i) > H(i)(\varphi(1)+(1-{\theta}/{b})\varphi(2)-\varepsilon). \end{align}
Recall that
$\xi_k>0$
,
$k\ge 1$
by (11). Then, by some easy computation, we have
\begin{align} \frac{H(n)}{H(i)H(i+1,n)} & = \frac{\sum_{j=1}^{n+1}\xi^{-1}_j\cdots\xi^{-1}_n} {\big(\sum_{j=1}^{i+1}\xi^{-1}_j\cdots\xi^{-1}_i\big)\big(\sum_{j=i+1}^{n+1}\xi^{-1}_j\cdots\xi^{-1}_n\big)} \nonumber \\ & = \frac{\sum_{j=1}^{n+1}\xi_1\cdots\xi_{j-1}} {\big(\sum_{j=1}^{i+1}\xi_1\cdots\xi_{j-1}\big)\big(\sum_{j=i+1}^{n+1}\xi_{i+1}\cdots\xi_{j-1}\big)} \ge \frac{1}{\sum_{j=i+1}^{n+1}\xi_{i+1}\cdots\xi_{j-1}}. \end{align}
It follows from (31) that, for all
$i> N_6$
and
$j-i\ge N_5+2$
,
\begin{align*} \xi_{i+1}\cdots \xi_{j-1}\le c_8 \varrho(M_{i+1})^{-1}\cdots \varrho(M_{j-1})^{-1}.\end{align*}
Thus, for all
$i> N_6$
,
\begin{equation} \sum_{j=i+N_5+2}^{n+1}\xi_{i+1}\cdots\xi_{j-1} < c_{8}\sum_{j=i+N_5+2}^{n+1}\varrho(M_{i+1})^{-1}\cdots\varrho(M_{j-1})^{-1}. \end{equation}
Then, under the assumption
$\varrho(M_{i+1})\ge 1$
, we have
\begin{align} \sum_{j=i+N_5+2}^{n+1}\xi_{i+1}\cdots \xi_{j-1}\le {c_{8}(n-i-N_5)}. \end{align}
On the other hand, since
$\xi_n\rightarrow{\varrho_1}/({a\theta-bd})\,=\!:\,\xi>0$
as
$n\rightarrow\infty$
, there exists a constant
$K_2$
such that, for all
$n\ge K_2$
,
$\xi_n<\xi+1$
. As a result, for all
$i>K_2$
,
\begin{align*}\sum_{j=i+1}^{i+N_5+1}\xi_{i+1}\cdots \xi_{j-1}\le N_5(\xi+1)^{N_5}.\end{align*}
Consulting (43), (44), and (45), we have, for all
$i>K_3\,:\!=\,\max\{K_2,N_6\}$
,
\begin{equation*} \frac{H(n)}{H(i)H(i+1,n)}\ge \frac{c}{n-i+1}. \end{equation*}
In view of (41), we have thus shown that, for all
$i\ge K\,:\!=\,\max\{K_3,K_1\}$
and
$n-i> K_1$
,
\begin{equation*} \frac{G(n)}{G(i)G(i+1,n)}\ge \frac{c}{n-i+1}. \end{equation*}
Taking this and (40) together, we get, for
$m>\log{K}$
(which implies
$2^{m-1}+1>K$
),
\begin{align*} b_m & = \min_{2^m<n\le 2^{m+1}}\sum_{i=2^{m-1}+1}^nP(i\in C\mid A_{m,m+1}>0,l_m=n) \\ & \ge c\min_{2^m<n\le 2^{m+1}}\sum_{i=2^{m-1}+1}^{n-K_1-1}\frac{1}{n-i+1} \\ & = c\min_{2^m<n\le 2^{m+1}}\sum_{j=K_1+2}^{n-2^{m-1}}\frac{1}{j} = c\sum_{j=K_1+2}^{2^{m-1}}\frac{1}{j} \ge c\int_{K_1+2}^{2^{m-1}+1}\frac{1}{x}\,\mathrm{d}x \ge cm\log 2. \end{align*}
Substituting this into (39), using Lemma 9 and (42), we see that
\begin{align} \sum_{m=K+1}^{\infty}P(A_{m,m+1}>0) & \le \sum_{m=K+1}^{\infty}\frac{1}{b_m}\sum_{j=2^{m-1}+1}^{2^{m+1}}P(j\in C) \nonumber \\ & = \sum_{m=K+1}^{\infty}\frac{1}{b_m}\sum_{j=2^{m-1}+1}^{2^{m+1}}\frac1{G(j)} \nonumber \\ & \le c\sum_{m=K+1}^{\infty}\frac{1}{m}\sum_{j=2^{m-1}+1}^{2^{m+1}}\frac{1}{H(j)} \nonumber \\ & \le c\sum_{m=K+1}^{\infty}\sum_{j=2^{m-1}+1}^{2^{m+1}}\frac{1}{H(j)\log j} \le c\sum_{n=2^K+1}^\infty\frac{1}{H(n)\log n}. \end{align}
Note that under the condition in case (i),
$\sum_{n=2}^\infty{1}/({L(n)\log n})<\infty$
. Thus, it follows from (32) that the right-hand side side of (46) is finite, so is
$\sum_{m=K+1}^{\infty}P(A_{m,m+1}>0)$
. Applying the Borel–Cantelli lemma, we conclude that with probability 1, at most finitely many of the events
$\{A_{m,m+1}>0\}$
,
$m\ge1$
, occur, which completes the first part of Theorem 2.
Next, we turn to the second part. Suppose there exists some
$\delta>0$
such that
$L(n)\le \delta n\log n$
for n large enough and
$\sum_{n=2}^\infty{1}/({L(n)\log n})=\infty$
.
We also use Borel–Cantelli Lemma to prove the result in this case, but here we need to estimate not only the sum of
$P(A_j)$
, but also the sum of
$P(A_jA_l)$
.
First, let’s study the probability
$P(A_j)$
. For
$j\ge1$
, let
$n_j=[j\log j]$
be the integer part of
$j\log j$
and set
$A_j=\{n_j\in C_k\}$
. For fixed
$\varepsilon>0$
, in view of Lemma 3 there exist constants
$L_1>k_0$
and
$L_2$
such that, for all
$n-k\ge L_1$
,
$k\ge k_0$
,
\begin{equation} \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) - \varepsilon \le \frac{G(k,n)}{H(k,n)} \le \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) + \varepsilon, \end{equation}
and, for all
$m>L_2$
,
\begin{equation} \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) - \varepsilon \le \frac{G(1,m)}{H(1,m)} \le \varphi(1) + \bigg(1-\frac{\theta}{b}\bigg)\varphi(2) + \varepsilon. \end{equation}
Notice that the sequence
$a_n+b_n$
,
$n\ge0$
, is bounded away from 0 and positive. Then, taking (48) and Lemma 9 into account, we obtain
\begin{equation} \sum_{j=L_2}^{\infty}P(A_j) = \sum_{j=L_2}^{\infty}\frac1{G(1,n_j)}\prod_{i=n_j+1}^{n_j+k-1}\frac{1}{1+a_i+b_i} \ge c\sum_{j=L_2}^{\infty}\frac{1}{H([j\log j])}. \end{equation}
Under the assumption
$\varrho(M_j)\ge 1$
for all
$j\ge1$
, we can see that L(n) is increasing from (37). Applying [Reference Csáki, Földes and Révész6, Lemma 2.2], we conclude that
$\sum_{j=2}^{\infty}{1}/({L([j\log j])})$
and
$\sum_{j=2}^{\infty}{1}/({L(j)\log j})$
converge or diverge simultaneously. As a result, it follows from (49) and Lemma 8 that
\begin{equation} \sum_{j=\max\{L_2,N_7\}}^{\infty}P(A_j) \ge c\sum_{j=\max\{L_2,N_7\}}^{\infty}\frac{1}{L([j\log j])} = \infty. \end{equation}
Second, we study the probability
$P(A_jA_l)$
. Define
$\mathcal C_k = \{(j,l)\colon 2\le j\lt l, l\log l \gt j\log j+k\}$
. Note that when
$j>\mathrm{e}^{\max\{L_1,L_2\}+k}$
and
$l\ge j+1$
, we have
$n_l-n_j-k> L_1$
and
$n_l>L_2$
. It thus follows from Lemma 9 and (47) that for the
$\varepsilon$
above, when
$(j,l)\in \mathcal C_k$
satisfying
$j>\mathrm{e}^{\max\{L_1,L_2\}+k}$
,
\begin{align*} P(A_jA_l) & = P(n_j\in C_k, n_l\in C_k) \\ & = \frac1{G(n_j)}\frac1{G(n_j+k,n_l)}\prod_{i=n_j+1}^{n_j+k-1}\frac{1}{1+a_i+b_i} \prod_{i=n_l+1}^{n_l+k-1}\frac1{1+a_{i}+b_{i}} \\ & = P(A_j)P(A_l) \frac{G(n_l)}{G(n_j+k,n_l)} \\ & \le P(A_j)P(A_l) \frac{H(n_l)}{H(n_j+k,n_l)}\frac{\varphi(1)+(1-{\theta}/{b})\varphi(2)+\varepsilon} {\varphi(1)+(1-{\theta}/{b})\varphi(2)-\varepsilon} \\ & = P(A_j)P(A_l)\frac{H(n_l)}{H(n_j+k,n_l)}(1+c\varepsilon). \end{align*}
Then, taking (38) and the fact
$\log(1-x)\le -x$
for all
$0<x<1$
into account, we have
\begin{equation} P(A_jA_l) \le P(A_j)P(A_l)\Bigg(1-\exp\Bigg\{{-}\sum_{i=n_j+k-1}^{n_l}\frac{1}{H(i)}\Bigg\}\Bigg)^{-1} (1+c\varepsilon). \end{equation}
For the above
$\varepsilon>0$
, let
\begin{align*} \ell = \min\Bigg\{l\ge j+1\colon\sum_{i=n_j+k-1}^{n_l}\frac{1}{H(i)}\ge\log\frac{1+\varepsilon}{\varepsilon}\Bigg\}. \end{align*}
Obviously, for
$l\ge\ell$
,
$\big(1-\exp\big\{{-}\sum_{i=n_j+k-1}^{n_l}{1}/{H(i)}\big\}\big)^{-1}\le 1+\varepsilon$
. Thus, it follows from (51) that
\begin{equation} P(A_jA_l) \le (1+c\varepsilon)(1+\varepsilon)P(A_j)P(A_l) \le (1+c\varepsilon)P(A_j)P(A_l) \text{ for all } l\ge\ell,\ (j,l)\in \mathcal C_k. \end{equation}
Next, suppose
$l<\ell$
. Note that for
$0<u<\log(({1+\varepsilon})/{\varepsilon})$
we have
$1-\mathrm{e}^{-u}\ge cu$
for some
$c\,:\!=\,c(\varepsilon)>0$
small enough. Then, in view of (51) and (32), we have
\begin{align} P(A_jA_l) & \le c(1+c\varepsilon)P(A_j)P(A_l)\Bigg(\sum_{i=n_j+k-1}^{n_l}\frac{1}{H(i)}\Bigg)^{-1} \nonumber \\ & \le c(1+c\varepsilon)P(A_j)P(A_l)\Bigg(\sum_{i=n_j+k-1}^{n_l}\frac{1}{L(i)}\Bigg)^{-1} \quad \text{for} \ j>N_7. \end{align}
Since L(n) is increasing, we have
\begin{align*}\Bigg(\sum_{i=n_j+k-1}^{n_l}\frac{1}{L(i)}\Bigg)^{-1}\le \frac{L(n_l)}{n_l-n_j-k+2}\end{align*}
for all
$j\ge N_7$
. Again by (32), we have
\begin{align*}\Bigg(\sum_{i=n_j+k-1}^{n_l}\frac{1}{L(i)}\Bigg)^{-1}\le\frac{1}{c_{9}} \frac{H(n_l)}{n_l-n_j-k+2}.\end{align*}
Therefore, taking (53) and (48) into account, we get that for
$(j,l)\in\mathcal C_k$
satisfying
$\ell\ge l\ge j+1$
and
$j\ge \max\{N_7, \mathrm{e}^{\max\{L_1,L_2\}+k}\}\,=\!:\,M$
,
\begin{align*} P(A_jA_l) & \le c\frac{G(n_l)}{n_l-n_j-k+2}P(A_j)P(A_l) \\ & = c\Bigg(\prod_{i=1}^{k-1}\frac1{1+a_{n_l+i}+b_{n_l+i}}\Bigg)\frac{P(A_j)}{n_l-n_j-k+2} \le \frac{cP(A_j)}{l\log l-j\log j}. \end{align*}
Consequently, for
$j\ge M$
,
\begin{align} \sum_{j+1\le l <\ell, (j,l)\in \mathcal C_k}P(A_jA_l) & \le \sum_{j+1\le l< \ell, (j,l)\in \mathcal C_k}\frac{cP(A_j)}{l\log l-j\log j} \nonumber \\ & \le cP(A_j)\sum_{l=j+1}^{\ell-1}\frac{1}{l\log l-j\log j} \nonumber \\ & \le cP(A_j)\frac{1}{\log j}\sum_{l=j+1}^{\ell-1}\frac{1}{l-j} \le cP(A_j)\frac{\log \ell}{\log j}. \end{align}
Recall that
\begin{equation} \sum_{i=n_j+k-1}^{n_l}\frac{1}{H(i)}< \log \frac{1+\varepsilon}{\varepsilon}, \quad j+1\le l<\ell, \end{equation}
and
$L(n)\le \delta n\log n$
for some
$\delta>0$
and n large enough. We claim that if j is large enough, then
\begin{equation} \ell < j^\gamma \quad \text{if } \gamma > \bigg(\frac{1+\varepsilon}{\varepsilon}\bigg)^{c_{10}\delta}+\varepsilon. \end{equation}
Suppose on the contrary that
$\ell \ge j^\gamma$
. Then, for
$j>N_7$
,
\begin{align*} \sum_{i=n_j+k-1}^{n_{\ell}}\frac{1}{H(i)} & \ge \sum_{i=n_j+k-1}^{n_{\ell}}\frac{1}{c_{10}L(i)} \\ & \ge \frac{1}{c_{10}\delta} \sum_{i=n_j+k-1}^{n_{\ell}}\frac{1}{i\log i} \\ & \ge \frac{1}{c_{10}\delta}(\log\log n_{\ell}-\log\log (n_j+k-1 )) \\ & \ge \frac1{c_{10}\delta}(\log\log n_{\ell}-\log\log n_{j+k}) \\ & \ge \frac1{c_{10}\delta}\log \frac{\gamma\log j+\log\gamma+\log\log j}{\log (j+k)+\log\log (j+k)} \ge \frac1{c_{10}\delta}\log(\gamma -\varepsilon) \end{align*}
for j large enough. Since
$\gamma > (({1+\varepsilon})/{\varepsilon})^{c_{10}\delta}+\varepsilon$
, we have
\begin{align*}\sum_{i=n_j+k-1}^{n_{\ell}}\frac{1}{H(i)}\ge \log \frac{1+\varepsilon}{\varepsilon},\end{align*}
which contradicts (55). This means (56) is right.
Applying (56) and (54), we obtain, for j large enough,
\begin{equation*} \sum_{j+1\le l< \ell, (j,l)\in \mathcal C_k}P(A_jA_l) \le cP(A_j). \end{equation*}
Taking this together with (52), we conclude that, for some
$j_0>0$
,
\begin{equation*} \sum_{j=j_0}^n\sum_{j<l\le n, (j,l)\in \mathcal C_k}P(A_jA_l) \le \sum_{j=j_0}^n\sum_{j<l\le n, (j,l)\in \mathcal C_k}(1+c\varepsilon)P(A_j)P(A_l)+c\sum_{j=j_0}^n P(A_j). \end{equation*}
Therefore, taking (50) into account, we have
\begin{align*} \alpha & \,:\!=\, \varliminf_{n\rightarrow\infty} \frac{\sum_{j=j_0}^n\sum_{j<l\le n, (j,l)\in \mathcal C_k}P(A_jA_l) - \sum_{j=j_0}^n\sum_{j<l\le n, (j,l)\in \mathcal C_k}(1+c\varepsilon)P(A_j)P(A_l)} {\big(\sum_{j=j_0}^n P(A_j)\big)^2} \\ & \le \varliminf_{n\rightarrow\infty} \frac{c}{\sum_{j=j_0}^n P(A_j)}=0. \end{align*}
An application of the Borel–Cantelli lemma [Reference Petrov22, p. 235] yields
\begin{align*} P(A_j,\,j\ge 1\text{ occur infinitely often}) & \ge P(A_j,\,j\ge j_0\text{ occur infinitely often}) \\ & \ge \frac{1}{1+\varepsilon +2\alpha} \ge \frac{1}{1+\varepsilon}. \end{align*}
Since
$\varepsilon>0$
is arbitrary, we can conclude that
$P(A_j,\,j\ge 1\text{ occur infinitely often})=1$
. So, the second part of the theorem is proved.
5. Examples
For
$n\ge1$
, let
$q_{n},p_n>0$
be numbers such that
$q_{n}+p_n=1$
. Suppose that
$\mathbf{Z}_n$
,
$n\ge0$
, is a two-type branching process with immigration satisfying
$\mathbf{Z}_0=0$
, and there is a fixed immigration
${{\mathbf{e}_1}}$
in each generation, with offspring distributions
\begin{align*} \mathbb{P}(\mathbf{Z}_{n}=(0,j)\mid\mathbf{Z}_{n-1} = \mathbf{e}_{1}) & = q_{n}^{j}p_{n}, \\ \mathbb{P}(\mathbf{Z}_{n}=(1,j)\mid\mathbf{Z}_{n-1} = \mathbf{e}_{2}) & = q_{n}^{j}p_{n}, \quad j\ge0,\,n\ge1.\end{align*}
Some computation yields the mean matrix
\begin{equation*} M_n= \begin{pmatrix} 0 & \quad b_n \\ 1 & \quad b_n \end{pmatrix}\end{equation*}
with
$b_n={q_{n}}/{p_{n}}$
,
$n\ge1$
. Then
$\varrho(M_k)=(b_k+\sqrt{b_k^2+4b_k})/2$
.
Fix
$B\ge 0$
. Set
$i_0\,:\!=\,\min\big\{i\colon {B}/{3i}<\frac23 \big\}$
and let
\begin{align*} p_i\,:\!=\,\left\{\begin{array}{l@{\quad}l} \frac23 - {B}/{3i}, \ & i\ge i_0, \\[4pt] \frac23, & i< i_0. \end{array}\right.\end{align*}
Theorem 3. Fix
$B\ge 0$
. If
$B\ge 1$
, then
$\{\mathbf{Z}_n\}$
has finitely many regeneration times, almost surely. If
$B<1$
, then
$\{\mathbf{Z}_n\}$
has infinitely many k-strong regeneration points, almost surely.
Proof. For
$B\ge0$
, let
$r_n={B}/{3n}$
. It is easy to see that
$\lim_{n\rightarrow\infty}n^2(r_n-r_{n+1})={B}/{3}$
. Thus, by some computation, we obtain
\begin{align*}|b_{k+1}-b_k|\sim|r_{n+1}-r_n|\sim\frac1{n^2},\quad n\to\infty,\end{align*}
which implies that
$\sum_{k=1}^\infty|b_{k+1}-b_k|<\infty$
. Since
$p_k=\frac{2}{3}- r_k$
,
$k\ge 1$
, we see that
$b_k\ge\frac12$
. As a result,
$\varrho(M_k)\ge 1$
. Thus, the conditions in Theorem 2 are fulfilled.
By Taylor expansion of
$\varrho(M_k)$
at 0, we get
$\varrho(M_k)=1+ 3r_k+O(r_k^2)$
as
$k\rightarrow\infty$
. And then, by Euler’s asymptotic formula for the harmonic series, we get that
\begin{equation} \varrho(M_1)\cdots\varrho(M_n)\sim c n^B \quad \text{as } n\rightarrow\infty. \end{equation}
When
$B>1$
,
$c\int_{k_0}^n1/{x^B}\,\mathrm{d}x$
is convergence, so is
$\sum_{k=k_0}^n\varrho(M_1)^{-1}\cdots\varrho(M_k)^{-1}$
by (57). Then it follows from (57) that
\begin{equation*} L(n) = \sum_{k=1}^n\varrho(M_k)\cdots\varrho(M_n) = \varrho(M_1)\cdots\varrho(M_n)\sum_{k=k_0}^n\varrho(M_1)^{-1}\cdots\varrho(M_{k-1})^{-1} \sim c n^B \end{equation*}
as
$n\rightarrow\infty$
, which implies that
$\sum_{n=2}^{\infty}1/({L(n)\log n})<\infty$
. So the conditions in Theorem 2(i) are satisfied. Then, by Theorem 2(i), the branching process has finitely many regeneration times almost surely.
When
$B\le 1$
,
$\int_{i_0}^n1/{x^B}\,\mathrm{d}x$
is divergent, so is
$\sum_{k=k_0}^n\varrho(M_1)^{-1}\cdots\varrho(M_{k-1})^{-1}$
, and we have
$\sum_{k=k_0}^n\varrho(M_1)^{-1}\cdots\varrho(M_{k-1})^{-1}\sim \int_{i_0}^n1/{x^B}\,\mathrm{d}x$
by (57), while
\begin{equation} \lim_{n\rightarrow\infty}\int_{i_0}^n\frac1{x^B}\,\mathrm{d}x = \left\{ \begin{array}{l@{\quad}l} \dfrac{1}{1-B}n^{1-B} - \dfrac{1}{(1-B)}i_0^{1-B},\ & B < 1, \\[9pt] \log n - \log i_0, & B = 1. \end{array} \right. \end{equation}
In view of (57), we thus have
\begin{equation} L(n) \sim \left\{ \begin{array}{l@{\quad}l} cn, & B < 1, \\[4pt] cn\log n,\ & B = 1 \end{array} \right. \quad \text{as } n\rightarrow\infty. \end{equation}
So if
$B=1$
, then
$\sum_{n=2}^\infty{1}/({L(n)\log n})<\infty$
. Applying Theorem 2(i), we can see that the branching process has finitely many regeneration times almost surely.
Assuming
$B<1$
, it follows from (59) that
$\sum_{n=2}^{\infty}1/({L(n)\log n})=\infty$
and
$L(n)\log n\le cn\log n$
for n large enough. Then, by Theorem 2(ii), we conclude that the process has infinitely many k-strong regeneration times almost surely.
Remark 5. Let
$\{\mathbf{Y}_n\}_{n\ge0}$
be a branching process in varying environments with
$\mathbf{Y}_0=\mathbf{e}_1$
, which shares the same branching mechanism as
$\{\mathbf{Z}_n\}_{n\ge0}$
in this section. By the results in [Reference Wang27, Theorem 1], we can see that the tail probability of surviving time
$\nu$
of the process
$\{\mathbf{Y}_n\}_{n\ge0}$
satisfies
\begin{align*}P(\nu>n)\sim\frac{c}{1+\sum_{k=1}^n\varrho(M_1)^{-1}\cdots\varrho(M_k)^{-1}}.\end{align*}
When
$B=1$
, it follows from (58) that
$P(\nu>n)\sim{c}/({n\log n})\rightarrow0$
. So
$\{\mathbf{Y}_n\}_{n\ge0}$
is extinct in this situition. Then we conclude that
$\{\mathbf{Z}_n\}_{n\ge0}$
should have a regeneration time. But, by Theorem 3, in this case, the process
$\{\mathbf{Z}_n\}_{n\ge0}$
has finitely many regeneration times. Such a phenomenon never happens for the time-homogenous branching process, since by the time-homogenous property, if the process owns one regeneration time, it must have infinitely many regeneration times.
When there are infinitely many regeneration times, we have established the asymptotic property of the number of regeneration times in [0,n] as follows.
Theorem 4. Fix
$0\le B<1$
. Then
\begin{equation} \lim_{n\rightarrow\infty}\frac{E\#\{k\colon k\in C\cap[0,n]\}}{\log n}=c>0 \end{equation}
and, for any
$\varepsilon>0$
,
\begin{equation} \lim_{n\rightarrow\infty}\frac{\#\{k\colon k\in C\cap[0,n]\}}{(\log n)^{1+\varepsilon}}=0 \end{equation}
almost surely.
Remark 6. Notice that Theorem 4 contains the case
$B=0$
. In this case,
$p_i\equiv \frac23$
and
$\varrho{(M_i)}\equiv 1$
for all
$i\ge1$
, so that
$\{\mathbf{Z}_n\}$
is indeed a critical Galton–Watson process with immigration. As shown by Theorem 4, it seems that, up to multiplication by a positive constant, the value of
$0\le B<1$
does not affect the order of the number of regeneration times in [0,n].
Proof. Let
$S_n=\#\{k\colon k\in C\cap[0,n]\}$
. By (14), we can see that
\begin{align*}E(S_n)=\sum_{i=1}^nP(Z_i=0)=\sum_{i=1}^n\frac1{G(i)}.\end{align*}
Consulting (16) and (32), there exist positive constants
$C_1$
and
$C_2$
such that
\begin{align*}C_1\sum_{i=1}^n\frac1{L(k)}\le\sum_{i=1}^n\frac1{G(i)}\le C_2\sum_{i=1}^n\frac1{L(k)}.\end{align*}
It follows from (59) that when
$B<1$
,
$L(n)\sim cn$
. As a result,
\begin{equation} E(S_n)\le \sum_{1\le i\le n}\frac{c}{i}. \end{equation}
We thus get (60).
Now we turn to the second part. Noticing that
$S_n$
is positive and nondecreasing, by (62) we have
$E(\max_{1\le k\le n}S_k) = E(S_n) < \sum_{1\le i\le n}{c}/{i}$
. We know that, for each
$\varepsilon>0$
,
$\sum_{i=2}^{\infty}1/({i(\log i)^{1+\varepsilon}})<\infty$
. Therefore, by [Reference Fazekas and Klesov8, Theorem 2.1], we have
\begin{align*}\frac{S_n}{(\log n)^{1+\varepsilon}}\rightarrow 0\end{align*}
almost surely as
$n\rightarrow\infty$
, which completes the proof of (61).
Acknowledgements
The authors would like to thank two referees who read the paper carefully and gave very good suggestions and comments which helped to improve the paper to a large extent.
Funding information
This project is supported by National Natural Science Foundation of China (Grant Nos. 12271043, 12001558) and the Nature Science Foundation of Anhui Educational Committee (Grant No. 2023AH040025).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
