No CrossRef data available.
Article contents
On the Popov–Pommerening conjecture for linear algebraic groups
Published online by Cambridge University Press: 09 October 2017
Abstract
Let 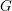 $G$ be a reductive group over an algebraically closed subfield
$G$ be a reductive group over an algebraically closed subfield 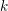 $k$ of
$k$ of 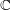 $\mathbb{C}$ of characteristic zero,
$\mathbb{C}$ of characteristic zero, 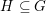 $H\subseteq G$ an observable subgroup normalised by a maximal torus of
$H\subseteq G$ an observable subgroup normalised by a maximal torus of 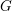 $G$ and
$G$ and 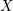 $X$ an affine
$X$ an affine 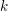 $k$-variety acted on by
$k$-variety acted on by 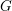 $G$. Popov and Pommerening conjectured in the late 1970s that the invariant algebra
$G$. Popov and Pommerening conjectured in the late 1970s that the invariant algebra 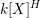 $k[X]^{H}$ is finitely generated. We prove the conjecture for: (1) subgroups of
$k[X]^{H}$ is finitely generated. We prove the conjecture for: (1) subgroups of 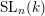 $\operatorname{SL}_{n}(k)$ closed under left (or right) Borel action and for: (2) a class of Borel regular subgroups of classical groups. We give a partial affirmative answer to the conjecture for general regular subgroups of
$\operatorname{SL}_{n}(k)$ closed under left (or right) Borel action and for: (2) a class of Borel regular subgroups of classical groups. We give a partial affirmative answer to the conjecture for general regular subgroups of 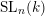 $\operatorname{SL}_{n}(k)$.
$\operatorname{SL}_{n}(k)$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2017


