Introduction
The creep phenomenon of snow is easily explained by the famous Nutting equation ![]() . The present author has expanded this equation into a formula which includes a temperature term and determined its constants experimentally. Thus, the tensile strain e was finally expressed by the expression
. The present author has expanded this equation into a formula which includes a temperature term and determined its constants experimentally. Thus, the tensile strain e was finally expressed by the expression

where σ is the stress, t the elapsed time, and T is temperature expressed in Celsius degrees. The constant of proportionality has to be decided by the snow quality.
We have also been able to observe the phenomenon of creep fracture on changing the stress or temperature, and the elongation and plastic flow-rate at the time of fracture were observed.
These phenomena can be interpreted if we assume that the tensile strain of snow is the accumulation of small deformations in the links between ice particles and that creep fracture is brought about by a momentary chain reaction following the breakage of a link.
Experimental measurements
The measurements were carried out in our low-temperature laboratory and we used preserved natural snow. Figure 1 shows the specially-made equipment. A snow sample as shown in the figure is cut by a mould and is held by two clamps (C1 and C2) which are placed on a piece of waxed paper. The surfaces of contact between the clamp and the snow are poked with a thin plate, while, at the same time, water and snow are supplied in order to make a condensed snow block. The contact areas are firmly frozen together after about thirty minutes. The clamp C1 is fixed by a ring and a holder, C2 is pulled by a strong thread which passes over a pulley P and from the other end of which a weight is suspended.

Fig. 1. Measuring equipment for tensile strain.
The creep strain activated the responsive needle of a displacement transducer which gave an output signal in the form of a voltage which was continuously recorded on a recorder. S in the figure is a stop to protect the responsive needle and terminal box T at the time of fracture.
The measurements were carried out by the following procedure.
The density of the sample was measured.
The apparatus was attached to the sample. In order to keep the equipment in the correct position, a small weight is attached to the thread throughout the time when the two shoulders of sample are congealing.
The weight was taken off after the shoulders had congealed; the responsive needle and terminal box were set and the recording apparatus started.
A weight is slowly and carefully attached.
Results
(1) Strain and elapsed time
In all our measurements the logarithm of expansion and of elapsed time were clearly related in a typical linear form.
In short, the strain e was related to time t by
The slope A always lay in the range 0.5-0.8, with average 0.64, so it may be approximated by 2⁄3. The intercept B is a constant which seems to be decided by snow quality, stress, and temperature. Thus the time dependence can be written in the form
(2) Strain and stress
The relation between deformation and stress was studied at about — 5°C by attaching different weights in order.
Figure 2 shows the measured values for a sample of density 0.39 g⁄cm3 and hardness 4.1 - 103 g⁄cm2. The weights are hung in ascending order, as shown on the right side of each line. The number in parentheses shows the slope of the line, which becomes almost constant if one hour elapses between application of one stress and the next.
The relation between the intercepts of the lines and the corresponding weights is shown by the line at the bottom right in Figure 2. According to the results of about 50 experiments, the slopes of these lines are distributed in the range of 0.9-2.0, with average 1.45, which may be approximated by 3⁄2. Thus the stress and time dependence of e can be written in the form

Fig. 2. Relation between stress and strain (expansion).
(3) Strain and temperature
The experiments on the effect of temperature were carried out by changing the laboratory temperature in steps.
Figure 3 shows the results for a fine-grained snow of density 0.42 g⁄cm3 and hardness 4.4 - 103 g⁄cm2, and the weight is always 7.5 kg. The time for one test is one hour and the next hour is used for rest as in the former measurement.
Each line is marked with the snow temperature and the slope. The intercepts of these lines are plotted on the right of Figure 3, and the relation is shown to be a straight line. It is known from about 40 experiments that the slopes of these lines are distributed in the range of —0.5 to —0.8 with average —0.67 which can be replaced with —2⁄3 Thus e can finally be written using the formula
(4) Creep fracture
According to Equation (4), the rate of expansion de⁄dt under a fixed stress and temperature is decreasing with the elapsing time, and snow is not expected to fracture. Thus, in order to bring about creep fracture of snow, it is necessary that the stress should be increased slowly or the temperature should be raised slowly.
Figure 4 shows a case in which a snow sample was fractured by increasing stress. The weight started at 8 kg and was increased at the rate of 500 g every 30 min, and these additional weights are shown with small arrow marks on the creep curve. Stress P1 is the tensile strength of this sample, P2 is the final stress, and F is the point of fracture. The left and right ordinate axes are respectively marked with the strain-rate and the viscosity. The viscosity is calculated from the slope of the creep curve, and is shown with open circles.
In a case in which snow temperature rose, snow can also be fractured as in Figure 5. The temperature is shown by open circles in the figure, and the creep curve and viscosity are respectively expressed by the thick line and the full circles.

Fig. 3. Relation between temperature and strain (expansion)
Through these fracture experiments, which take about 5-12 h, we have established the following facts.
(a) The creep curve can be changed into concave upward by a tension of over 80% of its centrifugal tensile strength at that time, and the average tension required for creep fracture is about 1.5 times as large as its tensile strength.
(b) The rate of expansion at the time of fracture is expressed as a percentage of the total length as follows:
Dry fine-grained snow 5–20 Wet fine-grained snow >15
Dry granular snow 3–8 Wet granular snow 3–5
(c) The average flow-rate for the final 10 min lay in the following range in units of percentage per hour (%⁄h).
Dry fine-grained snow 5–8 All wet snow >10
Dry granular snow 3–5
(d) The viscosity of dry snow and that of wet snow at the time of fracture are respectively under 104 and 103 g h⁄cm2.
Discussion
(1) Expansion of Nutting’s equation
The original form of Nutting’s equation for non-linear visco-elastic materials was given by Reference Nakaya and KuroiwaNakaya and Kuroiwa (1970, p. 26-27) as
where Φ, β, and α are constants. In this formula, Hooke’s law and Newton’s law are special cases obtained by inserting suitable values of β and α as follows: (Hooke’s law)
(Newton’s law)
(fig 4)(fig 5)where γ is the elastic modulus and η the viscosity, substituted of course, for Φ. So this equation is widely used for the explanation of visco-elastic behaviour.

Fig. 4. Creep fracture caused by a cumulative stress.

Fig. 5. Creep fracture caused by rising temperature.
According to our measurements, snow is a non-linear visco-elastic material and it is evident that the strain e is expressed by this equation. As mentioned above, the equation is a very useful one, but it does not have any temperature term and so its usefulness is limited to the case of fixed temperature.
In order to get rid of this limitation, the author introduced a factor of Tγ into the equation as follows:
where T is the snow temperature and γ is a constant. In our measurements, all the creep lines in a graph of log t against log e become almost parallel to each other, i.e. the temperature effect on strain can be expressed by moving the creep line in the direction of the log t axis on the logarithmic graph (this ability to convert the effects of time and temperature is called thermorheological simplicity).
If we use the conventional (i.e. Celsius) temperature T and γ in Equation (8), they become equal to — T and —α respectively as snow is a thermorheologically simple material. It thus seems that Nutting’s equation for snow can be expanded to the form
where, of course, the value of β and α are as determined by our measurements.
(2) Mechanism of tensile strain and fracture.
Snow consists of irregularly shaped ice grains and relatively big particles are mutually connected with a thin part which is called a “connecting bridge” or “link”. An ice particle is generally thick and strong, and it seems that the macroscopic expansion of a snow block is based on transformations of links.
When a snow sample is pulled by a large tension, the links are transformed in order of weakness, and the stress on an individual link is successively increased by this transformation, so the tension and the strain of a link is not constant even though the total tension is fixed. Thus, it seems that the stress σ and the strain e of a link in a creep test are as shown schematically in Figure 6.

Fig. 6. Variations of stress and strain on a link.
The elapsed time t is plotted as abscissa in this figure, t 1 is the time needed to apply the weights, and t2,t3,… are the times at which new stresses are applied. The ordinate in the figure is stress, f(1),f (2), … and f1, f2,… are respectively the actual stresses and yield stresses at times t 1, t 2…. The corresponding strains are shown in the figure below.
If f(i) is smaller than fi,as is the case for i = 1, 2, 3, the link will have only an elastic strain e i. If the stress suddenly exceeds the yield stress as in the case of i = 4 or i = 5, the link will be forced to extend by plastic flow.
These plastic deformations bring about a decrease of internal energy and a relief of stress, and the stress will go to a lower level after the large plastic expansion. The link is fractured by a stress which exceeds not only yield stress but also fracture stress, as in the case of i = 6, and only the plastic strain Δe will remain after the stress has been removed.
It seems that the tensile strain of snow is caused by the sum of the above-mentioned small deformations of the links, and can be expressed by the expanded Nutting equation. This reason will be considered as follows:
(a) Effect of elapsed time
The yield stress, the fracture stress, and the strain limit, drawn in on Figure 6, all increase with lapse of time. The reason for this may be that links are gradually becoming stronger by the effect of surface tension, sublimation, and sintering. According to Reference GriffithGriffith (1921, p. 170), the breaking strength of a plate R is expressed by
where E is Young’s modulus and c is the length of the focal line (i.e. the surrounding curve of the crack). We assume that this relation can be used for the ice link; c of a link is decreased by the above-mentioned effects. Besides, these effects also have the properties of making the links strong. Thus, the strength of a link under conditions of constant temperature and stress is increasing continuously with the lapse of time.
Now, if there are N links per unit volume of a sample at time t, and let us denote the number of links transformed during the time dt by dN, then dN is proportional to N and dt, and is also in inverse proportion to t because the links become stronger with time, and so we can write

The left side dN⁄N is the rate of transformation and is equal to the strain rate e, so e can be expressed as
where α is a constant. This form is part of Nutting’s formula.
(b) Effect of stress
According to our measurements, the strain of a sample following the application of weights is larger than the shrinkage at the time of the removal of stress, and the strain ratio between application and removal is 10 : 5-7.
It is also recognized that the recovered strain is in proportion to stress. But, when stress is applied, the deformation of links is brought about not only by elastic strain but also by plastic strain and microscopic fracture. During the creep test, the links are pulled in succession by further tension which is caused by the deformation of other links, and the strain may be brought about by elastic and plastic behaviour and fracture of links as was the case when the stress was first applied.
Then, in general, the strain-rate in a creep test can be expressed as
where, of course, the constant β must be larger than unity, and the value was determined as 3⁄2 by our tests.
(c) Effect of temperature
It is evident from the mechanical properties of ice that the strain limit, the yield stress, and the fracture stress of a link decrease with rising temperature. As mentioned before, snow is a thermorheologically simple material, so the strain at low temperature is small and is equal to the strain of a shorter elapsed time, and the strain at high temperature is large and corresponds to that of a long time.
If we use the value — T of the conventional Celsius temperature below freezing point, a rise of temperature will correspond to a decrease of — T. Then, if we remember that the strain-rate e is expressed as a power of the time t, it is natural that the relation between e and T should be shown as
where γ is a constant which, according to our theoretical consideration, equals the exponent of t as above mentioned.
(d) Creep fracture
According to the considerations above and the experimental results, e can be represented by
where T is snow conventional Celsius temperature. This is the expanded Nutting’s equation. According to this equation, de⁄dt decreases in inverse proportion to t1⁄3, i.e. if σ and T are kept constant, the rate of expansion will decrease with time and creep fracture cannot happen.
It is well known that a crack in snow cover appears at the point at which an inclination suddenly changes from gentle to steep and that many avalanches occur on warm days. This fact seems to be one proof of above-mentioned considerations, and our experiments on creep fracture were carried out from such a point of view.
Conclusion
Tensile strain of snow results from the sum of the deformations of connecting ice links, and conforms to the expanded Nutting’s formula.
According to experiment, the strain-rate e is approximately shown by the following proportional expression,
where, t is the elapsing time, σ is the stress, and T is the snow temperature.
If the chain reaction of the fracture of links develops rapidly into the sample, the rate of expansion reaches the maximum and the sample fractures. According to the above equation, the only way to increase the rate is either to increase stress or to raise the temperature, and experiments on creep fracture were carried out in both these ways.


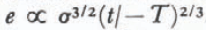 . It is evident from this expression that a creep fracture does not happen without either an increase of stress or a rise of temperature. We observed the phenomenon of creep fracture of snow by these two methods.
. It is evident from this expression that a creep fracture does not happen without either an increase of stress or a rise of temperature. We observed the phenomenon of creep fracture of snow by these two methods.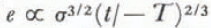 dargestellt werden. Dieser Ausdruck zeigt, dass Kriechbrüche nur bei wachsender Spannung oder zunehmender Temperatur eintreten. Durch beide Massnahmen konnten Kriechbrüche hervorgerufen werden.
dargestellt werden. Dieser Ausdruck zeigt, dass Kriechbrüche nur bei wachsender Spannung oder zunehmender Temperatur eintreten. Durch beide Massnahmen konnten Kriechbrüche hervorgerufen werden.





