No CrossRef data available.
Article contents
Maximum chordal subgraphs of random graphs
Part of:
Graph theory
Published online by Cambridge University Press: 03 May 2024
Abstract
We find asymptotics of the maximum size of a chordal subgraph in a binomial random graph 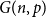 $G(n,p)$, for
$G(n,p)$, for 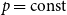 $p=\mathrm{const}$ and
$p=\mathrm{const}$ and 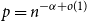 $p=n^{-\alpha +o(1)}$.
$p=n^{-\alpha +o(1)}$.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
*
Michael Krivelevich: Research supported in part by USA-Israel BSF grant 2018267.
References
Alon, N. and Füredi, Z. (1992) Spanning subgraphs of random graphs. Graph Comb. 8 91–94.CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Samotij, W. (2023) Largest subgraph from a hereditary property in a random graph. Discrete Math. 346(9) 113480.10.1016/j.disc.2023.113480CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B. (1998) Finding a large hidden clique in a random graph. Random Struct. Algor. 13 457–466.3.0.CO;2-W>CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs. Cambridge University Press, 2nd edition.10.1017/CBO9780511814068CrossRefGoogle Scholar
Bollobás, B. and Frieze, A. (1991) Spanning maximal planar subgraphs of random graphs. Random Struct. Algor. 2 225–231.10.1002/rsa.3240020206CrossRefGoogle Scholar
Brightwell, G., Panagiotou, K. and Steger, A. (2012) Extremal subgraphs of random graphs. Random Struct. Algor. 41 147–178.CrossRefGoogle Scholar
Buneman, P. (1974) A characterisation of rigid circuit graphs. Discrete Math. 9(3) 205–212.10.1016/0012-365X(74)90002-8CrossRefGoogle Scholar
Coja-Oghlan, A., Moore, C. and Sanwalani, V. (2006) Max
 $k$
-cut and approximating the chromatic number of random graphs. Random Struct. Algor. 28(3) 289–322.10.1002/rsa.20096CrossRefGoogle Scholar
$k$
-cut and approximating the chromatic number of random graphs. Random Struct. Algor. 28(3) 289–322.10.1002/rsa.20096CrossRefGoogle Scholar
Conlon, D. and Gowers, W. T. (2016) Combinatorial theorems in sparse random sets. Ann. Math. 184 367–454.10.4007/annals.2016.184.2.2CrossRefGoogle Scholar
Dekel, Y., Gurel-Gurevich, O. and Peres, Y. (2014) Finding hidden cliques in linear time with high probability. Comb. Prob. Comput. 23(1) 29–49.CrossRefGoogle Scholar
DeMarco, B. and Kahn, J. (2015) Mantel’s theorem for random graphs. Random Struct. Algor. 47 59–72.10.1002/rsa.20535CrossRefGoogle Scholar
Dembo, A., Montanari, A. and Sen, S. (2017) Extremal cuts of sparse random graphs. Ann. Probab. 45(2) 1190–1217.10.1214/15-AOP1084CrossRefGoogle Scholar
Diestel, R. (2017) Graph Theory. Springer, 5th edition.10.1007/978-3-662-53622-3CrossRefGoogle Scholar
Dirac, G. A. (1961) On rigid circuit graphs. Abh. Math. Semin. Univ. Hamburg 25 71–76.CrossRefGoogle Scholar
Erdős, P. and Laskar, R. (1985) A note on the size of a chordal subgraph. In Southeastern International Conference on Graphs, Combinatorics and Computing, Utilitas Mathematica Publishing Co., pp. 81–86.Google Scholar
Gamarnik, D. and Li, Q. (2018) On the max-cut of sparse random graphs. Random Struct. Algor. 52(2) 219–262.CrossRefGoogle Scholar
Garey, M. R. and Johnson, D. S. (1990) Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman & Co.Google Scholar
Gishboliner, L. (2022) Talk at the workshop “Recent advances in probabilistic and extremal combinatorics”, Ascona.Google Scholar
Gishboliner, L. and Sudakov, B. (2023) Maximal chordal subgraphs. Comb. Probab. Comput. 32(5) 724–741.CrossRefGoogle Scholar
Golumbic, M. C. (2004) Algorithmic Graph Theory and Perfect Graphs. Elsevier, 2nd edition.Google Scholar
Golumbic, M. C. (2021) Chordal graphs. In Topics in Algorithmic Graph Theory (Beineke, L. W., Golumbic, M. C. and Wilson, R. J., eds), Encyclopedia of Mathematics and its Applications, Cambridge University Press, pp. 130–151.10.1017/9781108592376.009CrossRefGoogle Scholar
Hoshen, I. and Samotij, W. (2023) Simonovits’s theorem in random graphs. arXiv: 2308.13455.Google Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs. J. Wiley & Sons.CrossRefGoogle Scholar
Juels, A. and Peinado, M. (2000) Hiding cliques for cryptographic security. Des. Codes Cryptogr. 20(3) 269–280.CrossRefGoogle Scholar
Krivelevich, M., Kronenberg, G. and Mond, A. (2023) Turán-type problems for long cycles in random and pseudo-random graphs. J. London Math. Soc. 107 1519–1551.CrossRefGoogle Scholar
Kučera, L. (1991) A generalised encryption scheme based on random graphs. In Graph-Theoretic Concepts in Computer Science, 18th International Workshop (WG 1992), Vol. 570, pp. 180–186.Google Scholar
Micali, S. and Vazirani, V. V. (1980) An
 $O(\sqrt{|V|}|E|)$
algorithm for finding maximum matching in general graphs. In 21st Annual Symposium on Foundations of Computer Science (FOCS 1980), pp. 17–27, Syracuse, NY, USA.10.1109/SFCS.1980.12CrossRefGoogle Scholar
$O(\sqrt{|V|}|E|)$
algorithm for finding maximum matching in general graphs. In 21st Annual Symposium on Foundations of Computer Science (FOCS 1980), pp. 17–27, Syracuse, NY, USA.10.1109/SFCS.1980.12CrossRefGoogle Scholar
Rose, D. J., Tarjan, R. E. and Lueker, G. S. (1976) Algorithmic aspects of vertex elimination on graphs. SIAM J. Comput. 5(2) 266–283.CrossRefGoogle Scholar
Ruciński, A. (1992) Matching and covering the vertices of a random graph by copies of a given graph. Discrete Math. 105 185–197.CrossRefGoogle Scholar
Schacht, M. (2016) Extremal results for random discrete structures. Ann. Math. 184(2) 333–365.CrossRefGoogle Scholar
Vandenberghe, L. and Andersen, M. S. (2015) Chordal graphs and semidefinite optimization. Found. Trends Optim. 1(4) 241–433.10.1561/2400000006CrossRefGoogle Scholar



