Introduction

A snow avalanche is the result of many complicated physical processes operating both in the snowpack and during the gravity-driven motion of the snow masses along the slope. Traditionally, an avalanche process can be divided into two stages, namely, origin and motion of the snow avalanche. In general, modelling of the instability of the snow masses on the slope and determining their motion along the track are carried out as separate units. At the same time, it is necessary to consider an avalanche process as a single event due to continuity of the overall process. To be precise, the output data concerning the problem of stability of snowpack on the slope are the input data for the models describing the avalanche motion. More specifically, for each unstable volume of snow initially made available for the motion, all basic dynamic characteristics of the avalanche are determined.

At the present time, there are a number of deterministic, physically proven, mathematical models that allow description of the processes of the avalanche origin and motion (Reference GrigoryanGrigoryan, 1979; Reference EglitEglit, 1986, Reference Eglit and Hestnes1998; Reference Bozhinskiy and LosevBozhinskiy and Losev, 1987; Reference Nefed’ev and BozhinskiyNefed’ev and Bozhinskiy, 1989). However, the parameters and input data of the models have both a regional and random nature. In the end, evaluation of the dynamic characteristics of the avalanche leads in many cases to large scatter of the output results. For this reason, it is necessary to construct the probabilistic models for the avalanche process. A random distribution of snow depth and strength of the snowpack in the avalanche starting zone leads to corresponding random distributions of the initial volume of snow that participates in the motion, and consequently yields random distributions of the dynamic characteristics of the avalanche, namely, velocity and depth of avalanche body, run-out distance and pressure on the protective structures. An approach in which parameters and/or input data of the deterministic mathematical model are considered as random variables was applied to estimate the stress state and stability of the snow cover on the slope (Reference BozhinskiyBozhinskiy, 1979; Reference Bozhinskiy and ChernoussBozhinskiy and Chernouss, 1986; Reference Chernouss and FedorenkoChernouss and Fedorenko, 1998). Reference BozhinskiyBozhinskiy (1992, Reference Bozhinskiy1994) obtained the probabilistic estimations of snow-avalanche and debris-flow velocities using this approach and deterministic analytical formulas for the velocities.

In this paper, a simplified version of a probabilistic model of snow-avalanche dynamics is developed. An initial volume of snow participating in the motion is prescribed as a random variable, which is an input parameter of the dynamic model. Generally, this volume must be determined by using the solution of the problem of equilibrium and stability of the snow cover on a mountain slope.

Probabiilistic Model

The deterministic one-dimensional hydraulic model is a basis for the probabilistic model of the avalanche motion. This model acts as an operator. The system of the model equations has the following form. The mass-conservation equation is

whilst the momentum-conservation equation is

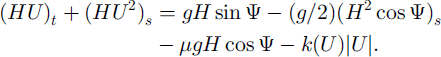
In Equations (1) and (2) H and U are the depth and velocity of the avalanche body, respectively, Ψ is the local slope angle, q_b is the rate of specific snow volume (per unit area of the bottom), g is the gravity acceleration, μ and k are the coefficients of dry and turbulent friction, respectively, s is the coordinate along the slope and t is time. The round brackets with attached lower index designate partial derivatives with respect to the variable, indicated by this index. The avalanche density p is assumed constant.

The specific volume of snow masses entrained into the motion is assumed to be proportional to the avalanche velocity

where me is the non-dimensional coefficient of entrainment. Finally, the snow-cover thickness during the avalanche motion on the slope diminishes according to

Let us consider the dynamic model, formulated above, as a probabilistic one, in such a way that the input data and/or the model parameters are random variables. Because the distribution laws of these variables are unknown in general, three kinds of distributions were considered (Reference VentselVentsel, 1969).

(i) Uniform law, u

where / is the probability density and M and D are the mathematical expectation and dispersion of the random variable a;, respectively.

(ii) Normal law, n

(iii) Exponential law, e

where A is the parameter of the distribution.

It should be emphasized that the uniform and normal laws are symmetric, whilst the exponential law is not. Thus, there is a sufficiently wide scope for description of output model characteristics. In order to compare the different distribution laws, it will be assumed that the mathematical expectations for all distribution laws of the input variables are equal:

For the dispersion coefficients this condition cannot fully be observed since

i.e. the dispersion coefficient of the exponential law, because of its structure, is three times higher than the dispersions of the uniform and normal laws.

Numerical Results and Discussion

The above probabilistic model of the snow-avalanche motion was used to evaluate the dynamic avalanche characteristics and run-out distance for the avalanche path No. 22 in Khibiny, Russia. This path is situated on the southern slope of the Yukspor mountains. It is a bow with west-northwestern-northern exposure. The starting zone has an average inclination of 33°, maximum width of 470 m and an area of 1.87 ×104m2. The avalanche slope consists of a rocky surface in the upper part and is covered by moss, lichen and bushes in the lower part. The average inclination of the run-out zone is 9°, and the maximum width is 175 m. The longitudinal profile of the avalanche path is depicted in Figure 1. Avalanche observations were started here in 1935 after a huge accident. The total number of registered avalanches is about 90, but only 30 of them were sufficiently described and analyzed in this paper. Usually, avalanches occur here a few times per year, and many of them are artificially triggered by mortar firing. In 1985, an avalanche protection was built in the run-out zone to protect rail and automobile roads and domestic buildings. The data used in the work were taken from such previous events.

Fig. 1. Longitudinal profile of avalanche path Mo. 22, Khibiny. The initial and final avalanche volumes are shown schematically in conditional units of thickness. s₀ is the position of the center of gravity of the initial volume; s* is the stop point of the avalanche front.

Two series of numerical experiments were carried out. In the first series the random variables were the thickness h of the snow cover, which lost stability in the starting zone (the input data), and the coefficient k of the turbulent friction (the model parameter). The other model parameters, length and location of the unstable zone were taken as deterministic. The ranges of the random variables h and k were prescribed, respectively, as follows: 0.1 ≤ h ≤ 1.3 m and 1 × 10∼³ ≤ k ≤ 11 × 10–³. Every range was divided into 10 equal intervals. Then the model Equations (1–4) were solved numerically. Thus, for the output model characteristics the square matrix of 10 × 10 values, corresponding to the intervals of division, was obtained. It was assumed that the random variables h and k are independent. Thus, the probability of the realization of each output model characteristic, corresponding to the matrix of values, was equal to the product of the probabilities h and k of the corresponding intervals (Reference VentselVentsel, 1969). For example, for a uniform distribution, the probability of realization of any element belonging to the matrix of values is equal to 0.01. For the two other distributions (normal and exponential), the probabilities of realization of the matrix element are different. Thus, for each dynamic characteristic, the artificial series consisting of 100 terms was constructed.

In the first series of numerical experiments, the value of dry-friction coefficient μ was equal to 0.25. The snow-cover thickness along the slope was 1 m and the coefficient of entrainment was equal to 0.003. The center of gravity of the initial released snow mass was situated at the point s₀ = 200 m on the profile (origin of coordinate is on the top point of profile; see Fig. 1). According to this set of the model parameters, a run-out distance of about 1400 m (along the slope) was achieved. This point on the profile corresponds to the beginning of the flatter part of the slope. The whole range of run-out distances was 1000–1400 m. In the numerical computations, the values of the front velocity, height and volume (per unit width) of the avalanche body were calculated at the points s =1000, 1200, 1300 m. At the stop points of the avalanche front, the location, maximum depth and volume (per unit width) of the avalanche deposits were determined.

The histograms and distribution functions were constructed using the matrix of values of the output model characteristics. The plots of the distribution functions of the front velocity at the position s = 1000 m are shown in Figure 2. The curves illustrate a relatively weak influence of the distribution laws for input data and model parameters on the distribution function for output data. The maximum difference occurs for moderate values of the velocity. For large values of the front velocities, differences are small, and the curves, corresponding to uniform, normal and exponential distribution laws of h and k, merge into a single curve. Similar results also arise for the distribution functions of other output characteristics, namely, the height of the front, the run-out distance, the depth and the volume of the avalanche deposits.

Fig. 2. Distribution functions of the avalanche front velocity at the slope point s = 1000 m. Symbols •, o, + correspond to uniform, normal and exponential distribution laws, respectively.

The three variables (the length I of snow slab in the starting zone and the coefficients of dry and turbulent friction) were taken as random variables during the second series of numerical experiments. The snow-cover thickness in the rupture zone was prescribed and set equal to the mean value 0.7 m, observed in the field conditions. This was due to a smaller coefficient of variation (C_h = 0.56) for the thickness of the ruptured snow slab in comparison with the coefficient of variation (Q = 1.39) for the length of snow slab that was set in motion. The other deterministic parameters were the same as in the first series of numerical tests. The uniform distribution law was assumed for all three random variables l,μ,k in the ranges: 100 ≤l ≤ 280 m, 0.20 ≤ _μ ≤ 0.45, 2.5 × 10–³ ≤ k \≤ 10 × 10–³. Every range was divided into six equal intervals. Therefore, for the output model characteristics the cubic matrix consisting of 6³ = 216 elements was obtained. Thus, the probability of realization of output characteristics from the matrix of values was set equal to 4.63 × 10–³. During the numerical modelling process, the location of the stop point of the avalanche front, the maximum depth and the volumes (per unit width) of the avalanche deposits were calculated.

The histogram of the stop points of the avalanche front (the run-out distance) is depicted in Figure 3. The distribution is characterized by positive asymmetry and negative excess. The modal value is shifted to the left. The model and empirical distribution functions, corresponding to the stop points of the avalanche front, are shown in Figure 4. The solid and dashed curves correspond to the three and two random parameters, respectively. The correlation between model (the solid curve) and field observations is good, practically over the whole range of the run-out distance. The exclusion occurs for small run-out distances, which are not overlapped by the deterministic model of avalanche motion under the assumed set of parameters. The dashed curve agrees with the field data within the large run-out distances. The maximum avalanche runout distance, derived by statistical modelling, was equal to 1387 m, whereas over the whole 50 year period of observations it was equal to 1373 m. The model and empirical distribution functions of the maximum depth of avalanche deposits are given in Figure 5. Here the model curve agrees also with field data, but in the whole, the calculated values of maximum depths of the avalanche deposits are about 1 m higher. The model and empirical distribution functions of the volumes (per unit width) of avalanche deposits are shown in Figure 6. The model overestimates and underestimates the volumes of avalanche deposits, respectively, for small and large probabilities close to unit. Thus, on the whole, the probabilistic model, which uses sufficiently restricted input information, gives good estimates of avalanche dynamic characteristics.

Fig. 3. Histogram of avalanche run-out distance.

Fig. 4. Model and empirical (•) distribution functions of avalanche run-out distance.

Fig. 5. Model and empirical (•) distribution functions for maximum thickness of avalanche deposits.

Fig. 6. Model and empirical (•) distribution functions for volumes (per unit width) of avalanche deposits.

Conclusions

The derived probabilistic model of snow-avalanche dynamics allows calculation of the probability of all dynamic characteristics of the avalanche body along the prescribed avalanche path. These characteristics are the velocity and the height of front, the pressure on any obstacle at any point of slope, the run-out distance, the maximum depth and the volume (per unit width) of avalanche deposits. By using these probabilistic estimations, the model provides the possibility of making a zoning of a territory with regard to the degree of avalanche danger. For model calculations, information about approximate ranges of released snow-slab volumes and several model parameters (coefficients of friction, and possibly coefficient of snow entrapment) is needed. As shown in this paper, and also before (Reference BozhinskiyBozhinskiy, 1992), the influence of the distribution laws for the input data and model parameters on the distribution function of the output model characteristics, especially near large, rather rare values, is relatively weak. Thus, the uniform (or normal) distribution law can be assumed for the input data and model parameters. The number of random input variables may be extended, but in this case the volume of the matrix of values for the output model characteristics will strongly increase.

Further advance in the development of the probabilistic models describing the origin and motion of snow avalanche is connected with the solution of a conjugate problem. The problem of determination of the stress state in the snow cover on the slope, and, correspondingly, of initial volume of snow entrained into the motion, must be matched with the dynamic problem.

Acknowledgement

This paper was financially supported by the Russian Fund of Basic Researches, grant Nos. 99–05–65166 and 00–15–98502.