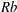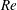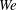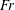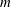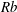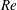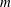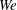1 Introduction
Nanofibres with diameters of less than a few hundred nanometres have remarkable properties such as immense surface-to-volume ratio, giving them significant applications in artificial tissues, carbon fibres, filtration membranes, sensors, to name a few (see e.g. Huang et al. Reference Huang, Zhang, Kotaki and Ramakrishna2003). One of the main factors in manufacturing nanofibres is the production technique, which influences the fibre shape, the fibre radius, the web porosity and the production rate. There exist several methods to produce nanofibres, which may be mainly categorized into four groups: electrospinning, melt blowing, bicomponent fibre spinning and centrifugal spinning (Nayak et al. Reference Nayak, Padhye, Kyratzis, Truong and Arnold2011). The three former techniques suffer from a variety of limitations such as low production rates (per nozzle), high operation costs and smaller ranges of material choice. Recently, centrifugal spinning methods have received considerable attention since they have the potential to eliminate these limitations.
Recent nanofibre fabrication techniques based on the centrifugal acceleration, such as Forcespinning® (Padron et al.
Reference Padron, Fuentes, Caruntu and Lozano2013) and rotary jet spinning (RJS) (Badrossamay et al.
Reference Badrossamay, Mcllwee, Goss and Parker2010), are conceptually similar in that fast rotation is employed to apply high stresses on the fibre to yield its considerable thinning rate. For example, in Forcespinning®, illustrated schematically in figure 1, a polymeric liquid (solution or melt) is loaded into a specially designed spinneret with several nozzles that rotates at a considerable speed, e.g.
$10^{3}{-}10^{4}$
r.p.m. The centrifugal force pushes the polymeric liquid through the spinneret nozzles, resulting in continuous polymer jets. The trajectories of these emerging jets are highly curved due to the rotational forces as they are stretched into very thin fibres, which will either break up or be collected as a fine web of nanofibres on the collectors positioned away from the rotation centre.
Figure 1. Schematic view of nanofibre formation through one of the recent methods of nanofibre fabrication by centrifugal spinning, i.e. Forcespinning®: (a) depiction of spinneret, orifices and rotating frame of reference; (b) closer view of the orifice and depiction of the jet with curvilinear coordinate system, fibre centreline and fibre angles in the horizontal (
$\unicode[STIX]{x1D6FC}$
) and vertical (
$\unicode[STIX]{x1D6FD}$
) planes.
There exist a few scholarly articles that experimentally study nanofibre fabrication by various centrifugal spinning methods, essentially to evaluate the effects of the process parameters such as fibre temperature (Sedaghat, Taheri-Nassaj & Naghizadeh Reference Sedaghat, Taheri-Nassaj and Naghizadeh2006; Wang et al. Reference Wang, Shi, Liu, Secret and Chen2011), polymer concentration (Lu et al. Reference Lu, Li, Zhang, Xu, Fu, Lee and Zhang2013; Ren et al. Reference Ren, Pandit, Elkin, Denman, Cooper and Kotha2013) as well as rotational speed and orifice size (Weitz et al. Reference Weitz, Harnau, Rauschenbach, Burghard and Kern2008; Badrossamay et al. Reference Badrossamay, Mcllwee, Goss and Parker2010; Vazquez, Vasquez & Lozano Reference Vazquez, Vasquez and Lozano2012; Mary et al. Reference Mary, Senthilram, Suganya, Nagarajan, Venugopal, Ramakrishna and Giri Dev2013). In a detailed study using high-speed photography, Padron et al. (Reference Padron, Fuentes, Caruntu and Lozano2013) explored the effects of several controllable parameters on fibre trajectory and final fibre radius, finding for example that both increasing spinneret angular velocity and decreasing polymer concentration result in thinner fibres. Although an experimental approach seems to be promising in uncovering the general effects of a number of parameters on nanofibre formation, this method is time consuming and the large number of the parameters involved makes it extremely hard to have a comprehensive understanding of the physics of the problem. This is where mathematical modelling comes to aid.
The literature of mathematical modelling of curved jets is mature thanks to the works of Decent, King & Wallwork (Reference Decent, King and Wallwork2002), Wallwork et al. (Reference Wallwork, Decent, King and Schulkes2002), Părău et al. (Reference Părău, Decent, Simmons, Wong and King2007), Marheineke & Wegener (Reference Marheineke and Wegener2009) and many other researchers, using asymptotic methods. There also exist a number of relevant studies concerning non-Newtonian fluids, e.g. Uddin, Decent & Simmons (Reference Uddin, Decent and Simmons2008), Uddin & Decent (Reference Uddin and Decent2009), Hawkins et al. (Reference Hawkins, Gurney, Decent, Simmons and Uddin2010), Uddin & Decent (Reference Uddin and Decent2010) and Marheineke et al. (Reference Marheineke, Liljegren-Sailer, Lorenz and Wegener2016). Although the majority of the previous studies have examined jet breakup through stability analyses, the analysis methods can well be used to study the trajectory and thinning of the radius of curved jets. These models are based on zeroth-order slender body theories (commonly referred to as ‘string’ models), whose small parameter is the ratio of the fibre radius to the radial position of the orifice, and they provide a relatively simple framework to analyse the fibre behaviours. While relatively simple, however, these models are known to suffer from debilitating limitations (e.g. near-orifice singularities) so that their applicability is only restricted to certain parameter ranges. For example, Götz et al. (Reference Götz, Klar, Unterreiter and Wegener2008) and Arne et al. (Reference Arne, Marheineke, Meister and Wegener2010) have proved that the string models have no physically relevant stationary solutions if
$Re\,Rb^{2}<1$
(see table 1 for definitions). As will be seen, the regime of moderate
$Re$
and small
$Rb$
is, however, the regime of high spinning speeds and viscous fibres, the most relevant regime in the production of nanofibres by all centrifugal spinning methods.
Table 1. Dimensionless parameter definitions and their approximate estimated ranges in centrifugal spinning methods with polymer solutions.
a These values are estimated based on the rheology of poly(ethylene oxide) solutions (Ebagninin, Benchabane & Bekkour Reference Ebagninin, Benchabane and Bekkour2009) at relevant polymer concentrations which have been used for nanofibre fabrication experiments (Padron et al. Reference Padron, Fuentes, Caruntu and Lozano2013).
So far, a few studies have been performed to overcome the string model limitations, e.g. the development of rod models (see e.g. Mahadevan & Keller (Reference Mahadevan and Keller1996), Ribe (Reference Ribe2004) and Ribe, Habibi & Bonn (Reference Ribe, Habibi and Bonn2006)), where fully coupled conservative equations of mass, linear and angular momentum are solved to predict the twisting and coiling of a curved jet. More relevant to our work, for glass wool spinning applications, Arne et al. (Reference Arne, Marheineke, Meister and Wegener2010) developed a Cosserat rod theory to model a curved jet in a two-dimensional stationary frame. Despite their superiority, the rod models are increasingly harder to derive as more dimensionless parameters (especially non-Newtonian ones) are included, and the equations are numerically stiffer than for the corresponding string models. For very thin fibres (i.e. small slenderness parameter) and fast rotations, the principal gain of rod models is the removal of the near-orifice singularity, making stable solutions possible, while the model equations revert to the string equations slightly away from the orifice. Another approach to remove the singularity of the string models is to omit the fibre angle boundary condition in favour of an interface condition to ensure the regularity of the string quantities (see e.g. Arne, Marheineke & Wegener Reference Arne, Marheineke and Wegener2011). The other alternative is to employ a regularized model, recently proposed by Taghavi & Larson (Reference Taghavi and Larson2014) for two-dimensional Newtonian flows (without surface tension), where the main idea is to add a simple regularization term resulting from higher-order terms to the string equations, yielding their stable solutions.
In centrifugal spinning methods, the industrially important features of nanofibres such as fibre radius and defect formation are governed by the spinneret angular velocity, orifice radius, viscosity, shear thinning and viscoelastic properties, surface tension, temperature, evaporation, etc. By thoughtfully varying these parameters, satisfactory control over the fibre radius and the web morphology may become possible. In this work, we develop a general regularized string model that overcomes past numerical limitations and allows determination of the three-dimensional steady fibre jet features while considering centrifugal, Coriolis, inertial, viscous, shear-thinning, surface tension and gravitational forces of arbitrary magnitudes. For our application of interest, the relevant ranges of the dimensionless groups formed by these forces are presented in table 1. String theory has so far failed to provide steady solutions for these parameter ranges.
Before we proceed, it is worth highlighting a distinction between the current work and the previous studies that extend the slender jet theory of Wallwork (Reference Wallwork2001) (e.g. Decent et al. (Reference Decent, King and Wallwork2002), Părău et al. (Reference Părău, Decent, Simmons, Wong and King2007), etc.). Inspired by their industrial applications (e.g. the prilling process) and experimental observations (Wallwork et al.
Reference Wallwork, Decent, King and Schulkes2002), this body of work concentrates on liquid jets that quickly break up into droplets (due to flow instabilities), on a length scale of the order of the spinneret radius. Even though Wallwork’s (Reference Wallwork2001) steady state equations are not generally valid in the limit of small
$Rb$
(due to the singularities discussed above), for certain parameters their analysis based on the time-dependent wave motion reveals that a jet either does not form at all or is extremely short and rapidly atomizes into droplets due to capillary instability. On the other hand, the experimental observations in centrifugal spinning processes suggest a large jet breakup length in many applications, and this length is a function of many factors, e.g. polymer solution properties, which may stabilize the flow or slow the growth of the capillary instability. Therefore, the parameter regime of interest in this paper considers a different small-
$Rb$
scenario, with low Reynolds number that is not accessible to the analysis of Wallwork, and where the jet is expected to be less susceptible to capillary breakup due to its higher viscosity.
The outline of the paper is as follows. In § 2, the geometry of the problem, the governing equations, the asymptotic method to derive the reduced model equations and the regularization approach are discussed. In § 3, our model results and discussion are presented for the dimensionless parameter ranges associated with nanofibre fabrication by centrifugal spinning methods. The effects of each parameter are evaluated on the fibre behaviours and fibre radius thinning regimes are presented where possible. Section 4 concludes the paper with a brief summary.
2 Problem formulation
In this section, we derive the asymptotic model equations of a single curved jet, which emerges with a normal speed of
$U$
from a nozzle of a cylinder/spinneret of radius
$s_{0}$
rotating about its axis of symmetry. The rotation angular speed,
$\unicode[STIX]{x1D6FA}$
, is constant in the counter-clockwise direction (see figure 1
a). In most experimental situations, there are several liquid jets that emerge from the nozzles of the spinneret; however, in the current study, we neglect the effects of the liquid jets on one another by focusing on one nozzle. We assume that the orifice of the nozzle is circular, with radius
$a_{0}$
, which is typically much smaller than the radius of the spinneret,
$s_{0}$
. We assume that the initial cross-sectional area of the fibre is equal to that of the circular orifice while the fibre radius,
$R$
, also always satisfies
$R/s_{0}\ll 1$
. Motivated by our application, we also consider that the fibre stretches and becomes very long before reaching the collectors away from the rotation centre. In this work, we consider the effects of centrifugal, Coriolis, gravity, surface tension, viscous and non-Newtonian power-law rheology on the fibre key features. Although for simplicity, we neglect the possible effects of mass transfer, heat transfer, viscoelasticity and air drag, we highlight that our formulation should allow us to include these effects, without any inherent difficulties, e.g. without the well-known singularities observed in similar asymptotic models.
We also note that the details of the fibre behaviour near the orifice depend on the flow inside the orifice and on the local contact line dynamics. The latter affects the fibre flow at the liquid–solid–gas contact line, which can have significant effects within an arc length of
$O(l_{c})$
with
$l_{c}$
being the characteristic capillary length. We acknowledge that in this work, in accordance with previous mathematical studies of similar fibre flows, we neglect the complex near-orifice behaviours, including the effects of the contact angle between the solid surface and the free-surface flow at the nozzle exit.
To write the governing equations in our system, we consider a reference frame with the coordinate system
$(x,y,z)$
that rotates with the angular speed
$\unicode[STIX]{x1D6FA}$
so that the orifice from which the liquid jet emerges is fixed (see figure 1
b). Therefore, the equations of motion and continuity in the rotating frame can be expressed as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}p+\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}+\boldsymbol{g}-2\unicode[STIX]{x1D74E}\times \boldsymbol{u}-\unicode[STIX]{x1D74E}\times (\unicode[STIX]{x1D74E}\times \boldsymbol{r}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
where
$t$
denotes time,
$\unicode[STIX]{x1D70C}$
the fluid density and
$p$
the pressure within the liquid jet. Also,
$\boldsymbol{g}=(0,-g,0)$
,
$\unicode[STIX]{x1D74E}=(0,\unicode[STIX]{x1D6FA},0)$
,
$\boldsymbol{r}^{\prime }=(x+s_{0},y,z)$
and
$\boldsymbol{u}$
and
$\unicode[STIX]{x1D64F}$
are the velocity field and the deviatoric stress tensor, respectively. We assume that the polymeric liquid fibre obeys a power-law model described by
$\unicode[STIX]{x1D64F}=k\dot{\unicode[STIX]{x1D6FE}}^{m-1}\dot{\unicode[STIX]{x1D6FE}}_{ij}$
, where
$k$
is the consistency,
$m$
the power-law index,
$\dot{\unicode[STIX]{x1D6FE}}_{ij}$
the shear-rate tensor and
$\dot{\unicode[STIX]{x1D6FE}}$
the second invariant.
Since the emerging trajectory is highly curved, it would be difficult to analyse the forces acting on the jet in a Cartesian coordinate system. For that reason, following Wallwork et al. (Reference Wallwork, Decent, King and Schulkes2002), to ease the analytical approach we track the curved jet in an orthogonal curvilinear coordinate system
$(s,n,\unicode[STIX]{x1D711})$
, in which
$s$
is the arc length along the centreline of the jet with respect to the orifice and
$(n,\unicode[STIX]{x1D711})$
are the plane polar coordinates in the radial and azimuthal directions within the cross-section of the jet. This coordinate system has the unit vectors indicated by
$\boldsymbol{e}_{s}$
,
$\boldsymbol{e}_{n}$
and
$\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
. The velocity vector can be therefore given as
$\boldsymbol{u}=u\boldsymbol{e}_{s}+v\boldsymbol{e}_{n}+w\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
. With its origin at the orifice centre, (denoted by
$O$
in figure 1
a), the position of the liquid jet centreline is described by Cartesian coordinates
$(X(s,t),Y(s,t),Z(s,t))$
. Note that in the coordinate system adopted, the
$x$
-axis is normal to the surface of the spinneret in the jet initial direction while the
$z$
-axis and
$y$
-axis are normal to the
$x$
-axis in the jet centreline planes. Therefore, along the arc length, positive values of
$z$
are in the direction opposite to the motion of the spinneret and negative values of
$y$
are in the direction of gravity. In this work, we focus on the steady state problem.
2.1 Equations in curvilinear coordinate system
We present the equations of motion and continuity in the curvilinear coordinate system, which is convenient to describe the fibre. To do so, we need to first determine the scale factors
$(h_{s},h_{n},h_{\unicode[STIX]{x1D711}})$
in such a system to derive the equations. More detail on the derivation of the scale factors in a three-dimensional frame in the orthogonal curvilinear coordinate system can be found in Wallwork (Reference Wallwork2001). These are
$$\begin{eqnarray}h_{n}=1,\quad h_{\unicode[STIX]{x1D711}}=n,\quad h_{s}=\left|\frac{\unicode[STIX]{x2202}\boldsymbol{r}}{\unicode[STIX]{x2202}s}\right|,\end{eqnarray}$$
where
$\boldsymbol{r}$
is the position vector relative to the orifice, i.e.
$\boldsymbol{r}=\int _{0}^{s}\boldsymbol{e}_{s}\,\text{d}s+n\boldsymbol{e}_{n}$
. Using the scale factors defined, we can now write the equations of motion at steady state in our orthogonal curvilinear coordinate system:
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{u_{i}}{h_{i}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}i}+\frac{u_{j}}{h_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}j}+\frac{u_{k}}{h_{k}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}k}-u_{j}\left(\frac{u_{j}}{h_{j}h_{i}}\frac{\unicode[STIX]{x2202}h_{j}}{\unicode[STIX]{x2202}i}-\frac{u_{i}}{h_{j}h_{i}}\frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}j}\right)-u_{k}\left(\frac{u_{k}}{h_{k}h_{i}}\frac{\unicode[STIX]{x2202}h_{k}}{\unicode[STIX]{x2202}i}-\frac{u_{i}}{h_{k}h_{i}}\frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}k}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{h_{i}\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}i}+V_{i}+G_{i}+RO_{i},\end{eqnarray}$$
in which
$i$
,
$j$
and
$k$
are index variables denoting the directions
$s$
,
$n$
and
$\unicode[STIX]{x1D711}$
. Furthermore,
$V$
,
$G$
and
$RO$
stand for viscous, gravitational and rotational (comprising Coriolis and centrifugal) terms, respectively, given in appendix A. The continuity equation in our curvilinear coordinate system can be expressed as follows:
$$\begin{eqnarray}n\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}s}+h_{s}v+nv\frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}n}+nh_{s}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}n}+w\frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}+h_{s}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}=0.\end{eqnarray}$$
2.2 Kinematic condition
The boundary condition at the surface of the jet is defined using a function
$R(s,\unicode[STIX]{x1D711})$
. According to the kinematic condition, a surface element can be characterized through
$(\text{D}/\text{D}t)(n-R(s,\unicode[STIX]{x1D711}))$
at
$n=R$
. Using the velocity vector and the material operator in the curvilinear coordinate system, the kinematic condition can be represented as
$$\begin{eqnarray}\frac{u}{h_{s}}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}s}+\frac{w}{n}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}=v.\end{eqnarray}$$
2.3 Stress conditions
Now, we proceed to derive the equations of the normal and tangential stress boundary conditions at the interface of the steady jet (
$n-R(s,\unicode[STIX]{x1D711})=0$
). The unit normal vector to the surface of the jet can be obtained as
$$\begin{eqnarray}\boldsymbol{n}=\frac{\unicode[STIX]{x1D735}(n-R(s,\unicode[STIX]{x1D711}))}{|\unicode[STIX]{x1D735}(n-R(s,\unicode[STIX]{x1D711}))|}=\frac{1}{E}\left(-\frac{1}{h_{s}}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}s},1,-\frac{1}{R}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right),\end{eqnarray}$$
where
$E$
is the magnitude of the normal vector:
$$\begin{eqnarray}E=\left(1+\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}s}\frac{1}{h_{s}}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\frac{1}{R}\right)^{2}\right).\end{eqnarray}$$
The tangent vectors at the interface can be derived as
$$\begin{eqnarray}\boldsymbol{t}_{\mathbf{1}}=\boldsymbol{e}_{\boldsymbol{s}}+\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}s}\frac{1}{h_{s}}\boldsymbol{e}_{\boldsymbol{n}},\quad \boldsymbol{t}_{\mathbf{2}}=\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\frac{1}{R}\boldsymbol{e}_{\boldsymbol{n}}+\boldsymbol{e}_{\unicode[STIX]{x1D711}}.\end{eqnarray}$$
Using the normal stress balance at the interface we can obtain
$$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{n}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D706},\end{eqnarray}$$
where
$\unicode[STIX]{x1D64F}$
is the stress tensor,
$\unicode[STIX]{x1D70E}$
is the surface tension and
$\unicode[STIX]{x1D706}$
is the free-surface curvature defined as
$$\begin{eqnarray}\unicode[STIX]{x1D706}=\frac{1}{nh_{s}}\left(-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left(\frac{n}{Eh_{s}}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}s}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}n}\left(\frac{nh_{s}}{E}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\left(\frac{h_{s}}{nE}\frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right)\right).\end{eqnarray}$$
The stress tensor components (
$\unicode[STIX]{x1D61B}_{ij}$
) in the curvilinear coordinate system can be obtained as (see e.g. Batchelor Reference Batchelor2000)
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D61B}_{ii}=-p+2\unicode[STIX]{x1D702}e_{ii},\\ \unicode[STIX]{x1D61B}_{jk}=\unicode[STIX]{x1D702}e_{jk},\end{array}\right\}\end{eqnarray}$$
where
$\unicode[STIX]{x1D702}$
is the apparent viscosity and
$e_{ii}$
and
$e_{jk}$
are the strain-rate components computed as (see e.g. Cobble, Smith & Mulholland (Reference Cobble, Smith and Mulholland1973) and Batchelor (Reference Batchelor2000))
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle e_{ii}=\frac{1}{h_{i}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{i}}+\frac{u_{j}}{h_{i}h_{j}}\frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{u_{k}}{h_{i}h_{k}}\frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}x_{k}},\\ \displaystyle e_{jk}=\frac{h_{k}}{2h_{j}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left(\frac{u_{k}}{h_{k}}\right)+\frac{h_{j}}{2h_{k}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{k}}\left(\frac{u_{j}}{h_{j}}\right),\quad e_{jk}=e_{kj}.\end{array}\right\}\end{eqnarray}$$
Note that the Einstein summation convention is not being used in (2.12) and (2.13). Ignoring the effects of air–jet interactions, the tangential stress conditions on the free surface are expressed as
$$\begin{eqnarray}\displaystyle & \boldsymbol{t}_{\mathbf{1}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{n}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{t}_{\mathbf{2}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}\boldsymbol{\cdot }\boldsymbol{n}=0. & \displaystyle\end{eqnarray}$$
In order to generalize our work, we shall proceed with the dimensionless form of our equations, using the following transformations where the bars indicate the dimensionless quantities:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \bar{u}=\frac{u}{U},\quad \bar{v}=\frac{v}{U},\quad \bar{w}=\frac{w}{U},\\ \displaystyle n=\frac{n}{a},\quad \bar{R}=\frac{R}{a},\\ \displaystyle \bar{s}=\frac{s}{s_{0}},\quad \bar{t}=\frac{tU}{s_{0}},\quad \bar{X}=\frac{X}{s_{0}},\quad \bar{Y}=\frac{Y}{s_{0}},\quad \bar{Z}=\frac{Z}{s_{0}},\\ \displaystyle \bar{p}=\frac{p}{\unicode[STIX]{x1D70C}U^{2}},\quad \bar{\unicode[STIX]{x1D702}}=\frac{\unicode[STIX]{x1D702}}{k\left({\displaystyle \frac{U}{s_{0}}}\right)^{(m-1)}}.\end{array}\right\}\end{eqnarray}$$
The definitions of the dimensionless groups resulting from the scalings above are listed in table 1. Hereafter, all the bars will be dropped for convenience.
2.4 Asymptotic analysis
We assume that the jet is a relatively long, slender, thin object which has an aspect ratio
$\unicode[STIX]{x1D700}=a_{0}/s_{0}$
. In nanofibre formation applications, the slenderness parameter
$\unicode[STIX]{x1D700}$
is very small, which may allow for the use of the leading-order terms as a reasonable estimate to the leading-order behaviours of the fibre. We therefore expand velocities, stresses and pressure in series of
$\unicode[STIX]{x1D700}n$
and
$R$
,
$X$
,
$Z$
,
$Y$
in series of
$\unicode[STIX]{x1D700}$
(see Eggers (Reference Eggers1997) and Hohman et al. (Reference Hohman, Shin, Rutledge and Brenner2001)). In this context,
$u$
,
$v$
,
$w$
and
$p$
are expanded in series with respect to
$\unicode[STIX]{x1D700}n$
and the rest of the variables are expanded in
$\unicode[STIX]{x1D700}$
:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u(s,n,\unicode[STIX]{x1D711})=u_{0}(s)+(\unicode[STIX]{x1D700}n)u_{1}(s,\unicode[STIX]{x1D711})+(\unicode[STIX]{x1D700}n)^{2}u_{2}(s,\unicode[STIX]{x1D711})+\cdots ,\\ v(s,n,\unicode[STIX]{x1D711})=(\unicode[STIX]{x1D700}n)v_{1}(s,\unicode[STIX]{x1D711})+(\unicode[STIX]{x1D700}n)^{2}v_{2}(s,\unicode[STIX]{x1D711})+\cdots ,\\ w(s,n,\unicode[STIX]{x1D711})=(\unicode[STIX]{x1D700}n)w_{1}(s,\unicode[STIX]{x1D711})+(\unicode[STIX]{x1D700}n)^{2}w_{2}(s,\unicode[STIX]{x1D711})+\cdots ,\\ p(s,n,\unicode[STIX]{x1D711})=p_{0}(s,\unicode[STIX]{x1D711})+(\unicode[STIX]{x1D700}n)p_{1}(s,\unicode[STIX]{x1D711})+\cdots ,\\ R(s,n,\unicode[STIX]{x1D711})=R_{0}(s)+\unicode[STIX]{x1D700}R_{1}(s,\unicode[STIX]{x1D711})+\cdots ,\\ X(s,n,\unicode[STIX]{x1D711})=X_{0}(s)+\unicode[STIX]{x1D700}X_{1}(s)+\cdots ,\\ Z(s,n,\unicode[STIX]{x1D711})=Z_{0}(s)+\unicode[STIX]{x1D700}Z_{1}(s)+\cdots ,\\ Y(s,n,\unicode[STIX]{x1D711})=Y_{0}(s)+\unicode[STIX]{x1D700}Y_{1}(s)+\cdots .\end{array}\right\}\end{eqnarray}$$
To derive the leading-order equations, we also need to determine and expand
$h_{s}$
(i.e. the scale factor associated with the
$s$
-direction) as function of
$s$
,
$n$
and
$\unicode[STIX]{x1D711}$
in our curvilinear coordinate system. Using the definition of the position vector and after some lengthy algebra,
$h_{s}$
can be obtained as
$$\begin{eqnarray}h_{s}=1+\unicode[STIX]{x1D700}n\cos (\unicode[STIX]{x1D711})\mathbb{S}_{0}+O(\unicode[STIX]{x1D700}^{2}),\end{eqnarray}$$
where
$\mathbb{S}_{0}=-\sqrt{X_{0ss}^{2}+Y_{0ss}^{2}+Z_{0ss}^{2}}$
with the subscript
$s$
representing a derivative with respect to
$s$
here and thereafter.
Finally, we proceed to obtain the leading- and first-order terms of the apparent viscosity to be used in our set of equations. Since the power-law constitutive equation is used to evaluate the shear-thinning effects on nanofibre formation, the dimensionless apparent viscosity can be represented as
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\dot{\unicode[STIX]{x1D6FE}}^{m-1},\end{eqnarray}$$
where the second invariant (
$\dot{\unicode[STIX]{x1D6FE}}$
) can be calculated as
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}}=\sqrt{2\mathop{\sum }_{i}\mathop{\sum }_{j}e_{ij}e_{ji}}.\end{eqnarray}$$
Note that for the flow in a slender-body filament, the extensional deformation is dominant and thus the term ‘extensional thinning’ or simply ‘strain-rate thinning’ may be more appropriate than the term ‘shear thinning’. However, for the sake of convention, we refer to our non-Newtonian fluid as a ‘shear-thinning fluid’, for the case
$m<1$
. Using
$h_{s}$
and the strain-rate equations (2.12) and (2.13), the apparent viscosity can be calculated after some manipulation as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}=|\sqrt{3}u_{0s}|^{m-1}\!\left(\!1-(\unicode[STIX]{x1D700}n)\frac{(m-1)}{u_{0s}}\!\left(\!w_{1}\sin (\unicode[STIX]{x1D711})\mathbb{S}_{0}+\!\left(\!u_{0}\frac{\tilde{\mathbb{S}}_{0}}{\mathbb{S}_{0}}+\frac{u_{0s}}{2}\mathbb{S}_{0}\!\right)\!\cos (\unicode[STIX]{x1D711})\!\!\right)\!+O((\unicode[STIX]{x1D700}n)^{2})\!\right)\!\!, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\tilde{\mathbb{S}}_{0}=X_{0ss}X_{0sss}+Y_{0ss}Y_{0sss}+Z_{0ss}Z_{0sss}$
. Now, substituting the expressions defined in (2.17) into our set of equations, the higher-order equations can be achieved. From the continuity equation (2.5) we have
$$\begin{eqnarray}\displaystyle & O(\unicode[STIX]{x1D700}n):\quad u_{0s}+2v_{1}+w_{1\unicode[STIX]{x1D711}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & O((\unicode[STIX]{x1D700}n)^{2}):\quad u_{1s}+3v_{2}+w_{2\unicode[STIX]{x1D711}}+(3v_{1}+w_{1\unicode[STIX]{x1D711}})\mathbb{S}_{0}\cos (\unicode[STIX]{x1D711})-w_{1}\mathbb{S}_{0}\sin (\unicode[STIX]{x1D711})=0. & \displaystyle\end{eqnarray}$$
From the second tangential stress condition, i.e. (2.15), we have:
$$\begin{eqnarray}\displaystyle & O(\unicode[STIX]{x1D700}n):\quad R_{0}^{3}v_{1\unicode[STIX]{x1D711}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & O((\unicode[STIX]{x1D700}n)^{2}):\quad 3R_{0}^{2}R_{1}v_{1\unicode[STIX]{x1D711}}+R_{0}^{4}(w_{2}+v_{2\unicode[STIX]{x1D711}})-2R_{0}^{2}R_{1\unicode[STIX]{x1D711}}w_{1\unicode[STIX]{x1D711}}=0. & \displaystyle\end{eqnarray}$$
Therefore
$v_{1\unicode[STIX]{x1D711}}=0$
and by differentiating (2.22) with respect to
$\unicode[STIX]{x1D711}$
it can be seen that
$w_{1\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}=0$
. According to the results,
$w_{1}$
must be independent of
$\unicode[STIX]{x1D711}$
and thus we find that
$v_{1}=-u_{0s}/2$
. From (2.25), we can then see that
$$\begin{eqnarray}w_{2}+v_{2\unicode[STIX]{x1D711}}=0.\end{eqnarray}$$
From the first tangential stress condition (2.14), we find
$$\begin{eqnarray}\displaystyle & O(\unicode[STIX]{x1D700}n):\quad u_{1}=u_{0}\mathbb{S}_{0}\cos (\unicode[STIX]{x1D711}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle O((\unicode[STIX]{x1D700}n)^{2}):\quad u_{2}=\frac{3}{2}u_{0s}\frac{R_{0s}}{R_{0}}+\frac{u_{0ss}}{4}. & \displaystyle\end{eqnarray}$$
By differentiating (2.26) with respect to
$\unicode[STIX]{x1D711}$
, we arrive at
$$\begin{eqnarray}w_{2\unicode[STIX]{x1D711}}=-v_{2\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}.\end{eqnarray}$$
Therefore,
$$\begin{eqnarray}v_{2\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}-3v_{2}=u_{1s}+3v_{1}\mathbb{S}_{0}\cos (\unicode[STIX]{x1D711})-w_{1}\sin (\unicode[STIX]{x1D711}).\end{eqnarray}$$
Substituting
$u_{1}$
and
$v_{1}$
with the corresponding expressions we find
$$\begin{eqnarray}v_{2\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}-3v_{2}=\left(u_{0}\mathbb{S}_{0s}-\frac{u_{0s}}{2}\mathbb{S}_{0}\right)\cos (\unicode[STIX]{x1D711})-w_{1}\mathbb{S}_{0}\sin (\unicode[STIX]{x1D711}).\end{eqnarray}$$
A periodic solution for
$w_{2}$
and
$v_{2}$
can result in
$$\begin{eqnarray}\displaystyle & \displaystyle v_{2}=\frac{1}{4}\left(\left(\frac{u_{0s}}{2}\mathbb{S}_{0}-u_{0}\mathbb{S}_{0s}\right)\cos (\unicode[STIX]{x1D711})+w_{1}\mathbb{S}_{0}\sin (\unicode[STIX]{x1D711})\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w_{2}=\frac{1}{4}\left(\left(\frac{u_{0s}}{2}\mathbb{S}_{0}-u_{0}\mathbb{S}_{0s}\right)\sin (\unicode[STIX]{x1D711})-w_{1}\mathbb{S}_{0}\cos (\unicode[STIX]{x1D711})\right). & \displaystyle\end{eqnarray}$$
The normal stress condition, equation (2.10), at the zeroth order and order
$\unicode[STIX]{x1D700}$
can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle p_{0}=-\frac{|\sqrt{3}u_{0s}|^{m-1}u_{0s}}{Re}+\frac{1}{R_{0}We}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{1}=\frac{1}{R_{0}We}\left(-\frac{R_{1\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}+R_{1}}{R_{0}^{2}}+\mathbb{S}_{0}\cos (\unicode[STIX]{x1D711})\right)+\frac{4|\sqrt{3}u_{0s}|^{m-1}v_{2}}{Re}. & \displaystyle\end{eqnarray}$$
From the kinematic condition, equation (2.6), we obtain
$$\begin{eqnarray}\frac{u_{0s}}{2}R_{0}+u_{0}R_{0s}=0.\end{eqnarray}$$
From this expression it can be concluded that
$R_{0}^{2}u_{0}$
is constant. Now, using the initial conditions (
$R_{0}(0)=1$
and
$u_{0}(0)=1$
) we find
$$\begin{eqnarray}R_{0}=\frac{1}{\sqrt{u_{0}}}.\end{eqnarray}$$
Using the aforementioned expressions, the motion equations at the leading order can be obtained. The motion equation associated with the arc length in the steady state frame is
$$\begin{eqnarray}u_{0}u_{0s}=-\frac{u_{0s}}{2We\sqrt{u_{0}}}-\frac{Y_{0s}}{Fr^{2}}+\frac{(X_{0}+1)X_{0s}+Z_{0}Z_{0s}}{Rb^{2}}+\frac{3|\sqrt{3}u_{0s}|^{m-1}}{Re}\left(mu_{0ss}-\frac{u_{0s}^{2}}{u_{0}}\right).\quad\end{eqnarray}$$
Finally, using the motion equation in the
$n$
-direction, a solvability condition can be found as follows:
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \mathbb{S}_{0}\left(\frac{(7-m)|\sqrt{3}u_{0s}|^{m-1}u_{0s}}{2Re}+\frac{1}{R_{0}We}-u_{0}^{2}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2u_{0}}{Rb}\left(\frac{Z_{0ss}X_{0s}-X_{0ss}Z_{0s}}{\mathbb{S}_{0}}\right)+\frac{(X_{0}+1)X_{0ss}+Z_{0}Z_{0ss}}{Rb^{2}\mathbb{S}_{0}}\nonumber\\ \displaystyle & & \displaystyle -\,(m-1)\frac{|\sqrt{3}u_{0s}|^{m-1}}{Re}\left(u_{0}\frac{\tilde{\mathbb{S}}_{0}}{\mathbb{S}_{0}}\right)-\frac{1}{Fr^{2}}\left(\frac{Y_{0ss}}{\mathbb{S}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\tan (\unicode[STIX]{x1D711})\left(\frac{(m-1)|\sqrt{3}u_{0s}|^{m-1}w_{1}}{Re}\mathbb{S}_{0}+\frac{2u_{0}}{Rb}\left(\frac{Y_{0ss}}{\mathbb{S}_{0}}\right)+\frac{1}{Fr^{2}}\left(\frac{Z_{0ss}X_{0s}-X_{0ss}Z_{0s}}{\mathbb{S}_{0}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{(X_{0}+1)(Y_{0ss}Z_{0s}-Z_{0ss}Y_{0s})+Z_{0}(X_{0ss}Y_{0s}-Y_{0ss}X_{0s})}{Rb^{2}\mathbb{S}_{0}}\vphantom{\frac{|\sqrt{3}u_{0s}|^{m-1}}{Re}}\right).\end{eqnarray}$$
It is seen that all the terms in (2.39) are independent of
$\unicode[STIX]{x1D711}$
except for the terms in the last parenthesis. Hence, the summation of the terms independent of
$\unicode[STIX]{x1D711}$
needs to be equal to zero. The same is true for the terms multiplied by
$\tan (\unicode[STIX]{x1D711})$
. Therefore, the equation above is finally reduced to
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \mathbb{S}_{0}^{2}\left(\frac{(7-m)|\sqrt{3}u_{0s}|^{m-1}u_{0s}}{2Re}+\frac{\sqrt{u_{0}}}{We}-u_{0}^{2}\right)+\frac{2u_{0}}{Rb}(Z_{0ss}X_{0s}-X_{0ss}Z_{0s})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{Rb^{2}}((X_{0}+1)X_{0ss}+Z_{0}Z_{0ss})-(m-1)\frac{|\sqrt{3}u_{0s}|^{m-1}}{Re}(u_{0}\tilde{\mathbb{S}}_{0})-\frac{Y_{0ss}}{Fr^{2}}.\end{eqnarray}$$
2.5 Projection approach
To ease the solution of our set of equations, we use projections onto a local system of tangential and normal coordinates (Panda Reference Panda2006). Since all the terms are of leading order, henceforth the subscript 0 will be dropped for simplicity. Introducing two fibre angles,
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
(see figure 1), we obtain
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}X_{s}=\cos (\unicode[STIX]{x1D6FC})\sin (\unicode[STIX]{x1D6FD}),\\ Z_{s}=-\sin (\unicode[STIX]{x1D6FC})\sin (\unicode[STIX]{x1D6FD}),\\ Y_{s}=\cos (\unicode[STIX]{x1D6FD}),\end{array}\right\}\end{eqnarray}$$
which can also automatically satisfy the standard arc length condition of the fibre, i.e.
$X_{s}^{2}+Y_{s}^{2}+Z_{s}^{2}=1$
. In fact, the rate of changes of
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
with respect to
$s$
are the local curvature components
$\unicode[STIX]{x1D705}_{1}$
(
$\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FC}$
) and
$\unicode[STIX]{x1D705}_{2}$
(
$\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FD}$
), respectively. Now, equation (2.38) can be expressed as
$$\begin{eqnarray}\displaystyle N_{s} & = & \displaystyle Re\left(\frac{uN}{3^{(m+1)/2}}\right)^{1/m}\left(1+\frac{1}{2u^{3/2}We}\right)+\frac{Re}{Fr^{2}}\frac{\cos (\unicode[STIX]{x1D6FD})}{u}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{Re}{Rb^{2}}\frac{[(X+1)\cos (\unicode[STIX]{x1D6FC})-Z\sin (\unicode[STIX]{x1D6FC})]\sin (\unicode[STIX]{x1D6FD})}{u},\end{eqnarray}$$
where
$N=(3^{(m+1)/2}u_{s}^{m})/u$
stands for tensile force. After substituting the projection expressions into (2.40), we arrive at
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \sin (\unicode[STIX]{x1D6FD})^{2}\unicode[STIX]{x1D705}_{1}^{2}\left(\frac{7-m}{6Re}uN+\frac{u^{1/2}}{We}-u^{2}\right)-\frac{2\unicode[STIX]{x1D705}_{1}u\sin (\unicode[STIX]{x1D6FD})^{2}}{Rb}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D705}_{1}\sin (\unicode[STIX]{x1D6FD})}{Rb^{2}}((X+1)\sin (\unicode[STIX]{x1D6FC})+Z\cos (\unicode[STIX]{x1D6FC}))-\unicode[STIX]{x1D705}_{1}\unicode[STIX]{x1D705}_{1s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}Re}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D705}_{2}^{2}\left(\frac{7-m}{6Re}uN+\frac{u^{1/2}}{We}-u^{2}\right)+\frac{\unicode[STIX]{x1D705}_{2}\cos (\unicode[STIX]{x1D6FD})}{Rb^{2}}((X+1)\cos (\unicode[STIX]{x1D6FC})+Z\sin (\unicode[STIX]{x1D6FC}))\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D705}_{2}\sin (\unicode[STIX]{x1D6FD})}{Fr^{2}}-\unicode[STIX]{x1D705}_{2}\unicode[STIX]{x1D705}_{2s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}Re}.\end{eqnarray}$$
A particular condition to satisfy (2.43) can be met by setting
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{1}=\frac{1}{q}\left(\!-\frac{2}{Rb}-\frac{1}{u\sin (\unicode[STIX]{x1D6FD})Rb^{2}}((X+1)\sin (\unicode[STIX]{x1D6FC})+Z\cos (\unicode[STIX]{x1D6FC}))-\unicode[STIX]{x1D705}_{1s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}u\sin (\unicode[STIX]{x1D6FD})^{2}Re}\right)\!,\hspace{-6.0pt} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{2}=\frac{1}{q}\left(\frac{\sin (\unicode[STIX]{x1D6FD})}{uFr^{2}}+\frac{\cos (\unicode[STIX]{x1D6FD})}{uRb^{2}}((X+1)\cos (\unicode[STIX]{x1D6FC})+Z\sin (\unicode[STIX]{x1D6FC}))-\unicode[STIX]{x1D705}_{2s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}uRe}\right)\!,\hspace{-6.0pt} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$q=uRe-((7-m)/6)N-Re/(u^{1/2}We)$
stands for the internal energy (sum of kinetic, viscous and surface tension energies).
So far, the three key reduced model equations are (2.42), which is an axial momentum balance (also conventionally called the
$s$
-momentum balance) and solvability conditions (2.44) and (2.45). Leading-order equations (2.42), (2.44) and (2.45) are commonly referred to as the ‘string’ equations.
2.6 General regularization approach
For fast rotations (small
$Rb$
), it can be mathematically demonstrated that the string equations developed so far do not have a physically relevant solution if
$q<0$
(e.g. see Götz et al. (Reference Götz, Klar, Unterreiter and Wegener2008) for the analysis of a two-dimensional Newtonian case). This implies that the near-orifice jet curvature is incorrect as the jet initially curves in the counter-clockwise direction, i.e. the fibre leads rather than trails. In fact, for a given fibre length, it is possible to accurately delineate the range of
$Rb$
,
$Re$
,
$We$
,
$Fr$
and
$m$
where the string model fails. However, we could also approximate the validity range of our string equations. For example, neglecting gravitational effects, in the vicinity of the orifice as
$s\rightarrow 0$
, we can crudely show that
$q=O(Re-Rb^{-2m}-Re\,We^{-1})$
, where
$u_{s}$
has been evaluated by a corresponding inviscid flow value. Therefore, the string model fails provided that
$Re^{-1}Rb^{-2m}+We^{-1}>1$
. For
$m=1$
and
$We\rightarrow \infty$
, this yields
$Re\,Rb^{2}<1$
, which is in accordance with the findings of Götz et al. (Reference Götz, Klar, Unterreiter and Wegener2008). Using the values given in table 1 for the ranges of the dimensionless parameters, we can easily see that
$q<0$
near the orifice for almost all the parameter ranges of nanofibre formation. Thus, the string model fails for all these practical ranges. Motivated by the important applications, here we develop a simple yet rigorous regularization approach for three-dimensional non-Newtonian fluids to remove the singularity issue and ensure the regularity of the string quantities.
Figure 2. Schematic diagram of stress tensor components
$\unicode[STIX]{x1D61B}_{ns}$
and
$\unicode[STIX]{x1D61B}_{sn}$
on a small jet element near the orifice, acting as moments of a couple causing the element to bend in the direction opposite to the spinneret rotation.
Conceptually, the underlining problem in the singularity issue of the string model is the fact that a viscous fibre would curve in the wrong direction near the orifice, implying that higher-order terms allowing for the correct near-orifice bending of the fibre have been ignored in the string equations. Thus, in order to find a way to remove the singularity, we need to examine the stress tensor component derivatives that would allow the fibre to bend. The stress tensor comprises of three normal components, i.e.
$\unicode[STIX]{x1D61B}_{ss}$
,
$\unicode[STIX]{x1D61B}_{nn}$
and
$\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}$
and six shear components, i.e.
$\unicode[STIX]{x1D61B}_{sn}$
,
$\unicode[STIX]{x1D61B}_{ns}$
,
$\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D711}n}$
,
$\unicode[STIX]{x1D61B}_{n\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D711}s}$
and
$\unicode[STIX]{x1D61B}_{s\unicode[STIX]{x1D711}}$
. The normal stress components are obviously irrelevant to bending whereas variations of the shear stress components along
$s$
,
$n$
and
$\unicode[STIX]{x1D711}$
can act as moments of a couple over an infinitesimal element of the jet, causing the fibre to bend or twist. The latter (i.e. twisting) is also immaterial in centrifugal spinning. Figure 2 shows a schematic diagram of a fibre close to the orifice, where the shear stress components
$\unicode[STIX]{x1D61B}_{ns}$
and
$\unicode[STIX]{x1D61B}_{sn}$
are depicted. As can be interpreted from the schematic, according to the beam theory, variations of
$\unicode[STIX]{x1D61B}_{ns}$
and
$\unicode[STIX]{x1D61B}_{sn}$
across the jet centreline or radius serve as bending moments to curve the fibre throughout the arc length. However, the expansion of the derivatives of
$\unicode[STIX]{x1D61B}_{ns}$
and
$\unicode[STIX]{x1D61B}_{sn}$
in the
$s$
-direction reveals that these stresses contain higher-order terms (removed from the string equations) responsible for significantly bending viscous fibres at very small arc lengths. Among the higher-order terms ignored, the term
$\unicode[STIX]{x1D702}v_{ss}(s,n,\unicode[STIX]{x1D711})$
is the only one that contains the highest-order derivatives of the centreline curvature. Therefore, it is logical to consider that the singularity issue of the solvability conditions (governing the curvature) originates from ignoring
$\unicode[STIX]{x1D702}v_{ss}(s,n,\unicode[STIX]{x1D711})$
, even though it plays a crucial role in the regions near the orifice, allowing the fibre to bend and stabilize the jet against Coriolis and centrifugal forces. Therefore, to cope with the singularity of the string model we must retain and take into account this higher-order term in the solvability equations (2.44) and (2.45). For our shear-thinning fluid, expanding
$\unicode[STIX]{x1D702}v_{ss}$
and using the asymptotic expressions, equation (2.32) and the projection expressions, the term
$\unicode[STIX]{x1D702}v_{ss}$
can be represented as a series of
$\unicode[STIX]{x1D705}_{1}$
and
$\unicode[STIX]{x1D705}_{2}$
derivatives:
$$\begin{eqnarray}\unicode[STIX]{x1D702}v_{ss}=-\frac{(\unicode[STIX]{x1D700}n)^{3}}{4Re}|\sqrt{3}u_{s}|^{m-1}u\left(\frac{\unicode[STIX]{x1D705}_{1}\sin (\unicode[STIX]{x1D6FD})^{2}\unicode[STIX]{x1D705}_{1sss}}{\sqrt{\sin (\unicode[STIX]{x1D6FD})^{2}\unicode[STIX]{x1D705}_{1}^{2}+\unicode[STIX]{x1D705}_{2}^{2}}}+\frac{\unicode[STIX]{x1D705}_{2}\unicode[STIX]{x1D705}_{2sss}}{\sqrt{\sin (\unicode[STIX]{x1D6FD})^{2}\unicode[STIX]{x1D705}_{1}^{2}+\unicode[STIX]{x1D705}_{2}^{2}}}+\cdots \right)+O(\unicode[STIX]{x1D700}^{4}),\end{eqnarray}$$
which we employ to modify and regularize our solvability equations. Therefore, after some algebra, the final set of our regularized string equations, including the axial momentum balance and solvability equations, will become
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{s}-Re\left(\frac{uN}{3^{(m+1)/2}}\right)^{1/m}\left(1+\frac{1}{2u^{3/2}We}\right)-\frac{Re\cos (\unicode[STIX]{x1D6FD})}{uFr}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{Re\sin (\unicode[STIX]{x1D6FD})[(X+1)\cos (\unicode[STIX]{x1D6FC})-Z\sin (\unicode[STIX]{x1D6FC})]}{uRb^{2}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{1sss}+q\unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{1s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}u\sin (\unicode[STIX]{x1D6FD})^{2}}+\frac{2Re}{Rb}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{Re[(X+1)\sin (\unicode[STIX]{x1D6FC})+Z\cos (\unicode[STIX]{x1D6FC})]}{uRb^{2}\sin (\unicode[STIX]{x1D6FD})}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{2sss}+q\unicode[STIX]{x1D705}_{2}+\unicode[STIX]{x1D705}_{2s}\frac{(m-1)(uN)^{(m-1)/m}}{3^{(m-1)/2m}u}-\frac{Re\sin (\unicode[STIX]{x1D6FD})}{uFr^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{Re\cos (\unicode[STIX]{x1D6FD})[(X+1)\cos (\unicode[STIX]{x1D6FC})+Z\sin (\unicode[STIX]{x1D6FC})]}{uRb^{2}}=0,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}=(\unicode[STIX]{x1D700}n)^{2}|\sqrt{3}u_{s}|^{m-1}/4$
.
Compared to a usual string model, two regularization terms involving the curvature third derivatives in the horizontal and vertical planes, i.e.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{1sss}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{2sss}$
, appear in the solvability equations. Here,
$\unicode[STIX]{x1D6FF}$
is a small regularization coefficient proportional to
$\unicode[STIX]{x1D700}^{2}$
. We find that this simple modification, i.e. including the regularization terms in the solvability conditions, completely removes the three-dimensional string model singularities, making a perfectly stable solution possible.
It is to be remembered that the stress term
$\unicode[STIX]{x1D702}v_{ss}$
at higher orders includes a series of
$\unicode[STIX]{x1D705}_{1}$
and
$\unicode[STIX]{x1D705}_{2}$
derivatives, among which the terms with the highest-order curvature derivatives have been kept in order to apply our regularization method. It may be mathematically intuitive that the terms containing the highest curvature derivatives are the only ones required to yield the stable solution in the limit of
$\unicode[STIX]{x1D700}\rightarrow 0$
and that the terms containing the lower-order curvature derivatives can be simply ignored. In order to verify this, figure 3 plots the magnitudes of the derivatives of
$\unicode[STIX]{x1D705}_{1}$
obtained from our numerical simulation for a typical fibre flow at small
$Rb$
. As observed, the magnitude of
$\unicode[STIX]{x1D705}_{1sss}$
is much larger than the other derivatives. Furthermore, it is seen that all these derivatives (including
$\unicode[STIX]{x1D705}_{1sss}$
) are only significant at small arc lengths (
$s\ll 1$
) and they all approach to zero at greater arc lengths.
Figure 3. Comparison between the magnitudes of the derivatives of
$\unicode[STIX]{x1D705}$
for
$Rb=0.01$
,
$Re=0.1$
,
$We\rightarrow \infty$
,
$Fr\rightarrow \infty$
and
$m=1$
. The regularization coefficient is chosen as
$\unicode[STIX]{x1D6FF}=10^{-3}$
.
In simple words, the regularization coefficient,
$\unicode[STIX]{x1D6FF}$
, represents the order of the thickness of the near-orifice boundary zone, which has negligible effects at larger arc lengths. In nanofibre formation applications, the jet is quite thin and, consequently, the boundary zone is very small. Thus, the solution away from the orifice becomes independent of the choice of a sufficiently small
$\unicode[STIX]{x1D6FF}$
. Figure 4 depicts our simulation results for the fibre trajectory (figure 4
a) and speed (figure 4
b) for different values of the regularization coefficient. According to the figure, at large
$\unicode[STIX]{x1D6FF}=1$
the fibre trajectory deviates from trajectories obtained for smaller values (
$\unicode[STIX]{x1D6FF}=10^{-2}$
and
$10^{-3}$
); this deviation is minor for
$\unicode[STIX]{x1D6FF}=10^{-1}$
. However, the fibre speed is less influenced by the magnitude of
$\unicode[STIX]{x1D6FF}$
. Therefore, we can conclude that the fibre key features are independent of the choice of the regularization coefficient as long as
$\unicode[STIX]{x1D6FF}$
is kept small, i.e. typically at
$10^{-2}$
, or lower. The fibre curvature and angle magnitudes near the orifice are expectedly affected by
$\unicode[STIX]{x1D6FF}$
even when it is small, a feature that quickly vanishes slightly away from the orifice. For all the simulation results presented in this paper, we fix
$\unicode[STIX]{x1D6FF}=10^{-3}$
.
Figure 4. Effect of the regularization coefficient,
$\unicode[STIX]{x1D6FF}$
, on (a) the fibre trajectory and (b) the fibre speed for
$Rb=0.01$
,
$Re=0.1$
,
$We\rightarrow \infty$
,
$Fr\rightarrow \infty$
and
$m=1$
, with
$\unicode[STIX]{x1D6FF}=1$
(dots),
$\unicode[STIX]{x1D6FF}=10^{-1}$
(dash-dot line),
$\unicode[STIX]{x1D6FF}=10^{-2}$
(dashed line) and
$\unicode[STIX]{x1D6FF}=10^{-3}$
(solid line).
From a modelling perspective, our regularized formulation presented is general in the terms of the following aspects.
-
(i) First, our model regularizes the solvability condition equations for a fully three-dimensional flow, using a regularization coefficient that is interestingly identical in both curvature equations.
-
(ii) Second, our formulation is applicable to both Newtonian and non-Newtonian fluids. The latter includes fluids described by the constitutive relations allowing for the term
$\unicode[STIX]{x1D702}v_{ss}$
to appear in the motion equations. Examples may include the Carreau–Yasuda (Aho & Syrjälä Reference Aho and Syrjälä2008) and the Cross–Williamson (Mishra et al.
Reference Mishra, Sonawane, Mukherji and Mruthyunjaya2006) models for the polymers with shear-thinning behaviours and the Song–Xia model (Song & Xia Reference Song and Xia1994) for the polymers showing also extension thinning/thickening behaviours. Note that
$v_{ss}$
(not
$\unicode[STIX]{x1D702}$
) is the heart of the regularization concept since it includes the third derivative of the curvature and the fibre thickness as parameters. Therefore, regardless of the functional dependence of
$\unicode[STIX]{x1D702}$
, a regularization term with a form of
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{sss}$
inevitability appears in the solvability conditions, where
$\unicode[STIX]{x1D705}_{sss}$
is the centreline curvature and
$\unicode[STIX]{x1D6FF}$
(as a regularization coefficient) can be an unknown function of
$\unicode[STIX]{x1D700}$
,
$n$
, non-Newtonian properties and so on, with the condition that
$\unicode[STIX]{x1D6FF}\rightarrow 0$
as
$\unicode[STIX]{x1D700}\rightarrow 0$
. Therefore,
$\unicode[STIX]{x1D6FF}$
is always a very small parameter in the asymptotic limit, used merely to remove the singularity and stabilize the solution.
The definitions of the dimensionless groups in (2.47)–(2.49) are introduced in table 1, which combine the design parameters in nanofibre formation by centrifugal spinning methods and serve as inputs of the model. Note that the slenderness parameter,
$\unicode[STIX]{x1D700}$
, which is of
$O(10^{-3})$
in centrifugal spinning methods, vanishes in the asymptotic limit so that it is not considered as a model parameter. On the other hand, for a sufficiently long fibre, which is also relevant to centrifugal spinning methods, it can be shown that the fibre key features are not governed by the end boundary conditions, implying that the fibre length,
$L$
, is also removed as a model input parameter (see § 2.7). The typical outputs of the model are introduced in table 2.
Table 2. Typical model outputs, which are functions of the arc length
$s$
. Note that all the model parameters are of leading order in
$\unicode[STIX]{x1D700}$
.
Before proceeding, it may be useful to note that although our model includes
$Rb$
,
$Re$
,
$Fr$
,
$We$
and
$m$
as the flow parameters, a dimensional analysis reveals that there are several additional dimensionless groups that govern the real fibre flow problem for nanofibre formation applications. Obvious examples may include the Weissenberg number (ratio of elastic to viscous stresses), the Schmidt number (ratio of viscous to molecular diffusion rate), the Nusselt number (ratio of convective to conductive heat transfer), etc. The general regularization formulation presented in this paper would allow us to include these dimensionless parameters in our model without any inherent difficulties e.g. the singularities observed in similar asymptotic models.
Finally, it is worth noting perhaps a few advantages of the regularized string model relative to a full rod model with bending terms included, which also removes the singularity at the nozzle. (i) There are generally more equations derived in a rod model, creating a stiff set of differential equations. (ii) It seems that the effects of surface tension and a variety of non-Newtonian constitutive equations can be more easily included in the regularized string model. (iii) The literature of the rod models for fibre spinning applications is less developed than that of the string models. The singularities in the latter may be simply removed using a regularization approach, implying that there may be opportunities for rapid development in the field. (iv) Regularized string models may be faster to solve numerically, especially for long fibres. For example, for a number of case studies for very small
$Rb$
, computational time of our model solution was, on average, four times less than that of the corresponding Cosserat rod model.
2.7 Boundary conditions and numerical scheme
To solve the system of differential equations (2.47)–(2.49), the physically acceptable boundary conditions at the nozzle exit are
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}X(0)=Y(0)=Z(0)=0,\\ \unicode[STIX]{x1D6FC}(0)=0\quad \text{and}\quad \unicode[STIX]{x1D6FD}(0)=\unicode[STIX]{x03C0}/2,\\ \unicode[STIX]{x1D705}_{1}(0)=\unicode[STIX]{x1D705}_{2}(0)=0,\\ u(0)=1.\end{array}\right\}\end{eqnarray}$$
However, our simulation results show that the solutions over a large
$s$
-domain are insensitive to the exact values of the end boundary conditions if the fibre is sufficiently long. In order to robustly solve the equations, one can set the fibre end boundary conditions as
$N(L)=\unicode[STIX]{x1D705}_{1s}(L)=\unicode[STIX]{x1D705}_{2s}(L)=\unicode[STIX]{x1D705}_{1ss}(L)=\unicode[STIX]{x1D705}_{2ss}(L)=0$
, the only consequence of which is that the solutions will slightly deviate as
$s$
approaches the vicinity of
$L$
, merely to satisfy the end boundary conditions. Therefore, the solutions in the main
$s$
-domain will be independent of the choice of a sufficiently large
$L$
.
For the numerical scheme, we set up systems of nonlinear equations using a Runge–Kutta collocation method combined with a Newton method, which is a fourth-order integration scheme to solve boundary value problems, e.g.
$\unicode[STIX]{x2202}_{s}\boldsymbol{y}=F(s,\boldsymbol{y})$
with boundary values defined as
$g(\boldsymbol{y}(a),\boldsymbol{y}(b))=0$
. We use the bvp4c routine in MATLAB R2015a to implement the method and discretize our system of nonlinear equations. We set the number of the collocation points typically between 100 and 1000, depending on the numerical stiffness of the equations. The convergence of the Newton method depends highly on the initial guess. To create a robust computational code, we start the solution procedure by solving the equations for a small value of
$L$
, which we gradually increase. Meanwhile, we update the initial guess at each step. We continue increasing
$L$
until the solutions in the main
$s$
-domain become independent of
$L$
. We have validated our model through comparisons against the results of Decent et al. (Reference Decent, King and Wallwork2002), Wallwork et al. (Reference Wallwork, Decent, King and Schulkes2002), Uddin et al. (Reference Uddin, Decent and Simmons2008), Arne et al. (Reference Arne, Marheineke, Meister and Wegener2010) and Arne et al. (Reference Arne, Marheineke and Wegener2011), finding excellent agreement. We have performed hundreds of simulations, from which we will present the main findings in this paper.
To better understand the effects of the end boundary conditions and the fibre length, figure 5 shows the two-dimensional fibre trajectory, angle, curvature, speed, tensile force and radius as a function of the arc length, for a set of parameters. Seven values of
$L$
are chosen, for which the end boundary conditions are applied. It can be seen that for larger
$L$
the solutions depend very weakly on
$L$
, i.e. the solutions slightly deviate only when
$s\rightarrow L$
. In fact, for a sufficiently large
$L$
, the solutions superpose and they are indistinguishable from one another. To explain the observed behaviour, a corresponding inviscid solution is also plotted in figure 5, for which the only boundary conditions are at the nozzle exit and no end boundary conditions are needed. For the highly viscous liquid jets (
$Re=0.1$
) of various lengths in this figure, it can be easily seen that the solutions approach their inviscid limit as
$L$
increases. This implies that for a sufficiently large
$L$
, the end boundary conditions are less relevant and
$L$
is also removed as a model parameter since the solution becomes nearly inviscid, which is a feature that is explained further in the following section. For further confirmation, we have also examined an inviscid scaling end boundary condition (Feng Reference Feng2002), finding that for a sufficiently long fibre the results are insensitive to the end boundary condition.
Figure 5. Simulation results for
$Rb=0.001$
,
$Re=0.1$
,
$We\rightarrow \infty$
and
$Fr\rightarrow \infty$
for
$L=0.05$
, 0.1, 0.2, 0.4, 0.6, 0.8, 1, shown by solid lines of progressively decreasing thickness. The dashed line in each plot shows the corresponding inviscid solution. The simulation results for
$L\geqslant 0.4$
are almost indistinguishable from one another.
3 Results and discussion
In this section, we will explore the effects of the flow parameters such as the rotation speed (quantified by
$Rb$
), viscosity (quantified by
$Re$
), gravity (quantified by
$Fr$
), surface tension (quantified by
$We$
) and shear-thinning properties (quantified by
$m$
), while focusing on the parameter ranges associated with nanofibre formation, given in table 1. Although the large number of the dimensionless parameters involved makes it hard to deliver quantitative predictions for all the possible flow features, we will attempt to provide essential understanding about the effects of each parameter and classify the regimes where possible.
Figure 6. Absolute value of each stress term in the axial momentum balance equation as a function of the arc length for typical flow parameters:
$Rb=0.01$
,
$Re=0.1$
,
$We=Fr=0.1$
,
$m=0.9$
. Centrifugal (dash-dot line), viscous (dashed line), inertial (solid line), surface tension (○) and gravitational (
$+$
) stress terms are shown. Vertical bold lines mark approximated transition arc lengths explained in the text.
Before we proceed to review the effects of the various dimensionless groups, it is useful to look into the variations of the stress terms versus the arc length in our reduced model. Figure 6 depicts the variation of the relative stress terms (absolute values) in the axial momentum balance equation for typical parameters in the centrifugal spinning process. Each term is the ratio of a stress to a characteristic inertial stress defined as
$\unicode[STIX]{x1D70C}U^{2}/s_{0}$
. The centrifugal stress term only increases very slowly with
$s$
. Meanwhile, the magnitude of the viscous stress term is initially equal to that of the centrifugal term but it starts to sharply decrease with
$s$
, after certain transition arc length which can roughly approximated by
$s\approx 3^{(m+1)/(2m+1)}2^{1/(2m+1)}Re^{2/(2m+1)}Rb^{-2/(2m+1)}$
, where the inertial stress sharply increases and takes over the viscous stress in balancing the centrifugal term. (This transition arc length is obtained through a simplified conceptual analysis, an example of which is explained at the end of this section.) The surface tension stress gradually decreases with
$s$
and drops below the inertial stress at certain transition arc length, which can be approximated by
$s\approx 3^{1/2}2^{-2/(3(m+1))}Rb^{2/(m+1)}Re^{-1/(m+1)}We^{-2/(3(m+1))}$
. The decrease in the viscous and surface tension stress terms as wells as the increase in the inertial term can be all attributed to the progressive increase of the fibre speed with the arc length. Finally, the gravitational stress initially increases slightly due to the falling of the fibre, but eventually reaches a small plateau value.
It may be crucially concluded from figure 6 that fibre key features at large arc lengths are mainly controlled by inertial effects. For example, it may be expected that, even for very viscous flows, the fibre radius will eventually approach a corresponding inviscid solution. A particularly relevant inviscid fibre radius solution is simply obtained for a Newtonian fibre with
$Rb\ll 1$
and
$Re\rightarrow \infty$
,
$We\rightarrow \infty$
,
$Fr\rightarrow \infty$
, i.e.
$R\approx \sqrt[4]{Rb^{2}/2s}$
at large
$s$
. Our results will demonstrate that this specific solution is more or less applicable, except for very small
$We$
flows, where the fibre does not follow a spiral trajectory and does not reach the inviscid limit at large
$s$
.
3.1 Effects of the Rossby number
Figure 7 shows the effects of
$Rb$
on the variation of the fibre radius versus the arc length. We observe that the fibre, which initially has a radius equal to that of the orifice, becomes progressively thin along the arc length. By decreasing
$Rb$
, two effects can be readily seen. First, the fibre starts to thin much more quickly for smaller
$Rb$
. Second, the thinning of the fibre is significantly enhanced as
$Rb$
decreases. Interestingly, each fibre radius at large arc lengths eventually approaches its own corresponding inviscid limit. Again, the lower
$Rb$
flow moves toward its inviscid limit much faster.
Figure 7. Simulation results of the fibre radius versus the arc length with
$m=1$
,
$Re=0.1$
and
$Fr=We=10$
for
$Rb=0.1$
(line),
$Rb=0.01$
(dashed line) and
$Rb=0.001$
(dash-dot line). The corresponding inviscid limit for the fibre radius (
$R\approx \sqrt[4]{Rb^{2}/2s}$
) is marked by dotted line.
3.2 Effects of the Reynolds number
Figure 8(a) shows the effects of varying
$Re$
(over two orders of magnitude) on the fibre radius. We may expect the lower
$Re$
flows to thin relatively more slowly, which is in fact the case at small arc lengths. However, counter-intuitively the fibre with the lower
$Re$
(more viscous flow) undergoes a relatively higher thinning rate at larger arc lengths so that it catches up with the less viscous flow at large arc lengths. Broadly speaking, the viscous fibres forget their history and they all eventually follow more or less the same corresponding inviscid limit for the fibre radius.
Figure 8. Simulation results with
$m=1$
,
$Rb=0.001$
and
$Fr=We=10$
for
$Re=0.001$
(line),
$Re=0.01$
(dashed line) and
$Re=0.1$
(dash-dot line). (a) Fibre radius versus the arc length. The corresponding inviscid limit for each fibre radius (
$R\approx \sqrt[4]{Rb^{2}/2s}$
) is marked by dotted line. (b) Tensile stress versus the arc length.
Figure 9. Simulation results for
$Rb=0.01$
,
$Re=0.1$
,
$m=1$
,
$We\rightarrow \infty$
, for
$Fr=0.01$
(line),
$Fr=0.02$
(dashed line) and
$Fr=1$
(dash-dot line). Each inset scale is semilogarithmic and has the same arc length range as the main panel.
To explain the behaviours observed, let us discuss figure 8(b), which shows the variation of the tensile stress (
$N/R^{2}$
) for the three different Reynolds numbers. We can distinguish a general trend for the different cases, i.e. the tensile stress grows, reaches a maximum (turning point) and then decreases gradually. For the higher
$Re$
flow, the initial increase of the tensile stress is extremely rapid and for the lower
$Re$
flow it is much slower. Our simulations show that while the fibre exhibits viscous characteristics before the turning point, the inertial behaviours become significant at the turning point and they completely take over slight thereafter. For the less viscous flow (higher
$Re$
), the tensile stress that balances the centrifugal stress is strong at first, causing the fibre to thin to a great degree. However, due to the decrease of the tensile stress after the turning point, the fibre thins with a much slower thinning rate. On the other hand, for the more viscous fibre (smaller
$Re$
), the centrifugal stress is also dissipated by the tensile stress, which is relatively much smaller at shorter arc lengths. Therefore, the fibre thins more slowly initially. Nevertheless, the tensile stress of the more viscous flow continues to grow and it eventually exceeds that of the less viscous flow, an effect which brings about two consequences. First, since the turning point for the more viscous fibre is reached at a larger arc length compared to the less viscous flow, the tensile stress for the more viscous flow remains significant over a wider range of the arc length, where it can progressively thin the fibre. Second, at larger arc lengths the more viscous fibre becomes thin at a higher rate than the less viscous fibre. Nonetheless, in all the cases the inertial stress finally controls the fibre behaviour at very large arc lengths.
Figure 10. Simulation results for
$Rb=0.01$
,
$Re=0.1$
,
$Fr\rightarrow \infty$
,
$m=1$
for
$We=0.001$
(solid line),
$We=0.01$
(dashed line) and
$We\rightarrow \infty$
(dash-dot line). (a)
$D_{c}$
denotes the circular trajectory diameter. (b) Shows the fibre angle and curvature (inset) in the
$X$
–
$Z$
plane. (c) Shows the fibre speed. (d) Shows the fibre radius and thinning rate (inset); the horizontal dotted line indicates the constant fibre radius limit (for the smallest Weber number) and the oblique dotted line shows the inviscid fibre radius limit (for the two larger Weber numbers). Each inset scale is semilogarithmic and has the same arc length range as the main panel.
3.3 Effects of the Froude number
Figure 9 shows the fibre three-dimensional trajectory, horizontal angle and curvature (inset), vertical angle and curvature (inset), radius and thinning rate (inset) as functions of
$s$
for three different values of
$Fr$
. As can be seen, at smaller
$Fr$
, the fibre falls under gravity faster than at larger
$Fr$
. However, the fibre horizontal angle and curvature do not much change with different values of
$Fr$
. The fibre vertical angle (
$\unicode[STIX]{x1D6FD}$
) and curvature (
$\unicode[STIX]{x1D705}_{2}$
) are more affected in the case of small
$Fr$
at small
$s$
but they reach nearly steady values at larger arc lengths. It is perhaps interesting to note the early oscillations in
$\unicode[STIX]{x1D6FD}$
(fibre angle in
$X$
–
$Y$
plane) compared to the monotonic decrease in
$\unicode[STIX]{x1D6FC}$
(fibre angle in
$X$
–
$Z$
plane). Moreover, comparing the curvatures (insets) reveals that the fibre curvature in the vertical plane is initially more affected than the curvature in the horizontal plane. However, the most important fibre features, i.e.
$R$
and
$|R_{s}|$
, are not significantly influenced by
$Fr$
. At larger
$s$
, the fibre radii approximately approach an inviscid solution that excludes all the parameters except for
$Rb$
. Therefore, for the parameter ranges of nanofibre formation, the effect of
$Fr$
on the fibre thinning remains minor throughout the arc length.
3.4 Effects of the Weber number
Figure 10 shows the effects of
$We$
on the fibre two-dimensional trajectory, angle, curvature (inset), speed, radius and thinning rate (inset). At
$We=0.01$
, the flow features are only slightly affected compared to
$We\rightarrow \infty$
. However,
$We=0.001$
significantly influences the jet behaviours: in particular the fibre trajectory is much tighter compared to the higher
$We$
flows, up to the point that the fibre even reaches a circular trajectory centred on the axis of rotation. Consequently, the fibre speed is also much smaller and at large
$s$
it reaches a nearly steady value after a few oscillations. The fibre thinning rate at shorter arc lengths is weaker for smaller
$We$
. Finally, whereas for higher
$We$
the fibre radius advances toward a corresponding inviscid limit (i.e.
$R\approx \sqrt[4]{Rb^{2}/2s}$
), for
$We=0.001$
it does not reach this limit but instead approaches an almost constant value.
Let us attempt to justify the behaviours observed at small and large Weber numbers. When
$We$
is very small, the surface energy of the fibre consumes a large portion of the centrifugal energy and thus the inertial energy cannot overtake the surface energy, causing the fibre to take a circular path, a constant speed and hence a constant radius. With increasing
$We$
, the surface energy decreases until a critical transition Weber number (
$We_{t}$
) is reached at which the inertial and surface energies are nearly equal, where the fibre begins to demonstrate a non-circular (spiral) trajectory instead of a circular one.
A final note is that at low Weber numbers, the steady fibre trajectory may be unstable to undulation and fibre breakup, which we do not consider in our analysis.
3.4.1 Simplified model for the circular trajectory regime
In order to analyse the circular trajectory regime, here we derive a simplified model with analytical expressions to predict the fibre behaviours in the circular trajectory regime, in the range of small Weber numbers. This implies that we will consider the flows for which the surface tension stress has a dominant effect. For simplicity, we concentrate on the condition where gravitational effects are negligible (
$Fr\rightarrow \infty$
) and the flow is Newtonian (
$m=1$
). We also concentrate on flows with
$Rb\ll 1$
, which is the regime of nanofibre formation. Table 3 shows the main outputs of the simplified model that will be presented in this subsection.
Provided that the fibre follows a circular path instead of a non-circular (spiral) one, we have
$$\begin{eqnarray}(X+1)^{2}+Z^{2}=\left(\frac{D_{c}}{2}\right)^{2}=\frac{1}{\unicode[STIX]{x1D705}_{c}^{2}}=\text{const.}\end{eqnarray}$$
Therefore, using (2.48) and the projection expressions (see § 2.5), we find the following equation that satisfies the circular trajectory:
$$\begin{eqnarray}\left(u-\frac{1}{\sqrt{u}We}\right)\unicode[STIX]{x1D705}_{c}+\frac{2}{Rb}+\frac{1}{uRb^{2}\unicode[STIX]{x1D705}_{c}}=0.\end{eqnarray}$$
On the other hand, by integrating motion equation (2.47), from zero to the arc length
$\ell _{c}$
where the trajectory becomes circular, we arrive at
$$\begin{eqnarray}\int _{0}^{\ell _{c}}uu_{s}\,\text{d}s+\int _{0}^{\ell _{c}}\frac{1}{2We}\frac{u_{s}}{\sqrt{u}}\,\text{d}s-\int _{0}^{\ell _{c}}\frac{(X+1)X_{s}+ZZ_{s}}{Rb^{2}}\,\text{d}s-\frac{3}{Re}{\int _{0}^{\ell _{c}}u\left(\frac{u_{s}}{u}\right)}_{s}\,\text{d}s=0.\end{eqnarray}$$
Using (3.1), all the terms in (3.3) can be readily integrated except for the viscous dissipative term (i.e. the fourth term), which is unknown. Crudely, to make the algebraic integration of the viscous term possible, the inviscid solutions without surface tension for velocity and its derivative for small
$Rb$
may be used as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle u\approx \frac{\sqrt{2s}}{Rb}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{s}\approx \frac{1}{\sqrt{2s}Rb}. & \displaystyle\end{eqnarray}$$
Table 3. Typical outputs of the simplified model for the circular trajectory regime. The model inputs are typically
$Rb$
,
$Re$
and
$We$
, while
$Fr\rightarrow \infty$
and
$m=1$
have been considered for simplicity.
In addition, again for the same purely inviscid flow,
$\ell _{c}$
can be coarsely linked to the fibre curvature of the circle through
$\sqrt{2\ell _{c}}\approx -1/\unicode[STIX]{x1D705}_{c}$
. It must be noted that the aforementioned inviscid expressions are only used to approximately integrate the dissipative viscous term and it does not mean that our flow is inviscid. After integrating and manipulating (3.3), we find
$$\begin{eqnarray}u_{c}^{2}-1+\frac{2\sqrt{u_{c}}}{We}-\frac{2}{We}+\frac{1}{Rb^{2}}-\frac{1}{Rb^{2}\unicode[STIX]{x1D705}_{c}^{2}}-\frac{6}{Re\,Rb\unicode[STIX]{x1D705}_{c}}=0.\end{eqnarray}$$
Solving (3.6) and (3.2) for
$\unicode[STIX]{x1D705}_{c}$
while ignoring non-physical solutions, we arrive at
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{c} & = & \displaystyle \frac{2u_{c}^{1/2}-2u_{c}+3Re^{-1}}{Rb(3u_{c}^{2}-2u_{c}^{3/2}-1+Rb^{-2})}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\sqrt{u_{c}^{2}+1-2u_{c}^{-1/2}+12Re^{-1}(u_{c}^{1/2}-u_{c})+9Re^{-2}+Rb^{-2}(2u_{c}^{-1/2}-1)}}{Rb(3u_{c}^{2}-2u_{c}^{3/2}-1+Rb^{-2})},\qquad\end{eqnarray}$$
where
$u_{c}$
, i.e. the fibre speed at the circle (equivalent to
$1/\sqrt{R_{c}}$
), is linked to
$We$
,
$Rb$
and
$\unicode[STIX]{x1D705}_{c}$
through
$$\begin{eqnarray}We=\frac{u_{c}^{1/2}\unicode[STIX]{x1D705}_{c}^{2}}{u_{c}^{2}\unicode[STIX]{x1D705}_{c}^{2}+2u_{c}Rb^{-1}\unicode[STIX]{x1D705}_{c}+Rb^{-2}}.\end{eqnarray}$$
Using (3.7) and (3.8), we can find the curvature of the circular trajectory (or the circle diameter) and the fibre speed (or the fibre radius) at the circle for a given set of
$We$
,
$Re$
and
$Rb$
.
Now, we can also proceed to compute the transition Weber number,
$We_{t}$
, at which the fibre starts to have a spiral trajectory instead of a circular one. Relation (3.7) has an imaginary part (i.e. a non-physical solution) when the term under the square root becomes negative, which suggests that there would be no circle-like trajectory that simultaneously satisfies the
$s$
-momentum and solvability equations. Therefore, we assume that the transition between a circular trajectory and a non-circular trajectory occurs when the term under the square root is zero (where also the maximum magnitude of the curvature can be reached). Applying this condition delivers two equations which can be solved to furnish a critical transition Weber number as
$$\begin{eqnarray}We_{t}=\frac{(2u_{t}^{3/2}-2u_{t}-3\sqrt{u_{t}}/Re)^{2}}{\sqrt{u_{t}}\left({\displaystyle \frac{2u_{t}^{2}}{Rb^{2}}}-{\displaystyle \frac{2}{Rb^{2}}}+{\displaystyle \frac{1}{Rb^{4}}}+{\displaystyle \frac{6u_{t}}{ReRb^{2}}}+{\displaystyle \frac{6u_{t}^{3}}{Re}}-{\displaystyle \frac{6u_{t}}{Re}}+{\displaystyle \frac{9u_{t}^{2}}{Re^{2}}}+(u_{t}^{2}-1)^{2}\right)},\end{eqnarray}$$
where
$u_{t}$
is the transition fibre speed which is linked to the Rossby and Reynolds numbers through
$$\begin{eqnarray}Rb=\sqrt{\frac{u_{t}-2\sqrt{u_{t}}}{{\displaystyle \frac{12u_{t}^{3/2}}{Re}}+u_{t}^{3}-{\displaystyle \frac{12u_{t}^{2}}{Re}}+{\displaystyle \frac{9u_{t}}{Re^{2}}}+u_{t}-2\sqrt{u_{t}}}}.\end{eqnarray}$$
Using the two equations above, we can find
$We_{t}$
as a function of
$Rb$
and
$Re$
.
Figure 11. (a) Fibre curvature of circular trajectory
$\unicode[STIX]{x1D705}_{c}$
(or equivalently inverse circle diameter
$D_{c}$
) versus
$We$
for
$Rb=0.001$
,
$Fr\rightarrow \infty$
and
$m=1$
. (b) Fibre radius (or speed) versus
$We$
for the same parameters as panel (a). In the two panels, the analytical approximate results are shown by lines and the simulation results by markers for
$Re=1$
(solid line, *),
$Re=0.1$
(dashed line,
$+$
) and
$Re=0.01$
(dash-dot line,
$\times$
).
We have analysed numerous simulation data and we have compared them with the simplified model results. Figure 11(a,b) compares the predictions of the simplified model with the simulation results. The circular trajectory curvature (or circle diameter) and the fibre radius (or speed) are shown versus
$We$
for a fixed
$Rb=0.001$
at different Reynolds numbers. The comparison between the simplified model curves and the simulation results is satisfactory, although for the smallest
$Re$
a deviation from the simplified model curve is observed, which is due to the simplifying assumptions explained earlier. Figure 11(a,b) shows that by increasing
$We$
, the absolute values of the fibre curvature and radius in a circular trajectory increase, which are both counter-intuitive. Loosely speaking, at very small
$We$
the surface energy is very large and larger centrifugal energy (and thus a larger circle diameter) is required to balance the surface energy, which also causes the fibre to have higher speed and therefore smaller fibre radius. However, with increasing
$We$
and thus smaller surface energy, the circle diameter required to maintain the necessary centrifugal force decreases, which in return results in a thicker fibre. By further increasing
$We$
, the inertial energy finally takes over the surface one at
$We_{t}$
, after which the fibre follows a spiral path and continuously thins along the arc length. In figure 11(a,b), the lines terminate at approximately the value of
$We_{t}$
, the Weber number at which the simplified model predicts that there no longer exists a physical circular trajectory satisfying the simplified equations.
Figure 12. Classification of the circular and spiral trajectory regimes in the plane of
$We$
and
$Rb$
(note that the critical transition values are plotted). The simplified model results are shown by lines and the simulation results by markers for
$Re=1$
(solid line, *),
$Re=0.1$
(dashed line,
$+$
) and
$Re=0.01$
(dash-dot line,
$\times$
).
Figure 12 classifies the circular and spiral trajectory regimes, by plotting
$We_{t}$
, from (3.9), against
$Rb$
for three different values of
$Re$
. The simplified model predictions are in good agreement with simulation results except for the smallest
$Re$
.
Although in this section we presented our simplified model for a Newtonian fluid (
$m=1$
), the same approach can be used to obtain
$We_{t}$
for a non-Newtonian fluid (
$m\neq 1$
). However, our simulation results (not shown) reveal that
$We_{t}$
is not greatly influenced by variations in
$m$
.
3.5 Effects of the power-law index
Figure 13 is aimed at describing the effects of the shear-thinning and shear-thickening power-law index on the fibre radius, for
$m=0.6$
, 0.8, 1 and 1.2. Figure 13(a) shows that the fibre trajectory is not significantly influenced by
$m$
. The fibre angles (not plotted for brevity) are likewise not much affected by
$m$
. Figure 13(b) shows the leading-order apparent viscosity versus
$s$
for the cases studied, revealing that the apparent viscosity is much lower for the flow with the smallest power-law index, which is expected. What is not a priori known is that for shear-thinning fluids the apparent viscosity varies non-monotonically with the arc length, initially decreasing, reaching a minimum, and eventually increasing with
$s$
. It is vividly seen that, unlike the shear-thinning cases (
$m<1$
), the apparent viscosity of the shear-thickening fluid (
$m=1.2$
) increases initially until it reaches a maximum and then decreases. Figure 13(c) also displays that the fibre radius for the smaller
$m$
flow initially lies below the one for the larger
$m$
flow. However, at large
$s$
the fibre radii for all the power-law index values reach nearly the same inviscid limit, independent of
$m$
(and of
$Re$
,
$Fr$
and
$We$
). Practically, one of the most significant effects of decreasing
$m$
is perhaps on the thinning rate of the fibre radius. Figure 13(d) shows the thinning rate versus the arc length, showing that the fibre thinning rate for
$m=0.6$
at small
$s$
is almost three times larger than that for
$m=1$
. Interestingly, while the thinning rate at the lower
$m$
is initially much larger compared to the higher
$m$
, at certain arc length,
$|-R_{s}|$
of the lower
$m$
flow falls below that of the higher
$m$
flow. The cross-over arc length is nearly the same for different values of
$m$
. However, the radius of all of these fibres is almost the same at large
$s$
.
Figure 13. Simulation results for
$Rb=0.01$
and
$Re=Fr=We=0.1$
, for
$m=0.6$
(solid line),
$m=0.8$
(dashed line),
$m=1$
(dash-dot line) and
$m=1.2$
(dotted line).
3.6 Zones of thinning of fibre radius
We have thus far found two main flow regimes for large and small Weber numbers, i.e. the spiral and circular trajectory regimes. To end our discussion section, we now present a thinning zone classification based on a simplified analysis, for perhaps the most crucial fibre feature, i.e. the fibre radius versus
$s$
. For simplicity, we neglect gravity, the effects of which on the flow were discussed above. In what follows, for the sake of clarity, we will use the ‘
$\varnothing$
’ symbol to denote a non-circular (spiral) trajectory flow and the ‘○’ symbol to indicate a circular trajectory flow.
Let us begin with the spiral trajectory regime, for which the effects of surface tension can be ignored. For these flows, we have observed that while the fibre radius initially remains close to unity at very small
$s$
(no-thinning regime), at a critical
$s$
the fibre transitions to a regime of significant thinning (intense-thinning regime), and finally at another larger critical
$s$
, the fibre reaches a third regime, which is nearly inviscid, with a much slower thinning rate (slow-thinning regime). To perform our simplified analysis, we concentrate only on the axial momentum balance equation. For small
$s$
, the viscous stress term in this equation is of order
$s^{-m-1}Re^{-1}3^{(m+1)/2}u$
balancing the centrifugal term that is of order
$Rb^{-2}$
, furnishing the fibre radius as
$$\begin{eqnarray}\overset{\varnothing }{R}_{it}\approx s^{-(m+1)/2}3^{(m+1)/4}Rb\,Re^{-1/2}.\end{eqnarray}$$
On the other hand, the fibre radius in the no-thinning and slow-thinning regimes are
$$\begin{eqnarray}\overset{\varnothing }{R}_{nt}\approx 1,\end{eqnarray}$$
and
$$\begin{eqnarray}\overset{\varnothing }{R}_{st}\approx \sqrt[4]{Rb^{2}/2s},\end{eqnarray}$$
respectively. Thus, the transition arc length between the no-thinning and intense-thinning regimes can be simply approximated through satisfying
$\overset{\varnothing }{R}_{nt}=\overset{\varnothing }{R}_{it}$
, furnishing
$$\begin{eqnarray}\overset{\varnothing }{s}_{nt-it}\approx 3^{1/2}Rb^{2/(m+1)}Re^{-1/(m+1)},\end{eqnarray}$$
while the transition arc length between the intense-thinning and slow-thinning regimes is similarly obtained through
$\overset{\varnothing }{R}_{it}=\overset{\varnothing }{R}_{st}$
, providing
$$\begin{eqnarray}\overset{\varnothing }{s}_{it-st}\approx 3^{(m+1)/(2m+1)}2^{1/(2m+1)}Re^{2/(2m+1)}Rb^{-2/(2m+1)}.\end{eqnarray}$$
To test the simple expressions developed, figure 14(a) compares a simulation fibre radius with a spiral trajectory against
$\overset{\varnothing }{R}_{nt}$
,
$\overset{\varnothing }{R}_{it}$
and
$\overset{\varnothing }{R}_{st}$
as well as the transition arc lengths, presenting reasonable agreement.
Figure 14. Comparison between the simulation fibre radii (thick lines) and the fibre radii of the three thinning zones (dash-lines) discussed in the text. The vertical dash-dot lines mark the transition between the zones. (a) Spiral trajectory flows for
$Rb=0.01$
,
$Re=Fr=We=0.1$
and
$m=0.6$
. (b) Circular trajectory flows for
$Rb=0.01$
,
$Re=0.1$
,
$Fr\rightarrow \infty$
,
$m=1$
and
$We=0.001$
.
Now for the circular trajectory regime, a similar approach can be employed and after some algebra, three fibre radius regimes can be found as
$$\begin{eqnarray}\overset{\bigcirc }{R}_{nt}\approx 1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overset{\bigcirc }{R}_{it} & {\approx} & \displaystyle \left(\vphantom{\frac{[Res^{2}]^{1/2^{L}}}{2^{2}WRb^{2}}}\frac{Re(3^{m-1}Res^{2(m+1)}Rb^{2}3^{-2m}+2^{3}3^{-(m+1)/2}We^{2}s^{(3+m)})}{2^{3}We^{2}s^{2}Rb^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{Re(3^{-(m+1)}Rbs^{(m+1)}[Res^{2}(Res^{2m}Rb^{2}+2^{4}3^{(m+1)/2}We^{2}s^{(m+1)})]^{1/2})}{2^{3}We^{2}s^{2}Rb^{2}}\right)^{-1/2}\!,\qquad\end{eqnarray}$$
and
$$\begin{eqnarray}\overset{\bigcirc }{R}_{ct}\approx R_{c},\end{eqnarray}$$
where the subscript ‘
$ct$
’ indicates a ceased-thinning regime, where the fibre radius approaches
$R_{c}$
, i.e. the fibre radius in the circular trajectory regime calculated earlier. On the other hand, the transition arc length between the no-thinning and intense-thinning regimes of circular trajectory flows,
$\overset{\bigcirc }{s}_{nt-it}$
, is the positive real root of
$$\begin{eqnarray}\overset{\bigcirc }{R}_{it}(Rb,Re,We,m,\overset{\bigcirc }{s}_{nt-it})-1=0,\end{eqnarray}$$
which can be readily found for a given set of dimensionless parameters. The transition arc length between the intense-thinning and ceased-thinning regimes for circular trajectory flows,
$\overset{\bigcirc }{s}_{it-ct}$
, can be calculated through finding the positive real root of
$$\begin{eqnarray}\overset{\bigcirc }{R}_{it}(Rb,Re,We,m,\overset{\bigcirc }{s}_{it-ct})-\overset{\bigcirc }{R}_{ct}=0,\end{eqnarray}$$
which can be likewise found for a given dimensionless parameter set. It must be noted that
$\overset{\bigcirc }{s}_{it-ct}$
is introduced here to maintain the integrity of the simplified analysis and place an arc length end boundary on the intense-thinning regime, although one could use the circular trajectory fibre arc length,
$\ell _{c}\approx 1/2\unicode[STIX]{x1D705}_{c}^{2}$
(discussed in § 3.4.1), as a more accurate prediction of the arc length where the constant fibre radius is reached.
To evaluate the performance of the simple expressions developed for the thinning zone classification of circular trajectory flows, figure 14(b) compares a simulation fibre radius against
$\overset{\bigcirc }{R}_{nt}$
,
$\overset{\bigcirc }{R}_{it}$
and
$\overset{\bigcirc }{R}_{ct}$
as well as the transition arc lengths, showing reasonable agreement.
4 Summary
In this work, we developed for the first time the three-dimensional string model equations for a shear-thinning power-law fluid, for which we implemented a general curvature regularization approach, enabling robust solutions for the parameter ranges of interest to nanofibre formation by centrifugal spinning methods. We exploited the model for a range of typical dimensionless parameters, i.e.
$Rb$
,
$Re$
,
$Fr$
,
$We$
and
$m$
, to provide a fundamental understanding about the curved jet features. We found that while decreasing
$Rb$
leads to thinner fibres throughout the arc length, decreasing
$Re$
merely influences the thinning at short arc lengths. In the same manner, shear-thinning properties strongly impact the fibre thinning rate only at small arc lengths. We also found that while gravity mainly influences the fibre vertical angle close to the orifice, the effects of surface tension can be more significant. In fact, we were able to classify in detail the circular and spiral trajectory flows, for which the transition occurs at a critical Weber number. Finally, as the arc length increases, we quantified boundaries of the no-thinning, intense-thinning and slow-thinning (for spiral trajectory flows) or ceased-thinning (for circular trajectory flows) zones describing the thinning of the fibre radius with fibre arc length. Future directions will include an extension of the model to include non-stationary solutions, viscoelastic constitutive models and stability analyses.
Acknowledgements
This research has been carried out at Université Laval, supported partially by the Canada foundation for innovation (grant nos GF112622, GQ113034 and GF517657) and the Discovery Grant of the Natural Sciences and Engineering Research Council of Canada (grant no. CG10915). R.G.L. gratefully acknowledges the support of the National Science Foundation under grant DMR 1403335. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. A partial doctoral scholarship support for S.N. provided by the Université Laval Aluminium Research Centre (REGAL-Laval) is greatly appreciated. Our special thanks are due to E. I. Părău for sharing useful mathematical derivations in personal communications and to the reviewers for their constructive and helpful comments.
Appendix A. Momentum stress terms
In this section, the stress terms in equation (2.4) are presented in detail. First, defining
$\mathbb{S}=-\sqrt{X_{ss}^{2}+Y_{ss}^{2}+Z_{ss}^{2}}$
and
$\tilde{\mathbb{S}}=X_{ss}X_{sss}+Y_{ss}Y_{sss}+Z_{ss}Z_{sss}$
, the viscous terms in the three directions (
$s$
,
$n$
and
$\unicode[STIX]{x1D711}$
) can be given:
$$\begin{eqnarray}\displaystyle V_{s} & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x1D702}}{nh_{s}}\left[\frac{n^{2}}{h_{s}^{2}}\cos (\unicode[STIX]{x1D711})\frac{\widetilde{\mathbb{S}}}{\mathbb{S}}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}s}+\mathbb{S}(v\cos (\unicode[STIX]{x1D711})-w\sin (\unicode[STIX]{x1D711}))\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n}{h_{s}}\left(-u\mathbb{S}+\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}s^{2}}+\mathbb{S}(v\cos (\unicode[STIX]{x1D711})-w\sin (\unicode[STIX]{x1D711}))+2\mathbb{S}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}s}\cos (\unicode[STIX]{x1D711})-\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}\sin (\unicode[STIX]{x1D711})\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\left.(1+2n\cos (\unicode[STIX]{x1D711})\mathbb{S})\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}n}+nh_{s}\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}n^{2}}-\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\sin (\unicode[STIX]{x1D711})\mathbb{S}+\frac{h_{s}}{n}\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{2}}\vphantom{\frac{\tilde{\mathbb{S}}}{h_{s}^{2}}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{\unicode[STIX]{x1D70C}h_{s}^{2}}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}s}+\mathbb{S}(v\cos (\unicode[STIX]{x1D711})-w\sin (\unicode[STIX]{x1D711}))\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}s}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}h_{s}}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}s}-\mathbb{S}\cos (\unicode[STIX]{x1D711})u+h_{s}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}n}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}n}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}n}\left(\frac{1}{n}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}+\frac{1}{h_{s}}\mathbb{S}\sin (\unicode[STIX]{x1D711})u+\frac{1}{h_{s}}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{n} & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x1D702}}{n}\left[\frac{n^{2}}{h_{s}^{2}}\cos (\unicode[STIX]{x1D711})\frac{\widetilde{\mathbb{S}}}{\mathbb{S}}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}s}\mathbb{S}u\cos (\unicode[STIX]{x1D711})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n}{h_{s}}\left(-v\mathbb{S}^{2}\cos ^{2}(\unicode[STIX]{x1D711})+\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}s^{2}}+\frac{\widetilde{\mathbb{S}}}{\mathbb{S}}\cos (\unicode[STIX]{x1D711})u-2\mathbb{S}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}s}\cos (\unicode[STIX]{x1D711})\right)\nonumber\\ \displaystyle & & \displaystyle +\,(1+2n\cos (\unicode[STIX]{x1D711})\mathbb{S})\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}n}+nh_{s}\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}n^{2}}+w\mathbb{S}^{2}\cos (\unicode[STIX]{x1D711})\sin (\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle -\left.\!\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}-w\right)\sin (\unicode[STIX]{x1D711})\mathbb{S}+\frac{h_{s}}{n}\left(\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{2}}-v-2\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right)\vphantom{\frac{\tilde{\mathbb{S}}}{h_{s}^{2}}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}h_{s}}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}s}-\mathbb{S}u\cos (\unicode[STIX]{x1D711})+h_{s}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}n}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}s}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2h_{s}}{\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}n}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}n}+\frac{h_{s}}{\unicode[STIX]{x1D70C}n}\left(\frac{1}{n}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}-\frac{w}{n}+\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}n}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D711}} & = & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x1D702}}{n}\left[\frac{n^{2}}{h_{s}^{2}}\cos (\unicode[STIX]{x1D711})\frac{\widetilde{\mathbb{S}}}{\mathbb{S}}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}+\mathbb{S}u\sin (\unicode[STIX]{x1D711})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n}{h_{s}}\left(-w\mathbb{S}^{2}\sin ^{2}(\unicode[STIX]{x1D711})+\frac{\unicode[STIX]{x2202}^{2}w}{\unicode[STIX]{x2202}s^{2}}-\frac{\widetilde{\mathbb{S}}}{\mathbb{S}}\sin (\unicode[STIX]{x1D711})u+2\mathbb{S}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}s}\sin (\unicode[STIX]{x1D711})\right)\nonumber\\ \displaystyle & & \displaystyle +\,(1+2n\cos (\unicode[STIX]{x1D711})\mathbb{S})\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}n}+nh_{s}\frac{\unicode[STIX]{x2202}^{2}w}{\unicode[STIX]{x2202}n^{2}}+w\mathbb{S}^{2}\cos (\unicode[STIX]{x1D711})\sin (\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle -\left.\!\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}+v\right)\sin (\unicode[STIX]{x1D711})\mathbb{S}+\frac{h_{s}}{n}\left(\frac{\unicode[STIX]{x2202}^{2}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{2}}-w+2\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right)\vphantom{\frac{\tilde{\mathbb{S}}}{h_{s}^{2}}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}h_{s}}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}+\mathbb{S}u\sin (\unicode[STIX]{x1D711})+\frac{h_{s}}{n}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}s}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{h_{s}}{n\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}-w+n\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}n}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}n}+\frac{2h_{s}}{\unicode[STIX]{x1D70C}n^{2}}\left(v+\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}.\end{eqnarray}$$
The gravitational terms in each direction can be derived as
$$\begin{eqnarray}\displaystyle & G_{s}=-gY_{s}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G_{n}=g\left(\frac{Z_{ss}X_{s}\sin (\unicode[STIX]{x1D711})-Z_{s}X_{ss}\sin (\unicode[STIX]{x1D711})+Y_{ss}\cos (\unicode[STIX]{x1D711})}{\mathbb{S}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle G_{\unicode[STIX]{x1D711}}=g\left(\frac{Z_{ss}X_{s}\cos (\unicode[STIX]{x1D711})-Z_{s}X_{ss}\cos (\unicode[STIX]{x1D711})+Y_{ss}\sin (\unicode[STIX]{x1D711})}{\mathbb{S}}\right). & \displaystyle\end{eqnarray}$$
Finally, the rotational terms are
$$\begin{eqnarray}\displaystyle RO_{s} & = & \displaystyle 2\unicode[STIX]{x1D6FA}\left(-\frac{v(Z_{s}X_{ss}\cos (\unicode[STIX]{x1D711})-Z_{ss}X_{s}\cos (\unicode[STIX]{x1D711})+Y_{ss}\sin (\unicode[STIX]{x1D711}))}{\mathbb{S}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{w(Z_{s}X_{ss}\sin (\unicode[STIX]{x1D711})-Z_{ss}X_{s}\sin (\unicode[STIX]{x1D711})-Y_{ss}\cos (\unicode[STIX]{x1D711}))}{\mathbb{S}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FA}^{2}\left(X_{s}(X+s_{0})+ZZ_{s}+nY_{s}\left(\frac{Z_{ss}X_{s}\sin (\unicode[STIX]{x1D711})-Z_{s}X_{ss}\sin (\unicode[STIX]{x1D711})+Y_{ss}\cos (\unicode[STIX]{x1D711})}{\mathbb{S}}\right)\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle RO_{n} & = & \displaystyle 2\unicode[STIX]{x1D6FA}\left(-\frac{u(Z_{ss}X_{s}\cos (\unicode[STIX]{x1D711})-Z_{s}X_{ss}\cos (\unicode[STIX]{x1D711})-Y_{ss}\sin (\unicode[STIX]{x1D711}))}{\mathbb{S}}-wY_{s}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FA}^{2}\left(\frac{(X+s_{0})(Z_{s}Y_{ss}\sin (\unicode[STIX]{x1D711})-Z_{ss}Y_{s}\sin (\unicode[STIX]{x1D711})+X_{ss}\cos (\unicode[STIX]{x1D711}))}{\mathbb{S}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{Z(Y_{s}X_{ss}\sin (\unicode[STIX]{x1D711})-Y_{ss}X_{s}\sin (\unicode[STIX]{x1D711})+Z_{ss}\cos (\unicode[STIX]{x1D711}))}{\mathbb{S}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n(((Z_{s}Y_{ss}-Z_{ss}Y_{s})\sin (\unicode[STIX]{x1D711})+X_{ss}\cos (\unicode[STIX]{x1D711}))^{2})}{\mathbb{S}^{2}}\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{n(((Y_{s}X_{ss}-Y_{ss}X_{s})\sin (\unicode[STIX]{x1D711})+Z_{ss}\cos (\unicode[STIX]{x1D711}))^{2})}{\mathbb{S}^{2}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle RO_{\unicode[STIX]{x1D711}} & = & \displaystyle 2\unicode[STIX]{x1D6FA}\left(-\frac{u(Z_{s}X_{ss}\sin (\unicode[STIX]{x1D711})-Z_{ss}X_{s}\sin (\unicode[STIX]{x1D711})-Y_{ss}\cos (\unicode[STIX]{x1D711}))}{\mathbb{S}}-vY_{s}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FA}^{2}\left(-\frac{(X+s_{0})(Z_{s}Y_{ss}\cos (\unicode[STIX]{x1D711})-Z_{ss}Y_{s}\cos (\unicode[STIX]{x1D711})-X_{ss}\sin (\unicode[STIX]{x1D711}))}{\mathbb{S}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{Z(Y_{s}X_{ss}\cos (\unicode[STIX]{x1D711})-Y_{ss}X_{s}\cos (\unicode[STIX]{x1D711})-Z_{ss}\sin (\unicode[STIX]{x1D711}))}{\mathbb{S}}\nonumber\\ \displaystyle & & \displaystyle +\,n\left(\frac{(Z_{s}Y_{ss}-Z_{ss}Y_{s})\sin (\unicode[STIX]{x1D711})+X_{ss}\cos (\unicode[STIX]{x1D711})}{\mathbb{S}^{2}((Z_{s}Y_{ss}-Z_{ss}Y_{s})\cos (\unicode[STIX]{x1D711})-X_{ss}\sin (\unicode[STIX]{x1D711}))^{-1}}\right)\nonumber\\ \displaystyle & & \displaystyle +\left.n\left(\frac{(Y_{s}X_{ss}-Y_{ss}X_{s})\sin (\unicode[STIX]{x1D711})+Z_{ss}\cos (\unicode[STIX]{x1D711})}{\mathbb{S}^{2}((Y_{s}X_{ss}-Y_{ss}X_{s})\cos (\unicode[STIX]{x1D711})-Z_{ss}\sin (\unicode[STIX]{x1D711}))^{-1}}\right)\right).\end{eqnarray}$$
