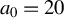1 Introduction
With the development and construction of high-power laser systems[ Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel1 – Reference Shen, Bu, Xu, Xu, Ji, Li and Xu3 ], the study of laser–plasma interactions is becoming increasingly important. One hot topic is electron acceleration. Conventional radio frequency (RF) accelerators are limited by the strength of the accelerating gradient supported by a specific material, thereby limiting the energy of the accelerated particles and the size of the facilities. However, high-intensity lasers can achieve higher acceleration gradients in laser-driven wakefield acceleration and direct laser acceleration[ Reference Kumar, Kant and Ghotra4 – Reference Tomkus, Girdauskas, Abedi-Varaki and Raciukaitis8 ]. Laser-driven electron acceleration has been of great significance for the realization of compact accelerators and radiation sources[ Reference Geddes, Toth, Van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans9 – Reference Ji, Pukhov, Kostyukov, Shen and Akli12 ] after the invention of the chirped pulse amplification (CPA) technology[ Reference Strickland and Mourou13 ]. Intense vortex beams, or Laguerre–Gaussian (LG) beams, have attracted the attention of the laser–plasma community because of their special properties, such as a twisted phase front, orbital angular momentum (OAM) carrying, hollow intensity distribution and spatially isolated longitudinal fields[ Reference Shi, Zhang, Arefiev and Shen14 ]. These properties can change the laser–plasma interactions in corresponding ways and produce different applications. To generate a relativistic intense twisted laser, one approach is to use a solid plasma with a ‘light fan’ structure to reflect the Gaussian laser and obtain a relativistic intense twisted laser, as proposed by Shi et al. in 2014[ Reference Shi, Shen, Zhang, Zhang, Wang and Xu15 ]. Porat et al.[ Reference Porat, Lightman, Cohen and Pomerantz16 ] demonstrated the feasibility of generating a relativistic intense twisted laser using a solid plasma with the ‘light fan’ structure in the laboratory in 2022. The experiment used a structured mirror based on microscale three-dimensional (3D) printing technology. An intense plane wave is obliquely incident on the ‘light fan’ to obtain the reflected vortex beam. In addition, several papers have been published on the generation of terawatt helical lasers using CPA systems[ Reference Chen, Zheng, Lu, Wang, Cai, Wang, Zheng, Ai, Leng, Xu and Fan17 , Reference Pan, Liang, Yu, Wang, Li and Li18 ]. Although the technology for generating higher-power helical beams has not yet been integrated into high-power laser facilities, these advances provide new opportunities and approaches for laser–plasma interactions and particle acceleration.
In previous work, a circularly polarized (CP) LG laser beam has been studied to generate high-quality electron pulse trains by the reflection of the laser from a high-density solid target[
Reference Shi, Blackman, Stutman and Arefiev19
–
Reference Pae, Kim, Pathak, Ryu and Nam22
]. The twist index
![]() $l$
of LG beams, often referred to as the topological charge, indicates the number of
$l$
of LG beams, often referred to as the topological charge, indicates the number of
![]() $2\pi$
phase shifts around the beam’s axis and determines the beam’s OAM, giving an OAM of
$2\pi$
phase shifts around the beam’s axis and determines the beam’s OAM, giving an OAM of
![]() $l\mathrm{\hslash}$
per photon[
Reference Shi, Zhang, Arefiev and Shen14
,
Reference Yao and Padgett23
,
Reference Allen, Padgett and Babiker24
]. When the twist index
$l\mathrm{\hslash}$
per photon[
Reference Shi, Zhang, Arefiev and Shen14
,
Reference Yao and Padgett23
,
Reference Allen, Padgett and Babiker24
]. When the twist index
![]() $l$
of the LG beam and the CP index
$l$
of the LG beam and the CP index
![]() $\sigma$
satisfy the condition
$\sigma$
satisfy the condition
![]() $l\times \sigma =-1$
, the spin angular momentum and the OAM are antiparallel, resulting in a longitudinal electromagnetic field along the axis for the twisted laser. Due to the hollow structure of the
$l\times \sigma =-1$
, the spin angular momentum and the OAM are antiparallel, resulting in a longitudinal electromagnetic field along the axis for the twisted laser. Due to the hollow structure of the
![]() ${\mathrm{LG}}_{01}$
helical wavefront and the strongest axial field along the axis, a spatial separation between longitudinal and transverse fields is possible. This feature is impossible for a conventional laser beam. For a given twist index, a linearly polarized (LP)-LG laser beam can be decomposed into a pair of CP-LG beams, where
${\mathrm{LG}}_{01}$
helical wavefront and the strongest axial field along the axis, a spatial separation between longitudinal and transverse fields is possible. This feature is impossible for a conventional laser beam. For a given twist index, a linearly polarized (LP)-LG laser beam can be decomposed into a pair of CP-LG beams, where
![]() ${\sigma =1,-1}$
represent the right-CP beam and the left-CP beam, respectively. According to the theoretical analysis, only a CP-LG beam with
${\sigma =1,-1}$
represent the right-CP beam and the left-CP beam, respectively. According to the theoretical analysis, only a CP-LG beam with
![]() ${l\times \sigma =-1}$
contributes to the longitudinal fields on the axis. Although their symmetry is broken at the position away from the axis, the longitudinal fields of an LP-LG beam still peak at the axis. While the strong high harmonic effect is unavoidable when an LP-LG laser beam interacts with solid plasma, it can still be used to generate electron pulse trains[
Reference Shi, Blackman, Zhu and Arefiev25
]. The scheme of accelerating electrons using relativistically strongly tightly focused radially polarized laser beams has also been investigated[
Reference Salamin26
–
Reference Zam, Thévenet, Lifschitz and Faure29
].
${l\times \sigma =-1}$
contributes to the longitudinal fields on the axis. Although their symmetry is broken at the position away from the axis, the longitudinal fields of an LP-LG beam still peak at the axis. While the strong high harmonic effect is unavoidable when an LP-LG laser beam interacts with solid plasma, it can still be used to generate electron pulse trains[
Reference Shi, Blackman, Zhu and Arefiev25
]. The scheme of accelerating electrons using relativistically strongly tightly focused radially polarized laser beams has also been investigated[
Reference Salamin26
–
Reference Zam, Thévenet, Lifschitz and Faure29
].
In this paper, we propose a scheme that combines the generation of the LG beam and the process of electron acceleration by the longitudinal fields. The basic idea is using the ‘light fan’ structure[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
] with a nanowire in the center (see Figure 1). The use of relativistic intense LG beam interaction with a nanowire target or micro-droplet to obtain attosecond beams has been studied[
Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao30
,
Reference Hu, Yu, Li, Yin, McKenna and Shao31
]. In experiments, silicon nano-integrated targets have been used to increase the total and cutoff energies of the resulting electron beams[
Reference Jiang, Ji, Audesirk, George, Snyder, Krygier, Poole, Willis, Daskalova, Chowdhury, Lewis, Schumacher, Pukhov, Freeman and Akli32
]. Here, we present the results of a 3D particle-in-cell (PIC) simulation for a CP Gaussian beam reflected from the ‘light fan’ structure above. The peak power of the CP laser beam is around 490 TW. The electrons from the nanowire can be extracted and injected into the reflected laser beam. The electrons injected near the laser axis can obtain longitudinal acceleration driven by a longitudinal electric field. Although the LG laser generated by reflection has a mixture of radial modes
![]() $p$
, which is bad for electron acceleration[
Reference Shi, Blackman and Arefiev20
,
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
], the longitudinal fields still have a remarkable acceleration effect. The most energetic bunch exhibits an energy of 310 MeV, with a spread of 6%. The bunch charge is 57 pC, the duration is 400 as and the angle of divergence is less than 50 mrad. By using a Gaussian beam, our proposed approach can potentially reduce the experimental complexity in demonstrating twisted laser-driven electron acceleration. These dense ultrashort bunches have the potential to be utilized in research and technology[
Reference Black, Niedermayer, Miao, Zhao, Solgaard, Byer and Leedle33
,
Reference Schönenberger, Mittelbach, Yousefi, McNeur, Niedermayer and Hommelhoff34
].
$p$
, which is bad for electron acceleration[
Reference Shi, Blackman and Arefiev20
,
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
], the longitudinal fields still have a remarkable acceleration effect. The most energetic bunch exhibits an energy of 310 MeV, with a spread of 6%. The bunch charge is 57 pC, the duration is 400 as and the angle of divergence is less than 50 mrad. By using a Gaussian beam, our proposed approach can potentially reduce the experimental complexity in demonstrating twisted laser-driven electron acceleration. These dense ultrashort bunches have the potential to be utilized in research and technology[
Reference Black, Niedermayer, Miao, Zhao, Solgaard, Byer and Leedle33
,
Reference Schönenberger, Mittelbach, Yousefi, McNeur, Niedermayer and Hommelhoff34
].

Figure 1 The target features a ‘light fan’ structure and a nanowire structure (blue part) at the center. The ‘light fan’ has eight parts, each with a uniform step height of
![]() $\Delta h={\lambda}_0/16$
. This setup emulates the effect of a spiral phase plate with
$\Delta h={\lambda}_0/16$
. This setup emulates the effect of a spiral phase plate with
![]() $\Delta h={\lambda}_0/2$
. The colors in green represent different phase changes that occur when a plane wave is incident normally. To prevent transmission of the laser pulse, the maximum thickness of the target is set to 1.6 μm.
$\Delta h={\lambda}_0/2$
. The colors in green represent different phase changes that occur when a plane wave is incident normally. To prevent transmission of the laser pulse, the maximum thickness of the target is set to 1.6 μm.
In the remainder of this paper, the setup of the 3D PIC simulation, the field structure of the reflected beam and the mode decomposition of the generated LG laser are first given in Section 2. In Section 3, the injection and initial acceleration of the electron bunches are discussed when the laser is reflected by the ‘light fan’ and interacts with the nanowire. The longitudinal momentum gain in a mixed longitudinal electric field mode is shown with the supporting theory in Section 4. Finally, we summarize the main conclusions and discuss potential applications in Section 5.
2 Simulation setup and mode structure of the reflected laser beam
In this section, we present the simulation setup using the PIC code SMILEI[
Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov, Aunai, Dargent, Riconda and Grech35
]. In our 3D PIC simulation, a CP Gaussian laser beam is reflected from the solid plasma with a ‘light fan’ structure that features a central integrated nanowire, as shown in Figure 1. We use a 490 TW CP Gaussian beam with
![]() $\sigma =+1$
, which propagates along the negative x-axis direction upon entering the simulation box. The focal plane of the beam is situated at
$\sigma =+1$
, which propagates along the negative x-axis direction upon entering the simulation box. The focal plane of the beam is situated at
![]() $x=0\ \mu \mathrm{m}$
, which coincides with the location of the target surface. The electron density is
$x=0\ \mu \mathrm{m}$
, which coincides with the location of the target surface. The electron density is
![]() ${n}_{\mathrm{e}}=120{n}_{\mathrm{c}}$
, where
${n}_{\mathrm{e}}=120{n}_{\mathrm{c}}$
, where
![]() ${n}_{\mathrm{c}}=1.74\times {10}^{27}\;{\mathrm{m}}^{-3}$
is the critical density for a laser with
${n}_{\mathrm{c}}=1.74\times {10}^{27}\;{\mathrm{m}}^{-3}$
is the critical density for a laser with
![]() ${\lambda}_0=0.8\ \mu \mathrm{m}$
. Because of the high energy of the incident beam, we assume that the target is completely ionized when the beam arrives, so the target is set up as a cold and preionized plasma. To track the acceleration of the electrons over an extended period, a moving window is utilized. The window size is set to encompass the entire simulation box and moves with a velocity of
${\lambda}_0=0.8\ \mu \mathrm{m}$
. Because of the high energy of the incident beam, we assume that the target is completely ionized when the beam arrives, so the target is set up as a cold and preionized plasma. To track the acceleration of the electrons over an extended period, a moving window is utilized. The window size is set to encompass the entire simulation box and moves with a velocity of
![]() $c$
, starting at
$c$
, starting at
![]() $t=25$
fs. The time
$t=25$
fs. The time
![]() $t=0$
is defined as the instant at which the peak of the laser envelope reaches
$t=0$
is defined as the instant at which the peak of the laser envelope reaches
![]() $x=0$
. The time resolution of the simulation is 0.012 laser cycles to better resolve the electron trajectories as well as to satisfy the Courant–Friedrichs–Lewy condition. Detailed parameters of the laser beam and the target are listed in Table 1. Through its ‘light fan’ structure, the wavefront of the reflected beam is twisted. In our scheme, we need to ensure the condition
$x=0$
. The time resolution of the simulation is 0.012 laser cycles to better resolve the electron trajectories as well as to satisfy the Courant–Friedrichs–Lewy condition. Detailed parameters of the laser beam and the target are listed in Table 1. Through its ‘light fan’ structure, the wavefront of the reflected beam is twisted. In our scheme, we need to ensure the condition
![]() $l\times \sigma =-1$
for the reflected beam to have a longitudinal electromagnetic field. For the CP beam with
$l\times \sigma =-1$
for the reflected beam to have a longitudinal electromagnetic field. For the CP beam with
![]() $\sigma =+1$
in our simulation, the wavefront should be twisted with index
$\sigma =+1$
in our simulation, the wavefront should be twisted with index
![]() $l=1$
by setting the handedness of the eight parts in Figure 1. Otherwise, there will be no longitudinal component of the electromagnetic field generated on the axis.
$l=1$
by setting the handedness of the eight parts in Figure 1. Otherwise, there will be no longitudinal component of the electromagnetic field generated on the axis.
Table 1 3D PIC simulation parameters.
![]() ${n}_{\mathrm{c}}=1.74\times {10}^{27}\;{\mathrm{m}}^{-3}$
is the critical density corresponding to the laser wavelength
${n}_{\mathrm{c}}=1.74\times {10}^{27}\;{\mathrm{m}}^{-3}$
is the critical density corresponding to the laser wavelength
![]() ${\lambda}_0$
. The initial temperatures for electrons and ions are set to zero.
${\lambda}_0$
. The initial temperatures for electrons and ions are set to zero.

To ensure that the longitudinal field of the reflected beam is of relativistic magnitude[ Reference Shi, Blackman and Arefiev20 ], the peak period-averaged power of the CP Gaussian beam should be greater than 80 TW. In this study, we utilized a high-density target and a modest intensity to mitigate the effects of self-focusing[ Reference Ghotra and Singh36 ] or target concavity, which needs further investigation in future work. Considering the limited computer resources, we also chose a small spot size and a short pulse width to set the simulation window as small. These limits provide an upper limit on peak power. Although higher peak power can result in higher energy gain, modest peak power is preferable for a proof-of-principle experiment from a technical challenge standpoint. That is why we set these parameters in our PIC simulation.
The structures of the electric and magnetic fields of the reflected beam in the
![]() $\left(x,z\right)$
-plane at time
$\left(x,z\right)$
-plane at time
![]() $t=$
50 fs are shown in Figure 2. The figures demonstrate the contrast in topology between the longitudinal and transverse field components. The longitudinal electric and magnetic fields attain their maximum amplitude on the axis of the reflected beam, as shown in Figures 2(a) and 2(c). Conversely, the transverse electric field diminishes to zero on the axis, as shown in Figure 2(b). Furthermore, the transverse field is positive and negative at corresponding positions on both sides of the axis (
$t=$
50 fs are shown in Figure 2. The figures demonstrate the contrast in topology between the longitudinal and transverse field components. The longitudinal electric and magnetic fields attain their maximum amplitude on the axis of the reflected beam, as shown in Figures 2(a) and 2(c). Conversely, the transverse electric field diminishes to zero on the axis, as shown in Figure 2(b). Furthermore, the transverse field is positive and negative at corresponding positions on both sides of the axis (
![]() $z=y=0$
), which is also a feature of the twist mode. A quantitative comparison shows that the maximum amplitude of the longitudinal electric field is about 20% of the maximum amplitude of the transverse electric field. Although the reflected laser beam is a mixture of different LG modes, as will be shown later, the ratio of 20% is close to our previous results based on a single mode[
Reference Shi, Blackman and Arefiev20
]. Due to the high peak power and the tight focus, the longitudinal field is still relativistic. The simulation results show that by integrating a nanowire structure at the center of the target, electrons can be efficiently injected and then accelerated during the twisted laser generation process, as shown in Figure 2(d). This will be discussed in Section 3.
$z=y=0$
), which is also a feature of the twist mode. A quantitative comparison shows that the maximum amplitude of the longitudinal electric field is about 20% of the maximum amplitude of the transverse electric field. Although the reflected laser beam is a mixture of different LG modes, as will be shown later, the ratio of 20% is close to our previous results based on a single mode[
Reference Shi, Blackman and Arefiev20
]. Due to the high peak power and the tight focus, the longitudinal field is still relativistic. The simulation results show that by integrating a nanowire structure at the center of the target, electrons can be efficiently injected and then accelerated during the twisted laser generation process, as shown in Figure 2(d). This will be discussed in Section 3.

Figure 2 The longitudinal slices of the electric and magnetic field components of the twisted laser beam are generated by the reflection of the plasma and the electron density from the PIC simulation. Panels (a) and (c) show the longitudinal electromagnetic field
![]() ${E}_x$
and
${E}_x$
and
![]() ${B}_x$
in the
${B}_x$
in the
![]() $\left(x,z\right)$
-plane at
$\left(x,z\right)$
-plane at
![]() $y=0$
. Panel (b) shows
$y=0$
. Panel (b) shows
![]() ${E}_y$
at the same location. The dashed lines in (b) and (c) are cuts that will be displayed as line-outs in (e) and (f). Panel (d) shows the electron density and the longitudinal electric field, where the blue and red contour lines represent
${E}_y$
at the same location. The dashed lines in (b) and (c) are cuts that will be displayed as line-outs in (e) and (f). Panel (d) shows the electron density and the longitudinal electric field, where the blue and red contour lines represent
![]() ${n}_{\mathrm{e}}=0.2{n}_{\mathrm{c}}$
and
${n}_{\mathrm{e}}=0.2{n}_{\mathrm{c}}$
and
![]() ${n}_{\mathrm{c}}$
, respectively. All the snapshots are taken at
${n}_{\mathrm{c}}$
, respectively. All the snapshots are taken at
![]() $t=50$
fs from the simulation with the parameters listed in Table 1. The line-outs are from those longitudinal slices in (b) and (c) and their corresponding spectral analysis. The red and the blue curves in panel (e) are the line-outs from the longitudinal slices of
$t=50$
fs from the simulation with the parameters listed in Table 1. The line-outs are from those longitudinal slices in (b) and (c) and their corresponding spectral analysis. The red and the blue curves in panel (e) are the line-outs from the longitudinal slices of
![]() ${E}_y$
(the cut shown as a dashed line at
${E}_y$
(the cut shown as a dashed line at
![]() $z=0$
in (b)) and
$z=0$
in (b)) and
![]() ${B}_x$
(the cut shown as a dashed line at
${B}_x$
(the cut shown as a dashed line at
![]() $z=0.6{w}_0$
in (c)), respectively. (f) The frequency spectra of
$z=0.6{w}_0$
in (c)), respectively. (f) The frequency spectra of
![]() ${E}_y$
(red curve) and
${E}_y$
(red curve) and
![]() ${B}_x$
(blue curve) from panel (e) were generated using the FFT. The dashed line represents the predicted attenuation curve of the high harmonic of the ROM mechanism
${B}_x$
(blue curve) from panel (e) were generated using the FFT. The dashed line represents the predicted attenuation curve of the high harmonic of the ROM mechanism
![]() ${I}_n\propto {n}^{-8/3}$
.
${I}_n\propto {n}^{-8/3}$
.
The reflected beam contains extreme nonlinear effects and obtains phase singularities in the interaction between the intense laser and the target plasma with a step-like structure. The reflected beam has been analyzed as a combination of different LG modes[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
]. The transverse scale of the nanowire is much smaller than the laser wavelength. Therefore, the proportion of different modes in the reflected beam should not be very different. However, the electron acceleration is sensitive to the LG modes according to our previous theory[
Reference Shi, Blackman and Arefiev20
,
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
,
Reference Shi, Blackman, Zhu and Arefiev25
]. After being injected into the longitudinal field, the electrons move at near-light speed in the beam. Because of the Gouy phase shift
![]() ${\varphi}_{p,l}\left(\tilde{x}\right)=\left(2p+|l|+1\right)\arctan \left(\tilde{x}\right)$
, which depends on the twist index
${\varphi}_{p,l}\left(\tilde{x}\right)=\left(2p+|l|+1\right)\arctan \left(\tilde{x}\right)$
, which depends on the twist index
![]() $l$
and the radial index
$l$
and the radial index
![]() $p$
, the phase velocity will be superluminous after the pulse reaches the focal plane. The
$p$
, the phase velocity will be superluminous after the pulse reaches the focal plane. The
![]() $\tilde{x}$
is defined as the longitudinal coordinate
$\tilde{x}$
is defined as the longitudinal coordinate
![]() $x$
being normalized to
$x$
being normalized to
![]() ${x}_{\mathrm{R}}$
, that is,
${x}_{\mathrm{R}}$
, that is,
![]() $\tilde{x}\equiv x/{x}_{\mathrm{R}}$
, where
$\tilde{x}\equiv x/{x}_{\mathrm{R}}$
, where
![]() ${x}_{\mathrm{R}}$
is the Rayleigh length. The fields that the electrons perceive are altered by the difference between their longitudinal velocity and the phase velocity of the reflected beam. Electrons that are accelerated at the start may later be decelerated and return energy to the field. It should be noted that a beam with different LG modes or different wavelengths would have different acceleration ranges. A mixture of LG modes or different frequency components can cause a degradation of the electron acceleration. To figure out the acceleration process in our simulation, it is necessary to perform a more comprehensive mode analysis of the reflected beam in the remainder of this section.
${x}_{\mathrm{R}}$
is the Rayleigh length. The fields that the electrons perceive are altered by the difference between their longitudinal velocity and the phase velocity of the reflected beam. Electrons that are accelerated at the start may later be decelerated and return energy to the field. It should be noted that a beam with different LG modes or different wavelengths would have different acceleration ranges. A mixture of LG modes or different frequency components can cause a degradation of the electron acceleration. To figure out the acceleration process in our simulation, it is necessary to perform a more comprehensive mode analysis of the reflected beam in the remainder of this section.
Before commencing the analysis of the LG modes, we need to examine the spectrum of the reflected fields in more detail. Figure 2(e) shows the plots of the longitudinal magnetic field along the axis (
![]() $y=0$
and
$y=0$
and
![]() $z=0$
, shown as a dashed line in Figure 2(c)) and the transverse electric field at an off-axis position (
$z=0$
, shown as a dashed line in Figure 2(c)) and the transverse electric field at an off-axis position (
![]() $y=0$
and
$y=0$
and
![]() $z=0.6{w}_0$
, shown as a dashed line in Figure 2(b)) of the reflected beam at
$z=0.6{w}_0$
, shown as a dashed line in Figure 2(b)) of the reflected beam at
![]() $t=50$
fs. The reason why
$t=50$
fs. The reason why
![]() ${B}_x$
is shown instead of
${B}_x$
is shown instead of
![]() ${E}_x$
is that it is difficult to separate the field of the electrons in the center from the longitudinal electric field of the laser. Since the transverse electric field in Figure 2(b) disappears on the axis of the reflected beam, it is displayed off-axis. The position of (
${E}_x$
is that it is difficult to separate the field of the electrons in the center from the longitudinal electric field of the laser. Since the transverse electric field in Figure 2(b) disappears on the axis of the reflected beam, it is displayed off-axis. The position of (
![]() $y\,{=}\,0,\ z=0.6{w}_0$
) is chosen to get the highest amplitude. Using the fast Fourier transform (FFT), we obtain the frequency spectra of
$y\,{=}\,0,\ z=0.6{w}_0$
) is chosen to get the highest amplitude. Using the fast Fourier transform (FFT), we obtain the frequency spectra of
![]() ${B}_x$
and
${B}_x$
and
![]() ${E}_y$
shown in Figure 2(f). The predicted high harmonic attenuation curve
${E}_y$
shown in Figure 2(f). The predicted high harmonic attenuation curve
![]() ${I}_n\propto {n}^{-8/3}$
in the relativistic oscillating mirror (ROM) mechanism is shown by the black dashed line[
Reference Lichters, Meyer-ter-Vehn and Pukhov37
]. Here,
${I}_n\propto {n}^{-8/3}$
in the relativistic oscillating mirror (ROM) mechanism is shown by the black dashed line[
Reference Lichters, Meyer-ter-Vehn and Pukhov37
]. Here,
![]() $n=\omega /{\omega}_0$
is the high harmonic order. It is evident that the descent rate of the spectrum for both
$n=\omega /{\omega}_0$
is the high harmonic order. It is evident that the descent rate of the spectrum for both
![]() ${E}_y$
(red line) and
${E}_y$
(red line) and
![]() ${B}_x$
(blue line) is faster than that of the predicted high harmonic attenuation curve (dashed line). It means that the high harmonic effect is weak in our case. Quantitatively, the proportion of high frequency is more than two orders of magnitude smaller than the fundamental frequency. It is different from the case using the LP-LG laser[
Reference Shi, Blackman, Zhu and Arefiev25
], where the high harmonic part is much stronger. So we can ignore the high-frequency portion of the reflected beam and consider the reflected beam to have the same spectrum as the incident beam. Existing theoretical analyses[
Reference Mendonça and Vieira38
] and experiments[
Reference Gariepy, Leach, Kim, Hammond, Frumker, Boyd and Corkum39
,
Reference Courtial, Dholakia, Allen and Padgett40
] strongly confirm that energy and momentum are conserved in high harmonic generation (HHG), and the physical mechanism indicates that angular momentum and frequency are not independently modulated[
Reference Vieira, Trines, Alves, Fonseca, Mendonça, Bingham, Norreys and Silva41
]. Therefore, it can be considered that the nth harmonic of a laser pulse with initial twist mode
${B}_x$
(blue line) is faster than that of the predicted high harmonic attenuation curve (dashed line). It means that the high harmonic effect is weak in our case. Quantitatively, the proportion of high frequency is more than two orders of magnitude smaller than the fundamental frequency. It is different from the case using the LP-LG laser[
Reference Shi, Blackman, Zhu and Arefiev25
], where the high harmonic part is much stronger. So we can ignore the high-frequency portion of the reflected beam and consider the reflected beam to have the same spectrum as the incident beam. Existing theoretical analyses[
Reference Mendonça and Vieira38
] and experiments[
Reference Gariepy, Leach, Kim, Hammond, Frumker, Boyd and Corkum39
,
Reference Courtial, Dholakia, Allen and Padgett40
] strongly confirm that energy and momentum are conserved in high harmonic generation (HHG), and the physical mechanism indicates that angular momentum and frequency are not independently modulated[
Reference Vieira, Trines, Alves, Fonseca, Mendonça, Bingham, Norreys and Silva41
]. Therefore, it can be considered that the nth harmonic of a laser pulse with initial twist mode
![]() $l$
and photon energy
$l$
and photon energy
![]() $\mathrm{\hslash}\omega$
has twist index
$\mathrm{\hslash}\omega$
has twist index
![]() $nl$
and energy
$nl$
and energy
![]() $n\mathrm{\hslash}\omega$
. Since higher-order twist modes are always associated with higher-order frequencies, we consider the reflected beam to have only one twist mode
$n\mathrm{\hslash}\omega$
. Since higher-order twist modes are always associated with higher-order frequencies, we consider the reflected beam to have only one twist mode
![]() $l=1$
.
$l=1$
.
It is convenient to represent the fields of the reflected laser beam as a combination of orthogonal LG modes. The transverse electric field of an LG mode with twist index
![]() $l$
and radial index
$l$
and radial index
![]() $p$
can be defined in cylindrical coordinates
$p$
can be defined in cylindrical coordinates
![]() $\left(r,\psi, x\right)$
as follows:
$\left(r,\psi, x\right)$
as follows:
 $$\begin{align}{\psi}_{p,l}&\equiv {C}_{p,l}f{\left(\tilde{x}\right)}^{\mid l\mid +1+2p}{\left(1+{\tilde{x}}^2\right)}^p{L}_p^{\mid l\mid}\left(\frac{2{\tilde{r}}^2}{1+{\tilde{x}}^2}\right) \nonumber\\&\quad \times {\left(\sqrt{2}\tilde{r}\right)}^{\mid l\mid}\exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)+ il\phi \right],\end{align}$$
$$\begin{align}{\psi}_{p,l}&\equiv {C}_{p,l}f{\left(\tilde{x}\right)}^{\mid l\mid +1+2p}{\left(1+{\tilde{x}}^2\right)}^p{L}_p^{\mid l\mid}\left(\frac{2{\tilde{r}}^2}{1+{\tilde{x}}^2}\right) \nonumber\\&\quad \times {\left(\sqrt{2}\tilde{r}\right)}^{\mid l\mid}\exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)+ il\phi \right],\end{align}$$
where
![]() $r$
and
$r$
and
![]() $\phi$
are the distance from the axis in the
$\phi$
are the distance from the axis in the
![]() $\left(y,z\right)$
-plane and the polar angle, respectively,
$\left(y,z\right)$
-plane and the polar angle, respectively,
![]() ${E}_0$
is the amplitude of the field,
${E}_0$
is the amplitude of the field,
![]() ${C}_{p,l}$
is the normalization factor,
${C}_{p,l}$
is the normalization factor,
![]() $g\left(\xi \right)$
is the pulsed envelope term and
$g\left(\xi \right)$
is the pulsed envelope term and
![]() ${L}_p^{\mid l\mid }$
is the generalized Laguerre polynomial term. Furthermore, the divergence angle of the beam is defined as
${L}_p^{\mid l\mid }$
is the generalized Laguerre polynomial term. Furthermore, the divergence angle of the beam is defined as
![]() ${\theta}_{\mathrm{d}}={w}_0/{x}_{\mathrm{R}}$
, and the Rayleigh length is
${\theta}_{\mathrm{d}}={w}_0/{x}_{\mathrm{R}}$
, and the Rayleigh length is
![]() ${x}_{\mathrm{R}}=\pi {w}_0^2/{\lambda}_0$
. The normalized transverse distance is
${x}_{\mathrm{R}}=\pi {w}_0^2/{\lambda}_0$
. The normalized transverse distance is
![]() $\tilde{r}\equiv r/{w}_0$
.
$\tilde{r}\equiv r/{w}_0$
.
Usually, without special settings, the field’s propagation information output by the PIC code only includes the real part. Using the Hilbert transform[
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
], we can get the complex field
![]() ${B}_z^{\mathrm{H}}$
from the real field
${B}_z^{\mathrm{H}}$
from the real field
![]() ${B}_z$
produced in the simulation. In our case, the incident beam is totally reflected by the target. The imaginary component of the result is the phase information associated with the propagation of the beam in the positive
${B}_z$
produced in the simulation. In our case, the incident beam is totally reflected by the target. The imaginary component of the result is the phase information associated with the propagation of the beam in the positive
![]() $x$
-axis direction. The percentage of each radial mode can be calculated from their ratios by obtaining the corresponding complex amplitudes
$x$
-axis direction. The percentage of each radial mode can be calculated from their ratios by obtaining the corresponding complex amplitudes
![]() ${b}_{p,l}$
of each mode. The complex amplitude
${b}_{p,l}$
of each mode. The complex amplitude
![]() ${b}_{p,l}$
corresponding to the mode of
${b}_{p,l}$
corresponding to the mode of
![]() $p$
can be obtained by the double integration:
$p$
can be obtained by the double integration:
 $$\begin{align}{b}_{p,l}\left(\xi \right)={\int}_0^{2\pi}\mathrm{d}\phi \left[{\int}_0^{\infty}\frac{\mid e\mid {B}_z^{\mathrm{H}}}{m_{\mathrm{e}}\omega }{\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\exp \left(- i\xi \right)\tilde{r}\mathrm{d}\tilde{r}\right].\end{align}$$
$$\begin{align}{b}_{p,l}\left(\xi \right)={\int}_0^{2\pi}\mathrm{d}\phi \left[{\int}_0^{\infty}\frac{\mid e\mid {B}_z^{\mathrm{H}}}{m_{\mathrm{e}}\omega }{\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\exp \left(- i\xi \right)\tilde{r}\mathrm{d}\tilde{r}\right].\end{align}$$
Here, the mode with different
![]() $l$
is assumed to be negligible by the previous discussion. Based on the mode decomposition from a snapshot of
$l$
is assumed to be negligible by the previous discussion. Based on the mode decomposition from a snapshot of
![]() ${B}_z$
(see Figure 3(a)) at
${B}_z$
(see Figure 3(a)) at
![]() $t=50$
fs in the simulation, the occupancy of the radial modes
$t=50$
fs in the simulation, the occupancy of the radial modes
![]() $p=$
0 and
$p=$
0 and
![]() $p=$
1 is shown in Figures 3(b) and 3(c), respectively. We have performed scanning calculations for
$p=$
1 is shown in Figures 3(b) and 3(c), respectively. We have performed scanning calculations for
![]() $p\in[0, 6]$
. The higher-order radial index modes can be ignored due to their relatively small proportions. Considering only
$p\in[0, 6]$
. The higher-order radial index modes can be ignored due to their relatively small proportions. Considering only
![]() $p=$
0, 1 and 2, the amplitude proportions of the
$p=$
0, 1 and 2, the amplitude proportions of the
![]() ${\mathrm{LG}}_{01}$
,
${\mathrm{LG}}_{01}$
,
![]() ${\mathrm{LG}}_{11}$
and
${\mathrm{LG}}_{11}$
and
![]() ${\mathrm{LG}}_{21}$
modes are about 65%, 22% and 13%, respectively (see the Appendix A). The percentage of
${\mathrm{LG}}_{21}$
modes are about 65%, 22% and 13%, respectively (see the Appendix A). The percentage of
![]() ${\mathrm{LG}}_{01}$
is similar to the 64.8% result provided by Shi et al.[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
].
${\mathrm{LG}}_{01}$
is similar to the 64.8% result provided by Shi et al.[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
].

Figure 3 The transverse magnetic field distribution of each mode obtained from the mode decomposition of the simulation results at the same time of Figure 2. (a) The distribution of the transverse magnetic field
![]() ${B}_z$
in the simulation in the
${B}_z$
in the simulation in the
![]() $\left(x,z\right)$
-plane at
$\left(x,z\right)$
-plane at
![]() $t=50$
fs. It is also the real part of the complex magnetic field
$t=50$
fs. It is also the real part of the complex magnetic field
![]() ${B}_z^{\mathrm{H}}$
in the
${B}_z^{\mathrm{H}}$
in the
![]() $\left(x,z\right)$
plane, which is the raw data of the Hilbert transform used to obtain (b) and (c). (b) The distribution of the main mode with
$\left(x,z\right)$
plane, which is the raw data of the Hilbert transform used to obtain (b) and (c). (b) The distribution of the main mode with
![]() $l=1$
and
$l=1$
and
![]() $p=0$
. (c) The distribution of another mode with
$p=0$
. (c) The distribution of another mode with
![]() $l=1$
and
$l=1$
and
![]() $p=1$
.
$p=1$
.
From the results of the spectrum analysis above, the amplitude of the second harmonic is more than two orders of magnitude smaller than that of the base mode. However, in the mode decomposition, the fraction of
![]() ${\mathrm{LG}}_{11}$
can be about 34% of
${\mathrm{LG}}_{11}$
can be about 34% of
![]() ${\mathrm{LG}}_{01}$
. A consequence of the significant contribution of the mode with
${\mathrm{LG}}_{01}$
. A consequence of the significant contribution of the mode with
![]() $p=$
1 is that the maximum transverse field of the reflected beam is significantly closer to the axis than for the modes with
$p=$
1 is that the maximum transverse field of the reflected beam is significantly closer to the axis than for the modes with
![]() $p=$
0. Therefore, in the spectrum analysis we take the maximum transverse electric field
$p=$
0. Therefore, in the spectrum analysis we take the maximum transverse electric field
![]() ${E}_y$
at
${E}_y$
at
![]() $r=\sqrt{z^2+{y}^2}=0.6{w}_0$
instead of
$r=\sqrt{z^2+{y}^2}=0.6{w}_0$
instead of
![]() $r=0.7{w}_0$
of the base mode. Based on these results, we will focus on the effects of the high-order radial modes and ignore the effect of HHG. In Section 4 we will analyze the effect of high
$r=0.7{w}_0$
of the base mode. Based on these results, we will focus on the effects of the high-order radial modes and ignore the effect of HHG. In Section 4 we will analyze the effect of high
![]() $p$
modes on the electron acceleration.
$p$
modes on the electron acceleration.
3 Electron injection into the twisted laser beam
In this section, we will study the origin of those accelerated electrons that can surf with the laser beam once the bunches are formed. Returning to the start of the laser beam reflection from the target, we will recover the process of ‘electron injection’. A 3D rendering of the electron density at
![]() $t=50$
fs is shown in Figure 4(a). Each electron bunch has a ring shape, where the blue and red isosurfaces represent
$t=50$
fs is shown in Figure 4(a). Each electron bunch has a ring shape, where the blue and red isosurfaces represent
![]() ${n}_{\mathrm{e}}=0.5{n}_{\mathrm{c}}$
and
${n}_{\mathrm{e}}=0.5{n}_{\mathrm{c}}$
and
![]() ${n}_{\mathrm{c}}$
, respectively. By setting the different species of electrons on the ‘light fan’ and the nanowire, we obtain that 98% of the electrons come from the nanowire for the bunches at
${n}_{\mathrm{c}}$
, respectively. By setting the different species of electrons on the ‘light fan’ and the nanowire, we obtain that 98% of the electrons come from the nanowire for the bunches at
![]() $t=248$
fs. On the back of the ‘light fan’ we also find some accelerated electrons. They have a broad energy spectrum and a large divergence angle. We think that they are accelerated by the transverse fields of the incident Gaussian beam. Since they quickly leave the acceleration region, we do not consider these electrons in this work. In our case, the results of a series of simulations indicate that the shape of the electron bunch is always annular or semi-annular, which is sensitive to the parameters of the laser and target.
$t=248$
fs. On the back of the ‘light fan’ we also find some accelerated electrons. They have a broad energy spectrum and a large divergence angle. We think that they are accelerated by the transverse fields of the incident Gaussian beam. Since they quickly leave the acceleration region, we do not consider these electrons in this work. In our case, the results of a series of simulations indicate that the shape of the electron bunch is always annular or semi-annular, which is sensitive to the parameters of the laser and target.

Figure 4 (a) 3D rendering of the electron density at
![]() $t=50$
fs, where the blue and red isosurfaces represent
$t=50$
fs, where the blue and red isosurfaces represent
![]() ${n}_{\mathrm{e}}=0.5{n}_{\mathrm{c}}$
and
${n}_{\mathrm{e}}=0.5{n}_{\mathrm{c}}$
and
![]() ${n}_{\mathrm{c}}$
, respectively. The early trajectories of some electrons, which were randomly selected from the central region in the third bunch at
${n}_{\mathrm{c}}$
, respectively. The early trajectories of some electrons, which were randomly selected from the central region in the third bunch at
![]() $t=248$
fs. The line color shows electron energy. (b) Representative electron trajectories in the
$t=248$
fs. The line color shows electron energy. (b) Representative electron trajectories in the
![]() $\left(y,z\right)$
transverse plane from time
$\left(y,z\right)$
transverse plane from time
![]() $t=0$
fs to time
$t=0$
fs to time
![]() $t=20$
fs. Images (c) and (d) are the trajectories of the same electrons in the longitudinal plane of
$t=20$
fs. Images (c) and (d) are the trajectories of the same electrons in the longitudinal plane of
![]() $\left(x,y\right)$
and
$\left(x,y\right)$
and
![]() $\left(x,z\right)$
, respectively.
$\left(x,z\right)$
, respectively.
Figures 4(b)–4(d) show the trajectory of 15 electrons that were traced back to represent the dynamics of the electrons in the third bunch. These representative electrons are selected at random from the central region in the third bunch at
![]() $t=248$
fs. To study the initial electron positions, we tracked these electrons back to the very beginning of our simulation, when the laser was just reflected off the target. The time step is 0.16 fs to ensure that more details are recovered. Since we are interested in the dynamics of the injection process, Figure 4 only provides trajectories from time
$t=248$
fs. To study the initial electron positions, we tracked these electrons back to the very beginning of our simulation, when the laser was just reflected off the target. The time step is 0.16 fs to ensure that more details are recovered. Since we are interested in the dynamics of the injection process, Figure 4 only provides trajectories from time
![]() $t=0$
to time
$t=0$
to time
![]() $t=20$
fs. Trajectories of representative electrons are shown in the transverse (
$t=20$
fs. Trajectories of representative electrons are shown in the transverse (
![]() $y$
-
$y$
-
![]() $z$
) plane in Figure 4(b). Figures 4(c) and 4(d) are the trajectories of the same electrons in the longitudinal plane of
$z$
) plane in Figure 4(b). Figures 4(c) and 4(d) are the trajectories of the same electrons in the longitudinal plane of
![]() $\left(y,x\right)$
and
$\left(y,x\right)$
and
![]() $\left(z,x\right)$
, respectively. The line color represents the electron energy. It can be seen that the electrons move in a helical motion in the early stage. The longitudinal displacement is about the length of the nanowire, which is
$\left(z,x\right)$
, respectively. The line color represents the electron energy. It can be seen that the electrons move in a helical motion in the early stage. The longitudinal displacement is about the length of the nanowire, which is
![]() $L_0 = 1.6\ \mu \mathrm{m} = 2{\lambda}_0$
. During the stage of helical motion, the electrons are not significantly accelerated. After detachment from the nanowire, they are accelerated by the longitudinal fields. At the same time, they stop their helical motion and approach the axis of the laser beam.
$L_0 = 1.6\ \mu \mathrm{m} = 2{\lambda}_0$
. During the stage of helical motion, the electrons are not significantly accelerated. After detachment from the nanowire, they are accelerated by the longitudinal fields. At the same time, they stop their helical motion and approach the axis of the laser beam.
Since the reflected beam is not strictly in the
![]() ${\mathrm{LG}}_{01}$
mode, the motion of the electron injection stage can only be predicted qualitatively by theory. Considering that the right-CP
${\mathrm{LG}}_{01}$
mode, the motion of the electron injection stage can only be predicted qualitatively by theory. Considering that the right-CP
![]() ${\mathrm{LG}}_{01}$
mode plays the major role, the transverse fields, which have
${\mathrm{LG}}_{01}$
mode plays the major role, the transverse fields, which have
![]() $y$
-polarized and
$y$
-polarized and
![]() $z$
-polarized beams with
$z$
-polarized beams with
![]() $\pi /2$
phase difference, can be written in the cylindrical coordinate system. The radial and polar components are as follows:
$\pi /2$
phase difference, can be written in the cylindrical coordinate system. The radial and polar components are as follows:
 $$\begin{align}{E}_{r,\phi}={E}_0\frac{\psi_{p,l}}{\exp \left( i l\phi \right)}g\left(\xi \right)\left\{\!\!\begin{array}{l}\exp \left( i\xi \right),\\ {}\exp \left[i\left(\xi -\pi /2\right)\right].\end{array}\right.\end{align}$$
$$\begin{align}{E}_{r,\phi}={E}_0\frac{\psi_{p,l}}{\exp \left( i l\phi \right)}g\left(\xi \right)\left\{\!\!\begin{array}{l}\exp \left( i\xi \right),\\ {}\exp \left[i\left(\xi -\pi /2\right)\right].\end{array}\right.\end{align}$$
According to Equation (5), it is obtained that both
![]() ${E}_r$
and
${E}_r$
and
![]() ${E}_{\phi }$
are independent of the polar angle (when
${E}_{\phi }$
are independent of the polar angle (when
![]() $l\times \sigma =-1$
), the periodic
$l\times \sigma =-1$
), the periodic
![]() ${E}_r$
may cause the electrons to be pulled out of the nanowire and the toroidal electric field
${E}_r$
may cause the electrons to be pulled out of the nanowire and the toroidal electric field
![]() ${E}_{\phi }$
explains the helical motion of the electrons in the early stage[
Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao30
]. The radial ponderomotive force in the vacuum laser acceleration (VLA) of the detached nanowire gives some electron convergence effect. That is why the electrons approach the laser axis during VLA. The whole process is different from LG laser interaction with dense plasma[
Reference Shi, Blackman, Stutman and Arefiev19
,
Reference Shi, Blackman and Arefiev20
,
Reference Shi, Blackman, Zhu and Arefiev25
] and the push–pull model[
Reference Thévenet, Vincenti and Faure42
]. It is similar to the process of electron injection in the interaction between the twisted laser beam and a nanowire[
Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao30
].
${E}_{\phi }$
explains the helical motion of the electrons in the early stage[
Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao30
]. The radial ponderomotive force in the vacuum laser acceleration (VLA) of the detached nanowire gives some electron convergence effect. That is why the electrons approach the laser axis during VLA. The whole process is different from LG laser interaction with dense plasma[
Reference Shi, Blackman, Stutman and Arefiev19
,
Reference Shi, Blackman and Arefiev20
,
Reference Shi, Blackman, Zhu and Arefiev25
] and the push–pull model[
Reference Thévenet, Vincenti and Faure42
]. It is similar to the process of electron injection in the interaction between the twisted laser beam and a nanowire[
Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao30
].
4 Electron acceleration in the reflected laser beam
In Section 3, we have shown that the reflected twisted beam generates dense electron bunches from the nanowire. The bunches can travel with the reflected beam and gain longitudinal momentum. This section will examine the phase velocity of the reflected beam and the longitudinal momentum gain in the acceleration process.
Figure 5(a) shows the line density of the electron bunches at
![]() $t=248$
fs and it is computed by choosing the near-axis region at
$t=248$
fs and it is computed by choosing the near-axis region at
![]() $r<3\;\mu \mathrm{m}$
. It shows the linear density of the third electron bunch is relatively high (the black dashed box marks), and its charge is 57 pC according to our simulation results. Therefore, the next analysis focuses on the third bunch. In further analysis of the areal density of the third bunch, as shown in Figure 5(b), it can be seen that the peak of areal density is semi-annular, which is consistent with the results discussed in Section 3. As shown in Figure 5(d), although the areal density of the third bunch has a special distribution shape, the data computed show that the divergence angle of the electrons is only related to the off-axis distance. It can be seen that most of the cell-averaged electron divergence angles are less than 50 mrad at the region about
$r<3\;\mu \mathrm{m}$
. It shows the linear density of the third electron bunch is relatively high (the black dashed box marks), and its charge is 57 pC according to our simulation results. Therefore, the next analysis focuses on the third bunch. In further analysis of the areal density of the third bunch, as shown in Figure 5(b), it can be seen that the peak of areal density is semi-annular, which is consistent with the results discussed in Section 3. As shown in Figure 5(d), although the areal density of the third bunch has a special distribution shape, the data computed show that the divergence angle of the electrons is only related to the off-axis distance. It can be seen that most of the cell-averaged electron divergence angles are less than 50 mrad at the region about
![]() $r<{w}_0$
. The divergence angle
$r<{w}_0$
. The divergence angle
![]() $\left\langle \theta \right\rangle \equiv \left\langle \arctan \left({p}_{\perp }/{p}_{\parallel}\right)\right\rangle$
is averaged on every mesh cell of the
$\left\langle \theta \right\rangle \equiv \left\langle \arctan \left({p}_{\perp }/{p}_{\parallel}\right)\right\rangle$
is averaged on every mesh cell of the
![]() $\left(y,z\right)$
-plane. The energy spectrum evolution and the final spectrum of the third bunch with
$\left(y,z\right)$
-plane. The energy spectrum evolution and the final spectrum of the third bunch with
![]() $r<1.5\;\mu \mathrm{m}$
are shown in Figure 5(c). Some particles experience continuous acceleration and gradually stabilize after injection into the beam. However, certain electrons are influenced by higher-order radial modes and enter a deceleration phase. This can be supported by the theoretical results that odd radial modes are not able to generate energetic electrons[
Reference Shi, Blackman and Arefiev20
]. The maximum energy of electrons can reach approximately 350 MeV and the peak energy is 310 MeV, with a spread of 6%.
$r<1.5\;\mu \mathrm{m}$
are shown in Figure 5(c). Some particles experience continuous acceleration and gradually stabilize after injection into the beam. However, certain electrons are influenced by higher-order radial modes and enter a deceleration phase. This can be supported by the theoretical results that odd radial modes are not able to generate energetic electrons[
Reference Shi, Blackman and Arefiev20
]. The maximum energy of electrons can reach approximately 350 MeV and the peak energy is 310 MeV, with a spread of 6%.

Figure 5 Acceleration results for the electron bunches in the reflected twisted beam. (a) The line density of electron bunches in the region of
![]() $r<3\;\mu \mathrm{m}$
. The black dashed box marks the third bunch. (b) The third electron bunch areal density
$r<3\;\mu \mathrm{m}$
. The black dashed box marks the third bunch. (b) The third electron bunch areal density
![]() ${\rho}_\mathrm{e}$
, in which the red dashed circle represents the region of
${\rho}_\mathrm{e}$
, in which the red dashed circle represents the region of
![]() $r<1.5\;\mu \mathrm{m}$
. (c) The background color image represents the time evolution of the third bunch electron energy spectrum inside the red dashed circle of (b). The final energy spectrum of the third electron bunch is represented by the solid red curve. The black dashed line represents the prediction of the electron energy gain from Equation (13) with
$r<1.5\;\mu \mathrm{m}$
. (c) The background color image represents the time evolution of the third bunch electron energy spectrum inside the red dashed circle of (b). The final energy spectrum of the third electron bunch is represented by the solid red curve. The black dashed line represents the prediction of the electron energy gain from Equation (13) with
![]() ${\Phi}_0=0.8\pi$
. The initiation time of the acceleration serves as a variable parameter. (d) The cell-averaged electron divergence angle
${\Phi}_0=0.8\pi$
. The initiation time of the acceleration serves as a variable parameter. (d) The cell-averaged electron divergence angle
![]() $\left\langle \theta \right\rangle$
of the third bunch. All plots are derived from the simulation results at
$\left\langle \theta \right\rangle$
of the third bunch. All plots are derived from the simulation results at
![]() $t=248$
fs.
$t=248$
fs.
The energy gain of electrons in the
![]() ${\mathrm{LG}}_{01}$
mode can already be approximately predicted theoretically, including the energy gain of electrons in higher-order radial modes[
Reference Shi, Blackman and Arefiev20
,
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
]. In the following, we will analyze the phase velocity and predict the energy gain of electrons in the mixed modes. To analyze the maximum effect of beam acceleration on electrons, we only analyze the maximum portion of the pulse envelope, which means we no longer consider the envelope shape. The longitudinal electric field is expressed as follows:
${\mathrm{LG}}_{01}$
mode can already be approximately predicted theoretically, including the energy gain of electrons in higher-order radial modes[
Reference Shi, Blackman and Arefiev20
,
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
]. In the following, we will analyze the phase velocity and predict the energy gain of electrons in the mixed modes. To analyze the maximum effect of beam acceleration on electrons, we only analyze the maximum portion of the pulse envelope, which means we no longer consider the envelope shape. The longitudinal electric field is expressed as follows:
where
![]() $\tilde{x}=x/{x}_{\mathrm{R}}$
,
$\tilde{x}=x/{x}_{\mathrm{R}}$
,
![]() ${x}_{\mathrm{R}}=\pi {w}_0^2/{\lambda}_0$
:
${x}_{\mathrm{R}}=\pi {w}_0^2/{\lambda}_0$
:
 $$\begin{align}{E}_{\parallel}^{\mathrm{max}}=2\sqrt{\frac{p+1}{\pi }}{\theta}_{\mathrm{d}}{E}_0=\frac{2}{\pi}\sqrt{\frac{p+1}{\pi }}\frac{\lambda_0}{w_0}{E}_0,\end{align}$$
$$\begin{align}{E}_{\parallel}^{\mathrm{max}}=2\sqrt{\frac{p+1}{\pi }}{\theta}_{\mathrm{d}}{E}_0=\frac{2}{\pi}\sqrt{\frac{p+1}{\pi }}\frac{\lambda_0}{w_0}{E}_0,\end{align}$$
where
![]() ${\Phi}_0$
represents the initial phase of electron injection at
${\Phi}_0$
represents the initial phase of electron injection at
![]() $x\approx 0$
,
$x\approx 0$
,
![]() $t\approx 0$
. The phase
$t\approx 0$
. The phase
![]() $\Phi$
is expressed as follows:
$\Phi$
is expressed as follows:
where the beam divergence angle
![]() ${\theta}_{\mathrm{d}}={w}_0/{x}_{\mathrm{R}}={\lambda}_0/\pi {w}_0$
. In our case, the beam is tightly focused to around three or four wavelengths, and it can be assumed that
${\theta}_{\mathrm{d}}={w}_0/{x}_{\mathrm{R}}={\lambda}_0/\pi {w}_0$
. In our case, the beam is tightly focused to around three or four wavelengths, and it can be assumed that
![]() ${\theta}_{\mathrm{d}}\ll 1$
. The phase velocity (
${\theta}_{\mathrm{d}}\ll 1$
. The phase velocity (
![]() ${v}_{\mathrm{ph}}$
) is defined as
${v}_{\mathrm{ph}}$
) is defined as
![]() $\mathrm{d}x/\mathrm{d}t$
when
$\mathrm{d}x/\mathrm{d}t$
when
![]() $\Phi =\mathrm{const}$
. Differentiating Equation (8), where
$\Phi =\mathrm{const}$
. Differentiating Equation (8), where
![]() $\Phi$
is held constant, we can obtain the relationship between the phase velocity and radial index
$\Phi$
is held constant, we can obtain the relationship between the phase velocity and radial index
![]() $p$
as follows:
$p$
as follows:
The electron is accelerated by the longitudinal electric field with
![]() ${v}_x<c$
, where
${v}_x<c$
, where
![]() ${v}_{\mathrm{ph}}>c$
, evidently
${v}_{\mathrm{ph}}>c$
, evidently
![]() ${v}_{\mathrm{ph}}>{v}_x$
. The electron slips relative to the wavefront are determined by
${v}_{\mathrm{ph}}>{v}_x$
. The electron slips relative to the wavefront are determined by
![]() ${v}_{\mathrm{ph}}-{v}_x$
. Equation (9) represents that the higher-order radial modes
${v}_{\mathrm{ph}}-{v}_x$
. Equation (9) represents that the higher-order radial modes
![]() $p$
correspond to a faster phase velocity while keeping the other quantities constant. Meanwhile, the phase velocity is superluminal after the focal plane and then decays to
$p$
correspond to a faster phase velocity while keeping the other quantities constant. Meanwhile, the phase velocity is superluminal after the focal plane and then decays to
![]() $c$
after several Rayleigh lengths. This affects the electrons gaining energy in the longitudinal field. Here,
$c$
after several Rayleigh lengths. This affects the electrons gaining energy in the longitudinal field. Here,
![]() $\Delta \Phi$
is the phase slip that the electrons experience from
$\Delta \Phi$
is the phase slip that the electrons experience from
![]() ${x}_0$
to
${x}_0$
to
![]() $x$
, which can be calculated by bringing
$x$
, which can be calculated by bringing
![]() $x={x}_0+c\left(t-{t}_0\right)$
into Equation (8), and obtaining the following:
$x={x}_0+c\left(t-{t}_0\right)$
into Equation (8), and obtaining the following:
where
![]() ${\tilde{x}}_0={x}_0/{x}_{\mathrm{R}}$
. With regards to
${\tilde{x}}_0={x}_0/{x}_{\mathrm{R}}$
. With regards to
![]() ${x}_0\ll {x}_{\mathrm{R}}$
, Equation (10) can be simplified as
${x}_0\ll {x}_{\mathrm{R}}$
, Equation (10) can be simplified as
![]() $\Delta \Phi =2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)$
. From Equation (10), it can be observed that the phase slip experienced by electrons is strongly correlated with the value of the radial index
$\Delta \Phi =2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)$
. From Equation (10), it can be observed that the phase slip experienced by electrons is strongly correlated with the value of the radial index
![]() $p$
. When
$p$
. When
![]() $p=0$
, the phase slip for electrons after a Rayleigh length is
$p=0$
, the phase slip for electrons after a Rayleigh length is
![]() $\Delta \Phi \approx -\pi$
[
Reference Shi, Blackman and Arefiev20
]. This implies that some electrons can still be in the accelerating phase of the longitudinal electric field. However, due to significant phase slip caused by higher-order radial modes, electrons quickly slide into the decelerating phase, and may even fail to gain energy from the electric field.
$\Delta \Phi \approx -\pi$
[
Reference Shi, Blackman and Arefiev20
]. This implies that some electrons can still be in the accelerating phase of the longitudinal electric field. However, due to significant phase slip caused by higher-order radial modes, electrons quickly slide into the decelerating phase, and may even fail to gain energy from the electric field.
By integrating the momentum balance equation
![]() $\mathrm{d}{p}_{\parallel }/\mathrm{d}t=-\mid e\mid {E}_{\parallel }$
with the assumption of
$\mathrm{d}{p}_{\parallel }/\mathrm{d}t=-\mid e\mid {E}_{\parallel }$
with the assumption of
![]() ${x}_0\ll {x}_{\mathrm{R}}$
, the momentum gain of the electron in
${x}_0\ll {x}_{\mathrm{R}}$
, the momentum gain of the electron in
![]() ${E}_{\parallel }$
can be obtained as follows:
${E}_{\parallel }$
can be obtained as follows:
 $$\begin{align}\Delta {p}_{\parallel}&=-\frac{\mid e\mid {E}_{\parallel}^{\mathrm{max}}{x}_{\mathrm{R}}}{2\left(p+1\right)c}\big\{\cos {\Phi}_0 \nonumber\\&\quad-\cos \left[{\Phi}_0-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\big\}.\end{align}$$
$$\begin{align}\Delta {p}_{\parallel}&=-\frac{\mid e\mid {E}_{\parallel}^{\mathrm{max}}{x}_{\mathrm{R}}}{2\left(p+1\right)c}\big\{\cos {\Phi}_0 \nonumber\\&\quad-\cos \left[{\Phi}_0-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\big\}.\end{align}$$
Equation (11) indicates that if the initial phase of the electron is appropriate, momentum gain can be continuously obtained from
![]() ${E}_{\parallel }$
. Electrons in other phases may lose energy due to entering the deceleration phase. Since the reflected beam contains multiple radial modes, we need to analyze the phase velocity evolution of the mixed-mode beam first. In Section 2, we obtain the proportion of radial modes with
${E}_{\parallel }$
. Electrons in other phases may lose energy due to entering the deceleration phase. Since the reflected beam contains multiple radial modes, we need to analyze the phase velocity evolution of the mixed-mode beam first. In Section 2, we obtain the proportion of radial modes with
![]() $p=$
0, 1 and 2. It is important to note that the longitudinal electric field maxima
$p=$
0, 1 and 2. It is important to note that the longitudinal electric field maxima
![]() ${E}_{\parallel}^{\mathrm{max}}$
are required for the analysis. Here,
${E}_{\parallel}^{\mathrm{max}}$
are required for the analysis. Here,
![]() ${E}_{\parallel }$
is the longitudinal electric field only containing radial modes with p = 0, 1 and 2, and the longitudinal field of each mode is represented by
${E}_{\parallel }$
is the longitudinal electric field only containing radial modes with p = 0, 1 and 2, and the longitudinal field of each mode is represented by
![]() ${E}_{\parallel, p}$
. The computational analysis determined that the
${E}_{\parallel, p}$
. The computational analysis determined that the
![]() $p=$
0, 1 and 2 modes contribute 55%, 24% and 19%, respectively, to the amplitude of the longitudinal electric field. We measure
$p=$
0, 1 and 2 modes contribute 55%, 24% and 19%, respectively, to the amplitude of the longitudinal electric field. We measure
![]() ${E}_{\parallel}^{\mathrm{max}}\approx 4m_{\mathrm{e}}c\omega/|e|$
when the longitudinal electric field variation becomes stable in the simulation result.
${E}_{\parallel}^{\mathrm{max}}\approx 4m_{\mathrm{e}}c\omega/|e|$
when the longitudinal electric field variation becomes stable in the simulation result.

Figure 6 Phase velocity
![]() ${v}_{\mathrm{ph}}$
analysis of reflected twisted beams. (a) The evolution of
${v}_{\mathrm{ph}}$
analysis of reflected twisted beams. (a) The evolution of
![]() ${v}_{\mathrm{ph}}$
of three beams with different modes under the same initial conditions. The black dashed curve represents
${v}_{\mathrm{ph}}$
of three beams with different modes under the same initial conditions. The black dashed curve represents
![]() ${v}_{\mathrm{ph}}$
with the
${v}_{\mathrm{ph}}$
with the
![]() ${\mathrm{LG}}_{01}$
mode. The solid blue curve represents
${\mathrm{LG}}_{01}$
mode. The solid blue curve represents
![]() ${v}_{\mathrm{ph}}$
with the
${v}_{\mathrm{ph}}$
with the
![]() ${\mathrm{LG}}_{11}$
mode. The red dashed curve is the analytical prediction for
${\mathrm{LG}}_{11}$
mode. The red dashed curve is the analytical prediction for
![]() ${v}_{\mathrm{ph}}$
of the reflected beam. (b) Evolution of the longitudinal electric field
${v}_{\mathrm{ph}}$
of the reflected beam. (b) Evolution of the longitudinal electric field
![]() ${E}_x$
on the axis with
${E}_x$
on the axis with
![]() $t$
. The solid black contours represent
$t$
. The solid black contours represent
![]() ${E}_x=0$
, while the red dashed curve is identical to that in (a).
${E}_x=0$
, while the red dashed curve is identical to that in (a).
In the reflected beam, two higher-order radial modes possess phase differences
![]() $\Delta {\vartheta}_{0,1},\Delta {\vartheta}_{0,2}$
from the base mode, where
$\Delta {\vartheta}_{0,1},\Delta {\vartheta}_{0,2}$
from the base mode, where
![]() $\Delta {\vartheta}_{0,1}$
is defined as the phase difference between
$\Delta {\vartheta}_{0,1}$
is defined as the phase difference between
![]() $p=0$
and
$p=0$
and
![]() $p=1$
, and
$p=1$
, and
![]() $\Delta {\vartheta}_{0,2}$
is defined as the phase difference between
$\Delta {\vartheta}_{0,2}$
is defined as the phase difference between
![]() $p=0$
and
$p=0$
and
![]() $p=2$
. This phase difference plays a very important role in the prediction of the energy gain. The expression for the longitudinal electric field can be updated to the following:
$p=2$
. This phase difference plays a very important role in the prediction of the energy gain. The expression for the longitudinal electric field can be updated to the following:
 $$\begin{align}{E}_{\parallel}&=\sum \limits_{p=0}^2-{E}_{\parallel, p}\sin \left[\xi +{\Phi}_0+\Delta {\vartheta}_{0,p}-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\nonumber\\& \quad \times {\left(1+{\tilde{x}}^2\right)}^{-1}.\end{align}$$
$$\begin{align}{E}_{\parallel}&=\sum \limits_{p=0}^2-{E}_{\parallel, p}\sin \left[\xi +{\Phi}_0+\Delta {\vartheta}_{0,p}-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\nonumber\\& \quad \times {\left(1+{\tilde{x}}^2\right)}^{-1}.\end{align}$$
By varying the phase difference
![]() $\Delta {\vartheta}_{0,1}\ \mathrm{and}\ \Delta {\vartheta}_{0,2}$
, we match the evolution of the longitudinal electric field in Equation (12) as closely as possible to the evolution of the longitudinal electric field of the reflected beam in the simulation results, as shown in Figure 6(b), where the solid black curve is the contour representing that the longitudinal electric field is zero. Although the phase difference information cannot be obtained directly in the simulation, the total phase velocity of the mixed mode can be calculated. In the previous analysis, the proportion of different radial modes was obtained. According to Equation (12), we can perform parameter scanning on the phase difference to make the calculated phase velocity curve (red dashed curve) closest to the phase velocity curve of the mixed mode (solid black curve) in Figure 6(b). The most appropriate phase difference is calculated as
$\Delta {\vartheta}_{0,1}\ \mathrm{and}\ \Delta {\vartheta}_{0,2}$
, we match the evolution of the longitudinal electric field in Equation (12) as closely as possible to the evolution of the longitudinal electric field of the reflected beam in the simulation results, as shown in Figure 6(b), where the solid black curve is the contour representing that the longitudinal electric field is zero. Although the phase difference information cannot be obtained directly in the simulation, the total phase velocity of the mixed mode can be calculated. In the previous analysis, the proportion of different radial modes was obtained. According to Equation (12), we can perform parameter scanning on the phase difference to make the calculated phase velocity curve (red dashed curve) closest to the phase velocity curve of the mixed mode (solid black curve) in Figure 6(b). The most appropriate phase difference is calculated as
![]() $\Delta {\vartheta}_{0,1}=0.3\pi$
and
$\Delta {\vartheta}_{0,1}=0.3\pi$
and
![]() $\Delta {\vartheta}_{0,2}=0.1\pi$
. As shown in Figure 6(a), the phase velocity of the reflected beam is compared with the phase velocity evolution of the
$\Delta {\vartheta}_{0,2}=0.1\pi$
. As shown in Figure 6(a), the phase velocity of the reflected beam is compared with the phase velocity evolution of the
![]() ${\mathrm{LG}}_{01}$
(black dashed curve) and
${\mathrm{LG}}_{01}$
(black dashed curve) and
![]() ${\mathrm{LG}}_{11}$
modes (blue curve), and it can be obtained that the phase slip of the reflected beam after a Rayleigh length is about 12% larger than that of the
${\mathrm{LG}}_{11}$
modes (blue curve), and it can be obtained that the phase slip of the reflected beam after a Rayleigh length is about 12% larger than that of the
![]() ${\mathrm{LG}}_{01}$
mode, but is still smaller than that of the
${\mathrm{LG}}_{01}$
mode, but is still smaller than that of the
![]() ${\mathrm{LG}}_{11}$
mode.
${\mathrm{LG}}_{11}$
mode.
The analysis of the phase velocity yields a phase difference among the three modes, which can be considered as having different initial phases
![]() ${\Phi}_0$
. Consequently, the formula for the momentum gain in the mixed mode is refined to the following expression:
${\Phi}_0$
. Consequently, the formula for the momentum gain in the mixed mode is refined to the following expression:
 $$\begin{align}&\Delta {p}_{\parallel}=\sum \limits_{p=0}^2-\frac{\mid e\mid {E}_{\parallel, p}^{\mathrm{max}}{x}_{\mathrm{R}}}{2\left(p+1\right)c}\left\{\cos \left({\Phi}_0+\Delta {\vartheta}_{0,p}\right)\right.\nonumber\\ {}&\left.\kern2.24em -\cos \left[{\Phi}_0+\Delta {\vartheta}_{0,p}-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\right\}.\end{align}$$
$$\begin{align}&\Delta {p}_{\parallel}=\sum \limits_{p=0}^2-\frac{\mid e\mid {E}_{\parallel, p}^{\mathrm{max}}{x}_{\mathrm{R}}}{2\left(p+1\right)c}\left\{\cos \left({\Phi}_0+\Delta {\vartheta}_{0,p}\right)\right.\nonumber\\ {}&\left.\kern2.24em -\cos \left[{\Phi}_0+\Delta {\vartheta}_{0,p}-2\left(p+1\right)\mathrm{arctan}\left(\tilde{x}\right)\right]\right\}.\end{align}$$
The phase difference
![]() $\Delta {\vartheta}_{0,1}=0.3\pi, \Delta {\vartheta}_{0,2}=0.1\pi$
and the initial phase
$\Delta {\vartheta}_{0,1}=0.3\pi, \Delta {\vartheta}_{0,2}=0.1\pi$
and the initial phase
![]() ${\Phi}_0=0.8\pi$
are brought into Equation (13) based on the proportion of the longitudinal electric fields of each radial mode. The energy gain can be obtained using
${\Phi}_0=0.8\pi$
are brought into Equation (13) based on the proportion of the longitudinal electric fields of each radial mode. The energy gain can be obtained using
![]() $\Delta {\varepsilon}_{\parallel}=c\Delta {p}_{\parallel }$
, and the mixed-mode energy gain prediction is plotted as the black dashed curve in Figure 5(c).
$\Delta {\varepsilon}_{\parallel}=c\Delta {p}_{\parallel }$
, and the mixed-mode energy gain prediction is plotted as the black dashed curve in Figure 5(c).

Figure 7 Electrons in the long-term trajectory, where the trajectory’s color represents the energy. (a) The trajectories of electron off-axis distance
![]() $r$
with
$r$
with
![]() $x$
, which are randomly selected from the third bunch that is situated close to the beam axis at
$x$
, which are randomly selected from the third bunch that is situated close to the beam axis at
![]() $t=248$
fs. (b) The variation of electron trajectories off-axis distance with
$t=248$
fs. (b) The variation of electron trajectories off-axis distance with
![]() $x$
, selected from the third bunch with the condition that energy is less than 150 MeV at
$x$
, selected from the third bunch with the condition that energy is less than 150 MeV at
![]() $t=248$
fs. (c) The trajectories of randomly selected electrons from the Figure 5(b) high-density region.
$t=248$
fs. (c) The trajectories of randomly selected electrons from the Figure 5(b) high-density region.
For the higher-order radial mode acceleration effect, Shi et al.[
Reference Shi, Blackman and Arefiev20
] concluded that for even radial modes, energy can be gained when the initial phase is
![]() ${\Phi}_0 \in [0.5\pi, 1.5\pi]$
. However, odd radial modes cannot result in energy gain. In the case of a pure radial mode
${\Phi}_0 \in [0.5\pi, 1.5\pi]$
. However, odd radial modes cannot result in energy gain. In the case of a pure radial mode
![]() $p=0$
, electrons with the appropriate initial phase can remain in the accelerating phase for several Rayleigh lengths due to the phase slip
$p=0$
, electrons with the appropriate initial phase can remain in the accelerating phase for several Rayleigh lengths due to the phase slip
![]() $\Delta \Phi = -\pi$
. Since the initial momentum gain is always negative for odd radial modes, electrons cannot be injected into the acceleration process. In our work, it can be found that the
$\Delta \Phi = -\pi$
. Since the initial momentum gain is always negative for odd radial modes, electrons cannot be injected into the acceleration process. In our work, it can be found that the
![]() ${\mathrm{LG}}_{01}$
mode dominated mixed mode can still accelerate electrons efficiently. However, the quality of the electron beam (maximum energy gain) is not as good as that of the
${\mathrm{LG}}_{01}$
mode dominated mixed mode can still accelerate electrons efficiently. However, the quality of the electron beam (maximum energy gain) is not as good as that of the
![]() ${\mathrm{LG}}_{01}$
mode, which is affected by the odd radial mode as well as the larger phase slip.
${\mathrm{LG}}_{01}$
mode, which is affected by the odd radial mode as well as the larger phase slip.
Figure 7 represents the long-range trajectory of electrons, which gain energy in a longitudinal field after being injected into the beam. However, due to the higher-order radial mode, electrons in different phases may have different energies after accelerating for about two Rayleigh lengths. Figure 7(a) shows the trajectory of 30 randomly selected electrons in the third bunch at
![]() $t=248$
fs close to the beam axis, where electrons can gain good acceleration. It is characterized by being in a paraxial position after being detached from the nanowire, being in an accelerated state without slowing down, and can accelerate to about 300 MeV. Figure 7(b) represents the trajectory of 30 electrons selected through energy limiting conditions in the third beam of electrons at
$t=248$
fs close to the beam axis, where electrons can gain good acceleration. It is characterized by being in a paraxial position after being detached from the nanowire, being in an accelerated state without slowing down, and can accelerate to about 300 MeV. Figure 7(b) represents the trajectory of 30 electrons selected through energy limiting conditions in the third beam of electrons at
![]() $t=248$
fs. It can be seen that these electrons have a maximum energy of about 150 MeV at
$t=248$
fs. It can be seen that these electrons have a maximum energy of about 150 MeV at
![]() $x\approx {x}_{\mathrm{R}}$
, and then enter the deceleration phase as predicted by our theory above. Figure 7(c) represents the trajectory of 30 electrons randomly selected from the Figure 7(b) high areal density region, which also accelerate to about 150 MeV and then decelerate. Due to the presence of the higher-order radial mode, the range of the acceleration phase is compressed, making it easier for electrons that deviate from the axis in the early stages to slip into the deceleration phase.
$x\approx {x}_{\mathrm{R}}$
, and then enter the deceleration phase as predicted by our theory above. Figure 7(c) represents the trajectory of 30 electrons randomly selected from the Figure 7(b) high areal density region, which also accelerate to about 150 MeV and then decelerate. Due to the presence of the higher-order radial mode, the range of the acceleration phase is compressed, making it easier for electrons that deviate from the axis in the early stages to slip into the deceleration phase.
We choose only one set of parameters to demonstrate our scheme. However, the scheme can work with a wide range of parameters. By using a higher peak power (
![]() $P$
[PW]), we can accelerate the electron bunches to higher energy (
$P$
[PW]), we can accelerate the electron bunches to higher energy (
![]() ${\varepsilon}^{\mathrm{term}}\left[\kern0.1em \mathrm{GeV}\kern0.1em \right]$
) according to a scaling relation of
${\varepsilon}^{\mathrm{term}}\left[\kern0.1em \mathrm{GeV}\kern0.1em \right]$
) according to a scaling relation of
![]() ${\varepsilon}^{\mathrm{term}}\left[\kern0.1em \mathrm{GeV}\kern0.1em \right]\approx 0.72\eta {P}^{1/2}\left[\kern0.1em \mathrm{PW}\kern0.1em \right]$
. Here
${\varepsilon}^{\mathrm{term}}\left[\kern0.1em \mathrm{GeV}\kern0.1em \right]\approx 0.72\eta {P}^{1/2}\left[\kern0.1em \mathrm{PW}\kern0.1em \right]$
. Here
![]() $\eta$
is the amplitude conversion rate from the Gaussian mode to the
$\eta$
is the amplitude conversion rate from the Gaussian mode to the
![]() ${\mathrm{LG}}_{01}$
mode. If we use a longer laser pulse
${\mathrm{LG}}_{01}$
mode. If we use a longer laser pulse
![]() ${\tau}_{\mathrm{g}}$
[fs] with other parameters unchanged, every cycle of the long pulse will accelerate one electron bunch. The total change (
${\tau}_{\mathrm{g}}$
[fs] with other parameters unchanged, every cycle of the long pulse will accelerate one electron bunch. The total change (
![]() ${Q}_{\mathrm{train}}\left[\mathrm{pC}\right]$
) that we can get in the ideal case is
${Q}_{\mathrm{train}}\left[\mathrm{pC}\right]$
) that we can get in the ideal case is
![]() ${Q}_{\mathrm{train}}\left[\mathrm{pC}\right]\approx 21{\tau}_{\mathrm{g}}\left[\mathrm{fs}\right]$
. Although the energy gain from the longitudinal fields is typically less than the energy from the laser wakefield acceleration at the same peak power, our scheme has several potential advantages. One advantage is that the long laser pulse can be used directly in vacuum without considering the self-modulation in the underdense plasma. As another advantage, a train of electron bunches with sub-femtosecond duration can find applications as an ultrafast probe beam[
Reference Zhang, Huang and Joshi43
] or in short-pulse backlight radiography[
Reference Bi, Zhou, Shan, Wei and Liu44
].
${Q}_{\mathrm{train}}\left[\mathrm{pC}\right]\approx 21{\tau}_{\mathrm{g}}\left[\mathrm{fs}\right]$
. Although the energy gain from the longitudinal fields is typically less than the energy from the laser wakefield acceleration at the same peak power, our scheme has several potential advantages. One advantage is that the long laser pulse can be used directly in vacuum without considering the self-modulation in the underdense plasma. As another advantage, a train of electron bunches with sub-femtosecond duration can find applications as an ultrafast probe beam[
Reference Zhang, Huang and Joshi43
] or in short-pulse backlight radiography[
Reference Bi, Zhou, Shan, Wei and Liu44
].
For high-power laser systems, laser pointing stability is an unavoidable issue. The results of the additional simulations with laser random offset show that our approach has a certain tolerance for laser pointing stability. When the incident beam is off-axis, the fraction of the
![]() ${\mathrm{LG}}_{01}$
mode in the reflected beam decreases[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
], which mainly affects the cutoff energy of the electron bunch.
${\mathrm{LG}}_{01}$
mode in the reflected beam decreases[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu15
], which mainly affects the cutoff energy of the electron bunch.
5 Summary and discussion
Using 3D PIC simulations, we have investigated the electron acceleration resulting from the reflection of a 490 TW CP Gaussian laser beam (
![]() $\sigma =+1$
) off a solid plasma integrated with a nanowire. The solid plasma with a ‘light fan’ structure imparts angular momentum to the reflected beam, endowing it with a helical wavefront structure, effectively generating LG beams. Analyzing the mode decomposition of the reflected beam reveals dominance of the
$\sigma =+1$
) off a solid plasma integrated with a nanowire. The solid plasma with a ‘light fan’ structure imparts angular momentum to the reflected beam, endowing it with a helical wavefront structure, effectively generating LG beams. Analyzing the mode decomposition of the reflected beam reveals dominance of the
![]() ${\mathrm{LG}}_{01}$
mode, accounting for 65% of the total. The longitudinal field of the generated relativistic intense laser is capable of accelerating injected electrons to an energy of several hundred MeV. We can get electron bunches with a low energy spread and a small divergence angle. The most energetic bunch exhibits an energy of 310 MeV, with a spread of 6%. The bunch charge is 57 pC, the duration is 400 as and the divergence angle is less than 50 mrad. We have also traced the origin of the electrons, revealing that over 97% of them originate from the nanowire. The unique structure of the nanowires not only enhances the amount of charge injected into the longitudinal field but also effectively suppresses the process of electron expulsion due to the transverse fields of Gaussian beam incidence.
${\mathrm{LG}}_{01}$
mode, accounting for 65% of the total. The longitudinal field of the generated relativistic intense laser is capable of accelerating injected electrons to an energy of several hundred MeV. We can get electron bunches with a low energy spread and a small divergence angle. The most energetic bunch exhibits an energy of 310 MeV, with a spread of 6%. The bunch charge is 57 pC, the duration is 400 as and the divergence angle is less than 50 mrad. We have also traced the origin of the electrons, revealing that over 97% of them originate from the nanowire. The unique structure of the nanowires not only enhances the amount of charge injected into the longitudinal field but also effectively suppresses the process of electron expulsion due to the transverse fields of Gaussian beam incidence.
Multi-radial mode LG beams can introduce intricate effects on electron acceleration. Twisted lasers with different radial indexes
![]() $p$
have different phase slips, resulting in different acceleration phases. We analyzed the effect of radial mode
$p$
have different phase slips, resulting in different acceleration phases. We analyzed the effect of radial mode
![]() $p=0$
, 1 and 2 on the electron acceleration effect based on the results of PIC simulations. Higher-order radial modes bring the transverse field closer to the axis and increase the rate of change of the beam phase velocity compared to the basic radial mode. This can lead to a decrease in the accelerated phase range of the electrons. However, the expected maximum energy of the electron bunch satisfies the prediction formula using mixed modes.
$p=0$
, 1 and 2 on the electron acceleration effect based on the results of PIC simulations. Higher-order radial modes bring the transverse field closer to the axis and increase the rate of change of the beam phase velocity compared to the basic radial mode. This can lead to a decrease in the accelerated phase range of the electrons. However, the expected maximum energy of the electron bunch satisfies the prediction formula using mixed modes.
By employing CP Gaussian beams, our proposed approach offers the potential to reduce experimental complexity in the demonstration of vortex laser-driven electron acceleration. From an experimental standpoint, generating relativistic twisted beams remains a significant challenge, as the majority of high-power laser setups currently only deliver Gaussian beams. The use of a solid plasma with the ‘light fan’ structure for generating twisted beams in the laboratory has been recently validated through experiments[ Reference Porat, Lightman, Cohen and Pomerantz16 ]. Our approach demonstrates that similar electron acceleration results to those achieved with twisted beams can be obtained using a CP Gaussian beam and a ‘light fan’ structure with a nanowire at the center.
With the progress in the use of microengineering techniques in the laser–plasma community[ Reference Porat, Lightman, Cohen and Pomerantz16 , Reference Jiang, Ji, Audesirk, George, Snyder, Krygier, Poole, Willis, Daskalova, Chowdhury, Lewis, Schumacher, Pukhov, Freeman and Akli32 , Reference Gheorghiu, Leca, Popa, Cernaianu and Stutman45 ], our proposal can take advantage of target fabrication and reduce the complexity of optical setups in large laser facilities. An array of small sacrificial ‘light fan’ mirrors can be made. A fresh area can be moved into the laser beam with each shot. Since large laser systems typically operate at low repetition rates, this sacrificial ‘light fan’ mirror array in the glass substrate can be realistic. Cost effectiveness can be another advantage over large-diameter mirrors. In particular, we can use kilojoule picosecond laser beams to obtain a train of electron bunches. For example, an 800 fs 500 TW CP-Gaussian laser beam contains about 300 cycles that could produce a similar number of bunches. The train of sub-femtosecond electron bunches can be directly used as an ultrafast probe beam[ Reference Zhang, Huang and Joshi43 ] or to generate high-brightness ultrafast X-ray radiation. Both can be used as an on-line diagnostic beam in facilities such as SG-II UP[ Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Liu, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Liu, Jiao, Huang and Lin46 ].
Appendix A. Mode decomposition
The field data output by the 3D PIC simulation can be represented as a combination of
![]() ${\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
modes with different twist indexes
${\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
modes with different twist indexes
![]() $l$
and radial indexes
$l$
and radial indexes
![]() $p$
. In the reflected beams of our case, all of these modes are along the
$p$
. In the reflected beams of our case, all of these modes are along the
![]() $x$
-axis positive direction of propagation. This indicates that their complex fields include the oscillation term
$x$
-axis positive direction of propagation. This indicates that their complex fields include the oscillation term
![]() $\exp \left( i\xi \right)=\exp \left( i kx- i\omega t\right)$
, where
$\exp \left( i\xi \right)=\exp \left( i kx- i\omega t\right)$
, where
![]() $k=2\pi /{\lambda}_0$
represents the wave vector. However, the information we obtain from the PIC code output contains only the real part of the complex field. This makes it challenging to perform mode decomposition on the reflected beam. Nevertheless, we can apply the Hilbert transform along the
$k=2\pi /{\lambda}_0$
represents the wave vector. However, the information we obtain from the PIC code output contains only the real part of the complex field. This makes it challenging to perform mode decomposition on the reflected beam. Nevertheless, we can apply the Hilbert transform along the
![]() $x$
-direction to the electromagnetic field information from the PIC code output, which allows us to recover the imaginary part of the field. The imaginary part represents the phase information of the beam propagating in the positive
$x$
-direction to the electromagnetic field information from the PIC code output, which allows us to recover the imaginary part of the field. The imaginary part represents the phase information of the beam propagating in the positive
![]() $x$
-axis direction[
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
]. We use the superscript H to represent the field obtained through the Hilbert transform. For example, the Hilbert transform can transform
$x$
-axis direction[
Reference Blackman, Shi, Klein, Cernaianu, Doria, Ghenuche and Arefiev21
]. We use the superscript H to represent the field obtained through the Hilbert transform. For example, the Hilbert transform can transform
![]() $f(t)=A\cdot \cos \left(\omega t+\varphi \right)$
into
$f(t)=A\cdot \cos \left(\omega t+\varphi \right)$
into
![]() ${f}^{\mathrm{H}}(t)=A\cdot {e}^{i\left(\omega t+\varphi \right)}$
, where
${f}^{\mathrm{H}}(t)=A\cdot {e}^{i\left(\omega t+\varphi \right)}$
, where
![]() $\operatorname{Re}\left[{f}^{\mathrm{H}}(t)\right]=f\left(\tilde{x}\right)=A\cdot \cos \left(\omega t+\varphi \right)$
and
$\operatorname{Re}\left[{f}^{\mathrm{H}}(t)\right]=f\left(\tilde{x}\right)=A\cdot \cos \left(\omega t+\varphi \right)$
and
![]() $\operatorname{Im}\left[{f}^{\mathrm{H}}(t)\right]=A\cdot \sin \left(\omega t+\varphi \right)$
.
$\operatorname{Im}\left[{f}^{\mathrm{H}}(t)\right]=A\cdot \sin \left(\omega t+\varphi \right)$
.
Because the influence of electrons on the electric field cannot be separated, we chose the magnetic field data
![]() ${B}_z$
for mode decomposition to increase the accuracy of the results. The field data through the Hilbert transform can be represented as a combination of the following:
${B}_z$
for mode decomposition to increase the accuracy of the results. The field data through the Hilbert transform can be represented as a combination of the following:
 $$\begin{align}\frac{\mid e\mid {B}_z^{\mathrm{H}}\left(\tilde{x},\tilde{r},\phi; t\right)}{m_{\mathrm{e}}\omega}=\sum \limits_{p=0}^{\infty}\left[\sum \limits_{l=-\infty}^{\infty }{b}_{p,l}\left(\xi \right){\psi}_{p,l}\Big(\tilde{x},\tilde{r},\phi \Big)\exp \left( i\xi \right)\right].\end{align}$$
$$\begin{align}\frac{\mid e\mid {B}_z^{\mathrm{H}}\left(\tilde{x},\tilde{r},\phi; t\right)}{m_{\mathrm{e}}\omega}=\sum \limits_{p=0}^{\infty}\left[\sum \limits_{l=-\infty}^{\infty }{b}_{p,l}\left(\xi \right){\psi}_{p,l}\Big(\tilde{x},\tilde{r},\phi \Big)\exp \left( i\xi \right)\right].\end{align}$$
Here the complex amplitude
![]() ${b}_{p,l}$
is dimensionless and includes both real and imaginary parts, and can be recovered through double integration if
${b}_{p,l}$
is dimensionless and includes both real and imaginary parts, and can be recovered through double integration if
![]() ${B}_z$
is known at time
${B}_z$
is known at time
![]() $t$
for the corresponding
$t$
for the corresponding
![]() $p$
:
$p$
:
 $$\begin{align}{b}_{p,l}\left(\xi \right)={\int}_0^{2\pi}\mathrm{d}\phi \left[{\int}_0^{\infty}\frac{\mid e\mid {B}_z^{\mathrm{H}}}{m_{\mathrm{e}}\omega }{\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\exp \left(- i\xi \right)\tilde{r}\mathrm{d}\tilde{r}\right].\end{align}$$
$$\begin{align}{b}_{p,l}\left(\xi \right)={\int}_0^{2\pi}\mathrm{d}\phi \left[{\int}_0^{\infty}\frac{\mid e\mid {B}_z^{\mathrm{H}}}{m_{\mathrm{e}}\omega }{\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\exp \left(- i\xi \right)\tilde{r}\mathrm{d}\tilde{r}\right].\end{align}$$
In this case, the complex form of the wave represented by
![]() ${b}_{p,l}$
can be explained as follows:
${b}_{p,l}$
can be explained as follows:
where
![]() ${B}_0{\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
represents the amplitudes of different modes of the LG beam, and
${B}_0{\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
represents the amplitudes of different modes of the LG beam, and
![]() $g\left(\xi \right)$
is the envelope term. The relative proportion of different LG modes (including envelope terms) can be obtained by plotting the real part of
$g\left(\xi \right)$
is the envelope term. The relative proportion of different LG modes (including envelope terms) can be obtained by plotting the real part of
![]() ${b}_{p,l}$
.
${b}_{p,l}$
.
The percentage of each radial mode can be calculated from their ratios by obtaining the corresponding complex amplitudes of each radial mode. We performed mode decomposition for radial modes
![]() $p= 0, 1, \ldots, 6 $
, and the results indicate that the dominant modes are
$p= 0, 1, \ldots, 6 $
, and the results indicate that the dominant modes are
![]() $p=0$
, 1 and 2, accounting for 65%, 22% and 13%, respectively, shown in Figure A1. We ran a benchmark in the PIC simulation where a multi-mode mixed beam containing radial modes
$p=0$
, 1 and 2, accounting for 65%, 22% and 13%, respectively, shown in Figure A1. We ran a benchmark in the PIC simulation where a multi-mode mixed beam containing radial modes
![]() $p=$
0, 1 and 2 (with proportions 4:2:1) with the same twist mode
$p=$
0, 1 and 2 (with proportions 4:2:1) with the same twist mode
![]() $l=1$
propagates along the positive
$l=1$
propagates along the positive
![]() $x$
-direction in vacuum. The mode decomposition method accurately determines the proportions of each radial mode.
$x$
-direction in vacuum. The mode decomposition method accurately determines the proportions of each radial mode.

Figure A1 The results of mode decomposition, in which the red solid line, black dashed line and blue dotted line represent the radial modes
![]() $p=0$
,
$p=0$
,
![]() $p=1$
and
$p=1$
and
![]() $p=2$
, respectively. Here,
$p=2$
, respectively. Here,
![]() ${b}_{p,l}$
is a dimensionless number that can be used to represent the relative proportions of different modes. The black dashed line indicates the position of the peak of the envelope.
${b}_{p,l}$
is a dimensionless number that can be used to represent the relative proportions of different modes. The black dashed line indicates the position of the peak of the envelope.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
PIC simulations were performed with the fully relativistic open-access 3D PIC code SMILEI[ Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov, Aunai, Dargent, Riconda and Grech35 ].
Acknowledgements
Y.S. acknowledges the support from the National Natural Science Foundation of China (Grant No. 12322513), USTC Research Funds of the Double First-Class Initiative and the CAS Project for Young Scientists in Basic Research (Grant No. YSBR060). The authors express their gratitude to Xuesong Geng from the Shanghai Institute of Optics and Fine Mechanics, and to the developers of SMILEI, for their invaluable assistance in utilizing the PIC code SMILEI. The Super Computing Center of USTC and Hefei Advanced Computing Center are acknowledged for computational support.