No CrossRef data available.
Article contents
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
Published online by Cambridge University Press: 27 August 2024
Abstract
Let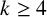 
$k\geq 4$ be an integer. We prove that the set 
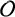$\mathcal {O}$ of all nonzero generalised octagonal numbers is a k-additive uniqueness set for the set of multiplicative functions. That is, if a multiplicative function 
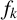$f_k$ satisfies the condition 
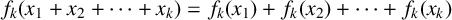$$ \begin{align*} f_k(x_1+x_2+\cdots+x_k)=f_k(x_1)+f_k(x_2)+\cdots+f_k(x_k) \end{align*} $$
for arbitrary 
$x_1,\ldots ,x_k\in \mathcal {O}$, then 
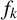$f_k$ is the identity function 
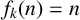$f_k(n)=n$ for all 
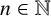$n\in \mathbb {N}$. We also show that 
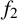$f_2$ and 
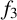$f_3$ are not determined uniquely.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by ADA University Faculty Research and Development Funds and by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1A2C1092930).
References
Chung, P. V., ‘Multiplicative functions satisfying the equation
$f({m}^2+{n}^2)=f({m}^2)+f({n}^2)$
’, Math. Slovaca 46(2–3) (1996), 165–171.Google Scholar
$f({m}^2+{n}^2)=f({m}^2)+f({n}^2)$
’, Math. Slovaca 46(2–3) (1996), 165–171.Google ScholarChung, P. V. and Phong, B. M., ‘Additive uniqueness sets for multiplicative functions’, Publ. Math. Debrecen 55(3–4) (1999), 237–243.CrossRefGoogle Scholar
Dubickas, A. and Šarka, P., ‘On multiplicative functions which are additive on sums of primes’, Aequationes Math. 86(1–2) (2013), 81–89.CrossRefGoogle Scholar
Fang, J.-H., ‘A characterization of the identity function with equation
$f(p+q+r)=f(p)+f(q)+f(r)$
’, Combinatorica 31(6) (2011), 697–701.CrossRefGoogle Scholar
$f(p+q+r)=f(p)+f(q)+f(r)$
’, Combinatorica 31(6) (2011), 697–701.CrossRefGoogle ScholarHasanalizade, E., ‘Multiplicative functions
$k$
-additive on generalized pentagonal numbers’, Integers 22 (2022), Article no. A43.Google Scholar
$k$
-additive on generalized pentagonal numbers’, Integers 22 (2022), Article no. A43.Google ScholarKim, B., Kim, J. Y., Lee, C. G. and Park, P.-S., ‘Multiplicative functions additive on generalized pentagonal numbers’, C. R. Math. Acad. Sci. Paris 356(2) (2018), 125–128.CrossRefGoogle Scholar
Kim, B., Kim, J. Y., Lee, C. G. and Park, P.-S., ‘Multiplicative functions additive on polygonal numbers’, Aequationes Math. 95 (2021), 601–621.CrossRefGoogle Scholar
Kim, D., Lee, J. and Oh, B.-H., ‘A sum of three nonzero triangular numbers’, Int. J. Number Theory 17(10) (2021), 2279–2300.CrossRefGoogle Scholar
Park, P.-S., ‘On
$k$
-additive uniqueness of the set of squares for multiplicative functions’, Aequationes Math. 92(3) (2018), 487–495.CrossRefGoogle Scholar
$k$
-additive uniqueness of the set of squares for multiplicative functions’, Aequationes Math. 92(3) (2018), 487–495.CrossRefGoogle ScholarPark, P.-S., ‘Multiplicative functions which are additive on triangular numbers’, Bull. Korean Math. Soc. 58(3) (2021), 603–608.Google Scholar
Park, P.-S., ‘On multiplicative functions which are additive on positive cubes’, Preprint, 2023, arXiv:2302.07461.Google Scholar
Spiro, C. A., ‘Additive uniqueness sets for arithmetic functions’, J. Number Theory 42(2) (1992), 232–246.CrossRefGoogle Scholar