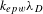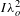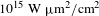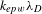1 Introduction
A major task of the laser–plasma interaction (LPI) community is to develop predictive means for the envisaged inertial confinement fusion (ICF) experiments such as National Ignition Facility (NIF)[Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter1–Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Doeppner, Hinkel, Hopkins, Kline, LePape, Ma, MacPhee, Milovich, Park, Park, Patel, Remington, Salmonson, Springer and Tommasini3], Laser MegaJoule (LMJ)[Reference Ebrardt and Chaput4] and ShengGuang (SG)[Reference He and Zhang5]. Among the dominant problems is an accurate evaluation of backscatter reflectivities, Brillouin (SBS) and Raman (SRS), for plasmas having an electron temperature of a few kilo electronvolts. Due to the complexity of the interaction numerical simulations should be the obvious means in order to understand fusion plasmas. However, the calculated reflectivity data do not always agree with the experimental data. A detailed comprehension of SBS and SRS is therefore necessary. First-principle simulations like the particle-in-cell (PIC) approach (mobile ions as well as electrons) should give a correct answer but cannot be performed for millimetre-cube plasmas and interaction times of several hundred picoseconds as they are too demanding for present-day computers. Nevertheless the kinetic approach is the most reasonable one as it can be expected that eventually models can be derived for the saturation of the parametric instabilities which in turn are incorporated in macroscopic, fluid-type, simulations of fusion plasmas.
In the present paper, parameters are considered which are of relevance for ICF. As the density is below the quarter-critical density both, SRS and SBS, will be present. The simultaneity of both instabilities raises questions concerning the relative importance, mutual influence and contribution to the total reflectivity. There seems to be emerging a consensus that kinetic effects are of relevance in order to determine the saturation of SRS as well as SBS. In particular, for high temperatures kinetic effects are supposed to be important for Raman backscattering. The full PIC-approach used allows for all possible decay processes admitted by the plasma. Although far from resolving this issue the simulations reported in this paper at least show the complexity of the scenario and the sensitivity to parameter changes. The issue of the nonlinear interaction between SBS and SRS is far from being understood in its details. It has been studied before using either reduced models[Reference Aldrich, Bezzerides, DuBois and Rose6–Reference Rose10] or by PIC simulations using small plasma and unrealistic mass ratios[Reference Estabrook, Kruer and Haines11]. Due to the intrinsic difficulty of resolving the different time scales involved in SBS and SRS, many studies prefer to focus either on SRS evolution and saturation[Reference Sanbonmatsu, Vu, DuBois and Bezzerides12–Reference Ellis, Strozzi, Winjum, Tsung, Grismayer, Mori, Fahlen and Williams18], or SBS evolution and saturation by itself [Reference Giacone and Vu19–Reference Chapman, Winjum, Brunner, Berger and Banks24]. The analysis of parametric instabilities in this paper is mostly of relevance to large-scale, homogeneous plasmas as in intense speckle in indirect-drive conditions[Reference Kirkwood, Moody, Kline, Dewald, Glenzer, Divol, Michel, Hinkel, Berger, Williams, Milovich, Yin, Rose, MacGowan, Landen, Rosen and Lindl25], or in the low-density part in shock-ignition conditions[Reference Atzeni, Ribeyre, Schurtz, Schmitt, Canaud, Betti and Perkins26–Reference Weber and Riconda29].
Considering low- and high-
$k{\it\lambda}_{D}$ regimes is of interest for several reasons. For example, it allows to compare the behaviour of parametric instabilities in the case of small-scale installations and fusion-type installations. There is a considerable difference as far as the electron temperature is concerned. In the case of shock-ignition, direct-drive approach the plasma corona spans all densities from zero to quarter-critical (limiting density for SRS). One therefore has a mixture of various 
$k{\it\lambda}_{D}$-regimes. In the case of indirect-drive hohlraum plasmas one encounters large-scale, more or less homogeneous, low densities (typically of the order of 
${\sim}0.1n_{c}$) with small temperature variations. This approach has only limited 
$k{\it\lambda}_{D}$-variations. In this paper, we consider a fixed density and vary the temperature. However, as 
$k{\it\lambda}_{D}$ is a linear function of the ratio 
$T_{e}/n_{e}$ to first order, the same regimes can also be obtained by varying the density for a given temperature.
The remainder of the paper is organized as follows. In Section 2, the basic formulae for SBS and SRS, as well as Langmuir decay are briefly reviewed as they will be used in the analysis of the results. The following section, Section 3, presents the numerical setup and discusses the issue of boundary conditions for the numerical simulations. Section 4 gives an overview of the reflectivity data obtained and the two extremes of Raman evolution. The main simulation results are presented in three sections (Sections 5, 7 and 8) characterized by the 
$k_{epw}{\it\lambda}_{D}$-regime used. The section on high electron temperature simulations (Section 5) is followed by a short section, Section 6, which points out some numerical limitations which can appear in PIC simulations for certain parameters. Section 9 looks at how the backscattering scenario changes if the laser intensity is increased strongly. Finally in the last section, Section 10, a summary and outlook on future necessary activities is given.
2 Basic framework for Raman and Brillouin backscattering
Table 1. An overview of the parameters of the numerical simulations discussed in this paper. The electron temperature 
$T_{e}$ is in keV and the intensity 
$I{\it\lambda}_{o}^{2}$ in 
$\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$. 
$b=$ backward, 
$f=$ forward, 
$sc=$ strong coupling, 
$wc=$ weak coupling. In addition to the cases listed below some of the runs have been done with artificial mass ratios of 
$m_{i}/m_{e}=10^{4}$ and 
$m_{i}/m_{e}=10^{5}$. In practical units one has 
$v_{osc}/v_{e}=0.611\times \sqrt{I/T_{e}}$ with intensity 
$I$ in units of 
$10^{15}~\text{W}/\text{cm}^{2}$ and 
$T_{e}$ in keV. The values for 
$k_{epw,b}{\it\lambda}_{D}$ and 
$k_{epw,f}{\it\lambda}_{D}$ were calculated using the approximations in Equation (6). N/a: not available as (1) the density is above the quarter-critical one or (2) the case is 
$sc$ (
$wc$) and not 
$wc$ (
$sc$). For all runs the density is set to 
$n/n_{c}=0.1$, except for case VIII which uses the density 
$n=0.3n_{c}$.
2.1 Raman and Brillouin
The present section gives a very brief overview of the dispersion relations and instability growth rates for Raman and Brillouin as they will be used in the discussion of the results in the subsequent sections. The general formulae given below can be found in the literature[Reference Forslund, Kindel and Lindman30, Reference Dautray and Watteau31].
Raman and Brillouin instabilities are based on the 3-wave coupling mechanism, i.e., the conservation equations for frequency, 
${\it\omega}_{o}={\it\omega}_{1}+{\it\omega}_{s}$, and wavevector, 
$k_{po}=k_{p1}+k_{s}$. Here 
${\it\omega}_{o}$, 
${\it\omega}_{1}$ and 
${\it\omega}_{s}$ are the frequencies of the pump, scattered electromagnetic wave and plasma response (ion-acoustic wave (IAW) or electron plasma wave (EPW)), respectively. Similarly, 
$k_{po}$, 
$k_{1}$ and 
$k_{s}$ are the corresponding wavevectors in the plasma with 
$k_{s}$ either the IAW vector 
$k_{cs}\approx 2k_{po}$ (in the case of backscattering) or the wavevector of the EPW 
$k_{epw}$. Each of the three implicated waves obeys its dispersion relation, which, taking into account finite temperature and 
$k{\it\lambda}_{D}$ effects read:
$$\begin{eqnarray}\displaystyle {\it\omega}_{o}^{2} & = & \displaystyle {\it\omega}_{pe}^{2}+k_{po}^{2}c^{2},\nonumber\\ \displaystyle {\it\omega}_{1}^{2} & = & \displaystyle {\it\omega}_{pe}^{2}+k_{1}^{2}c^{2},\nonumber\\ \displaystyle {\it\omega}_{cs}^{2} & = & \displaystyle k_{cs}^{2}c_{s}^{2}\left(\frac{1}{1+k_{cs}^{2}{\it\lambda}_{D}^{2}}+\frac{3T_{i}}{ZT_{e}}\right),\nonumber\\ \displaystyle {\it\omega}_{epw}^{2} & = & \displaystyle {\it\omega}_{pe}^{2}+3k_{epw}^{2}v_{e}^{2}\Rightarrow {\it\omega}_{epw}\nonumber\\ \displaystyle & = & \displaystyle {\it\omega}_{pe}(1+3k_{epw}^{2}{\it\lambda}_{D}^{2})^{1/2}.\end{eqnarray}$$ Here 
${\it\omega}_{pe}=\sqrt{4{\it\pi}ne^{2}/m_{e}}$ is the electron plasma frequency and 
$k_{po}=k_{o}\sqrt{1-n_{e}/n_{c}}$ is wavevector in the plasma with 
$n_{c}=n_{e}{\it\omega}_{o}^{2}/{\it\omega}_{pe}^{2}$ the critical density. Here one has mostly that 
$k_{po}=0.95k_{o}\approx k_{o}$ (i.e., for a plasma density of 
$n_{e}=0.1n_{c}$). 
${\it\lambda}_{D}=(kT_{e}/4{\it\pi}n_{e}^{2})^{1/2}$ is the Debye length.
Most of the cases considered (see Table 1) are in the strong-coupling regime. Only if the temperature is above 
$T_{e}\approx 5~\text{keV}$ the interaction is in the weak-coupling regime. The strong-coupling regime is characterized by 
$(v_{osc}/v_{e})^{2}>4k_{po}c_{s}{\it\omega}_{o}/{\it\omega}_{pe}^{2}$ with 
$v_{osc}=eE_{o}/{\it\omega}_{o}m_{e}$, 
$v_{e}=\sqrt{T_{e}/m_{e}}$ and 
$c_{s}=\sqrt{T_{e}/m_{i}}$ the electron quiver velocity, the electron thermal velocity and the ion-acoustic sound velocity, respectively. For given density and electron temperature strong coupling takes place whenever:
$$\begin{eqnarray}I_{14}{\it\lambda}_{o}^{2}>1.1\times 10^{-1}T_{e}^{3/2}~(\text{keV})(n_{c}/n_{e})(1-n_{e}/n_{c})^{1/2},\end{eqnarray}$$ where 
$I_{14}{\it\lambda}_{o}^{2}$ is the laser intensity in units of 
$10^{14}~\text{W}~{\rm\mu}\text{m}^{2}\!/\text{cm}^{2}$. According to this criterium the cases VIII, IX and X in Table 1 are weak coupling.
In the strong-coupling case the ion-acoustic plasma response is determined by the pump and is characterized by a quasi-mode rather than a real eigenmode of the system:
$$\begin{eqnarray}{\it\omega}_{sc}=\frac{1+i\sqrt{3}}{2}(k_{po}^{2}v_{osc}^{2}{\it\omega}_{pi}^{2}/{\it\omega}_{o})^{1/3}.\end{eqnarray}$$ 
${\it\omega}_{pi}=\sqrt{4{\it\pi}n_{i}Ze^{2}/m_{i}}$ is the ion plasma frequency. The instability growth rate in the strong-coupling regime follows from the imaginary part of Equation (3) and is given as 
${\it\gamma}_{sc}={\mathcal{I}}m({\it\omega}_{sc})=(\sqrt{3}/2)(k_{po}^{2}v_{osc}^{2}{\it\omega}_{pi}^{2}/{\it\omega}_{o})^{1/3}$, which in practical units reduces to:
$$\begin{eqnarray}{\it\gamma}_{sc}/{\it\omega}_{0}=2.95\times 10^{-3}\left(I_{14}{\it\lambda}_{o}^{2}\frac{Z}{A}\frac{n_{e}}{n_{c}}\frac{n_{c}-n_{e}}{n_{c}}\right)^{1/3}.\end{eqnarray}$$ Here 
$A$ is the mass ratio 
$m_{i}/m_{p}$ with 
$m_{p}$ the proton mass. Note that 
${\it\gamma}_{sc}$ is independent of the temperature.
By contrast, the SBS growth rate above threshold in the weak-coupling regime is given by 
${\it\gamma}_{wc}=k_{po}v_{osc}{\it\omega}_{pi}/\sqrt{2{\it\omega}_{cs}{\it\omega}_{o}}$ which results in 
${\it\gamma}_{wc}/{\it\omega}_{o}\approx v_{osc}{\it\omega}_{pi}/2{\it\omega}_{o}\sqrt{c_{s}c}$ and in practical units one has:
$$\begin{eqnarray}{\it\gamma}_{wc}/{\it\omega}_{0}=3.1\times 10^{-3}\sqrt{I_{14}}{\it\lambda}_{o}\left(\frac{n_{e}}{n_{c}}\right)^{1/2}\left(\frac{Z}{A}\right)^{1/4}\frac{1}{T_{e}^{1/4}~(\text{keV})}.\end{eqnarray}$$ For SBS the downshift of the backscattered electromagnetic wave is negligible as it is of the order of the frequency ratio 
${\it\omega}_{o}/{\it\omega}_{sc}\sim 1000$. For the wavevectors one has that 
$k_{cs}=2k_{po}=2k_{o}\sqrt{1-n_{e}/n_{c}}$.
In the case of SRS the frequency downshift for a density of 
$n_{e}=0.1n_{c}$ is 
${\it\omega}_{1}=3.16~{\it\omega}_{pe}$. For the wavevector in the case of backward Raman scattering one has 
$k_{epw}\sim k_{1}+k_{o}$. Neglecting Debye corrections the ratio of incident to backscattered electromagnetic wave is given as 
${\it\omega}_{1}/{\it\omega}_{o}=1-{\it\omega}_{pe}/{\it\omega}_{o}=1-\sqrt{n/n_{c}}$. One obtains a first-order wavevector of the form 
$k_{1}\approx (1/c)\sqrt{{\it\omega}_{1}^{2}-{\it\omega}_{pe}^{2}}=({\it\omega}_{o}/c)\sqrt{1-2\sqrt{n/n_{c}}}$. For the underdense plasma density of 
$n=0.1n_{c}$ mostly considered here one obtains 
$k_{1}\approx 0.6k_{o}$ and therefore 
$k_{epw,b}\approx 1.6k_{o}$. For forward Raman scattering the wavevector has the value: 
$k_{epw,f}\sim k_{o}-k_{1}\approx 0.4k_{o}$.
In practical units one obtains for the 
$k{\it\lambda}_{D}$-corrections for backward and forward SRS the following relations:
$$\begin{eqnarray}\displaystyle k_{epw,b}^{2}{\it\lambda}_{D}^{2} & = & \displaystyle \frac{1.96\times 10^{-3}T_{e}~(\text{keV})}{(n/n_{c})}\left[1+\sqrt{1-2\sqrt{\frac{n}{n_{c}}}}\right]^{2}\nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{7.83\times 10^{-3}T_{e}~(\text{keV})}{(n/n_{c})}\left[1-\sqrt{\frac{n}{n_{c}}}\right],\nonumber\\ \displaystyle k_{epw,f}^{2}{\it\lambda}_{D}^{2} & = & \displaystyle \frac{1.96\times 10^{-3}T_{e}~(\text{keV})}{(n/n_{c})}\left[1-\sqrt{1-2\sqrt{\frac{n}{n_{c}}}}\right]^{2}\nonumber\\ \displaystyle & {\approx} & \displaystyle 1.96\times 10^{-3}T_{e}~(\text{keV}).\end{eqnarray}$$ Whenever the condition 
${\it\gamma}_{o}<1.3{\it\omega}_{pe}$ is fulfilled the instability takes place in the convective regime. As this is the case for the densities and intensities used (see Table 1) the instability growth rate for SRS is given by: 
${\it\gamma}_{SRS}\approx {\it\gamma}_{o}\min (1,{\it\gamma}_{o}/{\it\gamma}_{\text{tot}})$. Here 
${\it\gamma}_{\text{tot}}={\it\gamma}_{L}+{\it\gamma}_{\text{coll}}$ is the total damping of the EPWs due to the Landau effect and collisions. Depending on whether it is backward or forward Raman, Landau damping takes the approximative form:
$$\begin{eqnarray}\displaystyle {\it\gamma}_{L,epw,b}/{\it\omega}_{o} & = & \displaystyle \frac{2\times 10^{2}(n/n_{c})^{2}\exp (-1/(2k_{epw,b}^{2}{\it\lambda}_{D}^{2}))}{T_{e}^{3/2}~(\text{keV})},\nonumber\\ \displaystyle {\it\gamma}_{L,epw,f}/{\it\omega}_{o} & = & \displaystyle \frac{1.6\times 10^{3}(n/n_{c})^{1/2}\exp (-1/(2k_{epw,f}^{2}{\it\lambda}_{D}^{2}))}{T_{e}^{3/2}~(\text{keV})},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$and the collisional contribution is given in practical units as:
$$\begin{eqnarray}{\it\gamma}_{\text{coll}}/{\it\omega}_{o}=\frac{2.74\times 10^{-5}\displaystyle \left(\frac{n_{e}}{n_{c}}\right)\ln {\rm\Lambda}_{ei}Z}{{\it\lambda}_{o}~({\rm\mu}\text{m})T_{e}^{3/2}~(\text{keV})}.\end{eqnarray}$$ Here 
$\ln {\rm\Lambda}_{ei}$ is the Coulomb logarithm which for the parameters used is of the order 10. 
${\it\gamma}_{o}$ itself is given by the expression:
$$\begin{eqnarray}{\it\gamma}_{o}/{\it\omega}_{o}=\frac{(k_{epw}/k_{o})(v_{osc}/c)}{2\left(\sqrt{\frac{n_{c}}{n_{e}}}-1\right)^{1/2}}.\end{eqnarray}$$ Evaluating for Stimulated Raman backscattering (SRBS) and Stimulated Raman forward scattering (SRFS) the above formulae shows that always the growth rate for Raman should be given by 
${\it\gamma}_{o}$ and is therefore temperature independent. The values in Table 1 are derived using Equation (9) using the corresponding 
$k$-vectors for backward and forward scattering.
Due to the dispersion relation for EPWs, Equation (1), SRS does not exist above the quarter-critical density. For backward SRS there also exists a lower limit given as a function of temperature in the way:
$$\begin{eqnarray}0.25>n/n_{c}>4.9\times 10^{-2}T_{e}~(\text{keV}).\end{eqnarray}$$ For high enough electron temperatures the damping of the EPW inhibits the excitation of SRS. For a plasma density 
$n=0.1n_{c}$ no strong Raman activity should be visible above 2 keV.
2.2 The Langmuir decay instability
The Langmuir decay instability was well known theoretically[Reference Oraevskii and Sagdeev32–Reference Obiki, Itatani and Otani34]. Experimentally it was observed more recently[Reference Labaune, Baldis, Bauer, Tikhonchuk and Laval35–Reference Kline, Montgomery, Bezzerides, Cobble, DuBois, Johnson, Rose, Yin and Vu38], although indirect evidence due to IAW damping on SRS[Reference Drake and Batha39–Reference Montgomery, Cobble, Fernandez, Focia, Johnson, Renard-LeGalloudec, Rose and Russell45] was available.
In the LDI-process a pump plasma wave 
$(k_{epw},{\it\omega}_{epw})$ decomposes into an IAW given by 
$(2k_{epw}-{\it\delta}k,{\it\omega}_{cs})$ (co-propagating with the original EPW) and an anti-Stokes daughter EPW (propagating in the opposite direction). The latter has a frequency downshifted by 
${\it\omega}_{cs}$ with respect to the original frequency and its wavevector is: 
$k_{epw1}=k_{epw}+{\it\delta}k$. 
${\it\delta}k=\frac{2}{3}(Zm_{e}/m_{i})^{1/2}/{\it\lambda}_{D}$ is the wavevector correction.
The LDI-process takes place if 
$k_{epw}{\it\lambda}_{D}>\frac{2}{3}(Zm_{e}/m_{i})^{1/2}\approx 0.02$[Reference Oraevskii and Sagdeev32, Reference Bonnaud, Pesme and Pellat46]. This condition is fulfilled for all the simulation runs of Table 1.
The maximum growth rate of LDI is given by:
$$\begin{eqnarray}{\it\gamma}_{LDI}=\frac{1}{2}\frac{e|E_{epw}|}{m_{e}{\it\omega}_{epw}}\frac{1}{v_{e}}\sqrt{{\it\omega}_{epw1}{\it\omega}_{cs}}.\end{eqnarray}$$ LDI, LDI cascade and Langmuir wave collapse dominate the nonlinear evolution of the EPW provided kinetic effects are of minor importance. In that case they play a role in saturating the SRS instability. In case the density fluctuations are below the wavebreaking limit, the condition 
$k_{epw}^{2}{\it\lambda}_{D}^{2}\ll 1$ amounts to neglecting kinetic effects. This would therefore be the regime where LDI and its influence on SRS is important[Reference Bezzerides, DuBois and Rose8, Reference Karttunen47–Reference Russell, DuBois and Rose51].
Figure 1. Reflectivity evolution: backscattered intensity normalized to incident intensity. The subfigures correspond to the following cases in Table 1: I (a), II (b), IIa (c), IIb (d), III (e), IV (f), IVa (g), V (h), Va (i), VI (j), VII (k), and VIII (l). The index a indicates that the plasma length was reduced to 
$40~{\rm\mu}\text{m}$, the index b to a doubling of the simulation time (i.e., 25 ps at half the number of particles per computational cell). N.B. reflectivity scales are not the same.
3 Numerical setup
3.1 General aspects
The physical parameters of electron temperature 
$T_{e}$, temperature ratio 
$ZT_{e}/T_{i}$, intensity 
$I{\it\lambda}_{o}^{2}$ (in the following all analysis is done with respect to 
${\it\lambda}_{o}=1~{\rm\mu}\text{m}$) were varied. By contrast the charge number 
$Z=1$ was kept constant. The mass ratio is the realistic value of 
$m_{i}/m_{e}=1836$. For some numerical tests this ratio was set to 
$10^{4}$ and 
$10^{5}$ as will be discussed in Section 6. The majority of the simulations used a plasma slab of 
$80~{\rm\mu}\text{m}$ length at 
$n=0.1n_{c}$. For most of the simulation the duration was 
$2.5\times 10^{4}{\it\omega}_{o}^{-1}$, corresponding to 12.5 ps. However, a few of longer duration were performed. Mostly two intensities were considered: 
$I{\it\lambda}_{o}^{2}=10^{15}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$ and 
$I{\it\lambda}_{o}^{2}=10^{16}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$. The time step for integration was set to 
${\rm\Delta}t=0.05{\it\omega}_{o}^{-1}$. Of the order of 40 particles were used per computational cell. The spatial resolution was set to 
$0.05c/{\it\omega}_{o}$. The cell size is therefore either resolving the Debye length for the high-temperature cases or is of the order of 
${\it\lambda}_{D}$ for 500 eV and 
$0.3n_{c}$.
Table 1 gives an overview of the parameters of the PIC-simulations performed.
3.2 Boundary conditions and their possible physical interpretation
The basic configuration used in the simulations is the exploding-foil configuration. The plasma plateau is surrounded on both sides by a large vacuum margin, 
$60~{\rm\mu}\text{m}$, in order to avoid any explicit boundary condition coming into play. The simulations are stopped before particles start to attain the limits of the simulation box. Depending on the parameters used in Raman PIC-simulations a hot tail can establish itself in the distribution function. These hot particles quickly reach the end of the plasma slab and are pulled around due to the inertia of the much more massive ions. This hot electron current interferes with Raman excitation and prevents new Raman bursts (see details below in the discussion of the results). At first view this might be considered to be an artificial artefact of the numerical setup. However, in a real fusion plasma a multi-speckle laser beam generated by a random phase plate (RPP) will produce hot spots everywhere. These hot spots will generate Raman bursts with subsequent hot electrons. These electrons will interact with other speckles in the plasma volume and affect the Raman instability. The fact that in the present simulations the hot electrons remain in the plasma slab can be interpreted as simulating what will happen in a multi-speckle plasma as far as Raman is concerned. The majority of the PIC-simulations use a plasma length of 
$80~{\rm\mu}\text{m}$. A speckle has a characteristic transverse size which is given as 
$l_{\bot }\approx 2f/k_{o}$ and a characteristic longitudinal (parallel) size of the order of 
$l_{\Vert }\approx 7f^{2}{\it\lambda}_{o}$[Reference Korotkevich, Lushnikov and Rose52]. For fusion plasmas such as NIF, operating at 
$3{\it\omega}_{o}$ and using a typical optical f/# of 7 one has 
$l_{\Vert }\approx 100~{\rm\mu}\text{m}$ which fits well the setup used here. The main effect of considering a two-dimensional (2D) configuration instead of a one-dimensional (1D) one for the parameters considered in this paper is to introduce side losses, as illustrated by various authors[Reference Rose53–Reference Winjum, Berger, Chapman, Banks and Brunner57]. However, the previous reasoning also applies to lateral losses so that the considered boundary conditions are still meaningful, although the precise value of the recurrence time for SRS can depend on the exact 2D configuration. 1D simulations exclude the two-plasmon decay instability which was studied in a complementary series of papers[Reference Weber and Riconda29, Reference Riconda, Weber, Tikhonchuk and Heron58, Reference Weber, Riconda, Klimo, Heron and Tikhonchuk59].
4 An overview for various parameters
4.1 Time evolution of the reflectivities
Figure 1 gives an overview of how much the reflectivity can vary with respect to changes in the basic parameters.
Figure 1 shows that the instantaneous reflectivities can vary enormously in their temporal behaviour and that they can attain values above 100%. Intensities above the incident intensities are possible as the backscattered pulse is bursty and can undergo amplification, i.e., it takes up energy from the still ongoing incident laser pulse. This phenomenon is known for both, SRS[Reference Maier, Kaiser and Giordmaine60] and SBS[Reference Weber, Riconda and Tikhonchuk61–Reference Weber, Lontano, Passoni, Riconda and Tikhonchuk63]. As expected, as the electron temperature 
$T_{e}$ increases SRS decreases. However, even when 
$k_{epw,b}{\it\lambda}_{D}$ is as large as 0.3, and EPWs therefore strongly damped, one can observe large SRS bursts: at the considered intensities inflationary SRS[Reference Vu, DuBois and Bezzerides15] sets in. This holds for values of 
$k_{epw,b}{\it\lambda}_{D}$ as large as 0.59. Increasing the electron temperature even further, 
$T_{e}=6{-}8~\text{keV}$ (not shown here), for the same intensity 
$I{\it\lambda}_{o}^{2}=10^{15}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$ and density, makes SRS disappear. In contrast, the largest bursts are obtained at low temperature and moderate intensities 
$I{\it\lambda}_{o}^{2}=3\times 10^{15}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$. SRS burst can be recursive if the simulations last long enough, as shown in Figure 1(d). Figure 1(d) shows the reflectivity evolution of case II in Table 1 on a longer time scale, 25 ps, twice the duration of the other cases. SRS burst can coexist with SBS when SBS starts growing; however, when SBS reaches large levels as in most of the simulations (up to 50%), SRS bursts are no longer observed, probably mainly due to pump depletion. As shown in Figure 1 for some cases (II, IV, V) a reduced plasma length of 
$40~{\rm\mu}\text{m}$ was considered as well (Figures 1(c), (g), and (i)). As can be seen, reducing the plasma size reduces the overall reflectivity, due to the convective character of the instabilities, and also because saturation for SRS is related to the modification of the electron distribution function. A longer plasma thus allows the instability to grow to larger values, before nonlinearities and kinetic effects as discussed in the next section limit the growth. Comparison of Figures 1(b) and (j) shows that increasing the intensity mainly affects the SBS time scales and the reflectivity. In these regimes inflation and kinetic saturation for SRS are such that they are already significant at 
$I{\it\lambda}_{o}^{2}=3\times 10^{15}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$. A general conclusion is that the integrated energy losses due to SRS in all these simulations are rather small, 
${<}5\%$. The dominant energy losses have to be attributed to SBS, which operates on longer time scales.
4.2 Time evolution of the distribution functions
Figure 2 shows the two extreme cases encountered in Raman backscattering. At low temperature and high intensity a bulk heating takes place for the electrons (a). By contrast, taking initially a high temperature does not modify the bulk plasma temperature but leads to the clear formation of high-energy tails in the distribution functions (b).
Figure 2. Parallel electron distribution functions. (a) Case IV for the times: 
$t=0$ (black), 
$(0.5\times 10^{4}){\it\omega}_{o}^{-1}$ (red), 
$(1.1\times 10^{4}){\it\omega}_{o}^{-1}$ (blue) and 
$(2\times 10^{4}){\it\omega}_{o}^{-1}$ (green). (b) Case VII for the times: 
$t=0$ (black), 
$(0.5\times 10^{4}){\it\omega}_{o}^{-1}$ (blue) and 
$(1\times 10^{4}){\it\omega}_{o}^{-1}$ (red).
In general, the hot electrons constitute only a few percent of the thermal background but their energy can go up to several tens of keV. Knowledge of the high-energy tail and the corresponding maximum energy of the electrons due to the generating parametric instabilities is essential for evaluating the possible preheat of the compressed shell during the implosion phase[Reference Riconda, Weber, Tikhonchuk and Heron58, Reference Weber, Riconda, Klimo, Heron and Tikhonchuk59]. In Figure 2, the time scales are such that recirculation already sets in.
Figure 3. Reflectivity evolution showing the effect of ion mass and electron temperature 
$T_{e}$ variation. First row with ion mass 
$1836$ with 1 keV (a), 2 keV (b), 4 keV (c), 8 keV (d). These cases correspond to the following runs in Table 1: (a) – I, (b) – VII, (c) – II, and (d) – X. Second row with ion mass 
$10^{4}$ with 1 keV (e), 2 keV (f), 4 keV (g), 8 keV (h). Third row with ion mass 
$10^{5}$ with 1 keV (i), 2 keV (j), 4 keV (k), 8 keV (l). All the simulations used a plasma of 
$80~{\rm\mu}\text{m}$. The 6 keV cases (not shown here) as function of the three mass ratios show reflectivities on the same level as the 8 keV cases. For all cases 
$I{\it\lambda}^{2}=10^{15}~\text{W}/\text{cm}^{2}$. Note: scales are not the same.
5 High 
$k_{epw}{\it\lambda}_{D}$-regime
The main characteristic of Raman in this regime is its bursty nature, in agreement with previous results[Reference Vu, DuBois and Bezzerides64, Reference Brunner and Valeo65]. In general, the duration of the bursts are of the order of a 
$1000{\it\omega}_{o}^{-1}$. The burst duration therefore seems not to be given by 
${\it\gamma}_{o}^{-1}$, where 
${\it\gamma}_{o}=\min ({\it\gamma}_{o},{\it\gamma}_{o}^{2}/{\it\gamma}_{L})$ as this would be of the order of 
$67{\it\omega}_{o}^{-1}$. Going up in intensity by a factor 10 reduces considerably the pulse duration, much more than can be accounted for by the corresponding variation in 
${\it\gamma}_{o}$ (which is of the order of 3).
If the forward travelling hot electrons are removed from the system by assuming open boundary conditions on the right hand side (i.e., hot electrons going out of the box are replaced by Maxwellian electrons, as if the simulated plasma was in contact with a thermal plasma at the initial temperature), the Raman bursts continue at regular intervals. They are only limited by SBBS which eventually might deplete the pump and prevent further Raman activity. Analysis of the transverse electromagnetic field activity shows that SRBS is located in the front of the plasma over a length of the order 
$l_{R}\approx 200{-}300~c/{\it\omega}_{o}$. The hot tail of the order of 100 keV corresponds to an electron velocity of the order of 
$v_{e}\approx 0.4c$. It was said that the presence of this tail locally inhibits new Raman build-up. The time it takes in order to reestablish locally the original distribution function over the length 
$l_{R}$ would be given approximately by 
$l_{R}/v_{e}\approx 500{-}800~{\it\omega}_{o}^{-1}$, consistent with the simulation results.
By contrast, if the hot electrons are kept in the system, they progressively build up a modified distribution function everywhere in space. Associated to the modified distribution function a number of phenomena can coexist: kinetic inflation[Reference Vu, DuBois and Bezzerides15], nonlinear frequency shift[Reference Vu, DuBois and Bezzerides64, Reference Vu, DuBois and Bezzerides66, Reference Vu, Yin, DuBois, Bezzerides and Dodd67], sidebands and trapped particle instabilities[Reference Brunner and Valeo65, Reference Vu, Yin, DuBois, Bezzerides and Dodd67–Reference Hara, Chapman, Banks, Brunner, Joseph, Berger and Boyd69], the latter contributing to the SRS saturation. It could therefore be conjectured that in the case of multi-speckles SRS would be self-limiting due to the modification of the distribution function by formation of a hot tail, after a transient state where inflation sets in. As the hot tail presents an electron temperature of the order of 100 keV collisions would be unable to restore the original distribution function.
Figure 4. Electron distribution functions for the case VII. (a) Snapshots averaged over the whole plasma slab. (b) Time resolved for a plasma slice of width 
$68c/{\it\omega}_{o}$ located roughly in the middle of the plateau.
6 Limitations of PIC-simulations at very high electron temperature
Figure 3 shows the effect of ion mass for various electron temperatures on the reflectivity for the standard numerical setup. At an electron temperature of 1 keV increasing the mass ratio (Figures 3(a), (e), and (i)) results above all in diminishing and finally disappearing SBBS activity as is to be expected. Nevertheless, one does notice some variation in the SRBS activity as far as number and height of peaks are concerned. Some influence of the ion mobility via a changing electrostatic field affects the Raman reflectivity. Nevertheless, there is no strong competition present between Raman and Brillouin backscattering in this initial stage. Rather the two instabilities seem to exist in parallel, even if the Raman contribution is reduced as soon as SBS sets in. For the standard mass ratio (Figure 3(a)) SBBS develops on a very fast time scale to a reflectivity level of over 40%. Any Raman activity, about 10%, is simply swamped by Brillouin. Increasing the mass ratio (Figure 3(e)) shows Raman peaks superposed on the Brillouin reflectivity curve. The two reflectivities basically just add. For an even larger mass ratio (right panel, top row) no Brillouin develops for the duration of the simulation and the Raman peaks are clearly visible (Figure 3(i)). Increasing the electron temperature to 2 keV shows a changing scenario (Figures 3(b), (f) and (j)). The distribution of peaks is different. Also in the second half of the simulation there is SRBS for the highest mass ratio but not for the intermediate case. The mass ratio does not enter into the growth factor of SRBS and the onset of the Raman-related reflectivity should be the same whatever the ion mass. At 4 keV strong differences can be seen in the duration of Raman and above all in its onset (Figures 3(c), (g) and (k)). Increasing the mass ratio delays Raman activity and, in the case of the largest mass ratio, no SRBS was obtained for the duration of the whole simulation. Doubling again the electron temperature results in no SRBS whatever the mass ratio (Figures 3(d), (h) and (l)). However, even for these temperatures Raman can exist in its bursty nature if the gain were increased by taking a longer plasma. The dependence of SRS on the mass ratio can be understood as a numerical effect, since the strength of numerical collisions is sensitive to the mass ratio and the number of particles per computational cell. The sensitivity to numerical collisions is confirmed by increasing the number of particles per cell to 1000 (not shown here). On the one hand, one observes that by reducing the noise the reflectivity burst develop and last on a longer time scale, as expected, but also increase in amplitude. Consistently with Figure 3 it is found that if the noise is too large (as in the case with artificial mass ratio), SRS is quenched. On the other hand, if the numerical noise is strongly reduced by increasing the number of particle per cell, one can see that the dependence on electron to ion mass ratio, even if it still exists, is much weaker. This has to be taken into account when using nonrealistic mass ratios for high-temperature plasmas, and the convergence of the simulations has to be studied carefully for a given parameter range.
7 Moderate $k_{epw}{\it\lambda}_{D}$-regime
In the moderate regime 
$k_{pew,b}{\it\lambda}_{D}\sim 0.3$ kinetic effects are very important. This is illustrated in Figure 4 that shows the spatial and temporal evolution of the parallel electron distribution functions.
As can be seen in Figure 4 the electron distribution function averaged over the whole plasma slab is representative of the local distribution function. If one plots the distribution function at different locations, for several times that correspond roughly to first backward Raman burst, one notices that while at the very beginning of the box the modification is transient (as the electron travel with the plasma wave) everywhere else the distribution function is flattened around the wave phase velocity, and one expects inflation to set in. This is confirmed by the reflectivity as function of time for this case (see Figure 1(k)). In this figure one observes a first reflectivity burst of around 10%, followed by a stronger burst at roughly 50% at time 
$t=6000{\it\omega}_{o}^{-1}$, while competing effects as mentioned in the previous section lead to saturation and subsequent bursts.
Figure 5 shows the frequency spectra over the whole simulation time in vacuum of the backscattered and transmitted transverse electromagnetic wave. The same four frequencies are of course also present inside the plasma itself (not shown here). The backscattered electromagnetic wave at 
$0.658{\it\omega}_{o}$ (counter-propagating to the incident laser direction) undergoes forward Raman scattering, which produces a secondary electromagnetic wave at the frequency 
${\sim}0.34{\it\omega}_{o}$, co-propagating with the primary scattered electromagnetic wave (note that for the calculation of the plasmons in both cases the backward and forward 
$k{\it\lambda}_{D}$ correction of Table 1 needs to be taken into account). This is called rescatter in Figure 5[Reference Langdon and Hinkel70].
As we can see both backward and forward Raman signals are present. The differences in value for Stokes and anti-Stokes in RBS and RFS are due to the different values of the 
$k_{epw}{\it\lambda}_{D}$-correction (see Table 1).
Figure 5. Logarithm of the frequency spectra (case VII) for backscattered light (a) and transmitted light (b). (a) The peaks 1 (
$0.336{\it\omega}_{o}$), 2 (
$0.658{\it\omega}_{o}$), 3 (
$1.0{\it\omega}_{o}$) and 4 (
$1.378{\it\omega}_{o}$) correspond to rescatter, RBS-Stokes, laser and RBS-anti-Stokes, respectively. (b) The peaks 1 (
$0.332{\it\omega}_{o}$), 2 (
$0.682{\it\omega}_{o}$), 3 (
$1.0{\it\omega}_{o}$) and 4 (
$1.319{\it\omega}_{o}$) correspond to rescatter, RFS-Stokes, laser and RFS-anti-Stokes, respectively.
Figure 6. Logarithm of the 
$k$-spectrum of the transverse electric field at 
$t=(5.5\times 10^{3}){\it\omega}_{o}^{-1}$ (case VII) showing the principal decay as well as the secondary decay of the electromagnetic wave. The spectrum comprises the whole computational box, i.e., plasma, left vacuum and right vacuum. The peaks are located at: 
$0.11k_{o}$ (1), 
$0.34k_{o}$ (2), 
$0.59k_{o}$ (3), 
$0.67k_{o}$ (4), 
$0.95k_{o}$ (5), 
$1.0k_{o}$ (6), 
$1.32k_{o}$ (7) and 
$1.39k_{o}$ (8). Peaks 1, 3, 5 and 7 exist in the plasma only, peaks 2, 4, 6 and 8 are the corresponding 
$k$-vectors in the vacuum.
Figure 7. 
$k$-spectra of the electrons (a, b, c) and ions (d, e, f) for the mass ratios 
$m_{i}/m_{e}$: 
$1836$ (a, d, case XI), 
$10^{4}$ (b, e) and 
$10^{5}$ (for c and f the electron temperature has been reduced even further to 125 eV). Note: LDI related to ion modes is located around 
$k\approx 3$, SRS around 
$k\approx 1.5$, and SBS around 
$k\approx 2$.
Figure 6 gives the corresponding 
$k$-spectrum for the time after the most intense Raman burst is observed. The plasma 
$k$-vectors correspond to the vacuum frequencies of Figure 5 via the standard relationship 
${\it\omega}^{2}/{\it\omega}_{o}^{2}=n/n_{c}+k^{2}/k_{o}^{2}$, showing the presence of both backward and forward Raman at this time.
Figure 8. Electron (a, d) and ion (b, e) 
$k$-spectra for the case XI and the corresponding reflectivities (c, f). Upper row for an 
$80~{\rm\mu}\text{m}$ plasma, lower row for a 
$40~{\rm\mu}\text{m}$ plasma.
8 Low $k_{epw}{\it\lambda}_{D}$-regime
In this regime we expect Raman saturation to occur because of the LDI instability acting on the SRS created EPW. This is because EPWs are very weakly damped and can grow above threshold, and kinetic effects are not expected to be very important, so that saturation can be attributed to a fluid-type decay such as LDI (see Section 2.2). In order to assess the importance of this saturation mechanism a set of simulations was performed with very low temperature, 
$T_{e}=250~\text{eV}$. The first column in Figure 7 (Figure 7(a) and (d)), corresponds to the Fourier transform of the ion and electron density for a realistic mass ratio, case XI of Table 1. The BRS-signal appears clearly at early time in the electron density spectrum as expected, around 
$1.5k/k_{o}$. However, it rapidly disappears while many diffuse ion-acoustic quasi-neutral modes (present in both ion and electrons density spectra) between 
$2.2k/k_{o}$ and 
$3.5k/k_{o}$ appear, with companion electron modes with 
$k/k_{o}$ slight below the original EPW wavevector, and features that can be related to the LDI cascade and turbulence. These modes are weak, and quickly the density spectra show a large ion-acoustic mode generated by SBS, around 
$2k/k_{o}$. This mode grows to very large values and no SRS signal appears anymore. It therefore seems that SRS saturation is due mainly to pump depletion due to SBS growth, even if LDI is present early. Keeping the temperature and increasing the mass ratio to 
$10^{4}$ affects both the LDI instability and the SBS growth, so that only the most unstable LDI mode should be present, and the saturation by SBS reduced. This is what can be observed, as the LDI-activity around 
$k\approx 3k_{o}$ is clearer and the first burst of Raman saturation can be attributed to LDI (Figures 7(b) and (e), 
$t<5000{\it\omega}_{o}^{-1}$). However, as the ion waves are damped, a second burst appears that this time seems to be affected by both LDI-decay and SBS growth. Reducing the temperature by a factor 2 and increasing the mass ratio to 
$10^{5}$ gives finally an almost isolated LDI signal at the location of the most unstable mode 
$k\approx 3k_{o}$. This mode contributes to the saturation of the EPW, although satellites in the EPW remind of a possible saturation of the SRS generated EPW by modulational type instability[Reference Brunner and Valeo65, Reference Yin, Daughton, Albright, Bezzerides, DuBois, Kindel and Vu68, Reference Hara, Chapman, Banks, Brunner, Joseph, Berger and Boyd69]. In conclusion, even if LDI can be observed as a mechanism contributing to SRS saturation in the low temperature plasma regime, it appears to be in competition with SBS and other instabilities.
This claim is further substantiated by Figure 8, where one can see that there can be an effect of LDI created IAW on SBS saturation. Here two different plasma lengths are used: 80 and 
$40~{\rm\mu}\text{m}$, for the case XI in Table 1 (the lower row corresponds to the first column of Figure 7, for longer time and larger Fourier scale). Both reflectivity images show a drop in reflectivity near the end of the simulation. In both cases a decay of the SBS driven IAW in fractional harmonics of the primary wave[Reference Riconda, Hüller, Myatt and Pesme20, Reference Chapman, Winjum, Brunner, Berger and Banks24, Reference Cohen, Lasinski, Langdon and Williams71–Reference Albright, Yin, Bowers and Bergen79] takes place and induces SBS saturation. However, the decay modes are not the same for the two cases. For the long plasma the decay fills the 
$k$-space with a series of distinct modes especially strong between 
$k=0$ and 
$k\approx 2k_{o}$. In contrast, for the short plasma the decay creates mode structures between the primary IAW 
$k$-vector 
$k\approx 2k_{o}$ and the first harmonic 
$k\approx 4k_{o}$. A correlation can be made to a possible seeding of these modes from IAW appearing at early time due to the LDI instability. For the long plasma a very strong Raman reflectivity burst of 100% is produced, with generation of high amplitude EPWs. The decay of these waves produces a very broad signal in 
$k$-space with many modes at low amplitude, and electron kinetic effects contribute to the saturation. The late time ion-acoustic decay of the SBS induced primary wave in this case is not affected by the earlier history. In the case of the short plasma the Raman burst produces a signal of just 15% and the decay produces an LDI-decay closer to the standard type. These modes last quite a long time and impose themselves as a preferential decay channel for the SBS produced IAW, as shown in Figures 8(d) and (e).
However, the plasma length does not affect the level of the SBS-reflectivity which is in both cases of the order of 60%.
In Figure 9 the 
${\it\omega}{-}k$ diagram for the short (a) and long (b) plasma is shown. As discussed, one observes different spectra for the decay-produced IAWs in the two cases, that appear as a result of the Raman activity. In particular, one can see in the short case the presence of a mode at 
$k=2.6k_{o}$ located on the negative branch of the 
${\it\omega}{-}k$ diagram, probably resulting from the first LDI cascade. One can also observe that the slope of the 
${\it\omega}{-}k$ diagram is less steep the long plasma case, consistent with an increased value of the ion-acoustic velocity due to electron heating. SBS saturation is also partially related to ion and electron kinetic effects and their interplay with the IAW decay into fractional harmonics[Reference Riconda, Heron, Pesme, Hüller, Tikhonchuk and Detering74, Reference Riconda, Heron, Pesme, Hüller, Tikhonchuk and Detering75], and discussed in more detail in recent studies including 1D and 2D simulations[Reference Chapman, Winjum, Brunner, Berger and Banks24, Reference Chapman, Brunner, Banks, Berger, Cohen and Williams78–Reference Berger, Brunner, Chapman, Divol, Still and Valeo80]. In fact, there is no fundamental difference between the two cases when analysing the ion phase space. Wavebreaking takes place for both plasma lengths, the density fluctuations are the same and limit in both cases the reflectivity to 60%. The only difference is that for the long plasma SBS is excited in two regions each comprising half of the plasma and giving rise to two backscattered electromagnetic waves. As the two regions are not excited simultaneously the reflectivity does crash as much as for the short plasma as the second region is still emitting. As a final conclusion one can say that there is therefore no real difference for the two plasmas as far as SBBS is concerned. The final difference seen in the 
${\it\omega}{-}k$-diagrams is a result of the difference in the Raman activity, and related LDI that can be present in this low 
$k_{epw}{\it\lambda}_{D}$-regime. Depending on the strength of the signal two different decay channels are chosen by the IAW, located in distinct regions of 
$k$-space.
Figure 9. The ion 
${\it\omega}{-}k$ diagram for the case XI with a 
$40~{\rm\mu}\text{m}$ plasma (a) and an 
$80~{\rm\mu}\text{m}$ plasma (b).
Figure 10. 
$k$-spectra for electrons (a, c, e, g) and ions (b, d, f, h) for the cases IV (0.5 keV, 
$80~{\it\lambda}_{o}$) (a, b), Va (
$1.5~\text{keV}$, 
$40~{\it\lambda}_{o}$) (c, d), V (1.5 keV, 
$80~{\it\lambda}_{o}$) (e, f) and VI (4 keV, 
$80~{\it\lambda}_{o}$) (g, h).
9 High-intensity simulations
For high intensity and at the same time high electron temperatures of a few keV the decay scenarios change as forward Raman becomes prominent. Figure 10 shows the electron- and ion-spectra as function of the electron temperature for the intensity 
$I=10^{16}~\text{W}/\text{cm}^{2}$.
The appearance of FRS is a function of the electron temperature and the length of the plasma. At 
$T_{e}=0.5~\text{keV}$ only the backward Raman burst is visible in the electron spectrum. Similarly for the case using 
$T_{e}=1.5~\text{keV}$ with a short plasma. However, doubling the plasma length produces an FRS-signal, at 
$k/k_{o}\approx 0.3$, weak compared to the BRS-signal, and some LDI-decay of the EPW associated to the FRS is visible[Reference Batha, Bradley, Drake, Estabrook, Kruer, Montgomery and Remington81]. Going up in temperature to 
$T_{e}=4~\text{keV}$ flips over the relative importance of forward to backward Raman. FRS is much more pronounced than BRS and a very strong LDI signal associated to the EPW produced by FRS can be seen. This is because the EPW associated with BRS is strongly damped in the linear phase because of the large 
$k$-vector and high temperature. The EPW wave associated to FRS instead, having a small wavevector, can grow to large values above the threshold for Langmuir decay: the ion spectrum even shows the harmonic of the LDI produced IAW that is around 
$0.7k/k_{o}$.
Figure 11. Snapshots of the electron (red) and ion (blue) phase space for the run VI: 
$(0.1\times 10^{4}){\it\omega}_{o}^{-1}$ (a), 
$(0.15\times 10^{4}){\it\omega}_{o}^{-1}$ (b), 
$(0.2\times 10^{4}){\it\omega}_{o}^{-1}$ (c), 
$(0.25\times 10^{4}){\it\omega}_{o}^{-1}$ (d), 
$(0.3\times 10^{4}){\it\omega}_{o}^{-1}$ (e), 
$(0.35\times 10^{4}){\it\omega}_{o}^{-1}$ (f), 
$(0.4\times 10^{4}){\it\omega}_{o}^{-1}$ (g), 
$(0.6\times 10^{4}){\it\omega}_{o}^{-1}$ (h), 
$(1.0\times 10^{4}){\it\omega}_{o}^{-1}$ (i) and 
$(1.5\times 10^{4}){\it\omega}_{o}^{-1}$ (j). Note: the figures have partially varying scales for the y-axis. In the main text the designations front and rear part of the plasma refer to the regions around 
$x\approx 400$ and 
$x\approx 800$, respectively. The laser is coming from the left.
For none of the high-intensity cases is any LDI-activity on the backward Raman process visible.
The very complex time evolution of the phase space of electrons and ions for the extreme case VI is shown in a sequence of snapshots up to the time displayed in the spectra (Figure 10) in Figure 11. Forward and backward Raman scatterings appear at the same time[Reference Bertrand, Ghizzo, Karttunen, Pättikangas, Salomaa and Shoucri82]. Figure 11(b) shows that BRS is localized at the front of the plasma and FRS at the rear. Whereas the BRS-activity remains rather limited, the FRS grows strongly (Figure 11(c)). The amplitude of the phase space modulation is so strong that even the backward part of the distribution function gets modulated. In the subsequent snapshot, Figure 11(d), the highly energetic particles which were created due to FRS have disappeared as the energy has been dumped into smaller spatial modes. This correlates exactly with the onset of LDI at 
$t\approx 2500{\it\omega}_{o}^{-1}$ (see Figure 10). At the same time of course LDI becomes visible in the ion phase space. The LDI-activity is localized roughly in the last 
$30{-}40~{\rm\mu}\text{m}$ of the plasma slab. The LDI-activity displays a burst-like behaviour and survives for roughly 
$7500{\it\omega}_{o}^{-1}$ before it disappears. Figure 11(h) shows that the ionic LDI-activity is at its maximum while the electronic one has disappeared in a thermalized background. Some heating of the electron plasma has taken place. Together with the onset of forward LDI, but uncorrelated, backward Brillouin starts to grow followed quickly by its harmonics. Figure 11(h) shows the simultaneous presence of two clearly distinct regions of the ion phase, both taking up about half of the plasma slab. In the front part can be seen the modulation due to the forward travelling IAW and in the rear part the strong modulation due to forward LDI. Starting from 
$t\approx 10\,000{\it\omega}_{o}^{-1}$ onwards the harmonics are significantly reduced in amplitude and the 
$k$-space between the fundamental and the first harmonic is filled by distinct fractional harmonics of the IAW which leads to a decay of the regular structure of the trapping circles and contributes to the SBS saturation. Figure 12 gives a blow-up for the ion phase space clearly showing the decay of the IAW.
Figure 12. Blow-up of the ion phase space at times 
$(1.05\times 10^{4}){\it\omega}_{o}^{-1}$ (a) and 
$(1.5\times 10^{4}){\it\omega}_{o}^{-1}$ (b) for case VI.
10 Conclusions and outlook
The main findings of the reported simulations on Raman–Brillouin can be summarized as follows:
(1) The interplay between Raman and Brillouin backscattering is strongly dependent on the parameter space. The main effect in the considered parameter range is pump depletion because of large SBS backscattering. However, in the low
$k_{epw}{\it\lambda}_{D}$ regime the presence of IAW due to LDI from the SRS created EPWs can seed the ion-fractional decay and affect the SBS saturation.(2) Raman backscattering is present for all intensities and electron temperatures but is a transient phenomenon. Forward Raman scattering is only pronounced at intensities approaching
$I{\it\lambda}_{o}^{2}=10^{16}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$. Depending on the initial electron temperature Raman either induces a strong bulk heating or generates a hot electron tail. This strong modification of the distribution function, albeit small as far as the absolute number density of particles involved, is at the origin of terminating Raman. Raman backscattering is simply self-limiting. For the intensities considered here, above $I{\it\lambda}_{o}^{2}=10^{15}~\text{W}~{\rm\mu}\text{m}^{2}/\text{cm}^{2}$, the temporal behaviour of Raman is bursty. Depending on the plasma parameters and the boundary conditions employed a sequence of bursts appears which can go on for tens of picoseconds with a quasi-periodicity.(3) The Langmuir decay instability is observed for very small
$k_{epw}{\it\lambda}_{D}$, corresponding to electron temperatures of the order of 100–500 eV. Also it is very sensitive to the mass ratio $m_{i}/m_{e}$. However, LDI is not directly responsible for saturation of Brillouin backscattering. It is much easier to generate LDI for high laser intensities but in this case it would always be forward LDI. For large homogeneous plasmas backward LDI is of very little importance as decay process for backward Raman scattering.(4) Particular care has to be taken when describing SRS in PIC-simulations at temperatures above
${\sim}4~\text{keV}$, especially if unrealistic mass ratios are used for computational reasons.(5) It is thought that boundary conditions involving non-thermal recycling of hot electrons are partially representative for a multi-speckle plasma, and have to be considered in that context.
(6) There is no doubt that kinetic effects are of prime importance for an understanding of Raman and Brillouin backscattering. As the fusion plasmas envisaged for LMJ and NIF are very hot, several keV, they have to be taken into account.
Open questions concern the role of inhomogeneous plasma profiles, 2D effects, such as e.g., competition with filamentation[Reference Pesme, Hüller, Myatt, Riconda, Maximov, Tikhonchuk, Labaune, Fuchs, Depierreux and Baldis83] or effects due to finite wave packets[Reference Fahlen, Winjum, Grismayer and Rose84] and collisions. The Raman backscattering scenario investigated here should not be affected by dimensionality as the burst time is short compared to the transverse transit time of a speckle. Similarly collisions should have no effect for Raman as the characteristic electron–ion collision frequency for a 1 keV plasma at 
$0.1n_{c}$ is of the order of 
$3\times 10^{-2}~\text{ps}^{-1}$. Unless at very low intensities Raman develops on a long picosecond time scale instead of being bursty, collisions can safely be neglected. However, they are expected to be important for Brillouin[Reference Rambo, Wilks and Kruer85, Reference Cohen, Divol, Langdon and Williams86]. In reality the plasma is inhomogeneous. This strongly affects the Raman behaviour. For a linear plasma profile the interplay of local self-focusing and SRS might change the nature of the backscattering process as Raman could become absolute unstable in hot spots. Nevertheless, in the indirect-drive approach the RPP-laser does encounter large homogeneous plasmas of millimetre size and the simulations should be representative for these regions.
Acknowledgements
C.R. acknowledges support from grant ANR-11-IDEX-0004-02 Plas@Par. S.W. acknowledges support from the project ELI: Extreme Light Infrastructure (CZ.02.1.01/0.0/0.0/15-008/0000162) from European Regional Development.
Open access
