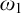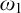Given an ideal
![]() $\mathcal {I}$
on a cardinal
$\mathcal {I}$
on a cardinal
![]() $\kappa $
, let
$\kappa $
, let
![]() $\mathbb {P}_{\mathcal {I}}={\wp }(\kappa )/\mathcal {I}$
. Forcing with
$\mathbb {P}_{\mathcal {I}}={\wp }(\kappa )/\mathcal {I}$
. Forcing with
![]() $\mathbb {P}_{\mathcal {I}}$
adds a V-ultrafilter on
$\mathbb {P}_{\mathcal {I}}$
adds a V-ultrafilter on
![]() $\kappa $
. An ideal
$\kappa $
. An ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\kappa $
is called precipitous if whenever
$\kappa $
is called precipitous if whenever
![]() $G\subseteq {\wp }(\kappa )$
is a
$G\subseteq {\wp }(\kappa )$
is a
![]() $\mathbb {P}_{\mathcal {I}}$
-generic ultrafilter,
$\mathbb {P}_{\mathcal {I}}$
-generic ultrafilter,
![]() $Ult(V, G)$
is well-founded.
$Ult(V, G)$
is well-founded.
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\lambda $
-complete if for any
$\lambda $
-complete if for any
![]() $\gamma <\lambda $
and
$\gamma <\lambda $
and
![]() $(A_\alpha : \alpha <\gamma )\subseteq \mathcal {I}$
,
$(A_\alpha : \alpha <\gamma )\subseteq \mathcal {I}$
,
![]() $\cup _{\alpha <\gamma } A_\alpha \in \mathcal {I}$
. If
$\cup _{\alpha <\gamma } A_\alpha \in \mathcal {I}$
. If
![]() $\mathcal {I}$
is a
$\mathcal {I}$
is a
![]() $\lambda $
-complete precipitous ideal on
$\lambda $
-complete precipitous ideal on
![]() $\kappa $
then the generic embedding,
$\kappa $
then the generic embedding,
![]() $j: V\rightarrow Ult(V, G)$
, produced by
$j: V\rightarrow Ult(V, G)$
, produced by
![]() $\mathcal {I}$
has a critical point
$\mathcal {I}$
has a critical point
![]() $\geq \lambda $
.
$\geq \lambda $
.
It is mentioned in [Reference Foreman, Magidor and Shelah2] that Jech asked whether supercompact cardinals imply that the non-stationary ideal on some cardinal
![]() $\kappa $
is precipitous. Theorem 33 of [Reference Foreman, Magidor and Shelah2] shows that this is not the case, as any normal precipitous ideal can be destroyed in a forcing extension. However, the following question remained open.
$\kappa $
is precipitous. Theorem 33 of [Reference Foreman, Magidor and Shelah2] shows that this is not the case, as any normal precipitous ideal can be destroyed in a forcing extension. However, the following question remained open.
Question 0.1. Do large cardinals imply that there exists a precipitous ideal on
![]() $\omega _1$
or on other regular cardinals?
$\omega _1$
or on other regular cardinals?
It is in fact not hard to show that sufficiently nice extender models do not carry precipitous ideals on
![]() $\omega _1$
. Theorem 0.2 was independently discovered by many inner model theorists. The proof generalizes to obtain stronger results on non-existence of precipitous ideals. To the author’s best knowledge, these results are unpublished and not due to the author. Because of this we will not dwell on them and will just give the prototypical argument.
$\omega _1$
. Theorem 0.2 was independently discovered by many inner model theorists. The proof generalizes to obtain stronger results on non-existence of precipitous ideals. To the author’s best knowledge, these results are unpublished and not due to the author. Because of this we will not dwell on them and will just give the prototypical argument.
Theorem 0.2. Suppose
![]() ${\mathcal {W} }$
is a countable
${\mathcal {W} }$
is a countable
![]() $\omega _1+1$
-iterable mouse and
$\omega _1+1$
-iterable mouse and
![]() $\kappa $
is a successor cardinal of
$\kappa $
is a successor cardinal of
![]() ${\mathcal {W} }$
such that
${\mathcal {W} }$
such that
![]() ${\mathcal {W} }\vDash$
“
${\mathcal {W} }\vDash$
“
![]() $\kappa ^{+2}$
exists” and there is
$\kappa ^{+2}$
exists” and there is
![]() $E\in \vec {E}^{\mathcal {W} }$
such that
$E\in \vec {E}^{\mathcal {W} }$
such that
![]() $\mathrm {crit }(E)>(\kappa ^{++})^{\mathcal {W} }$
. Then
$\mathrm {crit }(E)>(\kappa ^{++})^{\mathcal {W} }$
. Then
![]() ${\mathcal {W} }\vDash$
“
${\mathcal {W} }\vDash$
“
![]() $\kappa $
doesn’t carry a
$\kappa $
doesn’t carry a
![]() $\kappa $
-complete precipitous ideal.”
$\kappa $
-complete precipitous ideal.”
Proof Let
![]() $\phi $
be the following sentence (in the language of premice,
$\phi $
be the following sentence (in the language of premice,
![]() $\vec {E}$
is used for the extender sequence): there exists
$\vec {E}$
is used for the extender sequence): there exists
![]() $\nu $
such that:
$\nu $
such that:
-
1.
 $\nu $
is a successor cardinal,
$\nu $
is a successor cardinal, -
2.
 $\nu ^{++}$
exists,
$\nu ^{++}$
exists, -
3. there is an extender
 $E\in \vec {E}$
with
$E\in \vec {E}$
with
 $\mathrm {crit }(E)>\nu ^{++}$
,
$\mathrm {crit }(E)>\nu ^{++}$
, -
4. there is a
 $\nu $
-complete precipitious ideal on
$\nu $
-complete precipitious ideal on
 $\nu $
.
$\nu $
.
Towards a contradiction assume that in
![]() ${\mathcal {W} }$
,
${\mathcal {W} }$
,
![]() $\mathcal {I}$
is a
$\mathcal {I}$
is a
![]() $\kappa $
-complete precipitous ideal on
$\kappa $
-complete precipitous ideal on
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $E\in \vec {E}^{\mathcal {W} }$
be the least such that
$E\in \vec {E}^{\mathcal {W} }$
be the least such that
![]() $\mathrm {crit }(E)>(\kappa ^{++})^{\mathcal {W} }$
and let
$\mathrm {crit }(E)>(\kappa ^{++})^{\mathcal {W} }$
and let
![]() $\beta =index^{\mathcal {W} }(E)$
. Then
$\beta =index^{\mathcal {W} }(E)$
. Then
![]() $\mathcal {I}\in {\mathcal {W} }||\beta $
. It follows that without loss of generality we can assume that
$\mathcal {I}\in {\mathcal {W} }||\beta $
. It follows that without loss of generality we can assume that
![]() ${\mathcal {W} }={\mathcal {W} }||\beta $
,
${\mathcal {W} }={\mathcal {W} }||\beta $
,
![]() ${\mathcal {W} }$
is sound and
${\mathcal {W} }$
is sound and
![]() $\rho _\omega ({\mathcal {W} })=\omega $
and if
$\rho _\omega ({\mathcal {W} })=\omega $
and if
![]() ${\mathcal {W} }'\triangleleft {\mathcal {W} }$
then
${\mathcal {W} }'\triangleleft {\mathcal {W} }$
then
![]() ${\mathcal {W} }'\vDash \neg \phi $
.
${\mathcal {W} }'\vDash \neg \phi $
.
Let
![]() $j: {\mathcal {W} }\rightarrow {\mathcal {N}}\subseteq {\mathcal {W} }[g]$
be a generic embedding given by
$j: {\mathcal {W} }\rightarrow {\mathcal {N}}\subseteq {\mathcal {W} }[g]$
be a generic embedding given by
![]() $\mathcal {I}$
. Set
$\mathcal {I}$
. Set
![]() $\lambda =(\kappa ^{++})^{\mathcal {W} }$
and let
$\lambda =(\kappa ^{++})^{\mathcal {W} }$
and let
![]() $\eta $
be the predecessor of
$\eta $
be the predecessor of
![]() $\kappa $
. We have that:
$\kappa $
. We have that:
(1)
![]() $\lambda $
is a cardinal of
$\lambda $
is a cardinal of
![]() ${\mathcal {W} }[g]$
as
${\mathcal {W} }[g]$
as
![]() $\left |{\wp }(\kappa )\right |{}^{\mathcal {W} }=(\kappa ^{+})^{\mathcal {W} }$
.
$\left |{\wp }(\kappa )\right |{}^{\mathcal {W} }=(\kappa ^{+})^{\mathcal {W} }$
.
(2)
![]() $j(\lambda )=\lambda $
and
$j(\lambda )=\lambda $
and
![]() $j(\kappa )=(\eta ^+)^{\mathcal {N}}$
.
$j(\kappa )=(\eta ^+)^{\mathcal {N}}$
.
(3)
![]() ${\mathcal {W} }|\lambda \not \trianglelefteq j({\mathcal {W} }|\lambda )$
.
${\mathcal {W} }|\lambda \not \trianglelefteq j({\mathcal {W} }|\lambda )$
.
Notice that in V there is a real x that codes a premouse
![]() ${\mathcal { Q}}$
and an elementary embedding
${\mathcal { Q}}$
and an elementary embedding
![]() $\pi : {\mathcal { Q}}\rightarrow j({\mathcal {W} }|\lambda )$
such that:
$\pi : {\mathcal { Q}}\rightarrow j({\mathcal {W} }|\lambda )$
such that:
-
1.
 ${\mathcal {W} }|\eta \trianglelefteq {\mathcal { Q}}$
,
${\mathcal {W} }|\eta \trianglelefteq {\mathcal { Q}}$
, -
2.
 $\pi \restriction (\eta +1)=id$
,
$\pi \restriction (\eta +1)=id$
, -
3.
 ${\mathcal { Q}}\not \trianglelefteq j({\mathcal {W} }|\lambda )$
,
${\mathcal { Q}}\not \trianglelefteq j({\mathcal {W} }|\lambda )$
, -
4.
 $\pi (\lambda )=\lambda $
.
$\pi (\lambda )=\lambda $
.
Take for instance a real that codes
![]() $({\mathcal {W} }|\lambda , j\restriction {\mathcal {W} }|\lambda )$
. It follows by absoluteness that there is such a real in
$({\mathcal {W} }|\lambda , j\restriction {\mathcal {W} }|\lambda )$
. It follows by absoluteness that there is such a real in
![]() ${\mathcal {N}}^{Coll(\omega , j(\lambda ))}$
.
${\mathcal {N}}^{Coll(\omega , j(\lambda ))}$
.
Let
![]() $h\subseteq Coll(\omega , \lambda )$
be
$h\subseteq Coll(\omega , \lambda )$
be
![]() ${\mathcal {W} }$
-generic. It follows from elementarity that there is a pair
${\mathcal {W} }$
-generic. It follows from elementarity that there is a pair
![]() $({\mathcal R}, \sigma )\in {\mathcal {W} }[h]$
such that:
$({\mathcal R}, \sigma )\in {\mathcal {W} }[h]$
such that:
-
1.
 ${\mathcal {W} }|\eta \trianglelefteq {\mathcal R}$
,
${\mathcal {W} }|\eta \trianglelefteq {\mathcal R}$
, -
2.
 $\sigma :{\mathcal R}\rightarrow {\mathcal {W} }|\lambda $
is elementary,
$\sigma :{\mathcal R}\rightarrow {\mathcal {W} }|\lambda $
is elementary, -
3.
 $\sigma \restriction (\eta +1)=id$
,
$\sigma \restriction (\eta +1)=id$
, -
4.
 ${\mathcal R}\not ={\mathcal {W} }|\lambda $
, and
${\mathcal R}\not ={\mathcal {W} }|\lambda $
, and -
5.
 $\sigma (\lambda )=\lambda $
.
$\sigma (\lambda )=\lambda $
.
Because
![]() ${\mathcal {W} }$
is
${\mathcal {W} }$
is
![]() $\omega _1+1$
-iterable, it follows that the phalanx
$\omega _1+1$
-iterable, it follows that the phalanx
![]() $({\mathcal {W} }, {\mathcal R}, \eta +1)$
is
$({\mathcal {W} }, {\mathcal R}, \eta +1)$
is
![]() $\omega _1+1$
-iterable. We then compare
$\omega _1+1$
-iterable. We then compare
![]() ${\mathcal {W} }$
with
${\mathcal {W} }$
with
![]() $({\mathcal {W} }, {\mathcal R}, \eta +1)$
. Let
$({\mathcal {W} }, {\mathcal R}, \eta +1)$
. Let
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
be the iteration trees on
${\mathcal {U}}$
be the iteration trees on
![]() ${\mathcal {W} }$
and
${\mathcal {W} }$
and
![]() $({\mathcal {W} }, {\mathcal R}, \eta +1)$
that this comparison process produces. Because
$({\mathcal {W} }, {\mathcal R}, \eta +1)$
that this comparison process produces. Because
![]() $\rho _\omega ({\mathcal {W} })=\omega $
and
$\rho _\omega ({\mathcal {W} })=\omega $
and
![]() ${\mathcal {W} }$
is sound, the last model of
${\mathcal {W} }$
is sound, the last model of
![]() ${\mathcal {U}}$
is on the top of
${\mathcal {U}}$
is on the top of
![]() ${\mathcal R}$
. Let
${\mathcal R}$
. Let
![]() ${\mathcal R}'$
be the last model of
${\mathcal R}'$
be the last model of
![]() ${\mathcal {U}}$
and
${\mathcal {U}}$
and
![]() ${\mathcal {W} }'$
be the last model of
${\mathcal {W} }'$
be the last model of
![]() ${\mathcal {T}}$
.
${\mathcal {T}}$
.
Because
![]() $\sigma : {\mathcal R}\rightarrow {\mathcal {W} }|\lambda $
is elementary, it follows that
$\sigma : {\mathcal R}\rightarrow {\mathcal {W} }|\lambda $
is elementary, it follows that
![]() $(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
$(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
![]() ${\mathcal R}$
. We now want to argue that
${\mathcal R}$
. We now want to argue that
![]() ${\mathcal R}'={\mathcal R}$
. Assume not. Let E be the first extender of
${\mathcal R}'={\mathcal R}$
. Assume not. Let E be the first extender of
![]() ${\mathcal {U}}$
that is used on the
${\mathcal {U}}$
that is used on the
![]() ${\mathcal R}$
-to-
${\mathcal R}$
-to-
![]() ${\mathcal R}'$
branch. Then because
${\mathcal R}'$
branch. Then because
![]() $\mathrm {crit }(E)>\eta $
, we must have that there is a drop on the
$\mathrm {crit }(E)>\eta $
, we must have that there is a drop on the
![]() ${\mathcal R}$
-to-
${\mathcal R}$
-to-
![]() ${\mathcal R}'$
branch of
${\mathcal R}'$
branch of
![]() ${\mathcal {U}}$
, and hence
${\mathcal {U}}$
, and hence
![]() ${\mathcal R}'$
is not sound. It follows that we must have that
${\mathcal R}'$
is not sound. It follows that we must have that
![]() ${\mathcal {W} }'={\mathcal {W} }$
and
${\mathcal {W} }'={\mathcal {W} }$
and
![]() ${\mathcal {W} }\trianglelefteq {\mathcal R}'$
implying that
${\mathcal {W} }\trianglelefteq {\mathcal R}'$
implying that
![]() ${\mathcal {W} }\trianglelefteq {\mathcal R}$
. But then
${\mathcal {W} }\trianglelefteq {\mathcal R}$
. But then
![]() $\sigma ({\mathcal {W} })\triangleleft {\mathcal {W} }$
contradicting the minimality of
$\sigma ({\mathcal {W} })\triangleleft {\mathcal {W} }$
contradicting the minimality of
![]() ${\mathcal {W} }$
.
${\mathcal {W} }$
.
We thus have that
![]() ${\mathcal R}'={\mathcal R}$
and
${\mathcal R}'={\mathcal R}$
and
![]() ${\mathcal R}\trianglelefteq {\mathcal {W} }'$
. We now want to argue that
${\mathcal R}\trianglelefteq {\mathcal {W} }'$
. We now want to argue that
![]() ${\mathcal R}\trianglelefteq {\mathcal {W} }$
. Assume that this is false. Let
${\mathcal R}\trianglelefteq {\mathcal {W} }$
. Assume that this is false. Let
![]() $F=E_0^{\mathcal {T}}$
and let
$F=E_0^{\mathcal {T}}$
and let
![]() $\beta =index^{{\mathcal {W} }}(F)$
. It follows that:
$\beta =index^{{\mathcal {W} }}(F)$
. It follows that:
(4)
![]() $\beta \geq (\eta ^+)^{\mathcal R}$
Footnote
1
and
$\beta \geq (\eta ^+)^{\mathcal R}$
Footnote
1
and
![]() $\beta <Ord\cap {\mathcal R}=\lambda $
,
$\beta <Ord\cap {\mathcal R}=\lambda $
,
(5)
![]() $\beta $
is a cardinal of
$\beta $
is a cardinal of
![]() ${\mathcal {W} }'$
,
${\mathcal {W} }'$
,
(6)
![]() ${\mathcal {W} }'|\beta ={\mathcal {W} }|\beta $
, and
${\mathcal {W} }'|\beta ={\mathcal {W} }|\beta $
, and
(7)
![]() $\beta \leq (\eta ^{++})^{\mathcal R}$
.
$\beta \leq (\eta ^{++})^{\mathcal R}$
.
(7) is a consequence of (4), (5), and (6). Thus, it follows from (6) that we have two possibilities: either
![]() $\beta =(\eta ^{+})^{\mathcal R}$
or
$\beta =(\eta ^{+})^{\mathcal R}$
or
![]() $\beta =(\eta ^{++})^{\mathcal R}$
.
$\beta =(\eta ^{++})^{\mathcal R}$
.
Suppose now that
![]() $\beta =(\eta ^{++})^{\mathcal R}$
and set
$\beta =(\eta ^{++})^{\mathcal R}$
and set
![]() $\nu =(\eta ^{+++})^{Ult({\mathcal {W} }, F)}$
. Since
$\nu =(\eta ^{+++})^{Ult({\mathcal {W} }, F)}$
. Since
![]() $\beta <\lambda $
, we have that
$\beta <\lambda $
, we have that
![]() $\nu <\lambda $
. Since
$\nu <\lambda $
. Since
![]() $\nu '=_{def}(\eta ^{+++})^{{\mathcal {W} }'}\leq \nu $
Footnote
2
and
$\nu '=_{def}(\eta ^{+++})^{{\mathcal {W} }'}\leq \nu $
Footnote
2
and
![]() $(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
$(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
![]() ${\mathcal R}$
, we have that
${\mathcal R}$
, we have that
![]() ${\mathcal R}\trianglelefteq {\mathcal {W} }'|\nu '$
. Thus,
${\mathcal R}\trianglelefteq {\mathcal {W} }'|\nu '$
. Thus,
![]() $\lambda \leq \nu '\leq \nu <\lambda $
, contradiction.
$\lambda \leq \nu '\leq \nu <\lambda $
, contradiction.
Assume then that
![]() $\beta =(\eta ^+)^{\mathcal R}$
. Notice that
$\beta =(\eta ^+)^{\mathcal R}$
. Notice that
![]() ${\mathcal R}$
cannot be an initial segment of
${\mathcal R}$
cannot be an initial segment of
![]() $Ult({\mathcal {W} }, F)|\lambda $
because
$Ult({\mathcal {W} }, F)|\lambda $
because
![]() $\pi _F(\mathrm {crit }(F))\in (\eta , \lambda )$
is an inaccessible cardinal of
$\pi _F(\mathrm {crit }(F))\in (\eta , \lambda )$
is an inaccessible cardinal of
![]() $Ult({\mathcal {W} }, F)|\lambda $
whereas
$Ult({\mathcal {W} }, F)|\lambda $
whereas
![]() $(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
$(\eta ^{++})^{\mathcal R}$
is the largest cardinal of
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() $\lambda \subseteq {\mathcal R}$
. Thus,
$\lambda \subseteq {\mathcal R}$
. Thus,
![]() $G=_{def}E_1^{\mathcal {T}}$
is defined and if
$G=_{def}E_1^{\mathcal {T}}$
is defined and if
![]() $\gamma $
is the index of G in
$\gamma $
is the index of G in
![]() ${\mathcal {M}}_1^{\mathcal {T}}$
then
${\mathcal {M}}_1^{\mathcal {T}}$
then
-
(8)
 ${\mathcal R}|(\eta ^{++})^{\mathcal R}\trianglelefteq {\mathcal {M}}_1^{\mathcal {T}}|\gamma $
(notice that
${\mathcal R}|(\eta ^{++})^{\mathcal R}\trianglelefteq {\mathcal {M}}_1^{\mathcal {T}}|\gamma $
(notice that
 ${\mathcal {M}}_1^{\mathcal {T}}|\gamma ={\mathcal {W} }'|\gamma $
and
${\mathcal {M}}_1^{\mathcal {T}}|\gamma ={\mathcal {W} }'|\gamma $
and
 $\gamma $
is a cardinal of
$\gamma $
is a cardinal of
 ${\mathcal {W} }'$
).
${\mathcal {W} }'$
). -
(8) now implies that
 ${\mathcal R}\trianglelefteq {\mathcal {M}}_2^{\mathcal {T}}|(\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}$
, and therefore,
${\mathcal R}\trianglelefteq {\mathcal {M}}_2^{\mathcal {T}}|(\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}$
, and therefore,
 $\lambda \leq (\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}$
. However, as it was the case with
$\lambda \leq (\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}$
. However, as it was the case with
 $\beta $
,
$\beta $
,
 $\gamma <\lambda $
implying that
$\gamma <\lambda $
implying that
 $(\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}<\lambda $
.
$(\eta ^{+++})^{{\mathcal {M}}_2^{\mathcal {T}}}<\lambda $
.
We thus have shown that
![]() ${\mathcal {W} }'={\mathcal {W} }$
and that consequently,
${\mathcal {W} }'={\mathcal {W} }$
and that consequently,
![]() ${\mathcal R}\trianglelefteq {\mathcal {W} }$
. Therefore,
${\mathcal R}\trianglelefteq {\mathcal {W} }$
. Therefore,
![]() ${\mathcal R}={\mathcal {W} }|\lambda $
contradicting the fact that
${\mathcal R}={\mathcal {W} }|\lambda $
contradicting the fact that
![]() ${\mathcal R}\not ={\mathcal {W} }|\lambda $
.
${\mathcal R}\not ={\mathcal {W} }|\lambda $
.
Woodin showed that strong condensation, an axiom that he formulated, implies the non-existence of precipitous ideals on
![]() $\omega _1$
and cardinals below the least inaccessible cardinal. The proof is very similar to the one we gave above (see [Reference Woodin22, Definition 8.5] and [Reference Woodin22, Corollary 8.9]). The authors of [Reference Schimmerling and Velickovic10] say that Steel showed that in some extender models,
$\omega _1$
and cardinals below the least inaccessible cardinal. The proof is very similar to the one we gave above (see [Reference Woodin22, Definition 8.5] and [Reference Woodin22, Corollary 8.9]). The authors of [Reference Schimmerling and Velickovic10] say that Steel showed that in some extender models,
![]() $\kappa $
carries a precipitous ideal if and only if it is measurable. The authors of [Reference Schimmerling and Velickovic10] showed that in the minimal extender model with Woodin cardinal that is itself a limit of Woodin cardinals
$\kappa $
carries a precipitous ideal if and only if it is measurable. The authors of [Reference Schimmerling and Velickovic10] showed that in the minimal extender model with Woodin cardinal that is itself a limit of Woodin cardinals
![]() $\omega _1$
does not carry precipitous ideal (see [Reference Schimmerling and Velickovic10, Corollary 4]). The authors of [Reference Claverie and Schindler1] showed that if the extender model is a model of
$\omega _1$
does not carry precipitous ideal (see [Reference Schimmerling and Velickovic10, Corollary 4]). The authors of [Reference Claverie and Schindler1] showed that if the extender model is a model of
![]() $V=K$
then
$V=K$
then
![]() $\kappa $
carries a precipitous ideal if and only if it is a measurable cardinal (see [Reference Claverie and Schindler1, Theorem 0.3]).
$\kappa $
carries a precipitous ideal if and only if it is a measurable cardinal (see [Reference Claverie and Schindler1, Theorem 0.3]).
The proof of our main theorem, Theorem 0.5, uses a different type of argument that is not based on condensation. It is not clear to us how to prove Theorem 0.5 via condensation-like arguments or arguments based on the core model.
It is a well-known result of Woodin that if there is a Woodin cardinal
![]() $\delta $
then letting
$\delta $
then letting
![]() $\mathbb {Q}_\delta $
be the countable stationary tower forcing associated with
$\mathbb {Q}_\delta $
be the countable stationary tower forcing associated with
![]() $\delta $
(see [Reference Larson3]), there is
$\delta $
(see [Reference Larson3]), there is
![]() $G\subseteq \mathbb {Q}_\delta $
and an embedding
$G\subseteq \mathbb {Q}_\delta $
and an embedding
![]() $j: V\rightarrow M \subseteq V[G]$
definable in
$j: V\rightarrow M \subseteq V[G]$
definable in
![]() $V[G]$
such that:
$V[G]$
such that:
-
1.
 $\mathrm {crit }(j)=\omega _1$
and
$\mathrm {crit }(j)=\omega _1$
and -
2.
 $V[G]\vDash M^\omega \subseteq M$
.
$V[G]\vDash M^\omega \subseteq M$
.
The question on the existence of precipitous ideals on
![]() $\omega _1$
can be interpreted in at least two ways. One, of course, is the most direct interpretation. However, it can also be perceived as a question on the existence of generic embeddings that resemble the stationary tower embedding but are produced via small forcing, smaller than the size of the least Woodin cardinal.
$\omega _1$
can be interpreted in at least two ways. One, of course, is the most direct interpretation. However, it can also be perceived as a question on the existence of generic embeddings that resemble the stationary tower embedding but are produced via small forcing, smaller than the size of the least Woodin cardinal.
In this paper, we investigate this interpretation of the question.
Definition 0.3. Suppose
![]() $\delta $
is a Woodin cardinal which is not a limit of Woodin cardinals. Let
$\delta $
is a Woodin cardinal which is not a limit of Woodin cardinals. Let
![]() $\mu $
be the supremum of Woodin cardinals
$\mu $
be the supremum of Woodin cardinals
![]() $<\delta $
. We say there is a stationary-tower-like embedding (st-like-embedding) below
$<\delta $
. We say there is a stationary-tower-like embedding (st-like-embedding) below
![]() $\delta $
if there is a partial ordering
$\delta $
if there is a partial ordering
![]() $\mathbb {P}$
such that whenever
$\mathbb {P}$
such that whenever
![]() $g\subseteq \mathbb {P}$
is generic,
$g\subseteq \mathbb {P}$
is generic,
-
1.
 $\mu < \left |\mathbb {P}\right |<\delta $
,
$\mu < \left |\mathbb {P}\right |<\delta $
, -
2.
 $(\mu ^+)^V<\omega _1^{V[g]}$
,
$(\mu ^+)^V<\omega _1^{V[g]}$
, -
3. in
 $V[g]$
, there is an elementary embedding
$V[g]$
, there is an elementary embedding
 $j: V\rightarrow M\subseteq V[g]$
with the property that
$j: V\rightarrow M\subseteq V[g]$
with the property that
 $\mathrm {crit }(j)=\omega _1$
,
$\mathrm {crit }(j)=\omega _1$
,
 $\mathbb {R}^{V[g]}\subseteq M$
and for some regular cardinal
$\mathbb {R}^{V[g]}\subseteq M$
and for some regular cardinal
 $\nu <\delta $
,
$\nu <\delta $
,  $$ \begin{align*} M=\{ j(f)(s): s\in [\nu]^{<\omega}, f: [\nu]^{\left|s\right|}\rightarrow V \mbox{ and } f\in V\}.^{3} \end{align*} $$
$$ \begin{align*} M=\{ j(f)(s): s\in [\nu]^{<\omega}, f: [\nu]^{\left|s\right|}\rightarrow V \mbox{ and } f\in V\}.^{3} \end{align*} $$
The last portion of clause 3 above implies that
![]() $M=Ult(V, E)$
where
$M=Ult(V, E)$
where
It is worth noting that E may not be a short extender, and in the case of the countable stationary tower, it is not a short extender. If
![]() $\mathbb {Q}_{<\delta }$
is the countable stationary tower at
$\mathbb {Q}_{<\delta }$
is the countable stationary tower at
![]() $\delta $
and
$\delta $
and
![]() $j: V\rightarrow M$
is a generic ultrapower by some generic
$j: V\rightarrow M$
is a generic ultrapower by some generic
![]() $G\subseteq \mathbb {Q}_{<\delta }$
then setting
$G\subseteq \mathbb {Q}_{<\delta }$
then setting
![]() $\nu =\delta ^{+}$
, if E is the
$\nu =\delta ^{+}$
, if E is the
![]() $(\nu , \nu )$
extender derived from j, we have that
$(\nu , \nu )$
extender derived from j, we have that
![]() $Ult(V, E)$
and M agree on subsets of
$Ult(V, E)$
and M agree on subsets of
![]() $j(\delta )$
.Footnote
4
$j(\delta )$
.Footnote
4
The main question we deal with in this paper is the following.
Question 0.4. Assume there is a Woodin cardinal
![]() $\delta $
. Is there an st-like-embedding below
$\delta $
. Is there an st-like-embedding below
![]() $\delta $
?
$\delta $
?
The following is the main theorem of this paper.
Theorem 0.5. Let
![]() ${\mathcal {M}}$
be the minimal mouse with a Woodin cardinal that is a limit of Woodin cardinals. Let
${\mathcal {M}}$
be the minimal mouse with a Woodin cardinal that is a limit of Woodin cardinals. Let
![]() $\delta $
be the second Woodin cardinal of
$\delta $
be the second Woodin cardinal of
![]() ${\mathcal {M}}$
. Then there is no st-like-embedding below
${\mathcal {M}}$
. Then there is no st-like-embedding below
![]() $\delta $
.
$\delta $
.
We will need the following proposition.
Proposition 0.6. Suppose
![]() $\delta $
is a Woodin cardinal which is not a limit of Woodin cardinals, and let
$\delta $
is a Woodin cardinal which is not a limit of Woodin cardinals, and let
![]() $\mu $
be the supremum of the Woodin cardinals
$\mu $
be the supremum of the Woodin cardinals
![]() $<\delta $
. Let
$<\delta $
. Let
![]() $\kappa <\delta $
be the least
$\kappa <\delta $
be the least
![]() $<\delta $
-strong cardinal and let
$<\delta $
-strong cardinal and let
![]() $\xi $
be the least such that there is a poset
$\xi $
be the least such that there is a poset
![]() $\mathbb {P}\in V_\xi $
witnessing that there is an st-like-embedding below
$\mathbb {P}\in V_\xi $
witnessing that there is an st-like-embedding below
![]() $\delta $
. Then
$\delta $
. Then
![]() $\xi <\kappa $
.
$\xi <\kappa $
.
Proof Let
![]() $g\subseteq \mathbb {P}$
be generic and let
$g\subseteq \mathbb {P}$
be generic and let
![]() $j: V\rightarrow M$
be the st-like embedding in
$j: V\rightarrow M$
be the st-like embedding in
![]() $V[g]$
. Let
$V[g]$
. Let
![]() $\nu _0<\delta $
be such that
$\nu _0<\delta $
be such that
Let
![]() $\nu \in (\max (\nu _0, \xi ), \delta )$
be an inaccessible cardinal and let E be the
$\nu \in (\max (\nu _0, \xi ), \delta )$
be an inaccessible cardinal and let E be the
![]() $(\nu _0, \nu _0)$
-extender derived from j. More precisely,
$(\nu _0, \nu _0)$
-extender derived from j. More precisely,
Let F be an extender with critical point
![]() $\kappa $
witnessing that
$\kappa $
witnessing that
![]() $\kappa $
is
$\kappa $
is
![]() $\nu $
strong. Set
$\nu $
strong. Set
![]() $W=Ult(V, F)$
. We write
$W=Ult(V, F)$
. We write
![]() $W_\alpha $
for
$W_\alpha $
for
![]() $V_\alpha ^W$
. It follows that
$V_\alpha ^W$
. It follows that
![]() $E\in W[g]$
and because
$E\in W[g]$
and because
![]() $Ult(V, E)$
is well-founded,
$Ult(V, E)$
is well-founded,
![]() $Ult(W, E)$
is also well-founded.
$Ult(W, E)$
is also well-founded.
It is now not hard to verify that
![]() $\pi ^W_E: W\rightarrow Ult(W, E)$
is a st-like-embedding below
$\pi ^W_E: W\rightarrow Ult(W, E)$
is a st-like-embedding below
![]() $\delta $
(in
$\delta $
(in
![]() $W[g]$
). Because
$W[g]$
). Because
![]() $\mathbb {P}\in W_{\pi _F(\kappa )}$
, we have that
$\mathbb {P}\in W_{\pi _F(\kappa )}$
, we have that
![]() $\pi _F(\xi )<\pi _F(\kappa )$
. Hence,
$\pi _F(\xi )<\pi _F(\kappa )$
. Hence,
![]() $\xi <\kappa $
.
$\xi <\kappa $
.
Upon seeing the results of this paper, Woodin informed us that he already knew that in extender models there is no st-like-embedding below the first Woodin cardinal (in fact condensation style arguments give this). He also informed us that the answer was not known for the second Woodin cardinal and beyond. We could have chosen any Woodin cardinal
![]() $\delta $
such that the least cardinal
$\delta $
such that the least cardinal
![]() $\kappa $
that is
$\kappa $
that is
![]() $<\delta $
-strong is not a limit of Woodin cardinals. Our proof has all the main ideas, and this is not a vanity contest. Thus, we chose to work with the second Woodin cardinal.
$<\delta $
-strong is not a limit of Woodin cardinals. Our proof has all the main ideas, and this is not a vanity contest. Thus, we chose to work with the second Woodin cardinal.
We have not tried to prove results for overlapped Woodins, and believe that this is an interesting project. The methods of [Reference Sargsyan8] are probably relevant to this project.
Our methods are methods developed by inner model theorists for the last 60 years or so. We rely heavily on the writings of Mitchell and Steel. Readers familiar with the papers [Reference Mitchell and Steel5, Reference Steel18] can see their influence on the current paper.
We started thinking about generic embeddings in extender models because of Mathew Foreman. He informed us that it is not known if large cardinals imply the existence of precipitous ideals on
![]() $\omega _1$
. We thank him for asking us this question.
$\omega _1$
. We thank him for asking us this question.
Our motivation was just to show that inner model theory is a subject relevant to combinatorial set theory in a sense that a great deal of combinatorics beyond principles such as
![]() $\Diamond $
and
$\Diamond $
and
![]() $\square $
can be investigated and understood inside inner models. One only needs to try.
$\square $
can be investigated and understood inside inner models. One only needs to try.
Nevertheless, we do agree with the view that the internal combinatorial structure of extender models have not been very extensively studied beyond [Reference Schimmerling and Zeman11]. However, there are several papers in print that do investigate the internal structure of mice in different ways than [Reference Schimmerling and Zeman11] does. For instance, [Reference Schlutzenberg14] characterizes homogeneously Suslin sets in extender models, and [Reference Sargsyan and Schindler9] investigates grounds of certain types of extender models.
1 On S-reconstructible operators
Here we discuss some facts that describe the internal structure of a large class of mice. Suppose that:
-
1.
 ${\mathcal {M}}$
is a class size mouse over some set x satisfying a sentence
${\mathcal {M}}$
is a class size mouse over some set x satisfying a sentence
 $\phi $
,
$\phi $
, -
2. there is no active level
 ${\mathcal R}\trianglelefteq {\mathcal {M}}$
such that if E is the last extender of
${\mathcal R}\trianglelefteq {\mathcal {M}}$
such that if E is the last extender of
 ${\mathcal R}$
then
${\mathcal R}$
then
 ${\mathcal R}|\mathrm {crit }(E)\vDash \phi $
and
${\mathcal R}|\mathrm {crit }(E)\vDash \phi $
and -
3. there is an active mouse
 ${\mathcal R}$
such that if E is the last extender of
${\mathcal R}$
such that if E is the last extender of
 ${\mathcal R}$
then
${\mathcal R}$
then
 ${\mathcal R}|\mathrm { crit }(E)\vDash \phi $
.
${\mathcal R}|\mathrm { crit }(E)\vDash \phi $
.
Clause 3 above implies that
![]() ${\mathcal {M}}$
has a club of indiscernibles. We then say
${\mathcal {M}}$
has a club of indiscernibles. We then say
![]() ${\mathcal {M}}$
is the minimal class size x-mouse satisfying
${\mathcal {M}}$
is the minimal class size x-mouse satisfying
![]() $\phi $
if
$\phi $
if
![]() ${\mathcal {M}}$
is the hull of a club of indiscernibles. It is one of the most celebrated theorems of inner model theory that if there is a minimal class size x-mouse satisfying
${\mathcal {M}}$
is the hull of a club of indiscernibles. It is one of the most celebrated theorems of inner model theory that if there is a minimal class size x-mouse satisfying
![]() $\phi $
then it is unique. This can be shown via a standard comparison argument (see, for instance, [Reference Steel20, Theorem 3.11]). Just notice that if
$\phi $
then it is unique. This can be shown via a standard comparison argument (see, for instance, [Reference Steel20, Theorem 3.11]). Just notice that if
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() ${\mathcal {N}}$
are both minimal class size x-mice satisfying
${\mathcal {N}}$
are both minimal class size x-mice satisfying
![]() $\phi $
then their comparison has a club of fixed points all of which are indiscernibles.
$\phi $
then their comparison has a club of fixed points all of which are indiscernibles.
We say
![]() $\mathbb {M}: V\rightarrow V$
is a mouse operator if for some formula
$\mathbb {M}: V\rightarrow V$
is a mouse operator if for some formula
![]() $\phi $
,
$\phi $
,
-
1.
 $\mathrm {dom}(\mathbb {M})= \{x: L_{\omega }[x]\vDash "x$
is well-ordered”
$\mathrm {dom}(\mathbb {M})= \{x: L_{\omega }[x]\vDash "x$
is well-ordered”
 $\}\cap \{x:$
there is a minimal class size x-mouse satisfying
$\}\cap \{x:$
there is a minimal class size x-mouse satisfying
 $\phi \}$
,
$\phi \}$
, -
2. for each
 $x\in dom(\mathbb {M})$
,
$x\in dom(\mathbb {M})$
,
 $\mathbb {M}(x)$
is the minimal class size mouse satisfying
$\mathbb {M}(x)$
is the minimal class size mouse satisfying
 $\phi $
.
$\phi $
.
We also say that
![]() $\mathbb {M}$
is determined by
$\mathbb {M}$
is determined by
![]() $\phi $
and denote it by
$\phi $
and denote it by
![]() $\mathbb {M}_\phi $
. When
$\mathbb {M}_\phi $
. When
![]() $\phi $
is clear from context we drop it from our notation, and for
$\phi $
is clear from context we drop it from our notation, and for
![]() $x\in dom(\mathbb {M})$
, we let
$x\in dom(\mathbb {M})$
, we let
![]() ${\mathcal {M}}(x)=\mathbb {M}(x)$
. We say
${\mathcal {M}}(x)=\mathbb {M}(x)$
. We say
![]() $\mathbb {M}$
is total on a set X if
$\mathbb {M}$
is total on a set X if
![]() ${\mathcal {M}}(x)$
is defined for every
${\mathcal {M}}(x)$
is defined for every
![]() $x\in X\cap \{x: L_{\omega }[x]\vDash "x$
is well-ordered”
$x\in X\cap \{x: L_{\omega }[x]\vDash "x$
is well-ordered”
![]() $\}$
.
$\}$
.
We assume familiarity with [Reference Mitchell and Steel5] or with [Reference Steel20]. In particular, familiarity with [Reference Mitchell and Steel5, Chapter 11] will be very helpful. Recall from [Reference Mitchell and Steel5, Chapter 11] that the extenders used in the fully backgrounded construction are total and, hence, have measurable critical points in the sense that if
![]() ${\mathcal {N}}$
is a model appearing in the fully backgrounded construction and
${\mathcal {N}}$
is a model appearing in the fully backgrounded construction and
![]() $E\in \vec {E}^{\mathcal {N}}$
is a total extender then
$E\in \vec {E}^{\mathcal {N}}$
is a total extender then
![]() $\mathrm {crit }(E)$
is a measurable cardinal of
$\mathrm {crit }(E)$
is a measurable cardinal of
![]() ${\mathcal {N}}$
. Also, Lemma 11.1, Lemma 11.2, and Theorem 11.3 of [Reference Mitchell and Steel5] are very important for us. When we talk about fully backgrounded construction done inside a structure with a distinguished extender sequence, we tacitly assume that all extenders come from this extender sequence.
${\mathcal {N}}$
. Also, Lemma 11.1, Lemma 11.2, and Theorem 11.3 of [Reference Mitchell and Steel5] are very important for us. When we talk about fully backgrounded construction done inside a structure with a distinguished extender sequence, we tacitly assume that all extenders come from this extender sequence.
Definition 1.1. We say
![]() $\mathbb {M}_\phi $
is an
$\mathbb {M}_\phi $
is an
![]() ${\mathcal {S}}$
-reconstructible mouse operator if:
${\mathcal {S}}$
-reconstructible mouse operator if:
-
1.
 $dom(\mathbb {M}_\phi )=\{a\in HC: L_\omega [a]\vDash "a$
is well-ordered”
$dom(\mathbb {M}_\phi )=\{a\in HC: L_\omega [a]\vDash "a$
is well-ordered”
 $\}$
,
$\}$
, -
2. for each
 $a\in dom(\mathbb {M}_\phi )$
,
$a\in dom(\mathbb {M}_\phi )$
,
 ${\mathcal {M}}_\phi (a)$
has infinitely many Woodin cardinals the first
${\mathcal {M}}_\phi (a)$
has infinitely many Woodin cardinals the first
 $\omega $
of which are
$\omega $
of which are
 $(\delta _{a, i}:i\in \omega )$
,
$(\delta _{a, i}:i\in \omega )$
, -
3. for each
 $a\in dom(\mathbb {M}_\phi )$
, for each
$a\in dom(\mathbb {M}_\phi )$
, for each
 $i\in \omega $
, for each
$i\in \omega $
, for each
 ${\mathcal {M}}_\phi (a)$
-generic g for a poset of
${\mathcal {M}}_\phi (a)$
-generic g for a poset of
 ${\mathcal {M}}_\phi (a)$
-size
${\mathcal {M}}_\phi (a)$
-size
 $<\delta _{a, i}$
, for each
$<\delta _{a, i}$
, for each
 $x\in ({\mathcal {M}}_\phi (a)|\delta _{a, i})[g]$
, and for each
$x\in ({\mathcal {M}}_\phi (a)|\delta _{a, i})[g]$
, and for each
 $\eta <\delta _{a, i}$
such that
$\eta <\delta _{a, i}$
such that
 $x\in ({\mathcal {M}}_\phi (a)|\eta )[g]$
, letting:
$x\in ({\mathcal {M}}_\phi (a)|\eta )[g]$
, letting:-
(a)
 ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
 $({\mathcal {M}}_\phi (a)|\delta _{a, i})[g]$
done over x using extenders with critical points greater than
$({\mathcal {M}}_\phi (a)|\delta _{a, i})[g]$
done over x using extenders with critical points greater than
 $\eta $
and
$\eta $
and -
(b)
 ${\mathcal {N}}$
be the result of an S-construction that translates
${\mathcal {N}}$
be the result of an S-construction that translates
 ${\mathcal {M}}_\phi (a)$
into an x-mouse over
${\mathcal {M}}_\phi (a)$
into an x-mouse over
 ${\mathcal {P} }$
,
${\mathcal {P} }$
,
 ${\mathcal {N}}\vDash \phi $
.
${\mathcal {N}}\vDash \phi $
. -
S constructions are standard constructions in inner model theory. They were first considered by John Steel (hence the
![]() $"S"$
). The first known full treatment of S constructions was presented in [Reference Schindler and Steel12], where, for some truly unfortunate though fully understandable reasons,Footnote
5
they were called P constructions where P stands for nothing in particular. The reader can also consult [Reference Sargsyan7, Chapter 3.8].
$"S"$
). The first known full treatment of S constructions was presented in [Reference Schindler and Steel12], where, for some truly unfortunate though fully understandable reasons,Footnote
5
they were called P constructions where P stands for nothing in particular. The reader can also consult [Reference Sargsyan7, Chapter 3.8].
Our goal is to consider two particular kinds of mice,
![]() ${\mathcal {M}}_\omega $
and
${\mathcal {M}}_\omega $
and
![]() ${\mathcal {M}}_{wlw}$
. The first is the minimal class size mouse with
${\mathcal {M}}_{wlw}$
. The first is the minimal class size mouse with
![]() $\omega $
Woodin cardinals, and the second is the minimal class size mouse with a Woodin cardinal
$\omega $
Woodin cardinals, and the second is the minimal class size mouse with a Woodin cardinal
![]() $\delta $
that is a limit of Woodin cardinals. We will prove our theorems for S-reconstructible mice that have the internal covering property (see Definition 2.1). It is straightforward to check that both
$\delta $
that is a limit of Woodin cardinals. We will prove our theorems for S-reconstructible mice that have the internal covering property (see Definition 2.1). It is straightforward to check that both
![]() ${\mathcal {M}}_\omega $
and
${\mathcal {M}}_\omega $
and
![]() ${\mathcal {M}}_{wlw}$
satisfy our definition of S-reconstructible. Later we will show that they also satisfy the internal covering property (see Theorem 2.2).
${\mathcal {M}}_{wlw}$
satisfy our definition of S-reconstructible. Later we will show that they also satisfy the internal covering property (see Theorem 2.2).
Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Given
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Given
![]() $a\in dom(\mathbb {M}_\phi )$
, we let
$a\in dom(\mathbb {M}_\phi )$
, we let
We think of
![]() ${\mathcal {W} }$
as a function whose domain is
${\mathcal {W} }$
as a function whose domain is
![]() $dom(\mathbb {M}_\phi )$
. Given a transitive set N, let
$dom(\mathbb {M}_\phi )$
. Given a transitive set N, let
![]() ${\mathcal {W} }^N={\mathcal {W} }\restriction N$
. The following is a corollary to our definition. In general, the results of this section are not new and reformulations of similar results that appeared in [Reference Sargsyan7, Reference Steel18] (for example, see [Reference Sargsyan7, Chapter 3.1] and [Reference Steel18, Theorem 5.1]).
${\mathcal {W} }^N={\mathcal {W} }\restriction N$
. The following is a corollary to our definition. In general, the results of this section are not new and reformulations of similar results that appeared in [Reference Sargsyan7, Reference Steel18] (for example, see [Reference Sargsyan7, Chapter 3.1] and [Reference Steel18, Theorem 5.1]).
Corollary 1.2. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Fix
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Fix
![]() $a\in dom(\mathbb {M}_\phi )$
and
$a\in dom(\mathbb {M}_\phi )$
and
![]() $i\in \omega $
, and set
$i\in \omega $
, and set
![]() ${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
![]() $\delta =\delta _{a, i}$
. Then
$\delta =\delta _{a, i}$
. Then
![]() ${\mathcal {W} }^{{\mathcal {M}}|\delta }$
is uniformly definable over
${\mathcal {W} }^{{\mathcal {M}}|\delta }$
is uniformly definable over
![]() ${\mathcal {M}}|\delta $
. Moreover, there is a formula
${\mathcal {M}}|\delta $
. Moreover, there is a formula
![]() $\psi $
with the property that for any poset
$\psi $
with the property that for any poset
![]() $\mathbb {P}\in {\mathcal {M}}|\delta $
, for any
$\mathbb {P}\in {\mathcal {M}}|\delta $
, for any
![]() ${\mathcal {M}}$
-generic
${\mathcal {M}}$
-generic
![]() $g\subseteq \mathbb {P}$
, for any
$g\subseteq \mathbb {P}$
, for any
![]() $x\in HC^{{\mathcal {M}}[g]}$
, and for any
$x\in HC^{{\mathcal {M}}[g]}$
, and for any
![]() ${\mathcal R}$
,
${\mathcal R}$
,
It is clear what
![]() $\psi $
must be, it is just the formula defining the fully backgrounded constructions. Note that the language of
$\psi $
must be, it is just the formula defining the fully backgrounded constructions. Note that the language of
![]() ${\mathcal {M}}$
has a symbol for the extender sequence of
${\mathcal {M}}$
has a symbol for the extender sequence of
![]() ${\mathcal {M}}$
, and so
${\mathcal {M}}$
, and so
![]() $\psi $
may mention the extender sequence of
$\psi $
may mention the extender sequence of
![]() ${\mathcal {M}}|\delta $
. Results of Schlutzenberg suggest that
${\mathcal {M}}|\delta $
. Results of Schlutzenberg suggest that
![]() ${\mathcal {W} }$
maybe even be definable over the universe of
${\mathcal {W} }$
maybe even be definable over the universe of
![]() ${\mathcal {M}}|\delta $
(see [Reference Schlutzenberg13]). However, we do not need such fine calculations. Below we give an example of such a
${\mathcal {M}}|\delta $
(see [Reference Schlutzenberg13]). However, we do not need such fine calculations. Below we give an example of such a
![]() $\psi $
. Set
$\psi $
. Set
![]() $\psi [x, {\mathcal R}]: {\mathcal R}$
is an x-premouse and there is
$\psi [x, {\mathcal R}]: {\mathcal R}$
is an x-premouse and there is
![]() $\lambda <\delta $
such that for every
$\lambda <\delta $
such that for every
![]() $\eta \in (\lambda , \delta )$
, if
$\eta \in (\lambda , \delta )$
, if
![]() ${\mathcal {P} }$
is the output of the fully backgrounded construction of
${\mathcal {P} }$
is the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
![]() $>\eta $
,
$>\eta $
,
![]() ${\mathcal R}\trianglelefteq {\mathcal {P} }$
.
${\mathcal R}\trianglelefteq {\mathcal {P} }$
.
It can be shown that
![]() $\psi $
witnesses Corollary 1.2.
$\psi $
witnesses Corollary 1.2.
The next results show that
![]() ${\mathcal {M}}(a)$
in fact knows some fragments of its own strategy. The first lemma is a useful and easy lemma. We let
${\mathcal {M}}(a)$
in fact knows some fragments of its own strategy. The first lemma is a useful and easy lemma. We let
![]() $\delta _{a, -1}=0$
. We do not know the origin of this lemma but it has probably been discovered by many authors independently.
$\delta _{a, -1}=0$
. We do not know the origin of this lemma but it has probably been discovered by many authors independently.
Lemma 1.3. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Fix
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Fix
![]() $a\in dom(\mathbb {M}_\phi )$
and
$a\in dom(\mathbb {M}_\phi )$
and
![]() $i\in \omega $
, and set
$i\in \omega $
, and set
![]() ${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
![]() $\delta =\delta _{a, i}$
. Let
$\delta =\delta _{a, i}$
. Let
![]() $\mathbb {P}\in {\mathcal {M}}|\delta $
and suppose
$\mathbb {P}\in {\mathcal {M}}|\delta $
and suppose
![]() $g\subseteq \mathbb {P}$
is
$g\subseteq \mathbb {P}$
is
![]() ${\mathcal {M}}$
-generic. Let
${\mathcal {M}}$
-generic. Let
![]() $x\in {\mathcal {M}}|\delta [g]$
and
$x\in {\mathcal {M}}|\delta [g]$
and
![]() $\lambda \in (\max (\delta _{i-1}, \left |\mathbb {P}\right |{}^{\mathcal {M}}), \delta )$
be such that
$\lambda \in (\max (\delta _{i-1}, \left |\mathbb {P}\right |{}^{\mathcal {M}}), \delta )$
be such that
![]() $x\in {\mathcal {M}}|\lambda [g]$
. Let
$x\in {\mathcal {M}}|\lambda [g]$
. Let
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
![]() $>\lambda $
. Then
$>\lambda $
. Then
![]() ${\mathcal {P} }\vDash$
“there are no Woodin cardinals.”
${\mathcal {P} }\vDash$
“there are no Woodin cardinals.”
Proof Towards a contradiction, assume not. Let
![]() $\eta $
be the least Woodin cardinal of
$\eta $
be the least Woodin cardinal of
![]() ${\mathcal {P} }$
. Then
${\mathcal {P} }$
. Then
![]() ${\mathcal {M}}|\eta $
is generic over
${\mathcal {M}}|\eta $
is generic over
![]() ${\mathcal {P} }$
for the extender algebra at
${\mathcal {P} }$
for the extender algebra at
![]() $\eta $
that uses
$\eta $
that uses
![]() $\eta $
-generators. We claim that
$\eta $
-generators. We claim that
Claim.
![]() ${\mathcal {P} }[{\mathcal {M}}|\eta ]\vDash "\eta $
is a Woodin cardinal.”
${\mathcal {P} }[{\mathcal {M}}|\eta ]\vDash "\eta $
is a Woodin cardinal.”
Proof To see that
![]() ${\mathcal {P} }[{\mathcal {M}}|\eta ]\vDash "\eta $
is a Woodin cardinal,” let
${\mathcal {P} }[{\mathcal {M}}|\eta ]\vDash "\eta $
is a Woodin cardinal,” let
![]() $f: \eta \rightarrow \eta $
be a function in
$f: \eta \rightarrow \eta $
be a function in
![]() ${\mathcal {P} }[{\mathcal {M}}|\eta ]$
. Because the forcing that adds
${\mathcal {P} }[{\mathcal {M}}|\eta ]$
. Because the forcing that adds
![]() ${\mathcal {M}}|\eta $
has the
${\mathcal {M}}|\eta $
has the
![]() $\eta $
-cc, there is
$\eta $
-cc, there is
![]() $h:\eta \rightarrow \eta $
in
$h:\eta \rightarrow \eta $
in
![]() ${\mathcal {P} }$
such that for every
${\mathcal {P} }$
such that for every
![]() $\alpha <\eta $
,
$\alpha <\eta $
,
![]() $f(\alpha )<h(\alpha )$
. Let
$f(\alpha )<h(\alpha )$
. Let
![]() $E\in \vec {E}^{\mathcal {P} }$
be an extender such that
$E\in \vec {E}^{\mathcal {P} }$
be an extender such that
![]() $\nu =_{def}\nu _E$
is a
$\nu =_{def}\nu _E$
is a
![]() ${\mathcal {P} }$
-cardinal such that letting
${\mathcal {P} }$
-cardinal such that letting
![]() $\kappa =\mathrm { crit }(E)$
,
$\kappa =\mathrm { crit }(E)$
,
Let
![]() $F\in {\mathcal {M}}$
be the resurrection of E. Let
$F\in {\mathcal {M}}$
be the resurrection of E. Let
![]() ${\mathcal {S}}$
be the model appearing in the construction producing
${\mathcal {S}}$
be the model appearing in the construction producing
![]() ${\mathcal {P} }$
such that F is added to
${\mathcal {P} }$
such that F is added to
![]() ${\mathcal {S}}$
. We have that no further model appearing in the construction projects below
${\mathcal {S}}$
. We have that no further model appearing in the construction projects below
![]() $\nu $
(as
$\nu $
(as
![]() ${\mathcal {P} }|\nu $
is an initial segment of the final model of the construction). It follows that the canonical factor map
${\mathcal {P} }|\nu $
is an initial segment of the final model of the construction). It follows that the canonical factor map
![]() $k: Ult({\mathcal {P} }, E)\rightarrow \pi _F^{\mathcal {M}}({\mathcal {P} })$
has a critical point
$k: Ult({\mathcal {P} }, E)\rightarrow \pi _F^{\mathcal {M}}({\mathcal {P} })$
has a critical point
![]() $\geq \nu $
. Hence,
$\geq \nu $
. Hence,
![]() $k(\pi _E^{\mathcal {P} }(h)(\kappa ))=\pi ^{\mathcal {P} }_E(h)(\kappa )$
. It follows that
$k(\pi _E^{\mathcal {P} }(h)(\kappa ))=\pi ^{\mathcal {P} }_E(h)(\kappa )$
. It follows that
If
![]() $F\not \in \vec {E}^{{\mathcal {M}}|\eta }$
then for some
$F\not \in \vec {E}^{{\mathcal {M}}|\eta }$
then for some
![]() ${\mathcal {M}}$
-inaccessible
${\mathcal {M}}$
-inaccessible
![]() $\xi \in (\nu , \eta )$
,
$\xi \in (\nu , \eta )$
,
![]() $F\restriction \xi \in \vec {E}^{{\mathcal {M}}|\eta }$
. It follows that
$F\restriction \xi \in \vec {E}^{{\mathcal {M}}|\eta }$
. It follows that
![]() $F\restriction \xi $
witnesses Woodiness for f in
$F\restriction \xi $
witnesses Woodiness for f in
![]() ${\mathcal {P} }[{\mathcal {M}}|\eta ]$
.
${\mathcal {P} }[{\mathcal {M}}|\eta ]$
.
Notice now that
![]() ${\mathcal {W} }({\mathcal {M}}|\eta )\in {\mathcal {P} }[{\mathcal {M}}|\eta ]$
(this follows from S-reconstructibility). Hence,
${\mathcal {W} }({\mathcal {M}}|\eta )\in {\mathcal {P} }[{\mathcal {M}}|\eta ]$
(this follows from S-reconstructibility). Hence,
![]() ${\mathcal {W} }({\mathcal {M}}|\eta )\vDash "\eta $
is a Woodin cardinal.” It follows from [Reference Steel18, Remark 12.7] that
${\mathcal {W} }({\mathcal {M}}|\eta )\vDash "\eta $
is a Woodin cardinal.” It follows from [Reference Steel18, Remark 12.7] that
![]() ${\mathcal {W} }({\mathcal {M}}|\eta )$
is essentially the same as
${\mathcal {W} }({\mathcal {M}}|\eta )$
is essentially the same as
![]() ${\mathcal {M}}|\alpha $
where
${\mathcal {M}}|\alpha $
where
![]() $\alpha =(\eta ^+)^{\mathcal {M}}$
in the case
$\alpha =(\eta ^+)^{\mathcal {M}}$
in the case
![]() $\eta $
is a cutpoint and
$\eta $
is a cutpoint and
![]() $\alpha =lh(F)$
where
$\alpha =lh(F)$
where
![]() $F\in \vec {E}^{\mathcal {M}}$
is the first extender such that
$F\in \vec {E}^{\mathcal {M}}$
is the first extender such that
![]() $\eta \in (\mathrm {crit }(F), lh(F))$
. The point here is just that if there are partial extenders with critical point
$\eta \in (\mathrm {crit }(F), lh(F))$
. The point here is just that if there are partial extenders with critical point
![]() $\eta $
then they can be translated away.
$\eta $
then they can be translated away.
Suppose now that
![]() $\eta $
is a cutpoint. It follows from the above discussion that
$\eta $
is a cutpoint. It follows from the above discussion that
![]() ${\mathcal {W} }({\mathcal {M}}|\eta )={\mathcal {M}}|(\eta ^+)^{\mathcal {M}}$
and, hence,
${\mathcal {W} }({\mathcal {M}}|\eta )={\mathcal {M}}|(\eta ^+)^{\mathcal {M}}$
and, hence,
![]() $\eta $
is a Woodin cardinal of
$\eta $
is a Woodin cardinal of
![]() ${\mathcal {M}}$
, contradiction (there are no Woodin cardinals between
${\mathcal {M}}$
, contradiction (there are no Woodin cardinals between
![]() $\lambda $
and
$\lambda $
and
![]() $\delta $
). Next, suppose
$\delta $
). Next, suppose
![]() $\eta $
is not a cutpoint and let F be the least extender overlapping it. Then,
$\eta $
is not a cutpoint and let F be the least extender overlapping it. Then,
![]() $Ult({\mathcal {M}}, F)\vDash "\eta $
is a Woodin cardinal.” Hence,
$Ult({\mathcal {M}}, F)\vDash "\eta $
is a Woodin cardinal.” Hence,
![]() ${\mathcal {M}}|\mathrm { crit }(F)\vDash $
“there are unboundedly many Woodin cardinals.” Since
${\mathcal {M}}|\mathrm { crit }(F)\vDash $
“there are unboundedly many Woodin cardinals.” Since
![]() $\eta $
is a cardinal of
$\eta $
is a cardinal of
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() $\mathrm {crit }(F)$
is also a cardinal implying that
$\mathrm {crit }(F)$
is also a cardinal implying that
![]() ${\mathcal {M}}$
has Woodin cardinals in the interval
${\mathcal {M}}$
has Woodin cardinals in the interval
![]() $(\lambda , \delta )$
, contradiction!
$(\lambda , \delta )$
, contradiction!
The next proposition shows that some fragments of the iteration strategy are universally Baire inside the mouse operators. The proof is very much like the proofs used in [Reference Sargsyan7, Chapter 3.1]. Below given an iteration tree
![]() ${\mathcal {T}}$
on a premouse
${\mathcal {T}}$
on a premouse
![]() ${\mathcal {N}}$
, we let
${\mathcal {N}}$
, we let
![]() $C({\mathcal {T}})=\cup _{\alpha <lh({\mathcal {T}})}{\mathcal {M}}_\alpha ^{\mathcal {T}}|lh(E_\alpha ^{\mathcal {T}})$
. Usually
$C({\mathcal {T}})=\cup _{\alpha <lh({\mathcal {T}})}{\mathcal {M}}_\alpha ^{\mathcal {T}}|lh(E_\alpha ^{\mathcal {T}})$
. Usually
![]() $C({\mathcal {T}})$
is denoted by
$C({\mathcal {T}})$
is denoted by
![]() ${\mathcal {M}}({\mathcal {T}})$
which in this paper has a different meaning.
${\mathcal {M}}({\mathcal {T}})$
which in this paper has a different meaning.
Propositions 1.4–1.7 are all part of the standard literature. For example, see [Reference Steel18, Lemma 5.1] and [Reference Schlutzenberg14, Lemma 6.3].Footnote 6
Proposition 1.4. Suppose
![]() $\mathbb {M}_\phi $
is an
$\mathbb {M}_\phi $
is an
![]() ${\mathcal {S}}$
-reconstructible mouse operator and
${\mathcal {S}}$
-reconstructible mouse operator and
![]() ${a\in dom(\mathbb {M}_\phi )}$
. Fix
${a\in dom(\mathbb {M}_\phi )}$
. Fix
![]() $i\in \omega $
and set
$i\in \omega $
and set
![]() $\delta =\delta _{a, i}$
and
$\delta =\delta _{a, i}$
and
![]() ${\mathcal {M}}={\mathcal {M}}(a)$
. Let
${\mathcal {M}}={\mathcal {M}}(a)$
. Let
![]() $\Sigma $
be the unique iteration strategy of
$\Sigma $
be the unique iteration strategy of
![]() ${\mathcal {M}}$
. Suppose
${\mathcal {M}}$
. Suppose
![]() $\kappa \in (\delta _{a, i-1}, \delta )$
is an
$\kappa \in (\delta _{a, i-1}, \delta )$
is an
![]() ${\mathcal {M}}$
-cardinal and
${\mathcal {M}}$
-cardinal and
![]() $\Lambda $
is the fragment of
$\Lambda $
is the fragment of
![]() $\kern1pt\Sigma $
that acts on non-dropping trees on
$\kern1pt\Sigma $
that acts on non-dropping trees on
![]() ${\mathcal {M}}|\kappa $
that are above
${\mathcal {M}}|\kappa $
that are above
![]() $\delta _{a, i-1}$
. Then, for each
$\delta _{a, i-1}$
. Then, for each
![]() $j\in (i-1, \omega )$
,
$j\in (i-1, \omega )$
,
![]() $\Lambda \restriction ({\mathcal {M}}|\delta _{a, j})\in {\mathcal {M}}$
and whenever
$\Lambda \restriction ({\mathcal {M}}|\delta _{a, j})\in {\mathcal {M}}$
and whenever
![]() $g\subseteq Coll(\omega , \kappa )$
is
$g\subseteq Coll(\omega , \kappa )$
is
![]() ${\mathcal {M}}$
-generic,
${\mathcal {M}}$
-generic,
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
and
$\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
and
Furthermore, for every
![]() $j\in (i-1, \omega )$
, whenever h is
$j\in (i-1, \omega )$
, whenever h is
![]() ${\mathcal {M}}[g]$
-generic for a poset of size
${\mathcal {M}}[g]$
-generic for a poset of size
![]() $<\delta _{a, j}$
,
$<\delta _{a, j}$
,
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g*h]}$
is the canonical extension of
$\Lambda \restriction HC^{{\mathcal {M}}[g*h]}$
is the canonical extension of
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}$
.
$\Lambda \restriction HC^{{\mathcal {M}}[g]}$
.
Proof The representative case is when
![]() $i=0$
. When
$i=0$
. When
![]() $i>0$
we need to work over
$i>0$
we need to work over
![]() ${\mathcal {M}}|\delta _{a, i-1}$
. Here we assume
${\mathcal {M}}|\delta _{a, i-1}$
. Here we assume
![]() $i=0$
. Also, the proof of the case when
$i=0$
. Also, the proof of the case when
![]() $j>0$
is very similar to the proof of the case when
$j>0$
is very similar to the proof of the case when
![]() $j=0$
. The only difference is that for
$j=0$
. The only difference is that for
![]() $j>0$
, the fully backgrounded constructions we consider must use extenders with critical points
$j>0$
, the fully backgrounded constructions we consider must use extenders with critical points
![]() $>\delta _{a, j-1}$
.
$>\delta _{a, j-1}$
.
The fact that
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
follows from Corollary 1.2. Indeed, notice that given a tree
$\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
follows from Corollary 1.2. Indeed, notice that given a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {M}}|\kappa $
of limit length and according to
${\mathcal {M}}|\kappa $
of limit length and according to
![]() $\Lambda $
,
$\Lambda $
,
![]() $\Lambda ({\mathcal {T}})$
is the unique branch b such that
$\Lambda ({\mathcal {T}})$
is the unique branch b such that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
Footnote
7
exists and
${\mathcal { Q}}(b, {\mathcal {T}})$
Footnote
7
exists and
![]() ${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {W} }(C({\mathcal {T}}))$
. Thus, to define
${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {W} }(C({\mathcal {T}}))$
. Thus, to define
![]() $\Lambda $
in generic extensions of
$\Lambda $
in generic extensions of
![]() ${\mathcal {M}}$
, it is enough to know that the function
${\mathcal {M}}$
, it is enough to know that the function
![]() ${\mathcal {T}}\mapsto {\mathcal {W} }(C({\mathcal {T}}))$
is definable on the domain of
${\mathcal {T}}\mapsto {\mathcal {W} }(C({\mathcal {T}}))$
is definable on the domain of
![]() $\Lambda $
. This follows from Corollary 1.2. For the rest of the argument we assume that
$\Lambda $
. This follows from Corollary 1.2. For the rest of the argument we assume that
![]() $\kappa $
is a successor cardinal of
$\kappa $
is a successor cardinal of
![]() ${\mathcal {M}}$
. This assumption doesn’t cause loss of generality, since if
${\mathcal {M}}$
. This assumption doesn’t cause loss of generality, since if
![]() $\kappa $
is a limit cardinal then the conclusion of the proposition can be reached by using the conclusion of the proposition for
$\kappa $
is a limit cardinal then the conclusion of the proposition can be reached by using the conclusion of the proposition for
![]() $(\kappa ^+)^{\mathcal {M}}$
.
$(\kappa ^+)^{\mathcal {M}}$
.
As pointed out by the referee, we could define
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
as follows. Let T be the tree of attempts to build a triple
$\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}[g]$
as follows. Let T be the tree of attempts to build a triple
![]() $(x, y, z, \pi )$
such that x codes an iteration tree
$(x, y, z, \pi )$
such that x codes an iteration tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {M}}|\kappa $
, y codes a cofinal well-founded branch b of
${\mathcal {M}}|\kappa $
, y codes a cofinal well-founded branch b of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
exists, z codes a countable
${\mathcal { Q}}(b, {\mathcal {T}})$
exists, z codes a countable
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})\in {\mathcal {N}}$
,
${\mathcal { Q}}(b, {\mathcal {T}})\in {\mathcal {N}}$
,
![]() $\pi : {\mathcal {N}}\rightarrow {\mathcal {M}}|\delta $
and inside
$\pi : {\mathcal {N}}\rightarrow {\mathcal {M}}|\delta $
and inside
![]() ${\mathcal {N}}$
,
${\mathcal {N}}$
,
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
can be built via fully backgrounded constructions done over
${\mathcal { Q}}(b, {\mathcal {T}})$
can be built via fully backgrounded constructions done over
![]() $C({\mathcal {T}})$
. In this paper, especially in Propositions 1.5–1.7, we will need different sort of arguments, and so we present a somewhat more involved proof that exploits the idea of “iterating to the background constructions.”
$C({\mathcal {T}})$
. In this paper, especially in Propositions 1.5–1.7, we will need different sort of arguments, and so we present a somewhat more involved proof that exploits the idea of “iterating to the background constructions.”
Next we show that
![]() $\Lambda $
is
$\Lambda $
is
![]() $\delta $
-uB in
$\delta $
-uB in
![]() ${\mathcal {M}}[g]$
. Our generically absolute definition of
${\mathcal {M}}[g]$
. Our generically absolute definition of
![]() $\Lambda $
will also show the “furthermore” clause of the proposition. Let
$\Lambda $
will also show the “furthermore” clause of the proposition. Let
![]() $\lambda \in (\kappa , \delta )$
be a cardinal, and let
$\lambda \in (\kappa , \delta )$
be a cardinal, and let
![]() $\vec {C}=({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the models of fully backgrounded construction of
$\vec {C}=({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the models of fully backgrounded construction of
![]() ${\mathcal {M}}|\delta $
(or
${\mathcal {M}}|\delta $
(or
![]() ${\mathcal {M}}|\delta [g]$
) done over a in which extenders used have critical points
${\mathcal {M}}|\delta [g]$
) done over a in which extenders used have critical points
![]() $>\lambda $
. Let
$>\lambda $
. Let
![]() ${\mathcal R}_\delta $
be the output of
${\mathcal R}_\delta $
be the output of
![]() $\vec {C}$
. Thus, for
$\vec {C}$
. Thus, for
![]() $\alpha <\delta $
,
$\alpha <\delta $
,
![]() ${\mathcal R}_\delta ||\alpha $
is defined to be
${\mathcal R}_\delta ||\alpha $
is defined to be
![]() ${\mathcal R}_{\xi _\alpha }||\alpha $
where
${\mathcal R}_{\xi _\alpha }||\alpha $
where
![]() $\xi _\alpha $
is the least such that for all
$\xi _\alpha $
is the least such that for all
![]() $\zeta>\xi _\alpha $
,
$\zeta>\xi _\alpha $
,
![]() ${\mathcal R}_\zeta ||\alpha ={\mathcal R}_{\xi _\alpha }||\alpha $
. We claim that
${\mathcal R}_\zeta ||\alpha ={\mathcal R}_{\xi _\alpha }||\alpha $
. We claim that
Claim 1. For some
![]() $\xi $
,
$\xi $
,
![]() ${\mathcal R}_\xi $
is an iterate of
${\mathcal R}_\xi $
is an iterate of
![]() ${\mathcal {M}}|\kappa $
via a tree
${\mathcal {M}}|\kappa $
via a tree
![]() ${\mathcal {W} }$
such that
${\mathcal {W} }$
such that
![]() $\pi ^{\mathcal {W} }$
exists.
$\pi ^{\mathcal {W} }$
exists.
Proof Notice that as
![]() ${\mathcal {M}}|\kappa $
has no Woodin cardinals, if there was such a tree
${\mathcal {M}}|\kappa $
has no Woodin cardinals, if there was such a tree
![]() ${\mathcal {W} }$
then
${\mathcal {W} }$
then
![]() ${\mathcal {W} }\in {\mathcal {M}}$
. Now towards a contradiction assume our claim is false. We now compare
${\mathcal {W} }\in {\mathcal {M}}$
. Now towards a contradiction assume our claim is false. We now compare
![]() ${\mathcal {M}}|\kappa $
with the construction
${\mathcal {M}}|\kappa $
with the construction
![]() $({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
.Footnote
8
We use
$({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
.Footnote
8
We use
![]() $\Sigma _{{\mathcal {M}}|\kappa }$
on the
$\Sigma _{{\mathcal {M}}|\kappa }$
on the
![]() ${\mathcal {M}}|\kappa $
-side and
${\mathcal {M}}|\kappa $
-side and
![]() $\Sigma $
on the
$\Sigma $
on the
![]() ${\mathcal {M}}$
-side. The comparison produces a tree
${\mathcal {M}}$
-side. The comparison produces a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {M}}|\kappa $
according to
${\mathcal {M}}|\kappa $
according to
![]() $\Lambda $
with last model
$\Lambda $
with last model
![]() ${\mathcal {N}}$
and a non-dropping tree
${\mathcal {N}}$
and a non-dropping tree
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() ${\mathcal {M}}$
according to
${\mathcal {M}}$
according to
![]() $\Sigma $
with last model
$\Sigma $
with last model
![]() ${\mathcal {M}}_1$
such that
${\mathcal {M}}_1$
such that
![]() $\pi ^{\mathcal {U}}({\mathcal R}_\delta )\trianglelefteq {\mathcal {N}}$
.
$\pi ^{\mathcal {U}}({\mathcal R}_\delta )\trianglelefteq {\mathcal {N}}$
.
Indeed, if
![]() ${\mathcal {M}}|\kappa $
-side lost then the comparison would have stopped before reaching stage
${\mathcal {M}}|\kappa $
-side lost then the comparison would have stopped before reaching stage
![]() $\pi ^{\mathcal {U}}(\delta )$
, and so there would be some
$\pi ^{\mathcal {U}}(\delta )$
, and so there would be some
![]() $\xi $
such that the second model of
$\xi $
such that the second model of
![]() $\pi ^{\mathcal {U}}(\vec {C})(\xi )$
was an iterate of
$\pi ^{\mathcal {U}}(\vec {C})(\xi )$
was an iterate of
![]() ${\mathcal {M}}|\kappa $
. This fact would be witnessed inside
${\mathcal {M}}|\kappa $
. This fact would be witnessed inside
![]() ${\mathcal {M}}_1$
, and hence by elementarity our claim would be true in
${\mathcal {M}}_1$
, and hence by elementarity our claim would be true in
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
Because
![]() ${\mathcal {M}}|\kappa $
has no Woodin cardinals, we must have that
${\mathcal {M}}|\kappa $
has no Woodin cardinals, we must have that
![]() $rud({\mathcal {N}})\vDash "\pi ^{\mathcal {U}}(\delta )$
is not a Woodin cardinal.” Because all initial segments of
$rud({\mathcal {N}})\vDash "\pi ^{\mathcal {U}}(\delta )$
is not a Woodin cardinal.” Because all initial segments of
![]() ${\mathcal {M}}|\kappa $
are
${\mathcal {M}}|\kappa $
are
![]() $\phi $
-small, we have that if
$\phi $
-small, we have that if
![]() ${\mathcal R}$
is the result of S-construction that translates
${\mathcal R}$
is the result of S-construction that translates
![]() ${\mathcal {M}}_1$
into a mouse over
${\mathcal {M}}_1$
into a mouse over
![]() $\pi ^{\mathcal {U}}({\mathcal R}_\delta )$
then
$\pi ^{\mathcal {U}}({\mathcal R}_\delta )$
then
![]() ${\mathcal {N}}\trianglelefteq {\mathcal R}$
. However, because
${\mathcal {N}}\trianglelefteq {\mathcal R}$
. However, because
![]() $\pi ^{\mathcal {U}}(\delta )$
is a Woodin cardinal of
$\pi ^{\mathcal {U}}(\delta )$
is a Woodin cardinal of
![]() ${\mathcal {M}}_1$
, we have that
${\mathcal {M}}_1$
, we have that
![]() ${\mathcal R}\vDash "\pi ^{\mathcal {U}}(\delta )$
is a Woodin cardinal,” contradiction.
${\mathcal R}\vDash "\pi ^{\mathcal {U}}(\delta )$
is a Woodin cardinal,” contradiction.
We now use branch condensation of
![]() $\Lambda $
to get a generically absolute definition of
$\Lambda $
to get a generically absolute definition of
![]() $\Lambda $
.Footnote
9
Let
$\Lambda $
.Footnote
9
Let
![]() $g\subseteq Coll(\omega , \kappa )$
be
$g\subseteq Coll(\omega , \kappa )$
be
![]() ${\mathcal {M}}$
-generic. For each
${\mathcal {M}}$
-generic. For each
![]() $\lambda \in (\kappa , \delta )$
, let
$\lambda \in (\kappa , \delta )$
, let
![]() $\vec {C}_\lambda =({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the output of the fully backgrounded construction of
$\vec {C}_\lambda =({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over a in which extenders used have critical points
${\mathcal {M}}|\delta [g]$
done over a in which extenders used have critical points
![]() $>\lambda $
. Let
$>\lambda $
. Let
![]() $\xi _\lambda $
be such that
$\xi _\lambda $
be such that
![]() ${\mathcal R}_{\xi _\lambda }$
is an iterate of
${\mathcal R}_{\xi _\lambda }$
is an iterate of
![]() ${\mathcal {M}}|\kappa $
. This iteration must be according to
${\mathcal {M}}|\kappa $
. This iteration must be according to
![]() $\Sigma _{{\mathcal {M}}|\kappa }$
. Let
$\Sigma _{{\mathcal {M}}|\kappa }$
. Let
![]() $\pi _\lambda :{\mathcal {M}}|\kappa \rightarrow {\mathcal R}_{\xi _\lambda }$
.
$\pi _\lambda :{\mathcal {M}}|\kappa \rightarrow {\mathcal R}_{\xi _\lambda }$
.
Suppose now h is any
![]() ${\mathcal {M}}[g]$
-generic for a poset of size
${\mathcal {M}}[g]$
-generic for a poset of size
![]() $<\delta $
. Then given a non-dropping tree
$<\delta $
. Then given a non-dropping tree
![]() ${\mathcal {T}}\in {\mathcal {M}}|\delta [g][h]$
on
${\mathcal {T}}\in {\mathcal {M}}|\delta [g][h]$
on
![]() ${\mathcal {M}}|\kappa $
we say
${\mathcal {M}}|\kappa $
we say
![]() ${\mathcal {T}}$
is correct if for all limit
${\mathcal {T}}$
is correct if for all limit
![]() $\alpha <lh({\mathcal {T}})$
, for some
$\alpha <lh({\mathcal {T}})$
, for some
![]() $\eta $
such that
$\eta $
such that
![]() ${\mathcal {T}}\in {\mathcal {M}}|\eta [g][h]$
for all
${\mathcal {T}}\in {\mathcal {M}}|\eta [g][h]$
for all
![]() $\lambda \in (\eta , \delta )$
, there is an embedding
$\lambda \in (\eta , \delta )$
, there is an embedding
![]() $\sigma :{\mathcal {M}}^{{\mathcal {T}}}_\alpha \rightarrow {\mathcal R}_{\xi _\lambda }$
such that
$\sigma :{\mathcal {M}}^{{\mathcal {T}}}_\alpha \rightarrow {\mathcal R}_{\xi _\lambda }$
such that
Given a correct tree
![]() ${\mathcal {T}}\in {\mathcal {M}}[g*h]$
, we let
${\mathcal {T}}\in {\mathcal {M}}[g*h]$
, we let
![]() $\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
be the statement that for some
$\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
be the statement that for some
![]() $\eta <\delta $
for all
$\eta <\delta $
for all
![]() $\lambda \in (\eta , \delta )$
:
$\lambda \in (\eta , \delta )$
:
-
1. b is a cofinal well-founded branch of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 ${\mathcal { Q}}={\mathcal { Q}}(b, {\mathcal {T}})$
and
${\mathcal { Q}}={\mathcal { Q}}(b, {\mathcal {T}})$
and -
2. there is an embedding
 $\sigma : {\mathcal {M}}^{\mathcal {T}}_b\rightarrow {\mathcal R}_{\xi _\lambda }$
such that
$\sigma : {\mathcal {M}}^{\mathcal {T}}_b\rightarrow {\mathcal R}_{\xi _\lambda }$
such that
 $\pi _\lambda =\sigma \circ \pi ^{\mathcal {T}}_b$
.
$\pi _\lambda =\sigma \circ \pi ^{\mathcal {T}}_b$
.
Let
![]() $\psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
be the statement that
$\psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
be the statement that
![]() ${\mathcal {T}}$
is correct and
${\mathcal {T}}$
is correct and
![]() $\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
holds. Notice that
$\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
holds. Notice that
(1) in
![]() ${\mathcal {M}}[g]$
, whenever
${\mathcal {M}}[g]$
, whenever
![]() $\mathbb {P}$
is a poset of size
$\mathbb {P}$
is a poset of size
![]() $<\delta $
,
$<\delta $
,
![]() $\mathbb {P}$
forces that for any correct tree
$\mathbb {P}$
forces that for any correct tree
![]() ${\mathcal {T}}$
there is
${\mathcal {T}}$
there is
![]() $b, {\mathcal { Q}}$
such that
$b, {\mathcal { Q}}$
such that
![]() $\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
.Footnote
10
$\phi [{\mathcal {T}}, b, {\mathcal { Q}}]$
.Footnote
10
The branch condensation of
![]() $\Lambda $
implies that such a pair
$\Lambda $
implies that such a pair
![]() $(b, {\mathcal { Q}})$
must be unique. We then get that
$(b, {\mathcal { Q}})$
must be unique. We then get that
![]() $\psi $
is a generically correct definition of
$\psi $
is a generically correct definition of
![]() $\Lambda $
.
$\Lambda $
.
Claim 2. For a club of countable
![]() $X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
, letting
$X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
, letting
![]() $\pi _X: {\mathcal {N}}_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse of X, and letting
$\pi _X: {\mathcal {N}}_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse of X, and letting
![]() $h\in {\mathcal {M}}[g]$
be
$h\in {\mathcal {M}}[g]$
be
![]() ${\mathcal {N}}_X$
-generic for a poset of size
${\mathcal {N}}_X$
-generic for a poset of size
![]() $<\pi _X^{-1}(\delta )$
, for any
$<\pi _X^{-1}(\delta )$
, for any
![]() $({\mathcal {T}}, b, {\mathcal { Q}})\in {\mathcal {N}}_X[h]$
,
$({\mathcal {T}}, b, {\mathcal { Q}})\in {\mathcal {N}}_X[h]$
,
Proof Left to right direction is easy and we leave it to the reader. For the other direction, suppose that
![]() $({\mathcal {T}}, b, {\mathcal { Q}})\in {\mathcal {N}}_X[h]$
and
$({\mathcal {T}}, b, {\mathcal { Q}})\in {\mathcal {N}}_X[h]$
and
![]() ${\mathcal {M}}[g]\vDash \psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
. First we claim that
${\mathcal {M}}[g]\vDash \psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
. First we claim that
![]() ${\mathcal {N}}_X[h]\vDash "{\mathcal {T}}$
is correct.” Suppose otherwise. Then there is a limit
${\mathcal {N}}_X[h]\vDash "{\mathcal {T}}$
is correct.” Suppose otherwise. Then there is a limit
![]() $\alpha <lh({\mathcal {T}})$
such that
$\alpha <lh({\mathcal {T}})$
such that
![]() ${\mathcal {N}}_X[h]\vDash "{\mathcal {T}}\restriction \alpha $
is correct and
${\mathcal {N}}_X[h]\vDash "{\mathcal {T}}\restriction \alpha $
is correct and
![]() ${\mathcal {T}}\restriction \alpha +1$
is not correct.” It follows from (1) that there is
${\mathcal {T}}\restriction \alpha +1$
is not correct.” It follows from (1) that there is
![]() $c, {\mathcal { Q}}\in {\mathcal {N}}_X$
such that c is not the branch of
$c, {\mathcal { Q}}\in {\mathcal {N}}_X$
such that c is not the branch of
![]() ${\mathcal {T}}\restriction \alpha $
in
${\mathcal {T}}\restriction \alpha $
in
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {N}}_X\vDash \psi [{\mathcal {T}}\restriction \alpha , c, {\mathcal { Q}}]$
. It follows that
${\mathcal {N}}_X\vDash \psi [{\mathcal {T}}\restriction \alpha , c, {\mathcal { Q}}]$
. It follows that
![]() ${\mathcal {M}}[g]\vDash \psi [{\mathcal {T}}\restriction \alpha , c, {\mathcal { Q}}]$
implying that c is the branch of
${\mathcal {M}}[g]\vDash \psi [{\mathcal {T}}\restriction \alpha , c, {\mathcal { Q}}]$
implying that c is the branch of
![]() ${\mathcal {T}}\restriction \alpha $
in
${\mathcal {T}}\restriction \alpha $
in
![]() ${\mathcal {T}}$
. A similar argument shows that in fact
${\mathcal {T}}$
. A similar argument shows that in fact
![]() ${\mathcal {N}}_X\vDash \psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
.
${\mathcal {N}}_X\vDash \psi [{\mathcal {T}}, b, {\mathcal { Q}}]$
.
We now show that countable submodels also have universally Baire strategies.
Proposition 1.5. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible operator,
$\mathbb {M}_\phi $
is an S-reconstructible operator,
![]() $a\in dom(\mathbb {M}_\phi )$
, and
$a\in dom(\mathbb {M}_\phi )$
, and
![]() $i\in \omega $
. Set
$i\in \omega $
. Set
![]() ${\mathcal {M}}=_{def}{\mathcal {M}}_\phi (a)$
and
${\mathcal {M}}=_{def}{\mathcal {M}}_\phi (a)$
and
![]() $\delta =\delta _{a, i}$
. Let
$\delta =\delta _{a, i}$
. Let
![]() $\pi : {\mathcal {N}}\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}$
be a countable hull inside
$\pi : {\mathcal {N}}\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}$
be a countable hull inside
![]() ${\mathcal {M}}$
. Then
${\mathcal {M}}$
. Then
![]() ${\mathcal {M}}\vDash$
“
${\mathcal {M}}\vDash$
“
![]() ${\mathcal {N}}$
has a
${\mathcal {N}}$
has a
![]() $\delta $
-uB iteration strategy that acts on trees above
$\delta $
-uB iteration strategy that acts on trees above
![]() $\pi ^{-1}(\delta _{a, i-1})$
.”
$\pi ^{-1}(\delta _{a, i-1})$
.”
Proof Again, we only do the proof of the representative case
![]() $i=0$
. Let
$i=0$
. Let
![]() $\Sigma $
be the unique iteration strategy of
$\Sigma $
be the unique iteration strategy of
![]() ${\mathcal {M}}$
, and let
${\mathcal {M}}$
, and let
![]() $({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the models of the fully backgrounded constructions of
$({\mathcal {S}}_\xi , {\mathcal R}_\xi , F_\xi : \xi <\delta )$
be the models of the fully backgrounded constructions of
![]() ${\mathcal {M}}|\delta $
over a. We claim that for some
${\mathcal {M}}|\delta $
over a. We claim that for some
![]() $\xi <\delta $
there is an embedding
$\xi <\delta $
there is an embedding
![]() $\sigma : {\mathcal {N}}\rightarrow {\mathcal R}_\xi $
. To build such an embedding, we compare
$\sigma : {\mathcal {N}}\rightarrow {\mathcal R}_\xi $
. To build such an embedding, we compare
![]() ${\mathcal {N}}$
with the aforementioned construction of
${\mathcal {N}}$
with the aforementioned construction of
![]() ${\mathcal {M}}|\delta $
. We use the
${\mathcal {M}}|\delta $
. We use the
![]() $\pi $
-pullback of
$\pi $
-pullback of
![]() $\Sigma $
to iterate
$\Sigma $
to iterate
![]() ${\mathcal {N}}$
. We claim that the construction side wins the comparisons.
${\mathcal {N}}$
. We claim that the construction side wins the comparisons.
To see this, assume not. We then get a tree
![]() ${\mathcal {T}}$
on
${\mathcal {T}}$
on
![]() ${\mathcal {N}}$
and a tree
${\mathcal {N}}$
and a tree
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() ${\mathcal {M}}|\delta $
with last models
${\mathcal {M}}|\delta $
with last models
![]() ${\mathcal {N}}_1$
and
${\mathcal {N}}_1$
and
![]() ${\mathcal {M}}_1$
respectively such that
${\mathcal {M}}_1$
respectively such that
![]() $\pi ^{\mathcal {U}}$
exists and
$\pi ^{\mathcal {U}}$
exists and
![]() $\pi ^{\mathcal {U}}({\mathcal R}_\delta )\trianglelefteq {\mathcal {N}}_1$
. As there are no Woodin cardinals in
$\pi ^{\mathcal {U}}({\mathcal R}_\delta )\trianglelefteq {\mathcal {N}}_1$
. As there are no Woodin cardinals in
![]() ${\mathcal R}_\delta $
(see Lemma 1.3),
${\mathcal R}_\delta $
(see Lemma 1.3),
![]() $({\mathcal {T}}\restriction lh({\mathcal {T}})-1)\in {\mathcal {M}}_1$
. It follows that there is a tree
$({\mathcal {T}}\restriction lh({\mathcal {T}})-1)\in {\mathcal {M}}_1$
. It follows that there is a tree
![]() ${\mathcal {W} }\in {\mathcal {M}}$
on
${\mathcal {W} }\in {\mathcal {M}}$
on
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
![]() $C({\mathcal {W} })={\mathcal R}_\delta $
. It follows that
$C({\mathcal {W} })={\mathcal R}_\delta $
. It follows that
![]() ${\mathcal {M}}|(\omega _1)^{\mathcal {M}}\trianglelefteq {\mathcal {N}}$
, contradicting the fact that
${\mathcal {M}}|(\omega _1)^{\mathcal {M}}\trianglelefteq {\mathcal {N}}$
, contradicting the fact that
![]() ${\mathcal {N}}$
is countable in
${\mathcal {N}}$
is countable in
![]() ${\mathcal {M}}$
. This contradiction shows that there is
${\mathcal {M}}$
. This contradiction shows that there is
![]() $\sigma :{\mathcal {N}}\rightarrow {\mathcal R}_\xi $
for some
$\sigma :{\mathcal {N}}\rightarrow {\mathcal R}_\xi $
for some
![]() $\xi <\delta $
. The rest follows from Proposition 1.4.Footnote
11
It is not hard to show that the
$\xi <\delta $
. The rest follows from Proposition 1.4.Footnote
11
It is not hard to show that the
![]() $\sigma $
-pullback of the strategy of
$\sigma $
-pullback of the strategy of
![]() ${\mathcal R}_\xi $
induced by
${\mathcal R}_\xi $
induced by
![]() $\Sigma $
is
$\Sigma $
is
![]() $\delta $
-uB in
$\delta $
-uB in
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
We state, without a proof, a somewhat stronger version of Proposition 1.5.
Proposition 1.6. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator,
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator,
![]() $a\in dom(\mathbb {M}_\phi )$
, and
$a\in dom(\mathbb {M}_\phi )$
, and
![]() $i\in \omega $
. Set
$i\in \omega $
. Set
![]() $\delta =\delta _{a, i}$
and
$\delta =\delta _{a, i}$
and
![]() ${\mathcal {M}}={\mathcal {M}}_{\phi }(a)$
. Let
${\mathcal {M}}={\mathcal {M}}_{\phi }(a)$
. Let
![]() $\Sigma $
be the unique iteration strategy of
$\Sigma $
be the unique iteration strategy of
![]() ${\mathcal {M}}$
. Suppose g is
${\mathcal {M}}$
. Suppose g is
![]() ${\mathcal {M}}$
-generic for a poset of size
${\mathcal {M}}$
-generic for a poset of size
![]() $<\delta $
, and let
$<\delta $
, and let
![]() $\pi : {\mathcal {N}}[\bar {g}]\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be a countable hull in
$\pi : {\mathcal {N}}[\bar {g}]\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be a countable hull in
![]() ${\mathcal {M}}[g]$
. Then
${\mathcal {M}}[g]$
. Then
![]() ${\mathcal {M}}[g]\vDash \textit{"} {\mathcal {N}}$
has a
${\mathcal {M}}[g]\vDash \textit{"} {\mathcal {N}}$
has a
![]() $\delta $
-uB iteration strategy acting on trees that are above
$\delta $
-uB iteration strategy acting on trees that are above
![]() $\pi ^{-1}(\delta _{a, i-1})$
.”
$\pi ^{-1}(\delta _{a, i-1})$
.”
The next lemma shows that for any x, proper initial segments of
![]() ${\mathcal {W} }(x)$
have universally Baire iterations strategies (in
${\mathcal {W} }(x)$
have universally Baire iterations strategies (in
![]() ${\mathcal {M}}_\phi (a)$
). However, the function
${\mathcal {M}}_\phi (a)$
). However, the function
![]() $x\rightarrow {\mathcal {W} }(x)$
cannot be universally Baire. For this we need to collapse the first strong cardinal of
$x\rightarrow {\mathcal {W} }(x)$
cannot be universally Baire. For this we need to collapse the first strong cardinal of
![]() ${\mathcal {M}}(a)$
. The reason is that
${\mathcal {M}}(a)$
. The reason is that
![]() ${\mathcal {W} }(x)$
is the set of all OD subsets of x in the derived model of
${\mathcal {W} }(x)$
is the set of all OD subsets of x in the derived model of
![]() ${\mathcal {M}}(a)$
computed at
${\mathcal {M}}(a)$
computed at
![]() $\delta _{a, \omega }$
, and this derived model is a model in which all sets are ordinal definable from a real. For more on this we refer the reader to [Reference Steel18].
$\delta _{a, \omega }$
, and this derived model is a model in which all sets are ordinal definable from a real. For more on this we refer the reader to [Reference Steel18].
Proposition 1.7. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Let
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator. Let
![]() $a\in dom(\mathbb {M}_\phi )$
and
$a\in dom(\mathbb {M}_\phi )$
and
![]() $i\in \omega $
. Set
$i\in \omega $
. Set
![]() ${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
${\mathcal {M}}={\mathcal {M}}_\phi (a)$
and
![]() $\delta =\delta _{a, i}$
. Let g be
$\delta =\delta _{a, i}$
. Let g be
![]() ${\mathcal {M}}$
-generic for a poset of size
${\mathcal {M}}$
-generic for a poset of size
![]() $<\delta $
,
$<\delta $
,
![]() $x\in {\mathcal {M}}|\delta [g]\cap dom({\mathcal {W} })$
, and
$x\in {\mathcal {M}}|\delta [g]\cap dom({\mathcal {W} })$
, and
![]() ${\mathcal { Q}}\trianglelefteq {\mathcal {W} }(x)$
be such that
${\mathcal { Q}}\trianglelefteq {\mathcal {W} }(x)$
be such that
![]() $\rho _{\omega }({\mathcal { Q}})=\omega $
. Let
$\rho _{\omega }({\mathcal { Q}})=\omega $
. Let
![]() $\Lambda $
be the unique strategy of
$\Lambda $
be the unique strategy of
![]() ${\mathcal { Q}}$
. Then
${\mathcal { Q}}$
. Then
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}|\delta [g[$
and is
$\Lambda \restriction HC^{{\mathcal {M}}[g]}\in {\mathcal {M}}|\delta [g[$
and is
![]() $\delta $
-uB in
$\delta $
-uB in
![]() ${\mathcal {M}}$
in the stronger sense that for any
${\mathcal {M}}$
in the stronger sense that for any
![]() ${\mathcal {M}}[g]$
-generic h,
${\mathcal {M}}[g]$
-generic h,
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g*h]}$
is the canonical extension of
$\Lambda \restriction HC^{{\mathcal {M}}[g*h]}$
is the canonical extension of
![]() $\Lambda \restriction HC^{{\mathcal {M}}[g]}$
.
$\Lambda \restriction HC^{{\mathcal {M}}[g]}$
.
Proof We again do the proof in the representative case of
![]() $i=0$
. To prove the claim fix
$i=0$
. To prove the claim fix
![]() $g, x, {\mathcal { Q}}$
as in the statement of the proposition. Let
$g, x, {\mathcal { Q}}$
as in the statement of the proposition. Let
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points
![]() $>\lambda $
where
$>\lambda $
where
![]() $\lambda $
is some cardinal
$\lambda $
is some cardinal
![]() $<\delta $
bigger than the size of the poset. We have that
$<\delta $
bigger than the size of the poset. We have that
![]() ${\mathcal { Q}}\trianglelefteq {\mathcal {P} }$
. Thus, again, the iterability of
${\mathcal { Q}}\trianglelefteq {\mathcal {P} }$
. Thus, again, the iterability of
![]() ${\mathcal { Q}}$
reduces to the iterability of some
${\mathcal { Q}}$
reduces to the iterability of some
![]() ${\mathcal {M}}|\kappa $
for non-dropping trees where
${\mathcal {M}}|\kappa $
for non-dropping trees where
![]() $\kappa>\lambda $
is a regular cardinal of
$\kappa>\lambda $
is a regular cardinal of
![]() ${\mathcal {M}}$
. The rest of the claim follows from Propositions 1.4 and 1.5.
${\mathcal {M}}$
. The rest of the claim follows from Propositions 1.4 and 1.5.
2 The internal covering property
We will need to deal with S-reconstructible operators with a stronger property. Recall the
![]() ${\mathcal {W} }(x)$
function given by
${\mathcal {W} }(x)$
function given by
![]() ${\mathcal {W} }(x)={\mathcal {M}}(x)|(\left |x\right |{}^+)^{{\mathcal {M}}(x)}$
.
${\mathcal {W} }(x)={\mathcal {M}}(x)|(\left |x\right |{}^+)^{{\mathcal {M}}(x)}$
.
Definition 2.1. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator. We say
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator. We say
![]() $\mathbb {M}_\phi $
has the internal covering property if for any
$\mathbb {M}_\phi $
has the internal covering property if for any
![]() $a\in dom(\mathbb {M}_\phi )$
and
$a\in dom(\mathbb {M}_\phi )$
and
![]() $i\in \omega $
, letting
$i\in \omega $
, letting
![]() ${\mathcal {M}}={\mathcal {M}}(a)$
and
${\mathcal {M}}={\mathcal {M}}(a)$
and
![]() $\delta =\delta _{a, i}$
, for any
$\delta =\delta _{a, i}$
, for any
![]() $\mathbb {P}\in {\mathcal {M}}|\delta $
,
$\mathbb {P}\in {\mathcal {M}}|\delta $
,
![]() ${\mathcal {M}}$
-generic
${\mathcal {M}}$
-generic
![]() $g\subseteq \mathbb {P}$
,
$g\subseteq \mathbb {P}$
,
![]() $x\in {\mathcal {M}}|\delta [g]$
, and
$x\in {\mathcal {M}}|\delta [g]$
, and
![]() $\lambda \in (\delta _{a, i-1}, \delta )$
such that:
$\lambda \in (\delta _{a, i-1}, \delta )$
such that:
-
1.
 $a\in L_\omega [x]$
,
$a\in L_\omega [x]$
, -
2.
 $L_{\omega }[x]\vDash "x$
is well-ordered,”
$L_{\omega }[x]\vDash "x$
is well-ordered,” -
3.
 $x\in {\mathcal {M}}|\lambda [g]$
,
$x\in {\mathcal {M}}|\lambda [g]$
, -
4.
 ${\mathcal {M}}|\delta _{a, i-1}$
is generic over
${\mathcal {M}}|\delta _{a, i-1}$
is generic over
 ${\mathcal {W} }(x)$
,
${\mathcal {W} }(x)$
, -
5.
 $\mathbb {P}\in {\mathcal {M}}|\lambda $
.
$\mathbb {P}\in {\mathcal {M}}|\lambda $
.
Letting
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points greater than
${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points greater than
![]() $\lambda $
, for unboundedly many
$\lambda $
, for unboundedly many
![]() $\kappa <\delta $
,
$\kappa <\delta $
,
![]() $(\kappa ^+)^{\mathcal {P} }=(\kappa ^+)^{\mathcal {M}}$
.
$(\kappa ^+)^{\mathcal {P} }=(\kappa ^+)^{\mathcal {M}}$
.
Let
![]() $\mathbb {M}$
be either
$\mathbb {M}$
be either
![]() $x\rightarrow {\mathcal {M}}_\omega (x)$
or
$x\rightarrow {\mathcal {M}}_\omega (x)$
or
![]() $x\rightarrow {\mathcal {M}}_{wlw}(x)$
. Both of these operators are S-reconstructible. Here we show that they also have the internal covering property.
$x\rightarrow {\mathcal {M}}_{wlw}(x)$
. Both of these operators are S-reconstructible. Here we show that they also have the internal covering property.
Suppose
![]() ${\mathcal {M}}$
is a mouse,
${\mathcal {M}}$
is a mouse,
![]() $\kappa $
is an inaccessible cardinal of
$\kappa $
is an inaccessible cardinal of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $\rho _\omega ({\mathcal {M}})\geq \kappa $
, and
$\rho _\omega ({\mathcal {M}})\geq \kappa $
, and
![]() ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
![]() ${\mathcal {M}}|\kappa $
. We then let
${\mathcal {M}}|\kappa $
. We then let
![]() ${\mathcal {T}}^{\mathcal {M}}$
be the iteration tree on
${\mathcal {T}}^{\mathcal {M}}$
be the iteration tree on
![]() ${\mathcal {M}}$
that has the same tree structure as
${\mathcal {M}}$
that has the same tree structure as
![]() ${\mathcal {T}}$
and uses the same extenders as
${\mathcal {T}}$
and uses the same extenders as
![]() ${\mathcal {T}}$
.Footnote
12
Similarly, given an iteration tree on
${\mathcal {T}}$
.Footnote
12
Similarly, given an iteration tree on
![]() ${\mathcal {M}}$
that is below
${\mathcal {M}}$
that is below
![]() $\kappa $
, we let
$\kappa $
, we let
![]() ${\mathcal {T}}\restriction ({\mathcal {M}}|\kappa )$
be the iteration tree on
${\mathcal {T}}\restriction ({\mathcal {M}}|\kappa )$
be the iteration tree on
![]() ${\mathcal {M}}|\kappa $
that has the same tree structure and uses the same extenders as
${\mathcal {M}}|\kappa $
that has the same tree structure and uses the same extenders as
![]() ${\mathcal {T}}$
.
${\mathcal {T}}$
.
Theorem 2.2.
![]() $\mathbb {M}$
has the internal covering property.
$\mathbb {M}$
has the internal covering property.
Proof We show that
![]() ${\mathcal {M}}=_{def}{\mathcal {M}}(\emptyset )$
satisfies the internal covering property. Here the representative case is
${\mathcal {M}}=_{def}{\mathcal {M}}(\emptyset )$
satisfies the internal covering property. Here the representative case is
![]() $i=1$
, so we assume
$i=1$
, so we assume
![]() $i=1$
. Let
$i=1$
. Let
![]() $\delta _0=\delta _{\emptyset , 0}$
and
$\delta _0=\delta _{\emptyset , 0}$
and
![]() $\delta =\delta _{\emptyset , 1}$
. Let
$\delta =\delta _{\emptyset , 1}$
. Let
![]() $\phi $
be the obvious defining formula of
$\phi $
be the obvious defining formula of
![]() $\mathbb {M}$
.Footnote
13
$\mathbb {M}$
.Footnote
13
Let
![]() $\xi $
be the sup of the Woodin cardinals of
$\xi $
be the sup of the Woodin cardinals of
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() $g\subseteq Coll(\omega , <\xi )$
be generic over
$g\subseteq Coll(\omega , <\xi )$
be generic over
![]() ${\mathcal {M}}$
. Let W be the derived model of
${\mathcal {M}}$
. Let W be the derived model of
![]() ${\mathcal {M}}$
as computed in
${\mathcal {M}}$
as computed in
![]() ${\mathcal {M}}[g]$
. More precisely,
${\mathcal {M}}[g]$
. More precisely,
![]() $W=L(\Gamma , {\mathbb {R}}^*)$
where
$W=L(\Gamma , {\mathbb {R}}^*)$
where
![]() ${\mathbb {R}}^*=\cup _{\kappa <\xi }{\mathbb {R}}^{{\mathcal {M}}[g\cap Coll(\omega , <\kappa )]}$
and
${\mathbb {R}}^*=\cup _{\kappa <\xi }{\mathbb {R}}^{{\mathcal {M}}[g\cap Coll(\omega , <\kappa )]}$
and
![]() $\Gamma $
is the collection of all those sets of reals A of
$\Gamma $
is the collection of all those sets of reals A of
![]() ${\mathcal {M}}({\mathbb {R}}^*)$
such that
${\mathcal {M}}({\mathbb {R}}^*)$
such that
![]() $L(A, {\mathbb {R}}^*)\vDash AD^+$
. Woodin’s celebrated derived model theorem says that
$L(A, {\mathbb {R}}^*)\vDash AD^+$
. Woodin’s celebrated derived model theorem says that
![]() $L(\Gamma , {\mathbb {R}}^*)\vDash AD^+$
and in
$L(\Gamma , {\mathbb {R}}^*)\vDash AD^+$
and in
![]() ${\mathcal {M}}({\mathbb {R}}^*)$
,
${\mathcal {M}}({\mathbb {R}}^*)$
,
![]() ${\wp }({\mathbb {R}}^*)\cap W=\Gamma $
. In the case of
${\wp }({\mathbb {R}}^*)\cap W=\Gamma $
. In the case of
![]() ${\mathcal {M}}={\mathcal {M}}_\omega $
, W is just
${\mathcal {M}}={\mathcal {M}}_\omega $
, W is just
![]() $L({\mathbb {R}}^*)$
(see [Reference Steel19]).
$L({\mathbb {R}}^*)$
(see [Reference Steel19]).
Working in W, let
![]() $\nu $
be the supremum of
$\nu $
be the supremum of
![]() $OD^W$
prewellorderings of
$OD^W$
prewellorderings of
![]() ${\mathbb {R}}$
. Below we collect some facts that can be proved using
${\mathbb {R}}$
. Below we collect some facts that can be proved using
![]() $\mathrm {{HOD}}$
-analysis done inside W. The reader should consult [Reference Steel and Woodin21]. Giving the complete proofs of these facts is beyond this paper. Let
$\mathrm {{HOD}}$
-analysis done inside W. The reader should consult [Reference Steel and Woodin21]. Giving the complete proofs of these facts is beyond this paper. Let
![]() ${\mathcal { H}}=\mathrm {{HOD}}^W_{{\mathcal {M}}|\delta _0}$
and let
${\mathcal { H}}=\mathrm {{HOD}}^W_{{\mathcal {M}}|\delta _0}$
and let
![]() $\Sigma $
be the unique iteration strategy of
$\Sigma $
be the unique iteration strategy of
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
-
1.
 $V_\nu ^{\mathcal { H}}$
can be representedFootnote
14
as a
$V_\nu ^{\mathcal { H}}$
can be representedFootnote
14
as a
 $\Sigma $
-iterate of
$\Sigma $
-iterate of
 ${\mathcal {M}}|\delta $
via an iteration that is above
${\mathcal {M}}|\delta $
via an iteration that is above
 $\delta _0$
.
$\delta _0$
. -
2.
 ${\mathcal { H}}\vDash "\nu $
is a Woodin cardinal.”
${\mathcal { H}}\vDash "\nu $
is a Woodin cardinal.” -
3. Suppose
 $\mathbb {P}\in {\mathcal { H}}|\nu $
is a poset and
$\mathbb {P}\in {\mathcal { H}}|\nu $
is a poset and
 $g\subseteq \mathbb {P}$
is
$g\subseteq \mathbb {P}$
is
 ${\mathcal { H}}$
-generic. Then
${\mathcal { H}}$
-generic. Then
 ${\mathcal { H}}[g]\vDash "{\mathcal { H}}|\nu $
is
${\mathcal { H}}[g]\vDash "{\mathcal { H}}|\nu $
is
 $\nu +1$
-iterableFootnote
15
for trees that are in
$\nu +1$
-iterableFootnote
15
for trees that are in
 $L[{\mathcal { H}}|\nu ][g]$
.”
$L[{\mathcal { H}}|\nu ][g]$
.” -
4. Let
 ${\mathcal {S}}$
be the iterate of
${\mathcal {S}}$
be the iterate of
 ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
 ${\mathcal { H}}|\nu \trianglelefteq {\mathcal {S}}$
and if
${\mathcal { H}}|\nu \trianglelefteq {\mathcal {S}}$
and if
 $i: {\mathcal {M}}\rightarrow {\mathcal {S}}$
is the iteration embedding then the generators of i are contained inside
$i: {\mathcal {M}}\rightarrow {\mathcal {S}}$
is the iteration embedding then the generators of i are contained inside
 $\nu $
. Then the aforementioned strategy of
$\nu $
. Then the aforementioned strategy of
 ${\mathcal { H}}|\nu $
is
${\mathcal { H}}|\nu $
is
 $\Sigma _{\mathcal {S}}\restriction (L[{\mathcal { H}}|\nu ][g])$
.
$\Sigma _{\mathcal {S}}\restriction (L[{\mathcal { H}}|\nu ][g])$
.
Let now
![]() ${\mathcal {S}}$
be as in clause 4 above. We want to prove now that
${\mathcal {S}}$
be as in clause 4 above. We want to prove now that
![]() ${\mathcal {S}}$
satisfies the internal covering. We have that
${\mathcal {S}}$
satisfies the internal covering. We have that
![]() ${\mathcal {S}}|\nu ={\mathcal { H}}|\nu $
.
${\mathcal {S}}|\nu ={\mathcal { H}}|\nu $
.
Fix
![]() $\lambda \in (\delta _0, \nu )$
and let
$\lambda \in (\delta _0, \nu )$
and let
![]() $\mathbb {P}\in {\mathcal {S}}|\lambda $
be a poset. Let
$\mathbb {P}\in {\mathcal {S}}|\lambda $
be a poset. Let
![]() $g\subseteq \mathbb {P}$
be
$g\subseteq \mathbb {P}$
be
![]() ${\mathcal {S}}$
-generic and
${\mathcal {S}}$
-generic and
![]() $x\in {\mathcal {M}}|\lambda [g]$
be such that
$x\in {\mathcal {M}}|\lambda [g]$
be such that
![]() ${\mathcal {M}}|\delta _0$
is generic over
${\mathcal {M}}|\delta _0$
is generic over
![]() ${\mathcal {W} }(x)$
and
${\mathcal {W} }(x)$
and
![]() $L_\omega [x]\vDash "x$
is well-ordered.” Let
$L_\omega [x]\vDash "x$
is well-ordered.” Let
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points greater than
${\mathcal {M}}|\delta [g]$
done over x using extenders with critical points greater than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() ${\mathcal {W} }$
be the output of the fully backgrounded construction of
${\mathcal {W} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {P} }[{\mathcal {M}}|\delta _0]$
done over
${\mathcal {P} }[{\mathcal {M}}|\delta _0]$
done over
![]() ${\mathcal {M}}|\delta _0$
in which extenders used have critical points
${\mathcal {M}}|\delta _0$
in which extenders used have critical points
![]() $>\lambda $
. It is enough to show that in
$>\lambda $
. It is enough to show that in
![]() ${\mathcal {S}}$
,
${\mathcal {S}}$
,
![]() ${\mathcal {W} }$
computes unboundedly many successors correctly.
${\mathcal {W} }$
computes unboundedly many successors correctly.
We now compare
![]() ${\mathcal { H}}|\nu $
with
${\mathcal { H}}|\nu $
with
![]() ${\mathcal {W} }$
. On
${\mathcal {W} }$
. On
![]() ${\mathcal { H}}|\nu $
side we use the (
${\mathcal { H}}|\nu $
side we use the (
![]() $\nu +1$
)-strategy in
$\nu +1$
)-strategy in
![]() ${\mathcal { H}}$
that acts on iteration trees in
${\mathcal { H}}$
that acts on iteration trees in
![]() $L[{\mathcal { H}}|\nu ][g]$
. Let
$L[{\mathcal { H}}|\nu ][g]$
. Let
![]() $\Lambda $
be this strategy (which is a fragment of
$\Lambda $
be this strategy (which is a fragment of
![]() $\Sigma _{{\mathcal {S}}|\nu }$
). Notice that
$\Sigma _{{\mathcal {S}}|\nu }$
). Notice that
![]() $\Lambda $
induces a strategy for
$\Lambda $
induces a strategy for
![]() ${\mathcal {W} }$
(via the resurrection process described in [Reference Mitchell and Steel5, Chapter 12]). Let then
${\mathcal {W} }$
(via the resurrection process described in [Reference Mitchell and Steel5, Chapter 12]). Let then
![]() $\Psi $
be the strategy of
$\Psi $
be the strategy of
![]() ${\mathcal {W} }$
induced by
${\mathcal {W} }$
induced by
![]() $\Lambda $
. Both
$\Lambda $
. Both
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Psi $
act on trees of length
$\Psi $
act on trees of length
![]() $\leq \nu $
that are in
$\leq \nu $
that are in
![]() $L[{\mathcal { H}}|\nu ][g]$
.
$L[{\mathcal { H}}|\nu ][g]$
.
The aforementioned comparison process lasts at most
![]() $\nu +1$
steps.Footnote
16
Suppose first that the comparison process stops in
$\nu +1$
steps.Footnote
16
Suppose first that the comparison process stops in
![]() $<\nu $
-steps. Let
$<\nu $
-steps. Let
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
be the trees on
${\mathcal {U}}$
be the trees on
![]() ${\mathcal { H}}|\nu $
and
${\mathcal { H}}|\nu $
and
![]() ${\mathcal {W} }$
respectively with last models
${\mathcal {W} }$
respectively with last models
![]() ${\mathcal { H}}_1$
and
${\mathcal { H}}_1$
and
![]() ${\mathcal {W} }_1$
respectively. We must have that both
${\mathcal {W} }_1$
respectively. We must have that both
![]() $\pi ^{\mathcal {T}}$
and
$\pi ^{\mathcal {T}}$
and
![]() $\pi ^{\mathcal {U}}$
exist. It follows that there is a club of
$\pi ^{\mathcal {U}}$
exist. It follows that there is a club of
![]() $\xi $
such that
$\xi $
such that
![]() $\pi ^{\mathcal {T}}(\xi )=\xi =\pi ^{\mathcal {U}}(\xi )$
. For any such
$\pi ^{\mathcal {T}}(\xi )=\xi =\pi ^{\mathcal {U}}(\xi )$
. For any such
![]() $\xi $
we have that
$\xi $
we have that
which is what we wanted to show.
Suppose next that the comparison process lasts
![]() $\nu $
-steps. Let
$\nu $
-steps. Let
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
be the trees on
${\mathcal {U}}$
be the trees on
![]() ${\mathcal { H}}|\nu $
and
${\mathcal { H}}|\nu $
and
![]() ${\mathcal {W} }$
respectively. In order to apply
${\mathcal {W} }$
respectively. In order to apply
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Psi $
we must first show that both
$\Psi $
we must first show that both
![]() ${\mathcal {T}}, {\mathcal {U}}\in L[{\mathcal { H}}|\nu ][g]$
. Notice that for any limit
${\mathcal {T}}, {\mathcal {U}}\in L[{\mathcal { H}}|\nu ][g]$
. Notice that for any limit
![]() $\alpha <\nu $
, the branch chosen by
$\alpha <\nu $
, the branch chosen by
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
at stage
${\mathcal {U}}$
at stage
![]() $\alpha $
is determined by the corresponding
$\alpha $
is determined by the corresponding
![]() ${\mathcal { Q}}$
-structures. More precisely, if
${\mathcal { Q}}$
-structures. More precisely, if
![]() $b=\Lambda ({\mathcal {T}}\restriction \alpha )$
and
$b=\Lambda ({\mathcal {T}}\restriction \alpha )$
and
![]() $c=\Psi ({\mathcal {U}}\restriction \alpha )$
then both
$c=\Psi ({\mathcal {U}}\restriction \alpha )$
then both
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction \alpha )$
and
${\mathcal { Q}}(b, {\mathcal {T}}\restriction \alpha )$
and
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction \alpha )$
exist and are equal to respectively
${\mathcal { Q}}(c, {\mathcal {U}}\restriction \alpha )$
exist and are equal to respectively
![]() ${\mathcal { Q}}({\mathcal {T}}\restriction \alpha )$
and
${\mathcal { Q}}({\mathcal {T}}\restriction \alpha )$
and
![]() ${\mathcal { Q}}({\mathcal {U}}\restriction \alpha )$
. However, since
${\mathcal { Q}}({\mathcal {U}}\restriction \alpha )$
. However, since
![]() $C({\mathcal {T}})=C({\mathcal {U}})$
, we must have that
$C({\mathcal {T}})=C({\mathcal {U}})$
, we must have that
![]() ${\mathcal { Q}}({\mathcal {T}})={\mathcal { Q}}({\mathcal {U}})$
. Thus, the comparison process is definable over
${\mathcal { Q}}({\mathcal {T}})={\mathcal { Q}}({\mathcal {U}})$
. Thus, the comparison process is definable over
![]() ${\mathcal { H}}|\nu $
(for instance, see Corollary 1.4). It follows that indeed
${\mathcal { H}}|\nu $
(for instance, see Corollary 1.4). It follows that indeed
![]() ${\mathcal {T}}, {\mathcal {U}}\in L[{\mathcal { H}}|\nu ][g]$
.
${\mathcal {T}}, {\mathcal {U}}\in L[{\mathcal { H}}|\nu ][g]$
.
Let
![]() ${\mathcal {N}}$
be the output of the S-construction that translates
${\mathcal {N}}$
be the output of the S-construction that translates
![]() ${\mathcal {S}}$
into a mouse over
${\mathcal {S}}$
into a mouse over
![]() ${\mathcal {W} }$
. We have that
${\mathcal {W} }$
. We have that
![]() ${\mathcal {N}}\vDash \phi $
. Set
${\mathcal {N}}\vDash \phi $
. Set
![]() $b=\Lambda ({\mathcal {T}})$
and
$b=\Lambda ({\mathcal {T}})$
and
![]() $c=\Psi ({\mathcal {U}})$
.
$c=\Psi ({\mathcal {U}})$
.
Notice that
![]() ${\mathcal {N}}$
has an iteration strategy induced by
${\mathcal {N}}$
has an iteration strategy induced by
![]() $\Sigma _{\mathcal {S}}$
, and if
$\Sigma _{\mathcal {S}}$
, and if
![]() $\Psi ^+$
is this strategy then
$\Psi ^+$
is this strategy then
![]() $\Psi ^+({\mathcal {U}}^{\mathcal {N}})=c$
. Similarly,
$\Psi ^+({\mathcal {U}}^{\mathcal {N}})=c$
. Similarly,
![]() $\Sigma _{\mathcal {S}}({\mathcal {T}}^{\mathcal {S}})=b$
. Let
$\Sigma _{\mathcal {S}}({\mathcal {T}}^{\mathcal {S}})=b$
. Let
![]() ${\mathcal {T}}^+={\mathcal {T}}^{\mathcal {S}}$
and
${\mathcal {T}}^+={\mathcal {T}}^{\mathcal {S}}$
and
![]() ${\mathcal {U}}^+={\mathcal {U}}^{\mathcal {N}}$
.
${\mathcal {U}}^+={\mathcal {U}}^{\mathcal {N}}$
.
Claim 1.
![]() ${\mathcal {M}}^{\mathcal {T}}_b={\mathcal {M}}^{\mathcal {U}}_c$
.
${\mathcal {M}}^{\mathcal {T}}_b={\mathcal {M}}^{\mathcal {U}}_c$
.
Proof Because
![]() $\nu $
is inaccessible in
$\nu $
is inaccessible in
![]() ${\mathcal { H}}$
, we have that either
${\mathcal { H}}$
, we have that either
![]() ${\mathcal {M}}^{\mathcal {T}}_b\triangleleft {\mathcal {M}}^{\mathcal {U}}_c$
or
${\mathcal {M}}^{\mathcal {T}}_b\triangleleft {\mathcal {M}}^{\mathcal {U}}_c$
or
![]() ${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
.Footnote
17
Because both cases are symmetric let us deal with the case
${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
.Footnote
17
Because both cases are symmetric let us deal with the case
![]() ${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
and leave the other case (which actually is easier as
${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
and leave the other case (which actually is easier as
![]() ${\mathcal {T}}$
is a tree on the universe itself) to the reader.
${\mathcal {T}}$
is a tree on the universe itself) to the reader.
Again, the usual comparison argument for weasels (see, for example, Theorem 2.10 of [Reference Löwe and Steel4]) implies that either
![]() $\pi ^{{\mathcal {T}}^+}_b(\nu )>\nu $
or there is a drop on b. To see this, assume that
$\pi ^{{\mathcal {T}}^+}_b(\nu )>\nu $
or there is a drop on b. To see this, assume that
![]() $\pi ^{{\mathcal {T}}^+}_b$
exists and
$\pi ^{{\mathcal {T}}^+}_b$
exists and
![]() $\pi ^{{\mathcal {T}}^+}_b(\nu )=\nu $
. As
$\pi ^{{\mathcal {T}}^+}_b(\nu )=\nu $
. As
![]() ${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
, we have that
${\mathcal {M}}^{\mathcal {U}}_c\triangleleft {\mathcal {M}}^{\mathcal {T}}_b$
, we have that
![]() $Ord\cap {\mathcal {M}}^{\mathcal {U}}_c< \nu $
which implies that there is a drop in c. But then
$Ord\cap {\mathcal {M}}^{\mathcal {U}}_c< \nu $
which implies that there is a drop in c. But then
![]() ${\mathcal {W} }$
side cannot lose the comparison (once again see Theorem 2.10 of [Reference Löwe and Steel4]).
${\mathcal {W} }$
side cannot lose the comparison (once again see Theorem 2.10 of [Reference Löwe and Steel4]).
We thus have that either
![]() $\pi ^{{\mathcal {T}}^+}_b(\nu )>\nu $
or there is a drop on b. In both cases,
$\pi ^{{\mathcal {T}}^+}_b(\nu )>\nu $
or there is a drop on b. In both cases,
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
is defined. Now the usual comparison argument for weasels implies that c doesn’t have a drop and
${\mathcal { Q}}(b, {\mathcal {T}})$
is defined. Now the usual comparison argument for weasels implies that c doesn’t have a drop and
![]() $\pi ^{\mathcal {U}}_c(\nu )=\nu $
. It follows that
$\pi ^{\mathcal {U}}_c(\nu )=\nu $
. It follows that
![]() ${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash "\nu $
is a Woodin cardinal.” It then also follows that
${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash "\nu $
is a Woodin cardinal.” It then also follows that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
cannot have extenders overlapping
${\mathcal { Q}}(b, {\mathcal {T}})$
cannot have extenders overlapping
![]() $\nu $
as otherwise there will be Woodin cardinals in
$\nu $
as otherwise there will be Woodin cardinals in
![]() ${\mathcal {M}}^{\mathcal {U}}_c$
. Hence,
${\mathcal {M}}^{\mathcal {U}}_c$
. Hence,
![]() ${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {M}}({\mathcal {M}}^{\mathcal {U}}_c)$
. But since
${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {M}}({\mathcal {M}}^{\mathcal {U}}_c)$
. But since
![]() ${\mathcal {N}}\vDash \phi $
, we have that
${\mathcal {N}}\vDash \phi $
, we have that
![]() ${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash \phi $
, implying that in fact
${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash \phi $
, implying that in fact
![]() ${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {M}}^{{\mathcal {U}}^+}_c$
. Hence,
${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {M}}^{{\mathcal {U}}^+}_c$
. Hence,
![]() ${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash "\nu $
is not a Woodin cardinal,” contradiction.
${\mathcal {M}}^{{\mathcal {U}}^+}_c\vDash "\nu $
is not a Woodin cardinal,” contradiction.
We thus assume that
![]() ${\mathcal {M}}^{\mathcal {T}}_b={\mathcal {M}}^{\mathcal {U}}_c$
. In fact, the proof of the claim above shows that both
${\mathcal {M}}^{\mathcal {T}}_b={\mathcal {M}}^{\mathcal {U}}_c$
. In fact, the proof of the claim above shows that both
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
and
${\mathcal { Q}}(b, {\mathcal {T}})$
and
![]() ${\mathcal { Q}}(c, {\mathcal {U}})$
do not exist. Hence, both
${\mathcal { Q}}(c, {\mathcal {U}})$
do not exist. Hence, both
![]() $\pi ^{{\mathcal {T}}^+}_b$
and
$\pi ^{{\mathcal {T}}^+}_b$
and
![]() $\pi ^{{\mathcal {U}}^+}_c$
are defined and
$\pi ^{{\mathcal {U}}^+}_c$
are defined and
![]() $\pi ^{{\mathcal {T}}^+}_b(\nu )=\nu =\pi ^{{\mathcal {U}}^+}_c(\nu )$
. We then have that there is, in
$\pi ^{{\mathcal {T}}^+}_b(\nu )=\nu =\pi ^{{\mathcal {U}}^+}_c(\nu )$
. We then have that there is, in
![]() ${\mathcal { H}}[g]$
, an
${\mathcal { H}}[g]$
, an
![]() $\omega $
-club C of
$\omega $
-club C of
![]() $\xi <\nu $
such that:
$\xi <\nu $
such that:
-
1.
 $\pi ^{\mathcal {T}}_b(\xi )=\xi $
and
$\pi ^{\mathcal {T}}_b(\xi )=\xi $
and -
2.
 $\pi ^{{\mathcal {U}}}_c[\xi ]\subseteq \xi $
.
$\pi ^{{\mathcal {U}}}_c[\xi ]\subseteq \xi $
.
Claim 2. For each
![]() $\xi \in C$
,
$\xi \in C$
,
![]() $\pi ^{\mathcal {U}}_c(\xi )=\xi $
.
$\pi ^{\mathcal {U}}_c(\xi )=\xi $
.
Proof The claim follows from the following subclaim.
Subclaim. For each
![]() $\xi \in (\lambda , \nu )$
such that
$\xi \in (\lambda , \nu )$
such that
![]() $\mathrm {cf}^{{\mathcal { H}}[g]}(\xi )=\omega $
,
$\mathrm {cf}^{{\mathcal { H}}[g]}(\xi )=\omega $
,
![]() $\mathrm { cf}^{\mathcal {W} }(\xi )$
is not a measurable cardinal of
$\mathrm { cf}^{\mathcal {W} }(\xi )$
is not a measurable cardinal of
![]() ${\mathcal {W} }$
whose measurability is witnessed by an extender on the sequence of
${\mathcal {W} }$
whose measurability is witnessed by an extender on the sequence of
![]() ${\mathcal {W} }$
.
${\mathcal {W} }$
.
Proof To see this, fix
![]() $\xi $
as above and suppose
$\xi $
as above and suppose
![]() $\mathrm {cf}^{\mathcal {W} }(\xi )=\mu $
and there is a total extender
$\mathrm {cf}^{\mathcal {W} }(\xi )=\mu $
and there is a total extender
![]() $E\in \vec {E}^{\mathcal {W} }$
such that
$E\in \vec {E}^{\mathcal {W} }$
such that
![]() $\mathrm {crit }(E)=\mu $
. Let
$\mathrm {crit }(E)=\mu $
. Let
![]() $({\mathcal { K}}_\alpha , {\mathcal { K}}^{\prime }_\alpha , F_\alpha :\alpha <\nu )$
be the models of the fully backgrounded construction producing
$({\mathcal { K}}_\alpha , {\mathcal { K}}^{\prime }_\alpha , F_\alpha :\alpha <\nu )$
be the models of the fully backgrounded construction producing
![]() ${\mathcal {W} }$
. Let
${\mathcal {W} }$
. Let
![]() $\alpha $
be such that for all
$\alpha $
be such that for all
![]() $\beta \in [\alpha , \nu )$
,
$\beta \in [\alpha , \nu )$
,
![]() ${\mathcal { K}}_\alpha '|(\mu ^+)^{{\mathcal { K}}_\alpha '}={\mathcal {W} }|(\mu ^+)^{\mathcal {W} }$
. It then follows that E, as it is total over
${\mathcal { K}}_\alpha '|(\mu ^+)^{{\mathcal { K}}_\alpha '}={\mathcal {W} }|(\mu ^+)^{\mathcal {W} }$
. It then follows that E, as it is total over
![]() ${\mathcal {W} }$
, has been added after stage
${\mathcal {W} }$
, has been added after stage
![]() $\alpha $
and, therefore,
$\alpha $
and, therefore,
![]() $\mu $
is an inaccessible cardinal of
$\mu $
is an inaccessible cardinal of
![]() ${\mathcal { H}}$
. But as
${\mathcal { H}}$
. But as
![]() $\mathrm {cf}^{{\mathcal { H}}[g]}(\xi )=\omega $
,
$\mathrm {cf}^{{\mathcal { H}}[g]}(\xi )=\omega $
,
![]() $\mathrm {cf}^{{\mathcal { H}}[g]}(\mu )=\omega $
. As
$\mathrm {cf}^{{\mathcal { H}}[g]}(\mu )=\omega $
. As
![]() $\mu>\lambda $
, we get a contradiction!
$\mu>\lambda $
, we get a contradiction!
Thus, since for
![]() $\xi \in C$
,
$\xi \in C$
,
![]() $\mathrm {cf}^{\mathcal {W} }(\xi )$
is not a measurable cardinal of
$\mathrm {cf}^{\mathcal {W} }(\xi )$
is not a measurable cardinal of
![]() ${\mathcal {W} }$
,
${\mathcal {W} }$
,
![]() $\sup (\pi ^{\mathcal {U}}_c[\xi ])=\pi ^{\mathcal {U}}_c(\xi )$
implying that for
$\sup (\pi ^{\mathcal {U}}_c[\xi ])=\pi ^{\mathcal {U}}_c(\xi )$
implying that for
![]() $\xi \in C$
,
$\xi \in C$
,
![]() $\pi ^{\mathcal {U}}_c(\xi )=\xi $
.
$\pi ^{\mathcal {U}}_c(\xi )=\xi $
.
We now have that for each
![]() $\xi \in C$
,
$\xi \in C$
,
However, since
![]() $\pi ^{\mathcal {U}}_c$
is continuous at each
$\pi ^{\mathcal {U}}_c$
is continuous at each
![]() $(\xi ^+)^{\mathcal {W} }$
, we must indeed have that
$(\xi ^+)^{\mathcal {W} }$
, we must indeed have that
which is what we wanted to prove.Footnote 18
The above proof shows that in fact covering holds on a stationary set. The referee has pointed out that the proof of Theorem 2.2 uses arguments similar to those appearing in Chapter 3 of [Reference Steel17].
3 No towers resembling the stationary tower
Theorem 3.1. Suppose
![]() $\mathbb {M}_\phi $
is an S-reconstructible mouse operator with the internal covering property. Let
$\mathbb {M}_\phi $
is an S-reconstructible mouse operator with the internal covering property. Let
![]() $\alpha \in dom(\mathbb {M})$
and set
$\alpha \in dom(\mathbb {M})$
and set
![]() ${\mathcal {M}}={\mathcal {M}}(a)$
and
${\mathcal {M}}={\mathcal {M}}(a)$
and
![]() $\delta =\delta _{a, 1}$
. Then there is no st-like-embedding below
$\delta =\delta _{a, 1}$
. Then there is no st-like-embedding below
![]() $\delta $
.
$\delta $
.
Proof Towards a contradiction suppose
![]() $\mathbb {P}\in {\mathcal {M}}|\delta $
is such that
$\mathbb {P}\in {\mathcal {M}}|\delta $
is such that
![]() $\delta _{a, 0}<\left |\mathbb {P}\right |<\delta $
and whenever
$\delta _{a, 0}<\left |\mathbb {P}\right |<\delta $
and whenever
![]() $g\subseteq \mathbb {P}$
is generic, there is an elementary embedding
$g\subseteq \mathbb {P}$
is generic, there is an elementary embedding
![]() $j: {\mathcal {M}}\rightarrow {\mathcal {N}}\subseteq {\mathcal {M}}[g]$
in
$j: {\mathcal {M}}\rightarrow {\mathcal {N}}\subseteq {\mathcal {M}}[g]$
in
![]() ${\mathcal {M}}[g]$
with the property that:
${\mathcal {M}}[g]$
with the property that:
-
1.
 $\mathrm {crit }(j)=\omega _1^{\mathcal {M}}$
,
$\mathrm {crit }(j)=\omega _1^{\mathcal {M}}$
, -
2.
 $\mathbb {R}^{{\mathcal {M}}[g]}\subseteq {\mathcal {N}}$
,
$\mathbb {R}^{{\mathcal {M}}[g]}\subseteq {\mathcal {N}}$
, -
3.
 $\left |(\delta _{a, 0}^+)^{\mathcal {M}}\right |{}^{{\mathcal {M}}[g]}=\omega $
,
$\left |(\delta _{a, 0}^+)^{\mathcal {M}}\right |{}^{{\mathcal {M}}[g]}=\omega $
, -
4. for some
 ${\mathcal {M}}$
-regular cardinal
${\mathcal {M}}$
-regular cardinal
 $\nu _0<\delta $
,
$\nu _0<\delta $
,  $$ \begin{align*} {\mathcal{N}}=\{ j(f)(s): s\in [\nu_0]^{<\omega}, f: [\nu_0]^{\left|s\right|}\rightarrow {\mathcal{M}} \mbox{ and } f\in {\mathcal{M}}\}. \end{align*} $$
$$ \begin{align*} {\mathcal{N}}=\{ j(f)(s): s\in [\nu_0]^{<\omega}, f: [\nu_0]^{\left|s\right|}\rightarrow {\mathcal{M}} \mbox{ and } f\in {\mathcal{M}}\}. \end{align*} $$
Fix such a tuple
![]() $(g, {\mathcal {N}}, j)$
. Let
$(g, {\mathcal {N}}, j)$
. Let
![]() $\kappa =\omega _1^{\mathcal {M}}$
and let
$\kappa =\omega _1^{\mathcal {M}}$
and let
![]() $\lambda =\omega _1^{{\mathcal {M}}[g]}$
. Let
$\lambda =\omega _1^{{\mathcal {M}}[g]}$
. Let
![]() $\Sigma $
be the unique iteration strategy of
$\Sigma $
be the unique iteration strategy of
![]() ${\mathcal {M}}$
. Recall that we have set
${\mathcal {M}}$
. Recall that we have set
![]() ${\mathcal {W} }(x)={\mathcal {M}}(x)|(\left |x\right |{}^+)^{{\mathcal {M}}(x)}$
. We assume that
${\mathcal {W} }(x)={\mathcal {M}}(x)|(\left |x\right |{}^+)^{{\mathcal {M}}(x)}$
. We assume that
![]() $\mathbb {P}$
has the smallest possible rank.
$\mathbb {P}$
has the smallest possible rank.
Let
![]() ${\mathcal R}^*\trianglelefteq {\mathcal {N}}$
be the least such that
${\mathcal R}^*\trianglelefteq {\mathcal {N}}$
be the least such that
![]() $\rho _\omega ({\mathcal R}^*)=\omega $
and
$\rho _\omega ({\mathcal R}^*)=\omega $
and
![]() ${\mathcal {M}}|\kappa \triangleleft {\mathcal R}^*$
. Let
${\mathcal {M}}|\kappa \triangleleft {\mathcal R}^*$
. Let
![]() $\Phi $
be the
$\Phi $
be the
![]() $\delta $
-strategy of
$\delta $
-strategy of
![]() ${\mathcal R}^*$
in
${\mathcal R}^*$
in
![]() ${\mathcal {N}}$
. Corollary 1.2 implies that
${\mathcal {N}}$
. Corollary 1.2 implies that
![]() ${\mathcal {W} }\restriction {\mathcal {M}}|\delta $
is definable over
${\mathcal {W} }\restriction {\mathcal {M}}|\delta $
is definable over
![]() ${\mathcal {M}}|\delta $
. It then makes sense to write
${\mathcal {M}}|\delta $
. It then makes sense to write
![]() ${\mathcal {W} }^{\mathcal {N}}$
for the function given by the same definition over
${\mathcal {W} }^{\mathcal {N}}$
for the function given by the same definition over
![]() ${\mathcal {N}}|\delta $
.
${\mathcal {N}}|\delta $
.
Claim 1. Suppose
![]() $x\in HC^{{\mathcal {M}}|\delta [g]}$
is a transitive set such that
$x\in HC^{{\mathcal {M}}|\delta [g]}$
is a transitive set such that
![]() $L_{\omega }[x]\vDash "x$
is well-ordered.” Then
$L_{\omega }[x]\vDash "x$
is well-ordered.” Then
Proof Let
![]() ${\mathcal {W} }^*\trianglelefteq {\mathcal {W} }(x)$
be such that
${\mathcal {W} }^*\trianglelefteq {\mathcal {W} }(x)$
be such that
![]() $\rho _\omega ({\mathcal {W} }^*)=Ord\cap x$
. The proof of Proposition 1.7 shows that for some
$\rho _\omega ({\mathcal {W} }^*)=Ord\cap x$
. The proof of Proposition 1.7 shows that for some
![]() $\tau \in (\left |\mathbb {P}\right |, \delta )$
,
$\tau \in (\left |\mathbb {P}\right |, \delta )$
,
![]() ${\mathcal {W} }^*$
appears as a model of the fully backgrounded construction of
${\mathcal {W} }^*$
appears as a model of the fully backgrounded construction of
![]() ${\mathcal {M}}|(\tau ^+)^{\mathcal {M}}$
done using extenders with critical points
${\mathcal {M}}|(\tau ^+)^{\mathcal {M}}$
done using extenders with critical points
![]() $>\left |\mathbb {P}\right |$
. Working in
$>\left |\mathbb {P}\right |$
. Working in
![]() ${\mathcal {M}}[g]$
, let
${\mathcal {M}}[g]$
, let
![]() $\pi : \bar {{\mathcal {M}}}[\bar {g}]\rightarrow ({\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g])$
be such that
$\pi : \bar {{\mathcal {M}}}[\bar {g}]\rightarrow ({\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g])$
be such that
![]() $x\in \bar {{\mathcal {M}}}[\bar {g}]$
,
$x\in \bar {{\mathcal {M}}}[\bar {g}]$
,
![]() $\tau \in rng(\pi )$
and
$\tau \in rng(\pi )$
and
![]() $\bar {{\mathcal {M}}}$
is countable in
$\bar {{\mathcal {M}}}$
is countable in
![]() ${\mathcal {M}}[g]$
. Let
${\mathcal {M}}[g]$
. Let
![]() $\bar {\tau }=\pi ^{-1}(\tau )$
. We then have that
$\bar {\tau }=\pi ^{-1}(\tau )$
. We then have that
(*) the iterability of
![]() ${\mathcal {W} }^*$
reduces to the iterability of
${\mathcal {W} }^*$
reduces to the iterability of
![]() $\bar {{\mathcal {M}}}|(\bar {\tau }^+)^{\bar {{\mathcal {M}}}}$
for non-dropping trees that are above
$\bar {{\mathcal {M}}}|(\bar {\tau }^+)^{\bar {{\mathcal {M}}}}$
for non-dropping trees that are above
![]() $\left |\pi ^{-1}(\mathbb {P})\right |{}^{\bar {{\mathcal {M}}}}$
.
$\left |\pi ^{-1}(\mathbb {P})\right |{}^{\bar {{\mathcal {M}}}}$
.
By absoluteness we have
![]() $\sigma :\bar {{\mathcal {M}}}|(\bar {\tau }^+)^{\bar {{\mathcal {M}}}}\rightarrow j({\mathcal {M}}|(\tau ^+)^{\mathcal {M}})$
in
$\sigma :\bar {{\mathcal {M}}}|(\bar {\tau }^+)^{\bar {{\mathcal {M}}}}\rightarrow j({\mathcal {M}}|(\tau ^+)^{\mathcal {M}})$
in
![]() ${\mathcal {N}}$
. It follows from Proposition 1.4 that
${\mathcal {N}}$
. It follows from Proposition 1.4 that
![]() $j({\mathcal {M}}|(\tau ^+)^{\mathcal {M}})$
is
$j({\mathcal {M}}|(\tau ^+)^{\mathcal {M}})$
is
![]() $\delta +1$
-iterable in
$\delta +1$
-iterable in
![]() ${\mathcal {N}}$
(for non-dropping iterations that are above
${\mathcal {N}}$
(for non-dropping iterations that are above
![]() $\delta _{a, 0}$
), and hence
$\delta _{a, 0}$
), and hence
![]() ${\mathcal {W} }^*$
is
${\mathcal {W} }^*$
is
![]() $\delta $
-iterable in
$\delta $
-iterable in
![]() ${\mathcal {N}}$
(see (*)). Therefore,
${\mathcal {N}}$
(see (*)). Therefore,
![]() ${\mathcal {W} }^*\trianglelefteq {\mathcal {W} }^{\mathcal {N}}(x)$
.Footnote
19
${\mathcal {W} }^*\trianglelefteq {\mathcal {W} }^{\mathcal {N}}(x)$
.Footnote
19
The proof of Claim 1 is a prototypical argument that we will use again below. Recall that given an iteration tree
![]() ${\mathcal {T}}$
on a premouse
${\mathcal {T}}$
on a premouse
![]() ${\mathcal {N}}$
, we let
${\mathcal {N}}$
, we let
![]() $C({\mathcal {T}})=\cup _{\alpha <lh({\mathcal {T}})}{\mathcal {M}}_\alpha ^{\mathcal {T}}|lh(E_\alpha ^{\mathcal {T}})$
.
$C({\mathcal {T}})=\cup _{\alpha <lh({\mathcal {T}})}{\mathcal {M}}_\alpha ^{\mathcal {T}}|lh(E_\alpha ^{\mathcal {T}})$
.
Claim 2. There is a premouse
![]() ${\mathcal {X}}\in HC^{{\mathcal {M}}[g]}$
such that:
${\mathcal {X}}\in HC^{{\mathcal {M}}[g]}$
such that:
-
1.
 ${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
is generic over
${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
is generic over
 ${\mathcal {X}}$
,
${\mathcal {X}}$
, -
2. there is an iteration tree
 ${\mathcal { K}}$
on
${\mathcal { K}}$
on
 ${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
such that
${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
such that
 ${\mathcal { K}}$
is according to
${\mathcal { K}}$
is according to
 $\Sigma $
and either:
$\Sigma $
and either:-
(a) the iteration embedding
 $\pi ^{\mathcal { K}}$
exists and
$\pi ^{\mathcal { K}}$
exists and
 ${\mathcal {X}}$
is the last model of
${\mathcal {X}}$
is the last model of
 ${\mathcal { K}}$
, or
${\mathcal { K}}$
, or -
(b)
 ${\mathcal { K}}$
is of limit length,
${\mathcal { K}}$
is of limit length,
 ${\mathcal {W} }(C({\mathcal { K}}))\vDash "\delta ({\mathcal { K}})$
is a Woodin cardinal” and
${\mathcal {W} }(C({\mathcal { K}}))\vDash "\delta ({\mathcal { K}})$
is a Woodin cardinal” and
 ${\mathcal {X}}={\mathcal {W} }(C({\mathcal { K}}))$
,
${\mathcal {X}}={\mathcal {W} }(C({\mathcal { K}}))$
,
-
-
3. there is a sound
 ${\mathcal {X}}$
-premouse
${\mathcal {X}}$
-premouse
 ${\mathcal R}\in {\mathcal {M}}[g]$
such that
${\mathcal R}\in {\mathcal {M}}[g]$
such that
 $Ord\cap {\mathcal {X}}$
is a cardinal of
$Ord\cap {\mathcal {X}}$
is a cardinal of
 ${\mathcal R}$
and
${\mathcal R}$
and
 ${\mathcal {M}}[g]\vDash "{\mathcal R}$
is not
${\mathcal {M}}[g]\vDash "{\mathcal R}$
is not
 $\delta $
-iterable above
$\delta $
-iterable above
 $Ord\cap {\mathcal {X}}$
,” letting
$Ord\cap {\mathcal {X}}$
,” letting
 $\nu $
be the Woodin cardinal of
$\nu $
be the Woodin cardinal of
 ${\mathcal {X}}$
,
${\mathcal {X}}$
, -
4.
 ${\mathcal R}\vDash "\nu $
is a Woodin cardinal,”
${\mathcal R}\vDash "\nu $
is a Woodin cardinal,” -
5.
 $rud({\mathcal R})\vDash "Ord\cap {\mathcal {X}}$
Footnote
20
is not a cardinal,” and
$rud({\mathcal R})\vDash "Ord\cap {\mathcal {X}}$
Footnote
20
is not a cardinal,” and -
6.
 ${\mathcal {X}}$
and
${\mathcal {X}}$
and
 ${\mathcal R}$
are countable in
${\mathcal R}$
are countable in
 ${\mathcal {M}}[g]$
.
${\mathcal {M}}[g]$
.
Proof Let
![]() ${\mathcal {Y}}={\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
. Working inside
${\mathcal {Y}}={\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
. Working inside
![]() ${\mathcal {M}}[g]$
, we compare
${\mathcal {M}}[g]$
, we compare
![]() ${\mathcal {Y}}$
with
${\mathcal {Y}}$
with
![]() ${\mathcal R}^*$
.
${\mathcal R}^*$
.
![]() ${\mathcal {Y}}$
is not
${\mathcal {Y}}$
is not
![]() $\delta $
-iterable inside
$\delta $
-iterable inside
![]() ${\mathcal {M}}[g]$
.Footnote
21
However, it follows from Corollary 1.2 that the fragment of
${\mathcal {M}}[g]$
.Footnote
21
However, it follows from Corollary 1.2 that the fragment of
![]() $\Sigma _{\mathcal {Y}}\restriction ({\mathcal {M}}[g])$
that acts on short trees, i.e., trees
$\Sigma _{\mathcal {Y}}\restriction ({\mathcal {M}}[g])$
that acts on short trees, i.e., trees
![]() ${\mathcal {T}}$
for which
${\mathcal {T}}$
for which
![]() ${\mathcal { Q}}({\mathcal {T}})$
exists, is in
${\mathcal { Q}}({\mathcal {T}})$
exists, is in
![]() ${\mathcal {M}}[g]$
. We then want to use the aforementioned fragment of
${\mathcal {M}}[g]$
. We then want to use the aforementioned fragment of
![]() $\Sigma _{\mathcal {Y}}$
for the comparison that we would like to perform. Finally, we would like to incorporate
$\Sigma _{\mathcal {Y}}$
for the comparison that we would like to perform. Finally, we would like to incorporate
![]() ${\mathcal {Y}}$
-genericity iteration into the above mentioned comparison. More precisely, working inside
${\mathcal {Y}}$
-genericity iteration into the above mentioned comparison. More precisely, working inside
![]() ${\mathcal {M}}[g]$
we first iterate the least
${\mathcal {M}}[g]$
we first iterate the least
![]() ${\mathcal {Y}}$
-measurable cardinal
${\mathcal {Y}}$
-measurable cardinal
![]() $\delta _{a, 0}+1$
-times and get
$\delta _{a, 0}+1$
-times and get
![]() ${\mathcal {Y}}_1$
and then construct iteration trees
${\mathcal {Y}}_1$
and then construct iteration trees
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() ${\mathcal {Y}}_1$
and
${\mathcal {Y}}_1$
and
![]() ${\mathcal R}^*$
respectively such that:
${\mathcal R}^*$
respectively such that:
-
1.
 ${\mathcal {T}}$
is according to the short fragment of
${\mathcal {T}}$
is according to the short fragment of
 $\Sigma _{\mathcal {Y}}\restriction ({\mathcal {M}}[g])$
,
$\Sigma _{\mathcal {Y}}\restriction ({\mathcal {M}}[g])$
, -
2.
 ${\mathcal {U}}$
is according to
${\mathcal {U}}$
is according to
 $\Phi $
(recall that our hypothesis is that
$\Phi $
(recall that our hypothesis is that
 ${\mathbb {R}}^{{\mathcal {M}}[g]}={\mathbb {R}}^{\mathcal {N}}$
),
${\mathbb {R}}^{{\mathcal {M}}[g]}={\mathbb {R}}^{\mathcal {N}}$
), -
3. for
 $\alpha <\lambda $
, given
$\alpha <\lambda $
, given
 ${\mathcal {T}}\restriction \alpha +1$
and
${\mathcal {T}}\restriction \alpha +1$
and
 ${\mathcal {U}}\restriction \alpha +1$
we let:
${\mathcal {U}}\restriction \alpha +1$
we let:-
(a)
 $E^{\mathcal {T}}_{\alpha , 0}$
be the least extender, if it exists, on the sequence of
$E^{\mathcal {T}}_{\alpha , 0}$
be the least extender, if it exists, on the sequence of
 ${\mathcal {M}}^{\mathcal {T}}_\alpha $
that violates an identity in the relevant extender algebra,
${\mathcal {M}}^{\mathcal {T}}_\alpha $
that violates an identity in the relevant extender algebra, -
(b)
 $E^{\mathcal {T}}_{\alpha , 1}$
be the least extender, if it exists, that causes disagreement between
$E^{\mathcal {T}}_{\alpha , 1}$
be the least extender, if it exists, that causes disagreement between
 ${\mathcal {M}}^{\mathcal {T}}_\alpha $
and
${\mathcal {M}}^{\mathcal {T}}_\alpha $
and
 ${\mathcal {M}}^{\mathcal {U}}_\alpha $
,
${\mathcal {M}}^{\mathcal {U}}_\alpha $
,
-
-
4.
 $E^{\mathcal {T}}_\alpha $
is defined if either
$E^{\mathcal {T}}_\alpha $
is defined if either
 $E^{\mathcal {T}}_{\alpha , 0}$
or
$E^{\mathcal {T}}_{\alpha , 0}$
or
 $E^{\mathcal {T}}_{\alpha , 1}$
is defined and
$E^{\mathcal {T}}_{\alpha , 1}$
is defined and  $$ \begin{align*} E^{\mathcal{T}}_\alpha=\begin{cases} E^{\mathcal{T}}_{\alpha, 0}&: lh(E^{\mathcal{T}}_{\alpha, 0})\leq lh(E^{\mathcal{T}}_{\alpha, 1}),\\ E^{\mathcal{T}}_{\alpha, 1} &: lh(E^{\mathcal{T}}_{\alpha, 1})\leq lh(E^{\mathcal{T}}_{\alpha, 0}), \end{cases} \end{align*} $$
$$ \begin{align*} E^{\mathcal{T}}_\alpha=\begin{cases} E^{\mathcal{T}}_{\alpha, 0}&: lh(E^{\mathcal{T}}_{\alpha, 0})\leq lh(E^{\mathcal{T}}_{\alpha, 1}),\\ E^{\mathcal{T}}_{\alpha, 1} &: lh(E^{\mathcal{T}}_{\alpha, 1})\leq lh(E^{\mathcal{T}}_{\alpha, 0}), \end{cases} \end{align*} $$
-
5. if
 $E^{\mathcal {T}}_\alpha =E^{\mathcal {T}}_{\alpha , 1}$
then
$E^{\mathcal {T}}_\alpha =E^{\mathcal {T}}_{\alpha , 1}$
then
 $E^{\mathcal {U}}_\alpha =\vec {E}^{{\mathcal {M}}^{\mathcal {U}}_\alpha }(lh(E_\alpha ^{\mathcal {T}}))$
and otherwise
$E^{\mathcal {U}}_\alpha =\vec {E}^{{\mathcal {M}}^{\mathcal {U}}_\alpha }(lh(E_\alpha ^{\mathcal {T}}))$
and otherwise
 $E^{\mathcal {U}}_\alpha =E^{\mathcal {T}}_\alpha $
.
$E^{\mathcal {U}}_\alpha =E^{\mathcal {T}}_\alpha $
.
Because
![]() ${\mathcal R}^*\not \trianglelefteq {\mathcal {M}}$
we must have that
${\mathcal R}^*\not \trianglelefteq {\mathcal {M}}$
we must have that
![]() ${\mathcal R}^*$
-side must win any successful coiteration with
${\mathcal R}^*$
-side must win any successful coiteration with
![]() ${\mathcal {Y}}$
. Notice that Claim 1 implies that the construction of
${\mathcal {Y}}$
. Notice that Claim 1 implies that the construction of
![]() $({\mathcal {T}}, {\mathcal {U}})$
can be carried out inside
$({\mathcal {T}}, {\mathcal {U}})$
can be carried out inside
![]() ${\mathcal {N}}$
. It follows that our construction of
${\mathcal {N}}$
. It follows that our construction of
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
can last at most
${\mathcal {U}}$
can last at most
![]() $\omega _1^{\mathcal {N}}$
many steps producing trees
$\omega _1^{\mathcal {N}}$
many steps producing trees
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
. If now
${\mathcal {U}}$
. If now
![]() ${\mathcal {U}}$
is of limit length then because
${\mathcal {U}}$
is of limit length then because
![]() $\Phi $
acts on
$\Phi $
acts on
![]() ${\mathcal {U}}$
, we can let
${\mathcal {U}}$
, we can let
![]() $c=\Phi ({\mathcal {U}})$
. Let then
$c=\Phi ({\mathcal {U}})$
. Let then
![]() ${\mathcal R}_1$
be either the last model of
${\mathcal R}_1$
be either the last model of
![]() ${\mathcal {U}}$
(in case it has a last model) or
${\mathcal {U}}$
(in case it has a last model) or
![]() ${\mathcal {M}}_c^{\mathcal {U}}$
.
${\mathcal {M}}_c^{\mathcal {U}}$
.
We then must have one of the following cases (in
![]() ${\mathcal {M}}[g]$
): either:
${\mathcal {M}}[g]$
): either:
-
1.
 ${\mathcal {T}}$
has a last model
${\mathcal {T}}$
has a last model
 ${\mathcal {Y}}_2$
,
${\mathcal {Y}}_2$
,
 $\pi ^{\mathcal {T}}$
exists,
$\pi ^{\mathcal {T}}$
exists,
 ${\mathcal {Y}}$
is generic over the extender algebra of
${\mathcal {Y}}$
is generic over the extender algebra of
 ${\mathcal {Y}}_2$
at
${\mathcal {Y}}_2$
at
 $\pi ^{\mathcal {T}}(\delta _{a, 0})$
, and
$\pi ^{\mathcal {T}}(\delta _{a, 0})$
, and
 ${\mathcal {Y}}_2\triangleleft {\mathcal R}_1$
, or
${\mathcal {Y}}_2\triangleleft {\mathcal R}_1$
, or -
2.
 ${\mathcal {T}}$
is of limit length,
${\mathcal {T}}$
is of limit length,
 ${\mathcal { Q}}({\mathcal {T}})$
does not exist, and letting
${\mathcal { Q}}({\mathcal {T}})$
does not exist, and letting
 ${\mathcal {Y}}_2={\mathcal {W} }(C({\mathcal {T}}))$
,
${\mathcal {Y}}_2={\mathcal {W} }(C({\mathcal {T}}))$
,
 ${\mathcal {Y}}_2\trianglelefteq {\mathcal R}_1$
.
${\mathcal {Y}}_2\trianglelefteq {\mathcal R}_1$
.
Set
![]() ${\mathcal {X}}={\mathcal {Y}}_2$
. Notice that because
${\mathcal {X}}={\mathcal {Y}}_2$
. Notice that because
![]() $\rho _\omega ({\mathcal R}^*)=\omega $
, we must have that
$\rho _\omega ({\mathcal R}^*)=\omega $
, we must have that
![]() $rud({\mathcal R}_1)\vDash "\zeta $
is not a Woodin cardinal” where
$rud({\mathcal R}_1)\vDash "\zeta $
is not a Woodin cardinal” where
![]() $\zeta $
is the Woodin of
$\zeta $
is the Woodin of
![]() ${\mathcal {X}}$
. Let
${\mathcal {X}}$
. Let
![]() ${\mathcal R}_2\trianglelefteq {\mathcal R}_1$
be the longest such that
${\mathcal R}_2\trianglelefteq {\mathcal R}_1$
be the longest such that
![]() ${\mathcal R}_2\vDash "\zeta $
is a Woodin cardinal.” Let
${\mathcal R}_2\vDash "\zeta $
is a Woodin cardinal.” Let
![]() ${\mathcal R}\trianglelefteq {\mathcal R}_2$
be the longest such that
${\mathcal R}\trianglelefteq {\mathcal R}_2$
be the longest such that
![]() ${\mathcal R}\vDash "Ord\cap {\mathcal {X}}$
is a cardinal.” We claim that
${\mathcal R}\vDash "Ord\cap {\mathcal {X}}$
is a cardinal.” We claim that
![]() $({\mathcal {X}}, {\mathcal { K}}, {\mathcal R})$
is as desired where
$({\mathcal {X}}, {\mathcal { K}}, {\mathcal R})$
is as desired where
![]() ${\mathcal { K}}$
is the iteration tree on
${\mathcal { K}}$
is the iteration tree on
![]() ${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
producing
${\mathcal {M}}|(\delta _{a, 0}^+)^{\mathcal {M}}$
producing
![]() ${\mathcal {X}}$
. It follows from our construction that it is enough to show that:
${\mathcal {X}}$
. It follows from our construction that it is enough to show that:
-
(a)
 ${\mathcal R}$
is not
${\mathcal R}$
is not
 $\delta $
-iterable in
$\delta $
-iterable in
 ${\mathcal {M}}[g]$
above
${\mathcal {M}}[g]$
above
 $Ord\cap {\mathcal {X}}$
, and
$Ord\cap {\mathcal {X}}$
, and -
(b)
 ${\mathcal {X}}$
and
${\mathcal {X}}$
and
 ${\mathcal R}$
are countable in
${\mathcal R}$
are countable in
 ${\mathcal {N}}$
.
${\mathcal {N}}$
.
Assume that (a) fails. Let
![]() $\eta \in (\delta _{a, 0}, \delta )$
be an
$\eta \in (\delta _{a, 0}, \delta )$
be an
![]() ${\mathcal {M}}$
-cardinal such that
${\mathcal {M}}$
-cardinal such that
![]() $\mathbb {P}\in {\mathcal {M}}|\eta $
. Let
$\mathbb {P}\in {\mathcal {M}}|\eta $
. Let
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over
${\mathcal {M}}|\delta [g]$
done over
![]() ${\mathcal {X}}$
using extenders with critical point
${\mathcal {X}}$
using extenders with critical point
![]() $>\eta $
. Then
$>\eta $
. Then
![]() ${\mathcal R}\not \trianglelefteq {\mathcal {P} }$
which means that
${\mathcal R}\not \trianglelefteq {\mathcal {P} }$
which means that
![]() ${\mathcal R}$
must outiterate
${\mathcal R}$
must outiterate
![]() ${\mathcal {P} }$
(this can be shown by considering the comparison of
${\mathcal {P} }$
(this can be shown by considering the comparison of
![]() ${\mathcal R}$
with the construction producing
${\mathcal R}$
with the construction producing
![]() ${\mathcal {P} }$
). We then have a tree
${\mathcal {P} }$
). We then have a tree
![]() ${\mathcal {U}}'$
on
${\mathcal {U}}'$
on
![]() ${\mathcal R}$
such that
${\mathcal R}$
such that
![]() $C({\mathcal {U}}')={\mathcal {P} }$
implying that
$C({\mathcal {U}}')={\mathcal {P} }$
implying that
![]() ${\mathcal {P} }$
cannot compute unboundedly many successors correctly contradicting Theorem 2.2.Footnote
22
${\mathcal {P} }$
cannot compute unboundedly many successors correctly contradicting Theorem 2.2.Footnote
22
Finally we need to show that
![]() ${\mathcal {X}}$
and
${\mathcal {X}}$
and
![]() ${\mathcal R}$
are countable in
${\mathcal R}$
are countable in
![]() ${\mathcal {N}}$
. Assume not. We then must have that the construction of
${\mathcal {N}}$
. Assume not. We then must have that the construction of
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
lasts
${\mathcal {U}}$
lasts
![]() $\omega _1^{\mathcal {N}}$
steps. We now claim that we must also have a branch for
$\omega _1^{\mathcal {N}}$
steps. We now claim that we must also have a branch for
![]() ${\mathcal {T}}$
in
${\mathcal {T}}$
in
![]() ${\mathcal {N}}$
. Indeed, let
${\mathcal {N}}$
. Indeed, let
![]() $\pi : H\rightarrow {\mathcal {N}}|(\omega _2^{\mathcal {N}})$
be countable in
$\pi : H\rightarrow {\mathcal {N}}|(\omega _2^{\mathcal {N}})$
be countable in
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
![]() ${\mathcal {T}}, {\mathcal {U}}, c \in rng(\pi )$
. Then
${\mathcal {T}}, {\mathcal {U}}, c \in rng(\pi )$
. Then
![]() $\pi ^{-1}(c)\in H$
is the branch of
$\pi ^{-1}(c)\in H$
is the branch of
![]() $\pi ^{-1}({\mathcal {U}})$
. Let
$\pi ^{-1}({\mathcal {U}})$
. Let
![]() $\xi =\omega _1^H$
. Notice that
$\xi =\omega _1^H$
. Notice that
![]() ${\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
exists and the branch of
${\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
exists and the branch of
![]() ${\mathcal {T}}\restriction \xi $
chosen in
${\mathcal {T}}\restriction \xi $
chosen in
![]() ${\mathcal {T}}$
for
${\mathcal {T}}$
for
![]() ${\mathcal {T}}\restriction \xi $
is the unique branch d such that
${\mathcal {T}}\restriction \xi $
is the unique branch d such that
![]() ${\mathcal { Q}}(d, {\mathcal {T}}\restriction \xi )$
exists and is equal to
${\mathcal { Q}}(d, {\mathcal {T}}\restriction \xi )$
exists and is equal to
![]() ${\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
. But we have that
${\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
. But we have that
![]() $\pi ^{-1}({\mathcal R}_2)={\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
, and because
$\pi ^{-1}({\mathcal R}_2)={\mathcal { Q}}({\mathcal {T}}\restriction \xi )$
, and because
![]() $\pi ^{-1}({\mathcal R}_2)\in H$
, the branch of
$\pi ^{-1}({\mathcal R}_2)\in H$
, the branch of
![]() ${\mathcal {T}}\restriction \xi $
is in H. Let d be this branch. It then follows that
${\mathcal {T}}\restriction \xi $
is in H. Let d be this branch. It then follows that
![]() $\pi (d)$
is a branch of
$\pi (d)$
is a branch of
![]() ${\mathcal {T}}$
. The usual comparison argument now implies that the iteration must have lasted
${\mathcal {T}}$
. The usual comparison argument now implies that the iteration must have lasted
![]() $<\omega _1^{\mathcal {N}}$
steps.
$<\omega _1^{\mathcal {N}}$
steps.
Let
![]() $\Lambda $
be the strategy of
$\Lambda $
be the strategy of
![]() ${\mathcal R}$
in
${\mathcal R}$
in
![]() ${\mathcal {N}}$
. We have that
${\mathcal {N}}$
. We have that
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $(\delta , \delta )$
-strategy. We would like to find a
$(\delta , \delta )$
-strategy. We would like to find a
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal {S}}$
of
${\mathcal {S}}$
of
![]() ${\mathcal R}$
such that
${\mathcal R}$
such that
![]() ${\mathcal {S}}$
is a minimal counterexample to
${\mathcal {S}}$
is a minimal counterexample to
![]() $\delta $
-iterability. Below we define what this notion means.
$\delta $
-iterability. Below we define what this notion means.
Given a finite stack of normal trees
![]() ${\vec {\mathcal {T}}}\in {\mathcal {M}}|\delta [g]$
on
${\vec {\mathcal {T}}}\in {\mathcal {M}}|\delta [g]$
on
![]() ${\mathcal R}$
, we say
${\mathcal R}$
, we say
![]() ${\vec {\mathcal {T}}}$
is
${\vec {\mathcal {T}}}$
is
![]() $\Lambda $
-correct if in
$\Lambda $
-correct if in
![]() ${\mathcal {M}}[g]$
, there is a club of countable
${\mathcal {M}}[g]$
, there is a club of countable
![]() $X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
such that letting
$X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
such that letting
![]() $\pi _X: N_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse,
$\pi _X: N_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse,
![]() $\pi ^{-1}_X({\vec {\mathcal {T}}})$
is according to
$\pi ^{-1}_X({\vec {\mathcal {T}}})$
is according to
![]() $\Lambda $
. We now look for an iterate of
$\Lambda $
. We now look for an iterate of
![]() ${\mathcal R}$
that is a minimal counterexample to
${\mathcal R}$
that is a minimal counterexample to
![]() $<\delta $
-iterability among
$<\delta $
-iterability among
![]() $\Lambda $
-correct iterates of
$\Lambda $
-correct iterates of
![]() ${\mathcal R}$
. Below we make the notion more precise.
${\mathcal R}$
. Below we make the notion more precise.
Suppose
![]() ${\vec {\mathcal {T}}}\in {\mathcal {M}}|\delta [g]$
is a finite
${\vec {\mathcal {T}}}\in {\mathcal {M}}|\delta [g]$
is a finite
![]() $\Lambda $
-correct stack on
$\Lambda $
-correct stack on
![]() ${\mathcal R}$
with last model
${\mathcal R}$
with last model
![]() ${\mathcal { K}}$
. Let
${\mathcal { K}}$
. Let
![]() ${\mathcal {S}}\trianglelefteq {\mathcal { K}}$
. We say
${\mathcal {S}}\trianglelefteq {\mathcal { K}}$
. We say
![]() $({\vec {\mathcal {T}}}, {\mathcal {S}})$
is a minimal counterexample to
$({\vec {\mathcal {T}}}, {\mathcal {S}})$
is a minimal counterexample to
![]() $\delta $
-iterability if there is an
$\delta $
-iterability if there is an
![]() ${\mathcal {S}}$
-cardinal
${\mathcal {S}}$
-cardinal
![]() $\eta $
such that:
$\eta $
such that:
-
1.
 $\eta $
is a strong cutpoint in
$\eta $
is a strong cutpoint in
 ${\mathcal {S}}$
,Footnote
23
${\mathcal {S}}$
,Footnote
23
-
2.
 $\rho _\omega ({\mathcal {S}})\leq \eta $
and
$\rho _\omega ({\mathcal {S}})\leq \eta $
and
 ${\mathcal {S}}$
is
${\mathcal {S}}$
is
 $\eta $
-sound,
$\eta $
-sound, -
3. in
 ${\mathcal {M}}|\delta [g]$
,
${\mathcal {M}}|\delta [g]$
,
 ${\mathcal {S}}$
is not
${\mathcal {S}}$
is not
 $\delta $
-iterable above
$\delta $
-iterable above
 $\eta $
,
$\eta $
, -
4. whenever
 ${\mathcal {U}}\in {\mathcal {M}}|\delta [g]$
is a normal tree on
${\mathcal {U}}\in {\mathcal {M}}|\delta [g]$
is a normal tree on
 ${\mathcal {S}}$
above
${\mathcal {S}}$
above
 $\eta $
with last model
$\eta $
with last model
 ${\mathcal {W} }^*$
such that
${\mathcal {W} }^*$
such that
 ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
 $\Lambda $
-correct, for any
$\Lambda $
-correct, for any
 ${\mathcal {W} }$
such that
${\mathcal {W} }$
such that
 ${\mathcal {S}}|\eta \triangleleft {\mathcal {W} }\triangleleft {\mathcal {W} }^*$
and for any
${\mathcal {S}}|\eta \triangleleft {\mathcal {W} }\triangleleft {\mathcal {W} }^*$
and for any
 ${\mathcal {W} }$
-cardinal
${\mathcal {W} }$
-cardinal
 $\nu $
such that
$\nu $
such that
 $\nu $
is a strong cutpoint of
$\nu $
is a strong cutpoint of
 ${\mathcal {W} }$
and
${\mathcal {W} }$
and
 $\rho _\omega ({\mathcal {W} })\leq \nu $
,
$\rho _\omega ({\mathcal {W} })\leq \nu $
,
 ${\mathcal {M}}[g]\vDash "{\mathcal {W} }$
is
${\mathcal {M}}[g]\vDash "{\mathcal {W} }$
is
 $\delta $
-iterable above
$\delta $
-iterable above
 $\nu $
.”
$\nu $
.”
It is not difficult to see that there is a minimal counterexample to
![]() $\delta $
-iterability. Towards a contradiction, assume there is no minimal counterexample to
$\delta $
-iterability. Towards a contradiction, assume there is no minimal counterexample to
![]() $\delta $
-iterability. We know that
$\delta $
-iterability. We know that
![]() ${\mathcal R}$
is not a minimal counterexample to
${\mathcal R}$
is not a minimal counterexample to
![]() $\delta $
-iterability. We can then construct a sequence
$\delta $
-iterability. We can then construct a sequence
![]() $({\mathcal R}_i^+, {\mathcal R}_i, {\mathcal {T}}_i, \nu _i: i\in [1, \omega ))$
such that:Footnote
24
$({\mathcal R}_i^+, {\mathcal R}_i, {\mathcal {T}}_i, \nu _i: i\in [1, \omega ))$
such that:Footnote
24
-
1.
 ${\mathcal R}_i$
is a
${\mathcal R}_i$
is a
 $\nu _i$
-sound mouse over
$\nu _i$
-sound mouse over
 ${\mathcal R}_i|\nu _i$
such that
${\mathcal R}_i|\nu _i$
such that
 $\rho _\omega ({\mathcal R}_i)\leq \nu _i$
,
$\rho _\omega ({\mathcal R}_i)\leq \nu _i$
, -
2.
 $\nu _i$
is a strong cutpoint of
$\nu _i$
is a strong cutpoint of
 ${\mathcal R}_i$
,
${\mathcal R}_i$
, -
3.
 ${\mathcal {T}}_i$
is a tree on
${\mathcal {T}}_i$
is a tree on
 ${\mathcal R}_i$
above
${\mathcal R}_i$
above
 $\nu _i$
such that
$\nu _i$
such that
 $\oplus _{k\leq i}{\mathcal {T}}_k$
is
$\oplus _{k\leq i}{\mathcal {T}}_k$
is
 $\Lambda $
-correct,
$\Lambda $
-correct, -
4.
 ${\mathcal R}_{i+1}^+$
is the last model of
${\mathcal R}_{i+1}^+$
is the last model of
 ${\mathcal {T}}_i$
,
${\mathcal {T}}_i$
, -
5.
 ${\mathcal R}_{i+1}\triangleleft {\mathcal R}_{i+1}^+$
is such that for some
${\mathcal R}_{i+1}\triangleleft {\mathcal R}_{i+1}^+$
is such that for some
 $\nu _{i+1}$
,
$\nu _{i+1}$
,
 ${\mathcal R}_{i+1}$
is a
${\mathcal R}_{i+1}$
is a
 $\nu _{i+1}$
-sound mouse over
$\nu _{i+1}$
-sound mouse over
 ${\mathcal R}_{i+1}|\nu _{i+1}$
such that
${\mathcal R}_{i+1}|\nu _{i+1}$
such that
 $\rho _\omega ({\mathcal R}_{i+1})\leq \nu _{i+1}$
and
$\rho _\omega ({\mathcal R}_{i+1})\leq \nu _{i+1}$
and
 ${\mathcal R}_{i+1}$
is not
${\mathcal R}_{i+1}$
is not
 $\delta $
-iterable above
$\delta $
-iterable above
 $\nu _{i+1}$
in
$\nu _{i+1}$
in
 ${\mathcal {M}}[g]$
.
${\mathcal {M}}[g]$
.
Suppose then
![]() $X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
is such that it witnesses that for each i,
$X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
is such that it witnesses that for each i,
![]() $\oplus _{k\leq i}{\mathcal {T}}_k$
is
$\oplus _{k\leq i}{\mathcal {T}}_k$
is
![]() $\Lambda $
-correct. It follows that
$\Lambda $
-correct. It follows that
![]() $\pi _X^{-1}(\oplus _{i\in \omega }{\mathcal {T}}_i)$
witnesses that
$\pi _X^{-1}(\oplus _{i\in \omega }{\mathcal {T}}_i)$
witnesses that
![]() $\Lambda $
is not an iteration strategy for
$\Lambda $
is not an iteration strategy for
![]() ${\mathcal R}$
.
${\mathcal R}$
.
Let now
![]() ${\mathcal {S}}$
be a minimal counterexample to
${\mathcal {S}}$
be a minimal counterexample to
![]() $\delta $
-iterability and let
$\delta $
-iterability and let
![]() ${\vec {\mathcal {T}}}$
be the finite
${\vec {\mathcal {T}}}$
be the finite
![]() $\Lambda $
-correct stack on
$\Lambda $
-correct stack on
![]() ${\mathcal R}$
producing
${\mathcal R}$
producing
![]() ${\mathcal {S}}$
. Thus,
${\mathcal {S}}$
. Thus,
![]() ${\mathcal {S}}$
is an initial segment of the last model of
${\mathcal {S}}$
is an initial segment of the last model of
![]() ${\vec {\mathcal {T}}}$
. Let
${\vec {\mathcal {T}}}$
. Let
![]() $\eta $
be an
$\eta $
be an
![]() ${\mathcal {S}}$
-cardinal witnessing that
${\mathcal {S}}$
-cardinal witnessing that
![]() ${\mathcal {S}}$
is a minimal counterexample to
${\mathcal {S}}$
is a minimal counterexample to
![]() $\delta $
-iterability. We then have that
$\delta $
-iterability. We then have that
![]() $\eta $
is a strong cutpoint of
$\eta $
is a strong cutpoint of
![]() ${\mathcal {S}}$
,
${\mathcal {S}}$
,
![]() ${\mathcal {S}}$
is
${\mathcal {S}}$
is
![]() $\eta $
-sound, and
$\eta $
-sound, and
![]() $\rho _\omega ({\mathcal {S}})\leq \eta $
.
$\rho _\omega ({\mathcal {S}})\leq \eta $
.
Assume that
![]() ${\mathcal {S}}$
has a Woodin cardinal
${\mathcal {S}}$
has a Woodin cardinal
![]() $>\eta $
. Let
$>\eta $
. Let
![]() $\nu $
be its least Woodin cardinal
$\nu $
be its least Woodin cardinal
![]() $>\eta $
. Let
$>\eta $
. Let
![]() ${\mathcal {P} }$
be the output of the fully backgrounded construction of
${\mathcal {P} }$
be the output of the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
done over
${\mathcal {M}}|\delta [g]$
done over
![]() ${\mathcal {S}}|\eta $
using extenders with critical points
${\mathcal {S}}|\eta $
using extenders with critical points
![]() $>\eta $
. We now compare
$>\eta $
. We now compare
![]() ${\mathcal {S}}|\nu $
with the construction producing
${\mathcal {S}}|\nu $
with the construction producing
![]() ${\mathcal {P} }$
. The
${\mathcal {P} }$
. The
![]() ${\mathcal {P} }$
-side of such a comparison doesn’t move (for instance, see Lemma 2.11 of [Reference Sargsyan7]). However, since
${\mathcal {P} }$
-side of such a comparison doesn’t move (for instance, see Lemma 2.11 of [Reference Sargsyan7]). However, since
![]() ${\mathcal {S}}$
is not fully iterable, we need to describe a strategy for picking branches on the
${\mathcal {S}}$
is not fully iterable, we need to describe a strategy for picking branches on the
![]() ${\mathcal {S}}$
-side. Let
${\mathcal {S}}$
-side. Let
![]() $({\mathcal {P} }^*_\xi , {\mathcal {P} }_\xi , E_\xi : \xi <\delta )$
be the models of the aforementioned construction.
$({\mathcal {P} }^*_\xi , {\mathcal {P} }_\xi , E_\xi : \xi <\delta )$
be the models of the aforementioned construction.
Suppose then
![]() ${\mathcal {U}}\in {\mathcal {M}}|\delta [g]$
is a tree of limit length that has been built on
${\mathcal {U}}\in {\mathcal {M}}|\delta [g]$
is a tree of limit length that has been built on
![]() ${\mathcal {S}}$
via the aforementioned comparison process. We would like to describe a branch for it. As an inductive hypothesis, we maintain that
${\mathcal {S}}$
via the aforementioned comparison process. We would like to describe a branch for it. As an inductive hypothesis, we maintain that
![]() ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
![]() $\Lambda $
-correct. Thus, the branch b we pick for
$\Lambda $
-correct. Thus, the branch b we pick for
![]() ${\mathcal {U}}$
has to have the property that
${\mathcal {U}}$
has to have the property that
![]() ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}^\frown \{b\}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}^\frown \{b\}$
is
![]() $\Lambda $
-correct. There can be at most one such branch. It is then enough to show that there is such a branch. The description of b splits into two cases.
$\Lambda $
-correct. There can be at most one such branch. It is then enough to show that there is such a branch. The description of b splits into two cases.
First recall the definition of a fatal drop [Reference Sargsyan7, Definition 1.27]. Given a tree
![]() ${\mathcal {W} }$
on a premouse
${\mathcal {W} }$
on a premouse
![]() ${\mathcal { Q}}$
we say
${\mathcal { Q}}$
we say
![]() ${\mathcal {W} }$
has a fatal drop if there is
${\mathcal {W} }$
has a fatal drop if there is
![]() $\alpha <lh({\mathcal {W} })$
,
$\alpha <lh({\mathcal {W} })$
,
![]() $\xi $
, and
$\xi $
, and
![]() ${\mathcal { K}}\triangleleft {\mathcal {M}}^{\mathcal {T}}_\alpha $
such that
${\mathcal { K}}\triangleleft {\mathcal {M}}^{\mathcal {T}}_\alpha $
such that
![]() $\xi $
is a strong cutpoint of
$\xi $
is a strong cutpoint of
![]() ${\mathcal { K}}$
,
${\mathcal { K}}$
,
![]() $\rho _\omega ({\mathcal { K}})\leq \xi $
, and
$\rho _\omega ({\mathcal { K}})\leq \xi $
, and
![]() ${\mathcal {T}}_{\geq \alpha }$
is an iteration of
${\mathcal {T}}_{\geq \alpha }$
is an iteration of
![]() ${\mathcal { K}}$
above
${\mathcal { K}}$
above
![]() $\xi $
.
$\xi $
.
Case 1:
![]() ${\mathcal {U}}$
doesn’t have a fatal drop.
${\mathcal {U}}$
doesn’t have a fatal drop.
We have that there is some
![]() $\xi <\delta $
such that
$\xi <\delta $
such that
![]() $C({\mathcal {U}})\triangleleft {\mathcal {P} }_\xi $
. Because
$C({\mathcal {U}})\triangleleft {\mathcal {P} }_\xi $
. Because
![]() $\delta ({\mathcal {U}})<\delta $
, we have that
$\delta ({\mathcal {U}})<\delta $
, we have that
![]() ${\mathcal {M}}\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal.” It follows that there is a mouse
${\mathcal {M}}\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal.” It follows that there is a mouse
![]() ${\mathcal { Q}}$
over
${\mathcal { Q}}$
over
![]() $C({\mathcal {U}})$
that is obtained via the S-construction that translates
$C({\mathcal {U}})$
that is obtained via the S-construction that translates
![]() ${\mathcal {M}}$
into a mouse over
${\mathcal {M}}$
into a mouse over
![]() ${\mathcal {P} }_\xi |\delta ({\mathcal {U}})$
such that
${\mathcal {P} }_\xi |\delta ({\mathcal {U}})$
such that
![]() ${\mathcal { Q}}$
is
${\mathcal { Q}}$
is
![]() $\delta ({\mathcal {U}})$
-sound,
$\delta ({\mathcal {U}})$
-sound,
![]() $\rho _\omega ({\mathcal { Q}})\leq \delta ({\mathcal {U}})$
, and
$\rho _\omega ({\mathcal { Q}})\leq \delta ({\mathcal {U}})$
, and
![]() $rud({\mathcal { Q}})\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal.” We claim that
$rud({\mathcal { Q}})\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal.” We claim that
Claim 3. There is a branch b of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal { Q}}(b, {\mathcal {U}})$
exists and
${\mathcal { Q}}(b, {\mathcal {U}})$
exists and
![]() ${\mathcal { Q}}(b, {\mathcal {U}})={\mathcal { Q}}$
.
${\mathcal { Q}}(b, {\mathcal {U}})={\mathcal { Q}}$
.
Proof Indeed, let
![]() $X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be countable such that
$X\prec {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be countable such that
![]() ${\vec {\mathcal {T}}}, {\mathcal {S}}, {\mathcal {U}}, {\mathcal {P} }_\xi , {\mathcal { Q}} \in X$
, and letting
${\vec {\mathcal {T}}}, {\mathcal {S}}, {\mathcal {U}}, {\mathcal {P} }_\xi , {\mathcal { Q}} \in X$
, and letting
![]() $\pi _X:{\mathcal {N}}_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse of X,
$\pi _X:{\mathcal {N}}_X\rightarrow {\mathcal {M}}|(\delta ^+)^{\mathcal {M}}[g]$
be the transitive collapse of X,
![]() $\pi ^{-1}_X({\vec {\mathcal {T}}}^\frown {\mathcal {U}})$
is
$\pi ^{-1}_X({\vec {\mathcal {T}}}^\frown {\mathcal {U}})$
is
![]() $\Lambda $
-correct. Set
$\Lambda $
-correct. Set
![]() $\bar {{\mathcal { Q}}}=\pi ^{-1}({\mathcal { Q}})$
. Notice that it follows from Claim 1 and Proposition 1.7 that
$\bar {{\mathcal { Q}}}=\pi ^{-1}({\mathcal { Q}})$
. Notice that it follows from Claim 1 and Proposition 1.7 that
![]() $\bar {{\mathcal { Q}}}$
is
$\bar {{\mathcal { Q}}}$
is
![]() $\delta $
-iterable in
$\delta $
-iterable in
![]() ${\mathcal {N}}$
. Let then
${\mathcal {N}}$
. Let then
![]() $c=\Lambda (\pi _X^{-1}({\vec {\mathcal {T}}}^\frown {\mathcal {U}}))$
. We must have that
$c=\Lambda (\pi _X^{-1}({\vec {\mathcal {T}}}^\frown {\mathcal {U}}))$
. We must have that
![]() ${\mathcal { Q}}(c, \bar {{\mathcal {U}}})$
exists and
${\mathcal { Q}}(c, \bar {{\mathcal {U}}})$
exists and
![]() ${\mathcal { Q}}(c, \bar {{\mathcal {U}}})=\bar {{\mathcal { Q}}}$
. By absoluteness
${\mathcal { Q}}(c, \bar {{\mathcal {U}}})=\bar {{\mathcal { Q}}}$
. By absoluteness
![]() $c\in {\mathcal {N}}_X$
. It is now not hard to check that
$c\in {\mathcal {N}}_X$
. It is now not hard to check that
![]() $b=_{def}\pi _X(c)$
is as desired. b is the unique branch of
$b=_{def}\pi _X(c)$
is as desired. b is the unique branch of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal { Q}}(b, {\mathcal {U}})$
exists and
${\mathcal { Q}}(b, {\mathcal {U}})$
exists and
![]() ${\mathcal { Q}}(b, {\mathcal {U}})={\mathcal { Q}}$
.
${\mathcal { Q}}(b, {\mathcal {U}})={\mathcal { Q}}$
.
Case 2:
![]() ${\mathcal {U}}$
has a fatal drop.
${\mathcal {U}}$
has a fatal drop.
Let
![]() $\xi <lh({\mathcal {U}})$
be such that the fatal drop happens at
$\xi <lh({\mathcal {U}})$
be such that the fatal drop happens at
![]() ${\mathcal {M}}^{\mathcal {U}}_\xi $
. Let
${\mathcal {M}}^{\mathcal {U}}_\xi $
. Let
![]() $\zeta $
and
$\zeta $
and
![]() ${\mathcal {W} }\triangleleft {\mathcal {M}}^{\mathcal {U}}_\xi $
be such that
${\mathcal {W} }\triangleleft {\mathcal {M}}^{\mathcal {U}}_\xi $
be such that
![]() ${\mathcal {M}}^{\mathcal {U}}_\xi |\zeta \triangleleft {\mathcal {W} }$
,
${\mathcal {M}}^{\mathcal {U}}_\xi |\zeta \triangleleft {\mathcal {W} }$
,
![]() $\rho _\omega ({\mathcal {W} })=\zeta $
,
$\rho _\omega ({\mathcal {W} })=\zeta $
,
![]() $\zeta $
is a strong cutpoint of
$\zeta $
is a strong cutpoint of
![]() ${\mathcal {W} }$
, and
${\mathcal {W} }$
, and
![]() ${\mathcal {U}}_{\geq \xi }$
is an iteration tree on
${\mathcal {U}}_{\geq \xi }$
is an iteration tree on
![]() ${\mathcal {W} }$
above
${\mathcal {W} }$
above
![]() $\zeta $
. Because
$\zeta $
. Because
![]() ${\mathcal {S}}$
is a minimal counterexample to
${\mathcal {S}}$
is a minimal counterexample to
![]() $\delta $
-iterability, we have that
$\delta $
-iterability, we have that
![]() ${\mathcal {W} }$
is
${\mathcal {W} }$
is
![]() $\delta $
-iterable in
$\delta $
-iterable in
![]() ${\mathcal {M}}|\delta [g]$
. Let then b be the branch of
${\mathcal {M}}|\delta [g]$
. Let then b be the branch of
![]() ${\mathcal {U}}$
according to the unique strategy of
${\mathcal {U}}$
according to the unique strategy of
![]() ${\mathcal {W} }$
. Again a Skolem hull argument and Claim 1 show that
${\mathcal {W} }$
. Again a Skolem hull argument and Claim 1 show that
![]() ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}^\frown \{ b\}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}^\frown \{ b\}$
is
![]() $\Lambda $
-correct.
$\Lambda $
-correct.
This finishes our description of branches that player
![]() $II$
plays in the comparison game between
$II$
plays in the comparison game between
![]() ${\mathcal {S}}|\nu $
and the construction producing
${\mathcal {S}}|\nu $
and the construction producing
![]() ${\mathcal {P} }$
. Let then
${\mathcal {P} }$
. Let then
![]() ${\mathcal {U}}$
be the tree on
${\mathcal {U}}$
be the tree on
![]() ${\mathcal {S}}|\nu $
of maximal length constructed in the manner described above.
${\mathcal {S}}|\nu $
of maximal length constructed in the manner described above.
Notice that for unboundedly many
![]() $\theta < \delta $
,
$\theta < \delta $
,
![]() ${\mathcal {P} }$
computes
${\mathcal {P} }$
computes
![]() $\theta ^+$
correctly. This is because
$\theta ^+$
correctly. This is because
![]() ${\mathcal {X}}\in {\mathcal {P} }$
and if
${\mathcal {X}}\in {\mathcal {P} }$
and if
![]() ${\mathcal {P} }^*$
is the output of the fully backgrounded construction of
${\mathcal {P} }^*$
is the output of the fully backgrounded construction of
![]() ${\mathcal {P} }$
done over
${\mathcal {P} }$
done over
![]() ${\mathcal {X}}$
with large enough critical points then
${\mathcal {X}}$
with large enough critical points then
![]() ${\mathcal {P} }^*$
computes unboundedly many successors correctly (this is a consequence of the internal covering property).
${\mathcal {P} }^*$
computes unboundedly many successors correctly (this is a consequence of the internal covering property).
It now follows that
![]() $lh({\mathcal {U}})\not =\delta $
as then
$lh({\mathcal {U}})\not =\delta $
as then
![]() $C({\mathcal {U}})={\mathcal {P} }$
. Also,
$C({\mathcal {U}})={\mathcal {P} }$
. Also,
![]() ${\mathcal {U}}$
must have a last model
${\mathcal {U}}$
must have a last model
![]() ${\mathcal {S}}^*$
. Indeed, if
${\mathcal {S}}^*$
. Indeed, if
![]() ${\mathcal {U}}$
doesn’t have a last model then it is of limit length. Because
${\mathcal {U}}$
doesn’t have a last model then it is of limit length. Because
![]() $\delta ({\mathcal {U}})<\delta $
, we have that
$\delta ({\mathcal {U}})<\delta $
, we have that
![]() ${\mathcal {M}}\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal,” implying that our method of picking branches of
${\mathcal {M}}\vDash "\delta ({\mathcal {U}})$
is not a Woodin cardinal,” implying that our method of picking branches of
![]() ${\mathcal {U}}$
does produce a branch for
${\mathcal {U}}$
does produce a branch for
![]() ${\mathcal {U}}$
. Because the
${\mathcal {U}}$
. Because the
![]() ${\mathcal {S}}|\nu $
-side lost the comparison,
${\mathcal {S}}|\nu $
-side lost the comparison,
![]() $\pi ^{\mathcal {U}}$
must exist. Let
$\pi ^{\mathcal {U}}$
must exist. Let
![]() $\zeta =\pi ^{\mathcal {U}}(\nu )$
(because
$\zeta =\pi ^{\mathcal {U}}(\nu )$
(because
![]() ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
![]() $\Lambda $
-correct,
$\Lambda $
-correct,
![]() ${\mathcal {U}}$
can be applied to
${\mathcal {U}}$
can be applied to
![]() ${\mathcal {S}}$
).
${\mathcal {S}}$
).
Because
![]() ${\mathcal {M}}\vDash "\zeta $
is not a Woodin cardinal,” we can find sound
${\mathcal {M}}\vDash "\zeta $
is not a Woodin cardinal,” we can find sound
![]() ${\mathcal {S}}^*|\zeta $
-mouse
${\mathcal {S}}^*|\zeta $
-mouse
![]() ${\mathcal {W} }\in {\mathcal {M}}|\delta [g]$
such that
${\mathcal {W} }\in {\mathcal {M}}|\delta [g]$
such that
![]() $\rho _\omega ({\mathcal {W} })\leq \zeta $
,
$\rho _\omega ({\mathcal {W} })\leq \zeta $
,
![]() ${\mathcal {W} }\vDash "\zeta $
is a Woodin cardinal” and
${\mathcal {W} }\vDash "\zeta $
is a Woodin cardinal” and
![]() $rud({\mathcal {W} })\vDash "\zeta $
is not a Woodin cardinal.” Because we are in the no-fatal drop case,
$rud({\mathcal {W} })\vDash "\zeta $
is not a Woodin cardinal.” Because we are in the no-fatal drop case,
![]() ${\mathcal {W} }={\mathcal {S}}^*$
.
${\mathcal {W} }={\mathcal {S}}^*$
.
We claim that in
![]() ${\mathcal {M}}[g]$
,
${\mathcal {M}}[g]$
,
![]() ${\mathcal {W} }$
is
${\mathcal {W} }$
is
![]() $\delta $
-iterable above
$\delta $
-iterable above
![]() $\zeta $
. Notice that because
$\zeta $
. Notice that because
![]() ${\mathcal {W} }$
is obtained via S-constructions, for some
${\mathcal {W} }$
is obtained via S-constructions, for some
![]() $\beta $
,
$\beta $
,
![]() ${\mathcal {W} }$
is the result of the translation of
${\mathcal {W} }$
is the result of the translation of
![]() ${\mathcal {M}}||\beta $
into a mouse over
${\mathcal {M}}||\beta $
into a mouse over
![]() ${\mathcal {S}}^*|\zeta $
via S-constructions. It follows that
${\mathcal {S}}^*|\zeta $
via S-constructions. It follows that
![]() $\rho _{\omega }({\mathcal {M}}|\beta )\leq \zeta $
. Since
$\rho _{\omega }({\mathcal {M}}|\beta )\leq \zeta $
. Since
![]() ${\mathcal {M}}||\beta $
is
${\mathcal {M}}||\beta $
is
![]() $\delta $
-iterable above
$\delta $
-iterable above
![]() $\zeta $
,
$\zeta $
,
![]() ${\mathcal {W} }$
is also
${\mathcal {W} }$
is also
![]() $\delta $
-iterable above
$\delta $
-iterable above
![]() $\zeta $
(see Proposition 1.4). It follows from S-reconstructibility that for any
$\zeta $
(see Proposition 1.4). It follows from S-reconstructibility that for any
![]() $\xi \in (\zeta , \delta )$
,
$\xi \in (\zeta , \delta )$
,
![]() ${\mathcal {W} }$
can also be built by the fully backgrounded construction of
${\mathcal {W} }$
can also be built by the fully backgrounded construction of
![]() ${\mathcal {M}}|\delta [g]$
that uses extenders with critical points
${\mathcal {M}}|\delta [g]$
that uses extenders with critical points
![]() $>\xi $
. Let now
$>\xi $
. Let now
![]() $\xi _0<\xi _1$
be
$\xi _0<\xi _1$
be
![]() ${\mathcal {M}}$
-successor cardinals such that
${\mathcal {M}}$
-successor cardinals such that
![]() ${\mathcal {S}}^*|\zeta $
can be built by the fully backgrounded construction of
${\mathcal {S}}^*|\zeta $
can be built by the fully backgrounded construction of
![]() ${\mathcal {M}}|\xi _0[g]$
that uses extenders with critical points
${\mathcal {M}}|\xi _0[g]$
that uses extenders with critical points
![]() $>\eta $
, and
$>\eta $
, and
![]() ${\mathcal {W} }$
can be built by the fully backgrounded construction of
${\mathcal {W} }$
can be built by the fully backgrounded construction of
![]() ${\mathcal {M}}|\xi _1[g]$
that uses extenders with critical points
${\mathcal {M}}|\xi _1[g]$
that uses extenders with critical points
![]() $>\xi _0$
. It follows that iterability of
$>\xi _0$
. It follows that iterability of
![]() ${\mathcal {W} }$
can be reduced to the iterability of
${\mathcal {W} }$
can be reduced to the iterability of
![]() ${\mathcal {M}}|\xi _1$
for non-dropping trees that are above
${\mathcal {M}}|\xi _1$
for non-dropping trees that are above
![]() $\eta $
. Proposition 1.4 then implies that
$\eta $
. Proposition 1.4 then implies that
![]() ${\mathcal {W} }$
is
${\mathcal {W} }$
is
![]() $\delta $
-iterable in
$\delta $
-iterable in
![]() ${\mathcal {M}}[g]$
.
${\mathcal {M}}[g]$
.
This is a contradiction as in
![]() ${\mathcal {M}}[g]$
,
${\mathcal {M}}[g]$
,
![]() ${\mathcal {S}}$
is not
${\mathcal {S}}$
is not
![]() $\delta $
-iterable above
$\delta $
-iterable above
![]() $\eta $
, while because
$\eta $
, while because
![]() $\pi ^{\mathcal {U}}:{\mathcal {S}}\rightarrow {\mathcal {W} }$
, we get that in
$\pi ^{\mathcal {U}}:{\mathcal {S}}\rightarrow {\mathcal {W} }$
, we get that in
![]() ${\mathcal {M}}[g]$
,
${\mathcal {M}}[g]$
,
![]() ${\mathcal {S}}$
is in fact
${\mathcal {S}}$
is in fact
![]() $\delta $
-iterable above
$\delta $
-iterable above
![]() $\eta $
.
$\eta $
.
The case when
![]() ${\mathcal {S}}$
has no Woodin cardinals is very similar. Now we compare
${\mathcal {S}}$
has no Woodin cardinals is very similar. Now we compare
![]() ${\mathcal {S}}$
with the fully backgrounded constructions producing a tree
${\mathcal {S}}$
with the fully backgrounded constructions producing a tree
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() ${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
${\vec {\mathcal {T}}}^\frown {\mathcal {U}}$
is
![]() $\Lambda $
-correct. Because
$\Lambda $
-correct. Because
![]() ${\mathcal {S}}$
has no Woodin cardinals, handling limit stages of the construction of
${\mathcal {S}}$
has no Woodin cardinals, handling limit stages of the construction of
![]() ${\mathcal {U}}$
is very similar. Assuming
${\mathcal {U}}$
is very similar. Assuming
![]() ${\mathcal {U}}$
has been built up to stage
${\mathcal {U}}$
has been built up to stage
![]() $\gamma $
, we consider, as above, two cases. If
$\gamma $
, we consider, as above, two cases. If
![]() ${\mathcal {U}}\restriction \gamma $
has no fatal drops then we proceed as in the “no fatal drop case” of the above argument. Otherwise, we proceed in the “fatal drop” case of the above argument. We leave the details to the reader.
${\mathcal {U}}\restriction \gamma $
has no fatal drops then we proceed as in the “no fatal drop case” of the above argument. Otherwise, we proceed in the “fatal drop” case of the above argument. We leave the details to the reader.
We believe that the project of characterizing in mice the exact cardinals
![]() $\kappa $
that permit stationary tower like embeddings with critical point
$\kappa $
that permit stationary tower like embeddings with critical point
![]() $\kappa $
is a very nice project.
$\kappa $
is a very nice project.
Acknowledgments
The author is grateful to the referee for many useful comments. The author’s work was partially supported by the NSF Career Award DMS-1352034 and by the NSF Award DMS-1954149. The author is grateful to the Institute of Mathematics of the Polish Academy of Sciences for hosting him during the academic year 2020–2021, and for providing an excellent environment for conducting research. The author finished the paper while being at the institute.