Introduction
Iceland lies just south of the Arctic Circle in the North Atlantic Ocean and covers an area of roughly 103 000 km2, with a population of 260 000 (Fig. 1). The country is very mountainous and avalanche activity is common. The first recorded avalanche fatalities were in the year 1118 and since that time over 680 have occurred, a toll worse than that from any other type of land-based natural hazard in Iceland (Reference EgilssonEgilsson, 1997). During recent years it is the towns and villages in the northwest (the West Fjords) which have been most at risk from avalanching.
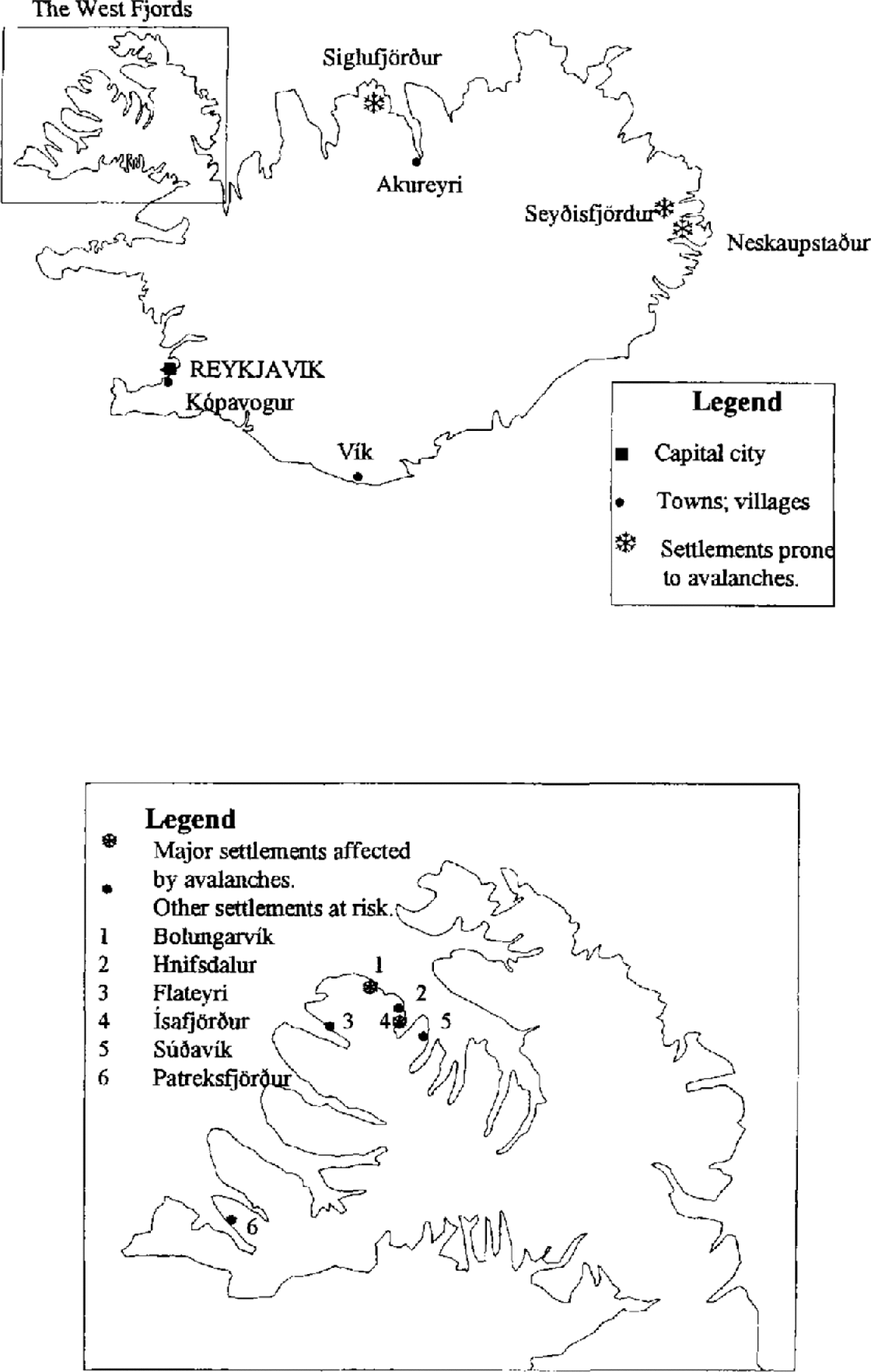
Fig. 1. Areas of Iceland prone to avalanching.
In the early hours of 26 October 1995, an avalanche devastated the village of Flateyri in the West Fjords. Nineteen houses, inhabited by 45 people, were struck, and 20 people out of a population of 379 were killed. This was the second such tragedy to strike in the West Fjords that year. On 16 January an avalanche destroyed or damaged 22 out of 70 houses in the village of Súðavík, killing 14 people, including eight children.
With such catastrophes occurring far too frequently, it is essential that tools are made available to the authorities that safeguard the development of settlements in mountainous regions. Risk analysis (Reference Einstein and BonnardEinstein, 1988; Reference FellFell, 1994) is one method of characterizing the probable losses from avalanching in such areas. Risk maps present the information in a manner that is easy to interpret and understand.
Various approaches have been employed around the world for determining hazard zones in avalanche terrain. Reference McClung and Schaerer.McClung and Schaerer (1993) provide a review of these methods. It is important to note that none of the existing zonation techniques adopt the risk approach explicitly. Perhaps the best-known scheme is the Swiss method which is based on a combination of information on avalanche impact pressure (derived from a dynamics model) and knowledge of probable avalanche return period (recurrence interval) at a given point in the terrain. This approach is risk-based, but docs not employ formal risk calculations such as we present in this paper.
Risk Analysis
Risk is defined as the probability of death or losses and is calculated as the product of three sub-components that take values between 0 and 1:
(1) Event frequency is defined by the spatial and temporal exceedance probability of avalanching as a function of location (downslope and across slope).
(2) Exposure is the fraction of time during which the objects or people concerned are potentially subjected to the phenomenon under consideration.
(3) Vulnerability is the fraction of damage to the elements concerned.
Risk is primarily a function of avalanche frequency as a function of location, which is dependent on both the spatial pattern of runout and the frequency of avalanches entering the runout zone. This component of risk forms the focus of our study. If one is dealing with the risk to residents, then the exposure is the fraction of time for which the building is occupied. An analysis of the risk to buildings uses an exposure value of 1 (the buildings are fixed objects in the avalanche path and are therefore permanently exposed). Vulnerability contains information about avalanche magnitude (destructive potential) and can be formulated to varying degrees of complexity. It is most simply defined as the statistical expectation of loss at a location, based on the frequency distribution of avalanche sizes and the estimated loss as a function of avalanche size.
It is very rare for avalanche records on a path to be sufficiently detailed for an accurate estimate of the probability distribution for runout to be made. Thus, data have to be pooled and a more general model, applicable to a larger area, developed. This model will represent an average case for the region concerned, ignoring major differences in path topography and weather. This is an inherent weakness of risk modelling and statistical approaches in general; one has to make a trade-off between sample size and degree of specificity.
Existing statistical approaches in the avalanche literature are used to estimate the expected runout of extreme avalanches, typically equated to a return period of 50–300 years (Reference McClung, Mears. and Schaerer.McClung and others, 1989; Reference Jóhannesson and HestnesJóhannesson, 1998a). A variety of such techniques exist (Reference Bovis and Mears.Bovis and Mears, 1976; Reference Lied and Bakkehøi.Lied and Bakkehøi, 1980; Reference Bakkehøi, Domaas. and Lied.Bakkehøi and others, 1983; Reference MartinelliMartinelli, 1986; Reference McClung and Lied.McClung and Lied, 1987; Reference McClung, Mears. and Schaerer.McClung and others, 1989; Reference McClung and Mears.McClung and Mears, 1991). These empirical approaches can be used to estimate maximum runout distance based on terrain variables and the historical record of extreme avalanche runout in a mountain range. However, none of these techniques permit the derivation of the variable of primary interest in risk studies: the relation between runout distance and return period along a single avalanche path. Furthermore, such methods do not incorporate destructive potential, which is required to assess risk.
In this paper we provide a mathematical simulation model containing information on return period and destructive potential as a function of position, based on avalanche occurrence data and the historical record of avalanche runout for a given mountain range. Thus, our approach has significant advantages over existing statistical approaches to avalanche runout.
Model Structure
Reference Banks, Carson. and Nelson.Banks and others (1996) define a simulation as “The imitation of the operation of a real-world process or system over time”. They further state that “Simulation involves the generation of an artificial history of a system, and the observation of that artificial history to draw inferences concerning the operating characteristics of the real system”. Thus, if one is able to simplify the real-world phenomenon into a set of mathematical or statistical relations, it is possible to develop a model to estimate properties ofthat system. By consideration of avalanche occurrence as a stochastic phenomenon, a statistical simulation model of avalanche risk can be produced.
Pooling of data obtained from a large number of avalanche paths provides sufficient information to permit avalanche runout and width information to be fitted to a specific probability density function (PDF). Since a model developed from such distributions is based on the historical record of avalanche occurrences, the results of a simulation should resemble the situation on an “average” avalanche path, in the spirit of risk modelling.
Before the avalanche data can be used to estimate risk, some form of avalanche size classification is required. This study uses the Canadian size classification, which is used by all observers in Canada and Iceland. This system is based on the potential destructive effects of avalanches. It is therefore directly connected to the vulnerability component of risk. The Canadian classification uses five sizes, although it is common for avalanche observers to use half-sizes. We have followed this procedure. The sizes and some associated properties are shown in Table 1.
Table 1. Canadian snow-avalanche size classification and typical factors from Reference McClung and Schaerer.McClung and Schaerer (1993)
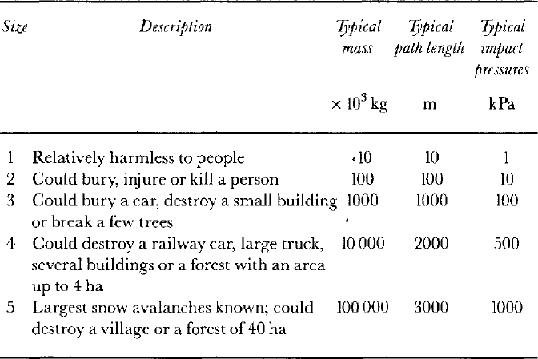
Figure 2 is a flow chart that outlines the structure of the model developed in this paper. More formally, risk is the product of event frequency (E), exposure and vulnerability. In this paper we take exposure to be 1.0 for risk to buildings (permanent structures) and 0.5 for individuals (50% occupancy time). Vulnerability can be simply evaluated from a look-up table linking avalanche size to probable damage. Evaluation of event frequency is more complex.

Fig. 2. Flow chart showing the structure of the risk model developed in this paper.
For an avalanche of a given size n, the event frequency (E) is given by:
where f is the average avalanche frequency (events per year) on the path, r n is the relative frequency of the given size and P(T) is the probability of an event reaching a target point T, with coordinates (T x, T y), where x is distance along the profile and y is distance perpendicular to the profile (Fig. 3). In our approach, f is typically determined by avalanche observation on the selected path, r is determined directly from the distribution for the relative frequency of different avalanche sizes and P(T x)n is found from the runout PDF for the given size. The evaluation of P(T y)n is more complex because this term reflects the interaction of variable avalanche width and differences in avalanche trajectory, both of which contribute to lateral variation in avalanche extent:
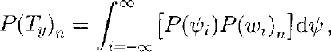
where P(ψ i) is the probability of the avalanche deviating from the centre line by ψ i metres and P(w i)n is the cumulative distribution function that defines the probability of an avalanche of size n attaining the required width w i defined as:
Figures 2 and 3 illustrate these relations. Once the above procedure has been applied to all sizes, the event frequency at a location has been determined. This theoretical structure is a flexible risk-modelling tool, a new approach in the avalanche literature. The model developed here exhibits a high degree of sophistication compared to several existing approaches in the natural hazards literature (Reference Morgan, Rawlings. and Sobkowicz.Morgan and others, 1992; Reference Sheridan and Macias.Sheridan and Macias, 1995).
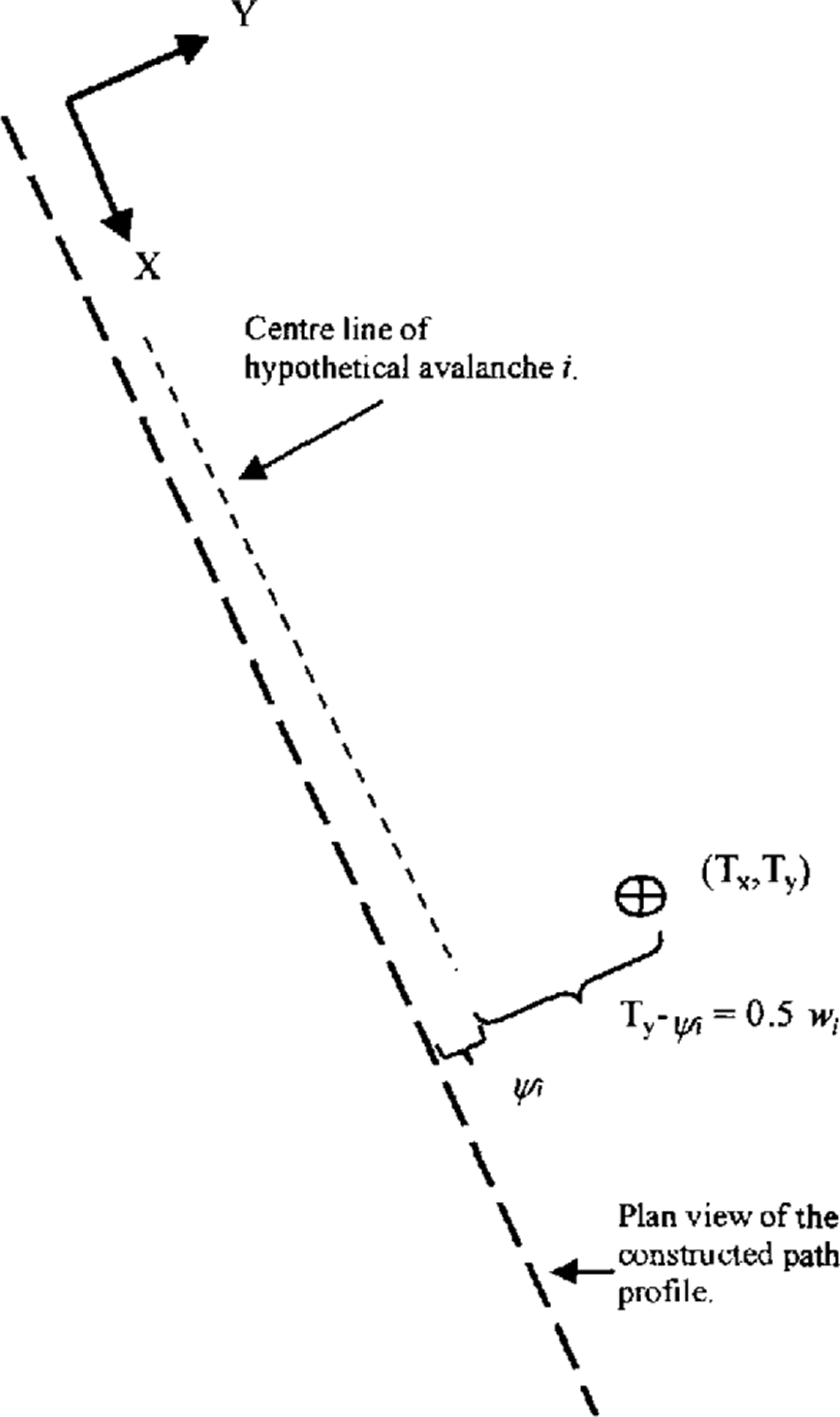
Fig. 3. The coordinate system and parameters used for combining avalanche-width and deviation information. The model is solved for a target location (T x, T y).
As a practical trial of this risk framework, the model has been applied to Icelandic avalanches. While the Icelandic avalanche database is expanding, the current shortage of available data makes it necessary to introduce some assumptions in order to develop the model.
Model Implementation
Average avalanche frequency
The avalanche frequency varies greatly between different climatic regions in Iceland. For example, in Neskaupstaður on the east coast, few events have been recorded since the major avalanche cycle of 1974, while at Flateyri five large events have been recorded on one path since the beginning of 1990. The quality of avalanche observations is variable around the country, but the range of different avalanche frequencies is such that real differences between regions are apparent, as are differences between paths. This intrinsic variability means that every effort should be made to formulate an average frequency of avalanche occurrence for each path, either directly from actual avalanche occurrences, by statistical methods (e.g. Reference Smith and McClung.Smith and McClung, 1997) or by theoretical approaches (Reference KeylockKeylock, 1996; Reference SólnesSólnes, 1997).
Equation (1) shows that the avalanche-frequency estimate (f) scales the event frequency (E i) to make the results for each size applicable to a particular path. For example, if at a specific location the avalanche exceedance probability (from the last three terms on the righthand side of Equation (1)) is calculated to be 0.01, then with an average frequency of one avalanche per year the return period at this location is 100 years. For a similar point on a different path where f equals two avalanches per year, the return period is 50 years.
Distribution for the relative frequency of different sizes
Unfortunately, there is no such thing as a complete, systematic, unbiased record of avalanching that utilizes an avalanche size classification appropriate for this study. In Iceland, the historical record of avalanching contains a bias due to the emphasis on events that caused damage to property and loss of life, the events with the largest widths and runout distances. At Rogers Pass and Revelstoke in British Columbia, Canada, there are systematic records of avalanching, each of the two datasets including over 5000 avalanches. However, the reason systematic records exist at these locations is that active control measures are in place. Such measures, if effective, will prevent major avalanches. Therefore, at such locations there is a bias towards smaller events. These effects can be clearly seen in the histograms presented in Figure 4.
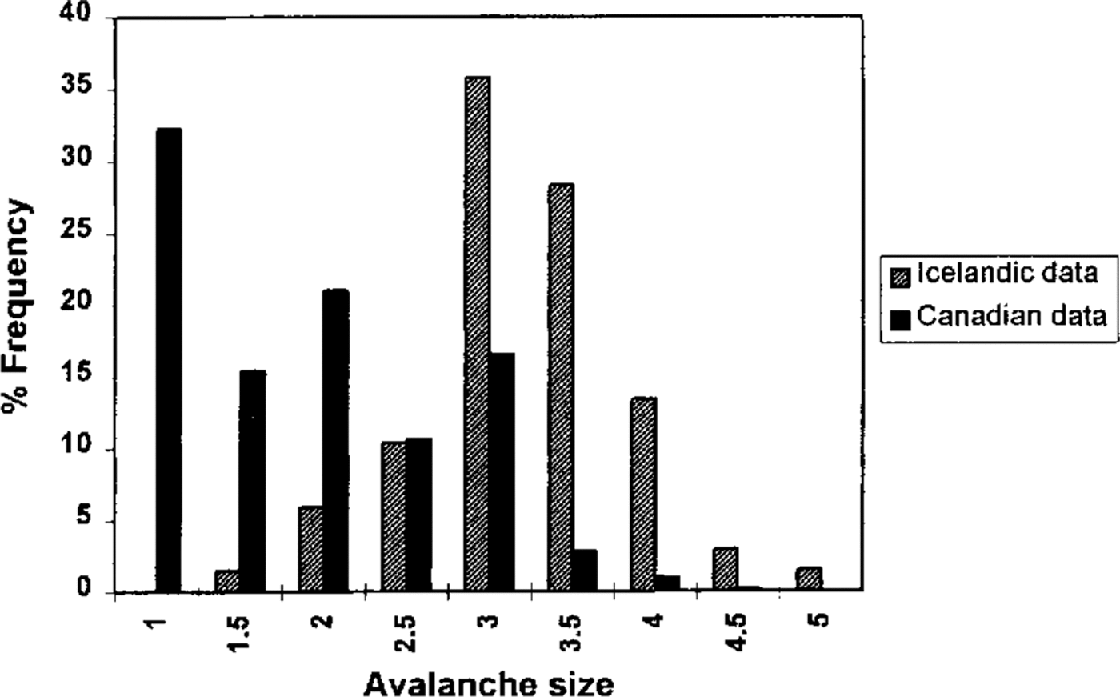
Fig. 4. Percentage frequency histograms of the relative frequency of different-sized avalanches in Canada and Iceland.
A compromise solution to this problem was adopted: the two records were amalgamated, the Icelandic data being employed for sizes 4 and above. Size 4 was chosen as the threshold condition because it seemed reasonable to suppose that the vast majority of size 4 events would have been observed in Iceland. It can be seen from the distributions derived in the next subsection that 80–90% of size 4 avalanches are expected to exceed the upslope limit of settlement in Iceland.
To combine the Canadian and Icelandic data, the size of the avalanches in Iceland had to be estimated. Where the deposit volume had been estimated, a “typical“ density value of 350 kg m−3 was used to calculate avalanche mass, with sizes allocated based on the mass values given in Table 1. Because the Canadian size classification is based on a logarithmic or power-law relationship, any error introduced by using a single density value should not be significant.
In many cases not all the deposit dimensions had been recorded for avalanches in Iceland. Commonly, the width and depth of the deposit had been measured, but not its length. To obtain an estimate of size for such events, simple least-squares regression was employed. The equation was derived from the 55 events where volume measurements had been taken. The regression was performed on log-transformed variables, with the product of deposit height and width related to volume. The resulting relation had an intercept of 3.63, a gradient of 1.07, a standard error of 0,60 and an r 2 of 0,83. This was thought quite acceptable given the power-law nature of the Canadian size classification.
Table 2 presents the distribution for the relative frequency of different sizes derived from a combination of the Canadian and Icelandic data. The method adopted was to note the proportion of avalanches in the Canadian record of size 4 or larger and then use this term to appropriately scale the Icelandic distribution for size 4 or larger. The main weakness in the practical implementation of our model at present is the use of this Canadian data. The relative frequency of different sizes is likely to differ between the two countries and this will affect our results. However, we preferred to employ the available data rather than to assume a specific theoretical distribution without recourse to data. Improvements have been made to avalanche observation in Iceland following the 1995 disasters, so it is hoped that this weakness can be eliminated once a complete frequency record can be derived for Iceland. Model sensitivity to the form of this distribution is explored in the model evaluation section.
Table 2. Relative frequency of the different avalanche size classes at the starting zone

Distributions for avalanche runout
Runout distance and avalanche-path profile data were obtained from a number of 1:5000 scale avalanche registration maps produced by the Icelandic Meteorological Office (IMO).The runout ratio of Reference McClung and Lied.McClung and Lied (1987) was used to standardize the data and to allow a comparison of avalanche events on different path,. The runout ratio technique defines a β point as the point on the slope profile where the local slope angle attains 10°, Analysis of avalanche-path parameters by Reference Lied and Bakkehøi.Lied and Bakkehøi (1980) and many subsequent workers has shown that this is the only statistically significant terrain parameter for runout-distance prediction. Thus, not only does the runout ratio permit inter-path comparison of runout distances, it also incorporates the significant terrain parameter. This ratio is defined as:
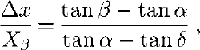
where Δx is the horizontal distance from the β point to the maximum reach of the avalanche, X β is the horizontal distance from the starting zone to the β point, α and β are the angles to the starting zone from the maximum reach of the avalanche and the β point, respectively, and δ is the angle from the maximum reach of the avalanche to the β point (Fig. 5).
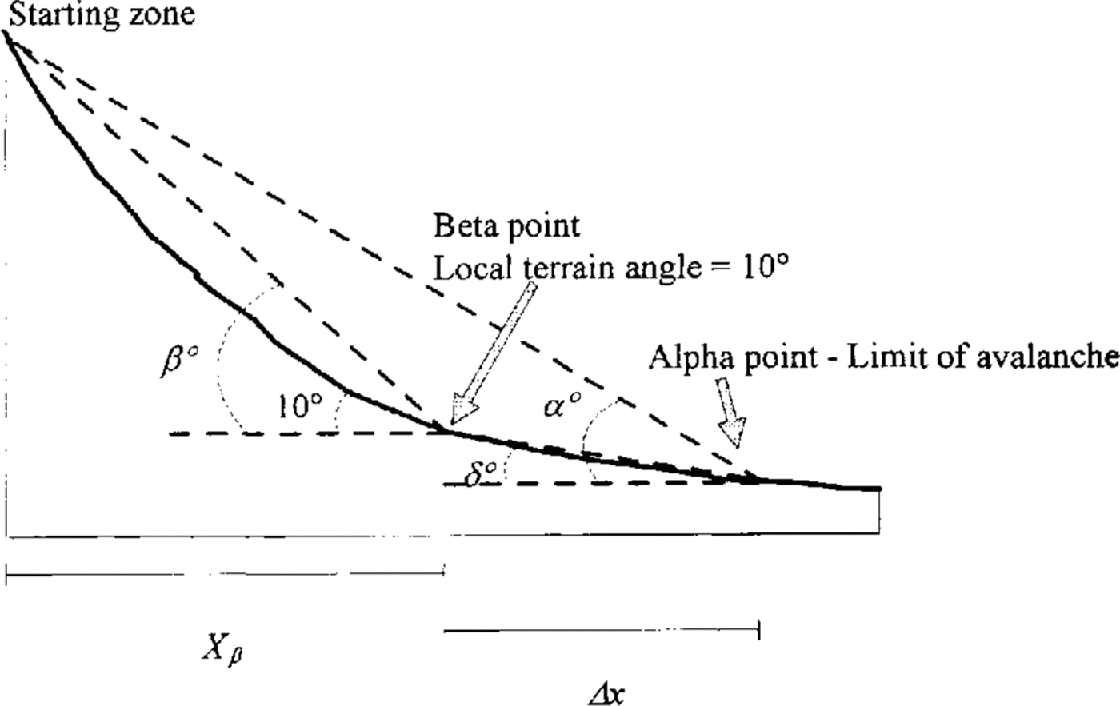
Fig. 5. Definition of slope-geometry parameters used for deriving the runout ratio.
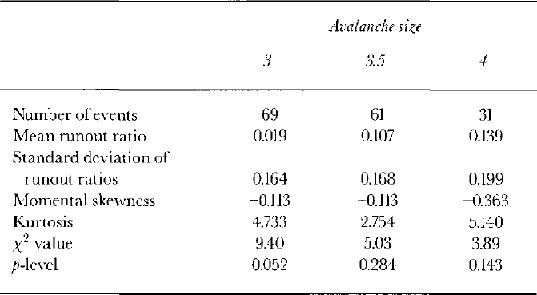
Once all measurements of runout have been converted to runout ratios and a size has been allocated to each event, runout ratios can be grouped by size, and distributions fitted to each assemblage. Only one size 5 and eight size 4.5 avalanches were recorded in Iceland, too few observations to permit a distribution to be fitted. This was also the case for events smaller than size 3 (14 size 2.5 events and one size 2 event had been observed). The fact that there were only enough avalanches in the Icelandic dataset to fit a distribution to three of the size classes (sizes 3, 3.5 and 4) is the second most important limitation of this study (see below). Altogether, 161 avalanche events from Iceland were employed in size–runout distribution fitting.
A priori it was hypothesized that a distribution exhibiting a certain amount of positive skew (e.g. a log-normal distribution) would best fit the data. However, inspection of the box plots presented in Figure 6 shows that there is no clear tendency for the collected data to exhibit a significant positive skew. The best-fit distribution to the runout distances for these three size classes was a normal distribution. The degree-of-fit was assessed by the χ 2 method where values of p ,0.05 suggest an insignificant degree of congruence between the data and the Gaussian model. Table 3 provides an assessment of the fits. With no obvious trend in skewness or kurtosis across these three size classes, it was not felt necessary to modify more than the first two moments of the distribution when estimating the parameters for other sizes.
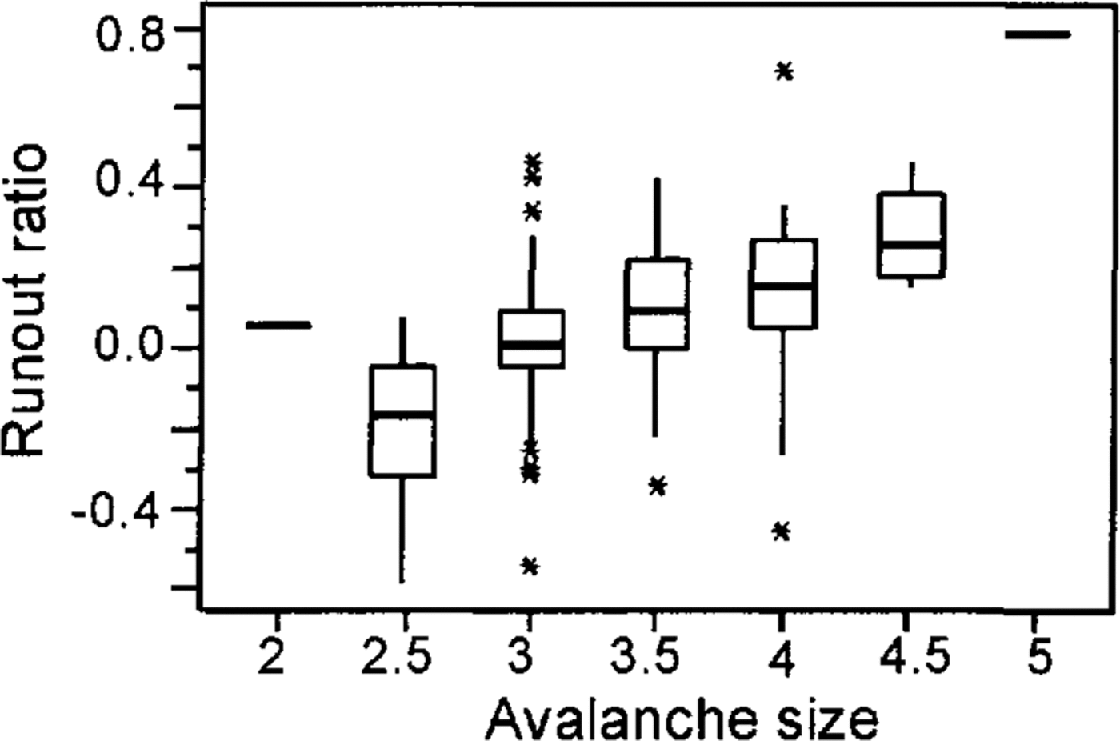
Fig. 6. Box plots of the observed runout data segregated by size. The top and bottom of the boxes represent the first and third quartiles; the central bar is the median.
Table 3. Runout ratio statistics for avalanche sizes 3–4, with an assessment of fit to the normal distribution
From the means and variances for these three fitted distributions, methods had to be devised to estimate parameters for other sizes where there were either no data or too few to permit distribution fitting. Observations at Rogers Pass would seem to suggest that, as size increases, runout distances increase in a logarithmic manner. This seems intuitively correct, in that for a given path there must be a theoretical maximum runout distance that will be approached asymptotically. Further support for this assumption comes from the Icelandic size 2.5 data where the median event has a runout ratio of –0.170, substantially less than the median value for size 3 (0.008). It was also clear that use of a linear fit drastically over-predicted the mean runout distance of the smallest avalanches (sizes 1–2). The difference between a linear and logarithmic fit in terms of risk is relatively small, as demonstrated in the model evaluation section below.
Applying a logarithmic relation to the mean values of the runout ratio (MR) and avalanche size (S) in Iceland gives Equation (5). This has an r 2 of 0.95. Application of this equation to all sizes yields the mean runout ratios given in Table 4.
For the second moment of the distribution, it was expected that the standard deviation would increase as the size increased, and this is borne out by the values in Table 3. With no additional information to guide the fitting procedure, a linear fit between the standard deviation of the runout ratios (SDR) and size was adopted with an r 2 of 0.82. The equation obtained by least-squares regression was:
The values derived from this relation are also given in Table 4.
Table 4. Derived parameters for normal distributions of the runout ratio for individual avalanche sizes
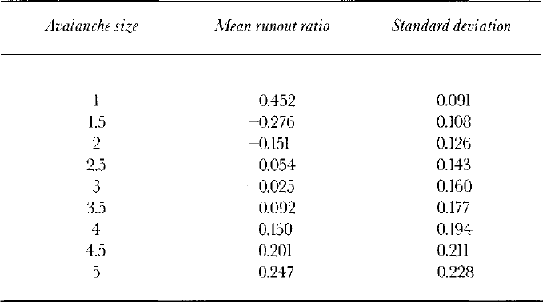
Figure 7 compares the available data and the fitted distributions. Agreement for sizes 2 and 5 is rather poor, but there are good reasons for this. The nature of the Icelandic data means that to be documented the single recorded size 2 event must have had an exceptional runout distance. The size 5 avalanche, at Ísafjörður in 1994, occurred on a path with a very unusual topography and was recently found to be the longest-running of recent major European avalanches by the Snow Avalanche Modelling and Mapping (SAME) working group (Barbolini, Gruber, Naaim, Keylock; unpublished information) on the basis of both statistical methods and dynamics model coefficients.
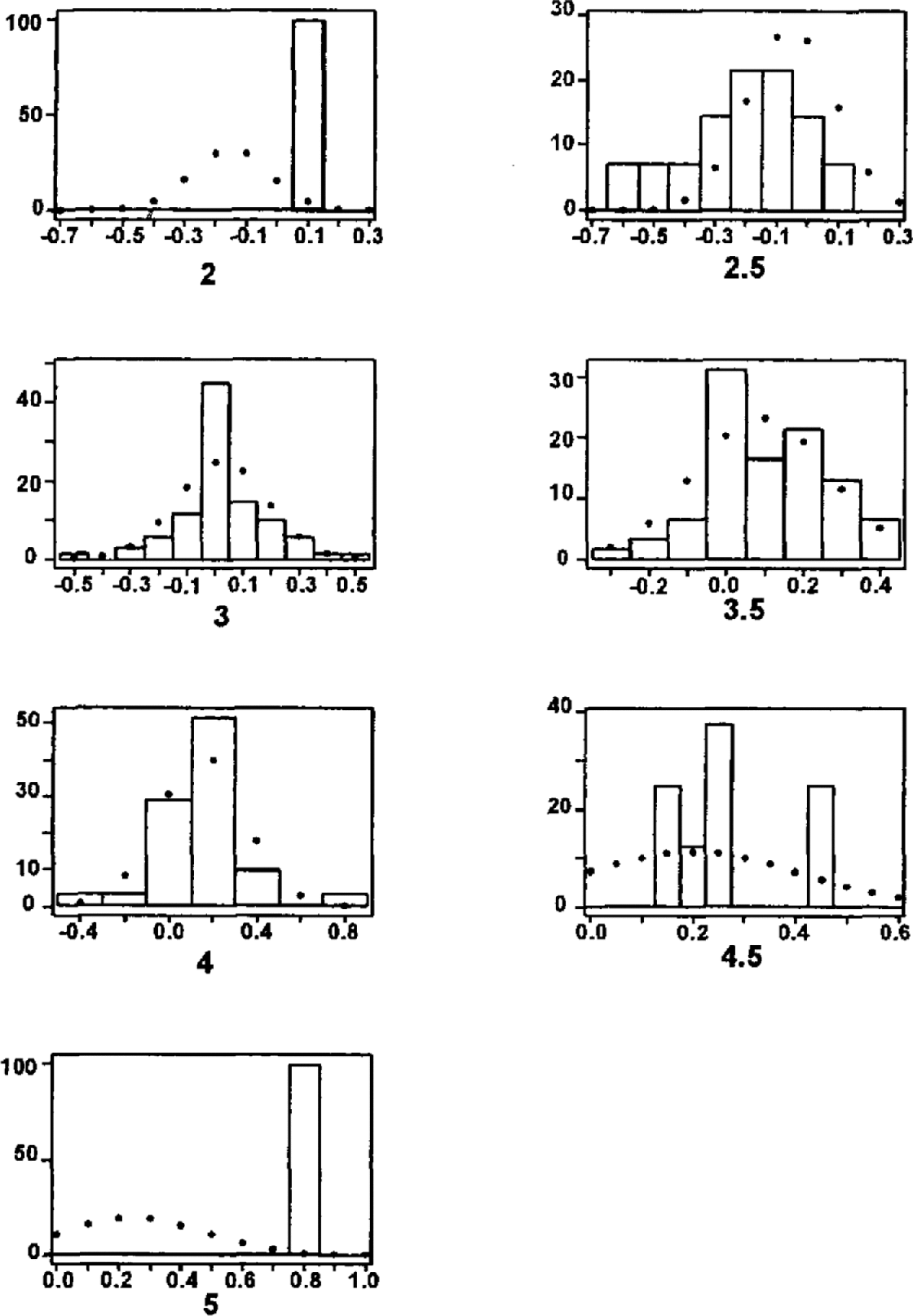
Fig. 7. Percentage histograms of available runout data and the fitted Gaussian distributions. For the seven sizes shown and in order of increasing size, the number of observed events was 1, 14, 69, 61, 31, 8, 1, respectively.
For avalanching in Iceland, one is mainly concerned with a region characterized by runout ratios of approximately 0.0–0.4. Using the distributions outlined in Table 4, it is simple to determine the percentage of avalanches of a given size that will exceed these runout ratios. When these values are weighted by the relative frequency of different sizes (Table 2), sizes 3–4 contribute 65% of avalanches at a runout ratio of 0.0, and 87% at a ratio of 0.4. Thus, while at the starting zone these three sizes represent only 20% of avalanches, by the time one reaches the region of concern for risk studies their significance has been greatly enhanced. Consequently, the limitation that there were sufficient data to attempt fits only to sizes 3, 3.5 and 4 is not as significant as might at first appear.
Figure 8 shows how the percentage of avalanches reaching or exceeding a specific runout ratio varies according to model simulation. This plot combines the relative size-frequency distribution listed in Table 2 with the runout distributions derived above. At this stage, width and direction effects are not included. The plot was constructed by determining the probability of exceeding a runout ratio value for each size–runout distribution and weighting this probability by the relative frequency of the given size. This calculation was performed for 100 different runout ratios between –0.8 and 0.8, sufficient to permit the points to be connected. There is no variability about the line, because the model was solved exactly for each point. It is evident that a runout ratio of 0.33 is exceeded by 1% of events according to the model.
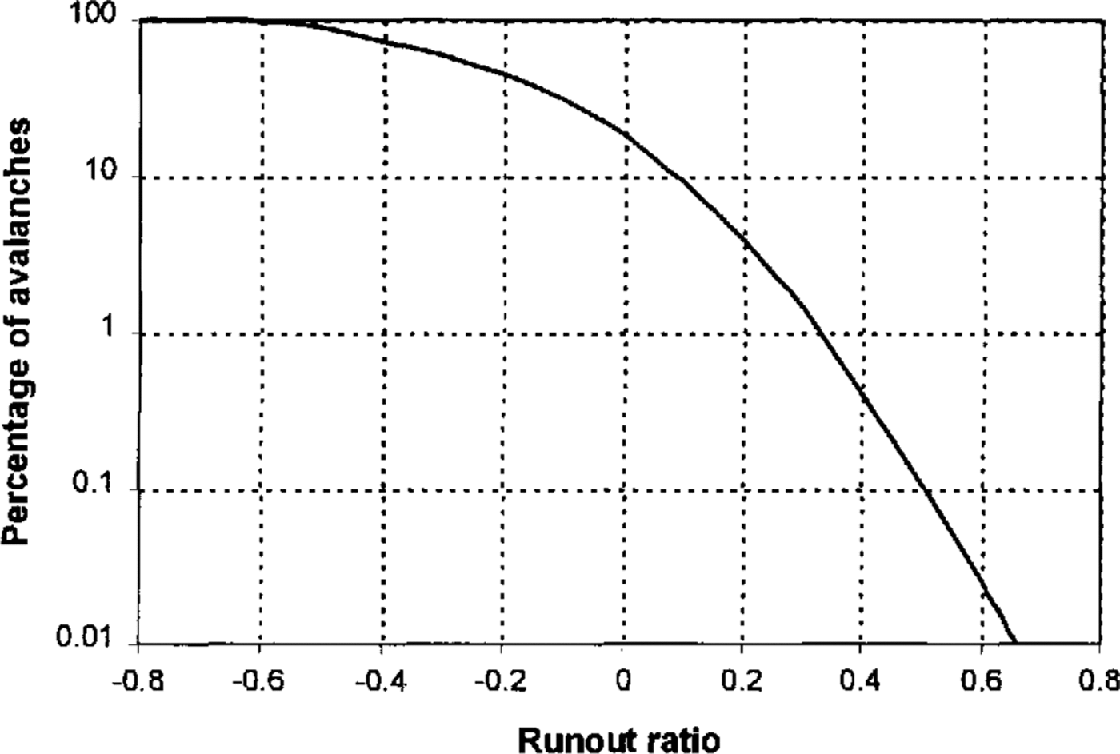
Fig. 8. Simulation model results for the percentage of avalanches attaining or exceeding a given runout ratio.
There is little available information concerning runout distances along a single avalanche path. However, Reference Föhn and Meister.Föhn and Meister (1981) suggest that annual maximum runout distances along the Salezertobel path in Switzerland, censored at an arbitrary location, conform to an extreme-value type I or Gumbel distribution (Reference GumbelGumbel, 1958). This result can be used as a preliminary test of the simulation model. To this end, 30 simulations were performed utilizing the size–runout distributions (Table 4) and the relative size–frequency distribution (Table 2). For each simulation, an assessment was made of the degree-of-fit of the resulting runout ratio distribution to a Gumbel distribution. Ten thousand avalanches were generated in each simulation. The procedure for each event was to randomly pick an avalanche size using the relative size–frequency distribution. For the selected size, a runout ratio was determined using the appropriate mean and standard deviation values (Table 4). Figure 9, showing one such simulation (with the runout ratios censored at 0.0), demonstrates that the model does indeed produce runout ratios that show a reasonable conformity to a Gumbel (rather than a Gaussian) distribution. The mean and standard deviations (in parentheses) for the scale and location parameters of the fitted Gumbel distribution for the 30 simulations were 0.103 (0.003) and –0.14.4 (0.006), respectively. The mean r 2 value was 0.982, with a standard deviation of 0.005. Therefore, our model appears to obey the same general distribution as the data from Salzertobel.
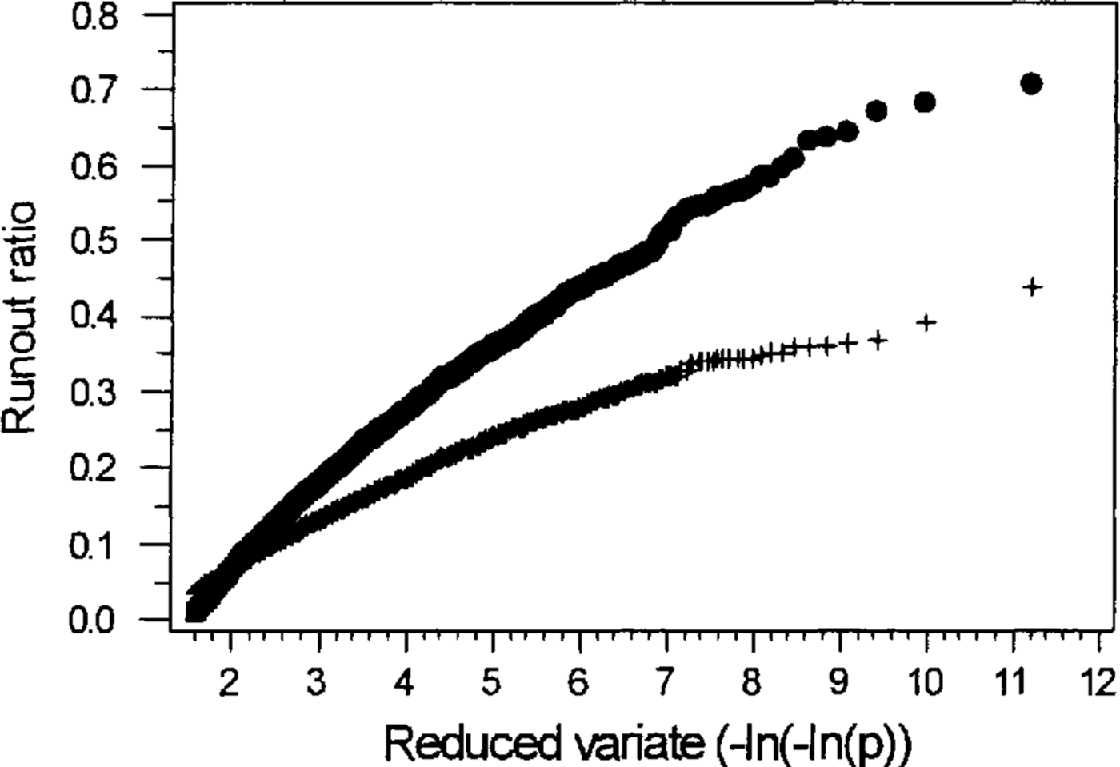
Fig. 9. Results for a model simulation (solid circles) compared to a Gaussian distribution (crosses) with the same mean and variance. The plot is scaled such that a Gumbel distribution will plot as a straight line. The data are censored at an arbitrary runout ratio (zero) in accordance with Reference Föhn and Meister.Föhn and Meister (1981).
Distributions for avalanche width
The approach used to develop the width simulation model was very similar to that used for the runout model. Distributions of avalanche-deposit widths were derived for each size of avalanche. These were then combined with the size–frequency distribution to simulate widths. The maximum width of the deposit can be determined with a high degree of precision compared to the fracture width or the width when the avalanche is in motion. It is also a variable that has been recorded in or may be inferred from the historical record. Employing the maximum width of the deposit provides the safest estimate of the area of terrain affected by the avalanche.
Instead of a normal distribution, the gamma distribution yielded the highest degree-of-fit to the data for sizes 3, 3.5 and 4 (the three sizes with enough data to permit an attempt at distribution fitting). Intuitively, this distribution is appealing, because avalanches cannot have zero or negative widths, values that are unacceptable for this distribution. Box plots of the available data are provided in Figure 10.
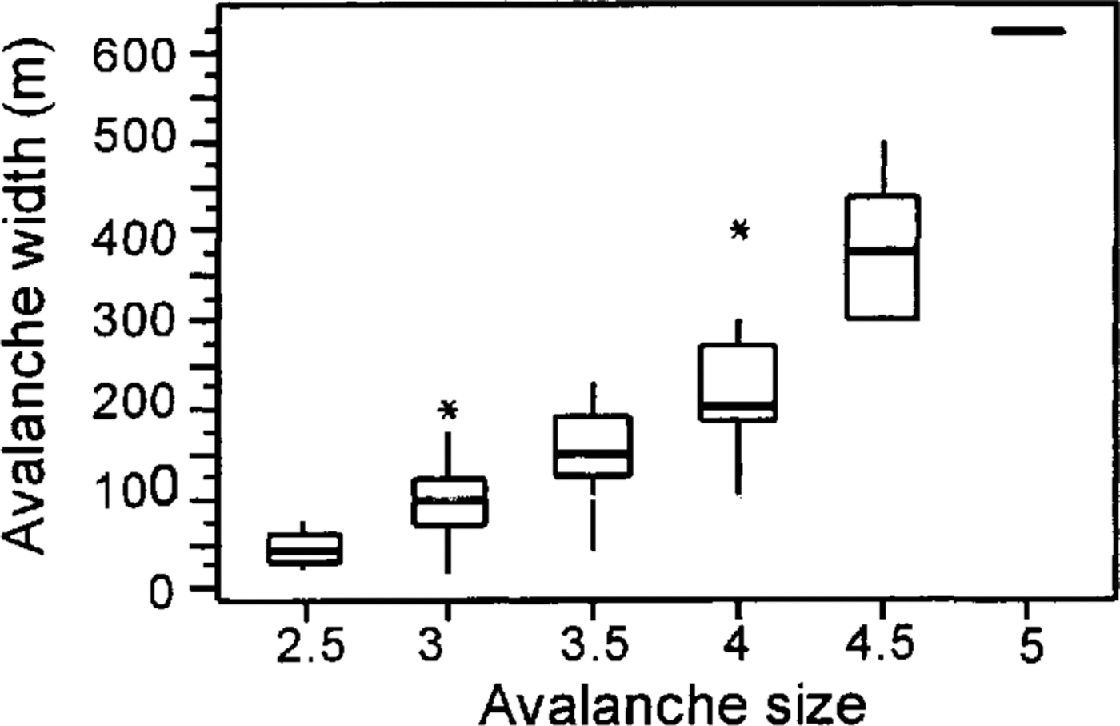
Fig. 10. Box plots of the observed width data segregated by size.
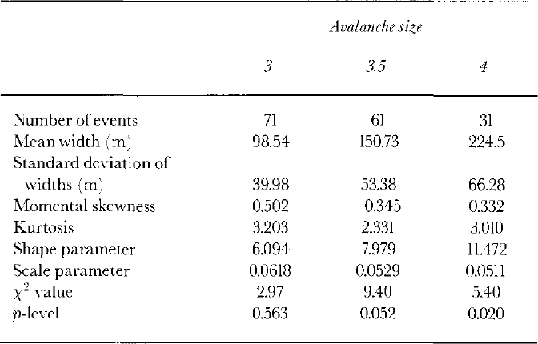
The degree-of-fit of the gamma distribution to the width data is given in Table 5, along with the distribution parameters. The goodness-of-fit is heavily influenced by the fact that many widths can only be estimated to one or two significant digits. This effect is particularly noticeable for the size 4 data where the mode incorporates the 200 m wide events and secondary peaks exist for the 300 and 250 m data classes. This lack of precision in the data results in a distortion that is reflected in the relatively poor fits to the larger sizes where width measurements are less accurately recorded.
Table 5. Deposit width statistics for avalanche sizes 3–4, with an assessment of fit to the gamma distribution
The regression relations used to derive values for the shape parameter (a) and the mean width (MW) for those sizes (5) with insufficient data for direct determination are given by Equations (7) and (8).
The resulting distribution parameters are given in Table 6, with comparisons between the models and the data provided in Figure 11. Very little information is available concerning the prediction of avalanche width, so Equations (7) and (8) were fitted to pass through the data points and to yield reasonable width estimates based on the available information. Figure 11 displays reasonable agreement between data and model.
Table 6. Estimated shape and scale parameters for gamma distributions of avalanche width

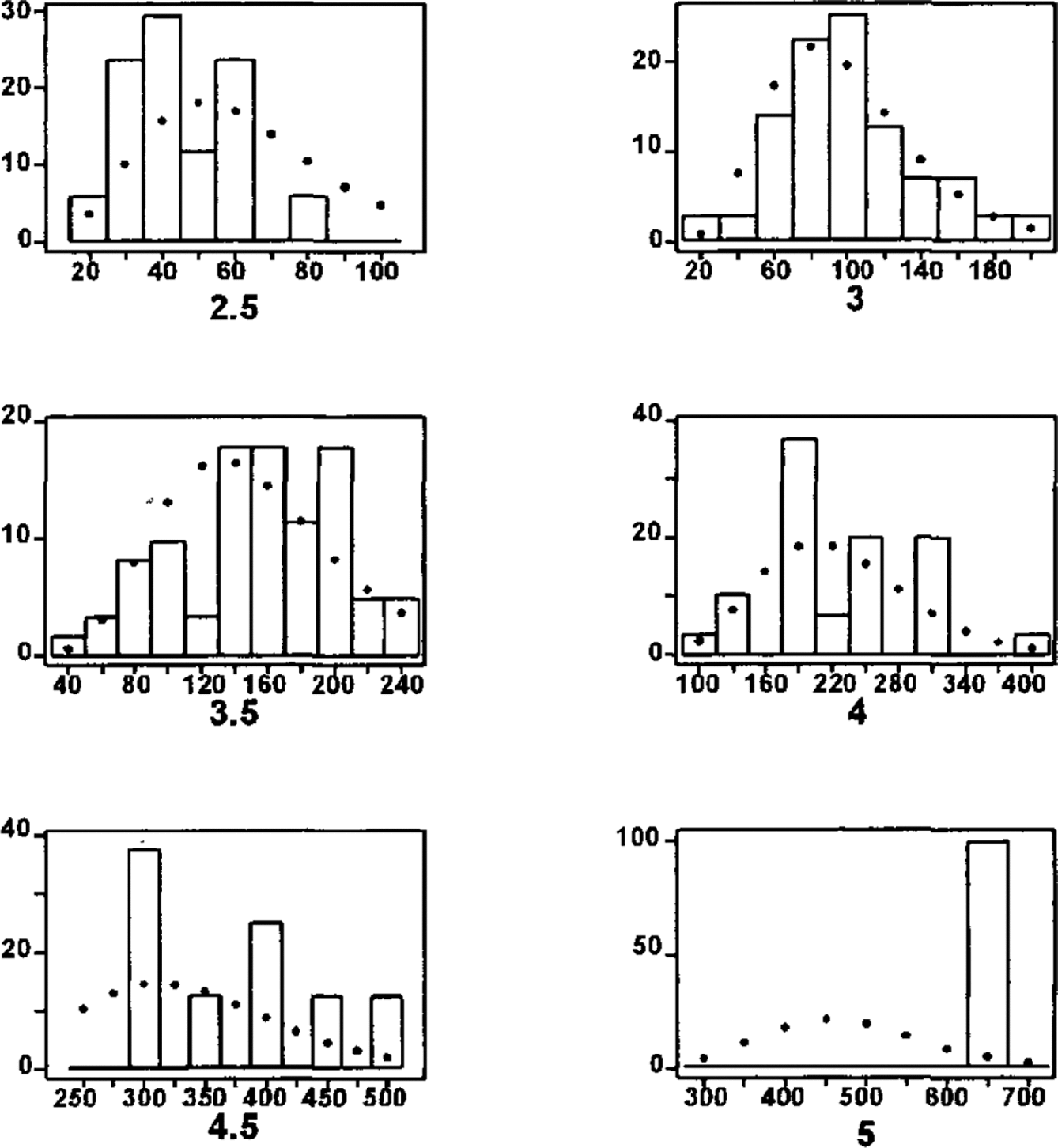
Fig. 11. Percentage histograms of available width data and the fitted gamma distributions. For the six sizes shown and in order of increasing size, the number of observed events was 17, 71, 61, 31, 8, 1, respectively.
Returning to Equation (2), P(w i)n may now he evaluated from the cumulative gamma distribution for a size n avalanche:

where a and λ are the shape and scale parameters of the gamma distribution (Table 6) and where the gamma function is:
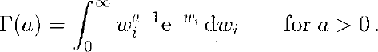
Avalanche direction
Owing to differences in release position, flow direction and the behaviour of individual avalanches, there is an inherent variability in avalanche direction along a path. For most paths with simple topography in the runout zone (as is common in Iceland), one would expect the mean of this deviation to be zero (the profile is constructed to represent the path of an “average” event). Defining an x coordinate as the horizontal component of the distance down the profile, and a y coordinate orthogonal to this, the deviation from the profile was formulated as the quantity L y/L x, where L y is the distance in the y direction from the constructed profile to the centre of the maximum extent of the deposit and L x is the distance down the profile from the starting zone to the maximum extent of the deposit. It was decided to define negative deviations as those that lay to the left of the profile when looking upslope.
In total, 54 events from eight paths were used in the analysis of this model component. All eight chosen paths had relatively simple runout topography (to be representative of the majority of Icelandic paths) and a relatively high number of recorded avalanches (to permit reasonable distribution fitting). A normal distribution with a mean of zero and a standard deviation of 0.053 (53 m for every 1000 m of travel) was found to best fit the data. Thus, the term P(ψ i) in Equation (2) is found from:
where σ dev is equal to 0.053 in Iceland.
Overview of event-frequency modelling
To evaluate Equation (2), it is necessary to establish some physical limits upon i. Size 5 avalanches tend to have the largest widths. From the distribution for P(w i)5 (parameters given in Table 6) it can be demonstrated that according to the model, an 1100 m wide size 5 avalanche has a probability of occurrence in a given year in the order of 10−6. Thus, a solution of Equation (2) using this value as a maximum for w i will be precise to five decimal places, sufficient for our purposes. This gives Equation (13), which may be solved numerically, discretizing the continuous distributions into 1m bins (±0.5 m) in order to evaluate the probability.
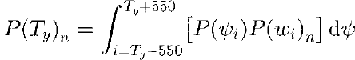
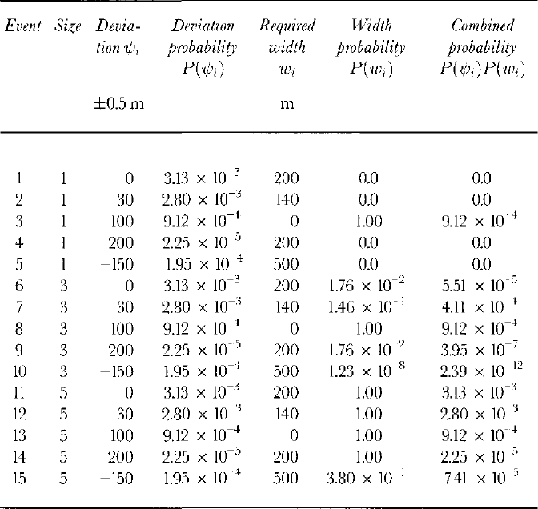
Table 7 provides an example of 15 hypothetical avalanche events of varying widths and deviations, for which the probabilities of hitting a hypothetical target point with coordinates (T x, T y) of (1200 m, 100 m) are evaluated. For the purposes of demonstration the evaluation of P(T x) is not mentioned here (this has already been discussed with reference to Figure 8). As Equation (13) shows, given that we are solving in 1 m increments, to evaluate P (T y) requires 1100 solutions to the product of the two distributions P(ψ i) and P(w i) for each of the nine avalanche sizes. The 15 events shown represent five of the 1100 calculations needed for three different size classes.
Table 7. Some hypothetical avalanche events of various sizes and deviations from the path profile, together with their combined probability of occurrence for a point 100 m to the side of the path profile and 1200 m down the profile
For a “typical” path in Iceland, where P β is in the order of 1200 m, the combined effect of width and deviation acts to diffuse the risk values laterally across the path. The runout simulation model gives a runout ratio of 0.33 for the 1:100 (1%) event (see Fig. 8). When width and deviation are included, the encounter probability at the centre line is reduced because some events that travel this far will have deviated sufficiently not to come into contact with the centre line. The 1:100 event now occurs at a runout ratio of 0.275. Thus, the deviation component of the model has an important impact on the attained risk values.
Vulnerability
Many different factors contribute to vulnerability, and a generalized study cannot take account of all such elements. However, the most important parts of the vulnerability term are the avalanche magnitude and the type of materials used in construction, and it is these two elements that are examined here.
The simulation models outlined above operate with avalanches segregated by size class. Given the Canadian avalanche-size system, it is relatively simple to incorporate avalanche magnitude into the vulnerability calculations by specifying an approximate relation between the fraction of damage and avalanche size. This may be expressed in terms of damage to the building or as percentage lives lost. These relations can then be modified for different construction materials. Since risk calculations are intended to be order-of-magnitude estimates, the vulnerability functions need not be highly precise.
Unfortunately, detailed information on how avalanches of particular sizes affect structures is very limited. This is partly because size classifications (such as the Canadian scheme) are not widely adopted, and also because little applied research has been performed in relation to this problem.
Risk analysis is more widely developed in the study of earthquakes, where a number of studies provide example vulnerability calculations. However, even here many simplifications are routinely made. There are obvious differences in the nature of the stresses and strains that avalanches and earthquakes induce upon structures. It is also difficult to translate between earthquake intensity and avalanche size. Owing to these limitations, one can only hope to approximate vulnerability. However, the information from Iceland on the degree of damage caused by avalanches can be used to scale the vulnerability values appropriately.
For earthquakes in Romania, Reference Fourner d’albe and KoridzeFourner d’Albe (1988) uses a relation between degree of damage (DD) and specific loss (SL) of:
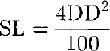
where DD is defined by the five classes given in Table 8 and SL is the cost of repair expressed as a proportion of cost of replacement of the structure. Fourner d’Albe then provides distributions that give the percentage frequency of events in each damage class for earthquakes of different magnitudes. This permits an overall average value of loss to be obtained for each size of seismic event.
Employing a similar approach to the size 4 Súðavík avalanche of January 1995, it was estimated that of the 22 houses struck, four could be classified as undergoing class 5 damage. Four more were allocated to class 4, three to class 3, four to class 2 and seven to class 1. The weighted average specific loss from this allocation of events was 39%. A similar estimate for the 1995 Flateyri event (size 4.5) gave a figure of 66%.
Before the 1995 avalanche, the 210 persons living in Súðavík occupied 70 houses. Thus, on average, one could expect that 66 people inhabited the 22 houses struck by the avalanche. In total, 14 persons or 21% of the inhabitants of the houses were killed. The fatalities were obviously concentrated in the few homes that bore the full force of the avalanche, but this is a useful average value that may be validly employed for large-scale risk assessment.
In the case of the 1995 Flateyri event, a size 4.5 avalanche killed 20 of the 45 inhabitants of 19 buildings severely damaged by the avalanche. Altogether, some 26 residential buildings were struck by the event, suggesting that the percentage fatalities from all buildings was some 33%.
Because avalanches smaller than size 2.5 are not sufficiently powerful to destroy a residence, it was assumed that for non-reinforced masonry buildings, no fatalities would arise for size 2 avalanches or smaller. Columns two and three of Table 9 show the values derived by interpolating and extrapolating from the available information concerning vulnerability and avalanche size.
Table 9. Vulnerability expressed as specific loss or proportion of fatalities for two different construction materials
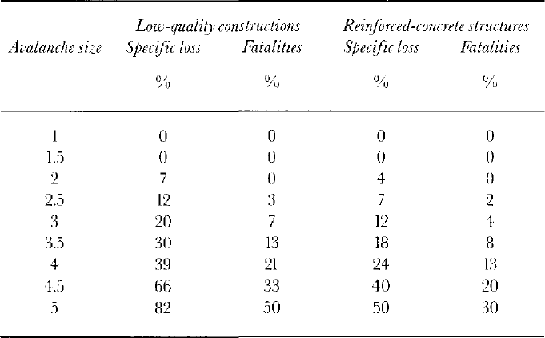
To allow for the fact that improved construction standards may be implemented in avalanche-prone areas in Iceland, an attempt was made to calculate vulnerability functions for reinforced structures. Reference Fourner d’albe and KoridzeFourner d’Albe (1988) provides data from Reference Sandi and Vasileseu.Sandi and Vasilescu (1982) concerning the difference in vulnerability to earthquakes between rein-forced-concrete and low-quality constructions in Bucharest. The data provided are comparable only for three earthquake intensities. However, it appears that on average the loss values for the concrete structures are 60% of those for the low-quality buildings, with no obvious trend across the three intensities. This correction is used in columns four and five of Table 9 to convert the vulnerability values for low-quality buildings into those for reinforced-concrete structures.
Model Evaluation
Because there is no direct means of evaluating the model, three different approaches are employed in this section. Firstly, the estimates of the exceedance probability (actually its inverse, the return period) of the October 1995 avalanche in Flatcyri are compared to estimates derived by Reference JóhannessonJóhannesson (1998b). Secondly, risk values from the model are compared to the recent history of fatality patterns in Iceland. Thirdly, the sensitivity of our results to a 10% perturbation of the distributions for all sizes is examined.
Table 8. Degree of damage to buildings from earthquakes in Montenegro, 1979. From Reference Fourner d’albe and KoridzeFourner d’Albe (1988)

Reference JóhannessonJóhannesson (1998b) derives an estimate for the return period of the 1995 Flateyri avalanche of 146 years using Gumbel statistics. This result agrees well with other calculations presented in that paper. How does the model derived here compare? Employing just the runout simulation model (i.e. assuming no deviation in avalanche direction) yields a return period for the 1995 event of 96 years. Including avalanche deviation gives a new estimate of 178 years. However the Skollahvilft path exhibits a certain amount of confinement, so the degree of deviation may be slightly less than average in Iceland. This would mean an estimate from our model would lie somewhere between these limit cases, yielding a good agreement with Jóhannesson’s study.
There is no direct means of comparing risk values from this model to other studies, as our work represents the first formal use of risk calculations in avalanche research. However, in the last 25 years there have been approximately 50 avalanche fatalities in Iceland from a population of 5000 people living in “at-risk” areas, of which 1000 are at “high risk” (personal communication from T. Jóhannesson, 1995). If one assumes the fatalities have occurred exclusively in the high-risk zone, the annual probability of death in this zone is approximately 2 × 103 [(50/25) × (1/1000)]. Inspection of Figure 12 shows risk values of this order in parts of Flateyri that both Icelandic and foreign avalanche experts have broadly-characterized as high-risk during discussion.
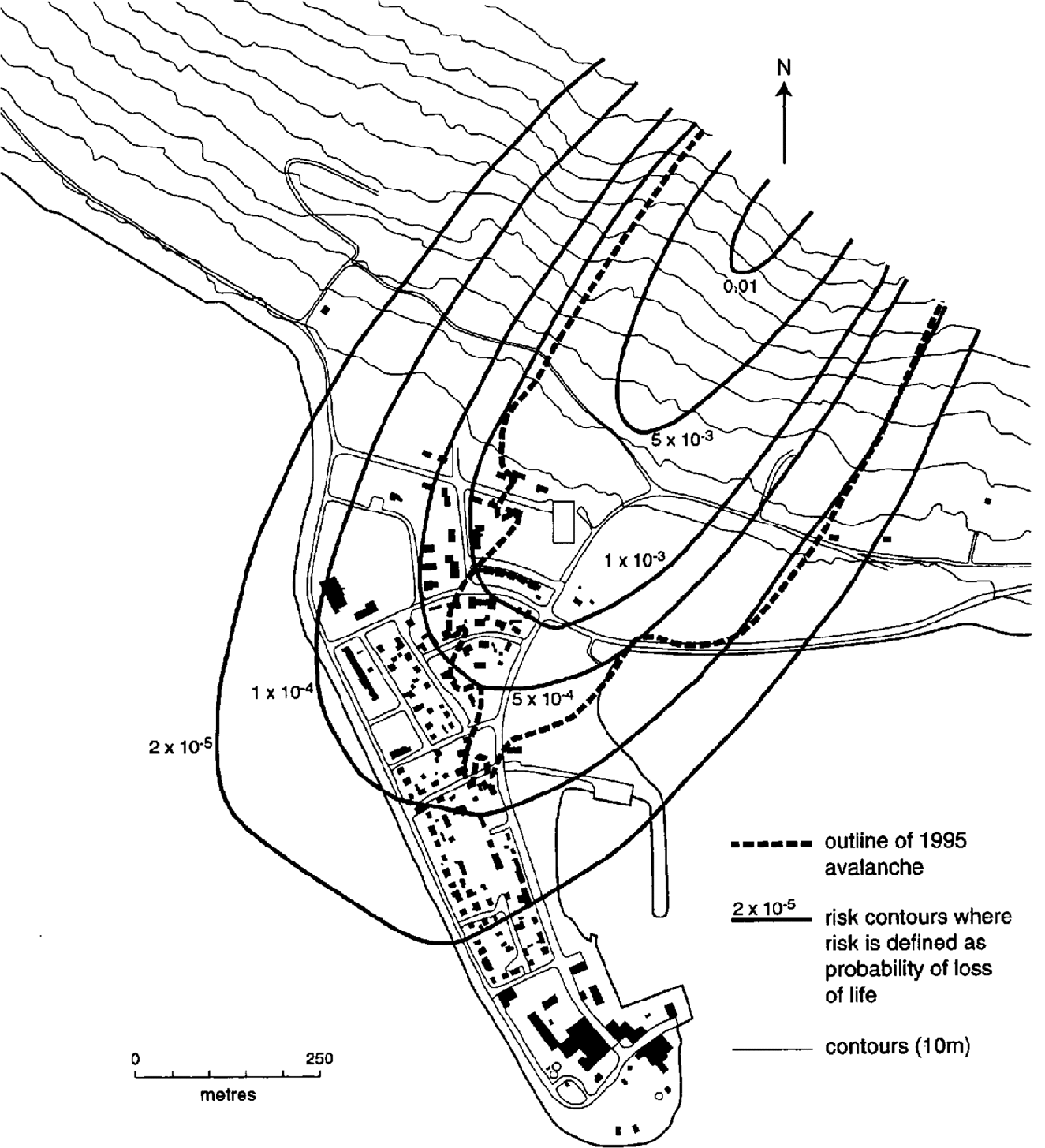
Fig. 12. A map of Flateyri showing the outline of the 1995 avalanche and risk contours produced using the approach outlined in this paper.
The results of the sensitivity analysis are displayed in Table 10. Each of the model distributions was perturbed by increasing parameter values by 10%. This was done for all sizes. Additionally, a second form for the mean values of the runout distribution was tried where a linear instead of a logarithmic fit to the data was attempted. The spurious effect of the unrealistically large runout distances of the smaller events is evident in this case.
Table 10. Sensitivity of the model to perturbations of distribution parameters

The above strategy was not valid for the distribution of the relative frequency of different sizes since it is cumulative. Therefore, as an alternative perturbation, the values for the larger sizes (>2.5) were increased by 10%, while the proportions for the smaller sizes were reduced by the same degree. The distribution was then renormalized to sum to unity. Because there is a fair degree of uncertainty in this distribution through the use of the Canadian data, a second, larger perturbation was introduced. The proportions for the larger sizes were increased by 30%, and those for the smaller sizes reduced by 10%.
The sensitivity analysis was performed at four loca1ions in the region of concern for risk studies in Iceland (runout ratios of 0.0 0.4 and deviations from the center line of 0.0 100 m). It is evident that different distributions behave in different ways. In general, the model appears to be fairly robust. Even the quite drastic change to the form of the relative frequency distribution appears to perturb the risk values by only 30%. As risk values are order-of-magnitude assessments, this appears quite reasonable. The changes to risk values and event frequencies caused by a +10% perturbation are less for most distributions than a 10% increase in the average avalanche frequency. Thus, one of the important limits on this model is the knowledge of the average avalanche frequency. The accuracy of our knowledge of this factor is likely to improve dramatically as a result of the recently improved avalanche observation in Iceland.
The theoretical model structure presented in this paper is very flexible. This has the advantage 1hat when one is implementing the model, distributions can be adjusted as the available data improve. We believe that the size–runout, size–width and deviation distributions derived here are reasonable reflections of the underlying population, even though an extrapolation from data for a small number of sizes was necessary. Even if this is not the case, the model is most sensitive to sizes 3–4, which make up the vast majority of events in the region of concern and contribute most to risk. Thus, the important sizes have been adequately characterized.
The greatest uncertainties lie with the estimation of average avalanche frequency and the relative frequency distribution. The former is always problematic, while it was necessary to employ Canadian data to derive the latter. Difficulties with the estimate of average avalanche frequency can be dealt with in practice by estimating the frequency at a point much further down the profile than the starting zone (e.g. the β point) and then making use of the model to reinterpret this as an estimate at the starting zone. Such a procedure is obviously not ideal, because a double reliance is placed on the model. The relative frequency distribution remains problematic in the application of our model to Iceland. Comfort can be taken from the general agreement between our estimates of return periods and those of Reference JóhannessonJóhannesson (1998b) and the sensitivity analysis presented in Table 10, which suggest that our characterisation is sufficiently accurate for an order-of-magnitude assessment of risk. However, active steps should be taken to increase knowledge of this distribution through improved avalanche observation.
Flateyri: a Case-Study
The catastrophic Flateyri avalanche of October 1995 was released from the Skollahvilft bowl at 650 m altitude. It proceeded to run down to the town along the Eyrarhryggur path and damaged or destroyed 29 houses. Figure 12 shows the town, together with various risk contours for this one particular path produced using the model outlined in this paper. It must be noted that another path also runs into the town, and thus the combined risk at any point is the sum of the two values.
The maximum extent of the avalanche deposit for the 1995 event was approximately 110 m to the side of the constructed path profile. Using the full model including width and deviation effects, the estimated exceedance probability at this point is 0.0036 (278 year return period). The corresponding exceedance probability for a location a similar distance downslope but lying upon the constructed path profile was 0.0056 (178 year return period). Table 11 gives risk and encounter probability estimates at these two locations.
Table 11. Risk and encounter probabilities for two locations at Flateyri where the runout distance equals that of the 1995 avalanche

It was decided in 1996 that an acceptable risk value for avalanching in Iceland is 2 × 105, where risk is evaluated as the probability of death. This has now been increased to 3 × 10−5, with the introduction of a value of 1 × 10−4 for avalanche risk for public buildings and work places (personal communication from T. Jóhannesson, 1998). The 2 × 105 and 1 × 10−4 contours (the range of risk values that have been considered acceptable) are plotted in Figure 12. It is evident that substantial avalanche protection measures are required in this village to mitigate the risk, with many residents at present facing a risk value of 1 × 103 according to the model we have presented. Thus, the major defence works currently under construction appear to be justified.
Conclusion
In this paper we have developed a simulation model for avalanche risk and have applied it to a town in Iceland. The model utilizes simulation techniques to sidestep the problem of insufficient records on a given path. Fortunately, the model is most sensitive to the most commonly documented avalanche sizes with relatively complete data records (sizes 3–4). The very small events have a negligible effect on risk calculation owing to restricted runout and damage potential, and the very large events are much less frequent.
The flexible structure of the model permits distributions to be updated as more and improved avalanche event data become available. In particular, it is hoped that improved avalanche observations will lead to a more accurate assessment of both avalanche frequency and the relative frequency of different-sized events in Iceland. This will obviate the need to employ the Canadian size–frequency information in the model.
During model formulation, we concentrated on the exceedance-probability component of risk. More complex formulations of vulnerability are necessary for case-by-case studies of avalanche risk. Our generalized risk model uses an average value for the whole area of terrain affected by the event, so it is useful for providing a first estimate of risk. For more detailed study it is preferable to vary the vulnerability over the affected part of the runout zone. This can be done by using a dynamics model to estimate impact pressures and hence scale vulnerability. T. Arnalds is currently performing such work at the IMO.
Acknowledgements
This research was supported by the Natural Sciences and Engineering Research Council of Canada and the IMO, with additional support from the European Union and the Peter Wall Institute of Advanced Studies at the University of British Columbia. We wish to acknowledge the assistance of J. G. Egilsson, T. Saemundsson and S. H. Haraldsdóttir of the IMO, who provided a great deal of help with the translation and interpretation of the avalanche records during summer 1995. This research has profited from subsequent discussions with T. Jóhannesson and K. Jónasson. We are grateful to O. Tucker for assisting with production of some of the diagrams. The comments of the scientific editor and three anonymous referees helped improve this paper.

























