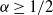1. Introduction
In recent years there has been increasing interest in using expectiles as an alternative risk measure to value at risk (VaR) in risk theory. Expectiles, a new least-squares analogue of quantiles introduced by [Reference Newey and Powell21], have recently become very popular in applications such as quantitative finance and risk management; see [Reference Bellini, Klar, Müller and Rosazza-Gianin4] and [Reference Ziegel32]. Indeed, the papers [Reference Bellini and Bignozzi3] and [Reference Ziegel32] have shown that expectiles with
$\alpha \geq 1/2$
are the only risk measures that are coherent and elicitable. For a given level
$\alpha \in (0,1)$
and an integrable random variable Y, the
$\alpha $
th expectile is defined as the minimizer of an asymmetrically weighted mean-squared deviation,
\begin{equation}e_{\alpha}(Y) = \underset{\theta}{\operatorname{argmin}} \mathbb{E}\left[\eta _{\alpha}(Y - \theta) - \eta_{\alpha}(Y)\right],\end{equation}
where
$\eta_{\alpha} (y)= |\alpha - \mathbb{1}_{\{y \leq 0\}}|y^{2}$
is the expectile check function. Subtracting
$\eta_{\alpha}(Y)$
in the expectation makes the integrand well-defined and finite without the need to assume that
$\mathbb{E}(Y^2)< \infty$
, while for Y we only require a finite first-order moment.
Expectiles have emerged as an important risk measure, especially in the study of extreme risks characterized by their low-probability, high-consequence nature. A paramount challenge in this area is data uncertainty, as the loss distribution is often only partially known or ambiguous. Typically, we only have access to limited information about the underlying distribution. This leads to the pivotal question in risk management: how can we robustly measure risk amidst such distributional uncertainties? In this paper, we investigate a worst-case expectile problem for datasets with ambiguous data, proposing a robust risk measure constrained by certain parameters. Recently, we have been confronted with a variety of extreme risks in many fields, such as finance, insurance, and environmental science. In many of these fields, the partial availability of distribution information can result in decisions that are overly sensitive to shifts in the underlying loss distribution, as pointed out in studies such as [Reference Embrechts, Wang and Wang10] and [Reference Pesenti, Millossovich and Tsanakas23]. Hence, the lack of complete information can render traditional risk measures, such as VaR and expectiles, less effective when based solely on stochastic data.
We aim to investigate the corresponding optimization problem based on a set of uncertain distributions, i.e., ambiguity sets. To address this problem, many researchers have proposed robust distribution optimization methods, the most widely used of which is the worst-case risk measure. Specifically, the worst-case risk measure is the worst risk measure calculated for all distributions under the ambiguity set. To be precise, for a random variable Y, given the level
$\alpha \geq 1/2$
, which corresponds to the case where
$e_{\alpha}$
is law-invariant and coherent [Reference Bellini, Klar, Müller and Rosazza-Gianin4], we define the worst-case value of the expectile (WCE) under a set
$\mathcal{M}$
as follows:
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{M}}=\sup\limits_{F_Y\in \mathcal{M}} e_\alpha(Y), \end{equation}
where
$F_{Y}$
denotes the distribution of Y and
$\mathcal{M}$
is a set of plausible distributions for Y.
This paper investigates the worst-case expectiles on two specified ambiguity sets, namely, moment-based and Wasserstein-metric-based ambiguity sets. These robust measures play a pivotal role in risk management, enabling market risk assessment under stressed scenarios. They offer insights into data modeling during financial crises through the worst-case approach. The worst-case expectile measure we introduce aligns with what has recently been termed the distributionally robust stochastic optimization problem. As shown in [Reference Shapiro26], there are two natural methods of constructing the ambiguity set
$\mathcal{M}$
. On the one hand, an ambiguity set of distributions can be defined as the set of all distributions that are in a neighborhood of a given reference distribution with respect to a transportation distance, such as the Wasserstein distance; this is discussed by [Reference Mohajerin-Esfahani and Kuhn19], [Reference Chen, Yu and Haskell7], and others. On the other hand, an alternative ambiguity set can be described by specifying the moments of the distributions, as discussed by [Reference Delage and Ye8] and [Reference Wiesemann, Kuhn and Sim30], among others. These two kinds of ambiguity sets are fundamentally different. In this paper we provide the worst-case expectiles under both scenarios.
The contributions of this paper are summarized as follows. First, we formally define the worst-case expectiles on the two types of ambiguity sets defined. Second, we transform the problem into a convex optimization problem for the ambiguity set specified by Wasserstein distance and a reference distribution G. Moreover, we obtain precise solutions to this problem in several special cases. Third, we focus on a more general ambiguity set defined by the moments of the distribution, i.e., where only the expectation and the pth-order central moment with
$p>1$
are acknowledged; this encompasses the scenario in which only the initial two moments are recognized. In addition, we derive some asymptotic behaviors of the worst-case expectiles for these two ambiguity sets.
The paper is organized as follows. In Section 2, we start with an overview of distortion risk measures and then transform the infinite-dimensional problem (1.2) into a finite one, focusing on the maximum of a series of worst-case distortion risk measures for two specified ambiguity sets induced by Wasserstein distance and moment constraints. In Section 3, we first give some precise results on the worst-case value of the expectile over the p-Wasserstein ball and analyze the asymptotic behavior of the worst-case expectile as
$\alpha$
tends to 1, with most circumstances taken into account. Then we compare our worst-case approach with the recently proposed ‘model aggregation’ approach of [Reference Mao, Wang and Wu18] and offer an alternative way of reformulating the problem (1.2), with full discussion. Finally, in Section 4 we discuss our findings and research perspectives. The proofs of all theoretical results and the details of extensive simulation studies are given in our supplementary material.
2. Reformulation of worst-case expectile through two important ambiguity sets
We first introduce some notation. Consider an atomless probability space
$(\Omega,\mathcal{F},\mathbb{P})$
and let
$\mathcal{L}^p$
be the set of all random variables in
$(\Omega,\mathcal{F},\mathbb{P})$
with finite pth moment,
$p \in (0,\infty)$
. We denote by
$\mathcal{L}^0$
the set of all random variables and by
$\mathcal{L}^\infty$
the set of essentially bounded random variables. In addition, we denote by
$\mathcal{M}^p$
the set of the distribution functions of random variables in
$\mathcal{L}^{p}$
, i.e.,
$\mathcal{M}^p=\{F_Y(y)\;:\; Y\in \mathcal{L}^p\}$
. For a random variable Y,
$F_{Y}(y)=\mathbb{P}(Y\leq y)$
represents its distribution function, and the corresponding left-continuous inverse is defined as
\begin{align*}{F_Y^{-1}(u)=\inf \{y \in \mathbb{R} \;:\; F_Y(y)\geq u\},\;u \in (0,1]}.\end{align*}
The mappings ess inf(
$\cdot$
) and ess sup(
$\cdot$
) on
$\mathcal{L}^0$
give the essential infimum and the essential supremum, respectively, of a random variable. For a distribution
$G \in \mathcal{M}^{1}$
, we denote its essential supremum and first moment by
$\textrm{ess sup}_{G}\;:\!=\;\textrm{ess sup} (G)$
and
$\mu_{G} \;:\!=\;\int x dG(x)$
, respectively. Throughout this paper, we denote the right and left derivatives of the function g at the point
$x_0$
(if they exist) by
$g^{\prime}_+(x_0)$
and
$g^{\prime}_-(x_0)$
. Similarly, we denote the left and right limits of the function g at
$x_0$
by
$g(x_0^-)$
and
$g(x_0^+)$
, respectively. For a real x, we denote its positive and negative parts by
$x^+$
and
$x^-$
, respectively; that is,
$x^+=\max(x,0)$
and
$x^-=\max(0,-x)$
.
2.1. Distortion risk measure
We now give the definition and some examples of distortion risk measures, which are commonly used in risk management. Recall that a non-decreasing function
$H:[0,1]\rightarrow[0,1]$
satisfying the boundary condition
$H(0) = 0, H(1)=1$
is called a distortion function. A precise definition and detailed discussion of the distortion risk measure associated with H can be found in [Reference Wang, Wang and Wei28] and [Reference Wang, Wei and Willmot29]. In particular, when H is continuous, the corresponding distortion risk measure
$\rho_H$
for the random variable Y has the following representation:
\begin{equation*} \rho_H(Y)=\int_0^1F_Y^{-1}(u)dH(u), \end{equation*}
if the integral is finite. Obviously, for
$Y\in \mathcal{L}^1$
, if we take
$H(u)=u$
, then
$\rho_H(Y)=\int_0^1F_Y^{-1}(u)du=\mathbb{E}[Y]$
.
Another important risk measure that is highly relevant to expectiles is the expected shortfall (ES). Given
$\alpha\in (0,1)$
, the expected shortfall at level
$\alpha$
[Reference Rockafellar and Uryasev25] is a distortion risk measure with
$H(u)=(1-\alpha)^{-1}(u-\alpha)^+$
. Specifically, for
$Y\in \mathcal{L}^1$
,
\begin{equation} \textrm{ES}_\alpha(Y)=\frac 1 {1-\alpha} \int_\alpha^1 F_Y^{-1}(u)du.\end{equation}
2.2. Reformulation
In addition to the original definition introduced in Equation (1.1), there are a number of other representations of the expectile, such as those mentioned in [Reference Bellini, Klar, Müller and Rosazza-Gianin4]. For our problem, a useful tool is the well-known Kusuoka representation, which expresses the expectile as the maximum of a convex combination of the expected shortfall at a certain level and the expectation.
Proposition 1. ([Reference Bellini, Klar, Müller and Rosazza-Gianin4, Proposition 9].) Let
$Y\in \mathcal{L}^1$
,
$\alpha\geq 1/2$
, and
$\beta= \alpha/{(1-\alpha)}$
; then
\begin{equation} e_\alpha(Y)=\max\limits_{\gamma \in [\frac1\beta,1]} \left\{(1-\gamma) \textrm{ES}_\tau(Y)+\gamma\mathbb{E}[Y]\right\},\end{equation}
where
$\tau=({\beta- 1/\gamma})\big/({\beta -1})$
.
Although there is no closed-form representation for the expectile, Proposition 1 allows us to reformulate the problem (1.2). Since a convex combination of two distortion risk measures is again a distortion risk measure, the expectile is actually the maximum of a one-parameter family of distortion risk measures indexed by
$\gamma\in[1/\beta,1]$
. Later, we will use
$\tau$
to represent
$({\beta- 1/\gamma})\big/({\beta -1})$
; we also use
$\tau(\gamma)$
to emphasize the interdependence between
$\gamma$
and
$\tau$
. Specifically, combining Proposition 1 and (2.1), we can rewrite
$\operatorname{WCE}_{\alpha}^{\mathcal{M}}$
as follows:
\begin{align} \operatorname{WCE}_{\alpha}^{\mathcal{M}}&=\sup\limits_{F_Y\in \mathcal{M}} e_\alpha(Y)\notag\\[5pt] &{=\sup\limits_{F_Y\in \mathcal{M}}\sup\limits_{\gamma \in [\frac 1 \beta,1]} \{(1-\gamma) \textrm{ES}_\tau(Y)+\gamma\mathbb{E}[Y]\}}\notag\\[5pt] &={\sup\limits_{\gamma \in [\frac 1 \beta,1]}}\sup\limits_{F_Y\in \mathcal{M}} \{(1-\gamma) \textrm{ES}_\tau(Y)+\gamma\mathbb{E}[Y]\}\notag\\[5pt] &={\sup\limits_{\gamma \in [\frac 1 \beta,1]}}\sup\limits_{F_Y\in \mathcal{M}} \left\{\frac{1-\gamma}{1-\tau}\int_0^1F_Y ^{-1}(u)\mathbb{1}_{(\tau,1)}(u)du+\gamma\int_0^1F_Y^{-1}(u)du\right\}\notag\\[5pt] & \;=\!:\;{\sup\limits_{\gamma \in [\frac 1 \beta,1]}}\sup\limits_{F_Y\in \mathcal{M}}\rho_{H_\gamma}(Y),\end{align}
where the distortion function
$H_\gamma(u)=\frac{1-\gamma}{1-\tau}(u-\tau)^++\gamma u$
. The inner supremum has been well studied for a wide variety of ambiguity sets [Reference Bernard, Pesenti and Vanduffel5, Reference Liu, Mao, Wang and Wei17, Reference Pesenti, Wang and Wang24]. If the inner problem has an explicit representation for
$\gamma$
, then the infinite-dimensional problem (1.2) is reduced to an optimization problem for some function of
$\gamma$
. For this reason, we start by introducing two ambiguity sets, defined in terms of the Wasserstein distance and moment conditions, respectively, and illustrate some existing results that we will use later.
2.3. Ambiguity set induced by the Wasserstein distance
The Wasserstein distance of order
$p \in [1, \infty)$
between two univariate distribution functions
$F_{1}, F_{2} \in \mathcal{M}^{p}$
is defined as the smallest
$\mathcal{L}^p$
distance between a pair of random variables with marginal distributions
$F_{1}, F_{2}$
, i.e.,
\begin{align*}W_p(F_1,F_2)= \inf \left\{\Big[\mathbb{E}\big|Y_1-Y_2\big|^p\Big]^{1/ p}\;:\; Y_{1} \sim F_{1}, Y_{2} \sim F_{2} \right\}.\end{align*}
For univariate distributions, the Wasserstein distance has the following closed-form expression:
\begin{equation*} W_p(F_1,F_2)=\left(\int_{0}^{1}\big|F_1^{-1}(u)-F_2^{-1}(u)\big|^p du\right)^{1/p},\;p\in [1,\infty).\end{equation*}
For details on the Wasserstein distance, see e.g. [Reference Villani27]. The ambiguity set induced by the Wasserstein distance is then defined as a ball centered on the reference distribution G with radius
$\varepsilon >0$
,
\begin{equation} \mathcal{W}_{p,G,\varepsilon}=\left\{F \in \mathcal{M}^{p}\;:\; W_p(F,G)\leq\varepsilon\right\}.\end{equation}
First we consider the reformulation (2.3) in the context of
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
. Note that the expectile reduces to expectation at the level of
$\alpha=1/2$
in Equation (1.1); hence the problem (1.2) is reduced to the following:
\begin{align} \operatorname{WCE}_{1/2}^{\mathcal{W}_{p,G,\varepsilon}}&\;:\!=\;\sup\limits_{F_Y\in \mathcal{W}_{p,G,\varepsilon}} e_{1/2}(Y)\notag =\sup\limits_{F_Y\in \mathcal{W}_{p,G,\varepsilon}}\int_0^1F_Y^{-1}(u)du\\[5pt] &=\sup\limits_{F\in \mathcal{W}_{p,G,\varepsilon}}\int_0^1\big(F^{-1}(u)-G^{-1}(u)\big)du+\int_0^1G^{-1}(u)du\notag\\[5pt] &\leq \sup\limits_{F\in \mathcal{W}_{p,G,\varepsilon}}\left(\int_{0}^{1}\big|F^{-1}(u)-G^{-1}(u)\big|^p du\right)^{1/p}+\mu_G\notag\\[5pt] &\leq \varepsilon+\mu_G,\end{align}
where the first inequality is due to the Hölder inequality. Then, letting
$F_0^{-1}(x)\;:\!=\;G^{-1}(x)+\varepsilon, x \in \mathbb{R}$
, we obtain the opposite inequality to (2.5); thus we have
\begin{equation*} \operatorname{WCE}_{1/2}^{\mathcal{W}_{p,G,\varepsilon}}=\varepsilon+\mu_G.\end{equation*}
As a result, we only need to concentrate on the case where
$\alpha > 1/2$
and
$\beta > 1$
. The following proposition is a special version of Proposition 4 in [Reference Liu, Mao, Wang and Wei17], giving the precise value for
$\sup\limits_{F_Y\in \mathcal{W}_{p, G,\varepsilon}}\rho_{H_\gamma}(Y)$
and an explicit expression for the distribution function at which the supremum is attained.
Proposition 2. For any fixed
$\gamma\in[1/\beta,1]$
, let
$H_\gamma(u)=\frac{1-\gamma}{1-\tau}(u-\tau)^++\gamma u$
. Let
$h_\gamma$
represent the left derivative of the distortion function
$H_\gamma$
, and let
$\Vert \cdot \Vert_q$
represent the standard q-norm. Then
\begin{equation} \sup\limits_{F_Y\in \mathcal{W}_{p,G,\varepsilon}}\rho_{H_\gamma}(Y)=\varepsilon\Vert h_\gamma\Vert_q+\int_0^1G^{-1}(u)h_\gamma(u)du,\end{equation}
where q is the conjugate index of p, i.e.,
$q= p/(p-1)$
with
$p> 1$
, and
$q=\infty$
with
$p=1$
. Moreover, the supremum in Equation (2.6) is attained by a certain distribution function, whose quantile function is given by
\begin{equation} F_{p,G,\varepsilon,\gamma}^{-1}(u)=G^{-1}(u)+C_{p,\gamma,\varepsilon}\left(\mathbb{1}_{\{0< u\leq\tau\}}+\beta^{q-1}\mathbb{1}_{\{\tau<u\leq 1\}}\right),\qquad p>1,\end{equation}
where
$C_{p,\gamma,\varepsilon}=\varepsilon/[\tau+\beta^q(1-\tau)]^{1/p}$
. For
$p=1$
, we have
\begin{equation} F_{1,G,\varepsilon,\gamma}^{-1}(u)=\begin{cases} G^{-1}(u)+\frac{\varepsilon}{1-\tau}\mathbb{1}_{\{\tau< u\leq1\}}& \text { if } \gamma<1, \\[5pt] G^{-1}(u)+\varepsilon & \text { if } \gamma=1. \end{cases}\end{equation}
The above proposition can easily be verified using Proposition 4 in [Reference Liu, Mao, Wang and Wei17], where the result for the worst-case value of a general distortion risk measure is provided. For convenience, let us write
\begin{equation} z_{p,G,\varepsilon}(\gamma) \;:\!=\; \varepsilon\Vert h_\gamma\Vert_q+\int_0^1G^{-1}(u)h_\gamma(u)du;\end{equation}
then, using the reformulation (2.3) and the setting
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
, we obtain that the problem (1.2) essentially becomes a convex optimization problem (the concavity of
$z_{p,G,\varepsilon}(\gamma)$
will be clarified in Theorem 1), i.e.,
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}={\sup\limits_{\gamma \in [\frac 1 \beta,1]}}z_{p,G,\varepsilon}(\gamma).\end{equation}
Therefore, we devote a great deal of space to describing the behavior of
$z_{p, G,\varepsilon}(\gamma)$
in the next section.
2.4. Ambiguity set induced by moment conditions
We now focus on another important ambiguity set, this one induced by moment conditions; for details see [Reference Chen, He and Zhang6] and [Reference Pesenti, Wang and Wang24]. Assume that
$p > 1$
,
$\mu\in\mathbb{R}$
, and
$\sigma$
is a positive real number. Specifically, we concentrate on the ambiguity set defined as follows:
\begin{equation} \mathcal{M}_{p,\mu,\sigma}=\left\{F\in\mathcal{M}^p\;:\;\int x dF(x)=\mu,\int \big|x-\mu\big|^pdF(x){\leq}\sigma^p\right\}.\end{equation}
Let
$Y\in\mathcal{L}^p$
be a random variable such that
$F_Y\in\mathcal{M}_{p,\mu,\sigma}$
; then its expectation is clarified by
$\mu$
, while its pth center moment is confirmed to have an upper bound
$\sigma^p$
. We would like to emphasize here that there are many other comparable versions of
$\mathcal{M}_{p,\mu,\sigma}$
, in one of which the restriction on the expectation is given by a pre-specified range rather than an equality; this indicates that the information about the expectation of an unknown distribution is not fully determined, which is often the case in parameter estimation problems. Many risk measures, including those explored in this article, share a similar structure in relation to the worst-case problem; thus we do not elaborate further here.
The case
$p\neq 2$
is less commonly discussed in literature than
$\mathcal{M}_{2,\mu,\sigma}$
. This is not just because the expectation and variance are the most fundamental attributes of random variables, but also because of computational convenience. For example, [Reference Mao, Wang and Wu18] establishes an explicit solution for
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{2,\mu,\sigma}}$
. However, it is still necessary to consider the general order condition when we have information on higher or lower moments than
$p=2$
. To the best of our knowledge, there is no literature concentrating on the worst-case value of the expectile through
$\mathcal{M}_{p,\mu,\sigma}$
when
$p\neq 2$
. Note that if
$\alpha=1/2$
, then obviously
$\operatorname{WCE}_{1/2}^{\mathcal{M}_{p,\mu,\sigma}}=\mu$
; therefore, we focus on the situation
$\mathcal{M}=\mathcal{M}_{p,\mu,\sigma}$
at level
$\alpha > 1/2$
, similarly to Section 2.3.
In parallel to Proposition 2, we can derive the following, which covers the case of a moment-constrained ambiguity set.
Proposition 3. Following the notation and definitions in Proposition 2, we have
\begin{equation*} \sup\limits_{F_Y\in \mathcal{M}_{p,\mu,\sigma}}\rho_{H_\gamma}(Y)=\mu+\min\limits_{x\in \mathbb{R}}\sigma\Vert h_\gamma-x\Vert_q=\mu+\sigma\lbrack h_\gamma\rbrack_q,\end{equation*}
where
$[h_\gamma]_q=\min\limits_{x\in \mathbb{R}}\Vert h_\gamma-x\Vert_q$
. Moreover, the above supremum can be attained by a two-point distribution, whose quantile function is defined by
\begin{equation} F_{p,\mu,\sigma,\gamma}^{-1}(u)=\mu+\frac{\sigma}{\left[\tau^{p-1}+(1-\tau)^{p-1}\right]^{1/p}}\left(-\frac{(1-\tau)^{1/q}}{\tau^{1/p}}\mathbb{1}_{\{0< u\leq\tau\}}+\frac{\tau^{1/q}}{(1-\tau)^{1/p}}\mathbb{1}_{\{\tau<u\leq 1\}}\right).\end{equation}
The specific form of the above quantile function requires careful computational verification and is essentially contained in the proof of Theorem 7; hence we omit its proof. According to Proposition 3, Equation (2.3) is reduced to
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}=\mu+\sigma{\sup\limits_{\gamma \in [\frac 1 \beta,1]}}[h_\gamma]_q.\end{equation}
Therefore, in the next section, we need to solve Equation (2.13), where the optimized function is not concave in general.
3. Main results
In this section, we first provide some exact results on the function
$z_{p, G,\varepsilon}(\gamma)$
, discussing both scenarios
$p=1$
and
$p>1$
in detail (see Theorems 1 and 2). Moreover, we find either a single distribution function
$F_{\alpha,\mathcal{M}}$
or a sequence of distribution functions
$F_{n,\alpha,\mathcal{M}}$
to attain or approximate the supremum in Equations (2.10) and (2.13), i.e., to satisfy
$e_{\alpha}(F_{\alpha,\mathcal{M}})$
$=\operatorname{WCE}_{\alpha}^{\mathcal{M}}$
or
$\lim_{n\rightarrow\infty}e_{\alpha}(F_{n,\alpha,\mathcal{M}})=\operatorname{WCE}_{\alpha}^{\mathcal{M}}$
, for
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
(Theorems 1 and 2) and
$\mathcal{M}=\mathcal{M}_{p,\mu,\sigma}$
(Theorem 7). As expected, the construction of these functions is extremely dependent on the behavior of the optimized functions. Unlike in most of the existing literature, which focuses on the exact worst-case value of certain risk measures, there is no explicit solution in most cases for the worst-case value of the expectile; we will explore this further below. However, when we consider extreme situations, i.e.,
$\alpha\rightarrow1$
, or equivalently
$\beta\rightarrow \infty$
, we can obtain asymptotic representations under extra conditions (see Theorems 3–7). In addition to studying
$\operatorname{WCE}_{\alpha}^{\mathcal{M}}$
, in Section 3.1.3 we give a concise introduction to an alternative approach called ‘model aggregation’ for prudent risk evaluation based on stochastic dominance, which was recently proposed in [Reference Mao, Wang and Wu18]. We then present a comprehensive comparison between model aggregation and our approach, simultaneously giving an upper bound to our problem for
$\mathcal{M}=\mathcal{W}_{p, G,\varepsilon}$
.
3.1. Results on
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
3.1.1. Some precise results
As shown in Equation (2.10),
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
is the supremum of a function
$z_{p,G,\varepsilon}(\gamma)$
on
$\left[1/\beta,1\right]$
. Unfortunately, there is no closed-form solution for this problem in general, because of extreme dependence on both the reference distribution G and the order p (even in some simple cases, such as when
$p=2$
and G is the standard normal distribution function). Fortunately, the function
$z_{p,G,\varepsilon}(\gamma)$
possesses good properties, in particular continuity and concavity, which implies that we can transform the infinite-dimensional problem (1.2) into a tractable one. Before we give the main results, it is worth mentioning that when
$p=1$
,
$l_p\left(\gamma\right) \;:\!=\; \Vert h_\gamma\Vert_q$
is neither continuous at
$\gamma=1$
nor strictly concave on
$\left(1/\beta,1\right)$
, which is different from the case
$p > 1$
. Consequently, we discuss the two cases of
$p>1$
and
$p=1$
separately.
Theorem 1. When
$p > 1$
,
$z_{p,G,\varepsilon}\left(\gamma\right)$
is continuous and strictly concave on
$\left[1/\beta,1\right]$
for any G; thus, its maximum value point
$\gamma^*$
exists and
$\gamma^* \in \left(1/\beta,1\right)$
, that is to say,
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}=z_{p,G,\varepsilon}\left(\gamma^*\right).\end{align*}
Moreover, we have
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}=e_{\alpha}(F_{p,G,\varepsilon,\gamma^*}),\end{align*}
where
$F_{p,G,\varepsilon,\gamma^*}$
is defined in (2.7).
Based on the fact that
$\tau$
is a strictly increasing function of
$\gamma$
that maps
$\left[1/\beta,1\right]$
into [0,1], we may seek the corresponding
$\tau^*$
instead of
$\gamma^*$
, i.e.,
\begin{equation} \tau^*=\sup_{\tau\in \left(0,1\right)}\left\{z^{\prime}_{p,G,\varepsilon-}\left(\gamma(\tau) \right)\geq0\right\}. \end{equation}
In the following, we focus on the situation when
$p=1$
. Noting that
$z_{1,G,\varepsilon}\left(1\right)=z_{1,G,\varepsilon}\left(1/\beta\right)=\varepsilon+\mu_G$
and
$\lim_{\gamma\rightarrow 1^-}z_{1,G,\varepsilon}\left(\gamma\right)=\varepsilon\beta+\mu_G>\varepsilon+\mu_G$
, we consider only
$\sup_{\gamma\in \left(\frac1\beta,1\right)}z_{1,G,\varepsilon}\left(\gamma\right)$
.
Theorem 2. When
$p = 1$
, we have the following:
-
(i) If
$\textrm{ess sup}_G \leq \mu_G+\varepsilon\beta$
, then
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\mu_G+\varepsilon\beta$
, and there exists a sequence of distribution functions
$F_{n,G,\varepsilon}$
such that
$\lim_{n\rightarrow \infty}e_{\alpha}(F_{n,G,\varepsilon})=\mu_G+\varepsilon\beta$
, whose quantile function is given by where
\begin{equation*} F_{n,G,\varepsilon}^{-1}(u)=G^{-1}(u)+\frac{\varepsilon}{1-\tau_n}\mathbb{1}_{\{\tau_n< u\leq1\}}, \end{equation*}
$\tau_n\in(0,1)$
is an arbitrary sequence tending to 1 as
$n\rightarrow\infty$
.
-
(ii) If
$\textrm{ess sup}_G > \mu_G+\varepsilon\beta$
, then
$z_{1,G,\varepsilon}\left(\gamma\right)$
attains its maximum on
$\gamma^* \in \left(1/\beta,1\right)$
and
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=z_{1,G,\varepsilon}\left(\gamma^*\right)$
. Analogously to Theorem 1, we have
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=e_{\alpha}(F_{1,G,\varepsilon,\gamma^*})$
, where
$F_{1,G,\varepsilon,\gamma^*}$
is as defined in (2.8).
Recalling Equations (2.7) and (2.8), we know that the quantile function that attains the supremum is in fact equal to the sum of
$G^{-1}$
and the quantile function corresponding to some non-negative two-point distribution indexed by
$\gamma^*$
, p, and
$\varepsilon$
. See Figure 3.1 for a numerical illustration.
Figure 3.1: Illustration of the distribution function at which the supremum is attained in Theorems 1 and 2: (a) Here
$p=1$
,
$\varepsilon=0.2$
, and
$\alpha=0.8$
; the standard normal distribution (green line) and exponential distribution (red line) and the corresponding transformed distributions
$F_{1, G,\varepsilon,\gamma^*}$
(purple and blue lines) are shown. (b) Here
$p=2$
,
$\varepsilon=1$
, and
$\alpha=0.9$
; the standard normal distribution (red line) and uniform distribution (purple line) and the corresponding transformed distributions
$F_{2, G,\varepsilon,\gamma^*}$
(green and blue lines) are shown.
Theorem 10 in [Reference Bellini, Klar, Müller and Rosazza-Gianin4] reveals that expectiles are Lipschitz with respect to the 1-Wasserstein metric, with Lipschitz constant
$\beta$
, i.e., for any distribution functions
$F_1, F_2\in \mathcal{M}^1$
, it holds that
\begin{equation} \left|e_{\alpha}(F_1)-e_{\alpha}(F_2)\right|\leq \beta W_1(F_1,F_2).\end{equation}
In conjunction with our Theorem 2, there are two counterintuitive aspects worth mentioning. First, there are circumstances in which the supremum in (1.2) may not be attained, which seems to contradict the fact that the expectile is a continuous functional under the 1-Wasserstein distance. However, this should not be surprising, because the Wasserstein ball is not compact under the induced Wasserstein topology (see Proposition 2.2.9 in [Reference Panaretos and Zemel22].) Second, one may conjecture that
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=e_{\alpha}(G)+\beta\varepsilon\end{equation}
from Equation (3.2). However, interestingly, this is clearly not the case, since from Theorem 2(i), it follows that under the condition
$\textrm{ess sup}_G \leq \mu_G+\varepsilon\beta$
, we have
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\mu_G+\beta\varepsilon,\end{align*}
which is strictly less than
$e_{\alpha}(G)+\beta\varepsilon$
, for any non-degenerate distribution function G. A natural question is under which assumptions on G and
$\varepsilon$
the Lipschitz bound (3.3) is optimal, and when it can be improved. The following proposition provides a detailed answer.
Proposition 4. If G is a non-degenerate distribution function, then
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}< e_{\alpha}(G)+\beta\varepsilon$
. By contrast, if
$G=\mathbb{1}_{\{x\geq x_0\}}$
, then
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=e_{\alpha}(G)+\beta\varepsilon$
.
Proposition 4 implies that the Lipschitz bound (3.3) is optimal if and only if G is degenerate, in which case the Wasserstein constraint is reduced to a restriction on the absolute first moment, i.e.,
$\mathcal{M}=\{F_Y,\mathbb{E}|Y-x_0|\leq\varepsilon\}$
for some real number
$x_0$
. The proof of this proposition is deferred to Appendix B, as a continuation of that of Theorem 2. In addition, we have the following corollary, which is a direct consequence of Theorem 2 and Proposition 4.
Corollary 1. When p=1, we have the following:
-
(i) If G is bounded from above, i.e.
$\textrm{ess sup}_G< \infty$
, then there exists some level
$\alpha$
close enough to 1 so that
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\varepsilon\beta+\mu_G$
. -
(ii) If G is not bounded from above, then
$z_{1,G,\varepsilon}\left(\gamma\right)$
attains its maximum on
$\left(1/\beta,1\right)$
, and (3.4)
\begin{equation} \varepsilon\beta+\mu_G<\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}} <\varepsilon\beta+e_{\alpha}(G). \end{equation}
3.1.2. Some asymptotic results
So far we have generally analyzed the properties of the function
$z_{p, G,\varepsilon}$
and obtained some precise results for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p, G,\varepsilon}}$
, along with a rough range (3.4) for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1, G,\varepsilon}}$
. The worst-case value of the expectile has a closed-form solution only in a few special circumstances, namely
$p=1$
and
$\textrm{ess sup}_G \leq \mu_G+\varepsilon\beta$
, which excludes a large class of distribution functions. It is clearly unsatisfactory simply to know that (2.10) is a convex optimization problem and can be calculated with respect to the specific reference distribution, since this does not provide meaningful understanding of the characteristics of the worst-case value of the expectile. Therefore, we take an alternative approach and explore its extreme behavior, i.e., we consider
$\alpha \rightarrow 1$
, which is a case often relevant in risk management. For this, we need to make some additional assumptions on the distribution function G. We start by collecting some notation.
Let
$\mathbb{E}^G[\!\cdot\!]$
represent taking the expectation under the distribution function G. Throughout this paper, the notation
$f(\alpha)=O(g(\alpha))$
means that there exists a constant c such that
$f(\alpha)/g(\alpha)\rightarrow c$
as
$\alpha \rightarrow 1.$
All limits are at
$\alpha \rightarrow 1$
, or equivalently
$\beta\rightarrow\infty$
, unless otherwise specified.
Theorem 3. When
$p = 1$
, if
$\mathbb{E}^G[(Y^+)^2]< \infty$
,
$G^{-1}$
is continuous, and
$\textrm{ess sup}_G=\infty$
, then
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\mu_G+\varepsilon\beta+o\left(1\right) \quad \text{as}\;\alpha \rightarrow 1.\end{align*}
Remark 1. From the proof in Appendix B, it can easily be seen that the remainder in Theorem 3 is actually
$O\Big(\beta\mathbb{E}^G\left[Y\mathbb{1}_{\{Y> {\varepsilon\beta}/2\}}\right]\Big)$
, which is of lower order than
$\varepsilon\beta$
because
$G\in \mathcal{M}^1$
. A trivial application of Chebyshev’s inequality implies that the higher the moments of G, the faster the residuals converge. In particular, when G is a normally distributed distribution function, the residuals are of exponential order infinitesimal. However, when G is a heavy-tailed distribution with an infinite moment of order
$p\in (1,2)$
, the residual term is large, which motivates us to relax the assumption that
$\mathbb{E}^G[(Y^+)^2]< \infty$
(see Theorem 4).
The following example shows that even if
$G\in\bigcap_{p\in(1,2)}\mathcal{M}^{2-\delta}$
for all
$\delta>0$
, but
$G\notin\mathcal{M}^2$
, the residual term is just O(1) rather than o(1).
Example 1. Let G be a Pareto distribution function with density
$2x^{-3}\mathbb{1}_{(1,\infty)}(x)$
; then we derive the following:
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\varepsilon\beta+2+1/\varepsilon+\textrm{o}(1). \end{align*}
Now we see that the approximation in Theorem 3 is valid only for
$\mathbb{E}^G[(Y^+)^2]< \infty$
. Therefore, we generally consider a class of heavy-tailed distributions whose survival function satisfies
\begin{equation} \overline G(x)\;:\!=\;1-G(x)=x^{-\theta}L(x),\end{equation}
where L(x) is a slowly varying function at infinity, i.e.,
$\lim_{x\rightarrow \infty}{L(cx)}/{L(x)}=1$
for any
$c>0$
. Intuitively,
$\overline G(x)$
is ‘almost’
$x^{-\theta}$
as
$x\rightarrow\infty$
, and the ‘tail’ becomes heavier as
$\theta\rightarrow 0$
. When
$\theta> 2$
, the condition in Theorem 3 is fulfilled. Moreover,
$\theta>1$
is required to guarantee that
$G\in\mathcal{M}^1$
. Consequently, we assume that
$\theta\in (1,2]$
. However, when
$\theta$
approaches 1, it seems difficult to give uniform and simple bounds connected to
$\theta$
. Worse still, when L is a general slowly varying function, the analysis is beyond the scope of this paper. Therefore, we impose additional restrictions on both
$\theta$
and L.
Theorem 4. Suppose that when x is large enough, the survival function of G has the representation (3.5), and assume
$3/2<\theta\leq2$
,
$\lim_{x\rightarrow\infty}L(x)\;=\!:\;\zeta>0$
. In addition, assume L is differentiable with
$\lim_{x\rightarrow\infty}x^{3-\theta}L^{\prime}(x)=0$
. Then
\begin{equation*} \operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\varepsilon\beta+\mu_G+\frac{\zeta\varepsilon^{1-\theta}}{\theta-1}\beta^{2-\theta}+o(1),\qquad{as \quad\alpha\rightarrow1}. \end{equation*}
Remark 2. Through a careful check of the proof in Appendix B, we can verify that our approximation for
$\tau^*$
only requires the assumption
$\lim_{x\rightarrow\infty}L(x)\;=\!:\;\zeta>0$
, which is not restrictive because there are large numbers of common heavy-tailed distributions satisfying these conditions. This is evidently the central condition to be checked as part of Theorem 4, excluding some irregular slowly varying functions such as
$\log(x)$
, which are difficult to analyze using our techniques. The other assumptions we made are utilized to guarantee that the residual term is o(1) rather than
$o(\beta^{2-\theta})$
. Even so, a large category of distributions is still included; see Table 1. A similar table can be found in [Reference Ahmad1].
It is easily confirmed from the above table that our assumption on
$L^{\prime}(x)$
is automatically satisfied whenever the parameter
$\theta> 1$
, except for the Burr distribution, which requires
$2-\alpha\beta-\alpha<0$
. Therefore, the assumptions in Theorem 4 should not be viewed as restrictive in practice.
Table 1. A list of heavy-tailed distributions satisfying the assumptions in Theorem 4 with corresponding
$\theta$
,
$\zeta$
, and
$L^{\prime}(x)$
. Here
$\Gamma(\cdot)$
and
$B(\cdot,\cdot)$
denote the gamma and beta functions, respectively.
We now turn to the case
$p>1$
. We can establish a more accurate approximation for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
when
$\textrm{ess sup}_G <\infty$
.
Theorem 5. If
$p> 1$
and G has bounded support, i.e.
$\textrm{ess sup}_{G} < \infty$
, then
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}=p^{-1} \big[\varepsilon\left(p-1\right)^{1/q}\beta^{1/p} +{\mu_G} \big]+q^{-1}{\textrm{ess sup}_G}+o\left(1\right),\qquad {as\quad\alpha\rightarrow1}. \end{equation}
In fact, as noted in Remark 1, the remainder o(1) in Equation (3.6) may also be replaced by a precise order of particular relevance to p and G, through a slight modification of the proof in Appendix B. However, tedious arguments are required to analyze the relationship between terms related to p and those related to G, or even both of them. The form of Theorem 5 is consistent with Theorem 2(i), in the sense that
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}\rightarrow \operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}$
as
$p\rightarrow1$
, regardless of the residual term. In detail,
$(p-1)^{1/q}\rightarrow 1$
as
$p\rightarrow1$
. We must inevitably make the strong assumption
$\textrm{ess sup}_G < \infty$
, since there are essential difficulties in tackling a general distribution G, on account of the complexity of
$z_{p,G,\varepsilon}$
and the entanglement of
$l_p$
and
$k_G$
, which are defined in the proof of Theorem 1. However, a broad class of distributions is still covered, including the empirical distribution, which has attracted considerable research interest recently. In the following supporting example, G is chosen to be a degenerate distribution function, and the restrictions related to the Wasserstein distance are effectively translated into moment constraints.
Example 2. Let G be the distribution function corresponding to a point measure
$\delta_{x_0}$
. Then we can provide a specific expression for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
as follows:
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}} = \begin{cases}\varepsilon\beta+x_0, &p=1,\\[5pt] \varepsilon p^{-1}{(p-1)^{1/q}}\beta^{1/p}\left(1+\frac{\beta-1}{\beta^q-\beta}\right) \left(1+\frac{1-\beta^{2-q}}{\beta-1}\right)^{1/q}+x_0, &p>1.\end{cases}\end{align*}
From Theorems 3–5, it appears that the worst-case value of the expectile through
$\mathcal{W}_{p,G,\varepsilon}$
is mainly influenced by the level
$\alpha$
when extreme risk is involved. On the one hand, it is intuitively clear that for a distribution G bounded from above, there is a bounded expectile at any level, and so it is reasonable to expect that at extreme levels, the effect of G on
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p, G,\varepsilon}}$
is limited. In detail, Theorems 3 and 5 quantitatively characterize this effect in terms of a weighted average of expectation and essential supremum, i.e.,
$\mu_G/p+\textrm{ess sup}_G/q$
(
$\mu_G$
by continuity when
$p=1$
). On the other hand, as the tail of the reference distribution becomes heavier and heavier, the ‘invasion’ of G becomes more and more prominent, because more and more terms related to G are included in the asymptotic expression for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}$
(see Theorems 3 and 4). An analogous phenomenon is found for
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}$
, which will be discussed in Section 3.2. Even if
$\varepsilon$
is small and G is a degenerate distribution, we find that the worst-case value of the expectile explodes as
$\alpha\rightarrow1$
. This is because the shape of the distribution may be greatly altered, regardless of how slight the perturbation induced by the Wasserstein distance is (see Figure 3.1 for a simple illustration). Specifically, we observe that the transformed distribution function
$F_{p, G,\varepsilon,\gamma^*}$
elongates the tail of G dramatically when
$\alpha$
is sufficiently close to 1; this can be theoretically verified in many cases. Indeed, in the several scenarios contemplated in Theorems 3–5,
$\tau^*\rightarrow1$
and
$\beta^{q-1}/[\tau^*+\beta^q(1-\tau^*)]^{1/p}\rightarrow\infty$
always hold when
$p>1$
, indicating that
$F_{p,G,\varepsilon,\gamma^*}^{-1}$
substantially elevates
$G^{-1}$
in an extremely narrow interval
$[\tau^*,1]$
. These results should be significant as a feature of model ambiguity at extreme levels.
3.1.3. Comparison with the model aggregation approach
As suggested by [Reference Mao, Wang and Wu18], instead of directly calculating the maximum (or supremum) of
$e_{\alpha}(F)$
over
$F\in\mathcal{M}$
, it may be better to calibrate a robust (conservative) distribution
$F^*$
from
$\mathcal{M}$
and calculate
$e_{\alpha}(F^*)$
; the latter is called the ‘model aggregation’ approach. As will be seen later, this element
$F^*$
does not necessarily belong to
$\mathcal{M}$
, although it ‘dominates’
$\mathcal{M}$
in some sense. In the presence of model uncertainty, a natural problem in risk management is how to generate such a robust model
$F^*$
from the collection of models generated by various scenarios. Indeed,
$F^*$
is typically referred to as a maximal element (or supremum) of the ambiguity set
$\mathcal{M}$
in the sense of stochastic dominance; it has been explicitly derived in many situations. Below, we will use the abbreviation ‘MA’ to refer to the model aggregation approach. It can be argued that both the worst-case approach and the MA approach are reasonable ways to assess the risk posed by model uncertainty, although they may yield different values over the same ambiguity set
$\mathcal{M}$
. Figure 1 in [Reference Mao, Wang and Wu18] illustrates the two methods.
Now we are in a position to properly formulate the MA approach by giving a partial order
$\preceq$
on
$\mathcal{M}^1$
. At this point,
$(\mathcal{M}^1,\preceq)$
is called an order set. The most commonly used partial orders in finance and economics are the usual stochastic order
$\preceq_{st}$
and the increasing convex order
$\preceq_{icx}$
, defined as follows.
Definition 1. For
$F_1$
,
$F_2$
$\in \mathcal{M}^1$
,
-
(i)
$F_1\preceq_{st}F_2$
if
$\int udF_1\leq \int udF_2$
for increasing functions u; -
(ii)
$F_1\preceq_{icx}F_2$
if
$\int udF_1\leq \int udF_2$
for increasing convex functions u.
A natural interpretation of a partial order is that
$F_2$
is riskier than
$F_1$
if
$F_1\preceq F_2$
. This is the case when
$F_1$
and
$F_2$
are viewed as loss distributions rather than wealth distributions: a larger element with respect to
$\preceq_{st}$
or
$\preceq_{icx}$
corresponds to higher risk. Thus, we expect the risk measure
$\rho$
to maintain the order, i.e.,
$\rho(F_1)\leq\rho(F_2)$
if
$F_1\preceq F_2$
, which is formally defined being as
$\preceq$
-consistent. The expectile is consistent with both
$\preceq_{st}$
and
$\preceq_{icx}$
. For an ambiguity set
$\mathcal{M}\in \mathcal{M}^1$
, the supremum of
$\mathcal{M}$
in
$\mathcal{M}^1$
is defined by
$\bigvee\mathcal{M}\in\mathcal{M}^1$
such that
$F_1\preceq \bigvee\mathcal{M}\preceq F_2$
for all
$F_1\in \mathcal{M}$
and for any
$F_2$
that dominates every element in
$\mathcal{M}$
. If such an
$F_2$
exists, we say that
$\mathcal{M}$
is bounded from above. In what follows, we denote the supremum of
$\mathcal{M}$
with respect to
$\preceq_{st}$
and
$\preceq_{icx}$
on
$\mathcal{M}^1$
by
$\bigvee_{st}\mathcal{M}$
and
$\bigvee_{icx}\mathcal{M}$
, respectively.
For an ambiguity set
$\mathcal{M}$
whose supremum
$\bigvee\mathcal{M}$
exists, we formally formulate the MA approach for an expectile, in parallel with (1.2), as
\begin{equation} \operatorname{MAE}_{\alpha,\preceq}^{\mathcal{M}}=e_{\alpha}\left(\bigvee\mathcal{M}\right),\end{equation}
and
$\operatorname{MAE}_{\alpha,\preceq}^{\mathcal{M}}=\infty$
if
$\mathcal{M}$
is not bounded from above. From the definition and the
$\preceq_{icx}$
-consistency of the expectile, it is easily verified that
$e_{\alpha}\left(\bigvee_{icx}\mathcal{M}\right)\geq e_{\alpha}(F)$
for any
$F\in \mathcal{M}$
. Moreover, since the expectile is consistent with the two partial orders
$\preceq_{st}$
and
$\preceq_{icx}$
, the MA approach with the stronger partial order
$\preceq_{st}$
leads to a higher risk evaluation, i.e.,
$\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{M}}\leq \operatorname{MAE}_{\alpha,\preceq_{st}}^{\mathcal{M}}$
. Combining these two statements, we have the chain of inequalities
\begin{equation} \operatorname{WCE}_{\alpha}^{\mathcal{M}}\leq \operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{M}}\leq \operatorname{MAE}_{\alpha,\preceq_{st}}^{\mathcal{M}},\end{equation}
which indicates that the MA approach may produce a more conservative risk evaluation. Although the supremum of Wasserstein balls with respect to
$\preceq_{st}$
and
$\preceq_{icx}$
is explicitly derived in [Reference Mao, Wang and Wu18, Theorem 6], there is no closed-form expression for the supremum under the partial order
$\preceq_{st}$
, and the
$\mathcal{W}_{p,G,\varepsilon}$
is not bounded from above under
$\preceq_{icx}$
when
$p = 1$
. Therefore, in the following we will restrict our attention to
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
with
$p>1$
and the partial order
$\preceq_{icx}$
. From [Reference Mao, Wang and Wu18, Theorem 6], the quantile function of
$\bigvee_{icx}\mathcal{W}_{p,G,\varepsilon}$
with
$p>1$
is given by
\begin{equation} {(F_{p,G,\varepsilon}^{icx})^{-1}(u)=G^{-1}(u)+\left(1-\frac 1p\right)(1-u)^{-1/p}\varepsilon,}\end{equation}
which is the sum of the quantile function
$G^{-1}$
and a Pareto quantile with a tail index
$p > 1$
. It is surprising that
$F_{p, G,\varepsilon}^{icx}$
is a heavy-tailed distribution even if the reference distribution G is light-tailed, while
$F_{p, G,\varepsilon,\gamma^*}$
is not so. Another significant difference between the worst-case approach and the MA approach is that the construction for
$F_{p, G,\varepsilon,\gamma^*}$
is highly dependent on the specific choice of risk measure, rather than simply arising from the ambiguity set
$\mathcal{W}_{p,G,\varepsilon}$
. Also, one may wonder whether the inequality in Equation (3.8) could be refined to an equality. The theorem below provides a negative answer, as well as an asymptotic representation for Equation (3.7), where
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
.
Theorem 6. Let
$p>1$
and let
$F_{p,G,\varepsilon}^{icx}$
be as defined in (3.9). Furthermore, let
$z_{p,G,\varepsilon}^{icx}(\gamma)=\int_0^1(F_{p,G,\varepsilon}^{icx})^{-1}(u)dH_{\gamma}(u)$
. Then the following hold:
-
(i) We have that
$z_{p,G,\varepsilon}^{icx}(\gamma)$
is continuous and strictly concave on
$[1/\beta,1]$
, and
\begin{align*}\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{W}_{p,G,\varepsilon}}=\max_{\gamma\in[1/\beta,1]}z_{p,G,\varepsilon}^{icx}(\gamma).\end{align*}
-
(ii) For any G,
$\varepsilon$
, and level
$\alpha>1/2$
,
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
is strictly less than
$\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{W}_{p,G,\varepsilon}}.$
-
(iii) If we further assume
$\textrm{ess sup}_G<\infty$
, then
\begin{align*}\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{W}_{p,G,\varepsilon}}=\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}+\frac{\varepsilon}{p}+\textrm{o}(1), \qquad as \quad \alpha\rightarrow1.\end{align*}
Parts (i) and (iii) are parallel to Theorems 1 and 5 respectively, in which the worst-case approach yields similar results. Moreover, they are proved via identical steps and using similar techniques; thus we only give the proof of Part (ii), which is deferred to Appendix B. Additionally, because of technical constraints, we can only obtain an asymptotic solution for
$\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{W}_{p, G,\varepsilon}}$
when
$\textrm{ess sup}_{G}$
is finite. Comparing these two methods, the MA approach yields a more cautious risk assessment, whereas our worst-case approach takes full advantage of the properties of expectiles. However, when extreme levels are considered, they are separated by almost a constant
$\varepsilon/p$
, which is negligible relative to the diverging term
$\operatorname{MAE}_{\alpha,\preceq_{icx}}^{\mathcal{W}_{p, G,\varepsilon}}$
.
3.1.4. Alternative formulation of
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
We present an alternative way of formulating
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
, based on the general results of [Reference Bartl, Drapeau and Tangpi2] on robust shortfall risk measures. As a particular category of risk measure, the utility-based shortfall risk measure (abbreviated as SR hereafter) was proposed by [Reference Föllmer and Schied11] and has attracted rapidly increasing interest in recent years [Reference Dunkel and Weber9, Reference Giesecke, Schmidt and Weber13, Reference Hu and Dali16]. We first give a brief definition of the shortfall risk measure, which is adopted from [Reference Guo and Xu15] with some slight modifications for simplicity. Let
$l\;:\; \mathbb{R}\rightarrow\mathbb{R}$
be a convex, increasing, and non-constant loss function, and let
$\lambda$
be a pre-specified constant in the interior of the range of l, indicating the risk level. Then the SR of
$X\in \mathcal{L}^1$
is defined as
\begin{equation} \operatorname{SR}_{\lambda,l}(X)=\inf\{t\in\mathbb{R}\;:\;\mathbb{E}(l(X-t))\leq\lambda\},\end{equation}
whenever
$\mathbb{E}(l(X-t))$
is finite for some
$t\in\mathbb{R}$
. Viewing
$-X$
as a financial position, we see from the definition that the SR is the smallest amount of cash that must be added to the position
$-X$
to make it below a certain risk level, i.e.,
$\mathbb{E}(l(\!-(\!-X+t)))\leq\lambda$
. Theorem 4.9 in [Reference Bellini and Bignozzi3] shows that the expectile is indeed a shortfall risk measure with
$l(t)=\alpha t^+-(1-\alpha)t^-$
and
$\lambda=0$
.
To hedge the risk arising from the ambiguity of the true probability distribution, much of the extant literature considers the distributionally robust shortfall risk measure (abbreviated as DRSR in the sequel); see [Reference Guo and Xu15, Reference Bartl, Drapeau and Tangpi2, Reference Wiesemann, Kuhn and Sim30]. Specifically, for an ambiguity set
$\mathcal{M}$
, we concentrate on the following problem:
\begin{equation}\operatorname{DRSR}_{\lambda,l}^{\mathcal{M}}=\inf\left\{t\in\mathbb{R}\;:\;\sup_{G\in \mathcal{M}}\mathbb{E}^G(l(X-t))\leq\lambda\right\}.\end{equation}
In [Reference Bartl, Drapeau and Tangpi2], Equation (3.11) is reformulated as a finite-dimensional problem with
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
and a different loss function l. In fact, we have
\begin{equation}\operatorname{DRSR}_{0,l}^{\mathcal{W}_{p,G,\varepsilon}}=\inf_{\mu\geq0}\operatorname{SR}_{0,l^{\mu p}+\mu\varepsilon^p}(X_G),\end{equation}
where
$X_G$
is an arbitrary random variable with distribution function G and
$l^{\mu p}$
is the
$\mu c$
-transform of function l with cost function
$c(x,y)=|x-y|^p$
, which is formally defined as
\begin{equation} l^{\mu p}(x)=\sup\left\{l(y)-\mu|x-y|^p, y\in\mathbb{R}\;\text{such that}\; l(y)<\infty\right\}.\end{equation}
Meanwhile, [Reference Guo and Xu15] reveals that the infimum and supremum in Equation (3.11) can be exchanged in many circumstances, and in particular for
$l(t)=\alpha t^+-(1-\alpha)t^-$
, which gives rise to an expectile. Indeed, we have
\begin{equation*}\operatorname{DRSR}_{\lambda,l}^{\mathcal{M}}=\sup_{G\in\mathcal{M}}\operatorname{SR}_{\lambda,l}(X_G),\end{equation*}
where the right-hand side is exactly the worst-case shortfall risk measure over
$\mathcal{M}$
. Now, by taking
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
and
$\lambda=0$
and combining this with Equation (3.12), we obtain the following reformulation:
\begin{equation}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}=\inf_{\mu\geq0}\operatorname{SR}_{-\mu\varepsilon^p,l_{\alpha}^{\mu p}}(X_G),\end{equation}
where
$l_{\alpha}^{\mu p}$
can be calculated explicitly from Equation (3.13) with
$l(y)=\alpha y^+-(1-\alpha)y^-$
. Specifically, when
$p>1$
we have
\begin{equation*} l_{\alpha}^{\mu p}= \begin{cases} \alpha x+\frac{\alpha^q}{q(\mu p)^{q-1}} & \text { if } x>\frac{1}{q(\mu p)^{q-1}}\left(\frac{\alpha^q-(1-\alpha)^q}{1-2\alpha}\right), \\[5pt] (1-\alpha)x+\frac{(1-\alpha)^q}{q(\mu p)^{q-1}} &\text { if } x\leq\frac{1}{q(\mu p)^{q-1}}\left(\frac{\alpha^q-(1-\alpha)^q}{1-2\alpha}\right). \end{cases}\end{equation*}
We believe it would be difficult to simplify Equation (3.14) further in this case, not only because of the complexity of
$l_{\alpha}^{\mu p}$
, but also because of the generality of G. However, when
$p=1$
, it is easy to obtain
$l_{\alpha}^{\mu 1}=l$
if
$\mu\geq\alpha$
and
$l_{\alpha}^{\mu p}=\infty$
otherwise, which further transforms Equation (3.14) into
\begin{equation}\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\inf_{\mu\geq\alpha}\inf\{t\in\mathbb{R}\;:\;\alpha\mathbb{E}^G(X-t)^+-(1-\alpha)\mathbb{E}^G(X-t)^-\leq -\mu\varepsilon\}.\end{equation}
Notice that the function
\begin{align*}g(t)=\alpha\mathbb{E}^G(X-t)^+-(1-\alpha)\mathbb{E}^G(X-t)^-=\alpha\int_t^{+\infty}(1-G(s))ds-(1-\alpha)\int_{-\infty}^tG(s)ds\end{align*}
is a strictly decreasing continuous function that tends to
$-\infty$
as
$t\rightarrow+\infty$
and tends to
$+\infty$
as
$t\rightarrow-\infty$
. Equation (3.15) can therefore be translated into a more concise form; that is,
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1, G,\varepsilon}}$
is the unique solution to the following equation:
\begin{equation} \alpha\int_t^{+\infty}(1-G(s))ds-(1-\alpha)\int_{-\infty}^tG(s)ds=-\alpha\varepsilon.\end{equation}
The above equation is quite succinct, although it is still difficult to use it to acquire general results for
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1, G,\varepsilon}}$
. However, if we assume
$\textrm{ess sup}_G\leq\beta\varepsilon+\mu_G$
and substitute
$\varepsilon\beta+\mu_G$
into Equation (3.16), we obtain
\begin{align*}&\alpha\int_{\varepsilon\beta+\mu_G}^{+\infty}(1-G(s))ds-(1-\alpha)\int_{-\infty}^{\varepsilon\beta+\mu_G}G(s)ds\\[5pt] =&-(1-\alpha)\left(\varepsilon\beta+\mu_G-G^{-1}(1)+\int_{-\infty}^{G^{-1}(1)}G(s)ds\right)\\[5pt] =&-(1-\alpha)\left(\varepsilon\beta+\mu_G-G^{-1}(1)+\int_{0}^{1}\left(G^{-1}(1)-G^{-1}(s)\right)ds\right)\\[5pt] =&-(1-\alpha)\varepsilon\beta=-\alpha\varepsilon,\end{align*}
which is consistent with Theorem 2(i), which shows that
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{1,G,\varepsilon}}=\varepsilon\beta+\mu_G$
.
In summary, Equations (2.10) and (3.14) are both tractable optimization problems that can be solved easily by many popular algorithms, once the distribution function G is provided. Nevertheless, it is clear that Equation (2.10) is easier to deal with, and it is possible to obtain a transformed distribution function whose expectile is exactly
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
by solving Equation (2.10). Moreover, when considering extreme levels, it is more difficult to obtain asymptotic results analogous to those of Theorems 3–7 by analyzing Equation (3.14).
3.2. Results on
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}$
We consider the problem (1.2) where
$\mathcal{M}=\mathcal{M}_{p,\mu,\sigma}$
. As in Section 3.1, we observe that there is no closed-form solution in most cases, apart from
$p=2$
. Another difficulty is that the function being optimized is not concave in general, so it is more fruitful to study the asymptotic nature of the solution than simply to discuss the solvability of the problem (2.13). In other words, we can obtain an asymptotic solution when
$\alpha \rightarrow 1$
, or equivalently
$\beta \rightarrow \infty$
. We show this in the following theorem.
Theorem 7. For any
$p>1$
, there exists only one
$\gamma^*\in (1/\beta,1)$
maximizing
$[h_{\gamma}]_q$
, and
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}=e_{\alpha}(F_{p,\mu,\sigma,\gamma^*})$
, where
$F_{p,\mu,\sigma,\gamma^*}$
is defined in (2.12). Moreover, we have the following:
-
If
$p=2$
, then
$\gamma^*=(1/\beta+1)/2$
and
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{M}_{2,\mu,\sigma}}=\mu+\sigma\frac{\beta-1}{2\sqrt{\beta}}.\end{align*}
-
If
$p \gt> 2$
, then
$\gamma^*=1/p+\textrm{o}(1)$
and
\begin{align*}\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}=\mu+\sigma {\frac{\left(\beta-1\right)^{1/p}}{p^{1/p}q^{1/q}}}+\textrm{o}\left(\beta^{2-p-1/p}\right),\qquad {as\quad\alpha\rightarrow1}.\end{align*}
-
If
$p \lt 2$
, then
$\gamma^*=1/p+\textrm{o}(1)$
and where
\begin{align*} \operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}=\mu+\sigma {\frac{\left(\beta-1\right)^{1/p}}{p^{1/p}q^{1/q}}}\left(1-\frac{\eta_1}{\beta^{p-1}}+\frac{\eta_2}{\beta^{2p-2}}\!\right)+\textrm{o}\left(\beta^{1/p-2p+2}\right)\!,\;\; {as\quad\alpha\rightarrow1}, \end{align*}
$\eta_1={p}^{-1}{(p-1)^{p-1}}$
and
\begin{align*}\eta_2={p^{-2}}{(p-1)^{2p-1}}+{p}^{-1}{(p-1)^{2p}}+(2p^{2})^{-1}{(p-1)^{p-1}(p+1)}.\end{align*}
The strategy of the proof is basically to use the same technique as in the proofs of Theorems 4 and 5, with some tiny modifications when dealing with the case
$p<2$
. The calculations are so tedious that we do not elaborate further here, deferring the proof to Appendix B; instead, we now discuss the results of the theorem in detail. Surprisingly, Theorems 5 and 7 indicate that the main terms of the asymptotic representations of
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}$
and
$\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}$
are of the same order, and the corresponding coefficients are also equal, when
$p>1$
,
$\textrm{ess sup}_{G} < \infty$
, and
$\sigma=\varepsilon$
(noting that
$p^{-1/p}q^{-1/q}=(p-1)^{1/q}/p$
). Alternatively, if we ignore the constants and the terms of lower order than
$\beta^{1/p}$
, the asymptotic behavior of
$\operatorname{WCE}_{\alpha}^{\mathcal{M}}$
is totally captured by
$Cp^{-1/p}q^{-1/q}\beta^{1/p}$
, where
$C=\varepsilon$
for
$\mathcal{M}=\mathcal{W}_{p,G,\varepsilon}$
and
$C=\sigma$
for
$\mathcal{M}_{p,\mu,\sigma}$
. We formally record this observation as follows.
Corollary 2. If
$p>1$
and
$\textrm{ess sup}_G <\infty$
, then
\begin{equation*} \lim_{\alpha\to1}\frac{\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}}{p^{-1/p}q^{-1/q}\beta^{1/p}}=\sigma,\qquad\qquad \lim_{\alpha\to1}\frac{\operatorname{WCE}_{\alpha}^{\mathcal{W}_{p,G,\varepsilon}}}{p^{-1/p}q^{-1/q}\beta^{1/p}}=\varepsilon.\end{equation*}
It can be seen from Equation (2.11) that for any given
$\mu$
and
$\sigma$
,
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p_1,\mu,\sigma}}<\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p_2,\mu,\sigma}}$
for any
$p_1>p_2>1$
. This roughly characterizes the effect of the reduction in ambiguity on the worst-case value of the expectile, while our results describe in detail the influence of p on
$\operatorname{WCE}_{\alpha}^{\mathcal{M}_{p,\mu,\sigma}}$
, at extreme levels. Regarding Theorem 7 alone, the first residual term
$\textrm{O}(\beta^{1/p-p+1})$
is
$o\left(1\right)$
if and only if
$p > ({\sqrt{5}+1})/{2} \approx 1.618$
, and the second residual term
$\textrm{O}(\beta^{1/p-2p+2})$
is
$o\left(1\right)$
if and only if
$p > ({\sqrt{3}+1})/{2} \approx 1.366$
. It seems that when
$p\rightarrow1$
, the error increases greatly and there are essential difficulties in finding uniform bounds to control the error.
4. Concluding remarks and future work
In this paper, we have presented the worst-case value of the expectile over two common ambiguity sets, one specified as a ball in the p-Wasserstein metric and the other specified by a moment constraint. We initially focus on the p-Wasserstein ball, for which we reformulate the problem as a convex optimization problem and provide a method of constructing elements that attain or approach the worst-case expectile. In this case, it is established that the precise value of the worst-case expectile can be derived only under specific conditions. However, the asymptotic behavior of the worst-case expectile at extreme levels is thoroughly understood for a wide range of distribution functions. The technical results and simulation studies described in the supplementary material show that our approximation is remarkably accurate, and the general trends of worst-case expectiles at extreme levels are independent of the reference distribution. Furthermore, we observe significant alterations in the shape of the distribution function within the p-Wasserstein ball for which the extreme worst-case expectile is achieved; this highlights a feature of distributional ambiguity.
We also compare our worst-case approach with the model aggregation approach in the case of the expectile; the latter relies not on a specific risk measure but on the choice of stochastic order. We observe that the model aggregation approach yields a more conservative risk evaluation at both fixed and extreme levels. Additionally, we attempt to reformulate our problem using the general results of [Reference Bartl, Drapeau and Tangpi2] on robust shortfall risk measures, and we re-derive Theorem 2(i) from this new perspective. In parallel, we apply our techniques to investigate the worst-case expectile over an ambiguity set with constraints on higher-order moments.
Although we have systematically studied the worst-case value of the expectile, there are still some restrictions on our results, which reveal a few promising directions for future study. First, we would like to remove the strong assumption
$\textrm{ess sup}_G<\infty$
in Theorems 5 and 6, which is essential for our proof. Second, one may want to offer more accurate and even unified approximations for the worst-case expectiles over both the p-Wasserstein ball and the moment-constrained ambiguity set, to describe their asymptotic behavior in a more general setting. Finally, a potential future problem would be to adapt the worst-case expectile to robust portfolio selection, a topic that has already attracted great interest in recent years [Reference Ghaoui, Oks and Oustry12, Reference Glasserman and Xu14, Reference Natarajan, Pachamanova and Sim20, Reference Zhu and Fukushima31].
Acknowledgements
The authors thank the editor and the anonymous referees for their helpful comments, which greatly improved the quality of this paper. Y. Chen and T. Mao are co-corresponding authors.
Funding information
This work is supported by the National Natural Science Foundation of China (Nos. 12371279, 12371476) and NSF of Anhui Province (Nos. 2208085MA05, 2208085MA07).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Supplementary material
The supplementary material for this article can be found at https://dx.doi.org/10.1017/apr.2024.10.
