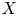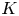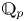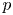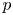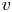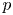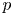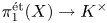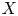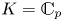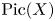1. Introduction
The Corlette–Simpson correspondence for a smooth projective variety ![]() $X$ over
$X$ over ![]() $\mathbb {C}$ is an equivalence of categories between finite-dimensional
$\mathbb {C}$ is an equivalence of categories between finite-dimensional ![]() $\mathbb {C}$-linear representations of the topological fundamental group
$\mathbb {C}$-linear representations of the topological fundamental group ![]() $\pi _1(X)$ of
$\pi _1(X)$ of ![]() $X(\mathbb {C})$ on the one hand, and semi-stable Higgs bundles on
$X(\mathbb {C})$ on the one hand, and semi-stable Higgs bundles on ![]() $X$ with vanishing (rational) Chern classes on the other hand [Reference SimpsonSim92, § 1]. For any
$X$ with vanishing (rational) Chern classes on the other hand [Reference SimpsonSim92, § 1]. For any ![]() $n\in \mathbb {N}$, there are natural complex analytic moduli spaces of the rank-
$n\in \mathbb {N}$, there are natural complex analytic moduli spaces of the rank-![]() $n$ objects on either side, and the correspondence induces a homeomorphism between them, see [Reference SimpsonSim92, Proposition 1.5] and [Reference SimpsonSim95, Theorem 7.18]. However, this map does not respect the complex analytic structures.
$n$ objects on either side, and the correspondence induces a homeomorphism between them, see [Reference SimpsonSim92, Proposition 1.5] and [Reference SimpsonSim95, Theorem 7.18]. However, this map does not respect the complex analytic structures.
Our first result is a very close ![]() $p$-adic analogue of this equivalence in rank one.
$p$-adic analogue of this equivalence in rank one.
Theorem 1.1
(i) Let
 $X$ be a connected smooth projective variety over
$X$ be a connected smooth projective variety over  $\mathbb {C}_p$ and fix a point
$\mathbb {C}_p$ and fix a point  $x\in X(\mathbb {C}_p)$. Then any choice of an exponential map for
$x\in X(\mathbb {C}_p)$. Then any choice of an exponential map for  $\mathbb {C}_p$ and of a flat
$\mathbb {C}_p$ and of a flat  $B_{\mathrm {dR}}^+/\xi ^2$-lift of
$B_{\mathrm {dR}}^+/\xi ^2$-lift of  $X$ induce an equivalence of categories
By passing to isomorphism classes, this induces an isomorphism of topological groups
$X$ induce an equivalence of categories
By passing to isomorphism classes, this induces an isomorphism of topological groups \[ \bigg\{\begin{array}{@{}c@{}l}\text{one-dimensional continuous}\\\text{$\mathbb{C}_p$-representations of $\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$} \end{array}\bigg\} {\tilde{\to}} \bigg\{\begin{array}{@{}c@{}l}\text{Higgs bundles on $X$ of rank one}\\\text{with vanishing Chern classes}\end{array}\bigg\}. \]
\[ \bigg\{\begin{array}{@{}c@{}l}\text{one-dimensional continuous}\\\text{$\mathbb{C}_p$-representations of $\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$} \end{array}\bigg\} {\tilde{\to}} \bigg\{\begin{array}{@{}c@{}l}\text{Higgs bundles on $X$ of rank one}\\\text{with vanishing Chern classes}\end{array}\bigg\}. \]
 \[ \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1^{{\mathrm{\acute{e}t}}}(X,x),\mathbb{C}_p^\times)\cong \operatorname{Pic}^{\tau}(X)\times H^0(X,\Omega^1(-1)). \]
\[ \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1^{{\mathrm{\acute{e}t}}}(X,x),\mathbb{C}_p^\times)\cong \operatorname{Pic}^{\tau}(X)\times H^0(X,\Omega^1(-1)). \]
(ii) More generally, let
 $X$ be a connected smooth proper rigid space over any complete algebraically closed field
$X$ be a connected smooth proper rigid space over any complete algebraically closed field  $K|\mathbb {C}_p$ and assume that the rigid analytic Picard functor of
$K|\mathbb {C}_p$ and assume that the rigid analytic Picard functor of  $X$ is representable by a rigid space
$X$ is representable by a rigid space  $\mathbf {Pic}_X$. Then the analogous statements as in part (i) hold when we replace the condition of ‘vanishing Chern classes’ by the strictly stronger condition that the underlying line bundle is ‘topologically torsion’ in
$\mathbf {Pic}_X$. Then the analogous statements as in part (i) hold when we replace the condition of ‘vanishing Chern classes’ by the strictly stronger condition that the underlying line bundle is ‘topologically torsion’ in  $\mathbf {Pic}_X(K)$.
$\mathbf {Pic}_X(K)$.
This is the first instance of a correspondence relating ![]() $p$-adic continuous representations to Higgs bundles with an explicit topological condition. It gives useful insights into what to expect in higher rank, e.g. that Chern classes do not define the correct condition in general.
$p$-adic continuous representations to Higgs bundles with an explicit topological condition. It gives useful insights into what to expect in higher rank, e.g. that Chern classes do not define the correct condition in general.
In order to clarify the statement of Theorem 1.1, we now elaborate on the terminology.
– An exponential map for
 $K$ is a continuous group homomorphism
$K$ is a continuous group homomorphism  $K\to 1+\mathfrak m_K$ splitting the
$K\to 1+\mathfrak m_K$ splitting the  $p$-adic logarithm
$p$-adic logarithm  $\log :1+\mathfrak m_K\to K$. Here
$\log :1+\mathfrak m_K\to K$. Here  $\mathfrak m_K$ is the maximal ideal of the ring of integers
$\mathfrak m_K$ is the maximal ideal of the ring of integers  $\mathcal {O}_K$ of
$\mathcal {O}_K$ of  $K$. An exponential exists since
$K$. An exponential exists since  $K$ is algebraically closed.
$K$ is algebraically closed.– We define
 $\operatorname {Pic}^{\tau }(X)$ as the group of isomorphism classes of line bundles
$\operatorname {Pic}^{\tau }(X)$ as the group of isomorphism classes of line bundles  $L$ on
$L$ on  $X$ for which there is
$X$ for which there is  $n\in \mathbb {N}$ such that
$n\in \mathbb {N}$ such that  $L^n$ defines a class in
$L^n$ defines a class in  $\mathbf {Pic}^0_X(K)$, where
$\mathbf {Pic}^0_X(K)$, where  $\mathbf {Pic}^0_X$ is the connected component of the identity of the rigid analytic Picard functor of
$\mathbf {Pic}^0_X$ is the connected component of the identity of the rigid analytic Picard functor of  $X$.
$X$.– The topological group structures in Theorem 1.1(i) come from regarding either side as
 $K$-points of natural rigid moduli spaces (see § 1.1), endowed with the canonical topology inherited from
$K$-points of natural rigid moduli spaces (see § 1.1), endowed with the canonical topology inherited from  $K$. For example,
$K$. For example,  $\operatorname {Pic}^{\tau }(X)$ inherits a topology from
$\operatorname {Pic}^{\tau }(X)$ inherits a topology from  $\mathbf {Pic}_X$.
$\mathbf {Pic}_X$.– The ‘topologically torsion’ condition in Theorem 1.1(ii) means that with respect to this topology on
 $\operatorname {Pic}^{\tau }(X)$, the line bundle
$\operatorname {Pic}^{\tau }(X)$, the line bundle  $L$ satisfies
$L$ satisfies  $L^{n!}\to 1$ for
$L^{n!}\to 1$ for  $n\to \infty$.
$n\to \infty$.
1.1 Geometrising the  $p$-adic Simpson correspondence of rank one
$p$-adic Simpson correspondence of rank one
The main aim of this article is to show that, surprisingly, Theorem 1.1 can be upgraded to a geometric statement about moduli spaces: we show that there is always a smooth rigid analytic moduli space ![]() $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ of topologically torsion line bundles. This is an open rigid subgroup of the Picard variety
$\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ of topologically torsion line bundles. This is an open rigid subgroup of the Picard variety ![]() $\mathbf {Pic}_{X}$ if the latter exists, but, in fact, we do not need representability of the Picard functor for the construction. Using the Hitchin base
$\mathbf {Pic}_{X}$ if the latter exists, but, in fact, we do not need representability of the Picard functor for the construction. Using the Hitchin base ![]() $\mathcal {A}$ of rank one, this allows us to define the ‘Dolbeault moduli space’ of topologically torsion Higgs line bundles
$\mathcal {A}$ of rank one, this allows us to define the ‘Dolbeault moduli space’ of topologically torsion Higgs line bundles
On the other side of the ![]() $p$-adic Simpson correspondence, we have the
$p$-adic Simpson correspondence, we have the ![]() $p$-adic character variety
$p$-adic character variety
defined as the internal Hom in ![]() $v$-sheaves over
$v$-sheaves over ![]() $K$, where the profinite group
$K$, where the profinite group ![]() $\pi _1^{\mathrm {\acute {e}t}}(X,x)$ is considered as a profinite
$\pi _1^{\mathrm {\acute {e}t}}(X,x)$ is considered as a profinite ![]() $v$-sheaf. As we explain in § 3.1, the functor
$v$-sheaf. As we explain in § 3.1, the functor ![]() $\mathbf {M}_{\mathrm {B}}$ is represented by a rigid group variety, playing the role of the ‘Betti moduli space’ in this context. We show the following.
$\mathbf {M}_{\mathrm {B}}$ is represented by a rigid group variety, playing the role of the ‘Betti moduli space’ in this context. We show the following.
Theorem 1.2 (Theorem 4.1)
Let ![]() $X$ be a connected smooth proper rigid space over
$X$ be a connected smooth proper rigid space over ![]() $K$ and fix
$K$ and fix ![]() $x\in X(K)$. Then there is a natural short exact sequence of rigid analytic groups
$x\in X(K)$. Then there is a natural short exact sequence of rigid analytic groups
On tangent spaces, the associated sequence of Lie algebras recovers the Hodge–Tate sequence
Here exactness of (1) is to be understood with respect to the étale topology. While the map ![]() $\mathrm {HTlog}$ in (1) can be defined explicitly using the
$\mathrm {HTlog}$ in (1) can be defined explicitly using the ![]() $p$-adic logarithm, the first map is more subtle: it generalises and geometrises a construction of Deninger and Werner [Reference Deninger and WernerDW05b], as well as of Song [Reference SongSon22] in the case of curves over
$p$-adic logarithm, the first map is more subtle: it generalises and geometrises a construction of Deninger and Werner [Reference Deninger and WernerDW05b], as well as of Song [Reference SongSon22] in the case of curves over ![]() $\overline {\mathbb {Q}}_p$ as we explain in § 4. It induces a generalised ‘Weil pairing’
$\overline {\mathbb {Q}}_p$ as we explain in § 4. It induces a generalised ‘Weil pairing’
namely a bilinear morphism of ![]() $v$-sheaves (or adic groups) where
$v$-sheaves (or adic groups) where ![]() $\underline {\pi _1^{{\mathrm {\acute {e}t}}}(X,x)}$ is the profinite
$\underline {\pi _1^{{\mathrm {\acute {e}t}}}(X,x)}$ is the profinite ![]() $v$-sheaf associated to the profinite group
$v$-sheaf associated to the profinite group ![]() $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. We refer to Theorem 4.1 for more details.
$\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. We refer to Theorem 4.1 for more details.
We use Theorem 1.2 to describe a geometric ![]() $p$-adic Simpson correspondence in rank one in terms of a comparison of moduli spaces: the projection
$p$-adic Simpson correspondence in rank one in terms of a comparison of moduli spaces: the projection ![]() $\mathbf {M}_{\mathrm {Dol}}\to \mathcal {A}$ may be interpreted as the Hitchin fibration. Theorem 1.2 now yields an analogous map
$\mathbf {M}_{\mathrm {Dol}}\to \mathcal {A}$ may be interpreted as the Hitchin fibration. Theorem 1.2 now yields an analogous map ![]() $\mathrm {HTlog}$ on the Betti side as follows.
$\mathrm {HTlog}$ on the Betti side as follows.

From this perspective, Theorem 1.2 says that both ![]() $\mathbf {M}_{\mathrm {B}}$ and
$\mathbf {M}_{\mathrm {B}}$ and ![]() $\mathbf {M}_{\mathrm {Dol}}$ are
$\mathbf {M}_{\mathrm {Dol}}$ are ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsors over
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsors over ![]() $\mathcal {A}$, but the latter is split, whereas we show that the former is never split outside of trivial cases. It follows that we can regard
$\mathcal {A}$, but the latter is split, whereas we show that the former is never split outside of trivial cases. It follows that we can regard ![]() $\mathbf {M}_{\mathrm {B}}$ as an étale twist of
$\mathbf {M}_{\mathrm {B}}$ as an étale twist of ![]() $\mathbf {M}_{\mathrm {Dol}}$. In fact, our main result is that one can more canonically compare these two torsors in a geometric fashion as follows.
$\mathbf {M}_{\mathrm {Dol}}$. In fact, our main result is that one can more canonically compare these two torsors in a geometric fashion as follows.
Theorem 1.3 (Theorem 5.4 and Corollary 4.6)
We have ![]() $\mathbf {M}_{\mathrm {B}}\not \cong \mathbf {M}_{\mathrm {Dol}}$ as rigid spaces except in the trivial case that
$\mathbf {M}_{\mathrm {B}}\not \cong \mathbf {M}_{\mathrm {Dol}}$ as rigid spaces except in the trivial case that ![]() $H^0(X,\Omega _X)=0$. Instead, any choice of a flat
$H^0(X,\Omega _X)=0$. Instead, any choice of a flat ![]() $B^+_{\mathrm {dR}}/\xi ^2$-lift
$B^+_{\mathrm {dR}}/\xi ^2$-lift ![]() $\mathbb {X}$ of
$\mathbb {X}$ of ![]() $X$ induces a natural
$X$ induces a natural ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor ![]() $\mathbb {L}_{\mathbb {X}}$ over
$\mathbb {L}_{\mathbb {X}}$ over ![]() $\mathcal {A}$ and a canonical isomorphism of rigid spaces
$\mathcal {A}$ and a canonical isomorphism of rigid spaces
Here the local system ![]() $\mathbb {L}_{\mathbb {X}}$ can roughly be thought of as a moduli space of exponentials, in the sense that it parametrises preimages of a certain logarithm map, see Definition 5.3. We also give a completely canonical variant of Theorem 1.3 over a moduli space of all lifts. These results explain the choices necessary in Faltings’
$\mathbb {L}_{\mathbb {X}}$ can roughly be thought of as a moduli space of exponentials, in the sense that it parametrises preimages of a certain logarithm map, see Definition 5.3. We also give a completely canonical variant of Theorem 1.3 over a moduli space of all lifts. These results explain the choices necessary in Faltings’ ![]() $p$-adic Simpson correspondence in a geometric fashion: any choice of an exponential induces a splitting of
$p$-adic Simpson correspondence in a geometric fashion: any choice of an exponential induces a splitting of ![]() $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on
$\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on ![]() $K$-points. We take this as a first sign that in the
$K$-points. We take this as a first sign that in the ![]() $p$-adic situation, a more geometric formulation of the
$p$-adic situation, a more geometric formulation of the ![]() $p$-adic Simpson correspondence is possible. We will pursue this further in [Reference HeuerHeu22c].
$p$-adic Simpson correspondence is possible. We will pursue this further in [Reference HeuerHeu22c].
Remark 1.4 A choice of ![]() $\mathbb {X}$ induces a choice of splitting of the Hodge–Tate sequence (2), see [Reference GuoGuo23, Proposition 7.2.5]. If we are given a model of
$\mathbb {X}$ induces a choice of splitting of the Hodge–Tate sequence (2), see [Reference GuoGuo23, Proposition 7.2.5]. If we are given a model of ![]() $X$ over a local field
$X$ over a local field ![]() $L|\mathbb {Q}_p$, this induces such a lift
$L|\mathbb {Q}_p$, this induces such a lift ![]() $\mathbb {X}$, and Theorem 1.3 then provides a completely canonical comparison.
$\mathbb {X}$, and Theorem 1.3 then provides a completely canonical comparison.
Remark 1.5 It is very surprising to us that the ![]() $p$-adic Simpson correspondence in rank one allows for a more refined comparison of the rigid analytic structures as in Theorem 1.3: if
$p$-adic Simpson correspondence in rank one allows for a more refined comparison of the rigid analytic structures as in Theorem 1.3: if ![]() $X$ is instead a smooth projective curve over
$X$ is instead a smooth projective curve over ![]() $\mathbb {C}$, the analogue of (1) is the exact sequence
$\mathbb {C}$, the analogue of (1) is the exact sequence
where the first map is defined as ![]() $\operatorname {Pic}^0(X)=\operatorname {Hom}(\pi _1(X),S^1)\to \operatorname {Hom}(H_1(X,\mathbb {Z}),\mathbb {C}^\times )$ using the decomposition
$\operatorname {Pic}^0(X)=\operatorname {Hom}(\pi _1(X),S^1)\to \operatorname {Hom}(H_1(X,\mathbb {Z}),\mathbb {C}^\times )$ using the decomposition ![]() $\mathbb {C}^\times =S^1\times \mathbb {R}^\times _+$; see [Reference SimpsonSim92, p. 21] and [Reference SimpsonSim93, § 2]. This is clearly only real-analytic and not complex-analytic. Instead, the only result we know in the literature that resembles Theorem 1.3 is Groechenig's result in the mod-
$\mathbb {C}^\times =S^1\times \mathbb {R}^\times _+$; see [Reference SimpsonSim92, p. 21] and [Reference SimpsonSim93, § 2]. This is clearly only real-analytic and not complex-analytic. Instead, the only result we know in the literature that resembles Theorem 1.3 is Groechenig's result in the mod-![]() $p$-Simpson correspondence that for curves over
$p$-Simpson correspondence that for curves over ![]() $\overline {\mathbb {F}}_p$, the de Rham moduli stack is a twist of the Dolbeault moduli stack [Reference GroechenigGro16].
$\overline {\mathbb {F}}_p$, the de Rham moduli stack is a twist of the Dolbeault moduli stack [Reference GroechenigGro16].
We now discuss the precise relation to previous results in the ![]() $p$-adic Simpson correspondence, and explain in more detail the topologically torsion condition and the moduli spaces.
$p$-adic Simpson correspondence, and explain in more detail the topologically torsion condition and the moduli spaces.
1.2 The conjectural  $p$-adic Simpson correspondence: known results
$p$-adic Simpson correspondence: known results
Let ![]() $K|\mathbb {Q}_p$ be any complete algebraically closed extension and let
$K|\mathbb {Q}_p$ be any complete algebraically closed extension and let ![]() $X$ be a connected smooth proper rigid space over
$X$ be a connected smooth proper rigid space over ![]() $K$ with fixed base-point
$K$ with fixed base-point ![]() $x\in X(K)$. In this setting, the conjectural
$x\in X(K)$. In this setting, the conjectural ![]() $p$-adic Simpson correspondence is expected to be an equivalence of categories (depending on choices)
$p$-adic Simpson correspondence is expected to be an equivalence of categories (depending on choices)
where ‘??’ is a condition yet to be identified. In order to construct a fully faithful functor from representations to Higgs bundles, Faltings [Reference FaltingsFal05] introduced a category of ‘generalised representations’ into which representations of ![]() $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ embed fully faithfully. This category can be shown to be equivalent to the category of
$\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ embed fully faithfully. This category can be shown to be equivalent to the category of ![]() $v$-vector bundles on
$v$-vector bundles on ![]() $X$ (see [Reference HeuerHeu22a, Proposition 2.3]). If we gloss over some technical differences in setups, then reformulated in this language, Faltings proved that if
$X$ (see [Reference HeuerHeu22a, Proposition 2.3]). If we gloss over some technical differences in setups, then reformulated in this language, Faltings proved that if ![]() $X$ is a smooth projective curve, there is an equivalence
$X$ is a smooth projective curve, there is an equivalence
More generally, such an equivalence has recently been constructed in [Reference HeuerHeu23, Theorem 1.1] for any smooth proper rigid space ![]() $X$ over
$X$ over ![]() $K$. Previously, Faltings constructed a ‘local’ version of this correspondence under additional ‘smallness’ assumptions, which was reinterpreted in terms of period rings and studied in detail by Abbes, Gros and Tsuji [Reference Abbes, Gros and TsujiAGT16]. There are other known instances of this, e.g. due to Wang for
$K$. Previously, Faltings constructed a ‘local’ version of this correspondence under additional ‘smallness’ assumptions, which was reinterpreted in terms of period rings and studied in detail by Abbes, Gros and Tsuji [Reference Abbes, Gros and TsujiAGT16]. There are other known instances of this, e.g. due to Wang for ![]() $X$ of good reduction [Reference WangWan23]. In rank one, we previously constructed the equivalence (5) for general
$X$ of good reduction [Reference WangWan23]. In rank one, we previously constructed the equivalence (5) for general ![]() $X$ by way of a ‘Hodge–Tate sequence for
$X$ by way of a ‘Hodge–Tate sequence for ![]() $\mathbb {G}_m$’ for the group
$\mathbb {G}_m$’ for the group ![]() $\operatorname {Pic}_v(X)$ of isomorphism classes of
$\operatorname {Pic}_v(X)$ of isomorphism classes of ![]() $v$-line bundles on
$v$-line bundles on ![]() $X$: a short exact sequence
$X$: a short exact sequence
see [Reference HeuerHeu22b]. We note that neither of the (conjectural) equivalences (4) and (5) is canonical, instead they will depend on choices of an exponential for ![]() $K$ and a flat
$K$ and a flat ![]() $B_{\mathrm {dR}}^+/\xi ^2$-lift of
$B_{\mathrm {dR}}^+/\xi ^2$-lift of ![]() $X$. For example, these choices induce a splitting of (6), which is not canonically split.
$X$. For example, these choices induce a splitting of (6), which is not canonically split.
Given correspondence (5), a fundamental open problem in ![]() $p$-adic non-abelian Hodge theory, raised by Faltings in [Reference FaltingsFal05, § 5], is to find the condition ‘??’.
$p$-adic non-abelian Hodge theory, raised by Faltings in [Reference FaltingsFal05, § 5], is to find the condition ‘??’.
Question 1.6 Which Higgs bundles on ![]() $X$ correspond to continuous representations of
$X$ correspond to continuous representations of ![]() $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ under the
$\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ under the ![]() $p$-adic non-abelian Hodge correspondence (5)?
$p$-adic non-abelian Hodge correspondence (5)?
In the case of vanishing Higgs field, this question had been studied by Deninger and Werner [Reference Deninger and WernerDW05b, Reference Deninger and WernerDW20] prior to Faltings’ article. Based on their work, Xu has recently made progress on Question 1.6 in the case of curves by identifying a condition for Higgs bundles to be ‘potentially Deninger–Werner’, from which he is able to construct a functor to representations [Reference XuXu22]. This raises the question if this condition has a more classical description that can be used in practice to see whether a Higgs bundle is ‘potentially Deninger–Werner.’
The construction of Deninger–Werner has been extended to the rigid analytic setup by Würthen [Reference WürthenWür23, § 3], whose results suggest that in the special case of vanishing Higgs field, pro-finite-étale vector bundles give the correct subcategory of Higgs bundles. Here a vector bundle is called pro-finite-étale if it becomes trivial on a pro-finite-étale cover in Scholze's pro-étale site [Reference ScholzeSch13] (we note that this is strictly stronger than being trivialised by a finite étale cover). Such vector bundles were further studied in [Reference Mann and WernerMW23]. We showed in [Reference HeuerHeu22b, § 5] that the pro-finite-étale condition also gives the correct category for all Higgs bundles in rank one, namely we constructed an equivalence as in (4) where the left-hand side consist of continuous characters and the right-hand side of Higgs line bundle whose underlying line bundle is pro-finite-étale. In [Reference Heuer, Mann and WernerHMW23], we deduced that on abelian varieties, the answer to Question 1.6 is given by pro-finite-étale Higgs bundles also in higher rank.
However, these results in turn raise the question how pro-finite-étale vector bundles can be characterised more classically, as it is a priori difficult to verify that a given vector bundle is pro-finite-étale. In [Reference HeuerHeu22b, § 5], we characterised pro-finite-étale line bundles as those admitting a reduction of structure group to a certain subsheaf ![]() $\mathbb {G}_m^{\mathrm {tt}}\subseteq \mathbb {G}_m$, but we left it open how such line bundles can be described more concretely, e.g. in terms of the Picard variety.
$\mathbb {G}_m^{\mathrm {tt}}\subseteq \mathbb {G}_m$, but we left it open how such line bundles can be described more concretely, e.g. in terms of the Picard variety.
Theorem 1.1 now gives a fully satisfactory answer to this question, thus to Question 1.6, for line bundles on any smooth proper rigid space. One reason why we think this description is the ‘correct’ one is that it is geometric, i.e. it can be phrased in terms of moduli spaces, opening up a completely new possibility for a geometric formulation of the ![]() $p$-adic Simpson correspondence: we believe that Theorem 1.3 stands a chance of being generalised to higher rank, as we will explore further in [Reference HeuerHeu22c]. Moreover, this suggests that a moduli-theoretic approach to non-abelian Hodge theory may help answer Question 1.6 in general.
$p$-adic Simpson correspondence: we believe that Theorem 1.3 stands a chance of being generalised to higher rank, as we will explore further in [Reference HeuerHeu22c]. Moreover, this suggests that a moduli-theoretic approach to non-abelian Hodge theory may help answer Question 1.6 in general.
1.3 A new geometric approach via diamantine Picard functors
We now elaborate on our strategy to prove Theorems 1.1–1.3, as well as on the construction of the moduli spaces, which yields additional results of independent interest.
A crucial new technical ingredient to this article are the diamantine Picard functors introduced for this purpose in [Reference HeuerHeu21a]: to motivate this, let us first mention that we show that a line bundle ![]() $L$ on
$L$ on ![]() $X$ is pro-finite-étale if and only if it extends to a line bundle on the adic space
$X$ is pro-finite-étale if and only if it extends to a line bundle on the adic space ![]() $X\times \underline {\widehat {\mathbb {Z}}}$ whose specialisation at each
$X\times \underline {\widehat {\mathbb {Z}}}$ whose specialisation at each ![]() $n\in \mathbb {Z}\subseteq \widehat {\mathbb {Z}}$ is isomorphic to
$n\in \mathbb {Z}\subseteq \widehat {\mathbb {Z}}$ is isomorphic to ![]() $L^n$. Here
$L^n$. Here ![]() $\underline {\widehat {\mathbb {Z}}}$ denotes the adic space over
$\underline {\widehat {\mathbb {Z}}}$ denotes the adic space over ![]() $\operatorname {Spa}(K)$ which represents the
$\operatorname {Spa}(K)$ which represents the ![]() $v$-sheaf
$v$-sheaf ![]() $\varprojlim _{N\in \mathbb {N}} \underline {\mathbb {Z}/N\mathbb {Z}}$ over
$\varprojlim _{N\in \mathbb {N}} \underline {\mathbb {Z}/N\mathbb {Z}}$ over ![]() $K$.
$K$.
We would like to say that this induces a morphism of adic spaces from ![]() $\underline {\widehat {\mathbb {Z}}}$ to the rigid Picard variety of
$\underline {\widehat {\mathbb {Z}}}$ to the rigid Picard variety of ![]() $X$. However,
$X$. However, ![]() $\underline {\widehat {\mathbb {Z}}}$ is no longer a rigid space, rather it is perfectoid. We therefore use the diamantine Picard functor
$\underline {\widehat {\mathbb {Z}}}$ is no longer a rigid space, rather it is perfectoid. We therefore use the diamantine Picard functor ![]() $\mathbf {Pic}_{X}$ defined on perfectoid test objects. More precisely, according to (6), there are two different such functors, one for étale line bundles, denoted by
$\mathbf {Pic}_{X}$ defined on perfectoid test objects. More precisely, according to (6), there are two different such functors, one for étale line bundles, denoted by ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$, the other for
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$, the other for ![]() $v$-line bundles, denoted by
$v$-line bundles, denoted by ![]() $\mathbf {Pic}_{X,v}$. Explicitly, for
$\mathbf {Pic}_{X,v}$. Explicitly, for ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$,
$\tau \in \{{\mathrm {\acute {e}t}},v\}$,
In order to characterise maps to ![]() $\mathbf {Pic}_{X,\tau }$ that ‘extend
$\mathbf {Pic}_{X,\tau }$ that ‘extend ![]() ${\widehat {\mathbb {Z}}}$-linearly’ as previously, we now define the following.
${\widehat {\mathbb {Z}}}$-linearly’ as previously, we now define the following.
Definition 1.7 For any ![]() $v$-sheaf
$v$-sheaf ![]() $F$ on
$F$ on ![]() $\operatorname {Perf}_K$, the topologically torsion subsheaf
$\operatorname {Perf}_K$, the topologically torsion subsheaf ![]() $F^\mathrm {tt}\subseteq F$ is the sheaf-theoretic image of the map
$F^\mathrm {tt}\subseteq F$ is the sheaf-theoretic image of the map ![]() $\underline {\mathrm {Hom}}(\underline {\widehat {\mathbb {Z}}},F)\to F$ given by evaluation at
$\underline {\mathrm {Hom}}(\underline {\widehat {\mathbb {Z}}},F)\to F$ given by evaluation at ![]() $1\in {\widehat {\mathbb {Z}}}$.
$1\in {\widehat {\mathbb {Z}}}$.
We give a more classical description of ![]() $F^\mathrm {tt}$ when
$F^\mathrm {tt}$ when ![]() $F$ is a rigid group: for example, the aforementioned topologically torsion subsheaf
$F$ is a rigid group: for example, the aforementioned topologically torsion subsheaf ![]() $\mathbb {G}_m^\mathrm {tt}\subseteq \mathbb {G}_m$ can be shown to be represented by the open subgroup generated by the open unit disc around
$\mathbb {G}_m^\mathrm {tt}\subseteq \mathbb {G}_m$ can be shown to be represented by the open subgroup generated by the open unit disc around ![]() $1$ and the roots of unity.
$1$ and the roots of unity.
These definitions, combined with a systematic study of topologically torsion subsheaves, allow us to give a much more conceptual characterisation of pro-finite-étale line bundles than that we gave previously in [Reference HeuerHeu22b, Theorem 5.7.3]: namely, in the category of diamonds, there is a universal pro-finite-étale cover ![]() $\widetilde X\to X$, a pro-finite-étale torsor under
$\widetilde X\to X$, a pro-finite-étale torsor under ![]() $\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$. The following result now describes which line bundles are trivialised by pro-finite-étale covers, or equivalently by
$\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$. The following result now describes which line bundles are trivialised by pro-finite-étale covers, or equivalently by ![]() $\widetilde X$ and, thus, give rise to
$\widetilde X$ and, thus, give rise to ![]() $p$-adic characters.
$p$-adic characters.
Theorem 1.8 (Theorem 3.6)
Let ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$. There is a short exact sequence of sheaves
$\tau \in \{{\mathrm {\acute {e}t}},v\}$. There is a short exact sequence of sheaves
on ![]() $\operatorname {Perf}_{K,\tau }$. The Cartan–Leray sequence of
$\operatorname {Perf}_{K,\tau }$. The Cartan–Leray sequence of ![]() $\widetilde X\to X$ thus induces a canonical isomorphism
$\widetilde X\to X$ thus induces a canonical isomorphism
Here we crucially use that ![]() $\mathbf {Pic}_{X,\tau }$ is defined on perfectoid test objects such as
$\mathbf {Pic}_{X,\tau }$ is defined on perfectoid test objects such as ![]() $\underline {\widehat {\mathbb {Z}}}$. On
$\underline {\widehat {\mathbb {Z}}}$. On ![]() $K$-points, we deduce that the line bundles on
$K$-points, we deduce that the line bundles on ![]() $X$ trivialised by
$X$ trivialised by ![]() $\widetilde X$ are given by
$\widetilde X$ are given by ![]() $\mathbf {Pic}^{\mathrm {tt}}_{X,{\mathrm {\acute {e}t}}}(K)=\operatorname {Pic}(X)^\mathrm {tt}$, i.e. those classes
$\mathbf {Pic}^{\mathrm {tt}}_{X,{\mathrm {\acute {e}t}}}(K)=\operatorname {Pic}(X)^\mathrm {tt}$, i.e. those classes ![]() $L$ in the topological group
$L$ in the topological group ![]() $\operatorname {Pic}(X)$ for which
$\operatorname {Pic}(X)$ for which ![]() $L^{n!}\to 1$ for
$L^{n!}\to 1$ for ![]() $n\to \infty$. To deduce Theorem 1.1, we show that for projective
$n\to \infty$. To deduce Theorem 1.1, we show that for projective ![]() $X$ over
$X$ over ![]() $\mathbb {C}_p$, we in fact have
$\mathbb {C}_p$, we in fact have
where ![]() $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}^{\tau }(X)$ is the group of line bundles with torsion Néron–Severi class. These are precisely the line bundles with vanishing (rational) Chern classes. To see (7), we use that
$\operatorname {Pic}_{{\mathrm {\acute {e}t}}}^{\tau }(X)$ is the group of line bundles with torsion Néron–Severi class. These are precisely the line bundles with vanishing (rational) Chern classes. To see (7), we use that ![]() $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is represented by an abelian variety
$\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is represented by an abelian variety ![]() $A$ over
$A$ over ![]() $\mathbb {C}_p$, and we show that
$\mathbb {C}_p$, and we show that ![]() $A^\mathrm {tt}(\mathbb {C}_p)=A(\mathbb {C}_p)$. For this, we use that the residue field of
$A^\mathrm {tt}(\mathbb {C}_p)=A(\mathbb {C}_p)$. For this, we use that the residue field of ![]() $\mathbb {C}_p$ is a union of finite fields, and that
$\mathbb {C}_p$ is a union of finite fields, and that ![]() $v_p(\mathbb {C}_p)=\mathbb {Q}$.
$v_p(\mathbb {C}_p)=\mathbb {Q}$.
On the other hand, this shows that finding the correct condition ‘??’ in (4) is very subtle.
Remark 1.9 Over any extension ![]() $K\supsetneq \mathbb {C}_p$, the inclusion
$K\supsetneq \mathbb {C}_p$, the inclusion ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)\subseteq \operatorname {Pic}^{\tau }(X)$ can become strict: if
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)\subseteq \operatorname {Pic}^{\tau }(X)$ can become strict: if ![]() $X$ is a curve of good reduction over
$X$ is a curve of good reduction over ![]() $K$ with Jacobian
$K$ with Jacobian ![]() $J=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$, then
$J=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$, then ![]() $J(K)^\mathrm {tt}$ are precisely those points of
$J(K)^\mathrm {tt}$ are precisely those points of ![]() $J(K)$ that reduce to a torsion point on the special fibre. This special case of curves with good reduction is implicit in Faltings’ discussion in [Reference FaltingsFal05, p. 856].
$J(K)$ that reduce to a torsion point on the special fibre. This special case of curves with good reduction is implicit in Faltings’ discussion in [Reference FaltingsFal05, p. 856].
Remark 1.10 Already over ![]() $\mathbb {C}_p$, the equality (7) and, thus, the first part of Theorem 1.1 can become false if we only assume that
$\mathbb {C}_p$, the equality (7) and, thus, the first part of Theorem 1.1 can become false if we only assume that ![]() $X$ is proper rather than projective, since
$X$ is proper rather than projective, since ![]() $\mathbf {Pic}^0_X$ is then no longer necessarily an abelian variety: for example, if
$\mathbf {Pic}^0_X$ is then no longer necessarily an abelian variety: for example, if ![]() $X$ is a Hopf variety, then
$X$ is a Hopf variety, then ![]() $\mathbf {Pic}_X=\mathbb {G}_m$ (see [Reference Hartl and LütkebohmertHL00, Remark 0.1.3]). However, we have
$\mathbf {Pic}_X=\mathbb {G}_m$ (see [Reference Hartl and LütkebohmertHL00, Remark 0.1.3]). However, we have ![]() $\mathbb {G}_m^\mathrm {tt}(\mathbb {C}_p)=\mathcal {O}_{\mathbb {C}_p}^\times \subsetneq \mathbb {C}_p^\times =\mathbb {G}_m(\mathbb {C}_p)$.
$\mathbb {G}_m^\mathrm {tt}(\mathbb {C}_p)=\mathcal {O}_{\mathbb {C}_p}^\times \subsetneq \mathbb {C}_p^\times =\mathbb {G}_m(\mathbb {C}_p)$.
Remark 1.11 In terms of rigid spaces in the sense of Tate, the map ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\hookrightarrow \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ may by (7) be an open bijective map that is no longer surjective when passing to adic spaces.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\hookrightarrow \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ may by (7) be an open bijective map that is no longer surjective when passing to adic spaces.
From this perspective, it arguably feels like a coincidence that ‘vanishing Chern classes’ are the correct answer to Question 1.6 for line bundles on projective varieties over ![]() $\mathbb {C}_p$. Instead, as already in rank one the cleanest formulation of the condition of ‘topologically torsion’ requires the geometric structure of
$\mathbb {C}_p$. Instead, as already in rank one the cleanest formulation of the condition of ‘topologically torsion’ requires the geometric structure of ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ as a rigid space, this suggests that in general, analytic moduli spaces may be necessary to answer Question 1.6 over general fields.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ as a rigid space, this suggests that in general, analytic moduli spaces may be necessary to answer Question 1.6 over general fields.
Structure of the article
In § 2 we introduce the notion of topologically torsion subsheaves and study these systematically. In particular, with an eye towards applications to Picard varieties, we study topologically torsion subsheaves of rigid groups.
In § 3 we introduce the ![]() $p$-adic character variety and explain why this is isomorphic to the topologically torsion subsheaf of the
$p$-adic character variety and explain why this is isomorphic to the topologically torsion subsheaf of the ![]() $v$-Picard functor, that is we prove Theorem 1.8.
$v$-Picard functor, that is we prove Theorem 1.8.
In § 4 we prove Theorem 1.2. We also give the application to Deninger and Werner's map by constructing a generalised Weil pairing. As a further application, we comment on applications to the study of the structure of rigid Picard functors.
In § 5, we prove the étale comparison of Betti and Dolbeault moduli spaces, Theorem 1.3, as well as several related comparison isomorphisms.
Notation
Throughout, let ![]() $K$ be a (complete) non-archimedean field of residue characteristic
$K$ be a (complete) non-archimedean field of residue characteristic ![]() $p$. We denote by
$p$. We denote by ![]() $\mathcal {O}_K=K^{\circ }$ the ring of integers consisting of power-bounded elements. More generally, we denote by
$\mathcal {O}_K=K^{\circ }$ the ring of integers consisting of power-bounded elements. More generally, we denote by ![]() $K^+\subseteq K$ any ring of integral elements. Let
$K^+\subseteq K$ any ring of integral elements. Let ![]() $\mathfrak {m}\subseteq K^+$ be the maximal ideal, and
$\mathfrak {m}\subseteq K^+$ be the maximal ideal, and ![]() $\Gamma$ the value group. From § 3 on,
$\Gamma$ the value group. From § 3 on, ![]() $K$ will be a perfectoid field extension of
$K$ will be a perfectoid field extension of ![]() $\mathbb {Q}_p$ in the sense of [Reference ScholzeSch12], and we then use almost mathematics with respect to
$\mathbb {Q}_p$ in the sense of [Reference ScholzeSch12], and we then use almost mathematics with respect to ![]() $\mathfrak {m}$.
$\mathfrak {m}$.
By a rigid space over ![]() $(K,K^+)$ we mean an adic space locally of topologically finite type over
$(K,K^+)$ we mean an adic space locally of topologically finite type over ![]() $\operatorname {Spa}(K,K^+)$. In the following, we often abbreviate
$\operatorname {Spa}(K,K^+)$. In the following, we often abbreviate ![]() $\operatorname {Spa}(K,K^+)$ by
$\operatorname {Spa}(K,K^+)$ by ![]() $\operatorname {Spa}(K)$ when the ring
$\operatorname {Spa}(K)$ when the ring ![]() $K^+$ is clear from the context. In particular, we then denote by
$K^+$ is clear from the context. In particular, we then denote by ![]() $\mathrm {SmRig}_{K}$ the category of smooth rigid spaces over
$\mathrm {SmRig}_{K}$ the category of smooth rigid spaces over ![]() $\operatorname {Spa}(K,K^+)$, by
$\operatorname {Spa}(K,K^+)$, by ![]() $\operatorname {Perf}_{K}$ the category of perfectoid spaces over
$\operatorname {Perf}_{K}$ the category of perfectoid spaces over ![]() $(K,K^+)$, and by
$(K,K^+)$, and by ![]() $\mathrm {LSD}_{K}$ the category of locally spatial diamonds over
$\mathrm {LSD}_{K}$ the category of locally spatial diamonds over ![]() $\mathrm {Spd}(K,K^+)$ in the sense of [Reference ScholzeSch18, § 11]. More generally, for any rigid space
$\mathrm {Spd}(K,K^+)$ in the sense of [Reference ScholzeSch18, § 11]. More generally, for any rigid space ![]() $X$ we denote by
$X$ we denote by ![]() $\mathrm {SmRig}_{X}$ the slice category of rigid spaces over
$\mathrm {SmRig}_{X}$ the slice category of rigid spaces over ![]() $X$. In accordance with this notation, for any two rigid spaces
$X$. In accordance with this notation, for any two rigid spaces ![]() $X$ and
$X$ and ![]() $Y$ over
$Y$ over ![]() $K$, we also write
$K$, we also write ![]() $Y_X:=Y\times _KX$. Similarly for the other categories.
$Y_X:=Y\times _KX$. Similarly for the other categories.
We denote by ![]() $\mathbb {B}^d$ the rigid unit polydisc of dimension
$\mathbb {B}^d$ the rigid unit polydisc of dimension ![]() $d$ over
$d$ over ![]() $(K,K^+)$, by
$(K,K^+)$, by ![]() $\mathbb {G}_m$ the rigid torus over
$\mathbb {G}_m$ the rigid torus over ![]() $(K,K^+)$ defined as the analytification of the algebraic torus, and similarly by
$(K,K^+)$ defined as the analytification of the algebraic torus, and similarly by ![]() $\mathbb {G}_a$ the rigid affine line with its additive structure. We denote by
$\mathbb {G}_a$ the rigid affine line with its additive structure. We denote by ![]() $\widehat {\mathbb {G}}_m$ the open unit disc around
$\widehat {\mathbb {G}}_m$ the open unit disc around ![]() $1$ in
$1$ in ![]() $\mathbb {G}_m$. These are all examples of rigid groups: by a rigid group we mean a group object in the category of rigid spaces over
$\mathbb {G}_m$. These are all examples of rigid groups: by a rigid group we mean a group object in the category of rigid spaces over ![]() $(K,K^+)$. In this article, we always assume this to be commutative without further mention. Similarly for adic groups.
$(K,K^+)$. In this article, we always assume this to be commutative without further mention. Similarly for adic groups.
There is a fully faithful diamondification functor ![]() $\mathrm {SmRig}_{K}\hookrightarrow \mathrm {LSD}_{K}$,
$\mathrm {SmRig}_{K}\hookrightarrow \mathrm {LSD}_{K}$, ![]() $X\mapsto X^\diamondsuit$, see [Reference ScholzeSch18, § 15.6], and we shall freely identify
$X\mapsto X^\diamondsuit$, see [Reference ScholzeSch18, § 15.6], and we shall freely identify ![]() $X$ with its image under this functor. In particular, we often drop the diamond
$X$ with its image under this functor. In particular, we often drop the diamond ![]() $-^\diamondsuit$ from notation. For example, we just write
$-^\diamondsuit$ from notation. For example, we just write ![]() $X_v$ for the
$X_v$ for the ![]() $v$-site
$v$-site ![]() $X^\diamondsuit _v$.
$X^\diamondsuit _v$.
For any formal scheme ![]() $\mathfrak S$ over
$\mathfrak S$ over ![]() $\operatorname {Spf}(K^+)$, we denote by
$\operatorname {Spf}(K^+)$, we denote by ![]() $\mathfrak S^\mathrm {ad}_{\eta }:=\mathfrak S^\mathrm {ad}\times _{\operatorname {Spa}(K^+,K^+)}\operatorname {Spa}(K,K^+)$ the adic generic fibre in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 2.2]. If
$\mathfrak S^\mathrm {ad}_{\eta }:=\mathfrak S^\mathrm {ad}\times _{\operatorname {Spa}(K^+,K^+)}\operatorname {Spa}(K,K^+)$ the adic generic fibre in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 2.2]. If ![]() $\mathfrak S$ is locally of topologically finite type over
$\mathfrak S$ is locally of topologically finite type over ![]() $\operatorname {Spf}(K^+)$, this is a rigid space over
$\operatorname {Spf}(K^+)$, this is a rigid space over ![]() $\operatorname {Spa}(K,K^+)$ in the above sense. We say that a rigid space has good reduction if it is isomorphic to
$\operatorname {Spa}(K,K^+)$ in the above sense. We say that a rigid space has good reduction if it is isomorphic to ![]() $\mathfrak S^\mathrm {ad}_{\eta }$ for some formal scheme
$\mathfrak S^\mathrm {ad}_{\eta }$ for some formal scheme ![]() $\mathfrak S$ that is smooth over
$\mathfrak S$ that is smooth over ![]() $\operatorname {Spf}(K^+)$.
$\operatorname {Spf}(K^+)$.
2. The topologically torsion subsheaf
The purpose of this section is to introduce a new technical device that plays a key role in this article: the topologically torsion subgroup of a ![]() $v$-sheaf.
$v$-sheaf.
2.1 Locally profinite  $v$-sheaves
$v$-sheaves
We start by recalling the definition of locally constant sheaves, and record some basic lemmas for later reference. For this it is beneficial to work in greater generality than in the introduction, over general non-archimedean fields ![]() $(K,K^+)$. We first adapt [Reference ScholzeSch18, Example 11.12] to this setting.
$(K,K^+)$. We first adapt [Reference ScholzeSch18, Example 11.12] to this setting.
Definition 2.1 Let ![]() $X$ be an adic space over
$X$ be an adic space over ![]() $\operatorname {Spa}(K,K^+)$. Then we have a natural injective map
$\operatorname {Spa}(K,K^+)$. Then we have a natural injective map ![]() $X(K,K^+)\hookrightarrow |X|$ sending a morphism
$X(K,K^+)\hookrightarrow |X|$ sending a morphism ![]() $x:\operatorname {Spa}(K,K^+)\to X$ to the image of the unique closed point under
$x:\operatorname {Spa}(K,K^+)\to X$ to the image of the unique closed point under ![]() $x$. We use this to endow
$x$. We use this to endow ![]() $X(K,K^+)$ with the subspace topology.
$X(K,K^+)$ with the subspace topology.
Definition 2.2 For any locally profinite set ![]() $G$ we define a locally profinite
$G$ we define a locally profinite ![]() $v$-sheaf
$v$-sheaf ![]() $\underline {G}$.
$\underline {G}$.
(i) If
 $G$ is a discrete topological space, then we associate to
$G$ is a discrete topological space, then we associate to  $G$ the locally constant sheaf
$G$ the locally constant sheaf  $\underline {G}$ on
$\underline {G}$ on  $\operatorname {Perf}_{K,v}$ that is the sheafification of the presheaf
$\operatorname {Perf}_{K,v}$ that is the sheafification of the presheaf  $X\mapsto G$. This is represented by the adic space
$X\mapsto G$. This is represented by the adic space  $\sqcup _G\operatorname {Spa}(K,K^+)$.
$\sqcup _G\operatorname {Spa}(K,K^+)$.(ii) If
 $G=\varprojlim _{i\in I} G_i$ is a profinite set where the
$G=\varprojlim _{i\in I} G_i$ is a profinite set where the  $G_i$ are finite sets considered as discrete topological spaces, then we associate to
$G_i$ are finite sets considered as discrete topological spaces, then we associate to  $G$ the
$G$ the  $v$-sheaf of sets
$v$-sheaf of sets  $\underline {G}:=\textstyle \varprojlim _{i\in I} \underline {G_i}$. By [Reference Scholze and WeinsteinSW13, Proposition 2.4.5], this is represented by the affinoid adic space
This is sheafy as by Lemma 2.3, any cover of
$\underline {G}:=\textstyle \varprojlim _{i\in I} \underline {G_i}$. By [Reference Scholze and WeinsteinSW13, Proposition 2.4.5], this is represented by the affinoid adic space
This is sheafy as by Lemma 2.3, any cover of \[ \underline{G}=\operatorname{Spa}(\operatorname{Map}_{{\operatorname{cts}}}(G,K),\operatorname{Map}_{{\operatorname{cts}}}(G,K^+))\sim \textstyle\varprojlim_{i\in I}\underline{G_i}. \]
\[ \underline{G}=\operatorname{Spa}(\operatorname{Map}_{{\operatorname{cts}}}(G,K),\operatorname{Map}_{{\operatorname{cts}}}(G,K^+))\sim \textstyle\varprojlim_{i\in I}\underline{G_i}. \]
 $|\underline {G}|$ admits a disjoint refinement.
$|\underline {G}|$ admits a disjoint refinement.(iii) In both the profinite and the discrete case, we have a natural homeomorphism
 $|\underline {G}|=|\operatorname {Spa}(K,K^+)|\times G$ by Lemma 2.3. Simultaneously generalising both parts (i) and (ii), we can therefore extend the definition to locally profinite sets
$|\underline {G}|=|\operatorname {Spa}(K,K^+)|\times G$ by Lemma 2.3. Simultaneously generalising both parts (i) and (ii), we can therefore extend the definition to locally profinite sets  $G$ by glueing.
$G$ by glueing.
If ![]() $G$ is a locally profinite group, then
$G$ is a locally profinite group, then ![]() $\underline {G}$ inherits the structure of an adic group: this is immediate from the observation that the functor
$\underline {G}$ inherits the structure of an adic group: this is immediate from the observation that the functor ![]() $\underline {\phantom {-}}$ commutes with finite products.
$\underline {\phantom {-}}$ commutes with finite products.
The following lemma was used in the definition.
Lemma 2.3 Let ![]() $G$ be a locally profinite set, then we have natural homeomorphisms
$G$ be a locally profinite set, then we have natural homeomorphisms
Proof. We can reduce to profinite sets ![]() $G=\varprojlim G_i$, for which we have
$G=\varprojlim G_i$, for which we have
This reduces us to the case of finite sets, where the statements are clear.
Lemma 2.4 Let ![]() $H$ be a locally profinite set, and let
$H$ be a locally profinite set, and let ![]() $G$ be any adic space over
$G$ be any adic space over ![]() $(K,K^+)$. Then
$(K,K^+)$. Then
functorially in ![]() $H$ and
$H$ and ![]() $G$. If
$G$. If ![]() $H$ is a locally profinite group and
$H$ is a locally profinite group and ![]() $G$ is an adic group for which
$G$ is an adic group for which ![]() $G(K,K^+)$ is a topological group, this induces
$G(K,K^+)$ is a topological group, this induces
Proof. The second part of the lemma will follow from the first by functoriality.
For the first part, evaluation on ![]() $(K,K^+)$-points defines by Lemma 2.3 a morphism
$(K,K^+)$-points defines by Lemma 2.3 a morphism
Here continuity is clear as ![]() $G(K,K^+)$ has the subspace topology of
$G(K,K^+)$ has the subspace topology of ![]() $|G|$, and
$|G|$, and ![]() $H$ that of
$H$ that of ![]() $|\underline {H}|$.
$|\underline {H}|$.
The map is clearly functorial in ![]() $H$ and
$H$ and ![]() $G$. To see that it is a bijection, we can therefore by glueing reduce to the case that
$G$. To see that it is a bijection, we can therefore by glueing reduce to the case that ![]() $H$ is profinite and
$H$ is profinite and ![]() $G$ is affinoid.
$G$ is affinoid.
Given a continuous map ![]() $\varphi :H\to G(K,K^+)$, there is an associated map of
$\varphi :H\to G(K,K^+)$, there is an associated map of ![]() $K^+$-algebras
$K^+$-algebras
that interprets ![]() $f\in \mathcal {O}^+(G)$ as a map
$f\in \mathcal {O}^+(G)$ as a map ![]() $f:G\to \mathbb {B}^1:=\operatorname {Spa}(K\langle X\rangle,K^+\langle X\rangle )$ and sends it to
$f:G\to \mathbb {B}^1:=\operatorname {Spa}(K\langle X\rangle,K^+\langle X\rangle )$ and sends it to
This is clearly functorial in ![]() $H$ and
$H$ and ![]() $G$. We have thus defined natural morphisms
$G$. We have thus defined natural morphisms
It is now formal from the functoriality that these compose to the identity: we can first reduce to the case ![]() $H=\{x\}$ and then to
$H=\{x\}$ and then to ![]() $G=\operatorname {Spa}(K,K^+)$, for which the statement is clear.
$G=\operatorname {Spa}(K,K^+)$, for which the statement is clear.
It remains to prove that the second map in the above composition is injective. For this, consider the topological space ![]() $H'$ whose underlying set is that of
$H'$ whose underlying set is that of ![]() $H$, but endowed with the discrete topology. There is by functoriality a natural map
$H$, but endowed with the discrete topology. There is by functoriality a natural map ![]() $\underline {H'}\to \underline {H}$, which on global sections
$\underline {H'}\to \underline {H}$, which on global sections
is injective. Consequently, so is the pullback ![]() $\operatorname {Map}(\underline {H},G)\to \operatorname {Map}(\underline {H},G)$ for affinoid
$\operatorname {Map}(\underline {H},G)\to \operatorname {Map}(\underline {H},G)$ for affinoid ![]() $G$. We are therefore reduced to the case of discrete
$G$. We are therefore reduced to the case of discrete ![]() $H$, where the lemma is clear.
$H$, where the lemma is clear.
2.2 Topologically torsion sheaves
From now on, let ![]() $K$ be a perfectoid field, and
$K$ be a perfectoid field, and ![]() $K^+\subseteq K$ a ring of integral elements as before. We work in the category of
$K^+\subseteq K$ a ring of integral elements as before. We work in the category of ![]() $v$-sheaves on
$v$-sheaves on ![]() $\operatorname {Perf}_K$. For a locally profinite set
$\operatorname {Perf}_K$. For a locally profinite set ![]() $G$, to simplify notation, from now on we also denote just by
$G$, to simplify notation, from now on we also denote just by ![]() $G$ the pro-constant
$G$ the pro-constant ![]() $v$-sheaf
$v$-sheaf ![]() $\underline {G}$ from Definition 2.2 when it is clear from the context what is meant.
$\underline {G}$ from Definition 2.2 when it is clear from the context what is meant.
Definition 2.5 Let ![]() $F$ be an abelian
$F$ be an abelian ![]() $v$-sheaf on
$v$-sheaf on ![]() $\operatorname {Perf}_K$.
$\operatorname {Perf}_K$.
(i) Consider the internal Hom sheaf
 $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F)$ where
is the profinite sheaf of Definition 2.2. There is a natural evaluation map at
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F)$ where
is the profinite sheaf of Definition 2.2. There is a natural evaluation map at \[ {\widehat{\mathbb{Z}}}:=\underline{{\widehat{\mathbb{Z}}}}=\varprojlim_{N\in\mathbb{N}} \underline{\mathbb{Z}/N\mathbb{Z}} \]
\[ {\widehat{\mathbb{Z}}}:=\underline{{\widehat{\mathbb{Z}}}}=\varprojlim_{N\in\mathbb{N}} \underline{\mathbb{Z}/N\mathbb{Z}} \]
 $1\in {\widehat {\mathbb {Z}}}$:
We define the topologically torsion subsheaf of
$1\in {\widehat {\mathbb {Z}}}$:
We define the topologically torsion subsheaf of \[ \mathrm{e}_F:\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},F)\to F. \]
\[ \mathrm{e}_F:\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},F)\to F. \]
 $F$ to be the abelian subsheaf
$F$ to be the abelian subsheaf
 \[ F^\mathrm{tt}=\mathrm{im}(\mathrm{e}_F)\subseteq F. \]
\[ F^\mathrm{tt}=\mathrm{im}(\mathrm{e}_F)\subseteq F. \]
(ii) We say that a
 $v$-sheaf
$v$-sheaf  $F$ is topologically torsion if
$F$ is topologically torsion if  $F^\mathrm {tt}\to F$ is an isomorphism.
$F^\mathrm {tt}\to F$ is an isomorphism.(iii) We say that
 $F$ is strongly topologically torsion if already
$F$ is strongly topologically torsion if already  $\mathrm e_F$ is an isomorphism.
$\mathrm e_F$ is an isomorphism.(iv) We say that
 $F$ is topologically torsionfree if
$F$ is topologically torsionfree if  $F^\mathrm {tt}=0$.
$F^\mathrm {tt}=0$.
Definition 2.6 We make analogous definitions for the topologically ![]() $p$-torsion subsheaf
$p$-torsion subsheaf
by replacing ![]() ${\widehat {\mathbb {Z}}}$ with
${\widehat {\mathbb {Z}}}$ with ![]() $\mathbb {Z}_p$. Via the natural projection
$\mathbb {Z}_p$. Via the natural projection ![]() ${\widehat {\mathbb {Z}}}\twoheadrightarrow \mathbb {Z}_p$, we see that
${\widehat {\mathbb {Z}}}\twoheadrightarrow \mathbb {Z}_p$, we see that ![]() $F\langle p^\infty \rangle \subseteq F^{\mathrm {tt}}\subseteq F$. In particular, if
$F\langle p^\infty \rangle \subseteq F^{\mathrm {tt}}\subseteq F$. In particular, if ![]() $F$ is topologically
$F$ is topologically ![]() $p$-torsion, it is automatically topologically torsion.
$p$-torsion, it is automatically topologically torsion.
Example 2.7 As we show in § 2.3, for the ![]() $v$-sheaf represented by the rigid group
$v$-sheaf represented by the rigid group ![]() $\mathbb {G}_m$, the sheaf
$\mathbb {G}_m$, the sheaf ![]() $\mathbb {G}_m\langle p^\infty \rangle \subseteq \mathbb {G}_m$ is given by the open unit disc
$\mathbb {G}_m\langle p^\infty \rangle \subseteq \mathbb {G}_m$ is given by the open unit disc ![]() $\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ of radius 1 around 1, and
$\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ of radius 1 around 1, and ![]() $\mathbb {G}_m^\mathrm {tt}$ is the open subgroup given by the translates by all roots of unity
$\mathbb {G}_m^\mathrm {tt}$ is the open subgroup given by the translates by all roots of unity ![]() $\mu _N\subseteq \mathbb {G}_m$ for
$\mu _N\subseteq \mathbb {G}_m$ for ![]() $N\in \mathbb {N}$.
$N\in \mathbb {N}$.
Remark 2.8 The construction of ![]() $F\langle p^\infty \rangle$ may be seen as an analogue for
$F\langle p^\infty \rangle$ may be seen as an analogue for ![]() $v$-sheaves of a related construction by Fargues [Reference FarguesFar19, §§ 1.6 and 2.4] for rigid groups in characteristic zero which gives rise to analytic
$v$-sheaves of a related construction by Fargues [Reference FarguesFar19, §§ 1.6 and 2.4] for rigid groups in characteristic zero which gives rise to analytic ![]() $p$-divisible groups in the sense of Fargues, cf. § 2.3. This is what motivates our notation.
$p$-divisible groups in the sense of Fargues, cf. § 2.3. This is what motivates our notation.
Lemma 2.9 For any abelian ![]() $v$-sheaf
$v$-sheaf ![]() $F$, the sheaf
$F$, the sheaf ![]() $F^\mathrm {tt}$ is itself topologically torsion. Sending
$F^\mathrm {tt}$ is itself topologically torsion. Sending ![]() $F\mapsto F^\mathrm {tt}$ thus defines a right-adjoint to the forgetful functor from topologically torsion abelian
$F\mapsto F^\mathrm {tt}$ thus defines a right-adjoint to the forgetful functor from topologically torsion abelian ![]() $v$-sheaves to abelian
$v$-sheaves to abelian ![]() $v$-sheaves. The analogous statements hold for
$v$-sheaves. The analogous statements hold for ![]() $F\langle p^\infty \rangle$.
$F\langle p^\infty \rangle$.
Proof. It suffices to show that the natural map ![]() $(F^{\mathrm {tt}})^\mathrm {tt}\to F^{\mathrm {tt}}$ is an isomorphism. It is then formal that this defines the unit of an adjunction with co-unit given by
$(F^{\mathrm {tt}})^\mathrm {tt}\to F^{\mathrm {tt}}$ is an isomorphism. It is then formal that this defines the unit of an adjunction with co-unit given by ![]() $F^\mathrm {tt}\to F$.
$F^\mathrm {tt}\to F$.
It suffices to show that the map is surjective, for which it suffices to prove that the map ![]() $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F^{\mathrm {tt}})\to F^{\mathrm {tt}}$ is surjective. For this it suffices to prove that the top map in the diagram
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F^{\mathrm {tt}})\to F^{\mathrm {tt}}$ is surjective. For this it suffices to prove that the top map in the diagram

is surjective. This holds because for any perfectoid space ![]() $T$ over
$T$ over ![]() $K$ and any
$K$ and any ![]() $T$-linear homomorphism
$T$-linear homomorphism ![]() $\varphi :{\widehat {\mathbb {Z}}}\times T\to F$, a preimage is given by the map
$\varphi :{\widehat {\mathbb {Z}}}\times T\to F$, a preimage is given by the map ![]() ${\widehat {\mathbb {Z}}}\times {\widehat {\mathbb {Z}}}\times T\to F$ defined by
${\widehat {\mathbb {Z}}}\times {\widehat {\mathbb {Z}}}\times T\to F$ defined by ![]() $(a,b,x)\mapsto \varphi (ab,x)$. Thus,
$(a,b,x)\mapsto \varphi (ab,x)$. Thus, ![]() $F^\mathrm {tt}$ is topologically torsion. The case of
$F^\mathrm {tt}$ is topologically torsion. The case of ![]() $F\langle p^\infty \rangle$ is analogous.
$F\langle p^\infty \rangle$ is analogous.
Example 2.10 The reason why we need both the notion of topologically torsion and strongly topologically torsion sheaves is that each has its advantages and pathologies.
(i) For an example where
 $F\langle p^\infty \rangle \neq \underline {\mathrm {Hom}}(\mathbb {Z}_p,F)$, consider the
$F\langle p^\infty \rangle \neq \underline {\mathrm {Hom}}(\mathbb {Z}_p,F)$, consider the  $v$-sheaf
$v$-sheaf  $F=\mathbb {Z}_p/\mathbb {Z}$ in the exact sequence
One can show that
$F=\mathbb {Z}_p/\mathbb {Z}$ in the exact sequence
One can show that \[ 0\to \mathbb{Z}\to \mathbb{Z}_p\to\mathbb{Z}_p/\mathbb{Z}\to 0. \]
\[ 0\to \mathbb{Z}\to \mathbb{Z}_p\to\mathbb{Z}_p/\mathbb{Z}\to 0. \]
 $\underline {\mathrm {Hom}}(\mathbb {Z}_p,F)=\underline {\mathbb {Q}_p}$ (see [Reference HeuerHeu21c, § 2.3]), but nevertheless
$\underline {\mathrm {Hom}}(\mathbb {Z}_p,F)=\underline {\mathbb {Q}_p}$ (see [Reference HeuerHeu21c, § 2.3]), but nevertheless  $F\langle p^\infty \rangle =F$. This also shows that the category of topologically torsion sheaves is not abelian, that subsheaves of topologically torsion sheaves need not be topologically torsion, and that in contrast to
$F\langle p^\infty \rangle =F$. This also shows that the category of topologically torsion sheaves is not abelian, that subsheaves of topologically torsion sheaves need not be topologically torsion, and that in contrast to  $\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$, the functor
$\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$, the functor  $-\langle p^\infty \rangle$ is neither left-exact nor right-exact.
$-\langle p^\infty \rangle$ is neither left-exact nor right-exact.(ii) On the other hand, the analogue of Lemma 2.9 does not hold for
 $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$, namely
is not an equivalence: indeed, by the Yoneda Lemma and the tensor-hom adjunction this follows from the fact that
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$, namely
is not an equivalence: indeed, by the Yoneda Lemma and the tensor-hom adjunction this follows from the fact that \[ \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},-))\to \operatorname{Hom}({\widehat{\mathbb{Z}}},-) \]
\[ \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},-))\to \operatorname{Hom}({\widehat{\mathbb{Z}}},-) \]
 ${\widehat {\mathbb {Z}}}\to {\widehat {\mathbb {Z}}}\otimes _{\mathbb {Z}}{\widehat {\mathbb {Z}}}$ is not an isomorphism of
${\widehat {\mathbb {Z}}}\to {\widehat {\mathbb {Z}}}\otimes _{\mathbb {Z}}{\widehat {\mathbb {Z}}}$ is not an isomorphism of  $v$-sheaves.
$v$-sheaves.
We show in § 2.3 that such pathologies cannot occur for ![]() $v$-sheaves represented by rigid spaces. However, we first prove some useful lemmas that hold in greater generality.
$v$-sheaves represented by rigid spaces. However, we first prove some useful lemmas that hold in greater generality.
Lemma 2.11
(i) The cokernel of
 $F^\mathrm {tt}\to F$ is torsionfree.
$F^\mathrm {tt}\to F$ is torsionfree.(ii) The cokernel of
 $F\langle p^\infty \rangle \to F$ is
$F\langle p^\infty \rangle \to F$ is  $p$-torsionfree.
$p$-torsionfree.
Proof. The ![]() $v$-sheaf
$v$-sheaf ![]() ${\widehat {\mathbb {Z}}}/\mathbb {Z}$ is uniquely divisible by a snake lemma argument. Thus,
${\widehat {\mathbb {Z}}}/\mathbb {Z}$ is uniquely divisible by a snake lemma argument. Thus, ![]() $\underline {\mathrm {Ext}}^1_v({\widehat {\mathbb {Z}}}/\mathbb {Z},F)$ is also uniquely divisible. The statement follows since we have an exact sequence
$\underline {\mathrm {Ext}}^1_v({\widehat {\mathbb {Z}}}/\mathbb {Z},F)$ is also uniquely divisible. The statement follows since we have an exact sequence
Similarly for the ![]() $v$-sheaf
$v$-sheaf ![]() $\mathbb {Z}_p/\mathbb {Z}$, which is uniquely
$\mathbb {Z}_p/\mathbb {Z}$, which is uniquely ![]() $p$-divisible.
$p$-divisible.
Lemma 2.12 The functors ![]() $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ and
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ and ![]() $\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$ preserve injectives in the category of abelian sheaves on
$\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$ preserve injectives in the category of abelian sheaves on ![]() $\operatorname {Perf}_{K,\tau }$ for
$\operatorname {Perf}_{K,\tau }$ for ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$.
$\tau \in \{{\mathrm {\acute {e}t}},v\}$.
Proof. Let ![]() $F\to G$ be an injection of abelian sheaves on
$F\to G$ be an injection of abelian sheaves on ![]() $\operatorname {Perf}_{K,\tau }$. Let
$\operatorname {Perf}_{K,\tau }$. Let ![]() $Q$ be an injective sheaf on
$Q$ be an injective sheaf on ![]() $\operatorname {Perf}_{K,\tau }$. Then
$\operatorname {Perf}_{K,\tau }$. Then ![]() $F\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}\to G\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}$ is injective as
$F\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}\to G\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}$ is injective as ![]() ${\widehat {\mathbb {Z}}}$ is a torsionfree sheaf and thus flat over
${\widehat {\mathbb {Z}}}$ is a torsionfree sheaf and thus flat over ![]() $\mathbb {Z}$. Hence,
$\mathbb {Z}$. Hence,

is surjective since ![]() $Q$ is injective.
$Q$ is injective.
Lemma 2.13 Let ![]() $F$ be a strongly topologically torsion v-sheaf. Let
$F$ be a strongly topologically torsion v-sheaf. Let ![]() $\pi :X\to \operatorname {Spa}(K,K^+)$ be a locally spatial diamond. Then the evaluation map
$\pi :X\to \operatorname {Spa}(K,K^+)$ be a locally spatial diamond. Then the evaluation map ![]() $\mathrm {e}:\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},R^1\pi _{\tau \ast }F)\to R^1\pi _{\tau \ast }F$ admits a splitting for
$\mathrm {e}:\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},R^1\pi _{\tau \ast }F)\to R^1\pi _{\tau \ast }F$ admits a splitting for ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$. In particular,
$\tau \in \{{\mathrm {\acute {e}t}},v\}$. In particular, ![]() $R^1\pi _{v\ast }F$ is topologically torsion.
$R^1\pi _{v\ast }F$ is topologically torsion.
Proof. There is a natural equivalence of functors on sheaves ![]() $\pi _{\tau \ast }\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\pi _{\tau \ast }-)$. By Lemma 2.12 this induces Grothendieck spectral sequences which yield a natural map
$\pi _{\tau \ast }\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\pi _{\tau \ast }-)$. By Lemma 2.12 this induces Grothendieck spectral sequences which yield a natural map
Since this equivalence is also natural in the first entry ![]() ${\widehat {\mathbb {Z}}}$, it is compatible with the evaluation map, which means that the above map defines the desired splitting.
${\widehat {\mathbb {Z}}}$, it is compatible with the evaluation map, which means that the above map defines the desired splitting.
2.3 Topologically torsion subgroups of rigid groups
Assume from now on that ![]() $K$ is a perfectoid field extension of
$K$ is a perfectoid field extension of ![]() $\mathbb {Q}_p$, and that the
$\mathbb {Q}_p$, and that the ![]() $v$-sheaf
$v$-sheaf ![]() $F$ is represented by a rigid group
$F$ is represented by a rigid group ![]() $G$. We recall that by our conventions, this means a group object in the category of adic space of locally finite presentation over
$G$. We recall that by our conventions, this means a group object in the category of adic space of locally finite presentation over ![]() $\operatorname {Spa}(K,K^+)$. In this case, the topologically
$\operatorname {Spa}(K,K^+)$. In this case, the topologically ![]() $p$-torsion subgroup
$p$-torsion subgroup ![]() $G\langle p^\infty \rangle$ can be described explicitly, and is often represented by an analytic
$G\langle p^\infty \rangle$ can be described explicitly, and is often represented by an analytic ![]() $p$-divisible subgroup in the sense of Fargues: namely, we prove the following extension of a result of Fargues [Reference FarguesFar19, Théorème 1.2] which shows that our notion of topologically torsion subsheaves generalises his notion of analytic
$p$-divisible subgroup in the sense of Fargues: namely, we prove the following extension of a result of Fargues [Reference FarguesFar19, Théorème 1.2] which shows that our notion of topologically torsion subsheaves generalises his notion of analytic ![]() $p$-divisible subgroups from rigid groups (in the sense of Tate) to general
$p$-divisible subgroups from rigid groups (in the sense of Tate) to general ![]() $v$-sheaves.
$v$-sheaves.
Proposition 2.14 Let ![]() $G$ be a rigid group over
$G$ be a rigid group over ![]() $(K,K^+)$. Then we have the following.
$(K,K^+)$. Then we have the following.
(i) We have
 $G\langle p^\infty \rangle =\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)\subseteq G$, and this subsheaf is represented by a rigid open subgroup that is strongly topologically torsion. Its
$G\langle p^\infty \rangle =\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)\subseteq G$, and this subsheaf is represented by a rigid open subgroup that is strongly topologically torsion. Its  $K$-points are characterised by
$K$-points are characterised by
 \[ \underline{\mathrm{Hom}}(\mathbb{Z}_p,G)(K,K^+)=\{x\in G(K,K^+)\mid p^n\cdot x\xrightarrow{n\to \infty} 0\}. \]
\[ \underline{\mathrm{Hom}}(\mathbb{Z}_p,G)(K,K^+)=\{x\in G(K,K^+)\mid p^n\cdot x\xrightarrow{n\to \infty} 0\}. \]
(ii) This open subgroup fits into a left-exact sequence of
 $v$-sheaves
If
$v$-sheaves
If \[ 0\to G[p^\infty]\to G\langle p^\infty\rangle\xrightarrow{\log}\mathrm{Lie}(G)\otimes_K \mathbb{G}_a. \]
\[ 0\to G[p^\infty]\to G\langle p^\infty\rangle\xrightarrow{\log}\mathrm{Lie}(G)\otimes_K \mathbb{G}_a. \]
 $[p]:G\to G$ is surjective, this sequence is also right-exact.
$[p]:G\to G$ is surjective, this sequence is also right-exact.(iii) We have
 $G^{\mathrm {tt}}=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)$ and this is represented by the open subgroup of
$G^{\mathrm {tt}}=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)$ and this is represented by the open subgroup of  $G$
If
$G$
If \[ G^{\mathrm{tt}}=\bigcup_{(N,p)=1} [N]^{-1}(G\langle p^\infty\rangle). \]
\[ G^{\mathrm{tt}}=\bigcup_{(N,p)=1} [N]^{-1}(G\langle p^\infty\rangle). \]
 $K$ is algebraically closed, we can more explicitly describe this as the union
$K$ is algebraically closed, we can more explicitly describe this as the union
 \[ G^{\mathrm{tt}}=G\langle p^\infty\rangle \cdot \bigcup_{(N,p)=1} G[N](K,K^+)\subseteq G. \]
\[ G^{\mathrm{tt}}=G\langle p^\infty\rangle \cdot \bigcup_{(N,p)=1} G[N](K,K^+)\subseteq G. \]
(iv) Assume that
 $G$ has good reduction, i.e. there is a formal group scheme
$G$ has good reduction, i.e. there is a formal group scheme  $\mathfrak G$ that is flat of topologically finite presentation over
$\mathfrak G$ that is flat of topologically finite presentation over  $K^+$ such that
$K^+$ such that  $\mathfrak G^{\mathrm {ad}}_{\eta }=G$. Let
$\mathfrak G^{\mathrm {ad}}_{\eta }=G$. Let  $\mathfrak G[p^\infty ]$ be the sheaf on
$\mathfrak G[p^\infty ]$ be the sheaf on  $p$-nilpotent
$p$-nilpotent  $K^+$-algebras
$K^+$-algebras  $R$ defined by
$R$ defined by  $\mathfrak G[p^\infty ](R)=\textstyle \varinjlim _{n\in \mathbb {N}} \mathfrak G[p^n](R)$. Then
is the adic generic fibre in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 2.2]. In particular,
$\mathfrak G[p^\infty ](R)=\textstyle \varinjlim _{n\in \mathbb {N}} \mathfrak G[p^n](R)$. Then
is the adic generic fibre in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 2.2]. In particular, \[ G\langle p^\infty\rangle=\mathfrak G[p^\infty]^{\mathrm{ad}}_{\eta} \]
\[ G\langle p^\infty\rangle=\mathfrak G[p^\infty]^{\mathrm{ad}}_{\eta} \]
 $G\langle p^\infty \rangle (K,K^+)$ (respectively,
$G\langle p^\infty \rangle (K,K^+)$ (respectively,  $G^\mathrm {tt}(K,K^+)$) consists of those points of
$G^\mathrm {tt}(K,K^+)$) consists of those points of  $\mathfrak G(K^+)$ which reduce to a
$\mathfrak G(K^+)$ which reduce to a  $p^\infty$-torsion point (respectively, torsion point) on the special fibre.
$p^\infty$-torsion point (respectively, torsion point) on the special fibre.
Remark 2.15 The aforementioned Theorem of Fargues asserts that for a (classical) rigid group over ![]() $(K,\mathcal {O}_K)$ of characteristic
$(K,\mathcal {O}_K)$ of characteristic ![]() $0$, there exists a rigid open subgroup
$0$, there exists a rigid open subgroup ![]() $U\subseteq G$ such that
$U\subseteq G$ such that
Proposition 2.14 recovers ![]() $U$ and shows that it is equal to
$U$ and shows that it is equal to ![]() $G\langle p^\infty \rangle$. Fargues also shows part (ii) in this case, and part (iv) is his point of view on the
$G\langle p^\infty \rangle$. Fargues also shows part (ii) in this case, and part (iv) is his point of view on the ![]() $p$-divisible group of
$p$-divisible group of ![]() $G$ (see [Reference FarguesFar19, § 0]).
$G$ (see [Reference FarguesFar19, § 0]).
From this perspective, the new aspects of Proposition 2.14 in the special case of classical rigid groups over ![]() $(K,\mathcal {O}_K)$ are the description of
$(K,\mathcal {O}_K)$ are the description of ![]() $U$ in terms of the
$U$ in terms of the ![]() $v$-sheaf
$v$-sheaf ![]() $\underline {\operatorname {Hom}}(\underline {\mathbb {Z}}_p,-)$ (which crucially uses the language of
$\underline {\operatorname {Hom}}(\underline {\mathbb {Z}}_p,-)$ (which crucially uses the language of ![]() $v$-sheaves), and the extension to coprime torsion via part (iii).
$v$-sheaves), and the extension to coprime torsion via part (iii).
Remark 2.16 In the second part of Proposition 2.14(iii), we form the disjoint union in the category of adic spaces. This is relevant because in the setting of classical rigid spaces in the sense of Tate, the subspaces ![]() $xG\langle p^\infty \rangle$ for
$xG\langle p^\infty \rangle$ for ![]() $x\in G[N](K)$ typically form a set-theoretic cover of
$x\in G[N](K)$ typically form a set-theoretic cover of ![]() $G$ that is not admissible. In the setting of adic spaces, this cover misses some points of rank two in
$G$ that is not admissible. In the setting of adic spaces, this cover misses some points of rank two in ![]() $G$ that are intentionally not included in
$G$ that are intentionally not included in ![]() $G^\mathrm {tt}$. See also § 2.4.
$G^\mathrm {tt}$. See also § 2.4.
Example 2.17
(i) To obtain an explicit description of
 $G\langle p^\infty \rangle$, it suffices by part (iv) to find an open subgroup of good reduction
$G\langle p^\infty \rangle$, it suffices by part (iv) to find an open subgroup of good reduction  $G_0\subseteq G$ such that
$G_0\subseteq G$ such that  $[p]^{-1}(G_0)\subseteq G_0$. For example, for
$[p]^{-1}(G_0)\subseteq G_0$. For example, for  $G=\mathbb {G}_m$, such an open subgroup is given by the affine torus
$G=\mathbb {G}_m$, such an open subgroup is given by the affine torus  $\mathfrak G=\mathbb {G}_{m,\mathcal {O}_K}$. This shows that
$\mathfrak G=\mathbb {G}_{m,\mathcal {O}_K}$. This shows that  $\mathbb {G}_m\langle p^\infty \rangle =\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ is the open disc of radius 1 around 1. In particular, by part (iv), we deduce that
$\mathbb {G}_m\langle p^\infty \rangle =\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ is the open disc of radius 1 around 1. In particular, by part (iv), we deduce that  $\mathbb {G}_m^{\mathrm {tt}}=\mu (K)\widehat {\mathbb {G}}_m$, justifying the description in Example 2.7.
$\mathbb {G}_m^{\mathrm {tt}}=\mu (K)\widehat {\mathbb {G}}_m$, justifying the description in Example 2.7.(ii) More generally, such an open subgroup exists for semi-abeloid varieties
 $A$, which are of interest in the context of Picard functors. By Raynaud uniformisation, there is a maximal open subgroup
$A$, which are of interest in the context of Picard functors. By Raynaud uniformisation, there is a maximal open subgroup  $A^+\subseteq A$ that admits a connected smooth formal model. We then let
$A^+\subseteq A$ that admits a connected smooth formal model. We then let  $G_0$ be the disjoint union of translates of
$G_0$ be the disjoint union of translates of  $A^+$ over points in
$A^+$ over points in  $A[p^\infty ]$. In fact, with this definition, the analogues of parts (i), (iii) and (iv) also hold in characteristic
$A[p^\infty ]$. In fact, with this definition, the analogues of parts (i), (iii) and (iv) also hold in characteristic  $p$.
$p$.(iii) If
 $G=\mathbb {G}_a$, then we cannot find an open subgroup of good reduction
$G=\mathbb {G}_a$, then we cannot find an open subgroup of good reduction  $G_0$ such that
$G_0$ such that  $[p]^{-1} (G_0)\subseteq G_0$. This is consistent with the fact that the
$[p]^{-1} (G_0)\subseteq G_0$. This is consistent with the fact that the  $\mathbb {G}_{a,\mathcal {O}_K}[p^n]$ do not form a
$\mathbb {G}_{a,\mathcal {O}_K}[p^n]$ do not form a  $p$-divisible group. Instead, in this case, we have
$p$-divisible group. Instead, in this case, we have  $\mathbb {G}_a\langle p^\infty \rangle =\mathbb {G}_a^{\mathrm {tt}}=\mathbb {G}_a$.
$\mathbb {G}_a\langle p^\infty \rangle =\mathbb {G}_a^{\mathrm {tt}}=\mathbb {G}_a$.(iv) The restriction to the rigid case is necessary: for example, set
 $G=\mathbb {Z}_l$ for
$G=\mathbb {Z}_l$ for  $l\neq p$. Here
$l\neq p$. Here  $G\langle p^\infty \rangle =0 \subseteq G$ is not open, rather it is closed. For part (iv), consider also the example of the formal scheme
$G\langle p^\infty \rangle =0 \subseteq G$ is not open, rather it is closed. For part (iv), consider also the example of the formal scheme  $\mathfrak G=\varprojlim _{[p]}\mathbb {G}_{m,K^+}$. Its adic generic fibre
$\mathfrak G=\varprojlim _{[p]}\mathbb {G}_{m,K^+}$. Its adic generic fibre  $G$ is a perfectoid group whose topologically torsion subgroup is given by the open subgroup
$G$ is a perfectoid group whose topologically torsion subgroup is given by the open subgroup  $\varprojlim _{[p]}\widehat {\mathbb {G}}_m$. This is closely related to the universal cover of
$\varprojlim _{[p]}\widehat {\mathbb {G}}_m$. This is closely related to the universal cover of  $\mu _{p^\infty }$ in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 3.1]. However, the description of
$\mu _{p^\infty }$ in the sense of Scholze and Weinstein [Reference Scholze and WeinsteinSW13, § 3.1]. However, the description of  $G\langle p^\infty \rangle$ in terms of torsion points of the special fibre is no longer valid as
$G\langle p^\infty \rangle$ in terms of torsion points of the special fibre is no longer valid as  $\mathfrak G$ is uniquely
$\mathfrak G$ is uniquely  $p$-divisible, and hence its special fibre is
$p$-divisible, and hence its special fibre is  $p$-torsionfree.
$p$-torsionfree.
Remark 2.18 We note that if ![]() $G$ is a rigid group, there is an alternative, ‘analytic’ description of
$G$ is a rigid group, there is an alternative, ‘analytic’ description of ![]() $G^\mathrm {tt}$, as follows. Using the
$G^\mathrm {tt}$, as follows. Using the ![]() $p$-adic logarithm, one can show that any morphism
$p$-adic logarithm, one can show that any morphism ![]() $\varphi :\mathbb {Z}_p\times T\to G$ in
$\varphi :\mathbb {Z}_p\times T\to G$ in ![]() $\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)(T)$ admits an analytic continuation locally. More precisely, for
$\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)(T)$ admits an analytic continuation locally. More precisely, for ![]() $n\gg 0$, the restriction of
$n\gg 0$, the restriction of ![]() $\varphi$ to
$\varphi$ to ![]() $p^n\mathbb {Z}_p\times T$ extends uniquely to a
$p^n\mathbb {Z}_p\times T$ extends uniquely to a ![]() $T$-linear homomorphism
$T$-linear homomorphism ![]() $\varphi :\mathbb {B}_n\times T\to G$ where
$\varphi :\mathbb {B}_n\times T\to G$ where ![]() $\mathbb {B}_n\subseteq \mathbb {G}_a$ is the closed disc of radius
$\mathbb {B}_n\subseteq \mathbb {G}_a$ is the closed disc of radius ![]() $\leq |p^n|$ with its additive structure. In other words, if
$\leq |p^n|$ with its additive structure. In other words, if ![]() $\mathbb {Z}_p(\epsilon )$ denotes for any
$\mathbb {Z}_p(\epsilon )$ denotes for any ![]() $\epsilon >0$ the open subgroup of
$\epsilon >0$ the open subgroup of ![]() $\mathbb {G}_a$ defined by the union of closed discs of radius
$\mathbb {G}_a$ defined by the union of closed discs of radius ![]() $\epsilon$ around
$\epsilon$ around ![]() $\mathbb {Z}_p\subseteq \mathbb {G}_a(K)$, then we have
$\mathbb {Z}_p\subseteq \mathbb {G}_a(K)$, then we have
Although we do not need this observation in this article, it is useful for other applications.
In light of Proposition 2.14, one can use the topologically ![]() $p$-torsion subsheaf to generalise the notion of ‘analytic
$p$-torsion subsheaf to generalise the notion of ‘analytic ![]() $p$-divisible groups’ in the sense of Fargues [Reference FarguesFar19, § 2 Définition 2]:
$p$-divisible groups’ in the sense of Fargues [Reference FarguesFar19, § 2 Définition 2]:
Definition 2.19
(i) We call a rigid group
 $G$ over
$G$ over  $(K,K^+)$ an analytic
$(K,K^+)$ an analytic  $p$-divisible group if
$p$-divisible group if  $G$ is topologically
$G$ is topologically  $p$-torsion (i.e.
$p$-torsion (i.e.  $G\langle p^\infty \rangle =G$) and
$G\langle p^\infty \rangle =G$) and  $[p]:G\to G$ is surjective.
$[p]:G\to G$ is surjective.(ii) We call a rigid group
 $G$ an analytic divisible group if
$G$ an analytic divisible group if  $G$ is topologically torsion (i.e.
$G$ is topologically torsion (i.e.  $G^\mathrm {tt}=G$) and
$G^\mathrm {tt}=G$) and  $[n]:G\to G$ is surjective for all
$[n]:G\to G$ is surjective for all  $n\in \mathbb {N}$.
$n\in \mathbb {N}$.
Examples of analytic divisible groups include ![]() $\mathbb {Q}/\mathbb {Z}$,
$\mathbb {Q}/\mathbb {Z}$, ![]() $\mathbb {G}_a$ and
$\mathbb {G}_a$ and ![]() $G^\mathrm {tt}$ for any rigid group
$G^\mathrm {tt}$ for any rigid group ![]() $G$ for which
$G$ for which ![]() $[n]:G\to G$ is surjective for all
$[n]:G\to G$ is surjective for all ![]() $n\in \mathbb {N}$, e.g. for abeloid varieties. One can then characterise
$n\in \mathbb {N}$, e.g. for abeloid varieties. One can then characterise ![]() $G^\mathrm {tt}$ as the maximal analytic divisible subgroup of
$G^\mathrm {tt}$ as the maximal analytic divisible subgroup of ![]() $G$, and similarly for
$G$, and similarly for ![]() $G\langle p^\infty \rangle$.
$G\langle p^\infty \rangle$.
We now start with the proof of Proposition 2.14. For this we use the following result.
Lemma 2.20 Let ![]() $G$ be any rigid group over
$G$ be any rigid group over ![]() $(K,K^+)$. Then
$(K,K^+)$. Then ![]() $G(K,K^+)$ is a complete topological group (complete with respect to the uniform structure given by open subgroups).
$G(K,K^+)$ is a complete topological group (complete with respect to the uniform structure given by open subgroups).
Proof. To simplify notation, let us just write ![]() $G(K)$ for
$G(K)$ for ![]() $G(K,K^+)$. We first note that
$G(K,K^+)$. We first note that ![]() $G(K)$ is a topological group: this is not completely obvious for adic groups since the map
$G(K)$ is a topological group: this is not completely obvious for adic groups since the map ![]() $|G\times G|\to |G|\times |G|$ is usually not a bijection. However, the continuous bijection
$|G\times G|\to |G|\times |G|$ is usually not a bijection. However, the continuous bijection
on ![]() $K$-points is indeed a homeomorphism: this follows from the fact that any rigid group admits a neighbourhood basis of
$K$-points is indeed a homeomorphism: this follows from the fact that any rigid group admits a neighbourhood basis of ![]() $0$ consisting of open rigid subgroups
$0$ consisting of open rigid subgroups ![]() $U\subseteq G$ such that
$U\subseteq G$ such that ![]() $U\cong \mathbb {B}^d$ as rigid spaces ([Reference FarguesFar19, § 1, Corollaire 4] over
$U\cong \mathbb {B}^d$ as rigid spaces ([Reference FarguesFar19, § 1, Corollaire 4] over ![]() $(K,\mathcal {O}_K)$, [Reference HeuerHeu22a, Corollary 3.7] in general). This also shows that
$(K,\mathcal {O}_K)$, [Reference HeuerHeu22a, Corollary 3.7] in general). This also shows that ![]() $G(K)$ is Hausdorff.
$G(K)$ is Hausdorff.
To see that ![]() $G(K)$ is complete, let
$G(K)$ is complete, let ![]() $(x_n)_{n\in \mathbb {N}}$ be any Cauchy sequence. Then for
$(x_n)_{n\in \mathbb {N}}$ be any Cauchy sequence. Then for ![]() $n,m\gg 0$, we have
$n,m\gg 0$, we have ![]() $x_n-x_m\in U$ and, thus,
$x_n-x_m\in U$ and, thus, ![]() $x_n\in x_m+U$. After translating by
$x_n\in x_m+U$. After translating by ![]() $x_m$, we may therefore assume
$x_m$, we may therefore assume ![]() $x_n\in U$ for all
$x_n\in U$ for all ![]() $n$. Now let
$n$. Now let ![]() $f\in \mathcal {O}^+(U)$ and consider the map
$f\in \mathcal {O}^+(U)$ and consider the map
For any ![]() $\epsilon >0$, let
$\epsilon >0$, let ![]() $V_{\epsilon }\subseteq U\times U$ be the pullback of the open ball
$V_{\epsilon }\subseteq U\times U$ be the pullback of the open ball ![]() $\mathbb {B}_{\epsilon }$ of radius
$\mathbb {B}_{\epsilon }$ of radius ![]() $\epsilon$ around
$\epsilon$ around ![]() $0$. Since
$0$. Since ![]() $U\times \{0\}\subseteq V_{\epsilon }$, and
$U\times \{0\}\subseteq V_{\epsilon }$, and ![]() $U\times \{0\}$ is the tilde limit of
$U\times \{0\}$ is the tilde limit of ![]() $\varprojlim _{n\in \mathbb {N}} U\times \mathbb {B}_{n}$ where
$\varprojlim _{n\in \mathbb {N}} U\times \mathbb {B}_{n}$ where ![]() $\mathbb {B}_n$ is the ball of radius
$\mathbb {B}_n$ is the ball of radius ![]() $|p^n|$, it follows from a standard approximation argument that there is an open subgroup
$|p^n|$, it follows from a standard approximation argument that there is an open subgroup ![]() $W_{\epsilon }\subseteq U$ such that
$W_{\epsilon }\subseteq U$ such that ![]() $U\times W_{\epsilon }\subseteq V_\epsilon$. For
$U\times W_{\epsilon }\subseteq V_\epsilon$. For ![]() $n,m\gg 0$, we then have
$n,m\gg 0$, we then have ![]() $x_m-x_n\in W_\epsilon$ which implies
$x_m-x_n\in W_\epsilon$ which implies ![]() $|f(x_m)-f(x_n)|\leq \epsilon$. Thus,
$|f(x_m)-f(x_n)|\leq \epsilon$. Thus, ![]() $f(x_m)$ is a Cauchy sequence in
$f(x_m)$ is a Cauchy sequence in ![]() $K^+$. It thus makes sense to define
$K^+$. It thus makes sense to define
One easily checks that this defines the desired limit ![]() $x_n\to x\in U(K,K^+)\subseteq G(K,K^+)$.
$x_n\to x\in U(K,K^+)\subseteq G(K,K^+)$.
Remark 2.21 With more work, one can show that ![]() $G(K,K^+)$ is a complete topological group for any adic group
$G(K,K^+)$ is a complete topological group for any adic group ![]() $G$ over
$G$ over ![]() $(K,K^+)$ satisfying the following mild technical assumption:
$(K,K^+)$ satisfying the following mild technical assumption: ![]() $G$ admits a basis of uniform affine open subspaces
$G$ admits a basis of uniform affine open subspaces ![]() $\mathcal {B}$ such that for each
$\mathcal {B}$ such that for each ![]() $U=\operatorname {Spa}(A,A^+)$ and
$U=\operatorname {Spa}(A,A^+)$ and ![]() $V=\operatorname {Spa}(B,B^+)$ in
$V=\operatorname {Spa}(B,B^+)$ in ![]() $\mathcal {B}$, the fibre product
$\mathcal {B}$, the fibre product ![]() $U\times _KV$ exists and is affinoid with
$U\times _KV$ exists and is affinoid with ![]() $\mathcal {O}(U\times _KV)=A\hat {\otimes }_K B$ the tensor product of complete normed
$\mathcal {O}(U\times _KV)=A\hat {\otimes }_K B$ the tensor product of complete normed ![]() $K$-vector spaces. For example, this holds for perfectoid groups. One then obtains the analogous description of
$K$-vector spaces. For example, this holds for perfectoid groups. One then obtains the analogous description of ![]() $K$-points of
$K$-points of ![]() $G\langle p^\infty \rangle$.
$G\langle p^\infty \rangle$.
Proof of Proposition 2.14 We begin by describing the ![]() $(K,K^+)$-points of
$(K,K^+)$-points of ![]() $G\langle p^\infty \rangle$ and
$G\langle p^\infty \rangle$ and ![]() $G^\mathrm {tt}$: By Lemma 2.4, we have
$G^\mathrm {tt}$: By Lemma 2.4, we have ![]() $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)(K)=\operatorname {Hom}_{{\operatorname {cts}}}({\widehat {\mathbb {Z}}},G(K))$. Let
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)(K)=\operatorname {Hom}_{{\operatorname {cts}}}({\widehat {\mathbb {Z}}},G(K))$. Let ![]() $\varphi :{\widehat {\mathbb {Z}}}\to G(K)$ be any continuous homomorphism. This is uniquely determined by the image
$\varphi :{\widehat {\mathbb {Z}}}\to G(K)$ be any continuous homomorphism. This is uniquely determined by the image ![]() $x=\varphi (1)$ of
$x=\varphi (1)$ of ![]() $1$. By continuity, since
$1$. By continuity, since ![]() $n!\to 0$ in
$n!\to 0$ in ![]() $\widehat {\mathbb {Z}}$, we have
$\widehat {\mathbb {Z}}$, we have ![]() $x^{n!}\to 0$ in
$x^{n!}\to 0$ in ![]() $G(K)$.
$G(K)$.
Conversely, let ![]() $x\in G(K)$ be such that
$x\in G(K)$ be such that ![]() $x^{n!}\to 0$. Let
$x^{n!}\to 0$. Let ![]() $f:\mathbb {Z}\to G(K)$ be the homomorphism defined by
$f:\mathbb {Z}\to G(K)$ be the homomorphism defined by ![]() $f(1)=x$. For any open subgroup
$f(1)=x$. For any open subgroup ![]() $U\subseteq G(K)$, we have
$U\subseteq G(K)$, we have ![]() $x^{n!}\in U$ for
$x^{n!}\in U$ for ![]() $n\gg 0$ and, thus,
$n\gg 0$ and, thus, ![]() $n!\mathbb {Z}\subseteq f^{-1}(U)$, so
$n!\mathbb {Z}\subseteq f^{-1}(U)$, so ![]() $f$ is continuous for the subspace topology on
$f$ is continuous for the subspace topology on ![]() $\mathbb {Z}\subseteq {\widehat {\mathbb {Z}}}$. By the universal property of the completion,
$\mathbb {Z}\subseteq {\widehat {\mathbb {Z}}}$. By the universal property of the completion, ![]() $f$ now extends to
$f$ now extends to ![]() ${\widehat {\mathbb {Z}}}$ as
${\widehat {\mathbb {Z}}}$ as ![]() $G(K)$ is complete by Lemma 2.20.
$G(K)$ is complete by Lemma 2.20.
The case of topological ![]() $p$-torsion is analogous. This gives the description of
$p$-torsion is analogous. This gives the description of ![]() $G\langle p^\infty \rangle (K,K^+)$.
$G\langle p^\infty \rangle (K,K^+)$.
By [Reference HeuerHeu22a, Proposition 3.5, Corollary 3.8], there exists an open subgroup ![]() $G_1\subseteq G$ of good reduction that admits an open immersion
$G_1\subseteq G$ of good reduction that admits an open immersion ![]() $\log :G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$. Let
$\log :G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$. Let
this is clearly an open adic subgroup of ![]() $G$. We claim that
$G$. We claim that ![]() $G_2=G\langle p^\infty \rangle$.
$G_2=G\langle p^\infty \rangle$.
To see that ![]() $G\langle p^\infty \rangle \subseteq G_2$, let
$G\langle p^\infty \rangle \subseteq G_2$, let ![]() $T=\operatorname {Spa}(S,S^+)$ be an affinoid perfectoid space over
$T=\operatorname {Spa}(S,S^+)$ be an affinoid perfectoid space over ![]() $(K,K^+)$ and let
$(K,K^+)$ and let
be any homomorphism over ![]() $T$. Then the preimage of
$T$. Then the preimage of ![]() $G_1\times T$ contains some neighbourhood
$G_1\times T$ contains some neighbourhood ![]() $p^n\underline {\mathbb {Z}}_p\times T$ of the identity because
$p^n\underline {\mathbb {Z}}_p\times T$ of the identity because ![]() $|\mathbb {Z}_p\times T|=\varprojlim |\mathbb {Z}/p^n\mathbb {Z}\times T|=\mathbb {Z}_p\times |T|$. By the definition of
$|\mathbb {Z}_p\times T|=\varprojlim |\mathbb {Z}/p^n\mathbb {Z}\times T|=\mathbb {Z}_p\times |T|$. By the definition of ![]() $G_2$, this implies that
$G_2$, this implies that ![]() $\varphi$ factors through
$\varphi$ factors through ![]() $G_2$.
$G_2$.
To see the converse, let now ![]() $\mathfrak G$ be the formal model of
$\mathfrak G$ be the formal model of ![]() $G_1$ and consider the open subgroup
$G_1$ and consider the open subgroup
We now invoke [Reference Scholze and WeinsteinSW13, Proposition 2.2.2.(ii)], which is written in the case that ![]() $K^+=\mathcal {O}_K$, but its proof goes through verbatim also for
$K^+=\mathcal {O}_K$, but its proof goes through verbatim also for ![]() $(K,K^+)$. This says that the points of
$(K,K^+)$. This says that the points of ![]() $G_0$ on perfectoid
$G_0$ on perfectoid ![]() $(K,K^+)$-algebras
$(K,K^+)$-algebras ![]() $(R,R^+)$ are given by the sheafification of the presheaf
$(R,R^+)$ are given by the sheafification of the presheaf
Suppose first that we are given any point ![]() $\varphi \in G_0(T)$. To prove that this is contained in
$\varphi \in G_0(T)$. To prove that this is contained in ![]() $G\langle p^\infty \rangle (T)\subseteq G(T)$, we may without loss of generality pass from
$G\langle p^\infty \rangle (T)\subseteq G(T)$, we may without loss of generality pass from ![]() $T$ to an analytic cover. By the above, we may therefore assume that
$T$ to an analytic cover. By the above, we may therefore assume that ![]() $\varphi$ has a formal model, i.e. comes from a group homomorphism
$\varphi$ has a formal model, i.e. comes from a group homomorphism ![]() $\varphi :\operatorname {Spf}(S^+)\to \mathfrak G$ that reduces mod
$\varphi :\operatorname {Spf}(S^+)\to \mathfrak G$ that reduces mod ![]() $p^n$ to compatible homomorphisms
$p^n$ to compatible homomorphisms
for all ![]() $n$. Taking the limit over
$n$. Taking the limit over ![]() $n$ and passing to the generic fibre, this gives the desired map
$n$ and passing to the generic fibre, this gives the desired map
Finally, we observe that given any ![]() $x\in G_2(T)$, there is
$x\in G_2(T)$, there is ![]() $n$ such that
$n$ such that ![]() $p^nx\in G_0(T)$. Let
$p^nx\in G_0(T)$. Let ![]() $\varphi :\underline {\mathbb {Z}}\times T\to G$ be the homomorphism sending
$\varphi :\underline {\mathbb {Z}}\times T\to G$ be the homomorphism sending ![]() $1\mapsto x$. As we have just shown, its restriction to
$1\mapsto x$. As we have just shown, its restriction to ![]() $p^n\underline {\mathbb {Z}}\times T$ extends uniquely to a map
$p^n\underline {\mathbb {Z}}\times T$ extends uniquely to a map ![]() $\widehat {\varphi }:p^n\underline {\mathbb {Z}}_p\times T\to G_0$. Using the short exact sequence
$\widehat {\varphi }:p^n\underline {\mathbb {Z}}_p\times T\to G_0$. Using the short exact sequence
of ![]() $v$-sheaves,
$v$-sheaves, ![]() $\varphi$ now extends uniquely to
$\varphi$ now extends uniquely to ![]() $\underline {\mathbb {Z}}_p\times T$ by the universal property of the cokernel.
$\underline {\mathbb {Z}}_p\times T$ by the universal property of the cokernel.
This proves part (i). Part (ii) follows from the open immersion ![]() $G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$, which can be uniquely extended to
$G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$, which can be uniquely extended to ![]() $G_2$ by sending
$G_2$ by sending ![]() $x\in G_0(T)$ with
$x\in G_0(T)$ with ![]() $p^nx\in G_1(T)$ to
$p^nx\in G_1(T)$ to ![]() $\log (x)=p^{-n}\log (p^nx)$. The statement about surjectivity follows as
$\log (x)=p^{-n}\log (p^nx)$. The statement about surjectivity follows as ![]() $\mathrm {Lie}(G)\otimes _K \mathbb {G}_a=\bigcup _{n\in \mathbb {N}}p^{-n}\log (G_1)$.
$\mathrm {Lie}(G)\otimes _K \mathbb {G}_a=\bigcup _{n\in \mathbb {N}}p^{-n}\log (G_1)$.
For part (iv), it remains to prove that any morphism ![]() $\varphi :\underline {\mathbb {Z}}_p\times T\to G$ factors through
$\varphi :\underline {\mathbb {Z}}_p\times T\to G$ factors through ![]() $G_0\subseteq G$. Since this is an open subgroup, we see as in the beginning of the proof that there is
$G_0\subseteq G$. Since this is an open subgroup, we see as in the beginning of the proof that there is ![]() $n$ such that
$n$ such that ![]() $\varphi (p^n\underline {\mathbb {Z}}_p\times T)\subseteq G_0$. However, in the case of good reduction, we also have
$\varphi (p^n\underline {\mathbb {Z}}_p\times T)\subseteq G_0$. However, in the case of good reduction, we also have ![]() $[p]_G^{-1}(G_0)=G_0$ by the above explicit description of
$[p]_G^{-1}(G_0)=G_0$ by the above explicit description of ![]() $G_0=\mathfrak G[p^\infty ]_{\eta }^{\mathrm {ad}}$. Thus,
$G_0=\mathfrak G[p^\infty ]_{\eta }^{\mathrm {ad}}$. Thus, ![]() $\varphi (\underline {\mathbb {Z}}_p\times T)\subseteq G_0$.
$\varphi (\underline {\mathbb {Z}}_p\times T)\subseteq G_0$.
To deduce part (iii), write ![]() ${\widehat {\mathbb {Z}}}=\mathbb {Z}_p\times {\widehat {\mathbb {Z}}}^{(p)}$ where
${\widehat {\mathbb {Z}}}=\mathbb {Z}_p\times {\widehat {\mathbb {Z}}}^{(p)}$ where ![]() ${\widehat {\mathbb {Z}}}^{(p)}=\varprojlim _{(N,p)=1} \mathbb {Z}/N$. It suffices to show the following.
${\widehat {\mathbb {Z}}}^{(p)}=\varprojlim _{(N,p)=1} \mathbb {Z}/N$. It suffices to show the following.
Lemma 2.22 Let ![]() $H=\varprojlim _{i\in I} H_i$ be any profinite group for which the order of each
$H=\varprojlim _{i\in I} H_i$ be any profinite group for which the order of each ![]() $H_i$ is coprime to
$H_i$ is coprime to ![]() $p$. Let
$p$. Let ![]() $G$ be any rigid group over
$G$ be any rigid group over ![]() $(K,K^+)$. Then we have
$(K,K^+)$. Then we have
Proof. Let ![]() $f:{H}\times T\to G$ be any homomorphism of adic groups over a perfectoid space
$f:{H}\times T\to G$ be any homomorphism of adic groups over a perfectoid space ![]() $T$. We need to prove that some open subgroup of
$T$. We need to prove that some open subgroup of ![]() $H$ gets sent to the identity. In the notation introduced previously, we can therefore assume that
$H$ gets sent to the identity. In the notation introduced previously, we can therefore assume that ![]() $f$ factors through the open subgroup
$f$ factors through the open subgroup ![]() $G_0=\mathfrak G[p^\infty ]^{\mathrm {ad}}_\eta \subseteq G$ and that
$G_0=\mathfrak G[p^\infty ]^{\mathrm {ad}}_\eta \subseteq G$ and that ![]() $f$ admits a formal model
$f$ admits a formal model ![]() ${H}\times \operatorname {Spf}(S^+)\to \mathfrak G$. We claim that
${H}\times \operatorname {Spf}(S^+)\to \mathfrak G$. We claim that ![]() $f$ is then trivial. To see this, we may reduce to
$f$ is then trivial. To see this, we may reduce to ![]() $T=\operatorname {Spa}(K,K^+)$. Then
$T=\operatorname {Spa}(K,K^+)$. Then ![]() $f$ corresponds to an inverse system of homomorphisms
$f$ corresponds to an inverse system of homomorphisms ![]() $H\to \mathfrak G(\mathcal {O}_K/p^n)[p^\infty ]$. Since the right-hand side is discrete, this factors through
$H\to \mathfrak G(\mathcal {O}_K/p^n)[p^\infty ]$. Since the right-hand side is discrete, this factors through ![]() $H_i$ for some
$H_i$ for some ![]() $i$. However,
$i$. However, ![]() $H_i$ is of order coprime to
$H_i$ is of order coprime to ![]() $p$, so this map is trivial.
$p$, so this map is trivial.
This finishes the proof of Proposition 2.14.
2.4 Topological torsion in abeloid varieties
An example of particular interest for our applications to the ![]() $p$-adic Simpson correspondence is the case of abeloid varieties, i.e. connected smooth proper rigid groups. For these we have the following curious special case.
$p$-adic Simpson correspondence is the case of abeloid varieties, i.e. connected smooth proper rigid groups. For these we have the following curious special case.
Proposition 2.23 Let ![]() $A$ be an abeloid variety over
$A$ be an abeloid variety over ![]() $K=\mathbb {C}_p$ or
$K=\mathbb {C}_p$ or ![]() $\mathbb {C}_p^\flat$. Then
$\mathbb {C}_p^\flat$. Then
Remark 2.24 This does not mean that the open immersion ![]() $A^\mathrm {tt}\to A$ is an isomorphism. Indeed, this is not the case; for example,
$A^\mathrm {tt}\to A$ is an isomorphism. Indeed, this is not the case; for example, ![]() $A$ is connected whereas
$A$ is connected whereas ![]() $A^\mathrm {tt}$ is an infinite disjoint union of open discs by Proposition 2.14. A closely related phenomenon is that the statement of Proposition 2.23 becomes false for any non-trivial extension of
$A^\mathrm {tt}$ is an infinite disjoint union of open discs by Proposition 2.14. A closely related phenomenon is that the statement of Proposition 2.23 becomes false for any non-trivial extension of ![]() $K$, already for Tate curves.
$K$, already for Tate curves.
This difference is relevant to the ![]() $p$-adic Simpson correspondence as it explains why the description in Theorem 1.1 in terms of vanishing Chern classes is only valid over
$p$-adic Simpson correspondence as it explains why the description in Theorem 1.1 in terms of vanishing Chern classes is only valid over ![]() $\mathbb {C}_p$.
$\mathbb {C}_p$.
Proof. If ![]() $A$ has good reduction with special fibre
$A$ has good reduction with special fibre ![]() $\overline {A}$ over the residue field
$\overline {A}$ over the residue field ![]() $\overline {\mathbb {F}}_p$, then by Proposition 2.14(iv), the specialisation map
$\overline {\mathbb {F}}_p$, then by Proposition 2.14(iv), the specialisation map ![]() $A(K)\to \overline {A}(\overline {\mathbb {F}}_p)$ induces a short exact sequence
$A(K)\to \overline {A}(\overline {\mathbb {F}}_p)$ induces a short exact sequence
where ![]() $\overline {A}(\overline {\mathbb {F}}_p)[\tfrac {1}{p}]:=\overline {A}(\overline {\mathbb {F}}_p)\otimes _{\mathbb {Z}}\mathbb {Z}[\tfrac {1}{p}]=\varinjlim _{[p]}\overline {A}(\overline {\mathbb {F}}_p)$. This is an abelian torsion group: indeed, the abelian variety
$\overline {A}(\overline {\mathbb {F}}_p)[\tfrac {1}{p}]:=\overline {A}(\overline {\mathbb {F}}_p)\otimes _{\mathbb {Z}}\mathbb {Z}[\tfrac {1}{p}]=\varinjlim _{[p]}\overline {A}(\overline {\mathbb {F}}_p)$. This is an abelian torsion group: indeed, the abelian variety ![]() $\overline {A}$ is already defined over a finite extension
$\overline {A}$ is already defined over a finite extension ![]() $\mathbb {F}_q$ of
$\mathbb {F}_q$ of ![]() $\mathbb {F}_p$ in
$\mathbb {F}_p$ in ![]() $\overline {\mathbb {F}}_p$ and, hence,
$\overline {\mathbb {F}}_p$ and, hence,
is a colimit of finite groups, where ![]() $k$ ranges through finite extensions of
$k$ ranges through finite extensions of ![]() $\mathbb {F}_q$ in
$\mathbb {F}_q$ in ![]() $\overline {\mathbb {F}}_p$. By the description of
$\overline {\mathbb {F}}_p$. By the description of ![]() $A^\mathrm {tt}$ in Proposition 2.14(iii), this shows that
$A^\mathrm {tt}$ in Proposition 2.14(iii), this shows that ![]() $A^\mathrm {tt}(K)=A(K)$ in this case.
$A^\mathrm {tt}(K)=A(K)$ in this case.
The general case follows from the case of good reduction via Raynaud uniformisation: By [Reference LütkebohmertLüt16, Theorem 7.6.4], we can write ![]() $A=E/M$ for some analytic short exact sequence
$A=E/M$ for some analytic short exact sequence
of rigid groups where ![]() $B$ is an abeloid variety of good reduction and
$B$ is an abeloid variety of good reduction and ![]() $T$ is a rigid torus, and where
$T$ is a rigid torus, and where ![]() $M\subseteq E(K)$ is a discrete lattice of rank equal to the rank of
$M\subseteq E(K)$ is a discrete lattice of rank equal to the rank of ![]() $T$. It is easy to see that this exact sequence of
$T$. It is easy to see that this exact sequence of ![]() $E$ becomes split over
$E$ becomes split over ![]() $B\langle p^\infty \rangle$, hence induces an exact sequence
$B\langle p^\infty \rangle$, hence induces an exact sequence
Let ![]() $M\cdot E\langle p^\infty \rangle \subseteq E$ be the open subgroup generated by
$M\cdot E\langle p^\infty \rangle \subseteq E$ be the open subgroup generated by ![]() $M$ and
$M$ and ![]() $E\langle p^\infty \rangle$. The composition
$E\langle p^\infty \rangle$. The composition
factors through ![]() $A\langle p^\infty \rangle$. Recall that the cokernel of
$A\langle p^\infty \rangle$. Recall that the cokernel of ![]() $A\langle p^\infty \rangle \to A^\mathrm {tt}$ is torsion by Proposition 2.14(iii), so to prove that
$A\langle p^\infty \rangle \to A^\mathrm {tt}$ is torsion by Proposition 2.14(iii), so to prove that ![]() $A^\mathrm {tt}(K)=A(K)$, it suffices to prove that the composition (10) is surjective on
$A^\mathrm {tt}(K)=A(K)$, it suffices to prove that the composition (10) is surjective on ![]() $K$-points after tensoring with
$K$-points after tensoring with ![]() $\mathbb {Q}$. Hence it suffices to prove the following.
$\mathbb {Q}$. Hence it suffices to prove the following.
Lemma 2.25 Let ![]() $A=E/M$ be an abeloid variety over
$A=E/M$ be an abeloid variety over ![]() $\mathbb {C}_p$ or
$\mathbb {C}_p$ or ![]() $\mathbb {C}_p^\flat$. Then
$\mathbb {C}_p^\flat$. Then
Proof. As we noted previously, the group ![]() $\overline B(\overline {\mathbb {F}}_p)$ is torsion, and thus
$\overline B(\overline {\mathbb {F}}_p)$ is torsion, and thus ![]() $\overline B(\overline {\mathbb {F}}_p)\otimes \mathbb {Q}=0$. By tensoring with
$\overline B(\overline {\mathbb {F}}_p)\otimes \mathbb {Q}=0$. By tensoring with ![]() $\mathbb {Q}$ the short exact sequence (8) in the case of
$\mathbb {Q}$ the short exact sequence (8) in the case of ![]() $A=B$, this proves the statement in the case of good reduction, where the lattice
$A=B$, this proves the statement in the case of good reduction, where the lattice ![]() $M$ is trivial.
$M$ is trivial.
The same argument shows that the inclusion ![]() $(1+\mathfrak {m}_K)\otimes \mathbb {Q}\to \mathcal {O}_{\mathbb {C}_p}^\times \otimes \mathbb {Q}$ is an isomorphism as
$(1+\mathfrak {m}_K)\otimes \mathbb {Q}\to \mathcal {O}_{\mathbb {C}_p}^\times \otimes \mathbb {Q}$ is an isomorphism as ![]() $\overline {\mathbb {F}}_p^\times$ is torsion. Consequently, the valuation on
$\overline {\mathbb {F}}_p^\times$ is torsion. Consequently, the valuation on ![]() $K$ defines a short exact sequence
$K$ defines a short exact sequence
If ![]() $M^\vee =\operatorname {Hom}(T,\mathbb {G}_m)$ denotes the character lattice of
$M^\vee =\operatorname {Hom}(T,\mathbb {G}_m)$ denotes the character lattice of ![]() $T$, we obtain from this and the pairing
$T$, we obtain from this and the pairing ![]() $M^\vee \times T(K)\to K^\times$ an exact sequence
$M^\vee \times T(K)\to K^\times$ an exact sequence
Now since ![]() $B\langle p^\infty \rangle (K)\otimes \mathbb {Q}=B(K)\otimes \mathbb {Q}$, we can use (9) to extend this to an exact sequence
$B\langle p^\infty \rangle (K)\otimes \mathbb {Q}=B(K)\otimes \mathbb {Q}$, we can use (9) to extend this to an exact sequence
Finally, we consider the composition
which is injective by duality theory of abeloids (see [Reference LütkebohmertLüt16, § 6.3, Proposition 6.1.8.c(ii)]). Consequently, tensoring with ![]() $\mathbb {Q}$ turns it into an injective homomorphism of
$\mathbb {Q}$ turns it into an injective homomorphism of ![]() $\mathbb {Q}$-vector spaces of the same dimension
$\mathbb {Q}$-vector spaces of the same dimension ![]() $\mathrm {rk} M=\mathrm {rk} T=\mathrm {rk} M^\vee$ and, hence, into an isomorphism. This shows that
$\mathrm {rk} M=\mathrm {rk} T=\mathrm {rk} M^\vee$ and, hence, into an isomorphism. This shows that ![]() $E\langle p^\infty \rangle (K)$ and
$E\langle p^\infty \rangle (K)$ and ![]() $M$ generate all of
$M$ generate all of ![]() $E(K)$ after tensoring with
$E(K)$ after tensoring with ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
3. Pro-finite-étale line bundles in families
Let ![]() $K$ be an algebraically closed non-archimedean field over
$K$ be an algebraically closed non-archimedean field over ![]() $\mathbb {Q}_p$ with ring of integral elements
$\mathbb {Q}_p$ with ring of integral elements ![]() $K^+$. Let
$K^+$. Let ![]() $\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space over
$\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space over ![]() $K$. Based on the preparations of the last section as well as the prequel articles [Reference HeuerHeu21a, Reference HeuerHeu22b], the goal of this section is to answer the following question in the case of line bundles.
$K$. Based on the preparations of the last section as well as the prequel articles [Reference HeuerHeu21a, Reference HeuerHeu22b], the goal of this section is to answer the following question in the case of line bundles.
Question 3.1 Which vector bundles on ![]() $X$ are trivialised by pro-finite-étale covers of
$X$ are trivialised by pro-finite-étale covers of ![]() $X$?
$X$?
As explained in detail in the introduction, this question is of interest in the ![]() $p$-adic Simpson correspondence, as it is known to lead to the answer of Question 1.6 in various situations, including the case of Higgs field
$p$-adic Simpson correspondence, as it is known to lead to the answer of Question 1.6 in various situations, including the case of Higgs field ![]() $0$, the case of line bundles and of abelian varieties [Reference WürthenWür23, Reference Mann and WernerMW23, Reference HeuerHeu22b, Reference Heuer, Mann and WernerHMW23]. Our aim is to give a complete answer to Question 3.1 in the case of line bundles, in terms of the topologically torsion subgroup of the Picard variety. This gives a more geometric, more explicit, and more conceptual description than that we previously gave in [Reference HeuerHeu22b, § 5]. Moreover, it naturally leads to a rigid moduli space of pro-finite-étale line bundles, without assuming that the rigid Picard functor is representable.
$0$, the case of line bundles and of abelian varieties [Reference WürthenWür23, Reference Mann and WernerMW23, Reference HeuerHeu22b, Reference Heuer, Mann and WernerHMW23]. Our aim is to give a complete answer to Question 3.1 in the case of line bundles, in terms of the topologically torsion subgroup of the Picard variety. This gives a more geometric, more explicit, and more conceptual description than that we previously gave in [Reference HeuerHeu22b, § 5]. Moreover, it naturally leads to a rigid moduli space of pro-finite-étale line bundles, without assuming that the rigid Picard functor is representable.
3.1 The rigid analytic character variety of  $\mathbb {G}_m$
$\mathbb {G}_m$
Our description of pro-finite-étale ![]() $v$-line bundles will be in terms of the
$v$-line bundles will be in terms of the ![]() $p$-adic analogue of the character variety, which we can define by an application of Proposition 2.14.
$p$-adic analogue of the character variety, which we can define by an application of Proposition 2.14.
Definition 3.2 Let ![]() $X$ be any connected smooth proper rigid space over
$X$ be any connected smooth proper rigid space over ![]() $(K,K^+)$. Let
$(K,K^+)$. Let ![]() $x\in X( K)$ be a base point and let
$x\in X( K)$ be a base point and let ![]() $\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$ be the étale fundamental group of
$\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$ be the étale fundamental group of ![]() $X$, a profinite group. Then the continuous character variety of
$X$, a profinite group. Then the continuous character variety of ![]() $X$ is the
$X$ is the ![]() $v$-sheaf on
$v$-sheaf on ![]() $\operatorname {Perf}_{K,v}$
$\operatorname {Perf}_{K,v}$
where ![]() $\pi _1(X)=\underline {\pi _1(X)}$ is considered as a profinite
$\pi _1(X)=\underline {\pi _1(X)}$ is considered as a profinite ![]() $v$-sheaf (Definition 2.2). Explicitly, the displayed sheaf sends
$v$-sheaf (Definition 2.2). Explicitly, the displayed sheaf sends ![]() $T\in \operatorname {Perf}_K$ to the set of
$T\in \operatorname {Perf}_K$ to the set of ![]() $T$-linear homomorphisms
$T$-linear homomorphisms ![]() $\underline {\pi _1(X)}\times T\to \mathbb {G}_m$, which we easily verify to be in bijection with the set of continuous group homomorphisms
$\underline {\pi _1(X)}\times T\to \mathbb {G}_m$, which we easily verify to be in bijection with the set of continuous group homomorphisms
Lemma 3.3 The continuous character variety is representable by a rigid analytic group whose identity component is non-canonically isomorphic to ![]() $\widehat {\mathbb {G}}_m^d$ for
$\widehat {\mathbb {G}}_m^d$ for ![]() $d=\dim _{\mathbb {Q}_p}H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)$ (here
$d=\dim _{\mathbb {Q}_p}H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)$ (here ![]() $\widehat {\mathbb {G}}_m$ is the open unit disc around
$\widehat {\mathbb {G}}_m$ is the open unit disc around ![]() $1$). Its group of connected components is torsion.
$1$). Its group of connected components is torsion.
If ![]() $\pi _1(X)$ is the profinite completion of a finitely generated group (e.g. if
$\pi _1(X)$ is the profinite completion of a finitely generated group (e.g. if ![]() $X$ is projective), then the proof shows that
$X$ is projective), then the proof shows that ![]() $\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is isomorphic to a finite disjoint union of copies of
$\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is isomorphic to a finite disjoint union of copies of ![]() $(\mathbb {G}_m^{\mathrm {tt}})^d$. Here the disjoint union accounts for torsion in the Néron–Severi group.
$(\mathbb {G}_m^{\mathrm {tt}})^d$. Here the disjoint union accounts for torsion in the Néron–Severi group.
Proof. Any continuous character ![]() $\pi _1(X)\to \mathcal {O}^\times (Y)$ for any perfectoid space
$\pi _1(X)\to \mathcal {O}^\times (Y)$ for any perfectoid space ![]() $Y$ factors through the maximal abelian quotient
$Y$ factors through the maximal abelian quotient ![]() $\pi ^{\mathrm {ab}}$ of
$\pi ^{\mathrm {ab}}$ of ![]() $\pi _1(X)$, so we have
$\pi _1(X)$, so we have
Let ![]() $T$ be the maximal torsionfree pro-
$T$ be the maximal torsionfree pro-![]() $p$-quotient of
$p$-quotient of ![]() $\pi ^{\mathrm {ab}}$. By [Reference HeuerHeu22b, Corollary 4.11],
$\pi ^{\mathrm {ab}}$. By [Reference HeuerHeu22b, Corollary 4.11], ![]() $T$ is a finite free
$T$ is a finite free ![]() $\mathbb {Z}_p$-module of rank
$\mathbb {Z}_p$-module of rank ![]() $d$ (the finiteness is based on [Reference ScholzeSch13, Theorem 1.1]). Thus,
$d$ (the finiteness is based on [Reference ScholzeSch13, Theorem 1.1]). Thus,
for some ![]() $p^\infty$-torsion group
$p^\infty$-torsion group ![]() $M$ and some profinite group
$M$ and some profinite group ![]() $N=\varprojlim N_i$ where each
$N=\varprojlim N_i$ where each ![]() $N_i$ has order coprime to
$N_i$ has order coprime to ![]() $p$. Hence,
$p$. Hence,
 \begin{align*}
\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)&=\underline{\mathrm{Hom}}(T,\mathbb{G}_m)\times
\underline{\mathrm{Hom}}(M,\mathbb{G}_m) \times \underline{\mathrm{Hom}}(N,\mathbb{G}_m)\\
&\cong\widehat{\mathbb{G}}_m^d\times \varinjlim\underline{\mathrm{Hom}}(N_i\times
M,\mathbb{G}_m) \end{align*}
\begin{align*}
\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)&=\underline{\mathrm{Hom}}(T,\mathbb{G}_m)\times
\underline{\mathrm{Hom}}(M,\mathbb{G}_m) \times \underline{\mathrm{Hom}}(N,\mathbb{G}_m)\\
&\cong\widehat{\mathbb{G}}_m^d\times \varinjlim\underline{\mathrm{Hom}}(N_i\times
M,\mathbb{G}_m) \end{align*}
3.2 Diamantine Picard functors
The second ingredient in our description of pro-finite-étale line bundles are the diamantine Picard functors introduced in [Reference HeuerHeu21a]. We therefore begin the discussion by recalling the definition and some basic properties.
Definition 3.4 Let ![]() $\pi :Y\to \operatorname {Spa}(K,K^+)$ be any locally spatial diamond and consider the associated morphism of big étale sites
$\pi :Y\to \operatorname {Spa}(K,K^+)$ be any locally spatial diamond and consider the associated morphism of big étale sites ![]() $\pi _{{\mathrm {\acute {e}t}}}:\mathrm {LSD}_{Y,{\mathrm {\acute {e}t}}}\to \operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Then we call
$\pi _{{\mathrm {\acute {e}t}}}:\mathrm {LSD}_{Y,{\mathrm {\acute {e}t}}}\to \operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Then we call
the étale diamantine Picard functor, where ![]() $\mathrm {Ab}$ is the category of abelian groups. Explicitly,
$\mathrm {Ab}$ is the category of abelian groups. Explicitly, ![]() $\mathbf {Pic}_{Y,{\mathrm {\acute {e}t}}}$ is the étale sheafification of the functor on
$\mathbf {Pic}_{Y,{\mathrm {\acute {e}t}}}$ is the étale sheafification of the functor on ![]() $\operatorname {Perf}_K$ that sends
$\operatorname {Perf}_K$ that sends ![]() $T\mapsto \operatorname {Pic}_{{\mathrm {\acute {e}t}}}(Y\times T)$.
$T\mapsto \operatorname {Pic}_{{\mathrm {\acute {e}t}}}(Y\times T)$.
Second, there is also a ![]() $v$-Picard functor which instead parametrises
$v$-Picard functor which instead parametrises ![]() $v$-line bundles, namely
$v$-line bundles, namely
the ![]() $v$-sheafification of
$v$-sheafification of ![]() $T\mapsto \operatorname {Pic}_{v}(Y\times T)$ where
$T\mapsto \operatorname {Pic}_{v}(Y\times T)$ where ![]() $T$ ranges through perfectoid spaces over
$T$ ranges through perfectoid spaces over ![]() $K$.
$K$.
We are most interested in the case that ![]() $Y=X$ is a smooth proper rigid space as before. In this case, the two main results of [Reference HeuerHeu21a] about these functors are as follows: we first proved that
$Y=X$ is a smooth proper rigid space as before. In this case, the two main results of [Reference HeuerHeu21a] about these functors are as follows: we first proved that ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is the ‘diamondification’ of the classical rigid analytic Picard functor defined on smooth rigid analytic test objects [Reference HeuerHeu21a, Theorem 1.1]. In particular, if the latter is represented by some rigid group
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is the ‘diamondification’ of the classical rigid analytic Picard functor defined on smooth rigid analytic test objects [Reference HeuerHeu21a, Theorem 1.1]. In particular, if the latter is represented by some rigid group ![]() $G$ (which conjecturally is always the case, and this is known, e.g., if
$G$ (which conjecturally is always the case, and this is known, e.g., if ![]() $X$ is projective), then
$X$ is projective), then ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by ![]() $G^\diamondsuit$. We therefore drop the additional
$G^\diamondsuit$. We therefore drop the additional ![]() $-^\diamondsuit$ used in [Reference HeuerHeu21a] from notation and write
$-^\diamondsuit$ used in [Reference HeuerHeu21a] from notation and write ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ instead of
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ instead of ![]() $\mathbf {Pic}^\diamondsuit _{X,{\mathrm {\acute {e}t}}}$.
$\mathbf {Pic}^\diamondsuit _{X,{\mathrm {\acute {e}t}}}$.
Second, we proved the following geometric version of the main theorem of [Reference HeuerHeu22b].
Theorem 3.5 [Reference HeuerHeu21a, Theorem 2.7 and Corollary 2.9]
There is a natural short exact sequence of abelian sheaves on ![]() $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$, functorial in
$\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$, functorial in ![]() $X$,
$X$,
In particular, this shows that ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is already a
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is already a ![]() $v$-sheaf and that
$v$-sheaf and that ![]() $\mathbf {Pic}_{X,v}$ is represented by a rigid group whenever
$\mathbf {Pic}_{X,v}$ is represented by a rigid group whenever ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is.
Note that in terms of the language introduced in the introduction, the last term in (11) can be interpreted as the ![]() $p$-adic Hitchin base
$p$-adic Hitchin base ![]() $\mathcal {A}$ in the context of line bundles.
$\mathcal {A}$ in the context of line bundles.
3.3 The pro-finite-étale universal cover
To make the connection to Question 3.1, we first reformulate the question slightly: recall that we have chosen a base point ![]() $x\in X(K)$. We consider the universal pro-finite-étale cover of
$x\in X(K)$. We consider the universal pro-finite-étale cover of ![]() $X$, defined as the spatial diamond
$X$, defined as the spatial diamond
where the index category is given by connected finite étale covers ![]() $(X',x')\to (X,x)$ with
$(X',x')\to (X,x)$ with ![]() $x'\in X'(K)$ a lift of
$x'\in X'(K)$ a lift of ![]() $x\in X(K)$. This is a pro-finite-étale
$x\in X(K)$. This is a pro-finite-étale ![]() $\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$-torsor. We refer to [Reference HeuerHeu22b, Definition 3.8] for further background.
$\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$-torsor. We refer to [Reference HeuerHeu22b, Definition 3.8] for further background.
By [Reference HeuerHeu22b, Lemma 4.8], we see that a vector bundle on ![]() $X$ is pro-finite-étale if and only if it becomes trivial after pullback to
$X$ is pro-finite-étale if and only if it becomes trivial after pullback to ![]() $\widetilde X\to X$. Moreover, we argued in [Reference HeuerHeu22b, § 5.2] that
$\widetilde X\to X$. Moreover, we argued in [Reference HeuerHeu22b, § 5.2] that ![]() $\widetilde X\to X$ plays a similar role for the
$\widetilde X\to X$ plays a similar role for the ![]() $p$-adic Simpson correspondence as the complex universal cover plays in the complex Simpson correspondence: there is an equivalence of categories
$p$-adic Simpson correspondence as the complex universal cover plays in the complex Simpson correspondence: there is an equivalence of categories
 \begin{align}\bigg\{\begin{array}{@{}c@{}l}\text{pro-finite-}{{\mathrm{\acute{e}tale}}}\\\text{$v$-vector bundles
on $X$} \end{array}\bigg\}&{\tilde{\to}}
\bigg\{\begin{array}{@{}c@{}l}\text{continuous
representations of
$\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$}\\\text{on finite-dimensional $K$-vector
spaces}\end{array}\bigg\}\\ V&\mapsto V(\widetilde X)
\end{align}
\begin{align}\bigg\{\begin{array}{@{}c@{}l}\text{pro-finite-}{{\mathrm{\acute{e}tale}}}\\\text{$v$-vector bundles
on $X$} \end{array}\bigg\}&{\tilde{\to}}
\bigg\{\begin{array}{@{}c@{}l}\text{continuous
representations of
$\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$}\\\text{on finite-dimensional $K$-vector
spaces}\end{array}\bigg\}\\ V&\mapsto V(\widetilde X)
\end{align}
since ![]() $\widetilde X\to X$ is a
$\widetilde X\to X$ is a ![]() $\pi _1(X)$-torsor and
$\pi _1(X)$-torsor and ![]() $\mathcal {O}(\widetilde X)=K$.
$\mathcal {O}(\widetilde X)=K$.
In order to describe the left-hand side for line bundles, we now use the diamantine Picard functor ![]() $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ of the universal cover. Namely, the main technical result of this article is that we can describe pro-finite-étale line bundles in terms of the topologically torsion subsheaf as defined in § 2 applied to the diamantine Picard functor of
$\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ of the universal cover. Namely, the main technical result of this article is that we can describe pro-finite-étale line bundles in terms of the topologically torsion subsheaf as defined in § 2 applied to the diamantine Picard functor of ![]() $X$:
$X$:
Here, we note that it makes sense to apply ![]() $-^\mathrm {tt}$ to
$-^\mathrm {tt}$ to ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ since this a
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ since this a ![]() $v$-sheaf by Theorem 3.5. Moreover,
$v$-sheaf by Theorem 3.5. Moreover, ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ has a close relation to the character variety from Definition 3.2.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ has a close relation to the character variety from Definition 3.2.
Theorem 3.6 Let ![]() $\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space.
$\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space.
(i) There is a short exact sequence of abelian sheaves on
 $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$
in which the first term can equivalently be described as
$\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$
in which the first term can equivalently be described as \[ 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^\mathrm{tt}\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\to \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}, \]
\[ 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^\mathrm{tt}\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\to \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}, \]
 $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}=R^1\pi _{{\mathrm {\acute {e}t}}\ast }(\mathbb {G}_m^\mathrm {tt})$.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}=R^1\pi _{{\mathrm {\acute {e}t}}\ast }(\mathbb {G}_m^\mathrm {tt})$.(ii) In the
 $v$-topology, we similarly have a short exact sequence
in which the first term can be naturally identified with the character variety
$v$-topology, we similarly have a short exact sequence
in which the first term can be naturally identified with the character variety \[ 0\to \mathbf{Pic}_{X,v}^\mathrm{tt}\to \mathbf{Pic}_{X,v}\to \mathbf{Pic}_{\widetilde X,v}, \]
\[ 0\to \mathbf{Pic}_{X,v}^\mathrm{tt}\to \mathbf{Pic}_{X,v}\to \mathbf{Pic}_{\widetilde X,v}, \]
 \[ \mathbf{Pic}_{X,v}^\mathrm{tt}=R^1\pi_{v\ast}(\mathbb{G}_m^\mathrm{tt})=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m). \]
\[ \mathbf{Pic}_{X,v}^\mathrm{tt}=R^1\pi_{v\ast}(\mathbb{G}_m^\mathrm{tt})=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m). \]
We prove Theorem 3.6 over the course of this section. First, we note that this gives the desired answer to Question 3.1 for line bundles: the pro-finite-étale line bundles on ![]() $X$ are precisely the topologically torsion
$X$ are precisely the topologically torsion ![]() $K$-points of the (classical) rigid-analytic Picard variety.
$K$-points of the (classical) rigid-analytic Picard variety.
Corollary 3.7 Assume that the rigid analytic Picard functor of ![]() $X$ is represented by a rigid group
$X$ is represented by a rigid group ![]() $G$. Then there is a left exact sequence
$G$. Then there is a left exact sequence
where ![]() $G(K)^\mathrm {tt}\subseteq G(K)$ is the subgroup of elements
$G(K)^\mathrm {tt}\subseteq G(K)$ is the subgroup of elements ![]() $x$ such that
$x$ such that ![]() $x^{n!}\to 1$ for
$x^{n!}\to 1$ for ![]() $n\to \infty$.
$n\to \infty$.
Proof. By [Reference HeuerHeu21a, Theorem 1.1], the assumption implies that also ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by the rigid group
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by the rigid group ![]() $G$. The result thus follows from Theorem 3.6(i) by evaluating at
$G$. The result thus follows from Theorem 3.6(i) by evaluating at ![]() $K$ and using that
$K$ and using that ![]() $G^\mathrm {tt}(K)=G(K)^\mathrm {tt}$ by Proposition 2.14(i) and (iii).
$G^\mathrm {tt}(K)=G(K)^\mathrm {tt}$ by Proposition 2.14(i) and (iii).
Remark 3.8
(i) If
 $K=\mathbb {C}_p$ and the identity component
$K=\mathbb {C}_p$ and the identity component  $G^0$ is abeloid, then by Proposition 2.23,
$G^0$ is abeloid, then by Proposition 2.23,  $G^\mathrm {tt}(\mathbb {C}_p)=G^\tau (\mathbb {C}_p)$ is generated by
$G^\mathrm {tt}(\mathbb {C}_p)=G^\tau (\mathbb {C}_p)$ is generated by  $G^0(\mathbb {C}_p)$ and torsion in the Néron–Severi group. In particular, these are then precisely the line bundles in
$G^0(\mathbb {C}_p)$ and torsion in the Néron–Severi group. In particular, these are then precisely the line bundles in  $\operatorname {Pic}(X)$ with vanishing Chern classes. However, this is no longer true over extensions of
$\operatorname {Pic}(X)$ with vanishing Chern classes. However, this is no longer true over extensions of  $\mathbb {C}_p$.
$\mathbb {C}_p$.(ii) Even without assuming any representability results,
 $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is always a small
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is always a small  $v$-sheaf (this follows from [Reference HeuerHeu22c, Theorem 7.13]), hence
$v$-sheaf (this follows from [Reference HeuerHeu22c, Theorem 7.13]), hence  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ always has the natural structure of a topological space by [Reference ScholzeSch18, Definition 12.8]. One can then still describe
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ always has the natural structure of a topological space by [Reference ScholzeSch18, Definition 12.8]. One can then still describe  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)$ as those
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)$ as those  $x$ in
$x$ in  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ such that
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ such that  $x^{n!}\to 1$ for
$x^{n!}\to 1$ for  $n\to \infty$.
$n\to \infty$.(iii) In general, the sequence is not right-exact: if
 $X$ is an abelian variety with good supersingular reduction
$X$ is an abelian variety with good supersingular reduction  $\overline {X}$, then
$\overline {X}$, then  $\operatorname {Pic}(\widetilde X)=\operatorname {Pic}(\overline {X})\otimes \mathbb {Q}$ by [Reference HeuerHeu21b, Theorem 4.1].
$\operatorname {Pic}(\widetilde X)=\operatorname {Pic}(\overline {X})\otimes \mathbb {Q}$ by [Reference HeuerHeu21b, Theorem 4.1].(iv) We cannot expect
 $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to be represented by an adic group: if
$\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to be represented by an adic group: if  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ and
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ and  $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ were both representable by adic groups, then the kernel of
$\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ were both representable by adic groups, then the kernel of  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ would be closed, a contradiction to Proposition 2.14 if
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ would be closed, a contradiction to Proposition 2.14 if  $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is a rigid group of dimension
$\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is a rigid group of dimension  $>0$. In fact, we show in [Reference HeuerHeu21b, § 6.5] that
$>0$. In fact, we show in [Reference HeuerHeu21b, § 6.5] that  $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ is typically not even a diamond.
$\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ is typically not even a diamond.
3.4 Relative universal property of the universal cover
The first step for the proof of Theorem 3.6 is to show that ![]() $\mathbb {G}_m^{\mathrm {tt}}$-torsors become trivial on the pro-finite-étale universal cover
$\mathbb {G}_m^{\mathrm {tt}}$-torsors become trivial on the pro-finite-étale universal cover ![]() $\widetilde X\to X$. This is part of the following analogue of the statement that the complex universal cover is simply connected. We recall that we write
$\widetilde X\to X$. This is part of the following analogue of the statement that the complex universal cover is simply connected. We recall that we write ![]() $\widetilde \pi :\widetilde X\to \operatorname {Spa}(K)$ for the structure map.
$\widetilde \pi :\widetilde X\to \operatorname {Spa}(K)$ for the structure map.
Proposition 3.9 Let ![]() $\mathcal {F}$ be any one of the
$\mathcal {F}$ be any one of the ![]() $v$-sheaves
$v$-sheaves ![]() $\mathcal {O}^{+a}/p^k$,
$\mathcal {O}^{+a}/p^k$, ![]() $\mathcal {O}^{+a}$,
$\mathcal {O}^{+a}$, ![]() $\mathcal {O}$,
$\mathcal {O}$, ![]() $\mathcal {O}^{\flat + a}$,
$\mathcal {O}^{\flat + a}$, ![]() $\mathcal {O}^\flat$,
$\mathcal {O}^\flat$, ![]() $\mathbb {G}_m\langle p^\infty \rangle$,
$\mathbb {G}_m\langle p^\infty \rangle$, ![]() $\mathbb {G}_m^{\mathrm {tt}}$, or
$\mathbb {G}_m^{\mathrm {tt}}$, or ![]() $\mathbb {Z}/N\mathbb {Z}$, where
$\mathbb {Z}/N\mathbb {Z}$, where ![]() $k,N\in \mathbb {N}$. Then for any affinoid perfectoid space
$k,N\in \mathbb {N}$. Then for any affinoid perfectoid space ![]() $Y$ over
$Y$ over ![]() $K$ and for
$K$ and for ![]() $n\in \{0,1\}$,
$n\in \{0,1\}$,
In particular, ![]() $\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=\mathcal {F}=\widetilde \pi _{v\ast }\mathcal {F}$ and
$\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=\mathcal {F}=\widetilde \pi _{v\ast }\mathcal {F}$ and ![]() $R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=0=R^1\widetilde \pi _{v\ast }\mathcal {F}$ on
$R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=0=R^1\widetilde \pi _{v\ast }\mathcal {F}$ on ![]() $\operatorname {Perf}_K$.
$\operatorname {Perf}_K$.
Remark 3.10 The restriction to ![]() $n\in \{0,1\}$ is necessary in general: the proposition does not hold for
$n\in \{0,1\}$ is necessary in general: the proposition does not hold for ![]() $n=2$ for any of the sheaves in the example of
$n=2$ for any of the sheaves in the example of ![]() $X=\mathbb {P}^1=\widetilde X$ and
$X=\mathbb {P}^1=\widetilde X$ and ![]() $Y{=}\operatorname {Spa}(K)$.
$Y{=}\operatorname {Spa}(K)$.
Proof. This is a relative version of [Reference HeuerHeu22b, Proposition 3.10], and the technical results of [Reference HeuerHeu21a, § 4] enable us to essentially follow the same line of argument: we start with ![]() $\mathcal {F}=\mathcal {O}^+/p^k$. By [Reference HeuerHeu21a, Proposition 4.12.2], which we recall as Lemma 3.11,
$\mathcal {F}=\mathcal {O}^+/p^k$. By [Reference HeuerHeu21a, Proposition 4.12.2], which we recall as Lemma 3.11,
where the ![]() $X'$ are as in the definition of
$X'$ are as in the definition of ![]() $\widetilde X$. By [Reference HeuerHeu21a, Corollary 4.6], this equals
$\widetilde X$. By [Reference HeuerHeu21a, Corollary 4.6], this equals
which vanishes because every class in ![]() $H^1_{\mathrm {\acute {e}t}}(X',\mathbb {Z}/p^k)$ is trivialised by a connected finite étale cover of
$H^1_{\mathrm {\acute {e}t}}(X',\mathbb {Z}/p^k)$ is trivialised by a connected finite étale cover of ![]() $X'$ and, thus, of
$X'$ and, thus, of ![]() $X$. This gives the case of
$X$. This gives the case of ![]() $n=1$.
$n=1$.
The case ![]() $n=0$ follows from Lemma 3.11 and [Reference HeuerHeu21a, Proposition 4.2.2.(iii)] which says that
$n=0$ follows from Lemma 3.11 and [Reference HeuerHeu21a, Proposition 4.2.2.(iii)] which says that
Next, consider ![]() $\mathcal {F}=\mathcal {O}^+$: the last equation implies that
$\mathcal {F}=\mathcal {O}^+$: the last equation implies that ![]() $R^1\varprojlim _{k\in \mathbb {N}} H^0(\widetilde X\times Y,\mathcal {O}^+/p^k)\stackrel {a}= 0$, so we deduce from the fact that the
$R^1\varprojlim _{k\in \mathbb {N}} H^0(\widetilde X\times Y,\mathcal {O}^+/p^k)\stackrel {a}= 0$, so we deduce from the fact that the ![]() $v$-site is replete and [Reference Bhatt and ScholzeBS15, Proposition 3.1.10] that
$v$-site is replete and [Reference Bhatt and ScholzeBS15, Proposition 3.1.10] that
The case of ![]() $\mathcal {O}$ follows. A similar limit argument gives the cases of
$\mathcal {O}$ follows. A similar limit argument gives the cases of ![]() $\mathcal {O}^{\flat +a}$ and then
$\mathcal {O}^{\flat +a}$ and then ![]() $\mathcal {O}^\flat$.
$\mathcal {O}^\flat$.
Since we have an injection ![]() $H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})\hookrightarrow H^1_{v}(\widetilde X\times Y,\mathcal {F})$, the result for
$H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})\hookrightarrow H^1_{v}(\widetilde X\times Y,\mathcal {F})$, the result for ![]() $H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})$ follows from the respective statements for
$H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})$ follows from the respective statements for ![]() $H^1_{v}(\widetilde X\times Y,\mathcal {F})$ for each of these sheaves.
$H^1_{v}(\widetilde X\times Y,\mathcal {F})$ for each of these sheaves.
For ![]() $\mathcal {F}=\mathbb {Z}/N\mathbb {Z}$, we know that étale and
$\mathcal {F}=\mathbb {Z}/N\mathbb {Z}$, we know that étale and ![]() $v$-topology agree. By [Reference ScholzeSch18, Proposition 14.9],
$v$-topology agree. By [Reference ScholzeSch18, Proposition 14.9],
For ![]() $n=0$, it follows from [Reference HeuerHeu21a, Corollary 4.8] that
$n=0$, it follows from [Reference HeuerHeu21a, Corollary 4.8] that ![]() $\widetilde \pi _{\ast }\mathbb {Z}/N\mathbb {Z}=\mathbb {Z}/N\mathbb {Z}$. To see the case of
$\widetilde \pi _{\ast }\mathbb {Z}/N\mathbb {Z}=\mathbb {Z}/N\mathbb {Z}$. To see the case of ![]() $n=1$, it thus suffices by the Leray sequence to prove that
$n=1$, it thus suffices by the Leray sequence to prove that ![]() $R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {Z}/N\mathbb {Z}=0$, which follows from the same cited result in the colimit over the
$R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {Z}/N\mathbb {Z}=0$, which follows from the same cited result in the colimit over the ![]() $X'$.
$X'$.
Finally, the case of ![]() $\mathbb {G}_m\langle p^\infty \rangle$ follows from that of
$\mathbb {G}_m\langle p^\infty \rangle$ follows from that of ![]() $\mu _{p^\infty }\cong \varinjlim \mathbb {Z}/p^k\mathbb {Z}$ (as
$\mu _{p^\infty }\cong \varinjlim \mathbb {Z}/p^k\mathbb {Z}$ (as ![]() $K$ is algebraically closed) and that of
$K$ is algebraically closed) and that of ![]() $\mathcal {O}$ by the logarithm sequence, and similarly for
$\mathcal {O}$ by the logarithm sequence, and similarly for ![]() $\mathbb {G}_m^\mathrm {tt}$ where we also include coprime-to-
$\mathbb {G}_m^\mathrm {tt}$ where we also include coprime-to-![]() $p$ torsion. This also shows that étale and
$p$ torsion. This also shows that étale and ![]() $v$-cohomology agree in this case.
$v$-cohomology agree in this case.
Lemma 3.11 Let ![]() $Y$ be any perfectoid space over
$Y$ be any perfectoid space over ![]() $K$ and let
$K$ and let ![]() $\widetilde X=\varprojlim _{i\in I} X_i$ be a diamond which is a limit of smooth quasi-compact quasi-separated (qcqs) rigid spaces over
$\widetilde X=\varprojlim _{i\in I} X_i$ be a diamond which is a limit of smooth quasi-compact quasi-separated (qcqs) rigid spaces over ![]() $K$ with finite étale transition maps. Then for the
$K$ with finite étale transition maps. Then for the ![]() $v$-sheaves
$v$-sheaves ![]() $\mathcal {F}=\mathcal {O}^{+a}/p$ or
$\mathcal {F}=\mathcal {O}^{+a}/p$ or ![]() $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$, we have for
$\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$, we have for ![]() $n\in \{0,1\}$:
$n\in \{0,1\}$:
Moreover, both sides stay the same when we exchange the ![]() $v$-topology for the étale topology.
$v$-topology for the étale topology.
Proof. For ![]() $\mathcal {F}=\mathcal {O}^{+a}/p$ and
$\mathcal {F}=\mathcal {O}^{+a}/p$ and ![]() $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$ this is [Reference HeuerHeu21a, Proposition 4.12.1 and 2] (where the latter sheaf was denoted by
$\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$ this is [Reference HeuerHeu21a, Proposition 4.12.1 and 2] (where the latter sheaf was denoted by ![]() $\overline {\mathcal {O}}^{\times }$). The case of
$\overline {\mathcal {O}}^{\times }$). The case of ![]() $\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$ follows by tensoring with
$\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$ follows by tensoring with ![]() $\mathbb {Q}$ since
$\mathbb {Q}$ since ![]() $\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}=(\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle )\otimes _{\mathbb {Z}} \mathbb {Q}$, see [Reference HeuerHeu22b, Lemma 2.16].
$\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}=(\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle )\otimes _{\mathbb {Z}} \mathbb {Q}$, see [Reference HeuerHeu22b, Lemma 2.16].
Corollary 3.12 The natural map ![]() $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,v}$ is injective.
$\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,v}$ is injective.
Proof. By Proposition 3.9, we have ![]() $\widetilde \pi _{\ast }\mathcal {O}=\mathcal {O}$ and, thus,
$\widetilde \pi _{\ast }\mathcal {O}=\mathcal {O}$ and, thus, ![]() $\widetilde \pi _{\ast }\mathbb {G}_m=\mathbb {G}_m$. We can therefore apply [Reference HeuerHeu21a, Lemma 4.13], which gives the following commutative diagram with short exact rows.
$\widetilde \pi _{\ast }\mathbb {G}_m=\mathbb {G}_m$. We can therefore apply [Reference HeuerHeu21a, Lemma 4.13], which gives the following commutative diagram with short exact rows.

As the first column is an isomorphism by [Reference Kedlaya and LiuKL16, Theorem 3.5.8], and the middle column is clearly injective, we can deduce that the last column is injective as well.
Remark 3.13 We do not know whether the map in Corollary 3.12 is an isomorphism in general. Although this is true for curves, it is certainly not always true that ![]() $v$-vector bundles on
$v$-vector bundles on ![]() $\widetilde X$ agree with étale vector bundles, as the example of
$\widetilde X$ agree with étale vector bundles, as the example of ![]() $X=\widetilde X=\mathbb {P}^1$ shows.
$X=\widetilde X=\mathbb {P}^1$ shows.
Remark 3.14 An alternative proof of Proposition 3.9 in the case of ![]() $\mathbb {Z}/N\mathbb {Z}$ and
$\mathbb {Z}/N\mathbb {Z}$ and ![]() $n=1$ would be to show that
$n=1$ would be to show that ![]() $(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$. One could deduce this from the following rigid analogue of a well-known algebraic statement: let
$(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$. One could deduce this from the following rigid analogue of a well-known algebraic statement: let ![]() $X$ be a connected proper rigid space and
$X$ be a connected proper rigid space and ![]() $Y$ any connected reduced rigid space. Then is the natural map
$Y$ any connected reduced rigid space. Then is the natural map ![]() $\pi ^{{\mathrm {\acute {e}t}}}_1(X\times Y)\to \pi _1^{{\mathrm {\acute {e}t}}}(X)\times \pi ^{{\mathrm {\acute {e}t}}}_1(Y)$ an isomorphism? We suspect that one could see this like in [Reference Grothendieck and RaynaudSGA1, X Corollaire 1.7], or using [Reference Scholze and WeinsteinSW20, § 16]. By an approximation argument, one could deduce that
$\pi ^{{\mathrm {\acute {e}t}}}_1(X\times Y)\to \pi _1^{{\mathrm {\acute {e}t}}}(X)\times \pi ^{{\mathrm {\acute {e}t}}}_1(Y)$ an isomorphism? We suspect that one could see this like in [Reference Grothendieck and RaynaudSGA1, X Corollaire 1.7], or using [Reference Scholze and WeinsteinSW20, § 16]. By an approximation argument, one could deduce that ![]() $(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$.
$(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$.
3.5 Topologically torsion line bundles
Next, we show that any pro-finite-étale line bundle admits a reduction of structure group from ![]() $\mathbb {G}_m$ to
$\mathbb {G}_m$ to ![]() $\mathbb {G}_m^\mathrm {tt}$. For this, we first show the following result.
$\mathbb {G}_m^\mathrm {tt}$. For this, we first show the following result.
Lemma 3.15 For any perfectoid space ![]() $Y$, there is for
$Y$, there is for ![]() $n\in \{0,1\}$ a natural isomorphism
$n\in \{0,1\}$ a natural isomorphism
Moreover, both sides remain the same when we exchange the ![]() $v$-topology for the étale topology.
$v$-topology for the étale topology.
Proof. We form the Cartan–Leray spectral sequence of the ![]() $\pi _1(X)$-torsor
$\pi _1(X)$-torsor ![]() $\widetilde X\times Y\to X\times Y$ for the sheaf
$\widetilde X\times Y\to X\times Y$ for the sheaf ![]() $\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, see [Reference HeuerHeu22b, Proposition 2.8]. Endow
$\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, see [Reference HeuerHeu22b, Proposition 2.8]. Endow ![]() $H^n_v(\widetilde X\times Y,\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})$ with the discrete topology, then by Lemma 3.11, we have for any profinite group
$H^n_v(\widetilde X\times Y,\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})$ with the discrete topology, then by Lemma 3.11, we have for any profinite group ![]() $G$:
$G$:
For ![]() $n=0$, the lemma follows by setting
$n=0$, the lemma follows by setting ![]() $G=\pi _1(X)$ and using the
$G=\pi _1(X)$ and using the ![]() $v$-sheaf property of
$v$-sheaf property of ![]() $\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$. For
$\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$. For ![]() $n=1$, this equation ensures that the conditions of [Reference HeuerHeu22b, Proposition 2.8.2] are satisfied. Setting
$n=1$, this equation ensures that the conditions of [Reference HeuerHeu22b, Proposition 2.8.2] are satisfied. Setting ![]() $G:=\pi _1(X)$ and
$G:=\pi _1(X)$ and ![]() $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, we thus obtain an exact sequence
$\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, we thus obtain an exact sequence
Since ![]() $G=\pi _1(X)$ is profinite and
$G=\pi _1(X)$ is profinite and ![]() $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ is a sheaf of
$\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ is a sheaf of ![]() $\mathbb {Q}$-vector spaces, the outer two groups vanish by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 1.6.2.c]. This gives the desired statement for the
$\mathbb {Q}$-vector spaces, the outer two groups vanish by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 1.6.2.c]. This gives the desired statement for the ![]() $v$-topology. The étale case follows from this by Lemma 3.11 and [Reference HeuerHeu21a, Proposition 4.12.1], or alternatively from the more general [Reference HeuerHeu22a, Proposition 4.8].
$v$-topology. The étale case follows from this by Lemma 3.11 and [Reference HeuerHeu21a, Proposition 4.12.1], or alternatively from the more general [Reference HeuerHeu22a, Proposition 4.8].
Lemma 3.16 [Reference HeuerHeu21a, Lemma 4.11.2]
We have ![]() $\pi _{\tau \ast }(\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ for
$\pi _{\tau \ast }(\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ for ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$.
$\tau \in \{{\mathrm {\acute {e}t}},v\}$.
Proof. The reference shows this for ![]() $\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$. The lemma follows by tensoring with
$\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$. The lemma follows by tensoring with ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
We can now complete the first steps of the proof of Theorem 3.6.
Proof of Theorem 3.6 Let ![]() $\tau \in \{{\mathrm {\acute {e}t}},v\}$ and consider the following morphism of exact sequences.
$\tau \in \{{\mathrm {\acute {e}t}},v\}$ and consider the following morphism of exact sequences.

Here the top left entry vanishes by Proposition 3.9. The right vertical morphism is injective by Lemma 3.15. The bottom left morphism is injective by Lemma 3.16.
This shows that we have a left-exact sequence:
We first consider ![]() $\tau ={\mathrm {\acute {e}t}}$. Note that (12) combines with Theorem 3.5 and Corollary 3.12 to show that
$\tau ={\mathrm {\acute {e}t}}$. Note that (12) combines with Theorem 3.5 and Corollary 3.12 to show that ![]() $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is the kernel of a morphism of
$R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is the kernel of a morphism of ![]() $v$-sheaves, hence it is itself a
$v$-sheaves, hence it is itself a ![]() $v$-sheaf. For Theorem 3.6(i), it remains to prove that
$v$-sheaf. For Theorem 3.6(i), it remains to prove that ![]() $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. This relies on the following key calculation, which crucially uses that our Picard functors use perfectoid test objects.
$R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. This relies on the following key calculation, which crucially uses that our Picard functors use perfectoid test objects.
Proposition 3.17 We have ![]() $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})=1$.
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})=1$.
Proof. For any affinoid perfectoid space ![]() $Y$ over
$Y$ over ![]() $K$, a section
$K$, a section ![]() $f\in \underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})(Y)$ is by definition of
$f\in \underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})(Y)$ is by definition of ![]() $\underline {\mathrm {Hom}}$ a morphism of sheaves on
$\underline {\mathrm {Hom}}$ a morphism of sheaves on ![]() $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$
$\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$
making the following diagram commute.

Here, in each row, ![]() $m$ denotes the multiplication morphism of abelian sheaves on
$m$ denotes the multiplication morphism of abelian sheaves on ![]() $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Denote by
$\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Denote by ![]() $q_1$ the morphism sending a map
$q_1$ the morphism sending a map ![]() $f:{\widehat {\mathbb {Z}}}\times Y\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to the composition
$f:{\widehat {\mathbb {Z}}}\times Y\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to the composition ![]() $m\circ (f\times f)$ in the diagram, and by
$m\circ (f\times f)$ in the diagram, and by ![]() $q_2$ the map sending
$q_2$ the map sending ![]() $f$ to
$f$ to ![]() $f\circ m$, then we can reformulate this description as saying that
$f\circ m$, then we can reformulate this description as saying that
We now use that for any ![]() $n\in \mathbb {N}$, we have, by Lemma 3.18 applied to
$n\in \mathbb {N}$, we have, by Lemma 3.18 applied to ![]() $F=\mathbb {G}_m$ and the composition
$F=\mathbb {G}_m$ and the composition ![]() $\widetilde X\times Y\times {\widehat {\mathbb {Z}}}^n\to Y\times {\widehat {\mathbb {Z}}}^n \to Y$, a natural identification
$\widetilde X\times Y\times {\widehat {\mathbb {Z}}}^n\to Y\times {\widehat {\mathbb {Z}}}^n \to Y$, a natural identification
It follows that the right-hand side of (13) equals the sheafification of the presheaf
on ![]() $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. We claim that this sheaf vanishes: let
$\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. We claim that this sheaf vanishes: let ![]() $g$ be the map defined as the composition
$g$ be the map defined as the composition
where ![]() $\pi _1$ is the projection to the first factor and
$\pi _1$ is the projection to the first factor and ![]() $r$ is the structure map. Invoking Lemma 3.18 again, we deduce that
$r$ is the structure map. Invoking Lemma 3.18 again, we deduce that
However, ![]() $R^1 \pi _{1,{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$ by Proposition 3.9. Hence,
$R^1 \pi _{1,{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$ by Proposition 3.9. Hence, ![]() $R^1g_{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$. It therefore suffices to prove that the presheaf on
$R^1g_{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$. It therefore suffices to prove that the presheaf on ![]() $\operatorname {Perf}_{K}$ given by
$\operatorname {Perf}_{K}$ given by
is trivial. For this, we use that by Lemma 3.11, we have for any ![]() $n\in \mathbb {N}$ an identification
$n\in \mathbb {N}$ an identification
where ![]() $\operatorname {Map}_{{\operatorname {lc}}}$ denotes the set of locally constant maps. Translating the morphisms
$\operatorname {Map}_{{\operatorname {lc}}}$ denotes the set of locally constant maps. Translating the morphisms ![]() $q_1$,
$q_1$, ![]() $q_2$ in (14) via this identification, we see that the presheaf (14) is precisely given by sending
$q_2$ in (14) via this identification, we see that the presheaf (14) is precisely given by sending ![]() $Y$ to
$Y$ to
However, the second argument is a ![]() $\mathbb {Q}$-vector space, so this group is trivial, as desired.
$\mathbb {Q}$-vector space, so this group is trivial, as desired.
Lemma 3.18 For any spatial diamonds ![]() $X$ and
$X$ and ![]() $Y$ over
$Y$ over ![]() $K$ and any profinite set
$K$ and any profinite set ![]() $S$, write
$S$, write
for the projections. Then for any abelian sheaf ![]() $F$ on
$F$ on ![]() $\mathrm {LSD}_{K,{\mathrm {\acute {e}t}}}$ and any
$\mathrm {LSD}_{K,{\mathrm {\acute {e}t}}}$ and any ![]() $n\geq 0$, we have
$n\geq 0$, we have
Proof. We claim that the functor ![]() $\pi _{2,{\mathrm {\acute {e}t}}\ast }$ from abelian sheaves on
$\pi _{2,{\mathrm {\acute {e}t}}\ast }$ from abelian sheaves on ![]() $(Y\times S)_{\mathrm {\acute {e}t}}$ to abelian sheaves on
$(Y\times S)_{\mathrm {\acute {e}t}}$ to abelian sheaves on ![]() $Y_{\mathrm {\acute {e}t}}$ is right-exact. Indeed, let
$Y_{\mathrm {\acute {e}t}}$ is right-exact. Indeed, let ![]() $F\to G$ be a surjection of sheaves on
$F\to G$ be a surjection of sheaves on ![]() $(Y\times S)_{\mathrm {\acute {e}t}}$ and let
$(Y\times S)_{\mathrm {\acute {e}t}}$ and let ![]() $\alpha \in \pi _{2,{\mathrm {\acute {e}t}}\ast }G(Y)=G(Y\times S)$, then there exists an étale cover
$\alpha \in \pi _{2,{\mathrm {\acute {e}t}}\ast }G(Y)=G(Y\times S)$, then there exists an étale cover ![]() $T\to Y\times S$ such that the image of
$T\to Y\times S$ such that the image of ![]() $\alpha$ in
$\alpha$ in ![]() $G(T)$ can be lifted to
$G(T)$ can be lifted to ![]() $F(T)$. Write
$F(T)$. Write ![]() $S=\varprojlim S_i$ for some finite sets
$S=\varprojlim S_i$ for some finite sets ![]() $S_i$, then
$S_i$, then ![]() $Y\times S=\varprojlim Y\times S_i$ in the category of diamonds. It follows using [Reference ScholzeSch18, Proposition 11.23] that the étale cover
$Y\times S=\varprojlim Y\times S_i$ in the category of diamonds. It follows using [Reference ScholzeSch18, Proposition 11.23] that the étale cover ![]() $T\to Y\times S$ can be refined by one of the form
$T\to Y\times S$ can be refined by one of the form ![]() $(Y'\times U_j\to Y\times S)_{j\in J}$ where
$(Y'\times U_j\to Y\times S)_{j\in J}$ where ![]() $Y'\to Y$ is an étale cover of
$Y'\to Y$ is an étale cover of ![]() $Y$ and
$Y$ and ![]() $\sqcup _{j\in J} U_j=S$ is a disjoint open cover of
$\sqcup _{j\in J} U_j=S$ is a disjoint open cover of ![]() $S$. Hence,
$S$. Hence, ![]() $\alpha$ also lifts to
$\alpha$ also lifts to
This shows that ![]() $\pi _{2,{\mathrm {\acute {e}t}}\ast }F\to \pi _{2,{\mathrm {\acute {e}t}}\ast }G$ is still surjective. It follows from this right-exactness that
$\pi _{2,{\mathrm {\acute {e}t}}\ast }F\to \pi _{2,{\mathrm {\acute {e}t}}\ast }G$ is still surjective. It follows from this right-exactness that ![]() $R\pi _{2,{\mathrm {\acute {e}t}}\ast }=\pi _{2,{\mathrm {\acute {e}t}}\ast }$. The lemma now follows from the Grothendieck spectral sequence.
$R\pi _{2,{\mathrm {\acute {e}t}}\ast }=\pi _{2,{\mathrm {\acute {e}t}}\ast }$. The lemma now follows from the Grothendieck spectral sequence.
To prove Theorem 3.6, we now apply the left-exact functor ![]() $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ to (12) and find
$\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ to (12) and find
by Proposition 3.17, hence
Since ![]() $\mathbb {G}_m^{\mathrm {tt}}$ is strongly topologically torsion by Proposition 2.14, Lemma 2.13 guarantees that the
$\mathbb {G}_m^{\mathrm {tt}}$ is strongly topologically torsion by Proposition 2.14, Lemma 2.13 guarantees that the ![]() $v$-sheaf
$v$-sheaf ![]() $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is topologically torsion, thus the left-hand side equals
$R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is topologically torsion, thus the left-hand side equals
This finishes the proof of part (i) of Theorem 3.6.
For the second part, we need to incorporate the character variety into the picture.
3.6 Relation to the character variety
Let ![]() $Y$ be an affinoid perfectoid space over
$Y$ be an affinoid perfectoid space over ![]() $K$. The Cartan–Leray short exact sequence for the
$K$. The Cartan–Leray short exact sequence for the ![]() $\pi _1(X)$-torsor
$\pi _1(X)$-torsor ![]() $\widetilde X\times Y\to X\times Y$ and the sheaf
$\widetilde X\times Y\to X\times Y$ and the sheaf ![]() $\mathbb {G}_m$ yields an exact sequence
$\mathbb {G}_m$ yields an exact sequence
By Proposition 3.9, ![]() $\mathbb {G}_m(\widetilde X\times Y)=\mathbb {G}_m(Y)$, so the first term equals
$\mathbb {G}_m(\widetilde X\times Y)=\mathbb {G}_m(Y)$, so the first term equals ![]() $\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),\mathbb {G}_m(Y))$. Using the character variety from Lemma 3.3, we thus obtain a left-exact sequence on
$\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),\mathbb {G}_m(Y))$. Using the character variety from Lemma 3.3, we thus obtain a left-exact sequence on ![]() $\operatorname {Perf}_{K,v}$
$\operatorname {Perf}_{K,v}$
We can describe the composition of the first map with ![]() $\mathrm {HTlog}$ more explicitly: recall that
$\mathrm {HTlog}$ more explicitly: recall that ![]() $\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)=\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}^\mathrm {tt}_m)$, so we can compose characters with
$\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)=\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}^\mathrm {tt}_m)$, so we can compose characters with ![]() $\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$.
$\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$.
Lemma 3.19 The following square is commutative and has a surjective diagonal.

Proof. By functoriality of the Cartan–Leray sequence (left square) and the definition of ![]() $\mathrm {HTlog}$ in [Reference HeuerHeu21a, Proposition 2.15] (right square), the following diagram commutes.
$\mathrm {HTlog}$ in [Reference HeuerHeu21a, Proposition 2.15] (right square), the following diagram commutes.

This shows commutativity. That the left map is surjective follows from Lemma 3.3 and surjectivity of ![]() $\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$. The map
$\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$. The map ![]() $\mathrm {HT}$ is surjective by [Reference HeuerHeu21a, Proposition 2.6].
$\mathrm {HT}$ is surjective by [Reference HeuerHeu21a, Proposition 2.6].
We can now put everything together: the diagram from Lemma 3.19 combines with (15) and the sequences from Theorems 3.5 and 3.6(i) to a commutative diagram

with left-exact rows. By Corollary 3.12, the morphism in the rightmost column is injective. By Lemma 3.19, the bottom dashed diagonal map is surjective. It follows from a diagram chase that ![]() $\mathbf {Pic}_{X,v}\to \mathbf {Pic}_{\widetilde X,v}$ admits a factorisation through the top dashed arrow: for example, it suffices to observe that by the snake lemma, the cokernels of the two horizontal maps in the top left square are isomorphic. Applying
$\mathbf {Pic}_{X,v}\to \mathbf {Pic}_{\widetilde X,v}$ admits a factorisation through the top dashed arrow: for example, it suffices to observe that by the snake lemma, the cokernels of the two horizontal maps in the top left square are isomorphic. Applying ![]() $\operatorname {Hom}({\widehat {\mathbb {Z}}},-)$, we deduce from Proposition 3.17 that this map becomes trivial, and we can thus argue as in the first part to deduce from the middle exact sequence that
$\operatorname {Hom}({\widehat {\mathbb {Z}}},-)$, we deduce from Proposition 3.17 that this map becomes trivial, and we can thus argue as in the first part to deduce from the middle exact sequence that
where the first equality follows from Lemma 3.3. This finishes the proof of Theorem 3.6(ii).
4. The morphism of Deninger and Werner
We now use Theorem 3.6 to give a reinterpretation, a generalisation, and a geometrisation of a construction of Deninger and Werner in the context of the ![]() $p$-adic Simpson correspondence.
$p$-adic Simpson correspondence.
Let ![]() $X$ be a connected smooth projective curve over
$X$ be a connected smooth projective curve over ![]() $\overline {\mathbb {Q}}_p$. We fix a base-point
$\overline {\mathbb {Q}}_p$. We fix a base-point ![]() $x\in X(\overline {\mathbb {Q}}_p)$. In [Reference Deninger and WernerDW05b], Deninger and Werner construct a functor from a certain category of vector bundles on
$x\in X(\overline {\mathbb {Q}}_p)$. In [Reference Deninger and WernerDW05b], Deninger and Werner construct a functor from a certain category of vector bundles on ![]() $X_{\mathbb {C}_p}$ to
$X_{\mathbb {C}_p}$ to ![]() $\mathbb {C}_p$-linear representations of the étale fundamental group
$\mathbb {C}_p$-linear representations of the étale fundamental group ![]() $\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ of
$\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ of ![]() $X$, thus defining a
$X$, thus defining a ![]() $p$-adic Simpson functor in the case of vanishing Higgs field, or in other words a partial analogue of Narasimhan–Seshadri theory. In [Reference Deninger and WernerDW05a], they go on to study this functor in the case of line bundles under the additional assumption that
$p$-adic Simpson functor in the case of vanishing Higgs field, or in other words a partial analogue of Narasimhan–Seshadri theory. In [Reference Deninger and WernerDW05a], they go on to study this functor in the case of line bundles under the additional assumption that ![]() $X$ has good reduction: in this case, their functor induces an injective continuous homomorphism
$X$ has good reduction: in this case, their functor induces an injective continuous homomorphism
where ![]() $A=\mathbf {Pic}^{0}_X(\mathbb {C}_p)$ is the Jacobian of
$A=\mathbf {Pic}^{0}_X(\mathbb {C}_p)$ is the Jacobian of ![]() $X$ and
$X$ and ![]() $TA^\vee$ is the adelic Tate module of its dual, i.e. of the Albanese. Deninger and Werner give an explicit description of
$TA^\vee$ is the adelic Tate module of its dual, i.e. of the Albanese. Deninger and Werner give an explicit description of ![]() $\alpha$ in terms of the Weil pairing of
$\alpha$ in terms of the Weil pairing of ![]() $A$, and extend their construction to any connected smooth proper algebraic variety
$A$, and extend their construction to any connected smooth proper algebraic variety ![]() $X$ over
$X$ over ![]() $\overline {\mathbb {Q}}_p$ satisfying a certain good reduction assumption (see [Reference Deninger and WernerDW05b, § 1.5]), obtaining more generally a morphism
$\overline {\mathbb {Q}}_p$ satisfying a certain good reduction assumption (see [Reference Deninger and WernerDW05b, § 1.5]), obtaining more generally a morphism ![]() $\alpha$ defined on the
$\alpha$ defined on the ![]() $\mathbb {C}_p$-points of the open and closed subgroup
$\mathbb {C}_p$-points of the open and closed subgroup ![]() $\mathbf {Pic}^{\tau }_X$ of the Picard variety whose image in the Néron–Severi group is torsion.
$\mathbf {Pic}^{\tau }_X$ of the Picard variety whose image in the Néron–Severi group is torsion.
In the case that ![]() $X$ is a curve over
$X$ is a curve over ![]() $\overline {\mathbb {Q}}_p$ with good reduction, Song [Reference SongSon22] has recently shown that the morphism
$\overline {\mathbb {Q}}_p$ with good reduction, Song [Reference SongSon22] has recently shown that the morphism ![]() $\alpha$ can be ‘geometrised’, i.e. interpreted as the
$\alpha$ can be ‘geometrised’, i.e. interpreted as the ![]() $\mathbb {C}_p$-points of a morphism of rigid group varieties.
$\mathbb {C}_p$-points of a morphism of rigid group varieties.
4.1 Geometrisation of Deninger and Werner's morphism
We now generalise and geometrise the results of Deninger and Werner and Song to any smooth proper rigid space ![]() $X$ of arbitrary dimension over any complete algebraically closed field
$X$ of arbitrary dimension over any complete algebraically closed field ![]() $K$ over
$K$ over ![]() $\mathbb {Q}_p$. For this we use a completely different method based on Theorems 3.5 and 3.6. Namely, we have the following result, which includes a topologically torsion version of Theorem 3.5.
$\mathbb {Q}_p$. For this we use a completely different method based on Theorems 3.5 and 3.6. Namely, we have the following result, which includes a topologically torsion version of Theorem 3.5.
Theorem 4.1 Let ![]() $X$ be a connected smooth proper rigid space over
$X$ be a connected smooth proper rigid space over ![]() $K$. Then we have the following.
$K$. Then we have the following.
(i) The topologically torsion Picard functor
is represented by a disjoint union of rigid analytic divisible groups. \[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}=R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}} \]
\[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}=R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}} \]
(ii) There is a natural short exact sequence of rigid group varieties
(16)where \begin{equation} 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\to \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)\xrightarrow{\mathrm{HTlog}} \mathcal{A}\to 0, \end{equation}
\begin{equation} 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\to \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)\xrightarrow{\mathrm{HTlog}} \mathcal{A}\to 0, \end{equation} $\mathcal {A}:=H^0(X,\Omega ^1_X(-1))\otimes \mathbb {G}_a$. It is functorial in
$\mathcal {A}:=H^0(X,\Omega ^1_X(-1))\otimes \mathbb {G}_a$. It is functorial in  $X\to \operatorname {Spa}(K)$ and canonically isomorphic to the topologically torsion part of the sequence (11) in Theorem 3.5.
$X\to \operatorname {Spa}(K)$ and canonically isomorphic to the topologically torsion part of the sequence (11) in Theorem 3.5.(iii) The exact sequence obtained from (16) by passing to Lie algebras, i.e. tangent spaces at the identity, is canonically identified with the Hodge–Tate sequence
 \[ 0\to H^1_{\mathrm{an}}(X,\mathcal{O})\to H^1_{{\mathrm{\acute{e}t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p} K\xrightarrow{\mathrm{HT}} H^0(X,\Omega^1(-1))\to 0. \]
\[ 0\to H^1_{\mathrm{an}}(X,\mathcal{O})\to H^1_{{\mathrm{\acute{e}t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p} K\xrightarrow{\mathrm{HT}} H^0(X,\Omega^1(-1))\to 0. \]
(iv) The first map of (16) induces a natural non-degenerate pairing of adic groups
 \[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \underline{\pi_1(X)}\to \mathbb{G}_m. \]
\[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \underline{\pi_1(X)}\to \mathbb{G}_m. \]
(v) If
 $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\tau }$ is an abeloid variety, then the pairing in part (iv) is the unique analytic continuation of the Weil pairing.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\tau }$ is an abeloid variety, then the pairing in part (iv) is the unique analytic continuation of the Weil pairing.
The first morphism in (16) generalises the map ![]() $\alpha$ of Deninger and Werner and Song. Indeed, if
$\alpha$ of Deninger and Werner and Song. Indeed, if ![]() $\mathbf {Pic}^{\tau }_{X,{\mathrm {\acute {e}t}}}$ is abeloid and
$\mathbf {Pic}^{\tau }_{X,{\mathrm {\acute {e}t}}}$ is abeloid and ![]() $K=\mathbb {C}_p$, then by Proposition 2.23, we have
$K=\mathbb {C}_p$, then by Proposition 2.23, we have ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(\mathbb {C}_p)=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}(\mathbb {C}_p)$.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(\mathbb {C}_p)=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}(\mathbb {C}_p)$.
However, this is no longer true over more general fields, where we need to use the topologically torsion subsheaf rather than all of ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\tau$ to define
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\tau$ to define ![]() $\alpha$. The last part is our analogue of the statement in [Reference Deninger and WernerDW05a, § 4] that
$\alpha$. The last part is our analogue of the statement in [Reference Deninger and WernerDW05a, § 4] that ![]() $\alpha$ is an extension of the Weil pairing in the case of curves.
$\alpha$ is an extension of the Weil pairing in the case of curves.
Remark 4.2 We note that in contrast to [Reference SongSon22, Theorem 1.0.1], the domain of our morphism is not ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ but the open subspace
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ but the open subspace ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$. For curves over
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$. For curves over ![]() $\mathbb {C}_p$, both spaces have the same
$\mathbb {C}_p$, both spaces have the same ![]() $\mathbb {C}_p$-points, but the latter has more points when considered as an adic space. In particular, the assumptions of [Reference SongSon22, Theorems 1.0.1 and 1.0.3] are never satisfied. Indeed, note that any morphism from the proper space
$\mathbb {C}_p$-points, but the latter has more points when considered as an adic space. In particular, the assumptions of [Reference SongSon22, Theorems 1.0.1 and 1.0.3] are never satisfied. Indeed, note that any morphism from the proper space ![]() $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ to
$\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ to ![]() $\mathbb {G}_m$ is trivial. That said, for curves, one can use Song's construction to explicitly define a map on
$\mathbb {G}_m$ is trivial. That said, for curves, one can use Song's construction to explicitly define a map on ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$.
Remark 4.3 As pointed out in Remark 1.5, in the setting of curves, the analogue of the short exact sequence of Theorem 4.1 in the complex analytic setting of the Corlette–Simpson correspondence is only real-analytic. This difference to the ![]() $p$-adic case can in part be attributed to the fact that the pro-étale fundamental group appearing in Theorem 4.1 is profinite and thus ignores the second factor in the decomposition
$p$-adic case can in part be attributed to the fact that the pro-étale fundamental group appearing in Theorem 4.1 is profinite and thus ignores the second factor in the decomposition ![]() $\mathbb {C}_p^\times =\mathcal {O}_{\mathbb {C}_p}^\times \times \mathbb {Q}$.
$\mathbb {C}_p^\times =\mathcal {O}_{\mathbb {C}_p}^\times \times \mathbb {Q}$.
Proof of Theorem 4.1 We first construct the exact sequence (16) in ![]() $v$-sheaves: as such, it arises from (11) by applying the functor
$v$-sheaves: as such, it arises from (11) by applying the functor ![]() $-^\mathrm {tt}$ from § 2.2. To see that this preserves exactness, we use that by [Reference HeuerHeu21a, Theorem 2.7.3], the sequence (11) is split over the open subgroup
$-^\mathrm {tt}$ from § 2.2. To see that this preserves exactness, we use that by [Reference HeuerHeu21a, Theorem 2.7.3], the sequence (11) is split over the open subgroup
defined by the image of ![]() $\underline {\mathrm {Hom}}(\pi _1(X),p\mathbb {G}_a^+)$ under the morphism
$\underline {\mathrm {Hom}}(\pi _1(X),p\mathbb {G}_a^+)$ under the morphism ![]() $\mathrm {HT}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_a)\to \mathcal {A}$. More explicitly, let
$\mathrm {HT}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_a)\to \mathcal {A}$. More explicitly, let ![]() $\mathbf {Pic}_{X,v}^+$ be the pullback under
$\mathbf {Pic}_{X,v}^+$ be the pullback under ![]() $\mathrm {HTlog}$ of
$\mathrm {HTlog}$ of ![]() $\mathcal {A}^+$, then the induced sequence
$\mathcal {A}^+$, then the induced sequence
is split and, in particular, exactness is preserved by the additive functor ![]() $-^{\mathrm {tt}}$. This shows left-exactness. Right-exactness follows from Lemma 3.19.
$-^{\mathrm {tt}}$. This shows left-exactness. Right-exactness follows from Lemma 3.19.
We deduce that ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ is the kernel of a morphism of rigid groups. Hence, it is itself representable by a rigid group. Since the other terms in (16) are disjoint unions of analytic divisible groups, so is
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ is the kernel of a morphism of rigid groups. Hence, it is itself representable by a rigid group. Since the other terms in (16) are disjoint unions of analytic divisible groups, so is ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$. We have thus shown parts (i) and (ii).
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$. We have thus shown parts (i) and (ii).
In order to deduce part (iii), we note that adding kernels to Lemma 3.19 induces the following morphism of short exact sequences.

Since the middle arrow is an isomorphism in a neighbourhood of the identity (because ![]() $\log$ is), this induces an isomorphism between the associated sequences on tangent spaces.
$\log$ is), this induces an isomorphism between the associated sequences on tangent spaces.
The pairing in part (iv) is associated to the map ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the adjunction of
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the adjunction of ![]() $\otimes$ and
$\otimes$ and ![]() $\underline {\mathrm {Hom}}$. It remains to prove part (v). Via the theory of the rigid Albanese variety developed in [Reference Hansen and LiHL20, § 4], and using the functoriality of Theorem 3.5, we can reduce to the case that
$\underline {\mathrm {Hom}}$. It remains to prove part (v). Via the theory of the rigid Albanese variety developed in [Reference Hansen and LiHL20, § 4], and using the functoriality of Theorem 3.5, we can reduce to the case that ![]() $X$ is itself an abeloid variety. We postpone the explicit description of the pairing in the abeloid case to the next subsection.
$X$ is itself an abeloid variety. We postpone the explicit description of the pairing in the abeloid case to the next subsection.
First, we give two corollaries. For this we first note the following very general fact.
Remark 4.4 Given any short exact sequence of rigid groups ![]() $0\to A\to B\xrightarrow {q} C\to 0$ (say, in the étale topology), we can forget the group structure on
$0\to A\to B\xrightarrow {q} C\to 0$ (say, in the étale topology), we can forget the group structure on ![]() $B$ and
$B$ and ![]() $C$ and regard the map
$C$ and regard the map ![]() $q:B\to C$ as an
$q:B\to C$ as an ![]() $A$-torsor in a natural way. (Slightly more precisely, it is a torsor in
$A$-torsor in a natural way. (Slightly more precisely, it is a torsor in ![]() $C_{\mathrm {\acute {e}t}}$ under the group object in
$C_{\mathrm {\acute {e}t}}$ under the group object in ![]() $C_{\mathrm {\acute {e}t}}$ represented by
$C_{\mathrm {\acute {e}t}}$ represented by ![]() $A\times C\to C$, but we still call this an
$A\times C\to C$, but we still call this an ![]() $A$-torsor.) Indeed, over any étale cover
$A$-torsor.) Indeed, over any étale cover ![]() $D\to C$ where
$D\to C$ where ![]() $q$ admits a splitting
$q$ admits a splitting ![]() $s:D\to B$ over
$s:D\to B$ over ![]() $C$, the natural map
$C$, the natural map ![]() $A\times D\to B\times _CD$ is an isomorphism with inverse
$A\times D\to B\times _CD$ is an isomorphism with inverse ![]() $(b,d)\mapsto (b-s(d),d)$.
$(b,d)\mapsto (b-s(d),d)$.
With Remark 4.4 in mind, we can deduce the following from combining Theorems 3.5 and 4.1.
Corollary 4.5
(i) The map
 $\mathrm {HTlog}:\mathbf {Pic}_{X,v}\to \mathcal {A}$ is an étale
$\mathrm {HTlog}:\mathbf {Pic}_{X,v}\to \mathcal {A}$ is an étale  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsor.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsor.(ii) The map
 $\mathrm {HTlog}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)\to \mathcal {A}$ is an étale
$\mathrm {HTlog}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)\to \mathcal {A}$ is an étale  $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsor.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsor.(iii) The torsor in part (i) is the pushout of the torsor in part (ii) along
 $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$.
Corollary 4.6 The sequences (11) and (16) are never split unless ![]() $H^0(X,\Omega _X^1)=0$. Indeed, any morphism
$H^0(X,\Omega _X^1)=0$. Indeed, any morphism ![]() $\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is constant.
$\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is constant.
Proof. Any splitting of (16) would be a morphism of rigid spaces ![]() $s:\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$. While its source is a product of copies of
$s:\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$. While its source is a product of copies of ![]() $\mathbb {G}_a$, each connected component of the target is contained in an affinoid subspace of
$\mathbb {G}_a$, each connected component of the target is contained in an affinoid subspace of ![]() $\mathbb {G}_m^d$ for some
$\mathbb {G}_m^d$ for some ![]() $d\in \mathbb {N}$. Hence,
$d\in \mathbb {N}$. Hence, ![]() $s$ is constant.
$s$ is constant.
The statement for (11) follows as we obtain (16) from (11) by applying the functor ![]() $-^\mathrm {tt}$.
$-^\mathrm {tt}$.
4.2 The Weil pairing from a pro-étale perspective
We now prove Theorem 4.1(v), namely that the pairing from part (iv) can be described as a unique analytic continuation of the Weil pairing if ![]() $X$ is abeloid. This is a pleasant application of Theorem 3.6 in its own right.
$X$ is abeloid. This is a pleasant application of Theorem 3.6 in its own right.
Remark 4.7 We note that it has long been known that such analytic Weil pairings exists: for abelian varieties of good reduction this is constructed in [Reference TateTat67, § 4]. Another related construction is by Fontaine [Reference FontaineFon03, Proposition 1.1] who gives for any abelian variety ![]() $A$ over a finite extension
$A$ over a finite extension ![]() $L$ of
$L$ of ![]() $\mathbb {Q}_p$ a natural continuous Galois-equivariant homomorphism that reinterpreted in our notation (via Propositions 2.23 and 2.14) is of the form
$\mathbb {Q}_p$ a natural continuous Galois-equivariant homomorphism that reinterpreted in our notation (via Propositions 2.23 and 2.14) is of the form
By comparing Fontaine's construction to ours, it is clear that (the topologically ![]() $p$-torsion part of) the analytic Weil pairing from Theorem 4.1 is a geometrisation of Fontaine's map.
$p$-torsion part of) the analytic Weil pairing from Theorem 4.1 is a geometrisation of Fontaine's map.
Let ![]() $A$ be an abeloid variety over
$A$ be an abeloid variety over ![]() $K$. The Weil pairing of
$K$. The Weil pairing of ![]() $A$ is the perfect pairing
$A$ is the perfect pairing
defined as follows: let ![]() $\mathcal {P}$ be the Poincaré bundle on
$\mathcal {P}$ be the Poincaré bundle on ![]() $A\times A^\vee$, then by bilinearity its restriction to
$A\times A^\vee$, then by bilinearity its restriction to ![]() $A\times A^\vee [N]$ has trivial
$A\times A^\vee [N]$ has trivial ![]() $N$th tensor power. It follows that
$N$th tensor power. It follows that ![]() $\mathcal {P}$ admits a canonical reduction of structure group to a
$\mathcal {P}$ admits a canonical reduction of structure group to a ![]() $\mu _N$-torsor
$\mu _N$-torsor ![]() $\mathcal {P}_N$ on
$\mathcal {P}_N$ on ![]() $A\times A^\vee$ that becomes trivial after pullback along
$A\times A^\vee$ that becomes trivial after pullback along ![]() $[N]:A\to A$. Consequently, we have a natural commutative diagram of bi-extensions
$[N]:A\to A$. Consequently, we have a natural commutative diagram of bi-extensions

and the Weil pairing is defined as the induced arrow on the left.
We can now extend this construction using the universal cover ![]() $\widetilde A$ of
$\widetilde A$ of ![]() $A$ from § 3.3. In the abeloid case, this is given by the space
$A$ from § 3.3. In the abeloid case, this is given by the space ![]() $\widetilde A=\textstyle \varprojlim _{[N],N\in \mathbb {N}}A$ and thus sits in an exact sequence
$\widetilde A=\textstyle \varprojlim _{[N],N\in \mathbb {N}}A$ and thus sits in an exact sequence
where ![]() $TA=\pi ^{\mathrm {\acute {e}t}}_1(A,0)=\varprojlim _{N\in \mathbb {N}} A[N]$ is the Tate module of
$TA=\pi ^{\mathrm {\acute {e}t}}_1(A,0)=\varprojlim _{N\in \mathbb {N}} A[N]$ is the Tate module of ![]() $A$. We now restrict to the open subspace
$A$. We now restrict to the open subspace ![]() $A\times A^{\vee \mathrm {tt}}\subseteq A\times A^\vee$. By Theorem 3.6(i), this is the locus where
$A\times A^{\vee \mathrm {tt}}\subseteq A\times A^\vee$. By Theorem 3.6(i), this is the locus where ![]() $\mathcal {P}$ admits a reduction of structure group to a
$\mathcal {P}$ admits a reduction of structure group to a ![]() $\mathbb {G}_m^{\mathrm {tt}}$-torsor
$\mathbb {G}_m^{\mathrm {tt}}$-torsor ![]() $\widehat {\mathcal {P}}$, which inherits from
$\widehat {\mathcal {P}}$, which inherits from ![]() $\mathcal {P}$ the structure of a bi-extension
$\mathcal {P}$ the structure of a bi-extension
Concretely, this means that it becomes an exact sequence of abelian sheaves on ![]() $\mathrm {LSD}_{A}$ and
$\mathrm {LSD}_{A}$ and ![]() $\mathrm {LSD}_{A^{\vee \mathrm {tt}}}$, respectively, when restricted to test objects relatively over either factor.
$\mathrm {LSD}_{A^{\vee \mathrm {tt}}}$, respectively, when restricted to test objects relatively over either factor.
By Theorem 3.6(i), this bi-extension becomes trivial upon pullback to ![]() $\widetilde A$. Using the short exact sequence of
$\widetilde A$. Using the short exact sequence of ![]() $\widetilde A$, we thus obtain a pushout diagram of adic groups relatively over
$\widetilde A$, we thus obtain a pushout diagram of adic groups relatively over ![]() $A^{\vee \mathrm {tt}}$
$A^{\vee \mathrm {tt}}$

where the middle arrow exists because ![]() $\mathcal {P}$ becomes split on
$\mathcal {P}$ becomes split on ![]() $\widetilde A\times A^{\vee \mathrm {tt}}$, and is unique because any two morphisms differ by a map from
$\widetilde A\times A^{\vee \mathrm {tt}}$, and is unique because any two morphisms differ by a map from ![]() $\widetilde A$ to
$\widetilde A$ to ![]() $\mathbb {G}_m^\mathrm {tt}$, which has to be trivial by Proposition 3.9.
$\mathbb {G}_m^\mathrm {tt}$, which has to be trivial by Proposition 3.9.
On the left, we thus obtain the desired bilinear pairing ![]() $\mathbf {e}:TA\times A^{\vee \mathrm {tt}}\to \mathbb {G}^\mathrm {tt}_m$. It is clear from the construction via pullback to
$\mathbf {e}:TA\times A^{\vee \mathrm {tt}}\to \mathbb {G}^\mathrm {tt}_m$. It is clear from the construction via pullback to ![]() $\widetilde A$ that this is precisely the pairing from Theorem 4.1. On the other hand, it is also clear from comparing to the pullback of (17) to
$\widetilde A$ that this is precisely the pairing from Theorem 4.1. On the other hand, it is also clear from comparing to the pullback of (17) to ![]() $\widetilde A$ that this gives an analytic continuation of the adelic Weil pairing
$\widetilde A$ that this gives an analytic continuation of the adelic Weil pairing
It remains to see that this property determines ![]() $\mathbf {e}$ uniquely: for this we use that by Proposition 2.14, for each
$\mathbf {e}$ uniquely: for this we use that by Proposition 2.14, for each ![]() $x\in TA$ the morphism
$x\in TA$ the morphism ![]() $\mathbf {e}(x,-)$ is uniquely determined by its value on prime-to-
$\mathbf {e}(x,-)$ is uniquely determined by its value on prime-to-![]() $p$ torsion and a morphism on the analytic
$p$ torsion and a morphism on the analytic ![]() $p$-divisible group
$p$-divisible group ![]() $A\langle p^\infty \rangle \to \mathbb {G}_m\langle p^\infty \rangle$. By fully faithfulness of Fargues’ functor from
$A\langle p^\infty \rangle \to \mathbb {G}_m\langle p^\infty \rangle$. By fully faithfulness of Fargues’ functor from ![]() $p$-divisible groups to analytic
$p$-divisible groups to analytic ![]() $p$-divisible groups [Reference FarguesFar19, Théorème 6.1], this is uniquely determined on
$p$-divisible groups [Reference FarguesFar19, Théorème 6.1], this is uniquely determined on ![]() $p$-torsion points, as desired.
$p$-torsion points, as desired.
Remark 4.8 As an application of Theorem 4.1, we point out that the geometric Simpson correspondence can, in turn, be used to study classical rigid analytic Picard functors.
It is expected that for any smooth proper rigid space ![]() $X$, the Picard functor
$X$, the Picard functor ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by a rigid group, and many instances of this are known, see [Reference HeuerHeu21a, § 1]. In all known cases, one additionally has the structural result that the identity component
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by a rigid group, and many instances of this are known, see [Reference HeuerHeu21a, § 1]. In all known cases, one additionally has the structural result that the identity component ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ is a semi-abeloid variety, i.e. an extension of an abeloid by a rigid torus, see especially [Reference Hartl and LütkebohmertHL00]. However, it currently seems an open question if one should expect such a description in general.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ is a semi-abeloid variety, i.e. an extension of an abeloid by a rigid torus, see especially [Reference Hartl and LütkebohmertHL00]. However, it currently seems an open question if one should expect such a description in general.
From this perspective, Theorem 4.1 gives the new result that a topologically torsion variant of the Picard functor is always representable. In particular, if ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is representable by a rigid group, this describes its open topologically torsion subgroup. From this we can deduce structural results on
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is representable by a rigid group, this describes its open topologically torsion subgroup. From this we can deduce structural results on ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ which provide evidence that
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ which provide evidence that ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ might always be representable by a semi-abeloid variety. Namely, Theorem 4.1 imposes concrete structural restrictions on what rigid groups can appear as Picard varieties, such as existence of an analytic Weil pairing on topological torsion, which are consistent with
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ might always be representable by a semi-abeloid variety. Namely, Theorem 4.1 imposes concrete structural restrictions on what rigid groups can appear as Picard varieties, such as existence of an analytic Weil pairing on topological torsion, which are consistent with ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$ being semi-abeloid.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$ being semi-abeloid.
As a basic example, we recover [Reference Hartl and LütkebohmertHL00, Lemma 3.1], which says ![]() $\operatorname {Hom}(\mathbb {G}_a,\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}})=0$. Indeed, as
$\operatorname {Hom}(\mathbb {G}_a,\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}})=0$. Indeed, as ![]() $\mathbb {G}_a=\mathbb {G}_a^\mathrm {tt}$, any such map factors through
$\mathbb {G}_a=\mathbb {G}_a^\mathrm {tt}$, any such map factors through ![]() $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\hookrightarrow \operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$, but
$\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\hookrightarrow \operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$, but ![]() $\operatorname {Hom}(\mathbb {G}_a,\mathbb {G}_m)=0$. Similarly, if
$\operatorname {Hom}(\mathbb {G}_a,\mathbb {G}_m)=0$. Similarly, if ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ was an open unit ball with additive structure, this would contradict it being the kernel of a map from
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ was an open unit ball with additive structure, this would contradict it being the kernel of a map from ![]() $\operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$ to an affine group.
$\operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$ to an affine group.
5. Comparison of analytic moduli spaces
In this final section, we use our main theorems to show that the ![]() $p$-adic Simpson correspondence in rank one admits a geometric description in terms of a comparison of moduli spaces. This also proves Theorem 1.1 and explains the necessary choices in a geometric way.
$p$-adic Simpson correspondence in rank one admits a geometric description in terms of a comparison of moduli spaces. This also proves Theorem 1.1 and explains the necessary choices in a geometric way.
As before, let ![]() $X$ be a connected smooth proper rigid space
$X$ be a connected smooth proper rigid space ![]() $X$ over an algebraically closed complete extension
$X$ over an algebraically closed complete extension ![]() $K$ of
$K$ of ![]() $\mathbb {Q}_p$ and choose a base-point
$\mathbb {Q}_p$ and choose a base-point ![]() $x\in X(K)$ to define
$x\in X(K)$ to define ![]() $\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. For simplicity, let us assume in this section that the classical rigid analytic Picard functor is representable (see Remark 4.8). As an application of Theorems 3.6 and 4.1, we can now define rigid analytic moduli spaces on both sides of the
$\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. For simplicity, let us assume in this section that the classical rigid analytic Picard functor is representable (see Remark 4.8). As an application of Theorems 3.6 and 4.1, we can now define rigid analytic moduli spaces on both sides of the ![]() $p$-adic Simpson correspondence, in very close analogy to Simpson's complex analytic moduli spaces of rank one [Reference SimpsonSim93, § 2].
$p$-adic Simpson correspondence, in very close analogy to Simpson's complex analytic moduli spaces of rank one [Reference SimpsonSim93, § 2].
Definition 5.1
(i) The coarse moduli space of
 $v$-line bundles on
$v$-line bundles on  $X$ is
$X$ is
 \[ \mathbf{Bun}_{v,1}:=\mathbf{Pic}_{X,v}. \]
\[ \mathbf{Bun}_{v,1}:=\mathbf{Pic}_{X,v}. \]
(ii) Write
 $\mathcal {A}:=H^0(X,\Omega ^1(-1))\otimes \mathbb {G}_a$, this is the Hitchin base of rank one. Then
is the coarse moduli space of Higgs line bundles on
$\mathcal {A}:=H^0(X,\Omega ^1(-1))\otimes \mathbb {G}_a$, this is the Hitchin base of rank one. Then
is the coarse moduli space of Higgs line bundles on \[ \mathbf{Higgs}_1:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\times \mathcal{A} \]
\[ \mathbf{Higgs}_1:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\times \mathcal{A} \]
 $X$.
$X$.(iii) We define the Betti moduli space to be the character variety of Lemma 3.3,
which is the moduli space of characters of \[ \mathbf{M}_{\mathrm{B}}:=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)=\mathbf{Pic}_{X,v}^{\mathrm{tt}}\subseteq \mathbf{Pic}_v, \]
\[ \mathbf{M}_{\mathrm{B}}:=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)=\mathbf{Pic}_{X,v}^{\mathrm{tt}}\subseteq \mathbf{Pic}_v, \]
 $\pi _1(X)$. Via Theorem 3.6(ii), we can equivalently see this as the coarse moduli space of topologically torsion
$\pi _1(X)$. Via Theorem 3.6(ii), we can equivalently see this as the coarse moduli space of topologically torsion  $v$-line bundles.
$v$-line bundles.(iv) We define the Dolbeault moduli space to be the coarse moduli space
of topologically torsion Higgs line bundles on \[ \mathbf{M}_{\mathrm{Dol}}:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \mathcal{A} \subseteq \mathbf{Higgs}_1 \]
\[ \mathbf{M}_{\mathrm{Dol}}:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \mathcal{A} \subseteq \mathbf{Higgs}_1 \]
 $X$.
$X$.
While a priori defined as ![]() $v$-sheaves on
$v$-sheaves on ![]() $\operatorname {Perf}_K$, Theorems 3.5, 4.1 and Lemma 3.3 combine to show that all of the above moduli functors are represented by smooth rigid spaces. This allows us to investigate a new perspective on the
$\operatorname {Perf}_K$, Theorems 3.5, 4.1 and Lemma 3.3 combine to show that all of the above moduli functors are represented by smooth rigid spaces. This allows us to investigate a new perspective on the ![]() $p$-adic Simpson correspondence, namely whether it admits a description in terms of moduli spaces.
$p$-adic Simpson correspondence, namely whether it admits a description in terms of moduli spaces.
This turns out to be the case: in this section, we note three slightly different ways in which we can compare ![]() $\mathbf {Bun}_{v,1}$ to
$\mathbf {Bun}_{v,1}$ to ![]() $\mathbf {Higgs}_1$, respectively
$\mathbf {Higgs}_1$, respectively ![]() $\mathbf {M}_{\mathrm {B}}$ to
$\mathbf {M}_{\mathrm {B}}$ to ![]() $\mathbf {M}_{\mathrm {Dol}}$. The basic idea for this comparison is that
$\mathbf {M}_{\mathrm {Dol}}$. The basic idea for this comparison is that ![]() $\mathrm {HTlog}$ on the Betti side, and the projection to
$\mathrm {HTlog}$ on the Betti side, and the projection to ![]() $\mathcal {A}$ on the Dolbeault side, define a diagram
$\mathcal {A}$ on the Dolbeault side, define a diagram

in which by Corollary 4.5, the second column consists of ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsors, and the first column consists of
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsors, and the first column consists of ![]() $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$-torsors. While the torsors on the bottom line are split, the torsors on the top line are typically not split according to Corollary 4.6. The first, rather primitive way in which the two sides can be compared is now the following ‘tautological comparison’, based on the observation that any extension becomes tautologically split after pullback to itself.
$\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$-torsors. While the torsors on the bottom line are split, the torsors on the top line are typically not split according to Corollary 4.6. The first, rather primitive way in which the two sides can be compared is now the following ‘tautological comparison’, based on the observation that any extension becomes tautologically split after pullback to itself.
Corollary 5.2 There is a canonical and functorial isomorphism of rigid groups
given by ![]() $(L_1,L_2)\mapsto ((L_1\otimes L_2^{-1},\mathrm {HTlog}(L_1)),L_2)$. It restricts to an isomorphism of rigid groups
$(L_1,L_2)\mapsto ((L_1\otimes L_2^{-1},\mathrm {HTlog}(L_1)),L_2)$. It restricts to an isomorphism of rigid groups
Our second comparison isomorphism is geometrically more refined but no longer completely canonical: it relies on the observation that the exact sequence (16) in Theorem 4.1 admits a reduction of structure groups to the ![]() $p$-torsion subsheaf
$p$-torsion subsheaf ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$.
Definition 5.3 Let ![]() $\mathbb {X}$ be any flat
$\mathbb {X}$ be any flat ![]() $B_{\mathrm {dR}}^+/\xi ^2$-lift of
$B_{\mathrm {dR}}^+/\xi ^2$-lift of ![]() $X$, which by Remark 1.4 induces a splitting
$X$, which by Remark 1.4 induces a splitting ![]() $s_{\mathbb {X}}$ of the Hodge–Tate sequence (2). Then we define the étale sheaf
$s_{\mathbb {X}}$ of the Hodge–Tate sequence (2). Then we define the étale sheaf ![]() $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ as the pullback
$\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ as the pullback

where ![]() $\widehat {\mathbb {G}}_m:=\mathbb {G}_m\langle p^\infty \rangle$ is the open disc of radius
$\widehat {\mathbb {G}}_m:=\mathbb {G}_m\langle p^\infty \rangle$ is the open disc of radius ![]() $1$ around
$1$ around ![]() $1$, and the bottom row is obtained by applying
$1$, and the bottom row is obtained by applying ![]() $\underline {\mathrm {Hom}}(\pi _1(X),-)$ to the logarithm sequence
$\underline {\mathrm {Hom}}(\pi _1(X),-)$ to the logarithm sequence ![]() $0\to \mu _{p^\infty }\to \widehat {\mathbb {G}}_m\xrightarrow {\log } \mathbb {G}_a\to 0$.
$0\to \mu _{p^\infty }\to \widehat {\mathbb {G}}_m\xrightarrow {\log } \mathbb {G}_a\to 0$.
The sheaf ![]() $\mathbb {L}_{\mathbb {X}}$ induces the following ‘étale comparison isomorphism’.
$\mathbb {L}_{\mathbb {X}}$ induces the following ‘étale comparison isomorphism’.
Theorem 5.4 There is a canonical isomorphism
It restrict to an isomorphism
Proof. The defining sequence of ![]() $\mathbb {L}_{\mathbb {X}}$ is a reduction of structure group of the short exact sequence from Theorem 4.1: this follows from combining Definition 5.3 with
$\mathbb {L}_{\mathbb {X}}$ is a reduction of structure group of the short exact sequence from Theorem 4.1: this follows from combining Definition 5.3 with

and the fact that ![]() $\mathrm {HT}\circ s_{\mathbb {X}}={\operatorname {id}}$. Since
$\mathrm {HT}\circ s_{\mathbb {X}}={\operatorname {id}}$. Since ![]() $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ is a
$\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ is a ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$ torsor, there is a canonical isomorphism
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$ torsor, there is a canonical isomorphism ![]() $\mathbb {L}_{\mathbb {X}}\times _{\mathcal {A}}\mathbb {L}_{\mathbb {X}}{\tilde{\to}} {\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]} \times \mathbb {L}_{\mathbb {X}}$, like in Corollary 5.2. Forming the pushout of the
$\mathbb {L}_{\mathbb {X}}\times _{\mathcal {A}}\mathbb {L}_{\mathbb {X}}{\tilde{\to}} {\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]} \times \mathbb {L}_{\mathbb {X}}$, like in Corollary 5.2. Forming the pushout of the ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor in the first factor along
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor in the first factor along ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ gives the second isomorphism. Pushing further along
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ gives the second isomorphism. Pushing further along ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ gives the first by Corollary 4.5.
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ gives the first by Corollary 4.5.
Finally, there is an étale version which is completely canonical, and which can be described as a universal version of Theorem 5.4 over the moduli space of all Hodge–Tate splittings.
Definition 5.5 Let ![]() $\mathcal {S}$ be the rigid affine space associated to the finite
$\mathcal {S}$ be the rigid affine space associated to the finite ![]() $K$-vector space
$K$-vector space
Set ![]() $\mathcal {A}_{\mathcal {S}}:=\mathcal {A}\times \mathcal {S}$. Then there is a tautological morphism
$\mathcal {A}_{\mathcal {S}}:=\mathcal {A}\times \mathcal {S}$. Then there is a tautological morphism
We use it to define a universal étale sheaf ![]() $\mathbb {L}\to \mathcal {A}_{\mathcal {S}}$ via the following commutative diagram.
$\mathbb {L}\to \mathcal {A}_{\mathcal {S}}$ via the following commutative diagram.

Then for any lift ![]() $\mathbb {X}$ of
$\mathbb {X}$ of ![]() $X$ corresponding to a point
$X$ corresponding to a point ![]() $x\in \mathcal {S}(K)$, the fibre of
$x\in \mathcal {S}(K)$, the fibre of ![]() $\mathbb {L}$ over
$\mathbb {L}$ over ![]() $\mathcal {A}\times x$ is
$\mathcal {A}\times x$ is ![]() $\mathbb {L}_{\mathbb {X}}$.
$\mathbb {L}_{\mathbb {X}}$.
We let ![]() $\mathcal {P}$ be the pushout of
$\mathcal {P}$ be the pushout of ![]() $\mathbb {L}$ along
$\mathbb {L}$ along ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$. This is an extension
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$. This is an extension
Note that this is completely canonical and does not depend on either lifts or exponentials.
We now have the following ‘universal comparison isomorphism’: in a way reminiscent of the Deligne–Hitchin twistor space in complex geometry [Reference SimpsonSim97, § 4], this exhibits ![]() $\mathbf {M}_{\mathrm {Dol}}$ as a ‘degeneration’ of
$\mathbf {M}_{\mathrm {Dol}}$ as a ‘degeneration’ of ![]() $\mathbf {M}_{\mathrm {B}}$ in the sense that there is an analytic morphism over a base
$\mathbf {M}_{\mathrm {B}}$ in the sense that there is an analytic morphism over a base ![]() $\mathcal {S}$ whose fibres are generically isomorphic to
$\mathcal {S}$ whose fibres are generically isomorphic to ![]() $\mathbf {M}_{\mathrm {B}}$, but whose fibre over a special point is equal to
$\mathbf {M}_{\mathrm {B}}$, but whose fibre over a special point is equal to ![]() $\mathbf {M}_{\mathrm {Dol}}$. (This is not to say that the universal comparison is directly related to
$\mathbf {M}_{\mathrm {Dol}}$. (This is not to say that the universal comparison is directly related to ![]() $\lambda$-connections over
$\lambda$-connections over ![]() $X$, whose closest known analogue are the
$X$, whose closest known analogue are the ![]() $q$-connections of Morrow and Tsuji [Reference Morrow and TsujiMT21, § 2].)
$q$-connections of Morrow and Tsuji [Reference Morrow and TsujiMT21, § 2].)
Proposition 5.6
(i) For any
 $B_{\mathrm {dR}}^+/\xi ^2$-lift
$B_{\mathrm {dR}}^+/\xi ^2$-lift  $\mathbb {X}$ of
$\mathbb {X}$ of  $X$, there is for the fibre
$X$, there is for the fibre  $\mathcal {P}_x$ of
$\mathcal {P}_x$ of  $\mathcal {P}$ over the associated point
$\mathcal {P}$ over the associated point  $x\in \mathcal {S}(K)$ a canonical isomorphism
$x\in \mathcal {S}(K)$ a canonical isomorphism
 \[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{B}}. \]
\[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{B}}. \]
(ii) For any morphism
 $x:H^1_{{\mathrm {\acute {e}t}}}(X,\Omega ^1)\to H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)\otimes K=\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),K)$ factoring through the Hodge–Tate filtration, we instead have a canonical isomorphism
$x:H^1_{{\mathrm {\acute {e}t}}}(X,\Omega ^1)\to H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)\otimes K=\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),K)$ factoring through the Hodge–Tate filtration, we instead have a canonical isomorphism
 \[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}. \]
\[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}. \]
(iii) There is a canonical and functorial isomorphism of rigid spaces
such that for any \[ c: \mathcal{P}\times_{\mathcal{A}_{\mathcal{S}}}\mathbb{L}{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}\times_{\mathcal{A}}\mathbb{L} \]
\[ c: \mathcal{P}\times_{\mathcal{A}_{\mathcal{S}}}\mathbb{L}{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}\times_{\mathcal{A}}\mathbb{L} \]
 $B_{\mathrm {dR}}^+/\xi ^2$-lift
$B_{\mathrm {dR}}^+/\xi ^2$-lift  $\mathbb {X}$ of
$\mathbb {X}$ of  $X$, the fibre of
$X$, the fibre of  $c$ over the associated point
$c$ over the associated point  $x\in \mathcal {S}(K)$ is canonically identified via part (i) with the isomorphism from Theorem 5.4.
$x\in \mathcal {S}(K)$ is canonically identified via part (i) with the isomorphism from Theorem 5.4.
The analogous statements hold for ![]() $\mathbf {Bun}_1$,
$\mathbf {Bun}_1$, ![]() $\mathbf {Higgs}_{1}$ instead of
$\mathbf {Higgs}_{1}$ instead of ![]() $\mathbf {M}_{\mathrm {B}}$,
$\mathbf {M}_{\mathrm {B}}$, ![]() $\mathbf {M}_{\mathrm {Dol}}$, respectively.
$\mathbf {M}_{\mathrm {Dol}}$, respectively.
Proof. We have a commutative diagram

inducing a natural map ![]() $\mathcal {P}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the universal property of the pushout.
$\mathcal {P}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the universal property of the pushout.
Part (i) follows from comparing the definition of ![]() $\mathbb {L}$ to that of Definition 5.3, since in this case the morphism on the right becomes the identity.
$\mathbb {L}$ to that of Definition 5.3, since in this case the morphism on the right becomes the identity.
To show part (ii), observe that in this case ![]() $\mathrm {HT}\circ s$ specialises to
$\mathrm {HT}\circ s$ specialises to ![]() $0$. Thus, there is a canonical morphism
$0$. Thus, there is a canonical morphism ![]() $\mathbb {L}_x\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ which induces a canonical splitting of
$\mathbb {L}_x\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ which induces a canonical splitting of ![]() $\mathcal{P}_x$. This is the same datum as an isomorphism
$\mathcal{P}_x$. This is the same datum as an isomorphism ![]() $\mathcal {P}_x{\tilde{\to}} \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\times \mathcal {A}=\mathbf {M}_{\mathrm {Dol}}$.
$\mathcal {P}_x{\tilde{\to}} \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\times \mathcal {A}=\mathbf {M}_{\mathrm {Dol}}$.
Finally, part (iii) follows from the tautological splitting
after pushout along ![]() $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. The last part of part (iii) about compatibility with Theorem 5.4 over
$\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. The last part of part (iii) about compatibility with Theorem 5.4 over ![]() $x\in \mathcal {S}(K)$ is clear from comparing the proofs.
$x\in \mathcal {S}(K)$ is clear from comparing the proofs.
It remains to note that this explains the choices in Theorem 1.1 in a geometric fashion.
Proof of Theorem 1.1 It is clear from the definition that any choice of exponential induces a continuous splitting ![]() $s$ of
$s$ of ![]() $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on
$\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on ![]() $K$-points, which induces the desired homeomorphism
$K$-points, which induces the desired homeomorphism
by taking ![]() $K$-points in Theorem 5.4 and considering the fibre over
$K$-points in Theorem 5.4 and considering the fibre over ![]() $s:\mathcal {A}(K)\to \mathbb {L}_{\mathbb {X}}(K)$.
$s:\mathcal {A}(K)\to \mathbb {L}_{\mathbb {X}}(K)$.
Remark 5.7 As an aside, Theorem 5.4 means that the term ‘geometric ![]() $p$-adic Simpson correspondence’ in the title may be interpreted quite literally: it provides a diagram
$p$-adic Simpson correspondence’ in the title may be interpreted quite literally: it provides a diagram
which is indeed an ‘étale correspondence’ in the sense of algebraic geometry.
Remark 5.8 The results of this section give an indication for what kind of geometric results one can expect also in higher rank. More precisely, we believe that the statements of Theorem 5.4, Proposition 5.6 and Remark 5.7 stand a chance to generalise: this suggests that the moduli space of ![]() $v$-vector bundles is an étale twist of the moduli space of Higgs bundles over the Hitchin base, and that the usual choices necessary for the formulation of the
$v$-vector bundles is an étale twist of the moduli space of Higgs bundles over the Hitchin base, and that the usual choices necessary for the formulation of the ![]() $p$-adic Simpson correspondence can be interpreted as leading to a trivialisation of this twist.
$p$-adic Simpson correspondence can be interpreted as leading to a trivialisation of this twist.
We show in [Reference HeuerHeu22c] that indeed, one can construct analytic moduli spaces of ![]() $v$-vector bundles and Higgs bundles in terms of small
$v$-vector bundles and Higgs bundles in terms of small ![]() $v$-stacks, and that both admit natural maps to the Hitchin base. This provides further evidence that the results of this article provide the first instance of a general moduli-theoretic approach to the
$v$-stacks, and that both admit natural maps to the Hitchin base. This provides further evidence that the results of this article provide the first instance of a general moduli-theoretic approach to the ![]() $p$-adic Simpson correspondence.
$p$-adic Simpson correspondence.
Acknowledgements
We would like to thank J. Anschütz, Y. Dutta, A.-C. Le Bras, L. Mann, P. Scholze, A. Thomas, A. Werner and M. Würthen for very helpful discussions. We thank the referee for very helpful comments.
Conflicts of interest
None.
Financial support
This work was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC-2047/1 – 390685813, and TRR 326 Geometry and Arithmetic of Uniformized Structures, project number 444845124. It was further supported by the DFG via the Leibniz-Preis of Peter Scholze.