No CrossRef data available.
Article contents
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
Published online by Cambridge University Press: 11 March 2024
Abstract
In this note, we present examples of non-quasi-geodesic metric spaces which are hyperbolic (i.e., satisfying Gromov’s 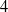 $4$-point condition) while the intersection of any two metric balls therein does not either ‘look like’ a ball or has uniformly bounded eccentricity. This answers an open question posed by Chatterji and Niblo.
$4$-point condition) while the intersection of any two metric balls therein does not either ‘look like’ a ball or has uniformly bounded eccentricity. This answers an open question posed by Chatterji and Niblo.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
Footnotes
†
JZ was partly supported by National Key R&D Program of China 2022YFA100700.
References
Bridson, M. R. and Haefliger, A., Metric space of non-positive curvature (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Chatterji, I. and Niblo, G. A., A characterization of hyperbolic spaces, Groups Geom. Dyn. 1(3) (2007), 281–299.CrossRefGoogle Scholar
Ghys, É. and de la Harpe, P. (Eds.), Sur les groupes hyperboliques d’après Mikhael Gromov,
Progress in Mathematics
, vol. 83 (Birkhäuser Boston Inc., Boston, MA, 1990),CrossRefGoogle Scholar
Gromov, M., Hyperbolic groups, in Essays in group theory (Springer, 1987), 75–263.CrossRefGoogle Scholar
Wenger, S., Characterizations of metric trees and Gromov hyperbolic spaces, Math. Res. Lett. 15(5) (2008), 1017–1026.CrossRefGoogle Scholar



