Introduction
IGESAT (the Ice, Cloud and Land Elevation Satellite) is scheduled for launch injuly 2001. It will have an orbital altitude of about 600 km and inclination of 94°. The Geoscience Laser Altimeter System (GLAS) instrument on the IGESAT mission has a 0.11 mrad beam divergence, so its footprint on the Earth’s surface is about 70 m. The GLAS shot-repetition rate is 40 Hz, giving a distance between consecutive footprints of about 170 m (Reference Schutz and PlagSchutz, 1998). One principal purpose of the GLAS instrument is to measure the height of the ground surface, particularly the surface of the ice sheets. There is a secondary characteristic of the ice sheets that is also of research interest: the roughness of their upper surfaces. As described further below, irregularities of the surface exist on several scales; here we are concerned with the roughness that has spectral wavelengths small compared with the diameter of the altimeter footprint.
Small-scale roughness has one source, i.e. the wind. Winds roughen the surface by processes of differential deposition and erosion. Generally speaking, the stronger the wind the rougher the surface, although in detail the relationship is complex. In a regional sense, then, the surface roughness can be taken as a measure, albeit imperfect, of the windiness of the region. The purpose of the algorithm discussed here is to determine the small-scale roughness from the spreading of the laser pulse that occurs because the impinging signal does not reach all of the surface simultaneously The rougher the surface, the more the returned pulse will be broadened relative to the outgoing pulse (Reference GardnerGardner, 1992).
There is an important complication. The pulse broadening reflects the different distances to different points within the footprint, so if the surface has a non-zero slope (as most ice-sheet surfaces do), then the pulse will be broadened upon reflection because of the slope-generated differences in surface height, even for a smooth surface. The effects on an idealized (Gaussian) pulse-broadening from simple models of roughness and slope are identical (see simulation results below). It follows that for real surfaces and pulses the two effects will be very similar, so it will not in practice be possible to distinguish between these two sources of pulse broadening solely from the analysis of pulse shapes. Only where the surface slope is otherwise known will it be possible to calculate the roughness (or vice versa). Fortunately, that slope will become known through the analysis of the surface-height measurements from the same instrument (some iteration may be required).
Roughness characteristics
At first glance the surfaces of the ice sheets appear smooth, but in reality they are roughened in three fundamentally different ways. On the smallest scale there is the roughness caused by the wind and variations in the rate of snow accumulation, which comprises irregular features called "sastrugi" and "snow dunes" (Reference KotlyakovKotlyakov, 1966; Reference Doumani and OuraDoumani, 1967). Sastrugi are erosional or erosional/depositional features that vary widely in size, both vertically and horizontally, depending on the wind characteristics and history in a particular region. In many areas the irregularities of the surface are 0.1m or less in height, with typical horizontal wavelengths on the order of several meters. Over parts of the interior of Antarctica, however, the sastrugi can reach heights of 1 m (e.g. Reference Endo and FujiwaraEndo and Fujiwara, 1973); horizontal wavelengths are larger, although not necessarily proportionally larger. Snow dunes (Reference KotlyakovKotlyakov, 1966) are accumulation features that are somewhat larger than sastrugi: they can be up to several meters in amplitude and tens of meters in wavelength. These physical features are larger than the meteorologically defined "surface roughness parameter", which typically has a value of 0.01 or so over a snow surface with sastrugi (Reference PatersonPaterson, 1994, p. 62-63), because of the streamlined shapes of the sastrugi and dunes.
Roughness due to sastrugi is anisotropic (Reference King and TurnerKing and Turner, 1997); sastrugi ridges are elongated in the direction of the wind, so the roughness characteristics are different along, and normal to, that direction.
An absence of surface roughness can also be an important characteristic of the ice-sheet surface. In particular, a smooth, glazed surface probably represents a region that has been free of snow accumulation for several years or more (Reference WatanabeWatanabe, 1978).
The second type of roughness has much longer wavelengths. This comprises the undulations (Reference Budd and CarterBudd and Garter, 1971; Reference MclntyreMclntyre, 1986) of the surface that result from the flow of the ice over topographic irregularities in the bed. Although the flow characteristics of the ice are such that the vertical scale of the relief of the surface is two orders of magnitude less than that of the bed, surface relief nevertheless exists and in many places is pronounced. Amplitudes of this relief are commonly a few meters to tens of meters, with horizontal wavelengths of hundreds of meters to many kilometers (Reference Budd and CarterBudd and Garter, 1971; Reference MclntyreMclntyre, 1986). The thickness of the ice sheet modulates the surface relief in two ways: the thicker the ice, the smaller the amplitude of the surface relief and the greater its dominant horizontal wavelengths. The ice sheet acts like a bandpass filter: subglacial relief of wavelengths short compared to the ice thickness is damped by the strength of the ice sheet, whereas very long wavelengths are attenuated by the plastic flow of the ice.
The third type of roughness stems from cracks in the surface, i.e. crevasses. These develop anywhere that the stresses in the ice from variations in flow exceed the breaking strength of the ice in tension. They are caused by lateral variations in flow speed and/or direction as the ice flows over basal topography, around bends in a subglacial channel, or through regions of rapid acceleration (longitudinal or transverse). Crevasses vary widely in scale, from millimeters to tens of meters across and from tens of meters to kilometers long (Reference SharpSharp, 1988). Spacings between crevasses are characteristically on the order of 100-200 m. Like the undulations, crevassing has a strong tendency to be more pronounced in locations nearer to the coast. In extreme cases (e.g. the Jakobshavn ice tongue in Greenland) the crevassing is so severe that the surface becomes a jumbled series of pinnacles, seemingly more crevasse than ice (Reference Lingle, Hughes and KollmeyerLingle and others, 1981).
Slope characteristics
The speed of outward ice flow from a steady-state ice sheet is sufficient largely to balance the incoming snowfall (when averaged over many centuries). In this way, ice sheets are able to maintain approximately parabolic profiles. The central regions are consequently very flat, with gradients on the order of 1:1000. Toward the ice margin, surface slopes and flow speeds are higher, the ice is thinner, and stresses from flow over the irregular subglacial bed make the ice surface more undulating. Within 200-300 km of the coast, the ice may become channeled, either through peripheral mountains where outlet glaciers develop, or through ice streams, fast-flowing zones within the ice sheet (Reference BentleyBentley, 1987). Here the slopes are highly variable, from as much as 1:10, where the ice is flowing slowly, to as little as 1:1000 on the fast-flowing, low-gradient ice streams. The coastal regions, with their widely variable slopes, are of particular importance in the context of global change, because it is here that any reaction of the ice sheets to changes in climate will first appear. More than half of Antarctica has gradients less than 1:300, and 90% has gradients less than 1.5%. Only 3% of the ice sheet, in the marginal areas, exhibits gradients larger than 3% (Reference Drewry, Mclntyre, Cooper and WoldenburgDrewry and others, 1985). Greenland has a similar distribution of slopes, except that the ratio of the marginal areas to the total is two or three times larger.
Algorithm
Our approach is based on the assumption that there is a spectral minimum in surface roughness that lies in the range of a few hundred meters and separates the wind-generated roughness at short wavelengths from the undulation generated by basal topography at longer wavelengths. (This assumption is unproven, although data have recently become available from Greenland (Reference VanderVeen, Krabill, Csatho and BolzanVan der Veen and others, 1998) that will be used to test it.) We can thus consider the surface within the footprint as characterized by a mean slope, which is a short segment of the long-wavelength undulations; superimposed on that slope are large wind-generated bumps of short wavelength. Correspondingly, we make two calculations, based on the alternate assumptions of (1) a rough, flat surface and (2) a smooth, linearly sloping surface.
We also assume a backscatter strength that is independent of the angle of incidence (diffuse scattering). This means that the effective reflectivity of the surface, i.e. the proportion of incident energy per unit cross-sectional area that is returned vertically, is the same everywhere within the footprint. Since we do not yet know how the GLAS instrument will affect the waveform, the instrumental effect has not been modeled in this paper.
Rough, flat surface
We assume that small-scale roughness has a Gaussian distribution, which also implies that there are enough bumps within the footprint to justify a statistical approach. Although there is no reason to suppose that this distribution of heights is realistic for the snow dunes and sastrugi that roughen the surface (since they tend to regularity of form and size within a small area (Reference Doumani and OuraDoumani, 1967)), there is no quantitative basis for any other assumption. It will require ground-truth experiments to provide a quantitative correlation between surface conditions and the roughness calculated from the GLAS algorithm. With this assumption, the shape of the returned pulse is given by the convolution of the outgoing pulse shape with the Gaussian function that represents the roughness.
We let σs, the standard deviation of surface heights, represent the surface roughness; the elevation probability density function can then be written as

where z is the height above the mean surface. As z = ct/2, where c is the speed of light and t is the two-way travel-time difference relative to the return from the mean surface, the surface-elevation probability density, expressed in terms of the time delay and as a function of time, can be written as

The Gaussian-shaped envelope of the transmitted pulse power can be expressed by Reference Abshire, McGarry, Pacini, Blair and ElmanAbshire and others (1994):

where σp is the half-width (standard deviation in time) of the pulse. Since the difference between the distance from the satellite to the center of the footprint and to its margin is negligibly small (about 1 mm for the GLAS beam width and orbit height), we may take as a valid approximation that the signal reaches the entire footprint simultaneously. In that case, the returned-pulse power Pr(t), can be expressed as the convolution of pt(t) and Rt(t) (Brown, Reference Brown1977):

where the scale A depends upon the amplitude of the outgoing pulse and other factors, such as the range to the surface, losses of transmission through the atmosphere and the optical system, and the surface reflectivity (Bufton, Reference Bufton1989).
By application of the Fourier transform (Stremler, Reference Stremler1990) this expression can be written explicitly as
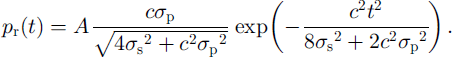
Smooth, sloping surface
For the purposes of algorithm development, we assume a linear slope. Since the dominant wavelengths of surface undulations are generally >10 km (Mclntyre, Reference Mclntyre1986), this should be a good approximation across the GLAS footprint (about 70 m). The shape of the returned pulse can then be described by the convolution of the outgoing-pulse shape with a function that represents the fraction of the total area within the footprint illuminated at a particular surface height. For a sloping surface the pulse no longer impinges on the whole footprint simultaneously, so the spatial shape of the pulse must be taken into account. We assume that the pulse spreads out uniformly in a right circular cone; if 9 is the angular distance from the axis of the cone and ae is the angular half-width, then the beam pattern can be expressed by a factor g(θ) given by Abshire and others (Reference Abshire, McGarry, Pacini, Blair and Elman1994),

We describe the surface, a tilted plane, by z(x, y) in a Cartesian coordinate system with its origin at the center of the footprint, z along the axis of the beam (positive upward), and x in the upslope direction. If the tilt of the plane is zero, the power illuminating the surface will be a function of x and y only, and its horizontal variation will be given by

where a is the distance on the surface subtended by angle σθ. If the detecting telescope on the satellite observes a circle of radius b on the horizontal plane centered at nadir, we can express the surface impulse response power from strips across that circle normal to the x axis, So(x), as

where
![]() is the half-width of the strip.
is the half-width of the strip.
To simplify this expression, we note that

where
![]() and erf (q), the error function, is defined by
and erf (q), the error function, is defined by

Then
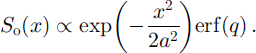
Now introduce a tilt a (slope tan α) along the x axis; then z = x tan α. Since z = ct/2, where t is now the return-time difference relative to that from nadir point, the impulse response power per unit time, as a function of time, Sa(t), is

where now

Finally, the returned power as a function of time is given again by the convolution of the transmitted pulse power, Pt(t), with Sα(t):

where A’ is analogous to A in Equation (3).
Combined effect
There is no way to ascertain from the shape of a signal returned pulse to what extent the pulse-broadening has been caused by the roughness and to what extent by the mean slope, because the theoretical effects of a linear slope and a Gaussian roughness are very similar (see below). We therefore make no attempt to combine the roughness and slope effects. In this study, we will calculate σs on the assumption of roughness alone, and calculate the mean slope on the assumption of a tilted planar surface. Clearly, the first calculation will overstate the actual roughness if there is a slope, and the second calculation will exaggerate the actual slope if the surface is rough.
The modeled waveform
Because the actual waveform will include noise and will not be a smooth curve, we add an average noise term and amplitude coefficient to the expression for the modeled waveform. We also normalize the waveform to its maximum; in this way we do not have to know the absolute amplitude of the waveform, which has been affected by the measuring instruments and the atmosphere. The modeled waveform can be written as

where P(t) = Pr(t) for the random case and P(t) =Ps{t) for the sloping case.
Inversion
Non-linear least squares will be used to extract model parameters by fitting the theoretical model to the observed waveform. Reference MenkeMenke (1989) described the non-linear least-squares fitting process in detail.
The fitting steps that will be used in our algorithm are as follows:
-
(1) make an initial estimate for the unknown model parameters;
-
(2) take a first-order Taylor-series expansion around the initial estimated values;
-
(3) find the least-squares solution for the correction to the initial estimated values;
-
(4) use the revised parameter values for a new estimate;
-
(5) repeat steps 2-4 until some exit criterion is satisfied.
The altimeter measured waveform is PO[n] (n = 1, 2, …,N), which represents N range-bin power values,

The modeled waveform is PM[n], calculated from the theoretical model,

There are four model parameters MP[m] (m = 1, 2, 3, 4) used here,

they are the mean surface position (referred to the peak of the model pulse), the surface roughness or the surface slope, the average noise level and the amplitude coefficient.The derivatives of the modeled power with respect to the four model parameters are represented by PD[n][m]:

Given the initial estimates of the four parameters, MPo[m], the Taylor expansion of PM[n] around PMo[n] can be written as

Define also B[n] = PO[n] - PMo[n] and A[n][m] = PDo [n] [m]; the matrix equation is then AX = B.The least-squares solution of that equation is A TAX = A TB = [A T A]−1 A TB. A new set of parameters can then be calculated by MP[m] = MPo[m] + X[m].
The covariance matrix,


where M = 4 is the number of parameters.
The derivatives of the modeled waveform with respect to the parameters are:

Then, for the random case:

For the sloping case, the derivatives are complicated integrals. We do not present them here, since in actuality the derivatives were calculated numerically during the inversion.
Simulation Results
Based on the assumptions that the laser-beam pattern and pulse shape are both Gaussian, a simulator has been constructed to study the waveforms of different surface topographies. The returned waveform is calculated by summing the returned power from the surface of a modeled three-dimensional topography within the laser footprint. The following function is used to generate surface topographies:
where A is the amplitude of the cosine topography, A, andA, are the wavelengths in the x and y directions, tan α is the surface slope, as is the surface roughness when A and a are zero, and random (x, y) generates random numbers at (x, y) that have zero mean and unit standard deviation. Different surfaces can be acquired by changing A, λx, λy, α and αs. For the purposes of this paper, A is set to zero. The simulator then can be used to test the relationship between surface slope and surface roughness by a non-linear least-squares inversion process.
Figures 1 and 2 show two groups of waveforms generated by the simulator using Equation (10) for different surface roughnesses and surface slopes. The waveforms change with the changing of surface parameters. Increasing surface roughness or surface slope broadens the waveforms and reduces the waveform amplitudes.
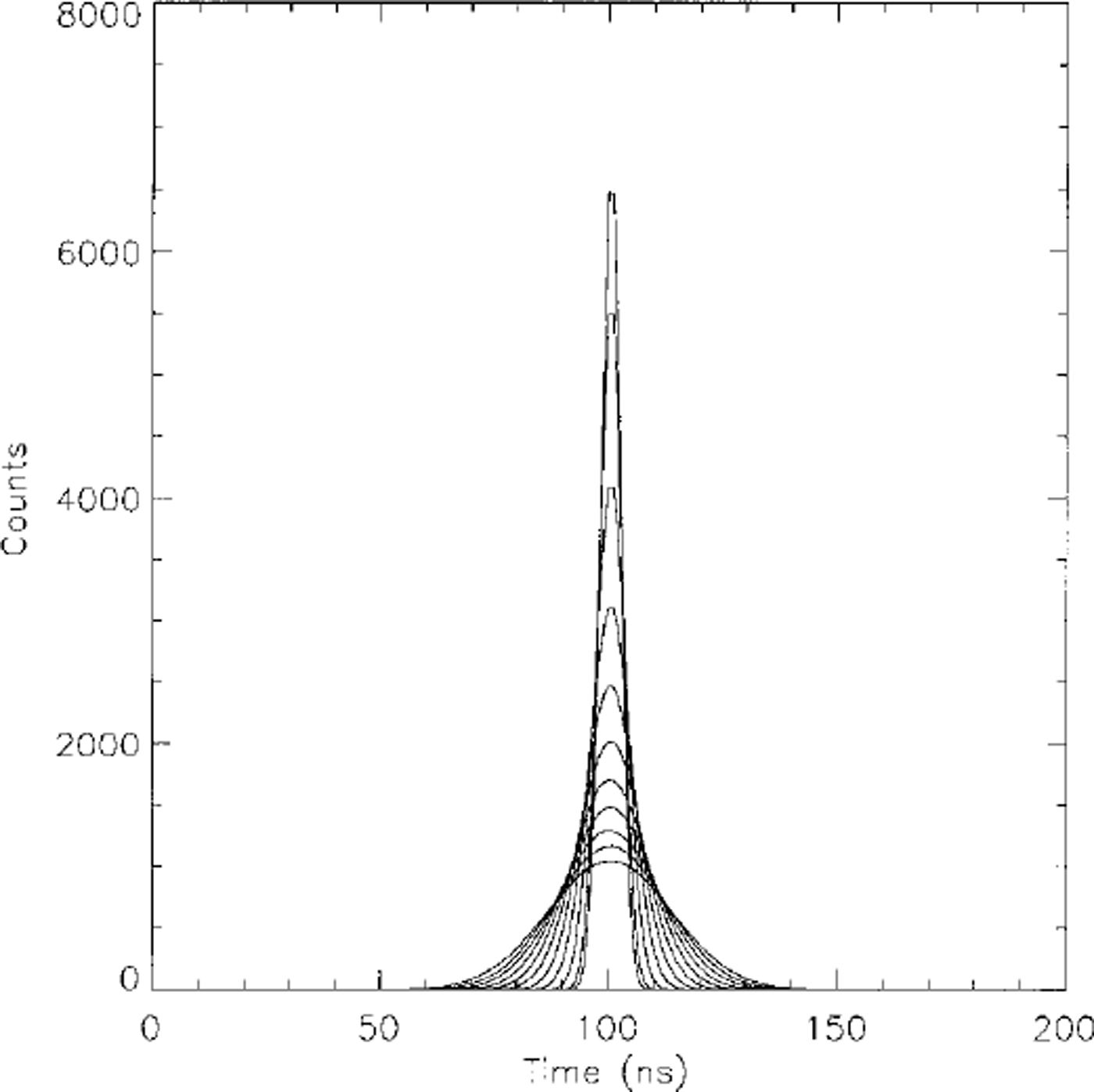
Fig. 1. Waveforms for flat, randomly rough surfaces. Surface roughness values range from 0 to 2 m in steps of 0.2 m. The waveform broadens and decrease in amplitude as the surface roughness increases.
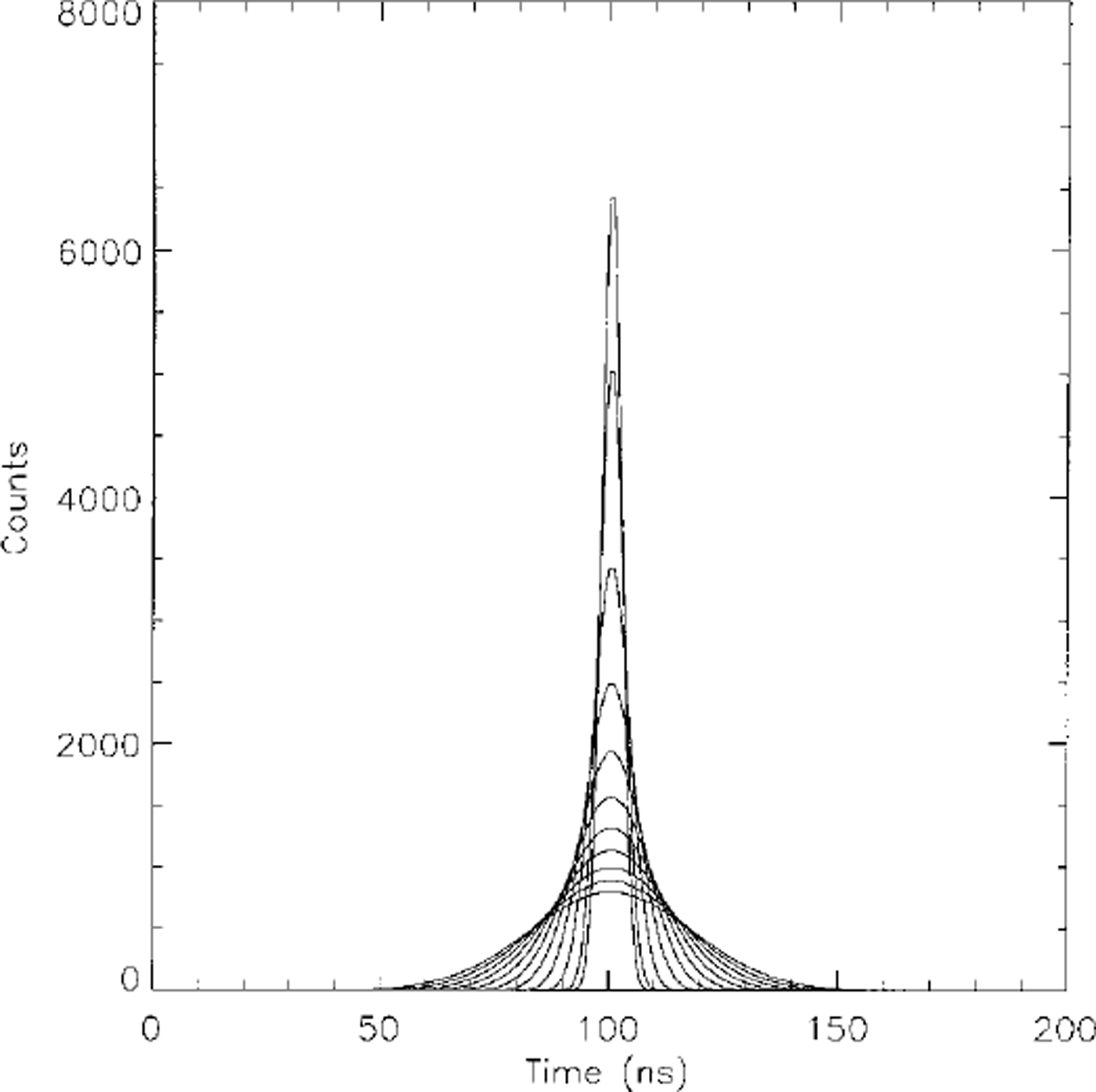
Fig. 2. Waveforms for smooth, sloping surfaces. Slopes range from 0° to 10° in steps of 1°. The waveform broadens and decreases in amplitude as the surface slope increases.
The non-linear least-squares inversion process was applied to waveforms generated by 100 flat, randomly rough surfaces (σs varying from 0 to 5 m at 0.05 m intervals, A = 0, a = 0 in Equation (10)) and 100 smooth, sloping surfaces (a varying from 0° to 10° at 0.1° intervals, A = 0, σs = 0 in Equation (10)). The results are shown in Figures 3 and 4, respectively. The calculated parameters match the given parameters very well except for very small slopes (<0.2°; Fig. 4). An alternate method is needed to calculate small slopes; one possibility is discussed at the end of this section.

Fig. 3. Surface roughness calculated from waveform fitting vs given surface roughness for flat, randomly rough surfaces. The mean difference is 0.003 m and the standard deviation of the difference is 0.008 m.

Fig. 4. Surface slope calculated from waveform fitting vs given surface slope for smooth surfaces. The mean difference is 0.018° and the standard deviation of the difference is 0.016°. The failure of the close linear relationship at very small slopes can barely be seen.
To investigate the effects of unmodeled slopes and roughness on our roughness-alone and slope-alone calculations, respectively, waveforms were generated using our simulator, for a series of sloping, rough surfaces. Slopes varied from 0° to 5° at 0.5° intervals, and roughnesses from 0 to 2 m at 0.2 m intervals. The results of the inversions are shown in Figure 5. The calculated surface slope depends on the surface roughness and vice versa; if one of the two terms (surface roughness or slope) is known through other means, the other term can be determined by the relationship shown in Figure 5. For a simulator-generated waveform, the fitted waveforms of the inversion process for the two models are very similar; the differences between them are <1 % of their amplitudes everywhere in the waveform. As the expected GLAS noise is >1% of its waveform amplitude, it will be impossible to distinguish between roughness-broadening and slope-broadening from analysis of pulse shape alone.
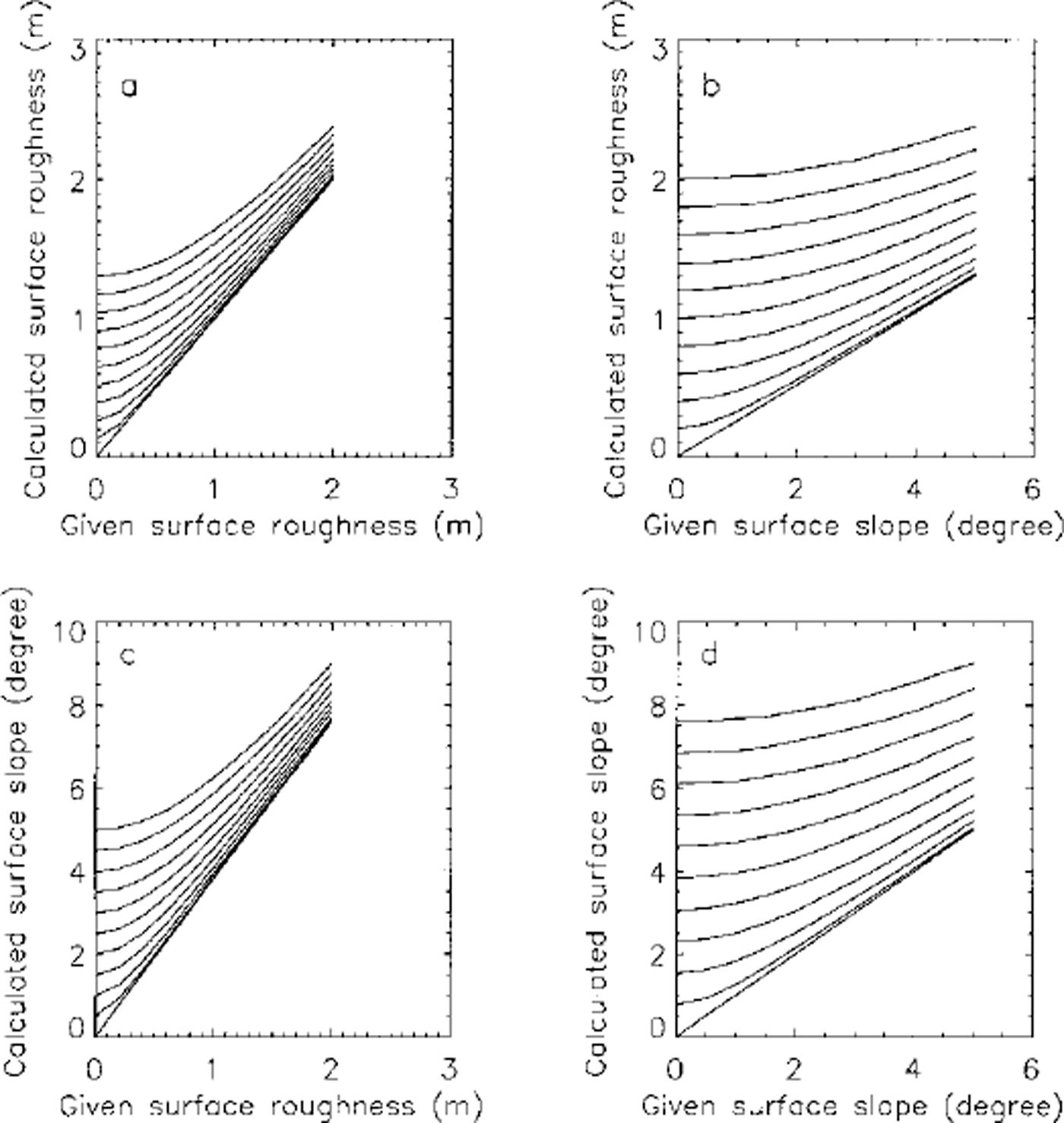
Fig. 5. Surface roughness and surface slope calculated from waveform fitting vs given surface roughness and surface slope. In (a) and (c) slope values 0, 0.5,1.0, …,5.0° refer to the lines in order from bottom to top. In (b) and (d) roughness values 0, 0.2, 0.4, …,2.0 m refer to the lines from bottom to top.
It can be shown analytically (from equations 9 and 14 in Zwally and others (in press)) that
where a is the radius of the laser footprint (determined by the laser-beam width and the satellite height) and a and σs are the surface slope and the surface roughness alternately calculated on the basis that the other is zero. Equation (11) was tested by calculating σs and a from roughness-alone and slope-alone model inversions and comparing a values with a calculated from Equation (11). The waveforms used in calculating Figure 6 are the same as used in calculating Figure 5. In Figure 6a the calculated surface slope (from inversion process) is plotted vs the calculated surface roughness (from inversion process). In Figure 6b the surface slope calculated by the inversion process is plotted vs the surface slope calculated by Equation (11). The two datasets matched very well. The standard deviation of the difference is 0.002°. Equation (11) may be used to calculate slope values when the surface slope is <0.2° and the fitting process, as pointed out earlier, does not give good results. Since the random-model fitting is faster than slope-model fitting, Equation (11) may also be used to calculate corresponding slope values and save computing time.
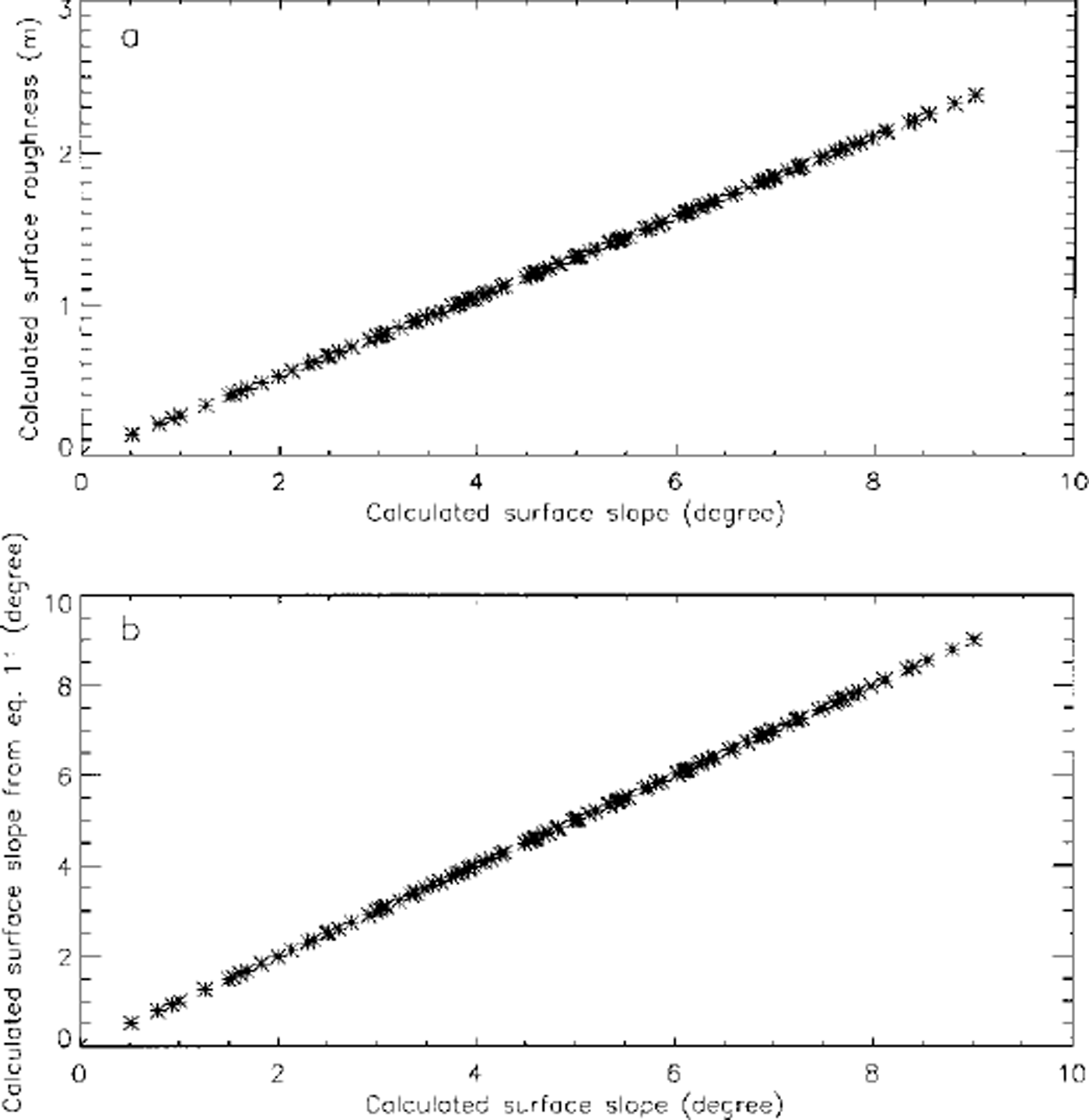
Fig. 6. (a) Surface slope and roughness, both calculated from waveform fitting, plotted against one another. Note the tight linear relationship, (b) Surface slope calculated from Equation (11) vs slope calculated from waveform fitting directly. The mean difference is 0.002° and the standard deviation of the difference is 0.002°.
Discussion
The random surface model and the sloping model are based on idealized surfaces and idealized instruments. If the transmitted pulse is not Gaussian we may not have analytical solutions for pr(t) in Equation (3) and ps(t) in Equation (8), in which case both surface roughness and slope must be calculated numerically. In practice, the calculated parameters must be compared with those measured by proven methods. The slope calculated by our algorithm depends upon the maximum and minimum surface heights within the footprint, which are assumed to he on opposite edges of the footprint. The error in this could be as great as 100% of the calculated slope in the case, for example, of a uniform mound centered in the footprint. We rely here on an assertion that the spectrum of surface irregularities has a minimum at wavelengths of a few hundred meters; these wavelengths are too long for wind-caused features but too short to reflect subglacial topography. There are no quantitative measurements to either prove or disprove this assertion. The actual surface has roughness characteristics that presumably he somewhere between a Gaussian distribution of irregularities and a uniform distribution of linear wavelike features. Various cases can be studied with the simulator by selecting different surface parameters in Equation (10).
Crevasses introduce a disturbance of the surface that is too complex to be modeled as any kind of roughness. In most crevassed regions most of the illuminated spots on the surface will fall between individual crevasses and will therefore not be affected at all. Where the spot overlaps the edge of an open crevasse there will probably be multiple returns from different levels of a discontinuous surface. No meaningful roughness can be calculated in such cases.
If the outgoing pulse is not circularly symmetric, the returned-pulse shape will contain a bias toward the part of the footprint illuminated by an excess of energy. J. Abshire (personal communication, 1995) calculated as an extreme case that a side lobe containing 10% of the outgoing energy on one edge of the beam would cause an error in a centroid detector of surface height of 18 cm on a surface with a 3° slope. This is about 5% of the height difference across the footprint. The relative error in surface slope to be expected would be of the same order of magnitude, which is small compared with other sources of error. For a flat surface of uniform roughness the error in the roughness calculation would be extremely small, because the entire footprint is illuminated at essentially the same instant. We conclude that spatial non-uniformity of the signal will not be a significant source of error in calculating slope and roughness.
A much more serious source of error arises from thin clouds or aerosols in the atmosphere, which cause forward scattering of the light beam. Forward scattering produces ray paths that are slightly longer than the straight-line path and thus causes a delayed arrival of some energy. This has the effect of broadening the pulse. Our surface-slope/roughness algorithm is based on pulse broadening, so forward scattering, if not recognized, will lead to overestimates of the roughness and/or slope. Calculations by J. Spinhirne and E. Eloranta (personal communications, 1998) indicate that the broadening could be as much as tens of ns; an error of this magnitude could completely obscure effects due to roughness or slope. Forward scattering will have to be dealt with, either by correcting for its effects or by deleting data that are affected.
Although the light signal does not penetrate the ice-sheet signal nearly as deeply as the signal from a radar altimeter, there nevertheless is some penetration that must be evaluated. Experiments in Greenland show that there is still measurable 1064 nm energy from sunlight at 50 mm depth below the surface in Greenland (personal communication from A. Nolin, 1996). This effect has not yet been evaluated quantitatively, but at a first guess we can estimate that volume scattering from within the upper 0.1m of the firn will broaden the return pulse by an amount comparable to that produced by a 0.1m roughness. This is another error source that requires further evaluation.
One of the principal purposes of laser altimetry is to produce a picture of the surface topography of the ice sheets. As the density of surface coverage increases, knowledge of the surface slope in the vicinity of a particular ground point will increase concomitantly. It may become increasingly possible to apply a correction to the pulse-spreading for the slope effect and to interpret the remainder as produced by surface roughness.
Acknowledgements
This work was supported by NASA for IGESAT/GLAS mission under contract No. NAS5-33015 to the University of Wisconsin-Madison. We wish to thank H.J. Zwally, J. B. Minster, A. G. Brenner and J. L. Saba for useful discussions.








