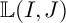1 Indecomposable rank 2 modules with tightly
 $3$
-interlacing layers
$3$
-interlacing layers
In [Reference Baur, Bogdanic and Elsener1], we studied the category
![]() ${\textrm {CM}}(B_{k,n})$
of Cohen–Macaulay modules over the completion of an algebra
${\textrm {CM}}(B_{k,n})$
of Cohen–Macaulay modules over the completion of an algebra
![]() $B_{k,n}$
, which is a quotient of the preprojective algebra of type
$B_{k,n}$
, which is a quotient of the preprojective algebra of type
![]() $A_{n-1}$
. The category
$A_{n-1}$
. The category
![]() ${\textrm {CM}}(B_{k,n})$
is important in a categorification of the cluster algebra structure on the homogeneous coordinate ring
${\textrm {CM}}(B_{k,n})$
is important in a categorification of the cluster algebra structure on the homogeneous coordinate ring
![]() $\mathbb C[Gr(k, n)]$
of the Grassmannian variety of k-dimensional subspaces in
$\mathbb C[Gr(k, n)]$
of the Grassmannian variety of k-dimensional subspaces in
![]() $\mathbb C^n$
(see [Reference Geiss, Leclerc and Schröer3]–[Reference Jensen, King and Su5]).
$\mathbb C^n$
(see [Reference Geiss, Leclerc and Schröer3]–[Reference Jensen, King and Su5]).
For the notation and background results used in this note, we refer the reader to [Reference Baur, Bogdanic and Elsener1, Sect. 1]. We thank Karin Erdmann and Alastair King for useful conversations about indecomposable modules.
In [Reference Baur, Bogdanic and Elsener1, Def. 4.2], we constructed a Cohen–Macaulay module of an arbitrary rank. In the case of rank 2, in [Reference Baur, Bogdanic and Elsener1, Lem. 5.12], we claimed that the constructed module is indecomposble. In fact, the rank 2 module from this lemma is not indecomposable. The aim of this note is to correct this mistake, that is, for given k-subsets I and J that are tightly
![]() $3$
-interlacing, to construct explicitly an indecomposable rank 2 Cohen–Macaulay module with filtration
$3$
-interlacing, to construct explicitly an indecomposable rank 2 Cohen–Macaulay module with filtration
![]() $L_I\mid L_J$
.
$L_I\mid L_J$
.
We show that this module is indecomposable by proving that its endomorphism ring does not have nontrivial idempotents.
Assume that we are in the case when I and J are tightly 3-interlacing k-subsets (
![]() $|I\setminus J|=|J\setminus I|=3$
and noncommon elements of I and J interlace). Write
$|I\setminus J|=|J\setminus I|=3$
and noncommon elements of I and J interlace). Write
![]() $I\setminus J$
as
$I\setminus J$
as
![]() $\{i_1,i_2,i_3\}$
and
$\{i_1,i_2,i_3\}$
and
![]() $J\setminus I=\{j_1,j_2,j_3\}$
so that
$J\setminus I=\{j_1,j_2,j_3\}$
so that
![]() $1\le i_1<j_1<i_2<j_2<i_3<j_3\le n$
.
$1\le i_1<j_1<i_2<j_2<i_3<j_3\le n$
.
The following construction covers all indecomposable rank 2 modules in case when the category
![]() ${\textrm {CM}}(B_{k,n})$
is tame and
${\textrm {CM}}(B_{k,n})$
is tame and
![]() $(k,n)=(3,9)$
.
$(k,n)=(3,9)$
.
We want to define a rank 2 module
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
in
$\operatorname {\mathbb {L}}\nolimits (I,J)$
in
![]() ${\textrm {CM}}(B_{k,n})$
in a similar way as rank 1 modules are defined in [Reference Jensen, King and Su5]. Let
${\textrm {CM}}(B_{k,n})$
in a similar way as rank 1 modules are defined in [Reference Jensen, King and Su5]. Let
![]() $V_i:=\operatorname {\mathbb {C}}\nolimits [|t|]\oplus \operatorname {\mathbb {C}}\nolimits [|t|]$
,
$V_i:=\operatorname {\mathbb {C}}\nolimits [|t|]\oplus \operatorname {\mathbb {C}}\nolimits [|t|]$
,
![]() $i=1,\dots , n$
. The module
$i=1,\dots , n$
. The module
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
has
$\operatorname {\mathbb {L}}\nolimits (I,J)$
has
![]() $V_i$
at each vertex
$V_i$
at each vertex
![]() $1,2,\dots , n$
of
$1,2,\dots , n$
of
![]() $\Gamma _n$
, where
$\Gamma _n$
, where
![]() $\Gamma _n$
is the quiver of the boundary algebra, that is, with vertices
$\Gamma _n$
is the quiver of the boundary algebra, that is, with vertices
![]() $1,2,\dots , n$
on a cycle and arrows
$1,2,\dots , n$
on a cycle and arrows
![]() $x_i: i-1\to i$
,
$x_i: i-1\to i$
,
![]() $y_i:i\to i-1$
. Observe the following matrices:
$y_i:i\to i-1$
. Observe the following matrices:
 $$ \begin{align*} \begin{array}{llll} A_1:=\begin{pmatrix} t & -2 \\ 0 & 1 \end{pmatrix}, & B_1:=\begin{pmatrix} t & 0 \\ 0 & 1 \end{pmatrix}, & C_1:= \begin{pmatrix} t & -1 \\ 0 & 1 \end{pmatrix}, & D_1:= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \\ A_2:=\begin{pmatrix} 1 & 2 \\ 0 & t \end{pmatrix}, & B_2:= \begin{pmatrix} 1 & 0 \\ 0 & t \end{pmatrix}, & C_2:= \begin{pmatrix} 1 & 1 \\ 0 & t \end{pmatrix}, & D_2:= \begin{pmatrix} t & 0 \\ 0 & t \end{pmatrix}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{llll} A_1:=\begin{pmatrix} t & -2 \\ 0 & 1 \end{pmatrix}, & B_1:=\begin{pmatrix} t & 0 \\ 0 & 1 \end{pmatrix}, & C_1:= \begin{pmatrix} t & -1 \\ 0 & 1 \end{pmatrix}, & D_1:= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \\ A_2:=\begin{pmatrix} 1 & 2 \\ 0 & t \end{pmatrix}, & B_2:= \begin{pmatrix} 1 & 0 \\ 0 & t \end{pmatrix}, & C_2:= \begin{pmatrix} 1 & 1 \\ 0 & t \end{pmatrix}, & D_2:= \begin{pmatrix} t & 0 \\ 0 & t \end{pmatrix}. \end{array} \end{align*} $$
Note that these are all matrix factorisations of
 $ \begin {pmatrix} t & 0 \\ 0 & t \end {pmatrix}$
:
$ \begin {pmatrix} t & 0 \\ 0 & t \end {pmatrix}$
:
 $A_1A_2=B_1B_2=C_1C_2=D_1D_2=\begin {pmatrix} t & 0 \\ 0 & t \end {pmatrix}$
.
$A_1A_2=B_1B_2=C_1C_2=D_1D_2=\begin {pmatrix} t & 0 \\ 0 & t \end {pmatrix}$
.
Definition 1.1. Let
![]() $I, J$
be tightly 3-interlacing k-subsets of
$I, J$
be tightly 3-interlacing k-subsets of
![]() $\{1,2,\dots ,n\}$
. At the vertices of
$\{1,2,\dots ,n\}$
. At the vertices of
![]() $\Gamma _n$
,
$\Gamma _n$
,
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
has the spaces
$\operatorname {\mathbb {L}}\nolimits (I,J)$
has the spaces
![]() $V_1,\dots , V_n$
. We define the maps
$V_1,\dots , V_n$
. We define the maps
![]() $x_i,y_i$
as follows:
$x_i,y_i$
as follows:
 $$ \begin{align*} x_i:V_{i-1}\to V_i \mbox{ acts as } \left\{ \begin{array}{rl} A_1, & \mbox{if}\ i=i_1, \\ B_2, & \mbox{if}\ i=j_1, \\ B_1, & \mbox{if}\ i=i_2, \\ C_2, & \mbox{if}\ i=j_2, \\ C_1, & \mbox{if}\ i=i_3, \\ A_2, & \mbox{if}\ i=j_3, \\ D_1, & \mbox{if}\ i\in I\cap J,\\ D_2, & \mbox{if}\ i\in I^c\cap J^c. \end{array}\right. \hskip.5cm y_i:V_{i}\to V_{i-1} \mbox{ acts as } \left\{ \begin{array}{rl} A_2, & \mbox{if}\ i=i_1, \\ B_1, & \mbox{if}\ i=j_1, \\ B_2, & \mbox{if}\ i=i_2, \\ C_1, & \mbox{if}\ i=j_2, \\ C_2, & \mbox{if}\ i=i_3, \\ A_1, & \mbox{if}\ i=j_3, \\ D_2, & \mbox{if}\ i\in I\cap J,\\ D_1, & \mbox{if}\ i\in I^c\cap J^c. \end{array}\right. \end{align*} $$
$$ \begin{align*} x_i:V_{i-1}\to V_i \mbox{ acts as } \left\{ \begin{array}{rl} A_1, & \mbox{if}\ i=i_1, \\ B_2, & \mbox{if}\ i=j_1, \\ B_1, & \mbox{if}\ i=i_2, \\ C_2, & \mbox{if}\ i=j_2, \\ C_1, & \mbox{if}\ i=i_3, \\ A_2, & \mbox{if}\ i=j_3, \\ D_1, & \mbox{if}\ i\in I\cap J,\\ D_2, & \mbox{if}\ i\in I^c\cap J^c. \end{array}\right. \hskip.5cm y_i:V_{i}\to V_{i-1} \mbox{ acts as } \left\{ \begin{array}{rl} A_2, & \mbox{if}\ i=i_1, \\ B_1, & \mbox{if}\ i=j_1, \\ B_2, & \mbox{if}\ i=i_2, \\ C_1, & \mbox{if}\ i=j_2, \\ C_2, & \mbox{if}\ i=i_3, \\ A_1, & \mbox{if}\ i=j_3, \\ D_2, & \mbox{if}\ i\in I\cap J,\\ D_1, & \mbox{if}\ i\in I^c\cap J^c. \end{array}\right. \end{align*} $$
One easily checks that
![]() $xy=yx$
and
$xy=yx$
and
![]() $x^k=y^{n-k}$
at all vertices and that
$x^k=y^{n-k}$
at all vertices and that
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
is free over the center of the boundary algebra. Hence, the following proposition holds.
$\operatorname {\mathbb {L}}\nolimits (I,J)$
is free over the center of the boundary algebra. Hence, the following proposition holds.
Proposition 1.2. The module
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
as constructed in Definition 1.1 is in
$\operatorname {\mathbb {L}}\nolimits (I,J)$
as constructed in Definition 1.1 is in
![]() ${\textrm {CM}}(B_{k,n})$
.
${\textrm {CM}}(B_{k,n})$
.
For the remainder of the paper, if
![]() $w=tv$
, then
$w=tv$
, then
![]() $t^{-1}w$
stands for v.
$t^{-1}w$
stands for v.
Proposition 1.3. Let I and J be tightly 3-interlacing,
![]() $n\ge 6$
arbitrary,
$n\ge 6$
arbitrary,
![]() $I\setminus J=\{i_1,i_2,i_3\}$
and
$I\setminus J=\{i_1,i_2,i_3\}$
and
![]() $J\setminus I=\{j_1,j_2,j_3\}$
where
$J\setminus I=\{j_1,j_2,j_3\}$
where
![]() $1\le i_1<j_1<i_2<j_2<i_3<j_3\le n$
. If
$1\le i_1<j_1<i_2<j_2<i_3<j_3\le n$
. If
![]() $\varphi =( \varphi _i)_{i=1}^n\in $
Hom
$\varphi =( \varphi _i)_{i=1}^n\in $
Hom
![]() $(\operatorname {\mathbb {L}}\nolimits (I,J),\operatorname {\mathbb {L}}\nolimits (I,J))$
, then
$(\operatorname {\mathbb {L}}\nolimits (I,J),\operatorname {\mathbb {L}}\nolimits (I,J))$
, then
 $$ \begin{align*} \varphi_{i_1}=\varphi_{i_2}=\varphi_{i_3}&=\begin{pmatrix}a & bt \\ c & d \end{pmatrix},\\ \varphi_{j_1}&=\begin{pmatrix} a & b \\ ct & d \end{pmatrix},\\ \varphi_{j_2}&=\begin{pmatrix} a+c & b+t^{-1}(d-a-c) \\ ct & d-c \end{pmatrix},\\ \varphi_{j_3}&=\begin{pmatrix} a+2c & b+2t^{-1}(d-a-2c) \\ ct & d-2c \end{pmatrix},\\ \varphi_{i}&=\varphi_{i-1}, \,\, \text{for } i\in (I^c \cap J^c)\cup (I\cap J), \end{align*} $$
$$ \begin{align*} \varphi_{i_1}=\varphi_{i_2}=\varphi_{i_3}&=\begin{pmatrix}a & bt \\ c & d \end{pmatrix},\\ \varphi_{j_1}&=\begin{pmatrix} a & b \\ ct & d \end{pmatrix},\\ \varphi_{j_2}&=\begin{pmatrix} a+c & b+t^{-1}(d-a-c) \\ ct & d-c \end{pmatrix},\\ \varphi_{j_3}&=\begin{pmatrix} a+2c & b+2t^{-1}(d-a-2c) \\ ct & d-2c \end{pmatrix},\\ \varphi_{i}&=\varphi_{i-1}, \,\, \text{for } i\in (I^c \cap J^c)\cup (I\cap J), \end{align*} $$
with
![]() $a,b,c,d\in \operatorname {\mathbb {C}}\nolimits [|t|]$
. Furthermore,
$a,b,c,d\in \operatorname {\mathbb {C}}\nolimits [|t|]$
. Furthermore,
![]() $t\mid c$
and
$t\mid c$
and
![]() $t\mid (a-d)$
.
$t\mid (a-d)$
.
Proof. First we prove the statement for
![]() $n=6$
,
$n=6$
,
![]() $I=\{1,3,5\}$
,
$I=\{1,3,5\}$
,
![]() $J=\{2,4,6\}$
, and
$J=\{2,4,6\}$
, and
![]() $\varphi \in $
End
$\varphi \in $
End
![]() $(\operatorname {\mathbb {L}}\nolimits (I,J))$
. Then
$(\operatorname {\mathbb {L}}\nolimits (I,J))$
. Then
![]() $\varphi =\left ( \varphi _1, \varphi _2, \ldots , \varphi _6 \right ),$
where each
$\varphi =\left ( \varphi _1, \varphi _2, \ldots , \varphi _6 \right ),$
where each
![]() $\varphi _i$
is an element of
$\varphi _i$
is an element of
![]() $M_2(\operatorname {\mathbb {C}}\nolimits [[t]])$
(matrices over the center).
$M_2(\operatorname {\mathbb {C}}\nolimits [[t]])$
(matrices over the center).
We check the relations which arise when we go from a peak of the rim of
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
to a valley of the rim:
$\operatorname {\mathbb {L}}\nolimits (I,J)$
to a valley of the rim:
 $$ \begin{align*} \begin{array}{clccl} (i) & x_2\varphi_1 = \varphi_2x_2, & \quad & (ii) & x_3\varphi_2 = \varphi_3x_3, \\ (iii) & x_4\varphi_3 = \varphi_4x_4, & & (iv) & x_5\varphi_4 = \varphi_5x_5, \\ (v) & x_6\varphi_5 = \varphi_6x_6, & & (vi) & x_1\varphi_6 = \varphi_1 x_1. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{clccl} (i) & x_2\varphi_1 = \varphi_2x_2, & \quad & (ii) & x_3\varphi_2 = \varphi_3x_3, \\ (iii) & x_4\varphi_3 = \varphi_4x_4, & & (iv) & x_5\varphi_4 = \varphi_5x_5, \\ (v) & x_6\varphi_5 = \varphi_6x_6, & & (vi) & x_1\varphi_6 = \varphi_1 x_1. \end{array} \end{align*} $$
Let
 $\varphi _1=\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
. The equalities
$\varphi _1=\begin {pmatrix} a & b \\ c & d \end {pmatrix}$
. The equalities
![]() $\varphi _1=\varphi _3=\varphi _5$
follow immediately from
$\varphi _1=\varphi _3=\varphi _5$
follow immediately from
![]() $t\varphi _3=\varphi _3B_1B_2=B_1B_2\varphi _1=t\varphi _1$
and
$t\varphi _3=\varphi _3B_1B_2=B_1B_2\varphi _1=t\varphi _1$
and
![]() $t\varphi _5=\varphi _5C_1C_2=C_1C_2\varphi _3=t\varphi _3$
.
$t\varphi _5=\varphi _5C_1C_2=C_1C_2\varphi _3=t\varphi _3$
.
If we consider matrices
![]() $x_i$
and
$x_i$
and
![]() $y_i$
as elements of the ring
$y_i$
as elements of the ring
![]() $M_2(\operatorname {\mathbb {C}}\nolimits ((t)))$
, where all of them are units, then from
$M_2(\operatorname {\mathbb {C}}\nolimits ((t)))$
, where all of them are units, then from
![]() $ x_2\varphi _1 = \varphi _2x_2$
follows that
$ x_2\varphi _1 = \varphi _2x_2$
follows that
 $$ \begin{align*}\varphi_2=x_2\varphi_1x_2^{-1}=\begin{pmatrix} 1 & 0 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & t^{-1} \end{pmatrix} = \begin{pmatrix} a & t^{-1}b \\ ct & d \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\varphi_2=x_2\varphi_1x_2^{-1}=\begin{pmatrix} 1 & 0 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & t^{-1} \end{pmatrix} = \begin{pmatrix} a & t^{-1}b \\ ct & d \end{pmatrix}.\end{align*} $$
Thus,
![]() $t\mid b$
, so if we replace b by
$t\mid b$
, so if we replace b by
![]() $bt$
, this yields
$bt$
, this yields
 $$ \begin{align*}\varphi_1=\begin{pmatrix} a & bt \\ c & d\end{pmatrix}, \quad \varphi_2=\begin{pmatrix} a & b \\ ct & d\end{pmatrix}.\end{align*} $$
$$ \begin{align*}\varphi_1=\begin{pmatrix} a & bt \\ c & d\end{pmatrix}, \quad \varphi_2=\begin{pmatrix} a & b \\ ct & d\end{pmatrix}.\end{align*} $$
Similarly, from
![]() $x_4\varphi _3 = \varphi _4x_4$
, we have
$x_4\varphi _3 = \varphi _4x_4$
, we have
 $$ \begin{align*}\varphi_4=x_4\varphi_3x_4^{-1}= \begin{pmatrix} 1 & 1 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & bt \\ c & d\end{pmatrix} \begin{pmatrix} 1 & -t^{-1} \\ 0 & t^{-1} \end{pmatrix} = \begin{pmatrix} a+c & b+t^{-1}(d-a-c) \\ ct & d-c \end{pmatrix} ,\end{align*} $$
$$ \begin{align*}\varphi_4=x_4\varphi_3x_4^{-1}= \begin{pmatrix} 1 & 1 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & bt \\ c & d\end{pmatrix} \begin{pmatrix} 1 & -t^{-1} \\ 0 & t^{-1} \end{pmatrix} = \begin{pmatrix} a+c & b+t^{-1}(d-a-c) \\ ct & d-c \end{pmatrix} ,\end{align*} $$
and from
![]() $x_6\varphi _5 = \varphi _6x_6$
, we have
$x_6\varphi _5 = \varphi _6x_6$
, we have
 $$ \begin{align*}\varphi_6=x_6\varphi_5x_6^{-1}=\begin{pmatrix} 1 & 2 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & bt \\ c & d\end{pmatrix} \begin{pmatrix} 1 & -2t^{-1} \\ 0 & t^{-1} \end{pmatrix} =\begin{pmatrix} a+2c & b+2t^{-1}(d-a-2c) \\ ct & d-2c \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\varphi_6=x_6\varphi_5x_6^{-1}=\begin{pmatrix} 1 & 2 \\ 0 & t \end{pmatrix} \begin{pmatrix} a & bt \\ c & d\end{pmatrix} \begin{pmatrix} 1 & -2t^{-1} \\ 0 & t^{-1} \end{pmatrix} =\begin{pmatrix} a+2c & b+2t^{-1}(d-a-2c) \\ ct & d-2c \end{pmatrix}.\end{align*} $$
The statement about the divisibility follows since we have the two properties
![]() $t\mid (d-c-a)$
and
$t\mid (d-c-a)$
and
![]() $t\mid (d-a-2c)$
. Combined, they imply
$t\mid (d-a-2c)$
. Combined, they imply
![]() $t\mid c$
and
$t\mid c$
and
![]() $t\mid d-a$
as claimed.
$t\mid d-a$
as claimed.
In the general case, the proof is almost the same as in the case
![]() $n=6$
. The only thing left to note is that if
$n=6$
. The only thing left to note is that if
![]() $i\in (I^c \cap J^c)\cup (I\cap J)$
, then
$i\in (I^c \cap J^c)\cup (I\cap J)$
, then
![]() $x_i$
is a scalar matrix (either identity or t times identity), so the equality
$x_i$
is a scalar matrix (either identity or t times identity), so the equality
![]() $x_{i}\varphi _{i-1}=\varphi _{i}x_{i}$
yields
$x_{i}\varphi _{i-1}=\varphi _{i}x_{i}$
yields
![]() $\varphi _{i-1}=\varphi _{i}$
.
$\varphi _{i-1}=\varphi _{i}$
.
Proposition 1.4. Let
![]() $I,J$
be tightly 3-interlacing,
$I,J$
be tightly 3-interlacing,
![]() $n\ge 6$
arbitrary. Then the module
$n\ge 6$
arbitrary. Then the module
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
is indecomposable.
$\operatorname {\mathbb {L}}\nolimits (I,J)$
is indecomposable.
Proof. We first consider
![]() $n=6$
. In this case, we can assume
$n=6$
. In this case, we can assume
![]() $I=\{1,3,5\}$
and
$I=\{1,3,5\}$
and
![]() $J=\{2,4,6\}$
. Take
$J=\{2,4,6\}$
. Take
![]() $\varphi =(\varphi _i)_i\in $
End
$\varphi =(\varphi _i)_i\in $
End
![]() $(\operatorname {\mathbb {L}}\nolimits (I,J))$
as in the previous proposition.
$(\operatorname {\mathbb {L}}\nolimits (I,J))$
as in the previous proposition.
To show the indecomposability, we assume that
![]() $\varphi $
is an idempotent endomorphism of
$\varphi $
is an idempotent endomorphism of
![]() $\operatorname {\mathbb {L}}\nolimits (I,J)$
and show that
$\operatorname {\mathbb {L}}\nolimits (I,J)$
and show that
![]() $\varphi $
is trivial (the identity or the zero endomorphism).
$\varphi $
is trivial (the identity or the zero endomorphism).
Assume that
![]() $\varphi _2^2=\varphi _2$
, that is
$\varphi _2^2=\varphi _2$
, that is
 $$ \begin{align*} \varphi_2^2=\begin{pmatrix} a^2+bct & (a+d)b \\ (a+d)ct & d^2+bct\end{pmatrix}= \begin{pmatrix}a & b \\ ct & d \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \varphi_2^2=\begin{pmatrix} a^2+bct & (a+d)b \\ (a+d)ct & d^2+bct\end{pmatrix}= \begin{pmatrix}a & b \\ ct & d \end{pmatrix}. \end{align*} $$
The equations
![]() $a^2+bct=a \quad \mbox {and} \quad d^2+bct=d$
on the diagonal entries give
$a^2+bct=a \quad \mbox {and} \quad d^2+bct=d$
on the diagonal entries give
![]() $a-a^2=d-d^2$
, that is,
$a-a^2=d-d^2$
, that is,
![]() $a-d=a^2-d^2=(a-d)(a+d)$
and hence
$a-d=a^2-d^2=(a-d)(a+d)$
and hence
![]() $a=d$
or
$a=d$
or
![]() $a+d=1$
. The equations also show that
$a+d=1$
. The equations also show that
![]() $t\mid a(1-a)$
and that
$t\mid a(1-a)$
and that
![]() $t\mid d(1-d)$
.
$t\mid d(1-d)$
.
Assume first
![]() $a=d$
. If
$a=d$
. If
![]() $b\ne 0$
, we get
$b\ne 0$
, we get
![]() $a=\frac {1}{2}$
, which contradicts to
$a=\frac {1}{2}$
, which contradicts to
![]() $t\mid a-a^2$
. Analogously for
$t\mid a-a^2$
. Analogously for
![]() $c\ne 0$
. Thus
$c\ne 0$
. Thus
![]() $b=c=0$
and
$b=c=0$
and
![]() $a=d=0$
or
$a=d=0$
or
![]() $a=d=1$
, the two trivial cases (note that if
$a=d=1$
, the two trivial cases (note that if
![]() $\varphi _2$
is trivial, then
$\varphi _2$
is trivial, then
![]() $x_{i}\varphi _{i-1}=\varphi _{i}x_{i}$
yields
$x_{i}\varphi _{i-1}=\varphi _{i}x_{i}$
yields
![]() $\varphi _2=\varphi _i$
, for all i).
$\varphi _2=\varphi _i$
, for all i).
So assume that
![]() $a\ne d$
and
$a\ne d$
and
![]() $d=1-a$
. Combining
$d=1-a$
. Combining
![]() $t\mid a(1-a)$
with the fact that t divides
$t\mid a(1-a)$
with the fact that t divides
![]() $a-d=2a-1$
implies that
$a-d=2a-1$
implies that
![]() $t\mid 1$
, which is a contradiction.
$t\mid 1$
, which is a contradiction.
For a general n, since
![]() $\varphi _i=\varphi _{i+1}$
for
$\varphi _i=\varphi _{i+1}$
for
![]() $i+1\in (I^c\cap J^c)\cup (I\cap J)$
, the proof follows as for
$i+1\in (I^c\cap J^c)\cup (I\cap J)$
, the proof follows as for
![]() $n=6$
.
$n=6$
.
The question of uniqueness of such a rank 2 indecomposable module is studied in [Reference Baur, Bogdanic and Li2]. For given tightly
![]() $3$
-interlacing I and J, there is a unique indecomposable rank 2 module with filtration
$3$
-interlacing I and J, there is a unique indecomposable rank 2 module with filtration
![]() $L_I\mid L_J$
. This statement is clear in case when the category
$L_I\mid L_J$
. This statement is clear in case when the category
![]() ${\textrm {CM}}(B_{k,n})$
is of finite representation type and in case when
${\textrm {CM}}(B_{k,n})$
is of finite representation type and in case when
![]() ${\textrm {CM}}(B_{k,n})$
is tame, with
${\textrm {CM}}(B_{k,n})$
is tame, with
![]() $(k,n)\in \{(3,9),\, (4,8)\}$
. Consequently, we have the following theorem.
$(k,n)\in \{(3,9),\, (4,8)\}$
. Consequently, we have the following theorem.
Theorem 1.5 [Reference Baur, Bogdanic and Li2, Th. 1.2].
Let
![]() $M\in {\textrm {CM}}(B_{k,n})$
be an indecomposable module with profile
$M\in {\textrm {CM}}(B_{k,n})$
be an indecomposable module with profile
![]() $I\mid J$
. Then, up to isomorphism, M is the unique indecomposable rank
$I\mid J$
. Then, up to isomorphism, M is the unique indecomposable rank
![]() $2$
module with filtration
$2$
module with filtration
![]() $I\mid J$
if and only if its poset is
$I\mid J$
if and only if its poset is
![]() $1^3\mid 2$
and I and J are almost tightly
$1^3\mid 2$
and I and J are almost tightly
![]() $3$
-interlacing.
$3$
-interlacing.
Acknowledgments
We thank the referees for helpful comments. Karin Baur and Ana Garcia Elsener would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme CAR where work on this paper was undertaken. This work was supported by EPSRC grant no EP/K032208/1.