1. Introduction
During the last decade, attempts to find solutions to the power exhaust problem in future tokamaks have led to emergence and analysis of several poloidal divertor configurations deviating significantly from a ‘standard’ single-null divertor configuration (e.g. Wesson & Campbell Reference Wesson and Campbell2011). Among them are: a cusp divertor (Takase Reference Takase2001) and its close ‘relative’ called an X-divertor (Kotschenreuther et al. Reference Kotschenreuther, Valanju, Wiley, Rognlien, Mahajan and Pekker2004, Reference Kotschenreuther, Valanju, Wiley and Mahajan2007), a Pitts divertor (Pitts et al. Reference Pitts, Duval, Loarte, Moret, Boedo, Coster, Furno, Horacek, Kukushkin, Reiter and Rommers2001), a snowflake divertor (Ryutov Reference Ryutov2007; Ryutov et al. Reference Ryutov, Cohen, Rognlien and Umansky2008) and a cloverleaf (Ryutov & Umansky Reference Ryutov and Umansky2013) divertor. All of them are utilizing poloidal flux expansion; the latter two also exploit the increased number of divertor channels and strike points. A desirable feature of the divertor magnetic field is a possibility to create it by remote coils situated sufficiently far from the divertor zone, behind the neutron shield and, desirably, even outside the toroidal field (TF) coils. General properties of the poloidal field (PF) created by distant currents impose some constraints on the realizable field geometry (Ryutov, Makowski & Umansky Reference Ryutov, Makowski and Umansky2010). Still, as was shown experimentally by Soukhanovskii et al. (Reference Soukhanovskii, Ahn, Bell, Gates, Gerhardt, Kaita, Kolemen, Leblanc, Maingi, Makowski, Maqueda, Mclean, Menard, Mueller, Paul, Raman, Roquemore, Ryutov, Sabbagh and Scott2011, Reference Soukhanovskii, Allen, Fenstermacher, Hill, Lasnier, Makowski, Mclean, Meyer, Kolemen, Groebner, Hyatt, Leonard, Osborne and Petrie2015), Reimerdes et al. (Reference Reimerdes, Canal, Duval, Labit, Lunt, Vijvers, Coda, De Temmerman, Morgan, Nespoli and Taland2013) and Vijvers et al. (Reference Vijvers, Canal, Labit, Reimerdes, Tal, Coda, De Temmerman, Duval, Morgan and Zielinski2014) for the case of a snowflake divertor, one can vary at will the divertor field structure even if the coils are situated far away from the divertor.
Here we explore an analogous issue for a cusp-like divertor and assess a variety of the related configurations.
Before proceeding to this analysis, we briefly describe the original cusp divertor, as presented in Takase (Reference Takase2001). It required producing PF nulls on each of the two branches of the separatrix of the standard divertor, as shown in figure 1 for some generic cusp divertor; for the original pictures with more detail, see figures 3 and 4 in Takase (Reference Takase2001) and figures 3 and 4 in Kotschenreuther et al. (Reference Kotschenreuther, Valanju, Wiley and Mahajan2007). As seen from figure 1, the divertor coils have been placed near the strike points in each divertor leg. As these coils are dipole-like, with the currents in the adjacent coils flowing in opposite directions, their magnetic field rapidly decreases with the distance, thereby making their effect on the main null and the core plasma minimal. A nice verbal summary of these features was presented in Kotschenreuther et al. (Reference Kotschenreuther, Valanju, Wiley and Mahajan2007): ‘this extra downstream X-point can be created with an extra pair of poloidal coils
![]() $\ldots .$
Each divertor leg (inside and outside) needs such a pair of coils
$\ldots .$
Each divertor leg (inside and outside) needs such a pair of coils
![]() $\ldots .$
The distant main plasma is hardly affected because the line flaring happens only near the extra coils’.
$\ldots .$
The distant main plasma is hardly affected because the line flaring happens only near the extra coils’.

Figure 1. A generic cusp divertor. The currents in the neighbouring coils flow in opposite directions, thereby minimizing the impact of these coils on the core plasma. In Takase (Reference Takase2001), additional coils (not shown in our schematic) that would squeeze the poloidal flux surfaces above the strike points have been considered, but the concept works nicely without them. Reproduced from Ryutov et al. (Reference Ryutov, Cohen, Rognlien, Soukhanovskii and Umansky2014b ) with permission of AIP Publishing, all rights reserved.
Now we want to produce a similar configuration with the coils situated far away from the divertor area. Specifically, we assume that the distance from the divertor PF nulls to the coils is larger than the distance between the nulls. In most of the existing reactor designs the PF coils, including the ones that control the divertor field, are placed outside the radiation shield and toroidal field coils. Or, putting it differently, our approach does not lead to an increase of the reactor size compared to reactors based on the standard single-null divertors of International Thermonuclear Experimental Reactor (ITER) type. It does not require the use of the PF coils interlinked with the TF coils.
The present study does not by any means pretend to propose ‘the best’ solution for the divertor problem: there already exist several promising ideas, some of which have been tested experimentally. Its purpose is much more modest: to identify and characterize several intriguing magnetic configurations and their features that may possibly provide a basis for modified divertor designs. These configurations may also be used to ‘probe’ the plasma properties at the plasma edge.
2. Magnetic field characterization
We assume that the plasma current in the divertor area is small, so that we are dealing with the vacuum magnetic field. In the zone whose dimension is small compared to the major radius, one can neglect the toroidicity and consider the field as planar, with two components,
![]() $B_{x}(x,y)$
and
$B_{x}(x,y)$
and
![]() $B_{y}(x,y)$
(the Cartesian coordinates
$B_{y}(x,y)$
(the Cartesian coordinates
![]() $x$
,
$x$
,
![]() $y$
are shown in figure 2). We choose the origin of the coordinate frame in the ‘main’ null, the one situated at the boundary of the confined plasma.
$y$
are shown in figure 2). We choose the origin of the coordinate frame in the ‘main’ null, the one situated at the boundary of the confined plasma.
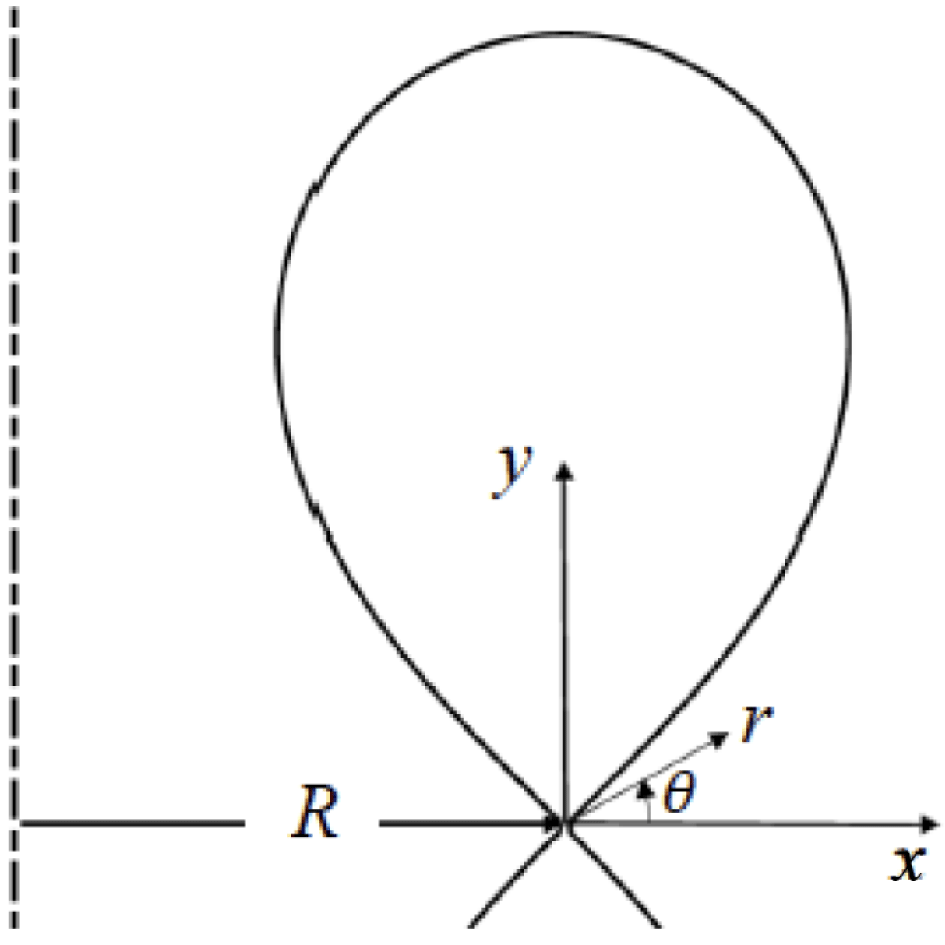
Figure 2. Coordinate frame used in our analysis. The origin coincides with the poloidal field null lying on the main separatrix.
The two-dimensional vacuum magnetic field can be conveniently described using complex variables (Brown & Churchill Reference Brown and Churchill2004). In the context of the divertor magnetic field, this approach has been used in Ryutov & Umansky (Reference Ryutov and Umansky2013) and Ryutov & Soukhanovskii (Reference Ryutov and Soukhanovskii2015). The complex variable
![]() $z$
is introduced as
$z$
is introduced as
![]() $z=x+\text{i}y$
; the presence of the conditions
$z=x+\text{i}y$
; the presence of the conditions
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
![]() $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}=0$
allows one to introduce a complex function
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}=0$
allows one to introduce a complex function
![]() $G(z)={\it\Psi}+\text{i}{\it\Phi}$
(a complex potential) and a function
$G(z)={\it\Psi}+\text{i}{\it\Phi}$
(a complex potential) and a function
![]() $F(z)=B_{x}(z)-\text{i}B_{y}(z)$
related to the complex potential
$F(z)=B_{x}(z)-\text{i}B_{y}(z)$
related to the complex potential
![]() $G$
by
$G$
by
With these definitions, one finds that
![]() ${\it\Phi}=\text{Im}\,G$
is a poloidal flux function,
${\it\Phi}=\text{Im}\,G$
is a poloidal flux function,
![]() $B_{x}=-\partial {\it\Phi}/\partial y$
,
$B_{x}=-\partial {\it\Phi}/\partial y$
,
![]() $B_{y}=\partial {\it\Phi}/\partial x$
, with the lines
$B_{y}=\partial {\it\Phi}/\partial x$
, with the lines
![]() ${\it\Phi}(x,y)=\text{const.}$
being the PF flux surfaces. The function
${\it\Phi}(x,y)=\text{const.}$
being the PF flux surfaces. The function
![]() ${\it\Psi}$
is a scalar potential. As the conductors that are generating the magnetic field in the divertor zone are situated far away from this zone, the functions
${\it\Psi}$
is a scalar potential. As the conductors that are generating the magnetic field in the divertor zone are situated far away from this zone, the functions
![]() $F$
and
$F$
and
![]() $G$
are regular functions.
$G$
are regular functions.
What we would like to produce is a configuration with three nearby nulls: one on the boundary of the main plasma, and two nulls on the two branches of the separatrix emerging from the ‘main’ null. In other words, we are interested in the configuration with three nearby nulls, of the type shown in figure 3 that depicts one of the configurations that appear as a result of our further analysis. This, in turn, means that the configuration will be close to the cloverleaf configuration (Ryutov & Umansky Reference Ryutov and Umansky2013), where the three nulls were merged into a third-order null. The trick is to find conditions under which this third-order null splits in the way shown in figure 3. An analysis presented in the present paper shows that such configurations do indeed exist. We also consider a structure of the nearby configurations and assess requirements to the location and the currents in the divertor coils.

Figure 3. A super-cusp divertor. The magnetic configuration is created by the coils situated at a significant distance from the divertor area. Fat black line represents the separatrix that passes through all three nulls. In the two lower nulls a cusp configuration is created. The confinement zone is indicated by a set of red flux surfaces, whereas the scrape-off layer is indicated by the yellow flux surfaces. In agreement with the original idea of Takase (Reference Takase2001) (see also Kotschenreuther et al. (Reference Kotschenreuther, Valanju, Wiley, Rognlien, Mahajan and Pekker2004, Reference Kotschenreuther, Valanju, Wiley and Mahajan2007)), there is a significant flux expansion in the area of the secondary nulls. In this case, the flux spreading occurs due to purely geometrical factors, not due to enhanced transport in the area of the weak field as in the models with very closely spaced nulls (Ryutov et al. Reference Ryutov, Cohen, Farmer, Rognlien, Soukhanovskii and Umansky2014a ). Shown in purple are two of many conceptually possible positions of the divertor plates.
A regular function in the area of interest for us can be represented as a third-order polynomial of the form
where
![]() $z_{1,2}$
are the secondary nulls, whereas the ‘main’ null, per our convention of the origin of the coordinate frame, is situated at
$z_{1,2}$
are the secondary nulls, whereas the ‘main’ null, per our convention of the origin of the coordinate frame, is situated at
![]() $z=0$
. We assume that
$z=0$
. We assume that
![]() $|z|$
,
$|z|$
,
![]() $|z_{1}|$
and
$|z_{1}|$
and
![]() $|z_{2}|$
are all small compared to the plasma minor radius
$|z_{2}|$
are all small compared to the plasma minor radius
![]() $a$
and the distances to the divertor coils. There is no reason to retain the higher-order terms in
$a$
and the distances to the divertor coils. There is no reason to retain the higher-order terms in
![]() $z$
as, for small
$z$
as, for small
![]() $z$
, they will be subdominant compared to the retained terms. The constant
$z$
, they will be subdominant compared to the retained terms. The constant
![]() $C$
is determined by the currents in the plasma and divertor coils. We represent it as
$C$
is determined by the currents in the plasma and divertor coils. We represent it as
where
![]() $B_{pm}$
is the poloidal magnetic field strength at the separatrix in the midplane and
$B_{pm}$
is the poloidal magnetic field strength at the separatrix in the midplane and
![]() $K$
is a dimensionless parameter that determines the rate of increase of the field at
$K$
is a dimensionless parameter that determines the rate of increase of the field at
![]() $|z|>|z_{1,2}|$
. If the divertor coils are situated at the distance
$|z|>|z_{1,2}|$
. If the divertor coils are situated at the distance
![]() ${\sim}a$
from the null, then this coefficient is of the order of unity. Its exact value depends on the global magnetic configuration. The parameter
${\sim}a$
from the null, then this coefficient is of the order of unity. Its exact value depends on the global magnetic configuration. The parameter
![]() ${\it\eta}$
determines the orientation of the branches of the separatrix with respect to the coordinate frame (see Ryutov & Soukhanovskii Reference Ryutov and Soukhanovskii2015). In what follows, we take it equal to
${\it\eta}$
determines the orientation of the branches of the separatrix with respect to the coordinate frame (see Ryutov & Soukhanovskii Reference Ryutov and Soukhanovskii2015). In what follows, we take it equal to
![]() ${\rm\pi}/2$
; as we show shortly, this corresponds to the location of the main plasma above the main null, i.e. the configuration looks like that in figure 3. The orientation of the field structure in a real device is determined by the location of the PF coils. For our selection of
${\rm\pi}/2$
; as we show shortly, this corresponds to the location of the main plasma above the main null, i.e. the configuration looks like that in figure 3. The orientation of the field structure in a real device is determined by the location of the PF coils. For our selection of
![]() ${\it\eta}$
and for
${\it\eta}$
and for
![]() $z_{1}=z_{2}=0$
, we recover an exact third-order null (figure 4) characteristic of the cloverleaf configuration described in Ryutov & Umansky (Reference Ryutov and Umansky2013).
$z_{1}=z_{2}=0$
, we recover an exact third-order null (figure 4) characteristic of the cloverleaf configuration described in Ryutov & Umansky (Reference Ryutov and Umansky2013).

Figure 4. An exact third-order null of the poloidal field (Kotschenreuther et al. Reference Kotschenreuther, Valanju, Wiley, Rognlien, Mahajan and Pekker2004). Eight branches of the separatrix are present with the confinement zone identified with the upper central octant. The presence of an apparent hole near the origin is a result of insufficient resolution of the printer.
3. Super-cusp configuration
We now want to deliberately distort an exact third-order-null configuration of figure 4, so that there would appear three nearby nulls, arranged in a special manner, like in figure 3 that shows a configuration symmetric with respect to the vertical axis. We will find the constraints under which such symmetric configuration and similar asymmetric configurations can be created by the distant coils. The configuration shown in figure 3 is very similar to the original cusp divertor, but has additional attractive features: first, it will be created by the coils that are much further from the divertor than the distance between the divertor nulls; second, the configuration will produce a clean cusp geometry, with one first-order null near each strike point, not a more complex configuration produced by the nearby coils. (In particular, in the case shown in figure 1, additional nulls are lurking around: in the vicinity of each strike point there are at least two nulls.) For these two reasons we suggest to call the configuration of figure 3 ‘a super-cusp’. Note also that significant compression of the flux surfaces occurs on the way from the main null to the secondary nulls, similarly to what has been discussed in the cusp- and X-divertor proposals (Takase Reference Takase2001; Kotschenreuther et al. Reference Kotschenreuther, Valanju, Wiley, Rognlien, Mahajan and Pekker2004, Reference Kotschenreuther, Valanju, Wiley and Mahajan2007). In the cusp divertor the effect was supposed to be further enhanced by additional coils situated between the main null and the secondary nulls.
For the analysis of the shape of the poloidal field flux surfaces, it is convenient to operate with the functions
![]() $F$
and
$F$
and
![]() $G$
divided by the coefficient
$G$
divided by the coefficient
![]() $KB_{pm}/a^{3}$
. So, the function
$KB_{pm}/a^{3}$
. So, the function
![]() $F$
becomes
$F$
becomes
Performing an integration, we find the corresponding function
![]() $G$
:
$G$
:
We take the additive constant equal to zero; then the equation
![]() $G(z)=0$
corresponds to the separatrix passing through the ‘main’ null,
$G(z)=0$
corresponds to the separatrix passing through the ‘main’ null,
![]() $z=0$
. To obtain a configuration of the type shown in figure 3, we need to find the situation where the same separatrix passes through two other nulls; in other words, we need to ensure that
$z=0$
. To obtain a configuration of the type shown in figure 3, we need to find the situation where the same separatrix passes through two other nulls; in other words, we need to ensure that
![]() $\text{Im}\,G(z_{1})=0$
,
$\text{Im}\,G(z_{1})=0$
,
![]() $\text{Im}\,G(z_{2})=0$
. We have accounted for the fact that the additive constant in (3.2) is zero for the ‘main’ null. These two equations then become
$\text{Im}\,G(z_{2})=0$
. We have accounted for the fact that the additive constant in (3.2) is zero for the ‘main’ null. These two equations then become
The positions of the two nulls will be characterized by their distances to the main null,
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
(both positive) and angles
$D_{2}$
(both positive) and angles
![]() ${\it\chi}_{1}$
,
${\it\chi}_{1}$
,
![]() ${\it\chi}_{2}$
formed by the segments
${\it\chi}_{2}$
formed by the segments
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
with the vertical axis (figure 5). With this convention, the positive signs of
$D_{2}$
with the vertical axis (figure 5). With this convention, the positive signs of
![]() ${\it\chi}_{1}$
,
${\it\chi}_{1}$
,
![]() ${\it\chi}_{2}$
mean that the nulls are situated on the opposite sides of the vertical axis. If
${\it\chi}_{2}$
mean that the nulls are situated on the opposite sides of the vertical axis. If
![]() ${\it\chi}_{1}$
is positive, whereas
${\it\chi}_{1}$
is positive, whereas
![]() ${\it\chi}_{2}$
is negative, the nulls are situated on the same (‘left’ side). The change of both signs corresponds simply to flipping the configuration with respect to the vertical axis. One more constraint on the values of
${\it\chi}_{2}$
is negative, the nulls are situated on the same (‘left’ side). The change of both signs corresponds simply to flipping the configuration with respect to the vertical axis. One more constraint on the values of
![]() ${\it\chi}_{1}$
,
${\it\chi}_{1}$
,
![]() ${\it\chi}_{2}$
is that both nulls should lie below the ‘main’ null, in the lower half-space, as is usually assumed in the divertor design. As
${\it\chi}_{2}$
is that both nulls should lie below the ‘main’ null, in the lower half-space, as is usually assumed in the divertor design. As
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
are positive, we have
$D_{2}$
are positive, we have

Figure 5. The two secondary nulls of the super-cusp configuration. Note the sign convention for the angles
![]() ${\it\chi}_{1,2}$
: both are positive when the corresponding null moves away from the vertical symmetry plane.
${\it\chi}_{1,2}$
: both are positive when the corresponding null moves away from the vertical symmetry plane.
Referring to figure 5 and the aforementioned definitions, we present the roots in the form
In this representation, (3.3a,b ) become
Here
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}>0$
. For
$D_{2}>0$
. For
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
satisfying (3.3), all three nulls lie on the same separatrix, an equation for which is
$z_{2}$
satisfying (3.3), all three nulls lie on the same separatrix, an equation for which is
![]() ${\it\Phi}=\text{Im}\,G=0$
. Substituting (3.5) into (3.2) and using the polar representation of
${\it\Phi}=\text{Im}\,G=0$
. Substituting (3.5) into (3.2) and using the polar representation of
![]() $z$
,
$z$
,
![]() $z=r\text{e}^{\text{i}{\it\theta}}$
, we find this equation in the polar coordinates
$z=r\text{e}^{\text{i}{\it\theta}}$
, we find this equation in the polar coordinates
![]() $r$
,
$r$
,
![]() ${\it\theta}$
:
${\it\theta}$
:
We first consider the case of symmetric location of secondary nulls,
![]() $D_{1}=D_{2}=D$
,
$D_{1}=D_{2}=D$
,
![]() ${\it\chi}_{1}={\it\chi}_{2}={\it\chi}$
(this is the case shown in figure 3). In this case (3.6) both lead to the same equation for the angle
${\it\chi}_{1}={\it\chi}_{2}={\it\chi}$
(this is the case shown in figure 3). In this case (3.6) both lead to the same equation for the angle
![]() ${\it\chi}$
:
${\it\chi}$
:
this yielding the following expression for
![]() $\cos {\it\chi}$
:
$\cos {\it\chi}$
:
or
![]() ${\it\chi}=0.97276$
. With that, the condition
${\it\chi}=0.97276$
. With that, the condition
![]() ${\it\Phi}=0$
leads to the following equation for the separatrix (see (3.7)):
${\it\Phi}=0$
leads to the following equation for the separatrix (see (3.7)):
The result is shown in figure 3. By putting divertor plates near the secondary nulls, one reduces the heat flux on the plates by strong flaring of the magnetic field. The distance
![]() $D$
is determined by the divertor coil configuration and the currents in these coils. We will return to this relation later.
$D$
is determined by the divertor coil configuration and the currents in these coils. We will return to this relation later.
We now show several examples of the asymmetric nulls, the ones that are described by (3.6). These equations cover a broad variety of the three-null super-cusp (and related) configurations. Taking as a parameter an angle
![]() ${\it\chi}_{1}$
, we can find from (3.6) the corresponding values of
${\it\chi}_{1}$
, we can find from (3.6) the corresponding values of
![]() ${\it\chi}_{2}$
and the ratios
${\it\chi}_{2}$
and the ratios
![]() $D_{2}/D_{1}$
and thereby get a family of configurations characterized by the parameter
$D_{2}/D_{1}$
and thereby get a family of configurations characterized by the parameter
![]() ${\it\chi}_{1}$
. As mentioned, distances
${\it\chi}_{1}$
. As mentioned, distances
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
are determined by the position of the divertor coils; for now, looking only for the shapes of these configurations, we normalize the distances to
$D_{2}$
are determined by the position of the divertor coils; for now, looking only for the shapes of these configurations, we normalize the distances to
![]() $D_{1}$
, making thereby
$D_{1}$
, making thereby
![]() $D_{1}=1$
.
$D_{1}=1$
.
Eliminating
![]() $D_{2}$
from (3.6), one finds the relation between
$D_{2}$
from (3.6), one finds the relation between
![]() ${\it\chi}_{1}$
and
${\it\chi}_{1}$
and
![]() ${\it\chi}_{2}$
:
${\it\chi}_{2}$
:
In the domain defined by (3.4a,b
), this equation describes several branches of solutions illustrated by figure 6. As mentioned, we are not interested in the secondary nulls lying above the primary null. Also, there is no need to consider negative
![]() ${\it\chi}_{1}$
– these configurations are obtained simply by flipping a configuration with
${\it\chi}_{1}$
– these configurations are obtained simply by flipping a configuration with
![]() ${\it\chi}_{1}>0$
around the vertical axis – hence the conditions of (3.4a,b
).
${\it\chi}_{1}>0$
around the vertical axis – hence the conditions of (3.4a,b
).
The second equation of (3.6) allows us to find
![]() $D_{2}$
in the form
$D_{2}$
in the form
As
![]() $D_{2}$
is positive (3.4c
), we have to consider solutions of (3.11) only in the domain where the right-hand side of (3.12) is positive; these domains are highlighted by a light shading in figure 6.
$D_{2}$
is positive (3.4c
), we have to consider solutions of (3.11) only in the domain where the right-hand side of (3.12) is positive; these domains are highlighted by a light shading in figure 6.
The solution describing the symmetric null of figure 3 corresponds to point 1 in figure 6. If one moves along the branch where this solution lies, the ratio
![]() $D_{2}/D_{1}$
increases in one direction (smaller
$D_{2}/D_{1}$
increases in one direction (smaller
![]() ${\it\chi}_{1}$
) and decreases in the opposite direction (larger
${\it\chi}_{1}$
) and decreases in the opposite direction (larger
![]() ${\it\chi}_{1}$
). An example is shown in figure 7(a) and corresponds to point 2. One of the two nulls is now situated significantly farther from the main plasma than the other. The configuration can be flipped around the vertical axis, if needed. Having different lengths of the divertor legs provides additional flexibility to the divertor design.
${\it\chi}_{1}$
). An example is shown in figure 7(a) and corresponds to point 2. One of the two nulls is now situated significantly farther from the main plasma than the other. The configuration can be flipped around the vertical axis, if needed. Having different lengths of the divertor legs provides additional flexibility to the divertor design.

Figure 7. Some of the asymmetric super-cusp configurations: (a) one divertor leg is much longer than the other. Corresponds to point 2 in figure 6 (
![]() ${\it\chi}_{1}=0.938$
,
${\it\chi}_{1}=0.938$
,
![]() ${\it\chi}_{2}=1.0484$
). Can be flipped around the vertical axis; (b) configuration with one of the secondary nulls merging with the primary null, thereby forming a snowflake configuration (
${\it\chi}_{2}=1.0484$
). Can be flipped around the vertical axis; (b) configuration with one of the secondary nulls merging with the primary null, thereby forming a snowflake configuration (
![]() ${\it\chi}_{1}={\rm\pi}/8$
,
${\it\chi}_{1}={\rm\pi}/8$
,
![]() ${\it\chi}_{2}=0.6545$
). A secondary null stands at some distance. Corresponds to point 3 in figure 6.
${\it\chi}_{2}=0.6545$
). A secondary null stands at some distance. Corresponds to point 3 in figure 6.
In the configuration of figure 7(b) (point 3 in figure 6), one of the secondary nulls merges with the primary null, thereby creating a second-order null (a snowflake) at the boundary of the confinement zone, with a first-order null situated nearby. Whether this peculiar configuration has an additional potential for the divertor improvement remains to be seen.
4. Other related configurations
Equations (3.6) also have solutions corresponding to configurations significantly different from the super-cusp. Among them there is a configuration of figure 8(a), where all three nulls lie on the boundary of the confinement zone (it corresponds to point 4 in figure 6). It may possess some interesting properties in terms of the core confinement and in terms of the divertor physics. For the latter, the presence of a long contact zone between the core and the private flux can be important. The present paper is, however, focused on the super-cusp geometry, and we will not dwell on this alternative.
The configuration shown in figure 8(b) (point 5 in figure 6) has two nulls lying on the same flux surface as the ‘main’ null, but only one of them connected to the scrape-off layer. So, they cannot serve in the same way as a cusp configuration of figure 3.

Figure 8. Some three-null configurations that do not possess super-cusp features. (a) corresponds to point 4 in figure 6 (
![]() ${\it\chi}_{1}={\rm\pi}/2$
,
${\it\chi}_{1}={\rm\pi}/2$
,
![]() ${\it\chi}_{2}=-0.9727$
), (b) corresponds to point 5 (
${\it\chi}_{2}=-0.9727$
), (b) corresponds to point 5 (
![]() ${\it\chi}_{1}=0.5632$
,
${\it\chi}_{1}=0.5632$
,
![]() ${\it\chi}_{2}=-0.1110$
).
${\it\chi}_{2}=-0.1110$
).
Although these configurations are indeed very different from the super-cusp of figure 3 or of figure 7(a), they belong to the same family of the magnetic configurations and can be transformed to the super-cusp by a mere rotation in the (
![]() $x,y$
) plane. The apparent difference is caused simply by the identification of the confinement zone, whereas the magnetic structures are essentially the same. The reader can easily imagine transforming the configurations of figures 7(b) and 8(a) by flipping them around the horizontal axis and shifting the origin. Still, with respect to divertor properties, these configurations are very different.
$x,y$
) plane. The apparent difference is caused simply by the identification of the confinement zone, whereas the magnetic structures are essentially the same. The reader can easily imagine transforming the configurations of figures 7(b) and 8(a) by flipping them around the horizontal axis and shifting the origin. Still, with respect to divertor properties, these configurations are very different.
Each of the nulls of the three-null configuration is a first-order null. The magnetic field in the immediate vicinity of such a null grows linearly with the distance from the null. Consider, for example, the vicinity of the ‘main’ null. For
![]() $|z|\ll |z_{1}|$
,
$|z|\ll |z_{1}|$
,
![]() $|z_{2}|$
, (2.2) yields
$|z_{2}|$
, (2.2) yields
![]() $F\approx Czz_{1}z_{2}$
, or
$F\approx Czz_{1}z_{2}$
, or
![]() $B_{p}=|C|rD_{1}D_{2}$
, where
$B_{p}=|C|rD_{1}D_{2}$
, where
![]() $r$
is the distance to the main null. Note that the absolute value of the poloidal field near the null does not depend upon direction, so that the derivative of
$r$
is the distance to the main null. Note that the absolute value of the poloidal field near the null does not depend upon direction, so that the derivative of
![]() $B_{p}$
over the distance is simply a constant:
$B_{p}$
over the distance is simply a constant:
where we used (2.3) for
![]() $C$
. This derivative characterizes the ‘flatness’ of the poloidal field near the null and is important for the evaluation of the zone of high poloidal beta in the vicinity of the null.
$C$
. This derivative characterizes the ‘flatness’ of the poloidal field near the null and is important for the evaluation of the zone of high poloidal beta in the vicinity of the null.
Remarkably, the flatness of the field in the other two nulls is the same as that defined by (4.1) for the first null. This is clear from an inspection of (2.2). This fact emphasizes that the nulls are not independent from each other: they belong to the same family and are ‘conversing’ with each other. This is another significant difference from the original cusp divertor.
The equal flatness of the poloidal field in all three nulls can also be used to test the approximation that the nulls are close to each other – an issue mentioned at the end of the introduction.
5. Geometry of the global field
In the previous sections we looked at the properties of the magnetic field in the zone situated far away from the currents generating this field. Now we consider the whole magnetic configuration that would include the plasma current and the current in the PF coils. The solution of the plasma equilibrium problem and determination of the shape of the separatrix in this situation are generally provided by the use of sophisticated equilibrium codes. On the other hand, some preliminary insights into geometry of the resulting system can be developed within a much simpler model, where the plasma and divertor currents are represented as a set of current-carrying wires. At the present stage of characterization of the super-cusp configuration we will limit ourselves to the wire model. With that, we will consider a relatively easily manageable symmetric situation.
The conductor imitating the plasma current will be situated at the distance
![]() $a$
from the ‘main’ null. Unlike a second-order null divertor (Ryutov Reference Ryutov2007), we need at least three divertor coils in order to control three PF nulls. We place these coils in the configuration used in the analysis of the cloverleaf divertor (Ryutov & Umansky Reference Ryutov and Umansky2013): two conductors are placed symmetrically with respect to the vertical axis, whereas the third conductor lies on the vertical axis (figure 9). The quantities
$a$
from the ‘main’ null. Unlike a second-order null divertor (Ryutov Reference Ryutov2007), we need at least three divertor coils in order to control three PF nulls. We place these coils in the configuration used in the analysis of the cloverleaf divertor (Ryutov & Umansky Reference Ryutov and Umansky2013): two conductors are placed symmetrically with respect to the vertical axis, whereas the third conductor lies on the vertical axis (figure 9). The quantities
![]() $a$
,
$a$
,
![]() $p$
,
$p$
,
![]() $q$
and
$q$
and
![]() $s$
shown in the figure are all positive. Adding more conductors would lead to a greater flexibility of configurations and will also allow one to reduce the currents per conductor, but for now we stay with the simplest configuration.
$s$
shown in the figure are all positive. Adding more conductors would lead to a greater flexibility of configurations and will also allow one to reduce the currents per conductor, but for now we stay with the simplest configuration.

Figure 9. Positions of conductors in the four-wire model and the global shape of the corresponding super-cusp configuration. Parameters of this configuration:
![]() $p=0.5a$
,
$p=0.5a$
,
![]() $q=0.2a$
,
$q=0.2a$
,
![]() $s=0.372a$
,
$s=0.372a$
,
![]() $I_{1}/I_{p}=0.424$
,
$I_{1}/I_{p}=0.424$
,
![]() $I_{2}/I_{p}=0.132$
,
$I_{2}/I_{p}=0.132$
,
![]() $D=0.098a$
. Note that for the geometry presented in this figure the minor radius is
$D=0.098a$
. Note that for the geometry presented in this figure the minor radius is
![]() ${\sim}0.5a$
.
${\sim}0.5a$
.
By adjusting the currents in the three conductors, one can create an exact third-order null at the origin, as was shown in Ryutov & Umansky (Reference Ryutov and Umansky2013). This reference also contains a characterization of the deviations from this state caused by the imposition of a uniform magnetic field. The arising magnetic configuration contains three nulls forming an equilateral triangle and never lying on the same separatrix. To generate a super-cusp configuration, one needs to adjust the currents in the coils in a different way, as considered below.
The complex potential for the set of coils shown in figure 9 is
The factor ‘
![]() $\text{i}$
’ makes the direction of the plasma field consistent with the current direction: we assume that the plasma current flows into the plane of the picture. The coil currents also flow in this direction. The currents are all positive. The current in each of the two symmetric conductors is
$\text{i}$
’ makes the direction of the plasma field consistent with the current direction: we assume that the plasma current flows into the plane of the picture. The coil currents also flow in this direction. The currents are all positive. The current in each of the two symmetric conductors is
![]() $I_{1}$
; the current in the conductor lying in the symmetry plane is
$I_{1}$
; the current in the conductor lying in the symmetry plane is
![]() $I_{2}$
. The total current in the divertor coils is
$I_{2}$
. The total current in the divertor coils is
![]() $2I_{1}+I_{2}$
.
$2I_{1}+I_{2}$
.
The field function is
where
![]() $\tilde{I} _{1,2}=I_{1,2}/I_{p}$
are the coil currents normalized to the plasma current. As before, we choose the ‘main’ null to be located at the origin. This immediately yields the following relation between the coil currents:
$\tilde{I} _{1,2}=I_{1,2}/I_{p}$
are the coil currents normalized to the plasma current. As before, we choose the ‘main’ null to be located at the origin. This immediately yields the following relation between the coil currents:
As is clear from (5.2), the condition
![]() $F=0$
that determines the location of the three field nulls is a cubic equation in
$F=0$
that determines the location of the three field nulls is a cubic equation in
![]() $z$
. With condition (5.3) satisfied, one of the three nulls lies at
$z$
. With condition (5.3) satisfied, one of the three nulls lies at
![]() $z=0$
. Then the positions of the other two nulls are determined from the quadratic equation that follows from (5.2) for
$z=0$
. Then the positions of the other two nulls are determined from the quadratic equation that follows from (5.2) for
![]() $\tilde{I} _{2}$
as in (5.3):
$\tilde{I} _{2}$
as in (5.3):
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle Q_{1}=\frac{1}{W}\left\{2q(1+s)-2\tilde{I} _{1}\left[1-q-s+\frac{(1-2q)qs}{p^{2}+q^{2}}\right]\right\},\\ \displaystyle Q_{2}=\frac{1}{W}[-q^{2}+p^{2}-qs-s(q^{2}+p^{2})+2\tilde{I} _{1}(q+s+qs)],\\ \displaystyle W=1+s+2\tilde{I} _{1}\left(1-\frac{qs}{p^{2}+q^{2}}\right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle Q_{1}=\frac{1}{W}\left\{2q(1+s)-2\tilde{I} _{1}\left[1-q-s+\frac{(1-2q)qs}{p^{2}+q^{2}}\right]\right\},\\ \displaystyle Q_{2}=\frac{1}{W}[-q^{2}+p^{2}-qs-s(q^{2}+p^{2})+2\tilde{I} _{1}(q+s+qs)],\\ \displaystyle W=1+s+2\tilde{I} _{1}\left(1-\frac{qs}{p^{2}+q^{2}}\right).\end{array}\right\}\end{eqnarray}$$
Here the parameters
![]() $p$
,
$p$
,
![]() $q$
and
$q$
and
![]() $s$
are normalized to
$s$
are normalized to
![]() $a$
(a distance of the plasma ‘wire’ from the origin).
$a$
(a distance of the plasma ‘wire’ from the origin).
If one makes both
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
zero, one creates an exact third-order null of Ryutov & Umansky (Reference Ryutov and Umansky2013). We, however, are now interested in a different situation, where the two secondary nulls would be separated from the primary null by some finite distance
$Q_{2}$
zero, one creates an exact third-order null of Ryutov & Umansky (Reference Ryutov and Umansky2013). We, however, are now interested in a different situation, where the two secondary nulls would be separated from the primary null by some finite distance
![]() $D$
and, at the same time, would be lying on the same separatrix as the main null, in the arrangement of figure 3. One can check that, by the order of magnitude,
$D$
and, at the same time, would be lying on the same separatrix as the main null, in the arrangement of figure 3. One can check that, by the order of magnitude,
![]() $Q_{1}\sim D$
,
$Q_{1}\sim D$
,
![]() $Q_{2}\sim D^{2}$
.
$Q_{2}\sim D^{2}$
.
As
![]() $Q_{1,2}$
are real, the nulls of (5.4) are symmetric with respect to the vertical axis. Therefore, the condition that they lie on the same separatrix as the main null imposes one constraint on the parameters of the system, namely that
$Q_{1,2}$
are real, the nulls of (5.4) are symmetric with respect to the vertical axis. Therefore, the condition that they lie on the same separatrix as the main null imposes one constraint on the parameters of the system, namely that
![]() $\text{Im}\,G(0)=\text{Im}\,G(z_{1})$
, where
$\text{Im}\,G(0)=\text{Im}\,G(z_{1})$
, where
![]() $z_{1}$
is, say, a ‘left one’ of the two secondary nulls (5.4). So, choosing the geometrical parameters
$z_{1}$
is, say, a ‘left one’ of the two secondary nulls (5.4). So, choosing the geometrical parameters
![]() $p$
,
$p$
,
![]() $q$
,
$q$
,
![]() $s$
, one can find a current
$s$
, one can find a current
![]() $I_{1}$
for which the desired configuration would form. An example is shown in figure 9 where the global separatrix is shown, with the super-cusp geometry formed near the ‘main’ null.
$I_{1}$
for which the desired configuration would form. An example is shown in figure 9 where the global separatrix is shown, with the super-cusp geometry formed near the ‘main’ null.
One can make the following observations regarding these results: (i) the total current in the divertor coils,
![]() $2I_{1}+I_{2}$
, is
$2I_{1}+I_{2}$
, is
![]() $0.98I_{p}$
. (ii) The distance from the main null to the secondary nulls can be substantial, up to a half of the minor radius (which is for this configuration
$0.98I_{p}$
. (ii) The distance from the main null to the secondary nulls can be substantial, up to a half of the minor radius (which is for this configuration
![]() ${\sim}0.5a$
), thereby allowing for a significant volume for deployment of the divertor components. With that, it is still within the applicability limit of a three-null model, with the distances to all the conductors being large compared to
${\sim}0.5a$
), thereby allowing for a significant volume for deployment of the divertor components. With that, it is still within the applicability limit of a three-null model, with the distances to all the conductors being large compared to
![]() $D$
.
$D$
.
Denoting by
![]() $I_{1}$
the difference between the current
$I_{1}$
the difference between the current
![]() $I_{1}^{\ast }$
that corresponds to the third-order null of Ryutov & Umansky (Reference Ryutov and Umansky2013) and the current
$I_{1}^{\ast }$
that corresponds to the third-order null of Ryutov & Umansky (Reference Ryutov and Umansky2013) and the current
![]() $I_{1}^{(cusp)}$
corresponding to the super-cusp configurations shown in figure 9, one finds that the distance
$I_{1}^{(cusp)}$
corresponding to the super-cusp configurations shown in figure 9, one finds that the distance
![]() $D$
between the secondary nulls and the primary null scales as
$D$
between the secondary nulls and the primary null scales as
![]() $D/p\sim \sqrt{{\rm\Delta}I_{1}/I_{1}^{\ast }}$
. So, for the case of figure 9 the current has to be changed by a few per cent compared to the current of an exact third-order null. The distance from the main null to the two secondary nulls is determined by the proximity of the currents to those that create an exact cloverleaf configuration. In order to have enough space to place the divertor targets in a way compatible with the presence of the two nulls, an overall size of the divertor would probably have to be
$D/p\sim \sqrt{{\rm\Delta}I_{1}/I_{1}^{\ast }}$
. So, for the case of figure 9 the current has to be changed by a few per cent compared to the current of an exact third-order null. The distance from the main null to the two secondary nulls is determined by the proximity of the currents to those that create an exact cloverleaf configuration. In order to have enough space to place the divertor targets in a way compatible with the presence of the two nulls, an overall size of the divertor would probably have to be
![]() $(1.5{-}2)D$
. In the example shown in figure 9, this would be
$(1.5{-}2)D$
. In the example shown in figure 9, this would be
![]() ${\sim}$
of order of 0.3–0.4 of the minor radius, i.e. comparable to the size used in the ITER design, e.g. Pitts et al. (Reference Pitts, Carpentier, Escourbiac, Hirai, Komarov, Lisgo, Kukushkin, Loarte, Merola, Baik, Mitteau, Sugihara, Bazylev and Stangeby2013). If needed, the parameter
${\sim}$
of order of 0.3–0.4 of the minor radius, i.e. comparable to the size used in the ITER design, e.g. Pitts et al. (Reference Pitts, Carpentier, Escourbiac, Hirai, Komarov, Lisgo, Kukushkin, Loarte, Merola, Baik, Mitteau, Sugihara, Bazylev and Stangeby2013). If needed, the parameter
![]() $D$
can be reduced by adjusting the currents in the divertor coils.
$D$
can be reduced by adjusting the currents in the divertor coils.
By deliberately making the current lower or higher than the value needed for the ‘perfect’ super-cusp, one finds the situations shown in figure 10, with the secondary separatrices split from the primary one. Similarly to a snowflake divertor, there are two different cases here: the secondary separatrix can either enclose the primary one as in figure 10(a) or be isolated from the primary one as in figure 10(b). By the analogy to the snowflake divertor, one can call the first (the second) case super-cusp-minus (super-cusp-plus).

Figure 10. The divertor area of the previous configuration but with the divertor coil current 2 % lower (a) and 2 % higher (b) from the exact super-cusp. In (a) two additional strike points are activated, similarly to the activation of additional strike points in the snowflake-minus divertor. Shown in yellow are scrape-off layer flux surfaces situated inside and outside the secondary separatrix. They are split between four divertor legs. This effect is absent in (b).
In the case of super-cusp-minus one can ‘activate’ four divertor legs without relying on plasma convection in the weak poloidal field zone (Ryutov et al. Reference Ryutov, Cohen, Farmer, Rognlien, Soukhanovskii and Umansky2014a ). Indeed, by choosing the current so that the secondary separatrix would go through a middle of the scrape-off layer, one would activate simultaneously the two outermost and two innermost divertor legs (four total), as seen from figure 10(a). This mechanism of the flux sharing has been discussed in relation to the snowflake divertor by Ryutov et al. (Reference Ryutov, Makowski and Umansky2010), and observed experimentally with the snowflake divertor in Soukhanovskii et al. (Reference Soukhanovskii, Ahn, Bell, Gates, Gerhardt, Kaita, Kolemen, Leblanc, Maingi, Makowski, Maqueda, Mclean, Menard, Mueller, Paul, Raman, Roquemore, Ryutov, Sabbagh and Scott2011, Reference Soukhanovskii, Allen, Fenstermacher, Hill, Lasnier, Makowski, Mclean, Meyer, Kolemen, Groebner, Hyatt, Leonard, Osborne and Petrie2015), Reimerdes et al. (Reference Reimerdes, Canal, Duval, Labit, Lunt, Vijvers, Coda, De Temmerman, Morgan, Nespoli and Taland2013) and Vijvers et al. (Reference Vijvers, Canal, Labit, Reimerdes, Tal, Coda, De Temmerman, Duval, Morgan and Zielinski2014).
Using divertor plates forming a small angle with the plasma flow, one recovers a conventional divertor configuration, but with four (instead of two) divertor legs. Note that if the magnetic field is small in a sufficiently large area near the main null, then a plasma convection can appear that would lead to the broadening of the plasma flow in each of the divertor legs, as discussed in Ryutov et al. (Reference Ryutov, Cohen, Farmer, Rognlien, Soukhanovskii and Umansky2014a ).
6. Discussion
In this article we explored a possibility of creating the cusp geometry similar to that of Takase (Reference Takase2001) by a set of remote coils. It turned out that this is indeed possible: by a proper adjustments of the current one can create configurations where additional nulls are produced downstream from the main X-point on both outgoing branches of the separatrix. This allows exploring the original idea of Takase (Reference Takase2001) and Kotschenreuther et al. (Reference Kotschenreuther, Valanju, Wiley, Rognlien, Mahajan and Pekker2004, Reference Kotschenreuther, Valanju, Wiley and Mahajan2007), of reducing the divertor heat flux by a strong flaring of the magnetic field lines in both strike points of a standard divertor, but without the coils situated near the targets.
Our approach is the same as that used before for the snowflake divertor: a representation of the field by a power series of the coordinates. If the secondary nulls are situated very close to the primary one, we recover a concept of a cloverleaf (third-order null) divertor of Ryutov & Umansky (Reference Ryutov and Umansky2013). If, however, the distance increases, the system would act as envisaged by Takase (Reference Takase2001), with the main effects on divertor operation coming from the flux expansion near two separate strike points.
The transition from one configuration to another can probably be studied with the same set of coils. The weak poloidal field at the divertor targets and the corresponding shallow intersection angle of the total magnetic field vector with a target may also provide conditions for the studies of specific sheath-driven instabilities strongly affected by this intersection angle (Farina, Pozzoli & Ryutov Reference Farina, Pozzoli and Ryutov1993; Cohen & Ryutov Reference Cohen and Ryutov1996). No analyses of these effects are available at present for the specific situation of a cusp or super-cusp divertors.
The control of the new configuration may be more complex than for the standard X-point or a snowflake configuration, since the control system has now to juggle with three nulls and keep them in the assigned positions. On the other hand, there is encouraging progress in development of advanced control algorithms for the two-null configurations (Kolemen et al. Reference Kolemen, Allen, Bray, Fenstermacher, Humphreys, Hyatt, Lasnier, Leonard, Makowski, Mclean, Maingi, Nazikian, Petrie, Soukhanovskii and Unterberg2015) and extrapolations to three-null systems may become possible.
Another issue with divertor performance may be associated with the constraints on the minimum angle between the magnetic field line and divertor plate at the strike point: at very small angle (that can be reached in the cusp divertor) imperfect flatness of the tiles may create ‘hot spots’ creating damage to the tiles. It was argued by Covele et al. (Reference Covele, Valanju, Kotschenreuther and Mahajan2014) that this constraint may actually become much less severe in the detached regimes.
Finally, concerns are sometime expressed regarding the divertor coil requirements associated with relatively high divertor currents needed for the multi-null systems compared to the single-null divertors. The solution here would probably come from increased number of coils and optimization of their positions, as has been done for the snowflake divertor, e.g. in Albanese, Ambrosino & Mattei (Reference Albanese, Ambrosino and Mattei2014) and Peng et al. (Reference Peng, Ye, Song, Mao, Chen and Qian2015). Increased number of the coils in the divertor area also provides more flexibility in controlling the magnetic field structure.
Acknowledgements
The author is grateful to Drs L. LoDestro, T. Rognlien, V. Soukhanovskii, M. Umansky and X. Xu for discussion of the results. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Security, LLC, Lawrence Livermore National Laboratory, under Contract DE-AC52-07NA27344.













