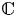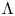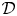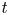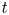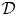1. Introduction
The regular Riemann–Hilbert correspondence (formulated and proved by Kashiwara [Reference KashiwaraKas84], and another proof given by Mebkhout [Reference MebkhoutMeb84]) states that the derived category of regular holonomic ![]() ${\mathcal {D}}$-modules is equivalent to the derived category of
${\mathcal {D}}$-modules is equivalent to the derived category of ![]() ${\mathbb {C}}$-constructible sheaves. Under this equivalence, the abelian category of regular holonomic
${\mathbb {C}}$-constructible sheaves. Under this equivalence, the abelian category of regular holonomic ![]() ${\mathcal {D}}$-modules is mapped to the abelian category of perverse sheaves introduced by Beilinson, Bernstein, Deligne and Gabber [Reference KashiwaraKas75, Reference Beĭlinson, Bernstein and DeligneBBD82, Reference Goresky and MacPhersonGM80].
${\mathcal {D}}$-modules is mapped to the abelian category of perverse sheaves introduced by Beilinson, Bernstein, Deligne and Gabber [Reference KashiwaraKas75, Reference Beĭlinson, Bernstein and DeligneBBD82, Reference Goresky and MacPhersonGM80].
After many efforts including understanding of formal and asymptotic structures [Reference MajimaMaj84, Reference SabbahSab00, Reference MochizukiMoc11, Reference KedlayaKed11], Stokes phenomena and Riemann–Hilbert correspondence for meromorphic connections [Reference MalgrangeMal83, Reference SibuyaSib90, Reference Deligne, Malgrange and RamisDMR07, Reference MochizukiMoc11, Reference SabbahSab13], sophistication of the regular Riemann–Hilbert correspondence [Reference Kashiwara and SchapiraKS01], and developments of ind-sheaves and the discovery of its relation to asymptotic behavior [Reference Kashiwara and SchapiraKS01, Reference Kashiwara and SchapiraKS03], in a seminal paper [Reference D'Agnolo and KashiwaraDK16], D’Agnolo and Kashiwara formulated and proved the irregular Riemann–Hilbert correspondence for holonomic ![]() ${\mathcal {D}}$-modules.
${\mathcal {D}}$-modules.
Theorem 1.1 (D'Agnolo and Kashiwara [Reference D'Agnolo and KashiwaraDK16])
For a complex manifold ![]() $X$, there exists a fully faithful embedding
$X$, there exists a fully faithful embedding
where the left-hand side is the derived category of cohomologically holonomic ![]() ${\mathcal {D}}$-modules and the right-hand side is the category of
${\mathcal {D}}$-modules and the right-hand side is the category of ![]() $\,\mathbb{R}$-constructible
$\,\mathbb{R}$-constructible ![]() ${\mathbb {C}}$-valued enhanced ind-sheaves. There also exists an explicit construction of a right quasi-inverse of the above embedding.
${\mathbb {C}}$-valued enhanced ind-sheaves. There also exists an explicit construction of a right quasi-inverse of the above embedding.
In the sequel [Reference D'Agnolo and KashiwaraDK19], they also introduced the notion of enhanced perverse ![]() $t$-structure on the right-hand side of the embedding and proved that the embedding is
$t$-structure on the right-hand side of the embedding and proved that the embedding is ![]() $t$-exact in a slightly generalized sense. Moreover, Mochizuki [Reference MochizukiMoc16] proved that the image of the equivalence can be characterized by testing on curves.
$t$-exact in a slightly generalized sense. Moreover, Mochizuki [Reference MochizukiMoc16] proved that the image of the equivalence can be characterized by testing on curves.
In this paper, we modify the right-hand side of the equivalence and make it closer to the form of the regular Riemann–Hilbert correspondence.
As mentioned in their paper, D’Agnolo and Kashiwara's clever definition and use of enhanced sheaves are inspired from the construction of Tamarkin [Reference TamarkinTam18]. Tamarkin's idea of adding one extra variable originally aimed to realize the Novikov ring action in sheaf theory as in Fukaya category [Reference Fukaya, Oh, Ohta and OnoFOOO09]. In this paper, we take a way which is closer to this original idea instead of the use of enhanced sheaves. The replacement for the right-hand side of (1.1) is expressed as graded modules (sheaves) over the ‘finite Novikov ring’ ![]() $\Lambda :=\mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ where
$\Lambda :=\mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ where ![]() $\mathbb {k}\subset {\mathbb {C}}$ is a field. An element of
$\mathbb {k}\subset {\mathbb {C}}$ is a field. An element of ![]() $\Lambda$ is expressed as a finite sum
$\Lambda$ is expressed as a finite sum ![]() $\sum _{a\in {\mathbb {R}}_{\geqslant 0}}c_aT^a$ where
$\sum _{a\in {\mathbb {R}}_{\geqslant 0}}c_aT^a$ where ![]() $T$ is the indeterminate. A priori, the hom-spaces
$T$ is the indeterminate. A priori, the hom-spaces ![]() $\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})$ of
$\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})$ of ![]() $\Lambda$-modules are defined over
$\Lambda$-modules are defined over ![]() $\Lambda$. By taking the tensor product
$\Lambda$. By taking the tensor product ![]() $\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})\otimes _{\Lambda }\mathbb {k}$ where
$\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})\otimes _{\Lambda }\mathbb {k}$ where ![]() $\Lambda \rightarrow \mathbb {k}$ is defined by
$\Lambda \rightarrow \mathbb {k}$ is defined by ![]() $T^a\mapsto 1$, we obtain a new category
$T^a\mapsto 1$, we obtain a new category ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. We will further modify this category to obtain
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. We will further modify this category to obtain ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We can consider
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We can consider ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ as an approximate description of
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ as an approximate description of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
The category ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian and has enough injective and flat objects. We define an abelian subcategory of
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian and has enough injective and flat objects. We define an abelian subcategory of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$: the category of irregular constructible sheaves
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$: the category of irregular constructible sheaves ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$. Then we set
$\mathrm {Mod}_{ic}(\Lambda _X)$. Then we set ![]() $D^b_{ic}(\Lambda _X)$ as the full subcategory of the bounded derived category
$D^b_{ic}(\Lambda _X)$ as the full subcategory of the bounded derived category ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ consisting of cohomologically irregular constructible sheaves. The meaning of irregular constructibility is as follows. As usual, there exists a
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ consisting of cohomologically irregular constructible sheaves. The meaning of irregular constructibility is as follows. As usual, there exists a ![]() ${\mathbb {C}}$-Whitney stratification and we have a sheaf which is locally constant as
${\mathbb {C}}$-Whitney stratification and we have a sheaf which is locally constant as ![]() $\Lambda$-module over each stratum, but moreover with particular gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem [Reference SabbahSab00, Reference MochizukiMoc11, Reference KedlayaKed11]. Then we have the following.
$\Lambda$-module over each stratum, but moreover with particular gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem [Reference SabbahSab00, Reference MochizukiMoc11, Reference KedlayaKed11]. Then we have the following.
Theorem 1.2
(i) The category
 $D^b_{ic}(\Lambda _X)$ has functors
$D^b_{ic}(\Lambda _X)$ has functors  $\mathop {{{\mathcal {H}}}om}\nolimits , \otimes , f^{-1}, f^!$ for any morphism
$\mathop {{{\mathcal {H}}}om}\nolimits , \otimes , f^{-1}, f^!$ for any morphism  $f$ and
$f$ and  $f_!$ for proper
$f_!$ for proper  $f$.
$f$.(ii) If
 $\,\mathbb{k}={\mathbb {C}}$, there exists an equivalence
(1.2)
$\,\mathbb{k}={\mathbb {C}}$, there exists an equivalence
(1.2) \begin{equation} D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq} D^b_{ic}(\Lambda_X). \end{equation}
\begin{equation} D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq} D^b_{ic}(\Lambda_X). \end{equation}
In our formulation, the data of exponential factors of solutions of irregular differential equations are encoded in the grading of ![]() $\Lambda$-modules. We would like to apply the following trivial fact to our setting. For a graded ring
$\Lambda$-modules. We would like to apply the following trivial fact to our setting. For a graded ring ![]() $R$, the grading-forgetful functor from the abelian category of graded
$R$, the grading-forgetful functor from the abelian category of graded ![]() $R$-modules to the abelian category of
$R$-modules to the abelian category of ![]() $R$-modules is exact. Although our category
$R$-modules is exact. Although our category ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$ has a modification of hom-spaces, we still have the following.
$\mathrm {Mod}_{ic}(\Lambda _X)$ has a modification of hom-spaces, we still have the following.
Theorem 1.3 There exists an exact functor ![]() $ {\mathfrak {F}}$ from
$ {\mathfrak {F}}$ from ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$ to the abelian category of
$\mathrm {Mod}_{ic}(\Lambda _X)$ to the abelian category of ![]() ${\mathbb {C}}$-constructible sheaves
${\mathbb {C}}$-constructible sheaves ![]() $\mathrm {Mod}_{c}(\mathbb {k}_X)$ such that, on the level of stalks, this is the composition of the grading-forgetful map and tensoring
$\mathrm {Mod}_{c}(\mathbb {k}_X)$ such that, on the level of stalks, this is the composition of the grading-forgetful map and tensoring ![]() $\mathbb {k}$ over
$\mathbb {k}$ over ![]() $\Lambda$.
$\Lambda$.
By using ![]() $ {\mathfrak {F}}$, we can define the support of an irregular constructible sheaf
$ {\mathfrak {F}}$, we can define the support of an irregular constructible sheaf ![]() $ {\mathcal {V}}$ by
$ {\mathcal {V}}$ by ![]() $\mathrm {supp}\, {\mathcal {V}}:=\mathrm {supp}\, {\mathfrak {F}}( {\mathcal {V}})$. By using this definition, we can define the irregular perverse
$\mathrm {supp}\, {\mathcal {V}}:=\mathrm {supp}\, {\mathfrak {F}}( {\mathcal {V}})$. By using this definition, we can define the irregular perverse ![]() $t$-structure by the same formula as in usual perverse sheaves. Let
$t$-structure by the same formula as in usual perverse sheaves. Let ![]() ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively
${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively ![]() ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of
${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of ![]() $D^b_{ic}(\Lambda _X)$ spanned by objects satisfying
$D^b_{ic}(\Lambda _X)$ spanned by objects satisfying
Theorem 1.4
(i) The pair
 $({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ defines a
$({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ defines a  $t$-structure of
$t$-structure of  $D^b_{ic}(\Lambda _X)$, which we call irregular perverse
$D^b_{ic}(\Lambda _X)$, which we call irregular perverse  $t$-structure.
$t$-structure.(ii) The heart of irregular perverse
 $t$-structure
$t$-structure  $\mathrm {Perv}_{ic}({\mathbb {C}}_X)$ over
$\mathrm {Perv}_{ic}({\mathbb {C}}_X)$ over  ${\mathbb {C}}$ is equivalent to the abelian category of holonomic
${\mathbb {C}}$ is equivalent to the abelian category of holonomic  ${\mathcal {D}}$-modules under the equivalence (1.2).
${\mathcal {D}}$-modules under the equivalence (1.2).
We also prove the corresponding results in the algebraic setting. Mostly, the statements are corollaries of analytic cases, although we also have ![]() $f_*$ and
$f_*$ and ![]() $f_!$ for any morphism and can prove stronger commutativity results for the Riemann–Hilbert functor (as in the case of algebraic regular Riemann–Hilbert correspondence).
$f_!$ for any morphism and can prove stronger commutativity results for the Riemann–Hilbert functor (as in the case of algebraic regular Riemann–Hilbert correspondence).
In the rest of this section, we would like to shortly discuss a conjectural explanation of the appearance of the Novikov ring. Recall that Tamarkin's introduction of additional ![]() $ {\mathbb {R}}$ was motivated by Floer theory/Fukaya category. Fukaya category is naturally enriched with the Novikov ring by estimating disk areas (Gromov's compactness theorem for holomorphic disks). We expect this appearance of the Novikov ring and the one in our construction can be identified as follows.
$ {\mathbb {R}}$ was motivated by Floer theory/Fukaya category. Fukaya category is naturally enriched with the Novikov ring by estimating disk areas (Gromov's compactness theorem for holomorphic disks). We expect this appearance of the Novikov ring and the one in our construction can be identified as follows.
We denote the derived category of regular holonomic ![]() ${\mathcal {D}}$-modules by
${\mathcal {D}}$-modules by ![]() $D^b_{\mathrm {reghol}}({\mathcal {D}}_X)$. Combining the regular Riemann–Hilbert correspondence with the Nadler–Zaslow equivalence [Reference Nadler and ZaslowNZ09], we have an embedding
$D^b_{\mathrm {reghol}}({\mathcal {D}}_X)$. Combining the regular Riemann–Hilbert correspondence with the Nadler–Zaslow equivalence [Reference Nadler and ZaslowNZ09], we have an embedding ![]() $D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b\operatorname {\mathfrak {Fuk}}^{NZ}(T^*X)$, where the right-hand side is Nadler and Zaslow's Fukaya category of conic Lagrangians in
$D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b\operatorname {\mathfrak {Fuk}}^{NZ}(T^*X)$, where the right-hand side is Nadler and Zaslow's Fukaya category of conic Lagrangians in ![]() $T^*X$.
$T^*X$.
We expect a similar claim for the holonomic case: there exists a Fukaya category ![]() $D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)$ enriched over
$D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)$ enriched over ![]() $\Lambda$ of
$\Lambda$ of ![]() $T^*X$ with nonconic Lagrangians which has a fully faithful embedding from the category
$T^*X$ with nonconic Lagrangians which has a fully faithful embedding from the category ![]() $D^b_{{ic},\Lambda }(\Lambda _X)$ which is a version of
$D^b_{{ic},\Lambda }(\Lambda _X)$ which is a version of ![]() $D^b_{ic}(\Lambda _X)$ enriched over
$D^b_{ic}(\Lambda _X)$ enriched over ![]() $\Lambda$. After the reduction of coefficient from
$\Lambda$. After the reduction of coefficient from ![]() $\Lambda$ to
$\Lambda$ to ![]() $\mathbb {k}$, we will obtain an embedding of
$\mathbb {k}$, we will obtain an embedding of ![]() $D^b_{ic}(\Lambda _X)$ into a version of Fukaya category. On the level of objects, the exponential
$D^b_{ic}(\Lambda _X)$ into a version of Fukaya category. On the level of objects, the exponential ![]() ${\mathcal {D}}_X$-module associated to a meromorphic function
${\mathcal {D}}_X$-module associated to a meromorphic function ![]() $f$ will correspond to the Lagrangian
$f$ will correspond to the Lagrangian ![]() $\mathrm {Graph}(df)$.
$\mathrm {Graph}(df)$.
If this expectation is true, one can imagine ![]() $K$-theory classes of objects of
$K$-theory classes of objects of ![]() $D\operatorname {\mathfrak {Fuk}}_{ic}(T^*X):=D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)\otimes _\Lambda \mathbb {k}$ as an irregular version of characteristic cycle. In the same vein, their supports can be considered as an irregular version of microsupports, which are no longer conic. Hence one can also imagine a generalization of microlocal analysis. Note that a version (real blown-up version) of the equivalence without
$D\operatorname {\mathfrak {Fuk}}_{ic}(T^*X):=D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)\otimes _\Lambda \mathbb {k}$ as an irregular version of characteristic cycle. In the same vein, their supports can be considered as an irregular version of microsupports, which are no longer conic. Hence one can also imagine a generalization of microlocal analysis. Note that a version (real blown-up version) of the equivalence without ![]() $\Lambda$ is already appeared if one fixes a formal type [Reference Shende, Treumann, Williams and ZaslowSTWZ15]. Also, another connection between Riemann–Hilbert correspondence and holomorphic Fukaya category is conjectured by Kontsevich [Reference KontsevichKon16], whose relation to our conjecture is also of interest.
$\Lambda$ is already appeared if one fixes a formal type [Reference Shende, Treumann, Williams and ZaslowSTWZ15]. Also, another connection between Riemann–Hilbert correspondence and holomorphic Fukaya category is conjectured by Kontsevich [Reference KontsevichKon16], whose relation to our conjecture is also of interest.
The organization of this paper is as follows. In § 2, we define and discuss the preliminary version of the category of sheaves with coefficients in ![]() $\Lambda$. In §§ 3 and 4, we define the (derived) category of sheaves with coefficients in
$\Lambda$. In §§ 3 and 4, we define the (derived) category of sheaves with coefficients in ![]() $\Lambda$ over topological spaces with boundary and consider various (derived) functorial operations as in usual sheaf theory. In § 5, we define our main objects irregular constructible sheaves and again see various functorial operations. We also note that irregular constructible sheaves are actually sheaves. In § 6, we construct the functor
$\Lambda$ over topological spaces with boundary and consider various (derived) functorial operations as in usual sheaf theory. In § 5, we define our main objects irregular constructible sheaves and again see various functorial operations. We also note that irregular constructible sheaves are actually sheaves. In § 6, we construct the functor ![]() $ {\mathfrak {F}}$ which relates irregular to usual sheaves. In § 7, we see the relationship between enhanced sheaves and our
$ {\mathfrak {F}}$ which relates irregular to usual sheaves. In § 7, we see the relationship between enhanced sheaves and our ![]() $\Lambda$-modules, which enables us to establish our version of Riemann–Hilbert correspondence using D’Agnolo and Kashiwara's theorem in § 8. We also prove some commutativity results for Riemann–Hilbert functor in § 8. In § 9, we define irregular perverse sheaves by using
$\Lambda$-modules, which enables us to establish our version of Riemann–Hilbert correspondence using D’Agnolo and Kashiwara's theorem in § 8. We also prove some commutativity results for Riemann–Hilbert functor in § 8. In § 9, we define irregular perverse sheaves by using ![]() $ {\mathfrak {F}}$ and import results in the theory of perverse sheaves to irregular perverse sheaves. In § 10, we discuss algebraic version of the above story.
$ {\mathfrak {F}}$ and import results in the theory of perverse sheaves to irregular perverse sheaves. In § 10, we discuss algebraic version of the above story.
2.  $\Lambda _X$-modules
$\Lambda _X$-modules
In this section, we introduce the ‘finite Novikov ring’ ![]() $\Lambda$ and its modules. We fix a field
$\Lambda$ and its modules. We fix a field ![]() $\mathbb {k}\subset {\mathbb {C}}$ once and for all.
$\mathbb {k}\subset {\mathbb {C}}$ once and for all.
2.1 The ring  $\Lambda$
$\Lambda$
Let us consider the set of nonnegative real numbers ![]() $\mathbb{R} _{\geqslant 0}$ as a semigroup by the addition. We denote the associated polynomial ring by
$\mathbb{R} _{\geqslant 0}$ as a semigroup by the addition. We denote the associated polynomial ring by ![]() $\Lambda :=\Lambda _\mathbb {k}:=\mathbb {k}[\mathbb{R} _{\geqslant 0}]$. For
$\Lambda :=\Lambda _\mathbb {k}:=\mathbb {k}[\mathbb{R} _{\geqslant 0}]$. For ![]() $a\in \mathbb{R} _{\geqslant 0}$, let us denote the corresponding indeterminate by
$a\in \mathbb{R} _{\geqslant 0}$, let us denote the corresponding indeterminate by ![]() $T^a$. We set
$T^a$. We set ![]() $\operatorname {Gr}^a\Lambda :=\mathbb {k}\cdot T^a\subset \Lambda$ for
$\operatorname {Gr}^a\Lambda :=\mathbb {k}\cdot T^a\subset \Lambda$ for ![]() $a\geqslant 0$, which gives an
$a\geqslant 0$, which gives an ![]() $ {\mathbb {R}}$-grading on
$ {\mathbb {R}}$-grading on ![]() $\Lambda$.
$\Lambda$.
Let ![]() $\mathrm {Mod}^0(\Lambda )$ be the abelian category of
$\mathrm {Mod}^0(\Lambda )$ be the abelian category of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules with degree
$\Lambda$-modules with degree ![]() $0$ morphisms. For an
$0$ morphisms. For an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module
$\Lambda$-module ![]() $V$, let
$V$, let ![]() $V\langle a\rangle$ be the grading shift of
$V\langle a\rangle$ be the grading shift of ![]() $M$ i.e.
$M$ i.e. ![]() $\operatorname {Gr}^bV\langle a\rangle :=\operatorname {Gr}^{a+b} V$. We set
$\operatorname {Gr}^bV\langle a\rangle :=\operatorname {Gr}^{a+b} V$. We set
for ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules. The category
$\Lambda$-modules. The category ![]() $\mathrm {Mod}^ {\mathbb {R}}(\Lambda )$ is consisting of
$\mathrm {Mod}^ {\mathbb {R}}(\Lambda )$ is consisting of ![]() $ {\mathbb {R}}$-graded modules with the hom-spaces defined by (2.1). We set
$ {\mathbb {R}}$-graded modules with the hom-spaces defined by (2.1). We set
2.2  $\Lambda _X$-modules
$\Lambda _X$-modules
Let ![]() $X$ be a complex manifold. Let
$X$ be a complex manifold. Let ![]() $\Lambda _X$ be the constant sheaf valued in
$\Lambda _X$ be the constant sheaf valued in ![]() $\Lambda$.
$\Lambda$.
Definition 2.1 A sheaf of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-module is a sheaf valued in
$\Lambda _X$-module is a sheaf valued in ![]() $\mathrm {Mod}^0(\Lambda )$.
$\mathrm {Mod}^0(\Lambda )$.
Let ![]() $\tilde {\mathcal{V} }$ be a sheaf of
$\tilde {\mathcal{V} }$ be a sheaf of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-modules. For an open subset
$\Lambda _X$-modules. For an open subset ![]() $U\subset X$, we have an
$U\subset X$, we have an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module
$\Lambda$-module ![]() $\tilde {\mathcal{V} }(U)$. For an inclusion
$\tilde {\mathcal{V} }(U)$. For an inclusion ![]() $U\hookrightarrow V$, we have a map
$U\hookrightarrow V$, we have a map ![]() $\tilde {\mathcal{V} }(V)\rightarrow \tilde {\mathcal{V} }(U)$ which respects the grading
$\tilde {\mathcal{V} }(V)\rightarrow \tilde {\mathcal{V} }(U)$ which respects the grading ![]() $\operatorname {Gr}^a\tilde {\mathcal{V} }(V)\rightarrow \operatorname {Gr}^a\tilde {\mathcal{V} }(U)$. Hence we have a sheaf of
$\operatorname {Gr}^a\tilde {\mathcal{V} }(V)\rightarrow \operatorname {Gr}^a\tilde {\mathcal{V} }(U)$. Hence we have a sheaf of ![]() $\mathbb {k}$-vector spaces
$\mathbb {k}$-vector spaces ![]() $\operatorname {Gr}^a\tilde {\mathcal{V} }$ and an isomorphism
$\operatorname {Gr}^a\tilde {\mathcal{V} }$ and an isomorphism ![]() $\tilde {\mathcal{V} }\cong {\bigoplus} _{a}\operatorname {Gr}^a\tilde {\mathcal{V} }$ as sheaves valued in
$\tilde {\mathcal{V} }\cong {\bigoplus} _{a}\operatorname {Gr}^a\tilde {\mathcal{V} }$ as sheaves valued in ![]() $\mathbb {k}$-vector spaces.
$\mathbb {k}$-vector spaces.
We denote the category of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-modules by
$\Lambda _X$-modules by ![]() $\mathrm {Mod}^0(\Lambda _X)$.
$\mathrm {Mod}^0(\Lambda _X)$.
Proposition 2.2 The category ![]() $\mathrm {Mod}^0(\Lambda _X)$ is abelian.
$\mathrm {Mod}^0(\Lambda _X)$ is abelian.
Proof. This is because ![]() $\mathrm {Mod}^0(\Lambda )$ is abelian.
$\mathrm {Mod}^0(\Lambda )$ is abelian.
Notation 2.1 ![]() $\tilde {\mathcal{V} }\langle a\rangle$ for
$\tilde {\mathcal{V} }\langle a\rangle$ for ![]() $a\in {\mathbb {R}}$ is
$a\in {\mathbb {R}}$ is ![]() $a$-shift of
$a$-shift of ![]() $\tilde {\mathcal{V} }$ as in the previous subsection. For
$\tilde {\mathcal{V} }$ as in the previous subsection. For ![]() $f\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }$,
$f\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }$, ![]() $f\langle a\rangle$ means the shifted morphism
$f\langle a\rangle$ means the shifted morphism ![]() $\tilde {\mathcal{V} }\langle a\rangle \rightarrow \tilde {\mathcal{W} }\langle a\rangle$.
$\tilde {\mathcal{V} }\langle a\rangle \rightarrow \tilde {\mathcal{W} }\langle a\rangle$.
We set
and
Note that ![]() $\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ is a
$\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ is a ![]() $\Lambda$-module. We see
$\Lambda$-module. We see ![]() $\mathbb {k}$ as a
$\mathbb {k}$ as a ![]() $\Lambda$-module by setting
$\Lambda$-module by setting ![]() $f\cdot c:=f|_{T=1}c$ for
$f\cdot c:=f|_{T=1}c$ for ![]() $f\in \Lambda$ and
$f\in \Lambda$ and ![]() $c\in \mathbb {k}$. We set
$c\in \mathbb {k}$. We set
Definition 2.3 The category ![]() $\mathrm {Mod}_{pre}^ {\mathfrak {I}}(\Lambda _X)$ is defined by the following data. The set of objects is the set of
$\mathrm {Mod}_{pre}^ {\mathfrak {I}}(\Lambda _X)$ is defined by the following data. The set of objects is the set of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-modules. For an
$\Lambda _X$-modules. For an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-module
$\Lambda _X$-module ![]() $\tilde {\mathcal{V} }$, the corresponding object in
$\tilde {\mathcal{V} }$, the corresponding object in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is denoted by
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is denoted by ![]() $[\tilde {\mathcal{V} }]$.
$[\tilde {\mathcal{V} }]$.
The hom-space between ![]() $[\tilde {\mathcal{V} }]$ and
$[\tilde {\mathcal{V} }]$ and ![]() $[\tilde {\mathcal{W} }]$ is
$[\tilde {\mathcal{W} }]$ is ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{V} }], [\tilde {\mathcal{W} }])$ defined in the above.
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{V} }], [\tilde {\mathcal{W} }])$ defined in the above.
There is a canonical functor ![]() $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which is the identity on objects and takes a morphism
$[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which is the identity on objects and takes a morphism ![]() $f$ to
$f$ to ![]() $f\otimes 1$.
$f\otimes 1$.
Remark 2.4 Here we would like to explain some motivations of Definition 2.3. We would like to consider usual sheaves endowed with a filtration indexed by ![]() $ {\mathbb {R}}$. A typical example is a sheaf
$ {\mathbb {R}}$. A typical example is a sheaf ![]() $\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\geqslant -a}$ (
$\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\geqslant -a}$ (![]() $a\in {\mathbb {R}}$) where
$a\in {\mathbb {R}}$) where ![]() $\phi$ is a continuous function on
$\phi$ is a continuous function on ![]() $X{\backslash } D$ where
$X{\backslash } D$ where ![]() $D$ is a divisor of
$D$ is a divisor of ![]() $X$. A typical
$X$. A typical ![]() $\phi$ is a meromorphic function with poles in
$\phi$ is a meromorphic function with poles in ![]() $D$ only determined up to adding a holomorphic function. This leads to considering
$D$ only determined up to adding a holomorphic function. This leads to considering ![]() $ {\mathbb {R}}$-filtrations up to a shift. Making the category of
$ {\mathbb {R}}$-filtrations up to a shift. Making the category of ![]() $ {\mathbb {R}}$-filtered vector spaces abelian is realized by the Rees trick which gives us
$ {\mathbb {R}}$-filtered vector spaces abelian is realized by the Rees trick which gives us ![]() $\Lambda$-modules. Flat modules are
$\Lambda$-modules. Flat modules are ![]() $ {\mathbb {R}}$-filtered vector spaces. Instead of ignoring shifts of gradings, we modify the notion of morphisms: the multiplication by
$ {\mathbb {R}}$-filtered vector spaces. Instead of ignoring shifts of gradings, we modify the notion of morphisms: the multiplication by ![]() $T^a\in \mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ becomes the identity to identify an object with its
$T^a\in \mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ becomes the identity to identify an object with its ![]() $a$-shift.
$a$-shift.
Definition 2.5 For an object ![]() $ {\mathcal {V}}$ in
$ {\mathcal {V}}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, a lift is a pair of an object
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, a lift is a pair of an object ![]() $\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$ and an isomorphism
$\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$ and an isomorphism ![]() $[\tilde {\mathcal{V} }]\xrightarrow {\cong } {\mathcal {V}}$. In the following, we usually do not write this isomorphism explicitly for simplicity.
$[\tilde {\mathcal{V} }]\xrightarrow {\cong } {\mathcal {V}}$. In the following, we usually do not write this isomorphism explicitly for simplicity.
Proposition 2.6 The category ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian category.
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian category.
To prove this proposition, we prepare some lemmas.
Lemma 2.7 Let ![]() $V$ be an
$V$ be an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module. Let
$\Lambda$-module. Let ![]() $s$ be a homogeneous element of
$s$ be a homogeneous element of ![]() $V$. If
$V$. If ![]() $T^a\cdot s \neq 0$ for any
$T^a\cdot s \neq 0$ for any ![]() $a\in {\mathbb {R}}\geqslant 0$, then
$a\in {\mathbb {R}}\geqslant 0$, then ![]() $s\otimes 1$ is nonzero in
$s\otimes 1$ is nonzero in ![]() $V\otimes _\Lambda \mathbb {k}$.
$V\otimes _\Lambda \mathbb {k}$.
Proof. Note that ![]() $l\cdot s$ is nonzero for any
$l\cdot s$ is nonzero for any ![]() $l\in \Lambda {\backslash }\{0\}$. We have an inclusion
$l\in \Lambda {\backslash }\{0\}$. We have an inclusion ![]() $\Lambda \cdot s\hookrightarrow V$. Since the left-hand side is a free
$\Lambda \cdot s\hookrightarrow V$. Since the left-hand side is a free ![]() $\Lambda$-module, the tensoring
$\Lambda$-module, the tensoring ![]() $(-)\otimes _\Lambda \mathbb {k}$ preserves the inclusion. Hence
$(-)\otimes _\Lambda \mathbb {k}$ preserves the inclusion. Hence ![]() $s\otimes 1$ is nonzero in
$s\otimes 1$ is nonzero in ![]() $V\otimes _\Lambda \mathbb {k}$.
$V\otimes _\Lambda \mathbb {k}$.
From Lemma 2.8 to Lemma 2.12, we will use the following notation: ![]() $ {\mathcal {V}}=[\tilde { {\mathcal {V}}}], {\mathcal {W}}=[\tilde {{\mathcal {W}}}]$.
$ {\mathcal {V}}=[\tilde { {\mathcal {V}}}], {\mathcal {W}}=[\tilde {{\mathcal {W}}}]$.
Lemma 2.8 For ![]() $f\in \operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$, if
$f\in \operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$, if ![]() $T^af\neq 0$ for any
$T^af\neq 0$ for any ![]() $a\in \mathbb{R} _{\geqslant 0}$, then
$a\in \mathbb{R} _{\geqslant 0}$, then ![]() $f$ is nonzero as an element in
$f$ is nonzero as an element in ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$.
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$.
Proof. This is a case of Lemma 2.7 by setting ![]() $V=\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ and
$V=\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ and ![]() $s:=f$.
$s:=f$.
Lemma 2.9 For ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists
$f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists ![]() $b\in {\mathbb {R}}$ such that there exists
$b\in {\mathbb {R}}$ such that there exists
which is a lift of ![]() $f$.
$f$.
Proof. Take a lift ![]() $f={\bigoplus} _{c}f_c\in {\bigoplus} _{c}\operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$. Since
$f={\bigoplus} _{c}f_c\in {\bigoplus} _{c}\operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$. Since ![]() $f_c$ is zero except for finite
$f_c$ is zero except for finite ![]() $c$, we can take
$c$, we can take ![]() $b$ to be a real number which is greater than or equal to the maximum of
$b$ to be a real number which is greater than or equal to the maximum of ![]() $c$ for which
$c$ for which ![]() $f_c$ is nonzero. Then we set
$f_c$ is nonzero. Then we set
Since ![]() $T^{b-c}=1$ on
$T^{b-c}=1$ on ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, the element
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, the element ![]() $f'$ represents
$f'$ represents ![]() $f$.
$f$.
Lemma 2.10 Let ![]() $f_i\in \operatorname {Hom}^{b_i}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$
$f_i\in \operatorname {Hom}^{b_i}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$ ![]() $(i=1,2)$ be lifts of
$(i=1,2)$ be lifts of ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$. Then there exists
$f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$. Then there exists ![]() $b_i\in \mathbb{R} _{\geqslant 0}$ such that
$b_i\in \mathbb{R} _{\geqslant 0}$ such that ![]() $T^{b_1}f_1=T^{b_2}f_2$.
$T^{b_1}f_1=T^{b_2}f_2$.
Proof. By multiplying some ![]() $T^a$ values we can assume that
$T^a$ values we can assume that ![]() $b_1=b_2$. Since
$b_1=b_2$. Since ![]() $f_1-f_2$ represents
$f_1-f_2$ represents ![]() $0$ in
$0$ in ![]() $\operatorname {Hom}_{\mathrm {Mod}_{pre}^{ {\mathfrak {I}}}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists
$\operatorname {Hom}_{\mathrm {Mod}_{pre}^{ {\mathfrak {I}}}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists ![]() $b\in \mathbb{R} _{\geqslant 0}$ such that
$b\in \mathbb{R} _{\geqslant 0}$ such that ![]() $T^b(f_1-f_2)=0$ by Lemma 2.8.
$T^b(f_1-f_2)=0$ by Lemma 2.8.
Lemma 2.11 For ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, let
$f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, let ![]() $f'\in \operatorname {Hom}^{b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$ be a lift. We view
$f'\in \operatorname {Hom}^{b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$ be a lift. We view ![]() $f'$ as a degree
$f'$ as a degree ![]() $0$ morphism between
$0$ morphism between ![]() $\tilde {\mathcal{V} }$ and
$\tilde {\mathcal{V} }$ and ![]() $\tilde {\mathcal{W} }\langle b\rangle$ in
$\tilde {\mathcal{W} }\langle b\rangle$ in ![]() $\mathrm {Mod}^0(\Lambda _X)$. The objects
$\mathrm {Mod}^0(\Lambda _X)$. The objects ![]() $[\ker (f')]$,
$[\ker (f')]$, ![]() $[\mathrm {im}(f')]$,
$[\mathrm {im}(f')]$, ![]() $[\operatorname {coker}(f')]$, and
$[\operatorname {coker}(f')]$, and ![]() $[\mathrm {coim}(f')]$ in
$[\mathrm {coim}(f')]$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ only depend on
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ only depend on ![]() $f$.
$f$.
Proof. By Lemma 2.10, it suffices to prove the objects defined for ![]() $f'$ and
$f'$ and ![]() $T^af'$ are isomorphic. We have morphisms
$T^af'$ are isomorphic. We have morphisms ![]() $f'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle b\rangle$ and
$f'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle b\rangle$ and ![]() $T^af'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle a+b\rangle$ in
$T^af'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle a+b\rangle$ in ![]() $\mathrm {Mod}^0(\Lambda _X)$. Note that
$\mathrm {Mod}^0(\Lambda _X)$. Note that ![]() $\ker f'\hookrightarrow \ker T^af'$. Hence for any
$\ker f'\hookrightarrow \ker T^af'$. Hence for any ![]() $\tilde {\mathcal{P} }\in \mathrm {Mod}^0(\Lambda _X)$, we have
$\tilde {\mathcal{P} }\in \mathrm {Mod}^0(\Lambda _X)$, we have
which induces a comparison morphism
It suffices to show that ![]() $c$ is an isomorphism.
$c$ is an isomorphism.
For any ![]() $g\in \operatorname {Hom}^b_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$, consider
$g\in \operatorname {Hom}^b_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$, consider ![]() $T^ag\in \operatorname {Hom}^{a+b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$. Since
$T^ag\in \operatorname {Hom}^{a+b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$. Since ![]() $f'\langle a+b\rangle \circ T^a g=T^af'\langle b\rangle \circ g=0$,
$f'\langle a+b\rangle \circ T^a g=T^af'\langle b\rangle \circ g=0$, ![]() $T^ag$ factors through
$T^ag$ factors through ![]() $\ker f'\langle a+b\rangle$ i.e.
$\ker f'\langle a+b\rangle$ i.e.
Hence ![]() $T^ag$ is in the image of
$T^ag$ is in the image of ![]() $\tilde {c}$. Since
$\tilde {c}$. Since ![]() $g$ and
$g$ and ![]() $T^ag$ represents the same morphism in
$T^ag$ represents the same morphism in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, we have the surjectivity of
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, we have the surjectivity of ![]() $c$.
$c$.
On the other hand, let ![]() $g\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }],[\ker f'])$ be zero in
$g\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }],[\ker f'])$ be zero in ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }], [\ker T^af'])$. For a lift
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }], [\ker T^af'])$. For a lift ![]() $g'$ of
$g'$ of ![]() $g$, we have
$g$, we have ![]() $T^bg'=0$ for some
$T^bg'=0$ for some ![]() $b\in \mathbb{R} _{\geqslant 0}$ by Lemma 2.8. Hence
$b\in \mathbb{R} _{\geqslant 0}$ by Lemma 2.8. Hence ![]() $g=0\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([P], [\ker f'])$. This gives the injectivity of
$g=0\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([P], [\ker f'])$. This gives the injectivity of ![]() $c$.
$c$.
Similar arguments prove the claims for ![]() $\mathrm {im}(f')$,
$\mathrm {im}(f')$, ![]() $\operatorname {coker}(f')$, and
$\operatorname {coker}(f')$, and ![]() $\mathrm {coim}(f')$.
$\mathrm {coim}(f')$.
Lemma 2.12 The objects defined in Lemma 2.11 actually give kernel, image, cokernel, and coimage in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$.
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$.
Proof. Again, we will only prove for kernel and the others can be proved by similar arguments.
Let ![]() ${\mathcal {P}}\xrightarrow {g} {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ satisfy
${\mathcal {P}}\xrightarrow {g} {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ satisfy ![]() $f\circ g=0$. We have lifts
$f\circ g=0$. We have lifts
in ![]() $\mathrm {Mod}^0(\Lambda _X)$. By replacing
$\mathrm {Mod}^0(\Lambda _X)$. By replacing ![]() $\tilde {\mathcal{W} }$ with
$\tilde {\mathcal{W} }$ with ![]() $\tilde {\mathcal{W} }\langle c\rangle$ with sufficiently large
$\tilde {\mathcal{W} }\langle c\rangle$ with sufficiently large ![]() $c$ and
$c$ and ![]() $\tilde {f}$ with
$\tilde {f}$ with ![]() $T^c\tilde {f}$, we can take so that
$T^c\tilde {f}$, we can take so that ![]() $\tilde {f}\circ \tilde {g}=0$ by Lemma 2.8. Then there exists a morphism
$\tilde {f}\circ \tilde {g}=0$ by Lemma 2.8. Then there exists a morphism ![]() $\tilde {\mathcal{P} }\rightarrow \ker \tilde {f}$ by the universality of the kernel. The commutative diagram
$\tilde {\mathcal{P} }\rightarrow \ker \tilde {f}$ by the universality of the kernel. The commutative diagram

descends to the commutative diagram

in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, hence we only have to check the uniqueness of the morphism
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, hence we only have to check the uniqueness of the morphism ![]() $h$.
$h$.
Let ![]() $h'\colon {\mathcal {P}}\rightarrow [\ker f']$ be another morphism in
$h'\colon {\mathcal {P}}\rightarrow [\ker f']$ be another morphism in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which fits into the following diagram.
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which fits into the following diagram.

We can lift ![]() $h'$ to
$h'$ to ![]() $\tilde {h}'\colon \tilde {\mathcal{P} }\rightarrow \ker \tilde {f}\langle a\rangle$ for some
$\tilde {h}'\colon \tilde {\mathcal{P} }\rightarrow \ker \tilde {f}\langle a\rangle$ for some ![]() $a\in \mathbb{R} _{\geqslant 0}$. Take
$a\in \mathbb{R} _{\geqslant 0}$. Take ![]() $b\in {\mathbb {R}}_{\geqslant 0}$ so that
$b\in {\mathbb {R}}_{\geqslant 0}$ so that ![]() $T^b\tilde {\iota }\langle a\rangle \circ \tilde {h}'=T^{a+b}\tilde {g}$ is satisfied. Then we again get a commutative diagram.
$T^b\tilde {\iota }\langle a\rangle \circ \tilde {h}'=T^{a+b}\tilde {g}$ is satisfied. Then we again get a commutative diagram.

On the other hand, we have the following commutative diagram.

By the universality of ![]() $\ker \tilde {f}\langle a+b\rangle$, we have
$\ker \tilde {f}\langle a+b\rangle$, we have ![]() $T^{a+b}\tilde {h}=T^b\tilde {h}'$. Hence
$T^{a+b}\tilde {h}=T^b\tilde {h}'$. Hence ![]() $h=h'$. This completes the proof.
$h=h'$. This completes the proof.
Proof Proof of Proposition 2.6
It remains to show that the isomorphism between ![]() $\mathrm {im}$ and
$\mathrm {im}$ and ![]() $\mathrm {coim}$. Let
$\mathrm {coim}$. Let ![]() $f$ be a morphism in
$f$ be a morphism in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ and
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ and ![]() $\tilde {f}$ be a lift of
$\tilde {f}$ be a lift of ![]() $f$. As shown in Lemma 2.12,
$f$. As shown in Lemma 2.12, ![]() $\mathrm {im} f$ is given by
$\mathrm {im} f$ is given by ![]() $[\mathrm {im} \tilde {f}]$ and
$[\mathrm {im} \tilde {f}]$ and ![]() $\mathrm {coim} f$ is given by
$\mathrm {coim} f$ is given by ![]() $[\mathrm {coim} \tilde {f}]$. Since
$[\mathrm {coim} \tilde {f}]$. Since ![]() $\mathrm {Mod}^0(\Lambda _X)$ is abelian, there exists a canonical isomorphism
$\mathrm {Mod}^0(\Lambda _X)$ is abelian, there exists a canonical isomorphism ![]() $\mathrm {im}\tilde {f}\cong \mathrm {coim}\tilde {f}$. This also induces an isomorphism between
$\mathrm {im}\tilde {f}\cong \mathrm {coim}\tilde {f}$. This also induces an isomorphism between ![]() $\mathrm {im} f$ and
$\mathrm {im} f$ and ![]() $\mathrm {coim} f$. This completes the proof.
$\mathrm {coim} f$. This completes the proof.
Corollary 2.13 The functor ![]() $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is exact.
$[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is exact.
Proof. This is obvious from Lemma 2.12.
It is useful to state a kind of the converse of the above corollary.
Lemma 2.14 Let
be an exact sequence of ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. Then there exists an exact sequence
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. Then there exists an exact sequence
in ![]() $\mathrm {Mod}^0(\Lambda _X)$ which is a lift of the above sequence.
$\mathrm {Mod}^0(\Lambda _X)$ which is a lift of the above sequence.
Proof. Take a lift ![]() $\tilde {\mathcal{V} }'\xrightarrow {\tilde {f}'}\tilde {\mathcal{W} }\xrightarrow {\tilde {g}'}\tilde {\mathcal{X} }'$ such that
$\tilde {\mathcal{V} }'\xrightarrow {\tilde {f}'}\tilde {\mathcal{W} }\xrightarrow {\tilde {g}'}\tilde {\mathcal{X} }'$ such that ![]() $\tilde {g}'\circ \tilde {f}'=0$. Set
$\tilde {g}'\circ \tilde {f}'=0$. Set ![]() $\tilde {\mathcal{V} }:=\ker \tilde {g}'$ and
$\tilde {\mathcal{V} }:=\ker \tilde {g}'$ and ![]() $\tilde {\mathcal{X} }:=\operatorname {im} \tilde {g}'$. Then we have an exact sequence
$\tilde {\mathcal{X} }:=\operatorname {im} \tilde {g}'$. Then we have an exact sequence
Here ![]() $\tilde {f}$ and
$\tilde {f}$ and ![]() $\tilde {g}$ are canonical morphisms. We have an associated morphism
$\tilde {g}$ are canonical morphisms. We have an associated morphism ![]() $\tilde {\mathcal{V} }'\rightarrow \tilde {\mathcal{V} }$. In
$\tilde {\mathcal{V} }'\rightarrow \tilde {\mathcal{V} }$. In ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, this associates a morphism
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, this associates a morphism ![]() $ {\mathcal {V}}\rightarrow [\tilde {\mathcal{V} }]=[\ker \tilde {g}']=\ker g$. By the exactness of the given sequence, we have
$ {\mathcal {V}}\rightarrow [\tilde {\mathcal{V} }]=[\ker \tilde {g}']=\ker g$. By the exactness of the given sequence, we have ![]() $ {\mathcal {V}}\xrightarrow {\cong } [\tilde {\mathcal{V} }]$. Hence
$ {\mathcal {V}}\xrightarrow {\cong } [\tilde {\mathcal{V} }]$. Hence ![]() $\tilde {\mathcal{V} }$ is a lift of
$\tilde {\mathcal{V} }$ is a lift of ![]() $ {\mathcal {V}}$. In a similar way, one can see that
$ {\mathcal {V}}$. In a similar way, one can see that ![]() $\tilde {\mathcal{X} }$ is a lift of
$\tilde {\mathcal{X} }$ is a lift of ![]() ${\mathcal {X}}$. This completes the proof.
${\mathcal {X}}$. This completes the proof.
3. The category  $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D)})$
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D)})$
In this section, we glue up ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ to obtain a modified category, especially for noncompact manifolds.
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ to obtain a modified category, especially for noncompact manifolds.
3.1 Topological space with boundary
We say a topological space is good if it is Hausdorff, locally compact, countable at infinity and has finite flabby dimension. In this paper, a topological space with boundary is a pair ![]() $(\bar {X},D_X)$ of a good topological space
$(\bar {X},D_X)$ of a good topological space ![]() $\bar {X}$ with a closed subset
$\bar {X}$ with a closed subset ![]() $D_X$ of
$D_X$ of ![]() $\bar {X}$. We say
$\bar {X}$. We say ![]() $D_X$ is the boundary of
$D_X$ is the boundary of ![]() $({\bar {X}},D_X)$ and
$({\bar {X}},D_X)$ and ![]() ${\bar {X}}{\backslash } D_X$ is the interior of
${\bar {X}}{\backslash } D_X$ is the interior of ![]() $({\bar {X}},D_X)$. A morphism between
$({\bar {X}},D_X)$. A morphism between ![]() $(\bar {X}, D_X)$ and
$(\bar {X}, D_X)$ and ![]() $(\bar {Y}, D_Y)$ is a continuous map
$(\bar {Y}, D_Y)$ is a continuous map ![]() $f$ between
$f$ between ![]() $\bar {X}$ and
$\bar {X}$ and ![]() $\bar {Y}$ preserving the interiors. We denote the interiors by
$\bar {Y}$ preserving the interiors. We denote the interiors by ![]() $X:={\bar {X}}{\backslash } D_X$ and
$X:={\bar {X}}{\backslash } D_X$ and ![]() $Y:={\bar {Y}}{\backslash } D_Y$. We also denote the induced map between interiors by
$Y:={\bar {Y}}{\backslash } D_Y$. We also denote the induced map between interiors by ![]() $f\colon X\rightarrow Y$ by the abuse of notation.
$f\colon X\rightarrow Y$ by the abuse of notation.
Example 3.1 (i) Our primary examples of topological spaces with boundaries are of the following class. For a topological space ![]() $Z$, consider a locally closed subset
$Z$, consider a locally closed subset ![]() $S$. Let
$S$. Let ![]() $\bar {S}$ be the closure of
$\bar {S}$ be the closure of ![]() $S$. Then
$S$. Then ![]() $(\bar {S}, \bar {S}{\backslash } S)$ is a topological space with boundary. We have a canonical map
$(\bar {S}, \bar {S}{\backslash } S)$ is a topological space with boundary. We have a canonical map ![]() $(\bar {S}, \bar {S}{\backslash } S)\rightarrow (Z,\varnothing )$ induced by the inclusion
$(\bar {S}, \bar {S}{\backslash } S)\rightarrow (Z,\varnothing )$ induced by the inclusion ![]() $\bar {S}\hookrightarrow Z$.
$\bar {S}\hookrightarrow Z$.
(ii) By the definition of morphisms of topological spaces with boundary, we have canonical maps ![]() $(X,\varnothing )\rightarrow ({\bar {X}}, D_X)$ and
$(X,\varnothing )\rightarrow ({\bar {X}}, D_X)$ and ![]() ${({\bar {X}}, D_X)}\rightarrow ({\bar {X}}, \varnothing )$ induced by the identity
${({\bar {X}}, D_X)}\rightarrow ({\bar {X}}, \varnothing )$ induced by the identity ![]() $\operatorname {id}\colon {\bar {X}}\rightarrow {\bar {X}}$. On the other hand, such a canonical map does not exist from
$\operatorname {id}\colon {\bar {X}}\rightarrow {\bar {X}}$. On the other hand, such a canonical map does not exist from ![]() ${({\bar {X}}, D_X)}$ to
${({\bar {X}}, D_X)}$ to ![]() $(X, \varnothing )$.
$(X, \varnothing )$.
Let ![]() $({\bar {X}}, D_X)$ be a topological space with boundary. The site
$({\bar {X}}, D_X)$ be a topological space with boundary. The site ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$ is defined by the following data: the underlying category is the category of open subsets of
$\mathrm {Open}_{({\bar {X}}, D_X)}$ is defined by the following data: the underlying category is the category of open subsets of ![]() ${\bar {X}}{\backslash } D_X$, a collection of open subsets
${\bar {X}}{\backslash } D_X$, a collection of open subsets ![]() $\{U_i\}_{i\in I}$ in
$\{U_i\}_{i\in I}$ in ![]() ${\bar {X}}{\backslash } D_X$ is said to define a cover of
${\bar {X}}{\backslash } D_X$ is said to define a cover of ![]() $U$ if there exists a subset
$U$ if there exists a subset ![]() $J$ of
$J$ of ![]() $I$ such that the subcollection
$I$ such that the subcollection ![]() $\{U_i\}_{i\in J}$ still defines an open covering of
$\{U_i\}_{i\in J}$ still defines an open covering of ![]() $U$ and is locally finite over
$U$ and is locally finite over ![]() ${\bar {X}}$.
${\bar {X}}$.
Remark 3.2 Here we explain some motivations of the definition of ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$. The essential point is the local finiteness at
$\mathrm {Open}_{({\bar {X}}, D_X)}$. The essential point is the local finiteness at ![]() $D_X$. If one does not introduce this finiteness, after the stackification below, all objects have trivial grading around
$D_X$. If one does not introduce this finiteness, after the stackification below, all objects have trivial grading around ![]() $D_X$. Since our grading encodes asymptotic behaviors of solutions of irregular
$D_X$. Since our grading encodes asymptotic behaviors of solutions of irregular ![]() ${\mathcal {D}}$-modules, we have to keep nontrivial gradings at
${\mathcal {D}}$-modules, we have to keep nontrivial gradings at ![]() $D_X$.
$D_X$.
A similar thing occurs even if you consider ind-sheaves. Since ind-sheaves are ind-objects of compactly supported sheaves, ind-sheaves on ![]() $X$ cannot encode the data around
$X$ cannot encode the data around ![]() $D_X$. To consider the data around
$D_X$. To consider the data around ![]() $D_X$, one has to consider compactly supported sheaves on
$D_X$, one has to consider compactly supported sheaves on ![]() ${\bar {X}}$ whose stalks can be nonzero only in
${\bar {X}}$ whose stalks can be nonzero only in ![]() $X$.
$X$.
The following is clear.
Lemma 3.3 The cover defined just before Remark 3.2 gives a Grothendieck topology on ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$.
$\mathrm {Open}_{({\bar {X}}, D_X)}$.
Remark 3.4 If ![]() ${\bar {X}}$ is compact and
${\bar {X}}$ is compact and ![]() $D_X=\varnothing$ then
$D_X=\varnothing$ then ![]() $\mathrm {Open}_{({\bar {X}},D_X)}$ coincides with the usual site of
$\mathrm {Open}_{({\bar {X}},D_X)}$ coincides with the usual site of ![]() ${\bar {X}}$.
${\bar {X}}$.
Lemma 3.5 Let ![]() $f\colon ({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$ is a morphism between topological spaces with boundary. Then there exists an induced morphism
$f\colon ({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$ is a morphism between topological spaces with boundary. Then there exists an induced morphism ![]() $\mathrm {Open}_{({\bar {Y}}, D_Y)}\rightarrow \mathrm {Open}_{({\bar {X}}, D_X)}$.
$\mathrm {Open}_{({\bar {Y}}, D_Y)}\rightarrow \mathrm {Open}_{({\bar {X}}, D_X)}$.
Proof. Let ![]() $\{U_i\}_{i\in I}$ be a cover of
$\{U_i\}_{i\in I}$ be a cover of ![]() $U$ in
$U$ in ![]() $\mathrm {Open}_{({\bar {Y}}, D_Y)}$. Let
$\mathrm {Open}_{({\bar {Y}}, D_Y)}$. Let ![]() $J\subset I$ be as in the definition of the cover. Then
$J\subset I$ be as in the definition of the cover. Then ![]() $\{f^{-1}(U_i)\}$ is an open covering of
$\{f^{-1}(U_i)\}$ is an open covering of ![]() $f^{-1}(U)$ in
$f^{-1}(U)$ in ![]() ${\bar {X}}$. Take
${\bar {X}}$. Take ![]() $x\in {\bar {X}}$, then there exists a small neighborhood
$x\in {\bar {X}}$, then there exists a small neighborhood ![]() $V$ of
$V$ of ![]() $f(y)$ such that
$f(y)$ such that ![]() $V$ only intersects with a finite subset of
$V$ only intersects with a finite subset of ![]() $\{U_j\}_{j\in J}$. Then
$\{U_j\}_{j\in J}$. Then ![]() $f^{-1}(V)$ also only intersects with a finite subset of
$f^{-1}(V)$ also only intersects with a finite subset of ![]() $\{f^{-1}(U_j)\}_{j\in J}$. Hence
$\{f^{-1}(U_j)\}_{j\in J}$. Hence ![]() $\{f^{-1}(U_i)\}_{i\in I}$ is a cover of
$\{f^{-1}(U_i)\}_{i\in I}$ is a cover of ![]() $f^{-1}(U)$ in
$f^{-1}(U)$ in ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$.
$\mathrm {Open}_{({\bar {X}}, D_X)}$.
Remark 3.6 The reader may consider the notion of topological spaces with boundary is similar to the notion of bordered spaces in [Reference D'Agnolo and KashiwaraDK16]. However, the role of these two notions are different: the former is about the base space and the latter is about the additional variable ![]() $ {\mathbb {R}}$.
$ {\mathbb {R}}$.
3.2 The category  $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$
Let ![]() $({\bar {X}}, D_X)$ be a topological space with boundary. We set
$({\bar {X}}, D_X)$ be a topological space with boundary. We set ![]() $X:={\bar {X}}{\backslash } D_X$. Let
$X:={\bar {X}}{\backslash } D_X$. Let ![]() $U\supset V$ be open subsets of
$U\supset V$ be open subsets of ![]() $X$. Then we have a restriction functor
$X$. Then we have a restriction functor
Lemma 3.7 This restriction functor is exact.
Proof. A short exact sequence in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _U)$ can be lifted to a short exact sequence in
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _U)$ can be lifted to a short exact sequence in ![]() $\mathrm {Mod}^0(\Lambda _U)$ by Corollary 2.13. Then we can restrict it to an exact sequence in
$\mathrm {Mod}^0(\Lambda _U)$ by Corollary 2.13. Then we can restrict it to an exact sequence in ![]() $\mathrm {Mod}^0(\Lambda _V)$. By Lemma 2.12, this also gives an exact sequence in
$\mathrm {Mod}^0(\Lambda _V)$. By Lemma 2.12, this also gives an exact sequence in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _V)$.
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _V)$.
These maps form a presheaf of categories over the site ![]() $\mathrm {Open}_{({\bar {X}},D_X)}$. This is not always a stack (even a prestack) because the tensor product
$\mathrm {Open}_{({\bar {X}},D_X)}$. This is not always a stack (even a prestack) because the tensor product ![]() $\otimes \mathbb {k}$ on the hom-space breaks the sheaf property.
$\otimes \mathbb {k}$ on the hom-space breaks the sheaf property.
Take the stackification (respectively prestackification) of this stack with respect to ![]() $\mathrm {Open}_{({\bar {X}},D_X)}$. We denote it by
$\mathrm {Open}_{({\bar {X}},D_X)}$. We denote it by ![]() $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ (respectively
$\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ (respectively ![]() ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{{({\bar {X}}, D_X)}}$).
${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{{({\bar {X}}, D_X)}}$).
Definition 3.8 The global section category of ![]() $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ is denoted by
$\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ is denoted by ![]() $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. For a manifold
$\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. For a manifold ![]() $X$, we set
$X$, we set ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X):=\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(X, \varnothing )})$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X):=\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(X, \varnothing )})$.
Proposition 3.9 The category ![]() $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$ is an abelian category for any
$\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$ is an abelian category for any ![]() $U\in \mathrm {Open}_{{({\bar {X}}, D_X)}}$.
$U\in \mathrm {Open}_{{({\bar {X}}, D_X)}}$.
Proof. We will only consider the case of kernels. A similar argument holds for cokernels, images and coimages.
Let ![]() $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism in
$f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$. Then there exists a covering
$\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$. Then there exists a covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $U$ such that we have a descent data
$U$ such that we have a descent data ![]() $f_i\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in
$f_i\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in ![]() ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_i)$. If it is necessary, we can replace the covering with a finer covering so that each
${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_i)$. If it is necessary, we can replace the covering with a finer covering so that each ![]() $f|_{U_i}$ is represented by a morphism
$f|_{U_i}$ is represented by a morphism ![]() $f_{i}\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in
$f_{i}\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{i})$. On each intersection
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{i})$. On each intersection ![]() $U_{i}\cap U_{j}$, we have a further covering
$U_{i}\cap U_{j}$, we have a further covering ![]() $\{U_{ijk}\}_k$ such that
$\{U_{ijk}\}_k$ such that ![]() $(f_i-f_j)|_{U_{ijk}}=0$.
$(f_i-f_j)|_{U_{ijk}}=0$.
Then we have ![]() $\ker (f_{i})$ since
$\ker (f_{i})$ since ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{i}})$ is an abelian category. Since the restriction functors are exact (Lemma 3.7), we have
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{i}})$ is an abelian category. Since the restriction functors are exact (Lemma 3.7), we have ![]() $\ker (f_i|_{U_{ij}})|_{U_{ijk}}=\ker (f_i|_{U_{ijk}})=\ker (f_j|_{U_{ijk}})=\ker (f_j|_{U_{ij}})|_{U_{ijk}}$ in
$\ker (f_i|_{U_{ij}})|_{U_{ijk}}=\ker (f_i|_{U_{ijk}})=\ker (f_j|_{U_{ijk}})=\ker (f_j|_{U_{ij}})|_{U_{ijk}}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{ijk}})$. Hence we have
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{ijk}})$. Hence we have ![]() $\ker (f_i)|_{U_{ij}}=\ker (f_i|_{U_{ij}})=\ker (f_j|_{U_{ij}})=\ker (f_j)|_{U_{ij}}$ in
$\ker (f_i)|_{U_{ij}}=\ker (f_i|_{U_{ij}})=\ker (f_j|_{U_{ij}})=\ker (f_j)|_{U_{ij}}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{{({\bar {X}}, D_X)}}(U_{ij})$. This further gives a descent data and glues up to an object
$\mathrm {Mod}^{\mathfrak {I}}_{{({\bar {X}}, D_X)}}(U_{ij})$. This further gives a descent data and glues up to an object ![]() ${\mathcal {K}}\in \mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$.
${\mathcal {K}}\in \mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$.
For a morphism ![]() $g\colon {\mathcal {X}}\rightarrow {\mathcal {V}}$ with
$g\colon {\mathcal {X}}\rightarrow {\mathcal {V}}$ with ![]() $f\circ g=0$, by taking a sufficiently fine cover
$f\circ g=0$, by taking a sufficiently fine cover ![]() $\{U_i\}$, we can represent
$\{U_i\}$, we can represent ![]() $f, g, {\mathcal {X}}, {\mathcal {V}}$ in
$f, g, {\mathcal {X}}, {\mathcal {V}}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_i})$. Then one gets a unique factorizing morphism
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_i})$. Then one gets a unique factorizing morphism ![]() ${\mathcal {X}}|_{U_i}\rightarrow \ker f_i$. Again by taking a finer covering as in the previous part of the proof and the universality, the set of these factorizing morphisms gives a descent data and can be glued up into the unique factorizing
${\mathcal {X}}|_{U_i}\rightarrow \ker f_i$. Again by taking a finer covering as in the previous part of the proof and the universality, the set of these factorizing morphisms gives a descent data and can be glued up into the unique factorizing ![]() ${\mathcal {X}}\rightarrow {\mathcal {K}}$. This shows
${\mathcal {X}}\rightarrow {\mathcal {K}}$. This shows ![]() ${\mathcal {K}}$ is
${\mathcal {K}}$ is ![]() $\ker f$.
$\ker f$.
Let ![]() $U$ be an open subset of
$U$ be an open subset of ![]() $X$. Let
$X$. Let ![]() $\alpha _U\colon \mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)\rightarrow \mathrm {Mod}^ {\mathfrak {I}}_{({\bar {X}},D)}(U)$ be the canonical functor.
$\alpha _U\colon \mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)\rightarrow \mathrm {Mod}^ {\mathfrak {I}}_{({\bar {X}},D)}(U)$ be the canonical functor.
Lemma 3.10 The functor ![]() $\alpha _U$ is an exact functor.
$\alpha _U$ is an exact functor.
Proof. Since kernels, cokernels, images, and coimages are defined locally, the assertion is obvious.
Lemma 3.11 If ![]() $\bar {U}$ is compact, the functor
$\bar {U}$ is compact, the functor ![]() $\alpha _U$ is fully faithful.
$\alpha _U$ is fully faithful.
Proof. We set ![]() $D_U:=D_X\cap \bar {U}$. To show the claim, it is enough to prove
$D_U:=D_X\cap \bar {U}$. To show the claim, it is enough to prove ![]() $\operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)}( {\mathcal {V}}, {\mathcal {W}})$ is a sheaf over the site
$\operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)}( {\mathcal {V}}, {\mathcal {W}})$ is a sheaf over the site ![]() $\mathrm {Open}_{(\bar {U},D_U)}$. Since
$\mathrm {Open}_{(\bar {U},D_U)}$. Since ![]() $\bar {U}$ is compact, any cover in
$\bar {U}$ is compact, any cover in ![]() $\mathrm {Open}_{(\bar {U}, D_U)}$ has a finite subcover.
$\mathrm {Open}_{(\bar {U}, D_U)}$ has a finite subcover.
We first assume that there exists a finite cover ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $U$ such that the restriction of
$U$ such that the restriction of ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$ to each open subset is zero. Let
$f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$ to each open subset is zero. Let ![]() $\tilde {f}\in \operatorname {Hom}_{\mathrm {Mod}^0(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ be a lift. Then the restriction of
$\tilde {f}\in \operatorname {Hom}_{\mathrm {Mod}^0(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ be a lift. Then the restriction of ![]() $f$ to each open subset
$f$ to each open subset ![]() $U_i$ is represented by
$U_i$ is represented by ![]() $\tilde {f}|_{U_i}$. Since
$\tilde {f}|_{U_i}$. Since ![]() $f|_{U_i}=0$, there exists a
$f|_{U_i}=0$, there exists a ![]() $T^a$ such that
$T^a$ such that ![]() $T^a\tilde {f}|_{U_i}=0$ by Lemma 2.8. Let
$T^a\tilde {f}|_{U_i}=0$ by Lemma 2.8. Let ![]() $A$ be the maximum of those
$A$ be the maximum of those ![]() $a$ values. Then
$a$ values. Then ![]() $T^A\tilde {f}=0$. Hence
$T^A\tilde {f}=0$. Hence ![]() $f=0$.
$f=0$.
Let ![]() $\{f_{i}\}\in \prod \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _{U_i})}( {\mathcal {V}}|_{U_i}, {\mathcal {W}}|_{U_i})$ satisfy the descent condition. Depending on
$\{f_{i}\}\in \prod \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _{U_i})}( {\mathcal {V}}|_{U_i}, {\mathcal {W}}|_{U_i})$ satisfy the descent condition. Depending on ![]() $i$, we have a set of lifts
$i$, we have a set of lifts ![]() $\tilde {f}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{W} }|_{U_i}\langle a_i\rangle$ in
$\tilde {f}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{W} }|_{U_i}\langle a_i\rangle$ in ![]() $\mathrm {Mod}^0(\Lambda _{U_i})$. In our situation, we can take
$\mathrm {Mod}^0(\Lambda _{U_i})$. In our situation, we can take ![]() $a_i=a_j$ for any
$a_i=a_j$ for any ![]() $i,j$, since the indexes are finite. Then we replace
$i,j$, since the indexes are finite. Then we replace ![]() $\tilde {\mathcal{W} }$ with
$\tilde {\mathcal{W} }$ with ![]() $\tilde {\mathcal{W} }\langle a_i\rangle$ by Lemma 2.12. On
$\tilde {\mathcal{W} }\langle a_i\rangle$ by Lemma 2.12. On ![]() $U_i\cap U_j$,
$U_i\cap U_j$, ![]() $\tilde {f}_i$ and
$\tilde {f}_i$ and ![]() $\tilde {f}_j$ may not coincide, but
$\tilde {f}_j$ may not coincide, but ![]() $f_i=[\tilde {f}_i]$ coincides with
$f_i=[\tilde {f}_i]$ coincides with ![]() $f_j=[\tilde {f}_j]$. Hence there exists
$f_j=[\tilde {f}_j]$. Hence there exists ![]() $T^{a_{ij}}$ such that
$T^{a_{ij}}$ such that ![]() $T^{a_{ij}}\tilde {f}_i=T^{a_{ij}}\tilde {f}_j$. By taking the maximum among
$T^{a_{ij}}\tilde {f}_i=T^{a_{ij}}\tilde {f}_j$. By taking the maximum among ![]() $a_{ij}$, we replace
$a_{ij}$, we replace ![]() $\tilde {f}_j$ with
$\tilde {f}_j$ with ![]() $T^a \tilde {f}_j$ then the set
$T^a \tilde {f}_j$ then the set ![]() $\{T^a \tilde {f}_i\}$ satisfies the descent condition in
$\{T^a \tilde {f}_i\}$ satisfies the descent condition in ![]() $\mathrm {Mod}^0(\Lambda _U)$. Hence we get a glued morphism.
$\mathrm {Mod}^0(\Lambda _U)$. Hence we get a glued morphism.
Corollary 3.12 If ![]() $X$ is compact,
$X$ is compact, ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian subcategory of
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian subcategory of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{X})$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{X})$.
Proof. The embedding is given by the proof of Lemma 3.11.
Let us denote the derived category by ![]() $D^{\bullet }(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ (
$D^{\bullet }(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ (![]() $\bullet =b, \pm$).
$\bullet =b, \pm$).
3.3 Forgetting shifts
Recall that we have the canonical functor ![]() $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. There also exists a canonical functor
$[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. There also exists a canonical functor ![]() $\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.
$\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.
Lemma 3.13 The functor ![]() $\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda )\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an exact functor.
$\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda )\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an exact functor.
For simplicity, we will denote ![]() $\alpha _X\circ [\cdot ]$ by
$\alpha _X\circ [\cdot ]$ by ![]() $[\cdot ]$. We denote the exact functor
$[\cdot ]$. We denote the exact functor ![]() $D^\bullet (\mathrm {Mod}^0(\Lambda _X))\rightarrow D^\bullet (\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ induced by
$D^\bullet (\mathrm {Mod}^0(\Lambda _X))\rightarrow D^\bullet (\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ induced by ![]() $[\cdot ]$ by the same notation.
$[\cdot ]$ by the same notation.
3.4 Finite limits and finite colimits
Since ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an abelian category, it admits finite limits and finite colimits.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an abelian category, it admits finite limits and finite colimits.
Lemma 3.14 Let ![]() $F\colon {\mathfrak {U}}\rightarrow \mathrm {Mod}^0(\Lambda _X)$ be a finite diagram without loops in
$F\colon {\mathfrak {U}}\rightarrow \mathrm {Mod}^0(\Lambda _X)$ be a finite diagram without loops in ![]() $\mathrm {Mod}^0(\Lambda _X)$. We have
$\mathrm {Mod}^0(\Lambda _X)$. We have
 \begin{equation} \begin{gathered} \big[\lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}[F],\\ \big[\lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}[F]. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \big[\lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}[F],\\ \big[\lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}[F]. \end{gathered} \end{equation}Proof. We will only prove the first equivalence. The second equivalence can be proved in a similar manner.
It is enough to show that the left-hand side satisfies the universality of the right-hand side. Let ![]() $ {\mathcal {V}}$ be an object which is over
$ {\mathcal {V}}$ be an object which is over ![]() $[F]$. Locally, we have a lift
$[F]$. Locally, we have a lift ![]() $\tilde {\mathcal{V} }\rightarrow F$. By the universality, we get a morphism
$\tilde {\mathcal{V} }\rightarrow F$. By the universality, we get a morphism ![]() $\tilde {\mathcal{V} }\rightarrow \displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F$, which induces a morphism
$\tilde {\mathcal{V} }\rightarrow \displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F$, which induces a morphism ![]() $ {\mathcal {V}}\rightarrow [\displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F]$ locally. The uniqueness of this morphism can be shown by a method similar to the proof of Lemma 2.12. The uniqueness glue up these local morphisms to obtain the desired result.
$ {\mathcal {V}}\rightarrow [\displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F]$ locally. The uniqueness of this morphism can be shown by a method similar to the proof of Lemma 2.12. The uniqueness glue up these local morphisms to obtain the desired result.
Remark 3.15 Contrary to the finite case, infinite (co)limits do not commute with ![]() $[\cdot ]$ in general. We give one example in the following. Let us set
$[\cdot ]$ in general. We give one example in the following. Let us set ![]() ${\bar {X}}=[0,\infty )$ and
${\bar {X}}=[0,\infty )$ and ![]() $D_X=\{0\}$. Consider
$D_X=\{0\}$. Consider ![]() $ {\mathcal {V}}_1:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x\}}$ and
$ {\mathcal {V}}_1:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x\}}$ and ![]() $ {\mathcal {V}}_2:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x^2\}}$. As we can see in the discussion of § 5 below, we have
$ {\mathcal {V}}_2:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x^2\}}$. As we can see in the discussion of § 5 below, we have ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}([ {\mathcal {V}}_2], [ {\mathcal {V}}_1])=0$. Let
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}([ {\mathcal {V}}_2], [ {\mathcal {V}}_1])=0$. Let ![]() $i_b\colon (b,\infty )\hookrightarrow [0, \infty )$ be the open embedding for
$i_b\colon (b,\infty )\hookrightarrow [0, \infty )$ be the open embedding for ![]() $b\in {\mathbb {R}}_{>0}$.
$b\in {\mathbb {R}}_{>0}$.
If ![]() $[\cdot ]$ and colimits commute, we have
$[\cdot ]$ and colimits commute, we have ![]() $[ {\mathcal {V}}_2]\cong \displaystyle {\lim _{\substack {\longrightarrow \\ b\rightarrow 0}}}[i_{b!}i_b^{-1} {\mathcal {V}}_2]$. Again, from the discussion of § 5, we can conclude
$[ {\mathcal {V}}_2]\cong \displaystyle {\lim _{\substack {\longrightarrow \\ b\rightarrow 0}}}[i_{b!}i_b^{-1} {\mathcal {V}}_2]$. Again, from the discussion of § 5, we can conclude
This is a contradiction.
3.5 Operations
In this section, we will develop the six functors. As above, ![]() $({\bar {X}}, D_X), ({\bar {Y}}, D_Y)$ are topological spaces with boundaries. We set
$({\bar {X}}, D_X), ({\bar {Y}}, D_Y)$ are topological spaces with boundaries. We set ![]() $X:={\bar {X}}{\backslash } D_X$ and
$X:={\bar {X}}{\backslash } D_X$ and ![]() $Y:={\bar {Y}}{\backslash } D_Y$. In the rest of this section, we use the following notation.
$Y:={\bar {Y}}{\backslash } D_Y$. In the rest of this section, we use the following notation.
Notation 3.1
–
 $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$.
$ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$.–
 ${\mathcal {Y}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$.
${\mathcal {Y}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$.–
 $\tilde {\mathcal{V} }_U, \tilde {\mathcal{W} }_U, \tilde {\mathcal{X} }_U\in \mathrm {Mod}^0(\Lambda _U)$ are lifts of
$\tilde {\mathcal{V} }_U, \tilde {\mathcal{W} }_U, \tilde {\mathcal{X} }_U\in \mathrm {Mod}^0(\Lambda _U)$ are lifts of  $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}}$ over
$ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}}$ over  $U$.
$U$.–
 $\{U_i\}_{i\in I}$ is a covering in
$\{U_i\}_{i\in I}$ is a covering in  $\mathrm {Open}_{({\bar {X}}, D_X)}$ with lifts
$\mathrm {Open}_{({\bar {X}}, D_X)}$ with lifts  $\{\tilde {\mathcal{V} }_i\}_{i\in I}, \{\tilde {\mathcal{W} }_i\}_{i\in I}, \{\tilde {\mathcal{X} }_i\}_{i\in I}$. Here
$\{\tilde {\mathcal{V} }_i\}_{i\in I}, \{\tilde {\mathcal{W} }_i\}_{i\in I}, \{\tilde {\mathcal{X} }_i\}_{i\in I}$. Here  $\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i, \tilde {\mathcal{X} }_i$ are abbreviations of
$\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i, \tilde {\mathcal{X} }_i$ are abbreviations of  $\tilde {\mathcal{V} }_{U_i}, \tilde {\mathcal{W} }_{U_i}, \tilde {\mathcal{X} }_{U_i}$ respectively.
$\tilde {\mathcal{V} }_{U_i}, \tilde {\mathcal{W} }_{U_i}, \tilde {\mathcal{X} }_{U_i}$ respectively.–
 $\{V_j\}_{j\in J}$ is a covering in
$\{V_j\}_{j\in J}$ is a covering in  $\mathrm {Open}_{({\bar {Y}}, D_Y)}$ with lifts
$\mathrm {Open}_{({\bar {Y}}, D_Y)}$ with lifts  $\{\tilde {\mathcal{Y} }_j\}_{j\in J}$. Here
$\{\tilde {\mathcal{Y} }_j\}_{j\in J}$. Here  $\tilde {\mathcal{Y} }_j$ are abbreviations of
$\tilde {\mathcal{Y} }_j$ are abbreviations of  $\tilde {\mathcal{V} }_{U_j}$ respectively.
$\tilde {\mathcal{V} }_{U_j}$ respectively.
The internal hom sheaf is defined by the assignment
for an open subset ![]() $U\subset X$. This is canonically an
$U\subset X$. This is canonically an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-module.
$\Lambda _X$-module.
There exists an open covering ![]() $\{U_i\}_{i\in I}$ of
$\{U_i\}_{i\in I}$ of ![]() $X$ in the site
$X$ in the site ![]() $\mathrm {Open}_{({\bar {X}},D_X)}$ with lifts
$\mathrm {Open}_{({\bar {X}},D_X)}$ with lifts ![]() $\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i$ over each
$\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i$ over each ![]() $U_i$. Then one has an
$U_i$. Then one has an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _{U_i}$-module
$\Lambda _{U_i}$-module ![]() $\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)$ over each
$\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)$ over each ![]() $U_i$.
$U_i$.
Lemma 3.16 The set ![]() $\{[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)]\}$ satisfies the descent and gives an object of
$\{[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)]\}$ satisfies the descent and gives an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by ![]() $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})$. This is independent of the choice of local lifts.
$\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})$. This is independent of the choice of local lifts.
Proof. On ![]() $U_{ij}:=U_i\cap U_j$, we have the isomorphism
$U_{ij}:=U_i\cap U_j$, we have the isomorphism ![]() $f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$ in
$f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$ in ![]() ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. Then there exists an open covering
${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. Then there exists an open covering ![]() $\{U_{ijk}\}$ of
$\{U_{ijk}\}$ of ![]() $U_{ij}$ where there exists a descent data
$U_{ij}$ where there exists a descent data ![]() $f_{ijk}\colon [\tilde {\mathcal{V} }_i|_{U_{ijk}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ijk}}]$ for the isomorphism
$f_{ijk}\colon [\tilde {\mathcal{V} }_i|_{U_{ijk}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ijk}}]$ for the isomorphism ![]() $f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}] \rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$.
$f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}] \rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$.
We can take a lift ![]() $\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle$ of this morphism and that of the inverse
$\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle$ of this morphism and that of the inverse ![]() $\tilde {g}_{ijk}\colon \tilde {\mathcal{V} }_j|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_i|_{U_{ijk}}\langle b\rangle$ for some
$\tilde {g}_{ijk}\colon \tilde {\mathcal{V} }_j|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_i|_{U_{ijk}}\langle b\rangle$ for some ![]() $a, b$. The difference
$a, b$. The difference ![]() $\tilde {g}_{ijk}\langle a\rangle \circ \tilde {f}_{ijk}-T^{a+b}$ and
$\tilde {g}_{ijk}\langle a\rangle \circ \tilde {f}_{ijk}-T^{a+b}$ and ![]() $\tilde {f}_{ijk}\langle b\rangle \circ \tilde {g}_{ijk}-T^{a+b}$ becomes
$\tilde {f}_{ijk}\langle b\rangle \circ \tilde {g}_{ijk}-T^{a+b}$ becomes ![]() $0$ after multiplying
$0$ after multiplying ![]() $T^c$ for sufficiently big
$T^c$ for sufficiently big ![]() $c$ by Lemma 2.8.
$c$ by Lemma 2.8.
For simplicity, let us assume that ![]() ${\mathcal {W}}$ has a global lift, i.e.
${\mathcal {W}}$ has a global lift, i.e. ![]() ${\mathcal {W}}=[\tilde {\mathcal{W} }]$, although we can do the same for general
${\mathcal {W}}=[\tilde {\mathcal{W} }]$, although we can do the same for general ![]() ${\mathcal {W}}$. We have the following induced morphisms:
${\mathcal {W}}$. We have the following induced morphisms:
 \begin{equation} \begin{gathered} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\xrightarrow{p(\tilde{g}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -b\rangle, \\ \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}}), \xrightarrow{p(\tilde{f}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -a\rangle, \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\xrightarrow{p(\tilde{g}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -b\rangle, \\ \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}}), \xrightarrow{p(\tilde{f}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -a\rangle, \end{gathered} \end{equation}
where ![]() $p(\tilde {f}_{ijk})$ and
$p(\tilde {f}_{ijk})$ and ![]() $p(\tilde {g}_{ijk})$ are precompositions of
$p(\tilde {g}_{ijk})$ are precompositions of ![]() $f$ and
$f$ and ![]() $g$. Since
$g$. Since ![]() $p(\tilde {f}_{ijk})\langle a\rangle \circ p(\tilde {g}_{ijk})-T^{a+b}\operatorname {id}$ and
$p(\tilde {f}_{ijk})\langle a\rangle \circ p(\tilde {g}_{ijk})-T^{a+b}\operatorname {id}$ and ![]() $p(\tilde {g}_{ijk})\circ p(\tilde {f}_{ijk})\langle b\rangle -T^{a+b}\operatorname {id}$ vanish by multiplying
$p(\tilde {g}_{ijk})\circ p(\tilde {f}_{ijk})\langle b\rangle -T^{a+b}\operatorname {id}$ vanish by multiplying ![]() $T^c$ for big
$T^c$ for big ![]() $c$, we can conclude
$c$, we can conclude ![]() $[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]\cong [\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_j|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]$. A similar argument as was done in Proposition 3.9 gives a gluing of these isomorphisms to give a global object in
$[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]\cong [\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_j|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]$. A similar argument as was done in Proposition 3.9 gives a gluing of these isomorphisms to give a global object in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The independence of the choice of local lifts is also clear.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The independence of the choice of local lifts is also clear.
Let us consider the assignment
for ![]() $V\subset U\in \mathrm {Open}_{({\bar {X}}, D_X)}$. Then this assignment does not depend on the choice of the lift
$V\subset U\in \mathrm {Open}_{({\bar {X}}, D_X)}$. Then this assignment does not depend on the choice of the lift ![]() $\tilde {\mathcal{V} }_U$. Hence one can associate a sheaf over
$\tilde {\mathcal{V} }_U$. Hence one can associate a sheaf over ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$. We write it
$\mathrm {Open}_{({\bar {X}}, D_X)}$. We write it ![]() $ {\mathcal {V}}\otimes \mathbb {k}$.
$ {\mathcal {V}}\otimes \mathbb {k}$.
Lemma 3.17 The sheaf ![]() $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\otimes \mathbb {k}$ over
$\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\otimes \mathbb {k}$ over ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$ is canonically isomorphic to
$\mathrm {Open}_{({\bar {X}}, D_X)}$ is canonically isomorphic to ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{\Lambda _{({\bar {X}}, D_X)}}}( {\mathcal {V}}, {\mathcal {W}})$.
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{\Lambda _{({\bar {X}}, D_X)}}}( {\mathcal {V}}, {\mathcal {W}})$.
Proof. This is obvious from the construction.
For ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules
$\Lambda$-modules ![]() $V$ and
$V$ and ![]() $W$, their tensor product is defined as follows:
$W$, their tensor product is defined as follows:
where the equivalence relations are generated by
where ![]() $\alpha \in \Lambda , v\in V, w\in W$ are homogeneous and
$\alpha \in \Lambda , v\in V, w\in W$ are homogeneous and ![]() $\operatorname {deg} \alpha +\operatorname {deg} v+\operatorname {deg} w=a$. The tensor product
$\operatorname {deg} \alpha +\operatorname {deg} v+\operatorname {deg} w=a$. The tensor product ![]() $V\otimes _\Lambda W:={\bigoplus} _a \operatorname {Gr}^a(V\otimes _\Lambda W)$ is canonically equipped with a
$V\otimes _\Lambda W:={\bigoplus} _a \operatorname {Gr}^a(V\otimes _\Lambda W)$ is canonically equipped with a ![]() $\Lambda$-module structure.
$\Lambda$-module structure.
Then the tensor product ![]() $\tilde {\mathcal{V} }\otimes \tilde {\mathcal{W} }$ is defined by the sheafification of the assignment
$\tilde {\mathcal{V} }\otimes \tilde {\mathcal{W} }$ is defined by the sheafification of the assignment
One has another ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _{U_i}$-module
$\Lambda _{U_i}$-module ![]() $\tilde {\mathcal{V} }_i\otimes _{\Lambda _X} \tilde {\mathcal{W} }_i$ over each
$\tilde {\mathcal{V} }_i\otimes _{\Lambda _X} \tilde {\mathcal{W} }_i$ over each ![]() $U_i$.
$U_i$.
Lemma 3.18 The set ![]() $\{[\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\tilde {\mathcal{W} }_i]\}$ satisfies the descent and gives an object of
$\{[\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\tilde {\mathcal{W} }_i]\}$ satisfies the descent and gives an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by ![]() $ {\mathcal {V}}\otimes {\mathcal {W}}$. This is independent of the choice of local lifts.
$ {\mathcal {V}}\otimes {\mathcal {W}}$. This is independent of the choice of local lifts.
Proof. We can prove in a similar manner as in the proof of Lemma 3.16.
Proposition 3.19 We have the following:
Proof. We have a canonical isomorphism
By tensoring ![]() $\mathbb {k}$ and taking sheafification over
$\mathbb {k}$ and taking sheafification over ![]() $\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$, we have an isomorphism
$\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$, we have an isomorphism
as a sheaf over ![]() $\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$. The isomorphisms over the
$\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$. The isomorphisms over the ![]() $U_i$ are glued up and give a desired result.
$U_i$ are glued up and give a desired result.
Corollary 3.20 In the same setting as above, we have the following:
Proof. From the above proposition, we have
 \begin{align} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}}))&\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}\otimes {\mathcal{W}} ,{\mathcal{X}})\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}},\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))). \end{align}
\begin{align} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}}))&\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}\otimes {\mathcal{W}} ,{\mathcal{X}})\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}},\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))). \end{align}Yoneda's lemma implies the desired statement.
We will define push-forwards for a class of morphisms.
In the following, we only consider the following class of maps.
Definition 3.21 We say a morphism ![]() $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ is tame if the underlying map
$f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ is tame if the underlying map ![]() $f\colon {\bar {X}}\rightarrow {\bar {Y}}$ is proper.
$f\colon {\bar {X}}\rightarrow {\bar {Y}}$ is proper.
Remark 3.22 For a locally closed subset ![]() $U\subset X$, a canonical morphism
$U\subset X$, a canonical morphism ![]() $(U, \varnothing )\rightarrow (X, \varnothing )$ is not tame in general. However
$(U, \varnothing )\rightarrow (X, \varnothing )$ is not tame in general. However ![]() $(\bar {U}, \bar {U}{\backslash } U)\rightarrow (X, \varnothing )$ is tame. In this sense, we will consider the latter one as a standard inclusion morphism.
$(\bar {U}, \bar {U}{\backslash } U)\rightarrow (X, \varnothing )$ is tame. In this sense, we will consider the latter one as a standard inclusion morphism.
Let ![]() $f$ be a tame map
$f$ be a tame map ![]() $({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$. We first assume that
$({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$. We first assume that ![]() $ {\mathcal {V}}$ has
$ {\mathcal {V}}$ has ![]() $\tilde {\mathcal{V} }$ with
$\tilde {\mathcal{V} }$ with ![]() $[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set
$[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set
where push-forward of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-module
$\Lambda _X$-module ![]() $\tilde {\mathcal{V} }$ is defined by
$\tilde {\mathcal{V} }$ is defined by ![]() $\operatorname {Gr}^af_*\tilde {\mathcal{V} }:=f_*\operatorname {Gr}^a\tilde {\mathcal{V} }$.
$\operatorname {Gr}^af_*\tilde {\mathcal{V} }:=f_*\operatorname {Gr}^a\tilde {\mathcal{V} }$.
Lemma 3.23 This is well defined.
Proof. Let ![]() $\tilde {\mathcal{V} }'$ be another lift. Take a covering
$\tilde {\mathcal{V} }'$ be another lift. Take a covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $\mathrm {Open}_{({\bar {X}}, D_X)}$ such that we have lifts of the isomorphisms
$\mathrm {Open}_{({\bar {X}}, D_X)}$ such that we have lifts of the isomorphisms ![]() $\tilde {g}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{V} }'\langle a_i\rangle |_{U_i}$ and
$\tilde {g}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{V} }'\langle a_i\rangle |_{U_i}$ and ![]() $\tilde {h}_i\colon \tilde {\mathcal{V} }'|_{U_i}\rightarrow \tilde {\mathcal{V} }|_{U_i}\langle b\rangle$ over each
$\tilde {h}_i\colon \tilde {\mathcal{V} }'|_{U_i}\rightarrow \tilde {\mathcal{V} }|_{U_i}\langle b\rangle$ over each ![]() $U_i$. Hence
$U_i$. Hence ![]() $\tilde {g}_i\langle b\rangle \circ \tilde {h}_i-T^{a+b}$ and
$\tilde {g}_i\langle b\rangle \circ \tilde {h}_i-T^{a+b}$ and ![]() $\tilde {h}_i\langle a\rangle \circ \tilde {g}_i-T^{a+b}$ vanish by large
$\tilde {h}_i\langle a\rangle \circ \tilde {g}_i-T^{a+b}$ vanish by large ![]() $T^c$. By pushing forward these equations, we have
$T^c$. By pushing forward these equations, we have
Hence we have ![]() $[f_*\iota _{i*}\tilde {\mathcal{V} }|_{U_i}]\cong [f_*\iota _{i*}\tilde {\mathcal{V} }'|_{U_i}]$ where
$[f_*\iota _{i*}\tilde {\mathcal{V} }|_{U_i}]\cong [f_*\iota _{i*}\tilde {\mathcal{V} }'|_{U_i}]$ where ![]() $\iota _i\colon U_i\rightarrow X$ is the inclusion map.
$\iota _i\colon U_i\rightarrow X$ is the inclusion map.
Let ![]() $ {\mathfrak {U}}$ be the Cech nerve of
$ {\mathfrak {U}}$ be the Cech nerve of ![]() $\{U_i\}$ and
$\{U_i\}$ and ![]() $\iota _U$ for
$\iota _U$ for ![]() $U\in {\mathfrak {U}}$ the inclusion map. Since
$U\in {\mathfrak {U}}$ the inclusion map. Since ![]() $f$ is tame,
$f$ is tame, ![]() $\{f(U_i)\}$ is locally finite in
$\{f(U_i)\}$ is locally finite in ![]() ${\bar {Y}}$ i.e. there exists a covering of
${\bar {Y}}$ i.e. there exists a covering of ![]() $Y$ in
$Y$ in ![]() $\mathrm {Open}_{({\bar {Y}}, D_Y)}$ such that there are only finite
$\mathrm {Open}_{({\bar {Y}}, D_Y)}$ such that there are only finite ![]() $U_i$ in each open subset. Hence we have
$U_i$ in each open subset. Hence we have
by Lemma 3.14. Combining with the first part of the proof, we get an isomorphism ![]() $[f_*\tilde {\mathcal{V} }]\cong [f_*\tilde {\mathcal{V} }']$.
$[f_*\tilde {\mathcal{V} }]\cong [f_*\tilde {\mathcal{V} }']$.
Since ![]() $f$ is tame, there exists a covering
$f$ is tame, there exists a covering ![]() $\{V_i\}$ of
$\{V_i\}$ of ![]() $Y$ and a finite cover
$Y$ and a finite cover ![]() $\{U_{ij}\}$ of each
$\{U_{ij}\}$ of each ![]() $f^{-1}(V_i)$ with lifts
$f^{-1}(V_i)$ with lifts ![]() $\tilde {\mathcal{V} }_{ij}$ of
$\tilde {\mathcal{V} }_{ij}$ of ![]() $ {\mathcal {V}}$.
$ {\mathcal {V}}$.
Let ![]() $ {\mathfrak {U}}_i$ be the Cech nerve of
$ {\mathfrak {U}}_i$ be the Cech nerve of ![]() $\{U_{ij}\}$. We set
$\{U_{ij}\}$. We set
Lemma 3.24 The collection ![]() $\{(f_* {\mathcal {V}})_i\}$ gives an object of
$\{(f_* {\mathcal {V}})_i\}$ gives an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y)$, denoted by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y)$, denoted by ![]() $f_* {\mathcal {V}}$. Moreover, it does not depend on the choice of coordinates and lifts.
$f_* {\mathcal {V}}$. Moreover, it does not depend on the choice of coordinates and lifts.
Proof. It can be proved by a similar argument as in Lemma 3.23.
Over ![]() $f^{-1}(V_i)$, we assign a sheaf
$f^{-1}(V_i)$, we assign a sheaf ![]() $[f^{-1}\tilde {\mathcal{Y} }_i]$ and these can glue up together. We will denote the resulting object by
$[f^{-1}\tilde {\mathcal{Y} }_i]$ and these can glue up together. We will denote the resulting object by ![]() $f^{-1}{\mathcal {Y}}$.
$f^{-1}{\mathcal {Y}}$.
Lemma 3.25 We have the following natural isomorphism:
Proof. It is enough to prove the statement over each ![]() $V_i$. There exists a finite covering
$V_i$. There exists a finite covering ![]() $\{U_j\}$ of
$\{U_j\}$ of ![]() $f^{-1}(V_i)$ with lifts
$f^{-1}(V_i)$ with lifts ![]() $\{\tilde {\mathcal{W} }_j\}$. Then
$\{\tilde {\mathcal{W} }_j\}$. Then ![]() $\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1} {\mathcal {V}}, {\mathcal {W}})$ is represented by
$\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1} {\mathcal {V}}, {\mathcal {W}})$ is represented by ![]() $\{\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1}\tilde {\mathcal{V} }_i|_{U_j}, \tilde {\mathcal{W} }_j)\}$.
$\{\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1}\tilde {\mathcal{V} }_i|_{U_j}, \tilde {\mathcal{W} }_j)\}$.
Let ![]() $ {\mathfrak {U}}$ be the Cech nerve of
$ {\mathfrak {U}}$ be the Cech nerve of ![]() $\{U_j\}$. By the definition of the push forward, we have
$\{U_j\}$. By the definition of the push forward, we have
Here ![]() $\tilde {\mathcal{V} }|_U$ means
$\tilde {\mathcal{V} }|_U$ means ![]() $\tilde {\mathcal{V} }_i|_U$ for some
$\tilde {\mathcal{V} }_i|_U$ for some ![]() $U\subset U_i$. We also have
$U\subset U_i$. We also have
 \begin{align} f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)&\simeq f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}\tilde{\mathcal{Y}}_i, i_{U*}\tilde{\mathcal{V}}|_U)\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{Y}}_i, f_*\iota_{U*}\tilde{\mathcal{V}}|_U) \end{align}
\begin{align} f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)&\simeq f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}\tilde{\mathcal{Y}}_i, i_{U*}\tilde{\mathcal{V}}|_U)\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{Y}}_i, f_*\iota_{U*}\tilde{\mathcal{V}}|_U) \end{align}
for ![]() $U\in {\mathfrak {U}}$. Hence
$U\in {\mathfrak {U}}$. Hence
 \begin{align} \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}([f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)])&\simeq \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*\iota_{U*}\tilde{\mathcal{V}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} [f_*\iota_{U*}\tilde{\mathcal{W}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*(\tilde{\mathcal{V}}|_{f^{{-}1}(V_i)})])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{Y}}, f_*{\mathcal{V}})|_{V_i}. \end{align}
\begin{align} \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}([f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)])&\simeq \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*\iota_{U*}\tilde{\mathcal{V}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} [f_*\iota_{U*}\tilde{\mathcal{W}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*(\tilde{\mathcal{V}}|_{f^{{-}1}(V_i)})])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{Y}}, f_*{\mathcal{V}})|_{V_i}. \end{align}This completes the proof.
Lemma 3.26 We have
Proof. Taking ![]() $\otimes \mathbb {k}$ and the global sections (as in the paragraph above Lemma 3.17) of both sides of Lemma 3.25, the right-hand side becomes
$\otimes \mathbb {k}$ and the global sections (as in the paragraph above Lemma 3.17) of both sides of Lemma 3.25, the right-hand side becomes ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}( {\mathcal {V}}, f_*{\mathcal {W}})$ and the left-hand side becomes
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}( {\mathcal {V}}, f_*{\mathcal {W}})$ and the left-hand side becomes
 \begin{align} (f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}) \otimes \mathbb{k}) (Y)&\cong f_*(\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}},{\mathcal{W}})\otimes \mathbb{k}) (Y)\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{({\bar{X}}, D_X)}}(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}). \end{align}
\begin{align} (f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}) \otimes \mathbb{k}) (Y)&\cong f_*(\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}},{\mathcal{W}})\otimes \mathbb{k}) (Y)\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{({\bar{X}}, D_X)}}(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}). \end{align}This completes the proof.
We first assume that ![]() $ {\mathcal {V}}$ has
$ {\mathcal {V}}$ has ![]() $\tilde {\mathcal{V} }$ with
$\tilde {\mathcal{V} }$ with ![]() $[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set
$[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set
Lemma 3.27 This is well defined.
Proof. This can be proved in the same way as the proof of Lemma 3.23.
Again by the same construction as in the case of push-forwards, we can define ![]() $f_! {\mathcal {V}}$ in general under the assumption of tameness.
$f_! {\mathcal {V}}$ in general under the assumption of tameness.
Assumption 3.28 In the following, when we consider ![]() $f_*$ or
$f_*$ or ![]() $f_!$, we always assume the tameness of
$f_!$, we always assume the tameness of ![]() $f$.
$f$.
4. Derived category of  $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$
4.1 Injectives and flats
In this section, we develop fundamentals about derived operations for ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. In this section, we will use Notation 3.1.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. In this section, we will use Notation 3.1.
Lemma 4.1 Let ![]() ${\mathcal {F}}$ be an
${\mathcal {F}}$ be an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module. For
$\Lambda$-module. For ![]() $x\in X$, the skyscraper sheaf
$x\in X$, the skyscraper sheaf ![]() $[{\mathcal {F}}_x]$ is an injective object. Moreover, the product
$[{\mathcal {F}}_x]$ is an injective object. Moreover, the product ![]() $[\prod _{x\in V}{\mathcal {F}}_x]$ for a subset
$[\prod _{x\in V}{\mathcal {F}}_x]$ for a subset ![]() $V\subset X$ is also an injective object.
$V\subset X$ is also an injective object.
Proof. The first part is almost trivial. Let us prove the second part.
Let ![]() $0\rightarrow {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}$ be an injection in the category
$0\rightarrow {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}$ be an injection in the category ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ with a map
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ with a map ![]() $ {\mathcal {V}}\xrightarrow {g} [\prod _{x\in X}{\mathcal {F}}_x]$. Let us take a locally finite covering
$ {\mathcal {V}}\xrightarrow {g} [\prod _{x\in X}{\mathcal {F}}_x]$. Let us take a locally finite covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $X$ with lifts
$X$ with lifts ![]() $0\rightarrow \tilde {\mathcal{V} }_i\xrightarrow {\tilde {f}_i} \tilde {\mathcal{W} }_i$ and
$0\rightarrow \tilde {\mathcal{V} }_i\xrightarrow {\tilde {f}_i} \tilde {\mathcal{W} }_i$ and ![]() $\tilde {\mathcal{V} }_i\xrightarrow {\tilde {g}_i} \prod _{x\in U_i}{\mathcal {F}}_x\langle a_i\rangle $. We also get a lift
$\tilde {\mathcal{V} }_i\xrightarrow {\tilde {g}_i} \prod _{x\in U_i}{\mathcal {F}}_x\langle a_i\rangle $. We also get a lift ![]() $\tilde {\mathcal{W} }_i\xrightarrow {\tilde {h}_i}\prod _{x\in U}{\mathcal {F}}_x\langle a_i\rangle $.
$\tilde {\mathcal{W} }_i\xrightarrow {\tilde {h}_i}\prod _{x\in U}{\mathcal {F}}_x\langle a_i\rangle $.
For each ![]() $x\in V$, we choose
$x\in V$, we choose ![]() $i_x$ from finite candidates of
$i_x$ from finite candidates of ![]() $i$ values satisfying
$i$ values satisfying ![]() $x\in U_i$. We set
$x\in U_i$. We set ![]() $\tilde {\mathcal{W} }_x:=(\tilde {\mathcal{W} }_{i_x})_x$. Over each
$\tilde {\mathcal{W} }_x:=(\tilde {\mathcal{W} }_{i_x})_x$. Over each ![]() $U_i$, the morphism
$U_i$, the morphism ![]() $\tilde {h}_i$ gives an element of
$\tilde {h}_i$ gives an element of ![]() $({\bigoplus} _{a\in {\mathbb {R}}}\prod _{x\in U_i}\operatorname {Hom}^{a}(\tilde {\mathcal{W} }_{x}, {\mathcal {F}}_x))\otimes _\Lambda k\cong \operatorname {Hom}(W|_{U_i}, [\prod _{x\in V}{\mathcal {F}}_x])$ which is zero on
$({\bigoplus} _{a\in {\mathbb {R}}}\prod _{x\in U_i}\operatorname {Hom}^{a}(\tilde {\mathcal{W} }_{x}, {\mathcal {F}}_x))\otimes _\Lambda k\cong \operatorname {Hom}(W|_{U_i}, [\prod _{x\in V}{\mathcal {F}}_x])$ which is zero on ![]() $i_x\neq i$. Then they are trivially glued up to give a desired lift of
$i_x\neq i$. Then they are trivially glued up to give a desired lift of ![]() $g$.
$g$.
Proposition 4.2 The category ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}},D_X)})$ has enough injectives.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}},D_X)})$ has enough injectives.
Proof. As usual, one can embed ![]() $\tilde {\mathcal{V} }_i$ to an injective object
$\tilde {\mathcal{V} }_i$ to an injective object ![]() $\tilde {\mathcal{I} }_i$ which is a product of skyscraper sheaves.
$\tilde {\mathcal{I} }_i$ which is a product of skyscraper sheaves.
Hence we have the inclusion ![]() $[\tilde {\mathcal{V} }_i]\hookrightarrow [\tilde {\mathcal{I} }_i]$. This induces the inclusion
$[\tilde {\mathcal{V} }_i]\hookrightarrow [\tilde {\mathcal{I} }_i]$. This induces the inclusion ![]() $ {\mathcal {V}}\hookrightarrow {\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$, where the latter is a locally finite direct sum hence it exits. By Lemma 4.1,
$ {\mathcal {V}}\hookrightarrow {\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$, where the latter is a locally finite direct sum hence it exits. By Lemma 4.1, ![]() ${\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$ is also an injective object. This completes the proof.
${\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$ is also an injective object. This completes the proof.
The above proof also shows the following.
Corollary 4.3 There exists an injective resolution ![]() $\tilde {\mathcal{I} }^\bullet :=\tilde {\mathcal{I} }^0\rightarrow \tilde {\mathcal{I} }^1\rightarrow \cdots$ of
$\tilde {\mathcal{I} }^\bullet :=\tilde {\mathcal{I} }^0\rightarrow \tilde {\mathcal{I} }^1\rightarrow \cdots$ of ![]() $\tilde {\mathcal{V} }$ giving an injective resolution
$\tilde {\mathcal{V} }$ giving an injective resolution ![]() $[\tilde {\mathcal{I} }^\bullet ]$ of
$[\tilde {\mathcal{I} }^\bullet ]$ of ![]() $[\tilde {\mathcal{V} }]$.
$[\tilde {\mathcal{V} }]$.
Lemma 4.4 Let ![]() $\tilde {\mathcal{F} }$ be a flat
$\tilde {\mathcal{F} }$ be a flat ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module. Then
$\Lambda$-module. Then ![]() $[\tilde {\mathcal{F} }]$ is a flat object.
$[\tilde {\mathcal{F} }]$ is a flat object.
Proof. Let ![]() $ {\mathcal {V}}\rightarrow {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an injection. Let us take an open covering
$ {\mathcal {V}}\rightarrow {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an injection. Let us take an open covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $X$ with lifts
$X$ with lifts ![]() $\{\tilde {\mathcal{V} }_i\}$,
$\{\tilde {\mathcal{V} }_i\}$, ![]() $\{\tilde {\mathcal{W} }_i\}$ and
$\{\tilde {\mathcal{W} }_i\}$ and ![]() $\tilde {f}_i\colon \tilde {\mathcal{V} }_i\rightarrow \tilde {\mathcal{W} }_i$. Here one can take
$\tilde {f}_i\colon \tilde {\mathcal{V} }_i\rightarrow \tilde {\mathcal{W} }_i$. Here one can take ![]() $\tilde {f}_i$ as an injection by Lemma 2.14. Then
$\tilde {f}_i$ as an injection by Lemma 2.14. Then ![]() $ {\mathcal {V}}\otimes [\tilde {\mathcal{F} }]$ (respectively
$ {\mathcal {V}}\otimes [\tilde {\mathcal{F} }]$ (respectively ![]() ${\mathcal {W}}\otimes [\tilde {\mathcal{F} }]$) is represented by
${\mathcal {W}}\otimes [\tilde {\mathcal{F} }]$) is represented by ![]() $\tilde {\mathcal{V} }_i\otimes \tilde {\mathcal{F} }|_{U_i}\rightarrow \tilde {\mathcal{W} }_i\otimes \tilde {\mathcal{F} }|_{U_i}$, which is an injection. Then by Lemma 2.12, the morphism
$\tilde {\mathcal{V} }_i\otimes \tilde {\mathcal{F} }|_{U_i}\rightarrow \tilde {\mathcal{W} }_i\otimes \tilde {\mathcal{F} }|_{U_i}$, which is an injection. Then by Lemma 2.12, the morphism ![]() $f\otimes [\tilde {\mathcal{F} }]$ is also an injection. This completes the proof.
$f\otimes [\tilde {\mathcal{F} }]$ is also an injection. This completes the proof.
Proposition 4.5 The category ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$ has enough flats.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$ has enough flats.
Proof. By the same construction as in [Reference Kashiwara and SchapiraKS90, Proposition 2.4.12], there exists a flat object ![]() $\tilde {\mathcal{F} }_i$ with a surjection
$\tilde {\mathcal{F} }_i$ with a surjection ![]() $\tilde {\mathcal{F} }_i\rightarrow \tilde {\mathcal{V} }_i$. Let
$\tilde {\mathcal{F} }_i\rightarrow \tilde {\mathcal{V} }_i$. Let ![]() $\iota _i\colon U_i\hookrightarrow X$ be the open imbedding. Hence
$\iota _i\colon U_i\hookrightarrow X$ be the open imbedding. Hence ![]() $[\iota _{i!}\tilde {\mathcal{F} }_i]$ is also a flat object by Lemma 4.4 and we have a surjection
$[\iota _{i!}\tilde {\mathcal{F} }_i]$ is also a flat object by Lemma 4.4 and we have a surjection ![]() ${\bigoplus} _i[\iota _{i!}\tilde {\mathcal{F} }_i]\rightarrow {\mathcal {V}}$. This completes the proof.
${\bigoplus} _i[\iota _{i!}\tilde {\mathcal{F} }_i]\rightarrow {\mathcal {V}}$. This completes the proof.
By a similar argument as in Corollary 4.3, we get the following.
Corollary 4.6 For ![]() $\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$, a flat resolution
$\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$, a flat resolution ![]() $\tilde {\mathcal{F} }^\bullet :=\tilde {\mathcal{F} }^0\leftarrow \tilde {\mathcal{F} }^{-1}\leftarrow \cdots$ of
$\tilde {\mathcal{F} }^\bullet :=\tilde {\mathcal{F} }^0\leftarrow \tilde {\mathcal{F} }^{-1}\leftarrow \cdots$ of ![]() $\tilde {\mathcal{V} }$ gives a flat resolution
$\tilde {\mathcal{V} }$ gives a flat resolution ![]() $[\tilde {\mathcal{F} }^\bullet ]$ of
$[\tilde {\mathcal{F} }^\bullet ]$ of ![]() $[\tilde {\mathcal{V} }]$.
$[\tilde {\mathcal{V} }]$.
4.2 Derived functors
Note that right and left exactness of various functors ![]() $f_*, f_!, f^{-1}, \mathop {{{\mathcal {H}}}om}\nolimits , \otimes$ are the same as in the case of
$f_*, f_!, f^{-1}, \mathop {{{\mathcal {H}}}om}\nolimits , \otimes$ are the same as in the case of ![]() $\mathbb {k}$-modules, according to Lemma 2.8.
$\mathbb {k}$-modules, according to Lemma 2.8.
We will use the following ‘derived’ notation of Notation 3.1.
Notation 4.1
–
 $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}}))$,
$ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}}))$,  ${\mathcal {Y}}, {\mathcal {Y}}_1, {\mathcal {Y}}_2\in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))$.
${\mathcal {Y}}, {\mathcal {Y}}_1, {\mathcal {Y}}_2\in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))$.–
 $\tilde {\mathcal{V} }, \tilde {\mathcal{W} }, \tilde {\mathcal{X} }\in D^b(\mathrm {Mod}^0(\Lambda _X))$,
$\tilde {\mathcal{V} }, \tilde {\mathcal{W} }, \tilde {\mathcal{X} }\in D^b(\mathrm {Mod}^0(\Lambda _X))$,  $\tilde {\mathcal{Y} }\in D^b(\mathrm {Mod}^0(\Lambda _Y))$.
$\tilde {\mathcal{Y} }\in D^b(\mathrm {Mod}^0(\Lambda _Y))$.
Lemma 4.7 We have
Proof. Since ![]() $[\cdot ]$ is an exact functor, it suffices to show the statements for an object
$[\cdot ]$ is an exact functor, it suffices to show the statements for an object ![]() $\mathrm {Mod}^0(\Lambda _X)$ by a standard argument in homological algebra. Then
$\mathrm {Mod}^0(\Lambda _X)$ by a standard argument in homological algebra. Then ![]() $\tilde {\mathcal{V} }$ has an injective resolution
$\tilde {\mathcal{V} }$ has an injective resolution ![]() $\tilde {\mathcal{I} }^\bullet$ such that
$\tilde {\mathcal{I} }^\bullet$ such that ![]() $[\tilde {\mathcal{I} }^\bullet ]$ is an injective resolution of
$[\tilde {\mathcal{I} }^\bullet ]$ is an injective resolution of ![]() $[\tilde {\mathcal{V} }]$ by Corollary 4.3. For
$[\tilde {\mathcal{V} }]$ by Corollary 4.3. For ![]() $F\in \{f_*, f_!, \mathop {{{\mathcal {H}}}om}\nolimits ([\tilde {\mathcal{W} }], -)\}$, we have
$F\in \{f_*, f_!, \mathop {{{\mathcal {H}}}om}\nolimits ([\tilde {\mathcal{W} }], -)\}$, we have
This completes the proof.
Lemma 4.8 We have ![]() $[f^{-1}\tilde {\mathcal{Y} }]\simeq f^{-1}[\tilde {\mathcal{Y} }]$.
$[f^{-1}\tilde {\mathcal{Y} }]\simeq f^{-1}[\tilde {\mathcal{Y} }]$.
Proof. It follows from the definition of ![]() $f^{-1}$ and its exactness on
$f^{-1}$ and its exactness on ![]() $\mathrm {Mod}^0(\Lambda _Y)$.
$\mathrm {Mod}^0(\Lambda _Y)$.
Lemma 4.9 We have ![]() $[\tilde {\mathcal{V} }\otimes ^{\mathbb{L} }\tilde {\mathcal{W} }]\simeq [\tilde {\mathcal{V} }]\otimes ^{\mathbb{L} } [\tilde {\mathcal{W} }]$.
$[\tilde {\mathcal{V} }\otimes ^{\mathbb{L} }\tilde {\mathcal{W} }]\simeq [\tilde {\mathcal{V} }]\otimes ^{\mathbb{L} } [\tilde {\mathcal{W} }]$.
Lemma 4.10 There exists the following isomorphism
Proof. This can be proved by a standard argument. Let us take a flat resolution ![]() ${\mathcal {F}}$ of
${\mathcal {F}}$ of ![]() ${\mathcal {W}}$ and an injective resolution
${\mathcal {W}}$ and an injective resolution ![]() ${\mathcal {I}}$ of
${\mathcal {I}}$ of ![]() ${\mathcal {X}}$. Then
${\mathcal {X}}$. Then ![]() ${\mathbb{R} \mathcal{H} om}({\mathcal {F}}, {\mathcal {I}})\simeq \mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {F}}, {\mathcal {I}})$ is again an injective object. Actually, we have
${\mathbb{R} \mathcal{H} om}({\mathcal {F}}, {\mathcal {I}})\simeq \mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {F}}, {\mathcal {I}})$ is again an injective object. Actually, we have
by Proposition 3.19. Then both sides of the equality in the statement is quasi-isomorphic to ![]() $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}\otimes {\mathcal {F}}, {\mathcal {I}})$. This completes the proof.
$\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}\otimes {\mathcal {F}}, {\mathcal {I}})$. This completes the proof.
Lemma 4.11 There exists the following isomorphism
Proof. By Lemma 3.26 and the exactness of ![]() $f^{-1}$ imply that push-forward of an injective is again injective. Also, pull-back of a flat object is again flat. Let
$f^{-1}$ imply that push-forward of an injective is again injective. Also, pull-back of a flat object is again flat. Let ![]() ${\mathcal {F}}$ be a flat resolution of
${\mathcal {F}}$ be a flat resolution of ![]() ${\mathcal {Y}}$ and
${\mathcal {Y}}$ and ![]() ${\mathcal {I}}$ be an injective resolution of
${\mathcal {I}}$ be an injective resolution of ![]() $ {\mathcal {V}}$. By replacing with these resolutions, we can work with underived functors, then Lemma 3.25 completes the proof.
$ {\mathcal {V}}$. By replacing with these resolutions, we can work with underived functors, then Lemma 3.25 completes the proof.
To construct exceptional inverse image, we follow the argument in [Reference Kashiwara and SchapiraKS90, 3.1].
Assume that ![]() $f_!\colon \mathrm {Mod}({\mathbb {Z}}_X)\rightarrow \mathrm {Mod}({\mathbb {Z}}_Y)$ has finite cohomological dimension. Let
$f_!\colon \mathrm {Mod}({\mathbb {Z}}_X)\rightarrow \mathrm {Mod}({\mathbb {Z}}_Y)$ has finite cohomological dimension. Let ![]() $\tilde {\mathcal{Z} }$ be an object of
$\tilde {\mathcal{Z} }$ be an object of ![]() $\mathrm {Mod}^0(\Lambda _Y)$ and
$\mathrm {Mod}^0(\Lambda _Y)$ and ![]() $K$ be a flat
$K$ be a flat ![]() $f$-soft
$f$-soft ![]() ${\mathbb {Z}}_X$-module. We define a presheaf by
${\mathbb {Z}}_X$-module. We define a presheaf by
This is actually a sheaf by [Reference Kashiwara and SchapiraKS90, Lemma 3.1.3]. We set ![]() $f^!_K\tilde {\mathcal{V} }:={\bigoplus} _{a\in {\mathbb {R}}}\operatorname {Gr}^a(f^!_K\tilde {\mathcal{V} })$ which is an object of
$f^!_K\tilde {\mathcal{V} }:={\bigoplus} _{a\in {\mathbb {R}}}\operatorname {Gr}^a(f^!_K\tilde {\mathcal{V} })$ which is an object of ![]() $\mathrm {Mod}^0(\Lambda _X)$. Let us moreover suppose
$\mathrm {Mod}^0(\Lambda _X)$. Let us moreover suppose ![]() $\tilde {\mathcal{Z} }$ be an injective object.
$\tilde {\mathcal{Z} }$ be an injective object.
Lemma 4.12 Under the above assumption, we have the following.
(i) The object
 $f_K^!\tilde {\mathcal{Z} }$ is an injective object of
$f_K^!\tilde {\mathcal{Z} }$ is an injective object of  $\mathrm {Mod}^0(\Lambda _{X})$.
$\mathrm {Mod}^0(\Lambda _{X})$.(ii) For any
 $\tilde {\mathcal{A} }\in \mathrm {Mod}^0(\Lambda _{X})$. we have a canonical isomorphism
(4.6)
$\tilde {\mathcal{A} }\in \mathrm {Mod}^0(\Lambda _{X})$. we have a canonical isomorphism
(4.6) \begin{equation} \operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_Y)}(f_!(\tilde{\mathcal{A}}\otimes_{\mathbb{Z}} K), \tilde{\mathcal{Z}})\xrightarrow{\simeq}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_X)}(\tilde{\mathcal{A}}, f^!_K\tilde{\mathcal{Z}}). \end{equation}
\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_Y)}(f_!(\tilde{\mathcal{A}}\otimes_{\mathbb{Z}} K), \tilde{\mathcal{Z}})\xrightarrow{\simeq}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_X)}(\tilde{\mathcal{A}}, f^!_K\tilde{\mathcal{Z}}). \end{equation}
Proof. This is done by the same argument as in the proof of [Reference Kashiwara and SchapiraKS90, Lemma 3.1.3].
In the following, we will use ![]() $K$ for the following complex.
$K$ for the following complex.
Lemma 4.13 [Reference Kashiwara and SchapiraKS90, Proposition 3.1.4]
The sheaf ![]() ${\mathbb {Z}}_X$ admits a finite flat
${\mathbb {Z}}_X$ admits a finite flat ![]() $f$-soft resolution
$f$-soft resolution ![]() $K$.
$K$.
Let ![]() $K^+(\mathrm {Mod}^0(\Lambda _X))$ be the homotopy category of injective complexes bounded below of objects in
$K^+(\mathrm {Mod}^0(\Lambda _X))$ be the homotopy category of injective complexes bounded below of objects in ![]() $\mathrm {Mod}^0(\Lambda _X)$. Then we have an equivalence
$\mathrm {Mod}^0(\Lambda _X)$. Then we have an equivalence ![]() $D^+(\mathrm {Mod}^0(\Lambda _X))\cong K^+(\mathrm {Mod}^0(\Lambda _X))$. We set the composition
$D^+(\mathrm {Mod}^0(\Lambda _X))\cong K^+(\mathrm {Mod}^0(\Lambda _X))$. We set the composition
Lemma 4.14 The functor ![]() $f^!$ is the right adjoint of
$f^!$ is the right adjoint of ![]() $ {\mathbb {R}} f_!$. We moreover have
$ {\mathbb {R}} f_!$. We moreover have
Proof. For ![]() $\tilde {\mathcal{W} }\in K^+(\mathrm {Mod}^0(\Lambda _X))\cong D^+(\mathrm {Mod}^0(\Lambda _X))$, we have
$\tilde {\mathcal{W} }\in K^+(\mathrm {Mod}^0(\Lambda _X))\cong D^+(\mathrm {Mod}^0(\Lambda _X))$, we have
by the above lemma. Since ![]() $f_!\tilde {\mathcal{W} }\otimes K\simeq {\mathbb {R}} f_!\tilde {\mathcal{W} }$, we complete the proof of the first assertion. The second assertion can also be proved by the argument of the proof of [Reference Kashiwara and SchapiraKS90, Proposition 3.1.10].
$f_!\tilde {\mathcal{W} }\otimes K\simeq {\mathbb {R}} f_!\tilde {\mathcal{W} }$, we complete the proof of the first assertion. The second assertion can also be proved by the argument of the proof of [Reference Kashiwara and SchapiraKS90, Proposition 3.1.10].
Let us now discuss the exceptional inverse image in ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$. Let
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$. Let ![]() ${\mathcal {Z}}$ be an object of
${\mathcal {Z}}$ be an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and ![]() $K$ be a
$K$ be a ![]() ${\mathbb {Z}}_X$-module.
${\mathbb {Z}}_X$-module.
Take a locally finite covering ![]() $\{V_i\}$ of
$\{V_i\}$ of ![]() $Y$ with lifts
$Y$ with lifts ![]() $\{\tilde {\mathcal{Z} }_i\}$. Hence we get
$\{\tilde {\mathcal{Z} }_i\}$. Hence we get ![]() $f_K^!\tilde {\mathcal{Z} }_i$.
$f_K^!\tilde {\mathcal{Z} }_i$.
Lemma 4.15 The data ![]() $\{[f_K^!\tilde {\mathcal{Z} }_i]\}$ gives an object of
$\{[f_K^!\tilde {\mathcal{Z} }_i]\}$ gives an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. We denote the resulting object by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. We denote the resulting object by ![]() $f^!_K{\mathcal {Z}}$.
$f^!_K{\mathcal {Z}}$.
Proof. Over ![]() $V_{ij}:=V_i\cap V_j$, we have
$V_{ij}:=V_i\cap V_j$, we have ![]() $f_{ij}\colon [\tilde {\mathcal{Z} }_i]|_{V_{ij}}\xrightarrow {\cong } [\tilde {\mathcal{Z} }_j]|_{V_{ij}}$. We can lift this map to
$f_{ij}\colon [\tilde {\mathcal{Z} }_i]|_{V_{ij}}\xrightarrow {\cong } [\tilde {\mathcal{Z} }_j]|_{V_{ij}}$. We can lift this map to ![]() $\tilde {f}_{ij}\colon \tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow \tilde {\mathcal{Z} }_j\langle a_{ij}\rangle |_{V_{ij}}$ (by taking a refined covering if necessary). We also have a lift of the inverse map
$\tilde {f}_{ij}\colon \tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow \tilde {\mathcal{Z} }_j\langle a_{ij}\rangle |_{V_{ij}}$ (by taking a refined covering if necessary). We also have a lift of the inverse map ![]() $\tilde {f}_{ji}$. Then
$\tilde {f}_{ji}$. Then ![]() $\tilde {f}_{ij}\circ \tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id}$ vanishes by multiplying some
$\tilde {f}_{ij}\circ \tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id}$ vanishes by multiplying some ![]() $T^a$. The map
$T^a$. The map ![]() $\tilde {f}_{ij}$ induces a map
$\tilde {f}_{ij}$ induces a map ![]() $f_K^!\tilde {f}_{ij}\colon f^!_K\tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow f^!_K\tilde {\mathcal{Z} }_j|_{V_{ij}}$. Then we also have
$f_K^!\tilde {f}_{ij}\colon f^!_K\tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow f^!_K\tilde {\mathcal{Z} }_j|_{V_{ij}}$. Then we also have ![]() $f_K^!\tilde {f}_{ji}$. Then
$f_K^!\tilde {f}_{ji}$. Then ![]() $f_K^!\tilde {f}_{ij}\circ f_K^!\tilde {f}_{ji}-T^{a_{ij}+{a_{ji}}}\operatorname {id}=f_K^!(\tilde {f}_{ij}\tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id})$ also vanishes by multiplying
$f_K^!\tilde {f}_{ij}\circ f_K^!\tilde {f}_{ji}-T^{a_{ij}+{a_{ji}}}\operatorname {id}=f_K^!(\tilde {f}_{ij}\tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id})$ also vanishes by multiplying ![]() $T^a$. This completes the proof.
$T^a$. This completes the proof.
Since ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ has injective resolutions, we have an equivalence
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ has injective resolutions, we have an equivalence ![]() $K^{+}(\Lambda _Y)\cong D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ where the left-hand side is the homotopy category of complexes bounded below of injective objects. We denote the composition
$K^{+}(\Lambda _Y)\cong D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ where the left-hand side is the homotopy category of complexes bounded below of injective objects. We denote the composition ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))\hookrightarrow K^{+}(\Lambda _Y)\xrightarrow {f^!_K}D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by the notation
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))\hookrightarrow K^{+}(\Lambda _Y)\xrightarrow {f^!_K}D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by the notation ![]() $f^!$.
$f^!$.
Proposition 4.16 The functor ![]() $f^!$ is an exact functor.
$f^!$ is an exact functor.
Proof. The exactness easily follows from the exactness of ![]() $f^!$ on
$f^!$ on ![]() $D^b(\mathrm {Mod}^0(\Lambda _Y))$.
$D^b(\mathrm {Mod}^0(\Lambda _Y))$.
Proposition 4.17 We have ![]() $f^![\tilde {\mathcal{V} }]\cong [f^!\tilde {\mathcal{V} }]$.
$f^![\tilde {\mathcal{V} }]\cong [f^!\tilde {\mathcal{V} }]$.
Proof. Replace ![]() $\tilde {\mathcal{V} }$ be an injective complex given in Lemma 4.1. Then
$\tilde {\mathcal{V} }$ be an injective complex given in Lemma 4.1. Then ![]() $[\tilde {\mathcal{V} }]$ is also an injective complex. By the definition of
$[\tilde {\mathcal{V} }]$ is also an injective complex. By the definition of ![]() $f^!$ for
$f^!$ for ![]() $\mathrm {Mod}^0(\Lambda _X)$ and
$\mathrm {Mod}^0(\Lambda _X)$ and ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we have
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we have ![]() $[f^!\tilde {\mathcal{V} }]\cong [f^!_K\tilde {\mathcal{V} }]\cong f^!_K[\tilde {\mathcal{V} }]\cong f^![\tilde {\mathcal{V} }]$. This completes the proof.
$[f^!\tilde {\mathcal{V} }]\cong [f^!_K\tilde {\mathcal{V} }]\cong f^!_K[\tilde {\mathcal{V} }]\cong f^![\tilde {\mathcal{V} }]$. This completes the proof.
Proposition 4.18 There exists a functorial isomorphism:
Proof. First, note that ![]() $ {\mathbb {R}} f_! {\mathcal {V}}\simeq f_!( {\mathcal {V}}\otimes K)$ which is deduced from the local consideration. Let
$ {\mathbb {R}} f_! {\mathcal {V}}\simeq f_!( {\mathcal {V}}\otimes K)$ which is deduced from the local consideration. Let ![]() ${\mathcal {I}}$ be an injective resolution of
${\mathcal {I}}$ be an injective resolution of ![]() ${\mathcal {Y}}$ and
${\mathcal {Y}}$ and ![]() $C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ be the category of bounded complexes of
$C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ be the category of bounded complexes of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. Then the left-hand side of the desired equality is
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. Then the left-hand side of the desired equality is
We also have a morphism
coming from the morphism ![]() ${\mathcal {Y}}\rightarrow {\mathcal {I}}$. We would like to prove this is an isomorphism. Let us work locally on
${\mathcal {Y}}\rightarrow {\mathcal {I}}$. We would like to prove this is an isomorphism. Let us work locally on ![]() $Y$. From the construction in Proposition 4.2, the complex
$Y$. From the construction in Proposition 4.2, the complex ![]() ${\mathcal {I}}$ is coming from an injective object
${\mathcal {I}}$ is coming from an injective object ![]() $\tilde {\mathcal{I} }$ locally. Hence we have an isomorphism
$\tilde {\mathcal{I} }$ locally. Hence we have an isomorphism
Here we used the fact that ![]() $[\cdot ]$ is exact and
$[\cdot ]$ is exact and ![]() $f^!\tilde {\mathcal{I} }$ is injective. Then Lemma 4.21 completes the proof.
$f^!\tilde {\mathcal{I} }$ is injective. Then Lemma 4.21 completes the proof.
Proposition 4.19 There exists a functorial isomorphism:
Proof. As usual sheaves, we have a canonical morphism ![]() $ {\mathbb {R}} f_*{\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})$. By the adjunction (Proposition 4.18), we have a morphism
$ {\mathbb {R}} f_*{\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})$. By the adjunction (Proposition 4.18), we have a morphism ![]() ${\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathcal {Y}})$. We would like to see the composition is an isomorphism. By a local consideration, this can be deduced from the usual case.
${\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathcal {Y}})$. We would like to see the composition is an isomorphism. By a local consideration, this can be deduced from the usual case.
Lemma 4.20 Let ![]() $\delta \colon X\rightarrow X\times X$ be the diagonal embedding. We have
$\delta \colon X\rightarrow X\times X$ be the diagonal embedding. We have
Proof. We can apply the same formula for usual sheaves to local representatives. Then we get the desired formula.
As in Lemma 3.17, we can relate ![]() $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits$ and usual
$ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits$ and usual ![]() $\operatorname {Hom}$ as follows. From
$\operatorname {Hom}$ as follows. From ![]() $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we can construct a complex of sheaves
$ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we can construct a complex of sheaves ![]() $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ as in the paragraph before Lemma 3.17.
$ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ as in the paragraph before Lemma 3.17.
Lemma 4.21 The space of global sections of ![]() ${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ is canonically isomorphic to
${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ is canonically isomorphic to ![]() $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathcal {W}})$.
$\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathcal {W}})$.
Proof. Let ![]() ${\mathcal {I}}$ be an injective resolution of
${\mathcal {I}}$ be an injective resolution of ![]() ${\mathcal {W}}$ and
${\mathcal {W}}$ and ![]() ${\mathcal {F}}$ be a flat resolution of
${\mathcal {F}}$ be a flat resolution of ![]() $ {\mathcal {V}}$. Then we have
$ {\mathcal {V}}$. Then we have
 \begin{align} \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{W}})&\cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{I}})\nonumber\\ &\cong H^0(\operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{\Lambda_{({\bar{X}}, D_X)}}}({\mathcal{V}},{\mathcal{I}})(X))\nonumber\\ &\cong H^0(\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{F}}, {\mathcal{I}})\otimes \mathbb{k}(X)). \end{align}
\begin{align} \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{W}})&\cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{I}})\nonumber\\ &\cong H^0(\operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{\Lambda_{({\bar{X}}, D_X)}}}({\mathcal{V}},{\mathcal{I}})(X))\nonumber\\ &\cong H^0(\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{F}}, {\mathcal{I}})\otimes \mathbb{k}(X)). \end{align}
Actually ![]() $\otimes \mathbb {k}$ is exact, as we will see in the proof of Lemma 6.1. This completes the proof.
$\otimes \mathbb {k}$ is exact, as we will see in the proof of Lemma 6.1. This completes the proof.
Lemma 4.22 For a tame morphism ![]() $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$, the following hold:
$f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$, the following hold:
(i)
 $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}\otimes ^{\mathbb {L}}{\mathcal {W}},{\mathcal {X}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {W}},{\mathcal {X}}))$;
$\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}\otimes ^{\mathbb {L}}{\mathcal {W}},{\mathcal {X}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {W}},{\mathcal {X}}))$;(ii)
 $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}(f^{-1}{\mathcal {Y}}, {\mathcal {W}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}( {\mathcal {V}}', {\mathbb {R}} f_* {\mathcal {V}})$;
$\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}(f^{-1}{\mathcal {Y}}, {\mathcal {W}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}( {\mathcal {V}}', {\mathbb {R}} f_* {\mathcal {V}})$;(iii)
 $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}(f_! {\mathcal {V}}, {\mathcal {Y}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, f^!{\mathcal {Y}})$.
$\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}(f_! {\mathcal {V}}, {\mathcal {Y}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, f^!{\mathcal {Y}})$.
Lemma 4.23 We have the following:
Proof. The assertions follow easily from Yoneda's Lemma.
We would like to state a useful lemma. Let ![]() $U$ be an open subset of
$U$ be an open subset of ![]() $X$ and
$X$ and ![]() $\bar {U}$ be the closure inside
$\bar {U}$ be the closure inside ![]() $\bar {X}$. Consider the map
$\bar {X}$. Consider the map ![]() $i\colon (\bar {U}, D_U:=\bar {U}{\backslash } U)\rightarrow {({\bar {X}}, D_X)}$. We denote the closed complement of
$i\colon (\bar {U}, D_U:=\bar {U}{\backslash } U)\rightarrow {({\bar {X}}, D_X)}$. We denote the closed complement of ![]() $U$ in
$U$ in ![]() $\bar {X}$ by
$\bar {X}$ by ![]() $V$. We denote the map
$V$. We denote the map ![]() $j\colon (V, V\cap D_X)\rightarrow {({\bar {X}}, D_X)}$.
$j\colon (V, V\cap D_X)\rightarrow {({\bar {X}}, D_X)}$.
Lemma 4.24 There exists an exact triangle in ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$:
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$:
Proof. Note that ![]() $i$ and
$i$ and ![]() $j$ are tame maps. Again, the statement follows from the corresponding statement for usual sheaves and the commutativity results for
$j$ are tame maps. Again, the statement follows from the corresponding statement for usual sheaves and the commutativity results for ![]() $[\cdot ]$ proved early in this subsection.
$[\cdot ]$ proved early in this subsection.
5. Irregular constructibility
In this section, we introduce the notion of ![]() ${\mathbb {C}}$-constructibility for objects in
${\mathbb {C}}$-constructibility for objects in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is defined in the same way for stratifications as in the case of usual constructible sheaves but with a strong assumption on gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem. In this section, we consider
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is defined in the same way for stratifications as in the case of usual constructible sheaves but with a strong assumption on gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem. In this section, we consider ![]() ${({\bar {X}}, D_X)}=(X, \varnothing )$ where
${({\bar {X}}, D_X)}=(X, \varnothing )$ where ![]() $X$ is a complex manifold. We denote
$X$ is a complex manifold. We denote ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ by ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
5.1 Formal structure
In this subsection, we recall as a motivation the theory of formal structures of meromorphic connections initiated by Sabbah [Reference SabbahSab00] and developed by Mochizuki (algebraic case) [Reference MochizukiMoc11] and Kedlaya (analytic case) [Reference KedlayaKed11].
Let ![]() $Z$ be a divisor in a complex manifold
$Z$ be a divisor in a complex manifold ![]() $X$ and
$X$ and ![]() $\hat {\mathcal{O} }_{x}$ be the formal completion of
$\hat {\mathcal{O} }_{x}$ be the formal completion of ![]() ${\mathcal {O}}_X$ at
${\mathcal {O}}_X$ at ![]() $x\in X$. Let
$x\in X$. Let ![]() ${\mathcal {M}}$ be a meromorphic connection over
${\mathcal {M}}$ be a meromorphic connection over ![]() $X$ with poles along
$X$ with poles along ![]() $Z$. We set
$Z$. We set ![]() $\hat {{\mathcal {M}}}_x={\mathcal {M}}_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$ and
$\hat {{\mathcal {M}}}_x={\mathcal {M}}_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$ and ![]() $\hat {\mathcal{O} }(*Z)_x:={\mathcal {O}}(*Z)_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$.
$\hat {\mathcal{O} }(*Z)_x:={\mathcal {O}}(*Z)_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$.
Definition 5.1
(i) For
 $\phi \in \hat {\mathcal{O} }(*Z)_{x}$, we set
$\phi \in \hat {\mathcal{O} }(*Z)_{x}$, we set  $\hat {{\mathcal {E}}}(\phi )$ to be
$\hat {{\mathcal {E}}}(\phi )$ to be  $\hat {\mathcal{O} }(*Z)_{x}$ as a
$\hat {\mathcal{O} }(*Z)_{x}$ as a  $\hat {\mathcal{O} }_x$-module with a connection
$\hat {\mathcal{O} }_x$-module with a connection  $\nabla$ over
$\nabla$ over  $\hat {\mathcal{O} }_x$ such that
(5.1)for the generator
$\hat {\mathcal{O} }_x$ such that
(5.1)for the generator \begin{equation} \nabla s:=\partial(\phi)\cdot s \end{equation}
\begin{equation} \nabla s:=\partial(\phi)\cdot s \end{equation} $s$.
$s$.(ii) We assume that
 $Z$ is a normal crossing divisor and take a local coordinate
$Z$ is a normal crossing divisor and take a local coordinate  $\{x_i\}_{i=1}^n$ such that
$\{x_i\}_{i=1}^n$ such that  $Z$ is defined by
$Z$ is defined by  $\prod _{i=1}^mx_i=0$. An
$\prod _{i=1}^mx_i=0$. An  $\hat {\mathcal{O} }(*Z)$-module
$\hat {\mathcal{O} }(*Z)$-module  $\hat {{\mathcal {R}}}$ with a connection
$\hat {{\mathcal {R}}}$ with a connection  $\nabla$ is regular if there exists an
$\nabla$ is regular if there exists an  $\hat {\mathcal{O} }_x$-submodule
$\hat {\mathcal{O} }_x$-submodule  ${\mathcal {L}}$ such that
${\mathcal {L}}$ such that  ${\mathcal {L}}\otimes _{\hat {\mathcal{O} }_x}\hat {\mathcal{O} }(*Z)_x\cong \hat {{\mathcal {R}}}$ and
${\mathcal {L}}\otimes _{\hat {\mathcal{O} }_x}\hat {\mathcal{O} }(*Z)_x\cong \hat {{\mathcal {R}}}$ and  $\nabla ({\mathcal {L}})\subset {\bigoplus} _{i=1}^m x^{-1}_i{\mathcal {L}}$.
$\nabla ({\mathcal {L}})\subset {\bigoplus} _{i=1}^m x^{-1}_i{\mathcal {L}}$.
Definition 5.2 We continue the notation in Definition 5.1(ii).
(i) A good decomposition of
 $\hat {{\mathcal {M}}}_x$ is an isomorphism
(5.2)where
$\hat {{\mathcal {M}}}_x$ is an isomorphism
(5.2)where \begin{equation} \hat{{\mathcal{M}}}_x\cong \bigoplus_{\alpha\in I}\hat{{\mathcal{E}}}(\phi_\alpha)\otimes_{\hat{\mathcal{O}}(*Z)_x}\hat{\mathcal{R}}_\alpha, \end{equation}
\begin{equation} \hat{{\mathcal{M}}}_x\cong \bigoplus_{\alpha\in I}\hat{{\mathcal{E}}}(\phi_\alpha)\otimes_{\hat{\mathcal{O}}(*Z)_x}\hat{\mathcal{R}}_\alpha, \end{equation} $\phi _\alpha \in \hat {\mathcal{O} }(*Z)_{x}$ and each
$\phi _\alpha \in \hat {\mathcal{O} }(*Z)_{x}$ and each  $\hat {\mathcal {R}}_\alpha$ is regular with the following conditions.
$\hat {\mathcal {R}}_\alpha$ is regular with the following conditions.
(a) Each
 $\phi _\alpha$ has the form
$\phi _\alpha$ has the form  $u\prod _{j=1}^mx_i^{-i_j}$ for some unit
$u\prod _{j=1}^mx_i^{-i_j}$ for some unit  $u\in \hat {\mathcal{O} }_x$ and nonnegative integers
$u\in \hat {\mathcal{O} }_x$ and nonnegative integers  $i_1,\ldots , i_m$.
$i_1,\ldots , i_m$.(b) For
 $\alpha , \beta \in I$, if
$\alpha , \beta \in I$, if  $\phi _a-\phi _\beta \not \in \hat {\mathcal{O} }_x$, then
$\phi _a-\phi _\beta \not \in \hat {\mathcal{O} }_x$, then  $\phi _\alpha -\phi _\beta$ has the form
$\phi _\alpha -\phi _\beta$ has the form  $u\prod _{j=1}^mx_i^{-i_j}$ for some unit
$u\prod _{j=1}^mx_i^{-i_j}$ for some unit  $u\in \hat {\mathcal{O} }_x$ and nonnegative integers
$u\in \hat {\mathcal{O} }_x$ and nonnegative integers  $i_1,\ldots , i_m$.
$i_1,\ldots , i_m$.
(ii) We say
 ${\mathcal {M}}$ admits a good decomposition at
${\mathcal {M}}$ admits a good decomposition at  $x\in Z$ if
$x\in Z$ if  $\hat {{\mathcal {M}}}_x$ admits a good decomposition.
$\hat {{\mathcal {M}}}_x$ admits a good decomposition.
In general, meromorphic connections do not have good decompositions as explained in [Reference SabbahSab00]. Sabbah's conjecture says that they do after modifications, which is proved by Mochizuki and Kedlaya.
Theorem 5.3 [Reference KedlayaKed11, Theorem 8.2.2]
For a point ![]() $x\in Z$, there exists an open neighborhood
$x\in Z$, there exists an open neighborhood ![]() $U$ of
$U$ of ![]() $z$ and a map
$z$ and a map ![]() $f\colon Y\rightarrow U$ which is a proper modification, and at each point of
$f\colon Y\rightarrow U$ which is a proper modification, and at each point of ![]() $f^{-1}(z)$, there exists a local covering
$f^{-1}(z)$, there exists a local covering ![]() $\pi$ ramified at
$\pi$ ramified at ![]() $f^{-1}(Z)$ such that
$f^{-1}(Z)$ such that ![]() $\pi ^*f^*{\mathcal {E}}$ admits a good decomposition at each point of
$\pi ^*f^*{\mathcal {E}}$ admits a good decomposition at each point of ![]() $y\in \pi ^{-1}f^{-1}(Z)$.
$y\in \pi ^{-1}f^{-1}(Z)$.
As explained in [Reference SabbahSab11], using Mochizuki's result, we have additional results. For ![]() $\hat {{\mathcal {M}}}_x$ which admits a good decomposition, let
$\hat {{\mathcal {M}}}_x$ which admits a good decomposition, let ![]() $\Phi _{x}$ be the subset of
$\Phi _{x}$ be the subset of ![]() $\hat {\mathcal{O} }(*Z)_x/ \hat {\mathcal{O} }_x$ consisting of the classes of
$\hat {\mathcal{O} }(*Z)_x/ \hat {\mathcal{O} }_x$ consisting of the classes of ![]() $\phi _\alpha$ values.
$\phi _\alpha$ values.
Theorem 5.4 [Reference SabbahSab11, Theorem 2.2.1]
The subset ![]() $\Phi _x$ is actually a subset of
$\Phi _x$ is actually a subset of ![]() ${\mathcal {O}}(*Z)_z/{\mathcal {O}}_x$. Moreover, there exists a neighborhood
${\mathcal {O}}(*Z)_z/{\mathcal {O}}_x$. Moreover, there exists a neighborhood ![]() $U$ of
$U$ of ![]() $x$ such that for any
$x$ such that for any ![]() $x'\in U$,
$x'\in U$, ![]() $\hat {{\mathcal {M}}}_{x'}$ has a good decomposition and
$\hat {{\mathcal {M}}}_{x'}$ has a good decomposition and ![]() $\Phi _{x'}$ is given by the restriction of representatives of
$\Phi _{x'}$ is given by the restriction of representatives of ![]() $\Phi _x$.
$\Phi _x$.
Let ![]() $\varpi \colon \tilde {X}(Z)\rightarrow X$ be the real blow-up of
$\varpi \colon \tilde {X}(Z)\rightarrow X$ be the real blow-up of ![]() $X$ along
$X$ along ![]() $Z$ (with real analytic structure specified in [Reference D'Agnolo and KashiwaraDK16]). Let
$Z$ (with real analytic structure specified in [Reference D'Agnolo and KashiwaraDK16]). Let ![]() $C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ be the subsheaf of the sheaf of
$C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ be the subsheaf of the sheaf of ![]() $C^\infty$-functions consisting of functions which are tempered at the exceptional divisor. Let further
$C^\infty$-functions consisting of functions which are tempered at the exceptional divisor. Let further ![]() ${\mathcal {A}}_{\tilde {X}(Z)}$ be the subsheaf of
${\mathcal {A}}_{\tilde {X}(Z)}$ be the subsheaf of ![]() $C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ consisting of functions whose restrictions on
$C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ consisting of functions whose restrictions on ![]() $X{\backslash } Z$ are holomorphic. We set
$X{\backslash } Z$ are holomorphic. We set ![]() ${\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}:={\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {O}}_X} {\mathcal {D}}_X$. For a
${\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}:={\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {O}}_X} {\mathcal {D}}_X$. For a ![]() ${\mathcal {D}}$-module
${\mathcal {D}}$-module ![]() ${\mathcal {N}}$ on
${\mathcal {N}}$ on ![]() $X$, we set
$X$, we set ![]() $\varpi ^*{\mathcal {N}}:={\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {D}}_X}\varpi ^{-1}{\mathcal {N}}$.
$\varpi ^*{\mathcal {N}}:={\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {D}}_X}\varpi ^{-1}{\mathcal {N}}$.
Suppose that ![]() ${\mathcal {M}}$ has a good decomposition
${\mathcal {M}}$ has a good decomposition ![]() ${\bigoplus} _{\alpha \in I}\hat {\mathcal {E}}(\phi _\alpha )\otimes \hat {\mathcal {R}}_\alpha$ at
${\bigoplus} _{\alpha \in I}\hat {\mathcal {E}}(\phi _\alpha )\otimes \hat {\mathcal {R}}_\alpha$ at ![]() $x$. For each
$x$. For each ![]() $\phi _\alpha$, by taking a lift locally around
$\phi _\alpha$, by taking a lift locally around ![]() $x$, we set
$x$, we set ![]() ${\mathcal {E}}(\phi _\alpha )$ to be a meromorphic connection
${\mathcal {E}}(\phi _\alpha )$ to be a meromorphic connection ![]() $({\mathcal {O}}(*Z), \nabla )$ defined by
$({\mathcal {O}}(*Z), \nabla )$ defined by ![]() $\nabla s:=\partial (\phi ) s$ for the generator
$\nabla s:=\partial (\phi ) s$ for the generator ![]() $s$. We also set
$s$. We also set ![]() ${\mathcal {R}}_\alpha$ to be a regular meromorphic connection defined locally around
${\mathcal {R}}_\alpha$ to be a regular meromorphic connection defined locally around ![]() $x$ corresponding to
$x$ corresponding to ![]() $\hat {{\mathcal {R}}}_\alpha$.
$\hat {{\mathcal {R}}}_\alpha$.
The following theorem is proved in [Reference MochizukiMoc11] and explained in [Reference SabbahSab13].
Theorem 5.5 [Reference SabbahSab13, Theorem 12.5], [Reference MochizukiMoc11, § 3]
There exists an open covering ![]() $\{U_i\}$ of a neighborhood of
$\{U_i\}$ of a neighborhood of ![]() $\varpi ^{-1}(x)$ such that each restriction
$\varpi ^{-1}(x)$ such that each restriction ![]() $(\varpi ^*{\mathcal {M}})|_{U_i}$ is isomorphic to
$(\varpi ^*{\mathcal {M}})|_{U_i}$ is isomorphic to ![]() $(\varpi ^*({\bigoplus} _{\alpha \in I}{\mathcal {E}}(\phi _\alpha )\otimes {\mathcal {R}}_\alpha ))|_{U_i}$.
$(\varpi ^*({\bigoplus} _{\alpha \in I}{\mathcal {E}}(\phi _\alpha )\otimes {\mathcal {R}}_\alpha ))|_{U_i}$.
5.2 Irregular constant sheaf  $\Lambda ^\phi$
$\Lambda ^\phi$
In this subsection, we prepare some preliminary lemmas concerning a class of modules.
Let ![]() ${(\bar {S}, D_S)}$ be a topological space with boundary. Let
${(\bar {S}, D_S)}$ be a topological space with boundary. Let ![]() $\phi$ be a
$\phi$ be a ![]() ${\mathbb {C}}$-valued continuous function over
${\mathbb {C}}$-valued continuous function over ![]() $S:=\bar {S}{\backslash } D_S$. We set
$S:=\bar {S}{\backslash } D_S$. We set
 \begin{equation} \begin{gathered} \operatorname{Gr}^a\Lambda^\phi_S:=p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi},\\ \Lambda^\phi_{S}:=\bigoplus_{a\in {\mathbb{R}}}p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi}, \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \operatorname{Gr}^a\Lambda^\phi_S:=p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi},\\ \Lambda^\phi_{S}:=\bigoplus_{a\in {\mathbb{R}}}p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi}, \end{gathered} \end{equation}
where ![]() $\mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi }$ is the constant sheaf supported on the set
$\mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi }$ is the constant sheaf supported on the set ![]() $\{(s, t)\in S\times {\mathbb {R}}\,|\, t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (s)\}$ and
$\{(s, t)\in S\times {\mathbb {R}}\,|\, t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (s)\}$ and ![]() $p\colon S\times {\mathbb {R}}\rightarrow S$ is the projection.
$p\colon S\times {\mathbb {R}}\rightarrow S$ is the projection.
Lemma 5.6 The sheaf ![]() $\Lambda ^\phi _{S}$ defines an object of
$\Lambda ^\phi _{S}$ defines an object of ![]() $\mathrm {Mod}^ {\mathbb {R}}(\Lambda _S)$. In particular, an object of
$\mathrm {Mod}^ {\mathbb {R}}(\Lambda _S)$. In particular, an object of ![]() $\Lambda ^\phi _{(\bar {S}, D_S)}:=[\Lambda ^\phi _S]\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.
$\Lambda ^\phi _{(\bar {S}, D_S)}:=[\Lambda ^\phi _S]\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.
Proof. Since the sheaf is globally presented as a direct sum, the restriction morphism preserves grading. The ![]() $\Lambda$-action is given as follows. For
$\Lambda$-action is given as follows. For ![]() $b\in \mathbb{R} _{\geqslant 0}$, we have a canonical morphism
$b\in \mathbb{R} _{\geqslant 0}$, we have a canonical morphism
This action gives the action of ![]() $T^b$.
$T^b$.
We would like to understand the structure of ![]() $\Lambda ^\phi _S$.
$\Lambda ^\phi _S$.
Lemma 5.7 Let ![]() $U$ be a connected open subset of
$U$ be a connected open subset of ![]() $S$ such that
$S$ such that ![]() $\phi |_U$ is bounded. Set
$\phi |_U$ is bounded. Set ![]() $b:=\inf _U {\mathop {\mathfrak {Re}}\nolimits } \phi$. Then
$b:=\inf _U {\mathop {\mathfrak {Re}}\nolimits } \phi$. Then ![]() $\Lambda ^\phi _S(U)\cong \Lambda \cdot T^b$.
$\Lambda ^\phi _S(U)\cong \Lambda \cdot T^b$.
Proof. Note that ![]() $\operatorname {Gr}^a\Lambda ^\phi _S(U)\cong \Gamma _{U\times [-a, \infty )}(U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. This is the kernel of the restriction morphism
$\operatorname {Gr}^a\Lambda ^\phi _S(U)\cong \Gamma _{U\times [-a, \infty )}(U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. This is the kernel of the restriction morphism ![]() $\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\rightarrow \Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. Since
$\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\rightarrow \Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. Since ![]() $U$ is connected, the set defined by
$U$ is connected, the set defined by ![]() $t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi$ is also connected. Hence we have
$t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi$ is also connected. Hence we have ![]() $\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong \mathbb {k}$. On the other hand,
$\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong \mathbb {k}$. On the other hand, ![]() $\Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong 0$ if and only if
$\Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong 0$ if and only if ![]() $U\times (-\infty , -a)\cap \{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi \}=\varnothing$. This is equivalent to
$U\times (-\infty , -a)\cap \{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi \}=\varnothing$. This is equivalent to ![]() $-a<\inf _U {\mathop {\mathfrak {Re}}\nolimits }\phi$. This completes the proof.
$-a<\inf _U {\mathop {\mathfrak {Re}}\nolimits }\phi$. This completes the proof.
For given ![]() $x\in S$, let us set
$x\in S$, let us set
 \begin{equation} \Lambda^{\phi(x)}:=\begin{cases} \mathop{{\displaystyle\bigoplus}}\limits_{{-}a\leqslant {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{if $x$ is a local minimum},\\ \mathop{{\displaystyle\bigoplus}}\limits_{{-}a< {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} \Lambda^{\phi(x)}:=\begin{cases} \mathop{{\displaystyle\bigoplus}}\limits_{{-}a\leqslant {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{if $x$ is a local minimum},\\ \mathop{{\displaystyle\bigoplus}}\limits_{{-}a< {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{otherwise}. \end{cases} \end{equation}
These are ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules with obvious gradings. Note that these are torsion-free
$\Lambda$-modules with obvious gradings. Note that these are torsion-free ![]() $\Lambda$-modules and the ring
$\Lambda$-modules and the ring ![]() $\Lambda$ has a valuation. Hence these modules are flat.
$\Lambda$ has a valuation. Hence these modules are flat.
From this lemma, the following is clear.
Corollary 5.8 For ![]() $x\in S$, the stalk
$x\in S$, the stalk ![]() $(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$.
$(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$.
Corollary 5.9 We have ![]() $\operatorname {Gr}^d\Lambda ^\phi _S\cong \mathbb {k}_{\mathrm {Int}\overline {\{ x| -d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$.
$\operatorname {Gr}^d\Lambda ^\phi _S\cong \mathbb {k}_{\mathrm {Int}\overline {\{ x| -d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$.
Proof. Let ![]() $x$ be a point with
$x$ be a point with ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)=-d$. The point
$ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)=-d$. The point ![]() $x$ is a local minimum if and only if
$x$ is a local minimum if and only if ![]() $x$ is in the interior of the closure of
$x$ is in the interior of the closure of ![]() $\{-x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}$. This completes the proof.
$\{-x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}$. This completes the proof.
Also, the module ![]() $\Lambda ^\phi _{(\bar {S}, D_S)}$ plays the role similar to the constant sheaves in the usual theory of sheaves. The following lemma explains this similarity.
$\Lambda ^\phi _{(\bar {S}, D_S)}$ plays the role similar to the constant sheaves in the usual theory of sheaves. The following lemma explains this similarity.
Lemma 5.10 The module ![]() $\Lambda ^\phi _{(\bar {S}, D_S)}$ is a flat object in
$\Lambda ^\phi _{(\bar {S}, D_S)}$ is a flat object in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{(\bar {S}, D_S)}})$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{(\bar {S}, D_S)}})$.
Proof. Let ![]() $ {\mathcal {V}}\rightarrow {\mathcal {W}}$ be an injective morphism in
$ {\mathcal {V}}\rightarrow {\mathcal {W}}$ be an injective morphism in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We would like to show the induced morphism
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We would like to show the induced morphism ![]() $ {\mathcal {V}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}\rightarrow {\mathcal {W}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}$ is again injective. There exists a covering
$ {\mathcal {V}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}\rightarrow {\mathcal {W}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}$ is again injective. There exists a covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $S$ which is locally finite in
$S$ which is locally finite in ![]() $\bar {S}$ such that there exist lifts
$\bar {S}$ such that there exist lifts ![]() $ {\mathcal {V}}_i, {\mathcal {W}}_i$ of
$ {\mathcal {V}}_i, {\mathcal {W}}_i$ of ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$ over each
${\mathcal {W}}$ over each ![]() $U_i$. It is enough to prove the injectivity over each
$U_i$. It is enough to prove the injectivity over each ![]() $U_i$.
$U_i$.
By Lemma 2.14, one can assume the restriction ![]() $ {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ is still injective. Since the tensor product commutes with taking stalks, it reduces to show that
$ {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ is still injective. Since the tensor product commutes with taking stalks, it reduces to show that ![]() $ {\mathcal {V}}_x\otimes (\Lambda ^\phi _S)_x\rightarrow {\mathcal {W}}_x\otimes (\Lambda ^\phi _S)_x$ is injective. Since
$ {\mathcal {V}}_x\otimes (\Lambda ^\phi _S)_x\rightarrow {\mathcal {W}}_x\otimes (\Lambda ^\phi _S)_x$ is injective. Since ![]() $(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$ (Corollary 5.8) is a torsion-free
$(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$ (Corollary 5.8) is a torsion-free ![]() $\Lambda$-module, this completes the proof.
$\Lambda$-module, this completes the proof.
Lemma 5.11 Let ![]() $\phi _1$ and
$\phi _1$ and ![]() $\phi _2$ be
$\phi _2$ be ![]() ${\mathbb {C}}$-valued continuous functions over connected
${\mathbb {C}}$-valued continuous functions over connected ![]() $S$ such that
$S$ such that ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded from above. Then there exists a canonical identification
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded from above. Then there exists a canonical identification
If moreover ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded, the two objects are isomorphic.
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded, the two objects are isomorphic.
Proof. Since ![]() $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2\}$ is bounded, there exists a large
$\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2\}$ is bounded, there exists a large ![]() $c\in {\mathbb {R}}$ such that
$c\in {\mathbb {R}}$ such that ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1$. The nonzero map
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1$. The nonzero map ![]() $\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t}\rightarrow \mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _{2}+c\geqslant t}$ coming from the inclusion
$\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t}\rightarrow \mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _{2}+c\geqslant t}$ coming from the inclusion ![]() $\{ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant t\}\subset \{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t\}$ induces a morphism
$\{ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant t\}\subset \{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t\}$ induces a morphism ![]() $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S\langle c\rangle $ of
$\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S\langle c\rangle $ of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _S$-modules. If
$\Lambda _S$-modules. If ![]() $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1\}$ is also bounded, in the same way, we also have a morphism
$\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1\}$ is also bounded, in the same way, we also have a morphism ![]() $\Lambda ^{\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\langle d\rangle $ for some
$\Lambda ^{\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\langle d\rangle $ for some ![]() $d\geqslant 0$. The composition
$d\geqslant 0$. The composition ![]() $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _1}_S\langle c+d\rangle $ is given by
$\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _1}_S\langle c+d\rangle $ is given by ![]() $T^{c+d}$. This is the identity of
$T^{c+d}$. This is the identity of ![]() $\Lambda ^\phi _{(\bar {S}, D_S)}$ in
$\Lambda ^\phi _{(\bar {S}, D_S)}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The same for the other direction. This completes the proof of the second part of the statement. We call morphism
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The same for the other direction. This completes the proof of the second part of the statement. We call morphism ![]() $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S$ of this kind as well as their scalar multiples standard morphisms. In the below, we will see there are only standard morphisms.
$\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S$ of this kind as well as their scalar multiples standard morphisms. In the below, we will see there are only standard morphisms.
Let ![]() $f$ be a nonzero morphism in
$f$ be a nonzero morphism in ![]() $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})$. Let us take a lift
$\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})$. Let us take a lift ![]() $\tilde {f}\colon \Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2+c}_S$ as a morphism of
$\tilde {f}\colon \Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2+c}_S$ as a morphism of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules locally on
$\Lambda$-modules locally on ![]() $U\subset S$. We can take
$U\subset S$. We can take ![]() $c$ such that
$c$ such that ![]() $c+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2> {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ and replace
$c+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2> {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ and replace ![]() $\phi _2$ with
$\phi _2$ with ![]() $\phi _2+c$ We consider
$\phi _2+c$ We consider ![]() $d\in {\mathbb {R}}$ such that the grading
$d\in {\mathbb {R}}$ such that the grading ![]() $d$-part of
$d$-part of ![]() $\tilde {f}$ is nonzero. To see this part more explicitly, let us prepare some notation.
$\tilde {f}$ is nonzero. To see this part more explicitly, let us prepare some notation.
Let us set ![]() $\mathrm {Int}\overline {\{ x\in U\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}=\sqcup _a S_{d,i}^a$ to be the decomposition into connected components. Since
$\mathrm {Int}\overline {\{ x\in U\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}=\sqcup _a S_{d,i}^a$ to be the decomposition into connected components. Since ![]() $\operatorname {Gr}^d\Lambda _U^\phi =\mathbb {k}_{\mathrm {Int}\overline {\{ x|-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$, we have
$\operatorname {Gr}^d\Lambda _U^\phi =\mathbb {k}_{\mathrm {Int}\overline {\{ x|-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$, we have ![]() $\operatorname {Gr}^d\Lambda _U^{\phi _i}={\bigoplus} _{a}\mathbb {k}_{S^a_{d,i}}$. We have
$\operatorname {Gr}^d\Lambda _U^{\phi _i}={\bigoplus} _{a}\mathbb {k}_{S^a_{d,i}}$. We have
There exists ![]() $d'\in \mathbb{R} _{\geqslant 0}$ such that there exists a connected component
$d'\in \mathbb{R} _{\geqslant 0}$ such that there exists a connected component ![]() $S_i$ of
$S_i$ of ![]() $\mathrm {Int}\overline {\{ x\,|\,-d'< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$ for each
$\mathrm {Int}\overline {\{ x\,|\,-d'< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$ for each ![]() $i$ such that
$i$ such that ![]() $S_i\supset \mathrm {Int}\overline {\{ x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$. Then we have a commutative diagram.
$S_i\supset \mathrm {Int}\overline {\{ x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$. Then we have a commutative diagram.

Since ![]() $S_1$ and
$S_1$ and ![]() $S_2$ are connected, the hom-space between them is one-dimensional. Hence
$S_2$ are connected, the hom-space between them is one-dimensional. Hence ![]() $\tilde {f}_d$ is induced by a standard morphism. This completes the proof.
$\tilde {f}_d$ is induced by a standard morphism. This completes the proof.
We prepare the following crucial lemma. The corresponding observation in the theory of enhanced ind-sheaves is a key to the formulation of irregular Riemann–Hilbert correspondence [Reference D'Agnolo and KashiwaraDK16].
Lemma 5.12 Let ![]() ${(\bar {S}, D_S)}$ be a topological space with boundary with
${(\bar {S}, D_S)}$ be a topological space with boundary with ![]() $S$ connected. Let
$S$ connected. Let ![]() $\phi _1, \phi _2$ be
$\phi _1, \phi _2$ be ![]() ${\mathbb {C}}$-valued continuous functions on
${\mathbb {C}}$-valued continuous functions on ![]() $S$. Assume that there exists an open subset
$S$. Assume that there exists an open subset ![]() $V$ of
$V$ of ![]() $S$ such that
$S$ such that ![]() $\bar {V}\cap D_S$ is nonempty and
$\bar {V}\cap D_S$ is nonempty and ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is divergent to
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is divergent to ![]() $-\infty$ on
$-\infty$ on ![]() $\bar {V}\cap D_S$. Then there exists no nonzero morphisms from
$\bar {V}\cap D_S$. Then there exists no nonzero morphisms from ![]() $\Lambda _{(\bar {S}, D_S)}^{\phi _1}$ to
$\Lambda _{(\bar {S}, D_S)}^{\phi _1}$ to ![]() $\Lambda _{(\bar {S}, D_S)}^{\phi _2}$.
$\Lambda _{(\bar {S}, D_S)}^{\phi _2}$.
Proof. For ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda _{(\bar {S}, D_S)}^{\phi _1}, \Lambda _{(\bar {S}, D_S)}^{\phi _2})$, let us take a lift
$f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda _{(\bar {S}, D_S)}^{\phi _1}, \Lambda _{(\bar {S}, D_S)}^{\phi _2})$, let us take a lift ![]() $\tilde {f}\colon \Lambda _{(\bar {S}, D_S)}^{\phi _1}\rightarrow \Lambda _{(\bar {S}, D_S)}^{\phi _2+c}$ as a morphism between
$\tilde {f}\colon \Lambda _{(\bar {S}, D_S)}^{\phi _1}\rightarrow \Lambda _{(\bar {S}, D_S)}^{\phi _2+c}$ as a morphism between ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _S$-modules. Since
$\Lambda _S$-modules. Since ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negatively divergent, there exists a neighborhood
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negatively divergent, there exists a neighborhood ![]() $U$ of
$U$ of ![]() $D_S$ such that
$D_S$ such that ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negative on
$ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negative on ![]() $U{\backslash } D_S$. Hence over
$U{\backslash } D_S$. Hence over ![]() $U{\backslash } D_S$, the restriction of
$U{\backslash } D_S$, the restriction of ![]() $\tilde {f}$ is zero there. By Lemma 5.11 and the connectedness of
$\tilde {f}$ is zero there. By Lemma 5.11 and the connectedness of ![]() $S$,
$S$, ![]() $f$ is zero everywhere.
$f$ is zero everywhere.
We also give the following.
Lemma 5.13 For ![]() $\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$
$\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ ![]() $(i=1,2)$, we have
$(i=1,2)$, we have ![]() $\Lambda ^{\phi _1}_{(\bar {S}, D_S)}\otimes \Lambda ^{\phi _2}_{(\bar {S}, D_S)}\cong \Lambda ^{\phi _1+\phi _2}_{(\bar {S}, D_S)}$. In particular,
$\Lambda ^{\phi _1}_{(\bar {S}, D_S)}\otimes \Lambda ^{\phi _2}_{(\bar {S}, D_S)}\cong \Lambda ^{\phi _1+\phi _2}_{(\bar {S}, D_S)}$. In particular, ![]() $\Lambda ^\phi _{(\bar {S}, D_S)}\otimes \Lambda ^{-\phi }_{(\bar {S}, D_S)}\cong \Lambda _{(\bar {S}, D_S)}$.
$\Lambda ^\phi _{(\bar {S}, D_S)}\otimes \Lambda ^{-\phi }_{(\bar {S}, D_S)}\cong \Lambda _{(\bar {S}, D_S)}$.
Proof. We have ![]() $\operatorname {Gr}^a\Lambda _S^{\phi _i}=\mathbb {k}_{\{ x| {\mathop {\mathfrak {Re}}\nolimits }\phi (x)>-a\}}$ for
$\operatorname {Gr}^a\Lambda _S^{\phi _i}=\mathbb {k}_{\{ x| {\mathop {\mathfrak {Re}}\nolimits }\phi (x)>-a\}}$ for ![]() $i=1,2$. Hence we have a map
$i=1,2$. Hence we have a map ![]() $\operatorname {Gr}^a\Lambda ^{\phi _1+\phi _2}_S\rightarrow \operatorname {Gr}^b\Lambda ^{\phi _1}_S\otimes _k\operatorname {Gr}^c\Lambda ^{\phi _2}_S$ for
$\operatorname {Gr}^a\Lambda ^{\phi _1+\phi _2}_S\rightarrow \operatorname {Gr}^b\Lambda ^{\phi _1}_S\otimes _k\operatorname {Gr}^c\Lambda ^{\phi _2}_S$ for ![]() $a=b+c$. Hence we get a map
$a=b+c$. Hence we get a map ![]() $m\colon \Lambda ^{\phi _1+\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\otimes \Lambda ^{\phi _2}_S$. By Corollary 5.8, the stalks of both sides at
$m\colon \Lambda ^{\phi _1+\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\otimes \Lambda ^{\phi _2}_S$. By Corollary 5.8, the stalks of both sides at ![]() $x\in X$ are
$x\in X$ are ![]() ${\bigoplus} _{-a\leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$ or
${\bigoplus} _{-a\leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$ or ![]() ${\bigoplus} _{-a< {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$. Hence the kernel and cokernel of
${\bigoplus} _{-a< {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$. Hence the kernel and cokernel of ![]() $m$ vanishes by multiplying
$m$ vanishes by multiplying ![]() $T^a$ for any
$T^a$ for any ![]() $a\in {\mathbb {R}}_{>0}$. Therefore the kernel and cokernel are zero in
$a\in {\mathbb {R}}_{>0}$. Therefore the kernel and cokernel are zero in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. This completes the proof.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. This completes the proof.
Similarly, we have
Lemma 5.14 For ![]() $\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$
$\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ ![]() $(i=1,2)$, we have
$(i=1,2)$, we have
Proof. One can prove in a similar way as in the proof of Lemma 5.13.
The following will be repeatedly used later.
Corollary 5.15 We have ![]() ${\mathbb{R} \mathcal{H} om}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})\simeq \Lambda ^{\phi _2-\phi _1}_{(\bar {S}, D_S)}$.
${\mathbb{R} \mathcal{H} om}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})\simeq \Lambda ^{\phi _2-\phi _1}_{(\bar {S}, D_S)}$.
Proof. Let ![]() ${\mathcal {I}}$ be an injective resolution of
${\mathcal {I}}$ be an injective resolution of ![]() $\Lambda ^{\phi _2}_{(\bar {S}, D_S)}$. We have the following:
$\Lambda ^{\phi _2}_{(\bar {S}, D_S)}$. We have the following:
 \begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\mathop{{{\mathcal{H}}}om}\nolimits(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})). \end{align}
\begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\mathop{{{\mathcal{H}}}om}\nolimits(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})). \end{align}
Here we used flatness of ![]() $\Lambda ^{\phi _1}_{(\bar {S}, D_S)}$.
$\Lambda ^{\phi _1}_{(\bar {S}, D_S)}$.
First, note that ![]() $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})\cong \Lambda ^{-\phi _1}_{(\bar {S}, D_S)}\otimes {\mathcal {I}}$ in
$\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})\cong \Lambda ^{-\phi _1}_{(\bar {S}, D_S)}\otimes {\mathcal {I}}$ in ![]() $C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)}))$. Second,
$C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)}))$. Second, ![]() ${\mathcal {I}}$ is locally given by
${\mathcal {I}}$ is locally given by ![]() $[\prod _x {\mathcal {F}}_x]$ where
$[\prod _x {\mathcal {F}}_x]$ where ![]() ${\mathcal {F}}_x$ is a skyscraper sheaf. Since
${\mathcal {F}}_x$ is a skyscraper sheaf. Since ![]() $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \prod _x{\mathcal {F}}_x)\cong \prod _x\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {F}}_x)$, the object
$\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \prod _x{\mathcal {F}}_x)\cong \prod _x\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {F}}_x)$, the object ![]() $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})$ is also injective. Hence we have
$\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})$ is also injective. Hence we have
 \begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}\Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{\phi_2-\phi_1}_{(\bar{S}, D_S)}). \end{align}
\begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}\Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{\phi_2-\phi_1}_{(\bar{S}, D_S)}). \end{align}This completes the proof.
5.3 Irregular local systems
Let ![]() $V$ be a neighborhood of
$V$ be a neighborhood of ![]() $0\in {\mathbb {C}}^n$ and consider a simple normal crossing
$0\in {\mathbb {C}}^n$ and consider a simple normal crossing ![]() $D_I={\bigcup} _{i\in I}\{z_i=0\}\cap V$. For
$D_I={\bigcup} _{i\in I}\{z_i=0\}\cap V$. For ![]() $A:=\{a_i\}\in {\mathbb {Z}}^{I}$,
$A:=\{a_i\}\in {\mathbb {Z}}^{I}$, ![]() $\Phi _A\colon {\mathbb {C}}^n\rightarrow {\mathbb {C}}^n$ is defined by
$\Phi _A\colon {\mathbb {C}}^n\rightarrow {\mathbb {C}}^n$ is defined by ![]() $(z_1^{a_1},\ldots , z_n^{a_n})$ where
$(z_1^{a_1},\ldots , z_n^{a_n})$ where ![]() $a_i=0$ for
$a_i=0$ for ![]() $i\not \in I$.
$i\not \in I$.
(i) A correspondence
 $f\colon V{\backslash } D_I\rightarrow {\mathbb {C}}$ is a multi-valued meromorphic function if there exists
$f\colon V{\backslash } D_I\rightarrow {\mathbb {C}}$ is a multi-valued meromorphic function if there exists  $A:=\{a_i\}\in {\mathbb {Z}}^{I}$ and a meromorphic function
$A:=\{a_i\}\in {\mathbb {Z}}^{I}$ and a meromorphic function  $f'$ on
$f'$ on  $\Phi _A^{-1}(V)$ with poles in
$\Phi _A^{-1}(V)$ with poles in  $\Phi _A^{-1}(D_I)$ such that
$\Phi _A^{-1}(D_I)$ such that  $f$ is equal to
$f$ is equal to  $z\mapsto \{ f'(z') \,|\, z'\in (\Phi _A)^{-1}(z)\}$.
$z\mapsto \{ f'(z') \,|\, z'\in (\Phi _A)^{-1}(z)\}$.(ii) A finite set of multi-valued meromorphic function is said to be good, if it satisfies the conditions in Definition 5.2 after taking the pull-backs along
 $\Phi _A$.
$\Phi _A$.
For a multi-valued meromorphic function ![]() $\phi$ and an open subset
$\phi$ and an open subset ![]() $U$ on which
$U$ on which ![]() $\phi$ is represented by a set of single-valued holomorphic functions
$\phi$ is represented by a set of single-valued holomorphic functions ![]() $\{\phi _k\}_{k\in K}$, we set
$\{\phi _k\}_{k\in K}$, we set ![]() $\Lambda ^\phi :={\bigoplus} _{k\in K}\Lambda ^{\phi _k}$.
$\Lambda ^\phi :={\bigoplus} _{k\in K}\Lambda ^{\phi _k}$.
For ![]() $S$ a locally closed complex submanifold
$S$ a locally closed complex submanifold ![]() $X$, consider
$X$, consider ![]() $(\bar {S}, D_S:=\bar {S}{\backslash } S)$ as a topological space with boundary.
$(\bar {S}, D_S:=\bar {S}{\backslash } S)$ as a topological space with boundary.
Definition 5.17 Let ![]() $ {\mathcal {V}}$ be an object of
$ {\mathcal {V}}$ be an object of ![]() $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We call
$\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We call ![]() $ {\mathcal {V}}$ a good irregular local system if the following hold.
$ {\mathcal {V}}$ a good irregular local system if the following hold.
(i) The boundary
 $D_S$ is normal crossing.
$D_S$ is normal crossing.(ii) For any point
 $x\in D_S$, there exists a neighborhood
$x\in D_S$, there exists a neighborhood  $U$ of
$U$ of  $x$ such that the restriction
$x$ such that the restriction  $ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf
$ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf  $\Lambda _U$.
$\Lambda _U$.(iii) For any point
 $x\in \bar {S}{\backslash } S$, there exist:
$x\in \bar {S}{\backslash } S$, there exist:
(a) a neighborhood
 $U$ of
$U$ of  $x$;
$x$;(b) a finite good set of multi-valued meromorphic functions
 $\{\phi _j\}_{j\in J}$ over
$\{\phi _j\}_{j\in J}$ over  $U$ with poles in
$U$ with poles in  $D_S$; and
$D_S$; and(c) a finite cover
 $\{U_k\}_{k\in K}$ of
$\{U_k\}_{k\in K}$ of  $U{\backslash } U\cap D_S$
$U{\backslash } U\cap D_S$
such that we have both the following.
• There exists an open covering
 $\{U_k'\}_{k\in K}$ of the real blow-up of
$\{U_k'\}_{k\in K}$ of the real blow-up of  $U$ along
$U$ along  $D_S$ (in the sense of [Reference D'Agnolo and KashiwaraDK16]) with
$D_S$ (in the sense of [Reference D'Agnolo and KashiwaraDK16]) with  $U_k=U_k'\cap (U{\backslash } D_S)$.
$U_k=U_k'\cap (U{\backslash } D_S)$.• Each restriction of
 $ {\mathcal {V}}|_{U_k}:= {\mathcal {V}}|_{(\overline {U_k}, \overline {U_k}\cap D_S)}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}^{-1} {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D_S)})$ is isomorphic to the finite direct sum
$ {\mathcal {V}}|_{U_k}:= {\mathcal {V}}|_{(\overline {U_k}, \overline {U_k}\cap D_S)}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}^{-1} {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D_S)})$ is isomorphic to the finite direct sum  ${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D_S)}$. Here
${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D_S)}$. Here  $\overline {U_k}$ means
$\overline {U_k}$ means  $U_k\cup (D_S\cap \overline {U_k})$ and
$U_k\cup (D_S\cap \overline {U_k})$ and  $\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}$ is the canonical map induced by the inclusion
$\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}$ is the canonical map induced by the inclusion  $\overline {U_k}\hookrightarrow \bar {S}$.
$\overline {U_k}\hookrightarrow \bar {S}$.
If the set of multi-valued functions is actually the set of meromorphic functions, we call it a unramified good irregular local system.
Lemma 5.18 Definition 5.17(iii) is equivalent to the following. For any point ![]() $x\in \bar {S}{\backslash } S$, there exist:
$x\in \bar {S}{\backslash } S$, there exist:
(a) a neighborhood
 $U$ of
$U$ of  $x=:0$ (with the notation used in Definition 5.16);
$x=:0$ (with the notation used in Definition 5.16);(b)
 $A:=\{a_i\}\in {\mathbb {Z}}^{I}$;
$A:=\{a_i\}\in {\mathbb {Z}}^{I}$;(c) a finite set of meromorphic functions
 $\{\phi _j\}_{j\in J}$ over
$\{\phi _j\}_{j\in J}$ over  $U':=\Phi _A^{-1}(U)$ with poles in
$U':=\Phi _A^{-1}(U)$ with poles in  $D':=\Phi _A^{-1}(D_I)$; and
$D':=\Phi _A^{-1}(D_I)$; and(d) a finite cover
 $\{U_k\}_{k\in K}$ of
$\{U_k\}_{k\in K}$ of  $U'{\backslash } U'\cap D'$
$U'{\backslash } U'\cap D'$
such that we have both the following.
• There exists an open covering
 $\{U_k'\}_{k\in K}$ of the real blow-up of
$\{U_k'\}_{k\in K}$ of the real blow-up of  $U$ along
$U$ along  $D'$ with
$D'$ with  $U_k=U_k'\cap (U{\backslash } D')$.
$U_k=U_k'\cap (U{\backslash } D')$.• Each restriction of
 $(\Phi _A^* {\mathcal {V}})|_{(\overline {U_k}, \overline {U_k}\cap D')}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D')}^{-1}(\Phi _A^* {\mathcal {V}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D')})$ is isomorphic to the finite direct sum
$(\Phi _A^* {\mathcal {V}})|_{(\overline {U_k}, \overline {U_k}\cap D')}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D')}^{-1}(\Phi _A^* {\mathcal {V}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D')})$ is isomorphic to the finite direct sum  ${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D')}$. Here
${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D')}$. Here  $\iota _{(\overline {U_k}, \overline {U_k}\cap D')}$ is the canonical map induced by the inclusion
$\iota _{(\overline {U_k}, \overline {U_k}\cap D')}$ is the canonical map induced by the inclusion  $\overline {U_k}\hookrightarrow \bar {S}$.
$\overline {U_k}\hookrightarrow \bar {S}$.
Proof. This is just from the definition of multi-valued meromorphic functions.
Definition 5.19 For a complex manifold ![]() $U$ with a divisor
$U$ with a divisor ![]() $D$, a modification of
$D$, a modification of ![]() $(U, D)$ is a morphism
$(U, D)$ is a morphism ![]() $f\colon ({U'}, D')\rightarrow (U, D)$ where
$f\colon ({U'}, D')\rightarrow (U, D)$ where ![]() $({U'}, D')$ is another complex manifold with a divisor and
$({U'}, D')$ is another complex manifold with a divisor and ![]() $f$ is a projective map between
$f$ is a projective map between ![]() ${U'}$ and
${U'}$ and ![]() $U$ preserving divisors and induces the identity map between
$U$ preserving divisors and induces the identity map between ![]() $U{\backslash } D$ and
$U{\backslash } D$ and ![]() ${U'}{\backslash } D'$.
${U'}{\backslash } D'$.
Definition 5.20 An object ![]() $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ is said to be an irregular local system if the following hold.
$ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ is said to be an irregular local system if the following hold.
(i) For any point
 $x\in S$, there exists a neighborhood
$x\in S$, there exists a neighborhood  $U$ of
$U$ of  $x$ such that the restriction
$x$ such that the restriction  $ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf
$ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf  $\Lambda _U$.
$\Lambda _U$.(ii) For any point
 $x\in D_S$, there exists a neighborhood
$x\in D_S$, there exists a neighborhood  $U$ of
$U$ of  $x$ and a modification
$x$ and a modification  $p\colon (U',D') \rightarrow ({U}, D_S\cap U)$ such that
$p\colon (U',D') \rightarrow ({U}, D_S\cap U)$ such that  $p^{-1}( {\mathcal {V}}|_{(U,D_S\cap U)})$ is a good irregular local system.
$p^{-1}( {\mathcal {V}}|_{(U,D_S\cap U)})$ is a good irregular local system.
Let ![]() $ {\mathcal {V}}$ be an irregular local system on
$ {\mathcal {V}}$ be an irregular local system on ![]() ${(\bar {S}, D_S)}$. Take a point
${(\bar {S}, D_S)}$. Take a point ![]() $x\in D_S$. Then by the definition of irregular local systems, there exists a relatively compact open neighborhood
$x\in D_S$. Then by the definition of irregular local systems, there exists a relatively compact open neighborhood ![]() $U$ of
$U$ of ![]() $x$ with a modification
$x$ with a modification ![]() $p\colon U'\rightarrow U$ such that for any
$p\colon U'\rightarrow U$ such that for any ![]() $y\in p^{-1}(D_S)=:D'$, there exists a finite cover
$y\in p^{-1}(D_S)=:D'$, there exists a finite cover ![]() $\{U_k\}_k$ of
$\{U_k\}_k$ of ![]() $U'{\backslash } D'$ given in the definition of good irregular local systems. We have
$U'{\backslash } D'$ given in the definition of good irregular local systems. We have ![]() $ {\mathcal {V}}|_{U_k}\cong {\bigoplus} _i\Lambda ^{\phi _i}_{(\overline {U_k}, \overline {U_k}\cap D')}$.
$ {\mathcal {V}}|_{U_k}\cong {\bigoplus} _i\Lambda ^{\phi _i}_{(\overline {U_k}, \overline {U_k}\cap D')}$.
Since ![]() $U'{\backslash } D'\cong U{\backslash } D_S$. we get a finite covering
$U'{\backslash } D'\cong U{\backslash } D_S$. we get a finite covering ![]() ${\mathcal {U}}$ of
${\mathcal {U}}$ of ![]() $U{\backslash } D_S$ such that
$U{\backslash } D_S$ such that ![]() $ {\mathcal {V}}|_{{\bar {U}}, D_S\cap {\bar {U}}}$ is isomorphic to a direct sum of irregular constant sheaves for each
$ {\mathcal {V}}|_{{\bar {U}}, D_S\cap {\bar {U}}}$ is isomorphic to a direct sum of irregular constant sheaves for each ![]() $U\in {\mathcal {U}}$.
$U\in {\mathcal {U}}$.
Definition 5.21 We call a finite covering ![]() ${\mathcal {U}}$ of
${\mathcal {U}}$ of ![]() $U{\backslash } D_S$ given above a sectorial covering for
$U{\backslash } D_S$ given above a sectorial covering for ![]() $ {\mathcal {V}}$ around
$ {\mathcal {V}}$ around ![]() $x$.
$x$.
Lemma 5.22 For ![]() $ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ and
$ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ and ![]() $x\in D_S$, there exists a neighborhood
$x\in D_S$, there exists a neighborhood ![]() $U$ of
$U$ of ![]() $x$ with a modification
$x$ with a modification ![]() $(U',D')\rightarrow (U, D)$ such that
$(U',D')\rightarrow (U, D)$ such that ![]() $p^{-1}( {\mathcal {V}}|_{(U, U\cap D_S)})$ and
$p^{-1}( {\mathcal {V}}|_{(U, U\cap D_S)})$ and ![]() $p^{-1}({\mathcal {W}}|_{(U, U\cap D_S)})$ are irregular local systems. In particular,
$p^{-1}({\mathcal {W}}|_{(U, U\cap D_S)})$ are irregular local systems. In particular, ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$ have a common sectorial covering.
${\mathcal {W}}$ have a common sectorial covering.
Proof. This is standard.
Next we would like to define one of the fundamental objects in this paper.
Definition 5.23 Let ![]() $ {\mathcal {V}}$ be an object of
$ {\mathcal {V}}$ be an object of ![]() $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)$. We say
$\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)$. We say ![]() $ {\mathcal {V}}$ is irregular constructible if the following hold. There exists a
$ {\mathcal {V}}$ is irregular constructible if the following hold. There exists a ![]() ${\mathbb {C}}$-analytic stratification
${\mathbb {C}}$-analytic stratification ![]() ${\mathcal {S}}$ of
${\mathcal {S}}$ of ![]() $X$ such that the restriction
$X$ such that the restriction ![]() $ {\mathcal {V}}|_{(\bar {S}, D_S:=\bar {S}{\backslash } S)}$ to each stratum
$ {\mathcal {V}}|_{(\bar {S}, D_S:=\bar {S}{\backslash } S)}$ to each stratum ![]() $S\in {\mathcal {S}}$ is an irregular local system as an object of
$S\in {\mathcal {S}}$ is an irregular local system as an object of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.
It is clear that the definition remains valid after refining the stratification. Let us denote the full subcategory of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ spanned by irregular constructible sheaves by
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ spanned by irregular constructible sheaves by ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$.
$\mathrm {Mod}_{ic}(\Lambda _X)$.
Proposition 5.24 The category ![]() $\mathrm {Mod}_{ic}({\Lambda _X})$ is abelian.
$\mathrm {Mod}_{ic}({\Lambda _X})$ is abelian.
Remark 5.25 This statement is a little bit interesting since the category of filtered vectors spaces is not abelian (see Remark 2.4).
Proof Proof of Proposition 5.24
Since ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian, it suffices to show kernels, cokernels, images, and coimages of morphisms between irregular constructible sheaves are also irregular constructible sheaves. Let
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian, it suffices to show kernels, cokernels, images, and coimages of morphisms between irregular constructible sheaves are also irregular constructible sheaves. Let ![]() $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism between irregular constructible sheaves. One can take a common
$f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism between irregular constructible sheaves. One can take a common ![]() ${\mathbb {C}}$-Whitney stratification for
${\mathbb {C}}$-Whitney stratification for ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$. Then it suffices to show Lemma 5.26 below.
${\mathcal {W}}$. Then it suffices to show Lemma 5.26 below.
Lemma 5.26 Kernels, cokernels, images, coimages of morphisms between irregular local systems are irregular local systems.
To prove Lemma 5.26, we prepare some notions and lemmas.
Definition 5.27 Let ![]() $\phi _i$ (
$\phi _i$ (![]() $i=1,2$) be meromorphic functions over
$i=1,2$) be meromorphic functions over ![]() $U$ with poles in
$U$ with poles in ![]() $D$. We say
$D$. We say ![]() $\phi _1$ and
$\phi _1$ and ![]() $\phi _2$ are equivalent if there exists a bounded holomorphic function
$\phi _2$ are equivalent if there exists a bounded holomorphic function ![]() $\phi$ over
$\phi$ over ![]() $U$ such that
$U$ such that ![]() $\phi _1=\phi _2+\phi$. We denote the set of meromorphic functions over
$\phi _1=\phi _2+\phi$. We denote the set of meromorphic functions over ![]() $(U, D)$ modulo this equivalence relation by
$(U, D)$ modulo this equivalence relation by ![]() $\mathrm {M}(U,D)$.
$\mathrm {M}(U,D)$.
Recall that ![]() $\Lambda ^{\phi _1}_{(U,D)}$ and
$\Lambda ^{\phi _1}_{(U,D)}$ and ![]() $\Lambda ^{\phi _2}_{(U, D)}$ are canonically isomorphic for
$\Lambda ^{\phi _2}_{(U, D)}$ are canonically isomorphic for ![]() $\phi _1=\phi _2\in M(U, D)$ by Lemma 5.11.
$\phi _1=\phi _2\in M(U, D)$ by Lemma 5.11.
Proof Proof of Lemma 5.26
Let ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$ be irregular local systems over
${\mathcal {W}}$ be irregular local systems over ![]() $(U,D)$. Since the definition of irregular local systems is local, we can consider locally on a open subset
$(U,D)$. Since the definition of irregular local systems is local, we can consider locally on a open subset ![]() $U$. There exists a modification
$U$. There exists a modification ![]() $p\colon (U', D')\rightarrow (U, D)$ such that
$p\colon (U', D')\rightarrow (U, D)$ such that ![]() $p^{-1} {\mathcal {V}}$ and
$p^{-1} {\mathcal {V}}$ and ![]() $p^{-1}{\mathcal {W}}$ are both good irregular local systems by Lemma 5.22.
$p^{-1}{\mathcal {W}}$ are both good irregular local systems by Lemma 5.22.
A morphism ![]() $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ induces a morphism over
$f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ induces a morphism over ![]() $U$ and we pull-back
$U$ and we pull-back ![]() $f$ by
$f$ by ![]() $p$. Then by the exactness of the pull-back, kernel cokernel, image, coimage (we denote those by
$p$. Then by the exactness of the pull-back, kernel cokernel, image, coimage (we denote those by ![]() $A$) of
$A$) of ![]() $p^{-1}f$ are pull-backs of those for
$p^{-1}f$ are pull-backs of those for ![]() $f$ i.e.
$f$ i.e. ![]() $p^{-1}A(f)\cong A(p^{-1}f)$.
$p^{-1}A(f)\cong A(p^{-1}f)$.
Furthermore, we can pull-back more by a covering map ![]() $\Phi _A$ to make
$\Phi _A$ to make ![]() $p^{-1} {\mathcal {V}}$ and
$p^{-1} {\mathcal {V}}$ and ![]() $p^{-1}{\mathcal {W}}$ unramified irregular local systems. Then again,
$p^{-1}{\mathcal {W}}$ unramified irregular local systems. Then again, ![]() $\Phi _A^{-1}p^{-1}A(f)\cong A(\Phi _A^{-1}\circ p^{-1}f)$. It suffices to show that this is an irregular local system.
$\Phi _A^{-1}p^{-1}A(f)\cong A(\Phi _A^{-1}\circ p^{-1}f)$. It suffices to show that this is an irregular local system.
So we reset the notation. Let ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$ be unramified good irregular local systems and
${\mathcal {W}}$ be unramified good irregular local systems and ![]() $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism. Then there exist sets of meromorphic functions
$f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism. Then there exist sets of meromorphic functions ![]() $\Phi _ {\mathcal {V}}$ and
$\Phi _ {\mathcal {V}}$ and ![]() $\Phi _{\mathcal {W}}$ over
$\Phi _{\mathcal {W}}$ over ![]() $(U, D)$ which are appeared in the definition of irregular local system.
$(U, D)$ which are appeared in the definition of irregular local system.
Take a point ![]() $x\in D$, a neighborhood
$x\in D$, a neighborhood ![]() $U$ of
$U$ of ![]() $x$, and a sectorial covering
$x$, and a sectorial covering ![]() ${\mathcal {U}}$ of
${\mathcal {U}}$ of ![]() $U{\backslash } D$ for
$U{\backslash } D$ for ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$. On each
${\mathcal {W}}$. On each ![]() $U\in {\mathcal {U}}$, we have isomorphisms
$U\in {\mathcal {U}}$, we have isomorphisms ![]() $ {\mathcal {V}}|_U\cong {\bigoplus} _{\phi \in \Phi _ {\mathcal {V}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi$ and
$ {\mathcal {V}}|_U\cong {\bigoplus} _{\phi \in \Phi _ {\mathcal {V}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi$ and ![]() ${\mathcal {W}}|_U\cong {\bigoplus} _{\psi \in \Phi _{\mathcal {W}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\psi$.
${\mathcal {W}}|_U\cong {\bigoplus} _{\psi \in \Phi _{\mathcal {W}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\psi$.
Suppose the following: there exists a sector ![]() $U\in {\mathcal {U}}$ such that the restriction of
$U\in {\mathcal {U}}$ such that the restriction of ![]() $f$ to the component
$f$ to the component ![]() $\Lambda ^{\phi }_{(\bar {U}, \bar {U}\cap D)}\rightarrow \Lambda ^\psi _{(\bar {U}, \bar {U}\cap D)}$ is nonzero where
$\Lambda ^{\phi }_{(\bar {U}, \bar {U}\cap D)}\rightarrow \Lambda ^\psi _{(\bar {U}, \bar {U}\cap D)}$ is nonzero where ![]() $\phi \in \Phi _ {\mathcal {V}}, \psi \in \Phi _{\mathcal {W}}$ with
$\phi \in \Phi _ {\mathcal {V}}, \psi \in \Phi _{\mathcal {W}}$ with ![]() $\phi \neq \psi$.
$\phi \neq \psi$.
Let ![]() $U'$ be the adjacent sector of
$U'$ be the adjacent sector of ![]() $U$. Then the restriction of
$U$. Then the restriction of ![]() $f$ to
$f$ to ![]() $\Lambda ^{\phi }_{(\overline {U'}, \overline {U'}\cap D)}\rightarrow \Lambda ^\psi _{(\overline {U'}, \overline {U'}\cap D)}$ is nonzero again. This implies
$\Lambda ^{\phi }_{(\overline {U'}, \overline {U'}\cap D)}\rightarrow \Lambda ^\psi _{(\overline {U'}, \overline {U'}\cap D)}$ is nonzero again. This implies ![]() $\max \{ {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\psi \}$ is bounded by Lemma 5.11. We can continue this procedure and we eventually will arrive at a sector on which
$\max \{ {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\psi \}$ is bounded by Lemma 5.11. We can continue this procedure and we eventually will arrive at a sector on which ![]() $\phi -\psi$ is negatively divergent since
$\phi -\psi$ is negatively divergent since ![]() $\phi \neq \psi$. This contradicts the supposition.
$\phi \neq \psi$. This contradicts the supposition.
Hence we cannot have such a morphism. This means ![]() $f|_{U}$ is diagonal with respect to indices
$f|_{U}$ is diagonal with respect to indices ![]() $M(U, D)\times M(U,D)$. Hence the morphism
$M(U, D)\times M(U,D)$. Hence the morphism ![]() $f|_{U}$ is represented by a sum of
$f|_{U}$ is represented by a sum of ![]() $c\cdot T^a\colon \Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi \rightarrow \Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$ where
$c\cdot T^a\colon \Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi \rightarrow \Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$ where ![]() $c\in k$ by Lemma 5.11. The
$c\in k$ by Lemma 5.11. The ![]() $A(c\cdot T^a)$ ia again of the form of a sum of
$A(c\cdot T^a)$ ia again of the form of a sum of ![]() $\Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$. This completes the proof.
$\Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$. This completes the proof.
We prepare the following lemma for the next subsection.
Lemma 5.28 The category ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$ is a thick subcategory of
$\mathrm {Mod}_{ic}(\Lambda _X)$ is a thick subcategory of ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.
Proof. Let
be an exact sequence in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ with
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ with ![]() $ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}_{ic}(\Lambda _X)$. Let
$ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}_{ic}(\Lambda _X)$. Let ![]() ${\mathcal {S}}$ be a common stratification of
${\mathcal {S}}$ be a common stratification of ![]() $ {\mathcal {V}}$ and
$ {\mathcal {V}}$ and ![]() ${\mathcal {W}}$. Since pull-backs are exact, we can reduce to the case that
${\mathcal {W}}$. Since pull-backs are exact, we can reduce to the case that ![]() $ {\mathcal {V}}, {\mathcal {W}}$ are irregular local systems on
$ {\mathcal {V}}, {\mathcal {W}}$ are irregular local systems on ![]() $(\bar {S}, D_S)$. For any point
$(\bar {S}, D_S)$. For any point ![]() $x\in D_S$, there exists a neighborhood
$x\in D_S$, there exists a neighborhood ![]() $U$ of
$U$ of ![]() $x$ such that
$x$ such that ![]() $U{\backslash } D_S$ has a finite sectorial covering
$U{\backslash } D_S$ has a finite sectorial covering ![]() $\{U_i\}$ and
$\{U_i\}$ and ![]() $ {\mathcal {V}}$ (respectively
$ {\mathcal {V}}$ (respectively ![]() ${\mathcal {W}}$) is isomorphic to
${\mathcal {W}}$) is isomorphic to ![]() ${\bigoplus} _j\Lambda ^{\phi _j}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$ (respectively
${\bigoplus} _j\Lambda ^{\phi _j}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$ (respectively ![]() ${\bigoplus} _{k}\Lambda ^{\psi _k}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$). Hence we have an exact sequence
${\bigoplus} _{k}\Lambda ^{\psi _k}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$). Hence we have an exact sequence
on each ![]() $U_i$.
$U_i$.
We have already seen that ![]() ${\mathbb{R} \mathcal{H} om}(\Lambda ^\psi _{(\overline {U_i}, \overline {U_i}\cap D_S)}, \Lambda ^\phi _{(\overline {U_i}, \overline {U_i}\cap D_S)})\simeq \Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}^{\phi -\psi }$ in Corollary 5.15. Then
${\mathbb{R} \mathcal{H} om}(\Lambda ^\psi _{(\overline {U_i}, \overline {U_i}\cap D_S)}, \Lambda ^\phi _{(\overline {U_i}, \overline {U_i}\cap D_S)})\simeq \Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}^{\phi -\psi }$ in Corollary 5.15. Then
 \begin{align} &\operatorname{Ext}^1_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi)\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi[1])\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^{\phi-\psi}[1])\nonumber\\ &\quad \cong 0, \end{align}
\begin{align} &\operatorname{Ext}^1_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi)\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi[1])\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^{\phi-\psi}[1])\nonumber\\ &\quad \cong 0, \end{align}
since ![]() $\Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}$ is free. This completes the proof.
$\Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}$ is free. This completes the proof.
5.4 Derived category and six operations
Definition 5.29 A cohomologically irregular constructible ![]() $\Lambda _{({\bar {X}}, D_X)}$-module is an object of
$\Lambda _{({\bar {X}}, D_X)}$-module is an object of ![]() $D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ such that all the cohomologies are irregular constructible sheaves. We denote the full subcategory spanned by those objects by
$D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ such that all the cohomologies are irregular constructible sheaves. We denote the full subcategory spanned by those objects by ![]() $D^b_{ic}(\Lambda _X)$.
$D^b_{ic}(\Lambda _X)$.
Proposition 5.30 The category ![]() $D^b_{ic}(\Lambda _X)$ is a triangulated category.
$D^b_{ic}(\Lambda _X)$ is a triangulated category.
Proof. This is a standard consequence of the thickness (Lemma 5.28).
We will now see Grothendieck six operations on this category. In the rest of subsection, ![]() $ {\mathcal {V}}, {\mathcal {W}}$ will be always objects of
$ {\mathcal {V}}, {\mathcal {W}}$ will be always objects of ![]() $D^b_{ic}(\Lambda _X)$.
$D^b_{ic}(\Lambda _X)$.
Proposition 5.31 We have ![]() $ {\mathcal {V}}\otimes ^{\mathbb{L} } {\mathcal {W}}\in D^b_{ic}(\Lambda _X)$.
$ {\mathcal {V}}\otimes ^{\mathbb{L} } {\mathcal {W}}\in D^b_{ic}(\Lambda _X)$.
Lemma 5.32 For an irregular constructible sheaf ![]() ${\mathcal {X}}$ on
${\mathcal {X}}$ on ![]() $(\bar {U}, D_U)$ (respectively
$(\bar {U}, D_U)$ (respectively ![]() $(V, V\cap D_S)$),
$(V, V\cap D_S)$), ![]() $i_!{\mathcal {X}}$ (respectively
$i_!{\mathcal {X}}$ (respectively ![]() $j_*{\mathcal {X}}$) is irregular constructible.
$j_*{\mathcal {X}}$) is irregular constructible.
Proof. By considering a stratification compatible with ![]() $U$ (respectively
$U$ (respectively ![]() $V$) and a stratification of
$V$) and a stratification of ![]() ${\mathcal {X}}$, the constructibility of
${\mathcal {X}}$, the constructibility of ![]() ${\mathcal {X}}$ implies the statement.
${\mathcal {X}}$ implies the statement.
For the constant map ![]() $a_X\colon X\rightarrow *$, we set
$a_X\colon X\rightarrow *$, we set ![]() $\omega _X^\Lambda :=a_X^!\Lambda \cong \Lambda \otimes _\mathbb {k} \omega _X\in D^b_{ic}(\Lambda _X)$ as usual. We also set
$\omega _X^\Lambda :=a_X^!\Lambda \cong \Lambda \otimes _\mathbb {k} \omega _X\in D^b_{ic}(\Lambda _X)$ as usual. We also set
First note the following.
Lemma 5.33 We have ![]() ${\mathbb {D}}\Lambda ^\phi _X\cong \Lambda ^{-\phi }_X\otimes _\mathbb {k}\omega _X$.
${\mathbb {D}}\Lambda ^\phi _X\cong \Lambda ^{-\phi }_X\otimes _\mathbb {k}\omega _X$.
Proof. This is a special case of Corollary 5.15.
Then we have the following.
Lemma 5.34 We have ![]() ${\mathbb {D}} {\mathcal {V}}\in D^b_{ic}(\Lambda _{X})$.
${\mathbb {D}} {\mathcal {V}}\in D^b_{ic}(\Lambda _{X})$.
Proof. Let ![]() ${\mathcal {S}}$ be a stratification of
${\mathcal {S}}$ be a stratification of ![]() $ {\mathcal {V}}$. Let
$ {\mathcal {V}}$. Let ![]() $U$ be the union of open subsets of
$U$ be the union of open subsets of ![]() ${\mathcal {S}}$. By applying Lemma 4.24, we have an exact triangle
${\mathcal {S}}$. By applying Lemma 4.24, we have an exact triangle
Then we have
 \begin{equation} \begin{gathered} {\mathbb{R}\mathcal{H} om}(i_!i^!{\mathcal{V}}, \omega^\Lambda_X)\simeq i_!{\mathbb{R}\mathcal{H} om}(i^{{-}1}{\mathcal{V}}, i^{{-}1}\omega^\Lambda_X),\\ {\mathbb{R}\mathcal{H} om}(j_!j^{{-}1}{\mathcal{V}}, \omega^\Lambda_X)\simeq j_*{\mathbb{R}\mathcal{H} om}(j^{{-}1}{\mathcal{V}}, j^!\omega^\Lambda_X). \end{gathered} \end{equation}
\begin{equation} \begin{gathered} {\mathbb{R}\mathcal{H} om}(i_!i^!{\mathcal{V}}, \omega^\Lambda_X)\simeq i_!{\mathbb{R}\mathcal{H} om}(i^{{-}1}{\mathcal{V}}, i^{{-}1}\omega^\Lambda_X),\\ {\mathbb{R}\mathcal{H} om}(j_!j^{{-}1}{\mathcal{V}}, \omega^\Lambda_X)\simeq j_*{\mathbb{R}\mathcal{H} om}(j^{{-}1}{\mathcal{V}}, j^!\omega^\Lambda_X). \end{gathered} \end{equation}By Lemma 5.32, we can prove the desired result by induction of the dimension of the strata and Lemma 5.33.
Lemma 5.35 The canonical morphism ![]() $ {\mathcal {V}}\rightarrow {\mathbb {D}}{\mathbb {D}} {\mathcal {V}}$ is an isomorphism.
$ {\mathcal {V}}\rightarrow {\mathbb {D}}{\mathbb {D}} {\mathcal {V}}$ is an isomorphism.
Proof. It is also enough to show the statement for irregular local systems. Then the statement is clear from ![]() ${\mathbb {D}}{\mathbb {D}}\Lambda _X^\phi =\Lambda _X^{\phi }$.
${\mathbb {D}}{\mathbb {D}}\Lambda _X^\phi =\Lambda _X^{\phi }$.
Lemma 5.36 We have
Proof. This is easy and the proof is left to the reader.
Corollary 5.37 The contravariant functor ![]() ${\mathbb {D}}\colon D^b_{ic}(\Lambda _X)\rightarrow D^b_{ic}(\Lambda _X)$ is a contravariant equivalence.
${\mathbb {D}}\colon D^b_{ic}(\Lambda _X)\rightarrow D^b_{ic}(\Lambda _X)$ is a contravariant equivalence.
Proof. The fully faithfulness of ![]() ${\mathbb {D}}$ is Lemma 5.36 and the essential surjectivity is Lemma 5.35.
${\mathbb {D}}$ is Lemma 5.36 and the essential surjectivity is Lemma 5.35.
Proposition 5.38 We have a natural isomorphism
Proof. This is easy and the proof is left to the reader.
Proposition 5.39 We have ![]() ${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}}), f^{-1} {\mathcal {V}}, f^! {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}}), f^{-1} {\mathcal {V}}, f^! {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
Proof. This is easy and the proof is left to the reader.
Let ![]() $i_{{({\bar {X}}, D_X)}}\colon {({\bar {X}}, D_X)}\rightarrow (X, \varnothing )$ be the canonical morphism.
$i_{{({\bar {X}}, D_X)}}\colon {({\bar {X}}, D_X)}\rightarrow (X, \varnothing )$ be the canonical morphism.
Lemma 5.40 The functor ![]() $i_{{({\bar {X}}, D_X)}!}\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{\bar {X}})$ is fully faithful embedding onto the full subcategory spanned by objects satisfying
$i_{{({\bar {X}}, D_X)}!}\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{\bar {X}})$ is fully faithful embedding onto the full subcategory spanned by objects satisfying ![]() $i_{D_X}^{-1} {\mathcal {V}}\simeq 0$. The functor
$i_{D_X}^{-1} {\mathcal {V}}\simeq 0$. The functor ![]() $i_{{({\bar {X}}, D_X)}*}$ is also fully faithful. In both cases, the left quasi-inverses are given by
$i_{{({\bar {X}}, D_X)}*}$ is also fully faithful. In both cases, the left quasi-inverses are given by ![]() $i_{({\bar {X}}, D_X)}^{-1}$.
$i_{({\bar {X}}, D_X)}^{-1}$.
Proof. This simply follows from Lemma 4.24
6. Forgetting grading
In this section, we discuss the relationship between irregular constructible sheaves and constructible sheaves. For a topological space with boundary ![]() ${({\bar {X}}, D_X)}$, we set
${({\bar {X}}, D_X)}$, we set ![]() $X:={\bar {X}}{\backslash } D_X$.
$X:={\bar {X}}{\backslash } D_X$.
6.1 Forgetting grading
Lemma 6.1 There exists an exact functor
satisfying the following. For an object ![]() $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$, take a local lift
$ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$, take a local lift ![]() $\tilde {\mathcal{V} }$ on an open subset
$\tilde {\mathcal{V} }$ on an open subset ![]() $U\subset X$. Let
$U\subset X$. Let ![]() $\tilde {\mathcal{V} }_{0}$ be the underlying ungraded
$\tilde {\mathcal{V} }_{0}$ be the underlying ungraded ![]() $\Lambda$-module of
$\Lambda$-module of ![]() $\tilde {\mathcal{V} }$. Then
$\tilde {\mathcal{V} }$. Then ![]() $ {\mathfrak {F}}( {\mathcal {V}})|_U\cong \tilde {\mathcal{V} }_0|_U\otimes _\Lambda \mathbb {k}$.
$ {\mathfrak {F}}( {\mathcal {V}})|_U\cong \tilde {\mathcal{V} }_0|_U\otimes _\Lambda \mathbb {k}$.
Proof. For an object ![]() $ {\mathcal {V}}$, let us take a locally finite covering
$ {\mathcal {V}}$, let us take a locally finite covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $X$ with lifts
$X$ with lifts ![]() $\{\tilde {\mathcal{V} }_i\}\subset \mathrm {Mod}^{\mathfrak {I}}_{pre} (\Lambda _X)$. There exists an isomorphism
$\{\tilde {\mathcal{V} }_i\}\subset \mathrm {Mod}^{\mathfrak {I}}_{pre} (\Lambda _X)$. There exists an isomorphism ![]() $f_{ij}\colon [\tilde {\mathcal{V} }_i]|_{U_i\cap U_j}\xrightarrow {\cong } [\tilde {\mathcal{V} }_j]|_{U_i\cap U_j}$ in
$f_{ij}\colon [\tilde {\mathcal{V} }_i]|_{U_i\cap U_j}\xrightarrow {\cong } [\tilde {\mathcal{V} }_j]|_{U_i\cap U_j}$ in ![]() ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. We can take a covering
${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. We can take a covering ![]() $\{U_{ijk}\}$ on which we have a descent data
$\{U_{ijk}\}$ on which we have a descent data ![]() $f_{ijk}\colon [\tilde {\mathcal{V} }_i]|_{U_{ijk}}\rightarrow [\tilde {\mathcal{V} }_j]|_{U_{ijk}}$ for
$f_{ijk}\colon [\tilde {\mathcal{V} }_i]|_{U_{ijk}}\rightarrow [\tilde {\mathcal{V} }_j]|_{U_{ijk}}$ for ![]() $f_{ij}$ in
$f_{ij}$ in ![]() $\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{ij})$. Let
$\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{ij})$. Let ![]() $\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle $ be a lift of
$\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle $ be a lift of ![]() $f_{ijk}$.
$f_{ijk}$.
Then ![]() $f_{ijk}|_{U_{ijk}\cap U_{ijl}}=f_{ijl}|_{U_{ijk}\cap U_{ijl}}$ means there exists
$f_{ijk}|_{U_{ijk}\cap U_{ijl}}=f_{ijl}|_{U_{ijk}\cap U_{ijl}}$ means there exists ![]() $b\in {\mathbb {R}}_{>0}$ such that
$b\in {\mathbb {R}}_{>0}$ such that ![]() $T^b\cdot ((\tilde {f}_{ijk}-\tilde {f}_{ijl})|_{U_{ijk}\cap U_{ijl}})=0$. This means
$T^b\cdot ((\tilde {f}_{ijk}-\tilde {f}_{ijl})|_{U_{ijk}\cap U_{ijl}})=0$. This means ![]() $\tilde {f}_{ijk}\otimes _\Lambda \mathbb {k} =\tilde {f}_{ijl}\otimes _\Lambda \mathbb {k}$. Hence the set
$\tilde {f}_{ijk}\otimes _\Lambda \mathbb {k} =\tilde {f}_{ijl}\otimes _\Lambda \mathbb {k}$. Hence the set ![]() $\{\tilde {f}_{ijk}\}$ gives an isomorphism
$\{\tilde {f}_{ijk}\}$ gives an isomorphism ![]() $f_{ij}\otimes _\Lambda \mathbb {k}\colon \tilde {\mathcal{V} }_i|_{U_{ij}}\otimes _\Lambda \mathbb {k}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ij}}\otimes _\Lambda \mathbb {k}$. Again, these morphisms can be glued up and give a
$f_{ij}\otimes _\Lambda \mathbb {k}\colon \tilde {\mathcal{V} }_i|_{U_{ij}}\otimes _\Lambda \mathbb {k}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ij}}\otimes _\Lambda \mathbb {k}$. Again, these morphisms can be glued up and give a ![]() $\mathbb {k}$-module sheaf
$\mathbb {k}$-module sheaf ![]() $ {\mathcal {V}}\otimes _\Lambda \mathbb {k}$. By a similar argument, one can actually see this does not depend on the choice of lifts.
$ {\mathcal {V}}\otimes _\Lambda \mathbb {k}$. By a similar argument, one can actually see this does not depend on the choice of lifts.
For ![]() $f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$, there exists a covering
$f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$, there exists a covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $X$ with lifts
$X$ with lifts ![]() $\{\tilde {f}_i\} \subset \mathrm {Mod}^ {\mathbb {R}}(\Lambda _{U_i})$. Then we get a set of morphisms
$\{\tilde {f}_i\} \subset \mathrm {Mod}^ {\mathbb {R}}(\Lambda _{U_i})$. Then we get a set of morphisms ![]() $\{\tilde {f}_i\otimes _{\Lambda _X} \mathbb {k}_X\}$. One can see these are glued up to a morphism in
$\{\tilde {f}_i\otimes _{\Lambda _X} \mathbb {k}_X\}$. One can see these are glued up to a morphism in ![]() $\mathrm {Mod}(\mathbb {k}_X)$ depending only on
$\mathrm {Mod}(\mathbb {k}_X)$ depending only on ![]() $f$ by a similar argument as above. The resulting morphism is denoted by
$f$ by a similar argument as above. The resulting morphism is denoted by ![]() $ {\mathfrak {F}}(f)$. It is clear that this correspondence preserves the compositions. Hence
$ {\mathfrak {F}}(f)$. It is clear that this correspondence preserves the compositions. Hence ![]() $ {\mathfrak {F}}$ gives a functor.
$ {\mathfrak {F}}$ gives a functor.
We would like to see the functor ![]() $ {\mathfrak {F}}$ is exact. Let
$ {\mathfrak {F}}$ is exact. Let
be an exact sequence in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is equivalent to that there exists a locally finite open covering
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is equivalent to that there exists a locally finite open covering ![]() $\{U_i\}$ of
$\{U_i\}$ of ![]() $X$ such that we have an exact sequence
$X$ such that we have an exact sequence
over each ![]() $U_i$. By Lemma 2.14, it can be lifted to an exact sequence of
$U_i$. By Lemma 2.14, it can be lifted to an exact sequence of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-modules
$\Lambda _X$-modules
Since tensor product is left exact, we get an exact sequence
It remains to show ![]() $\tilde {f}_i\otimes \operatorname {id}$ is injective. Let us take a homogeneous section of the kernel of
$\tilde {f}_i\otimes \operatorname {id}$ is injective. Let us take a homogeneous section of the kernel of ![]() $\tilde {f}_i\otimes \mathbb {k}$. Since it is a subsheaf of
$\tilde {f}_i\otimes \mathbb {k}$. Since it is a subsheaf of ![]() $\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\mathbb {k}_X$, it is locally represented by the form
$\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\mathbb {k}_X$, it is locally represented by the form ![]() $s\otimes 1$. If
$s\otimes 1$. If ![]() $s\otimes 1$ is nonzero, it means that
$s\otimes 1$ is nonzero, it means that ![]() $T^a\cdot s\neq 0$ in
$T^a\cdot s\neq 0$ in ![]() $\tilde {\mathcal{V} }_i$. Hence we have
$\tilde {\mathcal{V} }_i$. Hence we have ![]() $\Lambda _U\cdot s\hookrightarrow \tilde {\mathcal{V} }_i|_U$ where
$\Lambda _U\cdot s\hookrightarrow \tilde {\mathcal{V} }_i|_U$ where ![]() $U$ is the open set on which
$U$ is the open set on which ![]() $s$ is defined. If
$s$ is defined. If ![]() $\tilde {f}_i(s)\otimes 1=0$, we have some
$\tilde {f}_i(s)\otimes 1=0$, we have some ![]() $T^a$ such that
$T^a$ such that ![]() $T^a\tilde {f}_i(s)=0$ by Lemma 2.7. Hence we have a sequence of morphisms over
$T^a\tilde {f}_i(s)=0$ by Lemma 2.7. Hence we have a sequence of morphisms over ![]() $U$ of
$U$ of ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-modules
$\Lambda$-modules
whose composition is zero. Since ![]() $\Lambda _U\cdot s$ is nonzero in
$\Lambda _U\cdot s$ is nonzero in ![]() $\mathrm {Mod}^{\mathfrak {I}}(U_i)$, the morphism
$\mathrm {Mod}^{\mathfrak {I}}(U_i)$, the morphism ![]() $[T^a\tilde {f}_i]=[\tilde {f}_i]=f_i$ has a nontrivial kernel. This contradicts the injectivity of
$[T^a\tilde {f}_i]=[\tilde {f}_i]=f_i$ has a nontrivial kernel. This contradicts the injectivity of ![]() $f_i$. Hence
$f_i$. Hence ![]() $\tilde {f}_i\otimes \operatorname {id}$ is injective.
$\tilde {f}_i\otimes \operatorname {id}$ is injective.
Lemma 6.2 Let ![]() $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ be a map between topological spaces with boundaries. Then we have
$f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ be a map between topological spaces with boundaries. Then we have
Proof. For an ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda _X$-module
$\Lambda _X$-module ![]() $ {\mathcal {V}}$, let us consider
$ {\mathcal {V}}$, let us consider ![]() $f^{-1} {\mathcal {V}}$. The sheaf
$f^{-1} {\mathcal {V}}$. The sheaf ![]() $ {\mathfrak {F}}\circ f^{-1} {\mathcal {V}}(U)$ is a sheaf associated with the presheaf
$ {\mathfrak {F}}\circ f^{-1} {\mathcal {V}}(U)$ is a sheaf associated with the presheaf
On the other hand, the sheaf ![]() $f^{-1}\circ {\mathfrak {F}}( {\mathcal {V}})$ is a sheaf associated with the presheaf
$f^{-1}\circ {\mathfrak {F}}( {\mathcal {V}})$ is a sheaf associated with the presheaf
By the definition,
 \begin{align} f^{{-}1}{\mathcal{V}}(U)\otimes_{\Lambda}\mathbb{k}&\cong \bigg(\lim_{\substack{\longrightarrow \\ V\supset f(U)}}{\mathcal{V}}(V)\bigg) \otimes_\Lambda \mathbb{k}\nonumber\\ &\cong \lim_{\substack{\longrightarrow \\ V\supset f(U)}}({\mathcal{V}}(V)\otimes_{\Lambda}\mathbb{k})\nonumber\\ &\cong f^{{-}1}({\mathcal{V}}\otimes_{\Lambda_X} \mathbb{k}_X)(U). \end{align}
\begin{align} f^{{-}1}{\mathcal{V}}(U)\otimes_{\Lambda}\mathbb{k}&\cong \bigg(\lim_{\substack{\longrightarrow \\ V\supset f(U)}}{\mathcal{V}}(V)\bigg) \otimes_\Lambda \mathbb{k}\nonumber\\ &\cong \lim_{\substack{\longrightarrow \\ V\supset f(U)}}({\mathcal{V}}(V)\otimes_{\Lambda}\mathbb{k})\nonumber\\ &\cong f^{{-}1}({\mathcal{V}}\otimes_{\Lambda_X} \mathbb{k}_X)(U). \end{align}Hence they are the same.
Lemma 6.3 Let ![]() $ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an irregular local system. Then
$ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an irregular local system. Then ![]() $ {\mathfrak {F}}( {\mathcal {V}})$ is a local system.
$ {\mathfrak {F}}( {\mathcal {V}})$ is a local system.
Proof. There exists an open covering of ![]() $U$ such that
$U$ such that ![]() $ {\mathcal {V}}$ is represented by a direct sum of irregular constant sheaves
$ {\mathcal {V}}$ is represented by a direct sum of irregular constant sheaves ![]() $\Lambda ^\phi$. Hence the statement follows from that
$\Lambda ^\phi$. Hence the statement follows from that ![]() $\Lambda ^\phi \otimes _\Lambda \mathbb {k}$ is a rank 1 constant
$\Lambda ^\phi \otimes _\Lambda \mathbb {k}$ is a rank 1 constant ![]() $\mathbb {k}$-module on any enough small open subset.
$\mathbb {k}$-module on any enough small open subset.
Lemma 6.4 Let ![]() $G\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and
$G\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and ![]() $\tilde {G}\colon \mathrm {Mod}(\mathbb {k}_X)\rightarrow \mathrm {Mod}(\mathbb {k}_Y)$ be right (respectively left) exact functors such that
$\tilde {G}\colon \mathrm {Mod}(\mathbb {k}_X)\rightarrow \mathrm {Mod}(\mathbb {k}_Y)$ be right (respectively left) exact functors such that ![]() $ {\mathfrak {F}}\circ G\cong G\circ {\mathfrak {F}}$. Then we have
$ {\mathfrak {F}}\circ G\cong G\circ {\mathfrak {F}}$. Then we have ![]() $ {\mathfrak {F}}\circ {\mathbb {R}} G\simeq {\mathbb {R}} \tilde {G}\circ {\mathfrak {F}}$ (respectively
$ {\mathfrak {F}}\circ {\mathbb {R}} G\simeq {\mathbb {R}} \tilde {G}\circ {\mathfrak {F}}$ (respectively ![]() $ {\mathfrak {F}}\circ {\mathbb {L}} G\simeq {\mathbb {L}} \tilde {G}\circ {\mathfrak {F}}$).
$ {\mathfrak {F}}\circ {\mathbb {L}} G\simeq {\mathbb {L}} \tilde {G}\circ {\mathfrak {F}}$).
Proof. Let ![]() $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ and take an injective resolution
$ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ and take an injective resolution ![]() ${\mathcal {I}}^\bullet$ by using Proposition 4.2. Note that skyscraper sheaves
${\mathcal {I}}^\bullet$ by using Proposition 4.2. Note that skyscraper sheaves ![]() $\Lambda _x$ used in this injective resolution are mapped to skyscraper sheaves
$\Lambda _x$ used in this injective resolution are mapped to skyscraper sheaves ![]() $k_x$. Combining with the exactness of
$k_x$. Combining with the exactness of ![]() $ {\mathfrak {F}}$ (Lemma 6.1), we can conclude that
$ {\mathfrak {F}}$ (Lemma 6.1), we can conclude that ![]() $ {\mathfrak {F}}({\mathcal {I}}^\bullet )$ is an injective resolution of
$ {\mathfrak {F}}({\mathcal {I}}^\bullet )$ is an injective resolution of ![]() $ {\mathfrak {F}}( {\mathcal {V}})$. Hence we have
$ {\mathfrak {F}}( {\mathcal {V}})$. Hence we have
Similarly, for a free ![]() $ {\mathbb {R}}$-graded
$ {\mathbb {R}}$-graded ![]() $\Lambda$-module
$\Lambda$-module ![]() ${\mathcal {F}}$, the module
${\mathcal {F}}$, the module ![]() $ {\mathfrak {F}}({\mathcal {F}}_U)$ is a direct sum of
$ {\mathfrak {F}}({\mathcal {F}}_U)$ is a direct sum of ![]() $\mathbb {k}_U$, and hence is flat. By Lemma 4.4, we can do a similar argument as above. This completes the proof.
$\mathbb {k}_U$, and hence is flat. By Lemma 4.4, we can do a similar argument as above. This completes the proof.
Lemma 6.5 Let ![]() $f$ be a proper map
$f$ be a proper map ![]() $X\rightarrow Y$. We have an equality
$X\rightarrow Y$. We have an equality
of functors ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))\rightarrow D^b(\mathbb {k}_Y)$.
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))\rightarrow D^b(\mathbb {k}_Y)$.
Proof. By Lemma 6.4, it is enough to show the underived version. For ![]() $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)$ and an open subset
$ {\mathcal {V}}\in \mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)$ and an open subset ![]() $U$, both
$U$, both ![]() $f_!\circ {\mathfrak {F}}( {\mathcal {V}})$ and
$f_!\circ {\mathfrak {F}}( {\mathcal {V}})$ and ![]() $ {\mathfrak {F}}\circ f_!$ have
$ {\mathfrak {F}}\circ f_!$ have ![]() $ {\mathcal {V}}(f^{-1}(U))\otimes \mathbb {k}$ over
$ {\mathcal {V}}(f^{-1}(U))\otimes \mathbb {k}$ over ![]() $U$. This completes the proof.
$U$. This completes the proof.
Lemma 6.6 Let ![]() $i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical map and
$i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical map and ![]() $i_X\colon X\hookrightarrow {\bar {X}}$ be the inclusion. We have an equality
$i_X\colon X\hookrightarrow {\bar {X}}$ be the inclusion. We have an equality
Proof. Again, we only prove the underived version. One can prove in a similar way to Lemma 6.5.
6.2 The case of irregular constructible sheaves
Proposition 6.7 The functor ![]() $ {\mathfrak {F}}$ restricts to a functor
$ {\mathfrak {F}}$ restricts to a functor ![]() $\mathrm {Mod}_{ic}(\Lambda _X)\rightarrow \mathrm {Mod}_{c}(\mathbb {k}_X)$.
$\mathrm {Mod}_{ic}(\Lambda _X)\rightarrow \mathrm {Mod}_{c}(\mathbb {k}_X)$.
Proof. For ![]() $ {\mathcal {V}}\in \mathrm {Mod}_{ic}(\Lambda _X)$, let us take a stratification
$ {\mathcal {V}}\in \mathrm {Mod}_{ic}(\Lambda _X)$, let us take a stratification ![]() ${\mathcal {S}}$ of
${\mathcal {S}}$ of ![]() $X$. For each
$X$. For each ![]() $S\in {\mathcal {S}}$, let us denote the inclusions by
$S\in {\mathcal {S}}$, let us denote the inclusions by ![]() $i_{{(\bar {S}, D_S)}}\colon {(\bar {S}, D_S)}\hookrightarrow (X, \varnothing )$ and
$i_{{(\bar {S}, D_S)}}\colon {(\bar {S}, D_S)}\hookrightarrow (X, \varnothing )$ and ![]() $i_S\colon S\hookrightarrow X$. Then we have
$i_S\colon S\hookrightarrow X$. Then we have ![]() $i_S^{-1} {\mathfrak {F}}( {\mathcal {V}})\cong {\mathfrak {F}}(i_{(\bar {S}, D_S)}^{-1}( {\mathcal {V}}))$ by Lemma 6.2. By Lemma 6.3, this is a local system. Hence
$i_S^{-1} {\mathfrak {F}}( {\mathcal {V}})\cong {\mathfrak {F}}(i_{(\bar {S}, D_S)}^{-1}( {\mathcal {V}}))$ by Lemma 6.2. By Lemma 6.3, this is a local system. Hence ![]() $ {\mathfrak {F}}( {\mathcal {V}})$ is a constructible sheaf with respect to
$ {\mathfrak {F}}( {\mathcal {V}})$ is a constructible sheaf with respect to ![]() ${\mathcal {S}}$.
${\mathcal {S}}$.
We also denote the induced functor ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))\rightarrow D^b(\mathrm {Mod}(\mathbb {k}_X))$ by
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))\rightarrow D^b(\mathrm {Mod}(\mathbb {k}_X))$ by ![]() $ {\mathfrak {F}}$.
$ {\mathfrak {F}}$.
Corollary 6.8 The functor ![]() $ {\mathfrak {F}}$ restricts to
$ {\mathfrak {F}}$ restricts to ![]() $D^b_{ic}(\Lambda _X)\rightarrow D^b_c(\mathbb {k}_X)$.
$D^b_{ic}(\Lambda _X)\rightarrow D^b_c(\mathbb {k}_X)$.
Proof. For ![]() $ {\mathcal {V}}^\bullet \in D^b(\mathrm {Mod}_{ic}(\Lambda _X))$, since
$ {\mathcal {V}}^\bullet \in D^b(\mathrm {Mod}_{ic}(\Lambda _X))$, since ![]() $ {\mathfrak {F}}$ is exact on the abelian categories (Lemma 6.1), we have
$ {\mathfrak {F}}$ is exact on the abelian categories (Lemma 6.1), we have ![]() $H^i( {\mathfrak {F}}( {\mathcal {V}}^\bullet ))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))$. By Proposition 6.7, we have
$H^i( {\mathfrak {F}}( {\mathcal {V}}^\bullet ))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))$. By Proposition 6.7, we have ![]() $ {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))\in \mathrm {Mod}_c(\mathbb {k}_X)$.
$ {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))\in \mathrm {Mod}_c(\mathbb {k}_X)$.
Lemma 6.9 If we have ![]() $ {\mathfrak {F}}(E)\simeq 0$ for an irregular constructible sheaf
$ {\mathfrak {F}}(E)\simeq 0$ for an irregular constructible sheaf ![]() $E$, we have
$E$, we have ![]() $E\simeq 0$.
$E\simeq 0$.
Proof. We will argue on each stratum of a stratification of ![]() $E$. On the interior of a stratum, the irregular local system is locally isomorphic to
$E$. On the interior of a stratum, the irregular local system is locally isomorphic to ![]() ${\bigoplus} _{i\in I}\Lambda ^{\phi _i}$ for some
${\bigoplus} _{i\in I}\Lambda ^{\phi _i}$ for some ![]() $\phi _i$'s. Since
$\phi _i$'s. Since ![]() $ {\mathfrak {F}}({\bigoplus} _i\Lambda ^{\phi _i})\cong \mathbb {k}^{|I|}$,
$ {\mathfrak {F}}({\bigoplus} _i\Lambda ^{\phi _i})\cong \mathbb {k}^{|I|}$, ![]() $ {\mathfrak {F}}(E)\cong 0$ is equivalent to
$ {\mathfrak {F}}(E)\cong 0$ is equivalent to ![]() $|I|=0$. This means
$|I|=0$. This means ![]() $E\cong 0$. This completes the proof.
$E\cong 0$. This completes the proof.
We also would like to discuss the functor in the other direction. We consider the following functor
equipped with the trivial grading. We define ![]() $ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$ as the composition of the above with
$ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$ as the composition of the above with ![]() $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. It is clear that this induces an exact functor
$[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. It is clear that this induces an exact functor ![]() $ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$. We will denote its derived functor by the same notation
$ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$. We will denote its derived functor by the same notation ![]() $ {\mathfrak {G}}\colon D^b_c(\mathbb {k}_X)\rightarrow D^b_{ic}(\Lambda _X)$.
$ {\mathfrak {G}}\colon D^b_c(\mathbb {k}_X)\rightarrow D^b_{ic}(\Lambda _X)$.
Proposition 6.10 We have ![]() $ {\mathfrak {F}}\circ {\mathfrak {G}}\simeq \operatorname {id}$.
$ {\mathfrak {F}}\circ {\mathfrak {G}}\simeq \operatorname {id}$.
Proof. This again follows from the fact that ![]() $ {\mathfrak {F}}(\Lambda ^\phi )$ is a rank 1 constant
$ {\mathfrak {F}}(\Lambda ^\phi )$ is a rank 1 constant ![]() $\mathbb {k}$-module.
$\mathbb {k}$-module.
7. Enhanced sheaves and  $\Lambda$-modules
$\Lambda$-modules
7.1  $\mathbb{R}$-constructible enhanced ind-sheaves
$\mathbb{R}$-constructible enhanced ind-sheaves
In this section, we recall the definition of ![]() $ {\mathbb {R}}$-constructible enhanced ind-sheaves. For more detailed accounts, we refer to the original [Reference D'Agnolo and KashiwaraDK16] and the survey [Reference Kashiwara and SchapiraKS16]. Let
$ {\mathbb {R}}$-constructible enhanced ind-sheaves. For more detailed accounts, we refer to the original [Reference D'Agnolo and KashiwaraDK16] and the survey [Reference Kashiwara and SchapiraKS16]. Let ![]() $M$ be a real analytic manifold. Let
$M$ be a real analytic manifold. Let ![]() $\bar {\mathbb{R} }$ be the two point compactification of
$\bar {\mathbb{R} }$ be the two point compactification of ![]() $ {\mathbb {R}}$ i.e.
$ {\mathbb {R}}$ i.e. ![]() $ {\mathbb {R}}\cong (0,1)\hookrightarrow [0,1]=\bar {\mathbb{R} }$. The category of enhanced ind-sheaves is defined in two steps. First, we set
$ {\mathbb {R}}\cong (0,1)\hookrightarrow [0,1]=\bar {\mathbb{R} }$. The category of enhanced ind-sheaves is defined in two steps. First, we set
where ![]() $D^b(\mathrm {I}\mathbb {k}_M)$ is the bounded derived category of ind-sheaves over
$D^b(\mathrm {I}\mathbb {k}_M)$ is the bounded derived category of ind-sheaves over ![]() $M$ [Reference Kashiwara and SchapiraKS01]. We set
$M$ [Reference Kashiwara and SchapiraKS01]. We set ![]() $\mathbb {k}_{t\lesseqgtr 0}:=\mathbb {k}_{\{ (x,t)\in M\times \bar {\mathbb{R} }| t\in {\mathbb {R}}, t\lesseqgtr 0 \}}$. The definition of the convolution product
$\mathbb {k}_{t\lesseqgtr 0}:=\mathbb {k}_{\{ (x,t)\in M\times \bar {\mathbb{R} }| t\in {\mathbb {R}}, t\lesseqgtr 0 \}}$. The definition of the convolution product ![]() $\overset {+}{\otimes }$ can be extended to the objects in
$\overset {+}{\otimes }$ can be extended to the objects in ![]() $D^b(\mathrm {I}\mathbb {k}_{M\times (\bar {\mathbb{R} }, {\mathbb {R}})})$. We set
$D^b(\mathrm {I}\mathbb {k}_{M\times (\bar {\mathbb{R} }, {\mathbb {R}})})$. We set
The category of enhanced ind-sheaves over ![]() $X$ is defined by
$X$ is defined by
The triangulated category ![]() $E^b(\mathrm {I}\mathbb {k}_M)$ has monoidal operations
$E^b(\mathrm {I}\mathbb {k}_M)$ has monoidal operations ![]() $\overset {+}{\otimes }$ and
$\overset {+}{\otimes }$ and ![]() $\mathcal{I} hom^+$. For a morphism
$\mathcal{I} hom^+$. For a morphism ![]() $M\rightarrow N$ of real analytic manifolds, there are associated functors
$M\rightarrow N$ of real analytic manifolds, there are associated functors
They form adjoint pairs ![]() $Ef_{!!}\dashv Ef^!$ and
$Ef_{!!}\dashv Ef^!$ and ![]() $Ef^{-1}\dashv Ef_*$.
$Ef^{-1}\dashv Ef_*$.
We further set
as an object of ![]() $E^b({\mathrm {I}\mathbb {k}_M})$. As usual,
$E^b({\mathrm {I}\mathbb {k}_M})$. As usual, ![]() $\text{`}\lim\text{'}$ means Ind-colimit.
$\text{`}\lim\text{'}$ means Ind-colimit.
Definition 7.1
(i) An object
 ${\mathcal {E}}$ of
${\mathcal {E}}$ of  $E^b({\mathrm {I}\mathbb {k}_M})$ is said to be
$E^b({\mathrm {I}\mathbb {k}_M})$ is said to be  $ {\mathbb {R}}$-constructible if there exists an open covering
$ {\mathbb {R}}$-constructible if there exists an open covering  $\{U_i\}$ of
$\{U_i\}$ of  $M$ such that there exists an
$M$ such that there exists an  $ {\mathbb {R}}$-constructible sheaf
$ {\mathbb {R}}$-constructible sheaf  ${\mathcal {E}}_U$ over each
${\mathcal {E}}_U$ over each  $U\times {\mathbb {R}}$ such that
$U\times {\mathbb {R}}$ such that  ${\mathcal {E}}|_{U\times \bar {\mathbb{R} }}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_{U}$.
${\mathcal {E}}|_{U\times \bar {\mathbb{R} }}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_{U}$.(ii) An enhanced
 $ {\mathbb {R}}$-constructible ind-sheaf
$ {\mathbb {R}}$-constructible ind-sheaf  ${\mathcal {E}}$ of
${\mathcal {E}}$ of  $E^b({\mathrm {I}\mathbb {k}_M})$ is said to be
$E^b({\mathrm {I}\mathbb {k}_M})$ is said to be  ${\mathbb {C}}$-constructible if the following holds. There exists an open covering
${\mathbb {C}}$-constructible if the following holds. There exists an open covering  $\{U\}$ of
$\{U\}$ of  $M$ and a
$M$ and a  ${\mathbb {C}}$-stratification
${\mathbb {C}}$-stratification  ${\mathcal {S}}_U$ for each
${\mathcal {S}}_U$ for each  $U$ such that: (i) there exists an
$U$ such that: (i) there exists an  $ {\mathbb {R}}$-constructible sheaf
$ {\mathbb {R}}$-constructible sheaf  ${\mathcal {E}}_{U_i}$ such that
${\mathcal {E}}_{U_i}$ such that  ${\mathcal {E}}|_{U \times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes }\mathbb {k}^E_U$; (ii) each cohomology sheaf
${\mathcal {E}}|_{U \times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes }\mathbb {k}^E_U$; (ii) each cohomology sheaf  ${\mathcal {H}}^i({\mathcal {E}}_U|_S)$ for each
${\mathcal {H}}^i({\mathcal {E}}_U|_S)$ for each  $S\in {\mathcal {S}}_U$ is isomorphic to a direct sum of sheaves of the form
$S\in {\mathcal {S}}_U$ is isomorphic to a direct sum of sheaves of the form  $\mathbb {k}_{t\geqslant \phi (x)}$ for some continuous function
$\mathbb {k}_{t\geqslant \phi (x)}$ for some continuous function  $\phi$.
$\phi$.
We denote the full subcategory spanned by ![]() $ {\mathbb {R}}$-constructible (respectively
$ {\mathbb {R}}$-constructible (respectively ![]() ${\mathbb {C}}$-constructible) enhanced ind-sheaves by
${\mathbb {C}}$-constructible) enhanced ind-sheaves by ![]() $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ (respectively
$E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ (respectively ![]() $E^b_{{\mathbb {C}} - c}(\mathrm {I}\mathbb {k}_M)$). The category
$E^b_{{\mathbb {C}} - c}(\mathrm {I}\mathbb {k}_M)$). The category ![]() $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ has a contravariant autoequivalence
$E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ has a contravariant autoequivalence ![]() ${\mathbb {D}}$, analogous to the Verdier duality.
${\mathbb {D}}$, analogous to the Verdier duality.
7.2 From enhanced sheaves to  $\Lambda$-modules
$\Lambda$-modules
For a sheaf ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $X\times \bar {\mathbb{R} }$, let us consider the object
$X\times \bar {\mathbb{R} }$, let us consider the object ![]() ${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ where
${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ where ![]() $p\colon X\times {\mathbb {R}}\rightarrow X$ is the projection. It is equipped with the action of
$p\colon X\times {\mathbb {R}}\rightarrow X$ is the projection. It is equipped with the action of ![]() $\Lambda$ as follows. The action of
$\Lambda$ as follows. The action of ![]() $T^b$ on
$T^b$ on ![]() ${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ is the product of
${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ is the product of
induced by the canonical map ![]() $\mathbb {k}_{[-b-a,\infty )}\rightarrow \mathbb {k}_{[-a,\infty )}$.
$\mathbb {k}_{[-b-a,\infty )}\rightarrow \mathbb {k}_{[-a,\infty )}$.
Recall that ![]() $D^b(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}})$ is the derived category of
$D^b(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}})$ is the derived category of ![]() $\mathrm {Mod}(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}}):=\mathrm {Ind}(\mathrm {Mod}_c(\mathbb {k}_{M\times \bar { {\mathbb {R}}}}))$ where
$\mathrm {Mod}(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}}):=\mathrm {Ind}(\mathrm {Mod}_c(\mathbb {k}_{M\times \bar { {\mathbb {R}}}}))$ where ![]() $c$ means compactly supported sheaves. The left exact functor
$c$ means compactly supported sheaves. The left exact functor
 \begin{equation} \mathrm{Mod}_c(\mathbb{k}_{M\times \bar{{\mathbb{R}}}})\rightarrow \mathrm{Mod}^{\mathfrak{I}}(\Lambda_X); {\mathcal{E}}\mapsto \bigg[\bigoplus_{-a\in {\mathbb{R}}}p_*\Gamma_{[{-}a, \infty)}{\mathcal{E}}\bigg] \end{equation}
\begin{equation} \mathrm{Mod}_c(\mathbb{k}_{M\times \bar{{\mathbb{R}}}})\rightarrow \mathrm{Mod}^{\mathfrak{I}}(\Lambda_X); {\mathcal{E}}\mapsto \bigg[\bigoplus_{-a\in {\mathbb{R}}}p_*\Gamma_{[{-}a, \infty)}{\mathcal{E}}\bigg] \end{equation}induces
by taking ![]() $\mathrm {Ind}$ of all of them. This is again left exact [Reference Kashiwara and SchapiraKS06].
$\mathrm {Ind}$ of all of them. This is again left exact [Reference Kashiwara and SchapiraKS06].
We denote the right derived functor of ![]() $\tilde {M}$ by
$\tilde {M}$ by ![]() $ {\mathbb {R}}\tilde {M}\colon D^b(\mathrm {I}\mathbb {k}_{X\times \bar {\mathbb{R} }})\rightarrow D^b(\mathrm {Ind}(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)))$. Recall that there exist embeddings
$ {\mathbb {R}}\tilde {M}\colon D^b(\mathrm {I}\mathbb {k}_{X\times \bar {\mathbb{R} }})\rightarrow D^b(\mathrm {Ind}(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)))$. Recall that there exist embeddings
and
Composing these with ![]() $ {\mathbb {R}}\tilde {M}$, we get
$ {\mathbb {R}}\tilde {M}$, we get
Lemma 7.2 Let ![]() ${\mathcal {E}}$ be an
${\mathcal {E}}$ be an ![]() $ {\mathbb {R}}$-constructible sheaf over
$ {\mathbb {R}}$-constructible sheaf over ![]() $X\times {\mathbb {R}}$. Then we have
$X\times {\mathbb {R}}$. Then we have ![]() $M({\mathcal {E}}\overset {+}{\otimes } \mathbb {k}^E_X)\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$.
$M({\mathcal {E}}\overset {+}{\otimes } \mathbb {k}^E_X)\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$.
Proof. By the definition of ![]() $M$ and
$M$ and ![]() $\mathbb {k}^E_X$, it is enough to show that the natural morphisms
$\mathbb {k}^E_X$, it is enough to show that the natural morphisms
 \begin{equation} \bigg[ \bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a,\infty)}{\mathcal{E}}\bigg] \rightarrow \bigg[ \bigoplus_{-a\in {\mathbb{R}}} {\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,\infty)}{\mathcal{E}}\bigg] \end{equation}
\begin{equation} \bigg[ \bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a,\infty)}{\mathcal{E}}\bigg] \rightarrow \bigg[ \bigoplus_{-a\in {\mathbb{R}}} {\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,\infty)}{\mathcal{E}}\bigg] \end{equation}
are isomorphisms for any ![]() $c\in \mathbb{R} _{\geqslant 0}$. The cone is given by
$c\in \mathbb{R} _{\geqslant 0}$. The cone is given by
 \begin{equation} \bigg[\bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,-a)}{\mathcal{E}}\bigg]. \end{equation}
\begin{equation} \bigg[\bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,-a)}{\mathcal{E}}\bigg]. \end{equation}
Since ![]() $T^c\in \Lambda$ vanishes on this object, this is zero. Hence the morphisms are isomorphisms.
$T^c\in \Lambda$ vanishes on this object, this is zero. Hence the morphisms are isomorphisms.
Lemma 7.3 The functor ![]() $M$ restricts to a functor
$M$ restricts to a functor ![]() $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_X)\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$, which is also denoted by
$E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_X)\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$, which is also denoted by ![]() $M$.
$M$.
Proof. For an ![]() $ {\mathbb {R}}$-constructible enhanced ind-sheaf
$ {\mathbb {R}}$-constructible enhanced ind-sheaf ![]() ${\mathcal {E}}$, there exists a locally finite covering
${\mathcal {E}}$, there exists a locally finite covering ![]() ${\mathcal {U}}$ of
${\mathcal {U}}$ of ![]() $X$ such that we have
$X$ such that we have ![]() ${\mathcal {E}}|_{U\times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U$ and
${\mathcal {E}}|_{U\times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U$ and ![]() $(n+2)$-fold covers are empty where
$(n+2)$-fold covers are empty where ![]() $n=\dim X$. By the Cech construction,
$n=\dim X$. By the Cech construction, ![]() ${\mathcal {E}}$ is represented by a result of mapping cones of
${\mathcal {E}}$ is represented by a result of mapping cones of ![]() $i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U)$. This implies
$i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U)$. This implies ![]() $\tilde {M}({\mathcal {E}})$ is obtained as a finite mapping cones of
$\tilde {M}({\mathcal {E}})$ is obtained as a finite mapping cones of ![]() $\tilde {M}(i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}_U^E))$. By Lemma 7.2, this means that
$\tilde {M}(i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}_U^E))$. By Lemma 7.2, this means that ![]() $\tilde {M}({\mathcal {E}})$ is in
$\tilde {M}({\mathcal {E}})$ is in ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$. This completes the proof.
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$. This completes the proof.
Let ![]() $S$ be a locally closed subset in
$S$ be a locally closed subset in ![]() $X$ and
$X$ and ![]() $\bar {S}$ be the closure of
$\bar {S}$ be the closure of ![]() $S$ in
$S$ in ![]() $X$ and set
$X$ and set ![]() $D_S:=\bar {S}{\backslash } S$. Let
$D_S:=\bar {S}{\backslash } S$. Let ![]() $\phi$ be a continuous
$\phi$ be a continuous ![]() ${\mathbb {C}}$-valued function on
${\mathbb {C}}$-valued function on ![]() $S$. The inclusion
$S$. The inclusion ![]() $i_{(\bar {S}, D_S)}\colon {(\bar {S}, D_S)}\rightarrow X$ is a tame map, we get
$i_{(\bar {S}, D_S)}\colon {(\bar {S}, D_S)}\rightarrow X$ is a tame map, we get ![]() $i_{{(\bar {S}, D_S)} !}\Lambda ^\phi _{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We also set
$i_{{(\bar {S}, D_S)} !}\Lambda ^\phi _{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We also set ![]() ${\mathcal {E}}^\phi :=\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}\overset {+}{\otimes } \mathbb {k}^E_X\in E^b(\mathrm {I}\mathbb {k}_X)$.
${\mathcal {E}}^\phi :=\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}\overset {+}{\otimes } \mathbb {k}^E_X\in E^b(\mathrm {I}\mathbb {k}_X)$.
Lemma 7.4 We have ![]() $M({\mathcal {E}}^\phi )\cong i_{{(\bar {S}, D_S)} !}\Lambda ^\phi$.
$M({\mathcal {E}}^\phi )\cong i_{{(\bar {S}, D_S)} !}\Lambda ^\phi$.
Proof. By the definition of ![]() $M$,
$M$, ![]() $M({\mathcal {E}}^\phi )\cong \underset {a \rightarrow \infty }{\text {`{$\lim$ }'}}\big ( {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t+a}\big )$. From the proof of Lemma 7.2, this colimit stabilizes. In particular,
$M({\mathcal {E}}^\phi )\cong \underset {a \rightarrow \infty }{\text {`{$\lim$ }'}}\big ( {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t+a}\big )$. From the proof of Lemma 7.2, this colimit stabilizes. In particular, ![]() $M({\mathcal {E}}^\phi )\cong {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}=:i_{{(\bar {S}, D_S)}!}\Lambda ^\phi$
$M({\mathcal {E}}^\phi )\cong {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}=:i_{{(\bar {S}, D_S)}!}\Lambda ^\phi$
Lemma 7.5 There exists a canonical isomorphism
Proof. By Lemmas 5.11 and 5.12, we have
 \begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)}(i_{{(\bar{S}, D_S)} !}\Lambda^{\phi}, i_{{(\bar{S}, D_S)} !}\Lambda^{\phi'})\cong \begin{cases} \mathbb{k} & \text{$\max\{0, {\mathop{\mathfrak{Re}}\nolimits}\phi-{\mathop{\mathfrak{Re}}\nolimits}\phi'\}$ is bounded,}\\ 0 & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)}(i_{{(\bar{S}, D_S)} !}\Lambda^{\phi}, i_{{(\bar{S}, D_S)} !}\Lambda^{\phi'})\cong \begin{cases} \mathbb{k} & \text{$\max\{0, {\mathop{\mathfrak{Re}}\nolimits}\phi-{\mathop{\mathfrak{Re}}\nolimits}\phi'\}$ is bounded,}\\ 0 & \text{otherwise.} \end{cases} \end{equation}
It is easy to see that the right-hand side of (7.15) also has the same formula. In the case that ![]() $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\phi '\}$ is bounded, there exists
$\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\phi '\}$ is bounded, there exists ![]() $c\in \mathbb{R} _{\geqslant 0}$ such that
$c\in \mathbb{R} _{\geqslant 0}$ such that ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi < {\mathop {\mathfrak {Re}}\nolimits }\phi '+c$ everywhere. For a map
$ {\mathop {\mathfrak {Re}}\nolimits }\phi < {\mathop {\mathfrak {Re}}\nolimits }\phi '+c$ everywhere. For a map ![]() $f\in \operatorname {Hom}_{E^b(\mathrm {I}\mathbb {k}_X)}({\mathcal {E}}^\phi , {\mathcal {E}}^{\phi '})$, we have a lift
$f\in \operatorname {Hom}_{E^b(\mathrm {I}\mathbb {k}_X)}({\mathcal {E}}^\phi , {\mathcal {E}}^{\phi '})$, we have a lift ![]() $\tilde {f}\colon \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}\rightarrow \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '(x)+c\}}$ of usual
$\tilde {f}\colon \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}\rightarrow \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '(x)+c\}}$ of usual ![]() $ {\mathbb {R}}$-constructible sheaves. Then
$ {\mathbb {R}}$-constructible sheaves. Then ![]() $\tilde {f}$ induces a morphism
$\tilde {f}$ induces a morphism ![]() $i_{{(\bar {S}, D_S)} !}\Lambda ^\phi \rightarrow i_{{(\bar {S}, D_S)} !}\Lambda ^{\phi '}$. It is easy to see that the induced morphism only depends on the choice of
$i_{{(\bar {S}, D_S)} !}\Lambda ^\phi \rightarrow i_{{(\bar {S}, D_S)} !}\Lambda ^{\phi '}$. It is easy to see that the induced morphism only depends on the choice of ![]() $f$. By the proof of Lemma 5.11, this gives an isomorphism.
$f$. By the proof of Lemma 5.11, this gives an isomorphism.
8. Irregular Riemann–Hilbert correspondence
In this section, we will prove our version of the irregular Riemann–Hilbert correspondence as a corollary of D’Agnolo and Kashiwara's one. In this section, we will work over ![]() ${\mathbb {C}}$.
${\mathbb {C}}$.
8.1 An example
Before going to the general case, we would like to see some examples of the correspondence in ![]() $\dim =1$. We will freely use the standard language of Stokes phenomenon, for which one can refer to the standard reference, for example, [Reference SibuyaSib90].
$\dim =1$. We will freely use the standard language of Stokes phenomenon, for which one can refer to the standard reference, for example, [Reference SibuyaSib90].
We will consider the case when ![]() $X={\mathbb {D}}$ a disk around
$X={\mathbb {D}}$ a disk around ![]() $0\in {\mathbb {C}}$. Let
$0\in {\mathbb {C}}$. Let ![]() ${\mathcal {M}}$ be a meromorphic connection with poles in
${\mathcal {M}}$ be a meromorphic connection with poles in ![]() $0\in {\mathbb {D}}$. For the simplicity of the exposition, we assume that the formal completion of
$0\in {\mathbb {D}}$. For the simplicity of the exposition, we assume that the formal completion of ![]() ${\mathcal {M}}$ at
${\mathcal {M}}$ at ![]() $0$ is decomposed as
$0$ is decomposed as ![]() ${\bigoplus} _{\phi \in \Phi } {\mathcal {E}}(\phi )$ where
${\bigoplus} _{\phi \in \Phi } {\mathcal {E}}(\phi )$ where ![]() $\Phi$ is a set of meromorphic functions with poles in
$\Phi$ is a set of meromorphic functions with poles in ![]() $0\in {\mathbb {D}}$,
$0\in {\mathbb {D}}$, ![]() ${\mathcal {E}}(\phi )$ is a connection defined by
${\mathcal {E}}(\phi )$ is a connection defined by ![]() $d+\phi$. The set
$d+\phi$. The set ![]() $\Phi$ give a sectorial decomposition
$\Phi$ give a sectorial decomposition ![]() ${\mathbb {D}}{\backslash } 0={\bigcup} S_i$ by the Stokes rays and there exists a complete set of solutions
${\mathbb {D}}{\backslash } 0={\bigcup} S_i$ by the Stokes rays and there exists a complete set of solutions ![]() $\{s_{\phi }^i\}$ on each
$\{s_{\phi }^i\}$ on each ![]() $S_i$. On each Stokes ray, we have a transformation matrix between the sets of solutions. The transformed
$S_i$. On each Stokes ray, we have a transformation matrix between the sets of solutions. The transformed ![]() $s_\phi$ can have a component of
$s_\phi$ can have a component of ![]() $s_{\phi '}$ only if
$s_{\phi '}$ only if ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi \geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$ on the ray. We denote the transformation matrix on the Stokes ray
$ {\mathop {\mathfrak {Re}}\nolimits }\phi \geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$ on the ray. We denote the transformation matrix on the Stokes ray ![]() $r$ by
$r$ by ![]() $S_r$.
$S_r$.
Since
if ![]() $ {\mathop {\mathfrak {Re}}\nolimits }\phi \leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$, we can represent the transposition of
$ {\mathop {\mathfrak {Re}}\nolimits }\phi \leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$, we can represent the transposition of ![]() $S_r$ in
$S_r$ in ![]() $\operatorname {End}({\bigoplus} \Lambda ^\phi )$, as an isomorphism, locally around the ray
$\operatorname {End}({\bigoplus} \Lambda ^\phi )$, as an isomorphism, locally around the ray ![]() $r$. Gluing up
$r$. Gluing up ![]() ${\bigoplus} _\phi \Lambda ^\phi$ by the these morphisms, we get the Riemann–Hilbert dual object (i.e. the image of the ‘de Rham’ functor) of
${\bigoplus} _\phi \Lambda ^\phi$ by the these morphisms, we get the Riemann–Hilbert dual object (i.e. the image of the ‘de Rham’ functor) of ![]() ${\mathcal {M}}$ in terms of irregular constructible sheaves.
${\mathcal {M}}$ in terms of irregular constructible sheaves.
Of course, by the same procedure just replacing ![]() $\Lambda ^\phi$ with
$\Lambda ^\phi$ with ![]() ${\mathcal {E}}^\phi$ produces an enhanced ind-sheaf corresponding
${\mathcal {E}}^\phi$ produces an enhanced ind-sheaf corresponding ![]() ${\mathcal {E}}$ to by D’Agnolo and Kashiwara's functor [Reference D'Agnolo and KashiwaraDK16].
${\mathcal {E}}$ to by D’Agnolo and Kashiwara's functor [Reference D'Agnolo and KashiwaraDK16].
8.2 Notation for analytic  ${\mathcal {D}}$-modules
${\mathcal {D}}$-modules
We refer the theory of analytic ![]() ${\mathcal {D}}$-modules to [Reference KashiwaraKas03]. In this subsection, we simply recall the notation. For a complex manifold,
${\mathcal {D}}$-modules to [Reference KashiwaraKas03]. In this subsection, we simply recall the notation. For a complex manifold, ![]() ${\mathcal {D}}_X$ is the sheaf of differential operators,
${\mathcal {D}}_X$ is the sheaf of differential operators, ![]() $\mathrm {Mod}({\mathcal {D}}_X)$ is the category of left
$\mathrm {Mod}({\mathcal {D}}_X)$ is the category of left ![]() ${\mathcal {D}}$-modules, and
${\mathcal {D}}$-modules, and ![]() $D^b({\mathcal {D}}_X)$ is the bounded derived category of
$D^b({\mathcal {D}}_X)$ is the bounded derived category of ![]() ${\mathcal {D}}$-modules. We denote the full subcategory of
${\mathcal {D}}$-modules. We denote the full subcategory of ![]() $D^b({\mathcal {D}}_X)$ spanned by cohomologically holonomic
$D^b({\mathcal {D}}_X)$ spanned by cohomologically holonomic ![]() ${\mathcal {D}}$-modules by
${\mathcal {D}}$-modules by ![]() $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
$D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
The duality functor ![]() ${\mathbb {D}}$ is a contravariant autoequivalence of
${\mathbb {D}}$ is a contravariant autoequivalence of ![]() $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$. For a morphism of complex manifolds
$D^b_{\mathrm {hol}}({\mathcal {D}}_X)$. For a morphism of complex manifolds ![]() $f\colon X\rightarrow Y$, we can define the following functors,
$f\colon X\rightarrow Y$, we can define the following functors,
by using transfer ![]() ${\mathcal {D}}$-modules
${\mathcal {D}}$-modules ![]() ${\mathcal {D}}_{X\leftarrow Y}$ and
${\mathcal {D}}_{X\leftarrow Y}$ and ![]() ${\mathcal {D}}_{X\rightarrow Y}$. The functor
${\mathcal {D}}_{X\rightarrow Y}$. The functor ![]() $f^{\dagger}$ always preserves cohomologically holonomic modules. If
$f^{\dagger}$ always preserves cohomologically holonomic modules. If ![]() $f$ is proper,
$f$ is proper, ![]() $\int _f$ also preserves cohomologically holonomic modules. For a proper
$\int _f$ also preserves cohomologically holonomic modules. For a proper ![]() $f$, the pair of functors form an adjoint pair
$f$, the pair of functors form an adjoint pair ![]() $\int _f \dashv f^{\dagger}$. We also set
$\int _f \dashv f^{\dagger}$. We also set ![]() $f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}\colon D^b_{\mathrm {hol}}({\mathcal {D}}_Y)\rightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and
$f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}\colon D^b_{\mathrm {hol}}({\mathcal {D}}_Y)\rightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and ![]() $f_\star :={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then
$f_\star :={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then ![]() $f^\star \dashv f_\star$
$f^\star \dashv f_\star$
8.3 Irregular Riemann–Hilbert correspondence using enhanced sheaves
We recall the irregular Riemann–Hilbert correspondence by the result of D'Agnolo and Kashiwara.
Theorem 8.1 [Reference D'Agnolo and KashiwaraDK16]
There exists a contravariant embedding
Our convention is slightly different from the original one in [Reference D'Agnolo and KashiwaraDK16]. Let ![]() $\mathrm {Sol}^{{\mathbb {E}}}$ be the original one. We set
$\mathrm {Sol}^{{\mathbb {E}}}$ be the original one. We set ![]() $\mathrm {Sol}^E:=\mathrm {Sol}^{\mathbb {E}}[\dim X]$ We have
$\mathrm {Sol}^E:=\mathrm {Sol}^{\mathbb {E}}[\dim X]$ We have ![]() $\mathrm {Sol}^E:={\mathbb {D}}\circ {\mathrm {DR}}^E$ where
$\mathrm {Sol}^E:={\mathbb {D}}\circ {\mathrm {DR}}^E$ where ![]() ${\mathrm {DR}}^E$ is the same as the original one. We collect some properties of the irregular Riemann–Hilbert correspondence as follows.
${\mathrm {DR}}^E$ is the same as the original one. We collect some properties of the irregular Riemann–Hilbert correspondence as follows.
Proposition 8.2 [Reference D'Agnolo and KashiwaraDK16, Theorem 9.4.8, Proposition 9.4.10]
(i) There exists a canonical isomorphism
 ${\mathbb {D}}\circ {\mathrm {DR}}^E\simeq {\mathrm {DR}}^E\circ {\mathbb {D}}$.
${\mathbb {D}}\circ {\mathrm {DR}}^E\simeq {\mathrm {DR}}^E\circ {\mathbb {D}}$.(ii) For a morphism
 $f\colon X\rightarrow Y$ of complex manifolds, there exists an isomorphism
$f\colon X\rightarrow Y$ of complex manifolds, there exists an isomorphism  ${\mathrm {DR}}^E\circ f^{\dagger} \simeq Ef^!\circ {\mathrm {DR}}^E$.
${\mathrm {DR}}^E\circ f^{\dagger} \simeq Ef^!\circ {\mathrm {DR}}^E$.(iii) For a proper map
 $f\colon X\rightarrow Y$, we have
$f\colon X\rightarrow Y$, we have  ${\mathrm {DR}}^E\circ \int _f\simeq Ef_*\circ {\mathrm {DR}}^E$.
${\mathrm {DR}}^E\circ \int _f\simeq Ef_*\circ {\mathrm {DR}}^E$.(iv) There exists an isomorphism
 $\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$ for
$\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$ for  ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and
${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and  ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$.
${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$.
We will also use the following fundamental result. Let ![]() $Y$ be an analytic hypersurface of the complex manifold
$Y$ be an analytic hypersurface of the complex manifold ![]() $X$. Take a meromorphic function
$X$. Take a meromorphic function ![]() $\phi$ with poles in
$\phi$ with poles in ![]() $Y$;
$Y$; ![]() $\phi \in {\mathcal {O}}_X(*Y)$. We set
$\phi \in {\mathcal {O}}_X(*Y)$. We set ![]() ${\mathcal {E}}(\phi ):=({\mathcal {D}}_X\cdot e^\phi )(*Y)$.
${\mathcal {E}}(\phi ):=({\mathcal {D}}_X\cdot e^\phi )(*Y)$.
Our convention for ![]() $\mathrm {Sol}^E$ is shifted from D’Agnolo and Kashiwara's one so that the following holds.
$\mathrm {Sol}^E$ is shifted from D’Agnolo and Kashiwara's one so that the following holds.
Proposition 8.3 [Reference D'Agnolo and KashiwaraDK16, Lemma 9.3.1]
There exists an isomorphism
8.4 Irregular Riemann–Hilbert correspondence
Let us denote the essential image of ![]() $\mathrm {Sol}^E$ by
$\mathrm {Sol}^E$ by ![]() $E^b_{{\mathcal {D}}}(\mathrm {I}{\mathbb{C}} _X)$.
$E^b_{{\mathcal {D}}}(\mathrm {I}{\mathbb{C}} _X)$.
Lemma 8.4 The object ![]() $M({\mathcal {E}})$ is irregular constructible for
$M({\mathcal {E}})$ is irregular constructible for ![]() ${\mathcal {E}}\in E^b_{\mathcal {D}}(\mathrm {I}{\mathbb{C}} _X)$.
${\mathcal {E}}\in E^b_{\mathcal {D}}(\mathrm {I}{\mathbb{C}} _X)$.
Proof. We will prove by induction on the dimension of the support.
Let us take a holonomic ![]() ${\mathcal {D}}$-module
${\mathcal {D}}$-module ![]() ${\mathcal {M}}$ and consider
${\mathcal {M}}$ and consider ![]() ${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$.
${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$.
If the dimension of the support of ![]() $M({\mathcal {E}})$ is zero-dimensional, it is irregular constructible. We suppose that the statement is true for any
$M({\mathcal {E}})$ is zero-dimensional, it is irregular constructible. We suppose that the statement is true for any ![]() ${\mathcal {E}}'$ with
${\mathcal {E}}'$ with ![]() $\dim \mathrm {supp}\, M({\mathcal {E}}')<\dim \mathrm {supp}\, M({\mathcal {E}})$.
$\dim \mathrm {supp}\, M({\mathcal {E}}')<\dim \mathrm {supp}\, M({\mathcal {E}})$.
Since the question is local, we work locally. We set ![]() $Y:=\mathrm {supp}\,(M({\mathcal {E}}))$. Let
$Y:=\mathrm {supp}\,(M({\mathcal {E}}))$. Let ![]() $\pi \colon Y'\rightarrow Y$ be a resolution of singularities of
$\pi \colon Y'\rightarrow Y$ be a resolution of singularities of ![]() $Y$. Let
$Y$. Let ![]() $D$ be the inverse image of the union of singularities of
$D$ be the inverse image of the union of singularities of ![]() $Y$ and
$Y$ and ![]() ${\mathcal {M}}$. Then there exists a canonical morphism
${\mathcal {M}}$. Then there exists a canonical morphism
Since ![]() $(\pi ^\star {\mathcal {M}})(*D)$ is a meromorphic connection,
$(\pi ^\star {\mathcal {M}})(*D)$ is a meromorphic connection, ![]() $M(\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D)))$ is irregular constructible. Note that
$M(\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D)))$ is irregular constructible. Note that ![]() $\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D))$ has its support in the complement of
$\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D))$ has its support in the complement of ![]() $D$. Hence
$D$. Hence ![]() $M(\mathrm {Sol}^E({\mathcal {M}}_1'))$ has its support in the complement of
$M(\mathrm {Sol}^E({\mathcal {M}}_1'))$ has its support in the complement of ![]() $\pi (D)$ and is irregular constructible. The cone
$\pi (D)$ and is irregular constructible. The cone ![]() $C$ of this morphism is living on a divisor of
$C$ of this morphism is living on a divisor of ![]() $Y$. By the induction hypothesis,
$Y$. By the induction hypothesis, ![]() $M(\mathrm {Sol}^E(C))$ is irregular constructible. This completes the proof.
$M(\mathrm {Sol}^E(C))$ is irregular constructible. This completes the proof.
Lemma 8.5 For an irregular local system ![]() $ {\mathcal {V}}$, there exists an enhanced ind-sheaf
$ {\mathcal {V}}$, there exists an enhanced ind-sheaf ![]() $N( {\mathcal {V}})$ such that
$N( {\mathcal {V}})$ such that ![]() $M(N( {\mathcal {V}}))\cong {\mathcal {V}}$.
$M(N( {\mathcal {V}}))\cong {\mathcal {V}}$.
Proof. For an irregular local system ![]() $ {\mathcal {V}}$, one can find a sectorial covering (Definition 5.21). On each open subset in the covering, we have
$ {\mathcal {V}}$, one can find a sectorial covering (Definition 5.21). On each open subset in the covering, we have ![]() ${\bigoplus} {\mathcal {V}}\cong \Lambda ^\phi$. By Lemma 7.5, we can glue up
${\bigoplus} {\mathcal {V}}\cong \Lambda ^\phi$. By Lemma 7.5, we can glue up ![]() ${\bigoplus} {\mathcal {E}}^\phi$ by the corresponding morphisms gluing
${\bigoplus} {\mathcal {E}}^\phi$ by the corresponding morphisms gluing ![]() ${\bigoplus} \Lambda ^\phi$ up to make
${\bigoplus} \Lambda ^\phi$ up to make ![]() $ {\mathcal {V}}$. We denote the resulting enhanced ind-sheaf by
$ {\mathcal {V}}$. We denote the resulting enhanced ind-sheaf by ![]() $N( {\mathcal {V}})$.
$N( {\mathcal {V}})$.
Since the functor ![]() $M$ maps
$M$ maps ![]() ${\mathcal {E}}^\phi$ to
${\mathcal {E}}^\phi$ to ![]() $\Lambda ^\phi$ (Lemma 7.4) and the gluing maps are translated by Lemma 7.5, the enhanced ind-sheaf
$\Lambda ^\phi$ (Lemma 7.4) and the gluing maps are translated by Lemma 7.5, the enhanced ind-sheaf ![]() $N( {\mathcal {V}})$ satisfies
$N( {\mathcal {V}})$ satisfies ![]() $MN( {\mathcal {V}})\cong {\mathcal {V}}$.
$MN( {\mathcal {V}})\cong {\mathcal {V}}$.
Our version of an irregular Riemann–Hilbert correspondence is the following.
Theorem 8.6 The functor ![]() $M$ is a contravariant exact equivalence:
$M$ is a contravariant exact equivalence:
In particular, there exists a contravariant equivalence
Proof. First, we will prove the full faithfulness. Let ![]() ${\mathcal {M}}, {\mathcal {N}}$ be holonomic
${\mathcal {M}}, {\mathcal {N}}$ be holonomic ![]() ${\mathcal {D}}_X$-modules. Set
${\mathcal {D}}_X$-modules. Set ![]() ${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$ and
${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$ and ![]() ${\mathcal {F}}:=\mathrm {Sol}^E({\mathcal {N}})$. Then we have
${\mathcal {F}}:=\mathrm {Sol}^E({\mathcal {N}})$. Then we have
We would like to prove
Take a common stratification for ![]() ${\mathcal {E}}, {\mathcal {F}}$ and
${\mathcal {E}}, {\mathcal {F}}$ and ![]() $i\colon U\hookrightarrow X$ be the open stratum and
$i\colon U\hookrightarrow X$ be the open stratum and ![]() $j\colon V\hookrightarrow X$ be the complement. Then by Lemma 4.24, we have an exact triangle
$j\colon V\hookrightarrow X$ be the complement. Then by Lemma 4.24, we have an exact triangle
We also have the corresponding recollement for enhanced ind-sheaves
which is a direct consequence of the recollement on ![]() $X\times {\mathbb {R}}$. By the construction, this is the image of (8.11) under
$X\times {\mathbb {R}}$. By the construction, this is the image of (8.11) under ![]() $M$. Hence, it is enough to show the full faithfulness for irregular local systems.
$M$. Hence, it is enough to show the full faithfulness for irregular local systems.
For an irregular local system, we have locally a sectorial covering such that ![]() ${\mathcal {E}}, {\mathcal {F}}$ have the form
${\mathcal {E}}, {\mathcal {F}}$ have the form ![]() ${\bigoplus} {\mathcal {E}}^\phi$,
${\bigoplus} {\mathcal {E}}^\phi$, ![]() $M({\mathcal {E}}), M({\mathcal {F}})$ have the form
$M({\mathcal {E}}), M({\mathcal {F}})$ have the form ![]() ${\bigoplus} \Lambda ^\phi$, and these are related by Lemma 7.4. Hence we have the full faithfulness on each open cover by Lemma 7.5. Note also that
${\bigoplus} \Lambda ^\phi$, and these are related by Lemma 7.4. Hence we have the full faithfulness on each open cover by Lemma 7.5. Note also that ![]() $M$ is a morphism between stacks, which is clear from the definition. Hence we can glue up these isomorphisms to get the global full faithfulness.
$M$ is a morphism between stacks, which is clear from the definition. Hence we can glue up these isomorphisms to get the global full faithfulness.
To prove the essential surjectivity, we will use Mochizuki's curve test criterion [Reference MochizukiMoc16]. Since ![]() $\mathrm {Sol}^\Lambda$ is a fully faithful exact functor, by the recollement 4.24, it is enough to see
$\mathrm {Sol}^\Lambda$ is a fully faithful exact functor, by the recollement 4.24, it is enough to see ![]() $\mathrm {Sol}^\Lambda$ hits each irregular local system.
$\mathrm {Sol}^\Lambda$ hits each irregular local system.
Let ![]() $ {\mathcal {V}}$ be an irregular local system on
$ {\mathcal {V}}$ be an irregular local system on ![]() ${(\bar {S}, D_S)}\subset X$. Let
${(\bar {S}, D_S)}\subset X$. Let ![]() $\phi \colon \mathbf {D} \rightarrow X$ be a holomorphic disk satisfying
$\phi \colon \mathbf {D} \rightarrow X$ be a holomorphic disk satisfying ![]() $\phi ^{-1}(D_S)=\{ 0\}$. We set
$\phi ^{-1}(D_S)=\{ 0\}$. We set ![]() $x:=\phi (0)$.
$x:=\phi (0)$.
By the construction, ![]() $N( {\mathcal {V}})$ of Lemma 8.5 has a sectorial covering around
$N( {\mathcal {V}})$ of Lemma 8.5 has a sectorial covering around ![]() $x$ equipped with a set of multi-valued meromorphic functions. The pull-back of a sectorial covering is again sectorial. Hence
$x$ equipped with a set of multi-valued meromorphic functions. The pull-back of a sectorial covering is again sectorial. Hence ![]() $E\phi ^{-1}N( {\mathcal {V}})$ has a sectorial covering on which
$E\phi ^{-1}N( {\mathcal {V}})$ has a sectorial covering on which ![]() $E\phi ^{-1}N( {\mathcal {V}})$ restricts to the form
$E\phi ^{-1}N( {\mathcal {V}})$ restricts to the form ![]() ${\bigoplus} {\mathcal {E}}^\phi$ and the gluing data is the Stokes data. Since the situation is now one-dimensional, it is standard to see this is in the image of
${\bigoplus} {\mathcal {E}}^\phi$ and the gluing data is the Stokes data. Since the situation is now one-dimensional, it is standard to see this is in the image of ![]() $\mathrm {Sol}^E$ (e.g. by the discussion of [Reference D'Agnolo and KashiwaraDK19, 9.8]). Then Mochizuki's theorem [Reference MochizukiMoc16] tells us that there exists an object in
$\mathrm {Sol}^E$ (e.g. by the discussion of [Reference D'Agnolo and KashiwaraDK19, 9.8]). Then Mochizuki's theorem [Reference MochizukiMoc16] tells us that there exists an object in ![]() $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ such that
$D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ such that ![]() $\mathrm {Sol}^E({\mathcal {M}})=N( {\mathcal {V}})$. Hence we have
$\mathrm {Sol}^E({\mathcal {M}})=N( {\mathcal {V}})$. Hence we have ![]() $\mathrm {Sol}^\Lambda ({\mathcal {M}})=M\circ N( {\mathcal {V}})= {\mathcal {V}}$. This proves the essential surjectivity.
$\mathrm {Sol}^\Lambda ({\mathcal {M}})=M\circ N( {\mathcal {V}})= {\mathcal {V}}$. This proves the essential surjectivity.
Corollary 8.7 There exists an exact equivalence
In [Reference D'Agnolo and KashiwaraDK16], it is proved that the composition of ![]() $i_{\mathrm {reg}}\colon D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and
$i_{\mathrm {reg}}\colon D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and ![]() $\mathrm {Sol}^E$ is the same as the composition of the regular Riemann–Hilbert solution functor
$\mathrm {Sol}^E$ is the same as the composition of the regular Riemann–Hilbert solution functor ![]() $\mathrm {Sol}$ and
$\mathrm {Sol}$ and ![]() $D^b_c({\mathbb {C}}_X)\hookrightarrow E^b(\mathrm {I}{\mathbb{C}} _X)$. Here the last inclusion is obtained as
$D^b_c({\mathbb {C}}_X)\hookrightarrow E^b(\mathrm {I}{\mathbb{C}} _X)$. Here the last inclusion is obtained as ![]() $(\pi ^{-1}(-)\otimes {\mathbb {C}}_{X\times _{ {\mathbb {R}}_{\geqslant 0}}})\overset {+}{\otimes } {\mathbb {C}}^E_X$ where
$(\pi ^{-1}(-)\otimes {\mathbb {C}}_{X\times _{ {\mathbb {R}}_{\geqslant 0}}})\overset {+}{\otimes } {\mathbb {C}}^E_X$ where ![]() $\pi \colon M\times \bar { {\mathbb {R}}}\rightarrow M$. By the definition of
$\pi \colon M\times \bar { {\mathbb {R}}}\rightarrow M$. By the definition of ![]() $M$, the following corollary is clear.
$M$, the following corollary is clear.
Corollary 8.8 We have an identification ![]() $ {\mathfrak {G}}\circ \mathrm {Sol}\cong \mathrm {Sol}^\Lambda \circ i_{\mathrm {reg}}$.
$ {\mathfrak {G}}\circ \mathrm {Sol}\cong \mathrm {Sol}^\Lambda \circ i_{\mathrm {reg}}$.
8.5 Functors
In this subsection, we prove the commutativity between ![]() $\mathrm {Sol}^\Lambda$ and various functors. We assume that all the spaces are without boundary in this subsection.
$\mathrm {Sol}^\Lambda$ and various functors. We assume that all the spaces are without boundary in this subsection.
Proposition 8.9 Let ![]() $f\colon X\rightarrow Y$. We have
$f\colon X\rightarrow Y$. We have
In particular,
Proof. Since we know ![]() $Ef^*$ commutes with
$Ef^*$ commutes with ![]() $\mathrm {Sol}^E$, it is enough to see the commutativity with the functor
$\mathrm {Sol}^E$, it is enough to see the commutativity with the functor ![]() $M$. Let us take an
$M$. Let us take an ![]() $ {\mathbb {R}}$-constructible sheaf
$ {\mathbb {R}}$-constructible sheaf ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $X\times \bar {\mathbb{R} }$. Let
$X\times \bar {\mathbb{R} }$. Let ![]() $\bar {f}$ be the direct product of
$\bar {f}$ be the direct product of ![]() $f\colon X\rightarrow Y$ and
$f\colon X\rightarrow Y$ and ![]() $\operatorname {id}\colon \bar {\mathbb{R} }\rightarrow \bar {\mathbb{R} }$. Then we have
$\operatorname {id}\colon \bar {\mathbb{R} }\rightarrow \bar {\mathbb{R} }$. Then we have
Hence we have ![]() $M(\bar {f}^{-1}{\mathcal {E}})\simeq f^{-1}M({\mathcal {E}})$. This proves the first line.
$M(\bar {f}^{-1}{\mathcal {E}})\simeq f^{-1}M({\mathcal {E}})$. This proves the first line.
Lemma 8.10 We have
For ![]() ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and
${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and ![]() ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have
${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have
Proof. By [Reference D'Agnolo and KashiwaraDK16], we have ![]() $\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$. Hence it suffices to prove
$\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$. Hence it suffices to prove ![]() $M(\mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}}))\simeq M(\mathrm {Sol}^E({\mathcal {M}}))\boxtimes M(\mathrm {Sol}^E({\mathcal {N}}))$.
$M(\mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}}))\simeq M(\mathrm {Sol}^E({\mathcal {M}}))\boxtimes M(\mathrm {Sol}^E({\mathcal {N}}))$.
First, note that we have ![]() $p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[a,\infty )}({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})\simeq p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{t_1+t_2\geqslant a}({\mathcal {E}}\boxtimes {\mathcal {F}})$. We also have a map
$p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[a,\infty )}({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})\simeq p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{t_1+t_2\geqslant a}({\mathcal {E}}\boxtimes {\mathcal {F}})$. We also have a map
By combining these, we get a map ![]() $M({\mathcal {E}})\boxtimes M({\mathcal {F}})\rightarrow M({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})$. It suffices to show that this map is locally an isomorphism. For enhanced ind-sheaves
$M({\mathcal {E}})\boxtimes M({\mathcal {F}})\rightarrow M({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})$. It suffices to show that this map is locally an isomorphism. For enhanced ind-sheaves ![]() ${\mathcal {E}}^{\phi _1}, {\mathcal {E}}^{\phi _2}$, we have
${\mathcal {E}}^{\phi _1}, {\mathcal {E}}^{\phi _2}$, we have ![]() ${\mathcal {E}}^{\phi _1}\overset {+}{\boxtimes } {\mathcal {E}}^{\phi _2}\simeq {\mathcal {E}}^{\phi _1\oplus \phi _2}$. We also have
${\mathcal {E}}^{\phi _1}\overset {+}{\boxtimes } {\mathcal {E}}^{\phi _2}\simeq {\mathcal {E}}^{\phi _1\oplus \phi _2}$. We also have ![]() $\Lambda ^{\phi _1}\boxtimes \Lambda ^{\phi _2}\cong \Lambda ^{\phi _1\oplus \phi _2}$ from Lemma 5.13. Hence the morphism
$\Lambda ^{\phi _1}\boxtimes \Lambda ^{\phi _2}\cong \Lambda ^{\phi _1\oplus \phi _2}$ from Lemma 5.13. Hence the morphism ![]() $M({\mathcal {E}}^{\phi _1})\boxtimes M({\mathcal {E}}^{\phi _2})\rightarrow M({\mathcal {E}}^{\phi _1\oplus \phi _2})$ is an isomorphism. The general case can be reduced to this case by considering on each stratum.
$M({\mathcal {E}}^{\phi _1})\boxtimes M({\mathcal {E}}^{\phi _2})\rightarrow M({\mathcal {E}}^{\phi _1\oplus \phi _2})$ is an isomorphism. The general case can be reduced to this case by considering on each stratum.
Proposition 8.11 For ![]() ${\mathcal {M}}, {\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, we have
${\mathcal {M}}, {\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, we have
We also have
on ![]() $E^b_{{\mathcal {D}}}(\mathrm {I}\mathbb {k}_X)$
$E^b_{{\mathcal {D}}}(\mathrm {I}\mathbb {k}_X)$
Proof. Let ![]() $\delta \colon X\rightarrow X\times X$ be the diagonal embedding. Then
$\delta \colon X\rightarrow X\times X$ be the diagonal embedding. Then ![]() ${\mathcal {M}}\otimes {\mathcal {N}}\cong \delta ^{{\dagger} }({\mathcal {M}}\boxtimes {\mathcal {N}})$. Then we have,
${\mathcal {M}}\otimes {\mathcal {N}}\cong \delta ^{{\dagger} }({\mathcal {M}}\boxtimes {\mathcal {N}})$. Then we have,
 \begin{align} \mathrm{Sol}^\Lambda(\delta^{{{\dagger}}}({\mathcal{M}}\boxtimes {\mathcal{N}}))&\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}}\boxtimes {\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}})\boxtimes \mathrm{Sol}^\Lambda({\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \mathrm{Sol}^\Lambda({\mathcal{M}})\otimes \mathrm{Sol}^\Lambda({\mathcal{N}})[-\dim X], \end{align}
\begin{align} \mathrm{Sol}^\Lambda(\delta^{{{\dagger}}}({\mathcal{M}}\boxtimes {\mathcal{N}}))&\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}}\boxtimes {\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}})\boxtimes \mathrm{Sol}^\Lambda({\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \mathrm{Sol}^\Lambda({\mathcal{M}})\otimes \mathrm{Sol}^\Lambda({\mathcal{N}})[-\dim X], \end{align}where we used Lemmas 4.20 and 8.10. This proves the first claim. The second claim follows from the adjunction.
Proposition 8.12 Let ![]() $f\colon X\rightarrow Y$. We have
$f\colon X\rightarrow Y$. We have
Proof. The first equation is followed by the second one and Proposition 8.9.
We have
 \begin{align} {\mathbb{D}}\circ \mathrm{Sol}^\Lambda({\mathcal{E}})&\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\mathrm{Sol}^\Lambda({\mathcal{E}}), \omega^\Lambda_X)\nonumber\\ &\simeq M\circ \mathop{{{\mathcal{H}}}om}\nolimits^E(\mathrm{Sol}^E({\mathcal{E}}), \omega^E_X)\nonumber\\ &\simeq M\circ \mathrm{Sol}^E({\mathbb{D}}({\mathcal{E}}))\nonumber\\ &\simeq \mathrm{Sol}^\Lambda\circ {\mathbb{D}}({\mathcal{E}}), \end{align}
\begin{align} {\mathbb{D}}\circ \mathrm{Sol}^\Lambda({\mathcal{E}})&\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\mathrm{Sol}^\Lambda({\mathcal{E}}), \omega^\Lambda_X)\nonumber\\ &\simeq M\circ \mathop{{{\mathcal{H}}}om}\nolimits^E(\mathrm{Sol}^E({\mathcal{E}}), \omega^E_X)\nonumber\\ &\simeq M\circ \mathrm{Sol}^E({\mathbb{D}}({\mathcal{E}}))\nonumber\\ &\simeq \mathrm{Sol}^\Lambda\circ {\mathbb{D}}({\mathcal{E}}), \end{align}
where we used Proposition 8.11 and the commutativity of ![]() $\mathrm {Sol}^E$ with
$\mathrm {Sol}^E$ with ![]() ${\mathbb {D}}$ [Reference D'Agnolo and KashiwaraDK16]. This completes the proof of the third line.
${\mathbb {D}}$ [Reference D'Agnolo and KashiwaraDK16]. This completes the proof of the third line.
Proposition 8.13 Let ![]() $f\colon X\rightarrow Y$ be a proper map. Then we have
$f\colon X\rightarrow Y$ be a proper map. Then we have
Proof. By various adjunctions, we have
 \begin{align} \operatorname{Hom}\bigg( {\mathrm{DR}}^\Lambda\bigg(\int_{f!}{\mathcal{M}}\bigg), {\mathrm{DR}}^\Lambda({\mathcal{N}})\bigg)&\cong \operatorname{Hom} \bigg(\int_{f!}{\mathcal{M}},{\mathcal{N}} \bigg)\nonumber\\ &\cong \operatorname{Hom}({\mathcal{M}}, f^{\dagger}{\mathcal{N}})\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), {\mathrm{DR}}^\Lambda(f^{\dagger}{\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), f^!{\mathrm{DR}}^\Lambda ({\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}(f_!{\mathrm{DR}}^\Lambda({\mathcal{E}}), {\mathrm{DR}}^\Lambda {\mathcal{F}}). \end{align}
\begin{align} \operatorname{Hom}\bigg( {\mathrm{DR}}^\Lambda\bigg(\int_{f!}{\mathcal{M}}\bigg), {\mathrm{DR}}^\Lambda({\mathcal{N}})\bigg)&\cong \operatorname{Hom} \bigg(\int_{f!}{\mathcal{M}},{\mathcal{N}} \bigg)\nonumber\\ &\cong \operatorname{Hom}({\mathcal{M}}, f^{\dagger}{\mathcal{N}})\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), {\mathrm{DR}}^\Lambda(f^{\dagger}{\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), f^!{\mathrm{DR}}^\Lambda ({\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}(f_!{\mathrm{DR}}^\Lambda({\mathcal{E}}), {\mathrm{DR}}^\Lambda {\mathcal{F}}). \end{align}8.6 Corollaries
Proposition 8.14 Let ![]() $f\colon X\rightarrow Y$ be a proper morphism. Then
$f\colon X\rightarrow Y$ be a proper morphism. Then ![]() $f_* {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for
$f_* {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for ![]() $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
$ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
Proof. For ![]() $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, take
$ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, take ![]() $ {\mathcal {V}}':= {\mathcal {V}}\otimes _\mathbb {k}{\mathbb {C}}$. We set
$ {\mathcal {V}}':= {\mathcal {V}}\otimes _\mathbb {k}{\mathbb {C}}$. We set ![]() ${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda })^{-1}( {\mathcal {V}}')$. Then
${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda })^{-1}( {\mathcal {V}}')$. Then ![]() $\int _{f!}{\mathbb {D}}{\mathcal {M}}$ is holonomic. Proposition 8.13 tells us
$\int _{f!}{\mathbb {D}}{\mathcal {M}}$ is holonomic. Proposition 8.13 tells us ![]() ${\mathrm {DR}}^\Lambda (\int _{f!}{\mathbb {D}}{\mathcal {M}})\simeq f_!\circ {\mathrm {DR}}^\Lambda ({\mathbb {D}}\circ {\mathcal {M}})\simeq f_*\mathrm {Sol}^\Lambda ({\mathcal {M}})\simeq f_* {\mathcal {V}}'\otimes _\mathbb {k}{\mathbb {C}}$ is irregular constructible. Since the irregular constructibility is preserved under
${\mathrm {DR}}^\Lambda (\int _{f!}{\mathbb {D}}{\mathcal {M}})\simeq f_!\circ {\mathrm {DR}}^\Lambda ({\mathbb {D}}\circ {\mathcal {M}})\simeq f_*\mathrm {Sol}^\Lambda ({\mathcal {M}})\simeq f_* {\mathcal {V}}'\otimes _\mathbb {k}{\mathbb {C}}$ is irregular constructible. Since the irregular constructibility is preserved under ![]() $\otimes _{\mathbb {k}}{\mathbb {C}}$. This completes the proof.
$\otimes _{\mathbb {k}}{\mathbb {C}}$. This completes the proof.
Remark 8.15 To work with more general base fields, it is desirable to have a direct proof of the above result, which we do not have yet.
The following proposition says ‘an object of ![]() $D^b_{ic}(\Lambda _X)$ is actually a sheaf over
$D^b_{ic}(\Lambda _X)$ is actually a sheaf over ![]() $X$.’ It is logically not important, but conceptually makes us feel easy with irregular constructible sheaves. We use some results from the later sections to prove the following.
$X$.’ It is logically not important, but conceptually makes us feel easy with irregular constructible sheaves. We use some results from the later sections to prove the following.
Proposition 8.16 The essential image of ![]() $[\cdot ]\colon D^b(\mathrm {Mod}^0(\Lambda _X))\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ contains
$[\cdot ]\colon D^b(\mathrm {Mod}^0(\Lambda _X))\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ contains ![]() $D^b_{ic}(\Lambda _X)$.
$D^b_{ic}(\Lambda _X)$.
Proof. Let ![]() $ {\mathcal {V}}$ be an irregular constructible sheaf. Then we have
$ {\mathcal {V}}$ be an irregular constructible sheaf. Then we have ![]() $[ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))]\simeq {\mathcal {V}}\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by § 7.2 and Theorem 8.6. Since
$[ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))]\simeq {\mathcal {V}}\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by § 7.2 and Theorem 8.6. Since ![]() $[{\mathcal {E}}]\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ for
$[{\mathcal {E}}]\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ for ![]() ${\mathcal {E}}\in D^b(\mathrm {Ind}(\mathrm {Mod}^0(\Lambda _X)))$ if and only if
${\mathcal {E}}\in D^b(\mathrm {Ind}(\mathrm {Mod}^0(\Lambda _X)))$ if and only if ![]() ${\mathcal {E}}\in D^b(\mathrm {Mod}^0(\Lambda _X))$, we have
${\mathcal {E}}\in D^b(\mathrm {Mod}^0(\Lambda _X))$, we have ![]() $ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))\in D^b(\mathrm {Mod}^0(\Lambda _X))$. This completes the proof.
$ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))\in D^b(\mathrm {Mod}^0(\Lambda _X))$. This completes the proof.
9. Irregular perverse sheaves
In this section, we define the irregular perverse ![]() $t$-structure on the category of irregular constructible complexes. Over
$t$-structure on the category of irregular constructible complexes. Over ![]() ${\mathbb {C}}$, the heart is equivalent to the category of holonomic
${\mathbb {C}}$, the heart is equivalent to the category of holonomic ![]() ${\mathcal {D}}$-modules. We also prove
${\mathcal {D}}$-modules. We also prove ![]() $t$-exactness of various functors.
$t$-exactness of various functors.
9.1 Irregular perverse sheaves
For an object ![]() $ {\mathcal {V}}$ of
$ {\mathcal {V}}$ of ![]() $D^b_{ic}(\Lambda _X)$, we define the support by
$D^b_{ic}(\Lambda _X)$, we define the support by
Let us define the irregular perverse ![]() $t$-structure.
$t$-structure.
Definition 9.1 Let ![]() ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively
${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively ![]() ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of
${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of ![]() $D^b_{ic}(\Lambda _X)$ spanned by objects satisfying
$D^b_{ic}(\Lambda _X)$ spanned by objects satisfying
Let ![]() $({^p}D^{\leqslant 0}(\mathbb {k}_X), {^p}D^{\geqslant 0}(\mathbb {k}_X))$ be the perverse
$({^p}D^{\leqslant 0}(\mathbb {k}_X), {^p}D^{\geqslant 0}(\mathbb {k}_X))$ be the perverse ![]() $t$-structure of
$t$-structure of ![]() $D^b_c(\mathbb {k}_X)$.
$D^b_c(\mathbb {k}_X)$.
Lemma 9.2 We have ![]() $ {\mathfrak {F}}({^p}D_{ic}^{\leqslant 0}(\Lambda _X))\subset {^p}D^{\leqslant 0}(\mathbb {k}_X)$. Conversely, if
$ {\mathfrak {F}}({^p}D_{ic}^{\leqslant 0}(\Lambda _X))\subset {^p}D^{\leqslant 0}(\mathbb {k}_X)$. Conversely, if ![]() $ {\mathfrak {F}}( {\mathcal {V}})\in {^p}D^{\leqslant 0}(\mathbb {k}_X)$ for
$ {\mathfrak {F}}( {\mathcal {V}})\in {^p}D^{\leqslant 0}(\mathbb {k}_X)$ for ![]() $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, we have
$ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, we have ![]() $ {\mathcal {V}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$.
$ {\mathcal {V}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$.
Proof. Since ![]() $ {\mathfrak {F}}$ is
$ {\mathfrak {F}}$ is ![]() $t$-exact with respect to the standard
$t$-exact with respect to the standard ![]() $t$-structure (Lemma 6.1), we have
$t$-structure (Lemma 6.1), we have ![]() $H^i( {\mathfrak {F}}( {\mathcal {V}}))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}))$.
$H^i( {\mathfrak {F}}( {\mathcal {V}}))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}))$.
Proposition 9.3 The pair ![]() $({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ forms a
$({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ forms a ![]() $t$-structure.
$t$-structure.
To prove this proposition, we first prepare the following lemma.
Lemma 9.4 We have
for ![]() ${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and
${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ![]() ${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$.
${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$.
Proof. Note that the same statement for the usual perverse ![]() $t$-structure is known (e.g. [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 8.1.22]). By the commutativity proved in § 6, the first statement follows from Lemma 6.9. The second statement follows from the Verdier duality.
$t$-structure is known (e.g. [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 8.1.22]). By the commutativity proved in § 6, the first statement follows from Lemma 6.9. The second statement follows from the Verdier duality.
Proof Proof of Proposition 9.3
First, we will prove that for ![]() ${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and
${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ![]() ${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$, the vanishing
${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$, the vanishing
One can prove this just by mimicking the proof of [Reference Kashiwara and SchapiraKS90, Proposition 10.2.7].
It remains to show that there is a decomposition of objects in ![]() $D^b_{ic}(\Lambda _X)$. One can prove this by a usual argument for perverse sheaves as in [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 8.1.27].
$D^b_{ic}(\Lambda _X)$. One can prove this by a usual argument for perverse sheaves as in [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 8.1.27].
Definition 9.5 The heart of the ![]() $t$-structure is called the category of irregular perverse sheaves and denoted by
$t$-structure is called the category of irregular perverse sheaves and denoted by ![]() $\mathrm {Perv}_{ic}(k_X)$.
$\mathrm {Perv}_{ic}(k_X)$.
Theorem 9.6 The functor ![]() $\mathrm {Sol}^\Lambda$ restrict to a contravariant equivalence
$\mathrm {Sol}^\Lambda$ restrict to a contravariant equivalence
Lemma 9.7 Let ![]() ${\mathcal {D}}_i$
${\mathcal {D}}_i$ ![]() $(i=1,2)$ be triangulated categories with
$(i=1,2)$ be triangulated categories with ![]() $t$-structures
$t$-structures ![]() $(D^{\leqslant 0}_i, D_i^{\geqslant 0})$. Let
$(D^{\leqslant 0}_i, D_i^{\geqslant 0})$. Let ![]() $F\colon {\mathcal {D}}_1\rightarrow {\mathcal {D}}_2$ be a
$F\colon {\mathcal {D}}_1\rightarrow {\mathcal {D}}_2$ be a ![]() $t$-exact equivalence. Then
$t$-exact equivalence. Then ![]() $F$ gives an equivalence between
$F$ gives an equivalence between ![]() $t$-structures.
$t$-structures.
Proof. We have to show that ![]() $F\colon D^{\leqslant 0}_1\rightarrow D^{\leqslant 0}_2$ is essentially surjective. Let
$F\colon D^{\leqslant 0}_1\rightarrow D^{\leqslant 0}_2$ is essentially surjective. Let ![]() ${\mathcal {E}}$ be an object of
${\mathcal {E}}$ be an object of ![]() $D^{\leqslant 0}_2$. Then we have a standard triangle
$D^{\leqslant 0}_2$. Then we have a standard triangle
By applying ![]() $F$ again, we have
$F$ again, we have ![]() $F(\tau _{\geqslant 1}F^{-1}({\mathcal {E}}))\cong 0$ since
$F(\tau _{\geqslant 1}F^{-1}({\mathcal {E}}))\cong 0$ since ![]() ${\mathcal {E}}\in D^{\leqslant 0}_2$. Since
${\mathcal {E}}\in D^{\leqslant 0}_2$. Since ![]() $F$ is an equivalence, we have
$F$ is an equivalence, we have ![]() $\tau _{\geqslant 1}F^{-1}({\mathcal {E}})\cong 0$. Hence
$\tau _{\geqslant 1}F^{-1}({\mathcal {E}})\cong 0$. Hence ![]() $F^{-1}({\mathcal {E}})\in D^{\leqslant 0}_1$. We can prove for the positive part in a similar manner. This completes the proof.
$F^{-1}({\mathcal {E}})\in D^{\leqslant 0}_1$. We can prove for the positive part in a similar manner. This completes the proof.
Proof Proof of Theorem 9.6
By Lemma 9.7, it is enough to show that ![]() $\mathrm {Sol}^\Lambda$ is
$\mathrm {Sol}^\Lambda$ is ![]() $t$-exact. We only show the condition
$t$-exact. We only show the condition
for any holonomic ![]() ${\mathcal {D}}$-module
${\mathcal {D}}$-module ![]() ${\mathcal {M}}$. The other case follows from the Verdier duality.
${\mathcal {M}}$. The other case follows from the Verdier duality.
We will prove by induction on the dimension of the support of ![]() ${\mathcal {M}}$. Let
${\mathcal {M}}$. Let ![]() $Z'$ be the support of
$Z'$ be the support of ![]() ${\mathcal {M}}$ and
${\mathcal {M}}$ and ![]() $Z$ be the union of the component of the maximal dimension of
$Z$ be the union of the component of the maximal dimension of ![]() $Z'$. Take
$Z'$. Take ![]() $x\in Z$ and we will argue locally around
$x\in Z$ and we will argue locally around ![]() $x$.
$x$.
Take a divisor ![]() $D$ in
$D$ in ![]() $X$ such that
$X$ such that ![]() $D$ does not contain any component of
$D$ does not contain any component of ![]() $Z$ but the singularities of
$Z$ but the singularities of ![]() ${\mathcal {M}}$. We set
${\mathcal {M}}$. We set ![]() ${\mathcal {M}}_1:=\operatorname {im}({\mathcal {M}}\rightarrow {\mathcal {M}}(*D))$. Then we have two exact sequences
${\mathcal {M}}_1:=\operatorname {im}({\mathcal {M}}\rightarrow {\mathcal {M}}(*D))$. Then we have two exact sequences
Since the supports of ![]() $C_0, C_1$ are in
$C_0, C_1$ are in ![]() $D\cap Z$, the dimensions are less than
$D\cap Z$, the dimensions are less than ![]() $\dim Z$. By induction, (9.2) holds for
$\dim Z$. By induction, (9.2) holds for ![]() $C_0, C_1$. Hence it suffices to show (9.2) for
$C_0, C_1$. Hence it suffices to show (9.2) for ![]() ${\mathcal {M}}(*D)$.
${\mathcal {M}}(*D)$.
Let ![]() $p_1\colon (Z_1, D_1)\rightarrow (Z,D\cap Z)$ be a resolution of singularities of
$p_1\colon (Z_1, D_1)\rightarrow (Z,D\cap Z)$ be a resolution of singularities of ![]() $(Z, D\cap Z)$ and
$(Z, D\cap Z)$ and ![]() $p_2$ be a proper modification given by Theorem 5.3 for
$p_2$ be a proper modification given by Theorem 5.3 for ![]() $p_1^{\dagger} {\mathcal {M}}(*D)$. Then
$p_1^{\dagger} {\mathcal {M}}(*D)$. Then ![]() $p^{\dagger} {\mathcal {M}}(*D)$ (
$p^{\dagger} {\mathcal {M}}(*D)$ (![]() $p:=p_2\circ p_1$) satisfies (9.2), since its image under
$p:=p_2\circ p_1$) satisfies (9.2), since its image under ![]() $\mathrm {Sol}^\Lambda$ is an irregular local system. Now we note the following inequalities:
$\mathrm {Sol}^\Lambda$ is an irregular local system. Now we note the following inequalities:
 \begin{align} -j&\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda(p^{\dagger} {\mathcal{M}}(*D)))=\dim \mathrm{supp}\, {\mathcal{H}}^j(p^{{-}1}\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\nonumber\\ &=\dim \mathrm{supp}\, p^{{-}1}{\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D))). \end{align}
\begin{align} -j&\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda(p^{\dagger} {\mathcal{M}}(*D)))=\dim \mathrm{supp}\, {\mathcal{H}}^j(p^{{-}1}\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\nonumber\\ &=\dim \mathrm{supp}\, p^{{-}1}{\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D))). \end{align}
This shows ![]() ${\mathcal {M}}(*D)$ also satisfies (9.2). This completes the proof.
${\mathcal {M}}(*D)$ also satisfies (9.2). This completes the proof.
We would like to make a comparison with usual perverse sheaves.
Proposition 9.8 We have ![]() $ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$, By Proposition 6.10,
$ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$, By Proposition 6.10, ![]() $ {\mathfrak {F}}\circ {\mathfrak {G}}=\operatorname {id}$ on
$ {\mathfrak {F}}\circ {\mathfrak {G}}=\operatorname {id}$ on ![]() $\mathrm {Perv}(X)$.
$\mathrm {Perv}(X)$.
Proof. Since ![]() $ {\mathfrak {G}}$ is an exact functor, the condition in Definition 9.1 for
$ {\mathfrak {G}}$ is an exact functor, the condition in Definition 9.1 for ![]() $ {\mathfrak {G}}({\mathcal {E}})$ is equivalent to the condition for
$ {\mathfrak {G}}({\mathcal {E}})$ is equivalent to the condition for ![]() ${\mathcal {E}}$ to be a perverse sheaf. Hence we have
${\mathcal {E}}$ to be a perverse sheaf. Hence we have ![]() $ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$.
$ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$.
9.2  $t$-exactness of various operations
$t$-exactness of various operations
By using the functor ![]() $ {\mathfrak {F}}$, we can prove various
$ {\mathfrak {F}}$, we can prove various ![]() $t$-exactness properties in parallel with the theory of usual perverse
$t$-exactness properties in parallel with the theory of usual perverse ![]() $t$-structure. We only discuss some of them for illustration.
$t$-structure. We only discuss some of them for illustration.
Proposition 9.9 The Verdier duality functor ![]() ${\mathbb {D}}$ interchanges
${\mathbb {D}}$ interchanges ![]() ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and
${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ![]() ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$. In particular,
${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$. In particular, ![]() ${\mathbb {D}}$ restricts to a contravariant autoequivalence of
${\mathbb {D}}$ restricts to a contravariant autoequivalence of ![]() $\mathrm {Perv}_{ic}(\mathbb {k}_X)$.
$\mathrm {Perv}_{ic}(\mathbb {k}_X)$.
Proof. Since ![]() ${\mathbb {D}}^2\cong \operatorname {id}$, the condition in Definition 9.1 for
${\mathbb {D}}^2\cong \operatorname {id}$, the condition in Definition 9.1 for ![]() ${\mathbb {D}} {\mathcal {V}}$ is equivalent to that of
${\mathbb {D}} {\mathcal {V}}$ is equivalent to that of ![]() $ {\mathcal {V}}$.
$ {\mathcal {V}}$.
Proposition 9.10 Let ![]() $f\colon X\rightarrow Y$ be a morphism of complex manifolds. We assume that
$f\colon X\rightarrow Y$ be a morphism of complex manifolds. We assume that ![]() $f$ is proper for
$f$ is proper for ![]() $3$ and
$3$ and ![]() $4$. The following hold.
$4$. The following hold.
(i) For any
 $ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _Y)$, we have
$ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _Y)$, we have  $f^{-1} {\mathcal {V}}\in {^p}D_{ic}^{\leqslant \dim X-\dim Y}(\Lambda _X)$.
$f^{-1} {\mathcal {V}}\in {^p}D_{ic}^{\leqslant \dim X-\dim Y}(\Lambda _X)$.(ii) For any
 $ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _Y)$, we have
$ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _Y)$, we have  $f^{!} {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _X)$.
$f^{!} {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _X)$.(iii) For any
 $ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _X)$, we have
$ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _X)$, we have  $ {\mathbb {R}} f_* {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _Y)$.
$ {\mathbb {R}} f_* {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _Y)$.(iv) For any
 $ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _X)$, we have
$ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _X)$, we have  $ {\mathbb {R}} f_! {\mathcal {V}}\in {^p}D_{ic}^{\leqslant (\dim X-\dim Y)}(\Lambda _Y)$.
$ {\mathbb {R}} f_! {\mathcal {V}}\in {^p}D_{ic}^{\leqslant (\dim X-\dim Y)}(\Lambda _Y)$.
Proof. The statements (i), (iii) and (iv) can also be proved easily by using the commutativities of ![]() $ {\mathfrak {F}}$ with
$ {\mathfrak {F}}$ with ![]() $f^{-1}$ and
$f^{-1}$ and ![]() $f_!$ (§ 6) and Lemma 9.2. The statement (ii) is the Verdier dual of (i).
$f_!$ (§ 6) and Lemma 9.2. The statement (ii) is the Verdier dual of (i).
Remark 9.11 Other right/left ![]() $t$-exactness for various functors known in the theory of perverse sheaves can be also proved by using the argument used in Proposition 9.10.
$t$-exactness for various functors known in the theory of perverse sheaves can be also proved by using the argument used in Proposition 9.10.
Remark 9.12 Here we assumed the properness for (iii) and (iv) for simplicity. One can remove the assumption by working with ind/pro objects to define push-forwards for nontame morphisms.
10. Algebraic case
In this section, we deduce the algebraic version of the results.
10.1 Notation for algebraic  ${\mathcal {D}}$-modules
${\mathcal {D}}$-modules
For the theory of algebraic ![]() ${\mathcal {D}}$-modules, we refer to [Reference Hotta, Takeuchi and TanisakiHTT08]. For a smooth quasi-projective variety
${\mathcal {D}}$-modules, we refer to [Reference Hotta, Takeuchi and TanisakiHTT08]. For a smooth quasi-projective variety ![]() $X$, we denote the sheaf of algebraic differential operators by
$X$, we denote the sheaf of algebraic differential operators by ![]() ${\mathcal {D}}_X$. We denote the category of left
${\mathcal {D}}_X$. We denote the category of left ![]() ${\mathcal {D}}_X$-modules by
${\mathcal {D}}_X$-modules by ![]() $\mathrm {Mod}({\mathcal {D}}_X)$, the bounded derived category by
$\mathrm {Mod}({\mathcal {D}}_X)$, the bounded derived category by ![]() $D^b({\mathcal {D}}_X)$, and the full subcategory of cohomologically holonomic modules by
$D^b({\mathcal {D}}_X)$, and the full subcategory of cohomologically holonomic modules by ![]() $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
$D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
We denote the Verdier duality functor by ![]() ${\mathbb {D}}$. For a morphism of algebraic varieties
${\mathbb {D}}$. For a morphism of algebraic varieties ![]() $f\colon X\rightarrow Y$, we define
$f\colon X\rightarrow Y$, we define ![]() $\int _f$ and
$\int _f$ and ![]() $f^{\dagger}$ by the same formula as in the analytic case. In the algebraic case, both functors preserve holonomic objects without properness assumption. We set
$f^{\dagger}$ by the same formula as in the analytic case. In the algebraic case, both functors preserve holonomic objects without properness assumption. We set ![]() $f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}$ and
$f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}$ and ![]() $\int _{f!}:={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then we have two adjoint pairs
$\int _{f!}:={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then we have two adjoint pairs ![]() $f^\star \dashv \int _f$ and
$f^\star \dashv \int _f$ and ![]() $\int _{f!}\dashv f^{\dagger}$.
$\int _{f!}\dashv f^{\dagger}$.
Let ![]() $X^{{\mathrm {an}}}$ be the complex manifold associated with
$X^{{\mathrm {an}}}$ be the complex manifold associated with ![]() $X$. The analytification functor is an exact functor
$X$. The analytification functor is an exact functor ![]() $(\cdot )^{{\mathrm {an}}} \colon \mathrm {Mod}({\mathcal {D}}_X)\rightarrow \mathrm {Mod}({\mathcal {D}}_{X^{{\mathrm {an}}}})$. We also denote the induced functor on the derived categories by the same notation
$(\cdot )^{{\mathrm {an}}} \colon \mathrm {Mod}({\mathcal {D}}_X)\rightarrow \mathrm {Mod}({\mathcal {D}}_{X^{{\mathrm {an}}}})$. We also denote the induced functor on the derived categories by the same notation ![]() $(\cdot )^{\mathrm {an}}$. It preserves the holonomicity. We note the following.
$(\cdot )^{\mathrm {an}}$. It preserves the holonomicity. We note the following.
Lemma 10.1 [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 4.7.2]
Let ![]() $f\colon X\rightarrow Y$ be a morphism between algebraic varieties and
$f\colon X\rightarrow Y$ be a morphism between algebraic varieties and ![]() $f^{{\mathrm {an}}}\colon X^{{\mathrm {an}}}\rightarrow Y^{{\mathrm {an}}}$ be the associated morphisms between complex manifolds. Then the following hold.
$f^{{\mathrm {an}}}\colon X^{{\mathrm {an}}}\rightarrow Y^{{\mathrm {an}}}$ be the associated morphisms between complex manifolds. Then the following hold.
(i) For
 ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have a canonical isomorphism
${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have a canonical isomorphism  $(f^{\dagger} {\mathcal {M}})^{{\mathrm {an}}}\simeq (f^{{\mathrm {an}}})^{\dagger} ({\mathcal {M}})^{{\mathrm {an}}}$.
$(f^{\dagger} {\mathcal {M}})^{{\mathrm {an}}}\simeq (f^{{\mathrm {an}}})^{\dagger} ({\mathcal {M}})^{{\mathrm {an}}}$.(ii) If
 $f$ is proper, we have a canonical isomorphism
$f$ is proper, we have a canonical isomorphism  $\big (\int _f{\mathcal {N}}\big )^{\mathrm {an}} \simeq \int _{f^{\mathrm {an}}}({\mathcal {N}})^{\mathrm {an}}$ for
$\big (\int _f{\mathcal {N}}\big )^{\mathrm {an}} \simeq \int _{f^{\mathrm {an}}}({\mathcal {N}})^{\mathrm {an}}$ for  ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.
10.2 Algebraic irregular constructible sheaves
To consider irregular constructible sheaves, we will equip quasi-projective algebraic varieties with analytic topology. Let ![]() $X$ be a smooth quasi-projective variety. Let
$X$ be a smooth quasi-projective variety. Let ![]() ${\bar {X}}$ be a smooth projective variety with a Zariski open embedding
${\bar {X}}$ be a smooth projective variety with a Zariski open embedding ![]() $i_X\colon X\rightarrow {\bar {X}}$. We set
$i_X\colon X\rightarrow {\bar {X}}$. We set ![]() $j_{X}\colon D_X:={\bar {X}}{\backslash } X\hookrightarrow X$.
$j_{X}\colon D_X:={\bar {X}}{\backslash } X\hookrightarrow X$.
Definition 10.2 An object ![]() $ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is algebraic irregular constructible if the following holds: there exists an algebraic stratification
$ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is algebraic irregular constructible if the following holds: there exists an algebraic stratification ![]() ${\mathcal {S}}$ of
${\mathcal {S}}$ of ![]() ${\bar {X}}$ refining
${\bar {X}}$ refining ![]() ${\bar {X}}=X\sqcup D_X$ such that each restriction of
${\bar {X}}=X\sqcup D_X$ such that each restriction of ![]() $ {\mathcal {V}}$ to
$ {\mathcal {V}}$ to ![]() $S\in {\mathcal {S}}$ is an irregular local system.
$S\in {\mathcal {S}}$ is an irregular local system.
We denote the full subcategory of irregular constructible sheaves by ![]() $\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$. Let
$\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$. Let ![]() $i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical morphism, which is tame. We also denote the inclusion by
$i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical morphism, which is tame. We also denote the inclusion by ![]() $i_{D_X}\colon (D_X,\varnothing )\rightarrow ({\bar {X}}, \varnothing )$. The functors
$i_{D_X}\colon (D_X,\varnothing )\rightarrow ({\bar {X}}, \varnothing )$. The functors ![]() $i_{{({\bar {X}}, D_X)}!}, i_{{({\bar {X}}, D_X)}*}$ are fully faithful by Lemma 5.40.
$i_{{({\bar {X}}, D_X)}!}, i_{{({\bar {X}}, D_X)}*}$ are fully faithful by Lemma 5.40.
Lemma 10.3 The category ![]() $\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$ does not depend on the choice of
$\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$ does not depend on the choice of ![]() ${\bar {X}}$.
${\bar {X}}$.
Proof. We will prove the assertion in two steps. Let us first assume that ![]() $p\colon {\bar {X}}'\rightarrow {\bar {X}}$ is a map between two projective compactifications of
$p\colon {\bar {X}}'\rightarrow {\bar {X}}$ is a map between two projective compactifications of ![]() $X$ extending
$X$ extending ![]() $\operatorname {id}\colon X\rightarrow X$. Then it is clear that
$\operatorname {id}\colon X\rightarrow X$. Then it is clear that ![]() $p_*$ induces the desired equivalence of categories.
$p_*$ induces the desired equivalence of categories.
Now let ![]() ${\bar {X}}'$ be an arbitrary projective compactification of
${\bar {X}}'$ be an arbitrary projective compactification of ![]() $X$. Then there exists
$X$. Then there exists ![]() ${\bar {X}}''$ with maps
${\bar {X}}''$ with maps ![]() ${\bar {X}}''\rightarrow {\bar {X}}$ and
${\bar {X}}''\rightarrow {\bar {X}}$ and ![]() ${\bar {X}}''\rightarrow {\bar {X}}'$ extending
${\bar {X}}''\rightarrow {\bar {X}}'$ extending ![]() $\operatorname {id} \colon X\rightarrow X$. This can be done by taking a smooth blow-up replacement of the closure of the diagonal embedding
$\operatorname {id} \colon X\rightarrow X$. This can be done by taking a smooth blow-up replacement of the closure of the diagonal embedding ![]() $X\rightarrow {\bar {X}}\times {\bar {X}}'$. From the first part of this proof, we complete the proof.
$X\rightarrow {\bar {X}}\times {\bar {X}}'$. From the first part of this proof, we complete the proof.
We will denote the category of algebraic irregular constructible sheaves by ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$.
$\mathrm {Mod}_{ic}(\Lambda _X)$.
Lemma 10.4 The abelian subcategory ![]() $\mathrm {Mod}_{ic}(\Lambda _X)$ is thick in
$\mathrm {Mod}_{ic}(\Lambda _X)$ is thick in ![]() $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.
$\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.
Proof. One can prove the lemma by mimicking the proof of Lemma 5.28.
Let us denote the triangulated subcategory of ![]() $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ formed by cohomologically algebraic irregular constructible sheaves by
$D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ formed by cohomologically algebraic irregular constructible sheaves by ![]() $D^{b}_{ic}(\Lambda _X)$.
$D^{b}_{ic}(\Lambda _X)$.
Let ![]() $D^{b}_c(\mathbb {k}_X)$ be the category of cohomologically algebraic constructible complexes.
$D^{b}_c(\mathbb {k}_X)$ be the category of cohomologically algebraic constructible complexes.
Proposition 10.5 The functor ![]() $ {\mathfrak {F}}$ restricts to a functor
$ {\mathfrak {F}}$ restricts to a functor ![]() $ {\mathfrak {F}}\colon D^{b}_{ic}(\Lambda _X)\rightarrow D^{b}_c(\mathbb {k}_X)$.
$ {\mathfrak {F}}\colon D^{b}_{ic}(\Lambda _X)\rightarrow D^{b}_c(\mathbb {k}_X)$.
Proof. The proof of proposition 6.7 works for this case.
It is also clear that the results we proved in § 5.4 also hold for ![]() $D^{b}(\Lambda _X)$. In addition to these, we have the following.
$D^{b}(\Lambda _X)$. In addition to these, we have the following.
Let ![]() $f\colon X\rightarrow Y$ be a morphism between algebraic varieties. There exist compactifications
$f\colon X\rightarrow Y$ be a morphism between algebraic varieties. There exist compactifications ![]() $\bar {X},\bar {Y}$ such that
$\bar {X},\bar {Y}$ such that ![]() $f$ admits an extension
$f$ admits an extension ![]() $f\colon \bar {X}\rightarrow \bar {Y}$. Hence, considering the analytic topology,
$f\colon \bar {X}\rightarrow \bar {Y}$. Hence, considering the analytic topology, ![]() $f$ extends as a map
$f$ extends as a map ![]() $f\colon (\bar {X}, D_X)\rightarrow (\bar {Y}, D_Y)$. We set
$f\colon (\bar {X}, D_X)\rightarrow (\bar {Y}, D_Y)$. We set
 \begin{equation} \begin{gathered} f_*:=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_*i_{{({\bar{X}}, D_X)}*}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})),\\ f_! :=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_!i_{{({\bar{X}}, D_X)}!}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})). \end{gathered} \end{equation}
\begin{equation} \begin{gathered} f_*:=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_*i_{{({\bar{X}}, D_X)}*}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})),\\ f_! :=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_!i_{{({\bar{X}}, D_X)}!}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})). \end{gathered} \end{equation}Proposition 10.6 Let ![]() $f\colon X\rightarrow Y$ be a morphism between algebraic varieties. Then
$f\colon X\rightarrow Y$ be a morphism between algebraic varieties. Then ![]() $f_* {\mathcal {V}}, f_! {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for
$f_* {\mathcal {V}}, f_! {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for ![]() $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
$ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.
10.3 Algebraic Riemann–Hilbert correspondence
We first recall the following result due to Malgrange.
Theorem 10.7 [Reference MalgrangeMal04]
If ![]() $X$ is a smooth projective variety, analytic holonomic
$X$ is a smooth projective variety, analytic holonomic ![]() ${\mathcal {D}}_X$-modules are algebraic.
${\mathcal {D}}_X$-modules are algebraic.
By using this, we have the following algebraic version of irregular Riemann–Hilbert correspondence.
Theorem 10.8 There exists an exact equivalence
Proof. If ![]() $X$ is projective, there is nothing to prove by Theorem 10.7. We suppose
$X$ is projective, there is nothing to prove by Theorem 10.7. We suppose ![]() $X$ is quasi-projective and
$X$ is quasi-projective and ![]() $\bar {X}$ be a compactification of
$\bar {X}$ be a compactification of ![]() $X$. For
$X$. For ![]() ${\mathcal {M}}\in D^{b}_{\mathrm {hol}}({\mathcal {D}}_X)$, we have
${\mathcal {M}}\in D^{b}_{\mathrm {hol}}({\mathcal {D}}_X)$, we have ![]() $\int _{i_X}{\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_{\bar {X}})$ where
$\int _{i_X}{\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_{\bar {X}})$ where ![]() $i_X\colon X\hookrightarrow {\bar {X}}$ is the inclusion. Then we get a functor
$i_X\colon X\hookrightarrow {\bar {X}}$ is the inclusion. Then we get a functor
 \begin{align} \mathrm{Sol}^\Lambda_X&:= i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ({\cdot})^{{\mathrm{an}}} \circ\int_{i_X}\colon D^b_\mathrm{hol}({\mathcal{D}}_X)\rightarrow D^{b}_{ic}(\Lambda_{{\bar{X}}^{\mathrm{an}}})\nonumber\\ &= D^b_{ic}(\Lambda_{\bar{X}})\xrightarrow{i_{({\bar{X}}, D_X)}^{{-}1}} D^b_{ic}(\Lambda_{({\bar{X}}, D_X)}). \end{align}
\begin{align} \mathrm{Sol}^\Lambda_X&:= i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ({\cdot})^{{\mathrm{an}}} \circ\int_{i_X}\colon D^b_\mathrm{hol}({\mathcal{D}}_X)\rightarrow D^{b}_{ic}(\Lambda_{{\bar{X}}^{\mathrm{an}}})\nonumber\\ &= D^b_{ic}(\Lambda_{\bar{X}})\xrightarrow{i_{({\bar{X}}, D_X)}^{{-}1}} D^b_{ic}(\Lambda_{({\bar{X}}, D_X)}). \end{align}The middle equality is Chow's lemma. Note that the first three compositions are fully faithful.
Hence, to prove the full faithfulness of ![]() $\mathrm {Sol}^\Lambda _X$, it suffices to show that the image of
$\mathrm {Sol}^\Lambda _X$, it suffices to show that the image of ![]() $\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}\circ (\cdot )^{{\mathrm {an}}} \circ \int _{i_X}$ is zero under
$\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}\circ (\cdot )^{{\mathrm {an}}} \circ \int _{i_X}$ is zero under ![]() $i_{D_X}^{-1}$ by Lemma 5.40. Let
$i_{D_X}^{-1}$ by Lemma 5.40. Let ![]() ${\mathcal {S}}$ be a stratification of
${\mathcal {S}}$ be a stratification of ![]() $D_X$ such that each stratum is smooth. For
$D_X$ such that each stratum is smooth. For ![]() $S\in {\mathcal {S}}$, we have
$S\in {\mathcal {S}}$, we have ![]() $i_S^{{\dagger} }(\int _{i_X}{\mathcal {M}})\simeq 0$ where
$i_S^{{\dagger} }(\int _{i_X}{\mathcal {M}})\simeq 0$ where ![]() $i_S\colon S\hookrightarrow {\bar {X}}$ is the inclusion. Hence we have
$i_S\colon S\hookrightarrow {\bar {X}}$ is the inclusion. Hence we have
 \begin{align} i_S^{{-}1}\mathrm{Sol}^{\Lambda}_X({\mathcal{M}})&\simeq i_S^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{{\mathrm{an}}}\circ \int_{i_X}{\mathcal{M}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ i_{S}^{{{\dagger}}}\circ \bigg(\int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ \bigg( i_{S}^{{{\dagger}}}\circ \int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\simeq 0. \end{align}
\begin{align} i_S^{{-}1}\mathrm{Sol}^{\Lambda}_X({\mathcal{M}})&\simeq i_S^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{{\mathrm{an}}}\circ \int_{i_X}{\mathcal{M}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ i_{S}^{{{\dagger}}}\circ \bigg(\int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ \bigg( i_{S}^{{{\dagger}}}\circ \int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\simeq 0. \end{align}
Hence we can conclude that ![]() $i_{D_X}^{-1}\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}({\mathcal {M}})\simeq 0$. Then the full faithfulness of
$i_{D_X}^{-1}\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}({\mathcal {M}})\simeq 0$. Then the full faithfulness of ![]() $\mathrm {Sol}^\Lambda _X$ is evident from Lemma 5.40.
$\mathrm {Sol}^\Lambda _X$ is evident from Lemma 5.40.
To see the essential surjectivity, let us take an object ![]() $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$ and consider it as an object of
$ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$ and consider it as an object of ![]() $D^b_{ic}(\Lambda _{\bar {X}})=D^b_{ic}(\Lambda _{{\bar {X}}^{\mathrm {an}}})$. Then we have
$D^b_{ic}(\Lambda _{\bar {X}})=D^b_{ic}(\Lambda _{{\bar {X}}^{\mathrm {an}}})$. Then we have ![]() ${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda }_{{\bar {X}}^{{\mathrm {an}}}})^{-1}( {\mathcal {V}})\in D^b_{\mathrm {hol}}({\mathcal {D}}_{{\bar {X}}^{\mathrm {an}}})$. We set
${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda }_{{\bar {X}}^{{\mathrm {an}}}})^{-1}( {\mathcal {V}})\in D^b_{\mathrm {hol}}({\mathcal {D}}_{{\bar {X}}^{\mathrm {an}}})$. We set ![]() ${\mathcal {M}}^\mathrm {alg}:=((\cdot )^{\mathrm {an}})^{-1}({\mathcal {M}})$. Take a stratification
${\mathcal {M}}^\mathrm {alg}:=((\cdot )^{\mathrm {an}})^{-1}({\mathcal {M}})$. Take a stratification ![]() ${\mathcal {S}}$ of
${\mathcal {S}}$ of ![]() $D_X$ with smooth strata. To prove
$D_X$ with smooth strata. To prove ![]() ${\mathcal {M}}^\mathrm {alg}$ is isomorphic to
${\mathcal {M}}^\mathrm {alg}$ is isomorphic to ![]() $\int _{i_X}{\mathcal {N}}$ for
$\int _{i_X}{\mathcal {N}}$ for ![]() ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, it is enough to see
${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, it is enough to see ![]() $i_S^{{\dagger} }{\mathcal {M}}^{\mathrm {alg}}\simeq 0$ for each
$i_S^{{\dagger} }{\mathcal {M}}^{\mathrm {alg}}\simeq 0$ for each ![]() $S\in {\mathcal {S}}$. Note that
$S\in {\mathcal {S}}$. Note that ![]() $i_S^{\dagger} {\mathcal {M}}^\mathrm {alg}\simeq 0$ is equivalent to
$i_S^{\dagger} {\mathcal {M}}^\mathrm {alg}\simeq 0$ is equivalent to ![]() $(i_S^{\dagger} {\mathcal {M}}^\mathrm {alg})^{an}\simeq 0$. The latter can be shown as follows:
$(i_S^{\dagger} {\mathcal {M}}^\mathrm {alg})^{an}\simeq 0$. The latter can be shown as follows:
 \begin{align} \mathrm{Sol}_{S^{\mathrm{an}}}^\Lambda(i_S^{\dagger}{\mathcal{M}}^\mathrm{alg})^{{\mathrm{an}}}&\simeq \mathrm{Sol}^\Lambda_{S^{\mathrm{an}}}(i_{S^{\mathrm{an}}}^{\dagger}{\mathcal{M}}) \nonumber\\ &\simeq i_S^{{-}1}\mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}({\mathcal{M}})\nonumber\\ &\simeq i_S^{{-}1}{\mathcal{V}}\simeq 0. \end{align}
\begin{align} \mathrm{Sol}_{S^{\mathrm{an}}}^\Lambda(i_S^{\dagger}{\mathcal{M}}^\mathrm{alg})^{{\mathrm{an}}}&\simeq \mathrm{Sol}^\Lambda_{S^{\mathrm{an}}}(i_{S^{\mathrm{an}}}^{\dagger}{\mathcal{M}}) \nonumber\\ &\simeq i_S^{{-}1}\mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}({\mathcal{M}})\nonumber\\ &\simeq i_S^{{-}1}{\mathcal{V}}\simeq 0. \end{align}This completes the proof.
For the next subsection, we also prepare the following: we set ![]() ${\mathrm {DR}}^\Lambda _X:={\mathbb {D}}_{{({\bar {X}}, D_X)}}\circ \mathrm {Sol}^\Lambda _X$, which is an equivalence.
${\mathrm {DR}}^\Lambda _X:={\mathbb {D}}_{{({\bar {X}}, D_X)}}\circ \mathrm {Sol}^\Lambda _X$, which is an equivalence.
Lemma 10.9 There exist isomorphisms
Proof. We have
 \begin{align} {\mathrm{DR}}^\Lambda_X&\simeq {\mathbb{D}}_{{({\bar{X}}, D_X)}}\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ\int_{i_X}\nonumber\\ &\simeq i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathbb{D}}_{\bar{X}}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ\int_{i_X}\nonumber\\ &=i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X}.\end{align}
\begin{align} {\mathrm{DR}}^\Lambda_X&\simeq {\mathbb{D}}_{{({\bar{X}}, D_X)}}\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ\int_{i_X}\nonumber\\ &\simeq i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathbb{D}}_{\bar{X}}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ\int_{i_X}\nonumber\\ &=i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X}.\end{align}10.4 Comparisons of the functors
Let ![]() $X, Y$ be smooth quasi-projective varieties and
$X, Y$ be smooth quasi-projective varieties and ![]() $f\colon X\rightarrow Y$ be a morphism. Recall that holonomicity of algebraic
$f\colon X\rightarrow Y$ be a morphism. Recall that holonomicity of algebraic ![]() ${\mathcal {D}}$-modules is preserved by the six operations.
${\mathcal {D}}$-modules is preserved by the six operations.
Proposition 10.10 There exist canonical isomorphisms:
Proof. The third and fourth lines follow from the analytic cases. To prove the first and second lines, let us take a projective compactification ![]() $i_X\colon X\hookrightarrow {\bar {X}}$ and
$i_X\colon X\hookrightarrow {\bar {X}}$ and ![]() $i_Y\colon Y\hookrightarrow {\bar {Y}}$ and a map
$i_Y\colon Y\hookrightarrow {\bar {Y}}$ and a map ![]() $\bar {f}\colon {\bar {X}}\rightarrow {\bar {Y}}$ extending
$\bar {f}\colon {\bar {X}}\rightarrow {\bar {Y}}$ extending ![]() $f$. We have
$f$. We have
 \begin{align} {\mathrm{DR}}^\Lambda_Y\circ \int_{f!} &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_Y!}\circ \int_{f!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{\bar{f}}\circ \int_{i_X!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ \bar{f}_!\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ {\mathrm{DR}}^\Lambda_X. \end{align}
\begin{align} {\mathrm{DR}}^\Lambda_Y\circ \int_{f!} &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_Y!}\circ \int_{f!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{\bar{f}}\circ \int_{i_X!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ \bar{f}_!\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ {\mathrm{DR}}^\Lambda_X. \end{align}By using Lemma 10.9, one can prove the first formula in the same way.
10.5 Algebraic irregular perverse sheaves
In the same way as in Definition 9.1, we define ![]() $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ on
$({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ on ![]() $D^{b}_{ic}(\Lambda _X)$.
$D^{b}_{ic}(\Lambda _X)$.
Proposition 10.11 The following hold.
(i) The pair
 $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ forms a
$({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ forms a  $t$-structure on
$t$-structure on  $D^{b}_{ic}(\Lambda _X)$.
$D^{b}_{ic}(\Lambda _X)$.(ii) The heart
 $\mathrm {Perv}_{ic}(k_X)$ of the
$\mathrm {Perv}_{ic}(k_X)$ of the  $t$-structure
$t$-structure  $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ is equivalent to
$({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ is equivalent to  $\mathrm {Mod}_{\mathrm {hol}}({\mathcal {D}}_X)$ under the Riemann–Hilbert correspondence (Theorem 10.8).
$\mathrm {Mod}_{\mathrm {hol}}({\mathcal {D}}_X)$ under the Riemann–Hilbert correspondence (Theorem 10.8).(iii) The heart
 $\mathrm {Perv}_{ic}(\mathbb {k}_X)$ is stable under the Verdier duality. The
$\mathrm {Perv}_{ic}(\mathbb {k}_X)$ is stable under the Verdier duality. The  $t$-exactness in Proposition 9.10 also holds in this setting without the properness assumption.
$t$-exactness in Proposition 9.10 also holds in this setting without the properness assumption.
Proof. One can prove this in the same way as in the analytic setting except for nonproper setting of (iii). Let ![]() $f$ be a morphism
$f$ be a morphism ![]() $X\rightarrow Y$ and a compactification
$X\rightarrow Y$ and a compactification ![]() ${\bar {X}}\rightarrow {\bar {Y}}$. Then we have
${\bar {X}}\rightarrow {\bar {Y}}$. Then we have
by Lemmas 6.5 and 6.6. This proves the desired statement for ![]() $f_!$. The statement for
$f_!$. The statement for ![]() $f_*$ is obtained by taking the Verdier dual.
$f_*$ is obtained by taking the Verdier dual.
Acknowledgments
The author would like to thank Andrea D'Agnolo whose lectures three times (at Kashiwa, Berkeley, and Padova) gave him many insights about irregular Riemann–Hilbert correspondence. He also kindly pointed out some mistakes in an early draft. The author also would like to thank Takahiro Saito for having many discussions on many aspects of Riemann–Hilbert correspondence (at least once a week), and Takuro Mochizuki for kindly answering some questions. This work was supported by World Premier International Research Center Initiative (WPI), MEXT, Japan and JSPS KAKENHI Grant Number JP18K13405. The author would like to thank the referees for many comments to improve some expositions and proofs.