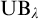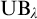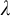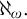1 Introduction
In [Reference Usuba5], Usuba introduced a new combinatorial principle, denoted
![]() $\mathrm {UB}_\lambda .$
Footnote
1
He showed that
$\mathrm {UB}_\lambda .$
Footnote
1
He showed that
![]() $\mathrm {UB}_\lambda $
holds for all regular uncountable cardinals and that for singular cardinals, some very weak assumptions like weak square or even
$\mathrm {UB}_\lambda $
holds for all regular uncountable cardinals and that for singular cardinals, some very weak assumptions like weak square or even
![]() $\mathrm {ADS}_\lambda $
imply it. It is known that
$\mathrm {ADS}_\lambda $
imply it. It is known that
![]() $\mathrm {ADS}_\lambda $
can fail for singular cardinals, for example if
$\mathrm {ADS}_\lambda $
can fail for singular cardinals, for example if
![]() $\kappa $
is supercompact and
$\kappa $
is supercompact and
![]() $\lambda> \kappa $
is such that
$\lambda> \kappa $
is such that
![]() $\mathrm {cf}(\lambda ) < \kappa $
. Motivated by this results, Usuba asked the following question:
$\mathrm {cf}(\lambda ) < \kappa $
. Motivated by this results, Usuba asked the following question:
Question 1.1. [Reference Usuba5, Question 2.11]
Is it consistent that
![]() $\mathrm {UB}_\lambda $
fails for some singular cardinal
$\mathrm {UB}_\lambda $
fails for some singular cardinal
![]() $\lambda $
?
$\lambda $
?
In this paper we give a positive answer to the above question by showing that Chang’s transfer principle
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _1, \aleph _0)$
implies the failure of
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _1, \aleph _0)$
implies the failure of
![]() $\mathrm { UB}_{\aleph _\omega }$
if
$\mathrm { UB}_{\aleph _\omega }$
if
![]() $\aleph _\omega $
is strong limit (see Theorem 3.1), where a stronger result is proved.
$\aleph _\omega $
is strong limit (see Theorem 3.1), where a stronger result is proved.
The paper is organized as follows. In Section 2, we present some preliminaries and results and then in Section 3, we prove our main result.
2 Some preliminaries
In this section we present some definitions and results that are needed for the later section of this paper. Let us start by introducing Usuba’s principle.
Definition 2.1. Let
![]() $\lambda $
be an uncountable cardinal. The principle
$\lambda $
be an uncountable cardinal. The principle
![]() $\mathrm {UB}_\lambda $
is the statement: there exists a function
$\mathrm {UB}_\lambda $
is the statement: there exists a function
![]() $f: [\lambda ^+]^{<\omega } \to \lambda ^+$
such that if
$f: [\lambda ^+]^{<\omega } \to \lambda ^+$
such that if
![]() $x, y \subseteq \lambda ^+$
are closed under f,
$x, y \subseteq \lambda ^+$
are closed under f,
![]() $x \cap \lambda =y \cap \lambda $
and
$x \cap \lambda =y \cap \lambda $
and
![]() $\sup (x \cap \lambda )=\lambda $
, then
$\sup (x \cap \lambda )=\lambda $
, then
![]() $x \subseteq y$
or
$x \subseteq y$
or
![]() $y \subseteq x.$
$y \subseteq x.$
It turned out this principle has many equivalent formulations. To state a few of it, let
![]() $S=\{x \subseteq \lambda : \sup (x)=\lambda \}$
,
$S=\{x \subseteq \lambda : \sup (x)=\lambda \}$
,
![]() $\theta> \lambda $
be large enough regular and let
$\theta> \lambda $
be large enough regular and let
![]() $\lhd $
be a well-ordering of
$\lhd $
be a well-ordering of
![]() $H(\theta )$
. Then we have the following.
$H(\theta )$
. Then we have the following.
Lemma 2.2. [Reference Usuba5]
The following are equivalent
![]() $:$
$:$
-
(1)
 $\mathrm {UB}_\lambda $
.
$\mathrm {UB}_\lambda $
. -
(2) If
 $M, N \prec (H(\theta ), \in , \lhd , \lambda , S, \ldots )$
are such that
$M, N \prec (H(\theta ), \in , \lhd , \lambda , S, \ldots )$
are such that
 $M \cap \lambda =N \cap \lambda \in S,$
then either
$M \cap \lambda =N \cap \lambda \in S,$
then either
 $M \cap \lambda ^+ \subseteq N \cap \lambda ^+$
or
$M \cap \lambda ^+ \subseteq N \cap \lambda ^+$
or
 $N \cap \lambda ^+ \subseteq M \cap \lambda ^+$
.
$N \cap \lambda ^+ \subseteq M \cap \lambda ^+$
. -
(3) If
 $M, N \prec (H(\theta ), \in , \lhd , \lambda , S, \ldots )$
are such that
$M, N \prec (H(\theta ), \in , \lhd , \lambda , S, \ldots )$
are such that
 $M \cap \lambda =N \cap \lambda \in S,$
and
$M \cap \lambda =N \cap \lambda \in S,$
and
 $\sup (M \cap \lambda ^+) \leq \sup (N \cap \lambda ^+)$
, then
$\sup (M \cap \lambda ^+) \leq \sup (N \cap \lambda ^+)$
, then
 $M \cap \lambda ^+$
is an initial segment of
$M \cap \lambda ^+$
is an initial segment of
 $N \cap \lambda ^+.$
$N \cap \lambda ^+.$
The principle
![]() $\mathrm {UB}_\lambda $
has many nice implications. Here we only consider its relation with Chang’s transfer principles which is also related to our work.
$\mathrm {UB}_\lambda $
has many nice implications. Here we only consider its relation with Chang’s transfer principles which is also related to our work.
Definition 2.3. Suppose
![]() $\lambda> \mu $
are infinite cardinal. Chang’s transfer principle
$\lambda> \mu $
are infinite cardinal. Chang’s transfer principle
![]() $(\lambda ^+, \lambda ) \twoheadrightarrow (\mu ^+, \mu )$
is the statement: if
$(\lambda ^+, \lambda ) \twoheadrightarrow (\mu ^+, \mu )$
is the statement: if
![]() $\mathcal L$
is a countable first-order language which contains a unary predicate U, then for any
$\mathcal L$
is a countable first-order language which contains a unary predicate U, then for any
![]() $\mathcal L$
-structure
$\mathcal L$
-structure
![]() $\mathcal M=(M, U^{\mathcal M}, \ldots )$
with
$\mathcal M=(M, U^{\mathcal M}, \ldots )$
with
![]() $|M|=\lambda ^+$
and
$|M|=\lambda ^+$
and
![]() $|U^{\mathcal M}|=\lambda $
, there exists an elementary submodel
$|U^{\mathcal M}|=\lambda $
, there exists an elementary submodel
![]() $\mathcal N= (N, U^{\mathcal N}, \ldots )$
of
$\mathcal N= (N, U^{\mathcal N}, \ldots )$
of
![]() $\mathcal M$
with
$\mathcal M$
with
![]() $|N|=\mu ^+$
and
$|N|=\mu ^+$
and
![]() $|U^{\mathcal N}|=\mu $
.
$|U^{\mathcal N}|=\mu $
.
Given an infinite cardinal
![]() $\nu ,$
the transfer principle
$\nu ,$
the transfer principle
![]() $(\lambda ^+, \lambda ) \twoheadrightarrow _{\leq \nu } (\mu ^+, \mu )$
is defined similarly, where we allow the language
$(\lambda ^+, \lambda ) \twoheadrightarrow _{\leq \nu } (\mu ^+, \mu )$
is defined similarly, where we allow the language
![]() $\mathcal L$
to have size at most
$\mathcal L$
to have size at most
![]() $\nu $
.
$\nu $
.
The next lemma shows the relation between
![]() $\mathrm {UB}_{\aleph _\omega }$
and Chang’s transfer principles.
$\mathrm {UB}_{\aleph _\omega }$
and Chang’s transfer principles.
Lemma 2.4. ([Reference Usuba5, Corollary 4.2])
Suppose
![]() $\mathrm {UB}_{\aleph _{\omega }}$
holds. Then the Chang transfer principles
$\mathrm {UB}_{\aleph _{\omega }}$
holds. Then the Chang transfer principles
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
fail for all
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
fail for all
![]() $1 \leq n < \omega .$
$1 \leq n < \omega .$
Remark 2.5. By [Reference Shelah4],
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
fails for all
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
fails for all
![]() $n \geq 3$
.
$n \geq 3$
.
Since the consistency of the transfer principle
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
is open for
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{n+1}, \aleph _n)$
is open for
![]() $n = 1, 2,$
one cannot use the above result to get the consistent failure of
$n = 1, 2,$
one cannot use the above result to get the consistent failure of
![]() $\mathrm {UB}_{\aleph _{\omega }}$
. In the next section we show that if
$\mathrm {UB}_{\aleph _{\omega }}$
. In the next section we show that if
![]() $\aleph _\omega $
is strong limit, then
$\aleph _\omega $
is strong limit, then
![]() $\mathrm {UB}_{\aleph _{\omega }}$
implies the failure of
$\mathrm {UB}_{\aleph _{\omega }}$
implies the failure of
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
as well, and hence by the results of [Reference Levinski, Magidor and Shelah3] (see also [Reference Eskew and Hayut1, Reference Hayut2], where the consistency of
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
as well, and hence by the results of [Reference Levinski, Magidor and Shelah3] (see also [Reference Eskew and Hayut1, Reference Hayut2], where the consistency of
![]() $\text {GCH}+(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
is proved using weaker large cardinal assumptions)
$\text {GCH}+(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
is proved using weaker large cardinal assumptions)
![]() $\mathrm {UB}_{\aleph _{\omega }}$
can fail. We also need the following notion.
$\mathrm {UB}_{\aleph _{\omega }}$
can fail. We also need the following notion.
Definition 2.6. An uncountable cardinal
![]() $\kappa $
is said to be Jonsson, if for every function
$\kappa $
is said to be Jonsson, if for every function
![]() $f:[\kappa ]^{<\omega } \to \kappa $
there exists a set
$f:[\kappa ]^{<\omega } \to \kappa $
there exists a set
![]() $H \subseteq \kappa $
of order type
$H \subseteq \kappa $
of order type
![]() $\kappa $
such that for each n,
$\kappa $
such that for each n,
![]() $f"[H]^n \neq \kappa .$
$f"[H]^n \neq \kappa .$
Notation 2.7. Given a model M and a subset A of M, by
![]() $cl(A, M)$
we mean the least substructure of M which includes A as a subset.
$cl(A, M)$
we mean the least substructure of M which includes A as a subset.
Lemma 2.8. Assume
![]() $\lambda $
is a singular strong limit cardinal of cofinality
$\lambda $
is a singular strong limit cardinal of cofinality
![]() $\kappa .$
Then there is a model
$\kappa .$
Then there is a model
![]() $M_0$
with vocabulary
$M_0$
with vocabulary
![]() $\mathcal L_0$
such that
$\mathcal L_0$
such that
![]() $:$
$:$
-
(a)
 $|\mathcal L_0|=\kappa $
and
$|\mathcal L_0|=\kappa $
and
 $|M_0|=\lambda ^+.$
$|M_0|=\lambda ^+.$
-
(b) If M is an
 $\mathcal L$
-structure which expands
$\mathcal L$
-structure which expands
 $M_0$
,
$M_0$
,
 $|\mathcal L|=\kappa $
, and M has Skolem functions, then for
$|\mathcal L|=\kappa $
, and M has Skolem functions, then for
 $\alpha _1, \alpha _2 < \lambda ^+,$
the following statements are equivalent
$\alpha _1, \alpha _2 < \lambda ^+,$
the following statements are equivalent
 $:$
$:$
-
(†)α1, α2 For some submodels
 $N_1, N_2$
of M we have:
$N_1, N_2$
of M we have:-
(α)
 $N_1 \cap \lambda =N_2 \cap \lambda $
is unbounded in
$N_1 \cap \lambda =N_2 \cap \lambda $
is unbounded in
 $\lambda $
,
$\lambda $
, -
(β)
 $\alpha _1 \in N_1 \setminus N_2$
and
$\alpha _1 \in N_1 \setminus N_2$
and
 $\alpha _2 \in N_2 \setminus N_1$
.
$\alpha _2 \in N_2 \setminus N_1$
.
-
-
(‡)α1, α2 If
 $V_\ell =cl(\{\alpha _\ell \}, M) \cap \lambda $
,
$V_\ell =cl(\{\alpha _\ell \}, M) \cap \lambda $
,
 $\ell =1, 2,$
and
$\ell =1, 2,$
and
 $V=V_1 \cup V_2$
, then
$V=V_1 \cup V_2$
, then  $$\begin{align*}\alpha_1 \notin cl(\{\alpha_2\} \cup V, M) \text{~}\& \text{~} \alpha_2 \notin cl(\{\alpha_1\} \cup V, M). \end{align*}$$
$$\begin{align*}\alpha_1 \notin cl(\{\alpha_2\} \cup V, M) \text{~}\& \text{~} \alpha_2 \notin cl(\{\alpha_1\} \cup V, M). \end{align*}$$
-
Proof Let
![]() $\langle \lambda _i: i<\kappa \rangle $
be an increasing sequence cofinal in
$\langle \lambda _i: i<\kappa \rangle $
be an increasing sequence cofinal in
![]() $\lambda $
such that for all
$\lambda $
such that for all
![]() $i<\kappa , 2^{\lambda _i} < \lambda _{i+1}$
. For each
$i<\kappa , 2^{\lambda _i} < \lambda _{i+1}$
. For each
![]() $0<n<\omega ,$
let
$0<n<\omega ,$
let
enumerate all functions from
![]() $\lambda _i$
into
$\lambda _i$
into
![]() $\lambda _i.$
Let
$\lambda _i.$
Let
![]() $M_0$
be defined as follows:
$M_0$
be defined as follows:
-
• the universe of
 $M_0$
is
$M_0$
is
 $\lambda ^+.$
$\lambda ^+.$
-
•
 $<^{M_0}= \{ (\alpha , \beta ): \alpha < \beta < \lambda ^+ \}$
.
$<^{M_0}= \{ (\alpha , \beta ): \alpha < \beta < \lambda ^+ \}$
. -
•
 $c_i^{M_0}=\lambda _i$
.
$c_i^{M_0}=\lambda _i$
. -
•
 $P^{M_0}=\{\alpha : \alpha < \lambda \}.$
$P^{M_0}=\{\alpha : \alpha < \lambda \}.$
-
•
 $F_n^{M_0}$
is an
$F_n^{M_0}$
is an
 $(n+1)$
-ary function such that:
$(n+1)$
-ary function such that:-
– if
 $i<\kappa , \alpha \in [\lambda _i, 2^{\lambda _i})$
and
$i<\kappa , \alpha \in [\lambda _i, 2^{\lambda _i})$
and
 $\beta _0, \cdots , \beta _{n-1} < \lambda _i$
, then
$\beta _0, \cdots , \beta _{n-1} < \lambda _i$
, then  $$\begin{align*}F_n^{M_0}(\beta_0, \ldots, \beta_{n-1}, \alpha)=F_{n, \alpha}(\beta_0, \ldots, \beta_{n-1}), \end{align*}$$
$$\begin{align*}F_n^{M_0}(\beta_0, \ldots, \beta_{n-1}, \alpha)=F_{n, \alpha}(\beta_0, \ldots, \beta_{n-1}), \end{align*}$$
-
– in all other cases,
 $F_n^{M_0}(\beta _0, \ldots , \beta _{n-1}, \beta _n)=\beta _n.$
$F_n^{M_0}(\beta _0, \ldots , \beta _{n-1}, \beta _n)=\beta _n.$
-
We show that the model
![]() $M_0$
is as required. Clause (a) clearly holds. To show that clause (b) is satisfied, let M be an
$M_0$
is as required. Clause (a) clearly holds. To show that clause (b) is satisfied, let M be an
![]() $\mathcal L$
-structure which expands
$\mathcal L$
-structure which expands
![]() $M_0$
,
$M_0$
,
![]() $|\mathcal L|=\kappa $
, and suppose M has Skolem functions. Let also
$|\mathcal L|=\kappa $
, and suppose M has Skolem functions. Let also
![]() $\alpha _1, \alpha _2 < \lambda ^+.$
$\alpha _1, \alpha _2 < \lambda ^+.$
First suppose that
![]() $(\dagger )_{\alpha _1, \alpha _2}$
holds, and suppose that the models
$(\dagger )_{\alpha _1, \alpha _2}$
holds, and suppose that the models
![]() $N_1, N_2$
witness it. Let also
$N_1, N_2$
witness it. Let also
![]() $V_\ell =cl(\{\alpha _\ell \}, M) \cap \lambda $
,
$V_\ell =cl(\{\alpha _\ell \}, M) \cap \lambda $
,
![]() $\ell =1, 2$
. Clearly each
$\ell =1, 2$
. Clearly each
![]() $V_\ell $
is an unbounded subset of
$V_\ell $
is an unbounded subset of
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $V=cl(V_1 \cup V_2, M) \cap \lambda $
and set
$V=cl(V_1 \cup V_2, M) \cap \lambda $
and set
![]() $N^*_\ell =cl(\{\alpha _\ell \} \cup V, M)$
.
$N^*_\ell =cl(\{\alpha _\ell \} \cup V, M)$
.
Claim 2.9.
![]() $N^*_\ell \subseteq N_\ell ,$
for
$N^*_\ell \subseteq N_\ell ,$
for
![]() $\ell =1, 2.$
$\ell =1, 2.$
Proof Fix
![]() $\ell .$
Sine
$\ell .$
Sine
![]() $\alpha _\ell \in N_\ell ,$
$\alpha _\ell \in N_\ell ,$
On the other hand,
![]() $N_1 \cap \lambda =N_2 \cap \lambda ,$
and hence
$N_1 \cap \lambda =N_2 \cap \lambda ,$
and hence
It follows that
![]() $V_1 \cup V_2 \subseteq N_\ell \cap \lambda ,$
and hence
$V_1 \cup V_2 \subseteq N_\ell \cap \lambda ,$
and hence
Thus, as
![]() $\{\alpha _\ell \} \cup V \subseteq N_\ell ,$
we have
$\{\alpha _\ell \} \cup V \subseteq N_\ell ,$
we have
The result follows.
Claim 2.10.
![]() $\alpha _1 \in N^*_1\setminus N^*_2$
and
$\alpha _1 \in N^*_1\setminus N^*_2$
and
![]() $\alpha _2 \in N^*_2\setminus N^*_1$
.
$\alpha _2 \in N^*_2\setminus N^*_1$
.
Proof Fix
![]() $\ell \in \{1, 2\}.$
Clearly
$\ell \in \{1, 2\}.$
Clearly
![]() $\alpha _\ell \in N^*_\ell $
. On the other hand, by our assumption,
$\alpha _\ell \in N^*_\ell $
. On the other hand, by our assumption,
![]() $\alpha _\ell \notin N_{3-\ell }$
, and by Claim 2.9,
$\alpha _\ell \notin N_{3-\ell }$
, and by Claim 2.9,
![]() $N^*_{3-\ell } \subseteq N_{3-\ell }.$
Thus
$N^*_{3-\ell } \subseteq N_{3-\ell }.$
Thus
![]() $\alpha _\ell \notin N^*_{3-\ell }$
.
$\alpha _\ell \notin N^*_{3-\ell }$
.
Thus
![]() $(\ddagger )_{\alpha _1, \alpha _2}$
is satisfied.
$(\ddagger )_{\alpha _1, \alpha _2}$
is satisfied.
Conversely suppose that
![]() $(\ddagger )_{\alpha _1, \alpha _2}$
holds, and for
$(\ddagger )_{\alpha _1, \alpha _2}$
holds, and for
![]() $\ell =1, 2,$
set
$\ell =1, 2,$
set
![]() $N_\ell =cl(\{\alpha _\ell \} \cup V, M)$
. By our assumption, clause (
$N_\ell =cl(\{\alpha _\ell \} \cup V, M)$
. By our assumption, clause (
![]() $\beta $
) of
$\beta $
) of
![]() $(\dagger )_{\alpha _1, \alpha _2}$
holds.
$(\dagger )_{\alpha _1, \alpha _2}$
holds.
Claim 2.11. For
![]() $\ell \in \{1, 2\}$
,
$\ell \in \{1, 2\}$
,
![]() $N_\ell \cap \lambda =V.$
$N_\ell \cap \lambda =V.$
Proof Fix
![]() $\ell \in \{1, 2\}$
. Clearly
$\ell \in \{1, 2\}$
. Clearly
![]() $N_\ell \cap \lambda \supseteq V.$
Now suppose towards a contradiction that
$N_\ell \cap \lambda \supseteq V.$
Now suppose towards a contradiction that
![]() $N_\ell \cap \lambda \neq V,$
and let
$N_\ell \cap \lambda \neq V,$
and let
![]() $\gamma \in N_\ell \cap \lambda \setminus V.$
As M has Skolem functions, there are
$\gamma \in N_\ell \cap \lambda \setminus V.$
As M has Skolem functions, there are
![]() $n, \beta _0, \ldots , \beta _{n-1} \in V$
and
$n, \beta _0, \ldots , \beta _{n-1} \in V$
and
![]() $(n+1)$
-ary function symbol F in
$(n+1)$
-ary function symbol F in
![]() $\mathcal L$
such that
$\mathcal L$
such that
As
![]() $\beta _0, \ldots , \beta _{n-1} \in V \subseteq \lambda $
and
$\beta _0, \ldots , \beta _{n-1} \in V \subseteq \lambda $
and
![]() $\gamma < \lambda $
, there is
$\gamma < \lambda $
, there is
![]() $i<\kappa $
such that
$i<\kappa $
such that
![]() $\beta _0, \ldots , \beta _{n-1}, \gamma < \lambda _i$
. Define an n-ary function
$\beta _0, \ldots , \beta _{n-1}, \gamma < \lambda _i$
. Define an n-ary function
![]() $G: \lambda _i \rightarrow \lambda _i$
as follows:
$G: \lambda _i \rightarrow \lambda _i$
as follows:
 $G(\xi _0, \cdots , \xi _{n-1})=\ \left \{ \begin {array}{l} F^M(\xi _0, \cdots , \xi _{n-1}, \alpha _\ell ), \hspace {0.8cm} \text { if } F^M(\xi _0, \ldots , \xi _{n-1}, \alpha _\ell ) < \lambda _i ,\\ 0, \hspace {3.64cm} \text { otherwise}. \end {array} \right.$
$G(\xi _0, \cdots , \xi _{n-1})=\ \left \{ \begin {array}{l} F^M(\xi _0, \cdots , \xi _{n-1}, \alpha _\ell ), \hspace {0.8cm} \text { if } F^M(\xi _0, \ldots , \xi _{n-1}, \alpha _\ell ) < \lambda _i ,\\ 0, \hspace {3.64cm} \text { otherwise}. \end {array} \right.$
Note that
![]() $G \in \{F_{n, \zeta }: \zeta \in [\lambda _i, 2^{\lambda _i}) \}$
. Let
$G \in \{F_{n, \zeta }: \zeta \in [\lambda _i, 2^{\lambda _i}) \}$
. Let
![]() $\zeta _*$
is well-defined and is definable in M (even in
$\zeta _*$
is well-defined and is definable in M (even in
![]() $M_0$
) from
$M_0$
) from
![]() $\alpha _\ell $
, so clearly
$\alpha _\ell $
, so clearly
![]() $\zeta _* \in cl(\{\alpha _\ell \}, M)$
.
$\zeta _* \in cl(\{\alpha _\ell \}, M)$
.
As
![]() $\zeta _* \in cl(\{\alpha _\ell \}, M) \cap \lambda = V_\ell \subseteq V$
and
$\zeta _* \in cl(\{\alpha _\ell \}, M) \cap \lambda = V_\ell \subseteq V$
and
![]() $\beta _0, \ldots , \beta _{n-1} \in V,$
so
$\beta _0, \ldots , \beta _{n-1} \in V,$
so
This contradicts our initial assumption that
![]() $\gamma \in N_\ell \cap \lambda \setminus V$
. The claim follows.
$\gamma \in N_\ell \cap \lambda \setminus V$
. The claim follows.
Claim 2.12.
![]() $N_1 \cap \lambda =N_2 \cap \lambda $
.
$N_1 \cap \lambda =N_2 \cap \lambda $
.
Proof By Claim 2.11, we have
![]() $ N_1 \cap \lambda =V=N_2 \cap \lambda ,$
which concludes the result.
$ N_1 \cap \lambda =V=N_2 \cap \lambda ,$
which concludes the result.
By Claim 2.12,
![]() $N_1 \cap \lambda =N_2 \cap \lambda $
, which implies clause (
$N_1 \cap \lambda =N_2 \cap \lambda $
, which implies clause (
![]() $\alpha $
) of
$\alpha $
) of
![]() $(\dagger )_{\alpha _1, \alpha _2}$
. Thus
$(\dagger )_{\alpha _1, \alpha _2}$
. Thus
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are as required in clause
$N_2$
are as required in clause
![]() $(\dagger )_{\alpha _1, \alpha _2}$
.
$(\dagger )_{\alpha _1, \alpha _2}$
.
This completes the proof of the lemma.
3
 $\mathrm {UB}_\lambda $
can fail at singular cardinals
$\mathrm {UB}_\lambda $
can fail at singular cardinals
In this section we prove the following theorem which answers Usuba’s Question 1.1.
Theorem 3.1. Assume
![]() $\lambda $
is a singular strong limit cardinal.
$\lambda $
is a singular strong limit cardinal.
![]() $\mathrm {UB}_\lambda $
fails if at least one of the following holds
$\mathrm {UB}_\lambda $
fails if at least one of the following holds
![]() $:$
$:$
-
(a)
 $\lambda =\aleph _\omega $
and Chang’s transfer principle
$\lambda =\aleph _\omega $
and Chang’s transfer principle
 $(\lambda ^+, \lambda ) \twoheadrightarrow (\aleph _1, \aleph _0)$
holds.
$(\lambda ^+, \lambda ) \twoheadrightarrow (\aleph _1, \aleph _0)$
holds. -
(b)
 $\lambda> \mu \geq \mathrm {cf}(\lambda )$
are such that
$\lambda> \mu \geq \mathrm {cf}(\lambda )$
are such that
 $(\lambda ^+, \lambda ) \twoheadrightarrow _{\leq \mathrm {cf}(\lambda )} (\mu ^+, \mu )$
holds.
$(\lambda ^+, \lambda ) \twoheadrightarrow _{\leq \mathrm {cf}(\lambda )} (\mu ^+, \mu )$
holds. -
(c)
 $\lambda> \mu \geq \mathrm {cf}(\lambda )$
and for every model M with universe
$\lambda> \mu \geq \mathrm {cf}(\lambda )$
and for every model M with universe
 $\lambda ^+$
and vocabulary of cardinality
$\lambda ^+$
and vocabulary of cardinality
 $\mathrm {cf}(\lambda )$
, we can find an increasing sequence
$\mathrm {cf}(\lambda )$
, we can find an increasing sequence
 $\vec {\alpha }=\langle \alpha _i: i < \mu ^+ \rangle $
of ordinals less than
$\vec {\alpha }=\langle \alpha _i: i < \mu ^+ \rangle $
of ordinals less than
 $\lambda ^+$
such that is stationary in
$\lambda ^+$
such that is stationary in $$\begin{align*}S^M_{\vec{\alpha}}=\{i<\mu^+: cl(\{\alpha_i\}, M) \cap \lambda \subseteq cl(\{\alpha_j: j<i \}, M) \} \end{align*}$$
$$\begin{align*}S^M_{\vec{\alpha}}=\{i<\mu^+: cl(\{\alpha_i\}, M) \cap \lambda \subseteq cl(\{\alpha_j: j<i \}, M) \} \end{align*}$$
 $\mu ^+$
.
$\mu ^+$
.
-
(d) There exists
 $\chi $
with
$\chi $
with
 $\lambda> \chi =\mathrm {cf}(\chi ) > \mathrm {cf}(\lambda )$
such that for every model M with universe
$\lambda> \chi =\mathrm {cf}(\chi ) > \mathrm {cf}(\lambda )$
such that for every model M with universe
 $\lambda ^+$
and vocabulary of cardinality
$\lambda ^+$
and vocabulary of cardinality
 $\mathrm {cf}(\lambda )$
, we can find an increasing sequence
$\mathrm {cf}(\lambda )$
, we can find an increasing sequence
 $\vec {\alpha }=\langle \alpha _i: i < \chi \rangle $
of ordinals less than
$\vec {\alpha }=\langle \alpha _i: i < \chi \rangle $
of ordinals less than
 $\lambda ^+$
such that is stationary in
$\lambda ^+$
such that is stationary in $$\begin{align*}S^M_{\vec{\alpha}}=\{i<\chi: cl(\{\alpha_i\}, M) \cap \lambda \subseteq cl(\{\alpha_j: j<i \}, M) \} \end{align*}$$
$$\begin{align*}S^M_{\vec{\alpha}}=\{i<\chi: cl(\{\alpha_i\}, M) \cap \lambda \subseteq cl(\{\alpha_j: j<i \}, M) \} \end{align*}$$
 $\chi $
.
$\chi $
.
-
(e) There is no sequence
 $\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
such that each
$\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
such that each
 $U_i \cap \lambda $
is a cofinal subset of
$U_i \cap \lambda $
is a cofinal subset of
 $\lambda $
,
$\lambda $
,
 $U_i \cap \lambda $
has size
$U_i \cap \lambda $
has size
 $\mathrm {cf}(\lambda )$
, and for every
$\mathrm {cf}(\lambda )$
, and for every
 $i<\lambda ^+$
there is a sequence
$i<\lambda ^+$
there is a sequence
 $\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
such that
$\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
such that
 $:$
$:$
-
•
 $\vec {X}_i$
has no repetition,
$\vec {X}_i$
has no repetition, -
•
 $\alpha _{i, j} \in U_i$
,
$\alpha _{i, j} \in U_i$
, -
•
 $\beta _{i, j} \in U_j \cap \lambda $
.
$\beta _{i, j} \in U_j \cap \lambda $
.
-
Furthermore, the statement
![]() $(e)$
is equivalent to
$(e)$
is equivalent to
![]() $\neg \mathrm {UB}_\lambda $
, provided that
$\neg \mathrm {UB}_\lambda $
, provided that
![]() $\mathrm {cf}(\lambda )$
is not a Jonsson cardinal.
$\mathrm {cf}(\lambda )$
is not a Jonsson cardinal.
Remark 3.2. The assumption “
![]() $\lambda $
is a strong limit cardinal” is only used in the proof of (e) implies
$\lambda $
is a strong limit cardinal” is only used in the proof of (e) implies
![]() $\neg \mathrm {UB}_\lambda $
.
$\neg \mathrm {UB}_\lambda $
.
Proof We prove the theorem by a sequence of claims. First note that:
Claim 3.3. Clause
![]() $(a)$
is a special case of clause
$(a)$
is a special case of clause
![]() $(b)$
, and clause
$(b)$
, and clause
![]() $(c) $
implies clause
$(c) $
implies clause
![]() $(d)$
.
$(d)$
.
Claim 3.4.
![]() $(b)$
implies
$(b)$
implies
![]() $(c)$
.
$(c)$
.
Proof Let M be a model with universe
![]() $\lambda ^+$
and vocabulary of cardinality at most
$\lambda ^+$
and vocabulary of cardinality at most
![]() $\mathrm {cf}(\lambda )$
. By (b), there exists an elementary submodel
$\mathrm {cf}(\lambda )$
. By (b), there exists an elementary submodel
![]() $N \prec M$
such that
$N \prec M$
such that
![]() $||N||=\mu ^+$
and
$||N||=\mu ^+$
and
![]() $|N \cap \lambda |=\mu .$
Let
$|N \cap \lambda |=\mu .$
Let
![]() $\vec {\alpha }=\langle \alpha _i: i<\mu ^+ \rangle $
list in increasing order the first
$\vec {\alpha }=\langle \alpha _i: i<\mu ^+ \rangle $
list in increasing order the first
![]() $\mu ^+$
elements of
$\mu ^+$
elements of
![]() $N.$
So for
$N.$
So for
![]() $i<\mu ^+$
we have
$i<\mu ^+$
we have
and since
![]() $N \cap \lambda $
has size
$N \cap \lambda $
has size
![]() $\mu $
, we can find some
$\mu $
, we can find some
![]() $i(*)< \mu ^+$
such that
$i(*)< \mu ^+$
such that
 $$\begin{align*}\forall i<\mu^+,~ cl(\{\alpha_i\}, M) \cap \lambda \subseteq \bigcup\limits_{j<i(*)}cl(\{\alpha_j\}, M). \end{align*}$$
$$\begin{align*}\forall i<\mu^+,~ cl(\{\alpha_i\}, M) \cap \lambda \subseteq \bigcup\limits_{j<i(*)}cl(\{\alpha_j\}, M). \end{align*}$$
Hence the set
![]() $S^M_{\vec {\alpha }}$
includes
$S^M_{\vec {\alpha }}$
includes
![]() $[i(*), \mu ^+)$
and so is stationary in
$[i(*), \mu ^+)$
and so is stationary in
![]() $\mu ^+$
, as requested.
$\mu ^+$
, as requested.
Claim 3.5.
![]() $(d)$
implies
$(d)$
implies
![]() $(e)$
.
$(e)$
.
Proof Suppose towards a contradiction that (d) holds but (e) fails. As (e) fails, we can find sequences
![]() $\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
and
$\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
and
![]() $\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
as in clause (e). Let M be a model in a vocabulary
$\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
as in clause (e). Let M be a model in a vocabulary
![]() $\mathcal L$
such that:
$\mathcal L$
such that:
-
(1)
 $|\mathcal L|=\mathrm {cf}(\lambda )$
,
$|\mathcal L|=\mathrm {cf}(\lambda )$
, -
(2) M has universe
 $\lambda ^+$
,
$\lambda ^+$
, -
(3)
 $M=(\lambda ^+, \langle \tau ^M_i: i<\mathrm {cf}(\lambda )\rangle , H^M )$
, where
$M=(\lambda ^+, \langle \tau ^M_i: i<\mathrm {cf}(\lambda )\rangle , H^M )$
, where-
(a)
 $\tau ^M_i=i,$
$\tau ^M_i=i,$
-
(b)
 $H^M$
is a 2-place function such that for all i,
$H^M$
is a 2-place function such that for all i,
 $U_i \cap \lambda = \{ H^M(i, \alpha ): \alpha < \mathrm {cf}(\lambda ) \}$
.
$U_i \cap \lambda = \{ H^M(i, \alpha ): \alpha < \mathrm {cf}(\lambda ) \}$
.
-
Now by (d) applied to the model M, we can find a sequence
![]() $\vec {\zeta }= \langle \zeta _i: i<\chi \rangle $
of ordinals less than
$\vec {\zeta }= \langle \zeta _i: i<\chi \rangle $
of ordinals less than
![]() $\lambda ^+$
such that the set
$\lambda ^+$
such that the set
![]() $S^M_{\vec {\zeta }}$
is stationary in
$S^M_{\vec {\zeta }}$
is stationary in
![]() $\chi $
. Let
$\chi $
. Let
![]() $\zeta =\sup \limits _{i<\chi }\zeta _i$
. Consider the sequence
$\zeta =\sup \limits _{i<\chi }\zeta _i$
. Consider the sequence
![]() $\vec {X}_\zeta =\langle (\alpha _{\zeta , \xi }, \beta _{\zeta , \xi }): \xi < \zeta \rangle $
.
$\vec {X}_\zeta =\langle (\alpha _{\zeta , \xi }, \beta _{\zeta , \xi }): \xi < \zeta \rangle $
.
For
![]() $i<\chi $
, let
$i<\chi $
, let
So
![]() $\langle W_i: i<\chi \rangle $
is a
$\langle W_i: i<\chi \rangle $
is a
![]() $\subseteq $
-increasing continuous sequence of sets each of cardinality
$\subseteq $
-increasing continuous sequence of sets each of cardinality
![]() $<\chi $
. Note that for each
$<\chi $
. Note that for each
![]() $i \in S^M_{\vec {\zeta }}$
,
$i \in S^M_{\vec {\zeta }}$
,
(The former inclusion
![]() $\subseteq $
holds because
$\subseteq $
holds because
![]() $\mathrm {cf}(\lambda ) \cup \{\zeta _i \} \subseteq cl(\{\zeta _i\}, M)$
and
$\mathrm {cf}(\lambda ) \cup \{\zeta _i \} \subseteq cl(\{\zeta _i\}, M)$
and
![]() $cl(\{\zeta _i\}, M)$
is closed under
$cl(\{\zeta _i\}, M)$
is closed under
![]() $H^M$
. The latter inclusion
$H^M$
. The latter inclusion
![]() $\subseteq $
holds because
$\subseteq $
holds because
![]() $i \in S^M_{\vec {\zeta }}$
.) Then since
$i \in S^M_{\vec {\zeta }}$
.) Then since
![]() $S^M_{\vec {\zeta }}$
is stationary in
$S^M_{\vec {\zeta }}$
is stationary in
![]() $\chi $
, there is
$\chi $
, there is
![]() $\beta _*$
such that
$\beta _*$
such that
is stationary. Moreover, since
![]() $|U_\zeta |=\mathrm {cf}(\lambda ) < \chi ,$
we get some
$|U_\zeta |=\mathrm {cf}(\lambda ) < \chi ,$
we get some
![]() $i_i < i_2$
in U such that
$i_i < i_2$
in U such that
![]() $\alpha _{\zeta , \zeta _{i_1}}=\alpha _{\zeta , \zeta _{i_2}}$
. This contradicts that
$\alpha _{\zeta , \zeta _{i_1}}=\alpha _{\zeta , \zeta _{i_2}}$
. This contradicts that
![]() $\vec {X}_\zeta $
has no repetition.
$\vec {X}_\zeta $
has no repetition.
Claim 3.6.
![]() $(e)$
implies
$(e)$
implies
![]() $\neg \mathrm {UB}_\lambda $
.
$\neg \mathrm {UB}_\lambda $
.
Proof Suppose not. Thus we can assume that both (e) and
![]() $\mathrm {UB}_\lambda $
hold. Let
$\mathrm {UB}_\lambda $
hold. Let
![]() $f: [\lambda ^+]^{<\omega } \to \lambda ^+$
witness
$f: [\lambda ^+]^{<\omega } \to \lambda ^+$
witness
![]() $\mathrm {UB}_\lambda .$
Choose a vocabulary
$\mathrm {UB}_\lambda .$
Choose a vocabulary
![]() $\mathcal L$
of size
$\mathcal L$
of size
![]() $\mathrm {cf}(\lambda )$
and an
$\mathrm {cf}(\lambda )$
and an
![]() $\mathcal L$
-model M such that:
$\mathcal L$
-model M such that:
-
(1) M has universe
 $\lambda ^+.$
$\lambda ^+.$
-
(2) M expands the model
 $M_0$
of Lemma 2.8, by expanding
$M_0$
of Lemma 2.8, by expanding
 $\mathcal L_0$
(the vocabulary of
$\mathcal L_0$
(the vocabulary of
 $M_0$
) using the constant symbols
$M_0$
) using the constant symbols
 $\langle d^M_i: i< \mathrm {cf}(\lambda ) \rangle $
and the function symbols
$\langle d^M_i: i< \mathrm {cf}(\lambda ) \rangle $
and the function symbols
 $( \langle F^M_n: n< \omega \rangle , p^M, G_1^M, G_2^M )$
, where:
$( \langle F^M_n: n< \omega \rangle , p^M, G_1^M, G_2^M )$
, where:-
(a)
 $d_i^M=i$
for
$d_i^M=i$
for
 $i<\mathrm {cf}(\lambda )$
,
$i<\mathrm {cf}(\lambda )$
, -
(b)
 $F^M_n$
is an n-ary function such that
$F^M_n$
is an n-ary function such that  $$\begin{align*}F^M_n(\alpha_0, \ldots, \alpha_{n-1}) = f(\{\alpha_0, \ldots, \alpha_{n-1} \}), \end{align*}$$
$$\begin{align*}F^M_n(\alpha_0, \ldots, \alpha_{n-1}) = f(\{\alpha_0, \ldots, \alpha_{n-1} \}), \end{align*}$$
-
(c)
 $p^M$
is a pairing function on
$p^M$
is a pairing function on
 $\lambda ^+,$
mapping
$\lambda ^+,$
mapping
 $\lambda \times \lambda $
onto
$\lambda \times \lambda $
onto
 $\lambda $
,
$\lambda $
, -
(d)
 $G_1^M$
and
$G_1^M$
and
 $G_2^M$
are 2-place functions such that for every
$G_2^M$
are 2-place functions such that for every
 $\alpha \in [\lambda , \lambda ^+)$
,
$\alpha \in [\lambda , \lambda ^+)$
,
 $\langle G_1(\beta , \alpha ): \beta < \alpha \rangle $
enumerates
$\langle G_1(\beta , \alpha ): \beta < \alpha \rangle $
enumerates
 $\lambda $
and
$\lambda $
and  $$\begin{align*}\big( \beta < \alpha ~\& ~ \gamma=G_1(\beta, \alpha) \big) \Rightarrow \beta=G_2(\gamma, \alpha). \end{align*}$$
$$\begin{align*}\big( \beta < \alpha ~\& ~ \gamma=G_1(\beta, \alpha) \big) \Rightarrow \beta=G_2(\gamma, \alpha). \end{align*}$$
-
By expanding M further, let us suppose that
-
(3) M contains Skolem functions.
For
![]() $\alpha < \lambda ^+,$
set
$\alpha < \lambda ^+,$
set
![]() $N_\alpha = cl(\{\alpha \}, M)$
.
$N_\alpha = cl(\{\alpha \}, M)$
.
![]() $(*)_1$
$(*)_1$
![]() $N_\alpha $
belongs to
$N_\alpha $
belongs to
![]() $[\lambda ^+]^{\mathrm {cf}(\lambda )}$
and it contains an unbounded subset of
$[\lambda ^+]^{\mathrm {cf}(\lambda )}$
and it contains an unbounded subset of
![]() $\lambda $
.
$\lambda $
.
Proof As
![]() $\mathcal L$
has size
$\mathcal L$
has size
![]() $\mathrm {cf}(\lambda )$
, so
$\mathrm {cf}(\lambda )$
, so
![]() $|N_\alpha | \leq \mathrm {cf}(\lambda )$
. On the other hand, by clause (2)(a),
$|N_\alpha | \leq \mathrm {cf}(\lambda )$
. On the other hand, by clause (2)(a),
![]() $\mathrm {cf}(\lambda ) \subseteq N_\alpha $
and hence
$\mathrm {cf}(\lambda ) \subseteq N_\alpha $
and hence
![]() $N_\alpha $
belongs to
$N_\alpha $
belongs to
![]() $[\lambda ^+]^{\mathrm {cf}(\lambda )}$
. Also as
$[\lambda ^+]^{\mathrm {cf}(\lambda )}$
. Also as
![]() $\{c_i^{M_0}: i < \mathrm {cf}(\lambda ) \} \subseteq N_\alpha $
(see the proof of Lemma 2.8) and
$\{c_i^{M_0}: i < \mathrm {cf}(\lambda ) \} \subseteq N_\alpha $
(see the proof of Lemma 2.8) and
![]() $\langle c_i^{M_0}: i < \mathrm {cf}(\lambda ) \rangle $
is an unbounded sequence in
$\langle c_i^{M_0}: i < \mathrm {cf}(\lambda ) \rangle $
is an unbounded sequence in
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $N_\alpha $
contains an unbounded subset of
$N_\alpha $
contains an unbounded subset of
![]() $\lambda $
.
$\lambda $
.
Let
E is clearly a club of
![]() $\lambda ^+$
and
$\lambda ^+$
and
![]() $E \cap \lambda =\emptyset .$
By Lemma 2.8, we have
$E \cap \lambda =\emptyset .$
By Lemma 2.8, we have
![]() $(*)_2$
Suppose
$(*)_2$
Suppose
![]() $\xi < \zeta $
are in E. Then
$\xi < \zeta $
are in E. Then
 $$\begin{align*}\xi \in cl\bigg(\{\zeta\} \cup (N_\xi \cap \lambda) \cup (N_\zeta \cap \lambda), M \bigg). \end{align*}$$
$$\begin{align*}\xi \in cl\bigg(\{\zeta\} \cup (N_\xi \cap \lambda) \cup (N_\zeta \cap \lambda), M \bigg). \end{align*}$$
Proof Suppose by the way of contradiction that
![]() $\xi \notin cl\big (\{\zeta \} \cup (N_\xi \cap \lambda ) \cup (N_\zeta \cap \lambda ), M \big ).$
Let
$\xi \notin cl\big (\{\zeta \} \cup (N_\xi \cap \lambda ) \cup (N_\zeta \cap \lambda ), M \big ).$
Let
![]() $V_1=N_\xi \cap \lambda $
,
$V_1=N_\xi \cap \lambda $
,
![]() $V_2=N_\zeta \cap \lambda $
and
$V_2=N_\zeta \cap \lambda $
and
![]() $V=V_1 \cup V_2$
. By our assumption,
$V=V_1 \cup V_2$
. By our assumption,
also, it is clear that
Thus by Lemma 2.8, we can find submodels
![]() $N^*_1, N^*_2$
of M such that:
$N^*_1, N^*_2$
of M such that:
-
(1)
 $N^*_1 \cap \lambda =N^*_2 \cap \lambda $
is unbounded in
$N^*_1 \cap \lambda =N^*_2 \cap \lambda $
is unbounded in
 $\lambda $
.
$\lambda $
. -
(2)
 $\xi \in N^*_1 \setminus N^*_2$
and
$\xi \in N^*_1 \setminus N^*_2$
and
 $\zeta \in N^*_2 \setminus N^*_1$
.
$\zeta \in N^*_2 \setminus N^*_1$
.
The models
![]() $N_1^*$
and
$N_1^*$
and
![]() $N^*_2$
are clearly f-closed, and by clause (1) above and
$N^*_2$
are clearly f-closed, and by clause (1) above and
![]() $\mathrm {UB}_\lambda $
, we have
$\mathrm {UB}_\lambda $
, we have
![]() $N^*_1 \subseteq N^*_2$
or
$N^*_1 \subseteq N^*_2$
or
![]() $N^*_2 \subseteq N^*_1$
, which contradicts clause (2) above.
$N^*_2 \subseteq N^*_1$
, which contradicts clause (2) above.
Let
![]() $\langle \sigma _i(x_0, \ldots , x_{n(i)-1}): i<\mathrm {cf}(\lambda ) \rangle $
list all terms of
$\langle \sigma _i(x_0, \ldots , x_{n(i)-1}): i<\mathrm {cf}(\lambda ) \rangle $
list all terms of
![]() $\mathcal {L}$
. By
$\mathcal {L}$
. By
![]() $(*)_2$
, for each
$(*)_2$
, for each
![]() $\xi < \zeta $
from E, we can choose some
$\xi < \zeta $
from E, we can choose some
![]() $i(\xi , \zeta ) < \mathrm {cf}(\lambda )$
together with sequences
$i(\xi , \zeta ) < \mathrm {cf}(\lambda )$
together with sequences
![]() $\vec {a}_{\xi , \zeta } \in (N_\zeta \cap \lambda )^{<\omega }$
and
$\vec {a}_{\xi , \zeta } \in (N_\zeta \cap \lambda )^{<\omega }$
and
![]() $\vec {b}_{\xi , \zeta } \in (N_\xi \cap \lambda )^{<\omega }$
such that
$\vec {b}_{\xi , \zeta } \in (N_\xi \cap \lambda )^{<\omega }$
such that
For
![]() $\xi \in E$
set
$\xi \in E$
set
![]() $U_\xi =N_\xi =cl(\{\xi \}, M).$
It follows that
$U_\xi =N_\xi =cl(\{\xi \}, M).$
It follows that
![]() $U_\xi =cl(U_\xi , M)$
. For
$U_\xi =cl(U_\xi , M)$
. For
![]() $ \xi < \zeta $
use the pairing function
$ \xi < \zeta $
use the pairing function
![]() $p^M$
to find
$p^M$
to find
![]() $\alpha _{\zeta , \xi }$
and
$\alpha _{\zeta , \xi }$
and
![]() $\beta _{\zeta , \xi }$
such that
$\beta _{\zeta , \xi }$
such that
![]() $\alpha _{\zeta , \xi }$
codes
$\alpha _{\zeta , \xi }$
codes
![]() $\langle i(\xi , \zeta ) \rangle ^{\frown } \vec {a}_{\xi , \zeta }$
and
$\langle i(\xi , \zeta ) \rangle ^{\frown } \vec {a}_{\xi , \zeta }$
and
![]() $\beta _{\zeta , \xi }$
codes
$\beta _{\zeta , \xi }$
codes
![]() $\vec {b}_{\xi , \zeta }$
.
$\vec {b}_{\xi , \zeta }$
.
Now the sequences
and
witness the failure of (e). We get a contradiction and the claim follows.
Thus so far we have shown that
Claim 3.7. Suppose that
![]() $\mathrm {cf}(\lambda )$
is not a Jonsson cardinal. Then
$\mathrm {cf}(\lambda )$
is not a Jonsson cardinal. Then
![]() $\neg \mathrm {UB}_\lambda $
implies
$\neg \mathrm {UB}_\lambda $
implies
![]() $(e)$
.
$(e)$
.
Proof Suppose towards a contradiction that (e) fails and let
![]() $\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
and
$\vec {X}=\langle U_i: i<\lambda ^+ \rangle $
and
![]() $\langle \vec {X}_i: i< \lambda ^+ \rangle $
, where
$\langle \vec {X}_i: i< \lambda ^+ \rangle $
, where
![]() $\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
as in clause (e) witness this failure. Let
$\vec {X}_i=\langle (\alpha _{i, j}, \beta _{i, j}): j<i \rangle $
as in clause (e) witness this failure. Let
![]() $\langle \lambda _i: i<\mathrm {cf}(\lambda ) \rangle $
be an increasing sequence cofinal in
$\langle \lambda _i: i<\mathrm {cf}(\lambda ) \rangle $
be an increasing sequence cofinal in
![]() $\lambda $
and define the function
$\lambda $
and define the function
![]() $c: \lambda \to \mathrm {cf}(\lambda )$
as
$c: \lambda \to \mathrm {cf}(\lambda )$
as
For
![]() $\xi < \lambda ^+$
let
$\xi < \lambda ^+$
let
![]() $\langle \gamma _{\xi , i}: i<\mathrm {cf}(\lambda ) \rangle $
enumerate
$\langle \gamma _{\xi , i}: i<\mathrm {cf}(\lambda ) \rangle $
enumerate
![]() $U_\xi $
such that each element of
$U_\xi $
such that each element of
![]() $U_\xi $
appears cofinally many often. Let
$U_\xi $
appears cofinally many often. Let
![]() $f: [\lambda ^+]^{<\omega } \to \lambda ^+$
be such that:
$f: [\lambda ^+]^{<\omega } \to \lambda ^+$
be such that:
-
(1) If
 $\xi < \zeta < \lambda ^+$
, then
$\xi < \zeta < \lambda ^+$
, then  $$\begin{align*}f(\alpha_{\zeta, \xi}, \beta_{\zeta, \xi}, \zeta)=\xi. \end{align*}$$
$$\begin{align*}f(\alpha_{\zeta, \xi}, \beta_{\zeta, \xi}, \zeta)=\xi. \end{align*}$$
-
(2) If
 $\zeta < \lambda ^+$
and
$\zeta < \lambda ^+$
and
 $\alpha < \lambda $
, then for arbitrary large
$\alpha < \lambda $
, then for arbitrary large
 $j< \mathrm {cf}(\lambda )$
, we have
$j< \mathrm {cf}(\lambda )$
, we have  $$\begin{align*}\sup\limits_{i<j}\lambda_i < \alpha < \lambda_j \implies f(\alpha, \zeta)=\gamma_{\zeta, j}. \end{align*}$$
$$\begin{align*}\sup\limits_{i<j}\lambda_i < \alpha < \lambda_j \implies f(\alpha, \zeta)=\gamma_{\zeta, j}. \end{align*}$$
-
(3) If
 $A \in [\mathrm {cf}(\lambda )]^{\mathrm {cf}(\lambda )}$
,
$A \in [\mathrm {cf}(\lambda )]^{\mathrm {cf}(\lambda )}$
,
 $c(\alpha _i)=i$
for
$c(\alpha _i)=i$
for
 $i \in A$
and
$i \in A$
and
 $j<\mathrm {cf}(\lambda ),$
then for some n and some sequence
$j<\mathrm {cf}(\lambda ),$
then for some n and some sequence
 $\vec \xi = \langle \xi _0, \ldots , \xi _{n-1} \rangle \in A^n$
, we have
$\vec \xi = \langle \xi _0, \ldots , \xi _{n-1} \rangle \in A^n$
, we have  $$\begin{align*}j =c (f(\alpha_{\xi_0}, \ldots, \alpha_{\xi_{n-1}})). \end{align*}$$
$$\begin{align*}j =c (f(\alpha_{\xi_0}, \ldots, \alpha_{\xi_{n-1}})). \end{align*}$$
Since
![]() $\mathrm {cf}(\lambda )$
is not a Jonsson cardinal, we can define such a function f.Footnote
2
Let us show that the pair
$\mathrm {cf}(\lambda )$
is not a Jonsson cardinal, we can define such a function f.Footnote
2
Let us show that the pair
![]() $(f, c)$
witnesses
$(f, c)$
witnesses
![]() $\mathrm {UB}_\lambda $
holds,Footnote
3
which contradicts our assumption. To see this, suppose
$\mathrm {UB}_\lambda $
holds,Footnote
3
which contradicts our assumption. To see this, suppose
![]() $x, y \subseteq \lambda ^+$
are closed under f,
$x, y \subseteq \lambda ^+$
are closed under f,
![]() $x \cap \lambda =y\cap \lambda $
and
$x \cap \lambda =y\cap \lambda $
and
![]() $\sup (x\cap \lambda )=\lambda .$
Assume towards a contradiction that
$\sup (x\cap \lambda )=\lambda .$
Assume towards a contradiction that
![]() $x \nsubseteq y$
and
$x \nsubseteq y$
and
![]() $y \nsubseteq x.$
Let
$y \nsubseteq x.$
Let
![]() $\xi =\min (x \setminus y)$
and
$\xi =\min (x \setminus y)$
and
![]() $\zeta =\min (y \setminus x)$
, and let us suppose that
$\zeta =\min (y \setminus x)$
, and let us suppose that
![]() $\xi < \zeta .$
$\xi < \zeta .$
By clause (3),
![]() $\mathrm {cf}(\lambda ) \subseteq y,$
and then by clause (2), and since
$\mathrm {cf}(\lambda ) \subseteq y,$
and then by clause (2), and since
![]() $y \cap \lambda $
is cofinal in
$y \cap \lambda $
is cofinal in
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $U_\zeta \subseteq y.$
Similarly
$U_\zeta \subseteq y.$
Similarly
![]() $U_\xi \subseteq x$
. As
$U_\xi \subseteq x$
. As
![]() $x \cap \lambda =y \cap \lambda $
and
$x \cap \lambda =y \cap \lambda $
and
![]() $U_\xi \subseteq \lambda ,$
we conclude that
$U_\xi \subseteq \lambda ,$
we conclude that
![]() $U_\xi \subseteq y$
as well. Thus by item (1), and since
$U_\xi \subseteq y$
as well. Thus by item (1), and since
![]() $\alpha _{\zeta , \xi }, \beta _{\zeta , \xi }, \zeta \in y$
we have
$\alpha _{\zeta , \xi }, \beta _{\zeta , \xi }, \zeta \in y$
we have
![]() $\xi \in y$
, which contradicts the choice of
$\xi \in y$
, which contradicts the choice of
![]() $\xi \in x \setminus y$
. This completes the proof of the claim.
$\xi \in x \setminus y$
. This completes the proof of the claim.
The theorem follows.
Remark 3.8. The above proof shows that the following are equivalent:
-
(1) clause (e) of Theorem 3.1,
-
(2) for each model M with universe
 $\lambda ^+$
and vocabulary of cardinality
$\lambda ^+$
and vocabulary of cardinality
 $\mathrm {cf}(\lambda ),$
there are substructures
$\mathrm {cf}(\lambda ),$
there are substructures
 $N_0, N_1$
of M such that
$N_0, N_1$
of M such that
 $N_0 \cap \lambda =N_1 \cap \lambda $
,
$N_0 \cap \lambda =N_1 \cap \lambda $
,
 $N_0 \nsubseteq N_1$
, and
$N_0 \nsubseteq N_1$
, and
 $N_1 \nsubseteq N_0.$
$N_1 \nsubseteq N_0.$
As we noticed earlier, it is consistent relative to the existence of large cardinals that Chang’s transfer principle
![]() $(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
holds with
$(\aleph _{\omega +1}, \aleph _\omega ) \twoheadrightarrow (\aleph _{1}, \aleph _0)$
holds with
![]() $\aleph _\omega $
being strong limit. Hence by our main theorem, we have the following corollary.
$\aleph _\omega $
being strong limit. Hence by our main theorem, we have the following corollary.
Corollary 3.9. It is consistent, relative to the existence of large cardinals, that
![]() $\mathrm {UB}_{\aleph _\omega }$
fails.
$\mathrm {UB}_{\aleph _\omega }$
fails.
Funding
The first author’s research has been supported by a grant from IPM (No. 1400030417). The second author’s research has been partially supported by Israel Science Foundation (ISF) grant no: 1838/19. This is publication 1216 of the second author.
Acknowledgments
The authors thank the referee of the paper for his/her very careful reading of the paper and detecting some essential errors in earlier versions of the paper.