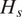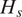Impact Statement
In the context of climate change, the climate of ocean waves has major socioeconomic and environmental implications. Since ocean waves are generated by the wind blowing at the ocean surface, understanding the relationship between wind and waves is critical to assessing the impact of climate change on ocean waves. This work contributes to understanding the spatiotemporal relationship between wind conditions and ocean waves using deep learning. We propose a fully data-driven empirical wind-wave model that predicts the significant wave height at a location in the Bay of Biscay using the North Atlantic wind conditions. The proposed method is computationally inexpensive and can provide long time series of future significant wave heights or complete historical data if wind data are available.
1. Introduction
Characterization of wave climate is required for many marine applications, such as the design of coastal and offshore structures and the planning of ship operations. Wind waves are generated by the surface wind, with the local wind creating the wind sea and wind from distant areas creating waves that propagate and form swells (Young, Reference Young1999). Waves in the Bay of Biscay depend on both local and large-scale wind conditions in the North Atlantic (Charles et al., Reference Charles, Idier, Delecluse, Déqué and Le Cozannet2012); however, swells generally dominate the sea state. Swells travel large distances and take up to 5 days to cross the Atlantic from Cape Hatteras to the Bay of Biscay (Ardhuin and Orfila, Reference Ardhuin and Orfila2018). Consequently, waves observed at a given location depend on wind conditions over the North Atlantic in a time window of several days, and it is challenging to reproduce this complex spatiotemporal relationship using machine learning. The goal of this work is to propose a deep learning approach that learns this relationship.
The advantage of deep learning methods (Goodfellow et al., Reference Goodfellow, Bengio and Courville2016) lies in their ability to build hierarchical representations of predictors. In particular, in the case of spatial data, convolutional neural networks (CNNs) allow to learn complex spatial features from the data (Gu et al., Reference Gu, Wang, Kuen, Ma, Shahroudy, Shuai, Liu, Wang, Wang, Wang, Cai and Chen2018). Moreover, long short-term memory (LSTM) (Hochreiter and Schmidhuber, Reference Hochreiter and Schmidhuber1997 has proven to be very successful in predicting time series and sequence data. In this work, we propose a nonexpensive data-driven approach that learns the underlying spatiotemporal structure of the relationship between wind and waves using a two-stage model based on CNNs and LSTM.
This paper is organized as follows. Section 2 presents the problem of downscaling of ocean waves and related works. Section 3 describes the data used in this work. Section 4 presents the proposed two-stage model, the architecture, and the training process. Section 5 discusses the results of this work. Finally, Section 6 presents the conclusions and future work directions.
2. Problem Statement and Related Work
The problem of improving the spatial resolution of climate variables is known under the name of downscaling (Maraun et al., Reference Maraun, Wetterhall, Ireson, Chandler, Kendon, Widmann, Brienen, Rust, Sauter, Themeßl and Venema2010). Downscaling approaches attempt to construct a link, either numerical or statistical, between large-scale and local-scale variables. The advantage of statistical downscaling (SD) over numerical models is primarily in terms of computational efficiency. A rigorous comparison of the two approaches can be found in Wang et al. (Reference Wang, Swail and Cox2010) and Laugel et al. (Reference Laugel, Menendez, Benoit, Mattarolo and Méndez2014).
In the case of ocean waves, wind (Obakrim et al., Reference Obakrim, Ailliot, Monbet and Raillard2022) or sea level pressure (SLP) (Camus et al., Reference Camus, Méndez, Losada, Menéndez, Espejo, Pérez, Rueda and Guanche2014) are commonly used to downscale ocean wave parameters. However, in order to establish a link function between the wind (or SLP) and the local ocean wave parameters, it is necessary to consider a large spatial and temporal coverage and, consequently, a large number of potential explanatory variables that are highly correlated. Some methods determine the wave generation area for any ocean location worldwide. For example, ESTELA (Pérez et al., Reference Pérez, Méndez, Menéndez and Losada2014) is a numerical model that uses spectral information to select the fraction of energy that travels to the target point from selected source points. The ESTELA method can be used to design SD methods. For instance, Camus et al. (Reference Camus, Méndez, Losada, Menéndez, Espejo, Pérez, Rueda and Guanche2014) and Hegermiller et al. (Reference Hegermiller, Antolinez, Rueda, Camus, Perez, Erikson, Barnard and Mendez2017) used the ESTELA method to define the predictors used in their SD model.
Obakrim et al. (Reference Obakrim, Ailliot, Monbet and Raillard2022) proposed a data-driven approach that determines the wave generation area by estimating the travel time of waves, generated in each considered sources point, that reach the target point. Then, the predictors were defined based on the wave generation area and finally, a SD model based on weather types was built.
As far as we know, the existing methods for SD of ocean wave parameters define a priori the spatiotemporal structure of the predictors, and then the SD model is built using these predictors. The aim of this study is to propose a deep learning approach that automatically learns the spatiotemporal relationship between wind and waves.
3. Data Preparation
The Climate Forecast System Reanalysis (CFSR) (Saha et al., Reference Saha, Moorthi, Pan, Wu, Wang, Nadiga, Tripp, Kistler, Woollen, Behringer and Liu2010) hourly wind data is considered in this study as a predictor. CFSR is a global reanalysis developed by the National Centers for Environmental Prediction (NCEP) that covers the period from 1979 to the present with an hourly time step and a spatial resolution of 0.5° by 0.5°. The historical
![]() $ {H}_s $
data is extracted from the hindcast database HOMERE (Boudière et al., Reference Boudière, Maisondieu, Ardhuin, Accensi, Pineau-Guillou and Lepesqueur2013) at the target location with spatial coordinates (45.2°N, 1.6°W) located in the Bay of Biscay. The temporal resolution of both wind and
$ {H}_s $
data is extracted from the hindcast database HOMERE (Boudière et al., Reference Boudière, Maisondieu, Ardhuin, Accensi, Pineau-Guillou and Lepesqueur2013) at the target location with spatial coordinates (45.2°N, 1.6°W) located in the Bay of Biscay. The temporal resolution of both wind and
![]() $ {H}_s $
data is up-scaled to 3-hourly data. The period from 1994 to 2016 is considered in this study, leading to a dataset with
$ {H}_s $
data is up-scaled to 3-hourly data. The period from 1994 to 2016 is considered in this study, leading to a dataset with
![]() $ n=67,208 $
observations.
$ n=67,208 $
observations.
Instead of using both zonal and meridional components as a predictor, we use the projected wind (Obakrim et al., Reference Obakrim, Ailliot, Monbet and Raillard2022) defined, at each location
![]() $ j $
and time
$ j $
and time
![]() $ t $
, as
$ t $
, as
 $$ {W}_j(t)={U}_j(t)\hskip0.1em {\cos}^2\left(\frac{1}{2}\left({b}_j-{\theta}_j(t)\right)\right), $$
$$ {W}_j(t)={U}_j(t)\hskip0.1em {\cos}^2\left(\frac{1}{2}\left({b}_j-{\theta}_j(t)\right)\right), $$
where
![]() $ {W}_j(t) $
is the projected wind,
$ {W}_j(t) $
is the projected wind,
![]() $ {U}_j(t) $
the wind speed,
$ {U}_j(t) $
the wind speed,
![]() $ {\theta}_j(t) $
the wind direction and
$ {\theta}_j(t) $
the wind direction and
![]() $ {b}_j $
is the great circle bearing from the source point
$ {b}_j $
is the great circle bearing from the source point
![]() $ j $
to the target point. Under the assumption that waves travel in great circle paths, grid points whose paths are blocked by land are neglected (Figure 1). Therefore, we define the global predictor at time
$ j $
to the target point. Under the assumption that waves travel in great circle paths, grid points whose paths are blocked by land are neglected (Figure 1). Therefore, we define the global predictor at time
![]() $ t $
as
$ t $
as
where
![]() $ p=5,651 $
is total number of grid points.
$ p=5,651 $
is total number of grid points.

Figure 1. The projected wind, defined in (1), in January 1, 1994, 00:00 hr. The black point represents the target point.
Following Obakrim et al. (Reference Obakrim, Ailliot, Monbet and Raillard2022), in order to capture the wind sea, we also define the local predictor as
where
![]() $ U(t) $
is the wind speed at the target point and
$ U(t) $
is the wind speed at the target point and
![]() $ F(t) $
is the fetch length at time
$ F(t) $
is the fetch length at time
![]() $ t $
, calculated as the minimum of the distance from the target point to shore in the direction from which the wind is blowing and
$ t $
, calculated as the minimum of the distance from the target point to shore in the direction from which the wind is blowing and
![]() $ 500\;\mathrm{km} $
. The fetch has an important effect on wind sea characteristics (Ardhuin and Orfila, Reference Ardhuin and Orfila2018); therefore, it is commonly used to construct empirical wind wave models.
$ 500\;\mathrm{km} $
. The fetch has an important effect on wind sea characteristics (Ardhuin and Orfila, Reference Ardhuin and Orfila2018); therefore, it is commonly used to construct empirical wind wave models.
4. Proposed Methodology
As mentioned in the last section, state of the art statistical methods for downscaling wave parameters usually use a preprocessing step to create features that take into account the wave generation area. In this study, we propose a deep-learning approach that automatically extracts these features. Since waves may take several days to reach the target point, the history and current wind can be used to predict
![]() $ {H}_s $
. An example of this type of model could have the following form:
$ {H}_s $
. An example of this type of model could have the following form:
where,
![]() $ {t}_{\mathrm{max}} $
can be interpreted as the maximum travel time of the waves and will be referred to as such in the following. However, this approach can be computationally challenging given the dimension of the predictor (5,651 in our case). Instead, in this study, we propose to use current wind conditions to estimate current and future
$ {t}_{\mathrm{max}} $
can be interpreted as the maximum travel time of the waves and will be referred to as such in the following. However, this approach can be computationally challenging given the dimension of the predictor (5,651 in our case). Instead, in this study, we propose to use current wind conditions to estimate current and future
![]() $ {H}_s $
.
$ {H}_s $
.
In order to describe the complex spatiotemporal relationship between wind and
![]() $ {H}_s $
, we propose the following two-stage model:
$ {H}_s $
, we propose the following two-stage model:
 $$ {\displaystyle \begin{array}{ll}\mathrm{First}\ \mathrm{stage}:\hskip0.3em & \left[{H}_s\left(t|{X}^{(g)}(t)\right),\dots, {H}_s\left(t+{t}_{\mathrm{max}}|{X}^{(g)}(t)\right)\right]=f\left({X}^{(g)}(t)\right)+\varepsilon (t),\hskip0.3em f:{\mathrm{\mathbb{R}}}^p\to {\mathrm{\mathbb{R}}}^{t_{\mathrm{max}}}\\ {}\mathrm{Second}\ \mathrm{stage}:\hskip0.3em & {H}_s(t)=g\left({X}^{(g)}(t),f\left({X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right),\dots, \hskip0.2em f\left({X}^{(g)}(t)\right)\right)+\varepsilon^{\prime }(t),\hskip0.3em g:{\mathrm{\mathbb{R}}}^{t_{\mathrm{max}}\times {t}_{\mathrm{max}}+8}\to \mathrm{\mathbb{R}}\end{array}}, $$
$$ {\displaystyle \begin{array}{ll}\mathrm{First}\ \mathrm{stage}:\hskip0.3em & \left[{H}_s\left(t|{X}^{(g)}(t)\right),\dots, {H}_s\left(t+{t}_{\mathrm{max}}|{X}^{(g)}(t)\right)\right]=f\left({X}^{(g)}(t)\right)+\varepsilon (t),\hskip0.3em f:{\mathrm{\mathbb{R}}}^p\to {\mathrm{\mathbb{R}}}^{t_{\mathrm{max}}}\\ {}\mathrm{Second}\ \mathrm{stage}:\hskip0.3em & {H}_s(t)=g\left({X}^{(g)}(t),f\left({X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right),\dots, \hskip0.2em f\left({X}^{(g)}(t)\right)\right)+\varepsilon^{\prime }(t),\hskip0.3em g:{\mathrm{\mathbb{R}}}^{t_{\mathrm{max}}\times {t}_{\mathrm{max}}+8}\to \mathrm{\mathbb{R}}\end{array}}, $$
where the notation
![]() $ {H}_s\left({t}_1|{X}^{(g)}\left({t}_2\right)\right) $
represents the contribution of wind conditions at time
$ {H}_s\left({t}_1|{X}^{(g)}\left({t}_2\right)\right) $
represents the contribution of wind conditions at time
![]() $ {t}_2 $
in
$ {t}_2 $
in
![]() $ {H}_s $
at time
$ {H}_s $
at time
![]() $ {t}_1 $
.
$ {t}_1 $
.
![]() $ \varepsilon $
and
$ \varepsilon $
and
![]() $ \varepsilon^{\prime } $
are the errors of the first stage and second stage, respectively. The first stage estimates the current and future
$ \varepsilon^{\prime } $
are the errors of the first stage and second stage, respectively. The first stage estimates the current and future
![]() $ {H}_s $
using current wind conditions. The second stage estimates
$ {H}_s $
using current wind conditions. The second stage estimates
![]() $ {H}_s $
using the past predictions obtained from the first stage. Along with the local predictor
$ {H}_s $
using the past predictions obtained from the first stage. Along with the local predictor
![]() $ {X}^{(g)} $
, the input for the second stage is a
$ {X}^{(g)} $
, the input for the second stage is a
![]() $ {t}_{\mathrm{max}}\times {t}_{\mathrm{max}} $
matrix of the form
$ {t}_{\mathrm{max}}\times {t}_{\mathrm{max}} $
matrix of the form
 $$ \left(\begin{array}{ccc}{\hat{H}}_s\left(t-{t}_{\mathrm{max}}|{X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right)& \dots & {\hat{H}}_s\left(t|{X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right)\\ {}\vdots & \ddots & \vdots \\ {}{\hat{H}}_s\left(t|{X}^{(g)}(t)\right)& \dots & {\hat{H}}_s\left(t+{t}_{\mathrm{max}}|{X}^{(g)}(t)\right)\end{array}\right), $$
$$ \left(\begin{array}{ccc}{\hat{H}}_s\left(t-{t}_{\mathrm{max}}|{X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right)& \dots & {\hat{H}}_s\left(t|{X}^{(g)}\left(t-{t}_{\mathrm{max}}\right)\right)\\ {}\vdots & \ddots & \vdots \\ {}{\hat{H}}_s\left(t|{X}^{(g)}(t)\right)& \dots & {\hat{H}}_s\left(t+{t}_{\mathrm{max}}|{X}^{(g)}(t)\right)\end{array}\right), $$
where
![]() $ {\hat{H}}_s\left({t}_1|{X}^{(g)}\left({t}_2\right)\right) $
represents the prediction, obtained from the first stage, of the contribution of wind conditions at time
$ {\hat{H}}_s\left({t}_1|{X}^{(g)}\left({t}_2\right)\right) $
represents the prediction, obtained from the first stage, of the contribution of wind conditions at time
![]() $ {t}_2 $
in the
$ {t}_2 $
in the
![]() $ {H}_s $
at time
$ {H}_s $
at time
![]() $ {t}_1 $
. When
$ {t}_1 $
. When
![]() $ {t}_1={t}_2 $
, this prediction represents the wind sea (first column of the matrix in equation (6)); for
$ {t}_1={t}_2 $
, this prediction represents the wind sea (first column of the matrix in equation (6)); for
![]() $ {t}_1>{t}_2 $
, on the other hand, the prediction represents the
$ {t}_1>{t}_2 $
, on the other hand, the prediction represents the
![]() $ {H}_s $
caused by swells.
$ {H}_s $
caused by swells.
The general structure of the model is shown in Figure 2. The first stage consists of a series of 3 × 3 convolutions followed by the ReLU activation function, 2 × 2 max pooling layer, Batch Normalization, then a flatten followed by a dense layer. The second stage starts with an LSTM layer that learns the long-term dependencies of the
![]() $ \left(t-{t}_{\mathrm{max}},\dots, t\right) $
outputs of the first stage. The output of the LSTM layer is then concatenated with the local predictor
$ \left(t-{t}_{\mathrm{max}},\dots, t\right) $
outputs of the first stage. The output of the LSTM layer is then concatenated with the local predictor
![]() $ {X}^l $
and fed into two fully connected layers. The dropout layer is used in both stages to prevent the network from overfitting. The loss function choosed in this study is the mean squared error (MSE) which is expressed as
$ {X}^l $
and fed into two fully connected layers. The dropout layer is used in both stages to prevent the network from overfitting. The loss function choosed in this study is the mean squared error (MSE) which is expressed as
 $$ {\displaystyle \begin{array}{l}\mathrm{MSE}\left(\mathrm{First}\ \mathrm{stage}\right)=\frac{1}{t_{\mathrm{max}}}\sum \limits_{i=0}^{t_{\mathrm{max}}}\frac{1}{n-{t}_{\mathrm{max}}-1}\sum \limits_{t=1}^{n-{t}_{\mathrm{max}}}{\left({H}_s\left(t+i\right)-{\hat{H}}_s\left(t+i|{X}^{(g)}(t)\right)\right)}^2,\\ {}\mathrm{MSE}\left(\mathrm{Second}\ \mathrm{stage}\right)=\frac{1}{n}\sum \limits_{t=1}^n{\left({H}_s(t)-{\hat{H}}_s(t)\right)}^2,\end{array}} $$
$$ {\displaystyle \begin{array}{l}\mathrm{MSE}\left(\mathrm{First}\ \mathrm{stage}\right)=\frac{1}{t_{\mathrm{max}}}\sum \limits_{i=0}^{t_{\mathrm{max}}}\frac{1}{n-{t}_{\mathrm{max}}-1}\sum \limits_{t=1}^{n-{t}_{\mathrm{max}}}{\left({H}_s\left(t+i\right)-{\hat{H}}_s\left(t+i|{X}^{(g)}(t)\right)\right)}^2,\\ {}\mathrm{MSE}\left(\mathrm{Second}\ \mathrm{stage}\right)=\frac{1}{n}\sum \limits_{t=1}^n{\left({H}_s(t)-{\hat{H}}_s(t)\right)}^2,\end{array}} $$
where
![]() $ n $
is the total number of observations and
$ n $
is the total number of observations and
![]() $ {\hat{H}}_s $
is the prediction of
$ {\hat{H}}_s $
is the prediction of
![]() $ {H}_s $
. The Keras framework with Tensorflow backend (Chollet et al., Reference Chollet2015) is used in this work to train the model, on a Nvidia K80s GPU using the Adam optimizer (Kingma and Ba, Reference Kingma and Ba2017) and mini batches of 64.
$ {H}_s $
. The Keras framework with Tensorflow backend (Chollet et al., Reference Chollet2015) is used in this work to train the model, on a Nvidia K80s GPU using the Adam optimizer (Kingma and Ba, Reference Kingma and Ba2017) and mini batches of 64.

Figure 2. Architecture of the two-stage model in equation (5).
5. Results
The period from 1994 to 2011 is used to train the two-stage model and the period from 2012 to 2014 serves as the validation period. The measures chosen in this paper to validate the analysis are the correlation coefficient (r), the root mean square error (RMSE), and the bias. Different values for the maximum travel time of waves
![]() $ {t}_{\mathrm{max}} $
are tested, and the results of k-fold cross-validation (with
$ {t}_{\mathrm{max}} $
are tested, and the results of k-fold cross-validation (with
![]() $ k=5 $
) are shown in Figure 3. The RMSE stabilizes approximately at
$ k=5 $
) are shown in Figure 3. The RMSE stabilizes approximately at
![]() $ {t}_{\mathrm{max}}=30\times 3\;\mathrm{hr} $
, which corresponds to about 3.3 days, and the gain is substantial compared to using
$ {t}_{\mathrm{max}}=30\times 3\;\mathrm{hr} $
, which corresponds to about 3.3 days, and the gain is substantial compared to using
![]() $ {t}_{\mathrm{max}}=5 $
. This means that wind conditions over a time window of at least 3.3 days must be considered to characterize the wave climate at the target location. In the following, the value of
$ {t}_{\mathrm{max}}=5 $
. This means that wind conditions over a time window of at least 3.3 days must be considered to characterize the wave climate at the target location. In the following, the value of
![]() $ {t}_{\mathrm{max}} $
is chosen equal to 30.
$ {t}_{\mathrm{max}} $
is chosen equal to 30.

Figure 3. Results of cross-validation using different values of
![]() $ {t}_{\mathrm{max}} $
. The blue line represents the mean of root mean square error (RMSE) and the red interval represents the minimum and maximum RMSE.
$ {t}_{\mathrm{max}} $
. The blue line represents the mean of root mean square error (RMSE) and the red interval represents the minimum and maximum RMSE.
Figure 4 shows the scatter plot of observed versus predicted values of
![]() $ {H}_s $
using the two-stage model (5). The RMSE in the validation period is equal to
$ {H}_s $
using the two-stage model (5). The RMSE in the validation period is equal to
![]() $ 0.21\;\mathrm{m} $
for an
$ 0.21\;\mathrm{m} $
for an
![]() $ {H}_s $
of mean
$ {H}_s $
of mean
![]() $ 1.9\;\mathrm{m} $
and standard deviation
$ 1.9\;\mathrm{m} $
and standard deviation
![]() $ 1.1\;\mathrm{m} $
. The model performs well in predicting
$ 1.1\;\mathrm{m} $
. The model performs well in predicting
![]() $ {H}_s $
and accounts for both wind and swell. The validation measures in the calibration and validation periods are almost the same. This means that the model does not overfit the training data and generalizes well the relationship between wind and waves. Furthermore, the seasonality of
$ {H}_s $
and accounts for both wind and swell. The validation measures in the calibration and validation periods are almost the same. This means that the model does not overfit the training data and generalizes well the relationship between wind and waves. Furthermore, the seasonality of
![]() $ {H}_s $
is well captured by the two-stage model, as can be seen in Figure 5.
$ {H}_s $
is well captured by the two-stage model, as can be seen in Figure 5.

Figure 4. Observed versus predicted
![]() $ {H}_s $
in the validation period (left panel) and calibration period (right panel).
$ {H}_s $
in the validation period (left panel) and calibration period (right panel).

Figure 5. Time series of observed (blue line) and predicted (red line)
![]() $ {H}_s $
in 2016.
$ {H}_s $
in 2016.
A comparison of the two-stage model with two other statistical approaches is done in Table 1. The first approach, described in Obakrim et al. (Reference Obakrim, Ailliot, Monbet and Raillard2022), is based on weather types (Maraun et al., Reference Maraun, Wetterhall, Ireson, Chandler, Kendon, Widmann, Brienen, Rust, Sauter, Themeßl and Venema2010). As for the present work, the local and global predictors were considered. However, in order to reduce the dimension of the predictor a single predictor is extracted at each spatial location
![]() $ j $
to predict
$ j $
to predict
![]() $ {H}_s $
at time
$ {H}_s $
at time
![]() $ t $
. It is defined a priori as
$ t $
. It is defined a priori as
 $$ {\displaystyle \begin{array}{c}{X}_j^{(g)}\left(t;{t}_j,{\alpha}_j\right)=\frac{1}{2{\alpha}_j+1}{\sum}_{i=t-{t}_j-{\alpha}_j}^{t-{t}_j+{\alpha}_j}{W}_j^2(i),\\ {}\hskip10.6em {t}_j+{\alpha}_j+1\le t\le {t}_j-{\alpha}_j+n,\end{array}} $$
$$ {\displaystyle \begin{array}{c}{X}_j^{(g)}\left(t;{t}_j,{\alpha}_j\right)=\frac{1}{2{\alpha}_j+1}{\sum}_{i=t-{t}_j-{\alpha}_j}^{t-{t}_j+{\alpha}_j}{W}_j^2(i),\\ {}\hskip10.6em {t}_j+{\alpha}_j+1\le t\le {t}_j-{\alpha}_j+n,\end{array}} $$
where
![]() $ {t}_j $
is the travel time of waves,
$ {t}_j $
is the travel time of waves,
![]() $ {\alpha}_j $
controls the length of the time window, and
$ {\alpha}_j $
controls the length of the time window, and
![]() $ {W}_j $
is the projected wind at location
$ {W}_j $
is the projected wind at location
![]() $ j $
. The parameters
$ j $
. The parameters
![]() $ {t}_j $
and
$ {t}_j $
and
![]() $ {\alpha}_j $
were estimated using the maximum correlation between
$ {\alpha}_j $
were estimated using the maximum correlation between
![]() $ {h}_s $
and the global predictor. The second method proposed by Michel et al., Reference Michel, Obakrim, Raillard, Ailliot and Monbet2022, called H-CNN, uses CNNs to predict
$ {h}_s $
and the global predictor. The second method proposed by Michel et al., Reference Michel, Obakrim, Raillard, Ailliot and Monbet2022, called H-CNN, uses CNNs to predict
![]() $ {H}_s $
using the same predictors as in Obakrim et al. (Reference Obakrim, Ailliot, Monbet and Raillard2022). Thus, the main difference with the approach proposed in this work is that the temporal dimension of the global predictor is reduced a priori using the preprocessing step based on the maximum correlation described above. The numerical results in Table 1 indicate that the two-stage model significantly outperforms the other two methods in term of the validation measures.
$ {H}_s $
using the same predictors as in Obakrim et al. (Reference Obakrim, Ailliot, Monbet and Raillard2022). Thus, the main difference with the approach proposed in this work is that the temporal dimension of the global predictor is reduced a priori using the preprocessing step based on the maximum correlation described above. The numerical results in Table 1 indicate that the two-stage model significantly outperforms the other two methods in term of the validation measures.
Table 1. Comparison of the two-stage model, weather types, and H-CNN methods.

Abbreviation: RMSE, root mean square error.
6. Conclusion
In this study, a two-stage model based on deep learning is proposed to predict
![]() $ {H}_s $
using wind conditions. The model is capable of learning automatically the underlying spatiotemporal structure of the relationship between wind and waves. The model does well in predicting
$ {H}_s $
using wind conditions. The model is capable of learning automatically the underlying spatiotemporal structure of the relationship between wind and waves. The model does well in predicting
![]() $ {H}_s $
and is computationally inexpensive (about 5 min using a computer of 30GB RAM, 2 cores CPU, and a 16GB GPU). The proposed methodology is based on two stages which are trained separately. A natural question that arises for future work, is whether we can estimate the parameters jointly using back-propagation and eventually speed up the training process and improving the results. Future work also includes using the method to predict other sea state parameters, such as wave direction and period.
$ {H}_s $
and is computationally inexpensive (about 5 min using a computer of 30GB RAM, 2 cores CPU, and a 16GB GPU). The proposed methodology is based on two stages which are trained separately. A natural question that arises for future work, is whether we can estimate the parameters jointly using back-propagation and eventually speed up the training process and improving the results. Future work also includes using the method to predict other sea state parameters, such as wave direction and period.
The proposed method can be used for climate and weather studies at any ocean location worldwide. For nearby locations, one can train only the second stage at each location, using the weights of one location as initialization for the others and leaving the first stage the same. The model can also learn from buoy data instead of hindcast data and eventually fill in the gaps and complete historical data.
Author Contributions
Conceptualization: S.O., V.M., N.R., P.A.; Data curation: S.O., N.R.; Data visualization: S.O.; Methodology: S.O., V.M., N.R., P.A.; Software: S.O.; Supervision: V.M., N.R., P.A.; Writing—original draft: S.O., V.M., N.R., P.A. All authors approved the final submitted draft.
Competing Interests
The authors declare no competing interests exist.
Data Availability Statement
The hindcast data Homere is available on their website: https://marc.ifremer.fr/produits/rejeu_d_etats_de_mer_homere. The wind data is available from the CFSR website: https://climatedataguide.ucar.edu/climate-data/climate-forecast-system-reanalysis-cfsr. For reasons of reproducibility, Python code and the processed data are available at https://github.com/SaidObakrim/Two-stage-CNN-LSTM-.
Ethics Statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding Statement
This work received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Provenance
This article is part of the Climate Informatics 2022 proceedings and was accepted in Environmental Data Science on the basis of the Climate Informatics peer review process.