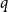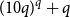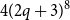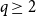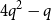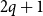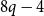1. Introduction
Quasirandom graphs play an important role in structural and extremal graph theory. The notion of quasirandom graphs can be traced to the works of Rödl [Reference Rödl42], Thomason [Reference Thomason46, Reference Thomason47] and Chung, Graham, and Wilson [Reference Chung, Graham and Wilson9] in the 1980s and is also deeply related to Szemerédi’s Regularity Lemma [Reference Simonovits and Sós44]. Indeed, the Regularity Lemma asserts that each graph can be approximated by partitioning it into a bounded number of quasirandom bipartite graphs. There is also a large body of literature concerning quasirandomness of various kinds of combinatorial structures such as groups [Reference Gowers24], hypergraphs [Reference Chung and Graham5, Reference Chung and Graham6, Reference Gowers22, Reference Gowers23, Reference Haviland and Thomason29, Reference Kohayakawa, Rödl and Skokan32, Reference Nagle, Rödl and Schaht41, Reference Rödl and Skokan43], permutations [Reference Chan, Král’, Noel, Pehova, Sharifzadeh and Volec4, Reference Cooper10, Reference Král’ and Pikhurko34, Reference Kureĉka35], Latin squares [Reference Cooper, Král’, Lamaison and Mohr11, Reference Eberhard, Manners and Mrazović17, Reference Garbe, Hancock, Hladký and Sharifzadeh20, Reference Gowers and Long25], subsets of integers [Reference Chung and Graham8], tournaments [Reference Bucić, Long, Shapira and Sudakov3, Reference Chung and Graham7, Reference Coregliano, Parente and Sato13, Reference Coregliano and Razborov14, Reference Grzesik, Il’kovič, Kielak and Král’26, Reference Hancock, Kabela, Král’, Martins, Parente, Skerman and Volec28], etc. Many of these notions have been treated in a unified way in the recent paper by Coregliano and Razborov [Reference Coregliano and Razborov15].
The starting point of our work is the following classical result on quasirandom graphs [Reference Chung, Graham and Wilson9]: a sequence of graphs
![]() $(G_n)_{n\in{\mathbb N}}$
is quasirandom with density
$(G_n)_{n\in{\mathbb N}}$
is quasirandom with density
![]() $p$
if and only if the homomorphism densities of the single edge
$p$
if and only if the homomorphism densities of the single edge
![]() $K_2$
and the 4-cycle
$K_2$
and the 4-cycle
![]() $C_4$
in
$C_4$
in
![]() $(G_n)_{n\in{\mathbb N}}$
converge to
$(G_n)_{n\in{\mathbb N}}$
converge to
![]() $p$
and
$p$
and
![]() $p^4$
, that is, to their expected densities in the Erdős-Rényi random graph with density
$p^4$
, that is, to their expected densities in the Erdős-Rényi random graph with density
![]() $p$
. In particular, quasirandomness is forced by homomorphism densities of graphs with at most
$p$
. In particular, quasirandomness is forced by homomorphism densities of graphs with at most
![]() $4$
vertices. In this paper, we consider a generalisation of quasirandom graphs, which corresponds to the stochastic block model in statistics. In this model, the edge density of a (large) graph is not homogeneous as in the Erdős-Rényi random graph model, however, the graph can be partitioned into
$4$
vertices. In this paper, we consider a generalisation of quasirandom graphs, which corresponds to the stochastic block model in statistics. In this model, the edge density of a (large) graph is not homogeneous as in the Erdős-Rényi random graph model, however, the graph can be partitioned into
![]() $q$
parts such that the edge density is homogeneous inside each part and between each pair of the parts. Lovász and Sós [Reference Lovász and Sós37] established that the structure of such graphs is forced by homomorphism densities of graphs with at most
$q$
parts such that the edge density is homogeneous inside each part and between each pair of the parts. Lovász and Sós [Reference Lovász and Sós37] established that the structure of such graphs is forced by homomorphism densities of graphs with at most
![]() $(10q)^q+q$
vertices. Lovász [Reference Lovász36, Theorem 5.33] refined this result by showing that homomorphism densities of graphs with at most
$(10q)^q+q$
vertices. Lovász [Reference Lovász36, Theorem 5.33] refined this result by showing that homomorphism densities of graphs with at most
![]() $4(2q+3)^8$
vertices suffice. Our main result, which we state below (we refer to Section 2 for not yet defined notation), improves this bound: the structure of generalised quasirandom graphs with
$4(2q+3)^8$
vertices suffice. Our main result, which we state below (we refer to Section 2 for not yet defined notation), improves this bound: the structure of generalised quasirandom graphs with
![]() $q\ge 2$
parts is forced by homomorphism densities of graphs with at most
$q\ge 2$
parts is forced by homomorphism densities of graphs with at most
![]() $4q^2-q$
vertices.
$4q^2-q$
vertices.
Theorem 1.
The following holds for every
![]() $q\ge 2$
and every
$q\ge 2$
and every
![]() $q$
-step graphon
$q$
-step graphon
![]() $W$
: if the density of each graph with at most
$W$
: if the density of each graph with at most
![]() $4q^2-q$
vertices in a graphon
$4q^2-q$
vertices in a graphon
![]() $W^{\prime}$
is the same as in
$W^{\prime}$
is the same as in
![]() $W$
, then the graphons
$W$
, then the graphons
![]() $W$
and
$W$
and
![]() $W^{\prime}$
are weakly isomorphic.
$W^{\prime}$
are weakly isomorphic.
We remark that our line of arguments to prove Theorem 1 substantially differs from that in [Reference Lovász36, Reference Lovász and Sós37], with the exception of initial application of Lemma 2. In particular, the key steps in our proof are more explicit and so of a more constructive nature, which is of importance in relation to applications [Reference Borgs, Chayes, Cohn and Ganguly2, Reference Gao, Lu and Zhou19, Reference Klopp, Tsybakov and Verzelen30, Reference Klopp and Verzelen31].
Spencer [Reference Spencer45] considered generalised quasirandom graphs with
![]() $q$
parts with an additional assumption that vertices in distinct parts have distinct degrees and established that the structure of such graphs is forced by homomorphism densities of graphs with at most
$q$
parts with an additional assumption that vertices in distinct parts have distinct degrees and established that the structure of such graphs is forced by homomorphism densities of graphs with at most
![]() $8q-4$
vertices. Addressing a question posed in [Reference Spencer45], we show (Theorem 11) that graphs with at most
$8q-4$
vertices. Addressing a question posed in [Reference Spencer45], we show (Theorem 11) that graphs with at most
![]() $2q+1$
vertices suffice in this restricted setting for any
$2q+1$
vertices suffice in this restricted setting for any
![]() $q\ge 2$
.
$q\ge 2$
.
We present our results and arguments using the language of the theory of graph limits, which is introduced in Section 2. We remark that similarly to arguments presented in [Reference Lovász36, Reference Lovász and Sós37], although not explicitly stated there, our arguments also apply in a more general setting of kernels in addition to graphons (see Section 2 for the definitions of the two notions). We present various auxiliary results in Section 3 and use them to prove our main result in Section 4. The case with the additional assumption that vertices in distinct parts have distinct degrees is analysed in Section 5.
2. Notation
We now introduce the notions and tools from the theory of graph limits that we need in our arguments; we refer the reader to the monograph by Lovász [Reference Lovász36] for a more comprehensive introduction and further details. We also rephrase results concerning quasirandom graphs and generalised quasirandom graphs with
![]() $q$
parts presented in Section 1 in the language of the theory of graph limits.
$q$
parts presented in Section 1 in the language of the theory of graph limits.
We start with fixing some general shorthand notation used throughout the paper. The set of the first
![]() $q$
positive integers is denoted by
$q$
positive integers is denoted by
![]() $[q]$
and more generally the set of integers between
$[q]$
and more generally the set of integers between
![]() $a$
and
$a$
and
![]() $b$
(inclusive) is denoted by
$b$
(inclusive) is denoted by
![]() $[a,b]$
. If
$[a,b]$
. If
![]() $H$
and
$H$
and
![]() $G$
are two graphs, the homomorphism density of
$G$
are two graphs, the homomorphism density of
![]() $H$
in
$H$
in
![]() $G$
, denoted by
$G$
, denoted by
![]() $t(H,G)$
, is the probability that a random function
$t(H,G)$
, is the probability that a random function
![]() $f\,:\,V(H)\to V(G)$
, with all
$f\,:\,V(H)\to V(G)$
, with all
![]() $|V(G)|^{|V(H)|}$
choices being equally likely, is a homomorphism of
$|V(G)|^{|V(H)|}$
choices being equally likely, is a homomorphism of
![]() $H$
to
$H$
to
![]() $G$
, that is,
$G$
, that is,
![]() $f(u)f(v)$
is an edge of
$f(u)f(v)$
is an edge of
![]() $H$
for every edge
$H$
for every edge
![]() $uv$
of
$uv$
of
![]() $G$
. A sequence
$G$
. A sequence
![]() $(G_n)_{n\in{\mathbb N}}$
of graphs is convergent if the number of vertices of
$(G_n)_{n\in{\mathbb N}}$
of graphs is convergent if the number of vertices of
![]() $G_n$
tends to infinity and the values of
$G_n$
tends to infinity and the values of
![]() $t(H,G_n)$
converge for every graph
$t(H,G_n)$
converge for every graph
![]() $H$
as
$H$
as
![]() $n\to \infty$
. A sequence
$n\to \infty$
. A sequence
![]() $(G_n)_{n\in{\mathbb N}}$
of graphs is quasirandom with density
$(G_n)_{n\in{\mathbb N}}$
of graphs is quasirandom with density
![]() $p$
if it is convergent and the limit of
$p$
if it is convergent and the limit of
![]() $t(H,G_n)$
is equal to
$t(H,G_n)$
is equal to
![]() $p^{|E(H)|}$
for every graph
$p^{|E(H)|}$
for every graph
![]() $H$
, where
$H$
, where
![]() $E(H)$
denotes the edge set of
$E(H)$
denotes the edge set of
![]() $H$
. If the particular value of
$H$
. If the particular value of
![]() $p$
is irrelevant or understood, we just say that a sequence of graphs is quasirandom instead of quasirandom with density
$p$
is irrelevant or understood, we just say that a sequence of graphs is quasirandom instead of quasirandom with density
![]() $p$
.
$p$
.
The theory of graph limits provides analytic ways of representing sequences of convergent graphs. A kernel is a bounded measurable function
![]() $U\,:\,[0,1]^2\to{\mathbb R}$
that is symmetric, that is,
$U\,:\,[0,1]^2\to{\mathbb R}$
that is symmetric, that is,
![]() $U(x,y)=U(y,x)$
for all
$U(x,y)=U(y,x)$
for all
![]() $(x,y)\in [0,1]^2$
. A graphon is a kernel whose values are restricted to
$(x,y)\in [0,1]^2$
. A graphon is a kernel whose values are restricted to
![]() $[0,1]$
. The homomorphism density of a graph
$[0,1]$
. The homomorphism density of a graph
![]() $H$
in a kernel
$H$
in a kernel
![]() $U$
is defined as follows:
$U$
is defined as follows:
where
![]() $\mbox{d} x_A$
for a set
$\mbox{d} x_A$
for a set
![]() $A=\{a_1,\dots,a_k\}$
is a shorthand for
$A=\{a_1,\dots,a_k\}$
is a shorthand for
![]() $\mbox{d} x_{a_1}\dots \mbox{d} x_{a_k}$
; we often just briefly say the density of a graph
$\mbox{d} x_{a_1}\dots \mbox{d} x_{a_k}$
; we often just briefly say the density of a graph
![]() $H$
in a kernel
$H$
in a kernel
![]() $U$
rather than the homomorphism density of
$U$
rather than the homomorphism density of
![]() $H$
in
$H$
in
![]() $U$
. A graphon
$U$
. A graphon
![]() $W$
is a limit of a convergent sequence
$W$
is a limit of a convergent sequence
![]() $(G_n)_{n\in{\mathbb N}}$
of graphs if
$(G_n)_{n\in{\mathbb N}}$
of graphs if
![]() $t(H,W)$
is the limit of
$t(H,W)$
is the limit of
![]() $t(H,G_n)$
for every graph
$t(H,G_n)$
for every graph
![]() $H$
. Every convergent sequence of graphs has a limit graphon and every graphon is a limit of a convergent sequence of graphs as shown by Lovász and Szegedy [Reference Lovász and Szegedy38]; also see [Reference Diaconis and Janson16] for relation to exchangeable arrays. Two kernels (or graphons)
$H$
. Every convergent sequence of graphs has a limit graphon and every graphon is a limit of a convergent sequence of graphs as shown by Lovász and Szegedy [Reference Lovász and Szegedy38]; also see [Reference Diaconis and Janson16] for relation to exchangeable arrays. Two kernels (or graphons)
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are weakly isomorphic if
$U_2$
are weakly isomorphic if
![]() $t(H,U_1)=t(H,U_2)$
for every graph
$t(H,U_1)=t(H,U_2)$
for every graph
![]() $H$
. Note that any two limits of the same convergent sequence of graphs are weakly isomorphic, and we refer particularly to [Reference Borgs, Chayes and Lovász1] for results on the structure of weakly isomorphic graphons and more generally kernels.
$H$
. Note that any two limits of the same convergent sequence of graphs are weakly isomorphic, and we refer particularly to [Reference Borgs, Chayes and Lovász1] for results on the structure of weakly isomorphic graphons and more generally kernels.
We phrase the results concerning quasirandom graphs using the language of the theory of graph limits. Observe that a sequence of graphs is quasirandom if and only if it converges to the graphon equal to
![]() $p$
everywhere. The following holds for every graphon
$p$
everywhere. The following holds for every graphon
![]() $W$
and every real
$W$
and every real
![]() $p\in [0,1]$
: a graphon
$p\in [0,1]$
: a graphon
![]() $W$
is weakly isomorphic to the constant graphon equal to
$W$
is weakly isomorphic to the constant graphon equal to
![]() $p$
if and only if
$p$
if and only if
![]() $t(K_2,W)=p$
and
$t(K_2,W)=p$
and
![]() $t(C_4,W)=p^4$
. This leads us to the following definition: a graphon
$t(C_4,W)=p^4$
. This leads us to the following definition: a graphon
![]() $U$
is forced by graphs contained in a set
$U$
is forced by graphs contained in a set
![]() $\mathcal{H}$
if every graphon
$\mathcal{H}$
if every graphon
![]() $U^{\prime}$
such that
$U^{\prime}$
such that
![]() $t(H,U^{\prime})=t(H,U)$
for every graph
$t(H,U^{\prime})=t(H,U)$
for every graph
![]() $H\in{\mathcal{H}}$
is weakly isomorphic to
$H\in{\mathcal{H}}$
is weakly isomorphic to
![]() $U$
. In particular, any constant graphon is forced by the graphs
$U$
. In particular, any constant graphon is forced by the graphs
![]() $K_2$
and
$K_2$
and
![]() $C_4$
. We refer particularly to [Reference Cooper, Král’ and Martins12, Reference Grzesik, Král’ and Lovász27, Reference Král’, Lovász, Noel and Sosnovec33, Reference Lovász and Szegedy39] for results on the structure of graphons forced by finite sets of graphs. Similarly, we say that a kernel
$C_4$
. We refer particularly to [Reference Cooper, Král’ and Martins12, Reference Grzesik, Král’ and Lovász27, Reference Král’, Lovász, Noel and Sosnovec33, Reference Lovász and Szegedy39] for results on the structure of graphons forced by finite sets of graphs. Similarly, we say that a kernel
![]() $U$
is forced by graphs from a set
$U$
is forced by graphs from a set
![]() $\mathcal{H}$
if every kernel
$\mathcal{H}$
if every kernel
![]() $U^{\prime}$
such that
$U^{\prime}$
such that
![]() $t(H,U^{\prime})=t(H,U)$
for every graph
$t(H,U^{\prime})=t(H,U)$
for every graph
![]() $H\in{\mathcal{H}}$
is weakly isomorphic to
$H\in{\mathcal{H}}$
is weakly isomorphic to
![]() $U$
. We emphasise that our results actually concern forcing kernels (rather than graphons), which makes them formally stronger.
$U$
. We emphasise that our results actually concern forcing kernels (rather than graphons), which makes them formally stronger.
A
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
is a kernel such that
$U$
is a kernel such that
![]() $[0,1]$
can be partitioned into
$[0,1]$
can be partitioned into
![]() $q$
non-null measurable sets
$q$
non-null measurable sets
![]() $A_1,\ldots,A_q$
such that
$A_1,\ldots,A_q$
such that
![]() $U$
is constant on
$U$
is constant on
![]() $A_i\times A_j$
for all
$A_i\times A_j$
for all
![]() $i,j\in [q]$
but there is no such partition with
$i,j\in [q]$
but there is no such partition with
![]() $q-1$
parts. A
$q-1$
parts. A
![]() $q$
-step graphon is a
$q$
-step graphon is a
![]() $q$
-step kernel that is also a graphon. If the number of parts is not important, we use a step kernel or a step graphon for brevity. Observe that step graphons correspond to stochastic block models and so to generalised quasirandom graphs discussed in Section 1. As mentioned in Section 1, Lovász and Sós [Reference Lovász and Sós37, Theorem 2.3] showed that every
$q$
-step kernel that is also a graphon. If the number of parts is not important, we use a step kernel or a step graphon for brevity. Observe that step graphons correspond to stochastic block models and so to generalised quasirandom graphs discussed in Section 1. As mentioned in Section 1, Lovász and Sós [Reference Lovász and Sós37, Theorem 2.3] showed that every
![]() $q$
-step graphon
$q$
-step graphon
![]() $W$
is forced by graphs with at most
$W$
is forced by graphs with at most
![]() $(10q)^q+q$
vertices, and Lovász [Reference Lovász36, Theorem 5.33] further improved the bound on the number of vertices to
$(10q)^q+q$
vertices, and Lovász [Reference Lovász36, Theorem 5.33] further improved the bound on the number of vertices to
![]() $4(2q+3)^8$
; we remark that the proof of either of the results can be adapted to the setting of step kernels. Our main result (Theorem 1) states that every
$4(2q+3)^8$
; we remark that the proof of either of the results can be adapted to the setting of step kernels. Our main result (Theorem 1) states that every
![]() $q$
-step graphon is forced by graphs with at most
$q$
-step graphon is forced by graphs with at most
![]() $\max \{4q^2-q,4\}$
vertices; our arguments also apply in the setting of step kernels as stated in Theorem 10.
$\max \{4q^2-q,4\}$
vertices; our arguments also apply in the setting of step kernels as stated in Theorem 10.
In the rest of this section, we introduce some technical notation needed to present our arguments. A
![]() $k$
-rooted graph is a graph with
$k$
-rooted graph is a graph with
![]() $k$
distinguished pairwise distinct vertices, and more generally an
$k$
distinguished pairwise distinct vertices, and more generally an
![]() $(s_1,\ldots,s_q)$
-rooted graph is an
$(s_1,\ldots,s_q)$
-rooted graph is an
![]() $(s_1+\cdots +s_q)$
-rooted graph whose roots are split into
$(s_1+\cdots +s_q)$
-rooted graph whose roots are split into
![]() $q$
groups, each of size
$q$
groups, each of size
![]() $s_i$
,
$s_i$
,
![]() $i\in [q]$
. If
$i\in [q]$
. If
![]() $H$
is a
$H$
is a
![]() $k$
-rooted graph with vertices
$k$
-rooted graph with vertices
![]() $v_1,\ldots,v_n$
such that its roots are
$v_1,\ldots,v_n$
such that its roots are
![]() $v_1,\ldots,v_k$
then the density of
$v_1,\ldots,v_k$
then the density of
![]() $H$
in a kernel
$H$
in a kernel
![]() $U$
when
$U$
when
![]() $x_1,\ldots,x_k\in [0,1]$
are chosen as the roots is defined as:
$x_1,\ldots,x_k\in [0,1]$
are chosen as the roots is defined as:
 \begin{equation*}t_{x_1,\ldots,x_k}(H,U)=\int _{[0,1]^{n-k}}\prod _{v_iv_j\in E(H)}U(v_i,v_j)\mbox {d} x_{[k+1,n]}.\end{equation*}
\begin{equation*}t_{x_1,\ldots,x_k}(H,U)=\int _{[0,1]^{n-k}}\prod _{v_iv_j\in E(H)}U(v_i,v_j)\mbox {d} x_{[k+1,n]}.\end{equation*}
By the Fubini–Tonelli Theorem, the integral exists for almost all choices of
![]() $x_1,\ldots,x_k$
and we will often ignore exceptional null sets in this paper. Note that for
$x_1,\ldots,x_k$
and we will often ignore exceptional null sets in this paper. Note that for
![]() $k=0$
this definition coincides with the definition of the density of an unrooted graph in a kernel. If the particular choice of the roots is understood, we write
$k=0$
this definition coincides with the definition of the density of an unrooted graph in a kernel. If the particular choice of the roots is understood, we write
![]() $t_{\star }(H,U)$
instead of
$t_{\star }(H,U)$
instead of
![]() $t_{x_1,\ldots,x_k}(H,U)$
. We sometimes think of and refer to the elements of
$t_{x_1,\ldots,x_k}(H,U)$
. We sometimes think of and refer to the elements of
![]() $[0,1]$
as vertices of a kernel, which justifies the definition of the density of a rooted graph in a kernel and leads to the following definition: the degree of a vertex
$[0,1]$
as vertices of a kernel, which justifies the definition of the density of a rooted graph in a kernel and leads to the following definition: the degree of a vertex
![]() $x\in [0,1]$
in a kernel
$x\in [0,1]$
in a kernel
![]() $U$
is the density
$U$
is the density
![]() $t_x(K_2^{\bullet },U)=\int _0^1 U(x,y)\mbox{d} y$
, where
$t_x(K_2^{\bullet },U)=\int _0^1 U(x,y)\mbox{d} y$
, where
![]() $K_2^{\bullet }$
is the
$K_2^{\bullet }$
is the
![]() $1$
-rooted graph obtained from
$1$
-rooted graph obtained from
![]() $K_2$
by choosing one of its vertices as the root.
$K_2$
by choosing one of its vertices as the root.
A quantum graph is a formal finite linear combination
![]() $Q=\sum _{i=1}^m c_i H_i$
of graphs; a graph
$Q=\sum _{i=1}^m c_i H_i$
of graphs; a graph
![]() $H_i$
with
$H_i$
with
![]() $c_i\not =0$
is called a constituent of
$c_i\not =0$
is called a constituent of
![]() $Q$
. More generally a quantum
$Q$
. More generally a quantum
![]() $k$
-rooted graph is a formal finite linear combination of
$k$
-rooted graph is a formal finite linear combination of
![]() $k$
-rooted graphs such that their roots induce the same (
$k$
-rooted graphs such that their roots induce the same (
![]() $k$
-vertex) subgraph in each of the constituents. The density of a (rooted) quantum graph
$k$
-vertex) subgraph in each of the constituents. The density of a (rooted) quantum graph
![]() $Q$
in a kernel
$Q$
in a kernel
![]() $U$
is the corresponding linear combination of the densities of the constituents forming
$U$
is the corresponding linear combination of the densities of the constituents forming
![]() $Q$
.
$Q$
.
For a
![]() $k$
-rooted graph
$k$
-rooted graph
![]() $H$
, let
$H$
, let
![]() $[\![ H]\!]_{}$
be the underlying unrooted graph. Note that it holds for every kernel
$[\![ H]\!]_{}$
be the underlying unrooted graph. Note that it holds for every kernel
![]() $U$
that
$U$
that
If
![]() $H$
and
$H$
and
![]() $H^{\prime}$
are
$H^{\prime}$
are
![]() $k$
-rooted graphs such that every pair of corresponding roots is joined by an edge in at most one of the graphs
$k$
-rooted graphs such that every pair of corresponding roots is joined by an edge in at most one of the graphs
![]() $H$
and
$H$
and
![]() $H^{\prime}$
, we define the product
$H^{\prime}$
, we define the product
![]() $H\times H^{\prime}$
as follows: let
$H\times H^{\prime}$
as follows: let
![]() $H^{\prime\prime}$
be the
$H^{\prime\prime}$
be the
![]() $k$
-rooted graph isomorphic to
$k$
-rooted graph isomorphic to
![]() $H^{\prime}$
that has the same roots as
$H^{\prime}$
that has the same roots as
![]() $H$
and is vertex disjoint otherwise, and let
$H$
and is vertex disjoint otherwise, and let
![]() $H\times H^{\prime}$
be the graph with the vertex set
$H\times H^{\prime}$
be the graph with the vertex set
![]() $V(H)\cup V(H^{\prime\prime})$
, the edge set
$V(H)\cup V(H^{\prime\prime})$
, the edge set
![]() $E(H)\cup E(H^{\prime})$
and the same set of roots. Note that
$E(H)\cup E(H^{\prime})$
and the same set of roots. Note that
![]() $H\times H^{\prime}$
does not have parallel edges as each pair of corresponding roots is joined by an edge in at most one of the graphs
$H\times H^{\prime}$
does not have parallel edges as each pair of corresponding roots is joined by an edge in at most one of the graphs
![]() $H$
and
$H$
and
![]() $H^{\prime}$
. Also observe that
$H^{\prime}$
. Also observe that
![]() $ |V(H\times H^{\prime})|=|V(H)|+|V(H^{\prime})|-k$
and it holds for every choice of roots and every kernel
$ |V(H\times H^{\prime})|=|V(H)|+|V(H^{\prime})|-k$
and it holds for every choice of roots and every kernel
![]() $U$
that
$U$
that
If
![]() $H=H^{\prime}$
, we may write
$H=H^{\prime}$
, we may write
![]() $H^2$
instead of
$H^2$
instead of
![]() $H\times H$
. The definition of the operator
$H\times H$
. The definition of the operator
![]() $[\![{\cdot}]\!]_{}$
and that of the product extend to rooted quantum graphs by linearity. Observe that, for every
$[\![{\cdot}]\!]_{}$
and that of the product extend to rooted quantum graphs by linearity. Observe that, for every
![]() $k$
-rooted quantum graph
$k$
-rooted quantum graph
![]() $Q$
and every kernel
$Q$
and every kernel
![]() $U$
, it holds that
$U$
, it holds that
![]() $t([\![ Q^2]\!]_{},U)\ge 0$
and the equality holds if and only if
$t([\![ Q^2]\!]_{},U)\ge 0$
and the equality holds if and only if
![]() $t_{\star }(Q,U)=0$
for almost every choice of roots.
$t_{\star }(Q,U)=0$
for almost every choice of roots.
3. Forcing step structure
We start with recalling a construction from [Reference Lovász36, Proposition 14.44], which forces the structure of a step kernel with at most
![]() $q$
parts. For
$q$
parts. For
![]() $k\in{\mathbb N}$
and
$k\in{\mathbb N}$
and
![]() $1\le i\lt j\le k$
, let
$1\le i\lt j\le k$
, let
![]() $Q_k^{ij}$
be the following
$Q_k^{ij}$
be the following
![]() $(2k)$
-rooted quantum graph with roots
$(2k)$
-rooted quantum graph with roots
![]() $v_1,\ldots,v_k$
and
$v_1,\ldots,v_k$
and
![]() $v^{\prime}_1,\ldots,v^{\prime}_k$
. The quantum graph
$v^{\prime}_1,\ldots,v^{\prime}_k$
. The quantum graph
![]() $Q_k^{ij}$
has four constituents, each with a single non-root vertex: the graph with the non-root vertex adjacent to
$Q_k^{ij}$
has four constituents, each with a single non-root vertex: the graph with the non-root vertex adjacent to
![]() $v_i$
and
$v_i$
and
![]() $v^{\prime}_i$
and the graph with the non-root vertex adjacent to
$v^{\prime}_i$
and the graph with the non-root vertex adjacent to
![]() $v_j$
and
$v_j$
and
![]() $v^{\prime}_j$
, both with coefficient
$v^{\prime}_j$
, both with coefficient
![]() $+1$
, as well as the graph with the non-root vertex adjacent to
$+1$
, as well as the graph with the non-root vertex adjacent to
![]() $v_i$
and
$v_i$
and
![]() $v^{\prime}_j$
and the graph with the non-root vertex adjacent to
$v^{\prime}_j$
and the graph with the non-root vertex adjacent to
![]() $v_j$
and
$v_j$
and
![]() $v^{\prime}_i$
, both with coefficient
$v^{\prime}_i$
, both with coefficient
![]() $-1$
. See Figure 1 for an example. Let
$-1$
. See Figure 1 for an example. Let
![]() $Q_k$
be the following quantum graph with each constituent having
$Q_k$
be the following quantum graph with each constituent having
![]() $2k+2\binom{k}{2}=k(k+1)$
vertices:
$2k+2\binom{k}{2}=k(k+1)$
vertices:
 \begin{equation*}Q_k=\left[\!\!\left[ \prod _{1\le i\lt j\le k} \left (Q_k^{ij}\right )^2\right]\!\!\right]_{}.\end{equation*}
\begin{equation*}Q_k=\left[\!\!\left[ \prod _{1\le i\lt j\le k} \left (Q_k^{ij}\right )^2\right]\!\!\right]_{}.\end{equation*}
The graph
![]() $Q_k$
is the graph obtained in the proof of [Reference Lovász36, Proposition 14.44] through an application [Reference Lovász36, Lemma 14.37]. This gives the following lemma, whose proof we sketch for completeness.
$Q_k$
is the graph obtained in the proof of [Reference Lovász36, Proposition 14.44] through an application [Reference Lovász36, Lemma 14.37]. This gives the following lemma, whose proof we sketch for completeness.

Figure 1. The
![]() $6$
-rooted quantum graph
$6$
-rooted quantum graph
![]() $Q_3^{12}$
.
$Q_3^{12}$
.
Lemma 2.
For every
![]() $q\in{\mathbb N}$
and every kernel
$q\in{\mathbb N}$
and every kernel
![]() $U$
, the following holds:
$U$
, the following holds:
![]() $t(Q_{q+1},U)=0$
if and only if
$t(Q_{q+1},U)=0$
if and only if
![]() $U$
is weakly isomorphic to a step kernel with at most
$U$
is weakly isomorphic to a step kernel with at most
![]() $q$
parts.
$q$
parts.
Proof. Observe that the value of
![]() $t(Q_{q+1},U)$
for a kernel
$t(Q_{q+1},U)$
for a kernel
![]() $U$
is equal to
$U$
is equal to
 \begin{equation} \int _{[0,1]^{2(q+1)}}\prod _{1\le i\lt j\le q+1}\!\!\left (\int _{[0,1]}\big (U(x_i,y)-U(x_j,y)\big )\big (U(x^{\prime}_i,y)-U(x^{\prime}_j,y)\big )\mbox{d} y\right )^2\!\!\mbox{d} x_{[q+1]} \mbox{d} x^{\prime}_{[q+1]}. \end{equation}
\begin{equation} \int _{[0,1]^{2(q+1)}}\prod _{1\le i\lt j\le q+1}\!\!\left (\int _{[0,1]}\big (U(x_i,y)-U(x_j,y)\big )\big (U(x^{\prime}_i,y)-U(x^{\prime}_j,y)\big )\mbox{d} y\right )^2\!\!\mbox{d} x_{[q+1]} \mbox{d} x^{\prime}_{[q+1]}. \end{equation}
If
![]() $U$
is a step kernel with at most
$U$
is a step kernel with at most
![]() $q$
parts, then for any choice of
$q$
parts, then for any choice of
![]() $x_1,\ldots,x_{q+1}$
, there exist
$x_1,\ldots,x_{q+1}$
, there exist
![]() $1\le i\lt j\le q+1$
such that
$1\le i\lt j\le q+1$
such that
![]() $x_i$
and
$x_i$
and
![]() $x_j$
are from the same part of
$x_j$
are from the same part of
![]() $U$
and so
$U$
and so
![]() $U(x_i,y)=U(x_j,y)$
for all
$U(x_i,y)=U(x_j,y)$
for all
![]() $y\in [0,1]$
. Consequently, the product in (1) is zero for any choice of roots
$y\in [0,1]$
. Consequently, the product in (1) is zero for any choice of roots
![]() $x_1,\ldots,x_{q+1}$
, which implies that
$x_1,\ldots,x_{q+1}$
, which implies that
![]() $t(Q_{q+1},U)=0$
.
$t(Q_{q+1},U)=0$
.
We now prove the other implication, that is, that if
![]() $t(Q_{q+1},U)=0$
, then
$t(Q_{q+1},U)=0$
, then
![]() $U$
is weakly isomorphic to a step kernel with at most
$U$
is weakly isomorphic to a step kernel with at most
![]() $q$
parts. Let
$q$
parts. Let
![]() $U$
be a kernel such that
$U$
be a kernel such that
![]() $t(Q_{q+1},U)=0$
. By (1), the following holds for almost all
$t(Q_{q+1},U)=0$
. By (1), the following holds for almost all
![]() $x_{[q+1]}\in [0,1]^{q+1}$
and
$x_{[q+1]}\in [0,1]^{q+1}$
and
![]() $x^{\prime}_{[q+1]}\in [0,1]^{q+1}$
:
$x^{\prime}_{[q+1]}\in [0,1]^{q+1}$
:
Using [Reference Lovász36, Proposition 13.23], we get that the following holds for almost all
![]() $x_{[q+1]}\in [0,1]^{q+1}$
:
$x_{[q+1]}\in [0,1]^{q+1}$
:
Let us consider an equivalence relation on
![]() $[0,1]$
defined as
$[0,1]$
defined as
![]() $x\equiv x^{\prime}$
if
$x\equiv x^{\prime}$
if
![]() $U(x,y)=U(x^{\prime},y)$
for almost all
$U(x,y)=U(x^{\prime},y)$
for almost all
![]() $y\in [0,1]$
. Observe that (2) holds for
$y\in [0,1]$
. Observe that (2) holds for
![]() $x_{[q+1]}\in [0,1]^{q+1}$
if and only if there exist
$x_{[q+1]}\in [0,1]^{q+1}$
if and only if there exist
![]() $1\le i\lt j\le q+1$
such that
$1\le i\lt j\le q+1$
such that
![]() $x_i\equiv x_j$
. Hence, (2) holds for almost all
$x_i\equiv x_j$
. Hence, (2) holds for almost all
![]() $x_{[q+1]}\in [0,1]^{q+1}$
if and only if the measure of the
$x_{[q+1]}\in [0,1]^{q+1}$
if and only if the measure of the
![]() $q$
largest equivalence classes of
$q$
largest equivalence classes of
![]() $\equiv$
is one, which is equivalent to
$\equiv$
is one, which is equivalent to
![]() $U$
being weakly isomorphic to a step kernel with at most
$U$
being weakly isomorphic to a step kernel with at most
![]() $q$
parts.
$q$
parts.
We next present two rather similar auxiliary lemmas; since their statements and constructions somewhat differ depending on the parity of
![]() $q$
, we state them separately for readability.
$q$
, we state them separately for readability.
Lemma 3.
For every even integer
![]() $q\ge 2$
and all integers
$q\ge 2$
and all integers
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists a graph
$s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists a graph
![]() $G$
with vertex set formed by
$G$
with vertex set formed by
![]() $q$
disjoint sets
$q$
disjoint sets
![]() $V_1,\ldots,V_q$
that satisfies the following:
$V_1,\ldots,V_q$
that satisfies the following:
-
• the size of
 $V_i$
is
$V_i$
is
 $s_i$
for each
$s_i$
for each
 $i\in [q]$
,
$i\in [q]$
, -
• the edge set of
 $G$
can be partitioned into four sets
$G$
can be partitioned into four sets
 $M_1,\ldots,M_4$
such that, for every
$M_1,\ldots,M_4$
such that, for every
 $1\le i\lt j\le q$
, each of the sets
$1\le i\lt j\le q$
, each of the sets
 $M_1$
and
$M_1$
and
 $M_2$
restricted to vertices of
$M_2$
restricted to vertices of
 $V_i\cup V_j$
, is a matching of size
$V_i\cup V_j$
, is a matching of size
 $q+2$
, and each of the sets
$q+2$
, and each of the sets
 $M_3$
and
$M_3$
and
 $M_4$
is a matching of size
$M_4$
is a matching of size
 $q$
, and
$q$
, and
-
• the chromatic number of
 $G$
is
$G$
is
 $q$
and the colour classes of every
$q$
and the colour classes of every
 $q$
-colouring of
$q$
-colouring of
 $G$
are precisely the sets
$G$
are precisely the sets
 $V_1,\ldots,V_q$
; in particular, each of the sets
$V_1,\ldots,V_q$
; in particular, each of the sets
 $V_i$
,
$V_i$
,
 $i\in [q]$
, is independent.
$i\in [q]$
, is independent.
Proof. Fix an even integer
![]() $q\ge 2$
and integers
$q\ge 2$
and integers
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
. Let
$s_1,\ldots,s_q\in [q+2,2q+2]$
. Let
![]() $V_i=\{i\}\times [s_i]$
; note that the first coordinate of a vertex determines which of the sets contains the vertex. We now describe the graph
$V_i=\{i\}\times [s_i]$
; note that the first coordinate of a vertex determines which of the sets contains the vertex. We now describe the graph
![]() $G$
by listing the edges between
$G$
by listing the edges between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
,
$V_j$
,
![]() $1\le i\lt j\le q$
, contained in the matchings
$1\le i\lt j\le q$
, contained in the matchings
![]() $M_1,\ldots,M_4$
, where we abbreviate
$M_1,\ldots,M_4$
, where we abbreviate
![]() $\{(a,b),(c,d)\}$
to
$\{(a,b),(c,d)\}$
to
![]() $(a,b)(c,d)$
.
$(a,b)(c,d)$
.
-
• The matching
 $M_1$
consists of the edge
$M_1$
consists of the edge
 $(i,1)(j,1)$
, the edge
$(i,1)(j,1)$
, the edge
 $(i,q+2)(j,q+2)$
, and the edges
$(i,q+2)(j,q+2)$
, and the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for even values
$(i,k+1)(j,k)$
for even values
 $k$
between
$k$
between
 $2$
and
$2$
and
 $q$
.
$q$
. -
• The matching
 $M_2$
consists of the edges
$M_2$
consists of the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for odd values
$(i,k+1)(j,k)$
for odd values
 $k$
between
$k$
between
 $1$
and
$1$
and
 $q+1$
.
$q+1$
. -
• The matching
 $M_3$
consists of the edges
$M_3$
consists of the edges
 $(i,k)(j,s_j-q+k)$
for all
$(i,k)(j,s_j-q+k)$
for all
 $k\in [q]$
.
$k\in [q]$
. -
• The matching
 $M_4$
consists of the edges
$M_4$
consists of the edges
 $(i,s_i-q+k)(j,k)$
for all
$(i,s_i-q+k)(j,k)$
for all
 $k\in [q]$
.
$k\in [q]$
.
Observe that the following edges are always present between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
,
$V_j$
,
![]() $1\le i\lt j\le q$
:
$1\le i\lt j\le q$
:
-
• the edges
 $(i,1)(j,1)$
,
$(i,1)(j,1)$
, -
• the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for
$(i,k+1)(j,k)$
for
 $k\in [q+1]$
, and
$k\in [q+1]$
, and -
• the edges
 $(i,k)(j,s_j-q+k)$
and
$(i,k)(j,s_j-q+k)$
and
 $(i,s_i-q+k)(j,k)$
for
$(i,s_i-q+k)(j,k)$
for
 $k\in [q]$
.
$k\in [q]$
.
Since the sets
![]() $V_1,\ldots,V_q$
are independent, the chromatic number of
$V_1,\ldots,V_q$
are independent, the chromatic number of
![]() $G$
is at most
$G$
is at most
![]() $q$
. On the other hand, the vertices
$q$
. On the other hand, the vertices
![]() $(i,1)$
,
$(i,1)$
,
![]() $i\in [q]$
form a complete graph of order
$i\in [q]$
form a complete graph of order
![]() $q$
, which implies that the chromatic number of
$q$
, which implies that the chromatic number of
![]() $G$
is at least
$G$
is at least
![]() $q$
and so it is equal to
$q$
and so it is equal to
![]() $q$
.
$q$
.
Consider an arbitrary
![]() $q$
-colouring of
$q$
-colouring of
![]() $G$
and let
$G$
and let
![]() $W_i$
,
$W_i$
,
![]() $i\in [q]$
, be the colour class containing the vertex
$i\in [q]$
, be the colour class containing the vertex
![]() $(i,1)$
. (Note that the vertices
$(i,1)$
. (Note that the vertices
![]() $(i,1)$
,
$(i,1)$
,
![]() $i\in [q]$
, are coloured with distinct colours as they form a complete graph.) We prove the following statement by induction on
$i\in [q]$
, are coloured with distinct colours as they form a complete graph.) We prove the following statement by induction on
![]() $k$
: for every
$k$
: for every
![]() $i\in [q]$
, if
$i\in [q]$
, if
![]() $k\le s_i$
, then the vertex
$k\le s_i$
, then the vertex
![]() $(i,k)$
belongs to
$(i,k)$
belongs to
![]() $W_i$
. If
$W_i$
. If
![]() $k=1$
, the statement follows from the definition of the sets
$k=1$
, the statement follows from the definition of the sets
![]() $W_i$
. If
$W_i$
. If
![]() $k\in [2,q+2]$
, for every
$k\in [2,q+2]$
, for every
![]() $i\in [q]$
, the existence of the edges
$i\in [q]$
, the existence of the edges
![]() $(j,k-1)(i,k)$
,
$(j,k-1)(i,k)$
,
![]() $j\in [q]\setminus \{i\}$
, and the induction assumption, which states that
$j\in [q]\setminus \{i\}$
, and the induction assumption, which states that
![]() $(j,k-1)$
belongs to
$(j,k-1)$
belongs to
![]() $W_j$
for
$W_j$
for
![]() $j\not =i$
, imply that the vertex
$j\not =i$
, imply that the vertex
![]() $(i,k)$
belongs to
$(i,k)$
belongs to
![]() $W_i$
. Finally, if
$W_i$
. Finally, if
![]() $k\in [q+3,s_i]$
,
$k\in [q+3,s_i]$
,
![]() $i\in [q]$
, the existence of the edges
$i\in [q]$
, the existence of the edges
![]() $(j,q+k-s_i)(i,k)$
,
$(j,q+k-s_i)(i,k)$
,
![]() $j\in [q]\setminus \{i\}$
, implies that the vertex
$j\in [q]\setminus \{i\}$
, implies that the vertex
![]() $(i,k)$
belongs to
$(i,k)$
belongs to
![]() $W_i$
(note that
$W_i$
(note that
![]() $q+k-s_i\le q$
and so
$q+k-s_i\le q$
and so
![]() $(j,q+k-s_i)\in W_j$
for
$(j,q+k-s_i)\in W_j$
for
![]() $j\not =i$
). Hence, the
$j\not =i$
). Hence, the
![]() $q$
-colouring of
$q$
-colouring of
![]() $G$
is unique up to a permutation of colour classes.
$G$
is unique up to a permutation of colour classes.
We next present the version of Lemma 4 for odd values of
![]() $q\ge 3$
.
$q\ge 3$
.
Lemma 4.
For every odd integer
![]() $q\ge 3$
and all integers
$q\ge 3$
and all integers
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists a graph
$s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists a graph
![]() $G$
with vertex set formed by
$G$
with vertex set formed by
![]() $q$
disjoint sets
$q$
disjoint sets
![]() $V_1,\ldots,V_q$
that satisfies the following:
$V_1,\ldots,V_q$
that satisfies the following:
-
• the size of
 $V_i$
is
$V_i$
is
 $s_i$
for each
$s_i$
for each
 $i\in [q]$
,
$i\in [q]$
, -
• the edge set of
 $G$
can be partitioned into four sets
$G$
can be partitioned into four sets
 $M_1,\ldots,M_4$
such that each of the sets
$M_1,\ldots,M_4$
such that each of the sets
 $M_1,\ldots,M_4$
restricted to vertices of
$M_1,\ldots,M_4$
restricted to vertices of
 $V_i\cup V_j$
,
$V_i\cup V_j$
,
 $1\le i\lt j\le q$
, is a matching of size
$1\le i\lt j\le q$
, is a matching of size
 $q+1$
, and
$q+1$
, and
-
• the chromatic number of
 $G$
is
$G$
is
 $q$
and the colour classes of every
$q$
and the colour classes of every
 $q$
-colouring of
$q$
-colouring of
 $G$
are precisely the sets
$G$
are precisely the sets
 $V_1,\ldots,V_q$
; in particular, each of the sets
$V_1,\ldots,V_q$
; in particular, each of the sets
 $V_i$
,
$V_i$
,
 $i\in [q]$
, is independent.
$i\in [q]$
, is independent.
Proof. Fix an odd integer
![]() $q\ge 3$
and integers
$q\ge 3$
and integers
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, and set
$s_1,\ldots,s_q\in [q+2,2q+2]$
, and set
![]() $V_i=\{i\}\times [s_i]$
. We describe the graph
$V_i=\{i\}\times [s_i]$
. We describe the graph
![]() $G$
by listing the edges between
$G$
by listing the edges between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
,
$V_j$
,
![]() $1\le i\lt j\le q$
, contained in the matchings
$1\le i\lt j\le q$
, contained in the matchings
![]() $M_1,\ldots,M_4$
.
$M_1,\ldots,M_4$
.
-
• The matching
 $M_1$
consists of the edge
$M_1$
consists of the edge
 $(i,1)(j,1)$
, the edge
$(i,1)(j,1)$
, the edge
 $(i,q+1)(j,q+1)$
, and the edges
$(i,q+1)(j,q+1)$
, and the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for even values
$(i,k+1)(j,k)$
for even values
 $k$
between
$k$
between
 $2$
and
$2$
and
 $q-1$
.
$q-1$
. -
• The matching
 $M_2$
consists of the edges
$M_2$
consists of the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for odd values
$(i,k+1)(j,k)$
for odd values
 $k$
between
$k$
between
 $1$
and
$1$
and
 $q$
.
$q$
. -
• The matching
 $M_3$
consists of the edges
$M_3$
consists of the edges
 $(i,k)(j,s_j-q-1+k)$
for all
$(i,k)(j,s_j-q-1+k)$
for all
 $k\in [q+1]$
unless
$k\in [q+1]$
unless
 $s_{j} = q + 2$
; if
$s_{j} = q + 2$
; if
 $s_{j} = q + 2$
, then the matching
$s_{j} = q + 2$
, then the matching
 $M_{3}$
consists of the edges
$M_{3}$
consists of the edges
 $(i, q + 1)(j, q + 2)$
,
$(i, q + 1)(j, q + 2)$
,
 $(i, q + 2)(j, 2)$
and
$(i, q + 2)(j, 2)$
and
 $(i, k)(j, k + 2)$
for
$(i, k)(j, k + 2)$
for
 $k \in [q - 1]$
.
$k \in [q - 1]$
. -
• The matching
 $M_4$
consists of the edges
$M_4$
consists of the edges
 $(i,s_i-q-1+k)(j,k)$
for all
$(i,s_i-q-1+k)(j,k)$
for all
 $k\in [q+1]$
unless
$k\in [q+1]$
unless
 $s_{i} = q + 2$
; if
$s_{i} = q + 2$
; if
 $s_{i} = q + 2$
, then the matching
$s_{i} = q + 2$
, then the matching
 $M_{4}$
consists of the edges
$M_{4}$
consists of the edges
 $(i, q + 2)(j, q + 1)$
,
$(i, q + 2)(j, q + 1)$
,
 $(i, 2)(j, q + 2)$
and
$(i, 2)(j, q + 2)$
and
 $(i, k + 2)(j, k)$
for
$(i, k + 2)(j, k)$
for
 $k \in [q - 1]$
.
$k \in [q - 1]$
.
Observe that the following edges are always present between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
,
$V_j$
,
![]() $1\le i\lt j\le q$
:
$1\le i\lt j\le q$
:
-
• the edges
 $(i,1)(j,1)$
,
$(i,1)(j,1)$
, -
• the edges
 $(i,k)(j,k+1)$
and
$(i,k)(j,k+1)$
and
 $(i,k+1)(j,k)$
for
$(i,k+1)(j,k)$
for
 $k\in [q]$
,
$k\in [q]$
, -
• the edges
 $(i,k)(j,s_j-q-1+k)$
for
$(i,k)(j,s_j-q-1+k)$
for
 $k = 2q + 3 - s_{j},\ldots, q + 1$
, and
$k = 2q + 3 - s_{j},\ldots, q + 1$
, and -
• the edges
 $(i, s_i - q - 1 + k)(j,k)$
for
$(i, s_i - q - 1 + k)(j,k)$
for
 $k = 2q + 3 - s_{i},\ldots, q + 1$
.
$k = 2q + 3 - s_{i},\ldots, q + 1$
.
The rest of the argument now follows exactly the lines of the corresponding part of the proof of Lemma 3.
We are now ready to prove the main lemma of this section.
Lemma 5.
For all integers
![]() $q\ge 2$
and
$q\ge 2$
and
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists an
$s_1,\ldots,s_q\in [q+2,2q+2]$
, there exists an
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
![]() $P_{s_1,\ldots,s_q}$
such that
$P_{s_1,\ldots,s_q}$
such that
-
• each constituent of
 $P_{s_1,\ldots,s_q}$
has
$P_{s_1,\ldots,s_q}$
has
 $2q(q-1)$
non-root vertices,
$2q(q-1)$
non-root vertices,
-
• the
 $s_1+\cdots +s_q$
roots of
$s_1+\cdots +s_q$
roots of
 $P_{s_1,\ldots,s_q}$
form an independent set,
$P_{s_1,\ldots,s_q}$
form an independent set,
-
• for every
 $q$
-step kernel
$q$
-step kernel
 $U$
, there exists
$U$
, there exists
 $d_0=d_0(U)\gt 0$
that does not depend on
$d_0=d_0(U)\gt 0$
that does not depend on
 $s_1,\ldots,s_q$
such that
$s_1,\ldots,s_q$
such that
 $t_{\star }(P_{s_1,\ldots,s_q},U)$
is either
$t_{\star }(P_{s_1,\ldots,s_q},U)$
is either
 $0$
or
$0$
or
 $d_0$
for all choices of roots, and it is non-zero if and only if all roots from each of the
$d_0$
for all choices of roots, and it is non-zero if and only if all roots from each of the
 $q$
groups of roots of
$q$
groups of roots of
 $P_{s_1,\ldots,s_q}$
are chosen from the same part of
$P_{s_1,\ldots,s_q}$
are chosen from the same part of
 $U$
but the roots from different groups are chosen from different parts.
$U$
but the roots from different groups are chosen from different parts.
Proof. For
![]() $q$
and
$q$
and
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, let
$s_1,\ldots,s_q\in [q+2,2q+2]$
, let
![]() $G$
be the graph from Lemma 3 or Lemma 4 (depending on the parity of
$G$
be the graph from Lemma 3 or Lemma 4 (depending on the parity of
![]() $q$
). Let
$q$
). Let
![]() $V_1,\ldots,V_q$
be the sets forming the vertex set of
$V_1,\ldots,V_q$
be the sets forming the vertex set of
![]() $G$
, and let
$G$
, and let
![]() $M_1,\ldots,M_4$
be the sets forming the edge set of G as given by the lemma. We identify the vertices of
$M_1,\ldots,M_4$
be the sets forming the edge set of G as given by the lemma. We identify the vertices of
![]() $V_i$
with the
$V_i$
with the
![]() $s_i$
roots in the
$s_i$
roots in the
![]() $i$
-th group. Let
$i$
-th group. Let
![]() $M^{ij}_k$
, for
$M^{ij}_k$
, for
![]() $1\le i\lt j\le q$
and
$1\le i\lt j\le q$
and
![]() $k\in [4]$
, consist of the edges of
$k\in [4]$
, consist of the edges of
![]() $M_k$
between
$M_k$
between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
, and let
$V_j$
, and let
![]() ${\mathcal{M}}^{ij}_k$
be the set of all
${\mathcal{M}}^{ij}_k$
be the set of all
![]() $2^{\left |M^{ij}_k\right |}$
subsets of
$2^{\left |M^{ij}_k\right |}$
subsets of
![]() $V_i\cup V_j$
such that each set in
$V_i\cup V_j$
such that each set in
![]() ${\mathcal{M}}^{ij}_k$
contains exactly one vertex from each edge of
${\mathcal{M}}^{ij}_k$
contains exactly one vertex from each edge of
![]() $M^{ij}_k$
. Next, if
$M^{ij}_k$
. Next, if
![]() $W\subseteq V_1\cup \cdots \cup V_q$
, we write
$W\subseteq V_1\cup \cdots \cup V_q$
, we write
![]() $P[W]$
for the
$P[W]$
for the
![]() $(s_1,\ldots,s_q)$
-rooted graph with a single non-root vertex such that the non-root vertex is adjacent to the roots in
$(s_1,\ldots,s_q)$
-rooted graph with a single non-root vertex such that the non-root vertex is adjacent to the roots in
![]() $W$
. Finally, we define the
$W$
. Finally, we define the
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
![]() $P_{s_1,\ldots,s_q}$
as follows:
$P_{s_1,\ldots,s_q}$
as follows:
Observe that each constituent of the quantum graph
![]() $P_{s_1,\ldots,s_q}$
has exactly
$P_{s_1,\ldots,s_q}$
has exactly
![]() $4\cdot \binom{q}{2}=2q(q-1)$
non-root vertices, and the
$4\cdot \binom{q}{2}=2q(q-1)$
non-root vertices, and the
![]() $s_1+\cdots +s_q$
roots form an independent set. We remark that the
$s_1+\cdots +s_q$
roots form an independent set. We remark that the
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
from the definition of
![]() $P_{s_1,\ldots,s_q}$
can also be obtained in the following alternative way, which gives additional insight into the definition of
$P_{s_1,\ldots,s_q}$
can also be obtained in the following alternative way, which gives additional insight into the definition of
![]() $P_{s_1,\ldots,s_q}$
. Let
$P_{s_1,\ldots,s_q}$
. Let
![]() $P^{\prime}[v]$
be the
$P^{\prime}[v]$
be the
![]() $(s_1,\ldots,s_q,1)$
-rooted graph such that
$(s_1,\ldots,s_q,1)$
-rooted graph such that
![]() $P^{\prime}[v]$
has no non-root vertices,
$P^{\prime}[v]$
has no non-root vertices,
![]() $v$
is a root contained in one of the first
$v$
is a root contained in one of the first
![]() $q$
groups of roots, and the only edge of
$q$
groups of roots, and the only edge of
![]() $P^{\prime}[v]$
is an edge joining the vertex
$P^{\prime}[v]$
is an edge joining the vertex
![]() $v$
and the single root contained in the last group. For
$v$
and the single root contained in the last group. For
![]() $1\le i\lt j\le q$
and
$1\le i\lt j\le q$
and
![]() $k\in [4]$
, the
$k\in [4]$
, the
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph (3) can be obtained from the
$(s_1,\ldots,s_q)$
-rooted quantum graph (3) can be obtained from the
![]() $(s_1,\ldots,s_q,1)$
-rooted graph
$(s_1,\ldots,s_q,1)$
-rooted graph
by changing the single root contained in the last group to a non-root vertex.
For the rest of the proof, fix a
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
and let
$U$
and let
![]() $z_i$
,
$z_i$
,
![]() $i\in [q]$
, be any vertex of
$i\in [q]$
, be any vertex of
![]() $U$
contained in the
$U$
contained in the
![]() $i$
-th part of
$i$
-th part of
![]() $U$
. Consider a choice
$U$
. Consider a choice
![]() $x_v$
,
$x_v$
,
![]() $v\in V(G)$
, of roots. Suppose that
$v\in V(G)$
, of roots. Suppose that
![]() $G$
has an edge
$G$
has an edge
![]() $uv$
such that
$uv$
such that
![]() $u\in V_i$
,
$u\in V_i$
,
![]() $v\in V_j$
,
$v\in V_j$
,
![]() $1\le i\lt j\le q$
,
$1\le i\lt j\le q$
,
![]() $uv\in M_k$
,
$uv\in M_k$
,
![]() $k\in [4]$
, and the vertices
$k\in [4]$
, and the vertices
![]() $x_u$
and
$x_u$
and
![]() $x_{v}$
belong to the same part of the kernel
$x_{v}$
belong to the same part of the kernel
![]() $U$
. Observe that
$U$
. Observe that
 \begin{align*} &\sum _{W\in{\mathcal{M}}^{ij}_k} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)\\ & \quad = \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)+ \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\v\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)\\ & \quad= \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)+ \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |-1}U(x_{v},y)\prod _{w\in W\setminus \{u\}}U(x_w,y)\\ & \quad= \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\left (U(x_u,y)-U(x_{v},y)\right )\prod _{w\in W\setminus \{u\}}U(x_w,y)\\ & \quad= \ 0. \end{align*}
\begin{align*} &\sum _{W\in{\mathcal{M}}^{ij}_k} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)\\ & \quad = \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)+ \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\v\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)\\ & \quad= \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\prod _{w\in W}U(x_w,y)+ \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |-1}U(x_{v},y)\prod _{w\in W\setminus \{u\}}U(x_w,y)\\ & \quad= \sum _{\substack{W\in{\mathcal{M}}^{ij}_k\\u\in W}} ({-}1)^{\left |W\cap V_i\right |}\left (U(x_u,y)-U(x_{v},y)\right )\prod _{w\in W\setminus \{u\}}U(x_w,y)\\ & \quad= \ 0. \end{align*}
It follows that
![]() $t_{x_{V(G)}}(P_{s_1,\ldots,s_q},U)=0$
if the colouring of the vertices of
$t_{x_{V(G)}}(P_{s_1,\ldots,s_q},U)=0$
if the colouring of the vertices of
![]() $G$
such that
$G$
such that
![]() $v$
is coloured with the part containing
$v$
is coloured with the part containing
![]() $x_v$
is not a proper colouring of
$x_v$
is not a proper colouring of
![]() $G$
. Either Lemma 3 or Lemma 4 (depending on the parity of
$G$
. Either Lemma 3 or Lemma 4 (depending on the parity of
![]() $q$
) implies that
$q$
) implies that
![]() $t_{x_{V(G)}}(P_{s_1,\ldots,s_q},U)\not =0$
only if all roots from each of the
$t_{x_{V(G)}}(P_{s_1,\ldots,s_q},U)\not =0$
only if all roots from each of the
![]() $q$
groups of roots are chosen from the same part of
$q$
groups of roots are chosen from the same part of
![]() $U$
and the roots from different groups are chosen from different parts. If this is indeed the case and
$U$
and the roots from different groups are chosen from different parts. If this is indeed the case and
![]() $q$
is odd, the properties of the graph
$q$
is odd, the properties of the graph
![]() $G$
given in Lemma 4 imply that
$G$
given in Lemma 4 imply that
 \begin{equation} t_{x_{V(G)}}\left(P_{s_1,\ldots,s_q},U\right)=\prod _{1\le i\lt j\le q}\left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q+1}\mbox{d} y\right )^4. \end{equation}
\begin{equation} t_{x_{V(G)}}\left(P_{s_1,\ldots,s_q},U\right)=\prod _{1\le i\lt j\le q}\left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q+1}\mbox{d} y\right )^4. \end{equation}
This is positive since for every distinct
![]() $i,j\in [q]$
there is a positive measure of
$i,j\in [q]$
there is a positive measure of
![]() $y$
with
$y$
with
![]() $U(z_i,y)\not = U(z_j,z)$
(as otherwise the
$U(z_i,y)\not = U(z_j,z)$
(as otherwise the
![]() $i$
-th and
$i$
-th and
![]() $j$
-th parts can be merged together contrary to the definition of a
$j$
-th parts can be merged together contrary to the definition of a
![]() $q$
-step kernel). Hence, the existence of
$q$
-step kernel). Hence, the existence of
![]() $d_0$
follows and it is equal to the right-hand side of (4), which does not depend on the values of
$d_0$
follows and it is equal to the right-hand side of (4), which does not depend on the values of
![]() $s_1,\ldots,s_q$
. Similarly, if
$s_1,\ldots,s_q$
. Similarly, if
![]() $q$
is even, the existence of
$q$
is even, the existence of
![]() $d_0$
follows from Lemma 3 and the definition of
$d_0$
follows from Lemma 3 and the definition of
![]() $P_{s_1,\ldots,s_q}$
, and its value is
$P_{s_1,\ldots,s_q}$
, and its value is
 \begin{equation} d_0=\prod _{1\le i\lt j\le q}\left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q+2}\mbox{d} y\right )^2 \left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q}\mbox{d} y\right )^2. \end{equation}
\begin{equation} d_0=\prod _{1\le i\lt j\le q}\left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q+2}\mbox{d} y\right )^2 \left (\int _{[0,1]}\left (U(z_i,y)-U(z_j,y)\right )^{q}\mbox{d} y\right )^2. \end{equation}
The proof of the lemma is now completed.
We emphasise that the value of
![]() $d_0$
from the statement of Lemma 5 depends on the kernel
$d_0$
from the statement of Lemma 5 depends on the kernel
![]() $U$
only, that is, it does not depend on
$U$
only, that is, it does not depend on
![]() $s_1,\ldots,s_q$
; namely,
$s_1,\ldots,s_q$
; namely,
![]() $d_0$
is given by the right-hand side of (4) or (5) depending on the parity of
$d_0$
is given by the right-hand side of (4) or (5) depending on the parity of
![]() $q$
, the number of parts of the step kernel
$q$
, the number of parts of the step kernel
![]() $U$
.
$U$
.
4. Main result
We start with a construction of a quantum graph that restricts the density of each part
![]() $A$
of a step kernel
$A$
of a step kernel
![]() $U$
, that is, the value of
$U$
, that is, the value of
![]() $U$
on
$U$
on
![]() $A\times A$
.
$A\times A$
.
Lemma 6.
For all integers
![]() $q\ge 2$
,
$q\ge 2$
,
![]() $k\in [q]$
and reals
$k\in [q]$
and reals
![]() $d_1,\ldots,d_k$
, there exists a quantum graph
$d_1,\ldots,d_k$
, there exists a quantum graph
![]() $R_{d_1,\ldots,d_k}$
such that each constituent of
$R_{d_1,\ldots,d_k}$
such that each constituent of
![]() $R_{d_1,\ldots,d_k}$
has
$R_{d_1,\ldots,d_k}$
has
![]() $3q^2$
vertices and the following holds for every
$3q^2$
vertices and the following holds for every
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
:
$U$
:
![]() $t\!\left(R_{d_1,\ldots,d_k},U\right)=0$
if and only if the density of each part of
$t\!\left(R_{d_1,\ldots,d_k},U\right)=0$
if and only if the density of each part of
![]() $U$
is one of the reals
$U$
is one of the reals
![]() $d_1,\ldots,d_k$
.
$d_1,\ldots,d_k$
.
Proof. Fix
![]() $q\ge 2$
and reals
$q\ge 2$
and reals
![]() $d_1,\ldots,d_k$
. Let
$d_1,\ldots,d_k$
. Let
![]() $P_{q+2,\ldots,q+2}$
be the graph from Lemma 5. Note that
$P_{q+2,\ldots,q+2}$
be the graph from Lemma 5. Note that
![]() $P_{q+2,\ldots,q+2}$
has
$P_{q+2,\ldots,q+2}$
has
![]() $q(q+2)+2q(q-1)=3q^2$
vertices. For
$q(q+2)+2q(q-1)=3q^2$
vertices. For
![]() $m\in [0,2k]$
, we set
$m\in [0,2k]$
, we set
![]() $P^{(m)}_{q+2,\ldots,q+2}$
to be a graph obtained from
$P^{(m)}_{q+2,\ldots,q+2}$
to be a graph obtained from
![]() $P_{q+2,\ldots,q+2}$
by adding arbitrary
$P_{q+2,\ldots,q+2}$
by adding arbitrary
![]() $m$
edges among the roots in the first group (without creating parallel edges); note that this is possible since
$m$
edges among the roots in the first group (without creating parallel edges); note that this is possible since
![]() $2k\le 2q\le \binom{q+2}{2}$
. Further, let
$2k\le 2q\le \binom{q+2}{2}$
. Further, let
![]() $p(x)$
be the polynomial defined as
$p(x)$
be the polynomial defined as
 \begin{equation*}p(x)=\prod _{i=1}^k(x-d_i)^2,\end{equation*}
\begin{equation*}p(x)=\prod _{i=1}^k(x-d_i)^2,\end{equation*}
and set
![]() $R_{d_1,\ldots,d_k}$
to be the quantum graph obtained from the expansion of
$R_{d_1,\ldots,d_k}$
to be the quantum graph obtained from the expansion of
![]() $p(x)$
into monomials by replacing each monomial
$p(x)$
into monomials by replacing each monomial
![]() $x^m$
, including
$x^m$
, including
![]() $x^0$
, with
$x^0$
, with
![]() $\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{}$
.
$\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{}$
.
Consider any
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
and let
$U$
and let
![]() $d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Observe that
$d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Observe that
 \begin{equation*}t\!\left (\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{},U\right )=d_0(q-1)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{i=1}^q p_i^m\right ),\end{equation*}
\begin{equation*}t\!\left (\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{},U\right )=d_0(q-1)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{i=1}^q p_i^m\right ),\end{equation*}
where
![]() $a_i$
is the measure and
$a_i$
is the measure and
![]() $p_i$
is the density of the
$p_i$
is the density of the
![]() $i$
-th part of
$i$
-th part of
![]() $U$
,
$U$
,
![]() $i\in [q]$
; note that the term
$i\in [q]$
; note that the term
![]() $(q-1)!$
counts possible choices of parts of
$(q-1)!$
counts possible choices of parts of
![]() $U$
for the second, third, etc. group of roots while the choices of the part for the first group of roots are accounted for by the last sum in the expression. It follows that
$U$
for the second, third, etc. group of roots while the choices of the part for the first group of roots are accounted for by the last sum in the expression. It follows that
 \begin{equation*}t\!\left (R_{d_1,\ldots,d_k},U\right )=d_0(q-1)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{i=1}^q p(p_i)\right ),\end{equation*}
\begin{equation*}t\!\left (R_{d_1,\ldots,d_k},U\right )=d_0(q-1)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{i=1}^q p(p_i)\right ),\end{equation*}
which, using
![]() $p(x)\ge 0$
for all
$p(x)\ge 0$
for all
![]() $x\in{\mathbb R}$
, is equal to zero if and only if
$x\in{\mathbb R}$
, is equal to zero if and only if
![]() $p(p_i)=0$
for every
$p(p_i)=0$
for every
![]() $i\in [q]$
. The latter holds if and only if each
$i\in [q]$
. The latter holds if and only if each
![]() $p_i$
is one of the reals
$p_i$
is one of the reals
![]() $d_1,\ldots,d_k$
(note that
$d_1,\ldots,d_k$
(note that
![]() $p(x)\gt 0$
unless
$p(x)\gt 0$
unless
![]() $x\in \{d_1,\ldots,d_k\}$
), and so the quantum graph
$x\in \{d_1,\ldots,d_k\}$
), and so the quantum graph
![]() $R_{d_1,\ldots,d_k}$
has the properties given in the statement of the lemma.
$R_{d_1,\ldots,d_k}$
has the properties given in the statement of the lemma.
The next lemma provides a quantum graph restricting densities between pairs of parts of a step kernel; its proof is similar to that of Lemma 6, however, we include it for completeness.
Lemma 7.
For all integers
![]() $q\ge 2$
,
$q\ge 2$
,
![]() $k\in [q(q-1)/2]$
and reals
$k\in [q(q-1)/2]$
and reals
![]() $d_1,\ldots,d_k$
, there exists a quantum graph
$d_1,\ldots,d_k$
, there exists a quantum graph
![]() $S_{d_1,\ldots,d_k}$
with
$S_{d_1,\ldots,d_k}$
with
![]() $3q^2$
vertices such that the following holds for every
$3q^2$
vertices such that the following holds for every
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
:
$U$
:
![]() $t\!\left(S_{d_1,\ldots,d_k},U\right)=0$
if and only if the density between each pair of distinct parts of
$t\!\left(S_{d_1,\ldots,d_k},U\right)=0$
if and only if the density between each pair of distinct parts of
![]() $U$
is one of the reals
$U$
is one of the reals
![]() $d_1,\ldots,d_k$
.
$d_1,\ldots,d_k$
.
Proof. Fix
![]() $q\ge 2$
and reals
$q\ge 2$
and reals
![]() $d_1,\ldots,d_k$
. Let
$d_1,\ldots,d_k$
. Let
![]() $P_{q+2,\ldots,q+2}$
be the graph from Lemma 5. Recall that
$P_{q+2,\ldots,q+2}$
be the graph from Lemma 5. Recall that
![]() $P_{q+2,\ldots,q+2}$
has
$P_{q+2,\ldots,q+2}$
has
![]() $q(q+2)+2q(q-1)=3q^2$
vertices. For
$q(q+2)+2q(q-1)=3q^2$
vertices. For
![]() $m\in [0,2k]$
, we set
$m\in [0,2k]$
, we set
![]() $P^{(m)}_{q+2,\ldots,q+2}$
to be a graph obtained from
$P^{(m)}_{q+2,\ldots,q+2}$
to be a graph obtained from
![]() $P_{q+2,\ldots,q+2}$
by adding arbitrary
$P_{q+2,\ldots,q+2}$
by adding arbitrary
![]() $m$
edges joining a root in the first group and a root in the second group without creating parallel edges; note that this is possible since
$m$
edges joining a root in the first group and a root in the second group without creating parallel edges; note that this is possible since
![]() $2k\le q(q-1)\le (q+2)^2$
. Further, let
$2k\le q(q-1)\le (q+2)^2$
. Further, let
![]() $p(x)$
be the polynomial defined as
$p(x)$
be the polynomial defined as
 \begin{equation*}p(x)=\prod _{i=1}^k(x-d_i)^2,\end{equation*}
\begin{equation*}p(x)=\prod _{i=1}^k(x-d_i)^2,\end{equation*}
and set
![]() $S_{d_1,\ldots,d_k}$
to be the quantum graph obtained from the expansion of
$S_{d_1,\ldots,d_k}$
to be the quantum graph obtained from the expansion of
![]() $p(x)$
by replacing
$p(x)$
by replacing
![]() $x^m$
with
$x^m$
with
![]() $\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{}$
.
$\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{}$
.
Consider a
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
and let
$U$
and let
![]() $d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Observe that
$d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Observe that
 \begin{equation*}t\!\left (\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{},U\right )=2d_0(q-2)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{1\le i\lt j\le q} p_{ij}^m\right ),\end{equation*}
\begin{equation*}t\!\left (\left[\!\!\;\left[ P^{(m)}_{q+2,\ldots,q+2}\right]\!\!\;\right]_{},U\right )=2d_0(q-2)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{1\le i\lt j\le q} p_{ij}^m\right ),\end{equation*}
where
![]() $a_i$
is the measure of the
$a_i$
is the measure of the
![]() $i$
-th part of
$i$
-th part of
![]() $U$
,
$U$
,
![]() $i\in [q]$
, and
$i\in [q]$
, and
![]() $p_{ij}$
is the density between the
$p_{ij}$
is the density between the
![]() $i$
-th and
$i$
-th and
![]() $j$
-th part of
$j$
-th part of
![]() $U$
,
$U$
,
![]() $1\le i\lt j\le q$
. It follows that
$1\le i\lt j\le q$
. It follows that
 \begin{equation*}t\!\left (S_{d_1,\ldots,d_k},U\right )=2d_0(q-2)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{1\le i\lt j\le q}p\!\left (p_{ij}\right )\right ),\end{equation*}
\begin{equation*}t\!\left (S_{d_1,\ldots,d_k},U\right )=2d_0(q-2)!\left (\prod _{i=1}^q a_i^{q+2}\right )\left (\sum _{1\le i\lt j\le q}p\!\left (p_{ij}\right )\right ),\end{equation*}
which (by
![]() $p\ge 0$
) is equal to zero if and only if
$p\ge 0$
) is equal to zero if and only if
![]() $p(p_{ij})=0$
for all
$p(p_{ij})=0$
for all
![]() $1\le i\lt j\le q$
. The latter holds if and only if each
$1\le i\lt j\le q$
. The latter holds if and only if each
![]() $p_{ij}$
,
$p_{ij}$
,
![]() $1\le i\lt j\le q$
, is one of the reals
$1\le i\lt j\le q$
, is one of the reals
![]() $d_1,\ldots,d_k$
, and so the quantum graph
$d_1,\ldots,d_k$
, and so the quantum graph
![]() $S_{d_1,\ldots,d_k}$
has the properties given in the statement of the lemma.
$S_{d_1,\ldots,d_k}$
has the properties given in the statement of the lemma.
We next present a construction of a rooted quantum graph that “tests” whether there is a permutation of parts of a step kernel matching densities in a given matrix
![]() $D$
. As the value of
$D$
. As the value of
![]() $d_0$
in Lemma 5, the value of
$d_0$
in Lemma 5, the value of
![]() $c_0$
in Lemma 8 does not depend on
$c_0$
in Lemma 8 does not depend on
![]() $s_1,\ldots,s_q$
, namely, it depends on the matrix
$s_1,\ldots,s_q$
, namely, it depends on the matrix
![]() $D$
and the kernel
$D$
and the kernel
![]() $U$
only.
$U$
only.
Lemma 8.
For all integers
![]() $q\ge 2$
,
$q\ge 2$
,
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
and a symmetric real matrix
$s_1,\ldots,s_q\in [q+2,2q+2]$
and a symmetric real matrix
![]() $D\in{\mathbb R}^{q\times q}$
, there exists an
$D\in{\mathbb R}^{q\times q}$
, there exists an
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
![]() $T_{s_1,\ldots,s_q}$
satisfying the following. Each constituent of
$T_{s_1,\ldots,s_q}$
satisfying the following. Each constituent of
![]() $T_{s_1,\ldots,s_q}$
has
$T_{s_1,\ldots,s_q}$
has
![]() $2q(q-1)$
non-root vertices, and if
$2q(q-1)$
non-root vertices, and if
![]() $U$
is a
$U$
is a
![]() $q$
-step kernel such that
$q$
-step kernel such that
-
• the density of each part of
 $U$
is one of the diagonal entries of
$U$
is one of the diagonal entries of
 $D$
, and
$D$
, and
-
• the density between each pair of the parts of
 $U$
is one of the off-diagonal entries of
$U$
is one of the off-diagonal entries of
 $D$
,
$D$
,
then there exists
![]() $c_0=c_0(D,U)\not =0$
, which does not depend on
$c_0=c_0(D,U)\not =0$
, which does not depend on
![]() $s_1,\ldots,s_q$
, such that
$s_1,\ldots,s_q$
, such that
![]() $t_{\star }\left(T_{s_1,\ldots,s_q},U\right)$
is either
$t_{\star }\left(T_{s_1,\ldots,s_q},U\right)$
is either
![]() $0$
or
$0$
or
![]() $c_0$
for all choices of roots and it is non-zero if and only if
$c_0$
for all choices of roots and it is non-zero if and only if
-
• all roots from each of the
 $q$
groups of roots are chosen from the same part of
$q$
groups of roots are chosen from the same part of
 $U$
,
$U$
, -
• roots from different groups are chosen from different parts of
 $U$
,
$U$
, -
•
 $D_{ii}$
is the density of the part of
$D_{ii}$
is the density of the part of
 $U$
that the
$U$
that the
 $i$
-th group of roots is chosen from, and
$i$
-th group of roots is chosen from, and
-
•
 $D_{ij}$
is the density between the parts of
$D_{ij}$
is the density between the parts of
 $U$
that the
$U$
that the
 $i$
-th and
$i$
-th and
 $j$
-th groups of roots are chosen from.
$j$
-th groups of roots are chosen from.
Proof. Fix integers
![]() $q\ge 2$
,
$q\ge 2$
,
![]() $s_1,\ldots,s_q\in [q+2,2q+2]$
, and a matrix
$s_1,\ldots,s_q\in [q+2,2q+2]$
, and a matrix
![]() $D$
. Let
$D$
. Let
![]() $Z_1$
be the set containing the values of diagonal entries of
$Z_1$
be the set containing the values of diagonal entries of
![]() $D$
and
$D$
and
![]() $Z_2$
the set containing the values of off-diagonal entries of
$Z_2$
the set containing the values of off-diagonal entries of
![]() $D$
. We next define a polynomial
$D$
. We next define a polynomial
![]() $p$
, whose
$p$
, whose
![]() $\binom{q+1}{2}$
are variables are indexed by pairs
$\binom{q+1}{2}$
are variables are indexed by pairs
![]() $ij$
with
$ij$
with
![]() $1\le i\le j\le q$
, as follows:
$1\le i\le j\le q$
, as follows:
 \begin{equation*}p\!\left(x_{11},x_{12},\ldots,x_{q-1,q},x_{q,q}\right)= \left (\prod _{i=1}^q\prod _{z\in Z_1\setminus \{D_{ii}\}}(x_{ii}-z)\right ) \left ( \prod _{1\le i\lt j\le q}\prod _{z\in Z_2\setminus \{D_{ij}\}}(x_{ij}-z)\right ).\end{equation*}
\begin{equation*}p\!\left(x_{11},x_{12},\ldots,x_{q-1,q},x_{q,q}\right)= \left (\prod _{i=1}^q\prod _{z\in Z_1\setminus \{D_{ii}\}}(x_{ii}-z)\right ) \left ( \prod _{1\le i\lt j\le q}\prod _{z\in Z_2\setminus \{D_{ij}\}}(x_{ij}-z)\right ).\end{equation*}
Let
![]() $P_{s_1,\ldots,s_q}$
be the graph from Lemma 5. For
$P_{s_1,\ldots,s_q}$
be the graph from Lemma 5. For
![]() $m_{ii}\in [0,|Z_1|]$
,
$m_{ii}\in [0,|Z_1|]$
,
![]() $i\in [q]$
, and
$i\in [q]$
, and
![]() $m_{ij}\in [0,|Z_2|]$
,
$m_{ij}\in [0,|Z_2|]$
,
![]() $1\le i\lt j\le k$
, let
$1\le i\lt j\le k$
, let
![]() $P^{m_{11},m_{12},\ldots,m_{q,q}}_{s_1,\ldots,s_q}$
be an
$P^{m_{11},m_{12},\ldots,m_{q,q}}_{s_1,\ldots,s_q}$
be an
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph obtained from
$(s_1,\ldots,s_q)$
-rooted quantum graph obtained from
![]() $P_{s_1,\ldots,s_q}$
by adding arbitrary
$P_{s_1,\ldots,s_q}$
by adding arbitrary
![]() $m_{ij}$
edges joining roots in the
$m_{ij}$
edges joining roots in the
![]() $i$
-th group and with the roots in the
$i$
-th group and with the roots in the
![]() $j$
-th group for
$j$
-th group for
![]() $1\le i\le j\le q$
(without creating parallel edges). The
$1\le i\le j\le q$
(without creating parallel edges). The
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
![]() $T_{s_1,\ldots,s_q}$
is obtained from the expansion of
$T_{s_1,\ldots,s_q}$
is obtained from the expansion of
![]() $p\!\left(x_{11},x_{12},\ldots,x_{q,q}\right)$
into monomials by replacing each monomial
$p\!\left(x_{11},x_{12},\ldots,x_{q,q}\right)$
into monomials by replacing each monomial
![]() $x_{11}^{m_{11}}x_{12}^{m_{12}}\cdots x_{q,q}^{m_{q,q}}$
with
$x_{11}^{m_{11}}x_{12}^{m_{12}}\cdots x_{q,q}^{m_{q,q}}$
with
![]() $P^{m_{11},m_{12},\ldots,m_{q,q}}_{s_1,\ldots,s_q}$
$P^{m_{11},m_{12},\ldots,m_{q,q}}_{s_1,\ldots,s_q}$
![]() $\big($
including the monomial
$\big($
including the monomial
![]() $x_{11}^0\cdots x_{q,q}^0\big)$
.
$x_{11}^0\cdots x_{q,q}^0\big)$
.
Fix a
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
such that
$U$
such that
-
• the density of each part of
 $U$
belongs to
$U$
belongs to
 $Z_1$
, and
$Z_1$
, and -
• the density between each pair of the parts of
 $U$
belongs to
$U$
belongs to
 $Z_2$
.
$Z_2$
.
Let
![]() $d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Note that
$d_0=d_0(U)\gt 0$
be the constant from Lemma 5. Note that
![]() $t_{\star }\left (T_{s_1,\ldots,s_q},U\right )=0$
unless
$t_{\star }\left (T_{s_1,\ldots,s_q},U\right )=0$
unless
-
• all roots from each of the
 $q$
groups of roots are chosen from the same part of
$q$
groups of roots are chosen from the same part of
 $U$
,
$U$
, -
• roots from different groups are chosen from different parts of
 $U$
,
$U$
, -
•
 $D_{ii}$
is the density of the part of
$D_{ii}$
is the density of the part of
 $U$
that the
$U$
that the
 $i$
-th group of roots is chosen from, and
$i$
-th group of roots is chosen from, and -
•
 $D_{ij}$
is the density between the parts of
$D_{ij}$
is the density between the parts of
 $U$
that the
$U$
that the
 $i$
-th and
$i$
-th and
 $j$
-th groups of roots are chosen from,
$j$
-th groups of roots are chosen from,
and if
![]() $t_{\star }\left (T_{s_1,\ldots,s_q},U\right )\not =0$
, then it is equal to
$t_{\star }\left (T_{s_1,\ldots,s_q},U\right )\not =0$
, then it is equal to
 \begin{equation*} c_0=d_0\left (\prod _{i=1}^q\prod _{z\in Z_1\setminus \{D_{ii}\}}(D_{ii}-z)\right ) \left ( \prod _{1\le i\lt j\le q}\prod _{z\in Z_2\setminus \{D_{ij}\}}(D_{ij}-z)\right )\not =0. \end{equation*}
\begin{equation*} c_0=d_0\left (\prod _{i=1}^q\prod _{z\in Z_1\setminus \{D_{ii}\}}(D_{ii}-z)\right ) \left ( \prod _{1\le i\lt j\le q}\prod _{z\in Z_2\setminus \{D_{ij}\}}(D_{ij}-z)\right )\not =0. \end{equation*}
Hence, the
![]() $(s_1,\ldots,s_q)$
-rooted quantum graph
$(s_1,\ldots,s_q)$
-rooted quantum graph
![]() $T_{s_1,\ldots,s_q}$
has the properties given in the statement of the lemma.
$T_{s_1,\ldots,s_q}$
has the properties given in the statement of the lemma.
To prove the main result of this paper, we need the following well-known result, which we state explicitly for reference.
Lemma 9.
For every
![]() $q\ge 1$
and reals
$q\ge 1$
and reals
![]() $z_1,\ldots,z_q$
, the following system of equations has at most one solution
$z_1,\ldots,z_q$
, the following system of equations has at most one solution
![]() $x_1,\ldots,x_q\in \mathbb R$
(up to a permutation of the values):
$x_1,\ldots,x_q\in \mathbb R$
(up to a permutation of the values):
 \begin{equation*} \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}l} x_1 & + & \cdots & + & x_q & = & z_1 \\ x_1^{2} & + & \cdots & + & x_q^{2} & = & z_2 \\ \vdots & & \vdots & & \vdots & & \vdots \\ x_1^{q} & + & \cdots & + & x_q^{q} & = & z_{q}. \end {array} \end{equation*}
\begin{equation*} \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}l} x_1 & + & \cdots & + & x_q & = & z_1 \\ x_1^{2} & + & \cdots & + & x_q^{2} & = & z_2 \\ \vdots & & \vdots & & \vdots & & \vdots \\ x_1^{q} & + & \cdots & + & x_q^{q} & = & z_{q}. \end {array} \end{equation*}
Proof. The system of equations gives the first
![]() $q$
power sums of
$q$
power sums of
![]() $x_1,\dots,x_q$
. By Newton’s identities (see e.g., [Reference Macdonald40, Equation (2.11
$x_1,\dots,x_q$
. By Newton’s identities (see e.g., [Reference Macdonald40, Equation (2.11
![]() $^{\prime}$
)]), this determines the first
$^{\prime}$
)]), this determines the first
![]() $q$
elementary symmetric polynomials, which are the coefficients of the polynomial
$q$
elementary symmetric polynomials, which are the coefficients of the polynomial
![]() $\prod _{i=1}^q(x+x_i)$
. Therefore any other solution
$\prod _{i=1}^q(x+x_i)$
. Therefore any other solution
![]() $y_1,\dots,y_q$
of the system satisfies that
$y_1,\dots,y_q$
of the system satisfies that
![]() $\prod _{i=1}^q(x+x_i)=\prod _{i=1}^q(x+y_i)$
, which yields the statement of the lemma because of the uniqueness of polynomial factorisation.
$\prod _{i=1}^q(x+x_i)=\prod _{i=1}^q(x+y_i)$
, which yields the statement of the lemma because of the uniqueness of polynomial factorisation.
We are now ready to prove our main result, which implies Theorem 1 stated in Section 1.
Theorem 10.
The following holds for every
![]() $q\ge 2$
and every
$q\ge 2$
and every
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
: if the density of each graph with at most
$U$
: if the density of each graph with at most
![]() $4q^2-q$
vertices in a kernel
$4q^2-q$
vertices in a kernel
![]() $U^{\prime}$
is the same as in
$U^{\prime}$
is the same as in
![]() $U$
, then the kernels
$U$
, then the kernels
![]() $U$
and
$U$
and
![]() $U^{\prime}$
are weakly isomorphic.
$U^{\prime}$
are weakly isomorphic.
Proof. Fix a
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
. Let
$U$
. Let
![]() $a_1,\ldots,a_q$
be the measures of the
$a_1,\ldots,a_q$
be the measures of the
![]() $q$
parts. Further let
$q$
parts. Further let
![]() $D\in{\mathbb R}^{q\times q}$
be the matrix such that
$D\in{\mathbb R}^{q\times q}$
be the matrix such that
![]() $D_{ii}$
is the density of the
$D_{ii}$
is the density of the
![]() $i$
-th part of
$i$
-th part of
![]() $U$
and
$U$
and
![]() $D_{ij}$
,
$D_{ij}$
,
![]() $i\not =j$
, is the density between the
$i\not =j$
, is the density between the
![]() $i$
-th and
$i$
-th and
![]() $j$
-th part.
$j$
-th part.
Consider a kernel
![]() $U^{\prime}$
such that
$U^{\prime}$
such that
![]() $t(H,U)=t(H,U^{\prime})$
for all graphs with at most
$t(H,U)=t(H,U^{\prime})$
for all graphs with at most
![]() $4q^2-q$
vertices. Since each constituent of the quantum graphs
$4q^2-q$
vertices. Since each constituent of the quantum graphs
![]() $Q_{q}$
and
$Q_{q}$
and
![]() $Q_{q+1}$
from Lemma 2 has
$Q_{q+1}$
from Lemma 2 has
![]() $q(q+1)$
and
$q(q+1)$
and
![]() $(q+1)(q+2)\le 4q^2-q$
vertices, respectively, it holds that
$(q+1)(q+2)\le 4q^2-q$
vertices, respectively, it holds that
![]() $t\!\left(Q_{q},U^{\prime}\right)\not =0$
and
$t\!\left(Q_{q},U^{\prime}\right)\not =0$
and
![]() $t\!\left(Q_{q+1},U^{\prime}\right)=0$
(as they are the same as the corresponding densities in
$t\!\left(Q_{q+1},U^{\prime}\right)=0$
(as they are the same as the corresponding densities in
![]() $U$
). We conclude using Lemma 2 that
$U$
). We conclude using Lemma 2 that
![]() $U^{\prime}$
is a
$U^{\prime}$
is a
![]() $q$
-step kernel.
$q$
-step kernel.
Let
![]() $R_{D_{11},\ldots,D_{qq}}$
be the quantum graph from the statement of Lemma 6; note that each constituent of
$R_{D_{11},\ldots,D_{qq}}$
be the quantum graph from the statement of Lemma 6; note that each constituent of
![]() $R_{D_{11},\ldots,D_{qq}}$
has
$R_{D_{11},\ldots,D_{qq}}$
has
![]() $3q^2\le 4q^2-q$
vertices. Since
$3q^2\le 4q^2-q$
vertices. Since
![]() $t(R_{D_{11},\ldots,D_{qq}},U^{\prime})=0$
(as the value is the same as for the kernel
$t(R_{D_{11},\ldots,D_{qq}},U^{\prime})=0$
(as the value is the same as for the kernel
![]() $U$
), Lemma 6 yields that the density of each part of
$U$
), Lemma 6 yields that the density of each part of
![]() $U^{\prime}$
is equal to one of the diagonal entries of
$U^{\prime}$
is equal to one of the diagonal entries of
![]() $D$
. Similarly, Lemma 7 applied with the off-diagonal entries of
$D$
. Similarly, Lemma 7 applied with the off-diagonal entries of
![]() $D$
yields that the density between any pair of parts of
$D$
yields that the density between any pair of parts of
![]() $U^{\prime}$
is equal to one of the off-diagonal entries of
$U^{\prime}$
is equal to one of the off-diagonal entries of
![]() $D$
. In addition, the
$D$
. In addition, the
![]() $(q+2,\ldots,q+2)$
-rooted quantum graph
$(q+2,\ldots,q+2)$
-rooted quantum graph
![]() $T_{q+2,\ldots,q+2}$
from Lemma 8 applied with the matrix
$T_{q+2,\ldots,q+2}$
from Lemma 8 applied with the matrix
![]() $D$
satisfies
$D$
satisfies
![]() $t\!\left([\![ T_{q+2,\ldots,q+2}]\!]_{},U\right)\not =0$
; thus it holds that
$t\!\left([\![ T_{q+2,\ldots,q+2}]\!]_{},U\right)\not =0$
; thus it holds that
![]() $t\!\left([\![ T_{q+2,\ldots,q+2}]\!]_{},U^{\prime}\right)\not =0$
. Hence, we derive using Lemma 8 that, after possibly permuting the parts of
$t\!\left([\![ T_{q+2,\ldots,q+2}]\!]_{},U^{\prime}\right)\not =0$
. Hence, we derive using Lemma 8 that, after possibly permuting the parts of
![]() $U^{\prime}$
, the density of the
$U^{\prime}$
, the density of the
![]() $i$
-th part of
$i$
-th part of
![]() $U^{\prime}$
is
$U^{\prime}$
is
![]() $D_{ii}$
and the density between the
$D_{ii}$
and the density between the
![]() $i$
-th and
$i$
-th and
![]() $j$
-th parts of
$j$
-th parts of
![]() $U^{\prime}$
is
$U^{\prime}$
is
![]() $D_{ij}$
.
$D_{ij}$
.
Let
![]() $d_0=d_0(U)\gt 0$
be the constant from Lemma 5 for the kernel
$d_0=d_0(U)\gt 0$
be the constant from Lemma 5 for the kernel
![]() $U$
. Observe that, for each
$U$
. Observe that, for each
![]() $k\in [0,q]$
, the following holds for the rooted quantum graph
$k\in [0,q]$
, the following holds for the rooted quantum graph
![]() $P_{q+k+2,q+2,\ldots,q+2}$
from Lemma 5:
$P_{q+k+2,q+2,\ldots,q+2}$
from Lemma 5:
 \begin{equation*} t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U\right )=d_0(q-1)!\left (\prod _{j=1}^qa_j^{q+2}\right )\left (\sum _{i=1}^q a_i^{k}\right ). \end{equation*}
\begin{equation*} t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U\right )=d_0(q-1)!\left (\prod _{j=1}^qa_j^{q+2}\right )\left (\sum _{i=1}^q a_i^{k}\right ). \end{equation*}
It follows that the following holds for every
![]() $k\in [q]$
:
$k\in [q]$
:
 \begin{equation*}\sum _{i=1}^q a_i^{k}=\frac {q\cdot t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U\right )}{t\!\left ([\![ P_{q+2,q+2,\ldots,q+2}]\!]_{},U\right )}.\end{equation*}
\begin{equation*}\sum _{i=1}^q a_i^{k}=\frac {q\cdot t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U\right )}{t\!\left ([\![ P_{q+2,q+2,\ldots,q+2}]\!]_{},U\right )}.\end{equation*}
Similarly, with
![]() $a^{\prime}_i$
denoting the measure of the
$a^{\prime}_i$
denoting the measure of the
![]() $i$
-th part of
$i$
-th part of
![]() $U^{\prime}$
, we obtain that
$U^{\prime}$
, we obtain that
 \begin{equation*}\sum _{i=1}^q \left (a^{\prime}_i\right )^{k}=\frac {q\cdot t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U^{\prime}\right )}{t\!\left ([\![ P_{q+2,q+2,\ldots,q+2}]\!]_{},U^{\prime}\right )}.\end{equation*}
\begin{equation*}\sum _{i=1}^q \left (a^{\prime}_i\right )^{k}=\frac {q\cdot t\!\left ([\![ P_{q+k+2,q+2,\ldots,q+2}]\!]_{},U^{\prime}\right )}{t\!\left ([\![ P_{q+2,q+2,\ldots,q+2}]\!]_{},U^{\prime}\right )}.\end{equation*}
Hence, Lemma 9 and the assumption that the homomorphism densities of all graphs with at most
![]() $q(q+2)+q+2q(q-1)=3q^2+q\le 4q^2-q$
vertices are the same in
$q(q+2)+q+2q(q-1)=3q^2+q\le 4q^2-q$
vertices are the same in
![]() $U$
and
$U$
and
![]() $U^{\prime}$
implies that the multisets
$U^{\prime}$
implies that the multisets
![]() $a_1,\ldots,a_q$
and
$a_1,\ldots,a_q$
and
![]() $a^{\prime}_1,\ldots,a^{\prime}_q$
are the same.
$a^{\prime}_1,\ldots,a^{\prime}_q$
are the same.
Let
![]() $c_0=c_0(D,U)\not =0$
be the constant from Lemma 8 for the kernel
$c_0=c_0(D,U)\not =0$
be the constant from Lemma 8 for the kernel
![]() $U$
and let
$U$
and let
![]() $\Pi _D$
be the set of all permutations
$\Pi _D$
be the set of all permutations
![]() $\pi$
of the parts of
$\pi$
of the parts of
![]() $U$
such that the densities inside the parts and between the parts in
$U$
such that the densities inside the parts and between the parts in
![]() $U$
and after applying
$U$
and after applying
![]() $\pi$
to the parts of
$\pi$
to the parts of
![]() $U$
are still as given by
$U$
are still as given by
![]() $D$
. Observe that it holds that
$D$
. Observe that it holds that
 \begin{equation*}t\!\left([\![ T_{s_1,\ldots,s_q}]\!]_{},U\right)=c_0\sum _{\pi \in \Pi _D}\prod _{i=1}^q a_{\pi (i)}^{s_i}.\end{equation*}
\begin{equation*}t\!\left([\![ T_{s_1,\ldots,s_q}]\!]_{},U\right)=c_0\sum _{\pi \in \Pi _D}\prod _{i=1}^q a_{\pi (i)}^{s_i}.\end{equation*}
Let
![]() $p(x_1,\ldots,x_q)$
be the polynomial defined as
$p(x_1,\ldots,x_q)$
be the polynomial defined as
 \begin{equation*}p(x_1,\ldots,x_q)=\left (\prod _{j=1}^q x_j^{q+2}\right )\left (\prod _{i=1}^q \prod _{a\in \{a_1,\dots,a_q\}\setminus \{a_i\}} (x_i-a)\right ).\end{equation*}
\begin{equation*}p(x_1,\ldots,x_q)=\left (\prod _{j=1}^q x_j^{q+2}\right )\left (\prod _{i=1}^q \prod _{a\in \{a_1,\dots,a_q\}\setminus \{a_i\}} (x_i-a)\right ).\end{equation*}
Note that each variable in each monomial of
![]() $p$
has degree between
$p$
has degree between
![]() $q+2$
and
$q+2$
and
![]() $2q+1$
. Since each
$2q+1$
. Since each
![]() $a_i$
is non-zero, we have for all
$a_i$
is non-zero, we have for all
![]() $q$
-tuples
$q$
-tuples
![]() $(x_1,\dots,x_q)$
of reals with
$(x_1,\dots,x_q)$
of reals with
![]() $\{x_1,\dots,x_q\}\subseteq \{a_1,\dots,a_q\}$
that
$\{x_1,\dots,x_q\}\subseteq \{a_1,\dots,a_q\}$
that
![]() $p(x_1,\ldots,x_q)=0$
if and only if there exists
$p(x_1,\ldots,x_q)=0$
if and only if there exists
![]() $i\in [q]$
such that
$i\in [q]$
such that
![]() $x_i\not =a_i$
. Let
$x_i\not =a_i$
. Let
![]() $T$
be the quantum graph obtained from the polynomial
$T$
be the quantum graph obtained from the polynomial
![]() $p$
by expanding it and then replacing each monomial
$p$
by expanding it and then replacing each monomial
![]() $x_1^{s_1}\cdots x_q^{s_q}$
with
$x_1^{s_1}\cdots x_q^{s_q}$
with
![]() $[\![ T_{s_1,\ldots,s_q}]\!]_{}$
(including the monomial
$[\![ T_{s_1,\ldots,s_q}]\!]_{}$
(including the monomial
![]() $x_1^0\cdots x_1^0$
). Note that the number of vertices of each constituent of
$x_1^0\cdots x_1^0$
). Note that the number of vertices of each constituent of
![]() $T$
is at most
$T$
is at most
![]() $q(2q+1)+2q(q-1)=4q^2-q$
and
$q(2q+1)+2q(q-1)=4q^2-q$
and
In particular, it holds that
![]() $t(T,U)\not =0$
and so
$t(T,U)\not =0$
and so
![]() $t(T,U^{\prime})\not =0$
. Along the same lines, we obtain that
$t(T,U^{\prime})\not =0$
. Along the same lines, we obtain that
where
![]() $c^{\prime}_0 =c_0(D,U^{\prime})\not =0$
is the constant from Lemma 8 for the kernel
$c^{\prime}_0 =c_0(D,U^{\prime})\not =0$
is the constant from Lemma 8 for the kernel
![]() $U^{\prime}$
and
$U^{\prime}$
and
![]() $\Pi ^{\prime}_D$
is the set of all permutations
$\Pi ^{\prime}_D$
is the set of all permutations
![]() $\pi$
of the parts of
$\pi$
of the parts of
![]() $U^{\prime}$
such that the densities of the parts and between the parts after applying
$U^{\prime}$
such that the densities of the parts and between the parts after applying
![]() $\pi$
are as given by
$\pi$
are as given by
![]() $D$
. Since it holds that
$D$
. Since it holds that
![]() $t(T,U^{\prime})\not =0$
, the set
$t(T,U^{\prime})\not =0$
, the set
![]() $\Pi ^{\prime}_D$
is non-empty. It follows that
$\Pi ^{\prime}_D$
is non-empty. It follows that
![]() $\Pi ^{\prime}_D$
contains a permutation
$\Pi ^{\prime}_D$
contains a permutation
![]() $\pi$
such that
$\pi$
such that
![]() $a^{\prime}_{\pi (i)}=a_i$
for all
$a^{\prime}_{\pi (i)}=a_i$
for all
![]() $i\in [q]$
, which implies that the kernels
$i\in [q]$
, which implies that the kernels
![]() $U$
and
$U$
and
![]() $U^{\prime}$
are weakly isomorphic.
$U^{\prime}$
are weakly isomorphic.
5. Parts with different degrees
In this section, we show that a
![]() $q$
-step kernel such that its vertices contained in different parts have different degrees is forced by graphs with at most
$q$
-step kernel such that its vertices contained in different parts have different degrees is forced by graphs with at most
![]() $2q+1$
vertices.
$2q+1$
vertices.
Theorem 11.
The following holds for every
![]() $q\ge 2$
and every
$q\ge 2$
and every
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
such that the degrees of vertices in different parts are different: if the density of each graph with at most
$U$
such that the degrees of vertices in different parts are different: if the density of each graph with at most
![]() $2q+1$
vertices in a kernel
$2q+1$
vertices in a kernel
![]() $U^{\prime}$
is the same as in
$U^{\prime}$
is the same as in
![]() $U$
, then the kernels
$U$
, then the kernels
![]() $U$
and
$U$
and
![]() $U^{\prime}$
are weakly isomorphic.
$U^{\prime}$
are weakly isomorphic.
Proof. Fix
![]() $q\ge 2$
, a
$q\ge 2$
, a
![]() $q$
-step kernel
$q$
-step kernel
![]() $U$
and a kernel
$U$
and a kernel
![]() $U^{\prime}$
such that
$U^{\prime}$
such that
![]() $t(H,U)=t(H,U^{\prime})$
for every graph
$t(H,U)=t(H,U^{\prime})$
for every graph
![]() $H$
with at most
$H$
with at most
![]() $2q+1$
vertices. For
$2q+1$
vertices. For
![]() $i\in [q]$
, let
$i\in [q]$
, let
![]() $A_i$
be the
$A_i$
be the
![]() $i$
-th part of
$i$
-th part of
![]() $U$
,
$U$
,
![]() $a_i$
be the measure of
$a_i$
be the measure of
![]() $A_i$
, and let
$A_i$
, and let
![]() $d_i$
be the common degree of the vertices contained in
$d_i$
be the common degree of the vertices contained in
![]() $A_i$
.
$A_i$
.
Let
![]() $K_1^{\bullet }$
and
$K_1^{\bullet }$
and
![]() $K_2^{\bullet }$
be the
$K_2^{\bullet }$
be the
![]() $1$
-rooted graphs obtained from
$1$
-rooted graphs obtained from
![]() $K_1$
and
$K_1$
and
![]() $K_2$
, respectively, by choosing one of their vertices to be the root. Note that
$K_2$
, respectively, by choosing one of their vertices to be the root. Note that
![]() $t_x(K_2^{\bullet }-d K_1^{\bullet },V)=0$
if and only if the degree of
$t_x(K_2^{\bullet }-d K_1^{\bullet },V)=0$
if and only if the degree of
![]() $x$
in a kernel
$x$
in a kernel
![]() $V$
is
$V$
is
![]() $d$
. It follows that a kernel
$d$
. It follows that a kernel
![]() $V$
satisfies that
$V$
satisfies that
 \begin{equation} t\!\left (\left[\!\!\left[ \prod _{i\in [q]}\left (K_2^{\bullet }-d_i K_1^{\bullet }\right )^2\right]\!\!\right]_{},V\right )=0 \end{equation}
\begin{equation} t\!\left (\left[\!\!\left[ \prod _{i\in [q]}\left (K_2^{\bullet }-d_i K_1^{\bullet }\right )^2\right]\!\!\right]_{},V\right )=0 \end{equation}
if and only if the degree of almost every vertex of
![]() $V$
is one of the numbers
$V$
is one of the numbers
![]() $d_1,\ldots,d_q$
. Next observe that if a kernel
$d_1,\ldots,d_q$
. Next observe that if a kernel
![]() $V$
satisfies (6) and
$V$
satisfies (6) and
 \begin{equation} t\!\left (\left[\!\!\left[ \prod _{i\in [q]\setminus \{k\}}\left (K_2^{\bullet }-d_i K_1^{\bullet }\right )\right]\!\!\right]_{},V\right )= a_k \prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right ) \end{equation}
\begin{equation} t\!\left (\left[\!\!\left[ \prod _{i\in [q]\setminus \{k\}}\left (K_2^{\bullet }-d_i K_1^{\bullet }\right )\right]\!\!\right]_{},V\right )= a_k \prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right ) \end{equation}
for
![]() $k\in [q]$
, then the measure of the set of vertices of
$k\in [q]$
, then the measure of the set of vertices of
![]() $V$
with degree equal to
$V$
with degree equal to
![]() $d_k$
is
$d_k$
is
![]() $a_k$
. Since
$a_k$
. Since
![]() $U$
satisfies (6) and (7) for every
$U$
satisfies (6) and (7) for every
![]() $k\in [q]$
and the graphs appearing in (6) and (7) have at most
$k\in [q]$
and the graphs appearing in (6) and (7) have at most
![]() $2q+1$
and
$2q+1$
and
![]() $q$
vertices, respectively, the vertex set of the kernel
$q$
vertices, respectively, the vertex set of the kernel
![]() $U^{\prime}$
can be partitioned into
$U^{\prime}$
can be partitioned into
![]() $q$
(measurable) sets
$q$
(measurable) sets
![]() $A^{\prime}_1,\ldots,A^{\prime}_q$
and a null set
$A^{\prime}_1,\ldots,A^{\prime}_q$
and a null set
![]() $A^{\prime}_0$
such that the measure of
$A^{\prime}_0$
such that the measure of
![]() $A^{\prime}_k$
is
$A^{\prime}_k$
is
![]() $a_k$
and all vertices contained in
$a_k$
and all vertices contained in
![]() $A^{\prime}_k$
have degree equal to
$A^{\prime}_k$
have degree equal to
![]() $d_k$
for every
$d_k$
for every
![]() $k\in [q]$
.
$k\in [q]$
.
Let
![]() $G^{\bullet \bullet }$
,
$G^{\bullet \bullet }$
,
![]() $G^{\circ \bullet }$
and
$G^{\circ \bullet }$
and
![]() $G^{\bullet \circ }$
be the following
$G^{\bullet \circ }$
be the following
![]() $2$
-rooted graphs:
$2$
-rooted graphs:
![]() $G^{\bullet \bullet }$
consists of two isolated roots only,
$G^{\bullet \bullet }$
consists of two isolated roots only,
![]() $G^{\circ \bullet }$
is obtained from
$G^{\circ \bullet }$
is obtained from
![]() $G^{\bullet \bullet }$
by adding a non-root vertex adjacent to the first root, and
$G^{\bullet \bullet }$
by adding a non-root vertex adjacent to the first root, and
![]() $G^{\bullet \circ }$
is obtained from
$G^{\bullet \circ }$
is obtained from
![]() $G^{\bullet \bullet }$
by adding a non-root vertex adjacent to the second root. For
$G^{\bullet \bullet }$
by adding a non-root vertex adjacent to the second root. For
![]() $k,\ell \in [q]$
, let
$k,\ell \in [q]$
, let
![]() $H_{k\ell }$
be the
$H_{k\ell }$
be the
![]() $2$
-rooted quantum graph defined as
$2$
-rooted quantum graph defined as
 \begin{equation*}H_{k\ell }=\left (\prod _{i\in [q]\setminus \{k\}}\left (G^{\circ \bullet }-d_i G^{\bullet \bullet }\right )\right )\times \left (\prod _{j\in [q]\setminus \{\ell \}}\left (G^{\bullet \circ }-d_j G^{\bullet \bullet }\right )\right ),\end{equation*}
\begin{equation*}H_{k\ell }=\left (\prod _{i\in [q]\setminus \{k\}}\left (G^{\circ \bullet }-d_i G^{\bullet \bullet }\right )\right )\times \left (\prod _{j\in [q]\setminus \{\ell \}}\left (G^{\bullet \circ }-d_j G^{\bullet \bullet }\right )\right ),\end{equation*}
and observe that
 \begin{equation*} t_{xy}\left (H_{k\ell },U^{\prime}\right )=\left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ) \end{equation*}
\begin{equation*} t_{xy}\left (H_{k\ell },U^{\prime}\right )=\left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ) \end{equation*}
if the degree of
![]() $x$
is
$x$
is
![]() $d_k$
and the degree of
$d_k$
and the degree of
![]() $y$
is
$y$
is
![]() $d_\ell$
, and
$d_\ell$
, and
![]() $t_{xy}\left (H_{k\ell },U^{\prime}\right )=0$
otherwise. In particular, it follows that
$t_{xy}\left (H_{k\ell },U^{\prime}\right )=0$
otherwise. In particular, it follows that
 \begin{equation} t\!\left ([\![ H_{k\ell }]\!]_{},U^{\prime}\right )=a_ka_\ell \left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ). \end{equation}
\begin{equation} t\!\left ([\![ H_{k\ell }]\!]_{},U^{\prime}\right )=a_ka_\ell \left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ). \end{equation}
Note that each constituent of the
![]() $2$
-rooted quantum graph
$2$
-rooted quantum graph
![]() $H_{k\ell }$
has at most
$H_{k\ell }$
has at most
![]() $2q$
vertices. Let
$2q$
vertices. Let
![]() $H^{\prime}_{k\ell }$
be the
$H^{\prime}_{k\ell }$
be the
![]() $2$
-rooted quantum graph obtained from
$2$
-rooted quantum graph obtained from
![]() $H_{k\ell }$
by joining the two roots in each of its constituents by an edge. Similarly as above, one can show that
$H_{k\ell }$
by joining the two roots in each of its constituents by an edge. Similarly as above, one can show that
 \begin{equation} t\!\left ([\![ H^{\prime}_{k\ell }]\!]_{},U^{\prime}\right )=\left (\int _{A^{\prime}_k\times A^{\prime}_\ell } U^{\prime}(x,y)\mbox{d} x\mbox{d} y\right ) \left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ). \end{equation}
\begin{equation} t\!\left ([\![ H^{\prime}_{k\ell }]\!]_{},U^{\prime}\right )=\left (\int _{A^{\prime}_k\times A^{\prime}_\ell } U^{\prime}(x,y)\mbox{d} x\mbox{d} y\right ) \left (\prod _{i\in [q]\setminus \{k\}}\left (d_k-d_i\right )\right )\left ( \prod _{j\in [q]\setminus \{\ell \}}\left (d_\ell -d_j\right )\right ). \end{equation}
Using (8) and (9), we obtain that
that is, the average density between the parts
![]() $A^{\prime}_k$
and
$A^{\prime}_k$
and
![]() $A^{\prime}_\ell$
in the kernel
$A^{\prime}_\ell$
in the kernel
![]() $U^{\prime}$
is the same as the density between the parts
$U^{\prime}$
is the same as the density between the parts
![]() $A_k$
and
$A_k$
and
![]() $A_\ell$
in the kernel
$A_\ell$
in the kernel
![]() $U$
.
$U$
.
We now recall that each step kernel is the unique (up to weak isomorphism) minimiser of the density of
![]() $C_4$
among all kernels with the same number of parts of the same measures and the same density between them. This statement for step graphons with parts of equal measure appears in [Reference Cooper, Král’ and Martins12, Lemma 11] and the same proof applies for kernels with parts not necessarily having the same sizes; also see [Reference Lovász36, Propositions 14.13 and 14.14] for related results. Since
$C_4$
among all kernels with the same number of parts of the same measures and the same density between them. This statement for step graphons with parts of equal measure appears in [Reference Cooper, Král’ and Martins12, Lemma 11] and the same proof applies for kernels with parts not necessarily having the same sizes; also see [Reference Lovász36, Propositions 14.13 and 14.14] for related results. Since
![]() $t(C_4,U)=t(C_4,U^{\prime})$
, it follows that
$t(C_4,U)=t(C_4,U^{\prime})$
, it follows that
![]() $U^{\prime}$
is weakly isomorphic to
$U^{\prime}$
is weakly isomorphic to
![]() $U$
.
$U$
.
6. Concluding remarks
Theorem 10 asserts that every
![]() $q$
-step kernel is forced by graphs with at most
$q$
-step kernel is forced by graphs with at most
![]() $4q^2-q$
vertices. We do not know whether it suffices to consider homomorphism densities of graphs with
$4q^2-q$
vertices. We do not know whether it suffices to consider homomorphism densities of graphs with
![]() $o(q^2)$
vertices, both in the case of kernels and in the more restrictive case of graphons. We leave this as an open problem.
$o(q^2)$
vertices, both in the case of kernels and in the more restrictive case of graphons. We leave this as an open problem.
We finish by establishing that it is necessary to consider graphs with the number of vertices linear in
![]() $q$
. The argument is similar to that used in analogous scenarios, for example, in [Reference Erdős, Lovász and Spencer18, Reference Glebov, Grzesik, Klimošová and Král’21]. For reals
$q$
. The argument is similar to that used in analogous scenarios, for example, in [Reference Erdős, Lovász and Spencer18, Reference Glebov, Grzesik, Klimošová and Král’21]. For reals
![]() $a_1,\ldots,a_q\in (0,1)$
such that
$a_1,\ldots,a_q\in (0,1)$
such that
![]() $a_1+\cdots +a_q\lt 1$
, let
$a_1+\cdots +a_q\lt 1$
, let
![]() $U_{a_1,\ldots,a_q}$
be the
$U_{a_1,\ldots,a_q}$
be the
![]() $(q+1)$
-step graphon with parts of measures
$(q+1)$
-step graphon with parts of measures
![]() $a_1,\ldots,a_q$
and
$a_1,\ldots,a_q$
and
![]() $1-a_1-\cdots -a_q$
such that the graphon
$1-a_1-\cdots -a_q$
such that the graphon
![]() $U_{a_1,\ldots,a_q}$
is equal to one within each of the first
$U_{a_1,\ldots,a_q}$
is equal to one within each of the first
![]() $q$
parts and to zero elsewhere. Observe that if
$q$
parts and to zero elsewhere. Observe that if
![]() $H$
is a graph, which consists of
$H$
is a graph, which consists of
![]() $k$
components with
$k$
components with
![]() $n_1,\ldots,n_k$
vertices after the removal of isolated vertices, then
$n_1,\ldots,n_k$
vertices after the removal of isolated vertices, then
 \begin{equation*}t\!\left (H,U_{a_1,\ldots,a_q}\right )=\prod _{i=1}^k\sum _{j=1}^q a_j^{n_i}=\prod _{i=1}^kt\left (K_{n_i},U_{a_1,\ldots,a_q}\right ).\end{equation*}
\begin{equation*}t\!\left (H,U_{a_1,\ldots,a_q}\right )=\prod _{i=1}^k\sum _{j=1}^q a_j^{n_i}=\prod _{i=1}^kt\left (K_{n_i},U_{a_1,\ldots,a_q}\right ).\end{equation*}
It follows that if
then the homomorphism density of every graph with at most
![]() $q$
vertices is the same in
$q$
vertices is the same in
![]() $U_{a_1,\ldots,a_q}$
and in
$U_{a_1,\ldots,a_q}$
and in
![]() $U_{a^{\prime}_1,\ldots,a^{\prime}_q}$
. When
$U_{a^{\prime}_1,\ldots,a^{\prime}_q}$
. When
![]() $f\!\left(a_1,\dots,a_q\right)=\left(t\!\left(K_{\ell +1},U_{a_1,\ldots,a_q}\right)\right)_{\ell =1}^{q-1}$
is viewed as a function of
$f\!\left(a_1,\dots,a_q\right)=\left(t\!\left(K_{\ell +1},U_{a_1,\ldots,a_q}\right)\right)_{\ell =1}^{q-1}$
is viewed as a function of
![]() $a_1,\ldots,a_q$
, then its Jacobian matrix
$a_1,\ldots,a_q$
, then its Jacobian matrix
![]() $J$
with respect to the first
$J$
with respect to the first
![]() $q-1$
coordinates is
$q-1$
coordinates is
 \begin{equation} \left [\begin{array}{c@{\quad}c@{\quad}c} 2a_1&\cdots & 2 a_{q-1}\\ 3a_1^2&\cdots & 3 a_{q-1}^2\\ \vdots & &\vdots \\ q a_1^{q-1}&\cdots & q a_{q-1}^{a-1} \end{array}\right ] = \left [\begin{array}{c@{\quad}c@{\quad}c} 2\\ &\ddots \\ && q \end{array}\right ] \left [\begin{array}{c@{\quad}c@{\quad}c} 1&\cdots & 1\\ a_1&\cdots & a_{q-1}\\ \vdots & &\vdots \\ a_1^{q-2}&\cdots & a_{q-1}^{a-2} \end{array}\right ] \left [\begin{array}{c@{\quad}c@{\quad}c} a_1\\ &\ddots \\ && a_{q-1} \end{array}\right ]. \end{equation}
\begin{equation} \left [\begin{array}{c@{\quad}c@{\quad}c} 2a_1&\cdots & 2 a_{q-1}\\ 3a_1^2&\cdots & 3 a_{q-1}^2\\ \vdots & &\vdots \\ q a_1^{q-1}&\cdots & q a_{q-1}^{a-1} \end{array}\right ] = \left [\begin{array}{c@{\quad}c@{\quad}c} 2\\ &\ddots \\ && q \end{array}\right ] \left [\begin{array}{c@{\quad}c@{\quad}c} 1&\cdots & 1\\ a_1&\cdots & a_{q-1}\\ \vdots & &\vdots \\ a_1^{q-2}&\cdots & a_{q-1}^{a-2} \end{array}\right ] \left [\begin{array}{c@{\quad}c@{\quad}c} a_1\\ &\ddots \\ && a_{q-1} \end{array}\right ]. \end{equation}
Fix any distinct positive reals
![]() $a_1,\dots,a_q$
with sum less than
$a_1,\dots,a_q$
with sum less than
![]() $1$
. Note that the middle matrix in (11) is the Vandermonde matrix of
$1$
. Note that the middle matrix in (11) is the Vandermonde matrix of
![]() $(a_1,\dots,a_{q-1})$
and thus the Jacobian matrix
$(a_1,\dots,a_{q-1})$
and thus the Jacobian matrix
![]() $J$
is non-singular. By the Implicit Function Theorem, for every
$J$
is non-singular. By the Implicit Function Theorem, for every
![]() $a^{\prime}_q $
sufficiently close to
$a^{\prime}_q $
sufficiently close to
![]() $a_q$
there is a vector
$a_q$
there is a vector
![]() $\left(a^{\prime}_1,\ldots,a^{\prime}_{q-1}\right)$
close to
$\left(a^{\prime}_1,\ldots,a^{\prime}_{q-1}\right)$
close to
![]() $(a_1,\dots,q_q)$
such that (10) holds. By making
$(a_1,\dots,q_q)$
such that (10) holds. By making
![]() $a^{\prime}_q $
sufficiently close but not equal to
$a^{\prime}_q $
sufficiently close but not equal to
![]() $a_q$
, we can ensure that
$a_q$
, we can ensure that
![]() $a^{\prime}_q \not \in \{a_1,\dots,a_q\}$
and that all elements
$a^{\prime}_q \not \in \{a_1,\dots,a_q\}$
and that all elements
![]() $a^{\prime}_i $
are positive and sum to less than
$a^{\prime}_i $
are positive and sum to less than
![]() $1$
. Thus we obtain two
$1$
. Thus we obtain two
![]() $(q+1)$
-step graphons, namely
$(q+1)$
-step graphons, namely
![]() $U_{a_1,\dots,a_q}$
and
$U_{a_1,\dots,a_q}$
and
![]() $U_{a^{\prime}_1,\dots,a^{\prime}_q}$
, that have the same homomorphism density of every graph with at most
$U_{a^{\prime}_1,\dots,a^{\prime}_q}$
, that have the same homomorphism density of every graph with at most
![]() $q$
vertices but are not weakly isomorphic; the latter can be established by, for example, applying the proof of Theorem 10 to these two graphons (alternatively, it also follows from the general analytic characterisation of weakly isomorphic kernels [Reference Lovász36, Theorem 13.10]).
$q$
vertices but are not weakly isomorphic; the latter can be established by, for example, applying the proof of Theorem 10 to these two graphons (alternatively, it also follows from the general analytic characterisation of weakly isomorphic kernels [Reference Lovász36, Theorem 13.10]).
Acknowledgement
The authors would like to thank both anonymous reviewers for their comments that have improved the presentation of the results in the paper.