Introduction
The melting of glaciers is a subject important to alpine hydrology (Reference Fountain and WalderFountain and Walder, 1998), regional water supplies (Reference Röthlisberger, Lang, Gurnell and ClarkRöthlisberger and Lang, 1987) and global sea-level change (Reference MeierMeier, 1984). The specific conditions controlling melt and water runoff depend on local variations in the surface energy balance and the processes conveying the water through the glacier. Few studies have examined the processes controlling meltwater production on polar glaciers. Our study area is the McMurdo Dry Valleys (MDV), Antarctica (Fig. 1), where an intact terrestrial ecosystem thrives in an environment composed of soils, streams and lakes, and is maintained by meltwater generated on the surrounding polar glaciers (Reference PriscuPriscu, 1999). To understand the response of this ecosystem requires us to understand the controls on meltwater production. Taylor Glacier is an important source of meltwater for the adjacent Lake Bonney. Because of the large expanse of Taylor Glacier, it potentially can generate a huge water flux to the lake. However, little meltwater is observed on the glacier surface, despite the large surficial channels that characterize the lower part of the glacier (Fig. 2). In this paper, we examine the development of these deeply incised channels, and argue that the channels do not reflect past times of large water flux but instead themselves create the conditions for meltwater generation. Knowledge about channel formation is important to understanding water flow from this glacier and other similar polar glaciers.

Fig. 1. Taylor Valley in the McMurdo Dry Valleys. Inset (boxed) is its location in Antarctica.

Fig. 2. (a) Aerial photograph of Taylor Glacier showing the locations of the north and south channels (McMurdo Dry Valleys Long-Term Ecological Research, http://huey.colorado.edu/LTER/). (b) Aerial view looking up-glacier at the channels on Taylor Glacier. The vertical terminus cliff in the foreground is ∼20m high.
Taylor Glacier is an outlet glacier of the East Antarctic ice sheet and fills the western end of Taylor Valley, one of the MDV. Taylor Valley is a northeast–southwest-trending valley ∼35 km long (Fig. 1) and comprises exposed bedrock, sandy-gravelly soil, ice-covered lakes, and ephemeral streams that flow for up to 10 weeks each summer (Reference Conovitz, McKnight, MacDonald, Fountain, House and PriscuConovitz and others, 1998). The streams originate from polar alpine glaciers, which flow from the mountains that border Taylor Valley. The climate in Taylor Valley is that of a polar desert: cold, windy and dry. The mean annual air temperature and wind speed are –17.8˚C and 3.4 ms–1, respectively, and the mean annual relative humidity is 64% (Reference DoranDoran and others, 2002; Reference Nylen, Fountain and DoranNylen and others, 2004). The average annual precipitation at the valley bottom, occurring as snow, is <10cmw.e. (Reference Grenfell and PerovichKeys, 1980; Reference BromleyBromley, 1985).
Mass-balance studies indicate that glacier accumulation zones in the MDV gain about 10–30cm of snow, and ablation zones lose about 6–15 cm of ice, annually (Reference Fountain and WalderFountain and others, 1998). In the lowermost part of the glaciers, sublimation accounts for 40–80% of the total ablation, melt for 20–60% and calving <5% (Reference Fountain, Dana, Lewis, Vaughn, McKnight and PriscuFountain and others, 1998; Reference Lewis, Fountain and DanaLewis and others, 1998). The glacier termini often form cliffs ∼20m high. Ablation on the vertical cliffs is much higher than elsewhere on the glaciers. On Canada Glacier in Taylor Valley the non-calving ablation was 3–6 times greater than on the horizontal surface (Reference Lewis, Fountain and DanaLewis and others, 1998). Wind speeds along the cliff faces were nearly half those recorded on the glacier surface, and net radiation was greater. Together these factors favor melt over sublimation, a more efficient ablative process than melt. Reference ChinnChinn (1987) found similar results for vertical ice faces away from the terminus on Wright Lower Glacier in Wright Valley.
Satellite images and vertical aerial photography show that the channels originate from medial moraines whose path can be traced tens of km up-glacier from the terminus. Our work focuses on two of these channels within ∼10km of the terminus. The fieldwork consisted of measuring the geometry of the channels and the meteorological environment within the channel and on the adjacent glacier surface. From the meteorological measurements, the energy balance is calculated within and outside of the channels to estimate meltwater flux and to understand the development of the channels.
Field Methods
Fieldwork was conducted over two summer seasons (1999/2000 and 2000/01) on two channels, identified as the north and south channels (Fig. 2). To characterize the channel geometry, cross-sections were surveyed (global positioning system and optical surveys) on both channels, 15 on the north channel and 13 on the south channel, at roughly 0.5 km intervals. A longitudinal profile of both the channel bottom and surface adjacent to the channel was measured on the north channel. All survey errors were <4.5 cm. Surface albedo was measured at each surveyed point. The cross-section survey of the north channel began roughly 4 km down-glacier from the start of the south channel survey. All down-glacier distances reported in the paper are with respect to ablation stake 90 (Fig. 3).

Fig. 3. Location of ablation stakes (flags), cross-sections (hexagons and triangles) and the meteorological station (the cross located at stake 83) on Taylor Glacier. Stake 90 (boxed) is the datum for all distances down-glacier.
The meteorological station on Taylor Glacier, ‘Taylor Station’ near ablation stake 83, is our reference station and has recorded the standard variables (air and ice temperature (±0.02˚C), relative humidity (<1%), incoming and outgoing shortwave radiation (±3%), wind speed (±0.3ms–1) and wind direction (±3˚)) since the 1994/95 season. To define the local lapse rate, temperature loggers were installed during the 1999/2000 field season. Five Onset StowAway XTI temperature loggers (Onset Computer Corp.) were mounted 1 m above the ice surface on bamboo poles near ablation stakes, and temperatures were recorded hourly. A temporary meteorological station was established in the north channel, about 3 km down-glacier from Taylor Station and 193 m lower in elevation, from 22 November 2000 to 5 January 2001. A pair of temporary meteorological stations within the channel and at the channel periphery were deployed from 6 to 15 January 2001, and were located about 2 km down-glacier from Taylor Station. All the temporary stations recorded air temperature, wind speed and direction, incoming and outgoing shortwave radiation, and relative humidity.
Channel Geometry Results
The two channels begin to widen and deepen at about the same location ∼7 km down-glacier from stake 90. The width of the north channel increases from 10m to 110m over 2 km, and the width of the south channel (Fig. 4) increases from 10 m to 120 m over about 0.5 km. The depth increases from 1m to about 24m over roughly 1.3 and 2.5 km for the north and south channels, respectively. For the first 7 km down-glacier, the ratio of width to depth is relatively constant (∼˚) for the south channel (Fig. 4) and likely the same for the north channel. From about 7 to 8 km down-glacier, a region of transition ensues and the width-to-depth ratio increases dramatically. This is followed by a second relatively constant width-to-depth ratio (approaching 4) toward the end of the survey. Based on surface velocity measured at the ablation stakes (Fountain, unpublished data), the estimated travel time of the ice along the glacier surface, from stake 90 down-glacier to the survey end (∼10.5 km distance and about 3 km from the glacier terminus), is ∼1500 years for the south channel (Fig. 4). During the region of transition, lasting ∼160 years, channel widening is estimated to peak at about 1.5 ma–1, while the peak deepening rate is estimated to be about 0.15 ma–1.

Fig. 4. (a) Width, depth and width-to-depth ratio of south channel with distance down-glacier; and (b) rate of change in width, depth and width-to-depth ratio of south channel. The region of transition is hatched.
The average slopes of the north- and south-facing walls of the north channel are 7° and 13° from horizontal, respectively, until ∼7.5 km down-glacier, after which the slopes increase. The slope of the north-facing wall down-glacier increases to ∼30° and that of the south-facing wall to ∼25˚. However, the north-facing wall is composed of steps with 1–3 m rises averaging 60° from horizontal.
Meteorological Measurement Results
The air temperatures measured on the bamboo stakes were highly correlated with Taylor Station (r 2∼0.97). The air cools about 3˚C over roughly 9.2 km up-glacier, corresponding to a lapse rate of about –0.8˚C(100 m)–1. The air temperature at the location where channel incision begins in earnest is –4.4˚C. The rate of summer (∼2 months) surface ablation also changes, from –6.2cmw.e. up-glacier of this location to –12.5 cmw.e. down-glacier.
Comparing results from Taylor Station and the first temporary channel station shows that the average air temperatures were –4.5˚C (–0.02˚C) and –2.8˚C (±0.02˚C), respectively (Table 1). The average wind speed and relative humidity were reduced in the channel by 1.8 ms–1 (41%) and 9%, respectively. Net shortwave radiation was greater by ∼50Wm–2 (37%) in the channel. At both stations, wind direction was bimodal in the up- and down-valley directions.
Table 1. Summary of average meteorological variables at the surface and in the channels. T is air temperature, WSp is wind speed, RH is relative humidity and SWnet is net shortwave radiation. The time period t1 is 18–25 January 1999, t2 is 12 November 2000 to 5 January 2001, and t3 is 6–15 January 2001. Surface is either Taylor Station (t1 and t2) or a temporary periphery station (t3). Channel during t1 is located 5 km down-glacier from Taylor Station, during t2 is 3 km down-glacier from Taylor Station, and during t3 is 2 km down-glacier from Taylor Station (t3), running simultaneously with the periphery station at t3. Difference is the change from the surface to the channel

The paired temporary stations showed that air temperature was again warmer in the channel, by about 1.3˚C (20%), and wind speed was reduced by about 3.1 ms–1 (88%). Relative humidity was 5% greater in the channel, and the net shortwave radiation was greater at the glacier surface by an average 29 Wm–2 (27%). Meteorological data collected in a channel near the terminus of Taylor Glacier from 18 to 25 January 1999 are also presented as supplementary data in Table 1 (personal communication from K. Lewis, 2001). Overall, a microclimate develops in the channels different from the glacier surface: on average, the channels are warmer by about 1.7˚C, wind speed is reduced by about 2.4 ms–1, relative humidity is about the same, and net shortwave radiation is greater by about 14Wm–2.
Energy-Balance Model
We developed an energy-balance model to estimate the melt rate on the glacier surface and within the channels to determine the relative importance of the broad horizontal surfaces and the channels in meltwater generation. The model is one-dimensional and is based on Reference PatersonPaterson’s (1994) summary
where R is net radiation flux, S is sensible-heat flux, L is latent-heat flux, G is flux of heat through the ice column, P is energy flux supplied through precipitation, and M is energy of fusion (calculated as a residual). P is neglected because of the low rate of precipitation in the dry valleys, and its temperature is probably close to the ice surface temperature. All the terms in Equation (1) are in units of Wm–2, and the sign convention is positive for energy fluxes toward the glacier–air interface and negative for fluxes away from the interface. See the Appendix for details of the model and associated errors.
The average daily values for sensible heat, S, and latent heat, L, for summer 1994/95 at Taylor Station are similar to those reported by Reference LewisLewis (1996) at Canada Glacier. Average net radiation, R, was greater at Taylor Glacier by ∼11Wm–2, which is consistent with a higher overall solar flux in the upper reaches of Taylor Valley (Reference Dana, Wharton, Dubayah and PriscuDana and others, 1998). Ice heat flux, G, at Taylor was greater than on Canada Glacier, presumably because calculations on Taylor Glacier were based on estimated ice temperatures that resulted in a constant temperature difference between 0.2 m (surface) and 1 m depths and/or because of radiative heating of the thermistors on Canada Glacier. Comparison of the model results of estimated ablation (latent heat and melt) over the season (∼65 days) at Taylor Station with measured ablation at the nearby ablation stake was good, –7.8 and –7.0 cm, respectively. Of the estimated ablation, sublimation accounted for –4.4 cmw.e. (56%) and –3.4 cmw.e. (44%) of melt.
Results from the 2000/01 season, when temporary stations were placed within the channel and at the channel periphery, showed that net radiation was higher within the channel than on the periphery and both sensible- and latent-heat fluxes were much lower, as expected with the reduced wind speed (Fig. 5). Ice heat fluxes are similar at the two locations. These conditions result in modeled melt energy about eight times greater in the channel due to the reduced sublimation. The measured ablation at the stake closest to the temporary stations was –11.2 cmw.e. over a 65 day period. The modeled ablation at the channel periphery is –10.9 cmw.e., of which –2.7cmw.e. (25%) is sublimation and –8.2cmw.e. (75%) is melt. Unfortunately, the ablation within the channel was not measured. It was therefore estimated from measurements in the 2001/02 season, which showed that ablation in the channel was 4.5 times the measured surface ablation. Assuming this ratio applies to the 2000/01 season, ablation in the channel was about –50.4 cmw.e. The modeled ablation within the channel is about –55.9cmw.e., of which –0.3 cmw.e. (1%) is due to sublimation and –55.6 cm w.e. (99%) is due to melt. The error of the modeled ablation can be as high as 17cmw.e. over a season, which overwhelms the magnitude of measured ablation on the glacier surface. This large error is a consequence of the error accumulating in the melt term of Equation (1) and its relative size compared to the small magnitude of measured ablation.

Fig. 5. Energy-balance fluctuations within the channel and at the periphery for Taylor and Canada Glaciers, summer 2000/01. R is net radiation, S is sensible heat, L is latent heat, G is ice heat flux and M is melt energy calculated as a residual.
Meltwater Contribution to Lake Bonney
Stream-flow to Lake Bonney is monitored annually at streams that enter the lake. The last complete gauging record for streams entering Lake Bonney is from January 1998 to January 1999. The volume change in Lake Bonney over that period was 6.1 × 105m3 and the monitored stream input was 4.6×105m3 (McMurdo Dry Valleys Long-Term Ecological Research, http://huey.colorado.edu/LTER/). Much of the residual volume change of 1.5×105m3 must originate from the channels on Taylor Glacier which discharge directly into the lake and are unmeasured. We estimated the stream-flow from these channels using average surface and channel seasonal ablation, survey data to make a rough-estimate channel area, and fraction of melt from the energy balance within the channel. The average surface ablation on Taylor Glacier for the summer season 1998/99 was –9.0cmw.e. If we assume that the ratio of channel to surface ablation also applies to the 1998/99 season, and that about 99% of the ablation is attributable to melt (from energy-balance model results in the channel), then the estimated meltwater volume from the channels is 1.0×105m3, which accounts for two-thirds of the unmeasured runoff. The other third may come from unmeasured melt along the ice cliffs of glaciers between the measured streams.
Discussion and Conclusions
The deeply incised features in the lower ablation zone of Taylor Glacier are not unique in the MDV. However, these long parallel channels, traced tens of km, are distinctive and cover ∼40% of the lower ablation zone. As the channels are advected down-glacier they slowly widen (<0.1ma–1) and deepen (<0.01ma–1), maintaining a width-to-depth ratio of about ˚. The channels rapidly change configuration from shallow, narrow geometry to deep, wide features over about a 160 year period. Peak widening rate is ∼1.5ma–1 and peak deepening rate is 0.15 ma–1. After this rapid change in geometry, enlargement slows and approaches a width-to-depth ratio of ∼4 near the glacier terminus.
We hypothesize that the dark morainal material melts into the ice, forming the shallow channels observed for many kilometers. As the channel advects down-glacier into a warmer climate, increased ablation deepens the channel below some threshold, a wind shadow is formed against the cool surface winds, and a warmer microclimate develops. The location of rapid channel incision coincides with an increase in surface ablation and local air temperatures (2000/01) of –4.4˚C. This air temperature may be a threshold in these meteorological conditions for melt to begin to occur. The reduced wind in the channels reduces the turbulent heat losses via sensible and latent processes, and the multiple reflections of the shortwave radiation off the channel walls, as well as solar incident angle, increase ice temperature. Together these effects shift the energy balance from a turbulence-dominated heat loss to a melt-dominated environment. The more energy-efficient mass loss through melt (heat of fusion, 3.3×105 J kg–1) vs sublimation (heat of vaporization, 2.8×106 J kg–1) increases channel ablation over the ablation on the nearby glacier surface. Eventually, a steady state evolves between channel width and depth because, as the channels deepen, the bottom is increasingly shaded by the channel walls and the latter must widen before the channel continues to deepen. We believe that the channels developed from differences in energy balance initiated by differences in topography. It could be argued that channels might form by thermal erosion from flowing water. However, that process would form narrow slot canyons rather than the wide channels observed. Additionally, the onset of dramatic channel development occurs just down-glacier from a minor bottlenecking of the glacier and a slight overdeepening indicated by isolated ground-penetrating radar (P. Langevin, unpublished data). Therefore, lateral and longitudinal extension may work together to affect channel dynamics. However, more radar work would need to be done to confirm subglacial conditions.
The solar regime also plays a role in channel morphology. The solar ellipse (the path the sun traces in the Taylor Valley sky) during the melt season ranges between 11° (southern sky) and 36° (northern sky) above horizontal. As a result, the north-facing walls receive more intense radiation than the south-facing walls. The north-facing walls are, on average, more steeply inclined than the south-facing walls, and they also have steeply inclined regions whose average slope is 60˚, yielding a nearly perpendicular solar incident angle of 84° when the sun is at its maximum elevation. Therefore, the channels may be equilibrating to the solar regime in the valley.
In summary, although the channels observed on Taylor Glacier drain meltwater from the broad flat surface and route it off the glacier, the channels themselves are important sources of runoff to Lake Bonney, contributing an extra ∼20% to the measured runoff. The channels probably form due to a microclimate that develops in the shallow channels when they deepen sufficiently. The microclimate, unlike the climate on the broad glacier surface, favors melt over sublimation. This more effective ablative process within the channels results in a dramatic and rapid change in channel geometry. Whether the channels could eventually grow large enough to lose their distinctive microclimate and terminate growth is uncertain since they are advected to the glacier terminus before that eventuality.
Acknowledgements
Our work was supported by US National Science Foundation, Office of Polar Programs grant NSF OPP-9813061. Discussions with K. Lewis were valuable. We received great support from Raytheon Polar Services and in particular from J. Scanniello. We appreciate the support of, and discussions with, our colleagues on the McMurdo Dry Valleys Long-Term Ecological Research project. In addition, we are especially grateful for the thoughtful feedback from peer reviewers of this paper.
Appendix: Energy-Balance Model
Radiative flux
Net radiation at the glacier surface is
where SWnet and LWnet are net shortwave and longwave radiation, respectively. We formulated the net shortwave radiation calculation to take into account radiation absorbed in the surface layer of ice (Hobbs, 1974):
where α is surface albedo, SW# is the incoming radiation flux, j is the absorption coefficient (m–1) and z is the depth into the ice. The absorption coefficient used, j = 1.6 m–1, is a value adjusted, within reasonable limits, in calibrating the energy balance. The coefficient is a value that depends on several variables: wavelength, incident angle and ice structure. Hobbs (1974), Reference Grenfell and PerovichGrenfell and Perovich (1981) and Reference PerovichPerovich (1996) provide comprehensive treatments of this topic, and it is discussed below in the section on energy-balance error and sensitivity. The maximum value of z used is 1 m, consistent with Reference PatersonPaterson (1994). Because the ice is typically below 0˚C and translucent, the energy of absorbed radiation is important.
Net longwave radiation (LWnet) is the difference between incoming longwave radiation from the atmosphere and outgoing longwave radiation from the surface (LW↓ and LW↑ respectively):
where є a and є i are air and ice emissivity, respectively (dimensionless), σ is the Stefan–Boltzmann constant (5.67×10–8Wm–2 K–4), and T a and T i are air and ice temperature, respectively, in Kelvin (K). Ice emissivity is 0.95, an average for ice (Reference AryaArya, 2001). We calculated atmospheric emissivity based on an empirically derived formula:
(Reference SatterlundSatterlund, 1979), where V a is atmospheric vapor pressure in mbar and T a is air temperature (K). Atmospheric vapor pressure is
(Reference Goff and GratchGoff and Gratch, 1946), where

RH is relative humidity, and T o is the triple point of water, 273.16 K at 611.2 Pa.
Turbulent heat fluxes
Turbulent heat fluxes include sensible and latent heat. Sensible heat, S, is the vertical flux of heat through mechanical and natural convection (wind) and a temperature gradient between the ice and the air above it:
where A (= 0.001) is the transfer coefficient, P (= 9.74× 104 Pa) is the atmospheric pressure, u is wind speed (m s–1), and T a and T i are the air and ice temperatures (K), respectively.
The latent-heat term, L, represents the vertical transfer of heat through a phase change from solid or liquid to vapor, or the reverse:
where V a and V i are the atmospheric and ice surface vapor pressures (Pa), respectively. V i is calculated in the same way as V a (Equation (A5)), except that humidity at the ice surface is assumed to be saturated, and temperature is the ice temperature, T i.
Heat flux through the ice column
Valid ice temperatures are available only from the 1994/95 season at the established station on Taylor Glacier. We estimate ice temperature during the 2000/01 season by correlating summer air temperatures with ice temperatures for the 1994/95 season at the established station on Taylor Glacier and using the regression equation to estimate ice temperature in the 2000/01 season. Air temperatures at Taylor Station for summer 1994/95 were better correlated with 0.2m ice temperatures (r 2 = 0.79) than 1.0m ice temperatures (r 2 = 0.58). Both correlations are statistically significant at the 95% confidence level. Predictably, using a linear regression directly correlates ice and air temperatures with no time lag for conduction, resulting in a constant difference in 0.2m and 1m ice temperatures. However, because our model produces average energy-balance terms, which are then applied to the season as a whole, this method of estimating ice temperature will compensate for the induced errors. Ice temperatures were presumed constant and equal to the average annual air temperature of –16.6˚C at 15 m depth (Reference PatersonPaterson, 1994). We use the 0.2 m ice temperatures as surface temperatures.
The conduction of heat through the ice column is
where k is the thermal conductivity (Wm–1 K–1) of ice and ∂T/∂z is the ice temperature gradient (Km–1). The empirical formula for thermal conductivity of pure ice (Reference PatersonPaterson, 1994) is
We calculated k for the first-season Taylor Station data when the ice temperatures were correct, and used it in the model. For the energy balance within the channel, we calculated k using ice temperatures predicted by the regression equation.
Energy-balance error and sensitivity
In order to estimate error in the energy-balance results, errors associated with the meteorological instrumentation were propagated through the energy-balance equations using the general law of error propagation (Reference BairdBaird, 1962)

where σy is the error associated with the equation (y), ∂y/∂xi is the change in equation y with respect to each variable xi , i = 1 : n, where n is the number of variables in the equation, and σxi is the standard deviation associated with each variable.
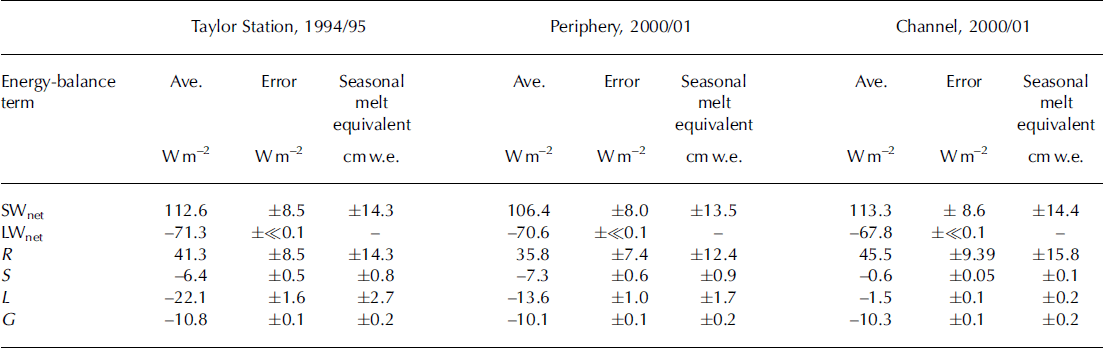
The very low error for net longwave radiation (Table 2) results from a ±0.02˚C error in temperature (Reference DoranDoran and others, 2002). The error in the net radiation term is dominated by error in the shortwave radiation and generates an error of ±12–15cmw.e. in melt calculated over the season. It is important to keep in mind that just 1 Wm–2 of energy produces 0.20 cmw.e. sublimation or 1.68 cmw.e. of melt over a summer season. A simple example of this sensitivity as it applies to the energy balance follows: The error associated with incoming shortwave radiation instrumentation is ±3%. The average incoming shortwave radiation for summer 1994/95 was ∼349Wm–2, 3% of which is ∼10Wm–2. This error magnitude alone amounts to ±17 cmw.e. of melt over the season, more than double the measured ablation.
Table 2. Error in the energy-balance modeling expressed as Wm–2 and as seasonal melt equivalent, assuming 65 days in the season. SWnet is net shortwave radiation, LWnet is net longwave radiation R is net radiation, S is sensible heat, L is latent heat and G is ice heat flux
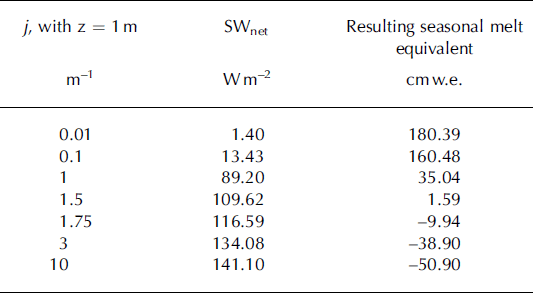
We arrived at a value of 1.6 m–1 for j by tuning it so that the calculated total ablation was approximately equal to the measured ablation of –7.0 cmw.e. over the 1994/95 season. The effect that altering j has on the net shortwave radiation at the glacier surface is illustrated in Table 3. For the 1994/95 summer season at Taylor Station, j had to be 1.5–2 to produce melt. The modeled seasonal melt for the 2000/01 season results from j values of 3.2 m–1 and 1.0 m–1 for the periphery and channel, respectively. These values are the same order of magnitude as the value of j used in calculating the energy balance at Taylor Station during the 1994/95 season.
Table 3. Sensitivity analysis in the value of the absorption coefficient, j, and the effect it has on net shortwave radiation and resulting melt equivalent. Altering j has no affect on sublimation