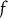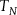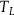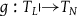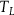Thus it appears that any tenable relationalism must incorporate a powerful, primitive notion of geometric modality. Manders (Reference Manders1982) provides the most promising route to such a relationalism. (Belot Reference Belot2000, 578)
1. Introduction
In this journal, Kenneth Manders has argued that the Newtonian conception of space, which postulates spatial points and treats them as fundamental, is theoretically equivalent to the Leibnizian modal conception, which treats spatial points as logically constructed from actual particles and possible configurations thereof (Manders Reference Manders1982). To demonstrate the equivalence between the substantival and the modal relationist metaphysics, Manders provides a translation from the language of the Newtonian theory of space
![]() ${T_N}$
into the language of Leibnizian modal relationism.
Footnote 1
He suggests that an adequate relationist theory
${T_N}$
into the language of Leibnizian modal relationism.
Footnote 1
He suggests that an adequate relationist theory
![]() ${T_L}$
can be found, namely, the translation of the Newtonian theory
${T_L}$
can be found, namely, the translation of the Newtonian theory
![]() ${T_N}$
(Manders Reference Manders1982, 589). However, the existence of a translation does not amount to a proof of equivalence under reasonable standards of formal equivalence. Although Manders defines a translation
${T_N}$
(Manders Reference Manders1982, 589). However, the existence of a translation does not amount to a proof of equivalence under reasonable standards of formal equivalence. Although Manders defines a translation
![]() $f:{T_N} \mapsto {T_L}$
, he does not show that there is a translation
$f:{T_N} \mapsto {T_L}$
, he does not show that there is a translation
![]() $g$
:
$g$
:
![]() ${T_L}$
${T_L}$
![]() $ \mapsto $
$ \mapsto $
![]() ${T_N}$
such that
${T_N}$
such that
![]() ${T_N} \models \phi \leftrightarrow g\left( {f\left( \phi \right)} \right)$
for all formulae
${T_N} \models \phi \leftrightarrow g\left( {f\left( \phi \right)} \right)$
for all formulae
![]() $\phi $
of
$\phi $
of
![]() ${T_N}$
(see Halvorson Reference Halvorson2019, 27). In fact, we show that there is no interpretation from
${T_N}$
(see Halvorson Reference Halvorson2019, 27). In fact, we show that there is no interpretation from
![]() ${T_L}$
to
${T_L}$
to
![]() ${T_N}$
(a translation that sends theorems into theorems).
${T_N}$
(a translation that sends theorems into theorems).
This result seems to show that the modal relationist introduces redundant structure, absent in the substantivalist theory. We substantiate this claim by using a criterion for comparing amounts of structure. The one we employ is inspired by a criterion for the equality of structure attributable to Barrett (Reference Barrett2022).
The philosophical conclusion of the article is that modal relationism ought to be abandoned on parsimony grounds. We base this recommendation on another principle of parsimony, whose most precise formulation is again attributable to Barrett (Reference Barrett2022), namely, that all else being equal, we should favor theories that posit less structure. We think that this principle is an improved form of Ockham’s razor and is both intrinsically plausible and exemplified by famous cases of theory choice. This combination of our structure-counting criterion and the parsimony principle of Barrett (Reference Barrett2022) is in tension with the requirement of Belot (Reference Belot2011) that a relationist theory should state truth conditions for all statements about space. If a systematic paraphrase is a translation function
![]() $f$
, then theories of the form
$f$
, then theories of the form
![]() $f\left( {{T_{{\rm{subst}}}}} \right)$
. cannot be superior on parsimony grounds.
$f\left( {{T_{{\rm{subst}}}}} \right)$
. cannot be superior on parsimony grounds.
2. The theories
 ${T_N}$
and
${T_N}$
and
 ${T_L}$
${T_L}$
Let us begin by describing the two systems
![]() ${T_N}$
and
${T_N}$
and
![]() ${T_L}$
. We follow Manders by identifying
${T_L}$
. We follow Manders by identifying
![]() ${T_N}$
with Tarski’s formalization of Euclidean geometry (see Tarski Reference Tarski, Henkin, Suppes and Tarski1959). The ontology of
${T_N}$
with Tarski’s formalization of Euclidean geometry (see Tarski Reference Tarski, Henkin, Suppes and Tarski1959). The ontology of
![]() ${T_N}$
consists of spatial points.
Footnote 2
The primitive extralogical predicates of the substantivalist language
${T_N}$
consists of spatial points.
Footnote 2
The primitive extralogical predicates of the substantivalist language
![]() ${L_N}$
are the following:
${L_N}$
are the following:
-
(a) A three-place predicate “Between
 ${v_1}{v_2}{v_3}$
” that holds of the points
${v_1}{v_2}{v_3}$
” that holds of the points
 ${v_1}$
,
${v_1}$
,
 ${v_2}$
, and
${v_2}$
, and
 ${v_3}$
when
${v_3}$
when
 ${v_2}$
stands between
${v_2}$
stands between
 ${v_1}$
and
${v_1}$
and
 ${v_3}$
on the segment connecting them
${v_3}$
on the segment connecting them -
(b) A four-place predicate “Congruence
 ${v_1}{v_2}{v_3}{v_4}$
” that holds of four points
${v_1}{v_2}{v_3}{v_4}$
” that holds of four points
 ${v_1},{v_2},{v_3}$
, and
${v_1},{v_2},{v_3}$
, and
 ${v_4}$
when the segment
${v_4}$
when the segment
 $\overline {{v_1}{v_2}} $
is as long as
$\overline {{v_1}{v_2}} $
is as long as
 $\overline {{v_3}{v_4}} $
$\overline {{v_3}{v_4}} $
The language
![]() ${L_L}$
of the relationist theory
${L_L}$
of the relationist theory
![]() ${T_L}$
contains two types of variables. The variables
${T_L}$
contains two types of variables. The variables
![]() ${x_1},{x_2}, \ldots ,{x_n}$
range over point particles. The variables
${x_1},{x_2}, \ldots ,{x_n}$
range over point particles. The variables
![]() ${c_1},{c_2}, \ldots ,{c_n}$
range over a new type of entity: possible configurations of point particles. Manders (Reference Manders1982) does not clarify whether the ontology of
${c_1},{c_2}, \ldots ,{c_n}$
range over a new type of entity: possible configurations of point particles. Manders (Reference Manders1982) does not clarify whether the ontology of
![]() ${T_L}$
includes only actual particles or both actual and merely possible particles. But as Field (Reference Field1984, 57) has pointed out, a “possible point particle” appears to behave in the relationist theory exactly like a space or a spacetime point. Because there is no distinction between particles and points, we cannot distinguish the merely possible particles from spatial points in terms of location. These “possible particles” seem to stand in exactly the same relations and satisfy exactly the same principles as points of space.
Footnote 3
If quantification over merely possible point particles is admitted, modal relationism appears to collapse immediately into substantivalism. Even if one could distinguish possible particles from spatial points, on philosophical grounds, merely possible point particles raise the same epistemological and parsimony objections as space or spacetime points. For this reason, we suppose that the particles that
${T_L}$
includes only actual particles or both actual and merely possible particles. But as Field (Reference Field1984, 57) has pointed out, a “possible point particle” appears to behave in the relationist theory exactly like a space or a spacetime point. Because there is no distinction between particles and points, we cannot distinguish the merely possible particles from spatial points in terms of location. These “possible particles” seem to stand in exactly the same relations and satisfy exactly the same principles as points of space.
Footnote 3
If quantification over merely possible point particles is admitted, modal relationism appears to collapse immediately into substantivalism. Even if one could distinguish possible particles from spatial points, on philosophical grounds, merely possible point particles raise the same epistemological and parsimony objections as space or spacetime points. For this reason, we suppose that the particles that
![]() ${T_L}$
quantifies over are only the actually existing ones. Possible configurations of particles will be described better later in the article, when we come to the predicates that apply to them. But they correspond roughly to possible worlds, or scenarios in which the particles are arranged in some fashion.
${T_L}$
quantifies over are only the actually existing ones. Possible configurations of particles will be described better later in the article, when we come to the predicates that apply to them. But they correspond roughly to possible worlds, or scenarios in which the particles are arranged in some fashion.
Language of
![]() ${T_L}$
: For every geometrical predicate
${T_L}$
: For every geometrical predicate
![]() ${R^n}$
of the Newtonian theory
${R^n}$
of the Newtonian theory
![]() ${T_N}$
, the language
${T_N}$
, the language
![]() ${L_L}$
has a predicate
${L_L}$
has a predicate
![]() ${R^{n + 1}}$
for point particles with an extra place for configurations. Because
${R^{n + 1}}$
for point particles with an extra place for configurations. Because
![]() ${L_N}$
contains two geometrical predicates of betweenness and congruence,
${L_N}$
contains two geometrical predicates of betweenness and congruence,
![]() ${T_L}$
contains the following two predicates:
${T_L}$
contains the following two predicates:
-
(1) A four-place predicate “Between
 ${\rm{'}}$
${\rm{'}}$
 ${c_1}{x_1}{x_2}{x_3}$
,” which holds of a configuration and three particles when the particle
${c_1}{x_1}{x_2}{x_3}$
,” which holds of a configuration and three particles when the particle
 ${x_2}$
is between the particles
${x_2}$
is between the particles
 ${x_1}$
and
${x_1}$
and
 ${x_3}$
in the configuration
${x_3}$
in the configuration
 ${c_1}$
${c_1}$
-
(2) A five-place predicate “Congruence
 ${\rm{'}}$
${\rm{'}}$
 ${c_1}{x_1}{x_2}{x_3}{x_4}$
,” which holds a configuration
${c_1}{x_1}{x_2}{x_3}{x_4}$
,” which holds a configuration
 ${c_1}$
and four particles
${c_1}$
and four particles
 ${x_1}{x_2}{x_3}{x_4}$
when the distance between
${x_1}{x_2}{x_3}{x_4}$
when the distance between
 ${x_1}$
and
${x_1}$
and
 ${x_2}$
is the same as the distance between
${x_2}$
is the same as the distance between
 ${x_3}$
and
${x_3}$
and
 ${x_4}$
in
${x_4}$
in
 ${c_1}$
${c_1}$
Moreover, the theory
![]() ${T_L}$
contains two other predicates:
${T_L}$
contains two other predicates:
-
(3) A four-place predicate “
 ${c_1}{x_1}\sim {c_2}{x_2}$
,” which holds two point particles and two configurations when the point particle
${c_1}{x_1}\sim {c_2}{x_2}$
,” which holds two point particles and two configurations when the point particle
 ${x_1}$
as it occurs in
${x_1}$
as it occurs in
 ${c_1}$
is in the same place of
${c_1}$
is in the same place of
 ${x_2}$
as it occurs in
${x_2}$
as it occurs in
 ${c_2}$
. We call this the same-place-as relation.
${c_2}$
. We call this the same-place-as relation. -
(4) A two-place predicate of membership “
 ${x_1}$
${x_1}$
 $ \in $
$ \in $
 ${c_1}$
,” which holds of a point particle and a configuration when the former is an element of the latter
${c_1}$
,” which holds of a point particle and a configuration when the former is an element of the latter
The same-place-as relation is crucial for the claim that
![]() ${T_L}$
is adequate to physics, and it is also the most unfamiliar. It requires, therefore, a more detailed explanation than the others. Manders (Reference Manders1982, 579–82) introduces it by drawing on intuitions about absolute space. Two particles in two respective configurations satisfy this relation if they stand in the same point of absolute space. However, this reference to absolute space is syncategorematic and does not require quantification over space, regions, or points. Configurations, in this sense of the word, are like possible assignments of the particles to absolute locations, rather than simply networks of relative distances. We can contrast this approach with another natural primitive: transworld congruence (Field Reference Field1989, 72). Four particles in two configurations are transworld congruent if they stand at the same distance in their respective configurations. In terms of transworld congruence, it is possible to define a weaker same-place relation: two particles
${T_L}$
is adequate to physics, and it is also the most unfamiliar. It requires, therefore, a more detailed explanation than the others. Manders (Reference Manders1982, 579–82) introduces it by drawing on intuitions about absolute space. Two particles in two respective configurations satisfy this relation if they stand in the same point of absolute space. However, this reference to absolute space is syncategorematic and does not require quantification over space, regions, or points. Configurations, in this sense of the word, are like possible assignments of the particles to absolute locations, rather than simply networks of relative distances. We can contrast this approach with another natural primitive: transworld congruence (Field Reference Field1989, 72). Four particles in two configurations are transworld congruent if they stand at the same distance in their respective configurations. In terms of transworld congruence, it is possible to define a weaker same-place relation: two particles
![]() $y$
and
$y$
and
![]() $y{\rm{'}}$
stand in the same place in two configurations
$y{\rm{'}}$
stand in the same place in two configurations
![]() $c$
and
$c$
and
![]() $c{\rm{'}}$
if they have the same number of particles and there is a one-to-one map that preserves congruence and maps
$c{\rm{'}}$
if they have the same number of particles and there is a one-to-one map that preserves congruence and maps
![]() $y$
to
$y$
to
![]() $y{\rm{'}}$
(fig. 1).
$y{\rm{'}}$
(fig. 1).

Figure 1.
![]() $c$
,
$c$
,
![]() $y$
,
$y$
,
![]() $c{\rm{'}}$
, and
$c{\rm{'}}$
, and
![]() $y{\rm{'}}$
need not stand in the same-place-as relation.
$y{\rm{'}}$
need not stand in the same-place-as relation.
In
![]() ${T_L}$
, particles stand in the same place independently of what other particles in the configurations are doing. The theory
${T_L}$
, particles stand in the same place independently of what other particles in the configurations are doing. The theory
![]() ${T_L}$
is consistent with the claim that there exist two isomorphic configurations, in the previous sense, with the particles in different places of absolute space. For example, there could be a configuration
${T_L}$
is consistent with the claim that there exist two isomorphic configurations, in the previous sense, with the particles in different places of absolute space. For example, there could be a configuration
![]() $c$
with three collinear particles,
$c$
with three collinear particles,
![]() $x,y,z$
, equally spaced, and also a configuration
$x,y,z$
, equally spaced, and also a configuration
![]() $c{\rm{'}}$
where the three particles are shifted by 5 cm to the left.
Footnote 4
$c{\rm{'}}$
where the three particles are shifted by 5 cm to the left.
Footnote 4
This same-place relation will pay its dividends when we come to motion and inertia. For an instant, let us add variables ranging over times
![]() ${t_1}, \ldots {\rm{\;}}{t_n}$
and a binary relation
${t_1}, \ldots {\rm{\;}}{t_n}$
and a binary relation
![]() $R\left( {t,c} \right)$
between times and the configuration realized at time
$R\left( {t,c} \right)$
between times and the configuration realized at time
![]() $t$
. The theory with transworld congruence does not seem to be able to define what it means for a symmetrical object to rotate around an axis. The contemplated extension of
$t$
. The theory with transworld congruence does not seem to be able to define what it means for a symmetrical object to rotate around an axis. The contemplated extension of
![]() ${T_L}$
can. It can state, for example, that
${T_L}$
can. It can state, for example, that
![]() $x$
remains in the same place at
$x$
remains in the same place at
![]() ${t_2}$
as it was at
${t_2}$
as it was at
![]() ${t_1}$
but that
${t_1}$
but that
![]() $y$
and
$y$
and
![]() $z$
have moved (fig. 2). It can also quantify the angle of rotation by contemplating a merely possible and unactualized configuration
$z$
have moved (fig. 2). It can also quantify the angle of rotation by contemplating a merely possible and unactualized configuration
![]() $c$
in which some particles
$c$
in which some particles
![]() $y{\rm{'}}$
and
$y{\rm{'}}$
and
![]() $z{\rm{'}}$
are located at
$z{\rm{'}}$
are located at
![]() ${t_2}$
where
${t_2}$
where
![]() $y$
and
$y$
and
![]() $z$
were in
$z$
were in
![]() ${t_1}$
. Therein lies the promise of physical adequacy.
${t_1}$
. Therein lies the promise of physical adequacy.

Figure 2. Rotation.
Ultimately, it is the axioms that fix the interpretation of the same-place relation. Manders states in the appendix that the postulates of
![]() ${T_L}$
are simply the translation of the axioms of
${T_L}$
are simply the translation of the axioms of
![]() ${T_N}$
, together with three axioms stating that the same-place-as relation is an equivalence relation on configurations (Manders Reference Manders1982, 589). Therefore, in order to specify the axioms, or postulates, of
${T_N}$
, together with three axioms stating that the same-place-as relation is an equivalence relation on configurations (Manders Reference Manders1982, 589). Therefore, in order to specify the axioms, or postulates, of
![]() ${T_L}$
, we need to specify the Mandersian translation first. In general, we can specify the axioms of a relationist theory by giving a translation and then taking the translation of the axioms of some substantivalist physical theory. Let us state explicitly the three equivalence relation axioms for the same-place-as relation:
${T_L}$
, we need to specify the Mandersian translation first. In general, we can specify the axioms of a relationist theory by giving a translation and then taking the translation of the axioms of some substantivalist physical theory. Let us state explicitly the three equivalence relation axioms for the same-place-as relation:
-
•
 ${\psi _1}$
is the formula
${\psi _1}$
is the formula
 $\forall {c_1}\forall {x_1}({x_1} \in {c_1} \to {x_1}{c_1}\sim {c_1}{x_1}$
).
$\forall {c_1}\forall {x_1}({x_1} \in {c_1} \to {x_1}{c_1}\sim {c_1}{x_1}$
). -
•
 ${\psi _2}$
is the formula
${\psi _2}$
is the formula
 $\forall {x_1}\forall {c_1}\forall {x_2}\forall {c_2}$
$\forall {x_1}\forall {c_1}\forall {x_2}\forall {c_2}$
 $\left( {{c_1}{x_1}\sim {c_2}{x_2} \to {c_2}{x_2}\sim {c_1}{x_1}} \right)$
.
$\left( {{c_1}{x_1}\sim {c_2}{x_2} \to {c_2}{x_2}\sim {c_1}{x_1}} \right)$
. -
•
 ${\psi _3}$
is
${\psi _3}$
is
 $\forall {x_1}\forall {c_1}\forall {x_2}\forall {c_2}\forall {x_3}\forall {c_3}$
$\forall {x_1}\forall {c_1}\forall {x_2}\forall {c_2}\forall {x_3}\forall {c_3}$
 $\left( {{c_1}{x_1}\sim {c_2}{x_2} \wedge {c_2}{x_2}\sim {c_3}{x_3} \to {c_1}{x_1}\sim {c_3}{x_3}} \right).$
$\left( {{c_1}{x_1}\sim {c_2}{x_2} \wedge {c_2}{x_2}\sim {c_3}{x_3} \to {c_1}{x_1}\sim {c_3}{x_3}} \right).$
Then,
![]() ${T_L}$
is the following theory:
${T_L}$
is the following theory:
The intuitive interpretation of the same-place-as relation may already raise suspicions that the resulting theory is “substantivalist” in some sense. However, it is important to note that the theory
![]() ${T_L}$
satisfies the classical definition of a relationist theory, as laid out in Field (Reference Field1984, 33): the theory does not postulate space or spacetime points, except as logical constructions out of aggregates of matter. If the theory is to be ruled substantivalist rather than relationist, the debate must be redefined. We will return to this point in the conclusion.
${T_L}$
satisfies the classical definition of a relationist theory, as laid out in Field (Reference Field1984, 33): the theory does not postulate space or spacetime points, except as logical constructions out of aggregates of matter. If the theory is to be ruled substantivalist rather than relationist, the debate must be redefined. We will return to this point in the conclusion.
3. The translation from
 ${T_N}$
to
${T_N}$
to
 ${T_L}$
${T_L}$
Manders sets out a translation from the Newtonian, or geometric, language
![]() ${L_N}$
into the Leibnizian language
${L_N}$
into the Leibnizian language
![]() ${L_L}$
of point particles and their possible configurations. A translation or interpretation
${L_L}$
of point particles and their possible configurations. A translation or interpretation
![]() $f$
of
$f$
of
![]() ${T_N}$
into
${T_N}$
into
![]() ${T_L}$
is entirely determined by a specification of the translation of the atomic formulae of
${T_L}$
is entirely determined by a specification of the translation of the atomic formulae of
![]() ${L_N}$
. Let us begin with the identity relation. Because the same-place-as relation is an equivalence relation, we can identify spatial points with the equivalence classes of pairs
${L_N}$
. Let us begin with the identity relation. Because the same-place-as relation is an equivalence relation, we can identify spatial points with the equivalence classes of pairs
![]() $\left( {x,c} \right)$
of a particle and a configuration under the same-place-as relation. After all, a particle in a configuration does indicate a position in absolute space. This suggests that the translation
$\left( {x,c} \right)$
of a particle and a configuration under the same-place-as relation. After all, a particle in a configuration does indicate a position in absolute space. This suggests that the translation
![]() $f$
should map the identity between points (i.e., formulae such as
$f$
should map the identity between points (i.e., formulae such as
![]() ${v_i} = {v_j}$
) into the same-place-as relation
${v_i} = {v_j}$
) into the same-place-as relation
![]() $\sim $
:
Footnote 5
$\sim $
:
Footnote 5
Definition of f for the identity between points.
Equivalently, in a Morita extension
![]() ${L_{N{\rm{'}}}}$
of
${L_{N{\rm{'}}}}$
of
![]() ${L_N}$
, new variables for spatial points may be introduced as equivalence classes of pairs of point particles and configurations under the same-place-as relation
${L_N}$
, new variables for spatial points may be introduced as equivalence classes of pairs of point particles and configurations under the same-place-as relation
![]() $\sim $
.
$\sim $
.
There are two other atomic formulae of the substantivalist theory
![]() ${T_N}$
: the two geometrical primitives of betweenness and congruence. If
${T_N}$
: the two geometrical primitives of betweenness and congruence. If
![]() $\phi \left( {{v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}}} \right)$
is “Between
$\phi \left( {{v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}}} \right)$
is “Between
![]() ${v_{{j_1}}}{v_{{j_2}}}{v_{{j_3}}}$
,” then its translation
${v_{{j_1}}}{v_{{j_2}}}{v_{{j_3}}}$
,” then its translation
![]() $f\left( \phi \right)$
states that there is a configuration
$f\left( \phi \right)$
states that there is a configuration
![]() $c{\rm{'}}$
in which the three points
$c{\rm{'}}$
in which the three points
![]() ${v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}}$
are occupied by particles, and the three particles located at these points satisfy the betweenness predicate in
${v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}}$
are occupied by particles, and the three particles located at these points satisfy the betweenness predicate in
![]() $c{\rm{'}}$
.
$c{\rm{'}}$
.
Definition of f for the predicate of Betweenness.
Explanation: The formula says that a point
![]() ${v_{{j_2}}}$
is between two points
${v_{{j_2}}}$
is between two points
![]() ${v_{{j_1}}}$
and
${v_{{j_1}}}$
and
![]() ${v_{{j_3}}}$
if and only if (iff) there is a configuration
${v_{{j_3}}}$
if and only if (iff) there is a configuration
![]() $c{\rm{'}}$
and three particles
$c{\rm{'}}$
and three particles
![]() ${x_{1}\!\!{\rm{'}}},{x_{2}\!\!{\rm{'}}}$
, and
${x_{1}\!\!{\rm{'}}},{x_{2}\!\!{\rm{'}}}$
, and
![]() ${x_{3}\!\!{\rm{'}}}$
, such that (i)
${x_{3}\!\!{\rm{'}}}$
, such that (i)
![]() ${x_{2}\!\!{\rm{'}}}$
is between
${x_{2}\!\!{\rm{'}}}$
is between
![]() ${x_{1}\!\!{\rm{'}}}$
and
${x_{1}\!\!{\rm{'}}}$
and
![]() ${x_{3}\!\!{\rm{'}}}$
in
${x_{3}\!\!{\rm{'}}}$
in
![]() $c{\rm{'}}$
, and (ii) the pairs of particles and configurations that correspond to the points
$c{\rm{'}}$
, and (ii) the pairs of particles and configurations that correspond to the points
![]() ${v_{{j_1}}},{v_{{j_2}}}$
, and
${v_{{j_1}}},{v_{{j_2}}}$
, and
![]() ${v_{j3}}$
are the same points as—that is, they stand, respectively, in the same-place relation to—the pairs
${v_{j3}}$
are the same points as—that is, they stand, respectively, in the same-place relation to—the pairs
![]() $x{{\rm{'}}_1}c{\rm{'}}$
,
$x{{\rm{'}}_1}c{\rm{'}}$
,
![]() $x{{\rm{'}}_2}c{\rm{'}}$
, and
$x{{\rm{'}}_2}c{\rm{'}}$
, and
![]() $x{{\rm{'}}_3}c{\rm{'}}$
(see fig. 3).
$x{{\rm{'}}_3}c{\rm{'}}$
(see fig. 3).

Figure 3. Betweenness in
![]() ${T_L}$
.
${T_L}$
.
Congruence: The translation
![]() $f$
is defined in a similar way when
$f$
is defined in a similar way when
![]() $\left( {{v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}},{v_{{j_4}}}} \right)$
is “
$\left( {{v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}},{v_{{j_4}}}} \right)$
is “
![]() ${\rm{Congruence}}{v_{{j_1}}}{v_{{j_2}}}{v_{{j_3}}}{v_{{j_4}}}$
.” There is a configuration
${\rm{Congruence}}{v_{{j_1}}}{v_{{j_2}}}{v_{{j_3}}}{v_{{j_4}}}$
.” There is a configuration
![]() $c{\rm{'}}$
in which the four points
$c{\rm{'}}$
in which the four points
![]() ${v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}},{v_{{j_4}}}$
are occupied, and the four particles located at these points satisfy the congruence predicate in
${v_{{j_1}}},{v_{{j_2}}},{v_{{j_3}}},{v_{{j_4}}}$
are occupied, and the four particles located at these points satisfy the congruence predicate in
![]() $c{\rm{'}}$
.
$c{\rm{'}}$
.
Definition of f for the predicate of Congruence.
The translation is extended, in the usual way, to complex formulae:
Definition of f for complex formulae.
Manders has given us a conservative translation
![]() $f$
from
$f$
from
![]() ${T_N}$
into
${T_N}$
into
![]() ${T_L}$
. Trivially, for any formula
${T_L}$
. Trivially, for any formula
![]() $\phi $
of the language of
$\phi $
of the language of
![]() ${T_N}$
, if
${T_N}$
, if
![]() $\phi $
is a theorem of
$\phi $
is a theorem of
![]() ${T_N}$
, then
${T_N}$
, then
![]() $f\left( \phi \right)$
is a theorem of
$f\left( \phi \right)$
is a theorem of
![]() ${T_L}$
. However, he has not shown how to translate the formulae of
${T_L}$
. However, he has not shown how to translate the formulae of
![]() ${L_L}$
back into
${L_L}$
back into
![]() ${L_N}$
. In other words, he has not shown that
${L_N}$
. In other words, he has not shown that
![]() ${T_N}$
and
${T_N}$
and
![]() ${T_L}$
are in fact theoretically equivalent. It is not difficult to see that there is in fact no reverse translation
${T_L}$
are in fact theoretically equivalent. It is not difficult to see that there is in fact no reverse translation
![]() ${f^{ - 1}}$
from the language
${f^{ - 1}}$
from the language
![]() ${L_L}$
to the language
${L_L}$
to the language
![]() ${L_N}$
that maps theorems into theorems.
Footnote 6
The reason is that the function
${L_N}$
that maps theorems into theorems.
Footnote 6
The reason is that the function
![]() $f$
is not essentially surjective:
$f$
is not essentially surjective:
Definition 1 Let
![]() $f$
:
$f$
:
![]() $T \to T'$
be a translation between theories.
$T \to T'$
be a translation between theories.
![]() $f$
is essentially surjective iff for each sentence
$f$
is essentially surjective iff for each sentence
![]() $\psi $
of
$\psi $
of
![]() ${L_{T'}}$
, there is a sentence
${L_{T'}}$
, there is a sentence
![]() $\phi $
of
$\phi $
of
![]() ${L_T}$
such that
${L_T}$
such that
![]() $T' \vdash \psi \leftrightarrow f\left( \phi \right)$
(Halvorson Reference Halvorson2019, 120; Barrett and Halvorson Reference Barrett and Halvorson2022, 7).
$T' \vdash \psi \leftrightarrow f\left( \phi \right)$
(Halvorson Reference Halvorson2019, 120; Barrett and Halvorson Reference Barrett and Halvorson2022, 7).
![]() ${T_L}$
talks about point particles and configurations, whereas
${T_L}$
talks about point particles and configurations, whereas
![]() ${T_N}$
has no resources to talk about either point particles or their configurations.
${T_N}$
has no resources to talk about either point particles or their configurations.
![]() ${T_L}$
is designed to describe relative distances between physical bodies, whereas
${T_L}$
is designed to describe relative distances between physical bodies, whereas
![]() ${T_N}$
is a purely geometrical theory and lacks any physical content. We can sketch a rigorous argument to see that
${T_N}$
is a purely geometrical theory and lacks any physical content. We can sketch a rigorous argument to see that
![]() $f$
is not essentially surjective and therefore that there cannot be such a reverse translation from
$f$
is not essentially surjective and therefore that there cannot be such a reverse translation from
![]() ${T_L}$
into
${T_L}$
into
![]() ${T_N}$
. This follows from the fact that
${T_N}$
. This follows from the fact that
![]() ${T_N}$
is complete but
${T_N}$
is complete but
![]() ${T_L}$
is incomplete.
Footnote 7
We will from now on omit the essentially identical arguments for extensions of these theories.
${T_L}$
is incomplete.
Footnote 7
We will from now on omit the essentially identical arguments for extensions of these theories.
Lemma 1 The Leibnizian theory
![]() ${T_{L}}$
is incomplete.
${T_{L}}$
is incomplete.
Proof. We show that there is a formula
![]() $\phi $
of the language of
$\phi $
of the language of
![]() ${T_L}$
and two models
${T_L}$
and two models
![]() $M$
and
$M$
and
![]() $M{\rm{'}}$
of
$M{\rm{'}}$
of
![]() ${T_L}$
such that
${T_L}$
such that
![]() $\phi $
is true in
$\phi $
is true in
![]() $M{\rm{'}}$
and
$M{\rm{'}}$
and
![]() $\neg \phi $
is true in
$\neg \phi $
is true in
![]() $M{\rm{''}}$
. The particles of
$M{\rm{''}}$
. The particles of
![]() $M$
consist of the set
$M$
consist of the set
![]() $\left\{ 1 \right\}$
. The particles of
$\left\{ 1 \right\}$
. The particles of
![]() $M{\rm{''}}$
consist of the set
$M{\rm{''}}$
consist of the set
![]() $\left\{ {1,2} \right\}$
. We take the configurations to be the functions from particles to
$\left\{ {1,2} \right\}$
. We take the configurations to be the functions from particles to
![]() ${\mathbb{R}^3}$
. The interpretations of the geometrical and same-place relations of
${\mathbb{R}^3}$
. The interpretations of the geometrical and same-place relations of
![]() ${T_L}$
are the obvious ones. We easily verify that the axioms of
${T_L}$
are the obvious ones. We easily verify that the axioms of
![]() ${T_L}$
hold in both
${T_L}$
hold in both
![]() $M$
and
$M$
and
![]() $M{\rm{'}}$
. Let
$M{\rm{'}}$
. Let
![]() $\phi $
be the formula that says “there is exactly one particle.”
$\phi $
be the formula that says “there is exactly one particle.”
![]() $\phi $
is true in
$\phi $
is true in
![]() $M$
, but it is false in
$M$
, but it is false in
![]() $M{\rm{'}}$
.
$M{\rm{'}}$
.
Proposition 1 The translation
![]() ${{f}}$
is not essentially surjective.
${{f}}$
is not essentially surjective.
Proof.
![]() ${T_N}$
is complete (see Schwabhäuser et al. Reference Schwabhäuser, Szmielew and Tarski1983, 218 ff.). Because
${T_N}$
is complete (see Schwabhäuser et al. Reference Schwabhäuser, Szmielew and Tarski1983, 218 ff.). Because
![]() ${T_L}$
is incomplete, take a sentence
${T_L}$
is incomplete, take a sentence
![]() $\psi $
that
$\psi $
that
![]() ${T_L}$
does not decide. Assume that
${T_L}$
does not decide. Assume that
![]() $f$
is essentially surjective so that there is a formula
$f$
is essentially surjective so that there is a formula
![]() $\phi $
of
$\phi $
of
![]() ${L_T}$
such that
${L_T}$
such that
![]() ${T_L} \vdash \psi \leftrightarrow f\left( \phi \right)$
. By completeness, either
${T_L} \vdash \psi \leftrightarrow f\left( \phi \right)$
. By completeness, either
![]() ${T_N} \vdash \phi $
, or
${T_N} \vdash \phi $
, or
![]() ${T_N} \vdash \neg \phi $
. Therefore, by definition of
${T_N} \vdash \neg \phi $
. Therefore, by definition of
![]() ${T_L}$
and
${T_L}$
and
![]() $f$
, either
$f$
, either
![]() ${T_L} \vdash f\left( \phi \right)$
, or
${T_L} \vdash f\left( \phi \right)$
, or
![]() $T{\rm{'}} \vdash \neg f\left( \phi \right)$
. By logic and the assumption, either
$T{\rm{'}} \vdash \neg f\left( \phi \right)$
. By logic and the assumption, either
![]() $T{\rm{'}} \vdash \psi $
, or
$T{\rm{'}} \vdash \psi $
, or
![]() $T{\rm{'}} \vdash \neg \psi $
. Contradiction.
$T{\rm{'}} \vdash \neg \psi $
. Contradiction.
□
Let us now state what we mean when we say that
![]() $g$
is an inverse to
$g$
is an inverse to
![]() $f$
:
$f$
:
Definition 2 If
![]() $f:T \to T'$
is a translation and
$f:T \to T'$
is a translation and
![]() $g:T' \to T$
is a translation, then
$g:T' \to T$
is a translation, then
![]() $g$
is an inverse of
$g$
is an inverse of
![]() $f$
iff for every closed formula
$f$
iff for every closed formula
![]() $\phi $
of
$\phi $
of
![]() ${L_T}$
and for every closed formula of
${L_T}$
and for every closed formula of
![]() ${L_{T'}}$
we have that
${L_{T'}}$
we have that
![]() $T \vdash \phi \leftrightarrow g\left( {f\left( \phi \right)} \right)$
and
$T \vdash \phi \leftrightarrow g\left( {f\left( \phi \right)} \right)$
and
![]() $T' \vdash \psi \leftrightarrow f\left( {g\left( \psi \right)} \right)$
.
$T' \vdash \psi \leftrightarrow f\left( {g\left( \psi \right)} \right)$
.
Corollary 1 There is no translation
![]() ${f^{ - 1}}$
that is an inverse to
${f^{ - 1}}$
that is an inverse to
![]() ${{f}}$
from the language of
${{f}}$
from the language of
![]() ${T_L}$
to the language of
${T_L}$
to the language of
![]() ${T_N}$
that preserves logical form and such that theorems of
${T_N}$
that preserves logical form and such that theorems of
![]() ${{{T}}_{{L}}}$
are mapped to theorems of
${{{T}}_{{L}}}$
are mapped to theorems of
![]() ${T_N}$
.
${T_N}$
.
Proof. Assume an inverse
![]() ${f^{ - 1}}$
exists. Let
${f^{ - 1}}$
exists. Let
![]() $\psi $
be a formula. Then
$\psi $
be a formula. Then
![]() ${T_L} \vdash f({f^{ - 1}}\left( {f\left( \psi \right)} \right) \leftrightarrow \psi $
. Therefore,
${T_L} \vdash f({f^{ - 1}}\left( {f\left( \psi \right)} \right) \leftrightarrow \psi $
. Therefore,
![]() $f$
is essentially surjective. Contradiction.
$f$
is essentially surjective. Contradiction.
4. Conclusion
In this last part of the article, we will argue that the theory
![]() ${T_L}$
is a worse theory than
${T_L}$
is a worse theory than
![]() ${T_N}$
and therefore ought to have been rejected in favor of substantivalism, even if classical mechanics had turned out to be empirically adequate.
${T_N}$
and therefore ought to have been rejected in favor of substantivalism, even if classical mechanics had turned out to be empirically adequate.
Because the only other modal relationist approach that is known to us—namely, the theory based on transworld congruence—is incapable of defining rotation and acceleration, this result casts doubt on modal relationism in general.
We will argue that
![]() ${T_L}$
is inferior on the grounds of parsimony. We have in mind a principle of theory choice like the following:
${T_L}$
is inferior on the grounds of parsimony. We have in mind a principle of theory choice like the following:
Structural parsimony. All other things equal, we should prefer theories that posit less structure (Barrett Reference Barrett2022, 296).
This principle explains, for instance, the fact that relativistic electrodynamics is better than Lorentz’s electrodynamics that posits the luminiferous aether, or an undetectable foliation of spacetime (Bradley Reference Bradley2021, 1055). Intuitively, a theory is more parsimonious than another if everything in the first theory is definable in the less parsimonious theory, but not the other way around (Barrett Reference Barrett2022, 307). The counting of structure at play has been rationally reconstructed in terms of category theory (Barrett Reference Barrett2022, 305), but this is equivalent to a condition in terms of translations (Barrett Reference Barrett2022, 310):
Equal structure. A theory
![]() $T$
posits the same amount of structure as a theory
$T$
posits the same amount of structure as a theory
![]() $T'$
iff there is an essentially surjective translation
$T'$
iff there is an essentially surjective translation
![]() $g:T \mapsto T'$
.
$g:T \mapsto T'$
.
This principle deals only with the case in which the two theories posit the same amount of structure. What we need is a similar criterion for when the structure posited by one theory is a proper part of the structure posited by the other. In such a situation, it is natural to assume that there is a translation
![]() $f:T \mapsto T{\rm{'}}$
, but there is no essentially surjective translation. This is equivalent to the following condition (by lemma 1 in Barrett and Halvorson [Reference Barrett and Halvorson2022, 8]):
$f:T \mapsto T{\rm{'}}$
, but there is no essentially surjective translation. This is equivalent to the following condition (by lemma 1 in Barrett and Halvorson [Reference Barrett and Halvorson2022, 8]):
Less structure. A theory
![]() $T$
posits less structure than a theory
$T$
posits less structure than a theory
![]() $T'$
iff there is an interpretation
$T'$
iff there is an interpretation
![]() $f:T \mapsto T'$
but there is no interpretation
$f:T \mapsto T'$
but there is no interpretation
![]() $g:T' \mapsto T$
.
Footnote 8
$g:T' \mapsto T$
.
Footnote 8
We will also assume this syntactical structure-counting criterion for many-sorted theories and employ generalized translations as well.
Barrett (Reference Barrett2023) has applied his parsimony principle to choose between nominalistic and Platonistic physical theories. He analyzes the requirement of Putnam (Reference Putnam1971) that a nominalistic physical theory must interpret standard Platonistic theories. He rejects it as unreasonable because it commits the nominalist to just as much structure as the Platonist. We will return to this point shortly.
The principle similarly indicts the theory
![]() ${T_L}$
of (Manders Reference Manders1982).
${T_L}$
of (Manders Reference Manders1982).
![]() ${T_L}$
posits more structure without any compensating explanatory gain, and therefore there is no reason to prefer it to the substantivalist theory
${T_L}$
posits more structure without any compensating explanatory gain, and therefore there is no reason to prefer it to the substantivalist theory
![]() ${T_N}$
.
${T_N}$
.
The relationist may insist that “not all else is equal,” but it is unclear what compensating advantages
![]() ${T_L}$
in Manders (Reference Manders1982) could have. The syntactical complexity of its axioms is clearly similar to that of the theory
${T_L}$
in Manders (Reference Manders1982) could have. The syntactical complexity of its axioms is clearly similar to that of the theory
![]() ${T_N}$
. The translation
${T_N}$
. The translation
![]() $f$
preserves logical structure. Manders (Reference Manders1982, 576) says that modal theories have a prima facie epistemological advantage. But it is unclear why because in order to code the physics, we need to add a functor
$f$
preserves logical structure. Manders (Reference Manders1982, 576) says that modal theories have a prima facie epistemological advantage. But it is unclear why because in order to code the physics, we need to add a functor
![]() $a\left( t \right)$
for the actual configuration at a time. We can then translate statements such as “the sun is at absolute rest” and “the sun is moving at 17,000 km/h” in the relationist language, and the translations will be similarly underdetermined by the evidence. Even if we adopt a Galilean invariant primitive of collinearity on an inertial line, for example, we will be left with what Dasgupta (Reference Dasgupta2015, 620–21) calls self-locational uncertainty and inexpressible ignorance about which of the infinitely many isometric configurations is the actual one. Finally, the complexity introduced by the possible ways of locating particles in space (Belot Reference Belot2000, 576) is matched by the redundancy in distinct configurations with the same particles and the same relative distances (see fig. 1).
$a\left( t \right)$
for the actual configuration at a time. We can then translate statements such as “the sun is at absolute rest” and “the sun is moving at 17,000 km/h” in the relationist language, and the translations will be similarly underdetermined by the evidence. Even if we adopt a Galilean invariant primitive of collinearity on an inertial line, for example, we will be left with what Dasgupta (Reference Dasgupta2015, 620–21) calls self-locational uncertainty and inexpressible ignorance about which of the infinitely many isometric configurations is the actual one. Finally, the complexity introduced by the possible ways of locating particles in space (Belot Reference Belot2000, 576) is matched by the redundancy in distinct configurations with the same particles and the same relative distances (see fig. 1).
The requirement of Putnam (Reference Putnam1971) that a nominalistic theory must translate a Platonistic theory has its relationist counterpart in the methodology of Belot (Reference Belot2011, 35–37), which requires a relationist theory to give truth conditions to all the geometric statements that its substantivalist counterpart can express. Is this requirement of interpreting the substantivalist theory reasonable or not?
The matter is partly a verbal dispute about the definition of relationism. It seems to us that there are two varieties of relationism. The first can be called eliminativism, and it simply denies the existence of space and time. In this view, the only entities that exist are material objects, and spacetime is banished from the ontology, together with the aether, quintessence, caloric, ghosts, and the like.
The second variety can be called reductive relationism, and it admits the existence of a substantial spacetime but treats it as ontologically derivative from matter. In this view, facts about spacetime regions are grounded on facts about material objects. Hartry Field (Reference Field1984) suggests that the relationist may view spacetime regions as logical constructions out of matter. A materialist might think in the same way that mental states are grounded on physical brain states. If one has this second view, then it makes sense to ask for a relational truthmaker for all or at least many basic facts about space or spacetime.
Gordon Belot (Reference Belot2011, appendix A; Reference Belot2012, 81) calls the first variety of relationism antirealism and reserves the term relationism for what we call reductive relationism. In this context, it makes sense to ask for a translation function
![]() $f$
from the standard formulation of mechanics into a reformulation that only quantifies over material objects. The goal is not to provide a rival theory but a more metaphysically perspicuous formulation of the same theory.
$f$
from the standard formulation of mechanics into a reformulation that only quantifies over material objects. The goal is not to provide a rival theory but a more metaphysically perspicuous formulation of the same theory.
However, none of these considerations saves the theory of Manders (Reference Manders1982) or modal relationism. If one wants to pursue the second strategy, one has to provide a theory that is genuinely equivalent to the standard version. The novel presentation should be a description of the same facts but show how some of them reduce to facts of a simpler sort. It should not introduce additional structure or posit additional facts. In other words, there should be a reverse translation
![]() ${f^{ - 1}}$
from modal relationist facts to substantival facts. This is precisely what we have shown to fail in the case of the theory
${f^{ - 1}}$
from modal relationist facts to substantival facts. This is precisely what we have shown to fail in the case of the theory
![]() ${T_L}$
of Manders (Reference Manders1982). Therefore, it does not matter whether one is an eliminativist or a reductionist relationist. Modal relationism is not the way to go.
${T_L}$
of Manders (Reference Manders1982). Therefore, it does not matter whether one is an eliminativist or a reductionist relationist. Modal relationism is not the way to go.
Acknowledgments
We would like to thank the audience of the Eidos Seminar, the audience of the Symmetry Group Seminar, and three anonymous referees for helpful comments.