1 Introduction
The present study is part of a broad effort at Princeton University to investigate the behaviour of hypersonic turbulent boundary layers, including the effects of roughness and transpiration. Previous experiments at Princeton have investigated some aspects of such high Mach number flows using the same experimental facility employed in the current study. Baumgartner (Reference Baumgartner1997) explored the mean flow properties of a Mach 7.5 boundary layer at near-adiabatic conditions, and Etz (Reference Etz1998) followed this work with measurements in a Mach 7.2 flow with a cooled wall.
Here, we report particle image velocimetry (PIV) and filtered Rayleigh scattering (FRS) measurements of a smooth, flat-plate, turbulent boundary layer with a free stream Mach number
$Ma=7.5$
, similar to that studied by Baumgartner (Reference Baumgartner1997). Of principal interest is the scaling of the turbulence statistics, and determination of the effects of Mach number.
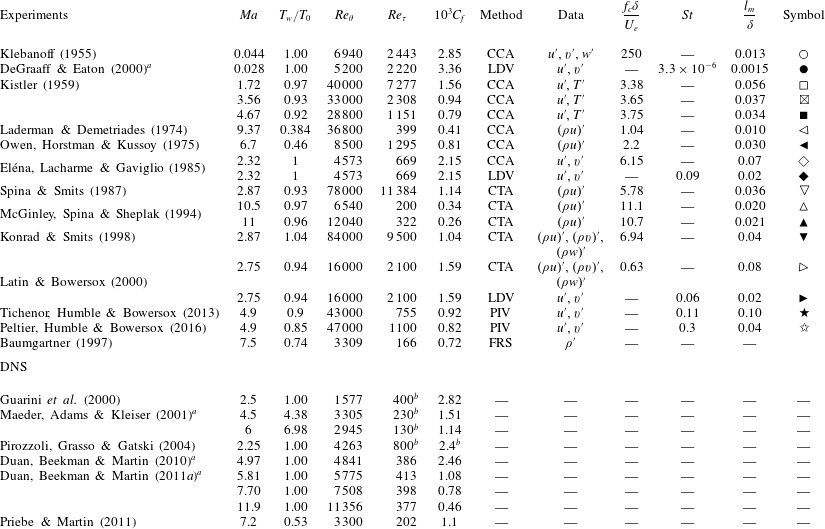
For the flow over a smooth wall with zero pressure gradient, previous experiments on hypersonic boundary layers have documented the general features of the mean flow, but even for this restricted case only a limited number of studies have reported turbulence measurements (see, for example, the review by Roy & Blottner Reference Roy and Blottner2006). A non-exclusive list of these experiments in high Mach number flows is given in table 1, together with some representative studies at lower Mach numbers. The subsonic case reported by Klebanoff (Reference Klebanoff1955) is included primarily because it has been widely used as a reference case, especially in the high-speed community. A number of direct numerical simulations (DNS) are also available for such flows, a subset of which are also shown in table 1 with an emphasis on higher Mach numbers. In this table,
$u^{\prime }$
,
$v^{\prime }$
and
$w^{\prime }$
are the velocity fluctuations in the streamwise, wall-normal and spanwise directions, respectively, and
$(\unicode[STIX]{x1D70C}u)^{\prime }$
,
$(\unicode[STIX]{x1D70C}v)^{\prime }$
and
$(\unicode[STIX]{x1D70C}w)^{\prime }$
are the corresponding mass-flux fluctuations. All other symbols are defined in the caption.
Table 1. Comparison database of high-speed turbulent boundary layer profiles. Here,
$Ma$
is the free stream Mach number,
$T_{w}$
and
$T_{0}$
are the wall and stagnation temperatures, respectively,
$Re_{\unicode[STIX]{x1D703}}$
(
$=U_{e}\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}_{e}$
) is the Reynolds number based on momentum thickness
$\unicode[STIX]{x1D703}$
,
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}_{w}$
,
$C_{f}$
(
$=\unicode[STIX]{x1D70F}_{w}/(\unicode[STIX]{x1D70C}_{e}U_{e}^{2}/2)$
) is the skin friction coefficient,
$\unicode[STIX]{x1D70F}_{w}$
is the wall shear stress, and
$\unicode[STIX]{x1D708}_{e}$
,
$\unicode[STIX]{x1D70C}_{e}$
and
$U_{e}$
are the free stream kinematic viscosity, density and velocity, respectively. Also,
$f_{c}$
is the hot-wire cutoff frequency,
$l_{m}$
is the size of the measurement sensor (wire length, streamwise dimension of LDV measurement volume, or PIV cross-correlation window size), and
$\unicode[STIX]{x1D6FF}$
is the boundary layer thickness as defined in each study. The particle Stokes number,
$St=U_{e}/(10\unicode[STIX]{x1D6FF}f_{p})$
, is defined using the particle frequency response,
$f_{p}$
. For Kistler (Reference Kistler1959), in the absence of other data,
$l_{m}$
was assumed to be the standard length, that is, 1 mm. CCA is constant current anemometry, CTA is constant temperature anemometry, LDV is laser-Doppler velocimetry, PIV is particle image velocimetry and FRS is filtered Rayleigh scattering.
a Only selected cases shown.
b Estimated value.
As to the scaling of the mean velocity, van Driest (Reference van Driest1951, Reference van Driest1956) derived a temperature–velocity relationship from the mean energy equation to define a transformed velocity
$U_{VD}$
that takes account of the fluid property variations across the layer. Here,
$$\begin{eqnarray}U_{VD}=\int _{U_{1}}^{U}\sqrt{\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{w}}}\,\text{d}U,\end{eqnarray}$$
where
$U$
is the mean streamwise component of velocity, and the suffix 1 denotes a location at the lower end of the validity range of the log law, which in inner scaling is given by
$$\begin{eqnarray}\frac{U_{VD}}{u_{\unicode[STIX]{x1D70F}}}=\frac{1}{\unicode[STIX]{x1D705}}\ln \frac{yu_{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D708}_{w}}+B.\end{eqnarray}$$
Here
$\unicode[STIX]{x1D705}$
and
$B$
are the usual von Kármán and additive constants, the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
is given by
$\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}_{w}}$
, and the viscous length scale is
$\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}$
, where
$\unicode[STIX]{x1D70C}_{w}$
and
$\unicode[STIX]{x1D708}_{w}$
are the density and kinematic viscosity evaluated at the wall temperature, respectively. While it is common for many studies to integrate this transformation from the wall, choosing a lower integration limit within the log layer acknowledges that the transformation is not expected to be valid in the near-wall viscous region (Smits & Dussauge Reference Smits and Dussauge2005).
According to Bushnell et al. (Reference Bushnell, Johnson, Harvey and Feller1969), the van Driest transformation appears to collapse zero pressure gradient turbulent boundary layer data at Mach numbers up to 12, and the constants in the logarithmic law appear unchanged from their subsonic values. The more detailed assessment of compressible turbulent boundary layer data by Fernholz & Finley (Reference Fernholz and Finley1976) confirmed this conclusion for flows up to a Mach number of 10, at least to the accuracy of the available data. That is, the transformed profile, when scaled with the friction velocity and the viscous length scale, appears to follow closely the incompressible behaviour. The intercept of the log law is now known to be sensitive to the level of wall-heat flux when integrating the van Driest transformation from the wall, and extensions have been proposed to account for this dependence using a semi-local wall-normal coordinate (Patel, Boersma & Pecnik Reference Patel, Boersma and Pecnik2016; Trettel & Larsson Reference Trettel and Larsson2016). These transformations have yet to be tested at hypersonic Mach numbers, however, and are difficult to apply to experimental data because the density and viscosity must both be known accurately throughout the near-wall buffer region. As a result, the van Driest transformation remains the most general transformation with which to compare compressible mean velocity profiles. For the datasets listed in table 1, all the mean velocity profiles follow this van Driest scaling, including the McGinley et al. (Reference McGinley, Spina and Sheplak1994) data taken in helium at a Mach number of 11.
The scaling with respect to the turbulence behaviour is not so clear. In subsonic flows, it is generally assumed that the turbulence in the near-wall region scales with the friction velocity and the viscous length scale (see, for example, Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015), and that the turbulence in the outer region scales with
$u_{\unicode[STIX]{x1D70F}}$
and the boundary layer thickness
$\unicode[STIX]{x1D6FF}$
. For high-speed flows, Morkovin (Reference Morkovin and Favre1961) proposed that the correct velocity scale for the turbulence ought to be the density-weighted velocity scale
$u_{\ast }=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}=u_{\unicode[STIX]{x1D70F}}\sqrt{\unicode[STIX]{x1D70C}_{w}/\unicode[STIX]{x1D70C}}$
, so that the scaling is applied to the turbulent stresses rather than the velocity variances. Morkovin showed that this scaling collapsed the streamwise turbulence intensity in the outer layer for Mach numbers up to 4.76, using the data of Kistler (Reference Kistler1959). As we shall see, however, the Kistler experiment had some shortcomings that cloud its use as a reference case.
For higher Mach numbers, no conclusive comparison with experiments has been possible, primarily because the existing data show very significant scatter. This scatter provides an important motivation for our study, which aims to examine the experimental support for Morkovin’s hypothesis. More broadly, we are interested in examining the structure of the hypersonic boundary layer, and determining the role of Mach number. Before we report our experimental results, we need to examine the available data, summarized in table 1, more closely.
2 Assessment of existing data
For the majority of the experiments listed in table 1 the turbulent fluctuations were measured using hot-wire anemometry. In compressible flows, hot-wires measure a combination of the fluctuating mass flux and the fluctuating total temperature (Smits, Hayakawa & Muck Reference Smits, Hayakawa and Muck1983). For example, a single normal wire is sensitive to the streamwise mass-flux fluctuation
$(\unicode[STIX]{x1D70C}u)^{\prime }$
and the total temperature fluctuation
$T_{0}^{\prime }$
, and to deduce, for instance, the root-mean-square (r.m.s.) streamwise velocity fluctuation
$\tilde{u} =\sqrt{\overline{{u^{\prime }}^{2}}}$
, it is necessary to either obtain data using a number of different overheat ratios (Kovasznay’s fluctuation diagram), or assume that the strong Reynolds analogy (SRA) holds. One form of the SRA states that the streamwise velocity fluctuations
$u^{\prime }$
and the temperature fluctuations
$T^{\prime }$
are related according to
$$\begin{eqnarray}\frac{\tilde{T}}{T}=\frac{\unicode[STIX]{x1D6FE}-1}{2}Ma^{2}\,\frac{\tilde{u} }{U},\end{eqnarray}$$
and
$$\begin{eqnarray}R_{uT}=-0.8,\end{eqnarray}$$
where
$R_{uT}$
is the correlation coefficient between
$u^{\prime }$
and
$T^{\prime }$
,
$\unicode[STIX]{x1D6FE}$
is the ratio of specific heats,
$\tilde{T}=\sqrt{\overline{{T^{\prime }}^{2}}}$
is the r.m.s. temperature fluctuation, and
$T$
is the local mean temperature (Smits & Dussauge Reference Smits and Dussauge2005). The SRA has been shown to hold for boundary layers at supersonic Mach numbers but its accuracy at Mach numbers greater than 5 has not been established unequivocally (see Guarini et al.
Reference Guarini, Moser, Shariff and Wray2000; Duan et al.
Reference Duan, Beekman and Martin2010). When using the fluctuation diagram or the SRA, it is also necessary to assume that the pressure fluctuations are small compared to the temperature and velocity fluctuations. Most of the experiments in table 1 used constant current anemometry (CCA) over a range of overheats to deduce
$\tilde{u}$
and
$\tilde{T}$
. The experiments by Konrad & Smits (Reference Konrad and Smits1998) used instead constant temperature anemometry (CTA) at a single, high overheat ratio and assumed that the SRA applied. The experiments by McGinley et al. (Reference McGinley, Spina and Sheplak1994) used CTA at a high overheat ratio, but only
$(\unicode[STIX]{x1D70C}u)^{\prime }$
values were reported. Values of
$\tilde{u}$
were therefore estimated using the SRA, allowing
$u_{\ast }^{+}=\tilde{u} /u_{\ast }$
to also be found. The relation of Walz (Reference Walz1969) was adopted to estimate the mean density profile in cases where this was not explicitly provided by the authors. Throughout this paper, the viscosity is calculated using the method of Keyes (Reference Keyes1951), as recommended by Roy & Blottner (Reference Roy and Blottner2006).
A limited number of more recent datasets employed PIV or laser Doppler velocimetry (LDV) to obtain direct measurements of velocity fluctuations up to Mach 5. These techniques circumvent the uncertainties associated with the mixed mode sensitivity of hot-wires, but come with their own experimental difficulties, which are addressed below.
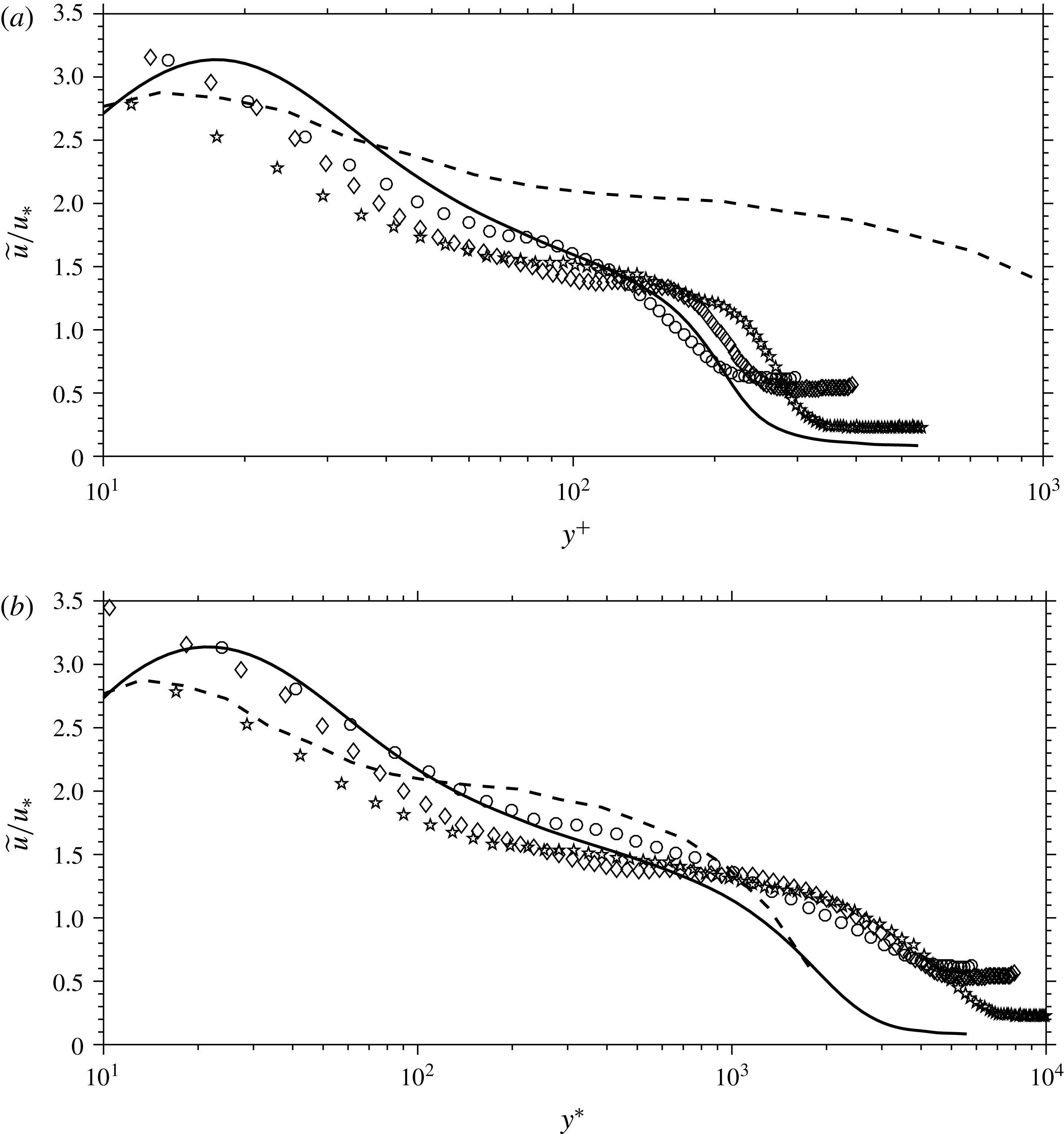
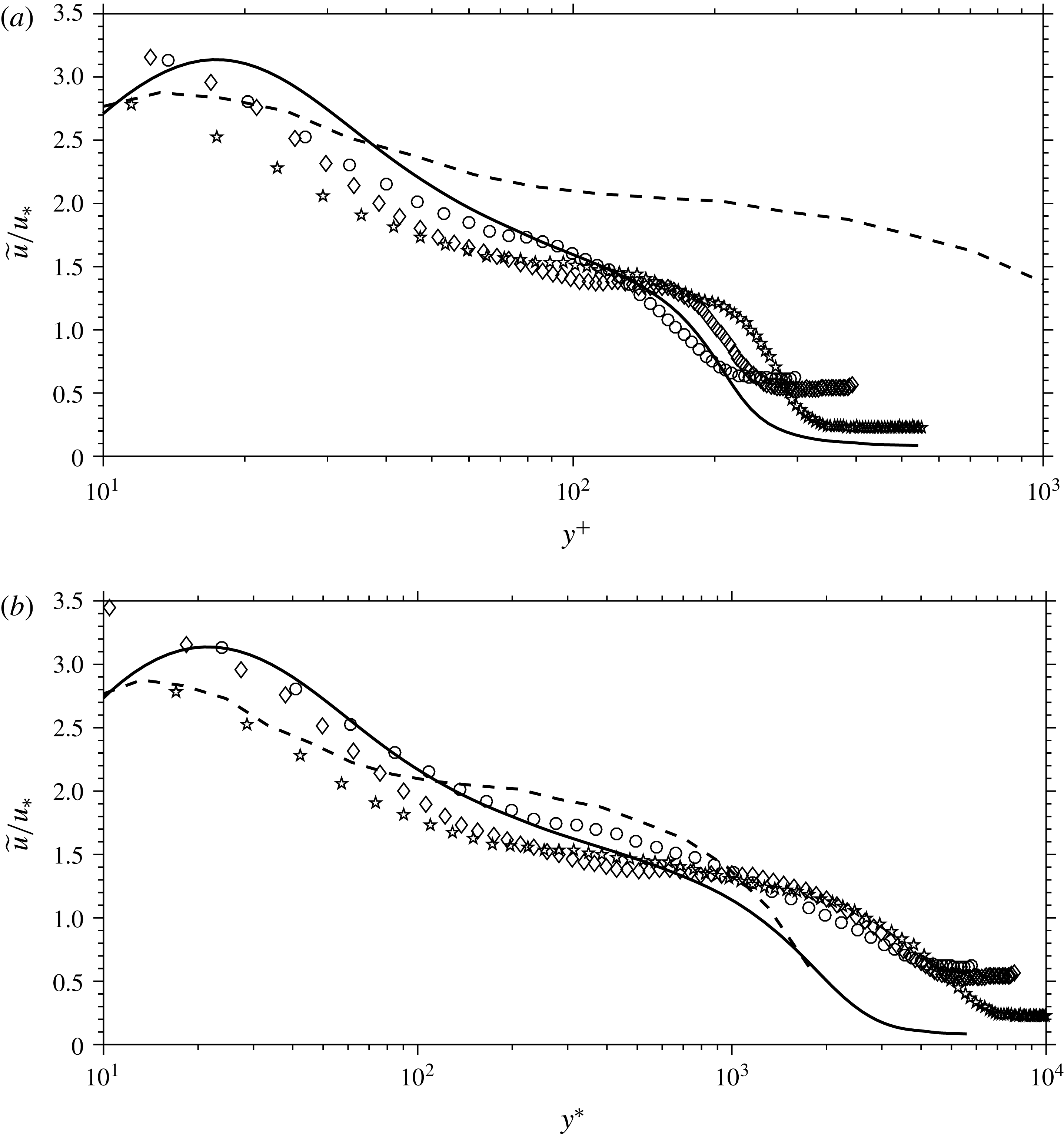
The streamwise fluctuation data from the experiments listed in table 1 are shown in figure 1 in conventional outer scaling (that is, scaling with
$u_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D6FF}$
), and in Morkovin scaling (that is, scaling with
$u_{\ast }$
and
$\unicode[STIX]{x1D6FF}$
). We will not use inner scaling because the data near the wall (if they exist) are almost always unreliable for a variety of reasons. While the collapse is slightly better using Morkovin scaling, the data are very far from demonstrating self-similarity. Even accounting for the different definitions of the boundary layer thickness employed by different authors, there is no discernible trend with increasing Mach number. Focussing on the Morkovin-scaled data, the lowest fluctuation levels are shown by the Laderman & Demetriades (Reference Laderman and Demetriades1974), Owen et al. (Reference Owen, Horstman and Kussoy1975) and McGinley et al. (Reference McGinley, Spina and Sheplak1994) data at Mach numbers of 6.7, 9.4 and 11, respectively. For the first two cases the wall was cooled, but even if these datasets were put aside, the experiments show great scatter and cannot be said to support Morkovin’s hypothesis with any degree of certainty. The particle-based measurements correspond more closely to the incompressible data in this scaling, but only two cases, obtained in the same facility, have a Mach number above 3, limiting our ability to draw firm conclusions about Mach number trends. It is not obvious whether the lack of collapse evident in figure 1 is due to measurement difficulties at high Mach numbers, shortcomings in the data analysis (such as the use of the SRA), or whether it reveals new flow physics associated with high Mach number turbulence. In that respect, DNS results may prove to be crucial, although experimental confirmation would certainly be desirable.
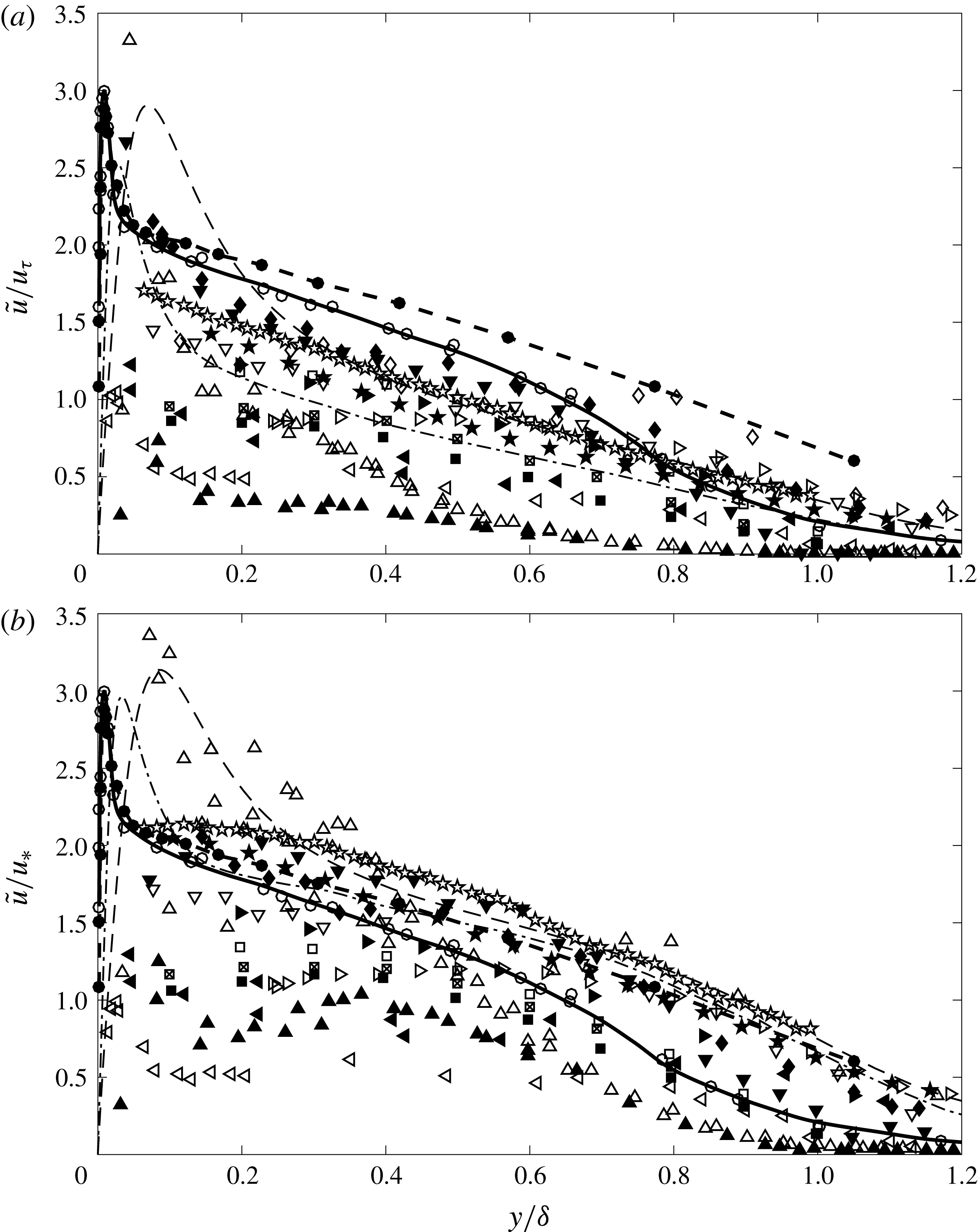
Figure 1. Streamwise turbulence intensities in (a) classical outer scaling and (b) transformed according to Morkovin. ——, ○ Klebanoff (Reference Klebanoff1955), -- – –, ● DeGraaff & Eaton (Reference DeGraaff and Eaton2000),
$Ma=0$
, – – –, Priebe & Martin (Reference Priebe and Martin2011),
$Ma=7.2$
, – - – - – Duan et al. (Reference Duan, Beekman and Martin2011a
) at
$Ma=7.7$
; other symbols as in table 1. Mach numbers range up to 11.
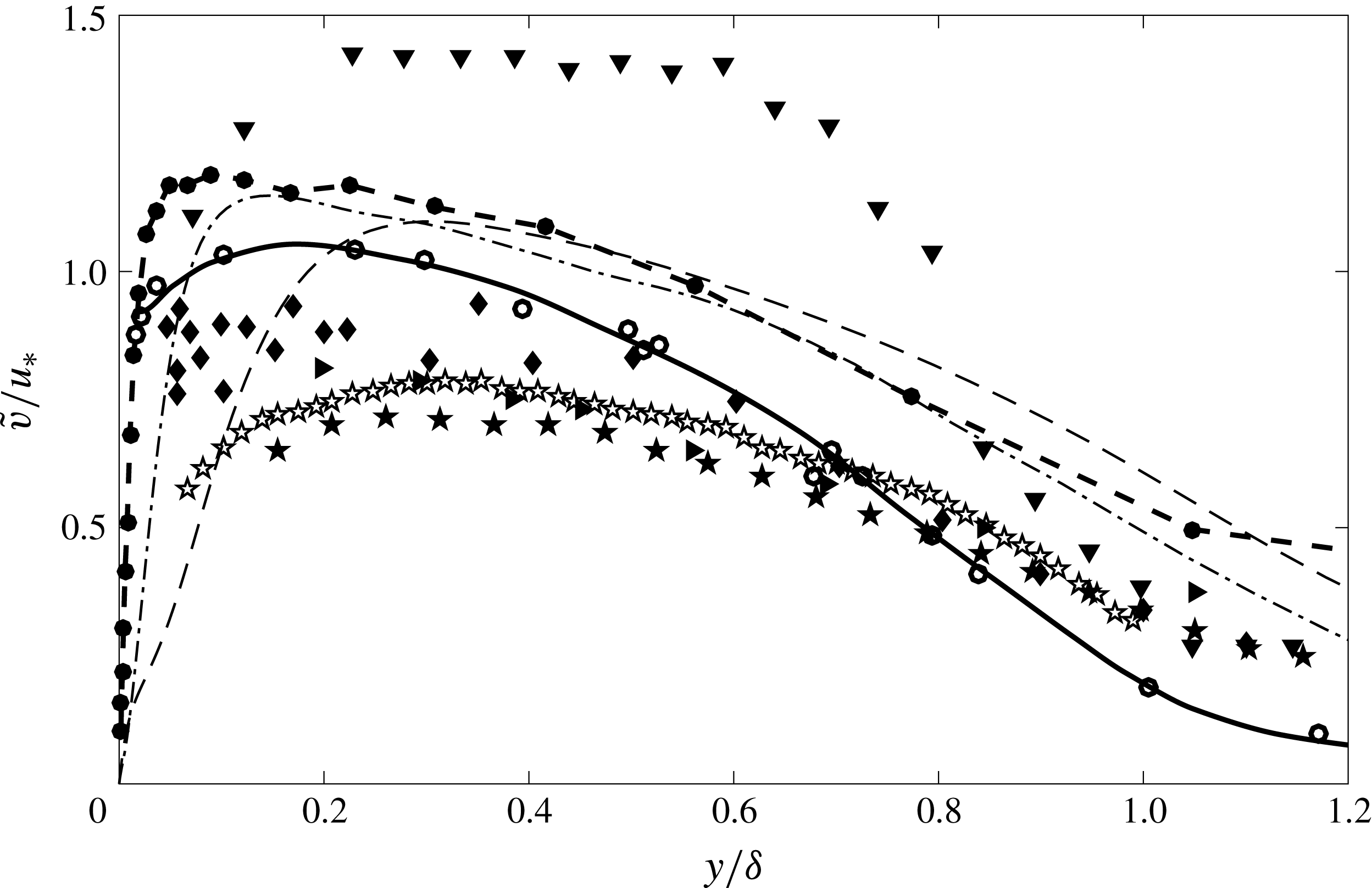
Figure 2. Wall-normal turbulence intensities in Morkovin scaling. ——, ○ Klebanoff (Reference Klebanoff1955), -- – –, ● DeGraaff & Eaton (Reference DeGraaff and Eaton2000),
$Ma=0$
, – – –, Priebe & Martin (Reference Priebe and Martin2011),
$Ma=7.2$
, – - – - – Duan et al. (Reference Duan, Beekman and Martin2011a
) at
$Ma=7.7$
; other symbols as in table 1. Mach numbers of experimental data are less than 5.
Figure 2 shows available experimental wall-normal fluctuation data in Morkovin scaling. The majority of the results were obtained using particle-based techniques such as LDV and PIV. The highest Mach number data available are from the studies by Tichenor et al. (Reference Tichenor, Humble and Bowersox2013) and Peltier et al. (Reference Peltier, Humble and Bowersox2016) at Mach 4.9, taken in the same facility. Again, the scatter is such that little can be said of Morkovin’s hypothesis with any degree of confidence, with much of the experimental data below the incompressible profiles and DNS simulations. It is apparent, however, that the measured wall-normal turbulence seems to reduce with increasing Mach number, especially in the lower half of the boundary layer. While this may be physical, it is thought to be more likely due to increasingly stringent particle frequency response requirements for the measurement of turbulence at high Mach number (Williams et al. Reference Williams, Nguyen, Schreyer and Smits2015).
We now examine the quality of the data more closely, beginning with those studies that employed hot-wires, which comprise the largest proportion of cases, especially at higher Mach numbers. McGinley et al. (Reference McGinley, Spina and Sheplak1994) reviewed the previous attempts to measure turbulent fluctuations using hot-wire anemometry in high Mach number flows, and made the observation that much of this work suffered from poor frequency response and/or suspect calibrations. To assess the frequency response, we use a criterion based on outer scaling, that is, the value of
$f_{c}\unicode[STIX]{x1D6FF}/U_{e}$
, where
$f_{c}$
is the system frequency response. Kistler (Reference Kistler1959) suggested that to measure
$\tilde{u}$
to better than 5 % accuracy,
$f_{c}\unicode[STIX]{x1D6FF}/U_{e}$
needed to be greater than 5. This criterion, however, ignores the Reynolds number and Mach number dependence of the frequency content, as well as variations with distance from the wall. In addition, as noted by Gaviglio, Anguillet & Eléna (Reference Gaviglio, Anguillet and Eléna1981), even if this criterion is satisfied, the bandwidth required for measuring the wall-normal component is greater because the
$v^{\prime }$
-spectrum is broader than the
$u^{\prime }$
-spectrum.
This criterion may be examined in more detail using the model spectra developed for subsonic flow by Smits (Reference Smits, Deville, Lê and Sagaut2009). The estimates for the ratio of the measured value of
$\tilde{u}$
(
$=\tilde{u} _{m}$
) to the actual value
$\tilde{u} _{0}$
are given in table 2 for two wall distances and one Reynolds number, along with the corresponding estimates for the wall-normal component,
$\tilde{v}_{m}/\tilde{v}_{0}$
. If we ignore Mach number effects, we see that the 5 % criterion suggested by Kistler will hold near the middle of the layer for
$\tilde{u}$
, but it fails closer to the wall, and it does not represent the accuracy of the
$\tilde{v}$
measurement well. When we compare these estimates for the effect of limited frequency response with the experiments in table 1 we see that the Kistler (Reference Kistler1959), Laderman & Demetriades (Reference Laderman and Demetriades1974) and Owen et al. (Reference Owen, Horstman and Kussoy1975) data for
$\tilde{u}$
are probably too low near
$y/\unicode[STIX]{x1D6FF}=0.5$
by about 12 %, 18 % and 25 %, respectively. Nevertheless, these possible errors do not explain the large scatter seen in figures 1 and 2.
Table 2. Estimated effect of anemometer frequency response on measurements of
$\tilde{u}$
and
$\tilde{v}$
. Based on subsonic spectral model by Smits (Reference Smits, Deville, Lê and Sagaut2009) at
$Re_{\unicode[STIX]{x1D70F}}=3300$
.
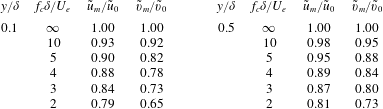
What about the effects of inadequate spatial resolution? To examine this aspect, we use the spatial filtering correlation suggested for subsonic turbulent boundary layers by Smits et al. (Reference Smits, Monty, Hultmark, Bailey, Hutchins and Marusic2011). The results for some representative wire lengths
$l_{m}$
and wall distances are given in table 3. When we compare these estimates for the effects due to spatial filtering with the experiments in table 1, we see that only the Laderman & Demetriades (Reference Laderman and Demetriades1974) and McGinley et al. (Reference McGinley, Spina and Sheplak1994)
$\tilde{u}$
data have less than 10 % error. According to these estimates, the Kistler (Reference Kistler1959) Mach 1.72 and the Eléna et al. (Reference Eléna, Lacharme, Gaviglio, Dybb and Pfund1985) datasets appear to have errors due to spatial filtering as high as 25 % on
$\tilde{u}$
in the middle of the boundary layer. The errors in the Kistler data are of particular concern because it was this dataset that was used by Morkovin to validate his scaling proposal. In the case of the Élena data, however, the measurements were repeated using laser-Doppler velocimetry, showing excellent agreement with the hot-wire results. This is somewhat surprising given the relatively poor spatial resolution of the hot-wire probes.
For particle-based techniques such as LDV and PIV, accurate measurements require that the particle response time scale
$\unicode[STIX]{x1D70F}_{p}$
is much less than the time scale of the energy-containing eddies
$\unicode[STIX]{x1D70F}_{f}$
. That is, we require
$St=\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{f}\ll 1$
. Samimy & Lele (Reference Samimy and Lele1991) used
$\unicode[STIX]{x1D70F}_{f}=10\unicode[STIX]{x1D6FF}/U_{e}$
, and concluded that for particles to faithfully follow such large scales the Stokes number should not exceed 0.1. In table 1, we show Stokes numbers for each of the particle-based measurements as they were given, or from estimates made using stated particle sizes. Four of the studies have Stokes numbers close to the limit suggested by Samimy & Lele.
As with hot-wire-based techniques, particle response limitations will have a greater influence on measurements of the wall-normal component than the streamwise component. In addition, Williams et al. (Reference Williams, Nguyen, Schreyer and Smits2015) showed that it was more difficult to obtain a satisfactory particle response at higher Mach numbers due to the low density of the flow. Hence, the effects of particle lag are most likely to be observed for the higher Mach number datasets and in measurements of the wall-normal component. Indeed, the two particle-based studies at Mach 4.9 display the lowest Morkovin-scaled wall-normal turbulence near the wall, possibly indicating that particle response adversely influenced these measurements. However, the streamwise velocity data for all particle-based studies lie close to the incompressible curves in Morkovin scaling, which suggests that the particle response in these cases was still adequate for the streamwise component.
Table 3. Effect of spatial filtering on measurements of
$\tilde{u}$
. Based on subsonic spatial filter model by Smits et al. (Reference Smits, Monty, Hultmark, Bailey, Hutchins and Marusic2011).
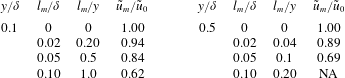
We see that the existing data are either of insufficient quality, or they do not cover a sufficient Mach number range to establish the validity of Morkovin scaling at high Mach number. In addition, the datasets are a mix of mass-weighted and velocity-based statistics that are inherently difficult to compare on a common basis. Hence, new experiments were performed at Mach 7.5 on a flat-plate model under near-adiabatic conditions (
$T_{w}/T_{r}\approx 0.8$
). Since hot-wire anemometry is clearly bedevilled by experimental difficulties at such a Mach number, PIV was used to measure the mean and turbulent velocities. As a complement to the PIV measurements, filtered Rayleigh scattering was used to visualize the instantaneous density field, and provide additional information on the outer layer instantaneous boundary layer structure. The measurements in this study cover a range of relatively low Reynolds numbers (
$3600\leqslant Re_{\unicode[STIX]{x1D703}}\leqslant 9340$
,
$180\leqslant Re_{\unicode[STIX]{x1D70F}}\leqslant 279$
) so that the flow is amenable to DNS.
We have already discussed particle frequency response as a potential limitation of PIV, especially at high Mach numbers. In this respect, recent work by Williams et al. (Reference Williams, Nguyen, Schreyer and Smits2015) used a combination of experiments and simulations to demonstrate a method to more accurately determine particle response variation across the boundary layer. In addition, for accurate PIV measurements the effects of spatial resolution, dynamic range, and high shear on PIV cross-correlation routines have also been considered (Williams Reference Williams2014). This experience will be used to improve the accuracy of the current study and to assess the overall error of the resulting measurements.
Finally, it is well known that transition and tripping become more difficult at higher Mach numbers. Larger tripping devices are needed, raising concerns that the resulting boundary layer statistics and structure may be influenced by these upstream effects. Williams & Smits (Reference Williams and Smits2017) recently conducted a parametric study of the effects of tripping on the mean velocity and streamwise turbulence profiles of the boundary layer that is the subject of the current study. It was demonstrated that the wake component of the mean velocity profile,
$\unicode[STIX]{x0394}U_{VD}^{+}$
, is a sensitive measure of under- or over-tripping. When correctly tripped, it was shown that the wake size follows the expected Reynolds number variation established by Coles (Reference Coles1962) for incompressible flow, when using the Reynolds number,
$Re_{\unicode[STIX]{x1D6FF}_{2}}=\unicode[STIX]{x1D70C}_{e}U_{e}\unicode[STIX]{x1D703}/\unicode[STIX]{x1D707}_{w}$
. With this knowledge, it has been possible to ensure that the current results are free from tripping effects with a high level of confidence.
3 Description of the experiment
The experiments were conducted in the low enthalpy Mach 8 Hypersonic Boundary Layer Facility at the Princeton Gas Dynamics Laboratory. Air was used as the working fluid. Baumgartner (Reference Baumgartner1997), Magruder (Reference Magruder1997) and Etz (Reference Etz1998) found that when the working section is empty, the Mach number is
$8.0\pm 0.1$
over the central 80 % of the cross-sectional area. With the flat-plate model in the tunnel, the free stream Mach number at the location of the measurement is approximately 7.5. The operating conditions for the current experiments are summarized in table 4. The Mach number was slightly higher in later experiments due to efforts to reduce downstream disturbances and improve ejector function, as described by Williams (Reference Williams2014), which otherwise did not change the flow. Under these conditions, air is expected to behave as a perfect gas.
The test section is made up of two 914 mm long, 229 mm inside-diameter stainless steel sections. One section is fitted with four orthogonal window cavities. The cavities are 127 mm
$\times$
206 mm rectangular sections, beginning 89 mm from the start of the section. The windows are recessed 38 mm from the wall of the test section. The flat-plate model is mounted on the centreline of the test section on a support that is fastened to a stainless steel plate that bolts to the side window cavity. The support has a diamond-shaped cross-section to minimize flow blockage. The mount was fixed to the plate at an approximately identical streamwise location in all cases, relative to the trailing edge of the plate. The windows are 225 mm
$\times$
137 mm
$\times$
12.7 mm in dimension and made of quartz. They are mounted into stainless steel window plates that fit over their respective window cavities. In previous experiments within this facility, the window cavities were found to cause disturbances that were detrimental to the starting of the tunnel (Etz Reference Etz1998). Inserts (see figure 3) that match the curvature of the inner tunnel wall were used to lessen this disturbance, leaving only small cutouts sufficient for optical access. The overall tunnel design is described in more detail by Baumgartner (Reference Baumgartner1997).
Table 4. Flow conditions and test plate geometry. Plate dimensions
$x_{tr}$
,
$x_{m}$
and
$x_{p}$
are defined as in figure 4. Uncertainty in other quantities represent variation during measurement acquisition. Mach numbers are accurate to within 0.1.
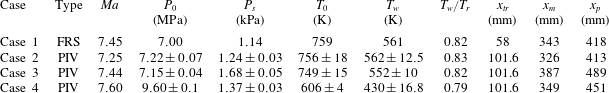
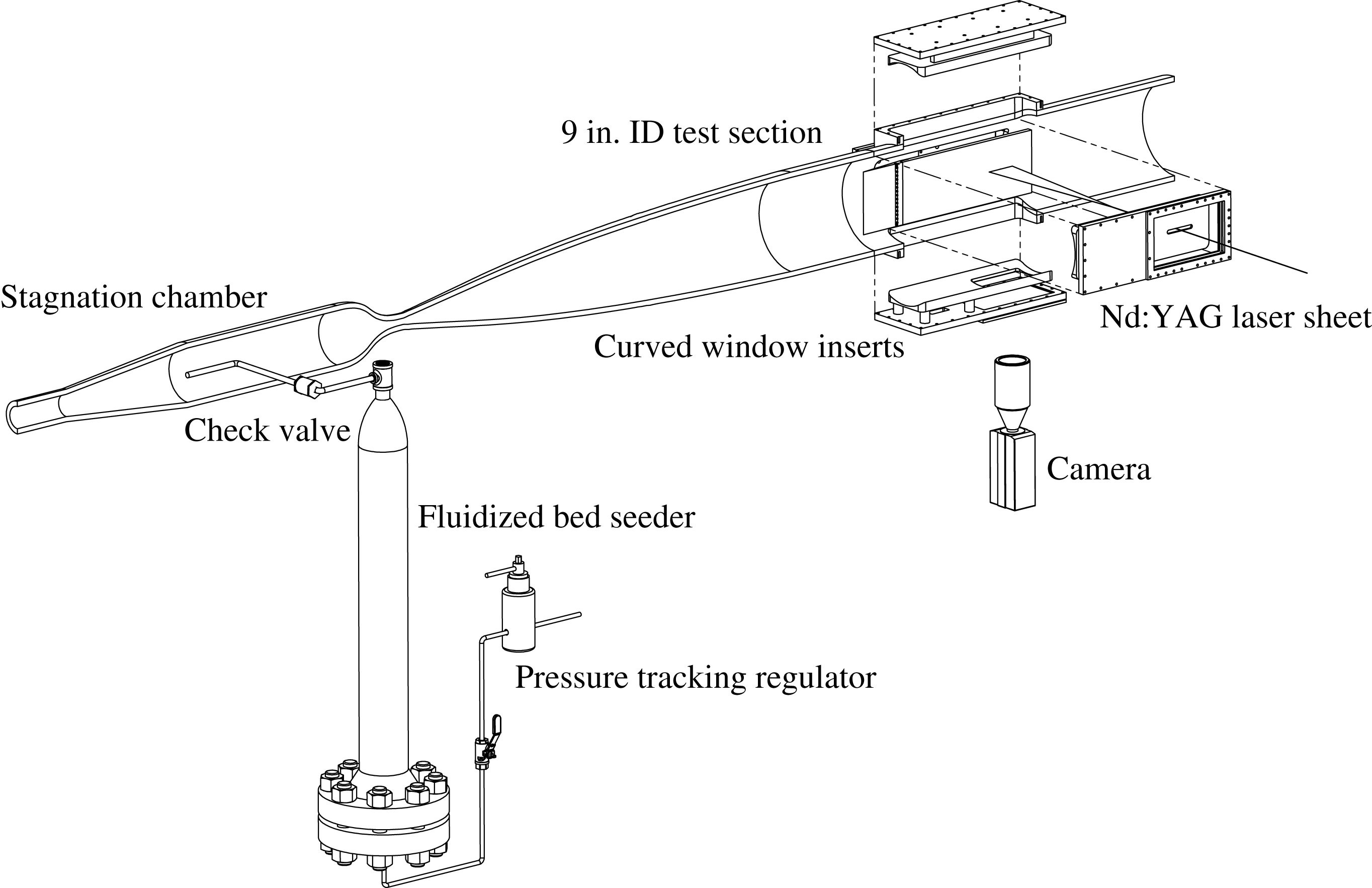
Figure 3. Schematic of the Mach 8 wind tunnel, PIV and seeding apparatus.
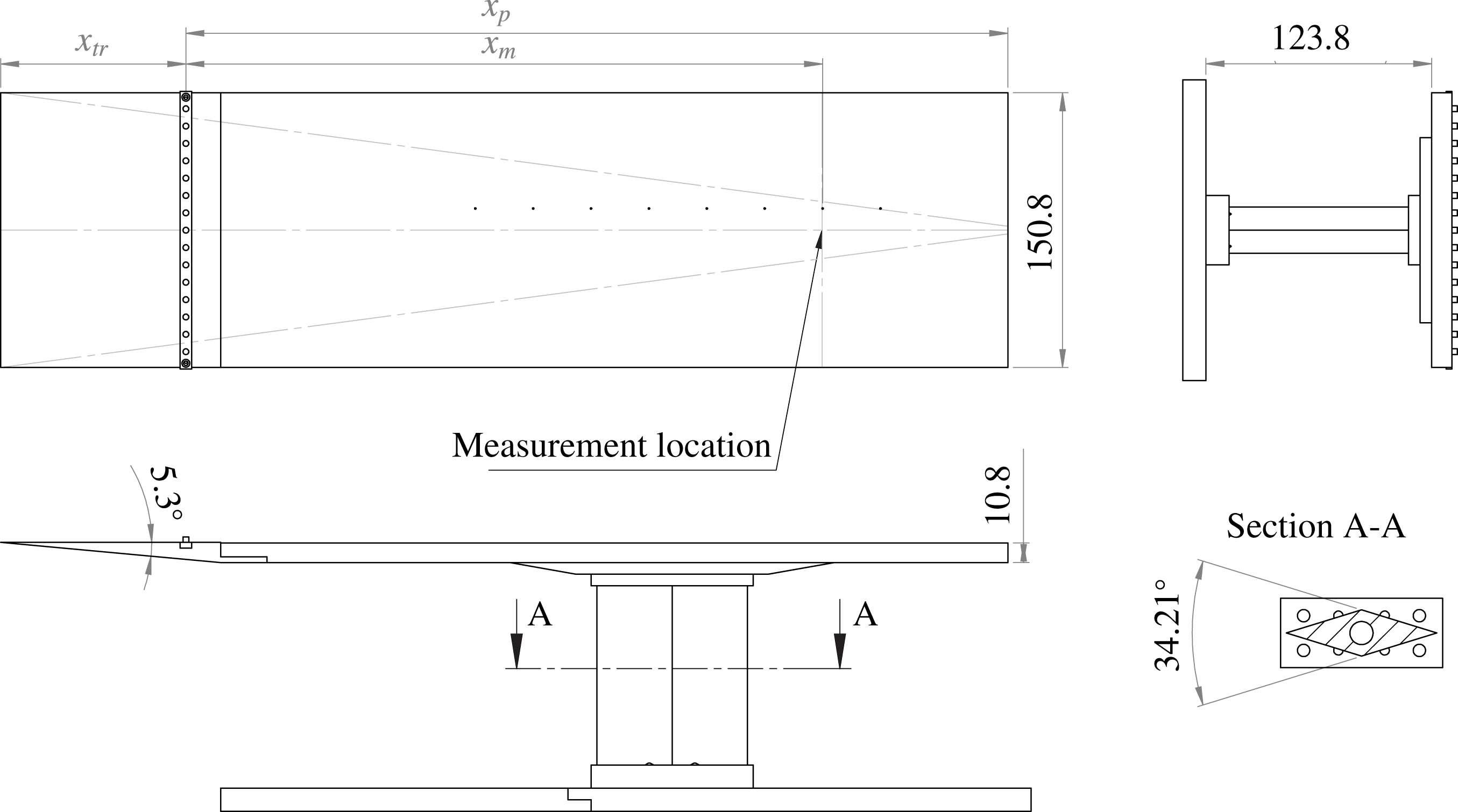
Figure 4. Geometry of test plate. The laminar, pre-trip distance, plate length and post-trip development length varied between cases as summarized in table 4. Mach lines originating from the corners of the leading edge are shown for Case 4. Dimensions in mm.
Four cases were studied: Case 1 employed filtered Rayleigh scattering for flow visualization, while PIV was used for Cases 2–4. All data were acquired on a brass flat-plate model that was 151 mm wide and 10.8 mm thick with a sharp leading edge (see figure 4). The r.m.s. surface roughness
$k$
of the model was estimated by Baumgartner (Reference Baumgartner1997) to be
${\leqslant}2~\unicode[STIX]{x03BC}\text{m}$
. Hence,
$ku_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}_{w}\leqslant 0.10$
and the plate was assumed to be smooth.
The pre- and post-trip development lengths (see table 4) and methods of tripping varied between the different cases. For Case 1, the boundary layer was tripped using a two-dimensional circular rod of 2.4 mm diameter which spanned the plate and was placed 58.4 mm from the leading edge. This case corresponds to Case III as described by Baumgartner (Reference Baumgartner1997). The remaining cases were tripped 101.6 mm from the leading edge using a three-dimensional trip consisting of cylindrical posts, each with a diameter of 3.2 mm, a height of 2.75 mm and spaced 7.2 mm apart. Measurements were acquired in line with one of the tripping posts. This trip was found by Williams & Smits (Reference Williams and Smits2017) to provide a fast transition to turbulent flow without overstimulating the layer, as measured by the development of the wake strength of the van Driest transformed mean velocity profile,
$\unicode[STIX]{x0394}U_{VD}^{+}$
. Case 4 of the current study was also considered by Williams & Smits (Reference Williams and Smits2017). As will be demonstrated in § 5,
$\unicode[STIX]{x0394}U_{VD}^{+}$
for each case lies close to the curve proposed by Coles (Reference Coles1962) for properly tripped boundary layers (at the corresponding value of
$Re_{\unicode[STIX]{x1D6FF}2}$
). We believe, therefore, that all four cases are free from transition/tripping effects and are thus differentiated only by Reynolds number and measurement considerations (such as resolution and dynamic range).
Edge effects and potential streamwise pressure gradients were also examined by Williams & Smits (Reference Williams and Smits2017). Edge effects originate close to the corners of the leading edge and propagate toward the centreline at approximately the Mach angle (Auvity, Etz & Smits Reference Auvity, Etz and Smits2001), as depicted in figure 4. Case 4 is the most stringent in this regard as this had the longest development length, but even then the measurement location was free from edge effects by this estimate. The Clauser (Reference Clauser1954) equilibrium pressure gradient parameter was found to be
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FF}_{k}^{\ast }/\unicode[STIX]{x1D70F}_{w})/(\text{d}p/\text{d}x)<0.05$
in initial tests, based on the incompressible version of the displacement thickness
$\unicode[STIX]{x1D6FF}_{k}^{\ast }$
. Streamwise pressure gradients are therefore considered to be negligible for all cases considered here.
Surface temperature (
$T_{w}$
) and wall static pressure (
$p_{w}$
) measurements were made at the streamwise locations,
$x_{m}$
, given in table 4. The thermocouple was affixed to a pocket on the underside of the plate on the centreline, within 1.6 mm (
$1/16$
in.) of the test surface. The static pressure tap was on the centreline for Cases 1 and 2 but offset in the spanwise direction by 3.6 mm for Cases 3 and 4. For the wall temperature measurements, a K-type thermocouple was used, and the pressure was measured using an Omegadyne PX309-005A5V, 0–0.34 bar transducer, accurate to 0.25 % of full scale. The settling chamber stagnation temperature
$T_{0}$
and the stagnation pressure
$p_{0}$
were measured with a K-type thermocouple and an Omega Engineering 0–137.9 bar pressure transducer, respectively. The stagnation pressure transducer has a relative uncertainty of 1 %. For all thermocouples, calibrated digital panel meters with an output of
$1~\text{mV}~\text{C}^{-1}$
. were used. Pressure and temperature data were digitized via a National Instruments data acquisition card controlled by LabVIEW software. Tunnel pressures and temperatures were continuously acquired and the values shown in table 4 are averages for the duration of the data acquisition. The bounds indicate the variation through the run, resulting from changes in tank supply pressure, heater temperature and heat transfer to the wall. The free stream Mach number is accurate to within
$0.1$
, based on the accuracies of the two pressure transducers.
The plate was heated prior to startup to help mitigate wall temperature changes during the run. The wall is considered isothermal due to the high thermal conductivity of its brass construction and this pre-heating process. For Cases 1–3, this was achieved by allowing stagnation air to flow through the heater and test section until the plate temperature reached
$523\,^{\circ }\text{K}$
(
$250\,^{\circ }\text{C}$
). For Case 4, resistive heating tape was used to pre-heat the wall to a temperature of
$373\,^{\circ }\text{K}$
(
$100\,^{\circ }\text{C}$
). This change was made to improve the repeatability in the location of the transition on the plate, as noted by Williams & Smits (Reference Williams and Smits2017), by more consistently fixing the location of the tunnel nozzle boundary layer transition.
3.1 Filtered Rayleigh scattering
The instantaneous boundary layer density field was visualized using filtered Rayleigh scattering (FRS). In FRS, a molecular filter is used to interrogate the Rayleigh signal, and by sweeping the laser over a range of frequencies it is possible to obtain, in a given plane, the flow velocity, density and temperature (Miles, Forkey & Lempert Reference Miles, Forkey and Lempert1992). For flow visualization it has the attractive feature of allowing background suppression by using a molecular filter to eliminate the signal from the stationary wall which has zero Doppler shift (Smith, Smits & Miles Reference Smith, Smits and Miles1989; Forkey et al.
Reference Forkey, Lempert, Bogdonoff and Miles1994). To enhance the Rayleigh signal in the low density flows studied here, liquid
$\text{CO}_{2}$
was injected into the tunnel air supply just downstream of the control valve (and upstream of the heater coil). For the data presented here, the mass flow of
$\text{CO}_{2}$
was
$0.03~\text{kg}~\text{s}^{-1}$
, or approximately 1 % of the mass flow of air. As the flow expands in the nozzle, the
$\text{CO}_{2}$
condenses and precipitates as sub-micron-sized particulates uniformly distributed throughout the free stream (Poggie et al.
Reference Poggie, Erbland, Smits and Miles2004). This provides a strong scattering signal when interrogated with a laser, where the intensity is related to the particle density. The
$\text{CO}_{2}$
clusters vaporize in the high temperature regions of the boundary layer near the wall, but they provide a strong signal in the outer part of the layer that can be used to study the turbulent structure. The laser was a Continuum Q-switched, injection-seeded, frequency-doubled Nd-YAG pulsed laser with pulse energies in the 300 mJ range. The laser could be tuned to frequencies from 520 nm to 550 nm, enabling the use of an iodine filter to eliminate the non-Doppler-shifted signal scattered from the wall. A survey of the boundary layer with the same quantity of
$\text{CO}_{2}$
injection used in the current study showed that the introduction of
$\text{CO}_{2}$
into the supply streams had no discernible effect on the mean velocity profile. More details are given by Smith & Smits (Reference Smith and Smits1995), Baumgartner (Reference Baumgartner1997) and Miles, Lempert & Forkey (Reference Miles, Lempert and Forkey2001).
Table 5. Comparison of PIV set-up parameters. Here,
$r^{+}$
is the spatial resolution of the measurement, in wall units, taking into account the windowing functions employed in DaVis. Also, % Cut. refers to the maximum number of missing vectors in any resulting vector field. All vector fields with a greater percentage of missing vectors were discarded.
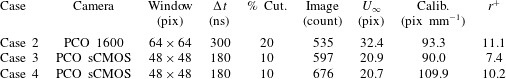
3.2 Particle image velocimetry
Measurements of the streamwise and wall-normal velocity components were obtained using planar, two-component, single-camera PIV, as shown in figure 3. The measurement parameters for each case can be found in table 5.
Case 2 employed a PCO 1600 camera (1600
$\times$
1200 pixels) with a Nikon 105 mm Macro lens and a
$2\times$
teleconverter resulting in a field of view of
$16\times 16~\text{mm}^{2}$
. An interframe time of 300 ns was used for this case. Cases 3 and 4 employed a PCO sCMOS camera that had higher resolution (2600
$\times$
2200 pixels) and a shorter interframe time of 180 ns. A Canon 200 mm Macro lens was used with this camera, resulting in a field of view of approximately
$20\times 22~\text{mm}^{2}$
. Each camera was operated at the fastest interframe time possible. For all cases, a New Wave Gemini PIV dual pulse ND:YAG laser system was used as the laser source. Each laser delivered approximately 100 mJ per pulse at a wavelength of 532 nm. The laser pulse width was 3–5 ns, with a jitter of
$\pm 0.5~\text{ns}$
. The lasers were operated at maximum power and a beam splitter was used to control their intensity to limit any potential bias error caused by differences in timing between triggering and emission of light by the Q-switch of the two lasers that would otherwise result from subtle differences in power settings (Bardet, André & Neal Reference Bardet, André and Neal2013). The resulting error in pulse separation was estimated to be less than 3 ns for this laser (Williams Reference Williams2014).
The flow was seeded using
$\text{TiO}_{2}$
particles (KRONOS 3333) in the stagnation chamber, upstream of the nozzle throat (see figure 3). A sieve was first used to break up the larger clumps that were greater than approximately 1 mm in size, and then the particles were dried in an oven to remove moisture. The particles were then suspended in a fluidized bed where high pressure air was fed from below (typically 11 bar above the tunnel stagnation pressure). The air flow entrained the particles, which then passed into the settling chamber of the tunnel through a 12.7 mm tube on the centreline. For Cases 2 and 3 this tube faced downstream, with its exit 450 mm from the nozzle throat. A mild improvement to seeding uniformity was achieved for Case 4 by turning this pipe to face upstream. The end of the tube was approximately 900 mm upstream of the nozzle throat in this case. Further details are given by Williams (Reference Williams2014).
The particle response was determined by Williams et al. (Reference Williams, Nguyen, Schreyer and Smits2015) by examining their motion as they passed through two shock waves of different strengths, corresponding to
$10^{\circ }$
and
$20^{\circ }$
turning at Mach 7.6. The frequency responses were found to be 36 and 77.2 kHz for the
$10^{\circ }$
and
$20^{\circ }$
cases, respectively. The particle trajectories were then simulated by solving the quasi-steady drag equation, using the formulation of Loth (Reference Loth2008) to account for changes in drag coefficient due to the finite Reynolds, Mach and Knudsen numbers on the flow around individual particles. By iteratively matching simulated particle response profiles to their measured counterparts the particle size and density were determined to be
$1.95~\unicode[STIX]{x03BC}\text{m}$
and
$950~\text{kg}~\text{m}^{-3}$
. The density is lower than that of pure
$\text{TiO}_{2}$
as the measured particles are an agglomeration of smaller primary crystals, leaving voids.
As noted by Williams et al. (Reference Williams, Nguyen, Schreyer and Smits2015), the particle frequency response depends on the perturbation strength, and thus the response to small disturbances, typical of turbulence, is much slower than the response to a shock wave. Such effects are rarely accounted for in previous high Mach number turbulence measurements but are essential to properly estimate particle response. The variation in Stokes number across the boundary layer was thus estimated for a small velocity disturbance
$({<}5\,\%U_{\infty })$
, accounting for changes in density and viscosity across the layer and assuming
$\unicode[STIX]{x1D70F}_{f}=10\unicode[STIX]{x1D6FF}/U_{\infty }$
. For the current study,
$\unicode[STIX]{x1D6FF}$
is defined as the 99 % thickness of the mean velocity profile. As shown in figure 5, the Stokes numbers are largest near to the wall due to the low densities in this region. The Stokes numbers are of order one in all three cases and thus some level of filtering appears inevitable. An estimate taken from Samimy & Lele (Reference Samimy and Lele1991) suggests that slip velocities could be upwards of 10 % of the local instantaneous velocity as a result. Nevertheless, Williams et al. (Reference Williams, Nguyen, Schreyer and Smits2015) indicated that particle frequency response limitations appear to have little effect on measurements of the streamwise turbulence under similar conditions as in the present experiments, while remaining likely to influence the wall-normal component.
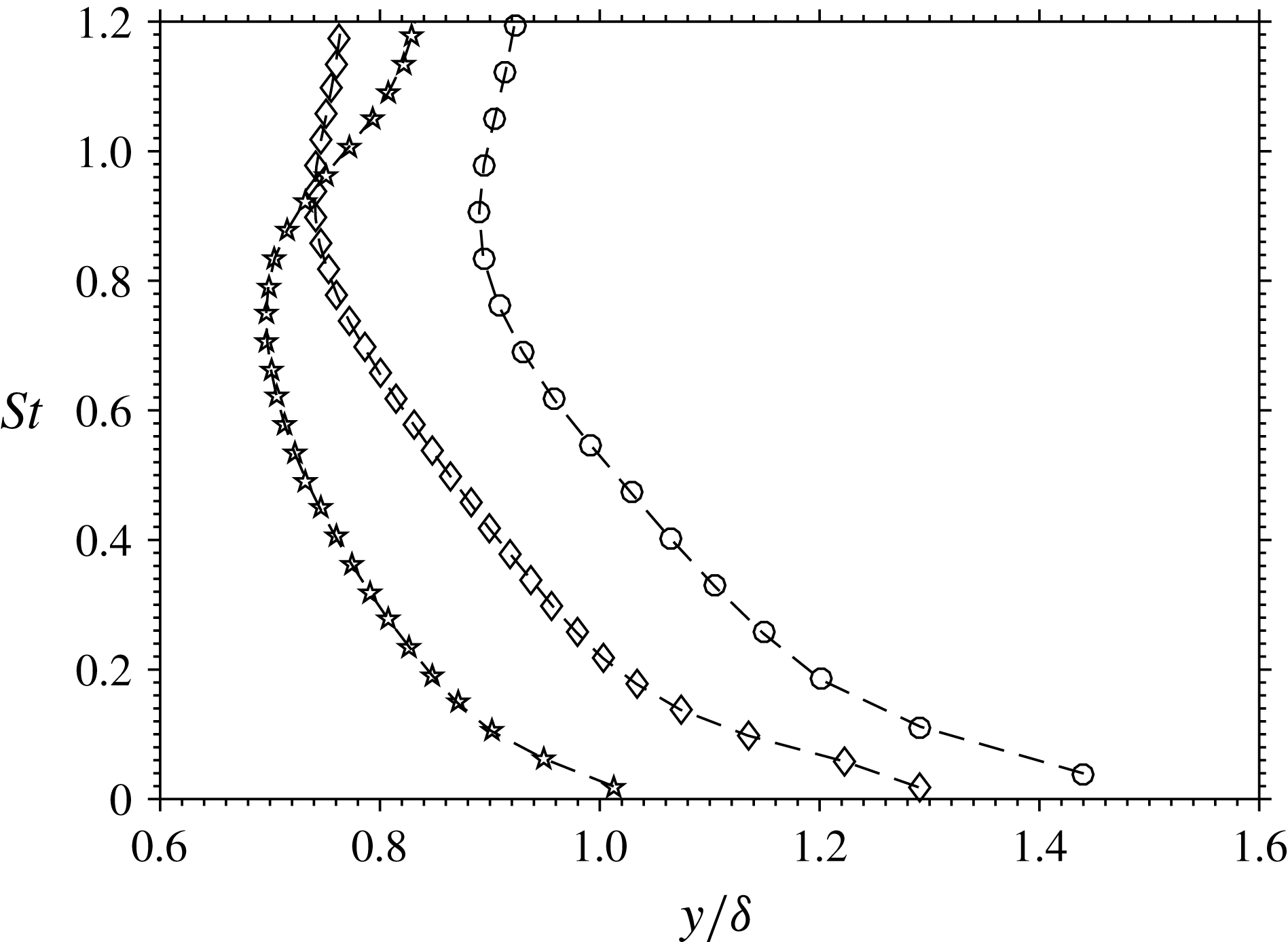
Figure 5. Outer layer Stokes number profiles. ○ Case 2, ♢ Case 3, ✩ Case 4.
A number of steps were necessary to process the raw PIV data for maximum accuracy and data yield. First, the location of the wall was normalized in each image using a cross-correlation of the laser wall reflection, accurate to approximately 1 pixel. This procedure corrected for wall movement due to thermal expansion and vibration, which otherwise could be as much as 30 pixels. Velocity fields were computed using a multi-grid, multi-pass cross-correlation method with iterative image deformation (Huang, Fiedler & Wang Reference Huang, Fiedler and Wang1993; Jambunathan et al.
Reference Jambunathan, Ju, Dobbins and Ashforth-Frost1995; Nogueira, Lecuona & Rodriguez Reference Nogueira, Lecuona and Rodriguez1999; Scarano Reference Scarano2002), as implemented in LaVision’s DaVis 8.2.3. This was the best performing code among a range of options (Williams Reference Williams2014) as it is designed to compensate for the high wall shear, with the image deformation scheme providing higher correlations in the near-wall region. Initial window sizes were 128
$\times$
128 pixels, reducing to 64
$\times$
64 pixels for Case 2 and 48
$\times$
48 pixels for Cases 3 and 4, and with a 50 % overlap in all cases. An iterative elliptical Gaussian windowing function with a maximum standard deviation of half the window size minus one pixel was applied to the final pass. Vectors were validated using a normalized median vector validation filter with a residual cutoff of 2.5 and a 7
$\times$
7 vector neighbourhood. The ratio between first and second correlation peaks was always greater than three. To ensure that vectors with non-physical velocities were not included, the expected range of particle displacements was also used as a filter. For Case 2, streamwise and wall-normal particle displacements were limited to 2–34 and
$\pm 3$
pixels, respectively, corresponding to
$0.06{-}1.05U_{\infty }$
and
$\pm 0.09U_{\infty }$
. For Cases 3 and 4, the range of allowable streamwise and wall-normal particle displacements was constrained to 2–24 and
$\pm 2$
pixels, that is,
$0.09{-}1.15U_{\infty }$
and
$\pm 0.09U_{\infty }$
, respectively.
PIV in high-speed flows commonly suffers from poor seeding uniformity, especially toward the end of a run. As such, all vector fields with greater than a specified percentage of missing vectors (‘% Cut’ in table 5) were eliminated from the dataset, to help ensure the validity of the normalized median filter. The cutoff was set as low as possible while still ensuring sufficient data remained to obtain good statistical convergence. A total of 603 images were retained on average, with a maximum of 676 for Case 4 (see table 5). Turbulent statistics were calculated by averaging the vector fields in the streamwise direction (a distance of approximately
$1.5\unicode[STIX]{x1D6FF}$
to
$2\unicode[STIX]{x1D6FF}$
). The velocity data were split into mean and fluctuating components using Reynolds averaging.
During a PIV run, the total temperature decreased by up to
$15\,^{\circ }\text{K}$
, leading to observed increases in the tunnel free stream velocity of up to
$12~\text{m}~\text{s}^{-1}$
(the Mach number remains constant). To account for these changes, a polynomial fit to the average free stream velocity in each vector field was used to normalize the free stream velocity of the entire run to its initial value at the beginning of acquisition. This correction was applied to all velocity vectors in each vector field, and although it had a negligible impact on the mean velocity profiles it lowered the value of the density-weighted free stream turbulence level (i.e. in Morkovin scaling) by 15–20 %. This correction was only applied to Cases 3 and 4 where the measurement of tunnel conditions was synchronized with PIV acquisition.
The PIV cases were designed to span a range of Reynolds numbers but also to evaluate the effects of measurement dynamic range and resolution in an effort to enhance and assess the accuracy of the measurement of wall-normal turbulence,
$\tilde{v}$
. As a result, the free stream particle displacements were chosen to be greater than 32 pixels for Case 2. With an estimated maximum
$\tilde{v}/U_{\infty }$
level of 4.5 %, the 32 pixel free stream displacement of Case 2 corresponds to a expected
$\tilde{v}$
displacement of approximately 1.5 pixels, and thus any significant truncation in this component is unlikely to be the result of dynamic range limitations. For Case 3, the dynamic range was reduced slightly to enhance the spatial resolution. With a free stream displacement of 21 pixels, it is estimated that
$\tilde{v}$
should still be approximately 0.9 pixels for Case 3. Case 4 has a higher Reynolds number, but a smaller field of view was used to ensure that the dynamic range was only slightly less than for Case 3. The dynamic range in all cases is thought to be sufficient because it is actually larger than other low-Reynolds number incompressible PIV studies where the wall-normal component was accurately measured (Williams et al.
Reference Williams, Hohman, Van Buren and Smits2017).
The resolution in inner units,
$r^{+}$
(see table 5), was estimated by taking account of the window size and the Gaussian weighting function applied to each image. Due to dynamic range choices as well as the use of a higher resolution camera, the resolution improved from 11.1 wall units for Case 2 to 7.4 for Case 3, even while the Reynolds number increased. Due to its higher Reynolds number, the resolution in Case 4 was 10.2 wall units. The resolution is therefore thought to be sufficient for all three cases, and actually better than many comparable hot-wire measurements.
The effect of particle frequency response will be discussed in greater detail in § 6, especially in relation to the accuracy of the measurement of wall-normal velocities. Due to the large particle displacements used in the current study, random errors are small since they are equal to approximately 5 % of the particle image diameter (Prasad et al.
Reference Prasad, Adrian, Landreth and Offutt1992), corresponding to
${\leqslant}0.5\,\%U_{\infty }$
. The sampling uncertainties of the streamwise and wall-normal velocity variances were approximately
$\pm 6.5\,\%$
for Cases 3 and 4, based on a 95 % confidence interval and assuming the data were uncorrelated for distances greater than half the boundary layer thickness (see Benedict & Gould (Reference Benedict and Gould1996)). For Case 2, this uncertainty was
$\pm 8.5\,\%$
. Bias errors due to laser pulse separation uncertainty were less than
$1.6\,\%U_{\infty }$
. Note that each of these error estimates are significantly less than those estimated for many previous experimental hot-wire datasets discussed in § 2, suggesting that the current data are significantly more accurate than previous experiments above Mach 5.
3.3 Flow conditions
Table 6 lists the properties of the boundary layer for each case. Here,
$Re^{\ast }=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}_{\infty }}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}_{\infty }$
is the semi-local friction Reynolds number at the outer edge of the boundary layer,
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$
is the boundary layer shape factor,
$\unicode[STIX]{x1D6FF}^{\ast }$
is the displacement thickness, and
$\unicode[STIX]{x0394}U_{VD}^{+}$
is the wake strength, that is, the maximum deviation of the van Driest transformed mean velocity profiles from the log law in the outer layer (see annotation in figure 9). The boundary layer properties for Case 1 were obtained by Baumgartner (Reference Baumgartner1997) using a Pitot probe. As can be seen, the Reynolds number increases from Case 1 to Case 4, covering a range of
$3600\leqslant Re_{\unicode[STIX]{x1D703}}\leqslant 9340$
, as a result of changing development lengths and stagnation conditions. Note that the Reynolds number of the FRS data, Case 1, is approximately equivalent to Case 2 if a different Reynolds number were considered (such as
$Re_{\unicode[STIX]{x1D70F}}$
). The results should be independent of differences in tripping device or development length, and since the wall temperature is fixed at approximately
$0.8T_{r}$
in each case, the Reynolds number is the only significantly varying property.
Table 6. Boundary layer properties. The boundary layer thickness,
$\unicode[STIX]{x1D6FF}$
, is defined as the distance from the wall at which the mean velocity reaches 99 % of the free stream value.
a Estimated from Pitot measurements of Baumgartner (Reference Baumgartner1997).
4 FRS results
We begin with a qualitative assessment of the outer layer turbulent structure using FRS. Figure 6 shows a montage of FRS images in the streamwise/wall-normal plane taken from Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997). Figure 7 shows a set of images in the streamwise/wall-parallel plane at
$y/\unicode[STIX]{x1D6FF}=0.77$
. The lighter areas are patches of free stream fluid penetrating toward the wall and the darker areas are the turbulent fluid. There are obvious similarities to subsonic boundary layers, and this comparison is made explicit in figure 8, where the hypersonic boundary layer FRS images are compared with the planar laser induced fluorescence (PLIF) visualizations of Delo (Reference Delo1996) in an incompressible boundary layer at a similar Reynolds number (
$Re_{\unicode[STIX]{x1D703}}=700$
,
$Re_{\unicode[STIX]{x1D70F}}=300$
). In the PLIF visualizations, the dye was injected sufficiently far upstream that it marks the turbulent–non-turbulent interface in the outer layer. See Delo, Kelso & Smits (Reference Delo, Kelso and Smits2004) for further details of this experiment. The qualitative similarity between the two boundary layers is striking; although the hypersonic boundary layer displays greater small-scale detail, this is expected of a flow with a higher Reynolds number toward the edge of the layer
$(Re_{\unicode[STIX]{x1D703}}=3600)$
. These comparisons are presented here primarily to illustrate the relatively minor effects of Mach number on the qualitative appearance of the boundary layer structure, when compared to the effects of Reynolds number.
Figure 6. Montage of flow visualizations in a plane perpendicular to the wall. Flow is from left to right and the wall is at the bottom of each image. The field of view is
$1.5\unicode[STIX]{x1D6FF}$
in the wall-normal direction and
$2.5\unicode[STIX]{x1D6FF}$
in the flow direction. From Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997).
Figure 7. Montage of flow visualizations in a plane parallel to the wall at
$y/\unicode[STIX]{x1D6FF}=0.77$
. Flow is from left to right. The field of view in each image is
$2.0\unicode[STIX]{x1D6FF}$
across the flow and
$2.0\unicode[STIX]{x1D6FF}$
in the flow direction. From Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997).
Figure 8. Comparisons of compressible/incompressible boundary layers. (a) Plan views (images are
$2\unicode[STIX]{x1D6FF}\times 2\unicode[STIX]{x1D6FF}$
). Numbers in lower right corner of each image indicate wall-normal position,
$y/\unicode[STIX]{x1D6FF}$
. (b) Plan views (images are
$2.5\unicode[STIX]{x1D6FF}\times 1.5\unicode[STIX]{x1D6FF}$
). In each case the FRS images from the Mach 7.2 flow are on the left, and the PLIF images from the incompressible flow are on the right. Compressible flow images are from Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997), and the incompressible flow images are from Delo (Reference Delo1996).
Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997) used these FRS images to obtain estimates of the intermittency profile and two-point correlations for the density field, as was done at Mach 2.5 by Smith & Smits (Reference Smith and Smits1995). The intermittency distribution agreed very well with Klebanoff’s (Reference Klebanoff1955) incompressible results, and the two-point correlations in the wall-normal planes yielded structure angles similar to those seen by Smits et al. (Reference Smits, Spina, Alving, Smith, Fernando and Donovan1989) in subsonic and supersonic boundary layers. The FRS correlations, which are indicative of the density field, followed trends from previous studies, which suggested that the streamwise length scales in wall-parallel planes tend to decrease with Mach number (Smits & Dussauge Reference Smits and Dussauge2005). As Smits & Dussauge (Reference Smits and Dussauge2005) point out, the scaling for the rate of decay of the correlations may be the time scale of the energy-containing eddies,
$\unicode[STIX]{x1D6EC}/u^{\prime }$
, where
$\unicode[STIX]{x1D6EC}$
is the integral length scale. Should
$\unicode[STIX]{x1D6EC}$
and
$u^{\prime }$
both decrease with Mach number so that their ratio remains approximately constant, the decrease in the streamwise length scales with Mach number could simply reflect the fact that the time scale of the large eddies remains constant as the absolute fluctuation level decreases. We will show that our PIV measurements do not support this trend, so that while the absolute value of
$u^{\prime }$
decreases with Mach number, the length scale does not.
5 Mean flow results
The mean velocity profiles were transformed according to van Driest. As is common with experimental data, the density profile was obtained using the relation of Walz (Reference Walz1969), which can be substituted into (1.1) and integrated to obtain a closed form equation for the van Driest transformed velocity (see Smits & Dussauge Reference Smits and Dussauge2005, p. 195). The friction velocity was determined using the Clauser chart method, matching a portion of the transformed velocity data to the semi-logarithmic profile, with von Kármán constant,
$\unicode[STIX]{x1D705}=0.4$
and additive constant
$B=5.1$
.
The wall was preheated to the highest feasible temperatures prior to tunnel startup. As a result, the wall temperature was approximately 80 % of the adiabatic recovery temperature. Possible changes in the log-law intercept for the current study due to the wall-heat flux are thus estimated to be considerably less than the observed increase of 0.7 (13 %) observed in the DNS study of Priebe & Martin (Reference Priebe and Martin2011) at the same Mach number, but where
$T_{w}/T_{r}\approx 0.5$
. Estimates of the friction velocity using the Clauser chart method and the van Driest transformation correspond to within 2.2 % of the value estimated using the van Driest II skin friction correlation (see Smits & Dussauge Reference Smits and Dussauge2005), further supporting this assessment.
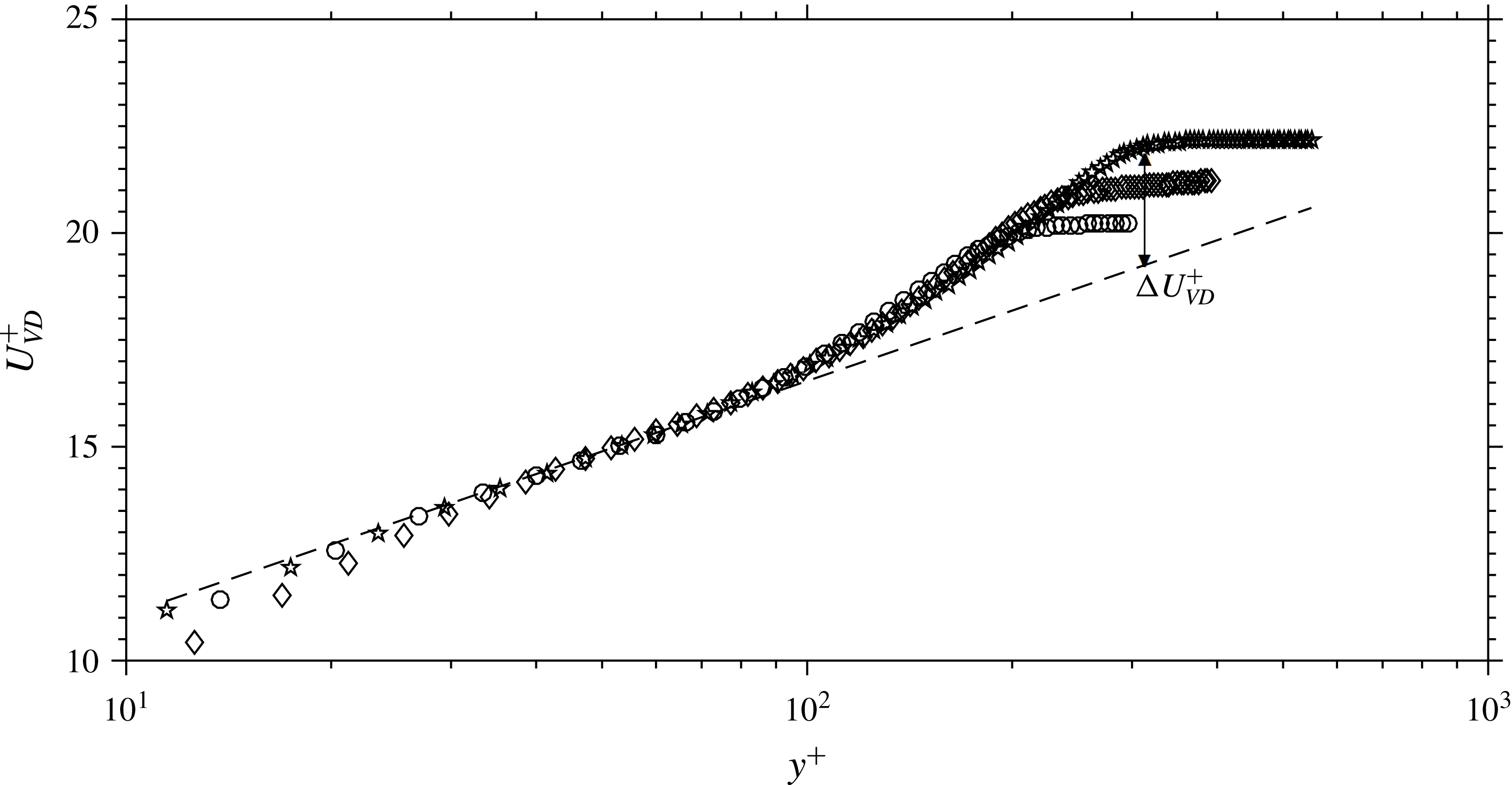
Figure 9. Mean velocity profiles transformed according to van Driest. – – –: equation (1.2) with
$\unicode[STIX]{x1D705}=0.4$
and
$B=5.1$
.
As seen in figure 9, the collapse of the mean velocity profiles in the semi-logarithmic region is excellent. As expected, the profiles extend to higher
$y^{+}=yu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}_{w}$
with increasing Reynolds number. As indicated earlier, the wake strength
$\unicode[STIX]{x0394}U_{VD}^{+}$
(see annotation of figure 9) was found to follow closely the expected Reynolds number trend for correctly tripped boundary layers determined by Coles (Reference Coles1962), when using
$Re_{\unicode[STIX]{x1D6FF}2}$
for the Reynolds number as proposed by Fernholz & Finley (Reference Fernholz and Finley1980). Near the wall, differences between the cases are to be expected due to higher measurement uncertainties in this region. In all, the mean velocity profiles follow the expected Reynolds number trends and highlight the success of the van Driest transformation.
6 Turbulence results
Root-mean-square velocity statistics and the turbulent shear stresses are presented in figure 10 in Morkovin scaling. For streamwise velocity fluctuations,
$\tilde{u} =\sqrt{\overline{{u^{\prime }}^{2}}}$
, and for the wall-normal direction
$\tilde{v}=\sqrt{\overline{{v^{\prime }}^{2}}}$
, where the bar indicates an ensemble average. The scaled turbulent shear stress is denoted as
$-\overline{u^{\prime }v^{\prime }}/u_{\ast }^{2}=-\unicode[STIX]{x1D70C}\overline{u^{\prime }v^{\prime }}/\unicode[STIX]{x1D70F}_{w}$
. The wall-normal distance,
$y$
, is scaled by the outer length scale
$\unicode[STIX]{x1D6FF}$
. The results are compared with the DNS simulations of Priebe & Martin (Reference Priebe and Martin2011) at the same Mach number but with a lower momentum thickness Reynolds number and wall temperature (
$Re_{\unicode[STIX]{x1D703}}=3300$
,
$T_{w}/T_{r}=0.53$
). The friction Reynolds number for the simulation lies between Cases 2 and 3 (
$Re_{\unicode[STIX]{x1D70F}}=194$
), and provides a baseline case for comparison and for examining Reynolds number effects. The incompressible profile of DeGraaff & Eaton (Reference DeGraaff and Eaton2000) at
$Re_{\unicode[STIX]{x1D703}}=5200$
is also shown.
6.1 Streamwise component
For the streamwise component of turbulence, figure 10(a) illustrates that the three PIV cases, the DNS and the incompressible data agree reasonably well with each other for approximately
$y/\unicode[STIX]{x1D6FF}>0.3$
. In particular, the Case 2 profile closely follows the DNS results of Priebe & Martin (Reference Priebe and Martin2011) across the entire boundary layer; these two cases also have the most similar Reynolds numbers. While the exact location and magnitude of the inner peak was not resolved in the current datasets, the maximum value of
$\tilde{u}$
is of similar magnitude for all cases and moves closer to the wall with increasing Reynolds number, following trends from incompressible flow. The inner peak for the hypersonic profiles is located further from the wall than what is seen in the incompressible data, but the temperature rise near the wall for the compressible flows naturally thickens the inner layer so this trend is as expected.
We see from figure 11(a) that by using inner scaling there is a better collapse of the data in the near-wall region, remembering that these data have the greatest uncertainty. The experimental profiles peak closer to the wall than the DNS data, but some differences should be expected because the wall temperatures for these cases are all somewhat different and temperature differences have the greatest influence on this region, as noted above.
Huang, Coleman & Bradshaw (Reference Huang, Coleman and Bradshaw1995) suggested that a better length scale for the inner region would allow the local stress and kinematic viscosity to vary with wall distance, creating the new coordinate,
$y^{\ast }=(yu_{\ast })/\unicode[STIX]{x1D708}$
. This has subsequently been called semi-local scaling and has been examined largely using DNS data. Patel et al. (Reference Patel, Boersma and Pecnik2016) and Trettel & Larsson (Reference Trettel and Larsson2016) used it to extend the van Driest transformation, as noted earlier, and it has been shown to approximately collapse the location of the near-wall turbulence peak in streamwise turbulence intensity in variable property, low Reynolds number, low Mach number channel flow (Modesti & Pirozzoli Reference Modesti and Pirozzoli2016; Patel et al.
Reference Patel, Boersma and Pecnik2016). Duan et al. (Reference Duan, Beekman and Martin2011a
) also demonstrated that this coordinate collapsed the locations of the near-wall peaks in the turbulent kinetic energy (TKE) budget terms for a range of supersonic boundary layers. In addition, a new Reynolds number for the outer layer can be defined in terms of the semi-local coordinate at the edge of the boundary layer,
$Re^{\ast }=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}_{\infty }}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}_{\infty }$
(see table 6), which suggests that the outer layer has characteristics of much higher Reynolds number than suggested by the conventional
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}_{w}$
.
Figure 11(b) demonstrates that Cases 2 and 3 agree closely with the DNS profile in the near-wall region when employing semi-local scaling, at least partially compensating for differences in near-wall viscosity and density between cases. Although Case 4 still shows some departures, the overall collapse of the near-wall streamwise turbulence data in this scaling is encouraging, with remaining variation between the current cases lying between the incompressible data and the high Mach number DNS.
While the criterion of Samimy & Lele (Reference Samimy and Lele1991) indicate that instantaneous particle motions could be reduced by up to 10 % based on previous particle response estimates, the current results suggest that this is a significant over-estimation for the measurement of streamwise turbulence. Differences between PIV, DNS and incompressible profiles are similar to the expected convergence error, especially in the outer layer, suggesting a significant improvement in accuracy over previous high Mach number hot-wire data. As a result, the current streamwise PIV results provide persuasive experimental support for the validity of Morkovin’s hypothesis above Mach 5 over a range of Reynolds numbers.
Figure 10. Turbulence profiles in outer layer Morkovin scaling. (a) Streamwise and (b) wall-normal velocity r.m.s. (c) Reynolds shear stress. Symbols as in table 6. ——, DNS by Priebe & Martin (Reference Priebe and Martin2011) (
$Ma=7.2$
,
$Re_{\unicode[STIX]{x1D703}}=3300$
,
$T_{w}/T_{r}=0.53$
);
-- – –, DeGraaff & Eaton (Reference DeGraaff and Eaton2000) (
$Ma=0$
,
$Re_{\unicode[STIX]{x1D703}}=5200$
).
6.2 Wall-normal component and shear stress
For the wall-normal component, figure 10(b) shows that all three cases agree closely with each other, but the measured level is approximately 60 % lower than the DNS and incompressible data. The shear stress (figure 10 c) is also significantly below its expected value. Assuming Morkovin’s hypothesis is accurate, the scaled magnitude of the shear stress should lie closer to a value of one near the wall, even at these low Reynolds numbers. Reductions in the wall-normal component cannot be attributed to dynamic range limitations because the maximum particle image displacements were purposely chosen to be large and varied between cases. Also, the spatial resolution was shown to be better than in many hot-wire experiments.
Reductions in measured wall-normal turbulence have been observed in previous particle-based velocimetry studies of supersonic flows, even when there was no apparent effect on the streamwise component. At Mach 5, for example, Tichenor et al. (Reference Tichenor, Humble and Bowersox2013) and Peltier et al. (Reference Peltier, Humble and Bowersox2016) observed a reduction in the measured wall-normal component of approximately 30 % in their PIV data when compared to DNS at the same Mach number (see figure 2). In a Mach 2 boundary layer, Lowe, Byun & Simpson (Reference Lowe, Byun and Simpson2014) observed reductions in Morkovin-scaled r.m.s. velocities of up to 70 % in both the wall-normal and spanwise directions using LDV. Indeed, this was the conclusion of Lowe et al. (Reference Lowe, Byun and Simpson2014) who demonstrated a better correspondence with DNS simulations by using a rudimentary correction for the particle response based on a Stokes drag model and example spectra.
As suggested earlier, particle response limitations can play a very important role because the
$v^{\prime }$
-spectrum is broader than its streamwise counterpart (Gaviglio et al.
Reference Gaviglio, Anguillet and Eléna1981). This disparity between the
$v^{\prime }$
- and the
$u^{\prime }$
-spectra also influences the accuracy of hot-wire measurements in the wall-normal direction. For particle-based techniques, this filtering of the wall-normal component is expected to increase with Mach number as the flow typically becomes more rarefied, since Knudsen number effects reduce particle drag coefficients (Williams et al.
Reference Williams, Nguyen, Schreyer and Smits2015).
Given the limitations of the
$v^{\prime }$
measurement, we will now focus on the behaviour of
$u^{\prime }$
when examining the structure of the hypersonic boundary layer.
6.3 Spatial correlations
The spatial structure of the streamwise velocity fluctuation field is investigated using the two-dimensional spatial correlation function,
$R_{uu}$
, defined by
$$\begin{eqnarray}R_{uu}(\unicode[STIX]{x0394}x,y,y_{ref})=\frac{\overline{u^{\prime }(x,y_{ref})u^{\prime }(x+\unicode[STIX]{x0394}x,y)}}{\tilde{u} (y_{ref})\tilde{u} (y)},\end{eqnarray}$$
where
$y_{ref}$
is the distance from the wall at which the correlation is computed, and
$\unicode[STIX]{x0394}x$
is the in-plane streamwise separation.
Figure 12. Correlations of streamwise velocity fluctuations for Case 4. Contours are shown between 0.2 and 0.7. (a)
$y/\unicode[STIX]{x1D6FF}=0.075$
, (b)
$y/\unicode[STIX]{x1D6FF}=0.15$
, (c)
$y/\unicode[STIX]{x1D6FF}=0.4$
, (d)
$y/\unicode[STIX]{x1D6FF}=0.6$
.
Contours of
$R_{uu}$
are shown in figure 12 for four wall-normal locations. We choose to highlight Case 4, but the other cases show a similar behaviour. At all four locations, the contours indicate a well-defined structure inclined at a shallow angle to the streamwise direction. Similar results have been observed in incompressible flows (see for example Smits et al.
Reference Smits, Spina, Alving, Smith, Fernando and Donovan1989; Volino, Schultz & Flack Reference Volino, Schultz and Flack2007) and supersonic flows at lower Mach number (Spina & Smits Reference Spina and Smits1987; Ganapathisubramani Reference Ganapathisubramani2007; Peltier et al.
Reference Peltier, Humble and Bowersox2016), but important differences exist.
Figure 13. (a) Wall-normal variation of mean streamwise length scale,
$L_{x}^{u}$
, for ○
$R_{uu}=0.2$
, ▫
$R_{uu}=0.3$
, ◃
$R_{uu}=0.4$
and ▵
$R_{uu}=0.5$
contours for Case 4. (b)
$L_{x}^{u}$
for
$R_{uu}=0.5$
contour.
$\times$
Volino et al. (Reference Volino, Schultz and Flack2007), [
$Ma=0$
,
$Re_{\unicode[STIX]{x1D6FF}2}=6000$
,
$0.1<y/\unicode[STIX]{x1D6FF}<0.5$
], ◃ Ganapathisubramani (Reference Ganapathisubramani2007) [
$Ma=2,Re_{\unicode[STIX]{x1D6FF}2}=11\,500$
,
$0.3<y/\unicode[STIX]{x1D6FF}<0.7$
], ▫ Duan, Beekman & Martin (Reference Duan, Beekman and Martin2011b
) [
$Ma=0$
–12,
$Re_{\unicode[STIX]{x1D6FF}2}=1500$
,
$y/\unicode[STIX]{x1D6FF}=0.1$
] ▵ Peltier et al. (Reference Peltier, Humble and Bowersox2016) [
$Ma=4.9$
,
$Re_{\unicode[STIX]{x1D6FF}2}=11\,200$
,
$y/\unicode[STIX]{x1D6FF}=0.1,0.2$
]. Other symbols for current dataset, as in table 6. Error bars indicate variability for indicated range of wall-normal locations.
Smits & Dussauge (Reference Smits and Dussauge2005) concluded on the basis of previous work that, within the scatter of available data, the integral length scale tends to increase with Reynolds number and decrease with Mach number. The integral length scales were always determined from hot-wire data and often involved the extrapolation of either
$u^{\prime }$
or
$(\unicode[STIX]{x1D70C}u)^{\prime }$
energy spectra to zero frequency (as low wavenumber hot-wire spectra are known to be often inaccurate), possibly contributing to this scatter. The field of view in our experiments is insufficient to determine the integral length scale, so we choose to examine
$L_{x}^{u}$
, the width of a given
$R_{uu}$
contour at
$y_{ref}$
. The variation of
$L_{x}^{u}$
with wall-normal distance is shown in figure 13(a) for the
$R_{uu}=0.2{-}0.5$
contours. For
$R_{uu}=0.2$
, the correlation length increases with distance from the wall, reaching a peak before decreasing toward the free stream. The location of this peak is sensitive to the contour level chosen, with the profile becoming flatter and located more toward the edge of the boundary layer for higher correlation contours.
For the
$R_{uu}=0.2$
contour,
$L_{x}^{u}$
is between 1.5 and
$2.5\unicode[STIX]{x1D6FF}$
over much of the layer. These values are much larger than the corresponding correlation length of the density field,
$L_{x}^{\unicode[STIX]{x1D70C}}=0.5\unicode[STIX]{x1D6FF}$
for
$R_{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70C}}=0.2$
, as determined by Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997) using FRS data similar to that shown in figures 6 and 7. Baumgartner et al.’s results were obtained in the same facility used in the current study and under conditions that correspond closely to Case 1. Their results were also similar to those obtained using FRS at Mach 2.5 by Smith & Smits (Reference Smith and Smits1995), suggesting a Mach number independence. While
$L_{x}$
is sensitive to measurement noise, especially for lower correlation levels, the differences between
$L_{x}$
determined from either the density or the velocity field cannot be explained in this way. In addition, the Reynolds number difference between the FRS and PIV data is also not significant enough to explain the difference, and so it appears that the structure of the velocity and density fields have a fundamentally different scaling.
To compare the current results with previous velocity correlation data, we now examine
$L_{x}^{u}$
for the
$R_{uu}=0.5$
contour where an approximate plateau was observed between
$0.3<y/\unicode[STIX]{x1D6FF}<0.7$
. Figure 13(b) shows the mean of
$L_{x}^{u}$
over this wall-normal range for Cases 2–4 in addition to results at other Mach numbers. Error bars indicate the variability of
$L_{x}^{u}$
across this range of wall-normal positions, when available. The overall accuracy of
$L_{x}^{u}$
was conservatively estimated to be
$\pm 0.075\unicode[STIX]{x1D6FF}$
for the
$R_{uu}=0.5$
contour, using estimates of the gradient in the correlation with streamwise separation at this contour. The Reynolds numbers for the cases shown vary between
$770<Re_{\unicode[STIX]{x1D6FF}2}<11\,500$
, with the current study and that of Duan et al. (Reference Duan, Beekman and Martin2011b
) at the lower end of this range and those of Ganapathisubramani (Reference Ganapathisubramani2007) and Peltier et al. (Reference Peltier, Humble and Bowersox2016) at the upper end. Cases 2–4 indicate a slight reduction in streamwise coherence with increasing Reynolds number, which is counter to the conclusions of Smits & Dussauge (Reference Smits and Dussauge2005), but this variation is minor compared to differences between the current data and the correlation length of Ganapathisubramani (Reference Ganapathisubramani2007) at higher Reynolds number.
Considering only the low Reynolds number data, our results indicate that the coherence length of streamwise velocity fluctuations only reduces slowly with Mach number. The data reviewed by Smits & Dussauge (Reference Smits and Dussauge2005) display a swifter reduction in length scale with Mach number, but the differences between our results based on PIV and those of Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997) based on FRS suggest that measures of coherence involving density, such as those obtained from mass-flux spectra, show greater reductions in coherence length than those based on velocity measurements. This assessment is further supported by the mass-flux correlations of Duan et al. (Reference Duan, Beekman and Martin2011b
), which indicate an approximately 50 % decrease in
$L_{x}^{\unicode[STIX]{x1D70C}u}$
from incompressible conditions to Mach 12 (at constant
$Re_{\unicode[STIX]{x1D6FF}2}$
). The reduction in
$L_{x}^{u}$
seen between the studies of Ganapathisubramani (Reference Ganapathisubramani2007) at Mach 2 and that of Peltier et al. (Reference Peltier, Humble and Bowersox2016) at Mach 4.9 may suggest that Mach number effects become more important at higher Reynolds numbers.
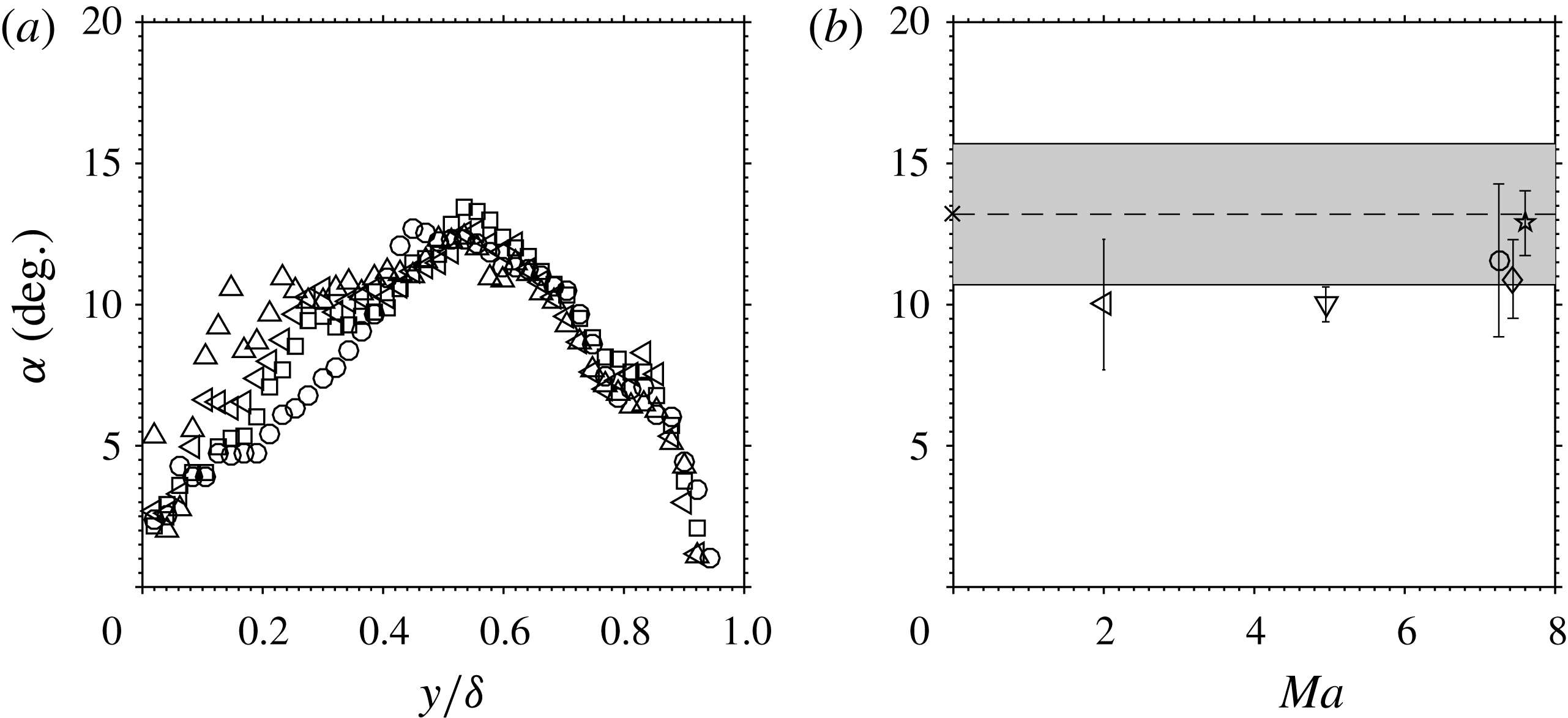
Figure 14. Inclination angle of the streamwise velocity correlation contours. (a) Variation with wall-normal distance for Case 4 and
$0.2<R_{uu}<0.5$
. Symbols as in figure 13(a). (b) Inclination of the
$R_{uu}=0.5$
contour from a range of studies. The shaded region indicates a range of incompressible results from Volino et al. (Reference Volino, Schultz and Flack2007). For this figure, the Peltier et al. (Reference Peltier, Humble and Bowersox2016) data represent an average for
$y/\unicode[STIX]{x1D6FF}=0.3{-}0.6$
, where the inclination angle was approximately constant. Other symbols and wall-normal locations as in figure 13(b). Error bars indicate variability for indicated range of wall-normal locations.
Also of interest is the inclination angle of the correlation contours, which is often linked to the inclination angle of hairpin packets in incompressible flows. Here, we define
$\unicode[STIX]{x1D6FC}$
as the angle of the semi-major axis of an ellipse fitted to a given contour and centred on the origin of the correlation. This is the conventional definition for such investigations as this measure is insensitive to noise in the correlation field. The variation of
$\unicode[STIX]{x1D6FC}$
with angle of attack is shown in figure 14(a) for
$R_{uu}=0.2{-}0.5$
. As previously, we highlight Case 4 since other cases show similar results. The angle is seen to increase with distance from the wall, reaching a broad maximum before decreasing once again toward the free stream. This trend mimics that seen at lower Mach number in the study of Peltier et al. (Reference Peltier, Humble and Bowersox2016). The angle is also seen to be insensitive to the chosen contour level, with the greatest variations in the near-wall region.
We can compare inclination angles between cases by determining the average angle across the broad outer layer maximum
$(0.3<y/\unicode[STIX]{x1D6FF}<0.7)$
. While the result is insensitive to contour level, we choose to examine the
$R_{uu}=0.5$
contour for consistency with the analysis of streamwise length scales. The results from Cases 2, 3, and 4 are shown in figure 14(b). Also shown is the range of angles observed in incompressible flow as summarized by Volino et al. (Reference Volino, Schultz and Flack2007)
$(13.2^{\circ }\pm 2.5)$
, as well as data at Mach 2 by Ganapathisubramani (Reference Ganapathisubramani2007) (
$0.3<y/\unicode[STIX]{x1D6FF}<0.7$
, estimated from figures), and at Mach 4.9 by Peltier et al. (Reference Peltier, Humble and Bowersox2016) (
$0.3<y/\unicode[STIX]{x1D6FF}<0.6$
). The error bars in each of these cases indicate the range of angles observed over the given range of wall-normal locations. The range of angles found by Volino et al. (Reference Volino, Schultz and Flack2007) (indicated by the shaded region) encompasses estimates of mean log-layer inclination angle obtained using a variety of methods for incompressible flows and are thought to be invariant with Reynolds number (see Marusic & Heuer Reference Marusic and Heuer2007).
The data indicate little or no change in the structure angle with Mach number when using correlations of streamwise velocity, at least within the scatter of the available data. Previous results based on correlations of streamwise mass flux suggest a different result, in that they indicate increases in structure angle with Mach number (Smits et al. Reference Smits, Spina, Alving, Smith, Fernando and Donovan1989; Duan et al. Reference Duan, Beekman and Martin2010), supporting our earlier observation that there appear to be fundamental differences between the velocity and density fields in compressible turbulent boundary layers.
6.4 Uniform momentum zones
The presence of uniform momentum zones (UMZs) separated by regions of high shear is now well established for incompressible flows (Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000), with the number of such zones increasing in a log-linear fashion with Reynolds number (de Silva, Hutchins & Marusic Reference de Silva, Hutchins and Marusic2016). Figure 15 reveals the presence of similar zones in hypersonic flows. Three regions of approximately uniform streamwise momentum can be observed in an instantaneous PIV velocity field for Case 4. These features can be further highlighted by comparing an instantaneous velocity profile with the mean profile as in figure 15(b). The velocities delineating each zone were determined using the minima between clearly defined peaks in the probability density histogram (p.d.f.) of instantaneous velocities (see figure 15 c), following procedures established by de Silva et al. (Reference de Silva, Hutchins and Marusic2016). To construct this p.d.f., the turbulent/non-turbulent interface (TNTI) was identified using the method of de Silva et al. (Reference de Silva, Philip, Chauhan, Meneveau and Marusic2013) to allow for the removal of vectors in the free stream, which would otherwise dominate the p.d.f. The entire field of view was used such that a sufficient number of velocity vectors were available to make the p.d.f. as smooth as possible. Additional instantaneous velocity fields with their associated UMZs are shown in figure 16. Such UMZs could be identified in a similar manner in any chosen PIV frame, and they are present ubiquitously throughout the PIV datasets.
We have not attempted to determine the mean number of UMZs or their distribution due to outstanding questions with regard to the correct field of view to use when examining UMZs in compressible flows, as well as the lower resolution and data yield of the current study when compared to, for example, the incompressible study of de Silva et al. (Reference de Silva, Hutchins and Marusic2016). Qualitative analysis of many instantaneous velocity fields, however, suggests that the mean number of UMZs in our Mach 7.5 boundary layer is similar to that expected for the
$Re_{\unicode[STIX]{x1D70F}}$
of this study (
$=2.85$
according to the empirical curve of de Silva et al. (Reference de Silva, Hutchins and Marusic2016)).
The current results represent broad experimental evidence for the presence of UMZs in hypersonic boundary layers and their qualitatively similar behaviour to incompressible flows. Such evidence has not previously been available and has been made possible by the direct measurement of the spatial velocity field using PIV.
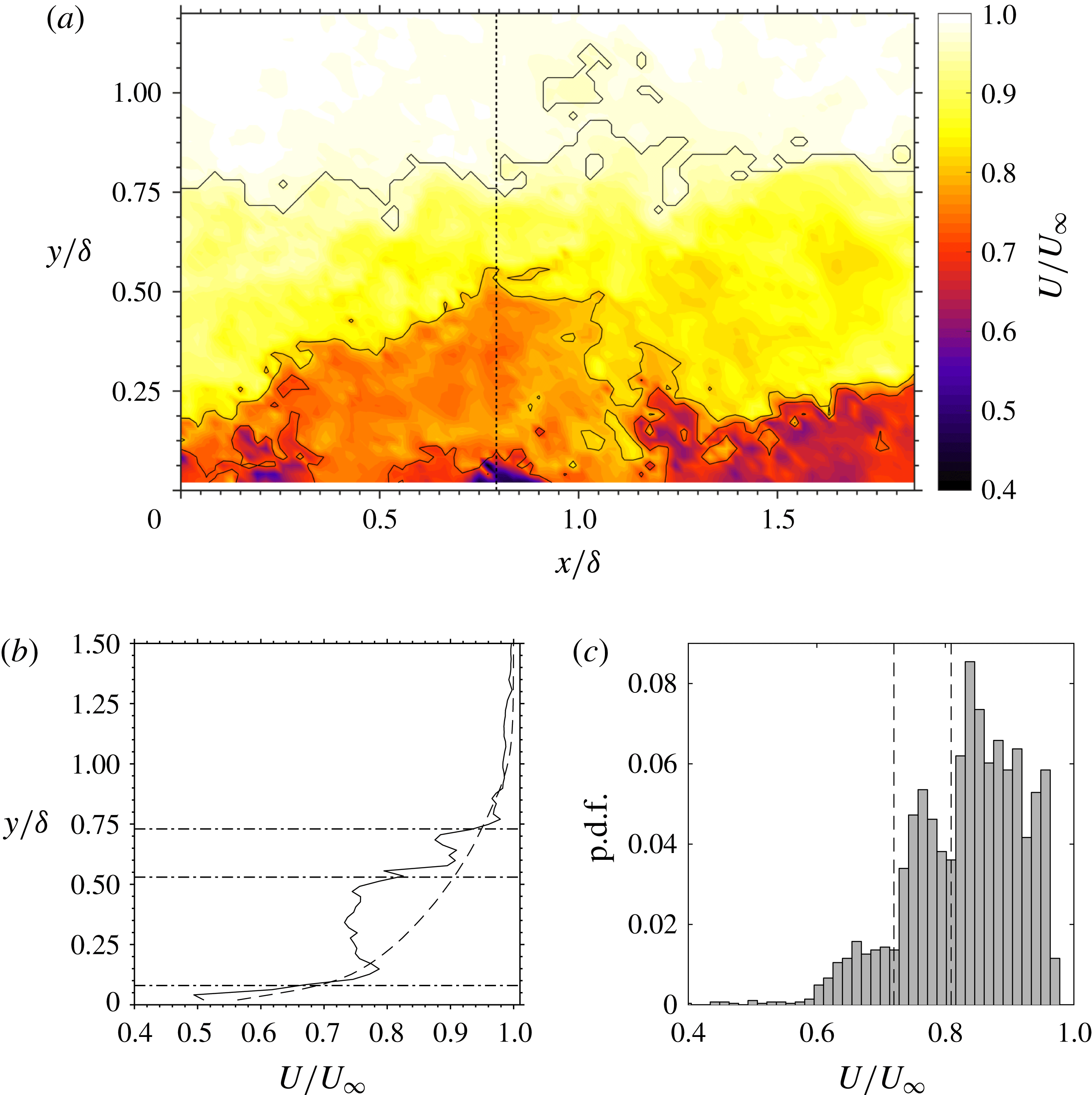
Figure 15. (a) Example of instantaneous streamwise velocity field from Case 4. Dark contours indicate the edge of each UMZ as found using the p.d.f. shown in part (c) and the TNTI as determined using the method of de Silva et al. (Reference de Silva, Philip, Chauhan, Meneveau and Marusic2013). (b) Comparison of instantaneous (——) and mean (- - - -) velocity profiles at the location indicated in part (a) (dotted line). Dot-dash lines delineate three different uniform momentum zones. (c) The p.d.f. of streamwise velocities in this instantaneous velocity field. Dashed lines indicate the edges of each UMZ. The non-turbulent free stream has been omitted when constructing this p.d.f.
Figure 16. Instantaneous streamwise velocity fields from Case 4 that further illustrate the presence of uniform momentum zones in hypersonic boundary layers. Dark lines indicate the bounds of each zone, as determined using the p.d.f. of the streamwise velocity vectors.
7 Discussion and conclusions
Measurements of the streamwise component of velocity in a Mach 7.5 turbulent boundary layer were obtained using PIV, thereby avoiding many of the difficulties that beset high Mach number hot-wire studies. The results were subject to extensive error analysis and validation tests, with particular attention paid to quantifying the particle response and any possible influence of the tripping device.
The streamwise turbulence results in Morkovin scaling were found to agree with DNS simulations in both inner and outer scaling, given known Reynolds number trends. The small scatter that remains appears related to the correct scaling of the wall-normal coordinate, with the semi-local inner scale
$y^{\ast }$
providing a better collapse in the near-wall region. Overall, the profiles are comparable to those seen for both DNS and incompressible boundary layers, providing direct experimental evidence that Morkovin scaling is valid for the streamwise turbulence at Mach numbers as high as 7.5.
In addition, we found that the overall structure of the turbulence appears to be largely independent of Mach number. For example, the streamwise length scales derived from velocity correlations were seen to decrease much more slowly with Mach number than suggested by previous studies (Smits & Dussauge Reference Smits and Dussauge2005). Similarly, the characteristic angle of inclination of the correlation contours of streamwise velocity is relatively insensitive to Mach number, whereas previous studies have suggested that this angle increases with Mach number (Smits et al. Reference Smits, Spina, Alving, Smith, Fernando and Donovan1989). These contrasting trends suggest significant differences in the properties of velocity and density fields at high Mach number, as many previous studies derived such length scales from mass-flux hot-wire data rather than velocity data per se. This assessment is further supported by the examination of streamwise length scales, where length scales derived from the correlation of streamwise velocities using PIV were three to five times longer than those measured from the density field using FRS by Baumgartner et al. (Reference Baumgartner, Erbland, Etz., Yalin, Muzas, Smits, Lempert and Miles1997) in a boundary layer nominally similar to Case 1 of the current study.
Instantaneous spatial structure was also found to mimic that at lower Mach number. The qualitative similarities between FRS images of the Mach 7.5 flow and PLIF visualizations of an incompressible boundary layer are striking. Greater detail of the spatial structure was extracted from PIV data, with the existence of Uniform Momentum Zones confirmed at Mach 7.5. These UMZs were ubiquitous throughout the PIV datasets and the average number of zones were similar to that seen in incompressible boundary layers at similar Reynolds numbers.
The data collected here cannot say much regarding the scaling of the wall-normal component of the velocity or the Reynolds shear stress. Particle frequency response limitations encountered in our experiments reduce the level of both, as has been seen in other particle-based velocimetry measurements at lower Mach numbers. In particular, our measurements were hampered by the higher frequency content of the wall-normal component compared to the streamwise component, and the low density of the flow which can lead to particle slip. Although we exercised great care in making the particles as small as possible while still being able to image them successfully, future improvements in imaging technology for PIV may make it possible to use smaller particles still, and thereby make it possible to acquire more accurate measurements of the wall-normal velocity component.
Acknowledgements
The support of NASA under Cooperative Agreement no. NNX08AB46A (Program Manager C. McGinley) is gratefully acknowledged. R. Bogart and D. Hoffman provided invaluable assistance setting up the experiments.
