1. Introduction
One of the main concerns for the safety of nuclear power plants is represented by earthquakes. During an earthquake, the main risk is that fuel assemblies start to move and potentially touch each other or prevent the drop of the control rods used to cool the core. To better understand the motion of fuel assemblies subjected to seismic forcing, fluid–structure interaction models are needed. In this paper, we present such a model, which has been developed with the objective of gaining insight into the complex fluid–structure interactions at play inside a nuclear reactor, while remaining computationally efficient.
A reactor core of a pressurised water reactor (PWR) is made of fuel assemblies (between ![]() $150$ and
$150$ and ![]() $250$ depending on the power of the reactor). Each fuel assembly gathers about 100 fuel rods, stands between four and five metres high, has a cross-section of about
$250$ depending on the power of the reactor). Each fuel assembly gathers about 100 fuel rods, stands between four and five metres high, has a cross-section of about ![]() $20\times 20\ {\rm cm}^{2}$, and weighs about 800 kg. The fuel rods, which contain pellets of uranium, have a diameter of about 1 cm for 4 m in height; the space between each pair of fuel rods in the assembly is about 3 mm. Fuel rods are held together by grids (between
$20\times 20\ {\rm cm}^{2}$, and weighs about 800 kg. The fuel rods, which contain pellets of uranium, have a diameter of about 1 cm for 4 m in height; the space between each pair of fuel rods in the assembly is about 3 mm. Fuel rods are held together by grids (between ![]() $8$ and
$8$ and ![]() $10$ depending on the power of the reactor) distributed along the height of the fuel assembly. Springs and dimples are used in between the grid and the rods to avoid any drop of the fuel rods (De Mario & Street Reference De Mario and Street1989).
$10$ depending on the power of the reactor) distributed along the height of the fuel assembly. Springs and dimples are used in between the grid and the rods to avoid any drop of the fuel rods (De Mario & Street Reference De Mario and Street1989).
The fuel assemblies are cooled by a strong axial flow. This water flow is upwards, with velocities of about ![]() $5\ {\rm m}\ {\rm s}^{-1}$ at 150 bar and
$5\ {\rm m}\ {\rm s}^{-1}$ at 150 bar and ![]() $310\,^{\circ }{\rm C}$. The flow regime is fully turbulent, with a Reynolds number based on the rod diameter of
$310\,^{\circ }{\rm C}$. The flow regime is fully turbulent, with a Reynolds number based on the rod diameter of ![]() $Re\approx 5\times 10^{5}$. Note that even if the main flow is upwards, the root-mean-square average of the transverse component is between 5 % and 15 % of the vertical velocity.
$Re\approx 5\times 10^{5}$. Note that even if the main flow is upwards, the root-mean-square average of the transverse component is between 5 % and 15 % of the vertical velocity.
The presence of the water flow gives rise to strongly coupled interactions between the fluid and the structure (Chen & Wambsganss Reference Chen and Wambsganss1972): the motion of the structure modifies the fluid flow, which itself exerts a force on the structure. A first attempt to describe fluid–structure interactions is to use the concepts of added mass and added damping. The added mass is the inertial mass added to a body because of the presence of a surrounding fluid. For simplicity, it can be viewed as a volume of fluid moving with the same velocity as the body, though in reality all fluid particles will be moving to various degrees (Buat Reference Buat1779; Lamb Reference Lamb1895). The added mass ![]() $M_a$ of a non-deformable body moving at velocity
$M_a$ of a non-deformable body moving at velocity ![]() $U$ through an unbounded fluid otherwise at rest can be defined such that the kinetic energy in the volume of fluid is
$U$ through an unbounded fluid otherwise at rest can be defined such that the kinetic energy in the volume of fluid is ![]() $E_k=(M_a U^{2})/{2}$, or equivalently,
$E_k=(M_a U^{2})/{2}$, or equivalently,
where ![]() $\boldsymbol {V}$ is the velocity field. A complete collection of added masses for different geometries and flow conditions can be found in Wendel (Reference Wendel1956) or Brennen (Reference Brennen1982), for instance.
$\boldsymbol {V}$ is the velocity field. A complete collection of added masses for different geometries and flow conditions can be found in Wendel (Reference Wendel1956) or Brennen (Reference Brennen1982), for instance.
While the added mass is due mainly to pressure forces exerted on the body, viscous forces and boundary layer separation give rise to drag and to an added damping effect. Taylor (Reference Taylor1952) proposed a model for the damping force on a slender structure, which has been used widely (e.g. Païdoussis Reference Païdoussis1966a; Triantafyllou & Cheryssostomidis Reference Triantafyllou and Cheryssostomidis1985; Gosselin & De Langre Reference Gosselin and De Langre2011; Singh, Michelin & De Langre Reference Singh, Michelin and De Langre2012). In Taylor's model, the damping force is decomposed into two terms: a normal force akin to drag, and a longitudinal force depending on the body surface and on the incident angle.
Generally, the total fluid force exerted on the non-deformable body is assumed to be decomposed into its added mass component (proportional to the acceleration) and its drag component (proportional to the square of the velocity). This decomposition, known as the Morison equation (Morison, Johnson & Schaaf Reference Morison, Johnson and Schaaf1950), can describe correctly experimental observations provided that drag and inertial coefficients are adjusted empirically (in general, they depend on the motion amplitude and frequency).
For deformable cylinders in axial flow, the concept of added mass does not apply directly. In that case, one can use slender body theory developed by Lighthill (Reference Lighthill1960a,Reference Lighthillb). This theory makes use of potential flow theory and arguments of momentum balance in slices of fluids along the slender body. The resulting normal force per unit length exerted by the fluid can be written in the limit of small displacement as
where ![]() $W(X,T)$ is the normal displacement,
$W(X,T)$ is the normal displacement, ![]() $U$ is the undisturbed axial flow velocity, and here,
$U$ is the undisturbed axial flow velocity, and here, ![]() $M_a$ is the added mass per unit length (
$M_a$ is the added mass per unit length (![]() $M_a=\rho {\rm \pi}A^{2}$ for a circular cylinder of radius
$M_a=\rho {\rm \pi}A^{2}$ for a circular cylinder of radius ![]() $A$). In the case of a solid body,
$A$). In the case of a solid body, ![]() $W$ has no
$W$ has no ![]() $X$ dependence and one recovers a force opposite to
$X$ dependence and one recovers a force opposite to ![]() $M_a\partial ^{2}_T W$, as expected.
$M_a\partial ^{2}_T W$, as expected.
Based on the work of Lighthill (Reference Lighthill1960b), Païdoussis (Reference Païdoussis1966a,Reference Païdoussisb) studied theoretically and experimentally the dynamics of a flexible slender cylinder clamped at its leading edge, which is immersed in an axial flow. He found that above a critical flow velocity, a flutter instability appears. Later, Païdoussis (Reference Païdoussis1973) and Païdoussis & Pettigrew (Reference Païdoussis and Pettigrew1979) extended this flutter stability analysis to confined geometries, by using the work of Classen (Reference Classen1972) and Chen & Wambsganss (Reference Chen and Wambsganss1972) on added mass in confined geometries.
The stability analysis of a single cylinder in axial flow has been later generalised to clusters of cylinders (Païdoussis Reference Païdoussis1973, Reference Païdoussis1979; Païdoussis & Suss Reference Païdoussis and Suss1977; Païdoussis, Suss & Pustejovsky Reference Païdoussis, Suss and Pustejovsky1977). If each cylinder is free to move independently, then the fluid acts as a coupling medium and the motions of the cylinders are synchronised. Above a critical flow velocity, the coupled pinned-pinned cylinders lose stability by divergence (unstable mode of eigenfrequency zero). For higher flow velocities, the system may be subjected to several divergence and flutter instabilities simultaneously. In recent years, this work of Païdoussis has been extended (e.g. De Langre et al. Reference De Langre, Païdoussis, Doaré and Modarres Sadeghi2007; Michelin & Smith Reference Michelin and Smith2009; Schouveiler & Eloy Reference Schouveiler and Eloy2009) and studied numerically both for a single cylinder (De Ridder et al. Reference De Ridder, Degroote, Van Tichelen and Vierendeels2013, Reference De Ridder, Doaré, Degroote, Van Tichelen, Schuurmans and Vierendeels2015) and for a cluster of cylinders (De Ridder et al. Reference De Ridder, Degroote, Van Tichelen and Vierendeels2017).
The flutter of a flexible cylinder in axial flow bears similarities with the flutter of an elastic plate often referred to as the flag instability. For a plate, two asymptotic limits can be studied: slender structures where Lighthill's slender body theory applies, and wide plates for which a two-dimensional approach is suited (Wu Reference Wu2001). For intermediate aspect ratios, the pressure distribution on a flexible plate can be solved by projecting the problem in Fourier space (Guo & Païdoussis Reference Guo and Païdoussis2000; Eloy, Souillez & Schouveiler Reference Eloy, Souillez and Schouveiler2007; Eloy et al. Reference Eloy, Lagrange, Souilliez and Schouveiler2008, Reference Eloy, Doaré, Duchemin and Schouveiler2010; Doaré, Mano & Bilbao Ludena Reference Doaré, Mano and Bilbao Ludena2011a; Doaré, Sauzade & Eloy Reference Doaré, Sauzade and Eloy2011b). With this projection, the approaches of slender body approximation and large span approximation can be generalised to any aspect ratio. In this paper, we will follow a similar approach to describe the flow around assemblies of flexible cylinders found in a PWR.
A different approach was proposed by Ricciardi et al. (Reference Ricciardi, Bellizzi, Collard and Cochelin2009) using a porous medium method. It now becomes possible to model both the fluid and the structure dynamics of a whole core. Some local information is lost compared to a direct numerical simulation, such as the vibrations of individual rods, but fluid-mediated interactions between fuel assemblies can be modelled. This model shows good agreement with experimental results on the response of the whole core to external forcing, but computational cost remains high.
At present, the models describing the fluid–structure interactions within a reactor core can be divided into two families: (1) complex numerical models with high computational costs, which usually hinder the understanding of physical mechanisms; and (2) linear models with low computational costs, which do not capture important mechanisms such as fluid-mediated interactions between assemblies. In this paper, we introduce a new model based on potential flow theory, with the objective of providing an accurate, computationally effective modelling of fluid–structure interactions within a reactor core.
The paper is organised as follows. In § 2, the model is presented and the mathematical methodology used to solve the problem is described. The model is then applied to a single cylinder in § 3, and compared to results of the literature for validation purposes. In § 4, it is applied to a multiple-cylinder geometry, replicating the geometry of an experimental facility. Numerical results are compared to experimental data and discussed in § 5. Finally, in § 6, some conclusions are drawn.
2. Potential flow model
In this section, we describe the proposed model where the fluid flow is treated as potential and the structure as an Euler–Bernoulli beam. The model is introduced for a single cylinder in axial flow, but as we shall see, it can be generalised to multiple cylinders.
2.1. Problem statement
We consider a pinned-pinned cylinder of length ![]() $L$ and radius
$L$ and radius ![]() $A$ (figure 1a). We will use two coordinate systems: a Cartesian system
$A$ (figure 1a). We will use two coordinate systems: a Cartesian system ![]() $(X,Y,Z)$ with its origin at the bottom of the cylinder, and a cylindrical system
$(X,Y,Z)$ with its origin at the bottom of the cylinder, and a cylindrical system ![]() $(R,\theta,Z)$ with the same origin (figure 1b).
$(R,\theta,Z)$ with the same origin (figure 1b).

Figure 1. Representation of a confined pinned-pinned cylinder deformed under axial flow in (a) real space and (b) Fourier space.
The cylinder is immersed in a uniform axial flow with velocity ![]() $U$ and bounded in the
$U$ and bounded in the ![]() $X$- and
$X$- and ![]() $Y$-directions by rigid walls at distances
$Y$-directions by rigid walls at distances ![]() $L_{x}$ and
$L_{x}$ and ![]() $L_{y}$ from the cylinder axis. Without loss of generality, we consider that the cylinder deflects in the
$L_{y}$ from the cylinder axis. Without loss of generality, we consider that the cylinder deflects in the ![]() $Y$-direction, and the deflection is called
$Y$-direction, and the deflection is called ![]() $W(Z,T)$ (figure 1a).
$W(Z,T)$ (figure 1a).
We use the linearised Euler–Bernoulli beam equation (Bauchau & Craig Reference Bauchau and Craig2009) to describe the dynamics of the cylinder deflection
where ![]() $M_s$ is the mass of the cylinder per unit length,
$M_s$ is the mass of the cylinder per unit length, ![]() $B=EI$ is the bending rigidity (
$B=EI$ is the bending rigidity (![]() $E$ being Young's modulus, and
$E$ being Young's modulus, and ![]() $I=({\rm \pi} A^{4})/{4}$ the second moment of area), and
$I=({\rm \pi} A^{4})/{4}$ the second moment of area), and ![]() $F_Y$ is the force per unit length that the fluid exerts on the cylinder in the
$F_Y$ is the force per unit length that the fluid exerts on the cylinder in the ![]() $Y$-direction.
$Y$-direction.
We assume that the forces exerted by the fluid on the structure originate mainly from pressure difference. Hence the force per unit length can be expressed as
where ![]() $P(R,\theta,Z,T)$ is the pressure field in cylindrical coordinates.
$P(R,\theta,Z,T)$ is the pressure field in cylindrical coordinates.
The problem is made dimensionless using the cylinder radius ![]() $A$, the flow velocity
$A$, the flow velocity ![]() $U$, and the fluid density
$U$, and the fluid density ![]() $\rho$ as characteristic length, speed and density. Dimensionless quantities are designated with lowercase letters such that, for instance,
$\rho$ as characteristic length, speed and density. Dimensionless quantities are designated with lowercase letters such that, for instance,
In dimensionless form, the linearised Euler–Bernoulli equation (2.1) becomes
where
The flow is assumed to be potential, inviscid and incompressible, such that the flow velocity is given by
where ![]() ${\boldsymbol {e}}_z$ is the unit vector along
${\boldsymbol {e}}_z$ is the unit vector along ![]() $z$, and
$z$, and ![]() $\varPhi (X,Y,Z,T)$ is the perturbation potential. In dimensionless units, this potential is
$\varPhi (X,Y,Z,T)$ is the perturbation potential. In dimensionless units, this potential is ![]() $\phi =\varPhi /(UA)$. To find the flow around the moving cylinder, one has to solve a Laplace problem with Neumann boundary conditions (linearised for small displacements):
$\phi =\varPhi /(UA)$. To find the flow around the moving cylinder, one has to solve a Laplace problem with Neumann boundary conditions (linearised for small displacements):
 $$\begin{gather}\left.\frac{\partial {\phi}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial {\phi}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$ $$\begin{gather}\left.\frac{\partial {\phi}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial {\phi}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$where (2.8) and (2.9) come from the impermeability of the walls, and (2.10) comes from the impermeability on the cylinder wall.
Using the linearised unsteady Bernoulli equation, the dimensionless pressure field can be linked to ![]() $\phi$ (Capanna Reference Capanna2018) by
$\phi$ (Capanna Reference Capanna2018) by
Using this relation and applying the operator ![]() $(\partial _{{t}}+\partial _{{z}})$ to the system (2.7)–(2.10) yields
$(\partial _{{t}}+\partial _{{z}})$ to the system (2.7)–(2.10) yields
 $$\begin{gather}\left.\frac{\partial {p}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial {p}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$ $$\begin{gather}\left.\frac{\partial {p}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial {p}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$
This shows that the pressure field is also a solution to a Laplace equation with Neumann boundary conditions. This is why the term ![]() $P/\rho$ is called the acceleration potential in aerofoil theory.
$P/\rho$ is called the acceleration potential in aerofoil theory.
2.2. Problem in Fourier space
To solve the set of equations (2.12)–(2.15), we will use the method proposed by Doaré et al. (Reference Doaré, Sauzade and Eloy2011b). It consists in expressing the Laplace problem in Fourier space along ![]() $z$ as
$z$ as
where ![]() $\hat {p}$ is the Fourier transform of
$\hat {p}$ is the Fourier transform of ![]() $p$, with
$p$, with ![]() $\mathcal {F}\left [ {{\cdot }} \right ]$ defined as
$\mathcal {F}\left [ {{\cdot }} \right ]$ defined as
together with the inverse Fourier transform
The convolution product along ![]() $z$, denoted
$z$, denoted ![]() $\star$, is also introduced
$\star$, is also introduced
In Fourier space, the three-dimensional Laplace problem is transformed into a two-dimensional Helmholtz problem:
 $$\begin{gather}\left.\frac{\partial \hat{p}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial \hat{p}}{\partial {x}}\right|_{|{x}|={l}_x} =0 , \end{gather}$$ $$\begin{gather}\left.\frac{\partial \hat{p}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$
$$\begin{gather}\left.\frac{\partial \hat{p}}{\partial {y}}\right|_{|{y}|={l}_y} =0 , \end{gather}$$
where ![]() $\hat {\gamma }(k,t)$ is the Fourier transform of the impermeability boundary condition, such that
$\hat {\gamma }(k,t)$ is the Fourier transform of the impermeability boundary condition, such that
Equation (2.2) relates the force per unit length exerted by the fluid on the cylinder and the pressure field. Using dimensionless quantities and taking the Fourier transform of (2.2), one obtains the equivalent in Fourier space:
where ![]() $\hat {f}_y$ is the Fourier transform of
$\hat {f}_y$ is the Fourier transform of ![]() $f_y$. Because the pressure
$f_y$. Because the pressure ![]() $\hat {p}$ is a solution of the linear Helmholtz problem (2.20)–(2.23), it is proportional to
$\hat {p}$ is a solution of the linear Helmholtz problem (2.20)–(2.23), it is proportional to ![]() $\hat {\gamma }(k, t)$. Hence (2.25) can be written as
$\hat {\gamma }(k, t)$. Hence (2.25) can be written as
where the function ![]() $\hat {\mu }(k)$ depends on
$\hat {\mu }(k)$ depends on ![]() $l_x$ and
$l_x$ and ![]() $l_y$ through the boundary conditions (2.21) and (2.22).
$l_y$ through the boundary conditions (2.21) and (2.22).
Equation (2.4) governing beam dynamics then becomes in Fourier space
showing that ![]() $\hat {\mu }$ plays the role of an added mass in Fourier space and that added damping
$\hat {\mu }$ plays the role of an added mass in Fourier space and that added damping ![]() $2{\rm i}k\hat {\mu }$ and added stiffness
$2{\rm i}k\hat {\mu }$ and added stiffness ![]() $-k^{2}\hat {\mu }$ are proportional to this added mass.
$-k^{2}\hat {\mu }$ are proportional to this added mass.
The objective now will be to calculate the added mass ![]() $\hat {\mu }(k)$. In practice, to calculate it, we can assume
$\hat {\mu }(k)$. In practice, to calculate it, we can assume ![]() $\hat {\gamma } = 1$, compute numerically the solution
$\hat {\gamma } = 1$, compute numerically the solution ![]() $\hat {p}$ of the Helmholtz problem (2.20)–(2.23) for different values of
$\hat {p}$ of the Helmholtz problem (2.20)–(2.23) for different values of ![]() $k$,
$k$, ![]() $l_x$ and
$l_x$ and ![]() $l_y$, and finally use (2.25) and (2.26) to compute
$l_y$, and finally use (2.25) and (2.26) to compute ![]() $\hat {\mu }(k)$.
$\hat {\mu }(k)$.
2.3. Modal decomposition and range of interest for  $k$
$k$
Considering an external forcing at a given frequency ![]() $\varOmega$, the displacement of the cylinder can be written in dimensionless form as
$\varOmega$, the displacement of the cylinder can be written in dimensionless form as
 \begin{equation} w(z,t) = \sum_{j=1}^{\infty}q_j(t)\,{\chi}j(z), \end{equation}
\begin{equation} w(z,t) = \sum_{j=1}^{\infty}q_j(t)\,{\chi}j(z), \end{equation}
where ![]() ${\chi}j (z)$ are the beam eigenmodes, and
${\chi}j (z)$ are the beam eigenmodes, and ![]() $q_j(t) = \eta _j\,{\rm e}^{{\rm i}\omega t}$ are the generalised coordinates, with
$q_j(t) = \eta _j\,{\rm e}^{{\rm i}\omega t}$ are the generalised coordinates, with ![]() $\eta _j$ the modal amplitudes (which do not depend on time), and
$\eta _j$ the modal amplitudes (which do not depend on time), and ![]() $\omega =\varOmega A/U$ the dimensionless forcing frequency.
$\omega =\varOmega A/U$ the dimensionless forcing frequency.
To determine the interesting range for ![]() $k$ for which
$k$ for which ![]() $\hat {\mu }$ should be computed, let us examine the eigenmodes
$\hat {\mu }$ should be computed, let us examine the eigenmodes ![]() ${\chi}j (z)$ and their Fourier transform
${\chi}j (z)$ and their Fourier transform ![]() $\hat {\chi }_j(k)$ for pinned-pinned beams. Eigenmodes are given by (Blevins Reference Blevins2015)
$\hat {\chi }_j(k)$ for pinned-pinned beams. Eigenmodes are given by (Blevins Reference Blevins2015)
where ![]() $l=L/A$ is the dimensionless cylinder length. Using this normalisation, the scalar product of two eigenmodes is
$l=L/A$ is the dimensionless cylinder length. Using this normalisation, the scalar product of two eigenmodes is
As figure 2(b) shows, ![]() $k$ values greater than
$k$ values greater than ![]() $10k_j$ have contributions at least 100 times smaller than low
$10k_j$ have contributions at least 100 times smaller than low ![]() $k$ values in Fourier space. Hence they can be truncated.
$k$ values in Fourier space. Hence they can be truncated.

Figure 2. (a) Eigenmodes for the first three modes of a pinned-pinned beam, and (b) their Fourier transforms.
Classical values for PWR beams are ![]() $A\in [10^{-3},10^{-2}]$ m and
$A\in [10^{-3},10^{-2}]$ m and ![]() $L\in [1,10]$ m. Hence classical slenderness ratios
$L\in [1,10]$ m. Hence classical slenderness ratios ![]() $l$ belong to
$l$ belong to ![]() $[10^{2},10^{4}]$, and dimensionless wavenumbers are
$[10^{2},10^{4}]$, and dimensionless wavenumbers are ![]() $k_j=j{\rm \pi} /l\in [3\times 10^{-4}, 0.3]$ when considering the first 10 modes. This implies that the interesting range for which
$k_j=j{\rm \pi} /l\in [3\times 10^{-4}, 0.3]$ when considering the first 10 modes. This implies that the interesting range for which ![]() $\hat {\mu }$ should be evaluated is roughly
$\hat {\mu }$ should be evaluated is roughly ![]() $k\in [10^{-4}, 10]$.
$k\in [10^{-4}, 10]$.
2.4. Equation of motion in generalised coordinates
Taking the Fourier transform of the modal decomposition (2.28), inserting it into the beam equation (2.27) in Fourier space, performing an inverse Fourier transform, and taking the scalar product (2.30) with the eigenmodes ![]() ${\chi}j$, gives a set of differential equations for the generalised coordinates
${\chi}j$, gives a set of differential equations for the generalised coordinates ![]() $q_i(t)$ that can be written in vector form as
$q_i(t)$ that can be written in vector form as
where ![]() $\boldsymbol {q}(t) = [q_1(t), q_2(t), \ldots ]^{\rm T}$ is the vector of generalised coordinates, the left-hand side corresponds to the unforced beam equation, and the right-hand side corresponds to the forcing by pressure forces. Here, we have omitted the external forcing term representing the seismic forcing.
$\boldsymbol {q}(t) = [q_1(t), q_2(t), \ldots ]^{\rm T}$ is the vector of generalised coordinates, the left-hand side corresponds to the unforced beam equation, and the right-hand side corresponds to the forcing by pressure forces. Here, we have omitted the external forcing term representing the seismic forcing.
The matrix ![]() $\boldsymbol{\mathsf{M}} = m \boldsymbol{\mathsf{I}}$, with
$\boldsymbol{\mathsf{M}} = m \boldsymbol{\mathsf{I}}$, with ![]() $\boldsymbol{\mathsf{I}}$ the identity matrix, is the mass matrix, and
$\boldsymbol{\mathsf{I}}$ the identity matrix, is the mass matrix, and ![]() $\boldsymbol{\mathsf{K}} = b\,\boldsymbol{\mathsf{diag}}(\{k_j^{4}\})$ is the stiffness matrix (where
$\boldsymbol{\mathsf{K}} = b\,\boldsymbol{\mathsf{diag}}(\{k_j^{4}\})$ is the stiffness matrix (where ![]() $\boldsymbol{\mathsf{diag}}(\{k_j^{4}\})$ means the diagonal matrix with
$\boldsymbol{\mathsf{diag}}(\{k_j^{4}\})$ means the diagonal matrix with ![]() $k_1^{4}$,
$k_1^{4}$, ![]() $k_2^{4}$, etc. on the diagonal). Equating the left-hand side of (2.31) to zero allows us to recover the eigenmodes and the eigenfrequencies
$k_2^{4}$, etc. on the diagonal). Equating the left-hand side of (2.31) to zero allows us to recover the eigenmodes and the eigenfrequencies ![]() $\omega _j = \sqrt {bk_j^{4}/m}$ of the beam in vacuum.
$\omega _j = \sqrt {bk_j^{4}/m}$ of the beam in vacuum.
The matrices ![]() $\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$,
$\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$, ![]() $\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and
$\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and ![]() $\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$ correspond to the added mass, added damping and added stiffness matrices, respectively. Their coefficients can be calculated as
$\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$ correspond to the added mass, added damping and added stiffness matrices, respectively. Their coefficients can be calculated as
where ![]() $\chi _j'$ and
$\chi _j'$ and ![]() $\chi _j''$ respectively denote first and second derivatives of
$\chi _j''$ respectively denote first and second derivatives of ![]() $\chi _j$,
$\chi _j$, ![]() $\mu = \mathcal {F}^{-1}\left [ {\hat \mu } \right ]$, and we have used the property (2.19) of the convolution product.
$\mu = \mathcal {F}^{-1}\left [ {\hat \mu } \right ]$, and we have used the property (2.19) of the convolution product.
We see here that knowledge of ![]() $\hat {\mu }(k)$ or
$\hat {\mu }(k)$ or ![]() $\mu (z)$ is enough to compute the matrices
$\mu (z)$ is enough to compute the matrices ![]() $\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$,
$\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$, ![]() $\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and
$\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and ![]() $\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$. In addition, these matrices depend only on the geometry of the problem (i.e. the wall distances
$\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$. In addition, these matrices depend only on the geometry of the problem (i.e. the wall distances ![]() $l_x$ and
$l_x$ and ![]() $l_y$) and not on the forcing. Finally, note that the Helmholtz problem (2.20) depends only on
$l_y$) and not on the forcing. Finally, note that the Helmholtz problem (2.20) depends only on ![]() $k^{2}$, which means that
$k^{2}$, which means that ![]() $\hat {\mu }(k)$ and
$\hat {\mu }(k)$ and ![]() $\mu (z)$ are real and even functions. The coefficients of the matrices
$\mu (z)$ are real and even functions. The coefficients of the matrices ![]() $\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$,
$\boldsymbol{\mathsf{M}}_{\boldsymbol{\mathsf{a}}}$, ![]() $\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and
$\boldsymbol{\mathsf{C}}_{\boldsymbol{\mathsf{a}}}$ and ![]() $\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$ are thus all real, as expected.
$\boldsymbol{\mathsf{K}}_{\boldsymbol{\mathsf{a}}}$ are thus all real, as expected.
3. Single cylinder
In this section, the numerical calculations performed for the single-cylinder geometry using the code implemented on FreeFEM![]() $++$ (Hecht Reference Hecht2012a,Reference Hechtb) will be presented. FreeFEM
$++$ (Hecht Reference Hecht2012a,Reference Hechtb) will be presented. FreeFEM![]() $++$ requires the weak formulation of problems. Problem (2.20)–(2.23) is then implemented as
$++$ requires the weak formulation of problems. Problem (2.20)–(2.23) is then implemented as
where ![]() $\partial \mathcal {C}$ denotes the rod's boundaries, and
$\partial \mathcal {C}$ denotes the rod's boundaries, and ![]() $\mathcal {D}$ denotes the fluid domain (see Appendix A).
$\mathcal {D}$ denotes the fluid domain (see Appendix A).
3.1. Meshing
As described previously, the numerical resolution of the problem takes advantage of the Fourier transform. This allows us to solve several two-dimensional problems, instead of solving a three-dimensional problem.
In this subsection, we present numerical solutions of the Helmholtz problem described by (2.20)–(2.23). Our objective is to compute the value of the function ![]() $\hat {\mu }(k;l_x,l_y)$ for different values of
$\hat {\mu }(k;l_x,l_y)$ for different values of ![]() $k$,
$k$, ![]() $l_x$ and
$l_x$ and ![]() $l_y$. Thanks to the symmetries of the problem, the equations may be solved on a quarter of the domain only (figure 3).
$l_y$. Thanks to the symmetries of the problem, the equations may be solved on a quarter of the domain only (figure 3).

Figure 3. Helmholtz problem represented in the FEM domain: limit conditions and example mesh for ![]() $k=0.01$,
$k=0.01$, ![]() $l_x=1.5$ and
$l_x=1.5$ and ![]() $l_y=2$.
$l_y=2$.
Before showing the results of these numerical computations, some considerations have to be made on the discretisation of the domain. A convergence study has been performed in order to find the optimal meshing for different combinations of wall distance and wavenumber. Typically, the size of the meshes must be decreased when the wavenumber ![]() $k$ is increased. In addition, the refinement of meshes will increase as the enclosure size decreases and when getting closer to the cylinder.
$k$ is increased. In addition, the refinement of meshes will increase as the enclosure size decreases and when getting closer to the cylinder.
Explored values are ![]() $k\in [10^{-5},10^{3}]$ and
$k\in [10^{-5},10^{3}]$ and ![]() $l_x,l_y\in [1.25,50]$. The variations of the number of cells in the mesh with
$l_x,l_y\in [1.25,50]$. The variations of the number of cells in the mesh with ![]() $l_x$ and
$l_x$ and ![]() $l_y$ do not depend on
$l_y$ do not depend on ![]() $k$: number of cells is maximum for
$k$: number of cells is maximum for ![]() $l_x=l_y=5$. This maximum is equal to 864 for
$l_x=l_y=5$. This maximum is equal to 864 for ![]() $k\leq 1$, and increases quadratically for
$k\leq 1$, and increases quadratically for ![]() $k>1$. The FreeFEM
$k>1$. The FreeFEM![]() $++$ code used in this study is included in Appendix A. Raw data can be found in the csv file attached to this paper; it contains the 2448 combinations of
$++$ code used in this study is included in Appendix A. Raw data can be found in the csv file attached to this paper; it contains the 2448 combinations of ![]() $l_x$,
$l_x$, ![]() $l_y$ and
$l_y$ and ![]() $k$ values, and the resulting
$k$ values, and the resulting ![]() $\hat {\mu }$ values.
$\hat {\mu }$ values.
3.2. General trends
Figure 4 shows the dependence of the added mass ![]() $\hat {\mu }$ on the wavenumber
$\hat {\mu }$ on the wavenumber ![]() $k$ for different values of the wall distances
$k$ for different values of the wall distances ![]() $l_x$ and
$l_x$ and ![]() $l_y$. It shows that the added mass does not change substantially for
$l_y$. It shows that the added mass does not change substantially for ![]() $k \lesssim 10^{-2}$ or
$k \lesssim 10^{-2}$ or ![]() $k \gtrsim 10^{2}$, for the enclosure sizes considered. This was expected because the only scales in the problem are the radius
$k \gtrsim 10^{2}$, for the enclosure sizes considered. This was expected because the only scales in the problem are the radius ![]() $a=1$ and the enclosure lengths
$a=1$ and the enclosure lengths ![]() $l_x$ and
$l_x$ and ![]() $l_y$, which are of order 1. Hence for
$l_y$, which are of order 1. Hence for ![]() $l_x$ and
$l_x$ and ![]() $l_y$ fixed, most variations of the added mass are expected to occur near
$l_y$ fixed, most variations of the added mass are expected to occur near ![]() $k\approx 1$. Note that the slenderness ratio of cylinders in a reactor core assembly is very large, and the range of relevant wavenumbers in this context is
$k\approx 1$. Note that the slenderness ratio of cylinders in a reactor core assembly is very large, and the range of relevant wavenumbers in this context is ![]() $k\in [3\times 10^{-4}, 0.3]$, as stressed already in § 2.3. For the sake of clarity, the raw data used for the plots in figure 4 are published online joint to this paper.
$k\in [3\times 10^{-4}, 0.3]$, as stressed already in § 2.3. For the sake of clarity, the raw data used for the plots in figure 4 are published online joint to this paper.

Figure 4. Value of ![]() $\hat {\mu }$ as function of the wavenumber
$\hat {\mu }$ as function of the wavenumber ![]() $k$ for different values of the wall distances
$k$ for different values of the wall distances ![]() $l_x$ and
$l_x$ and ![]() $l_y$. Dots denote computed values, and the solid line shows the fit (3.6), valid for
$l_y$. Dots denote computed values, and the solid line shows the fit (3.6), valid for ![]() $k\geq 10$. Wall distances are: (a)
$k\geq 10$. Wall distances are: (a) ![]() $l_x\leq 5$,
$l_x\leq 5$, ![]() $l_y\leq 5$; (b)
$l_y\leq 5$; (b) ![]() $l_x\leq 5$,
$l_x\leq 5$, ![]() $l_y > 5$; (c)
$l_y > 5$; (c) ![]() $l_x> 5$,
$l_x> 5$, ![]() $l_y> 5$; (d)
$l_y> 5$; (d) ![]() $l_x>5$,
$l_x>5$, ![]() $l_y\leq 5$.
$l_y\leq 5$.
3.3. Slender body limit
In the asymptotic limit of large wavelengths (![]() $k\ll 1$) and large enclosure sizes (
$k\ll 1$) and large enclosure sizes (![]() $l_x,l_y\gg 1$), we expect to recover the result of slender body theory (Lighthill Reference Lighthill1960b) given by (1.2), which in dimensionless form is
$l_x,l_y\gg 1$), we expect to recover the result of slender body theory (Lighthill Reference Lighthill1960b) given by (1.2), which in dimensionless form is
with ![]() $m_a = {\rm \pi}$, the added mass per unit length of a circular cylinder in dimensionless units. By analogy with (2.26), one thus expects
$m_a = {\rm \pi}$, the added mass per unit length of a circular cylinder in dimensionless units. By analogy with (2.26), one thus expects
and this is indeed what is found numerically when ![]() $l_x \gtrsim 10$,
$l_x \gtrsim 10$, ![]() $l_x \gtrsim 10$ and
$l_x \gtrsim 10$ and ![]() $k \lesssim 10^{-2}$ (figure 4c). This validates our numerical results for small wavenumbers
$k \lesssim 10^{-2}$ (figure 4c). This validates our numerical results for small wavenumbers ![]() $k$, in the limit of negligible enclosure sizes.
$k$, in the limit of negligible enclosure sizes.
3.4. Comparison with cylinder in annular enclosure
In the previous section, the numerical computations of the added mass have been validated in the limit of long wavelengths and large enclosure size by comparison with the slender body theory of Lighthill (Reference Lighthill1960b). In this section, we perform further comparisons with the theoretical results of Chen (Reference Chen1985) on a single cylinder confined in a concentric annular chamber. In a potential flow, the added mass of such a cylinder is
where ![]() $a_{ext}$ is the radius of the annular enclosure in dimensionless units.
$a_{ext}$ is the radius of the annular enclosure in dimensionless units.
We will compare this prediction with our numerical calculations of a cylinder in a square enclosure (![]() $l_x=l_y$). To perform this comparison, we need to relate the wall distances
$l_x=l_y$). To perform this comparison, we need to relate the wall distances ![]() $l_x=l_y$ to the annular radius
$l_x=l_y$ to the annular radius ![]() $a_{ext}$. One possibility is to use the hydraulic diameter equivalence, which leads to an annular radius
$a_{ext}$. One possibility is to use the hydraulic diameter equivalence, which leads to an annular radius
Alternatively, one can simply use the inscribed circle, which gives an annular radius ![]() $a_{insc}=l_x$. Finally, one can look for the best linear fit with the numerical data, which leads to
$a_{insc}=l_x$. Finally, one can look for the best linear fit with the numerical data, which leads to ![]() $a_{fit}=1.0775\,l_x$.
$a_{fit}=1.0775\,l_x$.
Figure 5 shows a comparison between our computations of the added mass for a square enclosure (![]() $l_x=l_y$ and
$l_x=l_y$ and ![]() $k\ll 1$) and the added mass predicted by (3.4) for an annular enclosure. This comparison shows that the effect of the square enclosure is equivalent to an annular enclosure with radius
$k\ll 1$) and the added mass predicted by (3.4) for an annular enclosure. This comparison shows that the effect of the square enclosure is equivalent to an annular enclosure with radius ![]() $a_{fit} = 1.0775\,l_x$. The hydraulic diameter equivalence gives a good estimate of the effect of the enclosure. This validates our numerical calculations in a square enclosure geometry in the limit
$a_{fit} = 1.0775\,l_x$. The hydraulic diameter equivalence gives a good estimate of the effect of the enclosure. This validates our numerical calculations in a square enclosure geometry in the limit ![]() $k\ll 1$.
$k\ll 1$.

Figure 5. Comparison between the computed added mass of a single cylinder in a square enclosure and the theoretical predictions of Chen (Reference Chen1985) for a concentric annular enclosure. (a) Geometry of the square enclosure (![]() $l_x=l_y=1.25$) superimposed with the three proposed annular enclosure radii:
$l_x=l_y=1.25$) superimposed with the three proposed annular enclosure radii: ![]() $a_{hydr}$,
$a_{hydr}$, ![]() $a_{insc}$ and
$a_{insc}$ and ![]() $a_{fit}$. (b) Comparison between our numerical results (dots) for
$a_{fit}$. (b) Comparison between our numerical results (dots) for ![]() $l_x=l_y$ and the prediction given by (3.4) for the three proposed radii (solid lines).
$l_x=l_y$ and the prediction given by (3.4) for the three proposed radii (solid lines).
3.5. Confinement effects
Figure 4 shows that ![]() $\hat {\mu }$ does change significantly for small values of
$\hat {\mu }$ does change significantly for small values of ![]() $k$, but still depends on the wall distances
$k$, but still depends on the wall distances ![]() $l_x$ and
$l_x$ and ![]() $l_y$ when
$l_y$ when ![]() $l_x \lesssim 5$ or
$l_x \lesssim 5$ or ![]() $l_y \lesssim 5$. Two extreme cases can be considered: (1) a small value of the wavenumber
$l_y \lesssim 5$. Two extreme cases can be considered: (1) a small value of the wavenumber ![]() $k= 10^{-5}$; and (2) a large value
$k= 10^{-5}$; and (2) a large value ![]() $k= 10$.
$k= 10$.
Figure 6 shows how the added mass depends on both ![]() $l_x$ and
$l_x$ and ![]() $l_y$ for the two extreme wavenumbers considered (
$l_y$ for the two extreme wavenumbers considered (![]() $k= 10^{-5}$ and
$k= 10^{-5}$ and ![]() $k=10$). For
$k=10$). For ![]() $k= 10^{-5}$, the enclosure length along the
$k= 10^{-5}$, the enclosure length along the ![]() $x$-direction has much more influence than its counterpart along the
$x$-direction has much more influence than its counterpart along the ![]() $y$-direction (figure 6a). For
$y$-direction (figure 6a). For ![]() $k=10$, it is the opposite. Note, however, that these effects have different magnitudes: for
$k=10$, it is the opposite. Note, however, that these effects have different magnitudes: for ![]() $k= 10^{-5}$, the value of
$k= 10^{-5}$, the value of ![]() $\hat {\mu }$ roughly triples between
$\hat {\mu }$ roughly triples between ![]() $l_x=10$ and
$l_x=10$ and ![]() $l_x=1.25$, while for
$l_x=1.25$, while for ![]() $k=10$,
$k=10$, ![]() $\hat {\mu }$ varies by only 15 % between
$\hat {\mu }$ varies by only 15 % between ![]() $l_y=10$ and
$l_y=10$ and ![]() $l_y=1.25$.
$l_y=1.25$.

Figure 6. Confinement effects for (a) small wavenumbers and (b) large wavenumbers.
Figure 4 thus shows that for large wavenumbers, the dependency on the enclosure size is weak. Assuming that ![]() $\hat {\mu }$ is independent of
$\hat {\mu }$ is independent of ![]() $l_x$ and
$l_x$ and ![]() $l_y$ for large
$l_y$ for large ![]() $k$ values, we can find a power-law approximation of
$k$ values, we can find a power-law approximation of ![]() $\hat {\mu }$ displayed as black solid line in figure 4:
$\hat {\mu }$ displayed as black solid line in figure 4:
For small wavenumbers, although the cylinder can move only in the ![]() $y$-direction, it is the wall distance along
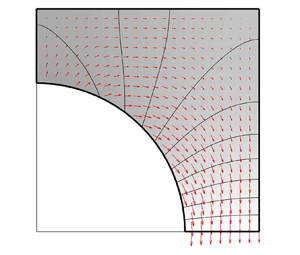
$y$-direction, it is the wall distance along ![]() $x$ that has the strongest influence. To better understand this paradoxical result, we plot the velocity field in the Fourier space (figure 7). For
$x$ that has the strongest influence. To better understand this paradoxical result, we plot the velocity field in the Fourier space (figure 7). For ![]() $k= 10^{-5}$, a strong flow in the
$k= 10^{-5}$, a strong flow in the ![]() $y$-direction (opposite to the cylinder displacement) is observed along the wall
$y$-direction (opposite to the cylinder displacement) is observed along the wall ![]() $x=l_x$ around the cylinder diameter (
$x=l_x$ around the cylinder diameter (![]() $y\approx 0$), as shown in figure 7(a). For large wavenumbers, however, no such flow is observed (figure 7b). By virtue of mass conservation, when the wall distance along
$y\approx 0$), as shown in figure 7(a). For large wavenumbers, however, no such flow is observed (figure 7b). By virtue of mass conservation, when the wall distance along ![]() $x$ is reduced, this flow increases. This is why there is a strong dependency of the fluid–structure interaction force on the
$x$ is reduced, this flow increases. This is why there is a strong dependency of the fluid–structure interaction force on the ![]() $x$-direction confinements for small wavenumbers.
$x$-direction confinements for small wavenumbers.

Figure 7. Velocity and pressure fields in Fourier space for both small and large wavenumbers.
Finally, for all the wavenumbers that have been considered and for all enclosure sizes, the added mass ![]() $\hat {\mu }$ appears to increase as the enclosure lengths decrease (in both directions). This observation is in agreement with the literature on channel flows by Chen & Wambsganss (Reference Chen and Wambsganss1972), Chen (Reference Chen1985) and Païdoussis & Pettigrew (Reference Païdoussis and Pettigrew1979).
$\hat {\mu }$ appears to increase as the enclosure lengths decrease (in both directions). This observation is in agreement with the literature on channel flows by Chen & Wambsganss (Reference Chen and Wambsganss1972), Chen (Reference Chen1985) and Païdoussis & Pettigrew (Reference Païdoussis and Pettigrew1979).
The calculations performed for a single-cylinder geometry allowed us to prove the reliability of the proposed simplified model. The introduction of the potential flow theory and the use of Fourier transforms are key to relate directly the cylinder displacement and the resulting pressure force.
This approach leads to fast calculations for any kind of geometry. In the next section, it will be applied to a group of cylinders and compared to experimental results in the same geometry.
4. Assemblies of cylinders
This section is dedicated to a geometry with multiple cylinders. This geometry is built to represent the four surrogate fuel bundles of the experimental facility ICARE that we used to validate our results.
4.1. ICARE experimental apparatus
The ICARE experimental facility is made of a closed water loop powered by a centrifugal pump, the test section, a compensation tank and a heat exchanger (figure 8). The test section is placed in vertical position with a square section measuring ![]() $22.5\ {\rm cm}\times 22.5\ {\rm cm}$, and hosts up to four fuel assemblies arranged in a
$22.5\ {\rm cm}\times 22.5\ {\rm cm}$, and hosts up to four fuel assemblies arranged in a ![]() $2 \times 2$ lattice. The length of the fuel assemblies is
$2 \times 2$ lattice. The length of the fuel assemblies is ![]() $L=2.57$ m. Each of them constitutes a square lattice of
$L=2.57$ m. Each of them constitutes a square lattice of ![]() $8\times 8$ rods, in which there are 60 rods simulating fuel rods made of acrylic, and four stainless steel guide tubes. The guide tubes are empty inside, and they are welded to five metallic spacer grids along the length of the assembly. The guide tubes have a structural function since they give rigidity to the assembly and they hold together fuel rods. Each assembly has a section measuring
$8\times 8$ rods, in which there are 60 rods simulating fuel rods made of acrylic, and four stainless steel guide tubes. The guide tubes are empty inside, and they are welded to five metallic spacer grids along the length of the assembly. The guide tubes have a structural function since they give rigidity to the assembly and they hold together fuel rods. Each assembly has a section measuring ![]() $10.1 \times 10.1\ {\rm cm}^{2}$, and the 60 rods constituting it have diameter
$10.1 \times 10.1\ {\rm cm}^{2}$, and the 60 rods constituting it have diameter ![]() $2A=9$ mm with pin pitch
$2A=9$ mm with pin pitch ![]() $P/(2A) = 1.39$. The top and bottom of the assembly are fixed rigidly to the guide tubes, and they are fixed to the test section through the lower and upper support plates.
$P/(2A) = 1.39$. The top and bottom of the assembly are fixed rigidly to the guide tubes, and they are fixed to the test section through the lower and upper support plates.

Figure 8. Scheme of the ICARE experimental facility. LDV, laser Doppler velocimetry.
A hydraulic actuator applies dynamic forcing to one of the four fuel assemblies (assembly [1] in figure 8). This forcing in one dimension aims to simulate an earthquake. The actuator is screwed into one of the grids of the assembly, and a force sensor is installed in between the actuator and the stem.
The test section is equipped with 24 linear variable differential transformer (LVDT) position sensors to measure the displacement of each grid in two directions (figure 9). For more details on the ICARE experiment, please refer to Capanna et al. (Reference Capanna, Ricciardi, Eloy and Sarrouy2019).

Figure 9. Scheme of the displacement sensors on the ICARE test section.
4.2. Problem geometry and meshing
The ICARE geometry is implemented in the code to allow for comparison with experiments with large (![]() $C=8$ mm) or small (
$C=8$ mm) or small (![]() $C=4$ mm) confinements (figures 10(a) and 10(b), respectively). Confinement size denotes the length of the gap between different assemblies and between the assemblies and the walls. For both confinement sizes, the distance in between the rods of the same assembly remains the same.
$C=4$ mm) confinements (figures 10(a) and 10(b), respectively). Confinement size denotes the length of the gap between different assemblies and between the assemblies and the walls. For both confinement sizes, the distance in between the rods of the same assembly remains the same.

Figure 10. Meshes for the two configurations simulating the ICARE set-up. These two geometries differ only by the value of the confinement ![]() $C$, as pictured. (a) Four assemblies in large confinement. (b) Four assemblies in small confinement.
$C$, as pictured. (a) Four assemblies in large confinement. (b) Four assemblies in small confinement.
Assemblies are numbered as depicted in figure 10(a). As in the experiments, the rods of assembly [1] are forced along the ![]() $x$-direction, and they all exhibit the same displacement
$x$-direction, and they all exhibit the same displacement ![]() $w_{x}^{[1]}(z,t)$. Those rods are assumed not to move along the
$w_{x}^{[1]}(z,t)$. Those rods are assumed not to move along the ![]() $y$-direction, and the rods in the other assemblies are assumed not to move.
$y$-direction, and the rods in the other assemblies are assumed not to move.
Based on § 3, the Helmholtz problem to solve is
where the superscripts ![]() $[n]$ refer to the assembly number,
$[n]$ refer to the assembly number, ![]() ${\partial}C^{[n]}$ denotes the boundaries of rods of assembly
${\partial}C^{[n]}$ denotes the boundaries of rods of assembly ![]() $[n]$ (with
$[n]$ (with ![]() $\theta$ the local polar angle for each rod), and
$\theta$ the local polar angle for each rod), and
As in § 3, the solution ![]() $\hat {p}$ of the Helmholtz problem (4.1) is proportional to
$\hat {p}$ of the Helmholtz problem (4.1) is proportional to ![]() ${\hat\omega}_{x}^{[1]}$, and one can define added masses
${\hat\omega}_{x}^{[1]}$, and one can define added masses ![]() $\hat {\mu }_x^{[n]}$ and
$\hat {\mu }_x^{[n]}$ and ![]() $\hat {\mu }_y^{[n]}$ from the forces exerted on each assembly:
$\hat {\mu }_y^{[n]}$ from the forces exerted on each assembly:
In practice, ![]() $\hat {\mu }_x^{[n]}$ and
$\hat {\mu }_x^{[n]}$ and ![]() $\hat {\mu }_y^{[n]}$ can be calculated by assuming
$\hat {\mu }_y^{[n]}$ can be calculated by assuming ![]() ${\hat\omega}_{x}^{[1]}=1$ and numerically solving the Helmholtz problem (4.1) for
${\hat\omega}_{x}^{[1]}=1$ and numerically solving the Helmholtz problem (4.1) for ![]() $\hat {p}$. The convergence of the calculations depends on the mesh size. We thus conducted a convergence study and found that convergence is ensured when the walls are divided into at least
$\hat {p}$. The convergence of the calculations depends on the mesh size. We thus conducted a convergence study and found that convergence is ensured when the walls are divided into at least ![]() $150$ sections, and the cylinder borders into
$150$ sections, and the cylinder borders into ![]() $50$ sections. The calculations presented here have been performed with
$50$ sections. The calculations presented here have been performed with ![]() $200$ divisions on the external walls and
$200$ divisions on the external walls and ![]() $75$ divisions on the cylinder borders, which corresponds to approximately 500 000 cells in the domain and a computing time of about 60 s.
$75$ divisions on the cylinder borders, which corresponds to approximately 500 000 cells in the domain and a computing time of about 60 s.
Figure 11 shows the results of these computations for ![]() $k\in [10^{-5}, 10]$. In Appendix B, we detail these results for individual rods. As in the single-cylinder case, the added masses do not change much for extreme values of
$k\in [10^{-5}, 10]$. In Appendix B, we detail these results for individual rods. As in the single-cylinder case, the added masses do not change much for extreme values of ![]() $k$, i.e.
$k$, i.e. ![]() $k\lesssim 10^{-2}$ or
$k\lesssim 10^{-2}$ or ![]() $k\gtrsim 1$, except for assembly
$k\gtrsim 1$, except for assembly ![]() $[1]$, the forced assembly. For large
$[1]$, the forced assembly. For large ![]() $k$, the added masses converge to zero.
$k$, the added masses converge to zero.

Figure 11. Added masses ![]() $\hat {\mu }_x^{[n]}$ (blue solid line) and
$\hat {\mu }_x^{[n]}$ (blue solid line) and ![]() $\hat {\mu }_y^{[n]}$ (red dashed line) on each assembly (in Fourier space) for different values of
$\hat {\mu }_y^{[n]}$ (red dashed line) on each assembly (in Fourier space) for different values of ![]() $k$.
$k$.
4.3. Equations of motion in real space
The functions ![]() $\hat {\mu }_x^{[n]}(k)$ and
$\hat {\mu }_x^{[n]}(k)$ and ![]() $\hat {\mu }_y^{[n]}(k)$ can be interpolated using piecewise sixth-order polynomials, which can then be used to calculate
$\hat {\mu }_y^{[n]}(k)$ can be interpolated using piecewise sixth-order polynomials, which can then be used to calculate ![]() ${\mu }_x^{[n]}(z)$ and
${\mu }_x^{[n]}(z)$ and ![]() ${\mu }_y^{[n]}(z)$ with an inverse Fourier transform (Appendix C). By analogy with the calculations for a single cylinder done in § 2.4, we can define added mass, added damping and added stiffness matrices for the assemblies too. There are 24 such matrices: 3 kinds (mass
${\mu }_y^{[n]}(z)$ with an inverse Fourier transform (Appendix C). By analogy with the calculations for a single cylinder done in § 2.4, we can define added mass, added damping and added stiffness matrices for the assemblies too. There are 24 such matrices: 3 kinds (mass ![]() $\boldsymbol{\mathsf{M}}$, damping
$\boldsymbol{\mathsf{M}}$, damping ![]() $\boldsymbol{\mathsf{C}}$, stiffness
$\boldsymbol{\mathsf{C}}$, stiffness ![]() $\boldsymbol{\mathsf{K}}$), 2 axes (
$\boldsymbol{\mathsf{K}}$), 2 axes (![]() $x$ and
$x$ and ![]() $y$, subscript
$y$, subscript ![]() $\circ$) and 4 assemblies, noted with the superscript
$\circ$) and 4 assemblies, noted with the superscript ![]() $[n]$. Similarly to (2.32a–c), these matrices are expressed using the added masses
$[n]$. Similarly to (2.32a–c), these matrices are expressed using the added masses ![]() ${\mu }_\circ ^{[n]}(z)$:
${\mu }_\circ ^{[n]}(z)$:
where ![]() $\chi _i(z)$ is the
$\chi _i(z)$ is the ![]() $i$th beam eigenmode defined in (2.29).
$i$th beam eigenmode defined in (2.29).
Because it is forced at mid-height, we can assume that assembly [1] moves mainly in its first beam eigenmode, i.e. ![]() $w_x^{[1]}(z,t) = q_x^{[1]}(t)\,\chi _1(z)$. We can assume further that the added mass and added stiffness matrices are diagonal, and that the added damping is negligible (Appendix C). With these hypotheses, the equation of motion for the
$w_x^{[1]}(z,t) = q_x^{[1]}(t)\,\chi _1(z)$. We can assume further that the added mass and added stiffness matrices are diagonal, and that the added damping is negligible (Appendix C). With these hypotheses, the equation of motion for the ![]() $x$-component of assembly [1] is
$x$-component of assembly [1] is
where ![]() $m_s=64m$ is the dimensionless mass of one assembly per unit length,
$m_s=64m$ is the dimensionless mass of one assembly per unit length, ![]() $k_s = 64 b k_1^{4}$ is its stiffness,
$k_s = 64 b k_1^{4}$ is its stiffness, ![]() $c_v$ accounts for the damping induced by the viscosity effect,
$c_v$ accounts for the damping induced by the viscosity effect, ![]() $m_x^{[1]}$ and
$m_x^{[1]}$ and ![]() $k_x^{[1]}$ denote the component
$k_x^{[1]}$ denote the component ![]() $(1,1)$ of the added matrices
$(1,1)$ of the added matrices ![]() $\boldsymbol{\mathsf{M}}_x^{[1]}$ and
$\boldsymbol{\mathsf{M}}_x^{[1]}$ and ![]() $\boldsymbol{\mathsf{K}}_x^{[1]}$, and
$\boldsymbol{\mathsf{K}}_x^{[1]}$, and ![]() $f_e\,{\rm e}^{{\rm i}\omega t}$ is the external forcing projected onto the first eigenmode, with
$f_e\,{\rm e}^{{\rm i}\omega t}$ is the external forcing projected onto the first eigenmode, with ![]() $f_e$ a scalar. The
$f_e$ a scalar. The ![]() $m_x^{[1]}$ and
$m_x^{[1]}$ and ![]() $k_x^{[1]}$ coefficients represent the added mass and stiffness encountered by an assembly that moves in its first mode in either the
$k_x^{[1]}$ coefficients represent the added mass and stiffness encountered by an assembly that moves in its first mode in either the ![]() $x$-direction or the
$x$-direction or the ![]() $y$-direction. Here, we consider only a weak coupling between the assemblies, such that we can neglect the hydrodynamic forces due to the motion of the other assemblies on assembly
$y$-direction. Here, we consider only a weak coupling between the assemblies, such that we can neglect the hydrodynamic forces due to the motion of the other assemblies on assembly ![]() $[1]$ (the validity of this assumption will be assessed below). The solution of (4.5) is simply
$[1]$ (the validity of this assumption will be assessed below). The solution of (4.5) is simply
with the transfer function
It is possible to estimate the motion of assemblies [2], [3] and [4] by considering the superimposition of the two following cases: still rods undergoing fluid forces induced by assembly [1] on the one hand, and moving rods undergoing fluid forces generated by their own movement while other assemblies stand still:
where the coefficients ![]() $m_x^{[1]}$,
$m_x^{[1]}$, ![]() $c_v$ and
$c_v$ and ![]() $k_x^{[1]}$ appear on the left-hand side because, by symmetry, they also correspond to the pressure force induced by the motion
$k_x^{[1]}$ appear on the left-hand side because, by symmetry, they also correspond to the pressure force induced by the motion ![]() $q_\circ ^{[n]}$ on the assembly
$q_\circ ^{[n]}$ on the assembly ![]() $[n]$ itself. The right-hand side represents the action of assembly [1] motion via the fluid.
$[n]$ itself. The right-hand side represents the action of assembly [1] motion via the fluid.
From (4.4c), we see that the added stiffness is ![]() $k_\circ ^{[n]} = -k_1^{2} m_\circ ^{[n]}$, with
$k_\circ ^{[n]} = -k_1^{2} m_\circ ^{[n]}$, with ![]() $k_1 = {\rm \pi}/l$ (since
$k_1 = {\rm \pi}/l$ (since ![]() $\chi _i'' = -k_i^{2} \chi _i$). We will now assume that
$\chi _i'' = -k_i^{2} \chi _i$). We will now assume that ![]() $\omega \gg k_1$, which is true here because typical values of
$\omega \gg k_1$, which is true here because typical values of ![]() $\omega$ are around 0.3, and
$\omega$ are around 0.3, and ![]() $l \approx 571$. This means that the added stiffness term
$l \approx 571$. This means that the added stiffness term ![]() $k_\circ ^{[n]}$ can be neglected compared to the added mass term
$k_\circ ^{[n]}$ can be neglected compared to the added mass term ![]() $-\omega ^{2} m_\circ ^{[n]}$ in (4.5) and (4.8). The values of the added masses
$-\omega ^{2} m_\circ ^{[n]}$ in (4.5) and (4.8). The values of the added masses ![]() $m_\circ ^{[n]}$ are given in table 1. From this table, we see that the ratio of added masses
$m_\circ ^{[n]}$ are given in table 1. From this table, we see that the ratio of added masses ![]() $m_\circ ^{[n]} / m_x^{[1]}$ is at most 21 % (for
$m_\circ ^{[n]} / m_x^{[1]}$ is at most 21 % (for ![]() $n>1$). This justifies neglecting the hydrodynamic forces due to the motion of the assemblies
$n>1$). This justifies neglecting the hydrodynamic forces due to the motion of the assemblies ![]() $[n]$ onto assembly
$[n]$ onto assembly ![]() $[1]$, which can be estimated as the square of this ratio and is thus of order 4 % at most.
$[1]$, which can be estimated as the square of this ratio and is thus of order 4 % at most.
Table 1. Added mass matrix coefficients for small and large confinements.

Under these hypotheses, we can calculate the displacement ratio at the forcing frequency ![]() $\omega$ as
$\omega$ as
 \begin{equation} \frac{q_\circ^{[n]}}{q_x^{[1]}} \approx{-}\frac{-\omega^{2} m_\circ^{[n]}}{-\omega^{2} (m_s + m_x^{[1]}) + {\rm i}\omega c_v + k_s}, \end{equation}
\begin{equation} \frac{q_\circ^{[n]}}{q_x^{[1]}} \approx{-}\frac{-\omega^{2} m_\circ^{[n]}}{-\omega^{2} (m_s + m_x^{[1]}) + {\rm i}\omega c_v + k_s}, \end{equation}
which becomes, at the resonant frequency ![]() $\omega _{res}$,
$\omega _{res}$,
 \begin{equation} \frac{q_\circ^{[n]}}{q_x^{[1]}} \approx{-}{\rm i} \omega_{res}\, \frac{m_\circ^{[n]}}{c_v}, \quad \mbox{with } {-\omega}_{res}^{2} (m_s + m_x^{[1]}) + k_s = 0. \end{equation}
\begin{equation} \frac{q_\circ^{[n]}}{q_x^{[1]}} \approx{-}{\rm i} \omega_{res}\, \frac{m_\circ^{[n]}}{c_v}, \quad \mbox{with } {-\omega}_{res}^{2} (m_s + m_x^{[1]}) + k_s = 0. \end{equation}
Note that this equation is applicable only to ![]() $n\neq$1.
$n\neq$1.
4.4. Comparison with a periodic assembly of cylinders
The model presented above allows us to compute the added mass of an assembly of cylinders organised in a square array. A qualitative comparison can be made with an infinite assembly made of a periodic arrangement of cylinders (Pettigrew & Taylor Reference Pettigrew and Taylor2003). In this case, by analogy with (3.4), the added mass of each cylinder is expressed as
 \begin{equation} \hat{\mu}={\rm \pi}\,\frac{a_{equiv}^{2}+1}{a_{equiv}^{2}-1}, \end{equation}
\begin{equation} \hat{\mu}={\rm \pi}\,\frac{a_{equiv}^{2}+1}{a_{equiv}^{2}-1}, \end{equation}
where ![]() $a_{equiv}$ is a measure of the equivalent confinement that can be approximated as
$a_{equiv}$ is a measure of the equivalent confinement that can be approximated as
with ![]() $p=P/A$, the period along
$p=P/A$, the period along ![]() $x$ and
$x$ and ![]() $y$ of the arrangement.
$y$ of the arrangement.
Using the value ![]() $P/A=2.78$ of the ICARE assemblies, (4.11) corresponds to an added mass per cylinder
$P/A=2.78$ of the ICARE assemblies, (4.11) corresponds to an added mass per cylinder ![]() $\hat {\mu }=4.26$. Considering an assembly made of 64 cylinders, the total added mass is
$\hat {\mu }=4.26$. Considering an assembly made of 64 cylinders, the total added mass is ![]() $m_x=274$. This value can be compared to the value
$m_x=274$. This value can be compared to the value ![]() $m_x^{[1]}=350$ obtained in our simulations (table 1). The two values are of the same order, but in the ICARE geometry, the presence of other assemblies and of the walls tends to increase the added mass.
$m_x^{[1]}=350$ obtained in our simulations (table 1). The two values are of the same order, but in the ICARE geometry, the presence of other assemblies and of the walls tends to increase the added mass.
5. Comparison with experimental results
This section compares results obtained using the simplified model and results from a set of experiments conducted on the ICARE facility described in § 4.1. Experiments are performed imposing a sine sweep ranging from 0 to 10 Hz with constant amplitude 1 mm and axial fluid velocity ![]() $1\ {\rm m}\ {\rm s}^{-1}$ when water is present. To catch the transfer function of a system using a swept sinusoidal excitation, the sweep rate needs to be small enough to avoid any transient phenomena and contamination of different harmonics in the system. For these experiments, a sweep rate of
$1\ {\rm m}\ {\rm s}^{-1}$ when water is present. To catch the transfer function of a system using a swept sinusoidal excitation, the sweep rate needs to be small enough to avoid any transient phenomena and contamination of different harmonics in the system. For these experiments, a sweep rate of ![]() $0.05\ {\rm Hz}\ {\rm s}^{-1}$ is applied, respecting the international standard ISO-7626 indications. The frequency range embraces assembly [1] first and second mode in water.
$0.05\ {\rm Hz}\ {\rm s}^{-1}$ is applied, respecting the international standard ISO-7626 indications. The frequency range embraces assembly [1] first and second mode in water.
5.1. Added mass
Let us consider the transfer function ![]() $H^{[1]}_{exp}$ between the displacement
$H^{[1]}_{exp}$ between the displacement ![]() $W^{[1]}_{x}$ along
$W^{[1]}_{x}$ along ![]() $x$ of the grid with vertical position
$x$ of the grid with vertical position ![]() $Z_w$, and the force
$Z_w$, and the force ![]() $F_{g}$ applied by the actuator on the grid with position
$F_{g}$ applied by the actuator on the grid with position ![]() $Z_f$. Since the data are acquired with a swept sinusoidal excitation, the transfer functions are calculated using the cross-correlation product, and are defined as
$Z_f$. Since the data are acquired with a swept sinusoidal excitation, the transfer functions are calculated using the cross-correlation product, and are defined as
 \begin{equation} H^{[1]}_{exp}=\left\|\frac{W^{[1]}_{x} \star W^{[1]}_{x}}{W^{[1]}_{x} \star F_{x}}\right\|, \end{equation}
\begin{equation} H^{[1]}_{exp}=\left\|\frac{W^{[1]}_{x} \star W^{[1]}_{x}}{W^{[1]}_{x} \star F_{x}}\right\|, \end{equation}
where ![]() $W^{[1]}_{x} \star W^{1]}_{x}$ is the spectral autocorrelation of the displacement signal of the first assembly along the
$W^{[1]}_{x} \star W^{1]}_{x}$ is the spectral autocorrelation of the displacement signal of the first assembly along the ![]() $x$-direction, and
$x$-direction, and ![]() $W^{[1]}_{x} \star F_{x}$ is the spectral cross-correlation between the displacement signal of the first assembly and the force imposed on the first assembly. Cross-correlation functions are calculated using an Hamming windowing filter (5000 points per windows) to clean up the noise from the signal.
$W^{[1]}_{x} \star F_{x}$ is the spectral cross-correlation between the displacement signal of the first assembly and the force imposed on the first assembly. Cross-correlation functions are calculated using an Hamming windowing filter (5000 points per windows) to clean up the noise from the signal.
The theoretical transfer function modulus for a one-degree-of-freedom system is given by
where ![]() $M_e$,
$M_e$, ![]() $C_e$ and
$C_e$ and ![]() $K_e$ are the coefficients of mass, damping and stiffness identified, and
$K_e$ are the coefficients of mass, damping and stiffness identified, and ![]() $\varOmega$ is the circular frequency.
$\varOmega$ is the circular frequency.
Assembly [1] is excited around its first mode; to identify its dynamical properties, one has to find ![]() $M_e$,
$M_e$, ![]() $C_e$ and
$C_e$ and ![]() $K_e$ that make
$K_e$ that make ![]() $H^{[1]}_{theo}$ fit the experimental data
$H^{[1]}_{theo}$ fit the experimental data ![]() $H^{[1]}_{exp}$. This can be achieved easily by a conjugate gradient optimisation method.
$H^{[1]}_{exp}$. This can be achieved easily by a conjugate gradient optimisation method.
Using an Euler–Bernoulli beam model for the rods as described in (2.1), one can write the virtual work of assembly [1] as
 \begin{align} &M_t\int^{L}_{0}\partial^{2}_T W^{[1]}_{x}\,\delta W\,{\rm d}Z+C_t\int^{L}_{0}\partial_T W^{[1]}_{x}\,\delta W\,{\rm d}Z+ B_t\int^{L}_{0}\partial^{2}_Z W^{[1]}_{x}\,\partial^{2}_Z\delta W\,{\rm d}Z\nonumber\\ &\quad=\int_0^{L}F_{g}\,\delta_{Z_f}\,\delta W\,{\rm d}Z, \end{align}
\begin{align} &M_t\int^{L}_{0}\partial^{2}_T W^{[1]}_{x}\,\delta W\,{\rm d}Z+C_t\int^{L}_{0}\partial_T W^{[1]}_{x}\,\delta W\,{\rm d}Z+ B_t\int^{L}_{0}\partial^{2}_Z W^{[1]}_{x}\,\partial^{2}_Z\delta W\,{\rm d}Z\nonumber\\ &\quad=\int_0^{L}F_{g}\,\delta_{Z_f}\,\delta W\,{\rm d}Z, \end{align}with
where ![]() $M_f$ and
$M_f$ and ![]() $B_f$ are respectively the participation of the fluid into mass and stiffness,
$B_f$ are respectively the participation of the fluid into mass and stiffness, ![]() $C_t$ is a linear damping coefficient, and the sum accounts for the 64 rods inside the assembly.
$C_t$ is a linear damping coefficient, and the sum accounts for the 64 rods inside the assembly.
When the structure vibrates on its ![]() $j{\rm th}$ natural mode,
$j{\rm th}$ natural mode,
with ![]() $X_j(Z)={\chi}j (Z/A)$, one can rewrite the energy of the system as
$X_j(Z)={\chi}j (Z/A)$, one can rewrite the energy of the system as
Noting that the experimental signal is
one can relate the mass per unit of length to the identified coefficient
 \begin{equation} M_t=\frac{X_1(Z_f)\,X_1(Z_w)}{\displaystyle\int^{L}_{0}X_1^{2}\,{\rm d}Z}\,M_e. \end{equation}
\begin{equation} M_t=\frac{X_1(Z_f)\,X_1(Z_w)}{\displaystyle\int^{L}_{0}X_1^{2}\,{\rm d}Z}\,M_e. \end{equation} Measurements take into account the effect of the fluid added mass ![]() $M_f$ and the mass of the structure
$M_f$ and the mass of the structure ![]() $M_s$, therefore to isolate the fluid added mass, the participation of the structure is subtracted, based on experimental results obtained in air. Finally, one then obtains the results listed in table 2 where added mass values are provided for the whole assembly,
$M_s$, therefore to isolate the fluid added mass, the participation of the structure is subtracted, based on experimental results obtained in air. Finally, one then obtains the results listed in table 2 where added mass values are provided for the whole assembly,
To get a comparison with results from numerical simulation obtained in § 4, the following transformation is applied
where ![]() $\rho =1000\ {\rm kg}\ {\rm m}^{-3}$ is the water density.
$\rho =1000\ {\rm kg}\ {\rm m}^{-3}$ is the water density.
Table 2. Values of added mass ![]() $M^{[1]}_x$.
$M^{[1]}_x$.

Table 2 shows the values of added mass for large and narrow confinement given by experiments and simulations. Both agree on the increase of added mass when the confinement gets narrower. Experiments give a large increase, more than double, whereas simulations predict an increase of about 10 %. Although the order of magnitude is respected, the differences observed could cast doubt on the validity of the model. To analyse these results properly, one has to keep in mind that the methodology used to obtain the experimental results is subject to uncertainties coming from the accuracy of measurement, the optimisation process, and the fact that we try to identify constants of a linear one-degree-of-freedom system from a complex nonlinear system. As a result, one could estimate that the added mass coefficient given by the simulations is a reasonable estimation.
The added stiffness is orders of magnitude smaller than the ‘in air’ structural stiffness: the added stiffness estimated from simulations in § 4 is about ![]() $4.7\ {\rm N}\ {\rm m}^{2}$, while the measured flexural stiffness of a fuel assembly is about
$4.7\ {\rm N}\ {\rm m}^{2}$, while the measured flexural stiffness of a fuel assembly is about ![]() $2300\ {\rm N}\ {\rm m}^{2}$. As a consequence, we cannot extract the added stiffness from the total stiffness measured experimentally.
$2300\ {\rm N}\ {\rm m}^{2}$. As a consequence, we cannot extract the added stiffness from the total stiffness measured experimentally.
5.2. Coupling
To characterise the coupling between the fuel assemblies induced by the fluid, let us consider the transfer function between the imposed displacement and the displacement of the other fuel assemblies at the third grid level in the two transverse directions. Similarly to (5.1), transfer functions are calculated as
 \begin{equation} H^{[n]}_{{\circ}}=\left\|\frac{W^{[n]}_{{\circ}} \star W^{[n]}_{{\circ}}}{W^{[n]}_{{\circ}} \star W^{[1]}_{x}}\right\|,\quad \circ{\in}\{x,y\}, \end{equation}
\begin{equation} H^{[n]}_{{\circ}}=\left\|\frac{W^{[n]}_{{\circ}} \star W^{[n]}_{{\circ}}}{W^{[n]}_{{\circ}} \star W^{[1]}_{x}}\right\|,\quad \circ{\in}\{x,y\}, \end{equation}
where ![]() $W^{[n]}$ is the displacement signal of the
$W^{[n]}$ is the displacement signal of the ![]() $n$th assembly along the
$n$th assembly along the ![]() $\circ$ direction.
$\circ$ direction.
For each transfer function, the maximum value – which occurs at the first natural frequency – is accounted for. These experimental results are compared to the displacement ratio given by (4.10), with the added mass coefficients ![]() $m_\circ ^{[n]}$ given in table 1, and
$m_\circ ^{[n]}$ given in table 1, and ![]() $c_v$ and
$c_v$ and ![]() $\omega _{res}$ estimated from identification of dynamical parameters using (5.6) as follows:
$\omega _{res}$ estimated from identification of dynamical parameters using (5.6) as follows:
 \begin{equation} C_v=\frac{X_1(Z_f)\,X_1(Z_w)}{\displaystyle\int^{L}_{0}X_1^{2}\,{\rm d}Z}\,C_e, \quad c_v=\frac{C_v}{\rho UA}, \quad \omega_{res}=\frac{A}{U}\sqrt{\frac{K_e}{M_e}}. \end{equation}
\begin{equation} C_v=\frac{X_1(Z_f)\,X_1(Z_w)}{\displaystyle\int^{L}_{0}X_1^{2}\,{\rm d}Z}\,C_e, \quad c_v=\frac{C_v}{\rho UA}, \quad \omega_{res}=\frac{A}{U}\sqrt{\frac{K_e}{M_e}}. \end{equation}
Experimental values give ![]() $c_v=69.2$ and
$c_v=69.2$ and ![]() $\omega _{res}=0.12$.
$\omega _{res}=0.12$.
Figure 12 compares graphically the displacement ratios as observed in the experiments with the ratios predicted by (4.10) with these values of ![]() $c_v$ and
$c_v$ and ![]() $\omega _{res}$. Experiments show a ratio of about 10 % for most of the fuel assemblies in the two directions except for fuel assembly [3], which shows a coupling of about 20 % in the direction of forcing. Although simulations seem to underestimate the values of coupling, they give a good prediction of the order of magnitude. Moreover, the general pattern is well reproduced, with a significantly more important coupling for fuel assembly [3] in the direction of forcing. Therefore, the methodology developed seems to be appropriate to simulate the coupling between fuel assemblies.
$\omega _{res}$. Experiments show a ratio of about 10 % for most of the fuel assemblies in the two directions except for fuel assembly [3], which shows a coupling of about 20 % in the direction of forcing. Although simulations seem to underestimate the values of coupling, they give a good prediction of the order of magnitude. Moreover, the general pattern is well reproduced, with a significantly more important coupling for fuel assembly [3] in the direction of forcing. Therefore, the methodology developed seems to be appropriate to simulate the coupling between fuel assemblies.

Figure 12. Displacement ratios obtained by experimental data (a) and approximated from numerical simulations (b) for four fuel assemblies in large confinement at first natural frequency.
6. Conclusions
In this paper, a new model for fluid–structure interaction of PWR fuel assemblies is proposed. The model used the well-known potential flow theory, and the equations are solved by using a Fourier approach. This approach leads to the important result of relating the fluid–structure interaction forces directly to the displacement of the structure itself. This result is an important achievement since it allows us to reduce computational time drastically, avoiding the necessity to solve fluid equations. As a drawback, it should be considered that the assumption of potential flow leads us to neglect completely the fuel grids, which introduce vorticity in the flow.
Calculations with a potential flow model are first performed for a single-cylinder geometry, and results have been compared with reference works in the literature. The model showed perfect agreement with the slender body model, and it also shows good predictions with respect to the confinement size. The model has been validated, thus the mathematical approach used to solve the equations has been demonstrated to be consistent and reliable. The model was thus improved for multiple-cylinder geometries.
Finally, in order to validate the multiple-cylinder model, calculations simulating the ICARE geometry are discussed and compared with experimental results. Modal parameters are identified as functions of the flow rates and compared with experimental ones. The model fits reasonably experimental data for the added mass, and gives a good estimation of the coupling between fuel assemblies.
Many perspectives are opened as a result of this work. As discussed in this paper, the model that has been implemented does not account for viscous forces. An improvement that would be of fundamental importance is to introduce with empirical factors the viscous forces in the model. One possible way to introduce viscosity in the model is to consider the axial water flow as the sum of two flows: a potential bulk flow and a viscous flow that has a defined empirical distribution. In this way, the viscous forces would be taken into account with an empirical formulation, and it would be extremely interesting to assess the effects of such improvements, especially on the added damping coefficient estimation.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2022.433.
Funding
The authors are grateful for the financial support of Electricité de France (EDF) and FRAMATOME.
Declaration of interests
The authors report no conflict of interest.
Appendix A. FreeFEM $++$ code for single cylinder
$++$ code for single cylinder

Appendix B. Qualitative analysis
After solving numerically the Helmholtz problem (4.1) for ![]() $\hat {\gamma }_x^{[1]} = 1$, the resulting forces on each rod
$\hat {\gamma }_x^{[1]} = 1$, the resulting forces on each rod ![]() $q$ of each assembly
$q$ of each assembly ![]() $n$ can be evaluated in both the
$n$ can be evaluated in both the ![]() $x$- and
$x$- and ![]() $y$-directions. From this, we can calculate the associated added masses
$y$-directions. From this, we can calculate the associated added masses ![]() $\hat {\mu }_x^{[n,q]}$ and
$\hat {\mu }_x^{[n,q]}$ and ![]() $\hat {\mu }_y^{[n,q]}$:
$\hat {\mu }_y^{[n,q]}$:
with ![]() ${\partial}C^{[n,q]}$ the boundary of rod
${\partial}C^{[n,q]}$ the boundary of rod ![]() $q$ in assembly
$q$ in assembly ![]() $n$. Note that
$n$. Note that ![]() $\hat {\mu }_x^{[n,q]}$ and
$\hat {\mu }_x^{[n,q]}$ and ![]() $\hat {\mu }_y^{[n,q]}$ are unchanged when
$\hat {\mu }_y^{[n,q]}$ are unchanged when ![]() $k$ is changed into
$k$ is changed into ![]() $-k$ since
$-k$ since ![]() $k$ always appears squared in the problem.
$k$ always appears squared in the problem.
These added masses are illustrated in figures 13 and 14 for the 8 mm confinement.

Figure 13. Added mass ![]() $\hat {\mu }_x^{[n,q]}$ along
$\hat {\mu }_x^{[n,q]}$ along ![]() $x$ for each rod for four values of
$x$ for each rod for four values of ![]() $k$, as labelled. Solid circles note positive values, hollow ones negative values. The confinement is 8 mm.
$k$, as labelled. Solid circles note positive values, hollow ones negative values. The confinement is 8 mm.

Figure 14. Same as figure 13 for the ![]() $y$-component of the added mass,
$y$-component of the added mass, ![]() $\hat {\mu }_y^{[n,q]}$.
$\hat {\mu }_y^{[n,q]}$.
Analogy with the single-cylinder case explains the positive values observed on assembly [1] for ![]() $\hat {\mu }_x^{[n,q]}$. Confinement size is about the rod diameter, which may be compared to
$\hat {\mu }_x^{[n,q]}$. Confinement size is about the rod diameter, which may be compared to ![]() $l_x = l_y=3$ in §§ 3.3 and 3.4 for which
$l_x = l_y=3$ in §§ 3.3 and 3.4 for which ![]() $\hat {\mu }>{\rm \pi}$ when
$\hat {\mu }>{\rm \pi}$ when ![]() $k\ll 1$. This is consistent with the values observed for assembly [1] (even though the rods are not confined properly). An interesting result is that rods in assemblies [2], [3] and [4] experience very small forces. As noted in § 3.5, this phenomenon is all the more true as
$k\ll 1$. This is consistent with the values observed for assembly [1] (even though the rods are not confined properly). An interesting result is that rods in assemblies [2], [3] and [4] experience very small forces. As noted in § 3.5, this phenomenon is all the more true as ![]() $k$ becomes large: pressure perturbations remain closer to the moving rods when
$k$ becomes large: pressure perturbations remain closer to the moving rods when ![]() $k$ is large, and interactions with far away rods are almost negligible.
$k$ is large, and interactions with far away rods are almost negligible.
Appendix C. Calculation of pressure forces in physical space
In § 4.3, we explained how to compute numerically the functions ![]() $\hat {\mu }_\circ ^{[n]}(k)$, which are then interpolated with piecewise sixth-order polynomials. These interpolations can be used to compute the added masses
$\hat {\mu }_\circ ^{[n]}(k)$, which are then interpolated with piecewise sixth-order polynomials. These interpolations can be used to compute the added masses ![]() ${\mu }_\circ ^{[n]}(z)$ with an inverse Fourier transform (figure 15).
${\mu }_\circ ^{[n]}(z)$ with an inverse Fourier transform (figure 15).

Figure 15. Added mass ![]() $\mu _x^{[n]}(z)$ (blue solid line) and
$\mu _x^{[n]}(z)$ (blue solid line) and ![]() $\mu _y^{[n]}(z)$ (red dashed line) as a function of
$\mu _y^{[n]}(z)$ (red dashed line) as a function of ![]() $z$ for the different assemblies (large confinement).
$z$ for the different assemblies (large confinement).
The functions ![]() ${\mu }_\circ ^{[n]}(z)$ are needed in (4.4a–c) to compute the added mass, added damping and added stiffness matrices. Note that the functions
${\mu }_\circ ^{[n]}(z)$ are needed in (4.4a–c) to compute the added mass, added damping and added stiffness matrices. Note that the functions ![]() $\mu _\circ ^{[n]}(z)$ are non-zero on an interval
$\mu _\circ ^{[n]}(z)$ are non-zero on an interval ![]() $\Delta z \lesssim 100$ (figure 15). This means that on a
$\Delta z \lesssim 100$ (figure 15). This means that on a ![]() $z$-scale of order
$z$-scale of order ![]() $l = L / A \approx 571$, these functions are almost proportional to a Dirac function, such that the convolution products between
$l = L / A \approx 571$, these functions are almost proportional to a Dirac function, such that the convolution products between ![]() $\mu _\circ ^{[n]}$ and
$\mu _\circ ^{[n]}$ and ![]() $\chi _j$,
$\chi _j$, ![]() $\chi _j'$ or
$\chi _j'$ or ![]() $\chi _j''$ appearing in (4.4a–c) can be approximated by simple product with
$\chi _j''$ appearing in (4.4a–c) can be approximated by simple product with ![]() $\int _{-\infty }^{\infty } \mu _\circ ^{[n]} \,{\rm d}z$.
$\int _{-\infty }^{\infty } \mu _\circ ^{[n]} \,{\rm d}z$.
As a consequence, the added mass matrix ![]() $\boldsymbol{\mathsf{M}}_\circ ^{[n]}$ and the added stiffness matrix
$\boldsymbol{\mathsf{M}}_\circ ^{[n]}$ and the added stiffness matrix ![]() $\boldsymbol{\mathsf{K}}_\circ ^{[n]}$ are almost diagonal (since
$\boldsymbol{\mathsf{K}}_\circ ^{[n]}$ are almost diagonal (since ![]() $\langle \chi _i, \chi _j\rangle = \delta _{ij}$) and the diagonal terms of the added damping matrix
$\langle \chi _i, \chi _j\rangle = \delta _{ij}$) and the diagonal terms of the added damping matrix ![]() $\boldsymbol{\mathsf{C}}_\circ ^{[n]}$ are almost zero (since
$\boldsymbol{\mathsf{C}}_\circ ^{[n]}$ are almost zero (since ![]() $\langle \chi _i, \chi _i'\rangle = 0$). This can be verified by computing the first
$\langle \chi _i, \chi _i'\rangle = 0$). This can be verified by computing the first ![]() $3\times 3$ terms of the matrices
$3\times 3$ terms of the matrices ![]() $\boldsymbol{\mathsf{M}}_x^{[n]}$ and
$\boldsymbol{\mathsf{M}}_x^{[n]}$ and ![]() $\boldsymbol{\mathsf{C}}_x^{[n]}$ for
$\boldsymbol{\mathsf{C}}_x^{[n]}$ for ![]() $n=1$ and
$n=1$ and ![]() $4$ (we chose assembly
$4$ (we chose assembly ![]() $[4]$ because it is the assembly for which the extension of
$[4]$ because it is the assembly for which the extension of ![]() ${\mu }_x^{[n]}(z)$ is widest; see figure 15):
${\mu }_x^{[n]}(z)$ is widest; see figure 15):
 $$\begin{gather} \boldsymbol{\mathsf{M}}_x^{[1]} = \begin{pmatrix} 350 & 0 & 0.0182 \\ 0 & 347 & 0 \\ 0.0182 & 0 & 342 \end{pmatrix}, \end{gather}$$
$$\begin{gather} \boldsymbol{\mathsf{M}}_x^{[1]} = \begin{pmatrix} 350 & 0 & 0.0182 \\ 0 & 347 & 0 \\ 0.0182 & 0 & 342 \end{pmatrix}, \end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{M}}_x^{[4]} = \begin{pmatrix}18.6 & 0 & 0.0882 \\ 0 & 17.4 & 0 \\ 0.0882 & 0 & 15.4 \end{pmatrix}, \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{M}}_x^{[4]} = \begin{pmatrix}18.6 & 0 & 0.0882 \\ 0 & 17.4 & 0 \\ 0.0882 & 0 & 15.4 \end{pmatrix}, \end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{C}}_x^{[1]} = \begin{pmatrix}0 & -3.26 & 0 \\ 3.26 & 0 & -5.79 \\ 0 & 5.79 & 0 \end{pmatrix}, \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{C}}_x^{[1]} = \begin{pmatrix}0 & -3.26 & 0 \\ 3.26 & 0 & -5.79 \\ 0 & 5.79 & 0 \end{pmatrix}, \end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{C}}_x^{[4]} = \begin{pmatrix}0 & -0.167 & 0 \\ 0.167 & 0 & -0.272 \\ 0 & 0.272 & 0 \end{pmatrix}. \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{C}}_x^{[4]} = \begin{pmatrix}0 & -0.167 & 0 \\ 0.167 & 0 & -0.272 \\ 0 & 0.272 & 0 \end{pmatrix}. \end{gather}$$Note that the matrices ![]() $\boldsymbol{\mathsf{K}}_\circ ^{[n]}$ satisfy
$\boldsymbol{\mathsf{K}}_\circ ^{[n]}$ satisfy ![]() $(\boldsymbol{\mathsf{K}}_\circ ^{[n]})_{ij} = -k_j^{2}\, (\boldsymbol{\mathsf{M}}_\circ ^{[n]})_{ij}$, such that they share the same characteristic of being almost diagonal with the matrices
$(\boldsymbol{\mathsf{K}}_\circ ^{[n]})_{ij} = -k_j^{2}\, (\boldsymbol{\mathsf{M}}_\circ ^{[n]})_{ij}$, such that they share the same characteristic of being almost diagonal with the matrices ![]() $\boldsymbol{\mathsf{M}}_\circ ^{[n]}$.
$\boldsymbol{\mathsf{M}}_\circ ^{[n]}$.