1. INTRODUCTION
Deep ice cores from polar ice sheets are one of the best climate archives available today. Mostly even and undisturbed annual layering of snow at the surface and physically, chemically and biologically stable conditions within the ice enable climate reconstructions at a resolution and precision unmatched by other geological archives. They are the only palaeoclimatic archive that permits the reconstruction of the greenhouse gas history of the past 800 000 a (800 ka) (Lüthi and others, Reference Lüthi2008). Ice cores contain information about the depositional and dynamical history of their ice sheets for the entire span for which ice can be recovered. However, in order to avoid interference with poorly known past variations in ice flow, drill sites are almost exclusively chosen in regions with assumed negligible dynamical variations and therefore only used to reconstruct the depositional history (e.g. Dahl-Jensen and others, Reference Dahl-Jensen1997; Marshall and Cuffey, Reference Marshall and Cuffey2000). In contrast, marine sedimentary records are routinely used to reconstruct not only the local surface climate but also dynamic variations in flow (Hay, Reference Hay1988).
Numerical ice-sheet modelling faces a somewhat complementary problem. Here, the simulated ice velocities are known with high precision at all locations in the ice sheet, but are very rarely compared with the well-known vertical profiles reconstructed from ice core archives. Replication of these high-quality archives may be an obvious target for the validation of numerical models, but the simulation of key variables like the age of the ice since its accumulation or oxygen isotopic ratios (δ 18O) faces technical difficulties that are fundamental enough to render this challenge virtually unsurmountable for most of the existing ice-sheet models (Greve, Reference Greve1997b; Tarasov and Peltier, Reference Tarasov and Peltier2002). Not only models would benefit from a better representation of englacial tracers. A synergistic effort would also allow for ice cores to be obtained from previously unsuitable regions and their records could be used more effectively to also infer past dynamical changes.
Geophysical modelling almost universally uses the Eulerian description of flow with its grid fixed in space. Discretization of differential equations on such a grid is known to produce spurious diffusion in the simulated fields, which is most detrimental in finely layered, highly variable fields such as the tracers along a vertical section through the Greenland ice sheet (GrIS). Past attempts to ameliorate this problem include representing tracer variables indirectly with provenance labels (Clarke and Marshall, Reference Clarke and Marshall2002). These fields of depositional latitude, longitude and time are much smoother and less prone to numerical diffusion. The record of when and where ice accumulated at the surface then permits reconstructions of the desired variables. As a refinement of this approach, Clarke and others (Reference Clarke, Lhomme and Marshall2005) replaced the Eulerian flow scheme with a semi-Lagrangian description, first proposed by Tarasov and Peltier (Reference Tarasov and Peltier2003). This further reduces diffusion by tracking tracer grid points backward in time and finding their location at the beginning of the current time step. The result is a good agreement with reconstructed ice core data when past boundary conditions at the surface are prescribed (Clarke and others, Reference Clarke, Lhomme and Marshall2005; Lhomme and others, Reference Lhomme, Clarke and Marshall2005). This method adds considerable computational cost due to the required interpolation in three-dimensional (3-D) space.
In this study, I present a new approach to tracer modelling in ice sheets. Instead of adding to the complexity of an existing model by separating the tracer transport from the calculation of ice flow, a new vertical discretization of the model grid is proposed. Vertical layers are not fixed in space as in the Eulerian description, but represent the accumulation of a certain period. Thus, they are fixed in time or isochronal. Over time, layers will thin with ice flow toward the margins, which allows younger layers to subside. Hence, vertical motion in the ice resembles the Lagrangian description of flow and does not require any flow across vertical layer boundaries, eliminating numerical diffusion entirely. Since flow in the horizontal is much faster than in the vertical and tracer fields are much smoother, advection in the lateral direction uses the common Eulerian description with grid points fixed in space. In its present form, the model represents a zonal section through the summit of the GrIS so that the flow in the single horizontal dimension is the same as through a pipe of variable diameter determined by the layer thickness.
The isochronal ice-sheet model is thoroughly tested by varying its key parameters. It is forced with accumulation and temperature as reconstructed for the past 50 ka from the GISP2 ice core (Cuffey and Clow, Reference Cuffey and Clow1997; Alley, Reference Alley2000b), and produces a good agreement with observed data for ice-surface topography, borehole temperature and δ 18O. It is shown that the latter ensures that also the internal structure of the ice sheet is correctly simulated, which can not be inferred from a good representation of the surface topography alone.
This paper is organized as follows. Section 2 describes the isochronal ice-sheet model in detail. The numerical robustness and accuracy of the model are documented for idealized simulations in Section 3. In Section 4, the simulated central Greenland ice core record and other observations are used to determine the optimal model parameters. One simulation with the best reproduction of the GISP2 δ 18O record is discussed in detail in Section 5. Finally, I discuss and conclude in Section 6.
2. THE ISOCHRONAL ICE-SHEET MODEL
The model presented here employs the shallow ice approximation with a temperature dependent flow law. The advection of ice in turn transports heat and creates heat by friction so that this model includes full thermodynamic coupling.
The ice-sheet model is set up to represent a zonal section through the summit of the GrIS. Although the basic concept of isochronal layers does not impede a simulation of the entire ice sheet in three dimensions, this simplified application allows the full complexity of the physical and numerical problems to be investigated at a viable numerical cost. The section through the summit is a reasonable approximation of the ice flow in the real world and more complex 3-D models (e.g., Greve, Reference Greve1997a), where the motion is mostly parallel to this 2-D plane due to much smaller ice surface gradients in the perpendicular direction. This situation did not fundamentally change during the last glacial cycle, during which the summit was approximately stationary (Tarasov and Peltier, Reference Tarasov and Peltier2003). Boundary conditions for surface climate and bed topography are based on the ETOPO1 dataset for present day (Amante and Eakins, Reference Amante and Eakins2009), averaged between 70°N and 75°N and adjusted for isostatic rebound.
2.1. Discretization
The vertical discretization of the model is the primary novelty of the isochronal model. The model grid is empty at the beginning of the simulation and is subsequently filled with layers of accumulated ice as the simulation time progresses. In contrast to existing ice-sheet models, the thickness of these accumulation layers is a prognostic model variable. Spacing between layers is not equidistant in space but in time, hence ‘isochronal’. Flow between layers does not occur so that they uniquely identify their time of deposition, comparable with a Lagrangian description of the flow field.
The horizontal discretization is equidistant in space with a regular spacing of 10 km. All model variables, including layer thickness, are advected along the horizontal as a finite-difference, Eulerian flow on a staggered grid (Fig. 1). Thus, the model mixes a Eulerian description in the horizontal with a Lagrangian flow in the vertical dimension and is therefore also ‘semi-Lagrangian’, although not in the traditional sense (e.g. Staniforth and Côté, Reference Staniforth and Côté1991) and fundamentally different from Tarasov and Peltier (Reference Tarasov and Peltier2003) and Clarke and others (Reference Clarke, Lhomme and Marshall2005).
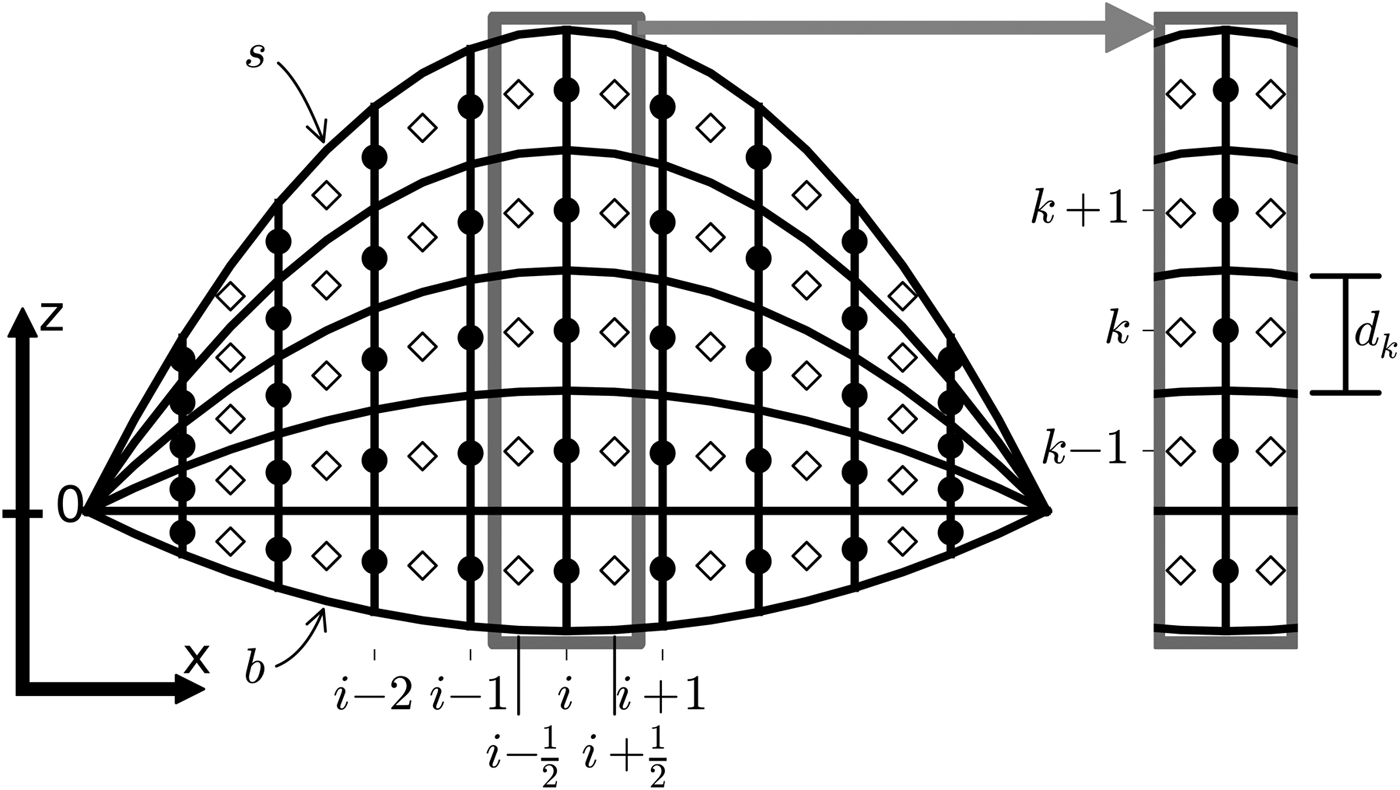
Fig. 1. Schematic of the ice-sheet model. Open diamonds represent the locations of grid box centres where all tracer quantities are calculated. Horizontal ice velocities are calculated at the boundaries of the grid boxes (black circles).
Simulations presented here run for 250 ka with accumulation layers representing 50 a each. This results in a total of 5000 vertical layers, considerably exceeding the resolution of commonly used ice-sheet models. This high level of detail is not required by the isochronal method but necessary to simulate the small-scale fluctuations found in ice core data (Table 1). The spacing of individual layers does not need to be equidistant (in time).
Table 1. List of model constants. Parameters that are varied in the ensemble simulations are highlighted

2.2. Calculation of ice flow velocities
Ice sheets are typically much thinner than their lateral extent, which makes it possible to neglect longitudinal stresses over the much greater shear stresses between horizontal layers of ice, the widely used shallow ice approximation (Hutter, Reference Hutter1983; Morland, Reference Morland1984). Using the empirical nonlinear flow law for ice by Glen (Reference Glen1955), the horizontal velocity can be integrated from the bottom up to any elevation z:
where u b is the velocity of basal sliding, ρ ice is the density of the ice, g the gravitational acceleration, and ∂ x s is the partial derivative of the surface elevation s in the horizontal direction, the surface slope. The elevation of the bedrock is denoted as b. The exponent n is empirically determined from data and commonly chosen to be 3. The flow velocity depends on the slope of the ice-surface elevation ∂ x s and the flow factor A that scales with temperature.
The temperature relative to the pressure melting point T* is defined such that melting always occurs at 0°C:
where the Clausius–Clapeyron constant γ accounts for the effect of the pressure of the overlying ice. The flow factor A is calculated as
where R is the universal gas constant, and A 0 and Q are constants to approximate the internal ice thermodynamics piecewise for temperatures above and below T* = −10°C (Paterson and Budd, Reference Paterson and Budd1982; Payne and others, Reference Payne2000):
This piecewise definition accounts for the increased plasticity near the pressure melting point.
![]() $E({z}^{\prime})$
in Eqn (1) is a somewhat arbitrary flow enhancement factor used to parameterize faster flow due to anisotropies and impurities in the ice crystal structure that are not accounted for by the theory (Fisher and Koerner, Reference Fisher and Koerner1986). The flow law by Glen (Reference Glen1955) is largely based on borehole closure rates in relatively clean recent ice. Ice accumulated during glacial times was probably subject to stronger winds and therefore higher deposition rates of dust on the GrIS (Paterson, Reference Paterson1991; Crowley and North, Reference Crowley and North1991), which would soften the ice and enhance the flow. In the simulations presented here, E has a default value of 3 for ice older and 1 for ice younger than 10 000 a. The sensitivity of the ice-sheet model to this parameter is explored below. A comprehensive derivation of the velocity Eqn (1) including a full description of the accompanying assumptions and relevant references is found in Greve and Blatter (Reference Greve and Blatter2009).
$E({z}^{\prime})$
in Eqn (1) is a somewhat arbitrary flow enhancement factor used to parameterize faster flow due to anisotropies and impurities in the ice crystal structure that are not accounted for by the theory (Fisher and Koerner, Reference Fisher and Koerner1986). The flow law by Glen (Reference Glen1955) is largely based on borehole closure rates in relatively clean recent ice. Ice accumulated during glacial times was probably subject to stronger winds and therefore higher deposition rates of dust on the GrIS (Paterson, Reference Paterson1991; Crowley and North, Reference Crowley and North1991), which would soften the ice and enhance the flow. In the simulations presented here, E has a default value of 3 for ice older and 1 for ice younger than 10 000 a. The sensitivity of the ice-sheet model to this parameter is explored below. A comprehensive derivation of the velocity Eqn (1) including a full description of the accompanying assumptions and relevant references is found in Greve and Blatter (Reference Greve and Blatter2009).
Because of the high vertical resolution of the ice-sheet model, especially near the bed where several of the above assumptions no longer apply, the flow at the lower boundary requires an additional parameterization that is not common in ice-sheet modelling. Similar to dust deposited on the top of the ice sheet, silt is taken up from its bed and admixed into the lower layers of ice, softening it significantly (Johnsen and Dansgaard, Reference Johnsen and Dansgaard1992). This enhances the vertical strain rate in this silty layer and effectively lubricates the flow above, resulting in much thinner layers close to the bed than would be expected from ice flow represented by Eqn (1) alone. Accounting for this lubrication improves the dating of ice cores (Johnsen and Dansgaard, Reference Johnsen and Dansgaard1992), and the comparison with independent dating methods suggests that the velocity at the bed is ~15% of that at the ice surface, although this ratio will likely have a geographic dependence. In the ice-sheet model, after integration of Eqn (1), velocities in the entire ice column are adjusted to be at least 15% of the surface velocity. The effect of this lubrication is qualitatively similar to basal sliding but at much smaller velocities. It is independent of the temperature of the ice.
Basal sliding is represented using a linear law (Payne and others, Reference Payne2000):
where A sl is the basal sliding parameter and h is the total ice thickness. Basal sliding is limited to regions where the temperature at the bed is at the pressure melting point (T* >0°C).
2.3. Horizontal advection of volume
Advection in the horizontal dimension resembles a flow through a pipe of variable diameter. Changes in the layer thickness d are a result of a divergence of the flow of volume F:
where ∂ t and ∂ x represent partial derivatives in time and space, respectively.
Equation (7) is discretized forward in time and upstream in space, using velocities at the border of the grid boxes (i ± 1/2; Fig. 1; also see Appendix). The total ice thickness is the sum of all layer thicknesses in the vertical dimension
The bedrock is known to subside under the load of thick ice sheets with potentially important effects on their surface climate and thereby their volume (Oerlemans, Reference Oerlemans1981, Reference Oerlemans1982). This effect can conveniently be described by the ice sinking toward hydrostatic equilibrium with a time delay expressed as a relaxation:
where τ
b is the relaxation time, ρ
rock the average density of the earth's crust and b
0 the equilibrium elevation of the relaxed bedrock without ice load. To obtain b
0, it is assumed that the GrIS is near equilibrium with its subsided bed in recent times. This is a good approximation because neither the surface height of the ice sheet nor its lateral extent changed dramatically during the last glacial cycle and through the Holocene, which is a long time compared with typical values of τ
b of 3000 a. Thus, b
0 is calculated by adding a third (
![]() $ \approx {\hskip-2pt} \rho _{{\rm ice}}/\rho _{{\rm rock}}$
) of the present ice thickness to the present bed elevation as provided in the ETOPO1 dataset (Amante and Eakins, Reference Amante and Eakins2009).
$ \approx {\hskip-2pt} \rho _{{\rm ice}}/\rho _{{\rm rock}}$
) of the present ice thickness to the present bed elevation as provided in the ETOPO1 dataset (Amante and Eakins, Reference Amante and Eakins2009).
After updating h and b in each model time step, the surface elevation is calculated as the sum of those two: s = b + h .
2.4. Horizontal advection of heat and passive tracers
The flow of the ice depends on its temperature (Eqn (1)), which evolves according to
where the first term represents horizontal heat advection due to the lateral heat transport Q, the second and the third terms are horizontal and vertical diffusion of heat, respectively, with the diffusivity α. Φ represents heating due to friction and geothermal heat flux. Vertical advection of heat is represented implicitly by the Lagrangian formulation of the vertical flow and is thus not explicitly included in Eqn (10). Given the conceptual separation of horizontal and vertical processes by the isochronal grid of the model, lateral transport of heat and other tracers is treated here, while vertical diffusion, friction and geothermal heating will be detailed separately in the next section.
For the relatively large horizontal grid spacing, heat diffusion in this dimension is negligible compared with advection. The horizontal heat transport equation thus simplifies to:
where E therm = d · T is the thermal energy stored in a grid box and Q = u · d · T the lateral transport of heat. Heat capacities on both sides cancel out. Separating the derivatives in Eqn (11) yields
and with (7) reduces to
Hence, temporal changes in temperature only depend on the advection of spatial variations in temperature, not variations in the flow itself or in layer thickness. This perhaps unexpectedly simple result is a consequence of the vertical discretization. As for the advection of volume, Eqn (13) is discretized forward in time and upstream in space and the result is solved implicitly. The transport of other tracers is solved in the same way.
2.5. Vertical diffusion of heat and frictional heating
Vertical advective heat transport is represented implicitly by the Lagrangian formulation of vertical flow. Thus, heat is transported implicitly by the downward motion of layers due to thinning below. As a consequence, in contrast to the horizontal dimension, vertical heat transport across layer boundaries is limited to diffusion:
with the thermal diffusivity of ice α. Solving this equation requires the calculation of a derivative of second order on the vertical grid, which has an uneven spacing (see Appendix). To avoid very small time steps, Eqn (14) is solved implicitly.
At the upper boundary, temperatures of the uppermost layer are relaxed to the average surface air temperature with a fixed relaxation time of 10 a. Strictly, this time should scale inversely with the layer thickness but given the slow flow of ice the chosen fixed value brings the upper layer close to thermal equilibrium with the lower atmosphere, even for the thickest simulated layers. This strong coupling is realistic in the absence of other sources of heat near the surface and therefore results are indistinguishable for relaxation times shorter than a couple of centuries.
The lower boundary condition for the vertical heat equation is provided by geothermal heat flux Q geo (Neumann type):
where k ′ is the thermal conductivity of ice. Temperatures close to the lower boundary are extrapolated linearly across the ice–bedrock interface to obtain a dummy temperature grid point T 0 that can be used in the implicit solver. If the location of T 0 is chosen to be at the same distance from the boundary as the lowermost point of the model domain T 1, their distance is the thickness of the bottom layer d 1:
Note that the sole intent of this relation is to implement the geothermal heat flux boundary condition. Physical details of the bedrock–ice interface are not of interest here in contrast to more sophisticated bed thermal models (Tarasov and Peltier, Reference Tarasov and Peltier2007; Willeit and Ganopolski, Reference Willeit and Ganopolski2015). However, here T 0 is not the temperature of the bedrock and the conductivity of the bedrock does not need to be taken into account.
Besides geothermal heat flux at the bottom, friction by shear within the ice and with the bedrock are important sources of heat. Following Paterson (Reference Paterson1999), heat created by vertical shear in the x-direction is proportional to the shear rate ε̇ xz and shear stress τ xz :
where c is the specific heat capacity of ice.
At the bottom at the ice–bedrock interface, no shear occurs as long as the ice is frozen to the bedrock. Therefore, frictional heating at the bottom only occurs with basal sliding when temperatures rise above the local pressure melting point. Based on energy conservation, it is assumed that the rate of thermal energy creation by the sliding is equal to the loss of potential energy stored in the ice column (Paterson, Reference Paterson1999):
Using
![]() $\partial _ts = - \partial _xs{\kern 1pt} u_{\rm b}$
yields
$\partial _ts = - \partial _xs{\kern 1pt} u_{\rm b}$
yields
which is included as an additional term for the bottom ice layer in the implicit solver of Eqn (14).
These different sources of heat may increase the ice temperature locally above the pressure-corrected melting point, T* > 0°C; (see Eqn (2)). In these cases, the excess thermal energy is used to melt ice:
where Δd is the amount of melt that is removed from the local grid box, T is the in-situ temperature and c fus the specific heat of fusion for ice. After that, the local temperature is set to T*. Since layers at the bottom may be very thin and internal friction considerably heats the lower interior region of the ice sheet, temperatures above freezing can occur at several points in the ice column, not just at the bottom. Therefore, Eqn (23) is applied to the entire model domain up to the time dependent surface.
2.6. Surface mass balance
The surface mass balance is calculated from daily temperature and precipitation fields of the ERA-interim reanalysis (Dee and others, Reference Dee2011), averaged between 1980 and 2010 and between 70°N and 75°N and linearly interpolated in the zonal dimension to the ice-sheet model grid points.
Accumulation is the aggregate amount of precipitation on days with an average temperature below 0°C, calculated at each ice-model gridpoint. Intra-daily temperature variations that could cause accumulation in spite of an average temperature above 0°C and refreezing of rain and meltwater are neglected. These simplifications have a limited impact, because the accumulation is constrained with reconstructed data. A spatially uniform offset is applied to match the reconstructed accumulation at the summit for the GISP2 ice core (Cuffey and Clow, Reference Cuffey and Clow1997; Alley, Reference Alley2000b). This reconstruction covers the past 50 ka, the period for which visual layer counting ensures the highest accuracy of the accumulation and the dating of the record (Meese and others, Reference Meese1997). For earlier times, ice core dating and hence accumulation estimates increasingly depend on models of ice flow that are impaired by poorly known boundary conditions like past positions of the ice-sheet margin and its thickness (Cuffey and Clow, Reference Cuffey and Clow1997). Thus, model years before 50 ka use the unvarying accumulation of that earliest date in the GISP2 record, 50 ka, representing a continuously dry glacial climate. Given that the amount of ice pre-dating the last glacial period in the GrIS is very small (MacGregor and others, Reference MacGregor2015), the effect of this simplification is probably negligible. The uncertainty in the reconstruction of accumulation will be explored by applying a ±10% offset.
The ERA-interim temperatures are also corrected for the past 50 ka, based on the same GISP2 ice core record (Cuffey and Clow, Reference Cuffey and Clow1997; Alley, Reference Alley2000b). In contrast to the correction of accumulation, not absolute temperatures are used but the anomaly with respect to the most recent date in the reconstruction, so that the simulation ends with the unaltered modern temperature profile of ERA-interim. Moreover, this offset is not applied uniformly over the entire model domain, but in the shape of an inverted parabola that ranges from zero at the boundaries to the reconstructed temperature anomaly at the location of GISP2, the modern summit. The non-uniform correction is motivated by the large temperature anomalies at the summit, which are not likely at lower elevations and closer to the ocean, although changes in the sea ice cover around Greenland have a potentially important impact on the GrIS temperatures (Merz and others, Reference Merz, Born, Raible and Stocker2016). The parabolic shape of the correction is chosen because it resembles the surface elevation of the GrIS more realistically than a linear increase, but differences from simulations using the linear function are minor (not shown). Again, before the simulation reaches the earliest date of the reconstruction, it uses the constant value of 50 ka.
Importantly, surface air temperatures are corrected for variations in time but not for changes of the simulated elevation of the ice surface with regard to a reference height. Thus, the imposed temperatures and their vertical gradient are consistent with an ice surface whose shape approximates that of the modern GrIS. Additional changes in the simulated ice elevation would have to be accounted for by correcting the air temperatures once more, this time for the atmospheric lapse rate. However, in combination with the constraint to match the reconstructed temperatures at the summit, this could lead to unrealistic results in case the shape of the simulated section significantly differed from todays, for example if the location of the ice divide was different. Multiple lines of evidence suggest that the summit remained close to its modern position throughout the last glaciation (Tarasov and Peltier, Reference Tarasov and Peltier2003; Zweck and Huybrechts, Reference Zweck and Huybrechts2005; Peltier and others, Reference Peltier, Argus and Drummond2015). In this case, the symmetric uncertainty in the elevation of past surface topographies reduces the lapse rate effect to a correction that is qualitatively similar to the offset for temporal changes in the temperature at the summit, the parabola mentioned above. Since the uncertainty of the temperature reconstruction of ±3°C is taken into account (see Section 4), and can accommodate several hundreds of meters of lapse-rate-corrected uncertainty in surface elevation, the latter is discarded in the simulations below.
After correcting the daily temperatures of the climatology with the annual average of the current simulation year as reconstructed from the GISP2 record, surface melting is parameterized with the positive degree-day (PDD) method (Reeh, Reference Reeh1991). Daily average temperatures above freezing are integrated over 1 a in units of °C to yield the PDD number. The result is multiplied by a constant factor β to estimate melt:
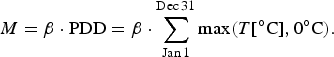 $$M = \beta \cdot {\rm PDD} = \beta \cdot \sum\limits_{{\rm Jan}{\kern 1pt} {\rm 1}}^{{\rm Dec}{\kern 1pt} {\rm 31}} {\rm max}(T[^{\circ} {\rm C}],0^{\circ} {\rm C}).$$
$$M = \beta \cdot {\rm PDD} = \beta \cdot \sum\limits_{{\rm Jan}{\kern 1pt} {\rm 1}}^{{\rm Dec}{\kern 1pt} {\rm 31}} {\rm max}(T[^{\circ} {\rm C}],0^{\circ} {\rm C}).$$
Reducing the surface energy balance to the single empirical factor β clearly is an oversimplification. Models that employ this method usually account for some complexity by using a higher melt rate for the relatively dark ice than for snow that is more reflective and a better thermal insulator (Hoinkes and Steinacker, Reference Hoinkes and Steinacker1975; Braithwaite and Olesen, Reference Braithwaite and Olesen1988). It has also been suggested to adjust melt factors to different climatic regions in Greenland (Braithwaite, Reference Braithwaite1995). Here, none of these adjustments is used. Following the focus on the new formulation of ice dynamics, the ice-sheet model does not include a surface module to simulate the transformation from accumulated snow to ice. The results below will show that the model is relatively insensitive to variations in β, because the accumulation is prescribed and the strongly positive ice-elevation feedback is not taken into account. Thus, the reduced complexity of the melt scheme is preferable to minimize uncertainties from sources other than the ice dynamics.
2.7. Surface boundary conditions for tracers
In addition to mass balance, conditions for temperature and passive tracers must be determined at the surface boundary. The GISP2-corrected climatological daily surface temperatures are used to calculate the annual average and the precipitation-weighted temperature. The former is used in the vertical heat diffusion (Section 2.5) while the latter determines the temperature of the newly accumulated layer of ice. The weights include the total precipitation, not just that below 0°C, because rain percolates through the upper layers and warms the ice even if it does not add to accumulation.
The ratio of the oxygen isotopic composition δ 18O at the surface is calculated as a linear function of surface elevation and average surface temperature (in °C), with coefficients estimated from observations on the GrIS (Dansgaard, Reference Dansgaard1961; Dansgaard and others, Reference Dansgaard, Johnsen, Clausen and Gundestrup1973; Johnsen and others, Reference Johnsen, Dansgaard and White1989):
This yields a distribution for the entire model domain, which, analogous to the reconstructed accumulation, is corrected by a constant offset to match the reconstructed δ 18O in the GISP2 record, covering the past 111 ka (Grootes and Stuiver, Reference Grootes and Stuiver1997). The constant value of δ 18O at 111 ka is used for ice accumulating earlier during the first part of the simulation. This maximum date corresponds to the maximum depth for which dating is possible in GISP2, 2800 m, ~240 m above the bed, with a dating error of ~±10% (Meese and others, Reference Meese1997). Below this depth, flow disturbances become too severe.
Lastly, a passive dye tracer is added to the model to illustrate the vertical motion by layer thinning and the outward flow within each layer. The value of this tracer alternates between −1 and +1 every 100 km at the surface and switches its sign every 2500 simulation years.
3. SIMULATIONS ON AN IDEALIZED DOMAIN
The EISMINT (European Ice Sheet Modelling INiTiative) protocol phase 1 defines a series of experiments to compare ice-sheet models of different complexity on a simplified symmetric domain and with idealized boundary conditions (Huybrechts and Payne, Reference Huybrechts and Payne1996). The benchmark experiments are used here to ensure the robustness of the isochronal discretization and to compare the results with ice-sheet models that use a cartesian vertical coordinate. The size of the domain is 1500 km, discretized to 31 equidistant grid points with a spacing of 50 km. The bedrock is completely flat and does not yield to the ice load above. In EISMINT 1, thermodynamics do not influence the flow factor A, which therefore has a constant value of 3.171 × 10−24 Pa−3 s−1. Basal sliding is disabled. This idealized setup and the simplified boundary conditions are inspired by analytical solutions (Vialov, Reference Vialov1958). A second set of benchmark simulations was proposed by phase 2 of EISMINT to evaluate these effects of thermomechanical coupling (Payne and others, Reference Payne2000), but they are defined only for models on a full 3-D grid. More importantly, the isochronal grid offers a complementary way to quantify the quality of the simulated thermal profile and its effect on the flow at different depths, which will be explored in detail in Section 4.
Two experiments were carried out with unvarying boundary conditions. The EISMINT fixed margin experiment prescribes a constant and homogeneous positive surface mass balance of 0.3 m a−1 for the entire model domain. The ice thickness at the lateral boundaries is set to zero. Three simulations were performed with different isochronal spacing and all three produce a symmetric ice sheet with a summit elevation of ~3600 m (Fig. 2a). This value as well as the shape of the surface elevation is in agreement with the EISMINT reference. No systematic influence of the isochronal resolution was found. Deviations in surface elevation between the three different resolutions can further be reduced to <4 m by enforcing compiler optimizations to be value-safe at the expense of computational efficiency. The elevation of the summit was stable in time and is therefore not negatively influenced by the constant addition of layers to the isochronal grid.

Fig. 2. Results for the EISMINT fixed (a) and moving (b) margin experiments after 200 000 model years. Results are symmetric and only half of the model domain is shown here. Each simulation was run with three different isochronal grids, 25, 50 and 100 a. The absolute surface elevation s is shown for the standard grid, deviations thereof Δs for the other two. The elevations at the summit of all simulations agree with the EISMINT reference within their uncertainty.
The surface mass balance in the EISMINT moving margin experiment is 0.5 m a−1 in the centre of the domain and decreases linearly for distances >450 km from the centre. Here too, the three simulations with the isochronal model agree with the summit elevation, the location of the ice margin and the shape of the reference (Fig. 2b). In both experiments, the influence of the isochronal resolution is minor and all six simulations maintain the symmetry of the surface elevation with regard to the summit. These results show that the dynamical core of the isochronal model produces results consistent with models that employ a vertical grid that is equidistant in space.
4. PERTURBED MODEL PARAMETERS, TUNING THE MODEL
Seven model parameters were selected to investigate the sensitivity of the new ice-sheet model, and to identify the most realistic set of parameters (Table 2). Three values are chosen for each of the seven parameters for a total of 37 = 2187 possible combinations.
Table 2. List of perturbed model parameters in the ensemble simulations
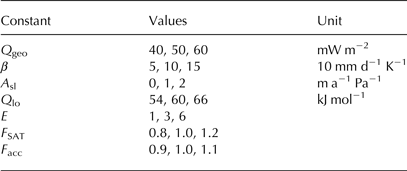
The focus here is on parameters that impact the flow of ice, either directly or through their relationship with the vertical temperature distribution. This includes the flow factor A. Since variations in A 0 have a negligible influence on A compared with changes in the exponential factor Q (Eqn (3)), only the latter is perturbed. Q lo is perturbed by 10% around its default value of 60 kJ mol−1. This is in agreement with variations found from laboratory measurements (Weertman, Reference Weertman, Whalley, Jones and Gold1973) and glacier ice (Paterson, Reference Paterson1977, Reference Paterson1999). Three matching values of Q hi are chosen to ensure a continuous profile for A at −10°C.
Geothermal heat flux Q geo below the GrIS is fairly homogeneous in the domain represented by the model, with a value of 50 mW m−2 (Shapiro and Ritzwoller, Reference Shapiro and Ritzwoller2004). However, this is not undebated (Rogozhina and others, Reference Rogozhina2012). Variations in Q geo have been found to considerably change the shape of the GrIS in earlier model studies (e.g., Greve and Hutter, Reference Greve and Hutter1995; Ritz and others, Reference Ritz, Fabre and Letréguilly1997). Here, variations ±10 mW m−2 are allowed. Possible values for the PDD factor β are 5, 10 and 15 mm d−1 K−1 in an attempt to balance the usually lower melt rates of snow and faster melting of exposed glacier ice (Ritz and others, Reference Ritz, Fabre and Letréguilly1997).
Further, the flow enhancement factor E is varied between 1, 3 and 6 for ice older than 10 ka before present. The first option is equivalent to eliminating
![]() $E({z}^{\prime})$
from Eqn (1), while a value of 3 is somewhat standard to represent ice accumulated during glacial times, originally proposed based on borehole measurements (Dahl-Jensen and Gundestrup, Reference Dahl-Jensen and Gundestrup1987; Paterson, Reference Paterson1999). The upper value of 6 is included to represent the upper limit of field measurements and recently found support from a flowline model using a comprehensive description of all relevant stresses in the ice (full-Stokes) (Ma and others, Reference Ma2010).
$E({z}^{\prime})$
from Eqn (1), while a value of 3 is somewhat standard to represent ice accumulated during glacial times, originally proposed based on borehole measurements (Dahl-Jensen and Gundestrup, Reference Dahl-Jensen and Gundestrup1987; Paterson, Reference Paterson1999). The upper value of 6 is included to represent the upper limit of field measurements and recently found support from a flowline model using a comprehensive description of all relevant stresses in the ice (full-Stokes) (Ma and others, Reference Ma2010).
The parameter for basal sliding A sl is perturbed to test the robustness of the simplified sliding law (Eqn (6)). As before, sliding only occurs where the ice-sheet bed reaches the local pressure melting point. Possible values are 0, 1 and 2 m a−1 Pa−1.
Lastly, the uncertainties in the reconstructions of surface air temperatures and accumulation rates are taken into account by scaling their default values. The uncertainty in the temperature reconstructions from oxygen isotopic ratios is difficult to quantify and potentially very large because they are influenced by multiple processes (Masson-Delmotte and others, Reference Masson-Delmotte2011; van de Berg and others, Reference van de Berg, van den Broeke, van Meijgaard and Kaspar2013; Merz and others, Reference Merz, Born, Raible, Fischer and Stocker2014a, Reference Merzb, Reference Merz, Born, Raible and Stocker2016). Independent reconstructions based on the differential diffusion of nitrogen isotopes in the firn (δ 15N) estimate the temperature difference between the last glaciation and the Holocene to be ~15°C with an uncertainty of ±3°C (Severinghaus and others, Reference Severinghaus, Sowers, Brook, Alley and Bender1998; Kindler and others, Reference Kindler2014). The relative uncertainty is thus ±20%, which is used here for the scaling factor F SAT applied to the GISP2 temperature anomaly with respect to present day.
The uncertainty of the reconstructed accumulation is largely due to the poorly known retreat of the ice-sheet margin after the last glacial maximum. Therefore, it is reasonable to assume accumulation rates of 10% above and below the most likely estimate (Cuffey and Clow, Reference Cuffey and Clow1997). This defines the scaling factor for accumulation F acc that is used to modify the absolute values of the accumulation.
All possible parameter combinations were run with the same input data as detailed in Section 2.6. In order to quantify model performance, three variables are analyzed that represent both the horizontal and vertical dimensions: (1) the surface elevation s, (2) the vertical profile of temperature at the modern summit and (3) the vertical profile of δ 18O at the same location.
The area of the GrIS and local deviations from the observed surface elevation are commonly used to evaluate model performance (Ritz and others, Reference Ritz, Fabre and Letréguilly1997; Stone and others, Reference Stone, Lunt, Rutt and Hanna2010; Robinson and others, Reference Robinson, Calov and Ganopolski2011). However, a good representation of the present day ice sheet does not ensure a realistic simulation of the vertical structure in the ice. As an example, too little accumulation during glacial times might be offset by too much snowfall during the Holocene, or vice versa, producing an ice surface that is indistinguishable from a more realistic simulation. In the vertical dimension, this deficiency would be obvious from a glacial-Holocene transition that is too deep in the ice. This motivates the analysis of δ 18O. The borehole temperature is included because it is a vertical profile that does include diffusion, unlike δ 18O, and because it is the variable that most directly constrains the choice of the geothermal heat flux at the lower boundary.
All three variables are 1-D curves that are analyzed for their cross correlation with the respective observed counterparts and their standard deviation. The results are readily illustrated in a Taylor diagram (Taylor, Reference Taylor2001) (Fig. 3). The vertical profiles of the model and reconstructed data are linearly interpolated onto a grid with a homogeneous resolution of 2 m. This is the resolution of the GISP2 δ 18O record. The GISP2 borehole temperature record has a resolution of 5 m. The shorter one of the model or data records is padded with its lowermost value to match the length of the other.

Fig. 3. Taylor diagram showing data of all ensemble simulations for ice-surface elevation (left), borehole temperature at GISP2 (middle) and the vertical profile of δ 18O (right). The radial distance of each dot from the origin is the standard deviation of the respective variable in this simulation. The standard deviation of the reconstructed data is marked with a dashed line. The azimuthal position of each dot quantifies the cross correlation between its simulation and the corresponding reconstruction. The RMSE is the distance from the reference (black dot, gray lines). The colour of dots corresponds to the RMSE of δ 18O and is the same in all three panels. The simulations with lowest RMSE are highlighted with a blue (surface elevation), red (borehole temperature) and green cross (δ 18O).
Most successful ensemble simulations achieve a relatively high correlation coefficient of above 0.95 for the surface elevation, because if an ice sheet is simulated at all it will have the correct rounded shape centered on the surface bounded by inaccessible ocean. However, the simulations vary widely in terms of standard deviation, which illustrates the wide range of simulated ice thicknesses. In contrast, δ 18O shows only small variations in standard deviation while the correlations are more diverse and generally lower. The accurate simulation of the observed standard deviation is expected because the same observations are used as a boundary condition at the ice surface. After that, the flow within the ice is unconstrained by observations so that the correct alignment of the simulated and observed curves can not be expected. Therefore, the cross correlation of the δ 18O profiles is an independent test of how fast the ice flows in the vertical dimension, complementary to the analysis of the surface topography that strongly depends on the velocity of the lateral ice flow.
The vertical profile of observed borehole temperatures shows low temperatures at the surface and throughout the ice and an approximately linear increase in the lowest 1000 m of ice (Johnsen and others, Reference Johnsen, Dahl-Jensen, Dansgaard and Gudenstrup1995). As before with the ice thickness, the general shape of the temperature curve is relatively easy to simulate correctly due to the geothermal heat flux that heats the ice from below. Therefore, the model achieves rather high correlation coefficients as well if the ice thickness is simulated reasonably well. However, where large mismatches between simulated and observed ice thicknesses lead to significant padding, quite low correlation coefficients are also possible.
The colour of the individual ensemble simulations in Figure 3 represents the RMSE of δ 18O. Taylor diagrams are constructed so that the RMSE is the distance from the perfect match at a correlation coefficient of one and a standard deviation that is equal to that of the independent reconstructed variable. This is illustrated by the gray curves in Figure 3. The colour of each simulation is the same in all three panels. This illustrates that the best simulations of δ 18O also tend to have a lower RMSE in ice thickness, but not always. Some blue dots that indicate a large mismatch with the vertical profile of δ 18O are among the best simulations in terms of present day surface elevation at the end of the simulation. A similar result is found for the borehole temperature.
Interesting detail is obtained from the analysis of individual model parameters (Fig. 4). The parameter with the greatest impact on model performance and stability is Q lo, which also determines Q hi and therefore the entire profile of A (Eqn (3)). For surface elevation and borehole temperature, low values of Q lo tend to yield a better agreement with the observed fields. For the RMSE of δ 18O, the lowest median is for the standard value of Q lo = 60 mJ mol−1.
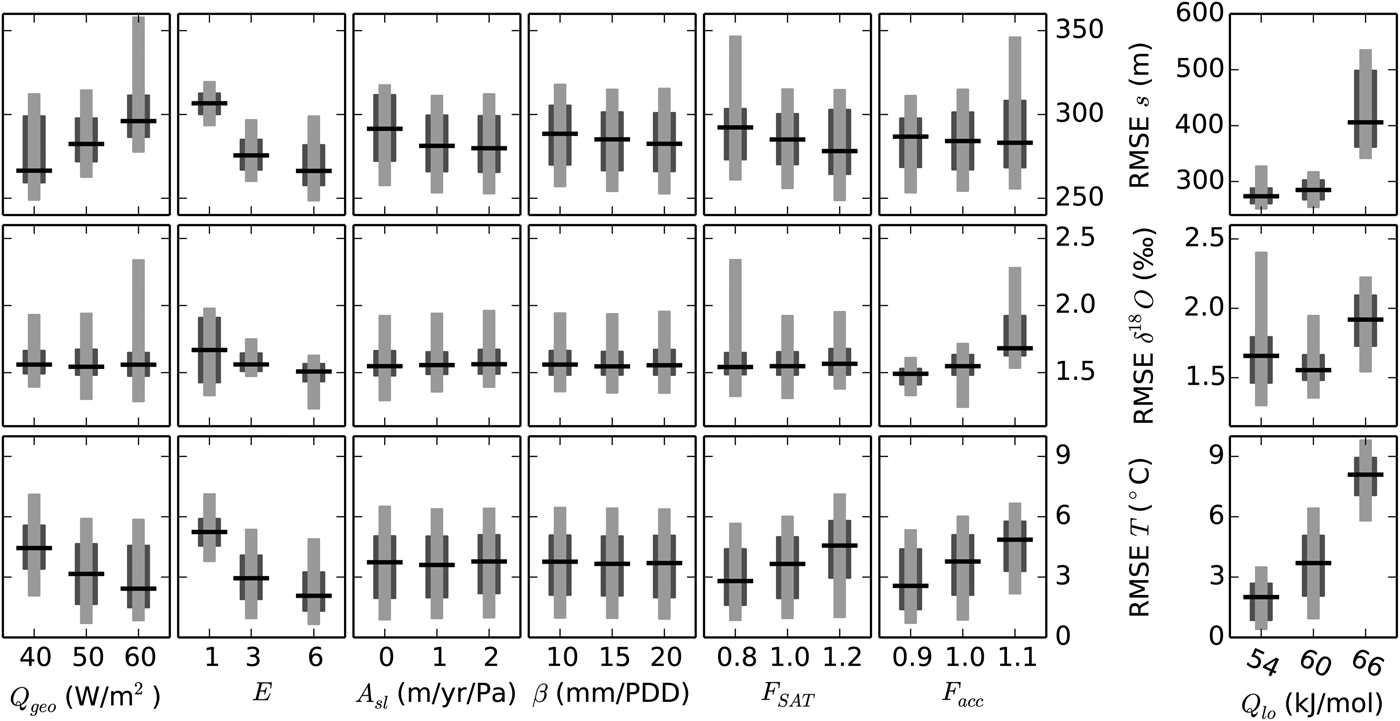
Fig. 4. RMSE for ice thickness (top row), δ 18O (middle row) and borehole temperature (bottom row), as a function of seven model parameters (columns). The single column on the right side shows the full ensemble for values of the Q lo parameter specified at the bottom. Due to its dominant impact on most variables, only the standard value for Q lo and hence A is used to assess the effect of the six remaining parameters on the left. Dark gray ranges contain 50% of the simulations, light gray 90%. The horizontal black line shows the median.
Given the dominant influence of A on the ice dynamics and therewith all three evaluation variables, the analysis of the other six parameters is limited to the default value of Q lo (Fig. 4, left), i.e., 36 = 729 parameter perturbations. The range of RMSE is generally smaller than for the full ensemble.
The three evaluation variables are sensitive to different aspects of the simulation and therefore respond differently to the six remaining model parameters. In some cases, the response is opposite. For example, RMSE s increases with higher values of Q geo while the median of RMSE T decreases with the same perturbations and RMSE δ 18O barely changes at all. This is explained by the direct impact of Q geo on the borehole temperature and its strong influence on the lateral flow that determines the shape of the surface elevation s. At the location of GISP2 close to the summit, the vertical profile of δ 18O depends mostly on the vertical advection of the ice that apparently is less sensitive to variations in Q geo. This is somewhat surprising because the geothermal heat flux does impact the lateral flow of ice, which in turn determines the rate of thinning of the layers and thus their vertical motion. In agreement with this picture, the flow enhancement parameter E, which has a similar effect on the lateral flow to that of Q geo, does cause a noticeable response in RMSE δ 18O. I speculate that this may be due to Q geo taking full effect only after the ice sheet is in thermal equilibrium, which is relatively late during the simulation and only felt by the lowermost part of the ice column, whereas the effect of different values of E is arguably opposite. Changes in E take effect from the beginning of the simulation and everywhere in the ice, but E is always 1 for ice younger than 10 000 a so changes do not affect the last part of the simulation. E also strongly influences RMSE T. All three metrics agree that the high values of E = 6 is generally the best, at least for the intermediate value of Q lo shown on the left side of Figure 4.
As a result of its dependence on the vertical flow of ice, RMSE δ 18O is sensitive to the accumulation rate F acc. Interestingly, the median of RMSE δ 18O is lowest when 80% of the reconstructed accumulation is applied, F acc = 0.9, but some simulations with F acc = 1.0 yield an even better agreement with the reconstructed profile as seen in the broader lower tail of the distribution. One possible interpretation is that a lower accumulation limits the negative effects of some of the other model parameters but does not in itself produce the best overall result. While the importance of F acc for RMSE s is limited, RMSE T clearly responds to changes in accumulation, because the borehole temperatures also strongly depend on the vertical flow of ice and heat.
F SAT has a similar effect on the vertical temperature to that of F acc, because it also directly changes the vertical temperature profile. As for Q geo, this also changes the horizontal flow of ice and therefore the surface elevation and the impact on RMSE T and RMSE s is opposite here too.
Basal sliding, A sl, has only limited impact on model performance, with the most noticeable effect in ice thickness. The reason for this is that under most configurations only relatively small regions reach the pressure melting point at the ice base and many only temporarily. Moreover, the silty layer parameterization already produces relatively large flow velocities near the bed and thus effectively removes heat that would otherwise warm the ice to the local pressure melting point.
Lastly, variations in the melting coefficient β are rather minor as well. Although this might be surprising because the amount and distribution of melting plays an important role for the surface area and volume of the GrIS and is related to a powerful positive feedback (e.g., Ritz and others, Reference Ritz, Fabre and Letréguilly1997; Born and Nisancioglu, Reference Born and Nisancioglu2012), this result is readily explained by the definition of accumulation and surface temperature of the model. The usually strong impact of β is due to the ice-elevation feedback that may lead to a runaway melting once the ice surface melts to lower and warmer elevations. As outlined in Section 2.6, this effect would easily overwhelm all other influences and produce surface temperatures and elevations that are in clear disagreement with reconstructions, in particular with the temperature reconstruction that is used to force the model. Therefore, in the simulations presented here, the surface temperature curve always resembles the temperatures on an ice-sheet surface with an approximate shape like the modern surface, scaled to match the reconstructed temperatures at GISP2. The additional lapse-rate correction to also match the variations in the actual simulated surface elevation is disregarded because combining this constraint with the reconstructed temperatures would result in either a small correction if the past surface elevation approximately resembled the shape of the modern GrIS, which it probably did (Tarasov and Peltier, Reference Tarasov and Peltier2003; Peltier and others, Reference Peltier, Argus and Drummond2015), or unrealistic values if it did not. As a result, these constraints on surface air temperature limit the impact of the PDD factor β.
The three simulations with the lowest RMSE for each of the three evaluation variables are each highlighted with a coloured cross in Figure 3 (Table 3). It is worth noting that there is no single simulation that excels in all three evaluation metrics. The best parameter sets for the two variables that directly depend on the flow of ice, surface elevation (BEST s ) and the oxygen isotopic profile (BESTδ 18O), agree on the values of the activation energy Q lo and the flow enhancement factor E. The two simulations use different values for the PDD factor β and the basal sliding parameter A sl, but these parameters were found to have a limited significance for model performance (Fig. 4). Interestingly, the best results for δ 18O and the borehole temperature are obtained by using the unperturbed reconstructed accumulation (F acc = 1). Since these two variables are very sensitive to variations in the vertical flow of ice and accumulation, this result suggests that the original reconstruction for accumulation is reasonable and does not need adjustment. However, none of the parameters is independent from the choice of the others so that considerable analysis would be required to ensure this result is unique and robust. Besides F acc, BEST T only shares the value of β with one other of the best-guess simulations. Since none of the evaluation variables is very sensitive to β, this result is of little relevance.
Table 3. Parameter sets with minimal RMSE for each of the three evaluation variables (boldface). Also shown are the corresponding correlation coefficients r and standard deviations σ
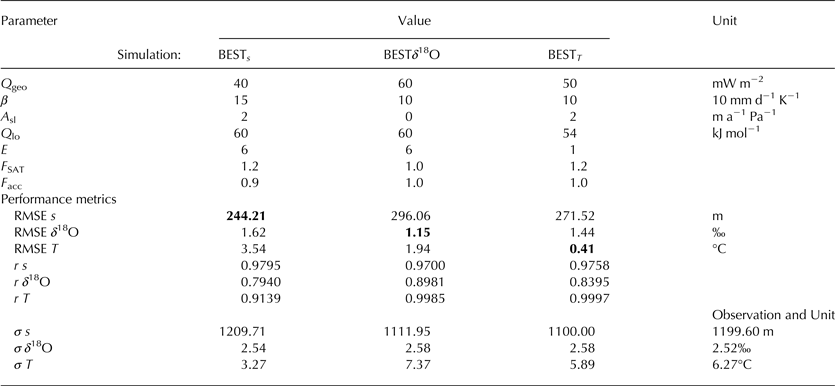
In summary, the analysis of the parameter sensitivity of the ensemble confirms that the ice-sheet model produces reasonable results. The explicit simulation of the vertical stratigraphy adds valuable detail to the simulations that can be used to quantify their quality. The following analysis will focus on the analyis of the simulation BEST δ 18O.
5. SIMULATION OF THE LAST GLACIAL CYCLE
Simulation BEST δ 18O is now analyzed in more detail. After initialization without ice and from a relaxed bedrock, the model runs for 200 ka with glacial accumulation and temperatures as reconstructed from GISP2 for 50 ka before present. Under these constant boundary conditions, ice accumulates rapidly and equilibrates its cross-sectional area within the first 40 ka of the simulation (Fig. 5). The oxygen isotopic ratio, which also uses a constant forcing until 111 ka before present, reaches a stable average in about the same time. In contrast, the average temperature of the ice does not fully stabilize during the first 150 ka of simulation time.
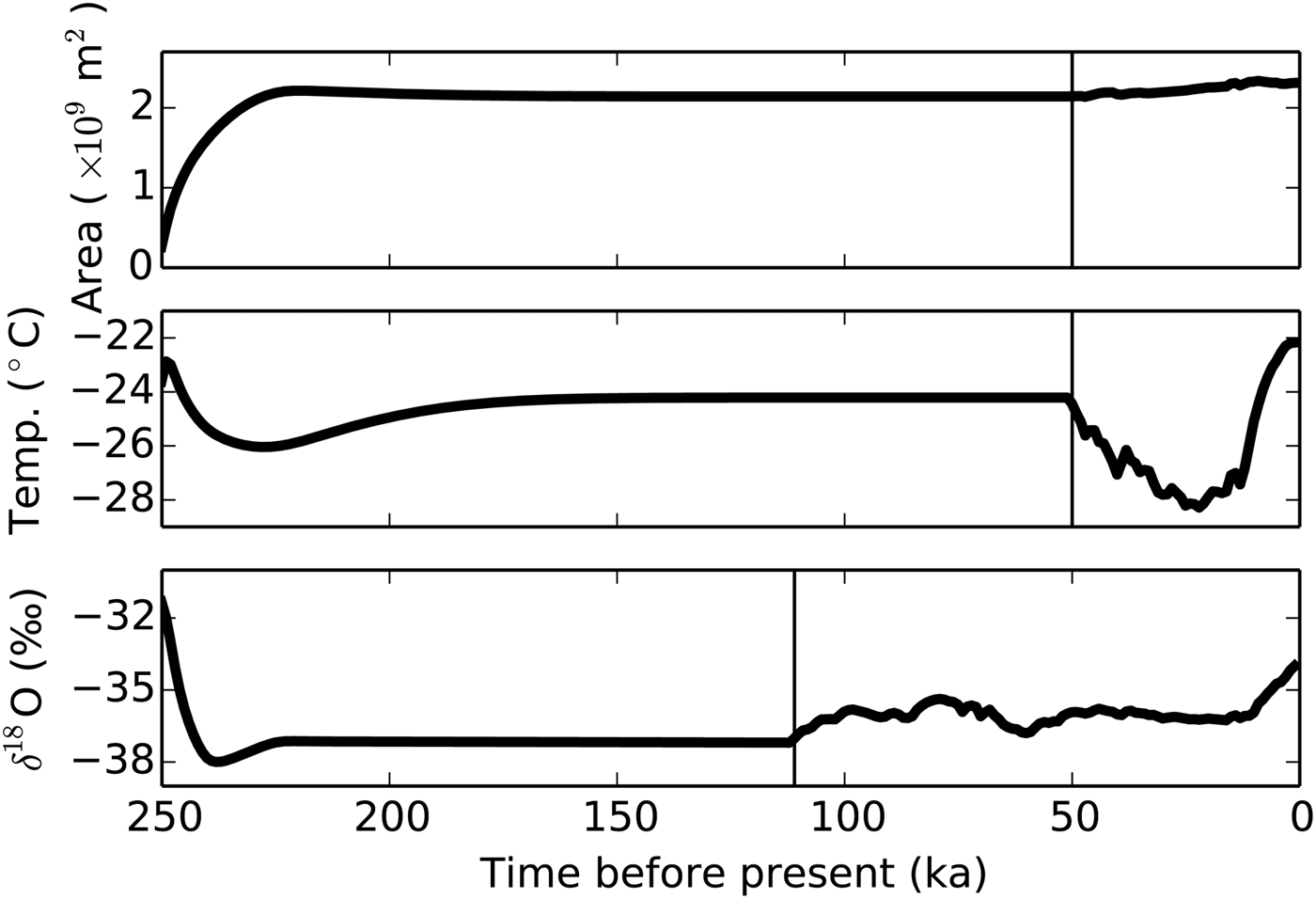
Fig. 5. Time evolution of the cross-sectional area, temperature and δ 18O of BEST δ 18O, averaged over the entire ice sheet. Vertical lines illustrate the onset of the transient forcing. The ice sheet quickly grows to its modern size (area) and the average oxygen isotopic composition equilibrates relatively soon after initializing from an ice-free start. However, the temperature distribution is not fully in equilibrium after 200 ka simulation time, just before the transient surface climate forcing begins. This is due to the slow warming by geothermal heat flux and its interaction with the ice flow.
After the onset of the transient forcing, the average ice temperature drops as the model approaches the last glacial maximum (LGM), ~20 ka ago. Simultaneously, ice volume slightly increases in spite of the coeval reduction in accumulation (not shown). The average temperature rises sharply and ice volume is reduced after the LGM. At the same time, average δ 18O also increases due to its dependence on temperature.
The LGM ice sheet is thinner than for present day, a result of the lower accumulation and slower lateral flow (Fig. 6). The present day topography compares well with the observed profile from ETOPO1 (Amante and Eakins, Reference Amante and Eakins2009), but too thick ice is found on both margins of the 2-D domain. This is partly due to comparing its topography with the average of observations between 70°N and 75°N. The GrIS is relatively narrow in the southern part of this range because of the presence of Scoresby Sund in the east and Uummannaq Fjord in the west that penetrate relatively far inland. Further north, fjord systems are less developed and the ice sheet is wider. The reference topography in Figure 6 represents the average across these two regions. However, the effective ice loss through narrow fjords and into floating outlet glaciers is not represented in this 2-D simulation, which explains why its surface topography looks more like the northern part of the comparison region (not shown). In addition, the ice in the model is forced to flow across the relatively high-bedrock topography in the east. Three-dimensional simulations show significant flow in the meridional direction in this region (Clarke and others, Reference Clarke, Lhomme and Marshall2005) that is neglected here. This adds to the simulated ice topography being too thick in most of the simulations as suggested by the too high standard deviation (Fig. 3).

Fig. 6. The simulated zonal section through the summit of the GrIS of simulation BEST δ 18O, for 20 ka before present (left) and today (right). West is on the left-hand side of the panels. The modern location of GISP2 is marked with a triangle. The modern ice and bedrock topographies are shown as green curves.
As a consequence of the stronger accumulation during the Holocene, the last 10 ka of the simulation, layer thicknesses are larger in the upper part of the ice sheet (Fig. 6). A marked transition to thicker layers is seen about halfway between bedrock and surface. The same conclusion is drawn from δ 18O and the dye tracer. At the LGM, horizontal bands are seen in δ 18O that correspond to the well-known Dansgaard–Oeschger events (Alley, Reference Alley2000a). This part has been compressed to the lower third of the ice at present day due to the accelerated accumulation. Strong doming of deeper ice layers is visible in both the dye tracer and δ 18O for the LGM. This illustrates how the vertical movement of the ice is much slower near the ice summit than closer to the margins and how this amplifies the surface slope as layers travel through the ice, although the rapid accumulation during the last 10 ka removes much of this effect.
Comparison of the simulated vertical section with the same data on the model grid before transformation further clarifies the basic concept of the model (Fig. 7). Since layers are added at a constant rate over the entire simulation time, the computational domain at the LGM is not yet full. Dynamic and thermodynamical processes change the thickness and tracer composition of each layer over time, but not its location in the isochronal model grid or in relation to other layers. Therefore, the same horizontal bands in δ 18O, Dansgaard–Oeschger events, are identified in the LGM and present day around layer number 3000 (100 ka before present). Around layer number 4000 (50 ka before present), the banding appears to have reduced at present day as compared with the LGM. This is due to the outward flow that pushes lighter isotopic values toward the margins and expands the low δ 18O region that was originally deposited in the centre of the ice sheet between ~600 and 900 km lateral distance. Note also that this visualization greatly exaggerates the importance of very thin layers near the ice bottom. The entire Holocene only covers the last 10 000a 50 a−1 = 200 layers on the top that correspond to more than half of the total ice thickness (Fig. 6).
The simulated ice in BEST δ 18O has approximately the correct thickness at the summit and the simulated vertical profiles at GISP2 compare well with the observed values (Fig. 8). As a result of the optimization exercise above, the vertical profile of δ 18O shows very good agreement over the depth range for which reconstructions exist. Although the depositional history of accumulation and δ 18O were used to constrain the surface boundary conditions of the model, a good agreement is not trivial because it also depends on the dynamical history of the entire ice sheet. If the lateral flow does not remove ice at the correct rate and from the correct depth at the depositional site, it will negatively affect the vertical profile of δ 18O even though the upper boundary conditions are prescribed. The correct reproduction of the reconstructed δ 18O record thus suggests that the ice dynamics are simulated correctly at every depth for which reconstructions are available. Moreover, since different layers of ice are accumulated at different times, the comparison of reconstructed and simulated vertical profiles also allows to quantify the model's sensitivity to a changing climate, for the entire time period that is covered by the reconstructions.

Fig. 8. Vertical profiles at the location of GISP2 at the end of the simulation BEST δ 18O (present). Observed borehole temperatures, δ 18O and layer-counted age scale are shown in red. The observed δ 18O record is shifted by 5‰ for better visibility. Thin red lines in (e) mark the ±10% uncertainty in reconstructed age below 2800 m.
Since the age of the ice is closely related to its δ 18O value in the model, the latter also is in good agreement with the reconstructed profile. The lowest 240 m of the GISP2 record are disturbed by non-laminar flow. The dating error was quantified as ±10% (Grootes and Stuiver, Reference Grootes and Stuiver1997; Meese and others, Reference Meese1997). This coincides with the range of a clear mismatch between model and data (Fig. 8e). It is important to highlight that at this close distance to the bedrock several processes influence the ice and its age that are not included in the model such as anisotropies in the ice that modify the flow and interaction with small-scale topography that folds the ice. However, probably the most important mechanism here is the meridional flow that is not included in the model. According to 3-D model studies (Clarke and others, Reference Clarke, Lhomme and Marshall2005, their Fig. 4), this flow component becomes increasingly important near the base of the ice sheet at the section that is simulated here.
The borehole temperature is reasonably well reproduced in BEST δ 18O. Note that the model in principle is capable of a more realistic simulation of this variable (BEST T ), but that simulation achieves worse results in terms of δ 18O. This partial incompatibility of different aspects of the model suggests a systematic shortcoming of the model either because of missing physical mechanisms or because it neglects the meridional flow. In the particular case of BEST δ 18O, the model must remove all ice that accumulates at GISP2 in the zonal direction in order to reproduce the reconstructed stratigraphy, because the meridional flow is not represented. To achieve a higher zonal flow rate while keeping a realistic surface gradient, the ice must be softer, which explains why BEST δ 18O estimates warmer temperatures and has the highest δ 18O of all BEST simulations.
As expected, the dye tracer is unaffected by numerical diffusion in the vertical dimension and therefore maintains its full amplitude almost over the entire depth range (Fig. 8c). Numerical diffusion does affect the horizontal flow because it uses a finite-difference scheme. As a result, the bottom 500 m of the ice column show dye tracer values that do not reach the full amplitude of ±1. This part of the ice column is affected by lateral flows because GISP2 is not exactly located at the ice divide and especially due to fast flow during the ice-free initialization of the model. Precipitation uses the modern distribution throughout the simulation, i.e., most ice accumulates near the coasts and flows toward the interior of Greenland during the first few millennia. This causes the disturbance in the dye tracer at the modern summit location. In support of this explanation, notably thicker layers and higher values of δ 18O are found near the glacier bed although the rate of accumulation and the surface δ 18O are constant during this early part of the simulation (Fig. 8a, d).
As suggested by the coloured dots in Figure 3, a good reproduction of the present day ice surface does not ensure the best possible simulation of the vertical profile of δ 18O. Too stiff ice during the glacial and the resulting overestimation of ice thickness might be offset by too little snowfall during the Holocene, possibly resulting in an indistinguishable ice surface at the end of the simulation. As an example, the ensemble includes a simulation that has a similar surface topography and ice thickness to those of BEST δ 18O. Although its RSME s (256.93 m) and σ s (1130.45 m) more closely match observations (Table 3), its δ 18O profile reveals that the internal layering beneath the summit clearly disagrees with the GISP2 reconstruction (RMSE δ 18O = 1.68, Fig. 9). This indicates a non-optimal sensitivity of this model version to variations in climate. Simulations of past and future ice volume would arguably yield less realistic results.

Fig. 9. Surface and bedrock elevation (left) and vertical profile of δ 18O at the location of GISP2 (right), for observations (red) and BEST δ 18O (black). The gray curves correspond to a simulation that has a lower RMSE s than BEST δ 18O but worse RMSE δ 18O. Arrows illustrate shifted curves for better visibility.
6. DISCUSSION AND CONCLUSIONS
A new ice-sheet model has been presented that employs a novel discretization in the vertical dimension. In contrast to traditional models, the vertical model dimension is not equidistant in space but in time. These isochronal layers of variable thickness uniquely identify individual periods of accumulation. Their number steadily increases as the simulation progresses while their thickness decreases with the lateral flow that moves ice toward the ice-sheet margins and into the ablation zones. The definition of model layers as isochrones prevents ice from moving through the model grid in the vertical direction, from one layer into the next. Instead, vertical flow only occurs because of thinning or thickening layers below. Thus, the model resembles the common perception of how ice is transported through an ice sheet, keeping isochronal layers intact. Folding of isochrones (Hindmarsh and others, Reference Hindmarsh, Leysinger Vieli, Raymond and Hilmar2006; Bell and others, Reference Bell2011, Reference Bell2014) is not simulated in the model.
The new discretization greatly improves the representation of vertical profiles of passively advected quantities such as the age of the ice since its accumulation or the oxygen isotopic ratio (δ 18O). It ensures a high-vertical resolution and entirely eliminates the negative effect of numerical diffusion, thereby enabling the simulation of ice cores. The simulated isochrones can directly be compared with comprehensive new datasets of englacial layers (MacGregor and others, Reference MacGregor2015) obtained from ground-penetrating radar observations (Bell and others, Reference Bell2011; Fujita and others, Reference Fujita2011; Sime and others, Reference Sime, Karlsson, Paden and Prasad Gogineni2014).
Similar attempts to simulate englacial tracers have successfully been made in the past by introducing semi-Lagrangian schemes (Tarasov and Peltier, Reference Tarasov and Peltier2003; Clarke and others, Reference Clarke, Lhomme and Marshall2005; Goelles and others, Reference Goelles, Grosfeld and Lohmann2014), where passive tracers are advected through the model grid as virtual particles. Their aims and quality of results are comparable with the method presented here, although the technical solution is entirely different. One advantage of the isochronal discretization is that it changes the definition of vertical layers from being a necessary and invariable part of the model design to a physically meaningful variable that is calculated prognostically. The model physics can be described at a very fine scale where necessary, for example to resolve annual layering. Since the ice flow dynamics work on an inhomogeneous grid that is constantly changing, the layer spacing does not need to be at constant time intervals. It is possible, albeit not used here, to finely resolve the layers of one period of interest after using broader isochrones for the spin-up phase. Similarly, several layers at the ice-sheet bed can be combined into one during the simulation to improve the model's performance.
Another notable difference between the two approaches is that the semi-Lagrangian scheme is an addition to a regular Eulerian ice sheet model. Therefore, the advection of passive tracers is independent from the calculation of the ice dynamics so that multiple simulations of the tracer field are possible without the computational overhead of the underlying ice-sheet model. The use of independent modular components also makes it easier to adapt the semi-Lagrangian scheme to one of the many existing ice-sheet models, or new developments. In contrast, the isochronal model presented here calculates the ice velocities on the same grid as the tracers, even if they represent very thin layers of ice, and the simulation of both velocities and tracers must be carried out at the same time. This is physically correct but numerically inefficient because ice velocities are relatively smooth fields that do not benefit from a high-vertical resolution. Future implementations might address this issue by calculating ice velocities on a coarser auxiliary grid defined by a subset of grid points and then interpolating the results. Taking this approach one step further, the ice velocities could also be calculated by an entirely different ice-sheet model, thus making the tracer advection independent from the ice dynamics and expanding potential applications. Lastly, since the advantages of the isochronal model are entirely due to its novel vertical discretization and do not depend on how the ice velocities are calculated, it is compatible with higher-order physics to represent longitudinal stresses. Multi-layered discretizations have been shown to be beneficial for the simulation of ice shelves (Jouvet, Reference Jouvet2015).
The isochronal discretization does not fully eliminate numerical diffusion, because only the vertical movement of entire layers follows the Lagrangian description of flow. Lateral volume flow within each layer is represented by an Eulerian advection scheme of first order, which is known to be very diffusive. This is evident from the white bands in the simulation of the dye tracer (Figs 6, 7). However, similar to diffusive processes in physics, numerical diffusion requires steep tracer gradients to act upon, so that the sharp transition from –1 to 1 of the dye tracer is the worst possible and an unrealistic case. Natural tracers like δ 18O are finely structured in the vertical but relatively smooth in the lateral dimension. This is why the isochronal discretization specifically addresses the vertical flow but keeps the common and computationally cheaper Eulerian flow in the lateral dimension. A special case where this method could fail is the merging of two ice sheets (Clarke and others, Reference Clarke, Lhomme and Marshall2005).
The new capability to simulate ice cores is used to constrain the model dynamics and its sensitivity to varying upper boundary conditions. Here, the simulated profile of δ 18O has been compared with the corresponding GISP2 record. While the values of δ 18O along the length of an ice core are due to changes in precipitation that accumulated at the top, the thickness of individual layers and their depth below the surface are determined by the 3-D flow of ice. Thus, the shape of the reconstructed ice core profile contains information on the ice dynamics at every depth and for all times since the ice accumulated. In contrast, the common model evaluation by comparison with the surface topography is ambiguous about the depth at which the ice is transported. More importantly, it only constrains the aggregate accumulation and ice flow until the present, with no information on timing. Too soft glacial ice could be offset by too stiff ice in the Holocene, leading to the same surface topography at present but an unrealistic sensitivity to changes in climate. Using a second reference period, for example the last interglaciation, ameliorates the problem somewhat, but relies on very uncertain reconstructions of the surface topography in the past (Robinson and others, Reference Robinson, Calov and Ganopolski2011). Moreover, two reference points are not enough to constrain a highly nonlinear system with multiple free parameters. The number of reference points for the vertical profiles is limited only by the resolution of the ice core.
It is important to emphasize that prescribing the reconstructed δ 18O from GISP2 as an upper boundary condition does not invalidate the test for ice dynamics, because it only constrains the depositional history. The dynamical history represented by the shape of the simulated δ 18O profile evolves freely and depends only on the model parameters to be tested. However, the location of the GISP2 ice core at the summit is not ideal because the influence of the divergent lateral flow is reduced to a thinning of layers that drives a slow vertical motion. Locations closer to the ice margins are more directly affected by the lateral flow because changes in the local surface slope advect material with a δ 18O signature that was deposited upstream.
While prescribing the δ 18O at the upper boundary is not problematic, forcing the model with accumulation reconstructed from GISP2 layer thickness data does slightly compromise the optimization exercise. To estimate the original thickness of each layer as it accumulated, the reconstruction assumes a thinning function that accounts for ice flow (Cuffey and Clow, Reference Cuffey and Clow1997). Thus, prescribing the reconstructed accumulation time series implicitly introduces a dynamical forcing component at the upper boundary. This undermines the independence between the prescribed depositional history and the simulated dynamics that the optimization is based on. Again, an ice core location further downstream from the reference point of the reconstructed accumulation is preferable because the shape of its δ 18O profile is less sensitive to layer thinning and more to lateral advection. Unfortunately, there are no other ice cores in the current 2-D model domain. It is not possible to define a flowline through more than one ice core location because this flowline likely changed during the last glacial cycle as a result of changes in surface topography gradients.
Although the majority of the ice flows zonally from the summit toward the margins, flow in the meridional direction is also important, especially in the lower part of the ice sheet (Greve, Reference Greve1997a; Clarke and others, Reference Clarke, Lhomme and Marshall2005). The latter is neglected in the 2-D domain of the isochronal model, causing ice to be removed too slowly from the interior of the ice sheet for a realistic simulation of the zonal surface gradient and ice stiffness. The incomplete description of the ice dynamics influences the optimization procedure because shortcomings in the limited model domain can not fully be separated from the impact of the optimization parameters. However, the effect is limited by the relatively small meridional flow. Importantly, the simplified domain was chosen only to facilitate the initial model development without compromising the model physics. The model includes all dynamical components to represent the full 3-D flow in future applications. Most of the necessary infrastructure, including a 2-D horizontal grid, has already been developed in parallel to the isochronal model in a second ice-sheet model (Neff and others, Reference Neff, Born and Stocker2016).
In summary, the new model overcomes the long-standing problem of excessive numerical diffusion in ice-sheet modelling with a radical redesign of the vertical flow of ice. The comparison of the thinning isochronals with previous approaches highlights the striking simplicity of its underlying concept. It approximates the intuitive understanding of ice-sheet flow that is used for many reconstruction techniques. Bridging this conceptual divide between modelling and reconstructions enables the investigation of several previously infeasible research questions. It opens the possibility to use ice core data not only for climate reconstructions but also to reconstruct past variations in ice flow and to constrain the model sensitivity. Simulations of the full 3-D stratigraphy are very timely because of the arrival of radar-based data of englacial layering. The convergence of model and data techniques unlocks the potential of new synergistic approaches to estimate both the past and future of ice sheets and sea level.
ACKNOWLEDGEMENTS
I am grateful to Thomas F. Stocker, Jakob Schwander and Alexander Robinson for helpful discussions, and to Joseph A. MacGregor and two anonymous reviewers for constructive comments. Gary Clow is acknowledged for providing the GISP2 borehole temperature data. The work has partly been funded by the European Commission under the Marie Curie Intra-European Fellowship ECLIPS (PIEF-GA-2011-300544).
APPENDIX
DISCRETIZATION OF LAYER THICKNESS EQUATION
Equation (7) is discretized forward in time and upstream in space, using velocities at the border of the grid boxes:
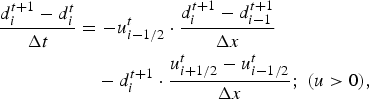 $$\eqalign{ \displaystyle{{d_i^{t + 1} - d_i^t} \over {\Delta t}}& = -u_{i - 1/2}^t \cdot \displaystyle{{d_i^{t + 1} - d_{i - 1}^{t + 1}} \over {\Delta x}} \cr & \quad - d_i^{t + 1} \cdot \displaystyle{{u_{i + 1/2}^t - u_{i - 1/2}^t} \over {\Delta x}};\;(u \gt 0),} $$
$$\eqalign{ \displaystyle{{d_i^{t + 1} - d_i^t} \over {\Delta t}}& = -u_{i - 1/2}^t \cdot \displaystyle{{d_i^{t + 1} - d_{i - 1}^{t + 1}} \over {\Delta x}} \cr & \quad - d_i^{t + 1} \cdot \displaystyle{{u_{i + 1/2}^t - u_{i - 1/2}^t} \over {\Delta x}};\;(u \gt 0),} $$
which takes the following form and is solved implicitly:
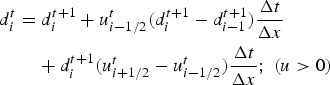 $$\eqalign{& d_i^t = d_i^{t + 1} + u_{i - 1/2}^t (d_i^{t + 1} - d_{i - 1}^{t + 1} )\displaystyle{{\Delta t} \over {\Delta x}} \cr & \qquad + d_i^{t + 1} (u_{i + 1/2}^t - u_{i - 1/2}^t )\displaystyle{{\Delta t} \over {\Delta x}};\;(u \gt 0)} $$
$$\eqalign{& d_i^t = d_i^{t + 1} + u_{i - 1/2}^t (d_i^{t + 1} - d_{i - 1}^{t + 1} )\displaystyle{{\Delta t} \over {\Delta x}} \cr & \qquad + d_i^{t + 1} (u_{i + 1/2}^t - u_{i - 1/2}^t )\displaystyle{{\Delta t} \over {\Delta x}};\;(u \gt 0)} $$
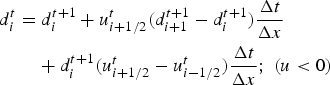 $$\eqalign{& d_i^t = d_i^{t + 1} + u_{i + 1/2}^t (d_{i + 1}^{t + 1} - d_i^{t + 1} )\displaystyle{{\Delta t} \over {\Delta x}} \cr & \qquad + d_i^{t + 1} (u_{i + 1/2}^t - u_{i - 1/2}^t )\displaystyle{{\Delta t} \over {\Delta x}};\;(u \lt 0)} $$
$$\eqalign{& d_i^t = d_i^{t + 1} + u_{i + 1/2}^t (d_{i + 1}^{t + 1} - d_i^{t + 1} )\displaystyle{{\Delta t} \over {\Delta x}} \cr & \qquad + d_i^{t + 1} (u_{i + 1/2}^t - u_{i - 1/2}^t )\displaystyle{{\Delta t} \over {\Delta x}};\;(u \lt 0)} $$
DISCRETIZATION OF VERTICAL HEAT EQUATION, 2ND DERIVATIVE ON AN UNEVEN GRID
The second derivative at a given depth z = i is
using
(A4) becomes
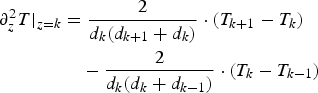 $$\eqalign{ \partial _z^2 T \vert _{z = k} &= \displaystyle{2 \over {d_k(d_{k + 1} + d_k)}} \cdot (T_{k + 1} - T_k) \cr & \quad - \displaystyle{2 \over {d_k(d_k + d_{k - 1})}} \cdot (T_k - T_{k - 1})} $$
$$\eqalign{ \partial _z^2 T \vert _{z = k} &= \displaystyle{2 \over {d_k(d_{k + 1} + d_k)}} \cdot (T_{k + 1} - T_k) \cr & \quad - \displaystyle{2 \over {d_k(d_k + d_{k - 1})}} \cdot (T_k - T_{k - 1})} $$
Thus, the vertical heat diffusion Eqn (14) is discretized as
and is solved implicitly.















