Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T11:22:48.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Moving beyond Moody

Published online by Cambridge University Press:  06 March 2018

Karen A. Flack
Karen A. Flack*
Affiliation:
Department of Mechanical Engineering, United States Naval Academy, Annapolis, MD 21402, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Thakkar et al. (J. Fluid Mech., vol. 837, 2018, R1) represents a significant advancement in the ability to computationally model rough wall flows. Direct numerical solution (DNS) of turbulent boundary layer flow over an industrial grit blasted surface at relevant roughness Reynolds numbers, from hydraulically smooth to fully rough regimes, is a path forward to parametrically study a wide range of surface roughness. The methodology described in this paper, coupled with validation experiments, ultimately should lead to improved frictional drag predictions.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
Focus on Fluids
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 1 - 4
Check for updates
Copyright
© Cambridge University Press 2018. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

1 Introduction

Engineers do not currently have the ability to accurately predict the drag of a generic rough surface. After decades of detailed measurements and recent computations of boundary layer flow over rough surfaces, the friction drag on a surface is only accurately known for the tested surfaces.

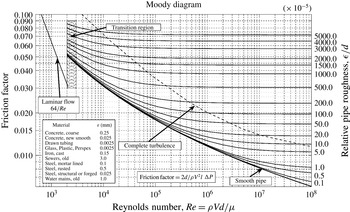
Figure 1. Reprinted with permission from L. F. Moody, Friction factors for pipe flow, Trans. ASME, vol. 66, 1944, pp. 671–684. Copyright 1944 ASME.

Engineering predictions of surface roughness is generally characterized by $k_{s}$ , the equivalent sand grain roughness height. This is the size of uniformly packed sand grains tested by Nikuradse (Reference Nikuradse1933) that produces the same frictional drag in the fully rough regime. Therefore, $k_{s}$ is a hydraulic scale, not a physical scale, and this is what is listed on the Moody diagram (Reference Moody1944) (figure 1) as $\unicode[STIX]{x1D716}$ , the equivalent roughness height. I suspect that the word equivalent has often been ignored and the words roughness height have been used. If this is the case, then which roughness height? The mean, the peak-to-trough, or the root mean square (r.m.s.) roughness height? Even if you select one of these roughness scales, all are dependent to some extent on the spatial sample size of your measurement region. Therefore, the Moody diagram is only accurate for surfaces with known $k_{s}$ in the fully rough regime.

The transitionally rough regime poses its own set of challenges. The transitionally rough regime is characterized by contributions from viscous and form drag on the roughness elements. At low Reynolds numbers, viscosity damps out flow disturbances caused by surface roughness. For these conditions, the flow is classified as hydraulically smooth. As Reynolds number increases, the turbulent eddies caused by the roughness elements are not fully damped by viscosity and form drag on the roughness contributes to the overall drag, increasingly with increased Reynolds number. Eventually, form drag is the dominant mechanism, and the flow becomes fully rough. The mechanisms responsible for this transition from hydraulically smooth to fully rough are not fully understood. Do roughness effects occur gradually as the roughness Reynolds number ( $k^{+}=U_{\unicode[STIX]{x1D70F}}k/\unicode[STIX]{x1D708}$ , where $k$ is the roughness height, $U_{\unicode[STIX]{x1D70F}}$ is the friction velocity and $\unicode[STIX]{x1D708}$ is the kinematic viscosity) increases, as assumed by the Colebrook (Reference Colebrook1939) roughness function (used in the Moody diagram), or is the onset of roughness effects more abrupt, occurring at a finite $k^{+}$ as represented by a Nikuradse (Reference Nikuradse1933) roughness function?

It has been shown that the onset of roughness effects, the shape of the roughness function in the transitionally rough regime and the Reynolds number where the flow becomes fully rough are highly dependent on roughness geometry (Flack & Schultz Reference Flack and Schultz2014). Since there are a myriad of roughness geometries, a way is needed to categorize surface roughness by easy to measure statistical or roughness feature properties. Additionally the measurement region upon which these properties are based should be identified, and potentially scales that do not contribute to the drag need to be removed before determining surface statistics. This filter should also be based on a roughness scale. There are a number of issues that need to be addressed before developing a robust engineering correlation, hence the reason that the contributions by Thakkar, Busse & Sandham (Reference Thakkar, Busse and Sandham2018) (for example, dispersive sheer stress as shown in the figure by the title) and other recent simulations of rough wall flows are so important. Realistic rough surfaces at relevant Reynolds numbers are being computed and there is hope in making headway towards identifying roughness scales to inform engineering predictions of surface drag.

2 Overview

A number of recent simulations over complex roughness have been performed with the goal of understanding the near wall turbulence and developing predictive correlations for drag. Mathematically generated surfaces with a range of scales allow for parametrically changing surface parameters. Anderson & Meneveau (Reference Anderson and Meneveau2011) performed a large eddy simulation (LES) for flow over a multi-scale, fractal-like roughness, similar to the range of scales in natural terrains. Realistic roughness was studied by Yuan & Piomelli (Reference Yuan and Piomelli2011) using LES for roughness replicated from hydraulic turbine blades, with surface features parametrically changed to study the influence of roughness slope on the surface drag. Three-dimensional sinusoidal roughness in the transitionally rough regime was investigated using direct numerical solution (DNS) by Chan et al. (Reference Chan, MacDonald, Chung, Hutchins and Ooi2015) and MacDonald et al. (Reference MacDonald, Chung, Chan, Hutchins and Ooi2016). It was shown in these studies that the roughness function could be accurately determined using the minimal-span channel technique (Chung et al. Reference Chung, Chan, MacDonald, Hutchins and Ooi2015) which allows for low Reynolds number simulations ( $Re_{\unicode[STIX]{x1D70F}}=U_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=180$ , where $h$ is the channel half height). This is encouraging since a large number of parameters can be investigated at a lower computational cost. Forooghi et al. (Reference Forooghi, Stroh, Magagnato, Jakirlic and Frohnapfel2017) also used DNS at low $Re_{\unicode[STIX]{x1D70F}}$ to determine the equivalent sand grain roughness for randomly distributed roughness elements of random size and prescribed shape. Correlations are presented considering roughness heights, slopes, density and moments of the surface elevation p.d.f.

Thakkar et al. (Reference Thakkar, Busse and Sandham2018) are the first to use DNS to study a realistic irregular roughness, similar to the sand grain roughness of Nikuradse (Reference Nikuradse1933), for the entire range of roughness Reynolds numbers from hydraulically smooth to fully rough. This is an extension of their previous work (Thakkar, Busse & Sandham Reference Thakkar, Busse and Sandham2017) where they presented roughness results in the upper part of the transitionally rough regime and the fully rough regime for grit blasted and graphite surfaces. DNS with engineering roughness is a true advancement, and they have developed techniques to tile these surfaces within the computational domain. The grit blasted surface is deemed Nikuradse-like because it follows the Nikuradse roughness function with $k_{s}^{+}=0.87k^{+}$ . The authors expect other sand-grain-like surfaces to have similar behaviour. The interesting question is what makes a surface sand-grain-like: sharp protrusions, close packing, a distinct range of scales, positive or negative skewness?

3 Future

Tremendous progress has been made in the prediction of frictional drag on rough surfaces. The way forward is to study both realistic roughness and mathematically generated surfaces that contain a range of surface features. Recent computations have shown that drag producing roughness scales can be adequately represented at relevant Reynolds numbers. Rough surfaces with a range of scales can be characterized by surface statistics or other mathematical parameters. These parameters can be derived from measured surface scans. Are the important features the r.m.s. height and the skewness of the p.d.f. (Flack & Schultz Reference Flack and Schultz2010), effective slope (Napoli, Armenio & De Marchis Reference Napoli, Armenio and De Marchis2008; Chan et al. Reference Chan, MacDonald, Chung, Hutchins and Ooi2015), distribution of peak roughness heights (Forooghi et al. Reference Forooghi, Stroh, Magagnato, Jakirlic and Frohnapfel2017) or others? Surely the roughness density and the sheltering that occurs as the roughness becomes more closely packed (i.e. MacDonald et al. Reference MacDonald, Chung, Chan, Hutchins and Ooi2016) must be important for sparse roughness.

The feature of the Moody diagram that should definitely be reconsidered is the Colebrook function in the transitionally rough regime. This function is a monotonic variation in the skin-friction, asymptotically approaching the limits of hydraulically smooth and fully rough regimes. While Colebrook’s experiments (Colebrook Reference Colebrook1939) on commercial pipes followed this function, more recent work on industrial pipes (Allen, Shockling & Smits Reference Allen, Shockling and Smits2005; Langelandsvik, Kunkel & Smits Reference Langelandsvik, Kunkel and Smits2008) and Nikuradse sand grains (Reference Nikuradse1933) did not display this behaviour. Gioia & Chakraborty (Reference Gioia and Chakraborty2006) discuss that the shape of the friction factor (or roughness function) is related to the size of eddies shed by the roughness elements. At low Reynolds numbers, dissipation of the small eddies shed from the roughness elements leads to a depressed value of the friction factor. The range of eddies become larger at higher Reynolds number resulting in more vigorous momentum transfer and increased drag. With an abundance of roughness geometries, it is likely that a wide range of friction factor shapes are possible in the transitionally rough regime.

Are we ready to move beyond the Moody diagram and characterizing the roughness by $k_{s}$ ? The equivalent sand grain roughness height is a convenient scale in the fully rough regime but not necessarily useful in the transitionally rough regime. Other scales may better characterize the onset of roughness effects, the shape of the roughness function and the transition to fully rough behaviour. This area of research is still very active and the ability to simulate realistic roughness with a wide range of surface parameters will ultimately lead to improved predictive tools.

References

Anderson, W. & Meneveau, C. 2011 Dynamic roughness model for large-eddy simulation of turbulent flow over multiscale, fractal-like rough surfaces. J. Fluid Mech. 679, 288–314.CrossRefGoogle Scholar
Allen, J. J., Shockling, M. A. & Smits, A. J. 2005 Evaluation of a universal transitional resistance diagram for pipes with honed surfaces. Phys. Fluids 17, 121702.CrossRefGoogle Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.CrossRefGoogle Scholar
Chung, D., Chan, L., MacDonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 41431.CrossRefGoogle Scholar
Colebrook, C. F. 1939 Turbulent flow in pipes, with particular reference to the transitional region between smooth and rough wall laws. J. Inst. Civil Engrs Lond. 11, 133–156.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. Trans. ASME J. Fluids Engng 132, 041203.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26, 101305.CrossRefGoogle Scholar
Forooghi, P., Stroh, A., Magagnato, F., Jakirlic, S. & Frohnapfel, B. 2017 Toward a universal roughness correlation. Trans. ASME J. Fluids Engng 139 (12), 121201.CrossRefGoogle Scholar
Gioia, G. & Chakraborty, P. 2006 Turbulent friction in rough pipes and the energy spectrum of the phenomenological theory. Phys. Rev. Lett. 96, 044502.CrossRefGoogle ScholarPubMed
Langelandsvik, L. I., Kunkel, G. J. & Smits, A. J. 2008 Flow in a commercial steel pipe. J. Fluid Mech. 595, 323–339.CrossRefGoogle Scholar
MacDonald, M., Chung, D., Chan, L., Hutchins, N. & Ooi, A. 2016 Turbulent flow over transitionally rough surfaces with varying roughness densities. J. Fluid Mech 804, 130–161.CrossRefGoogle Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.CrossRefGoogle Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. Translation from German published 1950 as NACA Tech. Memo. 1292.Google Scholar
Thakkar, M., Busse, A. & Sandham, N. 2017 Surface correlations of hydrodynamics drag for transitionally rough engineering surfaces. J. Turbul. 18 (2), 138–169.CrossRefGoogle Scholar
Thakkar, M., Busse, A. & Sandham, N. 2018 DNS of turbulent channel flow over a surrogate for Nikuradse-type roughness. J. Fluid Mech. 837, R1.CrossRefGoogle Scholar
Yuan, J. & Piomelli, U. 2011 Estimation and prediction of the roughness function of realistic surfaces. J. Turbul. 15 (6), 350–365.CrossRefGoogle Scholar
Figure 0

Figure 1. Reprinted with permission from L. F. Moody, Friction factors for pipe flow, Trans. ASME, vol. 66, 1944, pp. 671–684. Copyright 1944 ASME.