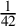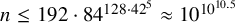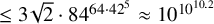1 Introduction
We work over the field of complex number
![]() $\mathbb C$
.
$\mathbb C$
.
Birkar famously proved the boundedness of n-complements for
![]() $\mathbb R$
-complementary varieties and pairs with hyperstandard coefficients [Reference Birkar3], which was later generalized to arbitrary DCC coefficients [Reference Han, Liu and Shokurov20] and arbitrary coefficients [Reference Shokurov40] under milder conditions. It is interesting to ask whether we can give an explicit bound of n, as such an explicit bound is expected to be useful for the moduli of log surfaces (cf. [Reference Alexeev and Liu1, Reference Kollár26, Reference Kollár28]) and threefold minimal log discrepancies [Reference Han, Liu and Luo19]. [Reference Shokurov39] shows that an
$\mathbb R$
-complementary varieties and pairs with hyperstandard coefficients [Reference Birkar3], which was later generalized to arbitrary DCC coefficients [Reference Han, Liu and Shokurov20] and arbitrary coefficients [Reference Shokurov40] under milder conditions. It is interesting to ask whether we can give an explicit bound of n, as such an explicit bound is expected to be useful for the moduli of log surfaces (cf. [Reference Alexeev and Liu1, Reference Kollár26, Reference Kollár28]) and threefold minimal log discrepancies [Reference Han, Liu and Luo19]. [Reference Shokurov39] shows that an
![]() $\mathbb R$
-complementary surface pair
$\mathbb R$
-complementary surface pair
![]() $(X,B)$
is n-complementary for some
$(X,B)$
is n-complementary for some
![]() $n\in \{1,2,3,4,6\}$
when B has standard coefficients and
$n\in \{1,2,3,4,6\}$
when B has standard coefficients and
![]() $(X,B)$
is not exceptional, but the question remained open in general for surfaces. In this paper, we provide an explicit upper bound of n for surfaces.
$(X,B)$
is not exceptional, but the question remained open in general for surfaces. In this paper, we provide an explicit upper bound of n for surfaces.
Theorem 1.1. Let
![]() $X/Z\ni z$
be an
$X/Z\ni z$
be an
![]() $\mathbb R$
-complementary surface. Then,
$\mathbb R$
-complementary surface. Then,
![]() $X/Z\ni z$
has an n-complement for some
$X/Z\ni z$
has an n-complement for some
![]() $n\leq 192\cdot 84^{128\cdot 42^5}$
. In particular, if Z is a point, then
$n\leq 192\cdot 84^{128\cdot 42^5}$
. In particular, if Z is a point, then
![]() $h^0(-nK_X)>0$
.
$h^0(-nK_X)>0$
.
The key ingredient of the proof of Theorem 1.1 is the following result which provides an explicit characterization of the singularities of exceptional pairs in any dimension. Recall that
![]() $\operatorname {lct}(d,\Gamma )$
is the set of lc thresholds for effective Weil divisors with respect to pairs of dimension d with coefficients in
$\operatorname {lct}(d,\Gamma )$
is the set of lc thresholds for effective Weil divisors with respect to pairs of dimension d with coefficients in
![]() $\Gamma $
.
$\Gamma $
.
Theorem 1.2. Let d be a positive integer and
![]() $\Gamma \subset [0,1]$
a DCC set. Let
$\Gamma \subset [0,1]$
a DCC set. Let
 $$ \begin{align*} \epsilon_1(d,\Gamma):=\inf\Bigg\{1-t\Biggm| \begin{array}{r@{}l}t<1, \text{there exists a pair }(W,\Delta+t\Psi)\text{ of dimension } d\text { such that }\\ (W,\Delta+t\Psi)\text{ is lc}, K_W+\Delta+t\Psi\equiv 0, \Delta\in\Gamma,\text{and }0\not=\Psi\in\mathbb N^+ \end{array}\Bigg\}, \end{align*} $$
$$ \begin{align*} \epsilon_1(d,\Gamma):=\inf\Bigg\{1-t\Biggm| \begin{array}{r@{}l}t<1, \text{there exists a pair }(W,\Delta+t\Psi)\text{ of dimension } d\text { such that }\\ (W,\Delta+t\Psi)\text{ is lc}, K_W+\Delta+t\Psi\equiv 0, \Delta\in\Gamma,\text{and }0\not=\Psi\in\mathbb N^+ \end{array}\Bigg\}, \end{align*} $$
and
![]() $\epsilon (d,\Gamma ):=\min \{\epsilon _1(d,\Gamma ),\epsilon _2(d,\Gamma )\}$
. Then, for any exceptional Fano type pair
$\epsilon (d,\Gamma ):=\min \{\epsilon _1(d,\Gamma ),\epsilon _2(d,\Gamma )\}$
. Then, for any exceptional Fano type pair
![]() $(X,B)$
of dimension d such that
$(X,B)$
of dimension d such that
![]() $B\in \Gamma $
and any
$B\in \Gamma $
and any
![]() $0\leq G\sim _{\mathbb R}-(K_X+B)$
,
$0\leq G\sim _{\mathbb R}-(K_X+B)$
,
![]() $(X,B+G)$
is
$(X,B+G)$
is
![]() $\epsilon (d,\Gamma )$
-lc. In particular,
$\epsilon (d,\Gamma )$
-lc. In particular,
![]() $(X,B)$
is
$(X,B)$
is
![]() $\epsilon (d,\Gamma )$
-lc.
$\epsilon (d,\Gamma )$
-lc.
We have the following corollary, which implies Theorem 1.1.
Corollary 1.3. Exceptional Fano type surfaces are
![]() $\frac {1}{42}$
-lc.
$\frac {1}{42}$
-lc.
With Corollary 1.3, we also provide an explicit upper bound of Tian’s
![]() $\alpha $
-invariant for surfaces:
$\alpha $
-invariant for surfaces:
Corollary 1.4. Tian’s
![]() $\alpha $
-invariant for any surface is
$\alpha $
-invariant for any surface is
![]() $\leq 3\sqrt {2}\cdot 84^{64\cdot 42^5}$
(when it is well-defined).
$\leq 3\sqrt {2}\cdot 84^{64\cdot 42^5}$
(when it is well-defined).
Although the bounds in Theorem 1.1 and Corollary 1.4 are expected to be far from being optimal, these are the first precise upper bounds of these two algebraic invariants for surfaces. Similar topics and alternative directions include the estimation of the lower bound n (cf. [Reference Esser, Totaro and Wang15, Reference Totaro and Wang42]), the boundedness of the the anti-canonical volume of Fano varieties (cf. [Reference Prokhorov35, Reference Prokhorov36, Reference Chen and Chen11, Reference Prokhorov37, Reference Chen12, Reference Prokhorov38, Reference Chen and Jiang13, Reference Chen and Jiang14, Reference Jiang and Zou23, Reference Jiang22, Reference Jiang and Zou24, Reference Birkar4]), estimation of
![]() $(\epsilon ,n)$
-complement [Reference Chen and Han9], the explicit McKernan-Shokurov conjecture [Reference Han, Jiang and Luo18], precise bounds of mlds [Reference Jiang21, Reference Liu and Xiao33, Reference Liu and Luo31], etc.
$(\epsilon ,n)$
-complement [Reference Chen and Han9], the explicit McKernan-Shokurov conjecture [Reference Han, Jiang and Luo18], precise bounds of mlds [Reference Jiang21, Reference Liu and Xiao33, Reference Liu and Luo31], etc.
Postscript
After the first version of this paper, 1) Totaro [Reference Totaro41] conjectured that the smallest Tian’s alpha invariant for del Pezzo surfaces is equal to
![]() $\frac {21}{2}$
, given by
$\frac {21}{2}$
, given by
![]() $X_{154}\subset \mathbb P(77,45,19,14)$
, and 2) The author and Shokurov [Reference Liu and Shokurov32] prove that
$X_{154}\subset \mathbb P(77,45,19,14)$
, and 2) The author and Shokurov [Reference Liu and Shokurov32] prove that
![]() $\epsilon (2,\{0\})=\frac {1}{13}$
. This result allows us to get better explicit bounds of the n-complements and the
$\epsilon (2,\{0\})=\frac {1}{13}$
. This result allows us to get better explicit bounds of the n-complements and the
![]() $\alpha $
-invariants. Nevertheless, in order to make the paper self-contained, we will not use any results in [Reference Liu and Shokurov32].
$\alpha $
-invariants. Nevertheless, in order to make the paper self-contained, we will not use any results in [Reference Liu and Shokurov32].
2 Preliminaries
We adopt the standard notation and definitions in [Reference Kollár and Mori29, Reference Birkar, Cascini, Hacon and McKernan6] and will freely use them. For the notation of (relative) pairs
![]() $(X/Z\ni z,B)$
and complements, we refer the reader to [Reference Chen and Han9].
$(X/Z\ni z,B)$
and complements, we refer the reader to [Reference Chen and Han9].
Definition 2.1. Let
![]() $(X/Z\ni z,B)$
be an
$(X/Z\ni z,B)$
be an
![]() $\mathbb {R}$
-complementary pair. We say that
$\mathbb {R}$
-complementary pair. We say that
![]() $(X/Z\ni z,B)$
is exceptional if
$(X/Z\ni z,B)$
is exceptional if
![]() $(X/Z\ni z,B+G)$
is klt for any
$(X/Z\ni z,B+G)$
is klt for any
![]() $G\geq 0$
such that
$G\geq 0$
such that
![]() $K_X+B+G\sim _{\mathbb R}0$
over a neighborhood of z.
$K_X+B+G\sim _{\mathbb R}0$
over a neighborhood of z.
Definition 2.2. Let d be a positive integer and
![]() $\Gamma \subset [0,1]$
a set. We let
$\Gamma \subset [0,1]$
a set. We let
 $$ \begin{align*} \epsilon_1(d,\Gamma):=\inf\Bigg\{1-t\Biggm|\begin{array}{r@{}l} t<1, \text{there exists a pair }(X,B+tC)\text{ of dimension } d\text { such that }\\ (X,B+tC)\text{ is lc}, K_X+B+tC\equiv 0, B\in\Gamma,\text{and }0\not=C\in\mathbb N^+ \end{array}\Bigg\}, \end{align*} $$
$$ \begin{align*} \epsilon_1(d,\Gamma):=\inf\Bigg\{1-t\Biggm|\begin{array}{r@{}l} t<1, \text{there exists a pair }(X,B+tC)\text{ of dimension } d\text { such that }\\ (X,B+tC)\text{ is lc}, K_X+B+tC\equiv 0, B\in\Gamma,\text{and }0\not=C\in\mathbb N^+ \end{array}\Bigg\}, \end{align*} $$
and
![]() $\epsilon (d,\Gamma ):=\min \{\epsilon _1(d,\Gamma ),\epsilon _2(d,\Gamma )\}$
. By [Reference Hacon, McKernan and Xu17, Theorem 1.5],
$\epsilon (d,\Gamma ):=\min \{\epsilon _1(d,\Gamma ),\epsilon _2(d,\Gamma )\}$
. By [Reference Hacon, McKernan and Xu17, Theorem 1.5],
![]() $\epsilon (d,\Gamma )>0$
when
$\epsilon (d,\Gamma )>0$
when
![]() $\Gamma $
is DCC.
$\Gamma $
is DCC.
Remark 2.3. Usually,
![]() $\epsilon _1(d,\Gamma )<\epsilon _2(d,\Gamma )$
, (e.g., when
$\epsilon _1(d,\Gamma )<\epsilon _2(d,\Gamma )$
, (e.g., when
![]() $\Gamma =D(\Gamma )$
[Reference Hacon, McKernan and Xu17, Lemma 11.2, Proposition 11.5]) and in such cases,
$\Gamma =D(\Gamma )$
[Reference Hacon, McKernan and Xu17, Lemma 11.2, Proposition 11.5]) and in such cases,
![]() $\epsilon (d,\Gamma )=\epsilon _1(d,\Gamma )$
.
$\epsilon (d,\Gamma )=\epsilon _1(d,\Gamma )$
.
Lemma 2.4 [Reference Kollár26, 5.3 Theorem, 5.4 Theorem]
Let
![]() $\Gamma :=\{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
. Then,
$\Gamma :=\{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
. Then,
-
1.
 $\epsilon _2(2,\Gamma )=\epsilon _2(2,\{0\})=\frac {1}{6}$
.
$\epsilon _2(2,\Gamma )=\epsilon _2(2,\{0\})=\frac {1}{6}$
. -
2.
 $\epsilon _1(2,\Gamma )=\frac {1}{42}\leq \epsilon _1(2,\{0\})$
.
$\epsilon _1(2,\Gamma )=\frac {1}{42}\leq \epsilon _1(2,\{0\})$
.
Remark 2.5. It was expected that
![]() $\epsilon _1(2,\{0\})=\frac {1}{13}$
(cf. [Reference Alexeev and Liu1, Notation 4.1], [Reference Kollár28, Reference Shokurov40]). After the first version of this paper, the author and Shokurov prove this result in [Reference Liu and Shokurov32]. It is interesting to ask whether
$\epsilon _1(2,\{0\})=\frac {1}{13}$
(cf. [Reference Alexeev and Liu1, Notation 4.1], [Reference Kollár28, Reference Shokurov40]). After the first version of this paper, the author and Shokurov prove this result in [Reference Liu and Shokurov32]. It is interesting to ask whether
![]() $\epsilon _1(d,\Gamma )$
is equal to the
$\epsilon _1(d,\Gamma )$
is equal to the
![]() $1$
-gap of mlds for pairs with coefficients in
$1$
-gap of mlds for pairs with coefficients in
![]() $\Gamma $
in dimension
$\Gamma $
in dimension
![]() $d+1$
(cf. [Reference Jiang21, Reference Liu and Xiao33, Reference Liu and Luo31]).
$d+1$
(cf. [Reference Jiang21, Reference Liu and Xiao33, Reference Liu and Luo31]).
Remark 2.6. When
![]() $\Gamma =\{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
is the standard set,
$\Gamma =\{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
is the standard set,
![]() $\epsilon (d,\Gamma )\leq \frac {1}{N_{d+2}-1}$
by considering the example
$\epsilon (d,\Gamma )\leq \frac {1}{N_{d+2}-1}$
by considering the example
![]() $(\mathbb P^d,\sum _{i=1}^{d+1}(1-\frac {1}{N_i})H_i+(1-\frac {1}{N_{d+2}-1})H_{d+2}))$
, where
$(\mathbb P^d,\sum _{i=1}^{d+1}(1-\frac {1}{N_i})H_i+(1-\frac {1}{N_{d+2}-1})H_{d+2}))$
, where
![]() $\{N_i\}_{i=1}^{+\infty }$
is the Sylvester sequence
$\{N_i\}_{i=1}^{+\infty }$
is the Sylvester sequence
![]() $2,3,7,43,\dots $
and
$2,3,7,43,\dots $
and
![]() $H_i$
are general hyperplanes of degree
$H_i$
are general hyperplanes of degree
![]() $1$
. It is also expected that
$1$
. It is also expected that
![]() $\epsilon (d,\Gamma )=\frac {1}{N_{d+2}-1}$
[Reference Kollár, Kollár, Lazarsfeld and Morrison27, 8.16].
$\epsilon (d,\Gamma )=\frac {1}{N_{d+2}-1}$
[Reference Kollár, Kollár, Lazarsfeld and Morrison27, 8.16].
Lemma 2.7 [(cf. [Reference Alexeev and Mori2, Proof of Lemma 3.7], [Reference Lai30, After Theorem A], [Reference Birkar4, Lemma 2.2]).]
Let
![]() $\epsilon $
be a positive real number and X an
$\epsilon $
be a positive real number and X an
![]() $\epsilon $
-lc Fano surface. Then,
$\epsilon $
-lc Fano surface. Then,
![]() $IK_X$
is Cartier for some positive integer
$IK_X$
is Cartier for some positive integer
![]() $I\leq 2\left (\frac {2}{\epsilon }\right )^{\frac {128}{\epsilon ^5}}.$
$I\leq 2\left (\frac {2}{\epsilon }\right )^{\frac {128}{\epsilon ^5}}.$
We will frequently use the following result to run minimal model programs:
Theorem 2.8 [Reference Birkar, Cascini, Hacon and McKernan6, Corollary 1.3.2]
Fano type varieties are Mori dream spaces. In particular, for any Fano type variety X and any
![]() $\mathbb {R}$
-Cartier
$\mathbb {R}$
-Cartier
![]() $\mathbb {R}$
-divisor D on X, any sequence of D-MMP terminates with either a good minimal model or a Mori fiber space.
$\mathbb {R}$
-divisor D on X, any sequence of D-MMP terminates with either a good minimal model or a Mori fiber space.
3 The nonexceptional case
Lemma 3.1. Let
![]() $X/Z\ni z$
be an
$X/Z\ni z$
be an
![]() $\mathbb {R}$
-complementary surface that is not exceptional. Then,
$\mathbb {R}$
-complementary surface that is not exceptional. Then,
![]() $X/Z\ni z$
has an n-complement for some
$X/Z\ni z$
has an n-complement for some
![]() $n\in \{1,2,3,4,6\}$
.
$n\in \{1,2,3,4,6\}$
.
Proof. There exists an lc but not klt pair
![]() $(X/Z\ni z,B)$
such that
$(X/Z\ni z,B)$
such that
![]() $K_X+B\sim _{\mathbb R,Z}0$
over a neighborhood of z. Let
$K_X+B\sim _{\mathbb R,Z}0$
over a neighborhood of z. Let
![]() $f: Y\rightarrow X$
be a dlt modification of
$f: Y\rightarrow X$
be a dlt modification of
![]() $(X/Z\ni z,B)$
and let
$(X/Z\ni z,B)$
and let
![]() $K_Y+B_Y:=f^*(K_X+B)$
. Then,
$K_Y+B_Y:=f^*(K_X+B)$
. Then,
![]() $\lfloor B_Y\rfloor \not =0$
. By [Reference Shokurov39, 2.3 Inductive Theorem],
$\lfloor B_Y\rfloor \not =0$
. By [Reference Shokurov39, 2.3 Inductive Theorem],
![]() $(Y/Z\ni z,\lfloor B_Y\rfloor )$
has a monotonic n-complement
$(Y/Z\ni z,\lfloor B_Y\rfloor )$
has a monotonic n-complement
![]() $(Y/Z\ni z,B_Y^+)$
for some
$(Y/Z\ni z,B_Y^+)$
for some
![]() $n\in \{1,2,3,4,6\}$
for any
$n\in \{1,2,3,4,6\}$
for any
![]() $z\in Z$
. Hence,
$z\in Z$
. Hence,
![]() $X/Z\ni z$
has an n-complement
$X/Z\ni z$
has an n-complement
![]() $(X/Z\ni z,f_*B_Y^+)$
for some
$(X/Z\ni z,f_*B_Y^+)$
for some
![]() $n\in \{1,2,3,4,6\}$
.
$n\in \{1,2,3,4,6\}$
.
Corollary 3.2. Let
![]() $X/Z\ni z$
be an
$X/Z\ni z$
be an
![]() $\mathbb {R}$
-complementary surface and
$\mathbb {R}$
-complementary surface and
![]() $\dim Z>0$
. Then,
$\dim Z>0$
. Then,
![]() $X/Z\ni z$
has an n-complement for some
$X/Z\ni z$
has an n-complement for some
![]() $n\in \{1,2,3,4,6\}$
.
$n\in \{1,2,3,4,6\}$
.
Proof. For any pair
![]() $(X/Z\ni z,B)$
such that
$(X/Z\ni z,B)$
such that
![]() $K_X+B\sim _{\mathbb R,Z}0$
over a neighborhood of z,
$K_X+B\sim _{\mathbb R,Z}0$
over a neighborhood of z,
![]() $(X/Z\ni z,B+tf^*z)$
is an lc but not klt pair such that
$(X/Z\ni z,B+tf^*z)$
is an lc but not klt pair such that
![]() $K_X+B+tf^*z\sim _{\mathbb R,Z}0$
over a neighborhood of z, where
$K_X+B+tf^*z\sim _{\mathbb R,Z}0$
over a neighborhood of z, where
![]() $t:=\operatorname {lct}(X,B;f^*z)$
. The corollary follows from Lemma 3.1.
$t:=\operatorname {lct}(X,B;f^*z)$
. The corollary follows from Lemma 3.1.
4 The exceptional case
4.1 Proof of Theorem 1.2 and Corollary 1.3
Lemma 4.1. Let d be a positive integer,
![]() $\Gamma \subset [0,1]$
a DCC set and
$\Gamma \subset [0,1]$
a DCC set and
![]() $\epsilon :=\epsilon (d,\Gamma )$
. Let
$\epsilon :=\epsilon (d,\Gamma )$
. Let
![]() $(X/Z,T+aS)$
be a pair such that X is of Fano type over Z,
$(X/Z,T+aS)$
be a pair such that X is of Fano type over Z,
![]() $-(K_X+T+aS)$
is nef
$-(K_X+T+aS)$
is nef
![]() $/Z$
,
$/Z$
,
![]() $T\in \Gamma $
,
$T\in \Gamma $
,
![]() $S\not =0$
is a reduced divisor and
$S\not =0$
is a reduced divisor and
![]() $a\in (1-\epsilon ,1)$
. Then, we may run a
$a\in (1-\epsilon ,1)$
. Then, we may run a
![]() $-(K_X+T+S)$
-MMP
$-(K_X+T+S)$
-MMP
![]() $/Z$
which consists of a sequence of divisorial contractions and flips
$/Z$
which consists of a sequence of divisorial contractions and flips
such that
-
1.
 $(X_i,T_i+S_i)$
is lc for each i,
$(X_i,T_i+S_i)$
is lc for each i, -
2.
 $S_n\not =0$
and
$S_n\not =0$
and -
3.
 $-(K_{X_n}+T_n+S_n)$
is nef
$-(K_{X_n}+T_n+S_n)$
is nef
 $/Z$
.
$/Z$
.
Here,
![]() $T_i$
and
$T_i$
and
![]() $S_i$
are the strict transforms of T and S on
$S_i$
are the strict transforms of T and S on
![]() $X_i$
respectively.
$X_i$
respectively.
Proof. By Theorem 2.8, we may run a
![]() $-(K_X+T+S)$
-MMP
$-(K_X+T+S)$
-MMP
![]() $/Z$
.
$/Z$
.
(1) Since
![]() $-(K_X+T+aS)$
is nef
$-(K_X+T+aS)$
is nef
![]() $/Z$
,
$/Z$
,
![]() $(X/Z,T+aS)$
is
$(X/Z,T+aS)$
is
![]() $\mathbb R$
-complementary. Hence,
$\mathbb R$
-complementary. Hence,
![]() $(X_i/Z,T_i+aS_i)$
is
$(X_i/Z,T_i+aS_i)$
is
![]() $\mathbb R$
-complementary for each i. In particular,
$\mathbb R$
-complementary for each i. In particular,
![]() $(X_i,T_i+aS_i)$
is lc for each i. By the definition of
$(X_i,T_i+aS_i)$
is lc for each i. By the definition of
![]() $\epsilon $
,
$\epsilon $
,
![]() $(X_i,T_i+S_i)$
is lc for each i.
$(X_i,T_i+S_i)$
is lc for each i.
(2) Since
![]() $-(K_X+T+aS)$
is nef
$-(K_X+T+aS)$
is nef
![]() $/Z$
, by the negativity lemma,
$/Z$
, by the negativity lemma,
![]() $X\dashrightarrow X_n$
is
$X\dashrightarrow X_n$
is
![]() $-(K_X+T+aS)$
-non-negapositive. Since
$-(K_X+T+aS)$
-non-negapositive. Since
![]() $X\dashrightarrow X_n$
is a
$X\dashrightarrow X_n$
is a
![]() $-(K_X+T+S)$
-MMP,
$-(K_X+T+S)$
-MMP,
![]() $X\dashrightarrow X_n$
is
$X\dashrightarrow X_n$
is
![]() $-(K_X+T+S)$
-negative. Hence,
$-(K_X+T+S)$
-negative. Hence,
![]() $X\dashrightarrow X_n$
is S-positive, and we get (2).
$X\dashrightarrow X_n$
is S-positive, and we get (2).
(3) Suppose not, then this MMP terminates with a
![]() $-(K_{X_n}+T_n+S_n)$
-Mori fiber space
$-(K_{X_n}+T_n+S_n)$
-Mori fiber space
![]() $X_n\rightarrow V$
. Then,
$X_n\rightarrow V$
. Then,
![]() $-(K_{X_n}+T_n+S_n)$
is anti-ample
$-(K_{X_n}+T_n+S_n)$
is anti-ample
![]() $/V$
. Since
$/V$
. Since
![]() $-(K_{X}+T+aS)$
is nef
$-(K_{X}+T+aS)$
is nef
![]() $/Z$
,
$/Z$
,
![]() $-(K_{X_n}+T_n+aS_n)$
is nef
$-(K_{X_n}+T_n+aS_n)$
is nef
![]() $/V$
and there exists a real number
$/V$
and there exists a real number
![]() $c\in [a,1)\subset (1-\epsilon ,1)$
such that
$c\in [a,1)\subset (1-\epsilon ,1)$
such that
![]() $K_{X_n}+T_n+cS_n\equiv _V0$
. By (1),
$K_{X_n}+T_n+cS_n\equiv _V0$
. By (1),
![]() $(X_n,T_n+cS_n)$
is lc. Let F be a general fiber of
$(X_n,T_n+cS_n)$
is lc. Let F be a general fiber of
![]() $X_n\rightarrow V$
,
$X_n\rightarrow V$
,
![]() $T_F:=T|_F$
and
$T_F:=T|_F$
and
![]() $S_F:=S|_F$
. Then,
$S_F:=S|_F$
. Then,
![]() $(F,T_F+cS_F)$
is lc and
$(F,T_F+cS_F)$
is lc and
![]() $K_F+T_F+cS_F\equiv 0$
. Thus,
$K_F+T_F+cS_F\equiv 0$
. Thus,
![]() $\epsilon \leq \epsilon _{1}(d,\Gamma )\leq \epsilon _1(\dim F,\Gamma )\leq 1-c$
, a contradiction.
$\epsilon \leq \epsilon _{1}(d,\Gamma )\leq \epsilon _1(\dim F,\Gamma )\leq 1-c$
, a contradiction.
Proof of Theorem 1.2
Let
![]() $a:={\operatorname {tmld}}(X,B+G)$
be the total minimal log discrepancy of
$a:={\operatorname {tmld}}(X,B+G)$
be the total minimal log discrepancy of
![]() $(X,B+G)$
, and E a divisor over X such that
$(X,B+G)$
, and E a divisor over X such that
![]() $a(E,X,B+G)=a$
. Suppose that
$a(E,X,B+G)=a$
. Suppose that
![]() $a<\epsilon :=\epsilon (d,\Gamma )$
. We let
$a<\epsilon :=\epsilon (d,\Gamma )$
. We let
![]() $c:=\operatorname {mult}_EG$
and let
$c:=\operatorname {mult}_EG$
and let
![]() $e:=1-a-c$
. If E is exceptional over X, then we let
$e:=1-a-c$
. If E is exceptional over X, then we let
![]() $f: Y\rightarrow X$
be a divisorial contraction which extracts E. If E is not exceptional over X, then we let
$f: Y\rightarrow X$
be a divisorial contraction which extracts E. If E is not exceptional over X, then we let
![]() $f: Y\rightarrow X$
be the identity morphism. Then, we have
$f: Y\rightarrow X$
be the identity morphism. Then, we have
![]() $K_Y+eE+B_Y=f^*(K_X+B)$
, where
$K_Y+eE+B_Y=f^*(K_X+B)$
, where
![]() $B_Y$
is the strict transform of B on Y. We let
$B_Y$
is the strict transform of B on Y. We let
![]() $G_Y:=f^*G$
.
$G_Y:=f^*G$
.
Claim 4.2. Y is of Fano type.
Proof. If
![]() $Y=X$
, then it is clear Y is of Fano type. Otherwise, there exists a klt pair
$Y=X$
, then it is clear Y is of Fano type. Otherwise, there exists a klt pair
![]() $(X,\Delta )$
such that
$(X,\Delta )$
such that
![]() $-(K_X+\Delta )$
is big and nef. Let
$-(K_X+\Delta )$
is big and nef. Let
![]() $\Delta _Y:=f^{-1}_*\Delta $
and let
$\Delta _Y:=f^{-1}_*\Delta $
and let
![]() $a':=a(E,X,\Delta )$
. Then,
$a':=a(E,X,\Delta )$
. Then,
![]() $a'\leq a<\epsilon <1$
, so
$a'\leq a<\epsilon <1$
, so
![]() $(Y,\Delta _Y+(1-a')E)$
is a klt pair such that
$(Y,\Delta _Y+(1-a')E)$
is a klt pair such that
![]() $-(K_Y+\Delta _Y+(1-a')E)$
is big and nef. Thus, Y is of Fano type.
$-(K_Y+\Delta _Y+(1-a')E)$
is big and nef. Thus, Y is of Fano type.
Proof of Theorem 1.2 continued. Since
![]() $-(K_Y+(1-a)E+B_Y)\sim _{\mathbb R}G_Y-cE\geq 0$
, by Claim 4.2 and Theorem 2.8, we may run a
$-(K_Y+(1-a)E+B_Y)\sim _{\mathbb R}G_Y-cE\geq 0$
, by Claim 4.2 and Theorem 2.8, we may run a
![]() $-(K_Y+(1-a)E+B_Y)$
-MMP which terminates with a model T such that
$-(K_Y+(1-a)E+B_Y)$
-MMP which terminates with a model T such that
![]() $-(K_T+(1-a)E_T+B_T)$
is nef, where
$-(K_T+(1-a)E_T+B_T)$
is nef, where
![]() $E_T,B_T$
are the strict transforms of
$E_T,B_T$
are the strict transforms of
![]() $E,B$
on T, respectively. Since E is not a component of
$E,B$
on T, respectively. Since E is not a component of
![]() $G_Y-cE$
and the MMP only contracts divisors that are contained in
$G_Y-cE$
and the MMP only contracts divisors that are contained in
![]() $\operatorname {Supp}(G_Y-cE)$
,
$\operatorname {Supp}(G_Y-cE)$
,
![]() $E_T\not =0$
. By Lemma 4.1, we may run a
$E_T\not =0$
. By Lemma 4.1, we may run a
![]() $-(K_T+E_T+B_T)$
-MMP which terminates with a model V, such that
$-(K_T+E_T+B_T)$
-MMP which terminates with a model V, such that
![]() $(V,E_V+B_V)$
is lc,
$(V,E_V+B_V)$
is lc,
![]() $E_V\not =0$
and
$E_V\not =0$
and
![]() $-(K_V+E_V+B_V)$
is nef, where
$-(K_V+E_V+B_V)$
is nef, where
![]() $E_V,B_V$
are the strict transforms of
$E_V,B_V$
are the strict transforms of
![]() $E_T,B_T$
on V, respectively. Since X is of Fano type, V is of Fano type. It is clear that
$E_T,B_T$
on V, respectively. Since X is of Fano type, V is of Fano type. It is clear that
![]() $(V,E_V+B_V)$
is not exceptional.
$(V,E_V+B_V)$
is not exceptional.
For any prime divisor D over X, we have
 $$ \begin{align*} a(D,X,B)&\geq a(D,Y,(1-a)E+B_Y)\geq a(D,T,(1-a)E_T+B_T)\\ &\geq a(D,T,E_T+B_T)\geq a(D,V,E_V+B_V). \end{align*} $$
$$ \begin{align*} a(D,X,B)&\geq a(D,Y,(1-a)E+B_Y)\geq a(D,T,(1-a)E_T+B_T)\\ &\geq a(D,T,E_T+B_T)\geq a(D,V,E_V+B_V). \end{align*} $$
By [Reference Birkar3, Lemma 2.17], X is not exceptional, a contradiction.
Remark 4.3. The proof of Theorem 1.2 also works for generalized pairs [Reference Birkar and Zhang5]. For simplicity, we omit the proof.
Corollary 4.4. Let
![]() $(X,B+G)$
be a pair such that
$(X,B+G)$
be a pair such that
![]() $(X,B)$
is exceptional, X is a Fano type surface,
$(X,B)$
is exceptional, X is a Fano type surface,
![]() $B\in \{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
and
$B\in \{1-\frac {1}{n}\mid n\in \mathbb N^+\}\cup \{1\}$
and
![]() $0\leq G\sim _{\mathbb R}-(K_X+B)$
. Then,
$0\leq G\sim _{\mathbb R}-(K_X+B)$
. Then,
![]() $(X,B+G)$
is
$(X,B+G)$
is
![]() $\frac {1}{42}$
-lc. In particular,
$\frac {1}{42}$
-lc. In particular,
![]() $(X,B)$
and X are
$(X,B)$
and X are
![]() $\frac {1}{42}$
-lc.
$\frac {1}{42}$
-lc.
Corollary 4.5. For any exceptional Fano surface X, there exists
![]() $I\leq 2\cdot 84^{128\cdot 42^5}$
such that
$I\leq 2\cdot 84^{128\cdot 42^5}$
such that
![]() $IK_X$
is Cartier. In particular,
$IK_X$
is Cartier. In particular,
![]() $K_X^2\geq \frac {1}{I}$
.
$K_X^2\geq \frac {1}{I}$
.
4.2 Exceptional surface complements
Lemma 4.6. Let
![]() $(X:=\mathbb P^1,B)$
be a pair such that
$(X:=\mathbb P^1,B)$
be a pair such that
![]() $\deg (K_X+B)\leq 0$
and
$\deg (K_X+B)\leq 0$
and
![]() $B\in \{\frac {k}{12}\mid k\in \mathbb N^+,0\leq k\leq 12\}\cup \{1-\frac {1}{n}\mid n\in \mathbb N^+\}$
. Then,
$B\in \{\frac {k}{12}\mid k\in \mathbb N^+,0\leq k\leq 12\}\cup \{1-\frac {1}{n}\mid n\in \mathbb N^+\}$
. Then,
![]() $(X,B)$
has a monotonic n-complement such that
$(X,B)$
has a monotonic n-complement such that
![]() $12\mid n$
and
$12\mid n$
and
![]() $n\leq 276$
.
$n\leq 276$
.
Proof. We may write
![]() $B=C+D$
where
$B=C+D$
where
![]() $C,D\geq 0$
,
$C,D\geq 0$
,
![]() $C\in \{1-\frac {1}{n}\mid n\in \mathbb N^+, 12\nmid n\}$
,
$C\in \{1-\frac {1}{n}\mid n\in \mathbb N^+, 12\nmid n\}$
,
![]() $12D$
is integral and
$12D$
is integral and
![]() $C\wedge D=0$
. Then, the coefficients of C are
$C\wedge D=0$
. Then, the coefficients of C are
![]() $\geq \frac {4}{5}$
. In particular, C has at most
$\geq \frac {4}{5}$
. In particular, C has at most
![]() $2$
irreducible components. Possibly adding divisors of the form
$2$
irreducible components. Possibly adding divisors of the form
![]() $\frac {1}{12}p$
to D where p are general points on X, we may assume that
$\frac {1}{12}p$
to D where p are general points on X, we may assume that
![]() $0\geq \deg (K_X+B)>-\frac {1}{12}$
. We have the following cases.
$0\geq \deg (K_X+B)>-\frac {1}{12}$
. We have the following cases.
Case 1.
![]() $C=0$
. Then,
$C=0$
. Then,
![]() $(X,B)$
is a
$(X,B)$
is a
![]() $12$
-complement of itself.
$12$
-complement of itself.
Case 2. C has
![]() $1$
irreducible component
$1$
irreducible component
![]() $C_1$
. Then,
$C_1$
. Then,
![]() $C=aC_1$
for some
$C=aC_1$
for some
![]() $a\in (0,1)$
and
$a\in (0,1)$
and
![]() $(X,\frac {\lceil 12a\rceil }{12}C_1+D)$
is a monotonic
$(X,\frac {\lceil 12a\rceil }{12}C_1+D)$
is a monotonic
![]() $12$
-complement of
$12$
-complement of
![]() $(X,B)$
.
$(X,B)$
.
Case 3. C has
![]() $2$
irreducible components
$2$
irreducible components
![]() $C_1,C_2$
. We have
$C_1,C_2$
. We have
![]() $C=a_1C_1+a_2C_2$
. Possibly switching
$C=a_1C_1+a_2C_2$
. Possibly switching
![]() $C_1,C_2$
, we may assume that
$C_1,C_2$
, we may assume that
![]() $a_1\leq a_2$
. If
$a_1\leq a_2$
. If
![]() $D=0$
, then
$D=0$
, then
![]() $(X,C_1+C_2)$
is a monotonic
$(X,C_1+C_2)$
is a monotonic
![]() $1$
-complement of
$1$
-complement of
![]() $(X,B)$
. If
$(X,B)$
. If
![]() $D\not =0$
, then
$D\not =0$
, then
![]() $a_1\leq \frac {23}{24}$
. Let m be the denominator of
$a_1\leq \frac {23}{24}$
. Let m be the denominator of
![]() $a_1$
. Then,
$a_1$
. Then,
![]() $m\leq 24$
and
$m\leq 24$
and
![]() $(X,a_1C_1+(2-\deg D-a_1)C_2+D)$
is a monotonic
$(X,a_1C_1+(2-\deg D-a_1)C_2+D)$
is a monotonic
![]() $\operatorname {lcm}(12,m)$
-complement of
$\operatorname {lcm}(12,m)$
-complement of
![]() $(X,B)$
. Since
$(X,B)$
. Since
![]() $12\mid \operatorname {lcm}(12,m)$
and
$12\mid \operatorname {lcm}(12,m)$
and
![]() $\operatorname {lcm}(12,m)\leq 276$
, we are done.
$\operatorname {lcm}(12,m)\leq 276$
, we are done.
Theorem 4.7. Let X be an
![]() $\mathbb {R}$
-complementary exceptional surface.
$\mathbb {R}$
-complementary exceptional surface.
-
1. If
 $\kappa (-K_X)=0$
, then X has an n-complement for some
$\kappa (-K_X)=0$
, then X has an n-complement for some
 $n\leq 21$
.
$n\leq 21$
. -
2. If
 $\kappa (-K_X)=1$
, then X has an n-complement for some n such that
$\kappa (-K_X)=1$
, then X has an n-complement for some n such that
 $12\mid n$
and
$12\mid n$
and
 $n\leq 276$
.
$n\leq 276$
. -
3. If
 $\kappa (-K_X)=2$
, then X has an n-complement for some
$\kappa (-K_X)=2$
, then X has an n-complement for some
 $n\leq 192\cdot 84^{128\cdot 42^5}$
.
$n\leq 192\cdot 84^{128\cdot 42^5}$
.
Proof. There exists a klt pair
![]() $(X,B)$
such that
$(X,B)$
such that
![]() $K_X+B\sim _{\mathbb R}0$
. Thus,
$K_X+B\sim _{\mathbb R}0$
. Thus,
![]() $(X,(1+\delta )B)$
is klt for some
$(X,(1+\delta )B)$
is klt for some
![]() $0<\delta \ll 1$
, so we may run a
$0<\delta \ll 1$
, so we may run a
![]() $(K_X+(1+\delta )B)$
-MMP which terminates with good minimal model
$(K_X+(1+\delta )B)$
-MMP which terminates with good minimal model
![]() $X'$
. Since
$X'$
. Since
![]() $K_X+(1+\delta )B\sim _{\mathbb R}-\delta K_X$
, this is also a
$K_X+(1+\delta )B\sim _{\mathbb R}-\delta K_X$
, this is also a
![]() $-K_X$
-MMP. By abundance for klt surfaces,
$-K_X$
-MMP. By abundance for klt surfaces,
![]() $-K_{X'}$
is semi-ample. Possibly replacing X with
$-K_{X'}$
is semi-ample. Possibly replacing X with
![]() $X'$
, we may assume that
$X'$
, we may assume that
![]() $-K_{X}$
is semi-ample.
$-K_{X}$
is semi-ample.
If
![]() $\kappa (-K_X)=0$
, then
$\kappa (-K_X)=0$
, then
![]() $K_X\equiv 0$
. Hence,
$K_X\equiv 0$
. Hence,
![]() $nK_X\sim 0$
for some positive integer
$nK_X\sim 0$
for some positive integer
![]() $n\leq 21$
[Reference Blache7, Reference Zhang43, Reference Zhang44], and X is an n-complement of itself for some
$n\leq 21$
[Reference Blache7, Reference Zhang43, Reference Zhang44], and X is an n-complement of itself for some
![]() $n\leq 21$
.
$n\leq 21$
.
If
![]() $\kappa (-K_X)=1$
, then
$\kappa (-K_X)=1$
, then
![]() $-K_X$
defines a contraction
$-K_X$
defines a contraction
![]() $f: X\rightarrow Z$
. By Kodaira’s canonical bundle formula, we have
$f: X\rightarrow Z$
. By Kodaira’s canonical bundle formula, we have
such that
![]() $12M_Z$
is an integral divisor,
$12M_Z$
is an integral divisor,
![]() $B_Z\in \{1-\frac {1}{n}\mid n\in \mathbb N^+\}$
and
$B_Z\in \{1-\frac {1}{n}\mid n\in \mathbb N^+\}$
and
We may choose
![]() $M_Z$
such that
$M_Z$
such that
![]() $B_Z\wedge M_Z=0$
and
$B_Z\wedge M_Z=0$
and
![]() $(Z,B_Z+M_Z)$
is klt. Since
$(Z,B_Z+M_Z)$
is klt. Since
![]() $-K_X$
is semi-ample,
$-K_X$
is semi-ample,
![]() $\deg (K_Z+B_Z+M_Z)\leq 0$
. Hence, Z is either an elliptic curve or
$\deg (K_Z+B_Z+M_Z)\leq 0$
. Hence, Z is either an elliptic curve or
![]() $\mathbb P^1$
. If Z is an elliptic curve, then
$\mathbb P^1$
. If Z is an elliptic curve, then
![]() $B_Z=M_Z=0$
and
$B_Z=M_Z=0$
and
![]() $12K_X$
is base-point-free. Hence, X is a
$12K_X$
is base-point-free. Hence, X is a
![]() $12$
-complement of itself. If
$12$
-complement of itself. If
![]() $Z=\mathbb P^1$
, by Lemma 4.6, there exists an integer
$Z=\mathbb P^1$
, by Lemma 4.6, there exists an integer
![]() $n\leq 276$
such that
$n\leq 276$
such that
![]() $12\mid n$
and
$12\mid n$
and
![]() $(Z,B_Z+M_Z)$
has a monotonic n-complement
$(Z,B_Z+M_Z)$
has a monotonic n-complement
![]() $(Z,B_Z+G+M_Z)$
. By the construction of
$(Z,B_Z+G+M_Z)$
. By the construction of
![]() $B_Z$
,
$B_Z$
,
![]() $(X,f^*G)$
lc. Hence,
$(X,f^*G)$
lc. Hence,
![]() $(X,f^*G)$
is an n-complement of X.
$(X,f^*G)$
is an n-complement of X.
If
![]() $\kappa (-K_X)=2$
, then
$\kappa (-K_X)=2$
, then
![]() $-K_X$
defines a birational morphism
$-K_X$
defines a birational morphism
![]() $f: X\rightarrow Y$
. We have
$f: X\rightarrow Y$
. We have
![]() $K_X=f^*K_Y$
. Possibly replacing X with Y, we may assume that X is Fano. By Corollary 1.3, X is
$K_X=f^*K_Y$
. Possibly replacing X with Y, we may assume that X is Fano. By Corollary 1.3, X is
![]() $\frac {1}{42}$
-lc. By Lemma 2.7,
$\frac {1}{42}$
-lc. By Lemma 2.7,
![]() $IK_X$
is Cartier for some
$IK_X$
is Cartier for some
![]() $I\leq 2\cdot 84^{128\cdot 42^5}$
. By the effective base-point-freeness theorem ([Reference Fujino16, Theorem 1.1, Remark 1.2] [25, 1.1 Theorem]),
$I\leq 2\cdot 84^{128\cdot 42^5}$
. By the effective base-point-freeness theorem ([Reference Fujino16, Theorem 1.1, Remark 1.2] [25, 1.1 Theorem]),
![]() $|-96IK_X|$
is base-point-free. In particular, X has a
$|-96IK_X|$
is base-point-free. In particular, X has a
![]() $96I$
-complement.
$96I$
-complement.
5 Proof of the main theorems
Proof of Theorem 1.1
If
![]() $\dim Z>0$
or
$\dim Z>0$
or
![]() $\dim Z=0$
and X is not exceptional, the theorem follows from Lemma 3.1 and Corollary 3.2. Otherwise,
$\dim Z=0$
and X is not exceptional, the theorem follows from Lemma 3.1 and Corollary 3.2. Otherwise,
![]() $\dim Z=0$
and X is exceptional, and the theorem follows from Theorem 4.7.
$\dim Z=0$
and X is exceptional, and the theorem follows from Theorem 4.7.
Proof of Corollary 1.4
Recall that Tian’s
![]() $\alpha $
-invariant for a variety X is defined as
$\alpha $
-invariant for a variety X is defined as
We may assume that
![]() $\alpha (X)>1$
. If
$\alpha (X)>1$
. If
![]() $\kappa (-K_X)\leq 1$
, then by Theorem 4.7, X has an n-complement
$\kappa (-K_X)\leq 1$
, then by Theorem 4.7, X has an n-complement
![]() $(X,G)$
for some
$(X,G)$
for some
![]() $n\leq 276$
. Hence,
$n\leq 276$
. Hence,
![]() $(X,nG)$
is not klt, and
$(X,nG)$
is not klt, and
![]() $\alpha (X)\leq 276$
. Thus, we may assume that
$\alpha (X)\leq 276$
. Thus, we may assume that
![]() $\kappa (-K_X)=2$
. We may run a
$\kappa (-K_X)=2$
. We may run a
![]() $(-K_X)$
-MMP and replace X with the canonical model of
$(-K_X)$
-MMP and replace X with the canonical model of
![]() $-K_X$
, and assume that
$-K_X$
, and assume that
![]() $-K_X$
is ample. By Corollary 4.5,
$-K_X$
is ample. By Corollary 4.5,
![]() $K_X^2\geq \frac {1}{I}$
. Since
$K_X^2\geq \frac {1}{I}$
. Since
![]() $\alpha (X)^2\cdot \operatorname {vol}(-K_X)\leq 9$
(cf. [Reference Blum and Jonsson8, Theorems A,D]),
$\alpha (X)^2\cdot \operatorname {vol}(-K_X)\leq 9$
(cf. [Reference Blum and Jonsson8, Theorems A,D]),
![]() $\alpha (X)\leq 3\sqrt {I}\leq 3\sqrt {2}\cdot 84^{64\cdot 42^5}$
.
$\alpha (X)\leq 3\sqrt {I}\leq 3\sqrt {2}\cdot 84^{64\cdot 42^5}$
.
6 Further remarks
Remark 6.1 (Reasonable and optimal bounds)
Recall that we expect
![]() $\epsilon _1(2,\{0\})=\frac {1}{13}$
. If we can prove this, then the bound of n in Theorem 1.1 can be improved to
$\epsilon _1(2,\{0\})=\frac {1}{13}$
. If we can prove this, then the bound of n in Theorem 1.1 can be improved to
![]() $192\cdot 26^{128\cdot 13^5}\approx 10^{10^{7.8}}$
. This is much smaller than the current bound, albeit it is still expected to be far from optimal. However, if one can get a better bound for
$192\cdot 26^{128\cdot 13^5}\approx 10^{10^{7.8}}$
. This is much smaller than the current bound, albeit it is still expected to be far from optimal. However, if one can get a better bound for
![]() $I=I(\epsilon )$
in Lemma 2.7, then the bound of n may be greatly improved. For example, [Reference Liu and Xie34, Proof of Lemma 4.9] actually implies that the local Cartier index of any
$I=I(\epsilon )$
in Lemma 2.7, then the bound of n may be greatly improved. For example, [Reference Liu and Xie34, Proof of Lemma 4.9] actually implies that the local Cartier index of any
![]() $\frac {2}{5}$
-klt weak Fano surface is
$\frac {2}{5}$
-klt weak Fano surface is
![]() $\leq 19$
. With a little more effort, one can show that the global Cartier index of any
$\leq 19$
. With a little more effort, one can show that the global Cartier index of any
![]() $\frac {2}{5}$
-klt weak Fano surface is
$\frac {2}{5}$
-klt weak Fano surface is
![]() $\leq 385$
. This is much smaller than the bound given by Lemma 2.7 which is
$\leq 385$
. This is much smaller than the bound given by Lemma 2.7 which is
![]() $2\cdot 5^{12500}$
. By applying the arguments in this paper, we shall get
$2\cdot 5^{12500}$
. By applying the arguments in this paper, we shall get
![]() $n\leq 36960$
and
$n\leq 36960$
and
![]() $\alpha (X)\leq 3\sqrt {385}\approx 58.86$
for exceptional
$\alpha (X)\leq 3\sqrt {385}\approx 58.86$
for exceptional
![]() $\frac {2}{5}$
-klt surfaces.
$\frac {2}{5}$
-klt surfaces.
Remark 6.2 (Explicit bound for pairs)
One may also ask whether we can find an explicit bounded of n for n-complements of surface pairs
![]() $(X,B)$
.
$(X,B)$
.
For pairs with finite rational coefficients, the bound is computable via the methods introduced in [Reference Alexeev and Mori2], but may be much larger than the case when
![]() $B=0$
. This is because the bound
$B=0$
. This is because the bound
![]() $\epsilon (d,\Gamma )=\frac {1}{42}$
in Lemma 2.4 will be changed to a number which is very close to
$\epsilon (d,\Gamma )=\frac {1}{42}$
in Lemma 2.4 will be changed to a number which is very close to
![]() $1$
as in [Reference Alexeev and Mori2, 3.5] when
$1$
as in [Reference Alexeev and Mori2, 3.5] when
![]() $\Gamma $
is not the standard set. It is very difficult to represent that number in a very explicit function of the common denominator of the coefficient set (even when the coefficient set is
$\Gamma $
is not the standard set. It is very difficult to represent that number in a very explicit function of the common denominator of the coefficient set (even when the coefficient set is
![]() $\{0,\frac {1}{3}\}$
, for example). We also need to go through the inductive arguments as in [Reference Shokurov39, 2.3 Inductive Theorem] for nonexceptional complements.
$\{0,\frac {1}{3}\}$
, for example). We also need to go through the inductive arguments as in [Reference Shokurov39, 2.3 Inductive Theorem] for nonexceptional complements.
For pairs with finite (maybe irrational) coefficients or DCC coefficients, a theory on ‘explicit uniform rational polytopes’ (cf. [Reference Han, Liu and Shokurov20]) is needed, which is still unknown.
For pairs with coefficients in
![]() $[0,1]$
, one needs to go through all the previous simpler cases and check the details of the proof of [Reference Shokurov40, Theorem 3] and avoid using any inexplicit boundedness result. This is considered to be much more difficult. See [Reference Chen, Han and Xue10] for a similar result.
$[0,1]$
, one needs to go through all the previous simpler cases and check the details of the proof of [Reference Shokurov40, Theorem 3] and avoid using any inexplicit boundedness result. This is considered to be much more difficult. See [Reference Chen, Han and Xue10] for a similar result.
Remark 6.3 (Explicit bound of threefold mlds)
By Remark 6.2 and following the details of the proof of [Reference Han, Liu and Luo19], one will be able to provide a computable lower bound of the
![]() $1$
-gap of threefold mlds for pairs with finite rational coefficients (or, more generally, hyperstandard rational coefficients). This is because all other constants in the proof of [Reference Han, Liu and Luo19] can be explicitly bounded except the t in [Reference Han, Liu and Luo19, Lemma 6.4]. Here, an explicit boundedness of n-complement for threefold singularities is needed, but this just follows from Theorem 1.1 and Remark 6.2. Nevertheless, such bound will, again, be far from being optimal. For example, when we have standard coefficients, the
$1$
-gap of threefold mlds for pairs with finite rational coefficients (or, more generally, hyperstandard rational coefficients). This is because all other constants in the proof of [Reference Han, Liu and Luo19] can be explicitly bounded except the t in [Reference Han, Liu and Luo19, Lemma 6.4]. Here, an explicit boundedness of n-complement for threefold singularities is needed, but this just follows from Theorem 1.1 and Remark 6.2. Nevertheless, such bound will, again, be far from being optimal. For example, when we have standard coefficients, the
![]() $1$
-gap is expected to be
$1$
-gap is expected to be
![]() $\frac {1}{42}$
(by Remark 2.5 and Lemma 2.4), but we can only show that the
$\frac {1}{42}$
(by Remark 2.5 and Lemma 2.4), but we can only show that the
![]() $1$
-gap is
$1$
-gap is
![]() $\geq \epsilon $
for some
$\geq \epsilon $
for some
![]() $\epsilon \approx \frac {1}{192\cdot 42^{128\cdot 42^5}}$
.
$\epsilon \approx \frac {1}{192\cdot 42^{128\cdot 42^5}}$
.
Acknowledgements
The author thanks Guodu Chen, Jingjun Han, Kai Huang, Yuchen Liu, Yujie Luo, Fanjun Meng, Lingyao Xie, Qingyuan Xue, and Junyan Zhao for useful discussions. The author thanks Jingjun Han, Chen Jiang, and Yuchen Liu for proposing the question to the author in different occasions, and thanks Yuchen Liu for the reference [Reference Blum and Jonsson8]. The author thanks Jingjun Han, Chen Jiang, and Dae-Won Lee for comments on the first version of this paper. He thanks the referee for useful suggestions and revising his paper.
Author contributions
Jihao Liu is the sole author of the paper.
Competing interest
The authors have no competing interest to declare.
Data availability statement
No data nor code is used in this paper.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
None.