No CrossRef data available.
Article contents
Stable laws for random dynamical systems
Published online by Cambridge University Press: 14 February 2024
Abstract
In this paper, we consider random dynamical systems formed by concatenating maps acting on the unit interval 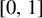 $[0,1]$ in an independent and identically distributed (i.i.d.) fashion. Considered as a stationary Markov process, the random dynamical system possesses a unique stationary measure
$[0,1]$ in an independent and identically distributed (i.i.d.) fashion. Considered as a stationary Markov process, the random dynamical system possesses a unique stationary measure 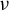 $\nu $. We consider a class of non-square-integrable observables
$\nu $. We consider a class of non-square-integrable observables 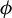 $\phi $, mostly of form
$\phi $, mostly of form 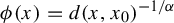 $\phi (x)=d(x,x_0)^{-{1}/{\alpha }}$, where
$\phi (x)=d(x,x_0)^{-{1}/{\alpha }}$, where 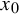 $x_0$ is a non-recurrent point (in particular a non-periodic point) satisfying some other genericity conditions and, more generally, regularly varying observables with index
$x_0$ is a non-recurrent point (in particular a non-periodic point) satisfying some other genericity conditions and, more generally, regularly varying observables with index 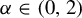 $\alpha \in (0,2)$. The two types of maps we concatenate are a class of piecewise
$\alpha \in (0,2)$. The two types of maps we concatenate are a class of piecewise 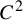 $C^2$ expanding maps and a class of intermittent maps possessing an indifferent fixed point at the origin. Under conditions on the dynamics and
$C^2$ expanding maps and a class of intermittent maps possessing an indifferent fixed point at the origin. Under conditions on the dynamics and 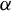 $\alpha $, we establish Poisson limit laws, convergence of scaled Birkhoff sums to a stable limit law, and functional stable limit laws in both the annealed and quenched case. The scaling constants for the limit laws for almost every quenched realization are the same as those of the annealed case and determined by
$\alpha $, we establish Poisson limit laws, convergence of scaled Birkhoff sums to a stable limit law, and functional stable limit laws in both the annealed and quenched case. The scaling constants for the limit laws for almost every quenched realization are the same as those of the annealed case and determined by 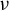 $\nu $. This is in contrast to the scalings in quenched central limit theorems where the centering constants depend in a critical way upon the realization and are not the same for almost every realization.
$\nu $. This is in contrast to the scalings in quenched central limit theorems where the centering constants depend in a critical way upon the realization and are not the same for almost every realization.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



