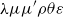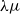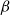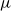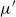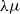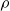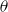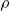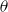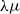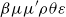1. Introduction
The works of Griffin (Reference Griffin and Allen1990) and Murthy (Reference Murthy1991) revealed in the nineties that the Curry–Howard correspondence can be extended to classical logic. Since then, many different calculi have appeared with the aim of representing natural deduction or Gentzen-style derivations in classical logic (Barbanera and Berardi Reference Barbanera and Berardi1994; Curien and Herbelin Reference Curien and Herbelin2000; Munch-Maccagnoni Reference Munch-Maccagnoni2013; Parigot Reference Parigot and Voronkov1992; Rehof and Sørensen Reference Rehof, Sørensen, Hagiya and Mitchell1994; Saurin Reference Saurin, Kaminski and Martini2008; Wadler Reference Wadler2003,Reference Wadler and Giesl2005). The systems based on the sequent calculus, like the
![]() $\overline{\lambda }\mu \tilde{\mu }$
-calculus of Curien-Herbelin (Curien and Herbelin Reference Curien and Herbelin2000), have the advantage of possessing symmetric reduction rules, which makes their study more pleasant. This is also the case for the system of Barbanera-Berardi (Barbanera and Berardi Reference Barbanera and Berardi1994), which is exclusively based on two connectives
$\overline{\lambda }\mu \tilde{\mu }$
-calculus of Curien-Herbelin (Curien and Herbelin Reference Curien and Herbelin2000), have the advantage of possessing symmetric reduction rules, which makes their study more pleasant. This is also the case for the system of Barbanera-Berardi (Barbanera and Berardi Reference Barbanera and Berardi1994), which is exclusively based on two connectives
![]() $\wedge$
and
$\wedge$
and
![]() $\vee$
. Parigot’s
$\vee$
. Parigot’s
![]() $\lambda \mu$
-calculus (Parigot Reference Parigot and Voronkov1992) was originally defined as a calculus for establishing connections between logical calculi and natural deduction-style proofs in second-order predicate logic. The
$\lambda \mu$
-calculus (Parigot Reference Parigot and Voronkov1992) was originally defined as a calculus for establishing connections between logical calculi and natural deduction-style proofs in second-order predicate logic. The
![]() $\lambda \mu$
-calculus can be considered as a simple extension of the
$\lambda \mu$
-calculus can be considered as a simple extension of the
![]() $\lambda$
-calculus: one obtains the
$\lambda$
-calculus: one obtains the
![]() $\lambda \mu$
-calculus by adding classical variables (so-called
$\lambda \mu$
-calculus by adding classical variables (so-called
![]() $\mu$
-variables) to the
$\mu$
-variables) to the
![]() $\lambda$
-calculus together with their term formation rules and reduction rules.
$\lambda$
-calculus together with their term formation rules and reduction rules.
The
![]() $\lambda \mu$
-calculus has two distinct presentations. One of them is the original calculus of Parigot, and the other one was introduced by de Groote by relaxing some of the term formation rules. The investigation of the difference between the two presentations in terms of normalization properties can be considered as the main aim of the paper. It turns out that, despite their great resemblance, the two calculi differ in important respects: if one adds to the
$\lambda \mu$
-calculus has two distinct presentations. One of them is the original calculus of Parigot, and the other one was introduced by de Groote by relaxing some of the term formation rules. The investigation of the difference between the two presentations in terms of normalization properties can be considered as the main aim of the paper. It turns out that, despite their great resemblance, the two calculi differ in important respects: if one adds to the
![]() $\beta$
-,
$\beta$
-,
![]() $\mu$
-, and
$\mu$
-, and
![]() $\mu '$
-reductions some structural rules, e.g., the
$\mu '$
-reductions some structural rules, e.g., the
![]() $\rho$
- or
$\rho$
- or
![]() $\varepsilon$
-rules, which are necessary to ensure the uniqueness of the representation of data, one can find that the Parigot-style calculus retains its strong normalization property, whereas the de Groote-style calculus does not. We will return to this question in several parts of the paper, and we will give the precise definitions for the different calculi in Sections 2 and 4.
$\varepsilon$
-rules, which are necessary to ensure the uniqueness of the representation of data, one can find that the Parigot-style calculus retains its strong normalization property, whereas the de Groote-style calculus does not. We will return to this question in several parts of the paper, and we will give the precise definitions for the different calculi in Sections 2 and 4.
Regarding the Parigot-style
![]() $\lambda \mu$
-calculus, originally, his system contains only two reductions (the
$\lambda \mu$
-calculus, originally, his system contains only two reductions (the
![]() $\beta$
- and
$\beta$
- and
![]() $\mu$
-rules). They stem from cut eliminations with respect to the implicational fragment of natural deduction both in the intuitionistic and in the classical case. He adds two more rules (
$\mu$
-rules). They stem from cut eliminations with respect to the implicational fragment of natural deduction both in the intuitionistic and in the classical case. He adds two more rules (
![]() $\rho$
and
$\rho$
and
![]() $\theta$
), which he calls simplification rules, and which correspond to cut elimination regarding negation. From a logical point of view, the
$\theta$
), which he calls simplification rules, and which correspond to cut elimination regarding negation. From a logical point of view, the
![]() $\lambda \mu$
-calculus makes it possible to easily encode the mathematical proofs. However, the calculus is not symmetric, which makes the examination of its properties more difficult. We note that we are concerned with the simply typed version of the
$\lambda \mu$
-calculus makes it possible to easily encode the mathematical proofs. However, the calculus is not symmetric, which makes the examination of its properties more difficult. We note that we are concerned with the simply typed version of the
![]() $\lambda \mu$
-calculus throughout the paper.
$\lambda \mu$
-calculus throughout the paper.
The simply typed
![]() $\lambda \mu$
-calculus enjoys many useful proof-theoretical properties, like confluence (Parigot Reference Parigot1993; Py Reference Py1998), subject reduction, and strong normalization (Parigot Reference Parigot1993). The calculus has, from the computer science point of view, a severe drawback: it does not meet the requirement of the unique representation of data. In the second-order typed
$\lambda \mu$
-calculus enjoys many useful proof-theoretical properties, like confluence (Parigot Reference Parigot1993; Py Reference Py1998), subject reduction, and strong normalization (Parigot Reference Parigot1993). The calculus has, from the computer science point of view, a severe drawback: it does not meet the requirement of the unique representation of data. In the second-order typed
![]() $\lambda$
-calculus, any term having the integer type
$\lambda$
-calculus, any term having the integer type
![]() $\mathcal{N}$
is
$\mathcal{N}$
is
![]() $\beta$
-equal to a Church numeral. This property enables the automatic generation of programs for the integers. In fact, a
$\beta$
-equal to a Church numeral. This property enables the automatic generation of programs for the integers. In fact, a
![]() $\lambda$
-term of type
$\lambda$
-term of type
![]() $\mathcal{N} \to \mathcal{N}$
is a program that represents a function for the integers: it takes a Church-integer and returns, after reduction, another one. This is no longer true in the
$\mathcal{N} \to \mathcal{N}$
is a program that represents a function for the integers: it takes a Church-integer and returns, after reduction, another one. This is no longer true in the
![]() $\lambda \mu$
-calculus: we can find normal terms of integer type that are not Church numerals. This should not come as a surprise, since we are able to prove that a type is
$\lambda \mu$
-calculus: we can find normal terms of integer type that are not Church numerals. This should not come as a surprise, since we are able to prove that a type is
![]() $\mathcal{N}$
by indirect reasoning. Hence, when we consider a type even as simple as
$\mathcal{N}$
by indirect reasoning. Hence, when we consider a type even as simple as
![]() $\mathcal{N}$
, it is only the intuitionistic proof of the type that we can recover by utilizing exclusively the existing reduction rules.
$\mathcal{N}$
, it is only the intuitionistic proof of the type that we can recover by utilizing exclusively the existing reduction rules.
There are several possible solutions to this problem. One can define an algorithm that, to every classical integer, assigns its value, which is represented by a Church numeral (Nour Reference Nour1997; Parigot Reference Parigot1993). The other possibility is to apply output operators in order to transform a classical integer into an intuitionistic one, namely, into a Church numeral (Nour Reference Nour1997; Parigot Reference Parigot1993). We choose here another solution which was also proposed by Parigot (Reference Parigot1993). If we add the reduction rule
![]() $\mu '$
to the
$\mu '$
to the
![]() $\lambda \mu$
-calculus, which is the symmetric counterpart of the
$\lambda \mu$
-calculus, which is the symmetric counterpart of the
![]() $\mu$
-rule and can be justified by the underlying logical rules, we get closer to reducing the Church integers to normal forms by simply applying the rules of the calculus. We discuss this question in more detail in Section 3. Similar assertions hold for the other algebraic data types defined formally in Krivine (Reference Krivine1994).
$\mu$
-rule and can be justified by the underlying logical rules, we get closer to reducing the Church integers to normal forms by simply applying the rules of the calculus. We discuss this question in more detail in Section 3. Similar assertions hold for the other algebraic data types defined formally in Krivine (Reference Krivine1994).
The calculus augmented with the
![]() $\mu '$
-rule preserves the subject reduction property (at least for the simply typed version), but confluence is lost. The
$\mu '$
-rule preserves the subject reduction property (at least for the simply typed version), but confluence is lost. The
![]() $\mu '$
-rule, however, plays an important role in the presentation of the call-by-value
$\mu '$
-rule, however, plays an important role in the presentation of the call-by-value
![]() $\lambda \mu$
-calculus. It permits a calculated value, as the functional part, to find its argument. de Groote (Reference de Groote1998) managed to integrate this rule with the
$\lambda \mu$
-calculus. It permits a calculated value, as the functional part, to find its argument. de Groote (Reference de Groote1998) managed to integrate this rule with the
![]() $\lambda \mu$
-calculus while preserving confluence. Py studied the call-by-value
$\lambda \mu$
-calculus while preserving confluence. Py studied the call-by-value
![]() $\mu '$
-reduction in his thesis (Py Reference Py1998). In particular, he proved confluence and strong normalization properties for
$\mu '$
-reduction in his thesis (Py Reference Py1998). In particular, he proved confluence and strong normalization properties for
![]() $\mu$
- and
$\mu$
- and
![]() $\mu '$
-reductions. He also enriched the syntax with new operators so that the subject reduction property was preserved and computational contents were given to the quantifiers.
$\mu '$
-reductions. He also enriched the syntax with new operators so that the subject reduction property was preserved and computational contents were given to the quantifiers.
Parigot (Reference Parigot1997) proved by an application of the Tait-Girard reducibility argument that the strong normalization property holds for the
![]() $\lambda \mu$
-calculus with second-order type assignments. It was a long standing open problem of Parigot whether the
$\lambda \mu$
-calculus with second-order type assignments. It was a long standing open problem of Parigot whether the
![]() $\mu \mu '$
-rules in the untyped calculus enjoy the strong normalization property. This was solved by David and the second author (David and Nour Reference David, Nour and Urzyczyn2005,Reference David and Nour2007). Subsequently, we have found in Battyányi and Nour (Reference Battyányi and Nour2020) another proof for this result. Until now, no simple weak normalization algorithm has been known for the
$\mu \mu '$
-rules in the untyped calculus enjoy the strong normalization property. This was solved by David and the second author (David and Nour Reference David, Nour and Urzyczyn2005,Reference David and Nour2007). Subsequently, we have found in Battyányi and Nour (Reference Battyányi and Nour2020) another proof for this result. Until now, no simple weak normalization algorithm has been known for the
![]() $\mu \mu '$
-reduction. In this paper, we also provide one.
$\mu \mu '$
-reduction. In this paper, we also provide one.
As was mentioned, there has mainly been two different presentations of the
![]() $\lambda \mu$
-calculus. Originally, Parigot defined his calculus with severe restrictions on the term formation rules. His syntax, however, does not make it possible to encode with typed
$\lambda \mu$
-calculus. Originally, Parigot defined his calculus with severe restrictions on the term formation rules. His syntax, however, does not make it possible to encode with typed
![]() $\lambda \mu$
-terms any proof of the classical tautology
$\lambda \mu$
-terms any proof of the classical tautology
![]() $\neg \neg A{\rightarrow } A$
without free variables of type
$\neg \neg A{\rightarrow } A$
without free variables of type
![]() $\neg \bot$
(similarly for some other classical tautologies). Furthermore, in this syntax with many reduction rules Böhm’s theorem does not hold. In fact, Py (Reference Py1998) gave two distinct closed normal terms
$\neg \bot$
(similarly for some other classical tautologies). Furthermore, in this syntax with many reduction rules Böhm’s theorem does not hold. In fact, Py (Reference Py1998) gave two distinct closed normal terms
![]() $M$
and
$M$
and
![]() $N$
for which there is no term
$N$
for which there is no term
![]() $L$
, such that
$L$
, such that
![]() $(L)M$
reduces to the first projection
$(L)M$
reduces to the first projection
![]() $\lambda x.\lambda y.x$
and
$\lambda x.\lambda y.x$
and
![]() $(L)N$
reduces to the second projection
$(L)N$
reduces to the second projection
![]() $\lambda x. \lambda y.y$
. De Groote proposed a syntax that is less restrictive than that of Parigot’s by splitting the rule concerning negation into two: one for the introduction and one for the elimination of negation and he even omitted certain restrictions that applied to the original calculus of Parigot. In this calculus, new rules can be considered like the
$\lambda x. \lambda y.y$
. De Groote proposed a syntax that is less restrictive than that of Parigot’s by splitting the rule concerning negation into two: one for the introduction and one for the elimination of negation and he even omitted certain restrictions that applied to the original calculus of Parigot. In this calculus, new rules can be considered like the
![]() $\varepsilon$
-rule, which allows to handle two consecutive proofs both leading to absurdity. The version proposed by de Groote (Reference de Groote1998) allowed him to construct an abstract machine for the
$\varepsilon$
-rule, which allows to handle two consecutive proofs both leading to absurdity. The version proposed by de Groote (Reference de Groote1998) allowed him to construct an abstract machine for the
![]() $\lambda \mu$
-calculus. Additionally, Saurin (Reference Saurin2012) proved that the de Groote version enjoys the separation property. Taking all these into account, we have adopted the de Groote-style calculus for the majority of our work. Our results also show that the two calculi are quite different: one of them has the strong normalization property while the other one only possesses the weak normalization property. The paper is structured in the following way.
$\lambda \mu$
-calculus. Additionally, Saurin (Reference Saurin2012) proved that the de Groote version enjoys the separation property. Taking all these into account, we have adopted the de Groote-style calculus for the majority of our work. Our results also show that the two calculi are quite different: one of them has the strong normalization property while the other one only possesses the weak normalization property. The paper is structured in the following way.
-
In the second section, we present the definitions necessary for our discussion.
-
The third section demonstrates the role of the structural rules: by making use of the additional rules we can prove that every term of integer type that weakly normalises behaves like a Church numeral in the sense that when it occurs in applications formed with terms of appropriate types it reduces to the well-known form of Church numerals.
-
The fourth section contains a proof that the Parigot-style
 $\lambda \mu$
-calculus enjoys the strong normalization property. The proof generalizes Py’s method (Py Reference Py1998): we prove that the simplification rules can be strongly postponed with respect to the
$\lambda \mu$
-calculus enjoys the strong normalization property. The proof generalizes Py’s method (Py Reference Py1998): we prove that the simplification rules can be strongly postponed with respect to the
 $\beta$
-,
$\beta$
-,
 $\mu$
- and
$\mu$
- and
 $\mu '$
-rules and then we resort to the already mentioned result of David and the second author, which states that the de Groote-style
$\mu '$
-rules and then we resort to the already mentioned result of David and the second author, which states that the de Groote-style
 $\lambda \mu \mu '$
-calculus enjoys the strong normalization property (David and Nour Reference David, Nour and Urzyczyn2005,Reference David and Nour2007). The Parigot-style
$\lambda \mu \mu '$
-calculus enjoys the strong normalization property (David and Nour Reference David, Nour and Urzyczyn2005,Reference David and Nour2007). The Parigot-style
 $\lambda \mu \mu '$
-calculus is a subsystem of the de Groote-style
$\lambda \mu \mu '$
-calculus is a subsystem of the de Groote-style
 $\lambda \mu \mu '$
-calculus, hence, its strong normalization property follows.
$\lambda \mu \mu '$
-calculus, hence, its strong normalization property follows. -
In the subsequent sections, we discuss the normalization properties of the de Groote version of the symmetric calculi
 $\mu \mu '$
and
$\mu \mu '$
and
 $\lambda \mu \mu '$
when augmented with the structural rules
$\lambda \mu \mu '$
when augmented with the structural rules
 $\rho$
,
$\rho$
,
 $\theta$
, and
$\theta$
, and
 $\varepsilon$
. We show by an example that
$\varepsilon$
. We show by an example that
 $\mu \mu '\rho \varepsilon$
-reduction is not strongly normalizing. Then we construct explicit algorithms in order to demonstrate that the weak normalization property for
$\mu \mu '\rho \varepsilon$
-reduction is not strongly normalizing. Then we construct explicit algorithms in order to demonstrate that the weak normalization property for
 $\mu \mu '\rho \varepsilon$
-reduction is still valid. We point out that our algorithm allows finding several normal forms for the same term.
$\mu \mu '\rho \varepsilon$
-reduction is still valid. We point out that our algorithm allows finding several normal forms for the same term. -
In the last section, we extend our result to the case of
 $\beta$
-reduction in the setting of typed calculus. More precisely, we show that, if we alternate our weak normalization algorithm for
$\beta$
-reduction in the setting of typed calculus. More precisely, we show that, if we alternate our weak normalization algorithm for
 $\mu \mu '\rho \varepsilon$
-reduction together with an arbitrary one for
$\mu \mu '\rho \varepsilon$
-reduction together with an arbitrary one for
 $\beta$
-reduction, the process necessarily terminates. In fact, performing these reductions strictly reduces the maximal rank of
$\beta$
-reduction, the process necessarily terminates. In fact, performing these reductions strictly reduces the maximal rank of
 $\beta$
-redexes. The proofs of this section are rather technical and are based on a fine analysis of the origin of the redexes in the reduction sequences. We observe that
$\beta$
-redexes. The proofs of this section are rather technical and are based on a fine analysis of the origin of the redexes in the reduction sequences. We observe that
 $\theta$
-reduction does not give rise to any particular problem and we can postpone it. Our method allows us to give a weak normalization algorithm for the complete calculus.
$\theta$
-reduction does not give rise to any particular problem and we can postpone it. Our method allows us to give a weak normalization algorithm for the complete calculus.
Some of the results of this paper, especially the results in Sections 4, 5, and 6, have already been presented in the thesis of the first author (Battyányi Reference Battyányi2007). We would like to clarify, however, that these results have not been published before and some of the proofs of the thesis were even incorrect. We found that it was very difficult to correct them using the same methods. The method applied here for proving the different variants of weak normalization properties are totally different. The proof of weak normalization of
![]() $\mu \mu '\rho \theta \varepsilon$
-reduction is direct and gives an easy algorithm. The demonstration of weak normalization of
$\mu \mu '\rho \theta \varepsilon$
-reduction is direct and gives an easy algorithm. The demonstration of weak normalization of
![]() $\beta \mu \mu '\rho \theta \varepsilon$
-reduction does not utilize residuals (which are quite complicated to properly formulate), rather we proceed, in most of the cases, by a simple induction on the structure of terms.
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction does not utilize residuals (which are quite complicated to properly formulate), rather we proceed, in most of the cases, by a simple induction on the structure of terms.
2. The
 $\lambda \mu$
-Calculus
$\lambda \mu$
-Calculus
The
![]() $\lambda \mu$
-calculus was introduced by Parigot (Reference Parigot and Voronkov1992) with the intention of providing a term encoding for classical natural deduction. In our paper, we restrict ourselves to the simply typed calculus. The
$\lambda \mu$
-calculus was introduced by Parigot (Reference Parigot and Voronkov1992) with the intention of providing a term encoding for classical natural deduction. In our paper, we restrict ourselves to the simply typed calculus. The
![]() $\lambda \mu$
-calculus possesses two kinds of variables: one of them is the original set of
$\lambda \mu$
-calculus possesses two kinds of variables: one of them is the original set of
![]() $\lambda$
-variables, the so called intuitionistic variables, and the other kind of variables is the set of
$\lambda$
-variables, the so called intuitionistic variables, and the other kind of variables is the set of
![]() $\mu$
-variables, which are termed classical variables. Parigot’s calculus has certain restrictions imposed on the term formation rules: namely, a
$\mu$
-variables, which are termed classical variables. Parigot’s calculus has certain restrictions imposed on the term formation rules: namely, a
![]() $\mu$
-abstraction must be followed by an application with a
$\mu$
-abstraction must be followed by an application with a
![]() $\mu$
-variable and vice versa. That is, a term
$\mu$
-variable and vice versa. That is, a term
![]() $\mu \alpha . M$
can only be of the form
$\mu \alpha . M$
can only be of the form
![]() $\mu \alpha . [\beta ] N$
for some
$\mu \alpha . [\beta ] N$
for some
![]() $N$
.
$N$
.
de Groote (Reference de Groote1998) has proposed a new version of the
![]() $\lambda \mu$
-calculus by modifying this syntax. Namely, the term formation rules became more flexible: a
$\lambda \mu$
-calculus by modifying this syntax. Namely, the term formation rules became more flexible: a
![]() $\mu$
-abstraction can now be followed by an arbitrary term (in the untyped version); hence, it does not need to be of the form
$\mu$
-abstraction can now be followed by an arbitrary term (in the untyped version); hence, it does not need to be of the form
![]() $\mu \alpha .[\beta ]N$
. Since in the greater part of the paper we are concerned with the de Groote version, we introduce the de Groote-style calculus in what follows. In Section 4, we deal with the Parigot-style calculus. We postpone defining the Parigot-style syntax until then.
$\mu \alpha .[\beta ]N$
. Since in the greater part of the paper we are concerned with the de Groote version, we introduce the de Groote-style calculus in what follows. In Section 4, we deal with the Parigot-style calculus. We postpone defining the Parigot-style syntax until then.
Definition 2.1. (
![]() $\lambda \mu$
-terms)
$\lambda \mu$
-terms)
-
1. Let
 $\mathcal{V}_{\lambda } = \{ x,y,z,\dots \}$
denote a set of
$\mathcal{V}_{\lambda } = \{ x,y,z,\dots \}$
denote a set of
 $\lambda$
-variables and
$\lambda$
-variables and
 $\mathcal{V}_{\mu } = \{\alpha,\beta,\gamma,\dots \}$
denote a set of
$\mathcal{V}_{\mu } = \{\alpha,\beta,\gamma,\dots \}$
denote a set of
 $\mu$
-variables, respectively. The
$\mu$
-variables, respectively. The
 $\lambda \mu$
-term formation rules are the following.
We decided to adopt Krivine’s notation for the applications, i.e., we write
$\lambda \mu$
-term formation rules are the following.
We decided to adopt Krivine’s notation for the applications, i.e., we write \begin{equation*} {\mathcal {T}} \;\; := \;\; \mathcal {V}_{\lambda } \;\; \mid \;\; \lambda \mathcal {V}_{\lambda }.{\mathcal {T}}\;\; \mid \;\; ({\mathcal {T}}){\mathcal {T}}\;\; \mid \;\; [\mathcal {V}_{\mu }]{\mathcal {T}} \;\; \mid \;\; \mu \mathcal {V}_{\mu }.{\mathcal {T}} \;\; \end{equation*}
\begin{equation*} {\mathcal {T}} \;\; := \;\; \mathcal {V}_{\lambda } \;\; \mid \;\; \lambda \mathcal {V}_{\lambda }.{\mathcal {T}}\;\; \mid \;\; ({\mathcal {T}}){\mathcal {T}}\;\; \mid \;\; [\mathcal {V}_{\mu }]{\mathcal {T}} \;\; \mid \;\; \mu \mathcal {V}_{\mu }.{\mathcal {T}} \;\; \end{equation*}
 $(M)N$
instead of
$(M)N$
instead of
 $(M\, N)$
if we apply
$(M\, N)$
if we apply
 $M$
to
$M$
to
 $N$
.
$N$
.
-
2. In a
 $\lambda \mu$
-term, the
$\lambda \mu$
-term, the
 $\lambda$
and
$\lambda$
and
 $\mu$
operators bind the variables in their scope. We therefore consider terms modulo equivalence, which allows to rename the variables bound by a
$\mu$
operators bind the variables in their scope. We therefore consider terms modulo equivalence, which allows to rename the variables bound by a
 $\lambda$
- or a
$\lambda$
- or a
 $\mu$
-abstraction.
$\mu$
-abstraction.
-
3. For every
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
, we define by induction on
$M$
, we define by induction on
 $M$
the set
$M$
the set
 $\textrm{fv}(M)$
of free
$\textrm{fv}(M)$
of free
 $\mu$
-variables of
$\mu$
-variables of
 $M$
:
$M$
:
 $\textrm{fv}(x)=\emptyset$
,
$\textrm{fv}(x)=\emptyset$
,
 $\textrm{fv}(\lambda x.M)=\textrm{fv}(M)$
,
$\textrm{fv}(\lambda x.M)=\textrm{fv}(M)$
,
 $\textrm{fv}((M)N)=\textrm{fv}(M) \cup \textrm{fv}((N)$
,
$\textrm{fv}((M)N)=\textrm{fv}(M) \cup \textrm{fv}((N)$
,
 $\textrm{fv}([\alpha ]M) = \textrm{fv}(M) \cup \{\alpha \}$
and
$\textrm{fv}([\alpha ]M) = \textrm{fv}(M) \cup \{\alpha \}$
and
 $\textrm{fv}(\mu \alpha . M) = \textrm{fv}(M)\setminus \{\alpha \}$
.
$\textrm{fv}(\mu \alpha . M) = \textrm{fv}(M)\setminus \{\alpha \}$
.
The notion of subterm plays a very important role in our paper. Many of our subsequent results require a fine analysis of the propagation and creation of certain subterms. A subterm
![]() $N$
of a term
$N$
of a term
![]() $M$
is a term that appears in the formation tree for
$M$
is a term that appears in the formation tree for
![]() $M$
. Obviously,
$M$
. Obviously,
![]() $M$
can contain several identical subterms. However, when we consider a subterm
$M$
can contain several identical subterms. However, when we consider a subterm
![]() $N$
of
$N$
of
![]() $M$
, we intend to take only one particular occurrence of
$M$
, we intend to take only one particular occurrence of
![]() $N$
in
$N$
in
![]() $M$
.
$M$
.
Definition 2.2. (Subterms)
-
1. We apply the notation
 $N \preceq M$
if
$N \preceq M$
if
 $N$
occurs as a subterm in the
$N$
occurs as a subterm in the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
. We call this occurrence strict and write
$M$
. We call this occurrence strict and write
 $N \prec M$
if, in addition,
$N \prec M$
if, in addition,
 $M\neq N$
.
$M\neq N$
. -
2. Let
 $N \preceq M$
and
$N \preceq M$
and
 $\alpha \in \mathcal{V}_{\mu }$
. An occurrence of the
$\alpha \in \mathcal{V}_{\mu }$
. An occurrence of the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $N$
in
$N$
in
 $M$
is said to be named with
$M$
is said to be named with
 $\alpha$
, if it is preceded by
$\alpha$
, if it is preceded by
 $[\alpha ]$
, that is,
$[\alpha ]$
, that is,
 $[\alpha ]N \preceq M$
for that occurrence.
$[\alpha ]N \preceq M$
for that occurrence.
Definition 2.3. (Type system)
The types are built from a set
![]() $\mathcal{V}_{\mathbb T}$
of atomic types and the constant
$\mathcal{V}_{\mathbb T}$
of atomic types and the constant
![]() $\bot$
with the connectives
$\bot$
with the connectives
![]() $\neg$
and
$\neg$
and
![]() $\rightarrow$
. The type formation rules are the following.
$\rightarrow$
. The type formation rules are the following.
In the definition below
![]() $\Gamma$
denotes a (possibly empty) context, that is, a finite set of declarations of the form
$\Gamma$
denotes a (possibly empty) context, that is, a finite set of declarations of the form
![]() $x:A$
(resp.
$x:A$
(resp.
![]() $\alpha :\neg A$
) for a
$\alpha :\neg A$
) for a
![]() $\lambda$
-variable
$\lambda$
-variable
![]() $x$
(resp. a
$x$
(resp. a
![]() $\mu$
-variable
$\mu$
-variable
![]() $\alpha$
) and type
$\alpha$
) and type
![]() $A$
such that a
$A$
such that a
![]() $\lambda$
-variable
$\lambda$
-variable
![]() $x$
(resp. a
$x$
(resp. a
![]() $\mu$
-variable
$\mu$
-variable
![]() $\alpha$
) occurs at most once in an expression
$\alpha$
) occurs at most once in an expression
![]() $x:A$
(resp.
$x:A$
(resp.
![]() $\alpha : \neg A$
) of
$\alpha : \neg A$
) of
![]() $\Gamma$
. The typing rules are as follows.
$\Gamma$
. The typing rules are as follows.

We say that the
![]() $\lambda \mu$
-term
$\lambda \mu$
-term
![]() $M$
is typable with type
$M$
is typable with type
![]() $A$
, if there is a context
$A$
, if there is a context
![]() $\Gamma$
and a derivation tree such that the uppermost nodes of the tree are axioms and the bottom node is
$\Gamma$
and a derivation tree such that the uppermost nodes of the tree are axioms and the bottom node is
![]() .
.
Observe that, in the typed
![]() $\lambda \mu$
-calculus, not every term is accepted as well typed. For example, we cannot write a
$\lambda \mu$
-calculus, not every term is accepted as well typed. For example, we cannot write a
![]() $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
![]() $([\alpha ]M)N$
or
$([\alpha ]M)N$
or
![]() $\mu \alpha . \lambda x.M$
.
$\mu \alpha . \lambda x.M$
.
In this paper, we work with several kinds of substitutions. All of them are implicitly understood with the necessary renaming of bound variables to avoid the capturing of the free variables coming from the substitution. We present
![]() $\mu$
-substitution in detail. We need it in Definition 2.6.
$\mu$
-substitution in detail. We need it in Definition 2.6.
Definition 2.4. (
![]() $\mu$
-substitution)
$\mu$
-substitution)
-
1. A
 $\mu$
-substitution is an expression of the form
$\mu$
-substitution is an expression of the form
 ${\sigma } =[\alpha :=_sN]$
where
${\sigma } =[\alpha :=_sN]$
where
 $s\in \{l,r\}$
,
$s\in \{l,r\}$
,
 $\alpha$
is a
$\alpha$
is a
 $\mu$
-variable and
$\mu$
-variable and
 $N$
is a
$N$
is a
 $\lambda \mu$
-term.
$\lambda \mu$
-term.
-
2. Let
 ${\sigma } =[\alpha :=_sN]$
and let
${\sigma } =[\alpha :=_sN]$
and let
 $M$
be a
$M$
be a
 $\lambda \mu$
-term. We define by induction the
$\lambda \mu$
-term. We define by induction the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M{\sigma }$
. We adopt the convention of renaming bound variables before a substitution so that no variable collision occurs. Then we can assume that the free variables of the
$M{\sigma }$
. We adopt the convention of renaming bound variables before a substitution so that no variable collision occurs. Then we can assume that the free variables of the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $N$
and variable
$N$
and variable
 $\alpha$
are not bound by any
$\alpha$
are not bound by any
 $\mu$
-abstraction in the
$\mu$
-abstraction in the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
.
$M$
.
-
If
 $M = x$
, then
$M = x$
, then
 $M{\sigma } = x$
.
$M{\sigma } = x$
. -
If
 $M = \lambda x.M'$
, then
$M = \lambda x.M'$
, then
 $M{\sigma } = \lambda x.M'{\sigma }$
.
$M{\sigma } = \lambda x.M'{\sigma }$
. -
If
 $M = (M_1)M_2$
, then
$M = (M_1)M_2$
, then
 $M{\sigma } = (M_1{\sigma })M_2{\sigma }$
.
$M{\sigma } = (M_1{\sigma })M_2{\sigma }$
. -
If
 $M = \mu \beta .M'$
, then
$M = \mu \beta .M'$
, then
 $M{\sigma } = \mu \beta .M'{\sigma }$
.
$M{\sigma } = \mu \beta .M'{\sigma }$
. -
If
 $M = [\beta ]M'$
and
$M = [\beta ]M'$
and
 $\beta \neq \alpha$
, then
$\beta \neq \alpha$
, then
 $M{\sigma } = [\beta ]M'{\sigma }$
.
$M{\sigma } = [\beta ]M'{\sigma }$
. -
If
 $M = [\alpha ]M'$
and
$M = [\alpha ]M'$
and
 $s = r$
, then
$s = r$
, then
 $M{\sigma } = [\alpha ](M'{\sigma })N$
.
$M{\sigma } = [\alpha ](M'{\sigma })N$
. -
If
 $M = [\alpha ]M'$
and
$M = [\alpha ]M'$
and
 $s = l$
, then
$s = l$
, then
 $M{\sigma } = [\alpha ](N)M'{\sigma }$
.
$M{\sigma } = [\alpha ](N)M'{\sigma }$
.
-
We adopt the convention that substitution has higher precedence than application and abstraction.
In order to define
![]() $\varepsilon$
-reduction, we need the following notion.
$\varepsilon$
-reduction, we need the following notion.
Definition 2.5. (
![]() $\alpha$
-translation)
$\alpha$
-translation)
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term and
$\lambda \mu$
-term and
![]() $\alpha$
a
$\alpha$
a
![]() $\mu$
-variable. We define the
$\mu$
-variable. We define the
![]() $\alpha$
-translation
$\alpha$
-translation
![]() $M_{\alpha }$
of
$M_{\alpha }$
of
![]() $M$
by induction on
$M$
by induction on
![]() $M$
.
$M$
.
-
If
 $M = x$
, then
$M = x$
, then
 $M_{\alpha }=x$
.
$M_{\alpha }=x$
. -
If
 $M = \lambda x.M'$
, then
$M = \lambda x.M'$
, then
 $M_{\alpha }=\lambda x.{M'}_{\alpha }$
.
$M_{\alpha }=\lambda x.{M'}_{\alpha }$
. -
If
 $M = (P)Q$
, then
$M = (P)Q$
, then
 $M_{\alpha }=(P_{\alpha })Q_{\alpha }$
.
$M_{\alpha }=(P_{\alpha })Q_{\alpha }$
. -
If
 $M = \mu \beta . M'$
, then
$M = \mu \beta . M'$
, then
 $M_{\alpha }=\mu \beta .{M'}_{\alpha }$
.
$M_{\alpha }=\mu \beta .{M'}_{\alpha }$
. -
If
 $M = [\beta ]M'$
and
$M = [\beta ]M'$
and
 $\beta \neq \alpha$
, then
$\beta \neq \alpha$
, then
 $M_{\alpha }=[\beta ]{M'}_{\alpha }$
.
$M_{\alpha }=[\beta ]{M'}_{\alpha }$
. -
If
 $M = [\alpha ]M'$
, then
$M = [\alpha ]M'$
, then
 $M_{\alpha }={M'}_{\alpha }$
.
$M_{\alpha }={M'}_{\alpha }$
.
Intuitively,
![]() $M_{\alpha }$
is the result of replacing every subterm
$M_{\alpha }$
is the result of replacing every subterm
![]() $[\alpha ]N$
in
$[\alpha ]N$
in
![]() $M$
with
$M$
with
![]() $N$
.
$N$
.
In what follows, we define the redexes examined in this paper and the reductions induced by them. Next, we recall some results about the
![]() $\lambda \mu$
-calculus. Regarding the necessary notions and definitions and the
$\lambda \mu$
-calculus. Regarding the necessary notions and definitions and the
![]() $\lambda$
-calculus analogues of the results listed below, the reader is referred to the standard textbooks, for example Reference Girard, Lafont and TaylorGirard et al. (1989),Krivine (Reference Krivine1993).
$\lambda$
-calculus analogues of the results listed below, the reader is referred to the standard textbooks, for example Reference Girard, Lafont and TaylorGirard et al. (1989),Krivine (Reference Krivine1993).
Definition 2.6. (Redex)
-
1. A
 $\beta$
-redex is a
$\beta$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $(\lambda x. M) N$
and we call
$(\lambda x. M) N$
and we call
 $M[x := N]$
its contractum. The
$M[x := N]$
its contractum. The
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M[x := N]$
is obtained from
$M[x := N]$
is obtained from
 $M$
by replacing every free occurrence of
$M$
by replacing every free occurrence of
 $x$
in
$x$
in
 $M$
by
$M$
by
 $N$
. This substitution is sometimes referred to as
$N$
. This substitution is sometimes referred to as
 $\beta$
-substitution.
$\beta$
-substitution.
-
2. A
 $\mu$
-redex is a
$\mu$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $(\mu \alpha . M) N$
and we call
$(\mu \alpha . M) N$
and we call
 $\mu \alpha .M[\alpha :=_r N]$
its contractum. Intuitively,
$\mu \alpha .M[\alpha :=_r N]$
its contractum. Intuitively,
 $M[\alpha :=_r N]$
is obtained from
$M[\alpha :=_r N]$
is obtained from
 $M$
by replacing every subterm in
$M$
by replacing every subterm in
 $M$
of the form
$M$
of the form
 $[\alpha ]P$
by
$[\alpha ]P$
by
 $[\alpha ](P)N$
.
$[\alpha ](P)N$
. -
3. A
 $\mu '$
-redex is a
$\mu '$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $(N)\mu \alpha . M$
and we call
$(N)\mu \alpha . M$
and we call
 $\mu \alpha .M[\alpha :=_l N]$
its contractum. Intuitively,
$\mu \alpha .M[\alpha :=_l N]$
its contractum. Intuitively,
 $M[\alpha :=_l N]$
is obtained from
$M[\alpha :=_l N]$
is obtained from
 $M$
by replacing every subterm in
$M$
by replacing every subterm in
 $M$
of the form
$M$
of the form
 $[\alpha ]P$
by
$[\alpha ]P$
by
 $[\alpha ](N)P$
.
$[\alpha ](N)P$
. -
4. A
 $\rho$
-redex is a
$\rho$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $[\beta ]\mu \alpha .M$
and we call
$[\beta ]\mu \alpha .M$
and we call
 $M[\alpha := \beta ]$
its contractum. The
$M[\alpha := \beta ]$
its contractum. The
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M[\alpha := \beta ]$
is obtained from
$M[\alpha := \beta ]$
is obtained from
 $M$
by replacing every free occurrence of
$M$
by replacing every free occurrence of
 $\alpha$
by
$\alpha$
by
 $\beta$
.
$\beta$
. -
5. A
 $\theta$
-redex is a
$\theta$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $\mu \alpha .[\alpha ]M$
where
$\mu \alpha .[\alpha ]M$
where
 $\alpha \not \in \textrm{fv}(M)$
and we call
$\alpha \not \in \textrm{fv}(M)$
and we call
 $M$
its contractum.
$M$
its contractum.
-
6. An
 $\varepsilon$
-redex is a
$\varepsilon$
-redex is a
 $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
 $\mu \alpha .\mu \beta .M$
and we call
$\mu \alpha .\mu \beta .M$
and we call
 $\mu \alpha .M_{\beta }$
its contractum.
$\mu \alpha .M_{\beta }$
its contractum.
The six reductions presented in Definition 2.6 can be justified by the cut elimination rules in natural deduction. This is why we will have type preservation property in the calculus (Theorem 2.10), which is also known as subject reduction property.
Remark 2.7.
-
1. The intuitive meaning of reducing
 $(\mu \alpha .M)N$
to
$(\mu \alpha .M)N$
to
 $\mu \alpha .M[\alpha : = _rN]$
is that the argument
$\mu \alpha .M[\alpha : = _rN]$
is that the argument
 $N$
of the function
$N$
of the function
 $\mu \alpha .M$
is passed as an argument to all the functions in
$\mu \alpha .M$
is passed as an argument to all the functions in
 $M$
named with the symbol
$M$
named with the symbol
 $[\alpha ]$
.
$[\alpha ]$
. -
2. The intuitive meaning of reducing
 $(N)\mu \alpha .M$
to
$(N)\mu \alpha .M$
to
 $\mu \alpha .M[\alpha : = _lN]$
is that the function
$\mu \alpha .M[\alpha : = _lN]$
is that the function
 $N$
having
$N$
having
 $\mu \alpha .M$
as argument becomes the functional part of the applications
$\mu \alpha .M$
as argument becomes the functional part of the applications
 $(N)P$
, where
$(N)P$
, where
 $P$
is a subterm of
$P$
is a subterm of
 $M$
named with the symbol
$M$
named with the symbol
 $[\alpha ]$
.
$[\alpha ]$
.
Definition 2.8. (Reduction and normalization)
Let
![]() $\mathcal{R} \subseteq \{\beta, \mu, \mu ', \rho, \theta, \varepsilon \}$
.
$\mathcal{R} \subseteq \{\beta, \mu, \mu ', \rho, \theta, \varepsilon \}$
.
-
1. Let
 $M$
and
$M$
and
 $M'$
be two
$M'$
be two
 $\lambda \mu$
-terms. We write
$\lambda \mu$
-terms. We write
 $M{\rightarrow }_{\mathcal{R}} M'$
, if
$M{\rightarrow }_{\mathcal{R}} M'$
, if
 $M'$
is obtained from
$M'$
is obtained from
 $M$
by replacing an
$M$
by replacing an
 $r$
-redex in
$r$
-redex in
 $M$
, where
$M$
, where
 $r \in \mathcal{R}$
, by its contractum. The reductions (on the redexes) take the following forms (the
$r \in \mathcal{R}$
, by its contractum. The reductions (on the redexes) take the following forms (the
 $\theta$
-redex has an additional condition).
$\theta$
-redex has an additional condition).

-
2. We denote by
 $\twoheadrightarrow _{\mathcal{R}}$
the reflexive, transitive closure of
$\twoheadrightarrow _{\mathcal{R}}$
the reflexive, transitive closure of
 ${\rightarrow }_{\mathcal{R}}$
. I.e.,
${\rightarrow }_{\mathcal{R}}$
. I.e.,
 $M \twoheadrightarrow _{\mathcal{R}} M'$
iff
$M \twoheadrightarrow _{\mathcal{R}} M'$
iff
 $M{\rightarrow }_{\mathcal{R}} M_1{\rightarrow }_{\mathcal{R}} M_2{\rightarrow } \cdots{\rightarrow }_{\mathcal{R}} M_k = M'$
. Finally, we write
$M{\rightarrow }_{\mathcal{R}} M_1{\rightarrow }_{\mathcal{R}} M_2{\rightarrow } \cdots{\rightarrow }_{\mathcal{R}} M_k = M'$
. Finally, we write
 $M{\rightarrow }^n_{\mathcal{R}} M'$
iff
$M{\rightarrow }^n_{\mathcal{R}} M'$
iff
 $M{\rightarrow }_{\mathcal{R}} M_1{\rightarrow }_{\mathcal{R}} M_2{\rightarrow }_{\mathcal{R}} \cdots{\rightarrow }_{\mathcal{R}} M_n = M'$
and
$M{\rightarrow }_{\mathcal{R}} M_1{\rightarrow }_{\mathcal{R}} M_2{\rightarrow }_{\mathcal{R}} \cdots{\rightarrow }_{\mathcal{R}} M_n = M'$
and
 $M{\rightarrow }^+_{\mathcal{R}} M'$
iff there is an
$M{\rightarrow }^+_{\mathcal{R}} M'$
iff there is an
 $n \gt 0$
such that
$n \gt 0$
such that
 $M{\rightarrow }^n_{\mathcal{R}} M'$
.
$M{\rightarrow }^n_{\mathcal{R}} M'$
. -
3. We denote by
 $\mathcal{NF}_{\mathcal{R}}$
the set of all
$\mathcal{NF}_{\mathcal{R}}$
the set of all
 $\lambda \mu$
-terms in
$\lambda \mu$
-terms in
 $\mathcal{R}$
-normal form, i.e.,
$\mathcal{R}$
-normal form, i.e.,
 $\lambda \mu$
-terms that do not contain an
$\lambda \mu$
-terms that do not contain an
 $r$
-redex for any
$r$
-redex for any
 $r \in \mathcal{R}$
.
$r \in \mathcal{R}$
. -
4. A
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
is said to be
$M$
is said to be
 $\mathcal{R}$
-weakly normalizable if there exists
$\mathcal{R}$
-weakly normalizable if there exists
 $M'\in \mathcal{NF}_{\mathcal{R}}$
such that
$M'\in \mathcal{NF}_{\mathcal{R}}$
such that
 $M \twoheadrightarrow _{\mathcal{R}} M'$
. We denote by
$M \twoheadrightarrow _{\mathcal{R}} M'$
. We denote by
 $\mathcal{WN}_{\mathcal{R}}$
the set of
$\mathcal{WN}_{\mathcal{R}}$
the set of
 $\mathcal{R}$
-weakly normalizable terms.
$\mathcal{R}$
-weakly normalizable terms.
-
5. A
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
is said to be
$M$
is said to be
 $\mathcal{R}$
-strongly normalizable, if there exists no infinite
$\mathcal{R}$
-strongly normalizable, if there exists no infinite
 $\mathcal{R}$
-reduction paths starting from
$\mathcal{R}$
-reduction paths starting from
 $M$
. That is, any possible sequence of reductions eventually leads to a normal term. We denote by
$M$
. That is, any possible sequence of reductions eventually leads to a normal term. We denote by
 $\mathcal{SN}_{\mathcal{R}}$
the set of
$\mathcal{SN}_{\mathcal{R}}$
the set of
 $\mathcal{R}$
-strongly normalizable terms.
$\mathcal{R}$
-strongly normalizable terms.
Remark 2.9. When talking about reductions, it is customary to define residuals, that is, the results of performing reductions in a term. However, in Section 6, when we examine the outcome of a reduction starting from a term
![]() $N$
and leading to
$N$
and leading to
![]() $N'$
, we are not interested in knowing about the residuals of a given subterm of
$N'$
, we are not interested in knowing about the residuals of a given subterm of
![]() $N$
occurring in
$N$
occurring in
![]() $N'$
(which is a one-to-many correspondence). Rather, we consider redexes of
$N'$
(which is a one-to-many correspondence). Rather, we consider redexes of
![]() $N'$
and we are interested in their possible origin in
$N'$
and we are interested in their possible origin in
![]() $N$
, that is, we trace back the reduction path, and this is a one-to-one correspondence. From the technical point of view, we do not need to formulate the notions of origin or residual to state the results of that section.
$N$
, that is, we trace back the reduction path, and this is a one-to-one correspondence. From the technical point of view, we do not need to formulate the notions of origin or residual to state the results of that section.
We list here the most important results that we are going to use in our paper. For the proofs of the next theorems, the interested reader is referred to Battyányi and Nour (Reference Battyányi and Nour2020),David and Nour (Reference David, Nour and Urzyczyn2005),Py (Reference Py1998).
Theorem 2.10.
The
![]() $\beta \mu \mu '\rho \theta \varepsilon$
-reduction preserves types, that is, if
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction preserves types, that is, if ![]() and
and
![]() $M \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } M'$
, then
$M \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } M'$
, then
![]() .
.
Theorem 2.11.
The
![]() $\mu \mu '$
-reduction is strongly normalizing for the untyped
$\mu \mu '$
-reduction is strongly normalizing for the untyped
![]() $\lambda \mu$
-terms.
$\lambda \mu$
-terms.
Theorem 2.12.
The
![]() $\beta \mu \mu '$
-reduction is strongly normalizing for the typed
$\beta \mu \mu '$
-reduction is strongly normalizing for the typed
![]() $\lambda \mu$
-terms.
$\lambda \mu$
-terms.
In the sequel, let IH be an abbreviation for the phrase “the induction hypothesis”.
3. Natural Numbers
The aim of this section is to justify our choices regarding the reduction rules. The major benefit of the “proof as program” paradigm (also known as Curry–Howard isomorphism) is that the proof itself ensures that the program extracted is correct (Krivine Reference Krivine1993; Leivant Reference Leivant1983). For example, in intuitionistic second-order
![]() $\lambda$
-calculus, to program functions on integers, it suffices to encode the proof of the totality of the function to extract the correct program. Since the only
$\lambda$
-calculus, to program functions on integers, it suffices to encode the proof of the totality of the function to extract the correct program. Since the only
![]() $\lambda$
-terms up to
$\lambda$
-terms up to
![]() $\beta$
-reduction that have an integer type are the Church numerals, to run the program one just has to apply it to a Church numeral and then reduce it to find the exact result. In classical logic the situation is different. Without
$\beta$
-reduction that have an integer type are the Church numerals, to run the program one just has to apply it to a Church numeral and then reduce it to find the exact result. In classical logic the situation is different. Without
![]() $\mu '$
-reduction we can have closed
$\mu '$
-reduction we can have closed
![]() $\lambda \mu$
-terms of integer type that are not Church numerals themselves (see Example 3.8). For data types, like integers, Parigot (Reference Parigot1993) observed that the classical integers (the terms that encode proofs of integer type) may contain subterms which can be discarded by simple reduction rules without changing the type. This phenomenon comes from the fact that one does not need double negation elimination in order to prove that these terms are well typed. Hence, the idea is to add rules to tidy up the terms for classical integers. We must keep in mind, however, that we are not able to do the same thing in higher order logics, since, in that case, the
$\lambda \mu$
-terms of integer type that are not Church numerals themselves (see Example 3.8). For data types, like integers, Parigot (Reference Parigot1993) observed that the classical integers (the terms that encode proofs of integer type) may contain subterms which can be discarded by simple reduction rules without changing the type. This phenomenon comes from the fact that one does not need double negation elimination in order to prove that these terms are well typed. Hence, the idea is to add rules to tidy up the terms for classical integers. We must keep in mind, however, that we are not able to do the same thing in higher order logics, since, in that case, the
![]() $\mu '$
-rule does not preserve the types. We emphasize that this method does not mean that every classical proof can be transformed into an intuitionistic one but, at least for many of the data types in the simply typed lambda calculus, it is possible. In higher order logics there exists another solution: one can give computational content to the quantifiers in such a way that the
$\mu '$
-rule does not preserve the types. We emphasize that this method does not mean that every classical proof can be transformed into an intuitionistic one but, at least for many of the data types in the simply typed lambda calculus, it is possible. In higher order logics there exists another solution: one can give computational content to the quantifiers in such a way that the
![]() $\mu '$
-rule preserves the types (Py Reference Py1998).
$\mu '$
-rule preserves the types (Py Reference Py1998).
Henceforth, we adopt the strategy of adding certain rules to the calculus, most notably the
![]() $\mu '$
-rule. In this section, we prove that in the presence of all of our mentioned rules, the only
$\mu '$
-rule. In this section, we prove that in the presence of all of our mentioned rules, the only
![]() $\lambda \mu$
-terms, regarding the de Groote syntax, that can be typed with integer type are the
$\lambda \mu$
-terms, regarding the de Groote syntax, that can be typed with integer type are the
![]() $\lambda \mu$
-terms that behave as Church numerals. In order to obtain the result, all the rules are necessary, that is, we consider
$\lambda \mu$
-terms that behave as Church numerals. In order to obtain the result, all the rules are necessary, that is, we consider
![]() $\beta \mu \mu '\rho \theta \varepsilon$
-reduction. The results of this section can be generalized to the various algebraic data types defined by Krivine (Reference Krivine1994). We omit their treatment in our paper.
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction. The results of this section can be generalized to the various algebraic data types defined by Krivine (Reference Krivine1994). We omit their treatment in our paper.
Definition 3.1. (Natural numbers)
-
1. Let
 $X$
be a variable type and
$X$
be a variable type and
 $\mathcal{N} = X{\rightarrow } ((X{\rightarrow } X){\rightarrow } X)$
be the integer type.
$\mathcal{N} = X{\rightarrow } ((X{\rightarrow } X){\rightarrow } X)$
be the integer type.
-
2. For every
 $n\in I\!N$
and
$n\in I\!N$
and
 $M,N \in \mathcal{T}$
, we define by induction the
$M,N \in \mathcal{T}$
, we define by induction the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $(M)^nN$
as follows:
$(M)^nN$
as follows:
 $(M)^0N = N$
and,
$(M)^0N = N$
and,
 $\forall \, k \in I\!N$
,
$\forall \, k \in I\!N$
,
 $(M)^{k+1}N = (M)(M)^{k}N$
; then
$(M)^{k+1}N = (M)(M)^{k}N$
; then
 $(M)^nN =\underbrace{(M) \dots (M)}_{n \; times} N$
.
$(M)^nN =\underbrace{(M) \dots (M)}_{n \; times} N$
. -
3. For every
 $n\in I\!N$
, we define the Church natural number (or Church numeral) as
$n\in I\!N$
, we define the Church natural number (or Church numeral) as
 $\underline{n} = \lambda x.\lambda f. (f)^nx$
.
$\underline{n} = \lambda x.\lambda f. (f)^nx$
. -
4. Let
 $\underline{s} = \lambda n.\lambda x. \lambda f. (f)((n)x)f$
. The
$\underline{s} = \lambda n.\lambda x. \lambda f. (f)((n)x)f$
. The
 $\lambda$
-term
$\lambda$
-term
 $\underline{s}$
is considered to be the successor function for Church numerals.
$\underline{s}$
is considered to be the successor function for Church numerals.
We remark that the successor function really behaves as the arithmetical operator on natural numbers: we can verify that, for all
![]() $n \in I\!N$
,
$n \in I\!N$
,
![]() $(\underline{s})\underline{n} \twoheadrightarrow _{\beta } \underline{n+1}$
.
$(\underline{s})\underline{n} \twoheadrightarrow _{\beta } \underline{n+1}$
.
The following results are valid for
![]() $\lambda$
-terms only. Later, we shall see examples of
$\lambda$
-terms only. Later, we shall see examples of
![]() $\lambda \mu$
-terms of type
$\lambda \mu$
-terms of type
![]() $\mathcal{N}$
(see Example 3.3).
$\mathcal{N}$
(see Example 3.3).
Theorem 3.2.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda$
-term. If
$\lambda$
-term. If
![]() , then,
, then,
![]() $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
![]() $M \twoheadrightarrow _{\beta } \underline{n}$
.
$M \twoheadrightarrow _{\beta } \underline{n}$
.
Proof. See Krivine (Reference Krivine1993).
With the introduction of the
![]() $\mu '$
-rule, we have lost confluence. It is easy to construct terms leading to different normal forms. More interestingly, we are able to define a
$\mu '$
-rule, we have lost confluence. It is easy to construct terms leading to different normal forms. More interestingly, we are able to define a
![]() $\lambda \mu$
-term of integer type that can evaluate to different integers. This permits us the coding of algorithms that can yield multiple possible results. The following example shows how a typed
$\lambda \mu$
-term of integer type that can evaluate to different integers. This permits us the coding of algorithms that can yield multiple possible results. The following example shows how a typed
![]() $\lambda \mu$
-term can be reduced to two different Church numerals. This phenomenon is not a shortcoming of the calculus. On the contrary, it even allows us the construction of programs that generate a set of solutions for a given problem.
$\lambda \mu$
-term can be reduced to two different Church numerals. This phenomenon is not a shortcoming of the calculus. On the contrary, it even allows us the construction of programs that generate a set of solutions for a given problem.
Example 3.3.
Let
![]() $n,m \in I\!N$
and
$n,m \in I\!N$
and
![]() $M = \mu \alpha .[\alpha ](\mu \gamma .[\alpha ]\underline{n})\mu \beta .[\alpha ]\underline{m}$
. We have
$M = \mu \alpha .[\alpha ](\mu \gamma .[\alpha ]\underline{n})\mu \beta .[\alpha ]\underline{m}$
. We have
-
 and
and
 , then
, then
 and
and
 , thus
, thus
 , therefore
, therefore
 ,
, -
 $M{{\rightarrow }}_{\mu } \; \mu \alpha .[\alpha ]\mu \gamma .[\alpha ]\underline{n} \;{{\rightarrow }}_{\rho } \; \mu \alpha . [\alpha ]\underline{n} \;{{\rightarrow }}_{\theta } \; \underline{n}$
,
$M{{\rightarrow }}_{\mu } \; \mu \alpha .[\alpha ]\mu \gamma .[\alpha ]\underline{n} \;{{\rightarrow }}_{\rho } \; \mu \alpha . [\alpha ]\underline{n} \;{{\rightarrow }}_{\theta } \; \underline{n}$
, -
 $M{{\rightarrow }}_{\mu '} \; \mu \alpha .[\alpha ]\mu \beta .[\alpha ]\underline{m} \;{{\rightarrow }}_{\rho } \; \mu \alpha . [\alpha ]\underline{m} \;{{\rightarrow }}_{\theta } \; \underline{m}$
.
$M{{\rightarrow }}_{\mu '} \; \mu \alpha .[\alpha ]\mu \beta .[\alpha ]\underline{m} \;{{\rightarrow }}_{\rho } \; \mu \alpha . [\alpha ]\underline{m} \;{{\rightarrow }}_{\theta } \; \underline{m}$
.
Lemmas 3.4 and 3.5 are technical and indispensable for obtaining the characterization of
![]() $\lambda \mu$
-terms of type
$\lambda \mu$
-terms of type
![]() $\mathcal{N}$
.
$\mathcal{N}$
.
Lemma 3.4.
Let
![]() $\Gamma = x : X, f : X{\rightarrow } X, \alpha : \neg X$
.
$\Gamma = x : X, f : X{\rightarrow } X, \alpha : \neg X$
.
-
1. There is no
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
such that
$M$
such that
 $M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
for any terms
$M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
for any terms
 $M_1,M_2$
and
$M_1,M_2$
and
 .
. -
2. There is no
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M$
such that
$M$
such that
 $M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
for any terms
$M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
for any terms
 $M_1,M_2$
and
$M_1,M_2$
and
 .
.
Proof.
-
1. By induction on
 $M$
. If
$M$
. If
 $\exists \, M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and
$\exists \, M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and
 , then,
, then,
 for some
for some
 $C$
. Since
$C$
. Since
 $M$
is normal and, by inspecting the typing rules,
$M$
is normal and, by inspecting the typing rules,
 $M_1 \neq x$
,
$M_1 \neq x$
,
 $M_1 \neq f$
,
$M_1 \neq f$
,
 $M_1\neq [\alpha ]M'_1$
,
$M_1\neq [\alpha ]M'_1$
,
 $M_1\neq \mu \beta .M'_1$
and
$M_1\neq \mu \beta .M'_1$
and
 $M_1 \neq \lambda y.M'_1$
. We deduce that
$M_1 \neq \lambda y.M'_1$
. We deduce that
 $M_1 = (M'_1)M'_2$
which is impossible by IH.
$M_1 = (M'_1)M'_2$
which is impossible by IH. -
2. If
 $\exists \, M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and
$\exists \, M = (M_1)M_2 \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and
 , then,
, then,
 . Since
. Since
 $M$
is normal and, by inspecting the typing rules,
$M$
is normal and, by inspecting the typing rules,
 $M_1 \neq x$
,
$M_1 \neq x$
,
 $M_1 \neq f$
,
$M_1 \neq f$
,
 $M_1\neq [\alpha ]M'_1$
,
$M_1\neq [\alpha ]M'_1$
,
 $M_1\neq \mu \beta .M'_1$
and
$M_1\neq \mu \beta .M'_1$
and
 $M_1 \neq \lambda y.M'_1$
. We deduce that
$M_1 \neq \lambda y.M'_1$
. We deduce that
 $M_1 = (M'_1)M'_2$
, which is impossible by 1.
$M_1 = (M'_1)M'_2$
, which is impossible by 1.
Lemma 3.5.
Let
![]() $\Gamma = x : X, f : X{\rightarrow } X, \alpha : \neg X$
. If
$\Gamma = x : X, f : X{\rightarrow } X, \alpha : \neg X$
. If
![]() $M \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
,
$M \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
,
![]() $M \neq \mu \beta .M'$
and
$M \neq \mu \beta .M'$
and
![]() , then
, then
![]() $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
![]() $M = (f)^nx$
.
$M = (f)^nx$
.
Proof.
By induction on
![]() $M$
.
$M$
.
-
Because of the typing rules and by our assumption,
 $M \neq [\alpha ]M'$
,
$M \neq [\alpha ]M'$
,
 $M \neq \mu \alpha .M'$
and
$M \neq \mu \alpha .M'$
and
 $M \neq \lambda y.M'$
.
$M \neq \lambda y.M'$
. -
If
 $M = x$
, then
$M = x$
, then
 $M = (f)^0x$
.
$M = (f)^0x$
. -
If
 $M = (M_1)M_2$
, then
$M = (M_1)M_2$
, then
 and
and
 . Since
. Since
 $M_1$
is normal and, if we take into account the typing rules, we find that
$M_1$
is normal and, if we take into account the typing rules, we find that
 $M_1 \neq [\alpha ]M'_1$
,
$M_1 \neq [\alpha ]M'_1$
,
 $M_1 \neq \mu \gamma .M'_1$
and
$M_1 \neq \mu \gamma .M'_1$
and
 $M_1 \neq \lambda y.M'_1$
. By Lemma 3.4, we have
$M_1 \neq \lambda y.M'_1$
. By Lemma 3.4, we have
 $M_1 \neq (M'_1)M'_2$
. If
$M_1 \neq (M'_1)M'_2$
. If
 $M_1$
is a
$M_1$
is a
 $\lambda$
-variable, then
$\lambda$
-variable, then
 $M_1 = f$
and
$M_1 = f$
and
 $A = X$
. Since
$A = X$
. Since
 and, by the fact that
and, by the fact that
 $M$
is normal,
$M$
is normal,
 $M_2 \neq \mu \gamma .M'_2$
, then, by IH,
$M_2 \neq \mu \gamma .M'_2$
, then, by IH,
 $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
 $M_2 = (f)^nx$
, thus
$M_2 = (f)^nx$
, thus
 $M = (f)^{n+1}x$
.
$M = (f)^{n+1}x$
.
We are now in a position to prove the main result in this section.
Theorem 3.6.
If
![]() $M \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and
$M \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
and ![]() , then
, then
![]() $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
![]() $M = (f)^nx$
.
$M = (f)^nx$
.
Proof.
If
![]() $M = \mu \alpha .M'$
, then
$M = \mu \alpha .M'$
, then
![]() . We prove by examining the form of the
. We prove by examining the form of the
![]() $\lambda \mu$
-term
$\lambda \mu$
-term
![]() $M'$
that
$M'$
that
![]() $M \neq \mu \alpha .M'$
.
$M \neq \mu \alpha .M'$
.
-
Since
 $M$
is normal, and because of the typing rules, we have
$M$
is normal, and because of the typing rules, we have
 $M' \neq x$
,
$M' \neq x$
,
 $M' \neq f$
,
$M' \neq f$
,
 $M' \neq \mu \beta .M''$
and
$M' \neq \mu \beta .M''$
and
 $M' \neq \lambda y.M''$
.
$M' \neq \lambda y.M''$
. -
If
 $M' = [\alpha ]M''$
, then
$M' = [\alpha ]M''$
, then
 $M'' \neq \mu \beta .N$
and
$M'' \neq \mu \beta .N$
and
 . By Lemma 3.5,
. By Lemma 3.5,
 $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
 $M'' = (f)^nx$
and
$M'' = (f)^nx$
and
 $M = \mu \alpha .[\alpha ](f)^nx$
which is a
$M = \mu \alpha .[\alpha ](f)^nx$
which is a
 $\theta$
-redex. Contradiction.
$\theta$
-redex. Contradiction. -
If
 $M' = (M_1')M_2'$
, then we obtain a contradiction by Lemma 3.4.
$M' = (M_1')M_2'$
, then we obtain a contradiction by Lemma 3.4.
We deduce that
![]() $M \neq \mu \alpha .M'$
, and we apply Lemma 3.5.
$M \neq \mu \alpha .M'$
, and we apply Lemma 3.5.
Hence, we obtain the following characterization of
![]() $\lambda \mu$
-terms of type
$\lambda \mu$
-terms of type
![]() $\mathcal{N}$
.
$\mathcal{N}$
.
Corollary 3.7.
Let
![]() $x,f$
be two different
$x,f$
be two different
![]() $\lambda$
-variables. If
$\lambda$
-variables. If
![]() and
and
![]() $((M)x)f \in \mathcal{WN}_{\beta \mu \mu '\rho \theta \varepsilon }$
, then
$((M)x)f \in \mathcal{WN}_{\beta \mu \mu '\rho \theta \varepsilon }$
, then
![]() $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
![]() $((M)x)f \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } (f)^nx$
.
$((M)x)f \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } (f)^nx$
.
Proof.
Let
![]() $N \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
such that
$N \in \mathcal{NF}_{\beta \mu \mu '\rho \theta \varepsilon }$
such that
![]() $((M)x)f \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } N$
. We have
$((M)x)f \twoheadrightarrow _{\beta \mu \mu '\rho \theta \varepsilon } N$
. We have
![]() , then, by Theorem 2.10,
, then, by Theorem 2.10,
![]() , and, by Theorem 3.6,
, and, by Theorem 3.6,
![]() $\exists \, n\in I\!N$
,
$\exists \, n\in I\!N$
,
![]() $N = (f)^nx$
.
$N = (f)^nx$
.
In the light of our subsequent results, the assumption
![]() $((M)x)f \in \mathcal{WN}_{\beta \mu \mu '\rho \theta \varepsilon }$
can in fact be omitted in the above corollary. Namely, we will show in the subsequent sections that
$((M)x)f \in \mathcal{WN}_{\beta \mu \mu '\rho \theta \varepsilon }$
can in fact be omitted in the above corollary. Namely, we will show in the subsequent sections that
![]() $\beta \mu \mu '\rho \theta \varepsilon$
-reduction is weakly normalizing. Hence, if we wish to obtain the corresponding Church numeral, it is enough to apply
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction is weakly normalizing. Hence, if we wish to obtain the corresponding Church numeral, it is enough to apply
![]() $M$
to the numeral
$M$
to the numeral
![]() $\underline{0}$
and to the successor
$\underline{0}$
and to the successor
![]() $\underline{s}$
, thus one arrives at the result
$\underline{s}$
, thus one arrives at the result
![]() $(\underline{s})^n\underline{0}$
, which reduces to
$(\underline{s})^n\underline{0}$
, which reduces to
![]() $\underline{n}$
.
$\underline{n}$
.
The following example presents a
![]() $\lambda \mu$
-term of integer type for which we need all reduction rules to obtain its value.
$\lambda \mu$
-term of integer type for which we need all reduction rules to obtain its value.
Example 3.8.
Let
![]() $M = \lambda x.\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x$
.
$M = \lambda x.\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x$
.
-
Let
 $x: X$
,
$x: X$
,
 $f : X{\rightarrow } X$
,
$f : X{\rightarrow } X$
,
 $g : X{\rightarrow } X$
,
$g : X{\rightarrow } X$
,
 $\alpha :\neg ((X{\rightarrow } X){\rightarrow } X)$
,
$\alpha :\neg ((X{\rightarrow } X){\rightarrow } X)$
,
 $\beta :\neg X$
and
$\beta :\neg X$
and
 $\gamma :\neg \bot$
, then we have the typing relation
$\gamma :\neg \bot$
, then we have the typing relation
 .
. -
In the rest of the paper, in order to make the reductions more readable, at each step we underline the successive redexes. We have
 \begin{align*} ((M)x)f&= (\underline{(\lambda x.\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x)x})f \\ &{{\rightarrow }}_{\beta }\underline{(\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x)f} \\ &{{\rightarrow }}_{\mu } \mu \alpha .[\alpha ](\lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\underline{(\lambda f.(f)x)f})f \\ &{{\rightarrow }}_{\beta } \mu \alpha .[\alpha ] \underline{(\lambda g.(g)\mu \beta .\mu \gamma .[\alpha ](f)x)f}\\ &{{\rightarrow }}_{\beta } \mu \alpha .[\alpha ](f) \underline{\mu \beta .\mu \gamma .[\alpha ](f)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \alpha .[\alpha ]\underline{(f) \mu \beta .[\alpha ](f)x}\\ &{{\rightarrow }}_{\mu '} \mu \alpha .\underline{[\alpha ]\mu \beta .[\alpha ](f)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \alpha .[\alpha ](f)x}\\ &{{\rightarrow }}_{\theta }(f)x. \end{align*}
\begin{align*} ((M)x)f&= (\underline{(\lambda x.\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x)x})f \\ &{{\rightarrow }}_{\beta }\underline{(\mu \alpha .[\alpha ] \lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\lambda f.(f)x)f} \\ &{{\rightarrow }}_{\mu } \mu \alpha .[\alpha ](\lambda g.(g)\mu \beta .\mu \gamma .[\alpha ]\underline{(\lambda f.(f)x)f})f \\ &{{\rightarrow }}_{\beta } \mu \alpha .[\alpha ] \underline{(\lambda g.(g)\mu \beta .\mu \gamma .[\alpha ](f)x)f}\\ &{{\rightarrow }}_{\beta } \mu \alpha .[\alpha ](f) \underline{\mu \beta .\mu \gamma .[\alpha ](f)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \alpha .[\alpha ]\underline{(f) \mu \beta .[\alpha ](f)x}\\ &{{\rightarrow }}_{\mu '} \mu \alpha .\underline{[\alpha ]\mu \beta .[\alpha ](f)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \alpha .[\alpha ](f)x}\\ &{{\rightarrow }}_{\theta }(f)x. \end{align*}
Remark 3.9. We recover the Church numerals directly from
![]() $M$
if we make use of the
$M$
if we make use of the
![]() $\nu$
-rule, which was introduced by Parigot (Reference Parigot1993). The rule can be presented as follows:
$\nu$
-rule, which was introduced by Parigot (Reference Parigot1993). The rule can be presented as follows:
If we consider again Example 3.8, we obtain the following reduction sequence.

We prefer not to use the
![]() $\nu$
-rule, however, since it contains a constraint on the type of a bound variable. If we considered the untyped calculus together with the
$\nu$
-rule, however, since it contains a constraint on the type of a bound variable. If we considered the untyped calculus together with the
![]() $\nu$
-rule, then the calculus would diverge for all
$\nu$
-rule, then the calculus would diverge for all
![]() $\lambda \mu$
-terms containing a
$\lambda \mu$
-terms containing a
![]() $\mu$
. We prefer a calculus where reduction does not depend on the types of terms, hence we omit the
$\mu$
. We prefer a calculus where reduction does not depend on the types of terms, hence we omit the
![]() $\nu$
-rule. In addition, the
$\nu$
-rule. In addition, the
![]() $\nu$
-rule is not strictly necessary for our main goal in this section, which is the demonstration that the introduction of certain rules suffices for finding the value of a term of integer type. We need
$\nu$
-rule is not strictly necessary for our main goal in this section, which is the demonstration that the introduction of certain rules suffices for finding the value of a term of integer type. We need
![]() $\beta \mu \mu '\rho \theta \varepsilon$
- reduction for this purpose, this is the statement of Corollary 3.7.
$\beta \mu \mu '\rho \theta \varepsilon$
- reduction for this purpose, this is the statement of Corollary 3.7.
4. The Parigot-Style
 $\lambda \mu$
-Calculus
$\lambda \mu$
-Calculus
Prior to turning to our main task and detailing the normalization results for
![]() $\beta \mu \mu '\rho \theta \varepsilon$
-reduction, we make a little detour and examine the original version of the
$\beta \mu \mu '\rho \theta \varepsilon$
-reduction, we make a little detour and examine the original version of the
![]() $\lambda \mu$
-calculus due to Parigot (Reference Parigot and Voronkov1992). We will refer to the calculus discussed in this section as the Parigot-style
$\lambda \mu$
-calculus due to Parigot (Reference Parigot and Voronkov1992). We will refer to the calculus discussed in this section as the Parigot-style
![]() $\lambda \mu$
-calculus as opposed to the one appearing in Definition 2.1, which was developed by de de Groote (Reference de Groote1998). The term formation rules of Parigot’s calculus differ from the ones discussed so far in the following manner: in Parigot’s calculus the forms of
$\lambda \mu$
-calculus as opposed to the one appearing in Definition 2.1, which was developed by de de Groote (Reference de Groote1998). The term formation rules of Parigot’s calculus differ from the ones discussed so far in the following manner: in Parigot’s calculus the forms of
![]() $\lambda \mu$
-terms are restricted in such a way that
$\lambda \mu$
-terms are restricted in such a way that
![]() $\mu$
-abstractions and applications with
$\mu$
-abstractions and applications with
![]() $\mu$
-variables are tied together. This is achieved by distinguishing named and unnamed
$\mu$
-variables are tied together. This is achieved by distinguishing named and unnamed
![]() $\lambda \mu$
-terms. Named
$\lambda \mu$
-terms. Named
![]() $\lambda \mu$
-terms are formulated from unnamed terms by an application of a
$\lambda \mu$
-terms are formulated from unnamed terms by an application of a
![]() $\mu$
-variable. Conversely,
$\mu$
-variable. Conversely,
![]() $\mu$
-abstracting over named terms returns unnamed terms. This is formalized in the definition below.
$\mu$
-abstracting over named terms returns unnamed terms. This is formalized in the definition below.
The typing rules are the same as in Definition 2.3, except that the last two rules are replaced with the following single rule:
Concerning the reduction rules, due to the syntax of
![]() $\lambda \mu$
-terms, the
$\lambda \mu$
-terms, the
![]() $\varepsilon$
-rule cannot be defined here, hence it is omitted.
$\varepsilon$
-rule cannot be defined here, hence it is omitted.
To better understand the difference between the Parigot and de Groote-style versions, we present an example that will be discussed in detail in the rest of the paragraph. We can check that the
![]() $\lambda \mu$
-term
$\lambda \mu$
-term
![]() $T=\lambda x.\mu \alpha .x$
is of type
$T=\lambda x.\mu \alpha .x$
is of type
![]() $\bot \to X$
. This term can be formulated in the de Groote syntax only, since, following the
$\bot \to X$
. This term can be formulated in the de Groote syntax only, since, following the
![]() $\mu \alpha$
, there is no
$\mu \alpha$
, there is no
![]() $[\beta ]$
. The
$[\beta ]$
. The
![]() $\lambda \mu$
-term
$\lambda \mu$
-term
![]() $T$
behaves quite interestingly. We can verify that, when we apply
$T$
behaves quite interestingly. We can verify that, when we apply
![]() $T$
to an arbitrarily long finite sequence of
$T$
to an arbitrarily long finite sequence of
![]() $\lambda \mu$
-terms, after some steps of
$\lambda \mu$
-terms, after some steps of
![]() $\mu$
-reduction we obtain
$\mu$
-reduction we obtain
![]() $\mu \alpha .P$
, provided
$\mu \alpha .P$
, provided
![]() $P$
was the first element of the list. Roughly speaking,
$P$
was the first element of the list. Roughly speaking,
![]() $T$
takes the first element of a list and erases the others. The second author has proved with Saber (Nour and Saber Reference Nour and Saber2009) that every
$T$
takes the first element of a list and erases the others. The second author has proved with Saber (Nour and Saber Reference Nour and Saber2009) that every
![]() $\lambda \mu$
-term of type
$\lambda \mu$
-term of type
![]() $\bot \to X$
enjoys the same property. The simplest proof of the formula
$\bot \to X$
enjoys the same property. The simplest proof of the formula
![]() $\bot \to X$
in the Parigot-style calculus turns out to be
$\bot \to X$
in the Parigot-style calculus turns out to be
![]() $T' = \lambda x.\mu \alpha . [\varphi ]x$
. The free variable
$T' = \lambda x.\mu \alpha . [\varphi ]x$
. The free variable
![]() $\varphi$
is of type
$\varphi$
is of type
![]() $\neg \bot$
, and it is quite embarrassing to acknowledge that we need to resort to a free variable of type
$\neg \bot$
, and it is quite embarrassing to acknowledge that we need to resort to a free variable of type
![]() $\neg \bot$
in order to construct a term of type
$\neg \bot$
in order to construct a term of type
![]() $\bot \rightarrow X$
, which is a classical tautology. Anyway, the
$\bot \rightarrow X$
, which is a classical tautology. Anyway, the
![]() $\lambda \mu$
-term
$\lambda \mu$
-term
![]() $T'$
behaves in the same way as
$T'$
behaves in the same way as
![]() $T$
.
$T$
.
In what follows, we prove that Parigot’s
![]() $\lambda \mu$
-calculus with
$\lambda \mu$
-calculus with
![]() $\rho \theta$
-reduction possesses the strong normalization property. First of all, we show that
$\rho \theta$
-reduction possesses the strong normalization property. First of all, we show that
![]() $\rho$
- and
$\rho$
- and
![]() $\theta$
-reduction can be strongly postponed with respect to
$\theta$
-reduction can be strongly postponed with respect to
![]() $\beta$
-,
$\beta$
-,
![]() $\mu$
-, and
$\mu$
-, and
![]() $\mu '$
-reduction.
$\mu '$
-reduction.
Definition 4.1. (Strong postponement)
Let
![]() ${\rightarrow }_1$
and
${\rightarrow }_1$
and
![]() ${\rightarrow }_2$
be two reduction relations. The reduction
${\rightarrow }_2$
be two reduction relations. The reduction
![]() ${\rightarrow }_2$
can be strongly postponed with respect to
${\rightarrow }_2$
can be strongly postponed with respect to
![]() ${\rightarrow }_1$
, if, for every
${\rightarrow }_1$
, if, for every
![]() $M$
,
$M$
,
![]() $N$
,
$N$
,
![]() $P\in \mathcal{T}$
such that
$P\in \mathcal{T}$
such that
![]() $M\twoheadrightarrow _{2}P{\rightarrow }^+_1N$
, we have
$M\twoheadrightarrow _{2}P{\rightarrow }^+_1N$
, we have
![]() $M{\rightarrow }^+_1Q\twoheadrightarrow _2 N$
for some
$M{\rightarrow }^+_1Q\twoheadrightarrow _2 N$
for some
![]() $Q$
.
$Q$
.
Our first aim is to demonstrate the following theorem.
Theorem 4.2.
In the Parigot-style calculus,
![]() $\rho \theta$
-reduction can be strongly postponed with respect to
$\rho \theta$
-reduction can be strongly postponed with respect to
![]() $\mu \mu '\beta$
.
$\mu \mu '\beta$
.
We prove the theorem in two steps. First, we establish that
![]() $\theta$
-reduction can be strongly postponed with respect to all the other rules, namely,
$\theta$
-reduction can be strongly postponed with respect to all the other rules, namely,
![]() $\beta, \mu, \mu ', \rho$
. We then show that the
$\beta, \mu, \mu ', \rho$
. We then show that the
![]() $\rho$
-rule can be strongly postponed with respect to
$\rho$
-rule can be strongly postponed with respect to
![]() $\mu$
,
$\mu$
,
![]() $\mu '$
, and
$\mu '$
, and
![]() $\beta$
.
$\beta$
.
First of all, we define two reductions that are special cases of
![]() $\mu$
- and
$\mu$
- and
![]() $\mu '$
-reductions. These new rules appear in the permutation lemmas that we are going to prove and are easy to handle.
$\mu '$
-reductions. These new rules appear in the permutation lemmas that we are going to prove and are easy to handle.
Definition 4.3. (
![]() $\mu _0$
and
$\mu _0$
and
![]() $\mu '_0$
-reduction)
$\mu '_0$
-reduction)
A
![]() $\mu _0$
-redex (resp.
$\mu _0$
-redex (resp.
![]() $\mu '_0$
-redex) is a
$\mu '_0$
-redex) is a
![]() $\lambda \mu$
-term of the form
$\lambda \mu$
-term of the form
![]() $(\mu \alpha . M) N$
(resp.
$(\mu \alpha . M) N$
(resp.
![]() $(N)\mu \alpha . M$
) where
$(N)\mu \alpha . M$
) where
![]() $\alpha$
occurs at most once in
$\alpha$
occurs at most once in
![]() $M$
, and we call
$M$
, and we call
![]() $\mu \alpha .M[\alpha :=_r N]$
(resp.
$\mu \alpha .M[\alpha :=_r N]$
(resp.
![]() $\mu \alpha .M[\alpha :=_l N]$
) its contractum. We write
$\mu \alpha .M[\alpha :=_l N]$
) its contractum. We write
![]() $M{\rightarrow }_{\mu _0} M'$
(resp.
$M{\rightarrow }_{\mu _0} M'$
(resp.
![]() $M{\rightarrow }_{\mu _0'} M'$
), if
$M{\rightarrow }_{\mu _0'} M'$
), if
![]() $M'$
is obtained from
$M'$
is obtained from
![]() $M$
by replacing a
$M$
by replacing a
![]() $\mu _0$
-redex (resp.
$\mu _0$
-redex (resp.
![]() $\mu _0'$
-redex) in
$\mu _0'$
-redex) in
![]() $M$
by its contractum. As usual, we define the reductions
$M$
by its contractum. As usual, we define the reductions
![]() $\twoheadrightarrow _{\mu _0}$
,
$\twoheadrightarrow _{\mu _0}$
,
![]() $\twoheadrightarrow _{\mu _0'}$
,
$\twoheadrightarrow _{\mu _0'}$
,
![]() ${\rightarrow }^n_{\mu _0}$
,
${\rightarrow }^n_{\mu _0}$
,
![]() ${\rightarrow }^n_{\mu _0'}$
,
${\rightarrow }^n_{\mu _0'}$
,
![]() ${\rightarrow }^+_{\mu _0}$
and
${\rightarrow }^+_{\mu _0}$
and
![]() ${\rightarrow }^+_{\mu _0'}$
.
${\rightarrow }^+_{\mu _0'}$
.
4.1 The case of
 $\theta$
-reduction
$\theta$
-reduction
We show that, in the Parigot-style
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\theta$
-reduction can be strongly postponed with respect to
$\theta$
-reduction can be strongly postponed with respect to
![]() $\beta \mu \mu '\rho$
-reduction. We prove for
$\beta \mu \mu '\rho$
-reduction. We prove for
![]() $\beta$
-,
$\beta$
-,
![]() $\mu$
-,
$\mu$
-,
![]() $\mu '$
-, and
$\mu '$
-, and
![]() $\rho$
-reductions, one by one, that the execution of a
$\rho$
-reductions, one by one, that the execution of a
![]() $\theta$
-reduction followed by either of the mentioned reductions can be replaced by a reduction sequence where the respective reductions precede
$\theta$
-reduction followed by either of the mentioned reductions can be replaced by a reduction sequence where the respective reductions precede
![]() $\theta$
-reduction (Lemmas 4.4, 4.5, 4.6, 4.7). Additionally, new
$\theta$
-reduction (Lemmas 4.4, 4.5, 4.6, 4.7). Additionally, new
![]() $\mu _0$
- or
$\mu _0$
- or
![]() $\mu _0'$
-redexes may be created, but these redexes can be executed before the
$\mu _0'$
-redexes may be created, but these redexes can be executed before the
![]() $\theta$
-redex. We can generalize the results on swapping
$\theta$
-redex. We can generalize the results on swapping
![]() $\theta$
-reduction with
$\theta$
-reduction with
![]() $\beta \mu \mu '\rho$
-reductions to reduction sequences by reasoning by induction on the length of the reduction sequences. This is stated in Theorem 4.9.
$\beta \mu \mu '\rho$
-reductions to reduction sequences by reasoning by induction on the length of the reduction sequences. This is stated in Theorem 4.9.
The following lemma shows how
![]() $\theta$
-reduction relates to the
$\theta$
-reduction relates to the
![]() $\beta$
-rule. In the next lemma, we observe the usefulness of the new
$\beta$
-rule. In the next lemma, we observe the usefulness of the new
![]() $\mu _0$
-reduction rule.
$\mu _0$
-reduction rule.
Lemma 4.4.
Let
![]() $M{\rightarrow }_{\theta }P{\rightarrow }_{\beta }N$
. Then either we have a
$M{\rightarrow }_{\theta }P{\rightarrow }_{\beta }N$
. Then either we have a
![]() $Q$
such that
$Q$
such that
![]() $M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\theta }N$
, or there are
$M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\theta }N$
, or there are
![]() $R$
,
$R$
,
![]() $Q$
for which
$Q$
for which
![]() $M{\rightarrow }_{\mu _0}R{\rightarrow }_{\beta }Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\mu _0}R{\rightarrow }_{\beta }Q{\rightarrow }_{\theta }N$
.
Proof.
By induction on
![]() $M$
.
$M$
.
-
The cases
 $M=[\alpha ]M_1$
,
$M=[\alpha ]M_1$
,
 $M=\mu \alpha . M_1$
and
$M=\mu \alpha . M_1$
and
 $M=\lambda x.M_1$
are straightforward.
$M=\lambda x.M_1$
are straightforward. -
Assume
 $M=(M_1)M_2$
.
$M=(M_1)M_2$
.
-
– If
 $M_1{\rightarrow }_{\theta }M_1'$
, the only nontrivial case is
$M_1{\rightarrow }_{\theta }M_1'$
, the only nontrivial case is
 $M_1'=\lambda x.M_3$
and
$M_1'=\lambda x.M_3$
and
 $M_1=\mu \alpha . [\alpha ]M_1'$
with
$M_1=\mu \alpha . [\alpha ]M_1'$
with
 $\alpha \not \in \textrm{fv}(M'_1)$
. Now we obtain
$\alpha \not \in \textrm{fv}(M'_1)$
. Now we obtain
 $M = (\mu \alpha . [\alpha ]\lambda x.M_3)M_2{\rightarrow }_{\mu _0} \mu \alpha . [\alpha ](\lambda x.M_3)M_2$
$M = (\mu \alpha . [\alpha ]\lambda x.M_3)M_2{\rightarrow }_{\mu _0} \mu \alpha . [\alpha ](\lambda x.M_3)M_2$
 ${\rightarrow }_{\beta } \mu \alpha . [\alpha ]M_3[x :=M_2]{\rightarrow }_{\theta } M_3[x :=M_2]$
.
${\rightarrow }_{\beta } \mu \alpha . [\alpha ]M_3[x :=M_2]{\rightarrow }_{\theta } M_3[x :=M_2]$
. -
– If
 $M_2{\rightarrow }_{\theta }M_2'$
, the only interesting case is
$M_2{\rightarrow }_{\theta }M_2'$
, the only interesting case is
 $M_1=\lambda x.M_3$
,
$M_1=\lambda x.M_3$
,
 $N=M_3[x:=M_2']$
. Then, with
$N=M_3[x:=M_2']$
. Then, with
 $Q=M_3[x:=M_2]$
, we have
$Q=M_3[x:=M_2]$
, we have
 $M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\theta }N$
.
$M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\theta }N$
.
-
The next lemma shows how
![]() $\theta$
-reduction commutes with
$\theta$
-reduction commutes with
![]() $\mu$
-reduction. We notice the appearance of
$\mu$
-reduction. We notice the appearance of
![]() $\mu _0$
-reduction.
$\mu _0$
-reduction.
Lemma 4.5.
-
1. Let
 $M{\rightarrow }_{\theta }P{\rightarrow }_{\mu }N$
. Then either we have a
$M{\rightarrow }_{\theta }P{\rightarrow }_{\mu }N$
. Then either we have a
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\theta }N$
or there are
$M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\theta }N$
or there are
 $R$
,
$R$
,
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu }Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu }Q{\rightarrow }_{\theta }N$
. -
2. Let
 $M{\rightarrow }_{\theta }P{\rightarrow }_{\mu _0}N$
. Then either
$M{\rightarrow }_{\theta }P{\rightarrow }_{\mu _0}N$
. Then either
 $M{\rightarrow }_{\mu _0}Q{\rightarrow }_{\theta }N$
for some
$M{\rightarrow }_{\mu _0}Q{\rightarrow }_{\theta }N$
for some
 $Q$
or there are
$Q$
or there are
 $R$
,
$R$
,
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu _0}Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu _0}Q{\rightarrow }_{\theta }N$
. -
3. Let
 $M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu _0}N$
. Then there is a
$M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu _0}N$
. Then there is a
 $Q$
such that
$Q$
such that
 $M\twoheadrightarrow _{\mu _0}Q{\rightarrow }_{\theta }^nN$
.
$M\twoheadrightarrow _{\mu _0}Q{\rightarrow }_{\theta }^nN$
.
Proof.
-
1. By induction on
 $M$
.
$M$
.
-
The cases
 $M=[\alpha ]M_1$
and
$M=[\alpha ]M_1$
and
 $M=\lambda x.M_1$
are straightforward. Regarding when
$M=\lambda x.M_1$
are straightforward. Regarding when
 $M=\mu \alpha .M_1$
, if
$M=\mu \alpha .M_1$
, if
 $M_1{\rightarrow }_{\theta } M_1'$
, then the IH applies. Otherwise,
$M_1{\rightarrow }_{\theta } M_1'$
, then the IH applies. Otherwise,
 $M_1=[\alpha ] M_2$
and
$M_1=[\alpha ] M_2$
and
 $M{\rightarrow }_{\theta } M_2 =P{\rightarrow }_{\beta } N$
. Then
$M{\rightarrow }_{\theta } M_2 =P{\rightarrow }_{\beta } N$
. Then
 $M{\rightarrow }_{\beta } \mu \alpha . [\alpha ]N{\rightarrow }_{\theta } N$
.
$M{\rightarrow }_{\beta } \mu \alpha . [\alpha ]N{\rightarrow }_{\theta } N$
. -
Assume
 $M=(M_1)M_2$
.
$M=(M_1)M_2$
.
-
– If
 $M_1=\mu \alpha [\alpha ]M_1'{\rightarrow }_{\theta }M_1'$
, the only interesting case is
$M_1=\mu \alpha [\alpha ]M_1'{\rightarrow }_{\theta }M_1'$
, the only interesting case is
 $M_1'=\mu \beta . M_3$
. Since
$M_1'=\mu \beta . M_3$
. Since
 $\alpha \notin M_1'$
, we have
$\alpha \notin M_1'$
, we have
 $M = (\mu \alpha . [\alpha ]\mu \beta . M_3)\;M_2{\rightarrow }_{\mu _0} \mu \alpha . [\alpha ] (\mu \beta . M_3)M_2$
$M = (\mu \alpha . [\alpha ]\mu \beta . M_3)\;M_2{\rightarrow }_{\mu _0} \mu \alpha . [\alpha ] (\mu \beta . M_3)M_2$
 ${\rightarrow }_{\mu } \mu \alpha . [\alpha ]\mu \beta . M_3[\beta :=_rM_2]\;{\rightarrow }_{\theta } \; \mu \beta . M_3[\beta :=_rM_2]$
.
${\rightarrow }_{\mu } \mu \alpha . [\alpha ]\mu \beta . M_3[\beta :=_rM_2]\;{\rightarrow }_{\theta } \; \mu \beta . M_3[\beta :=_rM_2]$
. -
– If
 $M_2=\mu \alpha [\alpha ]M_2'{\rightarrow }_{\theta }M_2'$
, the only interesting case is
$M_2=\mu \alpha [\alpha ]M_2'{\rightarrow }_{\theta }M_2'$
, the only interesting case is
 $M_1=\mu \beta . M_3$
,
$M_1=\mu \beta . M_3$
,
 $N=\mu \beta . M_3[\beta :=_rM_2']$
, where, with
$N=\mu \beta . M_3[\beta :=_rM_2']$
, where, with
 $Q=\mu \beta . M_3[\beta :=_rM_2]$
, we obtain
$Q=\mu \beta . M_3[\beta :=_rM_2]$
, we obtain
 $M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\theta }N$
.
$M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\theta }N$
.
-
-
-
3. The proof follows the pattern of point 1 of this lemma with the necessary changes implemented.
-
4. Applying case 2 of this lemma and proceeding by induction on
 $n$
.
$n$
.
The following lemma illustrates how
![]() $\theta$
-reduction commutes with
$\theta$
-reduction commutes with
![]() $\mu '$
- and
$\mu '$
- and
![]() $\mu '_0$
-reduction.
$\mu '_0$
-reduction.
Lemma 4.6.
-
1. Let
 $M{\rightarrow }_{\theta }P{\rightarrow }_{\mu '}N$
. Then either
$M{\rightarrow }_{\theta }P{\rightarrow }_{\mu '}N$
. Then either
 $M{\rightarrow }_{\mu '}Q\twoheadrightarrow _{\theta }N$
for some
$M{\rightarrow }_{\mu '}Q\twoheadrightarrow _{\theta }N$
for some
 $Q$
or there are
$Q$
or there are
 $R$
,
$R$
,
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\mu _0'}R{\rightarrow }_{\mu '}Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\mu _0'}R{\rightarrow }_{\mu '}Q{\rightarrow }_{\theta }N$
. -
2. Let
 $M{\rightarrow }_{\theta }P{\rightarrow }_{\mu _0'}N$
. Then either we have
$M{\rightarrow }_{\theta }P{\rightarrow }_{\mu _0'}N$
. Then either we have
 $M{\rightarrow }_{\mu _0'}Q{\rightarrow }_{\theta }N$
for some
$M{\rightarrow }_{\mu _0'}Q{\rightarrow }_{\theta }N$
for some
 $Q$
or there are
$Q$
or there are
 $R$
,
$R$
,
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\mu _0'}R{\rightarrow }_{\mu _0'}Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\mu _0'}R{\rightarrow }_{\mu _0'}Q{\rightarrow }_{\theta }N$
. -
3. Let
 $M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu '_0}N$
. Then there is a
$M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu '_0}N$
. Then there is a
 $Q$
such that
$Q$
such that
 $M\twoheadrightarrow _{\mu '_0}Q{\rightarrow }_{\theta }^nN$
.
$M\twoheadrightarrow _{\mu '_0}Q{\rightarrow }_{\theta }^nN$
.
Proof. Similar to Lemma 4.5.
The lemma below demonstrates that
![]() $\theta$
-reduction can be strongly postponed with respect to
$\theta$
-reduction can be strongly postponed with respect to
![]() $\rho$
-reduction.
$\rho$
-reduction.
Lemma 4.7.
Let
![]() $M{\rightarrow }_{\theta }P{\rightarrow }_{\rho }N$
. Then we have a
$M{\rightarrow }_{\theta }P{\rightarrow }_{\rho }N$
. Then we have a
![]() $Q$
such that
$Q$
such that
![]() $M{\rightarrow }_{\rho }Q{\rightarrow }_{\theta }N$
.
$M{\rightarrow }_{\rho }Q{\rightarrow }_{\theta }N$
.
Proof.
An obvious induction on
![]() $M$
.
$M$
.
We are now in a position to prove the next theorem, which describes how
![]() $\theta$
-reduction commutes with all the other rules.
$\theta$
-reduction commutes with all the other rules.
Theorem 4.8.
Let
![]() $M\twoheadrightarrow _{\theta }P{\rightarrow }_{\beta \mu \mu ' \rho }N$
. Then there exists
$M\twoheadrightarrow _{\theta }P{\rightarrow }_{\beta \mu \mu ' \rho }N$
. Then there exists
![]() $Q$
such that
$Q$
such that
![]() $M{\rightarrow }_{\beta \mu \mu ' \rho }^+Q\twoheadrightarrow _{\theta }N$
.
$M{\rightarrow }_{\beta \mu \mu ' \rho }^+Q\twoheadrightarrow _{\theta }N$
.
Proof.
Let
![]() $M{\rightarrow }^n_{\theta }P{\rightarrow }_{\beta \mu \mu ' \rho }N$
. The proof proceeds by induction on
$M{\rightarrow }^n_{\theta }P{\rightarrow }_{\beta \mu \mu ' \rho }N$
. The proof proceeds by induction on
![]() $n$
and by applying the previous lemmas. Let us suppose first that
$n$
and by applying the previous lemmas. Let us suppose first that
![]() $M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu }N$
.
$M{\rightarrow }_{\theta }^nP{\rightarrow }_{\mu }N$
.
-
 $n=0$
: the result is immediate.
$n=0$
: the result is immediate. -
 $n=m+1\gt 0$
: let
$n=m+1\gt 0$
: let
 $M{\rightarrow }_{\theta }^{m}K{\rightarrow }_{\theta }P$
for some
$M{\rightarrow }_{\theta }^{m}K{\rightarrow }_{\theta }P$
for some
 $K$
. By Lemma 4.5, either
$K$
. By Lemma 4.5, either
 $K{\rightarrow }_{\mu }R\twoheadrightarrow _{\theta }N$
or
$K{\rightarrow }_{\mu }R\twoheadrightarrow _{\theta }N$
or
 $K{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu }L{\rightarrow }_{\theta }N$
. In the former case, the IH applies to
$K{\rightarrow }_{\mu _0}R{\rightarrow }_{\mu }L{\rightarrow }_{\theta }N$
. In the former case, the IH applies to
 $M{\rightarrow }_{\theta }^{m}K{\rightarrow }_{\mu }R$
. In the latter case, by Lemma 4.5, there exists an
$M{\rightarrow }_{\theta }^{m}K{\rightarrow }_{\mu }R$
. In the latter case, by Lemma 4.5, there exists an
 $S$
such that
$S$
such that
 $M\twoheadrightarrow _{\mu _0}S{\rightarrow }_{\theta }^{m}R$
, and we can apply the IH to
$M\twoheadrightarrow _{\mu _0}S{\rightarrow }_{\theta }^{m}R$
, and we can apply the IH to
 $S{\rightarrow }_{\theta }^{m}R{\rightarrow }_{\mu }L$
.
$S{\rightarrow }_{\theta }^{m}R{\rightarrow }_{\mu }L$
.
The cases
![]() $P{\rightarrow }_{\mu '}N$
and
$P{\rightarrow }_{\mu '}N$
and
![]() $P{\rightarrow }_{\beta }N$
are analogous. Finally, the case
$P{\rightarrow }_{\beta }N$
are analogous. Finally, the case
![]() $P{\rightarrow }_{\rho }N$
is straightforward by Lemma 4.7.
$P{\rightarrow }_{\rho }N$
is straightforward by Lemma 4.7.
We have obtained the strong postponement of
![]() ${\rightarrow }_\theta$
with respect to
${\rightarrow }_\theta$
with respect to
![]() ${\rightarrow }_{\beta \mu \mu ' \rho }$
. This is stated in the next theorem.
${\rightarrow }_{\beta \mu \mu ' \rho }$
. This is stated in the next theorem.
Theorem 4.9.
Let
![]() $M\twoheadrightarrow _{\theta }P{\rightarrow }^+_{\beta \mu \mu ' \rho }N$
. Then there exists a
$M\twoheadrightarrow _{\theta }P{\rightarrow }^+_{\beta \mu \mu ' \rho }N$
. Then there exists a
![]() $Q$
for which
$Q$
for which
![]() $M{\rightarrow }_{\beta \mu \mu ' \rho }^+Q\twoheadrightarrow _{\theta }N$
.
$M{\rightarrow }_{\beta \mu \mu ' \rho }^+Q\twoheadrightarrow _{\theta }N$
.
Proof.
By induction on the reduction sequence
![]() $P{\rightarrow }^+_{\beta \mu \mu ' \rho }N$
using Theorem 4.8.
$P{\rightarrow }^+_{\beta \mu \mu ' \rho }N$
using Theorem 4.8.
Remark 4.10. We notice that the above proofs, hence Theorem 4.9, are also valid in the de Groote-style calculus. By contrast, the
![]() $\rho$
-rule exhibits a different behavior in de Groote’s calculus. In what follows, we show that
$\rho$
-rule exhibits a different behavior in de Groote’s calculus. In what follows, we show that
![]() $\rho$
-reduction can be strongly postponed with respect to
$\rho$
-reduction can be strongly postponed with respect to
![]() $\beta \mu \mu '$
-reduction in the simply typed Parigot calculus, and we demonstrate by giving counterexamples that this is not valid in the de Groote-style syntax.
$\beta \mu \mu '$
-reduction in the simply typed Parigot calculus, and we demonstrate by giving counterexamples that this is not valid in the de Groote-style syntax.
4.2 The case of
 $\rho$
-reduction
$\rho$
-reduction
Now we show that, in the simply typed Parigot-style
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\rho$
-reduction can be strongly postponed with respect to
$\rho$
-reduction can be strongly postponed with respect to
![]() $\beta \mu \mu '$
-reduction. The proofs of this subsection can also be found in Py (Reference Py1998). The presentation there, however, may differ in some places from ours. For the sake of completeness, we outline the proofs below. We prove that
$\beta \mu \mu '$
-reduction. The proofs of this subsection can also be found in Py (Reference Py1998). The presentation there, however, may differ in some places from ours. For the sake of completeness, we outline the proofs below. We prove that
![]() $\rho$
-reduction commutes with
$\rho$
-reduction commutes with
![]() $\beta$
-,
$\beta$
-,
![]() $\mu$
- and
$\mu$
- and
![]() $\mu '$
-reduction. This results in a reduction sequence starting with
$\mu '$
-reduction. This results in a reduction sequence starting with
![]() $\beta$
-reduction (or with a
$\beta$
-reduction (or with a
![]() $\mu$
- or
$\mu$
- or
![]() $\mu '$
-reduction, respectively) and ending in
$\mu '$
-reduction, respectively) and ending in
![]() $\rho$
-reduction (Lemmas 4.12 and 4.14). The subsection culminates in Theorem 4.16, which can be obtained from the above-mentioned results by induction on the length of the reduction sequences.
$\rho$
-reduction (Lemmas 4.12 and 4.14). The subsection culminates in Theorem 4.16, which can be obtained from the above-mentioned results by induction on the length of the reduction sequences.
The following lemma will be used in the proof of Lemma 4.12.
Lemma 4.11.
Let
![]() $M{\rightarrow }_{\rho }M'$
, then
$M{\rightarrow }_{\rho }M'$
, then
![]() $M[x :=N]{\rightarrow }_{\rho }M'[x:=N]$
.
$M[x :=N]{\rightarrow }_{\rho }M'[x:=N]$
.
Proof.
By induction on
![]() $M$
.
$M$
.
The next lemma proves postponement of
![]() $\rho$
-reduction with respect to
$\rho$
-reduction with respect to
![]() $\beta$
-reduction.
$\beta$
-reduction.
Lemma 4.12.
-
1. Let
 $M{\rightarrow }_{\rho }P{\rightarrow }_{\beta }N$
. Then there exists
$M{\rightarrow }_{\rho }P{\rightarrow }_{\beta }N$
. Then there exists
 $Q$
such that
$Q$
such that
 $M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\rho }N$
.
$M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\rho }N$
. -
2. Let
 $M\twoheadrightarrow _{\rho }P{\rightarrow }_{\beta }N$
. Then there exists
$M\twoheadrightarrow _{\rho }P{\rightarrow }_{\beta }N$
. Then there exists
 $Q$
for which
$Q$
for which
 $M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\rho }N$
.
$M{\rightarrow }_{\beta }Q\twoheadrightarrow _{\rho }N$
.
Proof.
-
1. By induction on
 $M$
.
$M$
.
-
The cases
 $M=\mu \alpha . M_1$
and
$M=\mu \alpha . M_1$
and
 $M=\lambda x.M_1$
are straightforward.
$M=\lambda x.M_1$
are straightforward. -
Assume
 $M=[\alpha ] M_1$
. If
$M=[\alpha ] M_1$
. If
 $M'=[\alpha ] M_1'$
and
$M'=[\alpha ] M_1'$
and
 $M_1{\rightarrow }_{ \rho } M_1'$
, the IH applies. Otherwise
$M_1{\rightarrow }_{ \rho } M_1'$
, the IH applies. Otherwise
 $M=[\alpha ] M_1=[\alpha ] \mu \beta M_2{\rightarrow }_{\rho }M_2[\beta :=\alpha ]=P{\rightarrow }_{\beta }N$
, which is also straightforward.
$M=[\alpha ] M_1=[\alpha ] \mu \beta M_2{\rightarrow }_{\rho }M_2[\beta :=\alpha ]=P{\rightarrow }_{\beta }N$
, which is also straightforward. -
Assume
 $M=(M_1)M_2$
.
$M=(M_1)M_2$
.
-
– If
 $M_1{\rightarrow }_{\rho }M_1'$
, we argue by induction on
$M_1{\rightarrow }_{\rho }M_1'$
, we argue by induction on
 $M_1$
.
$M_1$
.
-
 $\ast$
$\ast$
 $M_1'{\rightarrow }_\beta M_1''$
: we apply IH.
$M_1'{\rightarrow }_\beta M_1''$
: we apply IH. -
 $\ast$
$\ast$
 $M_2{\rightarrow }_\beta M_2'$
: straightforward.
$M_2{\rightarrow }_\beta M_2'$
: straightforward. -
 $\ast$
$\ast$
 $M_1=\lambda x.M_3$
:
$M_1=\lambda x.M_3$
:
 $M_1'=\lambda x.M_3'$
for some
$M_1'=\lambda x.M_3'$
for some
 $M_3{\rightarrow }_\rho M_3'$
and
$M_3{\rightarrow }_\rho M_3'$
and
 $N=M_3'[x:=M_2]$
. Then, by Lemma 4.11, we obtain
$N=M_3'[x:=M_2]$
. Then, by Lemma 4.11, we obtain
 $M{\rightarrow }_\beta M_3[x:=M_2]{\rightarrow }_\rho M_3'[x:=M_2]=N$
.
$M{\rightarrow }_\beta M_3[x:=M_2]{\rightarrow }_\rho M_3'[x:=M_2]=N$
. -
 $\ast$
$\ast$
 $M_1=[\alpha ]M_3$
: impossible by the term formation rules.
$M_1=[\alpha ]M_3$
: impossible by the term formation rules. -
 $\ast$
$\ast$
 $M_1=\mu \alpha .M_3$
or
$M_1=\mu \alpha .M_3$
or
 $M_1=(M_3)M_4$
: we apply IH.
$M_1=(M_3)M_4$
: we apply IH.
-
-
– Assume
 $M_2{\rightarrow }_{\rho }M_2'$
.
$M_2{\rightarrow }_{\rho }M_2'$
.
-
 $\ast$
If
$\ast$
If
 $M_1{\rightarrow }_\beta M_1'$
or
$M_1{\rightarrow }_\beta M_1'$
or
 $M_2'{\rightarrow }_\beta M_2''$
, we conclude by applying IH.
$M_2'{\rightarrow }_\beta M_2''$
, we conclude by applying IH. -
 $\ast$
$\ast$
 $M_2=\lambda x.M_3$
or
$M_2=\lambda x.M_3$
or
 $M_2=\mu \alpha .M_3$
: IH applies.
$M_2=\mu \alpha .M_3$
: IH applies. -
 $\ast$
$\ast$
 $M_2=[\alpha ]M_3$
: impossible by the term formation rules.
$M_2=[\alpha ]M_3$
: impossible by the term formation rules.
-
-
2. By the previous point of this lemma.
-
The following lemma is useful for proving Lemma 4.14.
Lemma 4.13.
Let
![]() $M{\rightarrow }_{\rho }M'$
and assume
$M{\rightarrow }_{\rho }M'$
and assume
![]() $\alpha \notin \textrm{fv}(N)$
. Then either
$\alpha \notin \textrm{fv}(N)$
. Then either
![]() $M[\alpha :=_rN]{\rightarrow }_{\rho }M'[\alpha :=_rN]$
(resp.
$M[\alpha :=_rN]{\rightarrow }_{\rho }M'[\alpha :=_rN]$
(resp.
![]() $M[\alpha :=_lN]{\rightarrow }_{\rho }M'[\alpha :=_lN]$
) or
$M[\alpha :=_lN]{\rightarrow }_{\rho }M'[\alpha :=_lN]$
) or
![]() $M[\alpha :=_rN]{\rightarrow }_{\mu }P{\rightarrow }_{\rho }M'[\alpha :=_rN]$
(resp.
$M[\alpha :=_rN]{\rightarrow }_{\mu }P{\rightarrow }_{\rho }M'[\alpha :=_rN]$
(resp.
![]() $M[\alpha :=_lN]{\rightarrow }_{\mu '}P{\rightarrow }_{\rho }M'[\alpha :=_lN]$
) for some
$M[\alpha :=_lN]{\rightarrow }_{\mu '}P{\rightarrow }_{\rho }M'[\alpha :=_lN]$
) for some
![]() $P$
.
$P$
.
Proof.
By induction on
![]() $M$
. The only interesting case is
$M$
. The only interesting case is
![]() $M=[\gamma ]\mu \beta . M_1$
.
$M=[\gamma ]\mu \beta . M_1$
.
-
If
 $\gamma \neq \alpha$
, then
$\gamma \neq \alpha$
, then
 $M[\alpha :=_rN]=[\gamma ]\mu \beta . M_1[\alpha :=_rN]{\rightarrow }_{\rho }M_1[\beta :=\gamma ][\alpha :=_rN]$
.
$M[\alpha :=_rN]=[\gamma ]\mu \beta . M_1[\alpha :=_rN]{\rightarrow }_{\rho }M_1[\beta :=\gamma ][\alpha :=_rN]$
. -
If
 $\gamma =\alpha$
, then
$\gamma =\alpha$
, then
 $M[\alpha :=_rN] = [\alpha ](\mu \beta . M_1[\alpha :=_rN])N$
$M[\alpha :=_rN] = [\alpha ](\mu \beta . M_1[\alpha :=_rN])N$
 ${\rightarrow }_{\mu } [\alpha ]\mu \beta . M_1[\alpha :=_rN][\beta :=_rN]{\rightarrow }_{\rho } M_1[\alpha :=_rN][\beta :=_rN][\beta :=\alpha ]$
${\rightarrow }_{\mu } [\alpha ]\mu \beta . M_1[\alpha :=_rN][\beta :=_rN]{\rightarrow }_{\rho } M_1[\alpha :=_rN][\beta :=_rN][\beta :=\alpha ]$
 $= M_1[\beta :=\alpha ][\alpha :=_rN]$
.
$= M_1[\beta :=\alpha ][\alpha :=_rN]$
.
The following lemma proves postponement of
![]() $\rho$
-reduction with respect to
$\rho$
-reduction with respect to
![]() $\mu$
- and
$\mu$
- and
![]() $\mu '$
-reductions.
$\mu '$
-reductions.
Lemma 4.14.
-
1. Let
 $M{\rightarrow }_{\rho }P{\rightarrow }_{\mu }N$
. Then there exists
$M{\rightarrow }_{\rho }P{\rightarrow }_{\mu }N$
. Then there exists
 $Q$
for which
$Q$
for which
 $M{\rightarrow }^+_{\mu }Q\twoheadrightarrow _{\rho }N$
.
$M{\rightarrow }^+_{\mu }Q\twoheadrightarrow _{\rho }N$
. -
2. Let
 $M{\rightarrow }_{\rho }P{\rightarrow }_{\mu '}N$
. Then there exists
$M{\rightarrow }_{\rho }P{\rightarrow }_{\mu '}N$
. Then there exists
 $Q$
for which
$Q$
for which
 $M{\rightarrow }^+_{\mu '}Q\twoheadrightarrow _{\rho }N$
.
$M{\rightarrow }^+_{\mu '}Q\twoheadrightarrow _{\rho }N$
. -
3. Let
 $M\twoheadrightarrow _{\rho }P{\rightarrow }_{\mu }N$
(resp.
$M\twoheadrightarrow _{\rho }P{\rightarrow }_{\mu }N$
(resp.
 $M\twoheadrightarrow _{\rho }P{\rightarrow }_{\mu '}N$
). Then there exists
$M\twoheadrightarrow _{\rho }P{\rightarrow }_{\mu '}N$
). Then there exists
 $Q$
such that
$Q$
such that
 $M{\rightarrow }^+_{\mu }Q\twoheadrightarrow _{\rho }N$
(resp.
$M{\rightarrow }^+_{\mu }Q\twoheadrightarrow _{\rho }N$
(resp.
 $M{\rightarrow }^+_{\mu '}Q\twoheadrightarrow _{\rho }N$
).
$M{\rightarrow }^+_{\mu '}Q\twoheadrightarrow _{\rho }N$
).
Proof. We only detail some of the more interesting cases of the first point.
-
1. By induction on
 $M$
.
$M$
.
-
The cases
 $M=\mu \alpha . M_1$
and
$M=\mu \alpha . M_1$
and
 $M=\lambda x.M_1$
are straightforward.
$M=\lambda x.M_1$
are straightforward. -
Assume
 $M=[\alpha ]M_1$
: if
$M=[\alpha ]M_1$
: if
 $M_1{\rightarrow }_\rho M_1'$
, we obtain the result by IH. Otherwise,
$M_1{\rightarrow }_\rho M_1'$
, we obtain the result by IH. Otherwise,
 $M=[\alpha ]\mu \beta .M_2{\rightarrow }_\rho M_2[\beta :=\alpha ]{\rightarrow }^R_\mu N$
. Then
$M=[\alpha ]\mu \beta .M_2{\rightarrow }_\rho M_2[\beta :=\alpha ]{\rightarrow }^R_\mu N$
. Then
 $M{\rightarrow }^{R'}_\mu [\alpha ]\mu \beta .M_3{\rightarrow }_\rho M_3[\beta :=\alpha ]=N$
for some
$M{\rightarrow }^{R'}_\mu [\alpha ]\mu \beta .M_3{\rightarrow }_\rho M_3[\beta :=\alpha ]=N$
for some
 $M_3$
, where
$M_3$
, where
 $R=R'[\beta :=\alpha ]$
.
$R=R'[\beta :=\alpha ]$
. -
Assume
 $M=(M_1)M_2$
.
$M=(M_1)M_2$
.
-
– If
 $M_1{\rightarrow }_{\rho }M_1'$
, we distinguish the following cases.
$M_1{\rightarrow }_{\rho }M_1'$
, we distinguish the following cases.
-
 $\ast$
$\ast$
 $M_1'{\rightarrow }_{\mu }M_1''$
: we apply IH.
$M_1'{\rightarrow }_{\mu }M_1''$
: we apply IH. -
 $\ast$
$\ast$
 $M_2{\rightarrow }_{\mu }M_2'$
: by IH.
$M_2{\rightarrow }_{\mu }M_2'$
: by IH. -
 $\ast$
$\ast$
 $M_1=\mu \gamma .M_3$
and
$M_1=\mu \gamma .M_3$
and
 $M_3{\rightarrow }_{\rho }M_3'$
and
$M_3{\rightarrow }_{\rho }M_3'$
and
 $N=\mu \gamma .M_3'[\gamma :=_r M_2]$
. Then, by Lemma 4.13, we have
$N=\mu \gamma .M_3'[\gamma :=_r M_2]$
. Then, by Lemma 4.13, we have
 $M=(\mu \gamma . M_3)M_2{\rightarrow }_{\mu } \mu \gamma . M_3[\gamma :=_rM_2] \twoheadrightarrow _{\mu } Q\;{\rightarrow }_{\rho } \; \mu \gamma . M_3'[\gamma :=_rM_2]$
for some
$M=(\mu \gamma . M_3)M_2{\rightarrow }_{\mu } \mu \gamma . M_3[\gamma :=_rM_2] \twoheadrightarrow _{\mu } Q\;{\rightarrow }_{\rho } \; \mu \gamma . M_3'[\gamma :=_rM_2]$
for some
 $Q$
.
$Q$
. -
 $\ast$
$\ast$
 $M_1=\lambda x.M_3$
: the IH applies.
$M_1=\lambda x.M_3$
: the IH applies. -
 $\ast$
$\ast$
 $M_1=[\alpha ]M_3$
: impossible by the term formation rules.
$M_1=[\alpha ]M_3$
: impossible by the term formation rules.
-
-
– The case
 $M=(M_1)M_2$
and
$M=(M_1)M_2$
and
 $M_2{\rightarrow }_{\rho }M_2'$
is similar to the above one. The only additional point is
$M_2{\rightarrow }_{\rho }M_2'$
is similar to the above one. The only additional point is
 $M_1=\mu \alpha . M_3$
and
$M_1=\mu \alpha . M_3$
and
 $N=\mu \alpha . M_3[\alpha :=_rM_2']$
. Then, with
$N=\mu \alpha . M_3[\alpha :=_rM_2']$
. Then, with
 $Q=\mu \alpha . M_3[\alpha :=_rM_2]$
,
$Q=\mu \alpha . M_3[\alpha :=_rM_2]$
,
 $M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\rho }N$
holds.
$M{\rightarrow }_{\mu }Q\twoheadrightarrow _{\rho }N$
holds.
-
2. Analogous to the above case. The proof makes use of Lemma 4.13.
-
3. By Points 1 and 2 of this lemma.
-
Remark 4.15. We emphasize that Lemmas 4.12 and 4.14 rely heavily on the fact that, in Parigot’s calculus, a
![]() $\mu$
-application must always be preceded by a
$\mu$
-application must always be preceded by a
![]() $\mu$
-abstraction. The lemmas mentioned are not valid in the de Groote-style
$\mu$
-abstraction. The lemmas mentioned are not valid in the de Groote-style
![]() $\lambda \mu$
-calculus which is shown by the following examples:
$\lambda \mu$
-calculus which is shown by the following examples:
-
Let
 $M=([\alpha ]\mu \beta .\lambda x.P)Q$
. Then
$M=([\alpha ]\mu \beta .\lambda x.P)Q$
. Then
 $M{\rightarrow }_\rho (\lambda x.P[\beta :=\alpha ])Q{\rightarrow }_\beta P[\beta :=\alpha ][x:=Q]$
, and we are not able to reverse the order of the
$M{\rightarrow }_\rho (\lambda x.P[\beta :=\alpha ])Q{\rightarrow }_\beta P[\beta :=\alpha ][x:=Q]$
, and we are not able to reverse the order of the
 $\beta$
- and
$\beta$
- and
 $\rho$
-reductions.
$\rho$
-reductions. -
Let
 $M=([\alpha ]\mu \beta .\mu \gamma .P)Q$
. Then
$M=([\alpha ]\mu \beta .\mu \gamma .P)Q$
. Then
 $M{\rightarrow }_\rho (\mu \gamma .P[\beta :=\alpha ])Q{\rightarrow }_\mu \mu \gamma . P[\beta :=\alpha ][\gamma :=_rQ]$
, and we are not able to reverse the order of the
$M{\rightarrow }_\rho (\mu \gamma .P[\beta :=\alpha ])Q{\rightarrow }_\mu \mu \gamma . P[\beta :=\alpha ][\gamma :=_rQ]$
, and we are not able to reverse the order of the
 $\mu$
- and
$\mu$
- and
 $\rho$
-reductions.
$\rho$
-reductions.
This phenomenon gives rise to the counterexample falsifying the strong normalization property of the de Groote-style calculus. We will discuss this in Section 5.
Now we can prove the theorem below, which asserts that the
![]() $\rho$
-rule can be strongly postponed with respect to
$\rho$
-rule can be strongly postponed with respect to
![]() $\beta \mu \mu '$
-reduction.
$\beta \mu \mu '$
-reduction.
Theorem 4.16.
Let
![]() $M\twoheadrightarrow _{\rho }P{\rightarrow }_{\beta \mu \mu '}^+N$
. Then there is a
$M\twoheadrightarrow _{\rho }P{\rightarrow }_{\beta \mu \mu '}^+N$
. Then there is a
![]() $Q$
for which
$Q$
for which
![]() $M{\rightarrow }_{\beta \mu \mu '}^+Q\twoheadrightarrow _{\rho }N$
.
$M{\rightarrow }_{\beta \mu \mu '}^+Q\twoheadrightarrow _{\rho }N$
.
Proof. A consequence of Lemmas 4.12 and 4.14.
Theorems 4.9 and 4.16 together yield Theorem 4.2.
4.3 Strong normalization
We are now in a position to state the main assertion of this section, which is Theorem 4.18.
Theorem 4.17.
The
![]() $\rho \theta$
-reduction is strongly normalizing.
$\rho \theta$
-reduction is strongly normalizing.
Proof.
Assume
![]() $M{\rightarrow }_{\rho \theta }M'$
. Then it is easy to observe that
$M{\rightarrow }_{\rho \theta }M'$
. Then it is easy to observe that
![]() $M'$
, as a word, consists of fewer symbols than
$M'$
, as a word, consists of fewer symbols than
![]() $M$
, which proves our assertion.
$M$
, which proves our assertion.
We are now ready to prove our strong normalization result.
Theorem 4.18.
In the simply typed Parigot-style
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\beta \mu \mu '\rho \theta$
-reduction is strongly normalizing.
$\beta \mu \mu '\rho \theta$
-reduction is strongly normalizing.
Proof.
It is known that de Groote’s simply typed
![]() $\lambda \mu$
-calculus with
$\lambda \mu$
-calculus with
![]() $\beta \mu \mu '$
-reduction is strongly normalizing (David and Nour Reference David, Nour and Urzyczyn2005). Since de Groote’s calculus is an extension of the original Parigot-style calculus, we immediately have the strong normalization property for the simply typed Parigot calculus with
$\beta \mu \mu '$
-reduction is strongly normalizing (David and Nour Reference David, Nour and Urzyczyn2005). Since de Groote’s calculus is an extension of the original Parigot-style calculus, we immediately have the strong normalization property for the simply typed Parigot calculus with
![]() $\beta \mu \mu '$
-reduction. Let
$\beta \mu \mu '$
-reduction. Let
![]() $\eta (M)$
denote the longest
$\eta (M)$
denote the longest
![]() $\beta \mu \mu '$
-reduction sequence starting from
$\beta \mu \mu '$
-reduction sequence starting from
![]() $M$
. Let
$M$
. Let
![]() $M$
be such that there is an infinite
$M$
be such that there is an infinite
![]() $\beta \mu \mu ' \rho \theta$
-reduction sequence starting from
$\beta \mu \mu ' \rho \theta$
-reduction sequence starting from
![]() $M$
and
$M$
and
![]() $\eta (M)$
is minimal. By Theorem 4.17, the infinite reduction sequence starting from
$\eta (M)$
is minimal. By Theorem 4.17, the infinite reduction sequence starting from
![]() $M$
must contain a
$M$
must contain a
![]() $\beta \mu \mu '$
-reduction, hence there is an
$\beta \mu \mu '$
-reduction, hence there is an
![]() $M'$
and
$M'$
and
![]() $M''$
such that
$M''$
such that
![]() $M\twoheadrightarrow _{\rho \theta }M'{\rightarrow }_{\beta \mu \mu '}M''$
and
$M\twoheadrightarrow _{\rho \theta }M'{\rightarrow }_{\beta \mu \mu '}M''$
and
![]() $M''$
has an infinite
$M''$
has an infinite
![]() $\beta \mu \mu ' \rho \theta$
-reduction sequence. If we apply Theorem 4.9 successively to the reduction sequence
$\beta \mu \mu ' \rho \theta$
-reduction sequence. If we apply Theorem 4.9 successively to the reduction sequence
![]() $M\twoheadrightarrow _{\rho \theta }M'{\rightarrow }_{\beta \mu \mu '}M''$
, then we obtain an
$M\twoheadrightarrow _{\rho \theta }M'{\rightarrow }_{\beta \mu \mu '}M''$
, then we obtain an
![]() $N$
and
$N$
and
![]() $P$
such that
$P$
such that
![]() $M\twoheadrightarrow _{\rho }N{\rightarrow }^+_{\beta \mu \mu '}P\twoheadrightarrow _{\theta }M''$
. Obviously,
$M\twoheadrightarrow _{\rho }N{\rightarrow }^+_{\beta \mu \mu '}P\twoheadrightarrow _{\theta }M''$
. Obviously,
![]() $P$
has an infinite
$P$
has an infinite
![]() $\beta \mu \mu ' \rho \theta$
-reduction sequence, since the reduction sequence
$\beta \mu \mu ' \rho \theta$
-reduction sequence, since the reduction sequence
![]() $P\twoheadrightarrow _{\theta }M''$
can be continued with the infinite reduction sequence starting from
$P\twoheadrightarrow _{\theta }M''$
can be continued with the infinite reduction sequence starting from
![]() $M''$
. We distinguish the following cases:
$M''$
. We distinguish the following cases:
-
 $M\twoheadrightarrow _{\rho }N$
is empty: since
$M\twoheadrightarrow _{\rho }N$
is empty: since
 $\eta (P)\lt \eta (M)$
, this contradicts the assumption on
$\eta (P)\lt \eta (M)$
, this contradicts the assumption on
 $M$
.
$M$
. -
 $M\twoheadrightarrow _{\rho }N$
is not empty: by Theorem 4.16, there is a
$M\twoheadrightarrow _{\rho }N$
is not empty: by Theorem 4.16, there is a
 $Q$
such that
$Q$
such that
 $M{\rightarrow }^+_{\beta \mu \mu '}Q\twoheadrightarrow _{\rho }P$
, then
$M{\rightarrow }^+_{\beta \mu \mu '}Q\twoheadrightarrow _{\rho }P$
, then
 $\eta (Q)\lt \eta (M)$
. This is a contradiction again.
$\eta (Q)\lt \eta (M)$
. This is a contradiction again.
5. The
 $\mu$
-Calculus
$\mu$
-Calculus
For the rest of the paper, we return to the de Groote-style syntax. With the creation of the
![]() $\lambda \mu$
-calculus, Parigot introduced a formal method to encode proofs in classical logic via terms of an appropriate calculus. The addition of the rules in connection with classical variables made it possible to represent the proof-theoretical machinery called reasoning by absurdity, which is very characteristic of classical reasoning. Parigot posed the question whether the rules corresponding to classical variables, that is, the rules without
$\lambda \mu$
-calculus, Parigot introduced a formal method to encode proofs in classical logic via terms of an appropriate calculus. The addition of the rules in connection with classical variables made it possible to represent the proof-theoretical machinery called reasoning by absurdity, which is very characteristic of classical reasoning. Parigot posed the question whether the rules corresponding to classical variables, that is, the rules without
![]() $\beta$
, are normalizing. In this spirit, we devote this section to the calculus with rules other than
$\beta$
, are normalizing. In this spirit, we devote this section to the calculus with rules other than
![]() $\beta$
. The rationale behind our choice is the expectation that examining the proof-theoretical properties can be simpler without the
$\beta$
. The rationale behind our choice is the expectation that examining the proof-theoretical properties can be simpler without the
![]() $\beta$
-rule, since we know that the
$\beta$
-rule, since we know that the
![]() $\beta$
-rule in the untyped case is not strongly normalizing and we know, for example, from Battyányi and Nour (Reference Battyányi and Nour2020) and David and Nour (Reference David, Nour and Urzyczyn2005) that the
$\beta$
-rule in the untyped case is not strongly normalizing and we know, for example, from Battyányi and Nour (Reference Battyányi and Nour2020) and David and Nour (Reference David, Nour and Urzyczyn2005) that the
![]() $\mu \mu '$
-calculus has the strong normalization property even in the untyped case. It looks quite tempting to try and prove the strong normalization property for the calculi obtained by adding more simplification rules like
$\mu \mu '$
-calculus has the strong normalization property even in the untyped case. It looks quite tempting to try and prove the strong normalization property for the calculi obtained by adding more simplification rules like
![]() $\rho$
-,
$\rho$
-,
![]() $\varepsilon$
-, and
$\varepsilon$
-, and
![]() $\theta$
-rules to the
$\theta$
-rules to the
![]() $\mu \mu '$
-rules. The
$\mu \mu '$
-rules. The
![]() $\theta$
-rule actually does not cause any difficulty, since it is strongly normalizing and, moreover, we can always move a
$\theta$
-rule actually does not cause any difficulty, since it is strongly normalizing and, moreover, we can always move a
![]() $\theta$
-redex to the end of a reduction sequence. However, contradicting our first guess,
$\theta$
-redex to the end of a reduction sequence. However, contradicting our first guess,
![]() $\mu \mu '$
-reduction fails to be strongly normalizing with the simplification rules
$\mu \mu '$
-reduction fails to be strongly normalizing with the simplification rules
![]() $\rho$
or
$\rho$
or
![]() $\varepsilon$
, however, innocent these rules may look. We demonstrate by examples that
$\varepsilon$
, however, innocent these rules may look. We demonstrate by examples that
![]() $\mu \mu '\rho$
- and
$\mu \mu '\rho$
- and
![]() $\mu \mu '\varepsilon$
-reductions are not strongly normalizing. We are able to prove, however, that weak normalization is preserved: in the second half of this section we show that
$\mu \mu '\varepsilon$
-reductions are not strongly normalizing. We are able to prove, however, that weak normalization is preserved: in the second half of this section we show that
![]() $\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing. We call the above calculus without
$\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing. We call the above calculus without
![]() $\beta$
-rule the
$\beta$
-rule the
![]() $\mu$
-calculus, that is, we consider
$\mu$
-calculus, that is, we consider
![]() $\mu \mu '\rho \varepsilon$
-reduction. In this respect, we talk about
$\mu \mu '\rho \varepsilon$
-reduction. In this respect, we talk about
![]() $\mu$
-normalization and
$\mu$
-normalization and
![]() $\mu$
-normal form if the reduction is clear from the context. Otherwise, we indicate explicitly the reductions we are dealing with. We could retain the structure of
$\mu$
-normal form if the reduction is clear from the context. Otherwise, we indicate explicitly the reductions we are dealing with. We could retain the structure of
![]() $\lambda \mu$
-terms by encoding a
$\lambda \mu$
-terms by encoding a
![]() $\lambda \mu$
-term with a
$\lambda \mu$
-term with a
![]() $\mu$
-term by inductively replacing the subterms of the form
$\mu$
-term by inductively replacing the subterms of the form
![]() $\lambda x.M$
with
$\lambda x.M$
with
![]() $((l)x)M$
, where
$((l)x)M$
, where
![]() $l$
is a constant. This way any
$l$
is a constant. This way any
![]() $\mu \mu '\rho \varepsilon$
-reduction of a
$\mu \mu '\rho \varepsilon$
-reduction of a
![]() $\lambda \mu$
-term would be simulated by an identical
$\lambda \mu$
-term would be simulated by an identical
![]() $\mu \mu '\rho \varepsilon$
-reduction of the appropriate
$\mu \mu '\rho \varepsilon$
-reduction of the appropriate
![]() $\mu$
-term. For the sake of simplicity, we abandon this option. Since only the typed
$\mu$
-term. For the sake of simplicity, we abandon this option. Since only the typed
![]() $\beta$
-reduction is strongly normalizing, in the last section, when we consider
$\beta$
-reduction is strongly normalizing, in the last section, when we consider
![]() $\beta$
-rule, we exclusively remain in the typed setting. Several results of this section, however, work in the untyped case as well. This is the reason why most of the present section will be concerned with the untyped calculus. Let us first define the
$\beta$
-rule, we exclusively remain in the typed setting. Several results of this section, however, work in the untyped case as well. This is the reason why most of the present section will be concerned with the untyped calculus. Let us first define the
![]() $\mu$
-terms, where we have deliberately omitted
$\mu$
-terms, where we have deliberately omitted
![]() $\lambda$
-abstractions, since they do not play any role concerning the normalization properties of the calculus without
$\lambda$
-abstractions, since they do not play any role concerning the normalization properties of the calculus without
![]() $\beta$
-rule.
$\beta$
-rule.
5.1 The reductions
 $\mu \mu '\rho$
and
$\mu \mu '\rho$
and
 $\mu \mu '\varepsilon$
$\mu \mu '\varepsilon$
It is already known that
![]() $\mu \mu '$
-reduction is strongly normalizing (Battyányi Reference Battyányi2007; Battyányi and Nour Reference Battyányi and Nour2020; David and Nour Reference David, Nour and Urzyczyn2005). We demonstrate in this section that this property is lost when we add either
$\mu \mu '$
-reduction is strongly normalizing (Battyányi Reference Battyányi2007; Battyányi and Nour Reference Battyányi and Nour2020; David and Nour Reference David, Nour and Urzyczyn2005). We demonstrate in this section that this property is lost when we add either
![]() $\rho$
- or
$\rho$
- or
![]() $\varepsilon$
-reduction to these rules. This phenomenon is actually a peculiarity of the de Groote-style syntax. In Theorems 5.1 and 5.3, we present examples of
$\varepsilon$
-reduction to these rules. This phenomenon is actually a peculiarity of the de Groote-style syntax. In Theorems 5.1 and 5.3, we present examples of
![]() $\mu$
-terms that are either not strongly or even not weakly normalizing. Both results appeared first in the thesis of the first author (Battyányi Reference Battyányi2007).
$\mu$
-terms that are either not strongly or even not weakly normalizing. Both results appeared first in the thesis of the first author (Battyányi Reference Battyányi2007).
Theorem 5.1.
The
![]() $\mu \mu ' \rho$
-reduction in the typed
$\mu \mu ' \rho$
-reduction in the typed
![]() $\mu$
-calculus is not strongly normalizing.
$\mu$
-calculus is not strongly normalizing.
Proof.
Let
![]() $P=\mu \alpha . [\alpha ][\alpha ]x$
,
$P=\mu \alpha . [\alpha ][\alpha ]x$
,
![]() $Q=\mu \beta . P$
and
$Q=\mu \beta . P$
and
![]() $M = (Q)P$
.
$M = (Q)P$
.
-
We observe that the term
 $M$
can be typed. Let
$M$
can be typed. Let
 $\alpha :\neg \bot$
and
$\alpha :\neg \bot$
and
 $\beta :\neg (\bot{\rightarrow } \bot )$
, then we have the typing relations
$\beta :\neg (\bot{\rightarrow } \bot )$
, then we have the typing relations  ,
,
 and
and  .
. -
The following reduction steps show that there exists an infinite reduction sequence starting from
 $M$
.
$M$
.

Remark 5.2.
-
1. Note that the
 $\mu$
-term
$\mu$
-term
 $M$
cannot be written in Parigot syntax because we will not be able to write two successive
$M$
cannot be written in Parigot syntax because we will not be able to write two successive
 $[\alpha ]$
s.
$[\alpha ]$
s. -
2. We remark that, when
 $\theta$
-reduction is allowed, the example above returns the initial
$\theta$
-reduction is allowed, the example above returns the initial
 $\mu$
-term
$\mu$
-term
 $M$
.
$M$
. -
3. We can normalize the
 $\mu$
-term
$\mu$
-term
 $M$
as follows :
$M$
as follows :
 $M =(Q)P{{\rightarrow }}_{\mu } Q$
.
$M =(Q)P{{\rightarrow }}_{\mu } Q$
. -
4. We can use this example to find a
 $\lambda \mu$
-term of integer type which is not strongly normalizable. Just consider the
$\lambda \mu$
-term of integer type which is not strongly normalizable. Just consider the
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $W = \lambda y. \lambda f. \mu \gamma .M[x:=[\gamma ]y]$
.
$W = \lambda y. \lambda f. \mu \gamma .M[x:=[\gamma ]y]$
.
Theorem 5.3.
The
![]() $\mu \mu ' \varepsilon$
-reduction in the typed
$\mu \mu ' \varepsilon$
-reduction in the typed
![]() $\mu$
-calculus is not strongly normalizing.
$\mu$
-calculus is not strongly normalizing.
Proof.
Let
![]() $K=\mu \alpha . [\alpha ][\alpha ]x$
,
$K=\mu \alpha . [\alpha ][\alpha ]x$
,
![]() $L=\mu \beta . [\beta ](z)[\beta ]y$
and
$L=\mu \beta . [\beta ](z)[\beta ]y$
and
![]() $N = \mu \gamma . (L)K$
.
$N = \mu \gamma . (L)K$
.
-
We first observe that the term
 $N$
can be typed. Let
$N$
can be typed. Let
 $\alpha :\neg \bot$
,
$\alpha :\neg \bot$
,
 $\beta :\neg (\bot{\rightarrow } \bot )$
and
$\beta :\neg (\bot{\rightarrow } \bot )$
and
 $\gamma : \neg \bot$
. We have the typing relations
$\gamma : \neg \bot$
. We have the typing relations
 ,
,
 and
and  .
. -
The following reductions show that there exists an infinite reduction sequence starting from
 $N$
.
$N$
.

To convince ourselves that this reduction can be continued without reaching a normal form, it is enough to observe that there is a certain analogy between lines 5 and 10. The idea of the proof of non-termination is roughly as follows. We have two occurrences of the subterm
 $K$
in the
$K$
in the
 $\mu$
-term
$\mu$
-term
 $ \mu \gamma .((z)(y)K)K$
, from which we can start an infinite reduction sequence. In the first stage of each iteration, we reduce exclusively the
$ \mu \gamma .((z)(y)K)K$
, from which we can start an infinite reduction sequence. In the first stage of each iteration, we reduce exclusively the
 $\mu$
- and
$\mu$
- and
 $\mu '$
-redexes lying around the second occurrence of
$\mu '$
-redexes lying around the second occurrence of
 $K$
until we arrive at the first occurrence of
$K$
until we arrive at the first occurrence of
 $K$
wrapped in a subterm
$K$
wrapped in a subterm
 $(z)(y)K$
. Then we distribute that copy of
$(z)(y)K$
. Then we distribute that copy of
 $(z)(y)K$
among all the subterms of the emerging
$(z)(y)K$
among all the subterms of the emerging
 $\mu '$
-redex which are named with
$\mu '$
-redex which are named with
 $\alpha$
, and afterwards we finish the actual iteration round with an
$\alpha$
, and afterwards we finish the actual iteration round with an
 $\varepsilon$
-reduction. Intuitively, none of the performed reduction steps decreases the total number of
$\varepsilon$
-reduction. Intuitively, none of the performed reduction steps decreases the total number of
 $\mu$
- and
$\mu$
- and
 $\mu '$
-redexes in the term, which anticipates that the reduction sequence cannot be terminating. Let us now properly formalize the proof. First of all we need some notations. For every sequence of
$\mu '$
-redexes in the term, which anticipates that the reduction sequence cannot be terminating. Let us now properly formalize the proof. First of all we need some notations. For every sequence of
 $\mu$
-terms
$\mu$
-terms
 $P,Q_0,\dots,Q_n$
, we define by induction on
$P,Q_0,\dots,Q_n$
, we define by induction on
 $n$
, the
$n$
, the
 $\mu$
-term
$\mu$
-term
 $\langle P;(P_0,\dots,P_n)\rangle$
by
$\langle P;(P_0,\dots,P_n)\rangle$
by
 $\langle P; (P_0) \rangle = ((z)(y)P)P_0$
and
$\langle P; (P_0) \rangle = ((z)(y)P)P_0$
and
 $\forall 1 \leq k \leq n$
,
$\forall 1 \leq k \leq n$
,
 $\langle P;(P_0,\dots,P_n) \rangle = \langle ((z)(y)P)P_n;(P_0,\dots,P_{n-1})\rangle$
. Intuitively
$\langle P;(P_0,\dots,P_n) \rangle = \langle ((z)(y)P)P_n;(P_0,\dots,P_{n-1})\rangle$
. Intuitively
 $\langle P;(P_0,\dots,P_n) \rangle$
$\langle P;(P_0,\dots,P_n) \rangle$
 $ =( (z)(y) \dots ( (z)(y) ((z)(y)P)P_n)P_{n-1} \dots )P_0$
.
$ =( (z)(y) \dots ( (z)(y) ((z)(y)P)P_n)P_{n-1} \dots )P_0$
.We define now two sequences of
 $\mu$
-terms
$\mu$
-terms
 $(Q_n)_n$
and
$(Q_n)_n$
and
 $(R_n)_n$
by :
$(R_n)_n$
by : $Q_0 = x$
,
$Q_0 = x$
,
 $\forall n\in I\!N$
,
$\forall n\in I\!N$
,
 $Q_{n+1} = \langle x;(Q_0,\dots,Q_n) \rangle$
and
$Q_{n+1} = \langle x;(Q_0,\dots,Q_n) \rangle$
and $\forall n\in I\!N$
,
$\forall n\in I\!N$
,
 $R_n= \mu \gamma .((z)(y)K) \langle K;(Q_0,\dots,Q_n) \rangle$
.
$R_n= \mu \gamma .((z)(y)K) \langle K;(Q_0,\dots,Q_n) \rangle$
.We have
 $R_0 = \mu \gamma .((z)(y)K) ((z)(y)K)x$
and
$R_0 = \mu \gamma .((z)(y)K) ((z)(y)K)x$
and
 $N \twoheadrightarrow ^+_{\mu \mu '\varepsilon } R_0$
.
$N \twoheadrightarrow ^+_{\mu \mu '\varepsilon } R_0$
.We prove that
 $\forall n\in I\!N$
,
$\forall n\in I\!N$
,
 $R_{n} \twoheadrightarrow ^+_{\mu \mu '\varepsilon } R_{n+1}$
.
$R_{n} \twoheadrightarrow ^+_{\mu \mu '\varepsilon } R_{n+1}$
.

Remark 5.4.
-
1. The variable
 $ z$
is used only to type the
$ z$
is used only to type the
 $\mu$
-term
$\mu$
-term
 $N$
.
$N$
. -
2. We can show that the
 $\mu$
-term
$\mu$
-term
 $N$
is not
$N$
is not
 $\mu \mu '\varepsilon$
-normalizable. We omit the rather technical proof of this result, since it is not needed in the sequel.
$\mu \mu '\varepsilon$
-normalizable. We omit the rather technical proof of this result, since it is not needed in the sequel.
We may guess that one of the reasons for the failure of strong normalization for the above terms could be the presence of two successive
![]() $\mu$
-applications
$\mu$
-applications
![]() $[.]$
(
$[.]$
(
![]() $M$
and
$M$
and
![]() $N$
contain
$N$
contain
![]() $[\alpha ][\alpha ]$
). To represent these terms in a typed environment, we need variables of type
$[\alpha ][\alpha ]$
). To represent these terms in a typed environment, we need variables of type
![]() $\neg \bot$
. We have already seen in the beginning of the previous section that terms of this type appear in the first works of Parigot with the aim of encoding classical tautologies with typed terms. Let us give another example to better understand this phenomenon. In Parigot’s syntax, it is not possible to write a
$\neg \bot$
. We have already seen in the beginning of the previous section that terms of this type appear in the first works of Parigot with the aim of encoding classical tautologies with typed terms. Let us give another example to better understand this phenomenon. In Parigot’s syntax, it is not possible to write a
![]() $\lambda \mu$
-term with type
$\lambda \mu$
-term with type
![]() $\neg \neg X \rightarrow X$
without using a free variable of type
$\neg \neg X \rightarrow X$
without using a free variable of type
![]() $\neg \bot$
. The simplest
$\neg \bot$
. The simplest
![]() $\lambda \mu$
-term he proposed is:
$\lambda \mu$
-term he proposed is:
![]() $\lambda y. \mu \alpha . [\varphi ] (y)\lambda x.\mu \delta .[\alpha ]x$
. In this term, the variable
$\lambda y. \mu \alpha . [\varphi ] (y)\lambda x.\mu \delta .[\alpha ]x$
. In this term, the variable
![]() $\varphi$
is free and has type
$\varphi$
is free and has type
![]() $\neg \bot$
. In de Groote’s syntax, we can write a term with type
$\neg \bot$
. In de Groote’s syntax, we can write a term with type
![]() $\neg \neg X \rightarrow X$
without free variables and without a variable of type
$\neg \neg X \rightarrow X$
without free variables and without a variable of type
![]() $\neg \bot$
. Here is an example:
$\neg \bot$
. Here is an example:
![]() $\lambda y. \mu \alpha . (y)\lambda x.[\alpha ]x$
. Many researchers have been interested in this kind of variables. For example, Ariola and Herbelin have made use of variables of type
$\lambda y. \mu \alpha . (y)\lambda x.[\alpha ]x$
. Many researchers have been interested in this kind of variables. For example, Ariola and Herbelin have made use of variables of type
![]() $\neg \bot$
in Ariola and Herbelin (Reference Ariola and Herbelin2003) (they called them variables for continuation) in order to establish translations between calculi based on classical logic. It is clear that due to the type of these variables, we can pile up two
$\neg \bot$
in Ariola and Herbelin (Reference Ariola and Herbelin2003) (they called them variables for continuation) in order to establish translations between calculi based on classical logic. It is clear that due to the type of these variables, we can pile up two
![]() $\mu$
-applications
$\mu$
-applications
![]() $[\alpha ][\alpha ]$
, which causes the loss of the strong normalization property. The first author studied a calculus in his thesis (Battyányi Reference Battyányi2007) where variables are not allowed to have type
$[\alpha ][\alpha ]$
, which causes the loss of the strong normalization property. The first author studied a calculus in his thesis (Battyányi Reference Battyányi2007) where variables are not allowed to have type
![]() $\neg \bot$
. He showed that the obtained calculus enjoys strong normalization.
$\neg \bot$
. He showed that the obtained calculus enjoys strong normalization.
5.2 Weak normalization of the
 $\mu$
-calculus
$\mu$
-calculus
In this section we show that
![]() $\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing. This result can be surprising in view of the results that we have discussed before, in particular, given that
$\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing. This result can be surprising in view of the results that we have discussed before, in particular, given that
![]() $\mu \mu '\varepsilon$
-reduction is not even normalizing. We will see that the normalization property of
$\mu \mu '\varepsilon$
-reduction is not even normalizing. We will see that the normalization property of
![]() $\mu \mu '\rho \varepsilon$
-reduction essentially originates from the structure of normal form terms with respect to all four rules. For the proof, we generalize our method for the weak normalization of
$\mu \mu '\rho \varepsilon$
-reduction essentially originates from the structure of normal form terms with respect to all four rules. For the proof, we generalize our method for the weak normalization of
![]() $\mu \mu '$
-calculus (Battyányi and Nour Reference Battyányi and Nour2020). We obtain a very simple normalization algorithm that is discussed in detail at the end of the section. The algorithm will be able to provide us with different normal forms of a given
$\mu \mu '$
-calculus (Battyányi and Nour Reference Battyányi and Nour2020). We obtain a very simple normalization algorithm that is discussed in detail at the end of the section. The algorithm will be able to provide us with different normal forms of a given
![]() $\mu$
-term. The main idea of our approach is to decide what to do when we face an application
$\mu$
-term. The main idea of our approach is to decide what to do when we face an application
![]() $(M)N$
. We start with normalizing the
$(M)N$
. We start with normalizing the
![]() $\mu$
-terms
$\mu$
-terms
![]() $M$
and
$M$
and
![]() $N$
separately to obtain the normal forms
$N$
separately to obtain the normal forms
![]() $M'$
and
$M'$
and
![]() $N'$
. The calculation can only continue if either
$N'$
. The calculation can only continue if either
![]() $M'$
or
$M'$
or
![]() $N'$
starts with
$N'$
starts with
![]() $\mu$
. This is where the necessity of studying the substitutions
$\mu$
. This is where the necessity of studying the substitutions
![]() $P[\alpha :=_sQ]$
, where
$P[\alpha :=_sQ]$
, where
![]() $s \in \{r,l\}$
and
$s \in \{r,l\}$
and
![]() $P,Q$
are in normal form, emerges. Lemma 5.7 characterizes the redexes that can be created in such substitutions, and Lemma 5.9 demonstrates how to handle them properly.
$P,Q$
are in normal form, emerges. Lemma 5.7 characterizes the redexes that can be created in such substitutions, and Lemma 5.9 demonstrates how to handle them properly.
We present the proofs in more detail in order to help the reader to easier understand the algorithm.
The following lemma depicts the
![]() $\mu$
-terms obtained by erasing
$\mu$
-terms obtained by erasing
![]() $\mu$
-variables from a normal form.
$\mu$
-variables from a normal form.
Lemma 5.5.
Let
![]() $M$
be a
$M$
be a
![]() $\mu$
-term and
$\mu$
-term and
![]() $\alpha$
a
$\alpha$
a
![]() $\mu$
-variable. If
$\mu$
-variable. If
![]() $M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
$M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
![]() $M_{\alpha } \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and, if
$M_{\alpha } \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and, if
![]() $M \neq \mu \beta .M'$
for some
$M \neq \mu \beta .M'$
for some
![]() $\beta$
, then there is no
$\beta$
, then there is no
![]() $\gamma$
such that
$\gamma$
such that
![]() $M_{\alpha } = \mu \gamma .M''$
.
$M_{\alpha } = \mu \gamma .M''$
.
Proof.
By induction on
![]() $M$
using Definition 2.5.
$M$
using Definition 2.5.
The next lemma is intuitive and has the consequence that we are not able to create a head
![]() $\mu$
-redex by a
$\mu$
-redex by a
![]() $\mu$
- or
$\mu$
- or
![]() $\mu '$
-substitution.
$\mu '$
-substitution.
Lemma 5.6.
Let
![]() $M,N$
be
$M,N$
be
![]() $\mu$
-terms and
$\mu$
-terms and
![]() $s \in \{r,l\}$
. If
$s \in \{r,l\}$
. If
![]() $M[\alpha :=_s N] = \mu \gamma .Q$
for some term
$M[\alpha :=_s N] = \mu \gamma .Q$
for some term
![]() $Q$
, then
$Q$
, then
![]() $M = \mu \gamma .P$
for some term
$M = \mu \gamma .P$
for some term
![]() $P$
.
$P$
.
Proof.
By induction on
![]() $M$
.
$M$
.
Now we characterize the redexes that can occur in a term of the form
![]() $M[\alpha :=_r N]$
or
$M[\alpha :=_r N]$
or
![]() $M[\alpha :=_l N]$
, where
$M[\alpha :=_l N]$
, where
![]() $M$
and
$M$
and
![]() $N$
are normal forms.
$N$
are normal forms.
Lemma 5.7.
Let
![]() $M,N$
be
$M,N$
be
![]() $\mu$
-terms such that
$\mu$
-terms such that
![]() $M,N \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
$M,N \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
![]() ${\sigma } = [\alpha :=_r N]$
and
${\sigma } = [\alpha :=_r N]$
and
![]() ${\sigma }' = [\alpha :=_l N]$
.
${\sigma }' = [\alpha :=_l N]$
.
-
1. We have
 $M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and the only possible
$M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and the only possible
 $\mu '$
-redexes of
$\mu '$
-redexes of
 $M{\sigma }$
are named with
$M{\sigma }$
are named with
 $\alpha$
and are of the form
$\alpha$
and are of the form
 $(L)N$
provided
$(L)N$
provided
 $N = \mu \gamma .K$
for some term
$N = \mu \gamma .K$
for some term
 $K$
. In particular,
$K$
. In particular,
 $M{\sigma } \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
if
$M{\sigma } \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
if
 $N \neq \mu \gamma .K$
.
$N \neq \mu \gamma .K$
. -
2. We have
 $M{\sigma }' \in \mathcal{NF}_{\mu '\rho \varepsilon }$
and the only possible
$M{\sigma }' \in \mathcal{NF}_{\mu '\rho \varepsilon }$
and the only possible
 $\mu$
-redexes of
$\mu$
-redexes of
 $M{\sigma }'$
are named with
$M{\sigma }'$
are named with
 $\alpha$
and are of the form
$\alpha$
and are of the form
 $(N)L$
provided
$(N)L$
provided
 $N = \mu \gamma .K$
for some term
$N = \mu \gamma .K$
for some term
 $K$
. In particular,
$K$
. In particular,
 $M{\sigma } \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
if
$M{\sigma } \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
if
 $N \neq \mu \gamma .K$
.
$N \neq \mu \gamma .K$
.
Proof.
We only prove the first point. The proof proceeds by induction on
![]() $M$
.
$M$
.
-
The result is obvious if
 $M = x$
.
$M = x$
. -
If
 $M = \mu \alpha . P$
, then
$M = \mu \alpha . P$
, then
 $P \neq \mu \beta . P'$
and
$P \neq \mu \beta . P'$
and
 $M{\sigma } = \mu \alpha .P{\sigma }$
. By IH,
$M{\sigma } = \mu \alpha .P{\sigma }$
. By IH,
 $P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
$P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
 $P{\sigma } \neq \mu \beta . Q$
, then
$P{\sigma } \neq \mu \beta . Q$
, then
 $M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
.
$M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
. -
If
 $M = [\beta ]P$
where
$M = [\beta ]P$
where
 $\beta \neq \alpha$
, then
$\beta \neq \alpha$
, then
 $P \neq \mu \gamma . P'$
and
$P \neq \mu \gamma . P'$
and
 $M{\sigma } = [\beta ]P{\sigma }$
. By IH,
$M{\sigma } = [\beta ]P{\sigma }$
. By IH,
 $P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
$P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
 $P{\sigma } \neq \mu \gamma . Q$
, then
$P{\sigma } \neq \mu \gamma . Q$
, then
 $M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
.
$M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
. -
If
 $M = [\alpha ]P$
, then
$M = [\alpha ]P$
, then
 $M{\sigma } = [\alpha ](P{\sigma })N$
. By IH,
$M{\sigma } = [\alpha ](P{\sigma })N$
. By IH,
 $P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
$P{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
 $P{\sigma } \neq \mu \beta . Q$
, then
$P{\sigma } \neq \mu \beta . Q$
, then
 $M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
.
$M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
. -
If
 $M = (P)Q$
, then
$M = (P)Q$
, then
 $M{\sigma } = (P{\sigma })Q{\sigma }$
and, since
$M{\sigma } = (P{\sigma })Q{\sigma }$
and, since
 $M$
is neither a
$M$
is neither a
 $\mu$
- and nor a
$\mu$
- and nor a
 $\mu '$
-redex, we have
$\mu '$
-redex, we have
 $P \neq \mu \beta . P'$
and
$P \neq \mu \beta . P'$
and
 $Q \neq \mu \beta . Q'$
. Using IH,
$Q \neq \mu \beta . Q'$
. Using IH,
 $P{\sigma },Q{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
$P{\sigma },Q{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and, by Lemma 5.6,
 $P{\sigma } \neq \mu \beta . P''$
,
$P{\sigma } \neq \mu \beta . P''$
,
 $Q{\sigma } \neq \mu \beta . Q''$
. Hence,
$Q{\sigma } \neq \mu \beta . Q''$
. Hence,
 $M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and the stipulation for the
$M{\sigma } \in \mathcal{NF}_{\mu \rho \varepsilon }$
and the stipulation for the
 $\mu '$
-redexes is valid for
$\mu '$
-redexes is valid for
 $M{\sigma }$
.
$M{\sigma }$
.
The requirement for the
![]() $\mu '$
-redex can be checked in all the above cases.
$\mu '$
-redex can be checked in all the above cases.
Definition 5.8. (
![]() $\mu$
and
$\mu$
and
![]() $\mu '$
-good)
$\mu '$
-good)
-
1. A
 $\mu$
-term
$\mu$
-term
 $M$
is said to be
$M$
is said to be
 $\mu$
-good if
$\mu$
-good if
 $M \in \mathcal{NF}_{\mu \rho \varepsilon }$
and its
$M \in \mathcal{NF}_{\mu \rho \varepsilon }$
and its
 $\mu '$
-redexes are named with
$\mu '$
-redexes are named with
 $\mu$
-variables.
$\mu$
-variables.
-
2. A
 $\mu$
-term
$\mu$
-term
 $M$
is said to be
$M$
is said to be
 $\mu '$
-good if
$\mu '$
-good if
 $M \in \mathcal{NF}_{\mu '\rho \varepsilon }$
and its
$M \in \mathcal{NF}_{\mu '\rho \varepsilon }$
and its
 $\mu$
-redexes are named with
$\mu$
-redexes are named with
 $\mu$
-variables.
$\mu$
-variables.
Let us now show how a
![]() $\mu$
-term that is
$\mu$
-term that is
![]() $\mu$
or
$\mu$
or
![]() $\mu '$
-good can be normalized.
$\mu '$
-good can be normalized.
Lemma 5.9.
-
1. If
 $M$
is
$M$
is
 $\mu$
-good, then
$\mu$
-good, then
 $\exists \, M' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, M' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $M \twoheadrightarrow _{\mu '\rho } M'$
and
$M \twoheadrightarrow _{\mu '\rho } M'$
and
 $M' = \mu \gamma .L$
for some term
$M' = \mu \gamma .L$
for some term
 $L$
iff
$L$
iff
 $M = \mu \gamma .K$
for some term
$M = \mu \gamma .K$
for some term
 $K$
; in particular
$K$
; in particular
 $M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
. -
2. If
 $M$
is
$M$
is
 $\mu '$
-good, then
$\mu '$
-good, then
 $\exists \, M' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, M' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $M \twoheadrightarrow _{\mu \rho } M'$
and
$M \twoheadrightarrow _{\mu \rho } M'$
and
 $M' = \mu \gamma .L$
for some term
$M' = \mu \gamma .L$
for some term
 $L$
iff
$L$
iff
 $M = \mu \gamma .K$
for some term
$M = \mu \gamma .K$
for some term
 $K$
; in particular
$K$
; in particular
 $M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
.
Proof.
We only prove the first point by induction on
![]() $M$
.
$M$
.
-
The result is obvious if
 $M = x$
.
$M = x$
. -
If
 $M = \mu \alpha . P$
, then
$M = \mu \alpha . P$
, then
 $P$
is
$P$
is
 $\mu$
-good and
$\mu$
-good and
 $P \neq \mu \beta .K$
. By IH,
$P \neq \mu \beta .K$
. By IH,
 $\exists \, P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $P \twoheadrightarrow _{\mu '\rho } P'$
and
$P \twoheadrightarrow _{\mu '\rho } P'$
and
 $P' \neq \mu \beta .L$
, then
$P' \neq \mu \beta .L$
, then
 $M \twoheadrightarrow _{\mu '\rho } \mu \alpha .P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu '\rho } \mu \alpha .P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
 $M = [\alpha ]P$
where
$M = [\alpha ]P$
where
 $P$
is not a
$P$
is not a
 $\mu '$
-redex, then
$\mu '$
-redex, then
 $P$
is
$P$
is
 $\mu$
-good and
$\mu$
-good and
 $P \neq \mu \beta .K$
. Because of IH,
$P \neq \mu \beta .K$
. Because of IH,
 $\exists \, P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $P \twoheadrightarrow _{\mu '\rho } P'$
and
$P \twoheadrightarrow _{\mu '\rho } P'$
and
 $P' \neq \mu \beta .L$
, then
$P' \neq \mu \beta .L$
, then
 $M \twoheadrightarrow _{\mu '\rho } [\alpha ]P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu '\rho } [\alpha ]P' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
If
 $M = [\alpha ](P)\mu \gamma .Q$
, then
$M = [\alpha ](P)\mu \gamma .Q$
, then
 $P,Q$
are
$P,Q$
are
 $\mu$
-good,
$\mu$
-good,
 $P \neq \mu \beta .K$
and
$P \neq \mu \beta .K$
and
 $Q \neq \mu \beta .L$
. By IH,
$Q \neq \mu \beta .L$
. By IH,
 $\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $P \twoheadrightarrow _{\mu '\rho } P'$
,
$P \twoheadrightarrow _{\mu '\rho } P'$
,
 $Q \twoheadrightarrow _{\mu '\rho } Q'$
,
$Q \twoheadrightarrow _{\mu '\rho } Q'$
,
 $P' \neq \mu \beta .K'$
and
$P' \neq \mu \beta .K'$
and
 $Q' \neq \mu \beta .L'$
. We have
$Q' \neq \mu \beta .L'$
. We have
 $M \twoheadrightarrow _{\mu '\rho } [\alpha ](P')\mu \gamma .Q'{\rightarrow }_{\mu '}[\alpha ]\mu \gamma .Q'[\gamma :=_l P']{\rightarrow }_{\rho } Q'[\gamma :=\alpha ][\alpha :=_l P']$
, and, by point 2 of Lemma 5.7,
$M \twoheadrightarrow _{\mu '\rho } [\alpha ](P')\mu \gamma .Q'{\rightarrow }_{\mu '}[\alpha ]\mu \gamma .Q'[\gamma :=_l P']{\rightarrow }_{\rho } Q'[\gamma :=\alpha ][\alpha :=_l P']$
, and, by point 2 of Lemma 5.7,
 $Q'[\gamma :=\alpha ][\alpha :=_l P'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$Q'[\gamma :=\alpha ][\alpha :=_l P'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
If
 $M = (P)Q$
, then
$M = (P)Q$
, then
 $P,Q$
are
$P,Q$
are
 $\mu$
-good,
$\mu$
-good,
 $P \neq \mu \beta .K$
and
$P \neq \mu \beta .K$
and
 $Q \neq \mu \beta .L$
. Applying IH,
$Q \neq \mu \beta .L$
. Applying IH,
 $\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $P \twoheadrightarrow _{\mu '\rho } P'$
,
$P \twoheadrightarrow _{\mu '\rho } P'$
,
 $Q \twoheadrightarrow _{\mu '\rho } Q'$
,
$Q \twoheadrightarrow _{\mu '\rho } Q'$
,
 $P' \neq \mu \beta . K'$
and
$P' \neq \mu \beta . K'$
and
 $Q' \neq \mu \beta . L'$
, thus
$Q' \neq \mu \beta . L'$
, thus
 $M \twoheadrightarrow _{\mu '\rho }(P')Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu '\rho }(P')Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
We can now prove our weak normalization result.
Theorem 5.10.
The
![]() $\mu$
-calculus is weakly normalizing.
$\mu$
-calculus is weakly normalizing.
Proof.
Let
![]() $M$
be any
$M$
be any
![]() $\mu$
-term. We prove by induction on
$\mu$
-term. We prove by induction on
![]() $M$
that
$M$
that
![]() $M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\mu \mu '\rho \varepsilon }$
.
-
The result is obvious if
 $M = x$
.
$M = x$
. -
If
 $M = \mu \alpha . N$
, then, by IH,
$M = \mu \alpha . N$
, then, by IH,
 $\exists \, N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $N \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N'$
. We have
$N \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N'$
. We have
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . N'$
. We distinguish two cases.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . N'$
. We distinguish two cases.
-
– If
 $N' \neq \mu \beta .K$
, then
$N' \neq \mu \beta .K$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
– If
 $N' = \mu \beta .K$
, then, by Lemma 5.5,
$N' = \mu \beta .K$
, then, by Lemma 5.5,
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . \mu \beta . K{\rightarrow }_{\varepsilon } \mu a. K_{\beta } \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha . \mu \beta . K{\rightarrow }_{\varepsilon } \mu a. K_{\beta } \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
-
-
If
 $M = [\alpha ]N$
, then, using IH,
$M = [\alpha ]N$
, then, using IH,
 $\exists \, N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $N \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N'$
. We have
$N \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N'$
. We have
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]N'$
. We distinguish two cases.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]N'$
. We distinguish two cases.
-
– If
 $N' \neq \mu \beta .K$
, then
$N' \neq \mu \beta .K$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]N' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
– If
 $N' = \mu \beta .K$
, then
$N' = \mu \beta .K$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]\mu \beta . K{\rightarrow }_{\rho } K[\beta :=\alpha ] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } [\alpha ]\mu \beta . K{\rightarrow }_{\rho } K[\beta :=\alpha ] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
-
-
If
 $M = (P)Q$
, then, by IH,
$M = (P)Q$
, then, by IH,
 $\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, P',Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $P \twoheadrightarrow _{\mu \mu '\rho \varepsilon } P'$
and
$P \twoheadrightarrow _{\mu \mu '\rho \varepsilon } P'$
and
 $Q \twoheadrightarrow _{\mu \mu '\rho \varepsilon } Q'$
. We have
$Q \twoheadrightarrow _{\mu \mu '\rho \varepsilon } Q'$
. We have
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } (P')Q'$
. We distinguish four cases.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } (P')Q'$
. We distinguish four cases.
-
– If
 $P' \neq \mu \alpha .K$
and
$P' \neq \mu \alpha .K$
and
 $Q' \neq \mu \beta .L$
, then
$Q' \neq \mu \beta .L$
, then
 $M \twoheadrightarrow (P')Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow (P')Q' \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
– If
 $P' =\mu \alpha .K$
and
$P' =\mu \alpha .K$
and
 $Q' \neq \mu \beta .L$
, then
$Q' \neq \mu \beta .L$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_rQ']$
. Recall that, by
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_rQ']$
. Recall that, by
 $P'\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
$P'\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
 $K\neq \mu \gamma K'$
. Hence, by Lemmas 5.7 and 5.6,
$K\neq \mu \gamma K'$
. Hence, by Lemmas 5.7 and 5.6,
 $K[\alpha :=_rQ'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
$K[\alpha :=_rQ'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
 $K[\alpha :=_rQ'] \neq \mu \gamma . O$
, then
$K[\alpha :=_rQ'] \neq \mu \gamma . O$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_rQ'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_rQ'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
– If
 $P' \neq \mu \alpha .K$
and
$P' \neq \mu \alpha .K$
and
 $Q' = \mu \beta .L$
, then
$Q' = \mu \beta .L$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .L[\alpha :=_lP']$
. By Lemmas 5.7 and 5.6,
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .L[\alpha :=_lP']$
. By Lemmas 5.7 and 5.6,
 $L[\alpha :=_lP'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
$L[\alpha :=_lP'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
 $L[\alpha :=_lP'] \neq \mu \gamma . O$
, then
$L[\alpha :=_lP'] \neq \mu \gamma . O$
, then
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .L[\alpha :=_lP'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .L[\alpha :=_lP'] \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
–
 $P' = \mu \alpha .K$
and
$P' = \mu \alpha .K$
and
 $Q' = \mu \beta .L$
, then we can conclude in two different ways.
$Q' = \mu \beta .L$
, then we can conclude in two different ways.
-
 $\ast$
We have
$\ast$
We have
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_r\mu \beta .L]$
. By Lemmas 5.7 and 5.6,
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .K[\alpha :=_r\mu \beta .L]$
. By Lemmas 5.7 and 5.6,
 $K[\alpha :=_r\mu \beta .L]$
is
$K[\alpha :=_r\mu \beta .L]$
is
 $\mu$
-good and
$\mu$
-good and
 $K[\alpha :=_r\mu \beta .L] \neq \mu \gamma .O$
, then, by Lemma 5.9,
$K[\alpha :=_r\mu \beta .L] \neq \mu \gamma .O$
, then, by Lemma 5.9,
 $\exists \, T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $K[\alpha :=_r\mu \beta .L] \twoheadrightarrow _{\mu '\rho } T$
and
$K[\alpha :=_r\mu \beta .L] \twoheadrightarrow _{\mu '\rho } T$
and
 $T \neq \mu \gamma .O'$
, thus
$T \neq \mu \gamma .O'$
, thus
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \alpha .T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. -
 $\ast$
We have
$\ast$
We have
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .L[\beta :=_l\mu \alpha .K]$
. By Lemmas 5.7 and 5.6,
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .L[\beta :=_l\mu \alpha .K]$
. By Lemmas 5.7 and 5.6,
 $V[\beta :=_l\mu \alpha .K]$
is
$V[\beta :=_l\mu \alpha .K]$
is
 $\mu '$
-good and
$\mu '$
-good and
 $L[\beta :=_l\mu \alpha .K] \neq \mu \gamma .O$
, then, by Lemma 5.9,
$L[\beta :=_l\mu \alpha .K] \neq \mu \gamma .O$
, then, by Lemma 5.9,
 $\exists \, T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
$\exists \, T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
such that
 $L[\beta :=_l \mu \alpha .K] \twoheadrightarrow _{\mu \rho } T$
and
$L[\beta :=_l \mu \alpha .K] \twoheadrightarrow _{\mu \rho } T$
and
 $T \neq \mu \gamma .O'$
, thus
$T \neq \mu \gamma .O'$
, thus
 $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } \mu \beta .T \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
.
-
-
Remark 5.11. Let us summarize the steps that we took to present a normalization algorithm. We proceed by induction on
![]() $\mu$
-terms.
$\mu$
-terms.
-
1. If
 $M= \mu \alpha . N$
, we normalize
$M= \mu \alpha . N$
, we normalize
 $N$
and, if we arrive at a normal form that begins with a
$N$
and, if we arrive at a normal form that begins with a
 $\mu \beta$
, then we reduce the
$\mu \beta$
, then we reduce the
 $\varepsilon$
-redex.
$\varepsilon$
-redex. -
2. If
 $M= [\alpha ] N$
, we normalize
$M= [\alpha ] N$
, we normalize
 $N$
and, if we arrive at a normal form that begins with a
$N$
and, if we arrive at a normal form that begins with a
 $\mu \beta$
, then we reduce the
$\mu \beta$
, then we reduce the
 $\rho$
-redex.
$\rho$
-redex. -
3. If
 $M= (M_1)M_2$
, we begin with normalizing
$M= (M_1)M_2$
, we begin with normalizing
 $M_1$
and
$M_1$
and
 $M_2$
, say, to normal forms
$M_2$
, say, to normal forms
 $N_1$
and
$N_1$
and
 $N_2$
. At this point, we distinguish four cases.
$N_2$
. At this point, we distinguish four cases.-
(a) If neither
 $N_1$
, nor
$N_1$
, nor
 $N_2$
begins with a
$N_2$
begins with a
 $\mu$
, the normalization is finished.
$\mu$
, the normalization is finished. -
(b) If
 $N_1 = \mu \alpha .N'_1$
and
$N_1 = \mu \alpha .N'_1$
and
 $N_2 \neq \mu \beta N'_2$
, then we reduce the
$N_2 \neq \mu \beta N'_2$
, then we reduce the
 $\mu$
-redex in order to obtain the normal form
$\mu$
-redex in order to obtain the normal form
 $\mu \alpha .N'_1[\alpha :=_rN_2]$
.
$\mu \alpha .N'_1[\alpha :=_rN_2]$
. -
(c) If
 $N_1 \neq \mu \alpha .N'_1$
and
$N_1 \neq \mu \alpha .N'_1$
and
 $N_2 = \mu \beta N'_2$
, the we reduce the
$N_2 = \mu \beta N'_2$
, the we reduce the
 $\mu '$
-redex. Hence, we obtain the normal form
$\mu '$
-redex. Hence, we obtain the normal form
 $\mu \beta .N'_2[\alpha :=_lN_1]$
.
$\mu \beta .N'_2[\alpha :=_lN_1]$
. -
(d) If
 $N_1 = \mu \alpha .N'_1$
and
$N_1 = \mu \alpha .N'_1$
and
 $N_2 = \mu \beta .N'_2$
, then
$N_2 = \mu \beta .N'_2$
, then
-
i. One can reduce the
 $\mu$
-redex so that one obtains a
$\mu$
-redex so that one obtains a
 $\mu$
-good term
$\mu$
-good term
 $\mu \alpha .N'_1[\alpha :=_rN_2]$
. It is now sufficient to reduce the remaining
$\mu \alpha .N'_1[\alpha :=_rN_2]$
. It is now sufficient to reduce the remaining
 $\mu '$
-redexes and then the created
$\mu '$
-redexes and then the created
 $\rho$
- and
$\rho$
- and
 $\varepsilon$
-redexes starting with the innermost ones.
$\varepsilon$
-redexes starting with the innermost ones. -
ii. Or one can reduce the
 $\mu '$
-redex so that one obtains a
$\mu '$
-redex so that one obtains a
 $\mu '$
-good term
$\mu '$
-good term
 $\mu \beta .N'_2[\alpha :=_lN_1]$
. It is now sufficient to reduce the remaining
$\mu \beta .N'_2[\alpha :=_lN_1]$
. It is now sufficient to reduce the remaining
 $\mu$
-redexes and then the created
$\mu$
-redexes and then the created
 $\rho$
- and
$\rho$
- and
 $\varepsilon$
-redexes starting with the innermost ones.
$\varepsilon$
-redexes starting with the innermost ones.
-
-
Observe that in case (d) we can obtain two different normal forms for
![]() $M$
.
$M$
.
We now take the
![]() $\mu$
-terms given in the proofs of Theorems 5.1 and 5.3 and normalize them with our algorithm.
$\mu$
-terms given in the proofs of Theorems 5.1 and 5.3 and normalize them with our algorithm.
Example 5.12.
-
1. Following the algorithm, we have two possibilities to normalize
 $M = (\mu \beta .\mu \alpha . [\alpha ][\alpha ]x)\mu \alpha . [\alpha ][\alpha ]x$
.
$M = (\mu \beta .\mu \alpha . [\alpha ][\alpha ]x)\mu \alpha . [\alpha ][\alpha ]x$
.
 \begin{align*} M &= (\underline{\mu \beta .\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\varepsilon } \underline{(\mu \beta .x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu } \mu \beta .x. \end{align*}
\begin{align*} M &= (\underline{\mu \beta .\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\varepsilon } \underline{(\mu \beta .x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu } \mu \beta .x. \end{align*}
 \begin{align*} M &= (\underline{\mu \beta .\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\varepsilon } \underline{(\mu \beta .x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \alpha . [\alpha ](\mu \beta .x)[\alpha ]\underline{(\mu \beta .x)x}\\ &{{\rightarrow }}_{\mu } \mu \alpha . [\alpha ](\mu \beta .x)\underline{[\alpha ]\mu \beta .x}\\ &{{\rightarrow }}_{\rho } \mu \alpha . [\alpha ]\underline{(\mu \beta .x)x} \end{align*}
\begin{align*} M &= (\underline{\mu \beta .\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\varepsilon } \underline{(\mu \beta .x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \alpha . [\alpha ](\mu \beta .x)[\alpha ]\underline{(\mu \beta .x)x}\\ &{{\rightarrow }}_{\mu } \mu \alpha . [\alpha ](\mu \beta .x)\underline{[\alpha ]\mu \beta .x}\\ &{{\rightarrow }}_{\rho } \mu \alpha . [\alpha ]\underline{(\mu \beta .x)x} \end{align*}
 \begin{align*} &{{\rightarrow }}_{\mu } \mu \alpha . \underline{[\alpha ]\mu \beta .x}\\ &{{\rightarrow }}_{\rho } \mu \alpha . x. \end{align*}
\begin{align*} &{{\rightarrow }}_{\mu } \mu \alpha . \underline{[\alpha ]\mu \beta .x}\\ &{{\rightarrow }}_{\rho } \mu \alpha . x. \end{align*}
-
2. Following the algorithm, we have two possibilities to normalize
 $N = \mu \gamma .(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x$
.
We note that we do not obtain the same normal form.
$N = \mu \gamma .(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x$
.
We note that we do not obtain the same normal form. \begin{align*} N &= \mu \gamma .\underline{(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \beta .[\beta ]((z)[\beta ]\underline{(y)\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \beta .[\beta ]((z)\underline{[\beta ]\mu \alpha . [\alpha ](y)[\alpha ](y)x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\rho } \mu \gamma .\mu \beta .[\beta ]\underline{((z)[\beta ](y)[\beta ](y)x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \beta .\underline{[\beta ]\mu \alpha . [\alpha ]((z)[\beta ](y)[\beta ](y)x)[\alpha ]((z)[\beta ](y)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \gamma .\mu \beta . [\beta ]((z)[\beta ](y)[\beta ](y)x)[\beta ]((z)[\beta ](y)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \gamma .((z)(y)(y)x)((z)(y)(y)x)x.\\[8pt] N &= \mu \gamma .\underline{(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \alpha . [\alpha ](\mu \beta . [\beta ](z)[\beta ]y)[\alpha ]\underline{(\mu \beta . [\beta ](z)[\beta ]y)x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \alpha . [\alpha ](\mu \beta . [\beta ](z)[\beta ]y)\underline{[\alpha ]\mu \beta . [\beta ]((z)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\rho } \mu \gamma .\mu \alpha . [\alpha ]\underline{(\mu \beta . [\beta ](z)[\beta ]y) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \alpha . \underline{[\alpha ]\mu \beta . [\beta ]((z)[\beta ](y) [\alpha ]((z)[\alpha ](y)x)x) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \gamma .\mu \alpha . [\alpha ]((z)[\alpha ](y) [\alpha ]((z)[\alpha ](y)x)x) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \gamma .((z)(y) ((z)(y)x)x) ((z)(y)x)x. \end{align*}
\begin{align*} N &= \mu \gamma .\underline{(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \beta .[\beta ]((z)[\beta ]\underline{(y)\mu \alpha . [\alpha ][\alpha ]x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \beta .[\beta ]((z)\underline{[\beta ]\mu \alpha . [\alpha ](y)[\alpha ](y)x})\mu \alpha . [\alpha ][\alpha ]x\\ &{{\rightarrow }}_{\rho } \mu \gamma .\mu \beta .[\beta ]\underline{((z)[\beta ](y)[\beta ](y)x)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \beta .\underline{[\beta ]\mu \alpha . [\alpha ]((z)[\beta ](y)[\beta ](y)x)[\alpha ]((z)[\beta ](y)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \gamma .\mu \beta . [\beta ]((z)[\beta ](y)[\beta ](y)x)[\beta ]((z)[\beta ](y)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \gamma .((z)(y)(y)x)((z)(y)(y)x)x.\\[8pt] N &= \mu \gamma .\underline{(\mu \beta . [\beta ](z)[\beta ]y)\mu \alpha . [\alpha ][\alpha ]x}\\ &{{\rightarrow }}_{\mu '} \mu \gamma .\mu \alpha . [\alpha ](\mu \beta . [\beta ](z)[\beta ]y)[\alpha ]\underline{(\mu \beta . [\beta ](z)[\beta ]y)x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \alpha . [\alpha ](\mu \beta . [\beta ](z)[\beta ]y)\underline{[\alpha ]\mu \beta . [\beta ]((z)[\beta ](y)x)x}\\ &{{\rightarrow }}_{\rho } \mu \gamma .\mu \alpha . [\alpha ]\underline{(\mu \beta . [\beta ](z)[\beta ]y) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\mu } \mu \gamma .\mu \alpha . \underline{[\alpha ]\mu \beta . [\beta ]((z)[\beta ](y) [\alpha ]((z)[\alpha ](y)x)x) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\rho } \underline{\mu \gamma .\mu \alpha . [\alpha ]((z)[\alpha ](y) [\alpha ]((z)[\alpha ](y)x)x) [\alpha ]((z)[\alpha ](y)x)x}\\ &{{\rightarrow }}_{\varepsilon } \mu \gamma .((z)(y) ((z)(y)x)x) ((z)(y)x)x. \end{align*}
6. The Case of
 $\beta$
-Reduction
$\beta$
-Reduction
In this section, we examine how the weak normalization property is preserved when we extend the calculus with
![]() $\beta$
-reduction. In what follows, since we include
$\beta$
-reduction. In what follows, since we include
![]() $\beta$
-reduction in our treatment again, instead of the abbreviations
$\beta$
-reduction in our treatment again, instead of the abbreviations
![]() $\mu$
-reduction and
$\mu$
-reduction and
![]() $\mu$
-normal form for
$\mu$
-normal form for
![]() $\mu \mu '\rho \varepsilon$
-reduction and
$\mu \mu '\rho \varepsilon$
-reduction and
![]() $\mu \mu '\rho \varepsilon$
-normal form, we explicitly indicate the particular reductions we are talking about. Although the algorithms of the previous section also work in the untyped setting, we now must consider a typed framework, since
$\mu \mu '\rho \varepsilon$
-normal form, we explicitly indicate the particular reductions we are talking about. Although the algorithms of the previous section also work in the untyped setting, we now must consider a typed framework, since
![]() $\beta$
-reduction is not weakly normalizing in the untyped form. Hence, all results we state in this section are for typed
$\beta$
-reduction is not weakly normalizing in the untyped form. Hence, all results we state in this section are for typed
![]() $\lambda \mu$
-terms. Our algorithm depends on the weak normalization algorithm presented in the previous section, and we also make use of the fact that the typed
$\lambda \mu$
-terms. Our algorithm depends on the weak normalization algorithm presented in the previous section, and we also make use of the fact that the typed
![]() $\lambda$
-calculus has the weak normalization property. The idea of the proof is as follows:
$\lambda$
-calculus has the weak normalization property. The idea of the proof is as follows:
-
We start from a
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M_1$
in
$M_1$
in
 ${\mu \mu ' \rho } \varepsilon$
-normal form, i.e., from a
${\mu \mu ' \rho } \varepsilon$
-normal form, i.e., from a
 $\lambda \mu$
-term in which there are no
$\lambda \mu$
-term in which there are no
 $\mu$
-,
$\mu$
-,
 $\mu '$
-,
$\mu '$
-,
 $\rho$
- or
$\rho$
- or
 $\varepsilon$
-redexes.
$\varepsilon$
-redexes. -
We eliminate all
 $\beta$
-redexes from
$\beta$
-redexes from
 $M_1$
by applying an arbitrary weak
$M_1$
by applying an arbitrary weak
 $\beta$
-normalization algorithm. Having done this, we arrive at a
$\beta$
-normalization algorithm. Having done this, we arrive at a
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M_2$
in
$M_2$
in
 $\beta$
-normal form.
$\beta$
-normal form. -
Next, we find a
 ${\mu \mu ' \rho }\varepsilon$
-normal form
${\mu \mu ' \rho }\varepsilon$
-normal form
 $M_3$
of
$M_3$
of
 $M_2$
by our weak normalization algorithm. The
$M_2$
by our weak normalization algorithm. The
 $\lambda \mu$
-term
$\lambda \mu$
-term
 $M_3$
may contain
$M_3$
may contain
 $\beta$
-redexes.
$\beta$
-redexes. -
We prove, however, that the maximum rank of
 $\beta$
-redexes in
$\beta$
-redexes in
 $M_1$
is strictly greater than that of
$M_1$
is strictly greater than that of
 $M_3$
. We will give the necessary definitions in the section.
$M_3$
. We will give the necessary definitions in the section.
By this, the process must terminate. Finally,
![]() $\theta$
-reduction causes no problem since it is strongly normalizing and does not create new redexes when applied to
$\theta$
-reduction causes no problem since it is strongly normalizing and does not create new redexes when applied to
![]() ${\mu \mu ' \rho }\varepsilon$
-normal forms.
${\mu \mu ' \rho }\varepsilon$
-normal forms.
We have to consider the evolution of types throughout the reduction. In order to simplify our presentation, we apply the typability relation of Church (Sørensen and Urzyczyn Reference Sørensen and Urzyczyn2006): we explicitly write the types of the variables in the abstractions together with the types of some of the subterms. To begin with, we present the reduction rules in the typed case. Recall that this evolution of types corresponds exactly to the notion of cut elimination in natural deduction proofs. We will not indicate the types of all subterms of a particular
![]() $\lambda \mu$
-term, but only the ones that are relevant for our purposes.
$\lambda \mu$
-term, but only the ones that are relevant for our purposes.

Definition 6.1.
The length of a type
![]() $A$
, which is denoted by
$A$
, which is denoted by
![]() $\textrm{lh}(A)$
, is defined as the number of arrows in
$\textrm{lh}(A)$
, is defined as the number of arrows in
![]() $A$
.
$A$
.
6.1 The origin of a
 $\mu$
-redex in a
$\mu$
-redex in a
 $\beta$
-reduction
$\beta$
-reduction
The aim of this section is to prove Corollary 6.7, which asserts that the creation of a
![]() $\mu$
-redex during
$\mu$
-redex during
![]() $\beta$
-reduction of a
$\beta$
-reduction of a
![]() $\mu \mu '\rho \varepsilon$
-normal term
$\mu \mu '\rho \varepsilon$
-normal term
![]() $M$
forces
$M$
forces
![]() $M$
to contain a
$M$
to contain a
![]() $\beta$
-redex of a particular type. We start from
$\beta$
-redex of a particular type. We start from
![]() $M$
and
$M$
and
![]() $M'$
, where
$M'$
, where
![]() $M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
$M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
![]() $M \twoheadrightarrow _{\beta } M'$
. We suppose that
$M \twoheadrightarrow _{\beta } M'$
. We suppose that
![]() $M'$
contains a
$M'$
contains a
![]() $\mu$
-redex
$\mu$
-redex
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A$
. We intend to say something about the term
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A$
. We intend to say something about the term
![]() $M$
, where
$M$
, where
![]() $M$
is such that the sequence of
$M$
is such that the sequence of
![]() $\beta$
-reductions leading to
$\beta$
-reductions leading to
![]() $M'$
has created a new
$M'$
has created a new
![]() $\mu$
-redex in
$\mu$
-redex in
![]() $M'$
. We show that
$M'$
. We show that
![]() $M$
must contain a
$M$
must contain a
![]() $\beta$
-redex
$\beta$
-redex
![]() $(\lambda x^C.P_2^D)Q_2^C$
with
$(\lambda x^C.P_2^D)Q_2^C$
with
![]() $\textrm{lh}(C \to D) \gt \textrm{lh}(A \to B)$
. We consider this
$\textrm{lh}(C \to D) \gt \textrm{lh}(A \to B)$
. We consider this
![]() $\beta$
-redex the origin of the
$\beta$
-redex the origin of the
![]() $\mu$
-redex. (In fact, a
$\mu$
-redex. (In fact, a
![]() $\beta$
-redex like that can be uniquely assigned to every
$\beta$
-redex like that can be uniquely assigned to every
![]() $\mu$
-redex of the above form, but we do not need this statement.) To establish this claim, we have to start from a more general assumption where the property
$\mu$
-redex of the above form, but we do not need this statement.) To establish this claim, we have to start from a more general assumption where the property
![]() $M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
is no longer valid.
$M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
is no longer valid.
The assertion of the following lemma explicitly shows the origins of
![]() $\beta$
- and
$\beta$
- and
![]() $\mu$
-redexes in a
$\mu$
-redexes in a
![]() $\beta$
-substitution.
$\beta$
-substitution.
Lemma 6.2.
-
1. If
 $(\lambda x. P)Q \preceq M[y:=N]$
, then
$(\lambda x. P)Q \preceq M[y:=N]$
, then
-
either
 $(\lambda x. P)Q\preceq N$
,
$(\lambda x. P)Q\preceq N$
, -
or
 $(\lambda x. P')Q' \preceq M$
,
$(\lambda x. P')Q' \preceq M$
,
 $P'[y:=N] = P$
and
$P'[y:=N] = P$
and
 $Q'[y:=N] = Q$
for some terms
$Q'[y:=N] = Q$
for some terms
 $P',Q'$
,
$P',Q'$
, -
or
 $(y)M' \preceq M$
,
$(y)M' \preceq M$
,
 $N = \lambda x. P$
and
$N = \lambda x. P$
and
 $M'[y:=N] = Q$
for some term
$M'[y:=N] = Q$
for some term
 $M'$
.
$M'$
.
-
2. If
 $(\mu \alpha . P)Q \preceq M[y:=N]$
, then
$(\mu \alpha . P)Q \preceq M[y:=N]$
, then
-
either
 $(\mu \alpha . P)Q \preceq N$
,
$(\mu \alpha . P)Q \preceq N$
, -
or
 $(\mu \alpha .P')Q' \preceq M$
,
$(\mu \alpha .P')Q' \preceq M$
,
 $P'[y:=N] = P$
and
$P'[y:=N] = P$
and
 $Q'[y:=N] = Q$
for some terms
$Q'[y:=N] = Q$
for some terms
 $P',Q'$
,
$P',Q'$
, -
or
 $(y)M' \preceq M$
,
$(y)M' \preceq M$
,
 $N = \mu \alpha . P$
and
$N = \mu \alpha . P$
and
 $M'[y:=N] = Q$
for some term
$M'[y:=N] = Q$
for some term
 $M'$
.
$M'$
.
-
Proof.
By induction on
![]() $M$
.
$M$
.
Lemmas 6.3 and 6.4 determine in some sense the origin of a
![]() $\beta$
- or
$\beta$
- or
![]() $\mu$
-redex in a
$\mu$
-redex in a
![]() $\beta$
-reduction while also stating important relations between the type of the redexes in the original term and in the resulting term, respectively. We can conclude that, during a
$\beta$
-reduction while also stating important relations between the type of the redexes in the original term and in the resulting term, respectively. We can conclude that, during a
![]() $\beta$
-reduction step, a
$\beta$
-reduction step, a
![]() $\mu$
-redex can stem from either a
$\mu$
-redex can stem from either a
![]() $\beta$
- or a
$\beta$
- or a
![]() $\mu$
-redex. When the origin is a
$\mu$
-redex. When the origin is a
![]() $\beta$
-redex, then it must be a redex of longer type. On the contrary, if we consider the origin of a
$\beta$
-redex, then it must be a redex of longer type. On the contrary, if we consider the origin of a
![]() $\beta$
-redex, then it must be a
$\beta$
-redex, then it must be a
![]() $\beta$
-redex again with type not smaller than that of the descendant. This is the statement of Lemma 6.4. Hence, if we examine a sequence of
$\beta$
-redex again with type not smaller than that of the descendant. This is the statement of Lemma 6.4. Hence, if we examine a sequence of
![]() $\beta$
-reductions starting from a term in
$\beta$
-reductions starting from a term in
![]() $\mu$
-normal form, the origin of a
$\mu$
-normal form, the origin of a
![]() $\mu$
-redex in the final term must be a
$\mu$
-redex in the final term must be a
![]() $\beta$
-redex in the original term of longer type (Corollary 6.7).
$\beta$
-redex in the original term of longer type (Corollary 6.7).
Lemma 6.3.
If
![]() $M{\rightarrow }_{\beta } M'$
and
$M{\rightarrow }_{\beta } M'$
and
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then either
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then either
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
![]() $(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
![]() $P_2,Q_2$
and some types
$P_2,Q_2$
and some types
![]() $C,D$
where
$C,D$
where
![]() $\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
Proof.
By induction on
![]() $M$
. The only nontrivial cases are
$M$
. The only nontrivial cases are
-
 $M=(M_1)M_2$
is not the reduced
$M=(M_1)M_2$
is not the reduced
 $\beta$
-redex and
$\beta$
-redex and
 $M' = (\mu \alpha .P_1)Q_1$
,
$M' = (\mu \alpha .P_1)Q_1$
,
-
– If
 $M_1 = \mu \alpha .P_1$
and
$M_1 = \mu \alpha .P_1$
and
 $M_2{\rightarrow }_{\beta } Q_1$
, then
$M_2{\rightarrow }_{\beta } Q_1$
, then
 $M = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })M_2^{A}$
.
$M = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })M_2^{A}$
. -
– If
 $M_1{\rightarrow }_{\beta } \mu \alpha .P_1$
and
$M_1{\rightarrow }_{\beta } \mu \alpha .P_1$
and
 $M_2 = Q_1$
, we only have two possible cases :
$M_2 = Q_1$
, we only have two possible cases :
-
 $\ast$
$\ast$
 $M_1 = \mu \alpha . P_2$
,
$M_1 = \mu \alpha . P_2$
,
 $P_2{\rightarrow }_{\beta } P_1$
and
$P_2{\rightarrow }_{\beta } P_1$
and
 $M = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })M_2^A$
.
$M = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })M_2^A$
. -
 $\ast$
$\ast$
 $M_1 = (\lambda y. P_2)Q_2{\rightarrow }_{\beta } \mu \alpha .P_1$
and
$M_1 = (\lambda y. P_2)Q_2{\rightarrow }_{\beta } \mu \alpha .P_1$
and
 $(\lambda y^{C}. P_2^{A{\rightarrow } B})Q_2^{C} \preceq M$
with
$(\lambda y^{C}. P_2^{A{\rightarrow } B})Q_2^{C} \preceq M$
with
 $\textrm{lh}(C{\rightarrow } (A{\rightarrow } B)) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } (A{\rightarrow } B)) \gt \textrm{lh}(A{\rightarrow } B)$
.
-
-
-
 $M =(\lambda y.M'_1)M_2$
is the reduced
$M =(\lambda y.M'_1)M_2$
is the reduced
 $\beta$
-redex and
$\beta$
-redex and
 $M' = M'_1[y:=M_2]$
. Then, by Lemma 6.2, we have three cases to examine.
$M' = M'_1[y:=M_2]$
. Then, by Lemma 6.2, we have three cases to examine.
-
– If
 $(\mu \alpha .P_1)Q_1 \preceq M_2$
, then we have the result.
$(\mu \alpha .P_1)Q_1 \preceq M_2$
, then we have the result. -
– If
 $(\mu \alpha .P_1)Q_1 = K[y:=M_2]$
where
$(\mu \alpha .P_1)Q_1 = K[y:=M_2]$
where
 $K=(\mu \alpha .P_2)Q_2 \preceq M'_1$
, then
$K=(\mu \alpha .P_2)Q_2 \preceq M'_1$
, then
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
.
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
. -
– If
 $(y)O \preceq M'_1$
,
$(y)O \preceq M'_1$
,
 $M_2 = \mu \alpha . P_1$
and
$M_2 = \mu \alpha . P_1$
and
 $O[y:=M_2] = Q_1$
, then
$O[y:=M_2] = Q_1$
, then
 $M = (\lambda y^{A{\rightarrow } B}.M'^{C}_1)M_2^{A{\rightarrow } B}$
and
$M = (\lambda y^{A{\rightarrow } B}.M'^{C}_1)M_2^{A{\rightarrow } B}$
and
 $\textrm{lh}((A{\rightarrow } B){\rightarrow } C) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}((A{\rightarrow } B){\rightarrow } C) \gt \textrm{lh}(A{\rightarrow } B)$
.
-
Lemma 6.4.
If
![]() $M{\rightarrow }_{\beta } M'$
and
$M{\rightarrow }_{\beta } M'$
and
![]() $(\lambda x^{A}.P_1^{B})Q_1^A \preceq M'$
, then
$(\lambda x^{A}.P_1^{B})Q_1^A \preceq M'$
, then
![]() $(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
![]() $P_2,Q_2$
and some types
$P_2,Q_2$
and some types
![]() $C,D$
where
$C,D$
where
![]() $\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(A{\rightarrow } B)$
.
Proof.
By induction on
![]() $M$
. The only nontrivial cases are
$M$
. The only nontrivial cases are
-
 $M=(M_1)M_2$
is not the reduced
$M=(M_1)M_2$
is not the reduced
 $\beta$
-redex and
$\beta$
-redex and
 $M' = (\lambda x.P_1)Q_1$
.
$M' = (\lambda x.P_1)Q_1$
.
-
– If
 $M_1 = \lambda x.P_1$
and
$M_1 = \lambda x.P_1$
and
 $M_2{\rightarrow }_{\beta } Q_1$
, then
$M_2{\rightarrow }_{\beta } Q_1$
, then
 $M = (\lambda x^{A}.P_1^{B})M_2^{A}$
.
$M = (\lambda x^{A}.P_1^{B})M_2^{A}$
. -
– If
 $M_1{\rightarrow }_{\beta } \lambda x.P_1$
and
$M_1{\rightarrow }_{\beta } \lambda x.P_1$
and
 $M_2 = Q_1$
, we have only two possible cases :
$M_2 = Q_1$
, we have only two possible cases :
-
 $\ast$
$\ast$
 $M_1 = \lambda x. P_2$
,
$M_1 = \lambda x. P_2$
,
 $P_1{\rightarrow }_{\beta } P_2$
and
$P_1{\rightarrow }_{\beta } P_2$
and
 $M = (\lambda x^{A}.P_2^{B})M_2^A$
.
$M = (\lambda x^{A}.P_2^{B})M_2^A$
. -
 $\ast$
$\ast$
 $M_1 = (\lambda y. P_2)Q_2{\rightarrow }_{\beta } \lambda x.P_1$
and
$M_1 = (\lambda y. P_2)Q_2{\rightarrow }_{\beta } \lambda x.P_1$
and
 $(\lambda y^{C}. P_2^{A{\rightarrow } B})Q_2^{C} \preceq M$
with
$(\lambda y^{C}. P_2^{A{\rightarrow } B})Q_2^{C} \preceq M$
with
 $\textrm{lh}(C{\rightarrow } (A{\rightarrow } B)) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } (A{\rightarrow } B)) \gt \textrm{lh}(A{\rightarrow } B)$
.
-
-
-
 $M =(\lambda y.M'_1)M_2$
is the reduced
$M =(\lambda y.M'_1)M_2$
is the reduced
 $\beta$
-redex and
$\beta$
-redex and
 $M' = M'_1[y:=M_2]$
. Then, by Lemma 6.2, we have three cases to examine.
$M' = M'_1[y:=M_2]$
. Then, by Lemma 6.2, we have three cases to examine.
-
– If
 $(\lambda x.P_1)Q_1 \preceq M_2$
, then we have the result.
$(\lambda x.P_1)Q_1 \preceq M_2$
, then we have the result. -
– If
 $(\lambda x.P_1)Q_1 = K[y:=M_2]$
where
$(\lambda x.P_1)Q_1 = K[y:=M_2]$
where
 $K=(\lambda x.P_2)Q_2 \preceq M'_1$
, then
$K=(\lambda x.P_2)Q_2 \preceq M'_1$
, then
 $(\lambda x^{A}.P_2^{B})Q_2^A \preceq M$
.
$(\lambda x^{A}.P_2^{B})Q_2^A \preceq M$
. -
– If
 $(y)O \preceq M'_1$
,
$(y)O \preceq M'_1$
,
 $M_2 = \lambda x. P_1$
and
$M_2 = \lambda x. P_1$
and
 $O[y:=M_2] = Q_1$
, then
$O[y:=M_2] = Q_1$
, then
 $M = (\lambda y^{A{\rightarrow } B}.M'^{C}_1)M_2^{A{\rightarrow } B}$
and
$M = (\lambda y^{A{\rightarrow } B}.M'^{C}_1)M_2^{A{\rightarrow } B}$
and
 $\textrm{lh}((A{\rightarrow } B){\rightarrow } C) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}((A{\rightarrow } B){\rightarrow } C) \gt \textrm{lh}(A{\rightarrow } B)$
.
-
We obtain the corollaries below about
![]() $\beta$
-reduction sequences. Intuitively, the origin of a
$\beta$
-reduction sequences. Intuitively, the origin of a
![]() $\mu$
-redex in a
$\mu$
-redex in a
![]() $\beta$
-reduction sequence is either a
$\beta$
-reduction sequence is either a
![]() $\mu$
-redex of the same type or a
$\mu$
-redex of the same type or a
![]() $\beta$
-redex of a type of greater length.
$\beta$
-redex of a type of greater length.
Corollary 6.5.
If
![]() $M \twoheadrightarrow _{\beta } M'$
and
$M \twoheadrightarrow _{\beta } M'$
and
![]() $(\lambda x^{A}.P_1^{B})Q_1^A \preceq M'$
, then
$(\lambda x^{A}.P_1^{B})Q_1^A \preceq M'$
, then
![]() $(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
![]() $P_2,Q_2$
and some types
$P_2,Q_2$
and some types
![]() $C,D$
where
$C,D$
where
![]() $\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(A{\rightarrow } B)$
.
Proof.
By induction on the length of the reduction
![]() $M \twoheadrightarrow _{\beta } M'$
using Lemma 6.4.
$M \twoheadrightarrow _{\beta } M'$
using Lemma 6.4.
Corollary 6.6.
If
![]() $M \twoheadrightarrow _{\beta } M'$
and
$M \twoheadrightarrow _{\beta } M'$
and
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then either
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then either
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
![]() $(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
![]() $P_2,Q_2$
and some types
$P_2,Q_2$
and some types
![]() $C,D$
where
$C,D$
where
![]() $\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
Proof.
By induction on the length of the reduction
![]() $M \twoheadrightarrow _{\beta } M'$
. If
$M \twoheadrightarrow _{\beta } M'$
. If
![]() $M= M'$
, the result is immediate. If
$M= M'$
, the result is immediate. If
![]() $M \twoheadrightarrow _{\beta } N{\rightarrow }_{\beta } M'$
, then, by Lemma 6.3, either
$M \twoheadrightarrow _{\beta } N{\rightarrow }_{\beta } M'$
, then, by Lemma 6.3, either
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_3^{\bot })Q_3^A \preceq N$
or
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_3^{\bot })Q_3^A \preceq N$
or
![]() $(\lambda x^E.P_3^F)Q_3^E \preceq N$
where
$(\lambda x^E.P_3^F)Q_3^E \preceq N$
where
![]() $\textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
.
-
If
 $(\lambda x^E.P_3^F)Q_3^E \preceq N$
where
$(\lambda x^E.P_3^F)Q_3^E \preceq N$
where
 $\textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
, then by Corollary 6.5,
$\textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
, then by Corollary 6.5,
 $(\lambda x^C.P_2^D)Q_2^C \preceq M$
where
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
where
 $\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \geq \textrm{lh}(E{\rightarrow } F) \gt \textrm{lh}(A{\rightarrow } B)$
. -
If
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_3^{\bot })Q_3^A \preceq N$
, the by IH, either
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_3^{\bot })Q_3^A \preceq N$
, the by IH, either
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^A \preceq M$
or
 $(\lambda x^C.P_2^D)Q_2^C \preceq M$
where
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
where
 $\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
Corollary 6.7.
If
![]() $M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
$M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
,
![]() $M \twoheadrightarrow _{\beta } M'$
, and
$M \twoheadrightarrow _{\beta } M'$
, and
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^A \preceq M'$
, then
![]() $(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
$(\lambda x^C.P_2^D)Q_2^C \preceq M$
for some terms
![]() $P_2,Q_2$
and some types
$P_2,Q_2$
and some types
![]() $C,D$
where
$C,D$
where
![]() $\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
$\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
.
Proof. Immediate from Corollary 6.6.
6.2 The origin of a
 $\beta$
-redex in a
$\beta$
-redex in a
 $\mu \mu '\rho \varepsilon$
-reduction
$\mu \mu '\rho \varepsilon$
-reduction
The aim of this section is to prove Corollary 6.17, which means that the creation of a
![]() $\beta$
-redex during a
$\beta$
-redex during a
![]() $\mu \mu '\rho \varepsilon$
-reduction sequence starting from a
$\mu \mu '\rho \varepsilon$
-reduction sequence starting from a
![]() $\beta$
-normal term
$\beta$
-normal term
![]() $M$
compels
$M$
compels
![]() $M$
to contain a
$M$
to contain a
![]() $\mu \mu '\rho \varepsilon$
-redex of a particular type. We start from
$\mu \mu '\rho \varepsilon$
-redex of a particular type. We start from
![]() $M$
and
$M$
and
![]() $N$
such that
$N$
such that
![]() $M \in \mathcal{NF}_{\beta }$
and
$M \in \mathcal{NF}_{\beta }$
and
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N$
. We assume that
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N$
. We assume that
![]() $N$
contains a
$N$
contains a
![]() $\beta$
-redex
$\beta$
-redex
![]() $(\lambda x^A.P_1^B)Q_1^A$
. We show that
$(\lambda x^A.P_1^B)Q_1^A$
. We show that
![]() $M$
must then contain a
$M$
must then contain a
![]() $\mu$
-redex
$\mu$
-redex
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A}$
. We consider this
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A}$
. We consider this
![]() $\mu$
-redex as the origin of the
$\mu$
-redex as the origin of the
![]() $\beta$
-redex. (In fact, a
$\beta$
-redex. (In fact, a
![]() $\mu$
-redex like that can be uniquely assigned to every
$\mu$
-redex like that can be uniquely assigned to every
![]() $\beta$
-redex of the above form, but we do not need this statement.) To establish this claim, we have to start from a more general assumption where
$\beta$
-redex of the above form, but we do not need this statement.) To establish this claim, we have to start from a more general assumption where
![]() $M \in \mathcal{NF}_{\beta }$
is no longer valid. We note that two cases can arise here: the origin of a
$M \in \mathcal{NF}_{\beta }$
is no longer valid. We note that two cases can arise here: the origin of a
![]() $\beta$
-redex with respect to a
$\beta$
-redex with respect to a
![]() $\mu \mu '\rho \varepsilon$
-reduction step can either be a
$\mu \mu '\rho \varepsilon$
-reduction step can either be a
![]() $\beta$
-redex or a
$\beta$
-redex or a
![]() $\mu$
-redex. When the origin of a
$\mu$
-redex. When the origin of a
![]() $\beta$
-redex is a
$\beta$
-redex is a
![]() $\mu$
-redex, then we have to resort to more subtle methods in our investigation. To this end, we introduce two notions: we describe when a term is
$\mu$
-redex, then we have to resort to more subtle methods in our investigation. To this end, we introduce two notions: we describe when a term is
![]() $\alpha$
-good and when it verifies condition
$\alpha$
-good and when it verifies condition
![]() $(A,B)$
for certain types
$(A,B)$
for certain types
![]() $A$
,
$A$
,
![]() $B$
(Definitions 6.9 and 6.12). Intuitively, these notions deal with the situation when the the name of the
$B$
(Definitions 6.9 and 6.12). Intuitively, these notions deal with the situation when the the name of the
![]() $\mu$
-variable changes because of a
$\mu$
-variable changes because of a
![]() $\rho$
-reduction.
$\rho$
-reduction.
The following lemma gives the location of
![]() $\beta$
- and
$\beta$
- and
![]() $\mu$
-redexes in a
$\mu$
-redexes in a
![]() $\mu$
-substitution.
$\mu$
-substitution.
Lemma 6.8.
Let
![]() $s \in \{l,r\}$
$s \in \{l,r\}$
-
1. If
 $(\lambda x. P)Q \preceq M[\beta :=_sN]$
, then
$(\lambda x. P)Q \preceq M[\beta :=_sN]$
, then
-
either
 $(\lambda x. P)Q \preceq N$
,
$(\lambda x. P)Q \preceq N$
, -
or
 $(\lambda x. P')Q' \preceq M$
,
$(\lambda x. P')Q' \preceq M$
,
 $P'[\beta :=_sN] = P$
and
$P'[\beta :=_sN] = P$
and
 $Q'[\beta :=_sN] = Q$
for some terms
$Q'[\beta :=_sN] = Q$
for some terms
 $P',Q'$
,
$P',Q'$
, -
or
 $s = r$
,
$s = r$
,
 $[\beta ]\lambda x.P' \preceq M$
,
$[\beta ]\lambda x.P' \preceq M$
,
 $N = Q$
and
$N = Q$
and
 $P'[\beta :=_rN] = P$
for some term
$P'[\beta :=_rN] = P$
for some term
 $P'$
,
$P'$
, -
or
 $s = l$
,
$s = l$
,
 $[\beta ]Q' \preceq M$
,
$[\beta ]Q' \preceq M$
,
 $N = \lambda x.P$
and
$N = \lambda x.P$
and
 $Q'[\beta :=_lN] = Q$
for some term
$Q'[\beta :=_lN] = Q$
for some term
 $Q'$
.
$Q'$
.
-
2. If
 $(\mu \alpha . P)Q \preceq M[\beta :=_sN]$
, then
$(\mu \alpha . P)Q \preceq M[\beta :=_sN]$
, then
-
either
 $(\mu \alpha . P)Q \preceq N$
,
$(\mu \alpha . P)Q \preceq N$
, -
or
 $(\mu \alpha . P')Q' \preceq M$
,
$(\mu \alpha . P')Q' \preceq M$
,
 $U'[\beta :=_sN] = U$
and
$U'[\beta :=_sN] = U$
and
 $Q'[\beta :=_sN] = Q$
for some terms
$Q'[\beta :=_sN] = Q$
for some terms
 $P',Q'$
,
$P',Q'$
, -
or
 $s = r$
,
$s = r$
,
 $[\beta ]\mu \alpha .P' \preceq M$
,
$[\beta ]\mu \alpha .P' \preceq M$
,
 $N = Q$
and
$N = Q$
and
 $P'[\beta :=_rN] = P$
for some term
$P'[\beta :=_rN] = P$
for some term
 $P'$
,
$P'$
, -
or
 $s = l$
,
$s = l$
,
 $[\beta ]Q' \preceq M$
,
$[\beta ]Q' \preceq M$
,
 $N = \mu \alpha .P$
and
$N = \mu \alpha .P$
and
 $Q'[\beta :=_lN] = Q$
for some term
$Q'[\beta :=_lN] = Q$
for some term
 $Q'$
.
$Q'$
.
Proof.
By induction on
![]() $M$
.
$M$
.
In what follows, we show that the origin of a
![]() $\mu$
-redex through a
$\mu$
-redex through a
![]() $\mu \mu '\rho \varepsilon$
-reduction sequence is always a
$\mu \mu '\rho \varepsilon$
-reduction sequence is always a
![]() $\mu$
-redex of the same type (Lemma 6.14). However, we need to add an auxiliary condition on the
$\mu$
-redex of the same type (Lemma 6.14). However, we need to add an auxiliary condition on the
![]() $\mu$
-redex to ensure this property during the search for the origin of a redex (Lemma 6.16). Hence, we give Definitions 6.9 and 6.12.
$\mu$
-redex to ensure this property during the search for the origin of a redex (Lemma 6.16). Hence, we give Definitions 6.9 and 6.12.
Definition 6.9.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term,
$\lambda \mu$
-term,
![]() $A,B$
types and
$A,B$
types and
![]() $\alpha ^{\neg (A \to B)} \in \textrm{fv}(M)$
. We say that
$\alpha ^{\neg (A \to B)} \in \textrm{fv}(M)$
. We say that
![]() $M$
is
$M$
is
![]() $\alpha$
-good if there exists an occurrence of
$\alpha$
-good if there exists an occurrence of
![]() $[\alpha ]$
such that
$[\alpha ]$
such that
-
either
 $[\alpha ]\lambda y^A.O^B \preceq M$
for some term
$[\alpha ]\lambda y^A.O^B \preceq M$
for some term
 $O$
, or
$O$
, or
-
 $[\alpha ]\mu \beta ^{\neg (A \to B)} .P^{\bot } \preceq M$
for some term
$[\alpha ]\mu \beta ^{\neg (A \to B)} .P^{\bot } \preceq M$
for some term
 $P$
which is
$P$
which is
 $\beta$
-good.
$\beta$
-good.
Intuitively a
![]() $\lambda \mu$
-term is
$\lambda \mu$
-term is
![]() $\alpha$
-good if it contains a subterm of the following form:
$\alpha$
-good if it contains a subterm of the following form:
![]() $[\alpha ]\mu \beta _1 \dots [\beta _1]\mu \beta _2 \dots [\beta _2]\mu \beta _3 \dots [\beta _n]\lambda y.O$
.
$[\alpha ]\mu \beta _1 \dots [\beta _1]\mu \beta _2 \dots [\beta _2]\mu \beta _3 \dots [\beta _n]\lambda y.O$
.
The next lemma helps understanding the notion of
![]() $\alpha$
-good with respect to a substitution and will be used in subsequent proofs.
$\alpha$
-good with respect to a substitution and will be used in subsequent proofs.
Lemma 6.10.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term.
$\lambda \mu$
-term.
-
1. Assume
 $M = P[\beta : =_s Q]$
,
$M = P[\beta : =_s Q]$
,
 $s \in \{l,r \}$
and
$s \in \{l,r \}$
and
 $\beta \neq \alpha$
.
$\beta \neq \alpha$
.-
(a) If
 $M$
is
$M$
is
 $\alpha$
-good, then either
$\alpha$
-good, then either
 $P$
is
$P$
is
 $\alpha$
-good or
$\alpha$
-good or
 $Q$
is
$Q$
is
 $\alpha$
-good.
$\alpha$
-good.
-
(b) If
 $P$
is
$P$
is
 $\alpha$
-good, then
$\alpha$
-good, then
 $M$
is
$M$
is
 $\alpha$
-good.
$\alpha$
-good.
-
(c) If
 $\beta \in \textrm{fv}(P)$
and
$\beta \in \textrm{fv}(P)$
and
 $Q$
is
$Q$
is
 $\alpha$
-good, then
$\alpha$
-good, then
 $M$
is
$M$
is
 $\alpha$
-good.
$\alpha$
-good.
-
-
2. If
 $\gamma ^{\neg \bot }$
is a
$\gamma ^{\neg \bot }$
is a
 $\mu$
-variable, then
$\mu$
-variable, then
 $M$
is
$M$
is
 $\alpha$
-good iff
$\alpha$
-good iff
 $M_{\gamma }$
is
$M_{\gamma }$
is
 $\alpha$
-good.
$\alpha$
-good.
-
3. If
 $\alpha \not \in \textrm{fv}(N)$
and
$\alpha \not \in \textrm{fv}(N)$
and
 $s \in \{l,r\}$
, then
$s \in \{l,r\}$
, then
 $M[\alpha :=_sN]$
is not
$M[\alpha :=_sN]$
is not
 $\alpha$
-good.
$\alpha$
-good.
Proof.
By induction on
![]() $M$
.
$M$
.
The following lemma intuitively means that we will not be able to create an
![]() $\alpha$
-good term by a
$\alpha$
-good term by a
![]() $\mu \mu '\rho \varepsilon$
-reduction.
$\mu \mu '\rho \varepsilon$
-reduction.
Lemma 6.11.
Let
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and assume
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and assume
![]() $M'$
is
$M'$
is
![]() $\alpha$
-good, then
$\alpha$
-good, then
![]() $M$
is
$M$
is
![]() $\alpha$
-good.
$\alpha$
-good.
Proof.
It is enough to examine the case of one-step reduction. We proceed by induction on
![]() $M$
. The cases
$M$
. The cases
![]() $M = \lambda x.N$
,
$M = \lambda x.N$
,
![]() $M = \mu \beta .N$
,
$M = \mu \beta .N$
,
![]() $M = (M_1)M_2$
, and
$M = (M_1)M_2$
, and
![]() $M = [\beta ]N$
, where
$M = [\beta ]N$
, where
![]() $\beta \neq \alpha$
, are treated by induction and using Lemma 6.10. Assume
$\beta \neq \alpha$
, are treated by induction and using Lemma 6.10. Assume
![]() $M = [\alpha ]N$
. We examine the form of
$M = [\alpha ]N$
. We examine the form of
![]() $N$
.
$N$
.
-
If
 $N = \lambda y.O$
, then
$N = \lambda y.O$
, then
 $M$
is
$M$
is
 $\alpha$
-good.
$\alpha$
-good. -
The case
 $N = [\beta ]O$
is impossible, since the type of
$N = [\beta ]O$
is impossible, since the type of
 $N$
differs from
$N$
differs from
 $\bot$
by reason of α :
$\bot$
by reason of α :
 $\neg (A\rightarrow B)$
.
$\neg (A\rightarrow B)$
. -
Assume
 $N = \mu \beta .O$
.
$N = \mu \beta .O$
.
-
– If
 $M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ]\mu \beta .O'=M'$
where
$M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ]\mu \beta .O'=M'$
where
 $O{\rightarrow }_{\mu \mu '\rho \varepsilon } O'$
, then
$O{\rightarrow }_{\mu \mu '\rho \varepsilon } O'$
, then
 $O'$
is
$O'$
is
 $\alpha$
-good or
$\alpha$
-good or
 $\beta$
-good, thus, by IH,
$\beta$
-good, thus, by IH,
 $O$
is
$O$
is
 $\alpha$
-good or
$\alpha$
-good or
 $\beta$
-good, therefore
$\beta$
-good, therefore
 $M$
is also
$M$
is also
 $\alpha$
-good.
$\alpha$
-good. -
– If
 $M = [\alpha ]\mu \beta .O{\rightarrow }_{\rho } O[\beta :=\alpha ]= M'$
, then
$M = [\alpha ]\mu \beta .O{\rightarrow }_{\rho } O[\beta :=\alpha ]= M'$
, then
 $O$
is
$O$
is
 $\alpha$
-good or
$\alpha$
-good or
 $\beta$
-good, thus
$\beta$
-good, thus
 $M$
is also
$M$
is also
 $\alpha$
-good.
$\alpha$
-good.
-
-
Assume
 $N = (N_1)N_2$
.
$N = (N_1)N_2$
.
-
– If
 $M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ](N_1')N_2 = M'$
where
$M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ](N_1')N_2 = M'$
where
 $N_1{\rightarrow }_{\mu \mu '\rho \varepsilon } N'_1$
, then
$N_1{\rightarrow }_{\mu \mu '\rho \varepsilon } N'_1$
, then
 $N'_1$
or
$N'_1$
or
 $N_2$
is
$N_2$
is
 $\alpha$
-good, thus, by IH,
$\alpha$
-good, thus, by IH,
 $N_1$
or
$N_1$
or
 $N_2$
is
$N_2$
is
 $\alpha$
-good, therefore
$\alpha$
-good, therefore
 $M$
is also
$M$
is also
 $\alpha$
-good.
$\alpha$
-good. -
– The case
 $M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ](N_1)N'_2 = M'$
where
$M{\rightarrow }_{\mu \mu '\rho \varepsilon } [\alpha ](N_1)N'_2 = M'$
where
 $N_2{\rightarrow }_{\mu \mu '\rho \varepsilon } N'_2$
is treated in the same way.
$N_2{\rightarrow }_{\mu \mu '\rho \varepsilon } N'_2$
is treated in the same way. -
– If
 $M = [\alpha ](\mu \beta .N_3)N_2{\rightarrow }_{\mu } [\alpha ]\mu \beta .N_3[\beta :=_rN_2] = M'$
, then, by Lemma 6.10,
$M = [\alpha ](\mu \beta .N_3)N_2{\rightarrow }_{\mu } [\alpha ]\mu \beta .N_3[\beta :=_rN_2] = M'$
, then, by Lemma 6.10,
 $N_3[\beta :=_rN_2]$
is not
$N_3[\beta :=_rN_2]$
is not
 $\beta$
-good, thus
$\beta$
-good, thus
 $N_3[\beta :=_rN_2]$
is
$N_3[\beta :=_rN_2]$
is
 $\alpha$
-good, and, by Lemma 6.10,
$\alpha$
-good, and, by Lemma 6.10,
 $N_3$
or
$N_3$
or
 $N_2$
is
$N_2$
is
 $\alpha$
-good, therefore
$\alpha$
-good, therefore
 $M$
is also
$M$
is also
 $\alpha$
-good.
$\alpha$
-good. -
– The case
 $M = [\alpha ](N_1)\mu \beta .N_2{\rightarrow }_{\mu '} [\alpha ]\mu \beta .N_2[\beta :=_lN_1] = M'$
is treated in the same way.
$M = [\alpha ](N_1)\mu \beta .N_2{\rightarrow }_{\mu '} [\alpha ]\mu \beta .N_2[\beta :=_lN_1] = M'$
is treated in the same way.
-
In the next definition, we give the condition that should be imposed on the
![]() $\mu$
-redex to ensure that our typability assertions hold throughout the reduction sequence. For a redex
$\mu$
-redex to ensure that our typability assertions hold throughout the reduction sequence. For a redex
![]() $(\mu \alpha .P)Q$
, we demand that there exists a chain, in the sense of Definition 6.9, that starts with
$(\mu \alpha .P)Q$
, we demand that there exists a chain, in the sense of Definition 6.9, that starts with
![]() $[\alpha ]$
and ends with a
$[\alpha ]$
and ends with a
![]() $\lambda$
-abstraction. We will see in the proof of Lemma 6.13 how this condition propagates and how it prevents the creation of certain
$\lambda$
-abstraction. We will see in the proof of Lemma 6.13 how this condition propagates and how it prevents the creation of certain
![]() $\mu$
-redexes.
$\mu$
-redexes.
Definition 6.12.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term and
$\lambda \mu$
-term and
![]() $A,B$
be types. We say that
$A,B$
be types. We say that
![]() $M$
verifies the condition
$M$
verifies the condition
![]() $(A,B)$
, or
$(A,B)$
, or
![]() $(A,B)$
holds for
$(A,B)$
holds for
![]() $M$
, if
$M$
, if
![]() $M$
contains a subterm of the form
$M$
contains a subterm of the form
![]() $(\mu \alpha ^{\neg (A \to B)}.P^{\bot })Q^A$
for some terms
$(\mu \alpha ^{\neg (A \to B)}.P^{\bot })Q^A$
for some terms
![]() $P,Q$
such that
$P,Q$
such that
![]() $P$
is
$P$
is
![]() $\alpha$
-good.
$\alpha$
-good.
Lemma 6.13.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term and
$\lambda \mu$
-term and
![]() $\gamma ^{\neg \bot }$
be a
$\gamma ^{\neg \bot }$
be a
![]() $\mu$
-variable, then
$\mu$
-variable, then
![]() $M$
verifies the condition
$M$
verifies the condition
![]() $(A,B)$
iff
$(A,B)$
iff
![]() $M_{\gamma }$
verifies the condition
$M_{\gamma }$
verifies the condition
![]() $(A,B)$
.
$(A,B)$
.
Proof.
By induction on
![]() $M$
.
$M$
.
Lemma 6.14.
Let
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and assume condition (A, B) holds for
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and assume condition (A, B) holds for
![]() $M'$
. Then condition
$M'$
. Then condition
![]() $(A,B)$
holds for
$(A,B)$
holds for
![]() $M$
.
$M$
.
Proof.
It is enough to examine the case of one-step reduction. We proceed by induction on
![]() $M$
. The cases
$M$
. The cases
![]() $M = \lambda x.N$
,
$M = \lambda x.N$
,
![]() $M = \mu \beta .N$
, and
$M = \mu \beta .N$
, and
![]() $M = [\beta ]N$
are treated by induction and using Lemma 6.13.
$M = [\beta ]N$
are treated by induction and using Lemma 6.13.
-
Assume
 $M = (M_1)M_2$
and
$M = (M_1)M_2$
and
 $M$
is not the reduced redex.
$M$
is not the reduced redex.
-
– The case
 $M' =(M_1)M'_2$
,
$M' =(M_1)M'_2$
,
 $M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
and
$M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
and
 $(A,B)$
holds for
$(A,B)$
holds for
 $M_1$
or for
$M_1$
or for
 $M'_2$
, then, using IH,
$M'_2$
, then, using IH,
 $(A,B)$
holds for
$(A,B)$
holds for
 $M_1$
or for
$M_1$
or for
 $M_2$
, thus
$M_2$
, thus
 $(A,B)$
holds for
$(A,B)$
holds for
 $M$
.
$M$
. -
– The case
 $M' =(M_1)M'_2$
,
$M' =(M_1)M'_2$
,
 $M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
,
$M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
,
 $M_1 = \mu \alpha ^{\neg (A \to B)}.P$
and
$M_1 = \mu \alpha ^{\neg (A \to B)}.P$
and
 $P$
is
$P$
is
 $\alpha$
-good, then
$\alpha$
-good, then
 $(A,B)$
holds for
$(A,B)$
holds for
 $M$
.
$M$
. -
– If
 $M' =(M'_1)M_2$
,
$M' =(M'_1)M_2$
,
 $M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
and
$M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
and
 $(A,B)$
holds for
$(A,B)$
holds for
 $M'_1$
or for
$M'_1$
or for
 $M_2$
, then, by IH,
$M_2$
, then, by IH,
 $(A,B)$
holds for
$(A,B)$
holds for
 $M_1$
or for
$M_1$
or for
 $M_2$
, thus
$M_2$
, thus
 $(A,B)$
holds for
$(A,B)$
holds for
 $M$
.
$M$
. -
– If
 $M' =(M'_1)M_2$
,
$M' =(M'_1)M_2$
,
 $M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
,
$M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
,
 $M'_1 = \mu \alpha ^{\neg (A \to B)}.P$
and
$M'_1 = \mu \alpha ^{\neg (A \to B)}.P$
and
 $P$
is
$P$
is
 $\alpha$
-good, then we examine the possible forms of
$\alpha$
-good, then we examine the possible forms of
 $M_1$
.
$M_1$
.
-
 $\ast$
The cases
$\ast$
The cases
 $M_1 = \lambda x.N$
and
$M_1 = \lambda x.N$
and
 $M_1 = [\beta ]N$
are impossible.
$M_1 = [\beta ]N$
are impossible. -
 $\ast$
If
$\ast$
If
 $M_1 = \mu \alpha . N$
and
$M_1 = \mu \alpha . N$
and
 $N{\rightarrow }_{\mu \mu '\rho \varepsilon } P$
, then, by Lemma 6.11,
$N{\rightarrow }_{\mu \mu '\rho \varepsilon } P$
, then, by Lemma 6.11,
 $N$
is
$N$
is
 $\alpha$
-good, thus
$\alpha$
-good, thus
 $M$
verifies the condition
$M$
verifies the condition
 $(A,B)$
.
$(A,B)$
. -
 $\ast$
If
$\ast$
If
 $M_1 = \mu \alpha .\mu \gamma .N{\rightarrow }_{\varepsilon } \mu \alpha .N_{\gamma } = \mu \alpha .P$
, then, by Lemma 6.10,
$M_1 = \mu \alpha .\mu \gamma .N{\rightarrow }_{\varepsilon } \mu \alpha .N_{\gamma } = \mu \alpha .P$
, then, by Lemma 6.10,
 $N$
is
$N$
is
 $\alpha$
-good, thus
$\alpha$
-good, thus
 $M_1$
verifies the condition
$M_1$
verifies the condition
 $(A,B)$
.
$(A,B)$
. -
 $\ast$
If
$\ast$
If
 $M_1 =(\mu \alpha .K)L{\rightarrow }_{\mu } \mu \alpha .K[\alpha :=_rL] = \mu \alpha .P$
, then
$M_1 =(\mu \alpha .K)L{\rightarrow }_{\mu } \mu \alpha .K[\alpha :=_rL] = \mu \alpha .P$
, then
 $K[\alpha :=_rL]$
would be
$K[\alpha :=_rL]$
would be
 $\alpha$
-good which is impossible according to Lemma 6.10.
$\alpha$
-good which is impossible according to Lemma 6.10. -
 $\ast$
If
$\ast$
If
 $M_1 =(L)\mu \alpha .K{\rightarrow }_{\mu '} \mu \alpha .K[\alpha :=_lL] = \mu \alpha .P$
, then
$M_1 =(L)\mu \alpha .K{\rightarrow }_{\mu '} \mu \alpha .K[\alpha :=_lL] = \mu \alpha .P$
, then
 $K[\alpha :=_lL]$
would be
$K[\alpha :=_lL]$
would be
 $\alpha$
-good which is impossible according to Lemma 6.10.
$\alpha$
-good which is impossible according to Lemma 6.10.
-
-
-
If
 $M = (\mu \beta ^{\neg (C{\rightarrow } D)}. M_3^{\bot }){M_2}^C$
is the reduced redex and
$M = (\mu \beta ^{\neg (C{\rightarrow } D)}. M_3^{\bot }){M_2}^C$
is the reduced redex and
 $M'=\mu \beta . M_3[\beta :=_rM_2]$
, then, by Lemma 6.8, we have three subcases to examine.
$M'=\mu \beta . M_3[\beta :=_rM_2]$
, then, by Lemma 6.8, we have three subcases to examine.
-
– The case where
 $(A,B)$
holds for
$(A,B)$
holds for
 $M_2$
is immediate.
$M_2$
is immediate. -
– If
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q^A=O[\beta :=_rM_2]$
for some
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q^A=O[\beta :=_rM_2]$
for some
 $O = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^{A} \preceq M_3$
and
$O = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^{A} \preceq M_3$
and
 $P_1[\beta :=_rM_2]$
is
$P_1[\beta :=_rM_2]$
is
 $\alpha$
-good, then, since
$\alpha$
-good, then, since
 $\alpha \not \in \textrm{fv}(M_2)$
, by Lemma 6.10,
$\alpha \not \in \textrm{fv}(M_2)$
, by Lemma 6.10,
 $P_1$
is
$P_1$
is
 $\alpha$
-good, thus
$\alpha$
-good, thus
 $M$
verifies the condition
$M$
verifies the condition
 $(A,B)$
.
$(A,B)$
. -
– If
 $[\beta ]\mu \alpha . P_1 \preceq M_3$
,
$[\beta ]\mu \alpha . P_1 \preceq M_3$
,
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1[\beta :=M_2]^{\bot })M_2^A \preceq M'$
and
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1[\beta :=M_2]^{\bot })M_2^A \preceq M'$
and
 $P_1[\beta :=M_2]$
is
$P_1[\beta :=M_2]$
is
 $\alpha$
-good, then
$\alpha$
-good, then
 $C{\rightarrow } D = A{\rightarrow } B$
and since
$C{\rightarrow } D = A{\rightarrow } B$
and since
 $\alpha \not \in \textrm{fv}(M_2)$
, by Lemma 6.10,
$\alpha \not \in \textrm{fv}(M_2)$
, by Lemma 6.10,
 $P_1$
is
$P_1$
is
 $\alpha$
-good, thus
$\alpha$
-good, thus
 $M$
verifies the condition
$M$
verifies the condition
 $(A,B)$
.
$(A,B)$
.
-
-
If
 $M = (M_1^{C{\rightarrow } D})\mu \beta ^{\neg C} .M_3^{\bot }$
is the reduced redex and
$M = (M_1^{C{\rightarrow } D})\mu \beta ^{\neg C} .M_3^{\bot }$
is the reduced redex and
 $M'=\mu \beta . M_3[\beta :=_lM_1]$
, then, by Lemma 6.8, we have three subcases to consider.
$M'=\mu \beta . M_3[\beta :=_lM_1]$
, then, by Lemma 6.8, we have three subcases to consider.
-
– The case where
 $(A,B)$
holds for
$(A,B)$
holds for
 $M_1$
is immediate.
$M_1$
is immediate. -
– If
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q^A=O[\beta :=_lM_1]$
for some
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q^A=O[\beta :=_lM_1]$
for some
 $O = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^{A} \preceq M_3$
and
$O = (\mu \alpha ^{\neg (A{\rightarrow } B)}.P_1^{\bot })Q_1^{A} \preceq M_3$
and
 $P_1[\beta :=_lM_1]$
is
$P_1[\beta :=_lM_1]$
is
 $\alpha$
-good, then, since
$\alpha$
-good, then, since
 $\alpha \not \in \textrm{fv}(M_1)$
, by Lemma 6.10,
$\alpha \not \in \textrm{fv}(M_1)$
, by Lemma 6.10,
 $P_1$
is
$P_1$
is
 $\alpha$
-good, thus
$\alpha$
-good, thus
 $M$
verifies the condition
$M$
verifies the condition
 $(A,B)$
.
$(A,B)$
. -
– If
 $M_1 = \mu \alpha . P$
,
$M_1 = \mu \alpha . P$
,
 $[\beta ]Q_1 \preceq M_3$
,
$[\beta ]Q_1 \preceq M_3$
,
 $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q_1[\beta :=_lM_1]^A \preceq M'$
and
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P^{\bot })Q_1[\beta :=_lM_1]^A \preceq M'$
and
 $P$
is
$P$
is
 $\alpha$
-good, then
$\alpha$
-good, then
 $C{\rightarrow } D = A{\rightarrow } B$
and
$C{\rightarrow } D = A{\rightarrow } B$
and
 $M$
verifies the condition
$M$
verifies the condition
 $(A,B)$
.
$(A,B)$
.
-
The lemma below will be applied in the proof of Lemma 6.16 in the case of
![]() $\varepsilon$
-reduction.
$\varepsilon$
-reduction.
Lemma 6.15.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term,
$\lambda \mu$
-term,
![]() $\gamma ^{\neg \bot }$
a
$\gamma ^{\neg \bot }$
a
![]() $\mu$
-variable and
$\mu$
-variable and
![]() $A,B$
be two types. Assume
$A,B$
be two types. Assume
![]() $(\lambda x^{A}.P^{B})Q^{A}\preceq M_{\gamma }$
. Then
$(\lambda x^{A}.P^{B})Q^{A}\preceq M_{\gamma }$
. Then
![]() $(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
for some terms
$(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
for some terms
![]() $P_1,Q_1$
.
$P_1,Q_1$
.
Proof.
By induction on
![]() $M$
.
$M$
.
The next lemma shows that the origin of a
![]() $\beta$
-redex of type
$\beta$
-redex of type
![]() $A\to B$
through a
$A\to B$
through a
![]() $\mu \mu '\rho \varepsilon$
-reduction sequence is either a
$\mu \mu '\rho \varepsilon$
-reduction sequence is either a
![]() $\beta$
-redex or a
$\beta$
-redex or a
![]() $\mu$
-redex verifying the condition
$\mu$
-redex verifying the condition
![]() $(A,B)$
of the same type.
$(A,B)$
of the same type.
Lemma 6.16.
If
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
and
![]() $(\lambda x^{A}.P^{B})Q^{A}\preceq M'$
, then either
$(\lambda x^{A}.P^{B})Q^{A}\preceq M'$
, then either
![]() $(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
for some terms
$(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
for some terms
![]() $P_1,Q_1$
or the condition
$P_1,Q_1$
or the condition
![]() $(A,B)$
holds for
$(A,B)$
holds for
![]() $M$
.
$M$
.
Proof.
By Lemma 6.14, it is enough to examine the case of one-step reduction. We proceed by induction on
![]() $M$
. The cases
$M$
. The cases
![]() $M = \lambda y.N$
,
$M = \lambda y.N$
,
![]() $M = \mu \beta .N$
, and
$M = \mu \beta .N$
, and
![]() $M = [\beta ]N$
are treated by induction and using Lemma 6.15.
$M = [\beta ]N$
are treated by induction and using Lemma 6.15.
-
Assume
 $M = (M_1)M_2$
and
$M = (M_1)M_2$
and
 $M$
is not the reduced redex.
$M$
is not the reduced redex.
-
– If
 $M' =(M'_1)M_2$
,
$M' =(M'_1)M_2$
,
 $M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
and
$M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_1$
and
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M'_1$
or
$(\lambda x^{A}.P^{B})Q^{A}\preceq M'_1$
or
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M_2$
, then, in the former case, we have the result by applying the IH. The latter case is trivial.
$(\lambda x^{A}.P^{B})Q^{A}\preceq M_2$
, then, in the former case, we have the result by applying the IH. The latter case is trivial. -
– If
 $M' =(M_1)M'_2$
,
$M' =(M_1)M'_2$
,
 $M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
and
$M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M'_2$
and
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M_1$
or
$(\lambda x^{A}.P^{B})Q^{A}\preceq M_1$
or
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M'_2$
, then either we have the result or we can apply the IH.
$(\lambda x^{A}.P^{B})Q^{A}\preceq M'_2$
, then either we have the result or we can apply the IH. -
– If
 $M' = (\lambda x^{A}.P^{B})M_2^{A}$
and
$M' = (\lambda x^{A}.P^{B})M_2^{A}$
and
 $M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } \lambda x.P$
, then the only possible case is
$M_1{\rightarrow }_{\mu \mu '\rho \varepsilon } \lambda x.P$
, then the only possible case is
 $M_1 = \lambda x. O$
and
$M_1 = \lambda x. O$
and
 $O{\rightarrow }_{\mu \mu '\rho \varepsilon } P$
, hence
$O{\rightarrow }_{\mu \mu '\rho \varepsilon } P$
, hence
 $M = (\lambda x^A. O^B)M_2^A$
.
$M = (\lambda x^A. O^B)M_2^A$
. -
– If
 $M' = (\lambda x^{A}.P^{B})M_3^{A}$
and
$M' = (\lambda x^{A}.P^{B})M_3^{A}$
and
 $M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M_3$
, then
$M_2{\rightarrow }_{\mu \mu '\rho \varepsilon } M_3$
, then
 $M = (\lambda x^A. P^B)M_2^A$
.
$M = (\lambda x^A. P^B)M_2^A$
.
-
-
If
 $M = (\mu \alpha ^{\neg (A{\rightarrow } B)}M_3^{\bot })M_2^A$
and
$M = (\mu \alpha ^{\neg (A{\rightarrow } B)}M_3^{\bot })M_2^A$
and
 $M{\rightarrow }_{\mu \mu '\rho \varepsilon } \mu \alpha . M_3[\alpha :=_rM_2]=M'$
, then, by Lemma 6.8, we also have three subcases to examine.
$M{\rightarrow }_{\mu \mu '\rho \varepsilon } \mu \alpha . M_3[\alpha :=_rM_2]=M'$
, then, by Lemma 6.8, we also have three subcases to examine.
-
– The case where
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M_2$
is immediate.
$(\lambda x^{A}.P^{B})Q^{A}\preceq M_2$
is immediate. -
– If
 $(\lambda x^{A}.P^{B})Q^{A}=O[\alpha :=_rM_2]$
for some
$(\lambda x^{A}.P^{B})Q^{A}=O[\alpha :=_rM_2]$
for some
 $O=(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M_3$
, then
$O=(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M_3$
, then
 $(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
, and we have the result.
$(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
, and we have the result. -
– If
 $[\alpha ]\lambda x^{A}.P_1^{B}\preceq M_3$
and
$[\alpha ]\lambda x^{A}.P_1^{B}\preceq M_3$
and
 $(\lambda x^{A}.P_1[\alpha :=_rM_2] ^{B})M_2^{A}\preceq M'$
, then
$(\lambda x^{A}.P_1[\alpha :=_rM_2] ^{B})M_2^{A}\preceq M'$
, then
 $M_3$
is
$M_3$
is
 $\alpha$
-good and the condition
$\alpha$
-good and the condition
 $(A,B)$
holds for
$(A,B)$
holds for
 $M$
.
$M$
.
-
-
If
 $M = (M_1^{A{\rightarrow } B})\mu \alpha ^{\neg A}.M_3^{\bot }$
,
$M = (M_1^{A{\rightarrow } B})\mu \alpha ^{\neg A}.M_3^{\bot }$
,
 $M{\rightarrow }_{\mu \mu '\rho \varepsilon } \mu \alpha . M_3[\alpha :=_lM_1]=M'$
, then, by Lemma 6.8, we have the subcases below.
$M{\rightarrow }_{\mu \mu '\rho \varepsilon } \mu \alpha . M_3[\alpha :=_lM_1]=M'$
, then, by Lemma 6.8, we have the subcases below.
-
– The case where
 $(\lambda x^{A}.P^{B})Q^{A}\preceq M_1$
is immediate.
$(\lambda x^{A}.P^{B})Q^{A}\preceq M_1$
is immediate. -
– If
 $(\lambda x^{A}.P^{B})Q^{A}=O[\alpha :=_lM_1]$
for some
$(\lambda x^{A}.P^{B})Q^{A}=O[\alpha :=_lM_1]$
for some
 $O=(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M_3$
, then
$O=(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M_3$
, then
 $(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
, and we have the result.
$(\lambda x^{A}.P_1^{B})Q_1^{A}\preceq M$
, and we have the result. -
– If
 $M_1 = \lambda x.P$
,
$M_1 = \lambda x.P$
,
 $[\alpha ]Q_1 \preceq M_3$
and
$[\alpha ]Q_1 \preceq M_3$
and
 $(\lambda x^{A}.P^{B})Q_1[\alpha :=_lM_1]^{A}\preceq M'$
, then
$(\lambda x^{A}.P^{B})Q_1[\alpha :=_lM_1]^{A}\preceq M'$
, then
 $M=(\lambda x^{A}.P^{B})\mu \alpha ^{\neg A}.M_3^{\bot }$
and our assertion follows.
$M=(\lambda x^{A}.P^{B})\mu \alpha ^{\neg A}.M_3^{\bot }$
and our assertion follows.
-
We obtain the following corollaries about
![]() $\mu \mu '\rho \varepsilon$
-reduction sequences. Intuitively, the origin of a
$\mu \mu '\rho \varepsilon$
-reduction sequences. Intuitively, the origin of a
![]() $\beta$
-redex through a
$\beta$
-redex through a
![]() $\mu \mu '\rho \varepsilon$
-reduction sequence is a
$\mu \mu '\rho \varepsilon$
-reduction sequence is a
![]() $\mu$
-redex of the same type.
$\mu$
-redex of the same type.
Corollary 6.17.
If
![]() $M \in \mathcal{NF}_{\beta }$
,
$M \in \mathcal{NF}_{\beta }$
,
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N$
and
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } N$
and
![]() $(\lambda x^A.P_1^B)Q_1^A \preceq N$
, then
$(\lambda x^A.P_1^B)Q_1^A \preceq N$
, then
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A} \preceq M$
for some terms
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A} \preceq M$
for some terms
![]() $P_2,Q_2$
.
$P_2,Q_2$
.
Proof. By Lemma 6.16.
6.3 Weak normalization
In this subsection, we state our main result (Theorem 6.24), which asserts that
![]() $\lambda \mu \mu '\rho \varepsilon \theta$
-reduction in the typed
$\lambda \mu \mu '\rho \varepsilon \theta$
-reduction in the typed
![]() $\lambda \mu$
-calculus is weakly normalizing.
$\lambda \mu$
-calculus is weakly normalizing.
We define the rank of a
![]() $\beta$
-redex first, and then the rank of a
$\beta$
-redex first, and then the rank of a
![]() $\lambda \mu$
-term. We could also define the rank of all the other redexes (and, especially, that of a
$\lambda \mu$
-term. We could also define the rank of all the other redexes (and, especially, that of a
![]() $\mu$
-redex), but we do not need this for our subsequent proofs.
$\mu$
-redex), but we do not need this for our subsequent proofs.
Definition 6.18.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term.
$\lambda \mu$
-term.
-
1. Let
 $r=(\lambda x^A.P^B)Q^A$
be a
$r=(\lambda x^A.P^B)Q^A$
be a
 $\beta$
-redex of
$\beta$
-redex of
 $M$
. The rank of
$M$
. The rank of
 $r$
in
$r$
in
 $M$
is defined by
$M$
is defined by
 $\textrm{rank}(r,M)=\textrm{lh}(A{\rightarrow } B)$
.
$\textrm{rank}(r,M)=\textrm{lh}(A{\rightarrow } B)$
. -
2. The rank of
 $M$
is
$M$
is
 $\textrm{rank}(M)=max\{\textrm{rank}(r,M)\;|\;r\textrm{is a}\ \beta \textrm{-redex in }M\}$
.
$\textrm{rank}(M)=max\{\textrm{rank}(r,M)\;|\;r\textrm{is a}\ \beta \textrm{-redex in }M\}$
.
At this point, we can combine all of our previous results on the creation of redexes to prove that
![]() $\beta \mu \mu '\rho \varepsilon$
-reduction is weakly normalizing (Theorem 6.21). In the statements below, we implicitly make use of the facts that typed
$\beta \mu \mu '\rho \varepsilon$
-reduction is weakly normalizing (Theorem 6.21). In the statements below, we implicitly make use of the facts that typed
![]() $\beta$
-reduction is strongly normalizing (Krivine Reference Krivine1993) (in fact, weak normalization suffices here) and that
$\beta$
-reduction is strongly normalizing (Krivine Reference Krivine1993) (in fact, weak normalization suffices here) and that
![]() $\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing (Theorem 5.10).
$\mu \mu '\rho \varepsilon$
-reduction is weakly normalizing (Theorem 5.10).
Corollary 6.19.
Let
![]() $M_1,M_3 \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
$M_1,M_3 \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
and
![]() $M_2 \in \mathcal{NF}_{\beta }$
such that
$M_2 \in \mathcal{NF}_{\beta }$
such that
![]() $M_3 \not \in \mathcal{NF}_{\beta }$
and
$M_3 \not \in \mathcal{NF}_{\beta }$
and
![]() $M_1 \twoheadrightarrow _{\beta } M_2 \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M_3$
, then
$M_1 \twoheadrightarrow _{\beta } M_2 \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M_3$
, then
![]() $\textrm{rank}(M_1) \gt \textrm{rank}(M_3)$
.
$\textrm{rank}(M_1) \gt \textrm{rank}(M_3)$
.
Proof.
Let
![]() $(\lambda x^A.P_1^B)Q_1^A$
be a
$(\lambda x^A.P_1^B)Q_1^A$
be a
![]() $\beta$
-redex of
$\beta$
-redex of
![]() $M_3$
having maximal rank. By Corollary 6.17,
$M_3$
having maximal rank. By Corollary 6.17,
![]() $(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A} \preceq M_2$
and, by Corollary 6.7,
$(\mu \alpha ^{\neg (A{\rightarrow } B)}.P_2^{\bot })Q_2^{A} \preceq M_2$
and, by Corollary 6.7,
![]() $(\lambda y^C.P_1'^D)Q_1'^C \preceq M_1$
where
$(\lambda y^C.P_1'^D)Q_1'^C \preceq M_1$
where
![]() $\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
. Hence
$\textrm{lh}(C{\rightarrow } D) \gt \textrm{lh}(A{\rightarrow } B)$
. Hence
![]() $\textrm{rank}(M_1) \gt \textrm{rank}(M_3)$
.
$\textrm{rank}(M_1) \gt \textrm{rank}(M_3)$
.
Corollary 6.20.
If
![]() $M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
$M \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
![]() $M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
Proof.
By induction on
![]() $\textrm{rank}(M)$
. If
$\textrm{rank}(M)$
. If
![]() $M \not \in \mathcal{NF}_{\beta }$
, then
$M \not \in \mathcal{NF}_{\beta }$
, then
![]() $M \twoheadrightarrow _{\beta } M'$
and
$M \twoheadrightarrow _{\beta } M'$
and
![]() $M' \in \mathcal{NF}_{\beta }$
for some
$M' \in \mathcal{NF}_{\beta }$
for some
![]() $M'$
. If
$M'$
. If
![]() $M' \not \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
$M' \not \in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
, then
![]() $M' \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M''$
and
$M' \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M''$
and
![]() $M''\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. Finally, if
$M''\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. Finally, if
![]() $M''\not \in \mathcal{NF}_{\beta }$
, by Corollary 6.19,
$M''\not \in \mathcal{NF}_{\beta }$
, by Corollary 6.19,
![]() $\textrm{rank}(M) \gt \textrm{rank}(M'')$
and, by IH,
$\textrm{rank}(M) \gt \textrm{rank}(M'')$
and, by IH,
![]() $M'' \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
, then
$M'' \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
, then
![]() $M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
We are now in a position to prove our weak normalization result.
Theorem 6.21.
In the typed
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\beta \mu \mu '\rho \varepsilon$
-reduction is weakly normalizing.
$\beta \mu \mu '\rho \varepsilon$
-reduction is weakly normalizing.
Proof.
Let
![]() $M$
be a
$M$
be a
![]() $\lambda \mu$
-term and
$\lambda \mu$
-term and
![]() $M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
where
$M \twoheadrightarrow _{\mu \mu '\rho \varepsilon } M'$
where
![]() $M'\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. By Corollary 6.20,
$M'\in \mathcal{NF}_{\mu \mu '\rho \varepsilon }$
. By Corollary 6.20,
![]() $M' \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
, hence
$M' \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
, hence
![]() $M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
$M \in \mathcal{WN}_{\beta \mu \mu '\rho \varepsilon }$
.
We can also extend our weak normalization algorithm for the
![]() $\theta$
-rule. First, we prove that
$\theta$
-rule. First, we prove that
![]() $\theta$
-reduction creates no
$\theta$
-reduction creates no
![]() $\beta \mu \mu '\rho \varepsilon$
-redex when the starting
$\beta \mu \mu '\rho \varepsilon$
-redex when the starting
![]() $\lambda \mu$
-term is in
$\lambda \mu$
-term is in
![]() $\beta \mu \mu '\rho \varepsilon$
-normal form. Hence,
$\beta \mu \mu '\rho \varepsilon$
-normal form. Hence,
![]() $\theta$
-reduction can be postponed.
$\theta$
-reduction can be postponed.
Lemma 6.22.
Let
![]() $M\in \mathcal{NF}_{\beta \mu \mu '\rho \varepsilon }$
. If
$M\in \mathcal{NF}_{\beta \mu \mu '\rho \varepsilon }$
. If
![]() $M\twoheadrightarrow _{\theta }M'$
, then
$M\twoheadrightarrow _{\theta }M'$
, then
![]() $M'\in \mathcal{NF}_{\beta \mu \mu '\rho \varepsilon }$
.
$M'\in \mathcal{NF}_{\beta \mu \mu '\rho \varepsilon }$
.
Proof.
It is enough to examine the case of one-step reduction. Let
![]() $\mu \alpha .[\alpha ]N$
be the
$\mu \alpha .[\alpha ]N$
be the
![]() $\theta$
-redex reduced in
$\theta$
-redex reduced in
![]() $M$
. We observe that if
$M$
. We observe that if
![]() $\mu \alpha .[\alpha ]N \prec M$
, then
$\mu \alpha .[\alpha ]N \prec M$
, then
![]() $\lambda x. \mu \alpha .[\alpha ]N \preceq M$
, and if
$\lambda x. \mu \alpha .[\alpha ]N \preceq M$
, and if
![]() $\lambda x. \mu \alpha .[\alpha ]N \prec M$
, then
$\lambda x. \mu \alpha .[\alpha ]N \prec M$
, then
![]() $[\beta ]\lambda x. \mu \alpha .[\alpha ]N \preceq M$
or
$[\beta ]\lambda x. \mu \alpha .[\alpha ]N \preceq M$
or
![]() $(Q)\lambda x. \mu \alpha .[\alpha ]N \preceq M$
, where
$(Q)\lambda x. \mu \alpha .[\alpha ]N \preceq M$
, where
![]() $Q \neq \lambda y.Q'$
and
$Q \neq \lambda y.Q'$
and
![]() $Q \neq \mu \gamma . Q'$
. Thus,
$Q \neq \mu \gamma . Q'$
. Thus,
![]() $\theta$
-reduction in
$\theta$
-reduction in
![]() $M$
cannot create other redexes.
$M$
cannot create other redexes.
Lemma 6.23.
Both in the typed and in the untyped
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\theta$
-reduction strongly normalizes.
$\theta$
-reduction strongly normalizes.
Proof.
We observe that
![]() $\theta$
-reduction decreases the size of the terms.
$\theta$
-reduction decreases the size of the terms.
Theorem 6.24.
In the typed
![]() $\lambda \mu$
-calculus,
$\lambda \mu$
-calculus,
![]() $\lambda \mu \mu '\rho \varepsilon \theta$
-reduction is weakly normalizing.
$\lambda \mu \mu '\rho \varepsilon \theta$
-reduction is weakly normalizing.
Proof. Follows from Theorem 6.21 and Lemmas 6.22 and 6.23.
7. Future Work
-
1. Apart from the fact that the
 $\mu '$
-rule destroys confluence, it has another flaw. It is the only rule (among the rules we have presented in this paper) that does not preserve second-order types (the classical counterparts of Girard’s system
$\mu '$
-rule destroys confluence, it has another flaw. It is the only rule (among the rules we have presented in this paper) that does not preserve second-order types (the classical counterparts of Girard’s system
 $\mathcal{F}$
and Krivine’s system
$\mathcal{F}$
and Krivine’s system
 $\mathcal{AF}_2$
). In Py (Reference Py1998), Py has presented an example of a
$\mathcal{AF}_2$
). In Py (Reference Py1998), Py has presented an example of a
 $\lambda \mu$
-term discovered by Raffalli which produces a
$\lambda \mu$
-term discovered by Raffalli which produces a
 $\lambda \mu$
-term of an arbitrary type starting from another
$\lambda \mu$
-term of an arbitrary type starting from another
 $\lambda \mu$
-term of a different type. The problem is caused exclusively by the
$\lambda \mu$
-term of a different type. The problem is caused exclusively by the
 $\mu '$
-rule. It would be interesting to find conditions under which, on the one hand, the
$\mu '$
-rule. It would be interesting to find conditions under which, on the one hand, the
 $\mu '$
-rule would preserve types, and, on the other hand, the uniqueness of the representation of integers and strong normalization would be retained.
$\mu '$
-rule would preserve types, and, on the other hand, the uniqueness of the representation of integers and strong normalization would be retained. -
2. In Nour and Ziadeh (Reference Nour and Ziadeh2017), the second author and Ziadeh have presented a realizability semantics for the
 $\lambda \mu$
-calculus equipped only with
$\lambda \mu$
-calculus equipped only with
 $\beta$
- and
$\beta$
- and
 $\mu$
-reduction rules. They have obtained a completeness result for this semantics. This type of semantics is interesting since, on the one hand, it characterizes the algorithmic behavior of typed
$\mu$
-reduction rules. They have obtained a completeness result for this semantics. This type of semantics is interesting since, on the one hand, it characterizes the algorithmic behavior of typed
 $\lambda \mu$
-terms and, on the other hand, it can be a tool for proving weak or strong normalization. Adding other reduction rules (even the simplest ones like
$\lambda \mu$
-terms and, on the other hand, it can be a tool for proving weak or strong normalization. Adding other reduction rules (even the simplest ones like
 $\rho$
- or
$\rho$
- or
 $\theta$
-rules) considerably complicates the study of these semantics. It would be interesting to find a good realizability semantics for the
$\theta$
-rules) considerably complicates the study of these semantics. It would be interesting to find a good realizability semantics for the
 $\lambda \mu$
-calculus with all rules discussed in this paper.
$\lambda \mu$
-calculus with all rules discussed in this paper. -
3. The second author has published (Nour Reference Nour2002) a calculus that encodes second order, classical natural deduction. This calculus also contains rules that permit the encoding of a parallel
 $or$
operator. It would be interesting to study the
$or$
operator. It would be interesting to study the
 $\mu '$
-rule in this calculus and prove its weak normalization.
$\mu '$
-rule in this calculus and prove its weak normalization.
Acknowledgements
We are grateful to T. Hirschowitz and F. Kamareddine, who helped us make the manuscript better, and we thank the referees for their thorough work and numerous comments which have greatly contributed to clarifying and improving the paper.