Methods to estimate the cost-effectiveness of technologies are well-established (Reference Drummond, Sculpher, Torrance, O'Brien and Stoddart1), and are now widely used to inform adoption and reimbursement decisions internationally (Reference O'Donnell, Pham, Pashos, Miller and Smith2). In England and Wales, the National Institute for Health and Clinical Excellence (NICE) issues guidance to the National Health Service and explicitly incorporates cost-effectiveness evidence into its technology appraisal process (3). A similar role is performed by the Scottish Medicines Consortium in Scotland (4).
These decisions are often taken in the absence of mature evidence on the effectiveness and cost-effectiveness of technologies. Research prioritization is determined by informal processes and trials are typically designed using frequentist approaches, which select a sample size such that the smallest clinically important difference can be determined at prespecified levels of statistical significance and power. These approaches may fail to convey all appropriate information to decision makers (Reference Claxton5). By explicitly estimating the value of alternative research designs and comparing these to the expected costs, expected value of information (EVI) methods enable joint consideration of adoption and research decisions in a way consistent with the objectives and constraints of the healthcare system (Reference Claxton5;Reference Eckermann, Karnon and Willan6). There is a large theoretical literature surrounding these techniques (Reference Claxton5–Reference Willan and Pinto10), but currently there is little evidence of their application in decision making.
In this study, we consider the usefulness of value of information methods to inform trial design in the context of a real clinical decision problem, relating to alternative techniques for the treatment of patients with a recent non-ST elevated myocardial infarction (NSTEMI). First, we describe the clinical decision problem and detail the construction of a pretrial economic model to summarize the current evidence. We then use the results from this model to consider the optimal design of a trial using EVI methods. We begin with a minimal model with simple but unrealistic assumptions then gradually introduce more realistic assumptions, illustrating the flexibility of EVI models and demonstrating the importance of the decision context in the estimation of sample size. Finally, a critical discussion is offered on the current usefulness of these methods in a real clinical setting based on this application.
Clinical Decision Problem
Coronary angiography is widely used to identify coronary narrowings (stenoses) and identify patients who may benefit from coronary revascularization. However, because the coronary angiogram is interpreted visually, judgments about stenosis severity are subjective, potentially leading to misdiagnosis and incorrect treatment decisions which have prognostic importance and resource implications. This problem is greatest in patients with multiple coronary narrowings where there is a need to distinguish between stenoses which do and do not cause ischemia.
The measurement of fractional flow reserve (FFR) using a coronary guidewire with a pressure sensor has the potential to improve diagnostic accuracy in coronary artery disease (CAD) and is now an established technique in the invasive management of people with stable CAD (Reference Kern, Lerman and Bech11). Results from recent studies in stable patients with long-term, chronic CAD such as angina, highlighted the benefits of FFR measurement to more accurately identify culprit lesions and guide stenting with improved outcomes compared with the visual interpretation of the angiogram alone (Reference Fearon, Bornschein and Tonino12;Reference Pijls, Fearon and Tonino13). Based on 1-year follow-up in the FAME study, FFR measurement was found to generate resource savings and promote improvements in health, and it has been posited that this outcome most probably arose from the large number of false positive patients who went on to receive percutaneous coronary intervention (PCI) unnecessarily in the angiogram only group (Reference Fearon, Bornschein and Tonino12). Although these trial results are not expected to be perfectly applicable to NSTEMI patients who differ in important respects from the patients in these trials, these results do suggest there is a potential for large clinical utility from a wider adoption of FFR measurement in NSTEMI patients.
METHODS
Economic Model
An economic model was constructed to reflect the predominant treatment and prognostic pathways of individuals with a recent NSTEMI who are at intermediate-high risk of further vascular events and are amenable to revascularization. The treatment options considered are coronary angiography alone (CA) and coronary angiography supported by FFR measurement (PW). Costs are expressed in GBP at a 2010 price base and benefits are expressed in quality-adjusted life-years (QALYs). A patient lifetime time horizon was used and costs and benefits were discounted at an annual rate of 3.5 percent based on NICE guidance (3). The model was probabilistic in that all input parameters were entered as probability distributions to reflect the uncertainty in the estimates of the population means. Monte Carlo simulation was used to propagate this uncertainty through the model.
In stage 1 of the model, individuals are allocated to index treatments based on the interpretation of the results of the diagnostic technologies and other complex criteria (e.g., medical history) by cardiologists. Four treatment options common to both treatment strategies are available: patients may be revascularized using PCI or a coronary artery bypass graft (CABG), a decision may be deferred until the results of further tests are available (DEFER) or medical therapy alone may be prescribed. In all cases, a common medical therapy package is assumed (see Table 1). PW is expected to change the distribution of index treatments by reducing diagnostic uncertainty. Odds ratios are applied separately to the probabilities of revascularization, PCI conditional on revascularization and DEFER conditional on no revascularization. In addition, the relative cost of PCI is allowed to differ between strategies, reflecting possible differences in average PCI procedures.
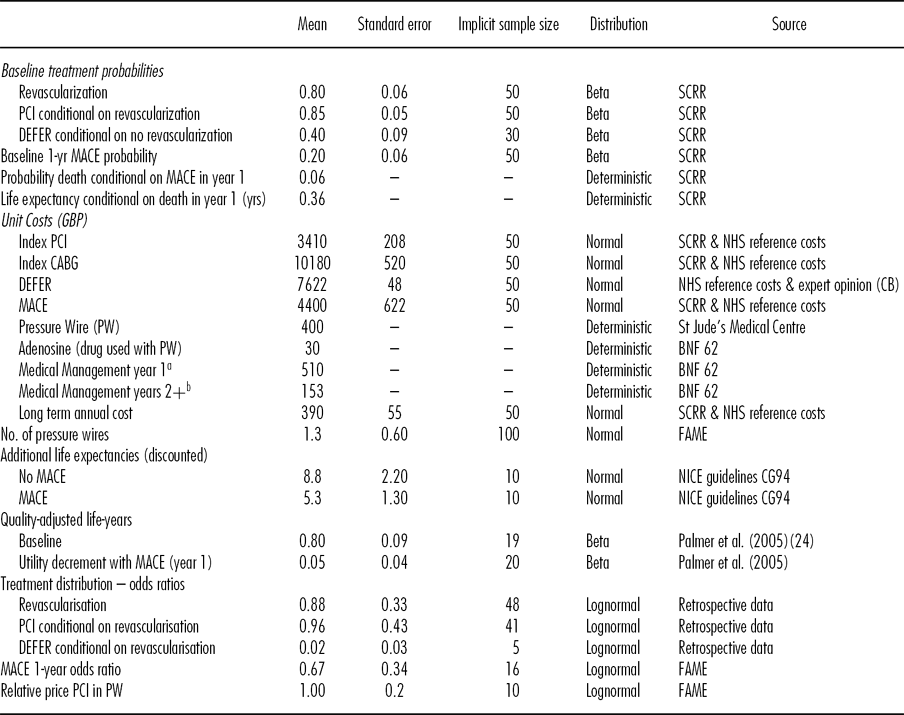
Table 1. Data Inputs in Economic Model

aAspirin (75mg), Bisoprolol (5mg), Ramipril (10mg), Simvastatin (40mg), Nitrate (20mg), Clopidogrel (90mg). All per day; bAs for year 1 but without Clopidogrel.
Individuals are at risk of further events, including death, myocardial infarction, stroke and revascularization (stage Reference O'Donnell, Pham, Pashos, Miller and Smith2). These are combined into a single composite major adverse cardiac event (14) outcome, which is assumed independent of the index treatment. The relative effect of FFR measurement on the risk of a MACE is restricted to 1-year based on the results of the FAME trial (Reference Fearon, Bornschein and Tonino12), expert opinion and model calibration. There is a utility decrement associated with a MACE and an additional loss of QALYs due to the risk of death in year 1. This 1-year treatment effect is extrapolated to a lifetime time horizon by modeling life expectancies conditional on the presence of a MACE event in the first year. A common cost and QALY tariff is applied to all additional years of death. Medical therapy is assumed to be received linearly over time for as long as the individual remains alive.
Baseline probabilities of the index treatments and of a MACE were estimated from data between 1st April 2006 and 31st May 2009 in the Scottish Cardiac Revascularisation Register (SCRR), which contains detailed information on all coronary angiograms, PCIs and CABGs in Scotland. Means and standard deviations for the costs of the index PCIs and CABGs and a MACE were estimated by combining detailed data from the SCRR with NHS Reference costs 2009–10 (15). The data are limited in several respects, including difficulties in attributing index treatments to individuals and the absence of important exclusion criteria, such that using the study size to estimate standard errors would underestimate the uncertainty in the derived estimates. Implicit sample sizes were used to better reflect the inherent uncertainty in the estimation of the above parameters. The costs of the DEFER option were estimated by assuming an average of four outpatient attendances, one hospital attendance, and one diagnostic test based on expert recommendation (C.B.).
The odds ratios applied to the index treatment probabilities were estimated using data from a retrospective study assessing how FFR measurement affects clinical decisions (Reference Carrick, Behan and Foo16). Briefly, three cardiologists each examined the angiogram results of 100 retrospective real patients and made a hypothetical recommendation based on their observations. FFR results were then revealed and the cardiologists were asked to state a new hypothetical treatment recommendation. The relative effect for the MACE probability at 1-year was taken from the FAME trial results (Reference Fearon, Bornschein and Tonino12). There are limits to the generalizability of the estimates from both sources. In particular, patients were selected into the retrospective study based on the presence of diagnostic uncertainty and so are not representative of NSTEMI patients as a whole and the effect of FFR measurement in the FAME study was based on a sample with stable CAD not NSTEMI. It is, therefore, necessary to discount sample sizes to reflect the additional uncertainty in these estimates.
Life expectancies at year 1 were taken from a previous model in patients with unstable angina or NSTEMI, with separate estimates for those who have a MACE in year 1 and those who do not. A common QALY tariff and cost is applied to all years after year 1. The cost consists of costs of further events, calculated in the same manner as described above, and continuing medical therapy (see Table 1).
We compare strategies according to the mean incremental net monetary benefit (INB) of PW compared with CA. Net monetary benefit for treatment i is calculated as the mean QALYs multiplied by the threshold value for a QALY, λ, minus mean costs: NBi = λqi − ci, where i = CA or PW. The threshold value should reflect the opportunity costs of implementation in the health service and a value of between GBP 20K and GBP 30K is commonly used in the United Kingdom. Incremental net monetary benefit (INB) is the difference in net monetary benefit (NMB) between the two strategies: INB = NMBPW − NMBCA. In this case, if INB is positive, PW is the expected cost-effective alternative and if it is negative, CA is the expected cost-effective strategy.
RESULTS
Economic Model
Owing to the additional cost of measuring FFR (GBP 550), PW is expected to increase costs in year 1 by GBP 168 per-person despite expected reductions in the index treatment costs (GBP 118) and costs of further events (GBP 264). By reducing the expected MACE rate in year 1, PW is expected to increase average life expectancy and consequently raise costs beyond year 1 by GBP 65. Overall, PW is expected to increase lifetime discounted costs by GBP 232 (SE GBP 527) per person.
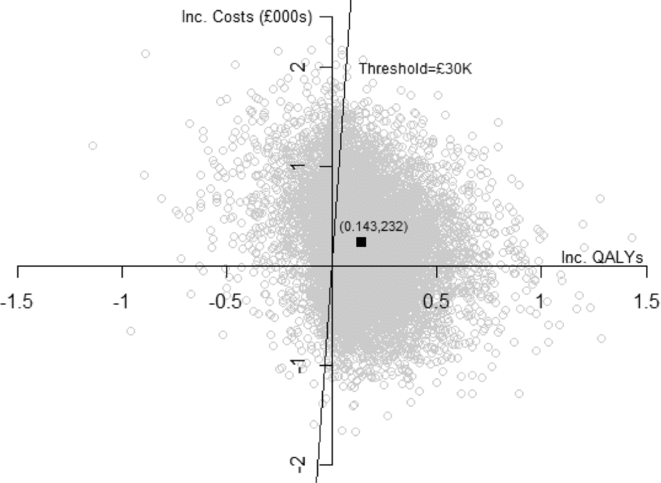
Expected discounted QALYs are greater with PW by 0.012 in year 1, and by 0.132 beyond 1 year, implying an overall expected increase in discounted QALYs of 0.143 (SE 0.203). The incremental net monetary benefit is increasing in λ and for λ = GBP 30,000 is GBP 4,069 ( = 30,000 × 0.143–232). For λ = GBP 20,000, INB = GBP 2,635. As illustrated in Figure 2, the mean estimate is subject to substantial uncertainty, with a standard deviation of GBP 6,233. The probability that PW is cost-effective is increasing in λ and for λ = GBP 20,000 is 0.75 and for λ = GBP 30,000 is 0.77.

Figure 1. Schematic of economic model.

Figure 2. Cost-effectiveness scatter plot.
Value of Information
Expected value of information methods explicitly compare expected costs of trialing with the expected benefits and have the potential to inform research prioritization and trial design in a way consistent with the constraints and objectives of the healthcare system. The optimal trial design is chosen such that the expected net gain (ENG), that is the difference between expected benefits and expected costs, is maximized.
Most applied research using value of information methods has focused on estimating the value of perfect information (EVPI), that is, the value of completely eliminating decision uncertainty (Reference Eckermann, Karnon and Willan6). In the case study considered, although PW is expected to be cost-effective, due to the uncertainty in this estimate, there is a probability of 0.23 given current evidence that, in fact, CA is cost-effective. If it is the case that CA is actually cost-effective and PW is adopted, then a loss is imposed equal to the true INB of CA relative to PW. The EVPI for a representative individual is the sum of the losses when CA is cost-effective weighted by the corresponding probabilities. EVPI provides an upper bound to the amount a decision maker should be willing to pay to eliminate decision uncertainty but is constrained in its ability to inform trial design because it does not consider the costs of trialing or the extent to which trials are actually able to reduce decision uncertainty. Trials are expected to reduce uncertainty in per-patient INB with the level of uncertainty expected to fall with increases in sample size. The individual expected value of sample information (EVSI) is the expected reduction in per-patient EVPI or opportunity loss pre- and post-trial, and can be estimated for a range of trial designs. As the sample size increases, the per-patient EVSI approaches per-patient EVPI. Here we use an analytic solution to the estimation of EVPI and EVSI which uses estimates of the mean INB, its variance and the between patient variance in the net benefit, estimated from the pretrial model (Reference Willan and Pinto10). The between-patient variance in net benefit was estimated from the model output by scaling up the observed variance in net benefit using an implicit sample size of 20. In this case study, EVPI for a representative individual is estimated to be GBP 964.
The expected value of information to the population is estimated by multiplying the expected value for an individual by the population expected to benefit. If the information was available immediately this would be every incident patient for as long as the technology was useful. The annual incidence of eligible individuals was estimated to be 20,000 based on the application of the trial exclusion criteria to BNF myocardial statistics for the United Kingdom (Reference Scarborough, Bhatnagar and Wickramasinghe17). The time horizon of the technology is assumed to be 10 years, reflecting possible future changes in technology, prices, and information (Reference Hoomans, Fenwick, Palmer and Claxton18). Over this time horizon, there would be 200,000 potential recipients of the information in the United Kingdom, which combined with the individual EVPI gives a population EVPI of GBP 193 m without discounting. For a 30-year time horizon, this would increase to 600,000 potential beneficiaries and the population EVPI to GBP 578 m.
The total costs of trialing are the sum of fixed costs (FC) of trialing, which are independent of sample size, and variable costs (VC), which represent costs of recruiting each patient. Based on trial planner advice we estimate the FC of trialing to be GBP 225,000 and a variable cost of GBP 200 associated with recruitment. Total costs for a trial of size n per-arm are, therefore, GBP 225,000 + 200 × 2n.
We consider a UK decision context where the decision-maker's problem is a choice between adopting PW, the technology expected to be cost-effective, now or delaying the adoption decision and undertaking a trial with a sample size to be specified (Reference Eckermann and Willan8). Initially we begin with the unrealistic assumption that all incident patients are recruited to the trial and that the information becomes available immediately after the trial concludes, such that the benefits of information accrue to all patients outside the trial. In this model, ENG is maximized at a sample size per-arm of 9,632 providing an expected GBP 121 m net gain.
Relaxing this assumption such that only a proportion of incident patients are recruited to the trial, increases the length of a trial of given size, and reduces the population EVSI for all sample sizes because fewer patients are now able to benefit from the information. Consequently, the optimal sample size is reduced. With 50 percent recruitment, the optimal size is reduced to 6,883 per-arm with an ENG of GBP 109 m. At a recruitment rate of 5 percent, as expected by trial planners, n = 1,767 with a maximum ENG of GBP 47 m. Modeling time for patient follow-up (Reference Drummond, Sculpher, Torrance, O'Brien and Stoddart1 year) and analysis of the data (6 months) further increases the length of a trial independent of sample size, reducing further the number of potential beneficiaries from the information and so leads to a further, albeit relatively small, reduction in optimal sample size to n = 1,593 with an ENG of GBP 35 m. Figure 3a plots each of the total costs, expected population EVSI and ENG as a function of the sample size per-arm. Financial costs of the trial are very low relative to the scale of benefit and have little influence on optimal sample size. For n below 1,593, the expected benefits from additional recruitment outweigh the expected costs, and for n above 1,593, the costs exceed the benefits. No improvement in ENG is possible at a sample size per-arm of 1,593.

Figure 3. Graphical representation of value of information models.
While the trial is ongoing, the patients not in the trial, or in the trial but randomized to CA, do not receive the technology expected to maximize net benefit. By not receiving PW, they have forgone the opportunity to benefit by an amount equal to the expected INB. We, therefore, expand the cost function to include these opportunity costs (OC). Now, additional recruitment, by lengthening a trial, imposes a substantially greater cost resulting from these forgone benefits (Reference Eckermann and Willan7). In this case study, the scale of the OCs is so large relative to the scale of benefit that the optimal decision becomes not to trial but instead to simply adopt PW. As presented in Figure 3b, the ENG is negative for any positive n.
In the framework considered thus far, it has been assumed that all patients and providers adopt the technology chosen by the decision maker. However, the extent to which adoption decisions are implemented in practice can be variable (Reference Drummond and Weatherly19). Nonadherence to decision-maker recommendations by patients and healthcare professionals may be caused by a variety of factors including knowledge, attitude and chance (Reference Hoomans, Fenwick, Palmer and Claxton18). Nevertheless, implementation can, at least in part, be expected to depend on the strength of evidence for the INB, and previous studies have modeled implementation as a function of the strength of evidence to allow for the estimation of optimal sample size (Reference Willan and Eckermann9;Reference Gittins and Pezeshk20). In particular, a sliding step function is used in which implementation depends on the standardized INB, that is, the mean INB divided by its standard deviation (Reference Willan and Eckermann9). Modeling the relationship between evidence and implementation in this way, increases the value of information at all sample sizes because now additional recruitment is not only expected to reduce uncertainty in the adoption decision but also to improve the implementation of PW. Furthermore, in our case study because 2.3 percent of patients currently receive PW, based on evidence from the SCRR, then even in the absence of further research the OC is slightly reduced for all sample sizes.
Based on the current observed implementation rate of 2.3 percent and the standardized INB estimated from the model, one additional point on the step function is required for the implementation function to be completely specified. We set this point assuming that implementation is perfect if the standardized net benefit is such that the null hypothesis that the INB ≤0 can be rejected at the 5 percent level. As can be observed graphically in Figure 3c, for n below 216, the costs of trialing exceed the benefits and so the ENG is negative and no trial is preferable. For sample sizes per-arm between 216 and 1,207, trialing is again optimal. ENG is maximized at a sample size of 626 per-arm, delivering an ENG of GBP 52 m. For n greater than 1,207, the expected costs of trialing again exceed the benefits and no trial is preferable.
For model 3c, the sensitivty of the sample size estimates to the economic model was considered through the mean and variance of the INB. A 50 percent increase in the mean INB reduces decision uncertainty and renders no trial optimal. A 50 percent reduction in the mean INB increases n to 705. A 50 percent increase in the variance leads to an optimal sample size of 590 per-arm, while under a 50 percent decrease, decision uncertainty has been reduced and trialling is not optimal. Changes to the annual incidence of disease, and fixed and variable costs had negligible impacts on the optimal sample size, while changes to the time horizon of the technology and the accrual rate have profound effects. For a 5-year time horizon, no trial is optimal, and for a time horizon of 15 years a larger trial with 889 patients per-arm is optimal. Halving the rate of accrual to the trial renders no trial optimal, while a 50 percent increase in accrual rate raises the optimal sample size per-arm to 1,222.
DISCUSSION
A pretrial model was constructed and used to consider the cost-effectiveness of PW relative to CA, the value of a trial and the optimal size of any such trial in the United Kingdom from a societal decision-making perspective. PW is expected to be cost-effective relative to CA, but there is considerable uncertainty in this estimate and consequently substantial benefits from the reduction of this uncertainty via a trial.
The optimal size of a trial has been shown to depend profoundly on the decision context and associated assumptions used to construct EVI models. We started from a set of unrealistic assumptions where all incident patients were assumed to be recruited, no follow-up and analysis time or associated opportunity costs of delay were allowed for and the decision maker was able to perfectly dictate clinical practice. Relaxing these assumptions to allow for recruitment and analysis time reduced the optimal sample size, and explicitly modeling the opportunity costs of trialing rendered no trial optimal. Trialing once again became optimal when imperfect implementation was assumed and a relationship between strength of evidence and implementation modeled. Currently, there is little evidence with which to inform the shape of such a function and the choice is somewhat arbitrary. EVI methods could benefit considerably from further research to enable the shape of such functions to be better specified.
This study has considered optimal trial design with value of information methods within a single jurisdiction, here the United Kingdom. However, the public information generated from a trial in the United Kingdom would be expected to have value in informing decision making in other jurisdictions, for example, Canada or Australia. Therefore, the expected value of the information from a UK perspective underestimates the global expected value of the information generated and the size of a globally optimal trial designed to inform local decisions across such jurisdictions (Reference Eckermann and Willan21). Value of information methods reflecting local decision contexts can be naturally extended to optimal trial design across jurisdictions where co-operation between jurisdictions allows the additional advantages of global trial design to be exploited. However, the successful application of these methods requires overcoming the practical difficulties associated with ensuring appropriate cooperation between jurisdictions.
In this case-study, EVSI has been calculated using a closed form solution which offers a flexible and relatively simple method with which to consider trial design. Alternative methods include simulation techniques (Reference Ades, Lu and Claxton22) which although considerably more complex and computationally intensive than the closed form solution possess several potential advantages. First, the closed-form solution assumes a trial informs INB directly, while trials, in reality, may collect information on only some of the parameters that constitute the INB. Simulation methods can restrict focus to subsets of parameters informed by a trial. Second, the closed-form approach makes the assumption that the INB is normally distributed. However, previous research has found that the appeal to the central limit theorem outperforms bootstrapping where sample sizes are small and data are skewed, while performing with the same asymptotic properties when sample sizes are large (Reference Nixon, Wonderling and Grieve23).
EVI methods require the specification of a large number of uncertain parameters compared with traditional frequentist approaches and are in some instances sensitive to these choices. However, many of these parameters, for example, the lifetime of the technology or the extent to which clinical practice will respond to evidence, are already implicit in funding decisions. EVI models require decision makers to be explicit about the assumptions used, improving the transparency of decision making.
EVI methods offer an appealing alternative to traditional frequentist methods for informing trial design and are more consistent with the constraints and objectives of the healthcare system. In addition they require decision makers to be explicit about the assumptions informing their decisions. The closed-form solution to the calculation of expected benefits offers a flexible method with which to consider alternative decision-making contexts. However, the real-world usefulness of these methods depends on the extent to which decision contexts are able to be realistically and practically represented. In this respect, an important challenge remaining to enable robust application of these methods is evidence for the relationship between trial evidence and implementation, where further research would be valuable.
CONTACT INFORMATION
Seamus Kent, BSc (Hons), MSc., MSc., ([email protected]), Researcher, Health Economics Research Centre, Department of Public Health, University of Oxford, Old Road Campus, Oxford, OX3 7LF
Andrew Briggs, BA (Hons), MSc., MSc., DPhil, Chair in Health Economis, Health Economics and Health Technology Assessment, University of Glasgow
Simon Eckermann, MdSc, Grad.Dip (H.Ec), PhD, Professor of Health Economics, Centre for Health Services Development, University of Wollongong
Colin Berry, BSc (Hons), MB ChB, MRCP, PhD, FRCP, FACC, Professor of Cardiology and Imaging, BHF Cardiovascular Research Centre, University of Glasgow
CONFLICTS OF INTEREST
Colin Berry reports a grant to his institution from Chief Scientist Office, NHS, Scotland for this work; and funding to his institution for consultancy, development of educational presentations, and travel expenses from St Jude Medical. The other authors report they have no potential conflicts of interest.