2.1. Transparency

The negotiations between the EU and United States over the TTIP started in June 2013, but the European Council’s detailed directives for the negotiations (“mandate”) were not made public. Increased pressure from the European Parliament and the EU Ombudsman (2015) led to a deal that allowed Parliament access to the negotiation texts under very strict conditions.

The European Commission (2013) argued that secrecy was inevitable as a matter of international relations, emphasizing the importance of secrecy as a prerequisite for trust among the negotiators. More importantly in the context of our analysis, the European Commission (2015) argued that increased openness would reduce social welfare by inefficient use of public resources.

The European Commission responded to the wave of criticism by civil society organizations against TTIP by releasing a long list of documents that it had previously kept secret. However, the most important TTIP documents remained unavailable, and many claims, both favorable and unfavorable toward TTIP, could not be substantiated. Increased openness in the EU about TTIP negotiations inspired various U.S. groups voicing similar concerns. More than 75 U.S. trade unions, political activist groups, and academics sent a letter to U.S. trade representative Michael Froman, requesting more openness in the TTIP negotiations, asking for the same level of transparency in the United States as in the EU (AFL-CIO, 2015).

2.2. Misinformation: an example from the European Union pathogen reduction treatments debate

The use of chlorine dioxide and other pathogen reduction treatments to remove surface contamination from poultry in U.S. slaughterhouses was one of the most prominent symbols of the European anti-TTIP movement used to convince European citizens of welfare loss that would result from TTIP.

BEUC, the European Consumer Organization, put forward many arguments against chlorination (Coynes, Reference Coynes2014), but the European Food Safety Agency (EFSA) itself had issued a scientific opinion proposing changes in the poultry meat inspection system (EFSA Panel on Biological Hazards, EFSA Panel of Contaminants in the Food Chain, and EFSA Panel on Animal Health and Welfare, 2012). Through inaccurate citing (BEUC made a generalization from the bacteria Campylobacter to all zoonotic pathogens, for which there is no support in EFSA’s article), BEUC inverted the content of EFSA’s opinion to support BEUC’s own view of the matter.

BEUC (Coynes, Reference Coynes2014) also turned around information from EFSA regarding the share of human cases of infection with Campylobacter that can be attributed to the different stages in the food value chain by inappropriately mixing up the results of different case studies in EFSA (EFSA Panel on Biological Hazards, 2010).

While BEUC remarked disparagingly about U.S. chicken (“chemically treated poultry”: Coynes, Reference Coynes2014), the European Medicines Agency (EMA, 2016) documented the use of antibiotics and other chemicals in European food production. Their figures showed that chicken production in Europe relied as much on antibiotics and other chemicals as other animal production lines. Even the European Parliament (2013) stated that it would be incorrect to view differences in food safety regulations in the EU and the United States as a general manifestation of fewer food safety concerns in the United States.

Matthews (Reference Matthews2016) argued that, in addition to the activities of the BEUC, the mainstream media also contributed to the provision of uncritical information. He provided examples from UK newspapers the Guardian and the Independent, which ran stories on the Greenpeace TTIP leaks without asking the European Commission for comments on the texts to provide balance, nor seeking to put the Greenpeace claims in context by querying independent experts for their opinions.

3.1. Game 1: a discrete choice model of citizen choices of facts among “spin”

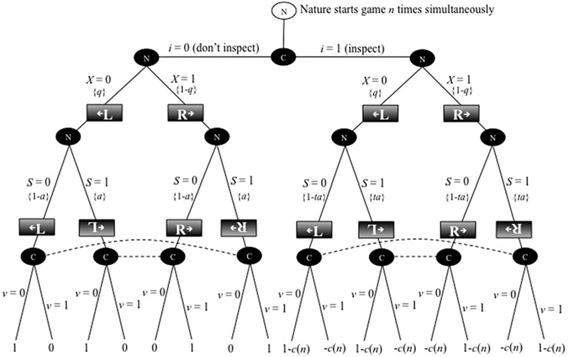
The first model is game 1, which is made up of n simultaneously played “one-fact” games (i.e., game 1.1, game 1.2, …, game 1.n). Figure 1 presents the extensive form of one-fact game 1.j. The n − 1 other one-fact games are identical to game 1.j. Game 1.j has two players: nature (N) and a citizen (C), and three periods. In period 1, the citizen decides whether to pay a per fact cost c(n) to “inspect” the results of upcoming plays by nature in the one-fact game. We assume ć(n) > 0; that is, the per fact cost of inspection is a monotonically increasing function of the number of facts that the citizen must inspect (i.e., in the number of one-fact games she must play simultaneously). This assumption represents the idea that the citizen’s fact-processing abilities are limited; limited brain power, time, energy, and so forth, make it so that when a citizen is confronted with the task of judging the veracity of many political claims, the more that must be judged, the less the amount of time, energy, and brain power that can be devoted to critically examining each claim.

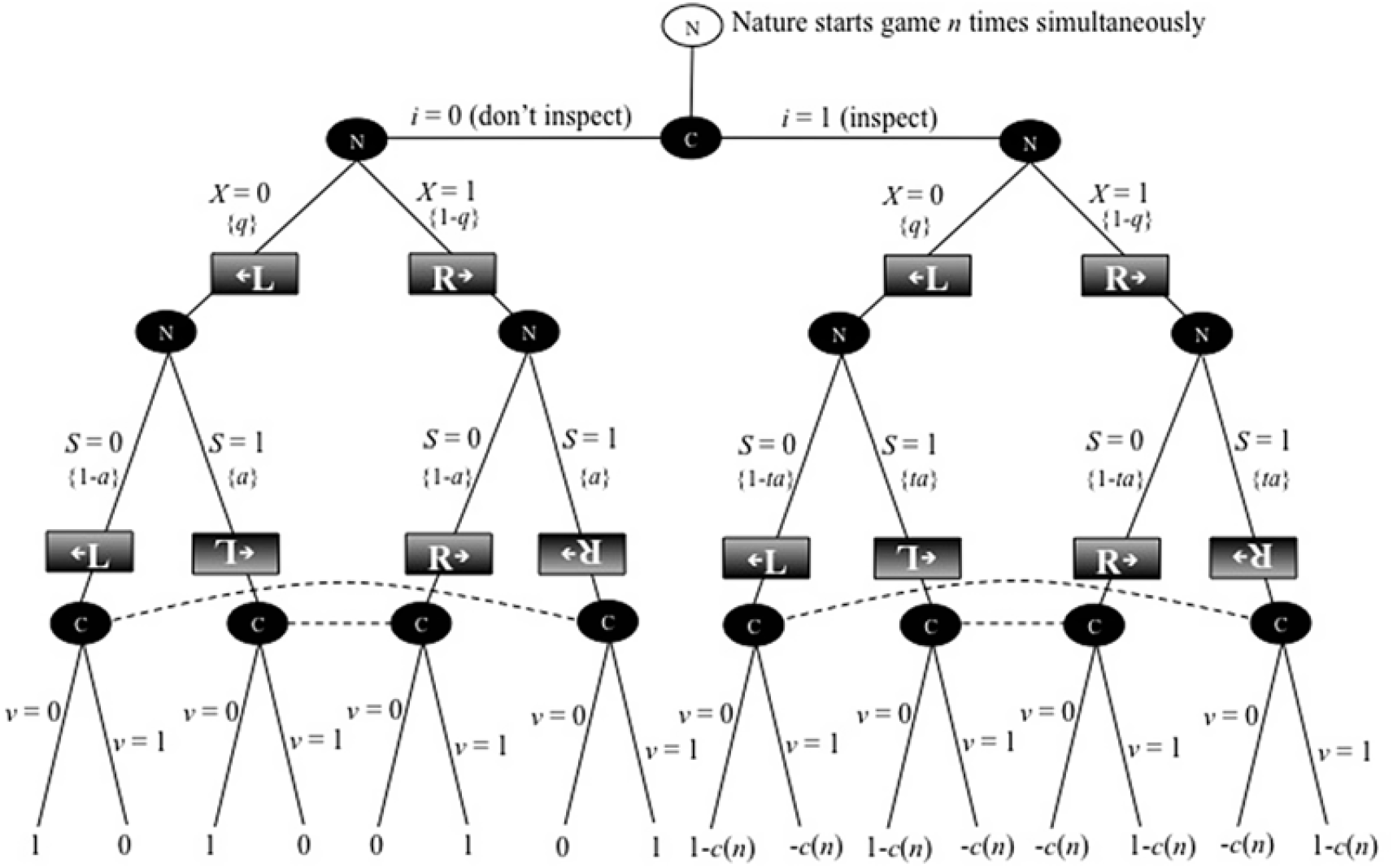
Figure 1. One of n identical one-fact games in game 1.

Period 2 of the one-fact game begins with nature drawing a “fact” from a binomial distribution of a random variable X. For any Q ∈ [0, 1], let b(X, Q) be the probability density function parameterized by Q:

(1) $b\left( {X,Q} \right) = {Q^{1 - X}}{\left( {1 - Q} \right)^X}\;{\rm{for }}\hskip 4ptX \in \left\{ {0,1} \right\}.$

When X = 0, we call X a “leftist fact,” and when X = 1, we call it a “rightist fact.” It will sometimes be useful to label facts by the symbols “←L” and “R→”.

At the same time that nature is generating the fact X, nature also chooses randomly whether to “spin” the fact. Consider another random variable, S (called “spin”), which is also generated from a binomial distribution parameterized by a real number a ∈ in [0, 1].

(2) $b\left( {S,a} \right) = {a^{1 - S}}{\left( {1 - a} \right)^S}\;{\rm{for\hskip 4pt }}S \in \left\{ {0,1} \right\}$

Consider the following function, which we call the “appearance function”:

(3) $$A\left( {X,S} \right) = \left\{ {\matrix{ {X\,{\rm{if}}\,S = 0} \cr {\left| {1 - X} \right|\,{\rm{if}}\,S = 1} \cr } } \right..$$

When S = 0, the fact X is “not spun,” and so it “appears” as its own value. When S = 1, the fact X is “spun,” and so if the fact is actually 0, it “appears” to be 1, and if the fact is actually 1, it appears to be 0. We might illustrate an agent who is “not fooled by appearances” as seeing the following:

• A(0, 0) = “←L”, A(0, 1) = “r→”, A(1, 0) = “R→”, and A(1, 1) = “←ᴚ”.

However, if the citizen is “fooled by appearances”, she simply sees the “arrows” and not the “letters” of the (spun or not spun) fact: A(0, 0) = “←”, A(0, 1) = “→”, A(1, 0) = “→”, and A(1, 1) = “←”. So, a spun fact appears as its opposite: a leftist fact appears to be rightist, and a rightist fact appears to be leftist. We assume that the citizen is “fooled by appearances.” We assume that the citizen knows the functional form of b(X, Q) and its domain but does not know the value of the draw q coming from the distribution. (We can call the value of q “the truth.”) If the citizen were to know the value of q, she would know b(X, q). We assume that the citizen also knows the probability with which facts are spun, a, and that spinning is generated by the binomial process defined in equation (2).

Next, we assume that the citizen’s objective is to observe a drawn (and potentially spun) fact and use it to estimate whether q is less than or equal to 0.5 and then use that estimate to “choose a government.” That is, the citizen is trying to figure out the “truth,” which may be leftist (if q ≤ 0.5) or rightist (if q > 0.5). If the truth is leftist, the consumer wants to choose a leftist government and does so by choosing v = 0. If the truth is rightist, the citizen wants to choose a rightist government by choosing v = 1.

Even though the citizen is fooled by appearances, we allow her to choose, at a cost, whether to “inspect” a “fact” (whether it has been spun or not). Her inspection choice variable is i, which when set to zero implies no inspection, and when set to one, the fact is inspected and “unspun.” That is, leftist facts that appeared to be rightist when not inspected are seen to be truly leftist after inspection, and rightist facts that appeared to be leftist when not inspected are revealed to be truly rightist after inspection. The cost of an inspection is c(n) > 0.

We assume that the citizen’s utility depends on whether she has chosen the correct kind of government. She receives one unit of utility (util) when she chooses government correctly (i.e., if she has chosen a leftist government if the truth is on the left and a rightist government if the truth is on the right). She receives no utils if she chooses government incorrectly. Her utility also depends on whether she has conducted an inspection. So the citizen’s utility is described by equation (4):

(4) ${U_C}\left( {i,v,X,n} \right) = - ic\left( n \right) + \left\{ {\matrix{ {0\,\,{\rm{if}}\,v \ne X} \cr {1\,\,{\rm{if}}\,v = X} \cr } } \right..$

We assume that the citizen chooses whether to inspect facts and how to vote, with the objective of maximizing her expected utility. Her choices, their outcomes, and the model’s random elements are illustrated in Figure 1, which shows an extensive form of a two-player game, where the players are nature (N) and the citizen (C). The citizen makes the first move, deciding before the fact “appears” whether to inspect or not to inspect the fact. Nature then generates a fact, drawing a leftist fact with probability q or a rightist fact with probability 1 − q. Then nature spins the fact, with probability a, or does not spin it, with probability 1 − a. If, however, the citizen chooses to inspect a fact, it reduces the probability that a spun fact “stays spun.” That is, instead of being “spun” with probability a, a fact is “effectively spun” (i.e., “spun” but not “unspun”) with probability ta, where t ∈ (0, 1).

It can be shown that the citizen depicted in Figure 1 will choose to inspect the fact if c(n) < (1 − t)a. That is, letting an asterisk denote an ex ante optimal decision,

(5) ${i^*} = \left\{ {\matrix{ {0\,\,{\rm{if}}\,c\left( n \right) > \left( {1 - t} \right)a} \cr {1\,\,{\rm{if}}\,c\left( n \right) < \left( {1 - t} \right)a} \cr } } \right..$

Note that the citizen is indifferent between inspecting and not inspecting if c(n) = (1 − t)a. The result shown in equation (5) is intuitive: The cost of inspecting a fact is c(n). The benefit of inspecting equals the value of choosing the correct government (which is 1) times the increase in the probability of finding a spin if one inspects, which is (1 − t)a. Because having to play additional one-fact games raises the per fact cost of inspection, it lowers the probability that the citizen installs the optimal government. For sufficiently high values of n, the per fact costs of inspection will be great enough to prevent the citizen from choosing to inspect the facts, and on average the government installed will deviate from the optimal government.

3.2. Game 2: a continuous choice model of citizen choices of facts among “spin”

Consider a random variable X = μ + ε, where μ is a constant real number, and ε ~ N(0, σ² ). Assume that draws from the distribution of ε are independent. Interpret any value of X as representing a “fact” about the effects of government policy. When X < μ, the fact is “leftist,” and when X > μ, the fact is a “rightist.”

Next, consider a citizen who obtains utility by choosing a government. C’s choice variable is v, which must be chosen from the real number line. C desires to install a government that is not too far “left” or too far “right”; that is, C wants to install a government that balances leftist and rightist facts to develop a policy based on evidence from the facts at hand. The citizen’s utility function is

(6) ${U_C}\left( {v,\mu } \right) = K - {\left[ {v - \mu } \right]^{{\kern 1pt} 2}},$

where K is a positive constant. When the citizen (C) chooses v, she does not know μ. Rather, she gains information about μ from draws of the random variable X out of its distribution. She knows that X is distributed normally but does not know the mean or variance of the distribution. In addition, C can learn about any fact by “inspecting it.” However, the inspection process is itself flawed, so that sometimes C perceives facts to be more “rightist” or more “leftist” than they actually are. C’s perceived value of a fact is determined by a random process, where the perceived value of a fact is its true value plus a normally distributed random variable: Y = X + ω, where the draws of ω are independent and identically distributed as ω ~ N(0, g(n)). Assume that g(n) is positive and monotonically increasing for all n. The idea is that the citizen is forced to inspect all the facts in a sample and must do so in a fixed amount of time or with a fixed amount of personal energy or resources. The greater the number (n) of facts inspected, the less time there is to spend on each fact, and so the greater is the variance of the size of the misjudgment. The citizen estimates μ by using the best unbiased estimate of it that is linear in the perceived values of the drawn facts. This is well known to be the sample mean:

$\hat \mu = \scale 150%{1 \over n}\sum\limits_{i = 1}^n {{Y_i}} .$

Solving the utility maximization is equivalent to solving the following problem:

$\mathop {Min}\limits_v \left\{ {{{\left[ {v - \hat \mu } \right]}^2}} \right\} = \mathop {Min}\limits_v \left\{ {{{\left[ {v - \scale 150%{1 \over n}\sum\limits_{i = 1}^n {{Y_i}} } \right]}^2}} \right\} = \mathop {Min}\limits_v \left\{ {{{\left[ {v - \scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {\mu + {\varepsilon _i} + {\omega _i}} \right)} } \right]}^2}} \right\}.$

The solution to the abovementioned problem is to set v equal to $\hat \mu $ , which is the mean of the sample of perceived values of the drawn facts. Note that (ε + ω) ∽ N(0, σ² + g(n)). The statistical properties of $\hat \mu $ under these assumptions are well known:

$v = \hat \mu = {1 \over n}\sum\limits_{i = 1}^n {\left( {\mu + {\varepsilon _i} + {\omega _i}} \right)}\ ∽\ N(0, σ2 + g(n)).

From equation (6), the realized utility of the consumer is

(7) ${U_C}\left( {v,\mu } \right) = K - {\left[ {\hat \mu - \mu } \right]^{{\kern 1pt} 2}} = K - {\left[ {\scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {\mu + {\varepsilon _i} + {\omega _i}} \right)} - \mu } \right]^{{\kern 1pt} 2}} = K - {\left[ {\scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {{\varepsilon _i} + {\omega _i}} \right)} } \right]^{{\kern 1pt} 2}}.$

and expected utility is

(8) $E{U_C}\left( n \right) = K - E\left( {{{\left[ {\scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {{\varepsilon _i} + {\omega _i}} \right)} } \right]}^{{\kern 1pt} 2}}} \right) = K - E\left( {\scale 150%{1 \over {{n^2}}}\left[ {\sum\limits_{i = 1}^n {\varepsilon _i^2 + \sum\limits_{i = 1}^n {\omega _i^2} } } \right]} \right) \hskip +30pt= K - \left( {\scale 150%{1 \over {{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\varepsilon _i}} \right)} } \right) - \left( {{1 \over {\scale 150%{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\omega _i}} \right)} } \right) = K - {{{\sigma ^2}} \over n} - {{g\left( n \right)} \over n}.$

Finally, note the effect of an increase in the sample size on expected utility:

(9) $${{dE{U_C}\left( n \right)} \over {dn}} = {{d\left[ {K{{{\sigma ^2}} \over n}{{g(n)} \over n}} \right]} \over {dn}} = - \left( {{{{\sigma ^2}} \over {{n^2}}} + {{g\left( n \right) - ng'\left( n \right)} \over {{n^2}}}} \right) = {{g'\left( n \right)} \over n} - {{{\sigma ^2} + g\left( n \right)} \over {{n^2}}}.$$

Because g is increasing in n, the sign of the expression is ambiguous. That is, increasing the sample size may decrease expected utility. The intuition behind this result is that, ceteris paribus, although increasing the sample size n (i.e., obtaining additional “facts”) provides the citizen with a better estimate of the mean of the distribution of facts X (which is also the mean of the distribution of the perceived facts Y), increasing sample size leaves less time per fact for inspection and so can increase the variance of the estimate of μ and decrease the accuracy of the citizen’s estimate of the optimal government to be installed. Thus, more “facts” need not make the citizen better off; because the citizen has limited resources with which to inspect the facts to estimate their mean, her assessment of the “facts” may worsen as the sample size increases.

3.3. Game 3: a model in which one interest group spins facts

Finally, we present a model in which a biased interest group can spin facts in an effort to win the political support of a representative citizen. We call this game 3. Like game 1, game 3 consists of n simultaneously played “one-fact” games (i.e., game 3.1, …, game 3.n). We show the extensive form of one such one-fact game in Figure 2.

Figure 2. The external form of one of n one-fact games played between a fact-spinning interest group and a citizen.

Without loss of generality, we assume that the interest group, denoted G_L , is leftist. Whether the truth is leftist or rightist depends once again on nature. When t = 0, the truth is leftist. When t = 1, the truth is rightist. G_L observes the truth and decides whether to spin the fact to make it appear other than it is. The citizen then sees the appearance of the truth in all of the one-fact games and must decide whether to vote for a leftist or rightist government. Payoff functions are shown in equations (12) and (13).

(10) $s\left( {a,t} \right) = \left\{ {\matrix{ {0\hskip +2pt{\rm{ if }}\hskip +2ptt = a} \cr {1\hskip +2pt{\rm{ if }}\hskip +2ptt \ne a} \cr } } \right.$

(11) $e\left( {v,t} \right) = \left\{ {\matrix{ {0\hskip +2pt{\rm{ if }}\hskip +2ptt \ne v} \cr {1\hskip +2pt{\rm{ if }}\hskip +2ptt = v} \cr } }\right.$

(12) ${U_{GL}}\left( {v,a,t} \right) = \left( {1 - v} \right) - {c_s}s\left( {a,t} \right)$

(13) ${U_C}\left( {v,i,t} \right) = e\left( {v,t} \right) - {c_i}i$

Game 3 is a type of signaling game, and as is common with signaling games, we use the pure-strategy Bayesian Nash equilibrium concept (Gibbons, Reference Gibbons1992). There are four potential types of such equilibria for the game: (1) “never spin,” (2) “always spin,” (3) “spin when you shouldn’t and don’t spin when you should,” and (4) “spin when the truth is inconvenient.”

It can be shown that the only pure-strategy perfect Bayesian Nash equilibrium in this game is the “spin when the truth is inconvenient” strategy. In game 3, because the interest group is biased left, the truth is “inconvenient” when nature generates a rightist fact. Only in this case will the leftist interest group attempt to spin the fact—and the group will do this only in the case in which inspection costs are sufficiently high (above 0.5). Because again we assume that per fact inspection costs increase with the number of facts that must be inspected, when nature generates more than some number of facts, it no longer is profitable for the citizen to inspect the facts. As a result, the citizen is more likely to be fooled by the interest group’s “spinning” of the facts and install a government that is leftist, which lowers social welfare when the truth is rightist.