2.1 Comments on Lanchester’s inability to publish

Frederick Lanchester is now well known as one of the great contributors to aerodynamic concepts and understanding. Unfortunately, as we will see, he was not well known for aerodynamics at the time he was conducting experiments. We will probably never know everything that Lanchester achieved while developing model flyers in the last decade of the 19th century, primarily because he was not able to get his work published until many years after he developed his concepts and theories. His earliest efforts at characterising vortical flow and lift had been presented in 1894 as a lecture during a meeting of the Birmingham Natural History and Philosophical Society, but his work was not accepted for publication by that society, and that lecture was subsequently never published (and no copies have been found since then) [Reference Von Karman3]. Prof. Theodore von Karman of Caltech, on the occasion of the first Lanchester Memorial Lecture in 1958, said that Lanchester revised his 1894 paper and submitted it to The Royal Society, which recommended it be submitted to The Physical Society, where it was rejected [Reference Von Karman3].

Lanchester did eventually succeed in being published by a Royal Society, however, but it was the Royal Society of Arts in 1909 [Reference Lanchester8]. This publication took place after he had completed publishing his two books on aerial flight: Aerodynamics in 1907 [Reference Lanchester9] and Aerodonetics in 1908 [Reference Lanchester10]. Apparently, not many people had been aware of Lanchester’s contributions to aerodynamics in the time between 1894 and 1907. For example, Prof Richard Southwell said in 1930, ‘I shall suggest that the kernel of all we yet know of fundamental aerodynamic theory was there to read in 1914’ [Reference Southwell11]. To which J. Laurence Pritchard wrote in 1957, ‘One might add, in 1894, if Lanchester had been listened to’ [Reference Pritchard12].

So why were Lanchester’s papers not being published in a timely fashion, even though we can now see they contained many important ideas? While there is little direct evidence for the reasons behind his inability to publish, there are many ideas and observations on the topic. In his book Aviation: An Historical Survey, Charles H. Gibbs-Smith said it was because his writing style was difficult to understand [Reference Gibbs-Smith13].

Prof Ludwig Prandtl of the University of Göttingen, on the occasion of giving the Wilbur Wright Memorial Lecture to the Royal Aeronautical Society in 1927, told the audience (which included Lanchester, which must have been awkward): ‘The truth of the matter, however, is that Lanchester’s treatment is difficult to follow, since it makes a very great demand on the reader’s intuitive perceptions, and only because we had been working on similar lines were we able to grasp Lanchester’s meaning at once’ [Reference Prandtl14].

Prof Theodore von Karman offers another reason for the lack of understanding towards Lanchester’s early papers:

Prof von Karman also comments that another fundamental reason for the misunderstanding of Lanchester’s work was that no accepted aerodynamic theory existed in the late 19th century and into the early 20th century, which made it difficult for reviewers to understand Lanchester’s ideas [Reference Von Karman3]. In other words, von Karman is saying that there really was not a solid, well accepted, theory of aerodynamics prior to Lanchester, and the various theories and fluid flow concepts that existed at the time were contradictory and lacking in accuracy. Reviewers of his paper or articles might have seen him as someone presenting ‘just another aerodynamic theory’, among so many other competing theories, which could easily be dismissed.

Von Karman adds yet another possible reason for the lack of publications when he states Lanchester just was not ‘mathematical’ enough, especially when compared with the work being developed on similar topics at the time by Martin Kutta [Reference Kutta15] and Nikolai Joukowski [Reference Joukowski16]:

In other words, while the more mathematical treatments of Kutta and Joukowski (who were both mathematicians/scientists) presented a theory for aerofoil circulation and lift, it was Lanchester’s description that made the theory practical and useful for airplanes. Also, Lanchester was the only one who extended the lift concept to three-dimensional wings, which was crucial for designing aircraft.

Philip Jarrett also has put forth a reason for Lanchester’s lack of publication success in an article from 2014: ‘Lanchester and The Great Divide’ [Reference Jarrett6]. In that paper Jarrett builds the case for a disconnect between those that were conducting mathematical/scientific research in the field of aeronautics and those that were interested in designing and building airplanes.

Certainly, the issues with translation and understanding of papers and books from English to German and vice versa caused delays in comprehension. Von Karman stated that this was definitely a problem for Prandtl, but it was not a problem at all for Carl Runge:

Another, less flattering, reason for Lanchester’s failure to publish is also possible. Could it be that Lanchester, being an engineer from the automotive industry, was the object of some level of class bias towards his work? Was he being ‘looked down upon’ because he was a practical engineer and not a mathematician or scientist? Certainly that is a possibility, and while some limited evidence exists for this perception, we probably will never know how much this impacted his ability to publish.

I hesitate to bring up a final possible reason for Lanchester’s inability to publish papers, one that does not seem to be mentioned very often in other sources. In reading Lanchester’s letters [17], (Ref. 17 is a treasure trove of Lanchester’s files, letter, and photos) I have noticed that he could, at times, be quite ‘prickly’ when communicating with people. While the catalog of letters I viewed did not include the letters he wrote while he was trying to publish his paper in 1894, they did include, among quite a few others, a letter he wrote to Prof A.V. Hill (the Secretary of the Royal Society) in 1939 [17]. In that letter Lanchester recounts the problems he had publishing his 1894 paper:

Lanchester was obviously still hurt by the events that had taken place many decades before, but he was also willing to lash out against people he believed had harmed him. In other parts of the same letter, Lanchester can be seen to be sarcastic, belittling and even rude. Of course, it is hard to put myself in his position and to fully understand what it must have felt like to have your work rejected. I would hope, however, that a more positive approach to communicating with others might have made the situation more productive.

A similar situation took place in 1908 when Lanchester decided to travel to France to meet and interact with Wilbur Wright, who was at Le Mans demonstrating the Wright Model A airplane (Wilbur Wright conducted his first flight in France in August 1908). Apparently that meeting did not go as well as planned, as evidenced by a letter Wilbur Wright wrote to Lanchester in January 1909 – the letter is shown in Fig. 3 [17].

Figure 3. Wilbur Wright’s letter to F.W. Lanchester, written 4 January 1909 from Le Mans, France [17] (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

A transcription of the letter follows:

Unfortunately, I could not find a copy of Lanchester’s letter of 29 December 1908, and their conversations during the time when the two met in France in August 1908 seems to have been limited to details about the design and manufacture of the Wright aircraft (of which Lanchester apparently was not overly impressed) [Reference Lanchester18]. We do know, however, what Lanchester thought about the meeting in France, because he described it in a letter to Col. J. Fullerton, the Secretary of the Aeronautical Society of Great Britain, written 24 November 1908 [17] (see Fig. 4).

Figure 4. Letter from Lanchester to Col. J. Fullerton, dated 24 November 1908 [17] (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

The letter begins with some small talk and details regarding a lecture Lanchester was to give at the society. Lanchester then begins talking about his meeting with Wilbur Wright:

And then a few sentences later:

Of course, Lanchester is describing the well-known reticence of Wilbur Wright to talk very much, especially about the details of his airplanes. Lanchester did state in his lecture that, ‘the reticence shown is perhaps no more than might be anticipated’ [Reference Lanchester18], so it is a little difficult to know his true feelings on that matter. Also, in Lanchester’s lecture about the Wright airplane [Reference Lanchester18] in December 1908 he includes many technical details that he learned from Wilbur Wright during his visit to Le Mans: ‘Mr Wright has admitted (at least to the author) that his gliding angle is about 7 degrees; this, at a gross weight of 1,100lbs., gives 140lbs thrust required, and at 58ft per sec, the thrust h.p. becomes 14.5’ [Reference Lanchester18].

Jarrett notes an important difference between Lanchester and Wilbur Wright [Reference Jarrett6]:

Lanchester did make several positive statements about the Wright airplane in his lecture, including, ‘On the whole the advantage certainly rests with the Wright machine from the aerodynamic standpoint’ [Reference Lanchester18]. In general, however, Lanchester had issues with the Wright approach and their airplane and was not afraid to voice those opinions in public. Apparently, Wilbur Wright also disagreed with Lanchester’s approach, but voiced his position in private.

The list of reasons for Lanchester’s inability to publish his work is long, with issues put forth from many well-known figures in the development of aerodynamic theories and concepts. Constraints such as Lanchester’s writing style and use of his own terminology, his non-theoretical approach, the lack of solid pre-existing theory, issues with the slowness of translation of books and papers between England and Germany, possible publication bias, and even Lanchester’s personality all might have contributed to his problems with publication. We will probably never know for sure which of these reasons is a main culprit, but it is possible that some or all of them may be correct to one extent or another. What we do know is that Lanchester made contributions to aerodynamics that we recognise today as being very important, even if others at the time did not recognise his contributions, for whatever reasons.

2.2 Lanchester’s writing style in historical context

Before proceeding to the specific details of Lanchester’s contributions to aerodynamic theory, I thought I would take a moment to investigate the theory that Lanchester was not a very clear writer. Certainly, Von Karman’s objections to Lanchester’s proclivity for making up his own technical terms is valid, but I wonder how correct the ‘bad writer’ complaint really is. As an un-scientific test for determining Lanchester’s writing ability (and how well he was understood), I have chosen three writing excerpts, all from the prefaces of early 20th century editions of fluids/aerodynamics books, and all written by native English speakers. Without looking ahead to the answer, perhaps you can determine which of these three excerpts was written by Lanchester:

To the early 21st century reader these three early 20th century excerpts certainly could all seem somewhat challenging to read. While we can only depend on what people said at the time, as discussed above in great detail, we do not know if people at that time believed anyone writing on aerodynamics was ‘easy to read’. So, which of these three excerpts were written by Lanchester? Excerpt A is from Horace Lamb’s book Hydrodynamics (4th Edition, 1916) [Reference Lamb19], Excerpt B is from William Lanchester’s book Aerodynamics (1907) [Reference Lanchester9] and Excerpt C is from Samuel Langley’s Experiments in Aerodynamics (2nd Edition, 1902) [Reference Langley20]. How did you do? Can you, as an early 21st century reader, tell the difference between these early 20th century technical writers? I have to admit that I cannot – they all require great attention and patience to understand in my opinion!

2.3 Aerofoil and wing theory

Lanchester spent a great deal of time experimenting with aerofoils and wings in the last decade of the 19th century. He was, by no means, unique in this endeavour, since many others had done the same thing before (and after) him, including Sir George Cayley, Otto Lilienthal, Horatio Phillips, Samuel Langley, Hiram Maxim, A.F. Zahm and the Wright Brothers (among others) [Reference Pritchard12]. What separated Lanchester from the others who were working on aerofoils, was his ability to deduce a theoretical cause for the performance of aerofoils, specifically the concept of circulation. Figure 5 shows a sketch made by Lanchester of flow over an aerofoil, and it includes several important concepts related to aerofoil aerodynamics: (1) the flow is changing direction upstream of the aerofoil; (2) the streamlines over the upper surface of the aerofoil are closer together than those under the lower surface (causing the flow to be faster over the upper surface than the lower surface); (3) the flow continues on a downward path after the trailing edge; and (4) there is a small wake behind the trailing edge due to viscous effects [Reference McCloskey7, Reference Lanchester21].

Figure 5. Flow over an aerofoil as described by Lanchester (public domain) [Reference Lanchester8].

Lanchester’s aerofoils, which had been developed based on his physical understanding described above, were actually very good aerofoils compared with other shapes of the time. Anderson points out that, ‘Lanchester’s aerofoil designs, obtained from his calculations, were tested in Prandtl’s wind tunnel at Göttingen University in 1912–13 and were found to produce a lift-to-drag ratio of 17; that was a 10% improvement over other models tested in that wind tunnel up to that time’ [Reference Anderson5].

While others had come up with some of these circulation concepts from a purely theoretical perspective, Lanchester saw what no one else at the time could understand: the two dimensional flow around the aerofoil section, when applied to a three dimensional wing, created a circulation pattern that continued in the vicinity of the wing tip, as shown in Fig. 6 (which he called ‘peripteral motion’). His final ‘visual’ representation of this three dimensional flow is shown in Fig. 7, which has been reproduced a great deal since the publication of his book.

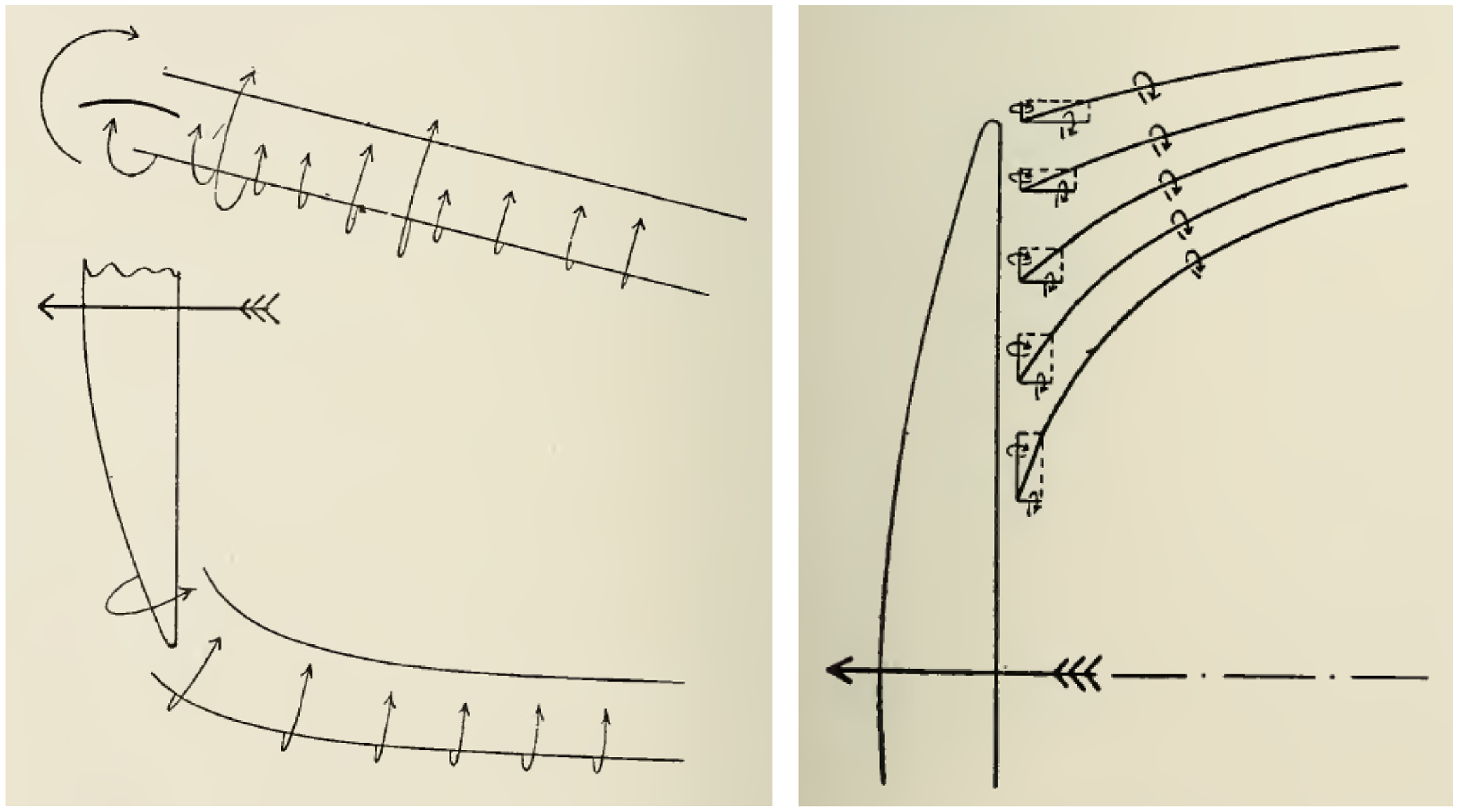
Figure 6. The circulation of flow around the aerofoil and in the vicinity of the wing tip (public domain) [Reference Lanchester8].

Figure 7. Lanchester’s sketch of the wing-tip vortex system (public domain) [Reference Lanchester8].

In addition, Lanchester knew that the three-dimensional flow in the vicinity of the wing tip would alter the flow of the aerofoils on the wing, thus creating an additional component of drag that we now call ‘induced’ or ‘vortex’ drag. He not only foresaw this new component of drag, he developed a way to find the magnitude of the induced drag using energy arguments. This clearly put Lanchester outside the realm of ‘tinkerer’ or ‘inventor’ and into the realm of a true aerodynamicist. Theodore von Karman later observed that,

1. 1. In the case of a finite aspect ratio wing two vortex trunks are formed at the wing tips.

2. 2. Each vortex trunk consists of a system composed of many individual vortices leaving the trailing edge of the wing along the span.

3. 3. The kinetic energy contained in this vortex system must be renewed by expending work continuously during uniform flight.

4. 4. The work required to maintain the same sustentation increases with decreasing aspect ratio [Reference Von Karman3].

Even Prandtl saw it necessary to comment on Lanchester’s contributions to wing theory upon the occasion of giving the Wilbur Wright Memorial Lecture in 1927.

Of course, Prandtl had to make sure there was no uncertainty in the uniqueness of his approach to wing theory, and that it had not been influenced by Lanchester’s approach. But he also was quick to give Lanchester credit for the first concept of wing theory, one which Prandtl would spend many years working on before coming up with his well-known ‘lifting line’ theory. Prandtl, however, notes that it was not the researchers in Germany who snubbed Lanchester and his concepts, but rather it was the scientific community in England who had done that.

2.4 Boundary layers, skin friction, and aircraft resistance

Boundary layer concepts represent yet another topic that linked Lanchester and Prandtl, since Lanchester also came up with concepts for boundary layers around the same time as Prandtl. According to J.A.D. Ackroyd, ‘Independently of Prandtl, Lanchester (1907) also proposes a boundary layer concept, although it seems unlikely that a date can be given to its inception. All that seems to be known is that, in 1905, Lanchester was carrying out experiments with model gliders with the specific intention of estimating skin friction’ [Reference Ackroyd4]. So, once again, Lanchester and Prandtl are linked, and in this case Lanchester had a practical application in mind, rather than just the development of a theory.

While there is a great deal of detail to Lanchester’s concepts for boundary layers [Reference Ackroyd4], the real goal of his work was to find relationships for laminar and turbulent skin friction drag so he could determine the resistance of a wing at various velocities. Lanchester states in Aerodynamics that part of his motivation is the observation by Samuel Langley that,

Lanchester completely agreed with the final sentence of Langley, but completely disagreed with the notion that power required would be less at higher velocities. Lanchester dives a little deeper into the experiments of Langley and finds that the following statement of Langley when discussing his experiments for a resultant pressure recorder, helps explain the paradox: ‘We may remark that they [his experimental data] incidentally show that the effect of the air friction is wholly insensible in such experiments as these’ [Reference Langley20]. At this point, Lanchester then states, ‘Unfortunately, the optimistic view propounded by Langley in his so-called law has not been realised. It is founded on the supposed negligibility of skin-friction, a supposition that can be no longer upheld’ [Reference Lanchester8].

At this point in his lecture, Lanchester then proceeded to develop the basic variation of resistance (drag) as a function of velocity, as shown in Fig. 8. He describes his experimental results showing that friction creates resistance proportional to V², and then he goes on to describe how other experiments show that another component of resistance (what we now call induced drag or vortex drag) varies with 1/V². Plotting both components of resistance shows one increasing steadily while the other decreases steadily. Lanchester goes on to say,

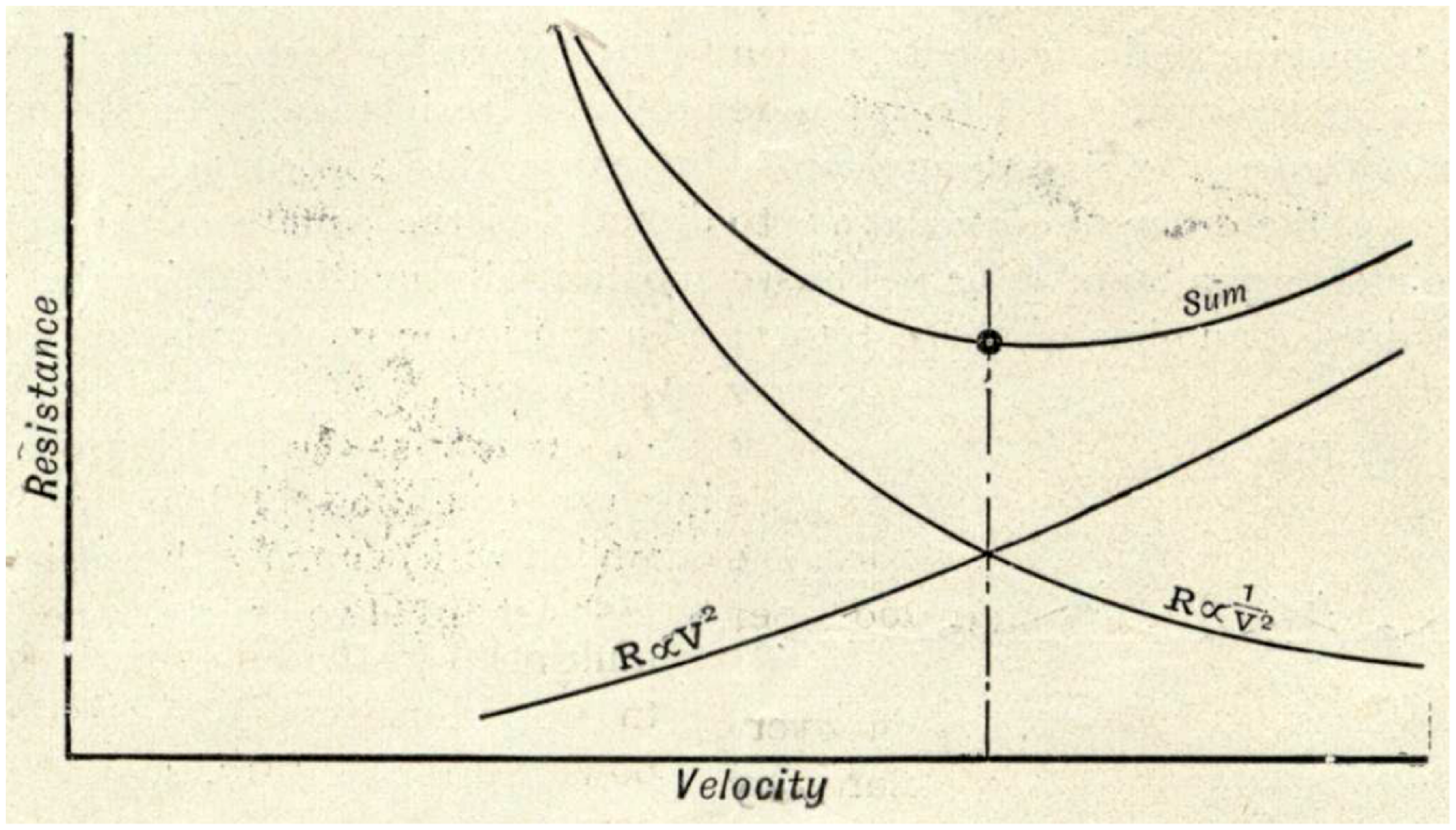
Figure 8. Resistance as a function of velocity for an airplane (public domain) [Reference Lanchester8].

Figure 9. Photographs of Lanchester’s model airplane catapult system from 1894 (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

This is, of course, how we view the situation today, and can be mathematically shown that the minimum thrust required for flight takes place when the parasite drag equals the drag due to lift. Furthermore, this point is where the lift-to-drag ratio (L/D) is maximised for the airplane. Lanchester had understood this ‘dual nature’ of resistance long before others.

2.5 Flight performance and mechanics

Lanchester had been conducting model airplane flights for many years (see Fig. 2 for pictures of his models), designed to measure model weight, speed, distance, velocity, flight path, glide angle, etc. He could use the model system to test different wing planforms and aerofoil shapes if needed. He launched his airplane models using a catapult system (see Fig. 9) and states that the flights began about 15 feet above the ground from a rear first story window of his house that faced west, down a slope of approximately 1 in 25 [Reference Lanchester10]. He states that about 20–30 flights were made during June and July of 1894, and he presents data for six of those flights. He had become quite adept at understanding the efficiency of an airplane wing and aerofoils through these measurements and comparing the performance of various shapes with each other. He used the data he collected for determining skin friction drag, lift-to-drag ratios, wing performance, etc. He also made observations of flight paths (with help from some ‘observers’ who sketched the vertical flight paths); Fig. 10 shows results from these flights (numbered 1–6). Anyone who has flown balsa wood gliders will recognise some of these flight paths. The recorded six flights made by Lanchester in 1894 using models with and without propellers are (references to figure numbers in the description are from Lanchester’s book, but have been retained here and in the figures for clarity) [Reference Lanchester10]:

Figure 10. Schematic of flight paths for six model airplane flights in 1894; Lanchester Aerodonetics, Fig. 23 (public domain) [Reference Lanchester10].

At this point a note should be made about the unusual forward vertical stabiliser seen in Fig. 8. Modern aircraft designers would look at this surface and realise it would create negative lateral stability to the aircraft (and wonder why Lanchester did not understand that fact). In fact, however, Lanchester fully understood that this surface was de-stabilising, and he used it for two purposes [Reference Lanchester9]:

• • They allowed Lanchester to control the location of the lateral neutral point in order to easily change the stability of his flying model without changing the baseline model.

• • These surfaces were the ‘test’ surfaces for each flight of the same aerodone – the baseline configuration provided a defined lift and drag, and the introduction of wing planforms and/or aerofoil shapes with these vertical surfaces allowed for measuring incremental lift and drag (and impact on performance).

Notice that Flights 2, 3 and 4 started fairly straight, and then Flight 2 started to turn toward the left as it traveled ‘280 or 290 yards’ (as shown in Fig. 9). What you do not see in Fig. 9, however, is what the airplane is doing in the pitch plane as it progresses along the horizontal flight path. For this information look at the top half of Fig. 10, which shows the recorded vertical flight path for Flight 2, and notice that the airplane is going through three cycles of fairly significant pitch up/pitch down motion before it impacts the ground. Also note that Flight 2 took place in fairly strong winds with large gusts (Lanchester later describes the wind as a head wind). Vertical flight path information for Flights 3 and 4 are also shown in Fig. 11, but they did not exhibit this cyclic motion, although these flights were slightly shorter at about 200 yards and conducted in calm winds.

Figure 11. Vertical flight paths for Flights 2, 3, and 4; Lanchester Aerodonetics, Figs 25 and 26 (for some reason this figure was published at an angle to the page orientation in the original book, the orientation has been adjusted in this presentation) (public domain) [Reference Lanchester10].

Figure 12. Extended vertical flight paths for Flights 2, 3 and 4 shown with dotted lines (backward in time) and dashed lines (forward in time), with the ‘mean gliding path’ shown with the long dashed line; Lanchester Aerodonetics, Fig. 27 (public domain) [Reference Lanchester10].

Now Lanchester does something quite ingenious. Looking at the cyclic pitch motion for Flight 2 in Fig. 10, he extends the motion both forward and back from the observed flight test data (extrapolating around a flight path centreline) to come up with a longer flight test as shown in Fig. 12. Lanchester observes,

Lanchester continues:

Lanchester then proceeds to perform this mathematical analysis assuming the airplane can be represented by a three degree-of-freedom longitudinal representation, and also assuming that the airplane loses no energy during the flight, but rather is able to trade kinetic energy for potential energy. Lanchester then proceeds to derive what he calls the ‘phugoid equation’ whose solutions are shown in Fig. 13. These phugoid motion curves show the various possible flight paths based on the preceding assumptions, and represents the first time someone had described this longitudinal dynamic mode of flight, that we still call the phugoid mode. Lanchester states ‘the author has not been able to reduce this expression to a form suitable for co-ordinate plotting’ [Reference Lanchester10].

Figure 13. Graphs of flight paths based on Lanchester’s phugoid motion theory; Θ is the angle of the flight path relative to the horizon, H is the vertical distance below the mean flight path (MFP on figure), H _n is the natural height, which is the fall distance required to make the velocity the natural velocity V _n (the value of velocity where the weight is balanced by lift), C is a constant determined from the flight data; the numbered curves represent different flight test cases (for example, Case 10 is for cos Θ = -1, H = 36ft, H _n = 64ft) (public domain) [Reference Lanchester10].

Figure 14. Lanchester sketchbook pages showing the design of a spring (left) and a universal joint (right); (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Figure 15. Lanchester sketchbook page showing the layout for an automobile (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

2.6 Gliders and airplane designs

In order to properly understand the breadth of capabilities displayed by Lanchester during his efforts at both automotive and aeronautical engineering, it will be beneficial to examine some of his notebooks. Within the Lanchester Interactive Archive [17] there are both notebooks (a total of 5 notebooks) and sketchbooks (a total of 13 sketchbooks plus a draughtsman’s sketchbook). The notebooks are smaller pocket-size books that Lanchester probably used while working in the shop to make quick observations, drawings and calculations. The sketchbooks are larger bound volumes of his detailed designs, including drawings (some to fairly detailed levels) and calculations. These sketchbooks are places where you can peer into Lanchester’s capabilities and breadth of activity. The sketchbooks are not sequenced by specific topics, rather they appear to be daily records of what he was working on, which is all the more impressive when you see that he might be working on a ‘variable leverage spring’ or a ‘universal joint’ for an automobile at one moment, as shown in Fig. 14, or the layout of an automobile the next moment, as shown in Fig. 15. Then, without warning, you might turn the page and find the design for an airplane landing gear, wing layout and propeller layout and calculations, as shown in Figs. 16 and 17.

Some of these concepts and ideas were probably to solve specific problems that came up as a new automobile was being designed, but others were for concepts that Lanchester would continue to develop and eventually patent. Lanchester eventually obtained 265 patents, mostly for motor cars and engines, but also for airplanes, sound recording, photography, firearms, etc. The breadth of his activity seemed to know very few bounds. For example, Fig. 18 shows the patent drawing for Patent 3,608 from 1897. The patent was titled, ‘Improvements in and relating to Aerial Machines’. Drawings for the patent include two distinct aircraft: a powered glider aircraft, and a fully powered airplane. The glider looks remarkably similar to streamlined glider designs that would become popular many decades later (with the exception of the forward vertical stabiliser).

Figure 16. Lanchester sketchbook pages for the design of a landing gear and wing/propeller/gear layout (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Figure 17. Lanchester sketchbook pages showing calculations for, and sketch of, the propeller for an aircraft, quite possibly the aircraft layout shown in Fig. 15 (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Figure 18. Lanchester patent for ‘Improvement in and relating to Aerial Machines’, Patent 3,608 from 1897 (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Two more Lanchester airplane design patents are shown in Figs 19 and 20, which are titled ‘Improvements in Aerodromes’ (Patent 9,413 from 1907) and ‘Improvements in Flying Machines’ (Patent 10,422 from 1909). ‘Improvements in Aerodromes’ looks at improved aircraft layout, including structural layout. ‘Improvements in Flying Machines’ concentrated on stability and control issues for airplanes. Notice that many of these designs include the structural aspects necessary for using monoplane wings, as well as pusher propellers and unique wing layouts. To say that Lanchester was extremely creative, and able to bring to the designs his experience in automobile design, would be an understatement. It is also interesting to note that many of these patents are from the same times Lanchester was trying to publish papers, giving aeronautical lectures, or writing his books. All of these activities are taking place at the same time he is an active participant in his automobile company and providing guidance and designs for those endeavors.

Figure 19. Lanchester patent for ‘Improvements in Aerodromes’, Patent 9,413 from 1907 (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Figure 20. Lanchester patent for ‘Improvements in Flying Machines’, Patent 10,422 from 1909 (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

3.1 Preface excerpts from Aerodynamics

While the various divides that existed at the time certainly impacted Lanchester and his ability to have his ideas heard, we do not have to spend much time trying to figure out why he wrote his book on aerodynamics. Lanchester’s first hints as to why he wrote Aerodynamics are found in the Preface to the book:

Lanchester believed that aeronautics would grow in importance and would lead to significant, interesting science and engineering problems. He believed those problems were among the most important applied science questions of the day; that certainly would be true in a very short time after he wrote his book. He then elaborates about national prestige and security issues that were at the forefront of his thoughts:

Amidst the various national security issues (all of which would come true in a very few years), Lanchester states that universities would soon need to develop programmes, courses and lectures in aerodynamics and aeronautics, and if that were true then having good books on the subject would be important for quality education of students. Also note that Lanchester claims that developing aircraft would be just as important as having a world-class navy! So how did Lanchester’s book fit into the landscape of other books in fluids/aerodynamics both prior to and after Lanchester’s books? That is the topic of the next section.

3.2 Related textbooks

What textbooks on aerodynamics existed at the time, both before and after, the publication of Lanchester’s Aerodynamics? And what sources did Lanchester use within his book, and how did he use them? While we’re answering those questions we can also keep in mind the discussion earlier about why Lanchester couldn’t publish his work, one reason of which was his inability to explain concepts in easy to understand descriptions.

The landscape of books (both textbooks and general books) on aerodynamics is shown in Fig. 23. Before looking at the specific books, however, certain historical items are included at the bottom of the figure to provide context, specifically some important flying events (such as Lilienthal’s and the Wright Brothers’ flights), as well as some initial lectures in aerodynamics and the universities where they were taught [Reference McCormick25]. That I was unaware how controversial it would be to find the first universities in the UK that taught aerodynamics courses, since at least three universities claim that distinction in one way or another. Looking beyond that controversy, however, we see that the first university aerodynamics lectures/classes were being taught in various countries as early as the period from 1909 through 1913. This is almost immediately after Lanchester wrote his books, and also shows how correct he was in seeing the development of aeronautical courses in universities. There is no doubt that lectures on aerodynamics were being taught in the UK by 1909 at Northampton Institute (now City, University of London), East London College (now St. Mary’s University), and Imperial College (see the bottom of Fig. 23), but the evidence for when degree programmes were fully established points to 1909–1910 at Northampton, where Frederick Handley Page was appointed as lecturer in 1910 [26–28].

Figure 23. The landscape of books on aerodynamics from 1870 through 1950.

In addition to the historical timeline just discussed, the type of book is also delineated between books that were ‘applied to airplanes’ and those that were ‘theoretical or scientific’; this is the divide that was described by Jarrett [Reference Jarrett6]. While I realise this is somewhat subjective, I found that it was fairly easy to see the difference between these two types of books, and some examples that show the difference will follow in later sections. I should also note that there were significant numbers of scientific papers being presented during this time period, but mainly on basic fluid dynamic topics and not as much on aerodynamics.

The landscape begins with three books that were theoretical or scientific in nature: Hydrodynamics by Horace Lamb which was first published in 1879 [Reference Lamb19], Original Solutions of Several Problems in Aerodynamics by Eli Blake in 1882 [Reference Blake29], and Experiments in Aerodynamics by Samuel Langley in 1891 [Reference Langley20]. These books were followed by two publications by Octave Chanute in the US: Aerial Navigation in 1891 [Reference Chanute30] and Progress in Flying Machines in 1894 [Reference Chanute31], both of which were very practical and applied.

A fairly significant gap takes place in aerodynamics books being published between 1894 and Lanchester’s books in 1907 and 1908. This also corresponds to the time period where significant progress was being made in the field where airplanes were being built and flight attempts were being made by many people. That makes Lanchester’s books fairly unique during this time period, and potentially very valuable to those who wanted to understand, and possibly teach, aerodynamics. Lanchester’s books were immediately followed by two more books on aerodynamics in 1907 (Moedebeck’s English translation of his book originally in German) [Reference Moedebeck32] and 1908 (Maxim’s handbook on how to build and fly airships) [Reference Maxim33], but by 1911–1920 there were a number of applied aerodynamics books that were published. This was in spite of the fact that The Great World War was taking place from 1914 to 1918, and in fact very few books seem to have been published during the war. Books by Lilienthal [Reference Lilienthal34] (this was an English translation of his book that originally came out in German), Hubbard [Reference Hubbard, Ledeboer and Turner35], Loening [Reference Loening36], (which mentions Lanchester’s skin friction method and references Aerodynamics) and Thurston [Reference Thurston37] all came out in 1911. All of these books were very practical and applied in nature, including presentations of aerodynamic data and applications. Near the end of, and right after, World War I, a number of new aerodynamics books came out that were also very practical in scope, including books by Judge [Reference Judge38] (which cites Lanchester throughout), Hayward [Reference Hayward39], Bairstow [Reference Bairstow40] (which mentions Lanchester’s phugoid oscillation concept) and Wilson [Reference Wilson41]. It should be noted that at least three of these books were specifically created to be textbooks, namely the books by Hubbard, Judge and Wilson, all of which have the word ‘text’ in their titles.

So, by 1920 almost all aerodynamics textbooks were similar in approach to Lanchester’s books. These books were published just before or just after World War I, and many of them were intended to be textbooks for universities. These applied books were fairly quickly followed by books by Warner [Reference Warner42], Wood [Reference Wood43], Jones [Reference Jones44] and Truitt [Reference Truitt45], all of which continued the trend of writing aerodynamics books that were very practical and applied, in the same vein as Lanchester’s Aerodynamics. What you will see if you continue looking at aerodynamics books after 1950 is that this very applied approach to teaching/writing about aerodynamics becomes a common approach primarily in aircraft design textbooks (as opposed to aerodynamics textbooks), pre-shadowed by the book by K.D. Wood, who would go on to write a well-known aircraft design book in 1943.

At the same time as this continuum of applied aerodynamics books were being written throughout the 1920s through 1940s, a very new type of book arrives on the scene: the theoretical or scientific publication. These publications (I use the term publication because Munk’s NACA paper of 1924 [Reference Munk46] was technically a report, but a report pretending to be a book) had a very different approach to aerodynamics. These books were similar to Lamb’s Hydrodynamics in approach, and lacking most of the features of the applied books we have been discussing. The series of theoretical books start with Munk’s treatise on aerodynamic theory [Reference Munk46] (Munk was a student of Prandtl), which was fairly quickly followed by books authored by Glauert [Reference Glauert47], (perhaps the first scientific aerodynamics book written in England) Diehl [Reference Diehl48], Prandtl & Tietjens [Reference Prandtl and Tietjens49, Reference Prandtl and Tietjens50], Durand [Reference Durand51] (which is a multi-volume series with many authors), Pavian [Reference Pavian52], Millikan [Reference Millikan53] and von Mises [Reference Von Mises54]. These books were followed into the 1950s by additional theoretical/scientific books, and eventually formed the basis for most modern aerodynamics textbooks. You could say this was the victory of the German approach to aerodynamics over the approach of the Lanchester, but if you realise that Lanchester’s approach largely found a home in aircraft design textbooks, then you can see that both approaches are still being followed today. In fact, in the US the German approach became the de facto aerodynamics approach, largely due to Prandtl’s students Max Munk and Theodore von Karman [Reference Von Karman55, Reference Hanle56].

Another way to look at Lanchester’s book is to see who he was citing as sources for his work. Was he only citing the applied work of his predecessors or was he citing a variety of sources? I have to admit to being quite surprised by the answer to this question, as I went through Aerodynamics looking for the number of mentions in the book, as shown in Fig. 24 (I use the term ‘mentions’ because Lanchester rarely formally cited someone’s work via a reference, but rather just mentioned their results or work). The results from most to fewest mentions are: Newton 107; Langley 104; Dine 92; Helmholtz 39; Rankine 32; Froude 32; Euler 27; Allen 26; Kelvin 25; Stokes 17; Lagrange 15; Hutton 13; Kirchhoff 12; Larmor 10; Lamb 8; Rayleigh 7; Lilienthal 7; Maxwell 7; Beaufoy 5; Reynolds 3; Robins 3; Chanute 2 (but not his book/lecture); Pilcher 1; Moilliard 1. Also, it is important to note that the following people were not cited by Lanchester at all: Wright, Cayley, Prandtl, Kutta, Navier, Bernoulli or Blake. These results do not point to someone who only cared about airplanes and applied engineering – this is a broad distribution of information from a wide variety of publications, both theoretical/scientific and airplane related. Leading the list with 107 citations is Isaac Newton, closely followed by Samuel Langley. In fact, Ackroyd notes about Lanchester’s while at university: ‘Lanchester seems to have spent much of that year in the library, reading the works of Newton and Rankine, an activity which was to have profound influence on his later work in aerodynamics’ [Reference Ackroyd4]. It seems that he has just as many citations of scientists as he does engineers. I do not believe this shows Lanchester to be sheltered or biased toward only one source of concepts and ideas – he is to be commended for this broad approach.

Figure 24. The number of times Lanchester mentions other works in Aerodynamics.

We will now look at how Lanchester’s approach in Aerodynamics compares with two other authors, specifically as how much scientific/mathematical information he includes.

3.2.1 Lamb’s hydrodynamics

Lanchester acknowledges in the Preface of Aerodynamics that Lamb’s Hydrodynamics is, ‘a work to which the author desires to acknowledge his indebtedness.’ As you look through the chapters of Aerodynamics you can see that Lanchester is depending on the theoretical developments that have been presented in Lamb’s classic book. Lanchester’s book does not have a Bibliography or Reference section, but rather uses footnotes to cite other works. As an example, when Lanchester presents Euler’s equations for inviscid flow (p. 79) he tells the reader, ‘For the full mathematical treatment reference should be made to “Hydrodynamics,” H. Lamb, Camb. University Press’ [Reference Lanchester9]. Again, for his presentation of fluid rotation (p. 86ff), Lanchester describes rotation with a paragraph and a single figure, but then refers the reader to Lamb and Lagrange, ‘The mathematical demonstration of this important fact will be found in “Hydrodynamics” (H. Lamb, Cambridge), or reference may be made to the original investigation (Lagrange, “Oeuvres”, T. IV., p. 714)’ [Reference Lanchester9, Reference LaGrange58]. In fact, throughout the book, in addition to citing Helmholtz, Kelvin and Thompson (among others; see Fig. 24 above), he cites Lamb’s mathematical derivations eight times. Does that mean Lanchester was unable to present the mathematical derivations within Aerodynamics, or does it simply mean the derivations were not the main point of his approach. Many have speculated about this over the years, including Von Karman who said [Reference Von Karman3],

It is true that because of this coincidence of their efforts [Prandtl and Lanchester] and Lanchester’s delayed publications, Lanchester’s clear priority for the circulation theory of sustentation was questioned; but it must be conceded that the mathematical theory gave more than he was able to deduce from his more or less qualitative arguments. On the other hand, he recognised the general mechanism of the lift and the induced drag also for the case of the aerofoil with finite span, for which the systematic mathematical theory needed approximately another decade of development.

von Karman said of Lanchester that, ‘He was a practical engineer, more or less an amateur mathematician, and by trade an automobile builder’ [Reference Von Karman and Edson57]. In case you feel the statement about being an ‘amateur mathematician’ is a slight against Lanchester, you should remember that von Karman said of Prandtl, ‘His control of mathematical methods and tricks was limited: many of his collaborators and followers surpassed him in solving difficult mathematical problems’ [Reference Von Karman and Edson57]. In fact, von Karman held Lanchester in high regard: ‘Of the three men I have named as pioneers in circulation theory, (Lanchester, Kutta, and Joukowski) only Lanchester went further than the problem of a wing of infinite span with constant section. He was the first man to attack the problem of a wing of finite span’ [Reference Von Karman and Edson57].

Here are some specific examples that show the vast difference between Lanchester’s Aerodynamics and Lamb’s Hydrodynamics. When describing the potential flow concept of a dipole (a source and a sink located equi-distance from the origin), Lanchester’s development contains no mathematics but does have a very nice image of the flowfield for the dipole (see Fig. 25(a)), while Lamb’s description contains pages of mathematical derivations using the complex stream function and complex analysis, as well as a more basic image of the flowfield than is presented by Lanchester (see Fig. 25(b)). Is one presentation better than the other? That completely depends on the purpose of the presentation and the intended audience.

Figure 25. Description of the potential flow for a dipole: (a) Lanchester’s approach; and (b) Lamb’s approach (public domain).

Figure 26. Description of flow over a cylinder: (a) Lanchester’s book; and (b) Lamb’s book (public domain).

Figure 27. Von Karman’s comparison of Lanchester’s approach for finite wings and Prandtl’s approach (left); Prandtl’s mathematical derivation as he determines the downwash caused by the trailing vortex system (right) [Reference Von Karman3, Reference Prandtl and Tietjens50].

Another example where Lanchester points to Lamb and does not develop any mathematical explanations is for flow over a cylinder (and flow over a sphere); see Fig. 26. Again, Lanchester’s figure is more complete than Lamb’s (Lanchester includes both the stream function and velocity potential equi-potential lines), but in this case Lanchester goes farther than Lamb by describing how, using energy conservation concepts, that the energy within the cylinder is equal to the energy outside of the cylinder, even to the extent that he shows each square inside the cylinder having a corresponding region outside of the cylinder that has the same energy. Of course, Lamb’s presentation includes pages of mathematical derivation and explanations that are nowhere to be found in Lanchester’s book.

3.3 Contents in Aerodynamics

One more way to understand Lanchester’s purpose in writing Aerodynamics is to simply look at the contents of the book. The Table of Contents for Lanchester’s Aerodynamics is quite remarkable – the breadth of topics covered is as wide as in any modern aerodynamics textbooks (with the exception of higher speed flight). Coupled with the contents of Aerodonetics, where he develops concepts in aircraft performance and flight mechanics, this is truly the first full coverage of airplane engineering concepts.

Figure 28. Early hand-written manuscript for a book titled Introduction to the Study of Flight (left); Introduction to the re-titled book The Fundamentals of Flight dated 1 May 1935 (right); (Coventry University, Lanchester Interactive Archive, Creative Commons (BY-NC-ND) 4.0 License).

Specifically, Lanchester’s Aerodynamics book includes the following chapter titles:

1. 1. Fluid Resistance and its Associated Phenomena

2. 2. Viscosity and Skin Friction

3. 3. The Hydrodynamics of Analytical Theory

4. 4. Wing Form and Motion in the Peripetery

5. 5. The Aeroplane – The Normal Plane

6. 6. The Inclined Aeroplane

7. 7. The Economics of Flight

8. 8. The Aerofoil

9. 9. On Propulsion, The Screw Propeller, and the Power Expended in Flight

10. 10. Experimental Aerodynamics

Lanchester clearly had a purpose and plan for writing Aerodynamics in 1907. Given the explosion of books on aerodynamics that followed his book, his purposes outlined in the Preface to the book were far seeing and on target. In fact, as you look through Aerodynamics and Aerodonetics you can see examples taken directly from his early flight experiments, as well as his designs and concepts from airplanes. What Lanchester could not have fully understood, is the immense social divide that his book was entering, which is probably what made him frustrated enough to write the book in the first place.

3.4 Lanchester’s plans for a new book in the 1930s

While looking through the immense holdings of the Lanchester Interactive Archive [17], I stumbled across an early manuscript for another book on aeronautics. Lanchester had written other books after Aerodynamics and Aerodonetics, including books titled Aircraft in Warfare: The Dawn of the Fourth Arm in 1911 and Relativity in 1931. I was not aware, however, of his detailed manuscript for another aerodynamics book. Figure 28 shows both an early hand-written manuscript for the book and a typed pre-publication version from 1935. Lanchester provides clues for why he was writing the new book.

Lanchester then states his personal purpose for writing this new book:

Lanchester still held the belief that aerodynamic knowledge was critical for developing aircraft and making progress in design. He also still believed that too much detail was not good for the average reader and practical aerodynamics was important, especially now that so much new research had been done by government labs in various countries. The handwritten draft for the new book is 161 pages long, and there is no telling how long the book would have become as Lanchester edited and revised the manuscript. As with Aerodynamics, there is very little theoretical development in the new book, but there are example calculations and methods. There are also callouts for many figures and illustrations in the manuscript, but those figures are not included in the manuscript. Even by the mid 1930s, Lanchester had not lost his desire to bring aerodynamics to the people who were really interested – I for one would have liked to read this book.

5.1 Are we using obsolescent approaches?

Sometimes it helps to see what we are doing by looking at the situation from a completely different perspective. I was reading an article on technological innovation, development, adoption and obsolescence and came across Fig. 28, which shows two related trend curves [Reference O’Leary64]. The maturity curve (known as the Gartner curve and shown with the dotted line) shows the development of any technology, starting with embryonic idea, the adolescent and early mainstream phases, the mature mainstream phase, the legacy phase, and finally obsolescence. Also on Fig. 29 there is the adoption of the product (known as the Cumulative Adoption S-curve and shown with the solid line), which initially is very low (and fairly constant) followed by a period of rapid growth, then a leveling off, and ending with a decrease of use once the technology becomes obsolescent.

Figure 29. Adoption curve and maturity curve with levels and adoption rates (used with permission of American Accounting Association, from O’Leary (2009), Ref. Reference O’Leary64; permission conveyed through Copyright Clearance Center, Inc.) [Reference O’Leary64].

My interest in these maturity and adoption curves is this: has our approach to aerodynamic education followed a similar trend, yet we have not replaced our approach with a new technology? The example of high-speed aerodynamics research seems instructive: a drop off in theoretical work took place in the 1960s, but this was followed by a sharp rise in computational research in the 1970s. One technology had been replaced by another! That does not mean all of the high-speed theories from the 1950s are completely obsolescent, but new ways to learn and expand knowledge had come onto the scene.

Here’s the problem: the new approaches used in research and design have not been updated in the undergraduate classroom (largely), and still haven’t been widely adopted. Computational fluid dynamics (CFD) largely replaced theory in high-speed aerodynamics research decades ago, but we still teach aerodynamics as if that did not happen. Why? Is it because theory was so important when current senior faculty were graduate students that they want all of their students to learn theory (and/or suffer through it) as well? Or perhaps we have a generation of aerodynamics faculty who largely were not exposed to CFD or more modern aerodynamic experimental techniques and cannot (or will not) bring those new approaches into the classroom. Or maybe the textbooks do not follow these modern approaches so the faculty, who are always pressed for time, just follow the textbook and do not supplement the material very much with new concepts or approaches.

Whatever the reason, I believe we need to change how we approach aerodynamics education, and there has long been a vocal minority who agree with this observation. For example, Murman, et al., made this statement in 2001:

I agree completely (for both aerodynamics education and textbooks), but realise there are a variety of impediments to making this change, and a number of challenges need to be overcome.

What does a potential new aerodynamics course (and textbook) look like (and is this new course closer to what Lanchester was doing all along)? How can aerodynamics be taught the way that it is currently used, with an integrated approach using theory, experiments and computational approaches? To help answer those questions, the AIAA Fluid Dynamics Technical Committee formed a working group in 2010 to explore how to include CFD in undergraduate education (and also for aerodynamics textbooks) [Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66]. The use of CFD in the design process is growing more prevalent each year, which was well illustrated by the testimony of Michael Garrett of The Boeing Company before the US Senate Committee on Commerce, Science, and Transportation in 2006. Mr. Garrett stated, ‘In 1980, Boeing tested 77 wings in wind tunnels to arrive at the final configuration of the 767. Just 25 years later, we built and tested 11 wings for the 787 – a reduction of over 80%’ [Reference Garrett67].

These changes in how aerodynamics was being done in industry, however, were not being followed in academia, as observed by the AIAA working group in 2014:

What would an undergraduate course and textbook look like to handle an integrated, three-pronged attack on aerodynamics using theoretical, experimental, and computational approaches? The AIAA working group conducted a survey of fluid/aerodynamic practioners and asked a number of questions about what students needed to know (similar to what Mason had done in 1992). Table 1 shows the results of the survey. In assessing the extent to which their new employees were prepared with these skills, the responses were (on a scale between 0 and 5, with 5 meaning ‘very prepared’): ‘Understanding of flow phenomena’ and ‘Post processing’ were fairly evenly rated (although the ratings are low), and ‘V&V’, ‘Grid generation’, and ‘Compressible flow methodology’ were rated essentially equally. Notice that the responses showed that students were relatively well prepared in using basic computer codes and geometry modelling, but not at the levels deemed necessary by the respondents. Thus, the perception of preparedness was quite low in every skill, but particularly in verification of solutions. Finally, the difference between the two responses is also shown in Table 1. Here a large difference would show a topic that was deemed important but that was not very evident in new graduates. Notice that the highest differences were for understanding flow phenomena (a physical understanding) and V&V (a computer code understanding) [Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66]. The working group went through a number of approaches to fulfilling these objectives, and examples of each were developed, as will be discussed in the next section.

Table 1. Overall results of survey of CFD customers (scale between 0 and 5, with 5 meaning very important/prepared) [Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66]

5.2 Strategies for incorporating CFD into undergraduate curriculum

The AIAA working group, which consisted of academics from a broad range of universities in the US, realised that ‘one size fits all’ was not going to be the correct answer for this problem. Every university is different, with different facilities and faculty experiences and capabilities, so the group tried to be realistic with their proposed curricular suggestions. Three basic approaches were proposed under areas labeled as: (1) CFD ‘Light’, (2) CFD ‘Moderate’, and (3) CFD ‘Heavy’. We will quickly look at each, but then also consider the implications of including CFD in aerodynamics education for textbooks.

5.2.2 CFD ‘Moderate’

At this intermediate level of CFD instruction, CFD modules are used to augment course material by substituting the module into an existing lecture for a fluid mechanics or aerodynamics course, or into the accompanying lab unit of the course. The CFD content is heavier than in the CFD light scenario, in that here the students are expected to compute the solutions before analysing them. As the following examples will suggest, this approach often makes use of free or in-house inviscid aerodynamic solvers (i.e. panel and/or vortex lattice codes) in order to compute aerodynamics and predict forces on lifting surfaces [Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66]. Examples of this approach were included in ‘A Best Practices Report on CFD Education in the Undergraduate Curriculum’ [Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66], and include specific course modules from three universities: University of Dayton, Saint Louis University and Boise State University. These approaches rely on the use of Matlab, or freely available software such as XFOIL [Reference Drela68] or OpenVSP [69], but in some cases actual CFD software was used as well. An example of a project that could be conducted using XFOIL is shown in Fig. 30, or an OpenVSP project is shown in Fig. 31, both of which do not require extra external computer resources (just student laptops) and are freely available.

Figure 30. XFOIL simulation of NACA 2412 aerofoil (courtesy of Mark Drela of MIT, GNU General Public License) [Reference Drela68].

Figure 31. Example aircraft input geometry for OpenVSP, which is then analysed by a vortex lattice method or other applications (NASA Open Source Agreement (NOSA) version 1.3) [69].

5.2.3 CFD ‘Heavy’

The section on ‘Heavy’ inclusion of CFD had multiple examples from the US Air Force Academy, University of Dayton, Saint Louis University, University of Vermont and Boise State University, as well as possible usage examples for laboratory and aircraft design courses. The only university (at the time of publication) with a required undergraduate course in computational aerodynamics, however, was the US Air Force Academy. While the course definitely required time for students to learn about how to use a production CFD code, there were also multiple aerodynamics concepts being presented. Specifically, students learned the following aerodynamic concepts while performing their projects [Reference Cummings23, Reference Eldredge, Senocak, Dawson, Canino, Liou, LeBeau, Hitt, Rumpfkeil and Cummings66].

• • boundary conditions and their relationship to flow type (viscous or inviscid)

• • boundary layer thickness, growth and velocity profiles

• • importance of understanding boundary-layer theory while doing CFD (sub-layer types and thicknesses, pressure gradients, etc.)

• • stagnation points and stagnation streamlines

• • flow separation and reattachment

• • laminar separation bubbles

• • aerofoil/wing stall

• • aerofoil pressure gradients as a function of angle-of-attack

• • aerofoil surface and off-surface pressures, circulation, and the resulting lift and drag variations with angle-of-attack

• • the relationship between pressure gradients and flow separation

• • pressure and skin friction drag

• • unsteady vortex shedding

• • the impact of wing-tip vortices

• • compressibility effects at subsonic Mach numbers.

In addition, the following aerodynamic theories and concepts are taught to the students while they are performing their projects (or are learned in a prior course):

• • NACA aerofoil designations and data

• • potential flow theory

• • Kutta-Joukowski theorem

• • thin aerofoil theory

• • lifting-line theory

So, while many faculty members might have believed they were giving up a great deal by teaching CA to their students in lieu of the more traditional syllabus, we found that many of the same concepts were still covered, but in different (and project-based) ways.

An example of the student project in our computational aerodynamics course is shown in Fig. 32. When aerofoil flowfields are computed using a Navier-Stokes solver (which is done at multiple angles of attack, including at least one post-stall angle-of-attack), the students now can see the flow (they can once again be the fluid particle rather than learn to derive the theory). They can also start to attain the outcomes of the respondents from the 1992 study conducted by Bill Mason and start to achieve ‘knowledge of flow physics’. By interrogating the boundary layer development along the chord of the aerofoil the students can see incipient flow separation and post-stall flows, as well as compare predictions of lift and drag with aerofoil data.

Figure 32. Flow field about an NACA 4412 aerofoil (left) and Comparison of CFD predictions with experimental data for an NACA 0012 aerofoil (right) [Reference Cummings23].

Now the students are ready to go beyond just deriving theories, but truly integrating theoretical fluid dynamics (TFD), experimental fluid dynamics (EFD) and computational fluid dynamics (CFD) approaches in project-based learning. An excellent example of integrating theory, experiments and computations is shown in Fig. 33, where the students have analysed a rectangular planform wing consisting of diamond-wedge aerofoils at supersonic speeds (in this case Mach 2.5). Experimental data was collected for the wing in the US Air Force Academy Tri-Sonic Wind Tunnel and compared with shock-expansion and Busemann’s theory for the 2D and 3D flow regions on the wing. The results are quite remarkable. Now true learning can take place, as a knowledge and ‘feel’ is developed, still based on theory, but also based on experiments and computations.

Figure 33. Comparison of TFD, EFD and CFD, for the 2D flow field over the diamond-wedge wing (left), and for the 3D flow field near the wing tip of the wing (right) [Reference Cummings23].

5.3 Implications for aerodynamics textbooks in the future

I think the list of topics covered in Section 5.2.3 is something that Lanchester would have wanted to see, since so many of those topics were included in Aerodynamics. The fact that this list was written over a decade ago, based on what we were doing at the US Air Force Academy with computational aerodynamics, is all the more interesting. In spite of that fact, the comparison of this list with Lanchester’s topics in Aerodynamics is quite informative, and makes me wonder if Lanchester might have seen that computational aerodynamics was helping to return aerodynamics books to his side of the ‘divide’. For example, as we began teaching computational aerodynamics to undergraduate students over twenty years ago, we realised there was no textbook appropriate for undergraduate students, so we ended up writing our own [Reference Cummings, Mason, Morton and McDaniel70]. This textbook still includes the results of aerodynamic theories (because we believe students still need to know those theories), but now takes them further into the aerodynamic triad of TFD/EFD/CFD. That will, hopefully, lead to students who are better prepared to tackle the problems associated with being an aerodynamicist (or performance or flight controls or structural engineer) in their future. Another textbook that incorporates computational simulations into an aerodynamics education is Flight Vehicle Aerodynamics by Mark Drela of MIT [Reference Drela71]. While the specific approaches are somewhat different in both books, the basic approach is similar: help students gain knowledge about aerodynamics using computational and theoretical approaches, something we hope Lanchester would have appreciated.