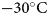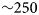Introduction
Mass loss from the Greenland Ice Sheet (GrIS) has significantly accelerated during the last several decades to become a major cryospheric contributor to global sea-level rise (Rignot and others, Reference Rignot, Velicogna, van den Broeke, Monaghan and Lenaerts2011; Jacob and others, Reference Jacob, Wahr, Pfeffer and Swenson2012; The IMBIE Team, 2019). Since 1991, 60% of GrIS mass loss has been attributed to surface meltwater runoff (van den Broeke and others, Reference van den Broeke2016), with total meltwater set to increase over the 21st century as Arctic warming accelerates (AMAP, 2017), the capacity of firn to refreeze percolating meltwater decreases (De La Peña and others, Reference De La Peña2015; Mikkelsen and others, Reference Mikkelsen2016; Noël and others, Reference Noël2017; Steger and others, Reference Steger2017) and the equilibrium line altitude moves inland (Leeson and others, Reference Leeson2015). These figures all emphasise the importance of developing a holistic understanding of the GrIS supraglacial hydrology system (Rennermalm and others, Reference Rennermalm2013).
Research on supraglacial lakes, which are one component of the supraglacial hydrology system, has advanced rapidly during the last decade (Chu, Reference Chu2014; Nienow and others, Reference Nienow, Sole, Slater and Cowton2017). However, the ways in which future warming will influence the lakes' spatial and temporal patterns (Box and Ski, Reference Box and Ski2007; McMillan and others, Reference McMillan, Nienow, Shepherd, Benham and Sole2007; Liang and others, Reference Liang2012; Johansson and others, Reference Johansson, Jansson and Brown2013; Fitzpatrick and others, Reference Fitzpatrick2014) and the surface-to-bed linkages for which they are frequently responsible (Das and others, Reference Das2008; Hoffman and others, Reference Hoffman2018), remain poorly constrained (Mayaud and others, Reference Mayaud, Banwell, Arnold and Willis2014; Banwell and others, Reference Banwell, Hewitt, Willis and Arnold2016; Koziol and others, Reference Koziol, Arnold, Pope and Colgan2017), and are gaining importance as supraglacial lakes are observed to be present over increasing portions of the ice sheet (Leeson and others, Reference Leeson2015; Gledhill and Williamson, Reference Gledhill and Williamson2017; Williamson and others, Reference Williamson, Banwell, Willis and Arnold2018a).
Greenland's supraglacial lakes can transiently occupy ${\sim }2.7\percnt$ of the ablation zone (Box and Ski, Reference Box and Ski2007) and form in the same locations year-on-year as a result of ice surface expression of basal topography (Echelmeyer and others, Reference Echelmeyer, Clarke and Harrison1991; Lampkin and VanderBerg, Reference Lampkin and VanderBerg2011). The lakes are observed to drain, either rapidly down hydro-fractured moulins (Das and others, Reference Das2008; Doyle and others, Reference Doyle2013) (${\sim }10\percnt$
of the ablation zone (Box and Ski, Reference Box and Ski2007) and form in the same locations year-on-year as a result of ice surface expression of basal topography (Echelmeyer and others, Reference Echelmeyer, Clarke and Harrison1991; Lampkin and VanderBerg, Reference Lampkin and VanderBerg2011). The lakes are observed to drain, either rapidly down hydro-fractured moulins (Das and others, Reference Das2008; Doyle and others, Reference Doyle2013) (${\sim }10\percnt$ of lakes; Selmes and others, Reference Selmes, Murray and James2013), or more gradually by over topping and incising their catchment (Tedesco and others, Reference Tedesco2013) (${\sim }50\percnt$
of lakes; Selmes and others, Reference Selmes, Murray and James2013), or more gradually by over topping and incising their catchment (Tedesco and others, Reference Tedesco2013) (${\sim }50\percnt$ of lakes; Selmes and others, Reference Selmes, Murray and James2013). The precise conditions that cause some, but not all, lakes to drain through hydrofracture remain elusive (Williamson and others, Reference Williamson, Willis, Arnold and Banwell2018b), though the overall effect of rapid lake drainage on ice velocity in land-terminating sectors of the GrIS is not as great as initially thought (Nienow and others, Reference Nienow, Sole, Slater and Cowton2017). The moulins they frequently open however, do exert long-lasting control on the subglacial hydrology system (Banwell and others, Reference Banwell, Hewitt, Willis and Arnold2016; Koziol and others, Reference Koziol, Arnold, Pope and Colgan2017; Williamson and others, Reference Williamson, Banwell, Willis and Arnold2018a). Many authors interested in supraglacial lake processes and effects assume that the ${\sim }40\percnt$
of lakes; Selmes and others, Reference Selmes, Murray and James2013). The precise conditions that cause some, but not all, lakes to drain through hydrofracture remain elusive (Williamson and others, Reference Williamson, Willis, Arnold and Banwell2018b), though the overall effect of rapid lake drainage on ice velocity in land-terminating sectors of the GrIS is not as great as initially thought (Nienow and others, Reference Nienow, Sole, Slater and Cowton2017). The moulins they frequently open however, do exert long-lasting control on the subglacial hydrology system (Banwell and others, Reference Banwell, Hewitt, Willis and Arnold2016; Koziol and others, Reference Koziol, Arnold, Pope and Colgan2017; Williamson and others, Reference Williamson, Banwell, Willis and Arnold2018a). Many authors interested in supraglacial lake processes and effects assume that the ${\sim }40\percnt$ of lakes that remain in situ at the end of the melt season (Selmes and others, Reference Selmes, Murray and James2013) either freeze entirely in winter (Johansson and others, Reference Johansson, Jansson and Brown2013; Selmes and others, Reference Selmes, Murray and James2013; Koziol and others, Reference Koziol, Arnold, Pope and Colgan2017), or freeze partially and play no future rule in the hydrology of the GrIS (Arnold and others, Reference Arnold, Banwell and Willis2014). This view is supported in remote sensing from Miles and others (Reference Miles, Willis, Benedek, Williamson and Tedesco2017) who suggest full winter freezing of lakes based on C-band Sentinel-1 satellite data, although they acknowledge this conclusion may be a result of the low penetration of the C-band radar (1–2 m).
of lakes that remain in situ at the end of the melt season (Selmes and others, Reference Selmes, Murray and James2013) either freeze entirely in winter (Johansson and others, Reference Johansson, Jansson and Brown2013; Selmes and others, Reference Selmes, Murray and James2013; Koziol and others, Reference Koziol, Arnold, Pope and Colgan2017), or freeze partially and play no future rule in the hydrology of the GrIS (Arnold and others, Reference Arnold, Banwell and Willis2014). This view is supported in remote sensing from Miles and others (Reference Miles, Willis, Benedek, Williamson and Tedesco2017) who suggest full winter freezing of lakes based on C-band Sentinel-1 satellite data, although they acknowledge this conclusion may be a result of the low penetration of the C-band radar (1–2 m).
Conversely Koenig and others (Reference Koenig2015) use L-band IceBridge airborne radar data to observe winter ‘buried lakes’ (sometimes called ‘subsurface lakes’) containing liquid water across the entire periphery of the GrIS, in the same location as MODIS detected summer lakes. These buried lakes are not normally observable from surface topography, although radar data shows an average overlying snow-depth of 0.65 m and an ice-lid thickness of 1.4 m (both are influenced by the timing of IceBridge flights). Russell (Reference Russell1993) also infers the presence of buried lakes from ice-sheet marginal meltwater release near Kangerlussuaq, concurrent with the development of two circular depressions where lakes had previously been observed 20–30 km inland. The first order estimate of 1.5 Gt of water accumulated in buried lakes (Koenig and others, Reference Koenig2015) is small in comparison with the 140 Gt believed to be in firn aquifers (Forster and others, Reference Forster2014), or the 100–300 Gt of melt lost through GrIS annual surface melt (Vernon and others, Reference Vernon2013). Nevertheless, a buried lake acts as a $0^{\circ }{\rm C}$ boundary whenever it is present, warming underlying ice even as a surface energy input decreases in winter, with potential implications for ice rheology and therefore fracture mechanics. A buried lake also acts as a store of water that may expedite the subsequent summer evolution of the supraglacial hydrological system. The thermal signature of lakes is important in cryo-hydrologic warming (Phillips and others, Reference Phillips, Rajaram and Steffen2010, Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013) as another way to warm the near-surface ice sheet, and for temperature analysis where surface features are found to exert a strong influence on temperature profiles (Catania and Neumann, Reference Catania and Neumann2010; Lüthi and others, Reference Lüthi2015; Hills and others, Reference Hills, Harper, Humphrey and Meierbachtol2017). These studies emphasise the need for a physically based and rigorous analysis of multi-year supraglacial lake evolution to provide better information for GrIS hydrology studies on the fate, and thermal effects, of lakes following the end of the summer melt season.
boundary whenever it is present, warming underlying ice even as a surface energy input decreases in winter, with potential implications for ice rheology and therefore fracture mechanics. A buried lake also acts as a store of water that may expedite the subsequent summer evolution of the supraglacial hydrological system. The thermal signature of lakes is important in cryo-hydrologic warming (Phillips and others, Reference Phillips, Rajaram and Steffen2010, Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013) as another way to warm the near-surface ice sheet, and for temperature analysis where surface features are found to exert a strong influence on temperature profiles (Catania and Neumann, Reference Catania and Neumann2010; Lüthi and others, Reference Lüthi2015; Hills and others, Reference Hills, Harper, Humphrey and Meierbachtol2017). These studies emphasise the need for a physically based and rigorous analysis of multi-year supraglacial lake evolution to provide better information for GrIS hydrology studies on the fate, and thermal effects, of lakes following the end of the summer melt season.
Here, a numerical modelling approach is used to gain a detailed understanding of the evolution of supraglacial lakes. GlacierLake is presented: an efficient and realistic model of supraglacial lake evolution, applicable across the ablation zone of any glacier (though modifications may be required for debris covered glaciers), but used here to investigate lake evolution on the GrIS. GlacierLake completes a year-long run in half a minute on a 3.2 GHz processor. This allows for GlacierLake's use across large areas, and allows coupling with broader hydrological models if required (e.g. Koziol and Arnold, Reference Koziol and Arnold2018). A fast run-time also enables extensive sensitivity testing which adds to the reliability and transparency of model results.
Existing models
Numerical models of snow, and of lakes underlain by ice or permafrost have been developed and applied over the last two decades. The earliest relevant model is from Ebert and Curry (Reference Ebert and Curry1993) who focused on meltwater lake formation atop sea ice, based on original equations by Maykut and Untersteiner (Reference Maykut and Untersteiner1971). Sea ice lake models improved over the decades (Morassutti and Ledrew, Reference Morassutti and Ledrew1996; Fetterer and Untersteiner, Reference Fetterer and Untersteiner1998; Taylor and Feltham, Reference Taylor and Feltham2004; Skyllingstad and others, Reference Skyllingstad, Paulson and Perovich2009) culminating in work by Scott and Feltham (Reference Scott and Feltham2010), who produced a fully 3-dimensional lake evolution model for first-year and multi-year sea ice. The terrestrial MyLake model of Saloranta and Andersen (Reference Saloranta and Andersen2007), originally developed for phosphorous-phytoplankton dynamics, performs well for temperature and ice lid thickness modelling, with a rapid run time. However the exclusion of a lower, spatially flexible phase boundary and underlying glacier-ice section means basal freeze-up and its effects on underlying temperature profiles cannot be constrained.
Models to simulate the evolution of supraglacial lakes began with Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) who derive their analysis from Ebert and Curry (Reference Ebert and Curry1993) and use the explicit heat equation discretisation from Alexiades and Solomon (Reference Alexiades and Solomon1993). Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) examined the abundance of supraglacial lakes in satellite imagery and combined this with the use of a 1-D model to examine the effects of a meltwater column on energy transfer, finding that the basal ablation of lakes is 110–170% that of the immediate surrounding bare ice. Benedek (Reference Benedek2014) used code from Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) to extend the length of the shortwave radiation path from the lake surface to the bed, based on refraction at the lake surface. Benedek (Reference Benedek2014) found this caused relatively little change to the overall evolution of the lakes, with parameter uncertainty (such as surface absorption of shortwave radiation) having a greater influence. The models of Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006), Tedesco and others (Reference Tedesco2012) and Benedek (Reference Benedek2014) were run for no longer than 30 days, and lid formation, allowance for a transition from bare ice to water, and lid collapse, were not incorporated. The explicit discretisation of these models means the time step was held below 6 min to avoid numerical instability, resulting in greater computational expense than with an implicit scheme. Lastly, Buzzard and others (Reference Buzzard, Feltham and Flocco2018) present currently the most physically comprehensive lake model, developed for ice shelves in Antarctica where firn compaction, saturation and refreezing are important. However, detailed modelling of these aspects increases the runtime of the model from minutes to hours and is not required when the lake forms atop solid ice following early snowmelt.
Model development
Model architecture
GlacierLake was written in MATLAB R2017b using the equations presented below, with source code and equations adapted from Benedek (Reference Benedek2014) (who adapted source code from Lüthje and others, Reference Lüthje, Feltham, Taylor and Worster2006), Buzzard and others (Reference Buzzard, Feltham and Flocco2018), Saloranta and Andersen (Reference Saloranta and Andersen2007) and Essery (Reference Essery2015). GlacierLake represents a single point in x, y space modelled as a $1\, {\rm m}^{2}$ column as any scaling factors cancel. The model is divided into five stages (Fig. 1 and Table 1). Movement through GlacierLake, and processes at each stage, are detailed in Table 2 and occur once a given threshold has been reached. The model is also allowed to move backwards through stages (for example stage 5 to 3 in Fig. 1) to mimic year-on-year evolution. The model was developed using weather data from the Program for Monitoring of the GrIS (PROMICE, vanAs and others, Reference van As and Fausto2010). The AWS UPE-U, at an elevation of 980 m a.s.l. and $72.89^{\circ }{\rm N}$
column as any scaling factors cancel. The model is divided into five stages (Fig. 1 and Table 1). Movement through GlacierLake, and processes at each stage, are detailed in Table 2 and occur once a given threshold has been reached. The model is also allowed to move backwards through stages (for example stage 5 to 3 in Fig. 1) to mimic year-on-year evolution. The model was developed using weather data from the Program for Monitoring of the GrIS (PROMICE, vanAs and others, Reference van As and Fausto2010). The AWS UPE-U, at an elevation of 980 m a.s.l. and $72.89^{\circ }{\rm N}$ , $53.58^{\circ }{\rm W}$
, $53.58^{\circ }{\rm W}$ , was used for development, as the record for this station was the most comprehensive of any PROMICE station in the ablation zone of the GrIS.
, was used for development, as the record for this station was the most comprehensive of any PROMICE station in the ablation zone of the GrIS.

Fig. 1. Schematic diagram of model stages with explanations in Table 1. Width of each stage schematically represents expected residence time. Segment shapes represent schematic evolution of phase throughout stage. The initial section of stage 4 is snow free to show that lid can function with or without snow cover. Height of each column indicates the overall depth of the model domain.
Table 1. Description of model stages

Table 2. Progression through model stages with brief descriptions of processes occurring at each stage

Trackers monitor events such as initialisation of snow layer to ensure repetition does not occur. Italicised text indicates setup and sub-functions, normal text indicates conditional statements.
GlacierLake comprises two modules. The main module contains cells of constant size throughout the model run (default 0.1 m for upper 15 m and, 1 m below). These cells are in one of three states: ice, water or ‘slush’, where ice and water coexist in a ratio dependent upon the total enthalpy of the cell. The density of water was used for slush, ice and water to avoid a change in cell depth with state as the difference is small (11%) and therefore assumed to be insignificant (Lüthje and others, Reference Lüthje, Feltham, Taylor and Worster2006; Benedek, Reference Benedek2014; Buzzard and others, Reference Buzzard, Feltham and Flocco2018). A second module deals with snow on the surface when present and incorporates the snow physics of Essery (Reference Essery2015) (see the Snow cover section and Fig. 2) to avoid computationally expensive resizing at each timestep as with Buzzard and others (Reference Buzzard, Feltham and Flocco2018). If the domain depth varies due to meltwater input, a temporary lake insert comprised cells of standard size is used within the main cell column (Fig. 2). A bucket filling method is used for each new cell to keep cell sizes uniform, so a new cell is only added when additional meltwater inflow exceeds 10 cm (as default). If the meltwater inflow input ceases, the lake insert is combined with the main column in a one-off operation to reduce complexity in subsequent stages.

Fig. 2. Construction of separate snow module (left) and the lake insert contained within the main module (right) during meltwater inflow. The lake insert size is increased discretely whereas the snow module size is increased continuously. The lake insert is combined with the main grid after meltwater inflow is complete. The grid size for snow/ice/slush cells remains constant in the upper section of the model but can increase in deeper cells (not shown in this figure).
Surface energy balance
Surface energy flux in ${\rm W}\, {\rm m}^{-2}$ is calculated after Buzzard and others (Reference Buzzard, Feltham and Flocco2018) who follow Ebert and Curry (Reference Ebert and Curry1993), as
is calculated after Buzzard and others (Reference Buzzard, Feltham and Flocco2018) who follow Ebert and Curry (Reference Ebert and Curry1993), as

where ɛ is the surface emissivity, $F_{{LW}_{{\rm in}}}$ is incoming longwave radiation (${\rm W}\, {\rm m}^{-2}$
is incoming longwave radiation (${\rm W}\, {\rm m}^{-2}$ ), α is albedo, $F_{{SW}}$
), α is albedo, $F_{{SW}}$ is incoming shortwave radiation (${\rm W}\, {\rm m}^{-2}$
is incoming shortwave radiation (${\rm W}\, {\rm m}^{-2}$ , separated into water-penetrating and surface radiation when a lake is present using eqn (12)), σ is the Stefan–Boltzmann constant (${\rm W}\, {\rm m}^{-2}\, {\rm K}^{-4}$
, separated into water-penetrating and surface radiation when a lake is present using eqn (12)), σ is the Stefan–Boltzmann constant (${\rm W}\, {\rm m}^{-2}\, {\rm K}^{-4}$ ), T is temperature (K), $F_{{\rm sen}}$
), T is temperature (K), $F_{{\rm sen}}$ is sensible heat flux (${\rm W}\, {\rm m}^{-2}$
is sensible heat flux (${\rm W}\, {\rm m}^{-2}$ ) and $F_{{\rm lat}}$
) and $F_{{\rm lat}}$ is latent heat flux (${\rm W}\, {\rm m}^{-2}$
is latent heat flux (${\rm W}\, {\rm m}^{-2}$ ). Sensible heat flux is calculated as
). Sensible heat flux is calculated as

where $\rho _{a}$ is the density of dry air ($1.275\, {\rm kg}\, {\rm m}^{-3}$
is the density of dry air ($1.275\, {\rm kg}\, {\rm m}^{-3}$ ), $C_{p}^{{\rm air}}$
), $C_{p}^{{\rm air}}$ is the specific heat capacity of dry air (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$
is the specific heat capacity of dry air (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$ ), $C_{T}$
), $C_{T}$ is a function of atmospheric stability described in Ebert and Curry (Reference Ebert and Curry1993) (eqns (4) and (5)), v is the wind speed (${\rm m}\, {\rm s}^{-1}$
is a function of atmospheric stability described in Ebert and Curry (Reference Ebert and Curry1993) (eqns (4) and (5)), v is the wind speed (${\rm m}\, {\rm s}^{-1}$ ) and $T_{a}$
) and $T_{a}$ and $T_{s}$
and $T_{s}$ are air and surface temperature respectively. Latent heat flux is calculated as
are air and surface temperature respectively. Latent heat flux is calculated as

where $L_{f}$ is the latent heat of fusion of ice (${\rm J}\, {\rm kg}^{-1}$
is the latent heat of fusion of ice (${\rm J}\, {\rm kg}^{-1}$ ), and $q_{a}$
), and $q_{a}$ and $q_{s}$
and $q_{s}$ are the air and surface specific humidities.
are the air and surface specific humidities.
$C_{T}$ is calculated as
is calculated as

where $C_{T_{s}} = 1.3\times 10^{-3}$ , $b' = 20$
, $b' = 20$ and c = 50.986 are constants and Ri is the bulk Richardson number,
and c = 50.986 are constants and Ri is the bulk Richardson number,

where $\Delta z$ is equal to 10 m following Ebert and Curry (Reference Ebert and Curry1993).
is equal to 10 m following Ebert and Curry (Reference Ebert and Curry1993).
Humidity is provided as relative (%) by PROMICE weather stations and converted to specific humidity by first obtaining the saturation vapour pressure, $e_{s}\lpar T\rpar$ at temperature T ($^{\circ }{\rm C}$
at temperature T ($^{\circ }{\rm C}$ ), following Tetens (Reference Tetens1930) as
), following Tetens (Reference Tetens1930) as

Vapour pressure is obtained using the definition of relative humidity (RH) as

The mixing ratio of water vapour, w, is calculated after American Meteorological Society (2012) as

where p is the pressure (Pa), $R_{d}$ is the specific gas constant for dry air (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$
is the specific gas constant for dry air (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$ ) and $R_{v}$
) and $R_{v}$ is the specific gas constant for water vapour (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$
is the specific gas constant for water vapour (${\rm J}\, {\rm kg}^{-1}\, {\rm K}^{-1}$ ). Lastly, the specific humidity, q, can be obtained after American Meteorological Society (2012) using
). Lastly, the specific humidity, q, can be obtained after American Meteorological Society (2012) using

Lake albedo, α, was calculated following Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) based on a two-stream approximation from Taylor and Feltham (Reference Taylor and Feltham2004) and adapted for the generally lower albedo for glacier ice than sea ice as

where $z_{l}$ is the depth of the lake.
is the depth of the lake.
Shortwave propagation
The Beer–Lambert law was used to calculate the transfer of shortwave radiation through water and ice as

where $F_{i}$ is the flux at cell i (${\rm W}\, {\rm m}^{-2}$
is the flux at cell i (${\rm W}\, {\rm m}^{-2}$ ), τ is the shortwave extinction coefficient (${\rm m}^{-1}$
), τ is the shortwave extinction coefficient (${\rm m}^{-1}$ ) and $z_{i}$
) and $z_{i}$ is the depth of cell i. $F_{b}$
is the depth of cell i. $F_{b}$ , the shortwave radiation entering the water column, is calculated from total incoming shortwave radiation as
, the shortwave radiation entering the water column, is calculated from total incoming shortwave radiation as
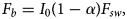
where $I_{0}$ is the proportion of shortwave radiation absorbed at the lake surface. The net radiation for the surface cell is then reduced to $\lpar 1- I_{0}\rpar \lpar 1-\alpha \rpar F_{{sw}}$
is the proportion of shortwave radiation absorbed at the lake surface. The net radiation for the surface cell is then reduced to $\lpar 1- I_{0}\rpar \lpar 1-\alpha \rpar F_{{sw}}$ .
.
Lake convection and indexing
The lake is modelled as turbulently convecting at ${\geq }0.1\, {\rm m}$ , following Buzzard and others (Reference Buzzard, Feltham and Flocco2018), using the four thirds rule,
, following Buzzard and others (Reference Buzzard, Feltham and Flocco2018), using the four thirds rule,
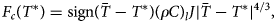
where $F_{c}\lpar T^{\ast }\rpar$ is the energy flux at the lake boundary of temperature $T^{\ast }$
is the energy flux at the lake boundary of temperature $T^{\ast }$ , $\bar {T}$
, $\bar {T}$ is the average lake temperature, $\lpar \rho C\rpar _{l}$
is the average lake temperature, $\lpar \rho C\rpar _{l}$ is the volumetric specific heat capacity of water and J is the turbulent heat flux factor ($1.907 \times 10^{-5}\, {\rm ms}^{1}\, {\rm K}^{-{1}/{3}}$
is the volumetric specific heat capacity of water and J is the turbulent heat flux factor ($1.907 \times 10^{-5}\, {\rm ms}^{1}\, {\rm K}^{-{1}/{3}}$ ). Turbulent heat flux is applied to the first slush or ice cell immediately surrounding the lake.
). Turbulent heat flux is applied to the first slush or ice cell immediately surrounding the lake.
To correctly apply turbulent mixing, correctly indexing slush, ice and water cells was necessary. This was implemented by progressing upwards from the base of the domain and recording the first and last instances of water between ice sections. This prevented two lakes being separated due to any transient appearance of one slush cell in the middle of the lake and encourages slush and ice encroachment from the upper and lower bounds of the lake.
Lake water is stratified based on temperature following the approach of Saloranta and Andersen (Reference Saloranta and Andersen2007) by using the UNESCO International Equation of State of Seawater (Loucks and van Beek, Reference Loucks and van Beek2005). This equation is applicable here as it deals with both saline content and temperature. Once lake input is complete in stage 3 the entire lake insert is combined with the main model domain in a one-off resizing to simplify model code in other stages.
Snow cover
The snow layer is adapted to be coupled to ice, rather than soil as developed by Essery (Reference Essery2015). Further details, including changing snow conductivity, compaction of snow over time, water content calculation and the initialisation of snow conductivity, can be found within Essery (Reference Essery2015). Realistic values for snow density ($200 {-} 500 \, {\rm kg}\, {\rm m}^{-3}$ ) are used for the conduction subfunction. Calculations for snow are completed at the beginning of each time step, to allow snow properties to be used subsequently in the conduction subfunction. When the snow layer becomes liquid, the snow layer is eliminated. Following results of sensitivity tests that found the influence of this water to be minor in comparison with meltwater flow into the lake, this water is not introduced into the lake. If refreezing occurs after partial melting of the snow layer, the density and thermal conductivity are updated to account for the proportion of the snow layer that is then solid ice based on the relative proportion of snow, ice and water.
) are used for the conduction subfunction. Calculations for snow are completed at the beginning of each time step, to allow snow properties to be used subsequently in the conduction subfunction. When the snow layer becomes liquid, the snow layer is eliminated. Following results of sensitivity tests that found the influence of this water to be minor in comparison with meltwater flow into the lake, this water is not introduced into the lake. If refreezing occurs after partial melting of the snow layer, the density and thermal conductivity are updated to account for the proportion of the snow layer that is then solid ice based on the relative proportion of snow, ice and water.
Enthalpy and heat diffusion
By default, the model is initialised as an ice column with temperature linearly interpolated between a surface and basal temperature specified by the user. Temperature is calculated from the cell's enthalpy as below, or in reverse if necessary as

where $T_{i}$ is the temperature at each grid cell (K), $E_{i}$
is the temperature at each grid cell (K), $E_{i}$ is the enthalpy at each grid cell (${\rm J}\, {\rm m}^{-2}$
is the enthalpy at each grid cell (${\rm J}\, {\rm m}^{-2}$ ), $\rho _{\rm water}$
), $\rho _{\rm water}$ is the density of water (${\rm kg}\, {\rm m}^{-3}$
is the density of water (${\rm kg}\, {\rm m}^{-3}$ ), $C_{\rm ice}$
), $C_{\rm ice}$ is the specific heat capacity of ice (${\rm J}\lpar {\rm kg}\, {\rm K}\rpar ^{-1}$
is the specific heat capacity of ice (${\rm J}\lpar {\rm kg}\, {\rm K}\rpar ^{-1}$ ), $C_{\rm water}$
), $C_{\rm water}$ is the specific heat capacity of water (${\rm J}\lpar {\rm kg}\, {\rm K}\rpar ^{-1}$
is the specific heat capacity of water (${\rm J}\lpar {\rm kg}\, {\rm K}\rpar ^{-1}$ ) and ${\rm d}z$
) and ${\rm d}z$ is the thickness of the cell. $E_{\rm ice_{i}}$
is the thickness of the cell. $E_{\rm ice_{i}}$ and $E_{\rm water_{i}}$
and $E_{\rm water_{i}}$ are the enthalpy thresholds for ice and water respectively (${\rm J}\, {\rm m}^{-2}$
are the enthalpy thresholds for ice and water respectively (${\rm J}\, {\rm m}^{-2}$ ). The model space uses unit metre squares in the x and y direction.
). The model space uses unit metre squares in the x and y direction.
The proportion of each cell that is water, $\lambda _{i}$ , is calculated as
, is calculated as

Heat diffusion is calculated using a backward-time, centred-space approach to enable much longer time steps (tested up to 2 h) whilst maintaining numerical stability when compared to the use of forward-time, centred-space after Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) and Alexiades and Solomon (Reference Alexiades and Solomon1993). The enthalpy change is calculated from temperature difference at each step, which remains valid unless a cell changes from ice to water or vice versa in one time step (an eventuality which depends on the time step and grid cell thickness and unlikely to occur whilst the model remains stable due to the high latent heat of melting/freezing). The one-dimensional heat diffusion equation,

(here excluding surface energy flux which is incorporated earlier in each timestep) is discretised to allow for non-uniform layer spacing as a result of meltwater input, snowfall and larger deep cells as

where n is the time step, i is the cell index, $\Delta x$ is the distance between the midpoints of two adjacent cells (m) and $\Delta t$
is the distance between the midpoints of two adjacent cells (m) and $\Delta t$ is the time step. The thermal diffusivity of each cell is calculated as
is the time step. The thermal diffusivity of each cell is calculated as

and the intermediate values between cells are obtained as depth weighted averages. For convenience, eqn (17) is simplified with the use of the $S_{i}^{n+1}$ term,
term,
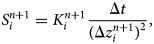
to give

A zero-flux boundary condition was specified for the base of the domain with the ice temperature of the bottom cell initially set at $-5^{\circ }{\rm C}$ . The default size of the upper cells is 0.1 m, enlarged to 1 m for the lowermost 30 cells to allow a large spatial domain without significantly increasing run-time. Equation (20) can then be entered into a system of simultaneous equations using a tridiagonal matrix generalised to a given number of model layers and solved as a matrix equation at each time step. The temperature of the surface cell is updated at each time step according to eqn (1) prior to heat diffusion.
. The default size of the upper cells is 0.1 m, enlarged to 1 m for the lowermost 30 cells to allow a large spatial domain without significantly increasing run-time. Equation (20) can then be entered into a system of simultaneous equations using a tridiagonal matrix generalised to a given number of model layers and solved as a matrix equation at each time step. The temperature of the surface cell is updated at each time step according to eqn (1) prior to heat diffusion.
Model testing
Sensitivity testing
Testing was conducted to determine the sensitivity of important GlacierLake outputs to parameter uncertainty. Normalised sensitivity coefficients for seven input parameters and six important output measures (Table 3) were calculated following Loucks and van Beek (Reference Loucks and van Beek2005) as

where $Q\lpar P_{0} \pm \Delta P\rpar$ is the output value Q when forced with a parameter of value $P_{0} \pm \Delta P$
is the output value Q when forced with a parameter of value $P_{0} \pm \Delta P$ , $P_{0}$
, $P_{0}$ is the initial parameter value and $\Delta P$
is the initial parameter value and $\Delta P$ is variation away from $P_{0}$
is variation away from $P_{0}$ .
.
Table 3. Parameters, parameter values and outputs used in sensitivity testing

Temperature units are ${}^{\circ }{\rm C}$ , depth and thickness in m and density in ${\rm kg}\, {\rm m}^{-3}$
, depth and thickness in m and density in ${\rm kg}\, {\rm m}^{-3}$ .
.
Figure 3 shows sensitivity coefficients. Most uncertainty is confined to albedo and the $I_{0}$ term (proportion of shortwave radiation absorbed at the lake surface) with the model output being fairly insensitive (sensitivity coefficient ≤0.2 excluding lake depth sensitivity to meltwater input) to other parameters. Many parameters are hard to obtain precisely and are subject to temporal and spatial variability, so this low sensitivity to parameter uncertainty promotes confidence in GlacierLake's results. The $I_{0}$
term (proportion of shortwave radiation absorbed at the lake surface) with the model output being fairly insensitive (sensitivity coefficient ≤0.2 excluding lake depth sensitivity to meltwater input) to other parameters. Many parameters are hard to obtain precisely and are subject to temporal and spatial variability, so this low sensitivity to parameter uncertainty promotes confidence in GlacierLake's results. The $I_{0}$ term merits further consideration and is covered in the discussion.
term merits further consideration and is covered in the discussion.

Fig. 3. Inter-comparison of sensitivity coefficients. Ordered by greatest sum uncertainty in columns and then rows. Abbreviations shown in Table 3. Note exponential scale for colour bar.
Tuning
The only published in-situ measurements of lake bottom ablation and lake depth come from Tedesco and others (Reference Tedesco2012); data which were also used by Banwell and others (Reference Banwell, Arnold, Willis, Tedesco and Ahlstrøm2012a). The record from Lake Ponting (69.589 N, −49.783 E, 962 m, data from 15th–19th June 2011) was compared to a GlacierLake run from 24th September 2009–1st August 2010, which was driven with GC-Net AWS data as processed by Banwell and others (Reference Banwell2012b), with incoming long wave radiation calculated at each time step within GlacierLake using equations from Banwell and others (Reference Banwell2012b). For precipitation input, RACMO2.3p2 was used (Noël and others, Reference Noël2018). The change in the $I_{0}$ value resulted in a large variation in the model output. An $I_{0}$
value resulted in a large variation in the model output. An $I_{0}$ value of 0.8, slightly greater than the value of 0.6 used by Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006), Tedesco and others (Reference Tedesco2012), Benedek (Reference Benedek2014) and Buzzard and others (Reference Buzzard, Feltham and Flocco2018) produced the output seen in Fig. 4. Values set as default following tuning can be found within the main function of the supplied code. GlacierLake is not intended to predict the evolution of specific, individual lakes with absolute accuracy, but this test shows that it is well suited for modelling broad trends and for understanding the behaviour of supraglacial lakes in Greenland. Large-scale comparison to remotely sensed lid thickness is beyond the scope of this study.
value of 0.8, slightly greater than the value of 0.6 used by Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006), Tedesco and others (Reference Tedesco2012), Benedek (Reference Benedek2014) and Buzzard and others (Reference Buzzard, Feltham and Flocco2018) produced the output seen in Fig. 4. Values set as default following tuning can be found within the main function of the supplied code. GlacierLake is not intended to predict the evolution of specific, individual lakes with absolute accuracy, but this test shows that it is well suited for modelling broad trends and for understanding the behaviour of supraglacial lakes in Greenland. Large-scale comparison to remotely sensed lid thickness is beyond the scope of this study.

Fig. 4. Comparison of modelled lake bottom ablation to measured lake bottom ablation data from Tedesco and others (Reference Tedesco2012). Dashed light grey is modelled basal ice ablation excluding lake formation, black is measured lake bottom ablation. Jumps in modelled ablation around day 175 result from threshold behaviour with cell enthalpy near the slush-water boundary.
Air temperature and precipitation variation
Precipitation and temperature vary across the spatial domain of lake occurrence in Greenland (Bromwich and others, Reference Bromwich, Chen, Bai, Cassano and Li2001; Gledhill and Williamson, Reference Gledhill and Williamson2017) and exert strong controls over ice lid formation within GlacierLake. While arbitrary, the following temperature and precipitation ranges were chosen to observe the behaviour of GlacierLake within, and slightly beyond, conditions where supraglacial lakes may reasonably be expected to form across the GrIS. Testing the relative importance of precipitation and temperature on lid formation enables a range of expected lid thicknesses at the beginning of the melt season to be obtained, as well as to find if any threshold behaviour is apparent. Weather data from PROMICE UPE U, with 2 m total of meltwater input (over 5 days using Lake Ponting data from Tedesco and others, Reference Tedesco2012) was used to form a lake with conditions varied upon lid formation to simulate the effect of precipitation and temperature differences on lid formation from a common starting point. Precipitation was multiplied by a factor ranging from 0 to 3 resulting in start of melt season snow depths between 0 and 3.45 m. Temperature from the day of lid formation to the end of the model run was added to or subtracted to with a range from $+10$ to $-20^{\circ }{\rm C}$
to $-20^{\circ }{\rm C}$ . Average temperature over this period with default settings is $-12.4^{\circ }{\rm C}$
. Average temperature over this period with default settings is $-12.4^{\circ }{\rm C}$ giving a range from $-2.4$
giving a range from $-2.4$ to $-32.4^{\circ }{\rm C}$
to $-32.4^{\circ }{\rm C}$ . The maximum lid thickness before lid breakup (or at 298 days of lid coverage if no lid breakup occurs) was recorded for a range of 25 inputs for precipitation and temperature giving 625 values in total.
. The maximum lid thickness before lid breakup (or at 298 days of lid coverage if no lid breakup occurs) was recorded for a range of 25 inputs for precipitation and temperature giving 625 values in total.
Figure 5 shows that a change in snow cover between 0 and 3.9 m over winter while air temperature is constant results in a greater range of ice lid thickness than a change in over-winter temperature between $+10$ and $-20^{\circ }{\rm C}$
and $-20^{\circ }{\rm C}$ (0.8–2.5 m against 1.4–2.3 m). Lid thickness varies smoothly with a parameter change with no threshold behaviour observed. Figure 5 also shows that even under the most extreme conditions tested (no snow cover and average winter temperatures of $-32.4^{\circ }{\rm C}$
(0.8–2.5 m against 1.4–2.3 m). Lid thickness varies smoothly with a parameter change with no threshold behaviour observed. Figure 5 also shows that even under the most extreme conditions tested (no snow cover and average winter temperatures of $-32.4^{\circ }{\rm C}$ ) lid thickness does not exceed 3.3 m. Koenig and others (Reference Koenig2015) find an average ice lid thickness of 1.4 m, with 0.65 m of snow cover present using observations obtained through Operation IceBridge. GlacierLake predicts lid thickness ranging from 1.7–2.7 m depending on temperature when snow cover at the start of the melt season reaches 0.65 m Koenig and others (Reference Koenig2015). This translates to thinner lids (1.5–2.5 m) during April and May when IceBridge flights are performed but suggests GlacierLake may slightly over predict lid thickness.
) lid thickness does not exceed 3.3 m. Koenig and others (Reference Koenig2015) find an average ice lid thickness of 1.4 m, with 0.65 m of snow cover present using observations obtained through Operation IceBridge. GlacierLake predicts lid thickness ranging from 1.7–2.7 m depending on temperature when snow cover at the start of the melt season reaches 0.65 m Koenig and others (Reference Koenig2015). This translates to thinner lids (1.5–2.5 m) during April and May when IceBridge flights are performed but suggests GlacierLake may slightly over predict lid thickness.

Fig. 5. Change in the maximum lid thickness with temperature and precipitation variation. Red vertical and horizontal lines indicate default UPE U conditions. White is where lid formation malfunctioned within GlacierLake. White contours show 0.5 m maximum thickness intervals.
Advection and basal freeze-up
Although GlacierLake does not have inbuilt allowance for advection, its effect was simulated by resetting ice temperature to its initial value on the day of lid formation, effectively removing the impact of warming earlier in the model run (Fig. 6). As surface energy flux is effectively isolated from the base upon lid formation this represents the earliest time in the model run where near-surface temperatures are not atmospherically controlled (e.g. cold wave in Fig. 6, left). A lower temperature limit of $-15^{\circ }{\rm C}$ was chosen as limited near-surface ice temperature profiles of land terminating sectors of the GrIS show this to be at the lower end of expected values (Meierbachtol and others, Reference Meierbachtol, Harper and Humphrey2013). Figure 7 shows that including advection increases basal freeze-up by at most 0.1 m compared to runs with no simulated advection. Total basal freeze-up with an initial ice temperature of $-15^{\circ }{\rm C}$
was chosen as limited near-surface ice temperature profiles of land terminating sectors of the GrIS show this to be at the lower end of expected values (Meierbachtol and others, Reference Meierbachtol, Harper and Humphrey2013). Figure 7 shows that including advection increases basal freeze-up by at most 0.1 m compared to runs with no simulated advection. Total basal freeze-up with an initial ice temperature of $-15^{\circ }{\rm C}$ is limited to 0.5 or 0.6 m with simulated advection. Altering the initial and advecting ice temperature made no difference to the magnitude of lid freezing (constant at 1.6 m throughout the test).
is limited to 0.5 or 0.6 m with simulated advection. Altering the initial and advecting ice temperature made no difference to the magnitude of lid freezing (constant at 1.6 m throughout the test).

Fig. 6. Simulated advection. Panels a and b: no alteration to ice temperature initially set at $-10^{\circ }{\rm C}$ . Panels c and d: a constant temperature of $-10^{\circ }{\rm C}$
. Panels c and d: a constant temperature of $-10^{\circ }{\rm C}$ was set initially, and repeated upon lid formation. Basal freeze-up was 0.4 and 0.5 m respectively. White space in panels b and d is free space before meltwater inflow input. Black line in panels a and c is snow depth, dashed blue line is water depth in snow layer.
was set initially, and repeated upon lid formation. Basal freeze-up was 0.4 and 0.5 m respectively. White space in panels b and d is free space before meltwater inflow input. Black line in panels a and c is snow depth, dashed blue line is water depth in snow layer.

Fig. 7. Total basal freeze-up whilst lid is present (stages 4–5) with and without simulated advection. Whilst the trend is upwards, small decreases in basal freeze-up are observed with and without advection included. This is a result of threshold behaviour between slush, water and ice within cells where the temperature is at, or within $0.05^{\circ }{\rm C}$ of $0^{\circ }{\rm C}$
of $0^{\circ }{\rm C}$ . For example a colder initial ice temperature may result in an increase of three slush cells above the ice-slush boundary but a decrease of one ice cell. Refer to Fig. 6 for test setup.
. For example a colder initial ice temperature may result in an increase of three slush cells above the ice-slush boundary but a decrease of one ice cell. Refer to Fig. 6 for test setup.
Temperature change at depth
The assumption that the warming influence of supraglacial lakes on underlying ice is not significant (Poinar and others, Reference Poinar, Joughin, Lenaerts and Van Den Broeke2017) has not been tested in the literature. We examine this by extending the 1 m deep cells at the bottom of the model to a total of 50 m (Fig. 8) making a 60 m domain in total. The initial temperature profile is set uniformly to $-10^{\circ }{\rm C}$ with weather data from PROMICE station UPE-U (Fausto and van As, Reference Fausto and van As2019). Figure 8 shows the lake exerts a strong influence (up to $8^{\circ }{\rm C}$
with weather data from PROMICE station UPE-U (Fausto and van As, Reference Fausto and van As2019). Figure 8 shows the lake exerts a strong influence (up to $8^{\circ }{\rm C}$ ) to around 10 m below the lake, however the warming effect beyond 15 m below the lake is limited at less than $1^{\circ }{\rm C}$
) to around 10 m below the lake, however the warming effect beyond 15 m below the lake is limited at less than $1^{\circ }{\rm C}$ .
.

Fig. 8. Ice temperature at depth using AWS data from the PROMICE UPE-U weather station, commencing 1st January 2010. Note the change in depth scale and jump from absolute temperature to temperature change from day 0 between panels b and c. Although the overall model domain extends to 60 m, only the upper 30 m are shown here. Black line in panel a is snow depth, blue dashed line is water depth.
GlacierLake behaviour at UPE-U AWS
To test steady-state behaviour, and the general behaviour of GlacierLake, it was run with PROMICE UPE-U data for 1000 days from 1st of January, 2010, repeating forcing data year on year. Figure 9 shows that although the thermal impact of a lake on underlying ice is limited beyond 15 m it is sufficient to prompt faster lake formation the following melt season. As annual melt exceeds annual refreezing, no steady state arises.

Fig. 9. Example model output including a short duration meltwater inflow input and snow cover, with data from PROMICE UPE-U AWS from 1st January 2010 repeating year-on-year for 1000 days. Panel a shows snow cover where black is snow depth and dashed blue is water depth. Panel b showsa lake temperature profile. White space in panel b is free space before meltwater inflow input.
Discussion
Temperature change at depth and multi-year behaviour
Warming of ice beneath lakes (Fig. 8) may influence lake drainage events on the GrIS as the fracture toughness of ice decreases with warming ice (Liu and Miller, Reference Liu and Miller1979), potentially lowering the stress threshold for fracture propagation beneath lakes (Krawczynski and others, Reference Krawczynski, Behn, Das and Joughin2009). However, further studies would be required to accurately assess this possibility. Figure 9 shows no steady state arises, consistent with melt rates of metres per year in the ablation zone. This points to lake drainage by fracture or over-topping being important controls in limiting the depth of lakes on the GrIS, as has been previously observed (Tedesco and Fettweis, Reference Tedesco and Fettweis2012) and also modelled (Banwell and others, Reference Banwell, Arnold, Willis, Tedesco and Ahlstrøm2012a). When buried, the lake top and bottom act as a $0^{\circ }{\rm C}$ boundaries, for both the underlying ice and the overlying ice lid. The consequence of this on the ice lid is to prevent very cold mid-winter temperatures due to an upward energy flux from latent heat of freezing of the water. This, with colder temperatures at the top of the water profile, contributes to lid freezing outpacing basal freeze-up.
boundaries, for both the underlying ice and the overlying ice lid. The consequence of this on the ice lid is to prevent very cold mid-winter temperatures due to an upward energy flux from latent heat of freezing of the water. This, with colder temperatures at the top of the water profile, contributes to lid freezing outpacing basal freeze-up.
$I_{0}$ term
term
Figures 3 and 4 show that model sensitivity to the value of $I_{0}$ is large, suggesting it should tested before model use where possible. The use of the $I_{0}$
is large, suggesting it should tested before model use where possible. The use of the $I_{0}$ term has moved away from its initial model implementation in Ebert and Curry (Reference Ebert and Curry1993) who use $I_{0}$
term has moved away from its initial model implementation in Ebert and Curry (Reference Ebert and Curry1993) who use $I_{0}$ in the Beer–Lambert law when calculating shortwave energy absorption in ice with brine pockets. When a meltwater lake is present Ebert and Curry (Reference Ebert and Curry1993) instead use the equation
in the Beer–Lambert law when calculating shortwave energy absorption in ice with brine pockets. When a meltwater lake is present Ebert and Curry (Reference Ebert and Curry1993) instead use the equation

where $a_{p}$ is the proportion of shortwave absorbed by the pond, $\alpha _{i}$
is the proportion of shortwave absorbed by the pond, $\alpha _{i}$ is bare ice albedo, $t_{p}$
is bare ice albedo, $t_{p}$ is the pond transmissivity as a function of depth and $I_{0}$
is the pond transmissivity as a function of depth and $I_{0}$ is the fraction of shortwave to penetrate the ice. They take an $I_{0}$
is the fraction of shortwave to penetrate the ice. They take an $I_{0}$ value that varies with cloud cover, with a maximum value of 0.35 under cloudy skies and a minimum value of 0.18 under clear skies, following Grenfell and Maykut (Reference Grenfell and Maykut1977). This reflects the fact that there is more incoming radiation in the infrared range under clear skies, most of which is absorbed in the upper 10 cm of the ice profile (Grenfell and Maykut, Reference Grenfell and Maykut1977).
value that varies with cloud cover, with a maximum value of 0.35 under cloudy skies and a minimum value of 0.18 under clear skies, following Grenfell and Maykut (Reference Grenfell and Maykut1977). This reflects the fact that there is more incoming radiation in the infrared range under clear skies, most of which is absorbed in the upper 10 cm of the ice profile (Grenfell and Maykut, Reference Grenfell and Maykut1977).
Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) deviate and take $I_{0}$ as the proportion of shortwave radiation that propagates below the surface water layer, as does this model. Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) use 0.6 as the value of $I_{0}$
as the proportion of shortwave radiation that propagates below the surface water layer, as does this model. Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) use 0.6 as the value of $I_{0}$ as Grenfell and Maykut (Reference Grenfell and Maykut1977) find the fraction of incident shortwave radiation above 700 nm (i.e. infrared) to be 40% (in disagreement with Kirk, Reference Kirk1988 who suggests a value of 50%). Their value of 0.6 is chosen as infrared radiation is strongly absorbed by the top 0.5 m of the water (Kirk, Reference Kirk1988). The calculation of Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) however, excludes reflection from the bare ice surface so may result in an oversupply of shortwave radiation to the upper ice layers beneath the lake. Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) do not run sensitivity tests of the $I_{0}$
as Grenfell and Maykut (Reference Grenfell and Maykut1977) find the fraction of incident shortwave radiation above 700 nm (i.e. infrared) to be 40% (in disagreement with Kirk, Reference Kirk1988 who suggests a value of 50%). Their value of 0.6 is chosen as infrared radiation is strongly absorbed by the top 0.5 m of the water (Kirk, Reference Kirk1988). The calculation of Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) however, excludes reflection from the bare ice surface so may result in an oversupply of shortwave radiation to the upper ice layers beneath the lake. Lüthje and others (Reference Lüthje, Feltham, Taylor and Worster2006) do not run sensitivity tests of the $I_{0}$ value and it is subsequently used in Tedesco and others (Reference Tedesco2012), Buzzard and others (Reference Buzzard, Feltham and Flocco2018) and the sea-ice lake model of Scott and Feltham (Reference Scott and Feltham2010), without further testing.
value and it is subsequently used in Tedesco and others (Reference Tedesco2012), Buzzard and others (Reference Buzzard, Feltham and Flocco2018) and the sea-ice lake model of Scott and Feltham (Reference Scott and Feltham2010), without further testing.
The $I_{0}$ term is important as it determines a proportion of incoming shortwave radiation, $F_{SW}\lpar 1 - I_{0}\rpar$
term is important as it determines a proportion of incoming shortwave radiation, $F_{SW}\lpar 1 - I_{0}\rpar$ , which will not be factored into the Beer–Lambert law and will therefore not be accessible to the underlying ice. The large sensitivity coefficients arises as a greater $I_{0}$
, which will not be factored into the Beer–Lambert law and will therefore not be accessible to the underlying ice. The large sensitivity coefficients arises as a greater $I_{0}$ means a greater energy flux for the upper ice cells, as shortwave infiltration is a faster transfer mechanism than turbulent heat transfer and heat diffusion. In effect, the use of the $I_{0}$
means a greater energy flux for the upper ice cells, as shortwave infiltration is a faster transfer mechanism than turbulent heat transfer and heat diffusion. In effect, the use of the $I_{0}$ term here is equivalent to an original $I_{0}$
term here is equivalent to an original $I_{0}$ value (as intended by Ebert and Curry, Reference Ebert and Curry1993) of 1 (i.e. all shortwave radiation enters the water column), with a certain fraction of light that penetrates to the lake base reflected backwards. In light of these points, the $I_{0}$
value (as intended by Ebert and Curry, Reference Ebert and Curry1993) of 1 (i.e. all shortwave radiation enters the water column), with a certain fraction of light that penetrates to the lake base reflected backwards. In light of these points, the $I_{0}$ term in its form used here was adjusted to obtain the closest match with measured basal ablation. Future models could re-incorporate the $I_{0}$
term in its form used here was adjusted to obtain the closest match with measured basal ablation. Future models could re-incorporate the $I_{0}$ definition of Ebert and Curry (Reference Ebert and Curry1993) or take note of the terms sensitivity. Discussion of the importance of the $I_{0}$
definition of Ebert and Curry (Reference Ebert and Curry1993) or take note of the terms sensitivity. Discussion of the importance of the $I_{0}$ term in low melt/ablation bare ice is covered in Hoffman and others (Reference Hoffman, Fountain and Liston2014).
term in low melt/ablation bare ice is covered in Hoffman and others (Reference Hoffman, Fountain and Liston2014).
Conclusion
This study has presented the first model for the full multi-year evolution of supraglacial lakes in the ablation zone of the GrIS. GlacierLake can replicate field data for ablation and lake formation from Tedesco and others (Reference Tedesco2012) with lid thickness slightly exceeding observations from Koenig and others (Reference Koenig2015) when a snow thickness of 0.65 m is used. GlacierLake shows that the sum of the ice-lid thickness and basal freeze-up is unlikely to exceed 3.9 m with no snow cover, or 2.8 m with 1 m of snow cover at the end of the melt season. This represents an important physically based confirmation of Koenig and others (Reference Koenig2015), i.e. that a large number of lakes can be expected to remain (at least partially) unfrozen throughout the winter, with implications for the development of the supraglacial hydrological system in the following melt season due to a pre-existing water stores. The computational efficiency of GlacierLake means it could be incorporated into a holistic model of Greenland supraglacial hydrology without impeding run time, and that it could be easily used in ice sheet-wide studies. GlacierLake could also be easily adapted to valley glacier or ice-cap supraglacial lakes. Sensitivity testing reveals the importance of the $I_{0}$ (proportion of shortwave radiation absorbed at the lake surface) term in determining energy transfer to the base of the lake. The results presented here are vital for better understanding the role of lakes for surrounding ice temperatures and in forming surface-bed links through lake hydrofracture. It is hoped that this study will provide an overall better understanding of GrIS surface-melt processes; such processes ultimately drive a significant and accelerating component of global sea-level rise.
(proportion of shortwave radiation absorbed at the lake surface) term in determining energy transfer to the base of the lake. The results presented here are vital for better understanding the role of lakes for surrounding ice temperatures and in forming surface-bed links through lake hydrofracture. It is hoped that this study will provide an overall better understanding of GrIS surface-melt processes; such processes ultimately drive a significant and accelerating component of global sea-level rise.
Code availability
Model code is available at: https://doi.org/10.17863/CAM.47791.
Acknowledgments
We thank two anonymous reviewers for insightful critiques of this paper. We thank Brice Noël and Michiel van den Broeke for providing the downscaled RACMO2.3p2 data. We thank Mikael Lüthje and Sammie Buzzard for supplying model code which was incorporated into GlacierLake. AWS data from PROMICE, setup by the Geological Survey of Denmark and Greenland, was invaluable in assembling this model. Andrew Williamson is thanked for advice during the study. The work by Robert Law was undertaken with support of the Debenham Scholarship at the Scott Polar Research Institute, University of Cambridge, and completed under NERC grant NE/L002507/1. Corinne Benedek acknowledges funding from the Howard Research Studentship through Sidney Sussex College, University of Cambridge. Alison Banwell acknowledges support from a Cooperative Institute for Research in Environmental Sciences (CIRES) Visiting Postdoctoral Fellowship.