Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-20T12:45:30.143Z Has data issue: false hasContentIssue false
  • English
  • Français

SELF-EMBEDDINGS OF MODELS OF ARITHMETIC; FIXED POINTS, SMALL SUBMODELS, AND EXTENDABILITY

Part of: Model theory Nonstandard models Proof theory and constructive mathematics

Published online by Cambridge University Press:  22 December 2022

SAEIDEH BAHRAMI Open the ORCID record for SAEIDEH BAHRAMI [Opens in a new window]
SAEIDEH BAHRAMI*
Affiliation:
SCHOOL OF MATHEMATICS INSTITUTE FOR RESEARCH IN FUNDAMENTAL SCIENCES (IPM) P.O. BOX 19395-5764 TEHRAN, IRAN
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we will show that for every cut I of any countable nonstandard model 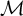$\mathcal {M}$ of 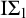$\mathrm {I}\Sigma _{1}$, each I-small 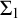$\Sigma _{1}$-elementary submodel of 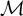$\mathcal {M}$ is of the form of the set of fixed points of some proper initial self-embedding of 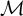$\mathcal {M}$ iff I is a strong cut of 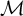$\mathcal {M}$. Especially, this feature will provide us with some equivalent conditions with the strongness of the standard cut in a given countable model 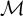$\mathcal {M}$ of 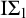$ \mathrm {I}\Sigma _{1} $. In addition, we will find some criteria for extendability of initial self-embeddings of countable nonstandard models of 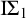$ \mathrm {I}\Sigma _{1} $ to larger models.

Keywords

Peano arithmeticnonstandard modelself-embeddingfixed pointstrong cutsmall submodel

MSC classification

Primary: 03C62: Models of arithmetic and set theory 03F30: First-order arithmetic and fragments 03H15: Nonstandard models of arithmetic
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 3 , September 2024 , pp. 1044 - 1066
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bahrami, S. and Enayat, A., Fixed points of self-embeddings of models of arithmetic . Annals of Pure and Applied Logic , vol. 169 (2018), pp. 487–513.CrossRefGoogle Scholar
Barwise, J. and Schlipf, J., On recursively saturated models of arithmetic, Model Theory and Algebra: A Memorial Tribute to A. Robinson (Saracino, D. and Weispfenning, V., editors), Lecture Notes in Mathematics, vol. 498, Springer, Berlin, 1976, pp. 42–55.CrossRefGoogle Scholar
Dimitracopoulos, C. and Paris, J., A note on a theorem of H. Friedman . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik , vol. 34 (1988), no. 1, pp. 13–17.CrossRefGoogle Scholar
Enayat, A., Automorphisms of models of arithmetic: A unified view . Annals of Pure and Applied Logic , vol. 145 (2007), pp. 16–36.CrossRefGoogle Scholar
Friedman, H., Countable models of set theories , Cambridge Summer School in Mathematical Logic (Mathias, A. R. D. and Rogers, H., editors), Lecture Notes in Mathematics, vol. 337, Springer, Berlin, 1973, pp. 539–573.CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First Order Arithmetic , Springer, Heidelberg, 1993.CrossRefGoogle Scholar
Kaye, R., Models of Peano Arithmetic , Oxford University Press, Oxford, 1991.CrossRefGoogle Scholar
Kaye, R., Kossak, R., and Kotlarski, H., Automorphisms of recursively saturated models of arithmetic . Annals of Pure and Applied Logic , vol. 55 (1991), pp. 67–99.CrossRefGoogle Scholar
Kirby, L. and Paris, J., ${\varSigma}_n$ -collection schemas in arithmetic , Logic Colloquium ’77 (A. Macintyre, L. Pacholski, and J. Paris, editors), North-Holland, Amsterdam, 1978, pp. 199–209.Google Scholar
Kossak, R. and Kotlarski, H., Results on automorphisms of recursively saturated models of $PA$ . Fundamenta Mathematicae , vol. 129 (1988), no. 1, pp. 9–15.CrossRefGoogle Scholar
Kossak, R. and Kotlarski, H., On extending automorphisms of models of Peano arithmetic . Fundamenta Mathematicae , vol. 149 (1996), no. 3, pp. 245–263.CrossRefGoogle Scholar
Kossak, R. and Schmerl, J., Arithmetically saturated models of arithmetic , Notre Dame Journal of Formal Logic , vol. 36 (1995), no. 4, pp. 531–546.CrossRefGoogle Scholar
Kossak, R. and Schmerl, J., The Structure of Models of Peano Arithmetic , Oxford Logic Guides, vol. 50, Clarendon Press, Oxford, 2006.CrossRefGoogle Scholar
Lascar, D., The small index property and recursively saturated models of Peano arithmetic , Automorphisms of First-Order Structures (Kaye, R. and Macpherson, D., editors), Oxford University Press, New York, 1994, pp. 281–292.CrossRefGoogle Scholar
Smoryński, C., Recursively saturated nonstandard models of arithmetic, this Journal, 46 (1981), no. 2, pp. 259–286.Google Scholar
Wilkie, A., On the theories of end-extensions of models of arithmetic , Set Theory and Hierarchy Theory V (Lachlan, A., Srebrny, M., and Zarach, A., editors), Lecture Notes in Mathematics, vol. 619, Springer, Berlin, 1977, pp. 305–310.CrossRefGoogle Scholar